The Extended H_∞ Particle Filter for Attitude Estimation Applied to Remote Sensing Satellite CBERS-4

Abstract

An extension of the linear $H_{\infty }$ filter, presented here as the extended $H_{\infty }$ particle filter (E$H_{\infty }$PF), is used in this work for attitude estimation, which presents a process and measurement model with nonlinear functions. The simulations implemented use orbit and attitude data from CBERS-4 (China–Brazil Earth Resources Satellite-4), making use of the robustness characteristics of the $H_{\infty }$ filter. The CBERS-4 is the fifth satellite of an advantageous international scientific interaction between Brazil and China for the development of remote sensing satellites used for strategic application in monitoring water resources and controlling deforestation in the Legal Amazon. In the extended $H_{\infty }$ particle filter (E$H_{\infty }$PF) the nature of the system, composed of dynamics and noises, seeks to degrade the state estimate. The E$H_{\infty }$PF deals with this by aiming for robustness, using a performance parameter in its cost function, in addition to presenting an advantageous feature of using a reduced number of particles for state estimation. The justification for the application of this method is because the non-Gaussian uncertainties that appear in the attitude sensors impair the estimation process and the E$H_{\infty }$PF minimizes in signal estimation the worst effects of disturbance signals without a priori knowledge of them, as shown in the results, in addition to presenting good precision within the prescribed requirements, with 100 particles representing a processing time 2.09 times less than the PF with 500 particles.

1. Introduction

Remote sensing satellite missions require pointing, so an accurate attitude determination and control system is a dominant factor for mission success. The attitude sensor determines how a given reference vector is oriented in relation to the satellite system [1]. After processing these vectors computationally, it is then possible to estimate the satellite’s orientation using attitude estimation techniques. With the advancement in technologies, the computational power and energy efficiency of microprocessors enables the use of increasingly computationally heavy models [2]. This strategy is especially advantageous in space systems.

The main objective of this research is to analyze the feasibility along with the advantages and disadvantages of implementing the E$H_{\infty }$PF for attitude estimation, highlighting and expanding the properties of the $H_{\infty }$ filter, showing its advantageous characteristics. In the E$H_{\infty }$PF the nature of the system, composed of dynamics and noises, seeks to deteriorate the state estimate, while at the same time seeking robustness through a coefficient of performance in its respective cost function. These characteristics of the method provide, with a reduced number of particles, a good processing time and good precision without sample impoverishment.

The justification for this research is given by the fact that many spacecraft missions, not only the remote sensing ones such as the CBERS-4 used in this research, necessitate precise sensor pointing and precise determination and attitude control in real time, which entails estimating attitude and gyros bias from attitude measurements provided by sensor outputs. The correct attitude determination directly influences the performance of the attitude control system and adjacent systems on the satellite that need this information. According to [3], because the determination of attitude is done using sensors, whose measurements always include some noise and non-Gaussian uncertainties, stochastic filters are more suitable approaches. The non-Gaussian uncertainties that appear in the process model are contained in the gyro’s measurements, which present noise and bias due to post-launch sensor misalignment, thermal expansion, fading, electro-mechanical degradation, etc. All these factors cause inaccuracies in the model and deteriorate the attitude estimation process. Thus, the E$H_{\infty }$PF deals well with this problem as shown in the results of this research.

The E$H_{\infty }$PF algorithm uses the $H_{\infty }$ robust filter concept so that external interference is overcome [4]. The $H_{\infty }$ filtering minimizes the worst-case estimation error using the concepts from the famous game theory approach [5,6,7]. The second-order linearization for the $H_{\infty }$ filtering was presented more recently in [8]. For the $H_{\infty }$ robust filtering, the parameter $\gamma$ has a special meaning for the method; it evaluates the upper threshold level and verifies the robustness of the $H_{\infty }$ robust filtering for the uncertain interference [3,4]. The performance is associated with the appropriate choice of the $\gamma$ parameter, which is directly associated with robustness and the average accuracy of the system [9], where you should always try to find a balance between these method properties. The finding is that with a higher the value of $\gamma$, the result will be closer to a normal filtering. The lower the associated $\gamma$ value, the more intense the filter robustness [4,10].

The CBERS-4 attitude and gyros bias estimation, which makes use of the PROPAT propagator [11], analyzing and comparing the mean error, standard deviation, root mean squared error (RMSE), and the processing time cost of the estimation methods used is the main aim of this research. The simulations are implemented with orbit and attitude data from 1 September 2015 provided by the Satellite Control Center of the Brazilian National Institute for Space Research (CCS-INPE). The quaternions are used to represent attitude [12], and two estimation methods are used and compared—PF and E$H_{\infty }$PF—which are modern methods that consider both the process model and the noisy measurement model. The application of these methods in real missions characterizes the main contribution of this work regarding the state-of-the-art estimation methods.

In aerospace engineering, it is possible to note important contributions related to the application of estimation methods: Ref. [12] presents a study on the satellite attitude estimation using the EKF; ref. [13] presents comparisons between two Kalman filters for nonlinear systems; ref. [14] analyses the results of the EKF in an instant mapping and localization process; ref. [15] research uses the EKF for attitude and gyros bias estimation but with real data and with a sampling time less than that the one used in this research; refs. [16,17] present a spacecraft attitude estimation through UKF, using quaternions and Euler angles; ref. [18] analyzes the UKF robustness for orbit determination through global positioning system signals; ref. [19] presents the orbit determination using nonlinear PF and GPS measurements; ref. [1] makes a comparison between the estimation methods of UKF, regularized particle filter (RegPF), and extended $H_{\infty }$ filter (E$H_{\infty }$F); and ref. [20] presents the Rao-Blackwellized particle filter (RaoBPF) attitude estimation and gyros bias for the CBERS 4 satellite, evaluating computational processing time cost and precision.

The structure of the article is as follows: Section 2 introduces the problem statement for nonlinear state estimation. Section 3 presents the general concepts of an extended $H_{\infty }$ particle filter (E$H_{\infty }$PF). Section 4 presents methods applied to gyros bias estimation and attitude estimation using the CBERS-4 orbit and attitude simulation data. The results are presented, analyzing the precision of the methods and the processing time of each one. Section 5 presents some conclusions and final comments.

2. Problem Statement

Assume the process model and the measurement model that represent a system of nonlinear equations described by:

$$\begin{array}{c}{\mathit{x}}_{k+1}=f_k({\mathit{x}}_k,{\mathit{u}}_k,{\mathit{w}}_k)\\ {\mathit{y}}_k=h_k({\mathit{x}}_k,{\mathit{\upsilon }}_k)\end{array}$$

(1)

where the term k is the time index, ${\mathit{x}}_k$ is the state vector, ${\mathit{u}}_k$ is associated with the control input, ${\mathit{w}}_k$ is the process noise, ${\mathit{y}}_k$ is the measurement vector, and ${\mathit{\upsilon }}_k$ is the measurement noise. The function $f_k(.)$ is commonly referred to as process equation, and $h_k(.)$ is commonly referred to as measurement equation; both functions are time-varying nonlinear vector systems. Both noises ${\mathit{w}}_k$ and ${\mathit{\upsilon }}_k$ are often considered Gaussian white noise and independently presented as a well-defined probability density function.

For applications of estimation methods, the process and measurement model may change from that presented by Equation (1), in which sometimes the process model is linear and the measurement model is nonlinear, or vice-versa. This happens for attitude estimation depending on the chosen parameterization. In this work, the attitude kinematic equation parameterized in quaternions will be used as a process model, which is a linear system, and the measurement model chosen is a nonlinear system.

2.1. Attitude Representation by Quaternions

The state vector is presented with the attitude representation parameterized in quaternion $\mathit{q}$ and the gyro bias $\mathit{\epsilon }$ represented by [21,22]:

$$\mathit{x}={\left[\begin{array}{cc}\mathit{q}& \mathit{\epsilon }\end{array}\right]}^T={\left[\begin{array}{ccccccc}{q}_1& q_2& q_3& q_4& {\mathit{\epsilon }}_x& {\mathit{\epsilon }}_y& {\mathit{\epsilon }}_z\end{array}\right]}^T$$

(2)

According to [23], the bias is an output component that has characteristics of both deterministic and stochastic behavior that is not tied to the input the sensor is connected to.

Then, the linear system that represents the process equation of the problem is given by [12,21]:

$$\left[\begin{array}{c}{\displaystyle \dot{\mathit{q}}}\\ \dot{\mathit{\epsilon }}\end{array}\right]=\left[\begin{array}{cc}{\displaystyle \frac{1}{2}{\mathsf{\Omega }}_{\omega }}& 0_{3\times 3}\\ & \\ 0_{3\times 4}& 0_{3\times 3}\end{array}\right]\left[\begin{array}{c}{\displaystyle \mathit{q}}\\ \mathit{\epsilon }\end{array}\right]+\mathit{w}$$

(3)

where ${\displaystyle \mathit{\omega }={\left[\begin{array}{ccc}{\omega }_x& {\omega }_y& {\omega }_z\end{array}\right]}^T}$ is the angular velocity vector in the body frame, and ${\mathsf{\Omega }}_{\omega }$ is an anti-symmetric matrix formed with the components of angular velocity and has dimension $4\times 4$, given by [12,21]:

$${\mathsf{\Omega }}_{\omega }=\left[\begin{array}{cccc}0& {\omega }_z& -{\omega }_y& {\omega }_x\\ -{\omega }_z& 0& {\omega }_x& {\omega }_y\\ {\omega }_y& -{\omega }_x& 0& {\omega }_z\\ -{\omega }_x& -{\omega }_y& -{\omega }_z& 0\end{array}\right]$$

(4)

In this work, the gyros model (rate integration gyros–RIGs) was used that has the classic representation [21,22] given by ${\mathit{\omega }}_i={\mathit{g}}_i-{\mathit{\epsilon }}_i+{\mathit{\upsilon }}_i$, where $(i=x,y,z)$, the term ${\mathit{g}}_i\left(t\right)$ is the gyro output vector, ${\mathit{\epsilon }}_i\left(t\right)$ are the components of the gyros bias defined as an output component unrelated to the input to which the sensor is subjected, and ${\mathit{\upsilon }}_i$ is the white Gaussian noise process, which covers all remaining non-modeled effects other than the random noises.

2.2. Mathematical Models of Attitude Sensors

The nonlinear system that represents the measurement equation of the problem is given by [24]:

$${\mathit{y}}_k=\left[\begin{array}{c}arctan\left(\frac{{\displaystyle -S_y}}{{\displaystyle S_{x}cos{60}^{\circ }+S_{z}cos{150}^{\circ }}}\right)\\ {24}^{\circ }+arctan\left(\frac{{\displaystyle S_x}}{{\displaystyle S_z}}\right)\\ \varphi \\ \theta \end{array}\right]+{\mathit{\upsilon }}_k$$

(5)

The first and second rows of the column matrix of Equation (5) contain the information provided by the digital sun sensor (DSS). This sensor provides the coupled pitch angle (${\alpha }_{\theta }$, first line term) and the coupled yaw angle (${\alpha }_{\psi }$, second line term); the direct measurement of an attitude angle is not trackable [16,17,24]. The terms $S_x$, $S_y$, $S_z$ are the solar vector components in the body frame, and these sensors are Chinese, made where this angle argument is associated with the field of view and resolution data sheet.

The third and fourth rows of the column matrix of Equation (5) are the information provided by the horizon sensor, commonly referred to as infrared earth sensors (IRES) [24]. Here, the roll angle measurement is given by $\varphi$ and the pitch angle measurement is given by $\theta$.

More information about the process and measurements equations can be found in [20].

3. The Extended ${\mathit{H}}_{\infty }$ Particle Filter

The theoretical foundation of an $H_{\infty }$ filter is based on a robust filter implementation [3,4] with the central goal of estimating the linear combination of the state ${\mathit{z}}_k$, which is given by

$${\mathit{z}}_k={\mathit{L}}_k{\mathit{x}}_k$$

(6)

where ${\mathit{L}}_k$ is a full rank positive definite matrix. Commonly, ${\mathit{L}}_k=\mathit{I}$ is used to perform a direct estimate of the state ${\mathit{x}}_k$, as in the Kalman filter. The state ${\mathit{z}}_k$, when estimated, is represented with the notation ${\widehat{\mathit{z}}}_k$; and the initial state ${\mathit{x}}_0$, when estimated, is represented with the notation ${\widehat{\mathit{x}}}_0$.

The central idea for the design criterion in E$H_{\infty }$PF is to find ${\widehat{\mathit{z}}}_k$ that minimizes $\left({\mathit{z}}_k-{\widehat{\mathit{z}}}_k\right)$ for any ${\mathit{w}}_k$, ${\mathit{\upsilon }}_k$, and ${\mathit{x}}_0$. The underlying concept brings the idea of a worst-case scenario; in other words, it is assumed that the nature of the system acts adversely in this estimation method, so it is necessary to find ${\mathit{w}}_k$, ${\mathit{\upsilon }}_k$, and ${\mathit{x}}_0$ to maximize $\left({\mathit{z}}_k-{\widehat{\mathit{z}}}_k\right)$ [3,8]. This extremization problem commonly uses a cost function, where it is more convenient to put the terms ${\mathit{w}}_k$, ${\mathit{\upsilon }}_k$, and ${\mathit{x}}_0$ in the denominator, represented by [3]:

$$J_1=\frac{{\displaystyle \sum _{k=0}^{\mathcal{N}-1}{∥{\mathit{z}}_k-{\widehat{\mathit{z}}}_k∥}_{{\mathit{S}}_k}^2}}{{\displaystyle {∥{\mathit{x}}_0-{\widehat{\mathit{x}}}_0∥}_{{\mathit{P}}_0^{-1}}^2+\sum _{k=0}^{\mathcal{N}-1}\left({∥{\mathit{w}}_k∥}_{{\mathit{Q}}_k^{-1}}^2+{∥{\mathit{\upsilon }}_k∥}_{{\mathit{R}}_k^{-1}}^2\right)}}$$

(7)

where $\mathcal{N}$ is the number associated with the filtering range, and $k=1,2,...,\mathcal{N}$. The notation ${∥{\mathit{x}}_k∥}_{{\mathit{S}}_k}^2$ is the standard representation of the weighted $L_2$ norm of ${\mathit{x}}_k$, i.e., ${∥{\mathit{x}}_k∥}_{{\mathit{S}}_k}^2={\mathit{x}}_k^T{\mathit{S}}_k{\mathit{x}}_k$. The expressions ${\mathit{P}}_0$, ${\mathit{Q}}_k$, ${\mathit{R}}_k$, and ${\mathit{S}}_k$ are the weighting matrices and, by definition, are symmetric positive matrices associated with the respective problem.

For the robust filter, the direct minimization of $J_1$ in Equation (7) is not commonly done; the strategy is to use a performance limit redefining the cost function of the problem to find an estimate ${\widehat{\mathit{z}}}_k$, which results in [1,3]

$$J_1<\frac{1}{\gamma }$$

(8)

where $\gamma \ge 0$ is the performance bound. Thus, rearranging the Equation (7) with this limiting factor results in

$$\begin{array}{ccc}\hfill J& =& {\displaystyle -\frac{1}{\gamma }{∥{\mathit{x}}_0-{\widehat{\mathit{x}}}_0∥}_{{\mathit{P}}_0^{-1}}^2}\hfill \\ \hfill & +& {\displaystyle \sum _{k=0}^{\mathcal{N}-1}\left[{∥{\mathit{z}}_k-{\widehat{\mathit{z}}}_k∥}_{{\mathit{S}}_k}^2-\frac{1}{\gamma }\left({∥{\mathit{w}}_k∥}_{{\mathit{Q}}_k^{-1}}^2+{∥{\mathit{\upsilon }}_k∥}_{{\mathit{R}}_k^{-1}}^2\right)\right]<1}\hfill \end{array}$$

(9)

The $minmax$ problem is given by the representation:

$$J^{\ast }=\underset{{\widehat{\mathit{z}}}_k}{min}\underset{{\mathit{w}}_k,{\mathit{\upsilon }}_k,{\mathit{x}}_0}{max}J$$

(10)

since ${\mathit{\upsilon }}_k={\mathit{y}}_k-h\left({\mathit{x}}_k\right)$, ${\mathit{z}}_k={\mathit{L}}_k{\mathit{x}}_k$, ${\widehat{\mathit{z}}}_k={\mathit{L}}_k{\widehat{\mathit{x}}}_k$ and defining ${\overline{\mathit{S}}}_k={\mathit{L}}_k^T{\mathit{S}}_k{\mathit{L}}_k$. Thus, Equations (9) and (10) can be rewritten as

$$J^{\ast }=\underset{{\widehat{\mathit{x}}}_k}{min}\underset{{\mathit{w}}_k,{\mathit{y}}_k,{\mathit{x}}_0}{max}J$$

(11)

where

$$\begin{array}{ccc}\hfill J& =& {\displaystyle -\frac{1}{\gamma }{∥{\mathit{x}}_0-{\widehat{\mathit{x}}}_0∥}_{{\mathit{P}}_0^{-1}}^2}\hfill \\ \hfill & +& {\displaystyle \sum _{k=0}^{\mathcal{N}-1}\left[{∥{\mathit{x}}_k-{\widehat{\mathit{x}}}_k∥}_{{\overline{\mathit{S}}}_k}^2-\frac{1}{\gamma }\left({∥{\mathit{w}}_k∥}_{{\mathit{Q}}_k^{-1}}^2+{∥{\mathit{y}}_k-h\left({\mathit{x}}_k\right)∥}_{{\mathit{R}}_k^{-1}}^2\right)\right]}\hfill \end{array}$$

(12)

According to [25], an optimal H${}_{\infty }$ filter is to find an estimate ${\mathit{x}}_k$ that minimizes J, under the condition ${\widehat{\mathit{x}}}_0=argmin{∥J∥}_{\infty }$. Since the analytical solution is by no means trivial, a suboptimal iterative algorithm is usually used to solve the optimal filter problem H${}_{\infty }$. In this way, we define a borderline value of performance coefficient $\gamma$, which meets ${∥J∥}_{\infty }=supJ\le {\gamma }^2$ since ${∥J∥}_{\infty }$ is the infinity-norm of J and sup is the supremum of a set [26].

3.1. Sample

Assuming a system composed of a process model and measurement model, both of which are nonlinear as shown in Equation (1), the method starts by randomly generating a considerable number N of state vectors, called particles or sample states, which will be associated with the initial probability density function (pdf) represented by $p\left({\mathit{x}}_0\right|{\mathit{Y}}_0)=p\left({\mathit{x}}_0\right)$ [3,27]. These particles or sample states are represented as ${\mathit{x}}_0^{+\left(i\right)}$$(i=1,2,...,N)$. This start is similar to a PF.

$${\mathit{x}}_0^{+\left(i\right)}\sim p\left({\mathit{x}}_0^{\left(i\right)}\right)\begin{array}{cccc}& & & \left(i=1,2,...,N\right)\end{array}$$

(13)

3.2. Prediction Step

The particles must be propagated at every step $k=1,2,...,\mathcal{N}$, which must be done using the process dynamics equation $f(.)$.

$${\mathit{x}}_k^{-\left(i\right)}=f_{k-1}({\mathit{x}}_{k-1}^{+\left(i\right)},{\mathit{w}}_{k-1}^{\left(i\right)})\begin{array}{cccc}& & & \left(i=1,2,...,N\right)\end{array}$$

(14)

where the ${\mathit{w}}_{k-1}^{\left(i\right)}$ is called a noise vector, which is randomly generated using the well known pdf of ${\mathit{w}}_{k-1}$ as seed.

3.3. Update Step

Once all measurements are obtained in time k, the conditional relative probabilities, also known as likelihood, of each particle ${\mathit{x}}_k^{-\left(i\right)}$ must be calculated by pdf $p\left({\mathit{y}}_k\right|{\mathit{x}}_k^{-\left(i\right)})$, which is obtained intrinsically by contributing the measurement model $h(.)$ and the noise measurements ${\mathit{\upsilon }}_k$, represented by [3,19,20,27].

$$\begin{array}{ccc}\hfill {\delta }_k^{\left(i\right)}& =& p\left({\mathit{y}}_k\right|{\mathit{x}}_k^{-\left(i\right)})\hfill \\ \hfill {\delta }_k^{\left(i\right)}& \sim & {\displaystyle {\delta }_{k-1}^{\left(i\right)}\frac{1}{det{\left(2\pi {\mathit{E}}_k^{-\left(i\right)}\right)}^{1/2}}exp\left(\frac{-{\left|\left|{\tilde{\mathit{y}}}_k^{\left(i\right)}\right|\right|}_{{\left({\mathit{E}}_k^{-\left(i\right)}\right)}^{-1}}^2}{2}\right)}\hfill \end{array}$$

(15)

where ${\tilde{\mathit{y}}}_k^{\left(i\right)}={\mathit{y}}_k-{\mathit{H}}_k^{\left(i\right)}{\mathit{x}}_k^{-\left(i\right)}$ is the measurement residues, and the term that weights the residues ${\mathit{E}}_k^{-\left(i\right)}={\mathit{H}}_k^{\left(i\right)}{\mathit{P}}_k^{-\left(i\right)}{\left({\mathit{H}}_k^{\left(i\right)}\right)}^T+{\mathit{R}}_k$ is the associated covariance matrix.

As a standard procedure, one should always normalize likelihood obtained by Equation (15) as follows:

$${\tilde{\delta }}_k^{\left(i\right)}=\frac{{\delta }_k^{\left(i\right)}}{{\sum }_{j=1}^N{\delta }_k^{\left(j\right)}},$$

(16)

in which it will be guaranteed that the sum of all likelihoods will be unitary.

The update of the covariance matrix and the state vector in this method is done using the extended H${}_{\infty }$ filter measurement update equations presented below.

$${\overline{\mathit{S}}}_k^{\left(i\right)}={\left({\mathit{L}}_k^{\left(i\right)}\right)}^T{\mathit{S}}_k^{\left(i\right)}{\mathit{L}}_k^{\left(i\right)}$$

(17)

$${\mathit{K}}_k^{\left(i\right)}={\mathit{P}}_k^{-\left(i\right)}{\left(\mathit{I}-\gamma {\overline{\mathit{S}}}_k^{\left(i\right)}{\mathit{P}}_k^{-\left(i\right)}+{\left({\mathit{H}}_k^{\left(i\right)}\right)}^T{\mathit{R}}_k^{-1}{\mathit{H}}_k^{\left(i\right)}{\mathit{P}}_k^{\left(i\right)}\right)}^{-1}{\left({\mathit{H}}_k^{\left(i\right)}\right)}^T{\mathit{R}}_k^{-1}$$

(18)

$${\mathit{x}}_k^{+\left(i\right)}=f({\mathit{x}}_k^{-\left(i\right)},{\mathit{\mu }}_k)+{\mathit{F}}_k^{\left(i\right)}{\mathit{K}}_k^{\left(i\right)}\left({\mathit{y}}_k-h\left({\mathit{x}}_k^{-\left(i\right)}\right)\right)$$

(19)

$${\mathit{P}}_k^{+\left(i\right)}={\mathit{F}}_k^{\left(i\right)}{\mathit{P}}_k^{-\left(i\right)}{\left(\mathit{I}-\gamma {\overline{\mathit{S}}}_k^{\left(i\right)}{\mathit{P}}_k^{-\left(i\right)}+{\left({\mathit{H}}_k^{\left(i\right)}\right)}^T{\mathit{R}}_k^{-1}{\mathit{H}}_k^{\left(i\right)}{\mathit{P}}_k^{\left(i\right)}\right)}^{-1}{\left({\mathit{F}}_k^{\left(i\right)}\right)}^T+{\mathit{Q}}_k$$

(20)

where ${\mathit{L}}_k^{\left(i\right)}$ and ${\mathit{S}}_k^{\left(i\right)}$ are positive matrices defined with full rank; the process and measurement Jacobians are represented by ${\mathit{F}}_k^{\left(i\right)}={\left.\frac{df}{d{\mathit{x}}_k}\right|}_{{\mathit{x}}_k={\mathit{x}}_k^{-\left(i\right)}}$ and ${\mathit{H}}_k^{\left(i\right)}={\left.\frac{dh}{d{\mathit{x}}_k}\right|}_{{\mathit{x}}_k={\mathit{x}}_k^{-\left(i\right)}}$; the performance coefficient $\gamma$ has a borderline value that must satisfy the Riccati inequality represented by Equation (21), i.e., the optimized value of ${\widehat{\mathit{x}}}_k$ will be guaranteed to be a local minimum of the problem’s cost function [3,8,25]:

$${\left({\mathit{P}}_k^{-\left(i\right)}\right)}^{-1}-\gamma {\overline{\mathit{S}}}_k^{\left(i\right)}+{\left({\mathit{H}}_k^{\left(i\right)}\right)}^T{\mathit{R}}_k^{-1}{\mathit{H}}_k^{\left(i\right)}>0$$

(21)

where Equation (21) must be positive definite.

Finally, the optimal state estimate and the associated error covariance matrix are calculated as:

$${\widehat{\mathit{x}}}_k=\sum _{i=1}^N{\tilde{\delta }}_k^{\left(i\right)}{\mathit{x}}_k^{+\left(i\right)}$$

(22)

$${\widehat{\mathit{P}}}_k=\sum _{i=1}^N{\tilde{\delta }}_k^{\left(i\right)}\left({\mathit{P}}_k^{+\left(i\right)}+\left({\mathit{x}}_k^{+\left(i\right)}-{\widehat{\mathit{x}}}_k\right){\left({\mathit{x}}_k^{+\left(i\right)}-{\widehat{\mathit{x}}}_k\right)}^T\right)$$

(23)

A cycle in the E$H_{\infty }$PF is completed with this logic. In summary, Equations (13)–(23) represent the steps used to obtain the a posteriori moments k from the a priori information $(k-1)$ at a given instant of time. However, some important information about the E$H_{\infty }$PF is listed here:

• The E$H_{\infty }$PF proposed here uses N particles with different values analyzing a possible sample impoverishment, a common problem for PF under the same conditions [3,20]. The idea is to analyze the processing time and the accuracy of the method.
• The weighting matrices ${\mathit{Q}}_k$, ${\mathit{R}}_k$, and ${\mathit{S}}_k$ in E$H_{\infty }$PF are designed as definite positive symmetric matrices and do not necessarily need to be diagonal, but the weighting matrices ${\tilde{\mathit{Q}}}_k$ and ${\tilde{\mathit{R}}}_k$ in EKF need to be configured as diagonals [3].
• Using the same weighting matrices ${\mathit{Q}}_k$ and ${\mathit{R}}_k$, it is observed that E$H_{\infty }$PF has more robust results compared to EKF. According to the theory, the EH${}_{\infty }$PF assumes that the process noise and measurement are both unmodeled, ${\mathit{w}}_k$ and ${\mathit{\upsilon }}_k$, respectively, and the initial condition ${\mathit{x}}_0$ will be chosen to maximize the cost function of the problem, i.e., considering the worst case scenario for the estimation process.
• For an $H_{\infty }$ filter, the threshold value of performance bound $\gamma$ controls the unfavorable conditions of the method. According to [4], in the error estimation of the method, when the restricted projected parameter $\gamma$ is reduced, the robustness characteristic of the filter is found. When the parameter $\gamma$ assumes large values tending to infinity, the $H_{\infty }$ filter has similar results to the standard Kalman filter.

4. Application and Results

The CBERS is a project for the development of remote sensing satellites administratively coordinated by the Brazilian Space Agency (AEB) and the China National Space Administration (CNSA), involving the scientific execution coordinated by the Brazilian National Institute for Space Research (INPE) and the Chinese Academy of Space Technology (CAST), which implements a world-class remote sensing system used by Brazil in strategic applications such as monitoring water resources, mapping the territory of both countries, and controlling deforestation in the Legal Amazon. In a first stage, the CBERS program started with two satellites, CBERS-1 and 2. With an agreement between Brazil and China, in November 2002, three satellites of the same category were built and launched, CBERS-2B, 3, and 4. In May 2015, a protocol for the development and launch of the CBERS 04A [28] was signed, and, more recently, in April 2023, an agreement was signed with the Chinese government to deepen scientific cooperation and collaborate on the development of the new CBERS-6 satellite. This satellite will have a new technology called synthetic aperture radar (SAR), which will increase and improve the monitoring of the Brazilian territory and biomes.

4.1. Parameters

The CBERS-4 satellite used in this research, the fifth satellite of the CBERS program, was launched on 7 December 2014 in a heliosynchronous and frozen orbit (see Figure 1). This configuration can provide global coverage: with low resolution cameras every 5 days, with medium resolution cameras every 26 days, and with high resolution cameras every 52 days [29].

In this work, in order to estimate the gyros bias and attitude, simulated orbit and attitude data from CBERS-4 were used, making use of the PROPAT propagator implemented in MatLab software. The PROPAT functions perform coordinate transformations, time and ephemeris conversion, orbital propagation, attitude transformations in various parameterizations, and attitude propagation [11]. The initial orbit and attitude conditions can be found in detail in [20]. In this article, the scope of the problem is expanded using a robust estimation method. This is supported by a series of additional simulations, including method comparison.

Table 1. CBERS-4 nominal orbital parameters [29].

Variable	Description	Values
a	Semi-major axis (average)	$7148.865$ km
e	Eccentricity	$1.1\times {10}^{-3}$
i	Inclination	$98.504$ deg
$\mathsf{\Omega }$	Right ascension of the	$333.3615$ deg
	ascending node (RAAN)
$\varpi$	Perigee argument	$117.4208$ deg
$t_{LTDN}$	Local time at the descending	10:30 a.m.
	node
$\tau$	Orbital period	$100.26$ min

presents CBERS-4 orbital parameters used for orbit simulation.

Table 2. Temporal parameters, CBERS-4 initial state, and initial variance parameters for estimation methods.

Variable	Description	Values
$\Delta$	Sampling rate	$0.5$ s
T	Observation time span	10 min
${\mathit{q}}_0^T$	Quaternions initial state	[0   0   0   1]
${\mathit{\epsilon }}_0^T$	Gyros bias initial state	[5.7   4.8   2.6] deg/h
${\mathit{\sigma }}_{P_q}^2$	Quaternions variance	$0.25$ deg2
${\mathit{\sigma }}_{P_b}^2$	Gyros bias variance	$1.0$ deg2/h2
$\gamma$	Specific performance bound	${\displaystyle \frac{1}{3}}$

presents the simulation data for the sampling rate $\Delta$; the observation time span T; the quaternions initial state ${\mathit{q}}_0$ and the gyros bias initial state ${\mathit{\epsilon }}_0$ that compose the initial state vector ${\mathit{x}}_0$; the quaternions variance ${\mathit{\sigma }}_{P_q}^2$ and the gyros bias variance ${\mathit{\sigma }}_{P_b}^2$ that compose the initial covariance matrix $P_0$; and $\gamma$, the user-specific performance bound for E$H_{\infty }$PF exclusively.

For CBERS-4, the telemetry data from the sensors arrives at the onboard computer in a fixed binary word length that translates into floating point values. The data sampling rates of the sensors are different and come asynchronously: 2 Hz for gyroscopes, 1 Hz for IRES-s, and 0.25 Hz for DSS-s. These telemetries recorded on board are downlinked and made available by the control center. We chose in the simulations to use a common sampling rate for all sensors; we chose gyros sampling rate of 2 Hz or 0.5 s, as shown in Table 2.

These data are used in all estimation methods of this work. It is important to say that the values of ${\mathit{\epsilon }}_0$ are typical drifts simulated for the CBERS-4 application. Thus, the initial state vector ${\mathit{x}}_0$ and the initial covariance matrix ${\mathit{P}}_0$ started in Table 2 are used in Equations (24) and (25) below:

$${\mathit{x}}_0={\left[\begin{array}{cc}{\mathit{q}}_0^T& {\mathit{\epsilon }}_0^T\end{array}\right]}^T$$

(24)

$${\mathit{P}}_0=diag\left(\begin{array}{ccccccc}{\mathit{\sigma }}_{P_q}^2& {\mathit{\sigma }}_{P_q}^2& {\mathit{\sigma }}_{P_q}^2& {\mathit{\sigma }}_{P_q}^2& {\mathit{\sigma }}_{P_b}^2& {\mathit{\sigma }}_{P_b}^2& {\mathit{\sigma }}_{P_b}^2\end{array}\right)$$

(25)

where $diag(.)$ means a diagonal matrix.

Table 3. CBERS-4 process noises variance parameters and measurements noises variance parameters for estimation methods.

Variable	Description	Values
${\mathit{\sigma }}_{Q_q}^2$	Quaternions process	$0.1\times {10}^{-3}$
	noises variance
${\mathit{\sigma }}_{Q_b}^2$	Gyros bias process	$0.1\times {10}^{-5}$ deg2/h2
	noises variance
${\mathit{\sigma }}_{R_{DSS}}^2$	DSS measurements	$0.36$ deg2
	noises variance
${\mathit{\sigma }}_{R_{IRES}}^2$	IRES measurements	$0.36\times {10}^{-2}$ deg2/h2
	noises variance

presents the quaternions process noise variance ${\mathit{\sigma }}_{Q_q}^2$, the gyros bias process noise variance ${\mathit{\sigma }}_{Q_b}^2$, the DSS measurements noise variance ${\mathit{\sigma }}_{R_{DSS}}^2$, and the IRES measurements process noise variance ${\mathit{\sigma }}_{R_{IRES}}^2$. These variances compose the initial diagonal process noise covariance matrix ${\mathit{Q}}_0$ and the initial diagonal measurements noise covariance matrix ${\mathit{R}}_0$.

These initial process noise covariance matrix ${\mathit{Q}}_0$ and the initial measurements noise covariance matrix ${\mathit{R}}_0$ are presented in Equations (26) and (27) below.

$${\mathit{Q}}_0=diag\left(\begin{array}{ccccccc}{\mathit{\sigma }}_{Q_q}^2& {\mathit{\sigma }}_{Q_q}^2& {\mathit{\sigma }}_{Q_q}^2& {\mathit{\sigma }}_{Q_q}^2& {\mathit{\sigma }}_{Q_b}^2& {\mathit{\sigma }}_{Q_b}^2& {\mathit{\sigma }}_{Q_b}^2\end{array}\right)$$

(26)

$${\mathit{R}}_0=diag\left(\begin{array}{cccc}{\mathit{\sigma }}_{R_{DSS}}^2& {\mathit{\sigma }}_{R_{DSS}}^2& {\mathit{\sigma }}_{R_{IRES}}^2& {\mathit{\sigma }}_{R_{IRES}}^2\end{array}\right)$$

(27)

These matrices are used in all estimation methods of this work, and for E$H_{\infty }$PF, the matrices ${\mathit{L}}_k={\mathit{I}}_{7\times 7}$ and ${\mathit{S}}_k={\mathit{I}}_{7\times 7}$ throughout the simulation, to have the direct estimation of the state vector according to the theory.

4.2. Filter Performance

Two metrics were defined to evaluate filter performance.

4.2.1. Mean Error

The mean error is represented by Equation (28).

$${\overline{\mathit{X}}}_k=\frac{1}{N}\sum _{i=1}^N{\tilde{\mathit{X}}}_k^{\left(i\right)}$$

(28)

where

$${\tilde{\mathit{X}}}_k^{\left(i\right)}={\widehat{\mathit{x}}}_k^{\left(i\right)}-{\mathit{x}}_k$$

(29)

Equation (29) represents the estimation error, the difference between the estimated state and the true state, and has been used to verify the accuracy of each filter’s estimate.

The respective standard deviation of mean error is represented by:

$${\mathit{\sigma }}_{X_k}=\sqrt{\frac{1}{N-1}\sum _{i=1}^N{\left({\tilde{\mathit{X}}}_k^{\left(i\right)}-{\overline{\mathit{X}}}_k\right)}^2}$$

(30)

4.2.2. Root Mean Squared Error

The root mean square error is represented by Equation (31).

$${\overline{\overline{\mathit{X}}}}_k=\sqrt{\frac{1}{N}\sum _{i=1}^N{\left({\tilde{\mathit{X}}}_k^{\left(i\right)}\right)}^2}$$

(31)

These two metrics were calculated for each iteration over a large number M of Monte Carlo simulations. It was employed to obtain the mean error, the standard deviation, and the root mean squared error of the simulation.

4.3. Methodology

The standard PF was implemented using re-sampling in a systematic way to increase particle diversity [3,30] with the intention of evaluating and measuring the performance of the proposed E$H_{\infty }$PF. More details about this estimation method and implementation can be found in [1,20,31]. The mean error, root mean square error (RMSE), and processing time cost of the estimation methods used were analyzed and compared.

In state estimation simulations, the standard PF used $N=500$ and 1000 particles, and the E$H_{\infty }$PF used $N=10,25,50,100,200,300$, and 500 particles (all with the specific performance bound $\gamma =\frac{1}{3}$). However, for the PF, only the results with 500 particles are presented, and for E$H_{\infty }$PF, only the results with 100 particles are presented for the estimation error state. The results with different particles number were used in scenario comparison estimation error and for analyzing the processing time cost.

4.4. Results

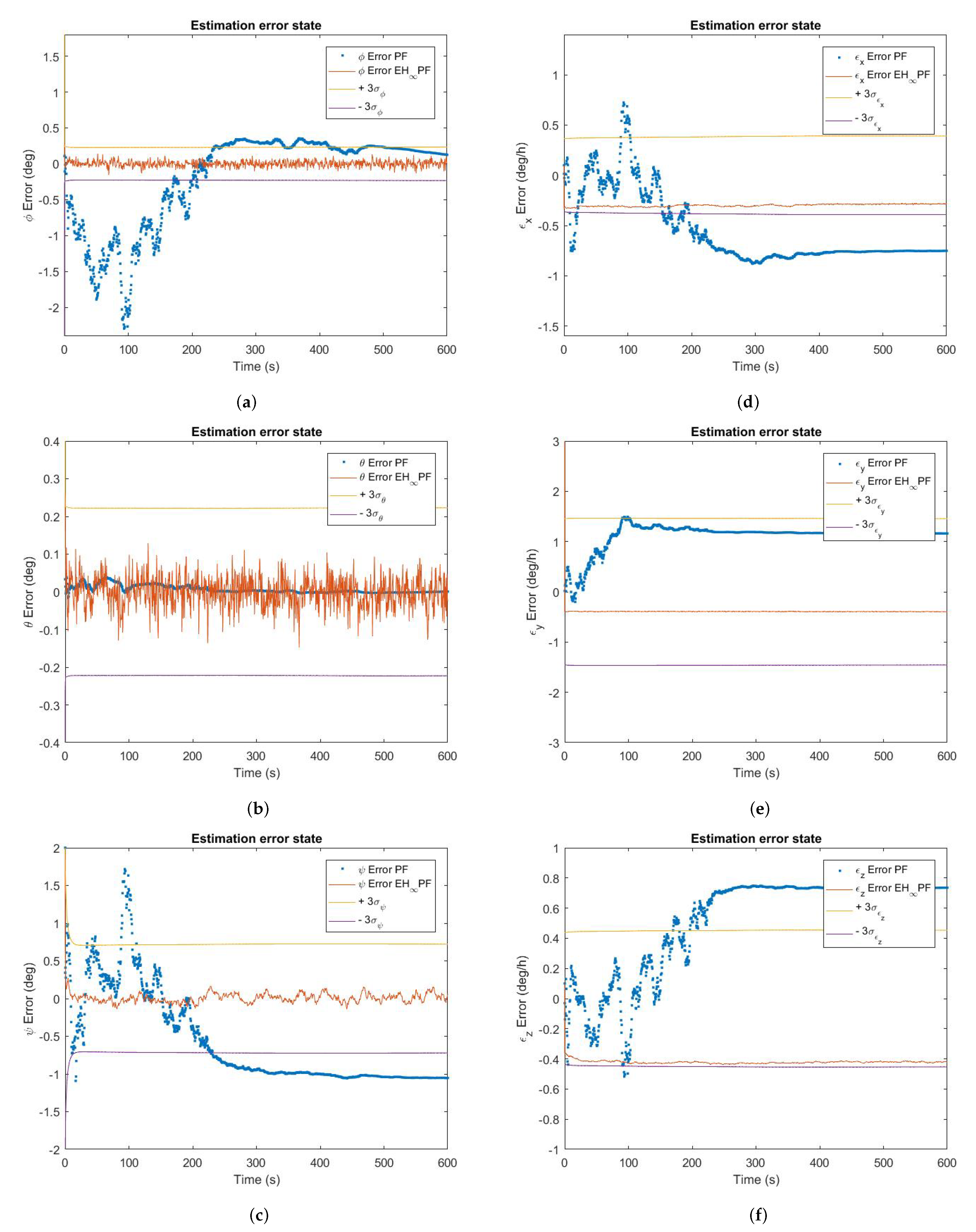
The attitude and gyros bias estimation error are presented in Figure 2a–f. The results were obtained in quaternions and transformed into Euler angles (ZYX sequence using roll $\varphi$, pitch $\theta$, and yaw $\psi$ angles), for better interpretation.

Figure 2a–c present only the attitude estimation error for the following estimation methods: PF (500 particles) in blue, E$H_{\infty }$PF (100 particles and $\gamma =\frac{1}{3}$) in red, and the results together with $\pm 3\sigma$ in yellow and magenta, representing a confidence interval considering the error as a normal probability distribution. In Figure 2d–f are present only the gyros bias estimation error following the same logic of representation and color code as in Figure 2a.

It is observed in Figure 2a–c that the E$H_{\infty }$PF (100 particles) presents excellent and competitive precision for the attitude estimation error with a mean close to zero with a reduced number of particles compared to the PF, with their results within $\pm 3\sigma$ standard deviations. For PF (500 particles), the results for attitude errors in roll and yaw extrapolate the reference standard deviation, but the attitude error in pitch visually presents a satisfactory result within the standard deviation considered and with precision superior to E$H_{\infty }$PF (100 particles and $\gamma =\frac{1}{3}$).

It is noted in Figure 2d–f that the E$H_{\infty }$PF (100 particles and $\gamma =\frac{1}{3}$) presents good precision for the gyros bias estimation error with results within $\pm 3\sigma$ standard deviations. The PF (500 particles) present good results only for the y-axis gyros bias estimation error in the limit of the considered standard deviation; for the x-axis gyros bias estimation error and z-axis gyros bias estimation error, they present results that extrapolate the reference standard deviation.

Figure 2 shows that in the PF process, the estimation error does not decrease with the filter process and eventually converges toward a value outside $\pm 3\sigma$. This discrepancy is associated with the number of particles used. Most of the time, for the PF to obtain good results, it is necessary to use a high number of particles, as few particles generate a problem called sample impoverishment.

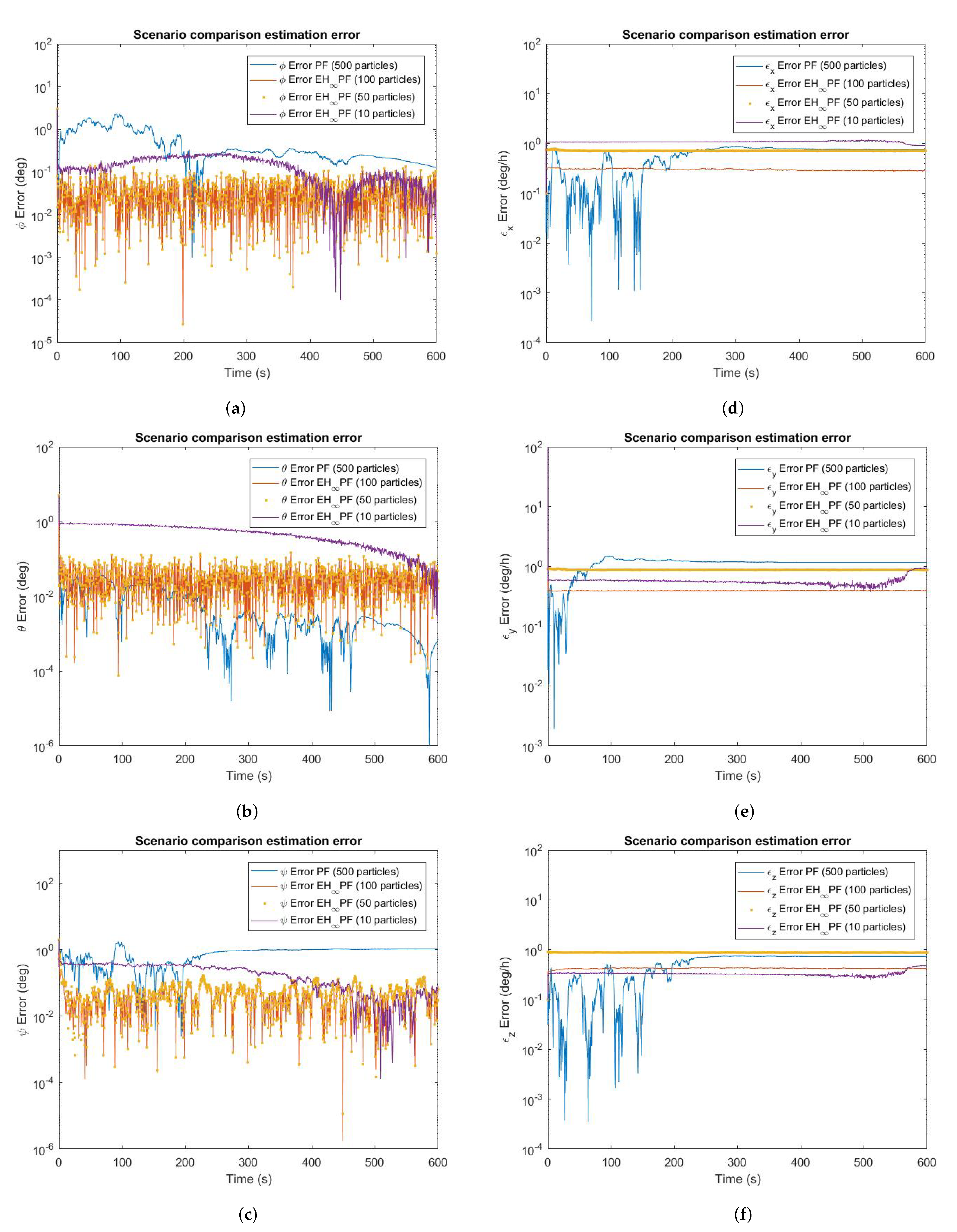
Monolog graphs (Figure 3a–f) represent the scenarios that make up the estimation errors between the estimation methods used, facilitating the visualization with the following representation: PF (500 particles) in blue, E$H_{\infty }$PF (100 particles) in red, E$H_{\infty }$PF (50 particles) in yellow, and E$H_{\infty }$PF (10 particles) in purple. All results for the E$H_{\infty }$PF uses specific performance bound $\gamma =\frac{1}{3}$.

Figure 3a–c show that even with 100 particles, the E$H_{\infty }$PF achieved a higher attitude determination accuracy in roll and yaw angle when compared to PF (500 particles). The standard PF did not achieve good accuracy even using a considerable number of particles, except for the pitch estimation error.

Comparing Figure 3d–f at the beginning of the simulation, the PF presents excellent results but it loses precision throughout the simulation. In this way, it is observed that the E$H_{\infty }$PF with 100 particles reached a higher precision and accuracy for gyros bias estimation error when compared with standard PF.

In general, the E$H_{\infty }$PF loses efficiency using a reduced number of particles, as can be seen in Figure 3a–f with 10 and 50 particles. For this attitude estimation application, the E$H_{\infty }$PF with 100 particles showed, in terms of accuracy, competitive and interesting results.

Table 4. Summary statistical information presented on simulation range, mean error, standard deviation, minimum and maximum error, root mean square error, and peak-to-peak error for PF.

	PF
	Mean Error	Stand. Dev.	Min. Error	Max. Error	RMSE	Peak to Peak Error
$\varphi$ (deg)	$-0.1938$	$0.6552$	$-2.2954$	$0.3544$	$0.3189$	$0.6299$
$\theta$ (deg)	$0.0063$	$0.0099$	$-0.0164$	$0.0390$	$0.0162$	$0.0424$
$\psi$ (deg)	$-0.5745$	$0.6302$	$-1.0919$	$1.7162$	$1.8425$	$3.6840$
${\epsilon }_{\varphi }$ (deg/h)	$-0.5500$	$0.3515$	$-0.8792$	$0.7237$	$2.1240$	$4.2480$
${\epsilon }_{\theta }$ (deg/h)	$1.1134$	$0.2754$	$-0.2004$	$1.4925$	$0.1472$	$2.2971$
${\epsilon }_{\psi }$ (deg/h)	$0.5042$	$0.3404$	$-0.5174$	$0.7483$	$0.0982$	$1.1864$

and

Table 5. Summary statistical information presented on simulation range, mean error, standard deviation, minimum and maximum error, root mean square error, and peak-to-peak error for E$H_{\infty }$PF.

	E${\mathit{H}}_{\mathit{\infty }}$PF
	Mean Error	Stand. Dev.	Min. Error	Max. Error	RMSE	Peak to Peak Error
$\varphi$ (deg)	$-0.0010$	$0.0416$	$-0.1474$	$0.1409$	$0.0010$	$0.320$
$\theta$ (deg)	$-0.0007$	$0.0410$	$-0.1475$	$0.2248$	$0.0009$	$0.4572$
$\psi$ (deg)	$0.0085$	$0.0632$	$-0.1352$	$0.7358$	$0.0049$	$1.573$
${\epsilon }_{\varphi }$ (deg/h)	$-0.2990$	$0.0118$	$-0.3307$	$-0.2769$	$0.0977$	$0.2894$
${\epsilon }_{\theta }$ (deg/h)	$-0.3926$	$0.0027$	$-0.4069$	$-0.3797$	$0.0824$	$0.1245$
${\epsilon }_{\psi }$ (deg/h)	$-0.4216$	$0.0093$	$-0.4386$	$-0.3614$	$0.7515$	$1.4569$

shows the mean error, standard deviation, minimal error, maximum error shown in Figure 2a–f, the RMSE, and peak to peak error in the attitude estimation and gyros bias estimation error for the PF (500 particles) and E$H_{\infty }$PF (100 particles and $\gamma =\frac{1}{3}$).

With the relation results of the estimation error, we found results of the order of ${10}^{-3}$ degrees on average (see Table 5) for the E$H_{\infty }$PF considered within the design requirements for pointing error [29].

Table 6. Comparative information on data processing time.

Nonlinear State Estimation Method	Processing Time (s)
PF ($N=500$ particles)	$47.3310$
PF ($N=1000$ particles)	$243.4860$
E$H_{\infty }$PF ($N=10$ particles)	$4.7782$
E$H_{\infty }$PF ($N=25$ particles)	$5.7672$
E$H_{\infty }$PF ($N=50$ particles)	$11.3551$
E$H_{\infty }$PF ($N=100$ particles)	$22.6254$
E$H_{\infty }$PF ($N=200$ particles)	$46.4539$
E$H_{\infty }$PF ($N=300$ particles)	$73.4110$
E$H_{\infty }$PF ($N=500$ particles)	$132.5640$

presents the comparative information on data processing time for an Intel${}^{\circledR }$ Core${}^{\mathrm{TM}}$ i7 processor with a maximum frequency of 4.10 GHz for the estimation methods used. In summary, PF (500 particles) has a data processing time for state estimation $2.09$ times greater than E$H_{\infty }$PF (100 particles).

5. Conclusions

The E$H_{\infty }$PF based on the $H_{\infty }$ filter is premised on minimizing the worst possible effects and conditions of disturbance signals associated with measurement noise through signal estimation error without a priori knowledge of these perturbations. The non-Gaussian uncertainties that appear in the process model are contained in the gyro’s measurements, which present noise and bias due to post-launch sensor misalignment, thermal expansion, fading, electro-mechanical degradation, etc. All these factors cause inaccuracies in the model and deteriorate the attitude estimation process. The E$H_{\infty }$PF proved to be effective for estimating attitude and showed greater accuracy when compared with the standard PF and results from previous studies using different estimation methods [1,16,17,20].

In summary, it is concluded that the E$H_{\infty }$PF algorithm implemented in this work presented an excellent and competitive precision for estimating attitude and gyros bias; the estimation error results are within a proposed confidence interval considering the error with a normalized Gaussian distribution. For E$H_{\infty }$PF with coefficient of performance $\gamma =\frac{1}{3}$ and with only 100 particles, it presents a low data processing time, $2.09$ times less than the standard PF with 500 particles. This represents an alternative to be used in embedded space systems. Both estimation methods converge without known sample impoverishment even using a reduced sample number, especially for E$H_{\infty }$PF, with robust and fast results, providing a kinematic attitude solution in addition to estimating the gyroscope bias with specified accuracy for the attitude determination control system (ADCS) according to the project requirements.

Other results that could be presented would be evaluating the variation of performance threshold values $\gamma$ as presented in [4] in order to verify the robustness of the E$H_{\infty }$PF method, as already stated and theoretically validated. Reduced values of the performance coefficient $\gamma$ would lead to the characteristic robustness of the filter. If the value of performance coefficient $\gamma$ approaches infinity, the E$H_{\infty }$PF would have results similar to the standard Kalman filter.

In future work, the research group intends to apply the attitude estimation method to other satellites such as the Amazônia I, from the National Institute for Space Research (INPE-Brasil); and in a cubesats scenario as for AlfaCrux [32] and SPLASH project—the Self-DePloyable FLexible AeroSHell for de-Orbiting and Space Re-entry [33]. Applications in other aerospace engineering dynamic systems will also be implemented, such as in-orbit estimation using GPS data and in aerodynamic coefficient estimation for unmanned aerial vehicles (UAV), for example. This application will analyze the precision, computational processing time cost, and feasibility to embedded systems.