Sensitivity of Optical Satellites to Estimate Windthrow Tree-Mortality in a Central Amazon Forest
Abstract
1. Introduction
2. Materials and Methods
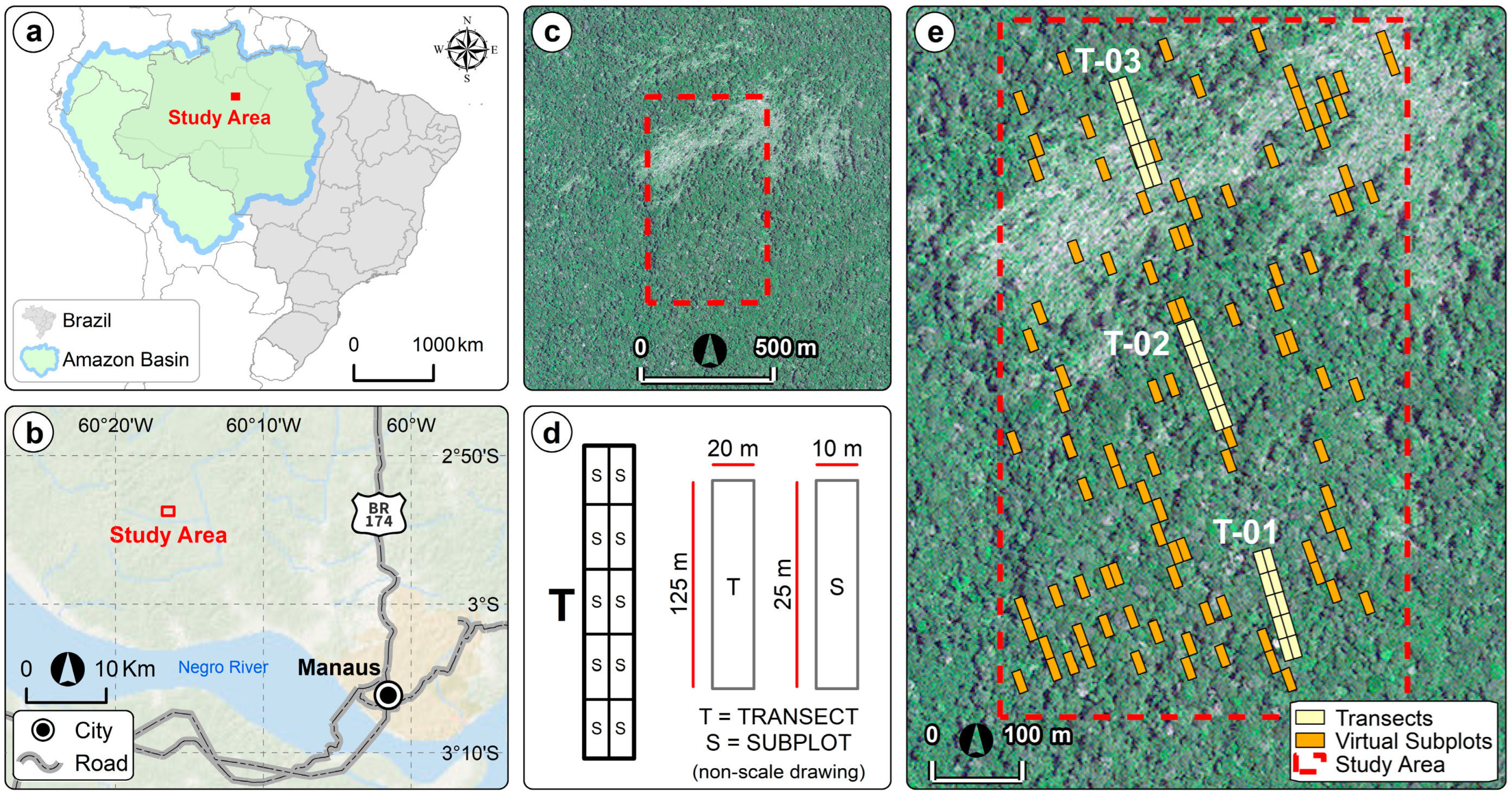
2.1. Study Area and Sampling Design
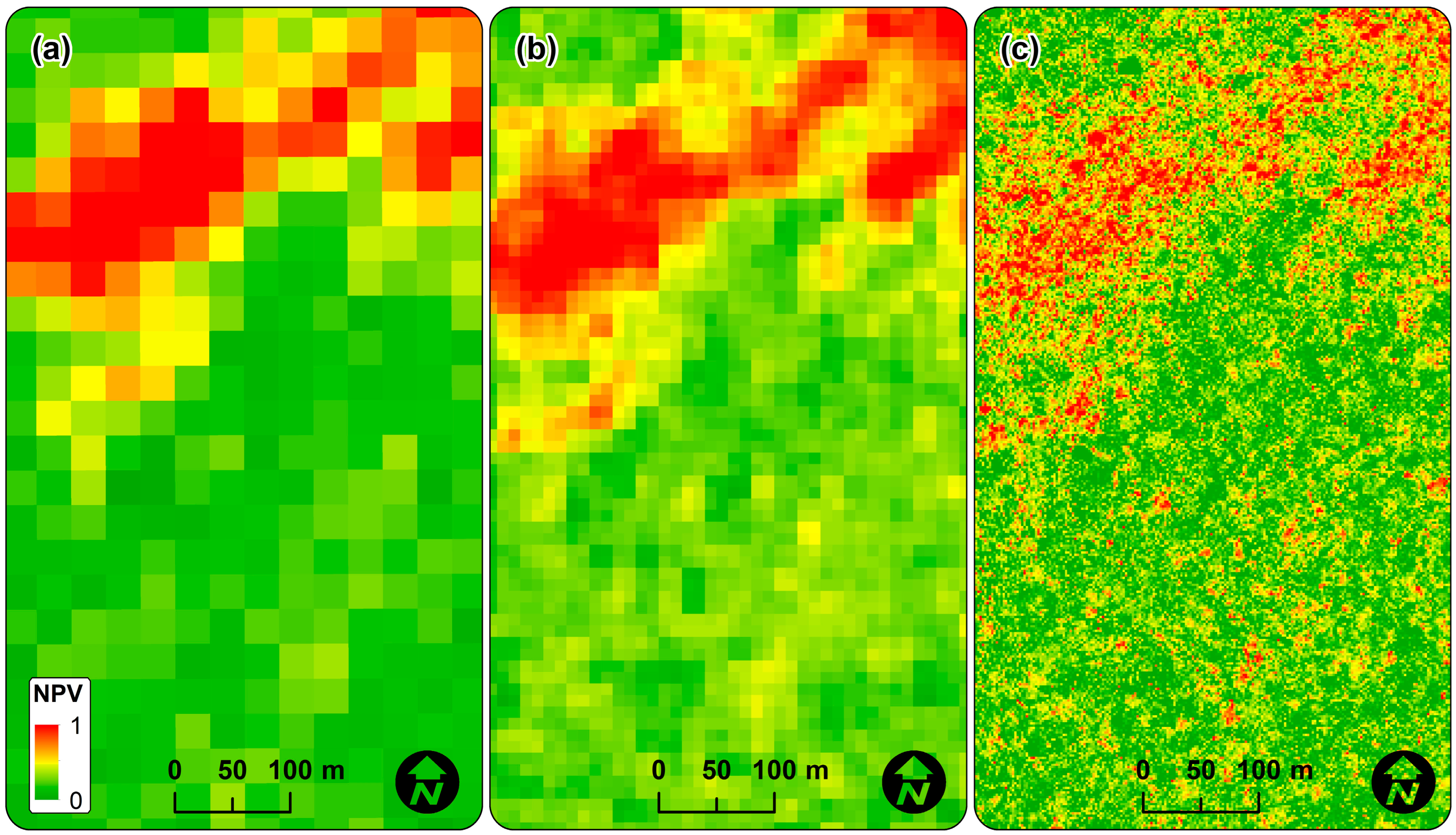
2.2. Spectral Mixture Analysis and Remote Sensing Estimates of Windthrow Tree-Mortality
2.3. Remote Sensing Estimates of Windthrow Tree Mortality
2.4. Statistical Analysis
3. Results
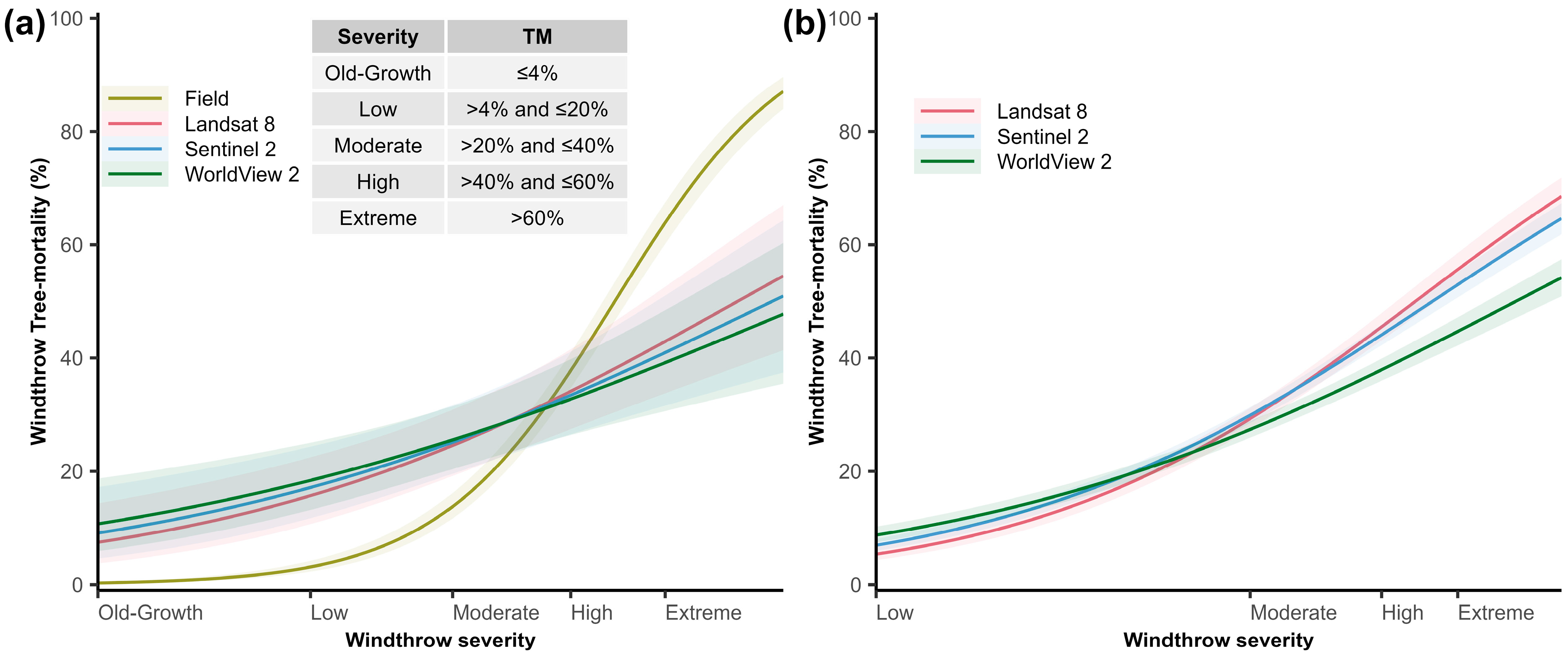
3.1. How Does Spatial Resolution Affect Satellite Estimates of Windthrow Tree-Mortality?
3.2. Which Sensor Produces the Most Reliable Estimates of Windthrow Tree-Mortality across an Extent Gradient of Windthrow Severity?
4. Discussion
4.1. Relating Satellite Data and Field Data
4.2. Trade-Off between Precision and Accuracy of Satellite Estimates
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Marra, D.M.; Chambers, J.Q.; Higuchi, N.; Trumbore, S.E.; Ribeiro, G.H.P.M.; Dos Santos, J.; Negrón-Juárez, R.I.; Reu, B.; Wirth, C. Large-Scale Wind Disturbances Promote Tree Diversity in a Central Amazon Forest. PLoS ONE 2014, 9, e103711. [Google Scholar] [CrossRef]
- Magnabosco Marra, D.; Trumbore, S.E.; Higuchi, N.; Ribeiro, G.H.P.M.P.M.; Negrón-Juárez, R.I.; Holzwarth, F.; Rifai, S.W.; dos Santos, J.; Lima, A.J.N.N.; Kinupp, V.F.; et al. Windthrows Control Biomass Patterns and Functional Composition of Amazon Forests. Glob. Chang. Biol. 2018, 24, 5867–5881. [Google Scholar] [CrossRef]
- Rifai, S.W.; Urquiza Muñoz, J.D.; Negrón-Juárez, R.I.; Ramírez Arévalo, F.R.; Tello-Espinoza, R.; Vanderwel, M.C.; Lichstein, J.W.; Chambers, J.Q.; Bohlman, S.A. Landscape-Scale Consequences of Differential Tree Mortality from Catastrophic Wind Disturbance in the Amazon. Ecol. Appl. 2016, 26, 2225–2237. [Google Scholar] [CrossRef]
- Urquiza Muñoz, J.D.; Magnabosco Marra, D.; Negrón-Juarez, R.I.; Tello-Espinoza, R.; Alegría-Muñoz, W.; Pacheco-Gómez, T.; Rifai, S.W.; Chambers, J.Q.; Jenkins, H.S.; Brenning, A.; et al. Recovery of Forest Structure Following Large-Scale Windthrows in the Northwestern Amazon. Forests 2021, 12, 667. [Google Scholar] [CrossRef]
- Rehbein, A.; Ambrizzi, T.; Mechoso, C.R. Mesoscale Convective Systems over the Amazon Basin. Part I: Climatological Aspects. Int. J. Clim. 2018, 38, 215–229. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Masson-Delmotte, V., Zhai, P., Pirani, A., Connors, S.L., Péan, C., Berger, S., Caud, N., Chen, Y., Eds.; IPCC: Geneva, Switzerland, 2021. [Google Scholar]
- Feng, Y.; Negrón-Juárez, R.I.; Romps, D.M.; Chambers, J.Q. Amazon Windthrow Disturbances Are Likely to Increase with Storm Frequency under Global Warming. Nat. Commun. 2023, 14, 101. [Google Scholar] [CrossRef]
- Aleixo, I.; Norris, D.; Hemerik, L.; Barbosa, A.; Prata, E.; Costa, F.; Poorter, L. Amazonian Rainforest Tree Mortality Driven by Climate and Functional Traits. Nat. Clim. Chang. 2019, 9, 384–388. [Google Scholar] [CrossRef]
- Chambers, J.Q.; Negron-Juarez, R.I.; Marra, D.M.; Di Vittorio, A.; Tews, J.; Roberts, D.; Ribeiro, G.H.P.M.; Trumbore, S.E.; Higuchi, N. The Steady-State Mosaic of Disturbance and Succession across an Old-Growth Central Amazon Forest Landscape. Proc. Natl. Acad. Sci. USA 2013, 110, 3949–3954. [Google Scholar] [CrossRef]
- Esquivel-Muelbert, A.; Phillips, O.L.; Brienen, R.J.W.; Fauset, S.; Sullivan, M.J.P.; Baker, T.R.; Chao, K.J.; Feldpausch, T.R.; Gloor, E.; Higuchi, N.; et al. Tree Mode of Death and Mortality Risk Factors across Amazon Forests. Nat. Commun. 2020, 11, 5515. [Google Scholar] [CrossRef]
- Gora, E.M.; Esquivel-Muelbert, A. Implications of Size-Dependent Tree Mortality for Tropical Forest Carbon Dynamics. Nat. Plants 2021, 7, 384–391. [Google Scholar] [CrossRef]
- Belward, A.S.; Skøien, J.O. Who Launched What, When and Why; Trends in Global Land-Cover Observation Capacity from Civilian Earth Observation Satellites. ISPRS J. Photogramm. Remote Sens. 2015, 103, 115–128. [Google Scholar] [CrossRef]
- Negrón-Juárez, R.I.; Holm, J.A.; Marra, D.M.; Rifai, S.W.; Riley, W.J.; Chambers, J.Q.; Koven, C.D.; Knox, R.G.; McGroddy, M.E.; Di Vittorio, A.V.; et al. Vulnerability of Amazon Forests to Storm-Driven Tree Mortality. Environ. Res. Lett. 2018, 13, 054021. [Google Scholar] [CrossRef]
- Negrón-Juárez, R.I.; Chambers, J.Q.; Guimaraes, G.; Zeng, H.; Raupp, C.F.M.; Marra, D.M.; Ribeiro, G.H.P.M.; Saatchi, S.S.; Nelson, B.W.; Higuchi, N. Widespread Amazon Forest Tree Mortality from a Single Cross-Basin Squall Line Event. Geophys. Res. Lett. 2010, 37, L16701. [Google Scholar] [CrossRef]
- Nelson, B.W.; Amaral, I. Destructive Wind Effects Detected in TM Images of the Amazon Basin. Int. Arch. Photg. Rem. Sens. 1994, 30, 339–343. [Google Scholar]
- Negrón-Juárez, R.; Jenkins, H.; Raupp, C.; Riley, W.; Kueppers, L.; Magnabosco Marra, D.; Ribeiro, G.; Monteiro, M.; Candido, L.; Chambers, J.; et al. Windthrow Variability in Central Amazonia. Atmosphere 2017, 8, 28. [Google Scholar] [CrossRef]
- Negron-Juarez, R.; Magnabosco-Marra, D.; Feng, Y.; Urquiza-Muñoz, J.D.; Riley, W.J.; Chambers, J.Q. Windthrow Characteristics and Their Regional Association with Rainfall, Soil, and Surface Elevation in the Amazon. Environ. Res. Lett. 2023, 18, 014030. [Google Scholar] [CrossRef]
- Roy, D.P.; Wulder, M.A.; Loveland, T.R.; Woodcock, C.E.; Allen, R.G.; Anderson, M.C.; Helder, D.; Irons, J.R.; Johnson, D.M.; Kennedy, R.; et al. Landsat-8: Science and Product Vision for Terrestrial Global Change Research. Remote Sens. Environ. 2014, 145, 154–172. [Google Scholar] [CrossRef]
- Coppin, P.; Jonckheere, I.; Nackaerts, K.; Muys, B.; Lambin, E. Digital Change Detection Methods in Ecosystem Monitoring: A Review. Int. J. Remote Sens. 2004, 25, 1565–1596. [Google Scholar] [CrossRef]
- Goward, S.; Arvidson, T.; Williams, D.; Faundeen, J.; Irons, J.; Franks, S. Historical Record of Landsat Global Coverage: Mission Operations, NSLRSDA, and International Cooperator Stations. Photogramm. Eng. Remote Sens. 2006, 72, 1155–1169. [Google Scholar] [CrossRef]
- Woodcock, C.E.; Strahler, A.H. The Factor of Scale in Remote Sensing. Remote Sens. Environ. 1987, 21, 311–332. [Google Scholar] [CrossRef]
- Coops, N.C.; Wulder, M.A.; White, J.C. Identifying and Describing Forest Disturbance and Spatial Pattern: Data Selection Issues and Methodological Implications. In Understanding Forest Disturbance and Spatial Pattern; Wulder, M.A., Franklin, S.E., Eds.; CRC Press: Boca Raton, FL, USA, 2006; pp. 31–61. [Google Scholar]
- Negrón-Juárez, R.I.; Chambers, J.Q.; Marra, D.M.; Ribeiro, G.H.P.M.; Rifai, S.W.; Higuchi, N.; Roberts, D. Detection of Subpixel Treefall Gaps with Landsat Imagery in Central Amazon Forests. Remote Sens. Environ. 2011, 115, 3322–3328. [Google Scholar] [CrossRef]
- Negrón-Juárez, R.I.; Holm, J.A.; Faybishenko, B.; Magnabosco-Marra, D.; Fisher, R.A.; Shuman, J.K.; de Araujo, A.C.; Riley, W.J.; Chambers, J.Q. Landsat Near-Infrared (NIR) Band and ELM-FATES Sensitivity to Forest Disturbances and Regrowth in the Central Amazon. Biogeosciences 2020, 17, 6185–6205. [Google Scholar] [CrossRef]
- Asner, G.P.; Kellner, J.R.; Kennedy-Bowdoin, T.; Knapp, D.E.; Anderson, C.; Martin, R.E. Forest Canopy Gap Distributions in the Southern Peruvian Amazon. PLoS ONE 2013, 8, e60875. [Google Scholar] [CrossRef] [PubMed]
- Asner, G.P.; Keller, M.; Pereira, R., Jr.; Zweede, J.C.; Silva, J.N.M. Canopy Damage and Recovery after Selective Logging in Amazonia: Field and Satellite Studies. Ecol. Appl. 2004, 14, 280–298. [Google Scholar] [CrossRef]
- Adams, J.B.; Gillespie, A.R. Remote Sensing of Landscapes with Spectral Images, 1st ed.; Adams, J.B., Gillespie, A.R., Eds.; Cambridge University Press: New York, NY, USA, 2006; ISBN 9780521662215. [Google Scholar]
- Turner, M.G. Landscape Ecology: The Effect of Pattern on Process. Annu. Rev. Ecol. Syst. 1989, 20, 171–197. [Google Scholar] [CrossRef]
- Wulder, M. Optical Remote-Sensing Techniques for the Assessment of Forest Inventory and Biophysical Parameters. Prog. Phys. Geogr. Earth Environ. 1998, 22, 449–476. [Google Scholar] [CrossRef]
- Townshend, J.R.G.; Justice, C.O. Selecting the Spatial Resolution of Satellite Sensors Required for Global Monitoring of Land Transformations. Int. J. Remote Sens. 1988, 9, 187–236. [Google Scholar] [CrossRef]
- Asner, G.P.; Warner, A.S. Canopy Shadow in IKONOS Satellite Observations of Tropical Forests and Savannas. Remote Sens. Environ. 2003, 87, 521–533. [Google Scholar] [CrossRef]
- Clark, D.B.; Castro, C.S.; Alvarado, L.D.A.; Read, J.M. Quantifying Mortality of Tropical Rain Forest Trees Using High-Spatial-Resolution Satellite Data. Ecol. Lett. 2004, 7, 52–59. [Google Scholar] [CrossRef]
- Clark, D.B.; Read, J.M.; Clark, M.L.; Cruz, A.M.; Dotti, M.F.; Clark, D.A. Application of 1-M and 4-M Resolution Satellite Data to Ecological Studies of Tropical Rain Forests. Ecol. Appl. 2004, 14, 61–74. [Google Scholar] [CrossRef]
- Dalagnol, R.; Phillips, O.L.; Gloor, E.; Galvão, L.S.; Wagner, F.H.; Locks, C.J.; Aragão, L.E.O.C. Quantifying Canopy Tree Loss and Gap Recovery in Tropical Forests under Low-Intensity Logging Using VHR Satellite Imagery and Airborne LiDAR. Remote Sens. 2019, 11, 817. [Google Scholar] [CrossRef]
- Fuller, D.O. Tropical Forest Monitoring and Remote Sensing: A New Era of Transparency in Forest Governance? Singap. J. Trop. Geogr. 2006, 27, 15–29. [Google Scholar] [CrossRef]
- Jackson, C.; Adam, E. Remote Sensing of Selective Logging in Tropical Forests: Current State and Future Directions. iForest-Biogeosci. For. 2020, 13, 286–300. [Google Scholar] [CrossRef]
- Espírito-Santo, F.D.B.; Keller, M.M.; Linder, E.; Oliveira Junior, R.C.; Pereira, C.; Oliveira, C.G. Gap Formation and Carbon Cycling in the Brazilian Amazon: Measurement Using High-Resolution Optical Remote Sensing and Studies in Large Forest Plots. Plant Ecol. Divers. 2014, 7, 305–318. [Google Scholar] [CrossRef]
- Espírito-Santo, F.D.B.; Gloor, M.; Keller, M.; Malhi, Y.; Saatchi, S.; Nelson, B.; Junior, R.C.O.; Pereira, C.; Lloyd, J.; Frolking, S.; et al. Size and Frequency of Natural Forest Disturbances and the Amazon Forest Carbon Balance. Nat. Commun. 2014, 5, 3434. [Google Scholar] [CrossRef]
- Fransson, J.E.S.; Walter, F.; Blennow, K.; Gustavsson, A.; Ulander, L.M.H. Detection of Storm-Damaged Forested Areas Using Airborne CARABAS-II VHF SAR Image Data. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2170–2175. [Google Scholar] [CrossRef]
- Dwyer, E.; Pasquali, P.; Holecz, F.; Arino, O. Mapping Forest Damage Caused by the 1999 Lothar Storm in Jura (France), Using SAR Interferometry. Earth Obs. Q. 2000, 65, 28–29. [Google Scholar]
- Weishampel, J.F.; Drake, J.B.; Cooper, A.; Blair, J.B.; Hofton, M. Forest Canopy Recovery from the 1938 Hurricane and Subsequent Salvage Damage Measured with Airborne LiDAR. Remote Sens. Environ. 2007, 109, 142–153. [Google Scholar] [CrossRef]
- Dalagnol, R.; Wagner, F.H.; Galvão, L.S.; Streher, A.S.; Phillips, O.L.; Gloor, E.; Pugh, T.A.M.; Ometto, J.P.H.B.; Aragão, L.E.O.C. Large-Scale Variations in the Dynamics of Amazon Forest Canopy Gaps from Airborne Lidar Data and Opportunities for Tree Mortality Estimates. Sci. Rep. 2021, 11, 1388. [Google Scholar] [CrossRef]
- Gorgens, E.B.; Keller, M.; Jackson, T.; Marra, D.M.; Reis, C.R.; de Almeida, D.R.A.; Coomes, D.; Ometto, J.P. Out of Steady State: Tracking Canopy Gap Dynamics across Brazilian Amazon. Biotropica 2023, 55, 755–766. [Google Scholar] [CrossRef]
- Simonetti, A.; Araújo, R.F.; Celes, C.H.; da Silva e Silva, F.R.; dos Santos, J.; Higuchi, N.; Trumbore, S.; Marra, D.M. Gap Geometry, Seasonality and Associated Losses of Biomass—Combining UAV Imagery and Field Data from a Central Amazon Forest. Biogeosci. Discuss, 2023; preprint. [Google Scholar] [CrossRef]
- Green, R.M. The Sensitivity of SAR Backscatter to Forest Windthrow Gaps. Int. J. Remote Sens. 1998, 19, 2419–2425. [Google Scholar] [CrossRef]
- Schwarz, M.; Steinmeier, C.; Holecz, F.; Stebler, O.; Wagner, H. Detection of Windthrow in Mountainous Regions with Different Remote Sensing Data and Classification Methods. Scand. J. For. Res. 2003, 18, 525–536. [Google Scholar] [CrossRef]
- Ping, D.; Dalagnol, R.; Galvão, L.S.; Nelson, B.; Wagner, F.; Schultz, D.M.; Bispo, P.d.C. Assessing the Magnitude of the Amazonian Forest Blowdowns and Post-Disturbance Recovery Using Landsat-8 and Time Series of PlanetScope Satellite Constellation Data. Remote Sens. 2023, 15, 3196. [Google Scholar] [CrossRef]
- Kislov, D.E.; Korznikov, K.A. Automatic Windthrow Detection Using Very-High-Resolution Satellite Imagery and Deep Learning. Remote Sens. 2020, 12, 1145. [Google Scholar] [CrossRef]
- Jaiswal, N.; Bucher, T.; Seiler, J.; Beckschäfer, P.; Bhattacharjee, P. Deep Learning Based Windthrow Detection for Winter Storms. In Proceedings of the Remote Sensing for Agriculture, Ecosystems, and Hydrology XXIV, Berlin, Germany, 5–7 September 2022; Neale, C.M., Maltese, A., Eds.; SPIE: Cergy, France, 2022; Volume 12262, p. 28. [Google Scholar]
- Galizia, L.; Nasrallah, A.; Elkhoury, C.; Coutu, S.; Castet, C.; Voituron, Q. Windthrow Detection with Moderate to High Resolution Optical Imageries across the European Forests. In Proceedings of the EGU General Assembly 2023, Vienna, Austria, 24–28 April 2023. [Google Scholar] [CrossRef]
- Deigele, W.; Brandmeier, M.; Straub, C. A Hierarchical Deep-Learning Approach for Rapid Windthrow Detection on PlanetScope and High-Resolution Aerial Image Data. Remote Sens. 2020, 12, 2121. [Google Scholar] [CrossRef]
- Hamdi, Z.M.; Brandmeier, M.; Straub, C. Forest Damage Assessment Using Deep Learning on High Resolution Remote Sensing Data. Remote Sens. 2019, 11, 1976. [Google Scholar] [CrossRef]
- Kislov, D.E.; Korznikov, K.A.; Altman, J.; Vozmishcheva, A.S.; Krestov, P. V Extending Deep Learning Approaches for Forest Disturbance Segmentation on Very High-resolution Satellite Images. Remote Sens. Ecol. Conserv. 2021, 7, 355–368. [Google Scholar] [CrossRef]
- Andreae, M.O.; Acevedo, O.C.; Araùjo, A.; Artaxo, P.; Barbosa, C.G.G.; Barbosa, H.M.J.; Brito, J.; Carbone, S.; Chi, X.; Cintra, B.B.L.; et al. The Amazon Tall Tower Observatory (ATTO): Overview of Pilot Measurements on Ecosystem Ecology, Meteorology, Trace Gases, and Aerosols. Atmos. Chem. Phys. 2015, 15, 10723–10776. [Google Scholar] [CrossRef]
- Stropp, J.; Van der Sleen, P.; Assunção, P.A.; da Silva, A.L.; Ter Steege, H. Tree Communities of White-Sand and Terra-Firme Forests of the Upper Rio Negro. Acta Amaz. 2011, 41, 521–544. [Google Scholar] [CrossRef]
- Targhetta, N.; Kesselmeier, J.; Wittmann, F. Effects of the Hydroedaphic Gradient on Tree Species Composition and Aboveground Wood Biomass of Oligotrophic Forest Ecosystems in the Central Amazon Basin. Folia Geobot 2015, 50, 185–205. [Google Scholar] [CrossRef]
- De Oliveira, A.N.; Amaral, I.L. do Florística e Fitossociologia de Uma Floresta de Vertente Na Amazônia Central, Amazonas, Brasil. Acta Amaz. 2004, 34, 21–34. [Google Scholar] [CrossRef]
- Braga, P.I.S. Subdivisão Fitogeográfica, Tipos de Vegetação, Conservação e Inventário Florístico Da Floresta Amazônica. Acta Amaz. 1979, 9, 53–80. [Google Scholar] [CrossRef]
- Higuchi, N.; Chambers, J.; Santos, J. Dos Dinâmica e Balanço Do Carbono Da Vegetação Primária Da Amazônia Central. Floresta 2004, 34, 295–304. [Google Scholar] [CrossRef]
- Telles, E.d.C.C.; de Camargo, P.B.; Martinelli, L.A.; Trumbore, S.E.; da Costa, E.S.; Santos, J.; Higuchi, N.; Oliveira, R.C. Influence of Soil Texture on Carbon Dynamics and Storage Potential in Tropical Forest Soils of Amazonia. Glob. Biogeochem. Cycles 2003, 17, 1040. [Google Scholar] [CrossRef]
- Carneiro, V.M.C. Composição Florística e Análise Estrutural Da Floresta Primária de Terra Firme Na Bacia Do Rio Cuieiras; Universidade Federal do Amazonas: Manaus, Brazil, 2004. [Google Scholar]
- Chambers, J.Q.; Robertson, A.L.; Carneiro, V.M.C.; Lima, A.J.N.; Smith, M.-L.; Plourde, L.C.; Higuchi, N. Hyperspectral Remote Detection of Niche Partitioning among Canopy Trees Driven by Blowdown Gap Disturbances in the Central Amazon. Oecologia 2009, 160, 107–117. [Google Scholar] [CrossRef]
- Pinto, A.C.; Higuchi, N.; Iida, S.; Santos, J.; Ribeiro, R.J.; Rocha, R.M.; Silva, R.P. Padrão de Distribuição Espacial de Espécies Florestais Que Ocorrem Na Região de Manaus. In Projeto Jacaranda Fase II—Pesquisas Florestais na Amazônia Central; Higuchi, N., Santos, J., Sampaio, P.T., Marenco, R.A., Ferraz, J., Sales, P.C., Saito, M., Matsumoto, S., Eds.; National Institute of Amazon Research: Manaus, Brazil, 2003; pp. 1–20. [Google Scholar]
- Anderson, A.B. White-Sand Vegetation of Brazilian Amazonia. Biotropica 1981, 13, 199. [Google Scholar] [CrossRef]
- Adeney, J.M.; Christensen, N.L.; Vicentini, A.; Cohn-Haft, M. White-sand Ecosystems in Amazonia. Biotropica 2016, 48, 7–23. [Google Scholar] [CrossRef]
- Luizão, F.J.; Schubart, H.O.R. Litter Production and Decomposition in a Terra-Firme Forest of Central Amazonia. Experientia 1987, 43, 259–265. [Google Scholar] [CrossRef]
- Ferraz, J.; Ohta, S.; de Sales, P.C. Distribuição Dos Solos Ao Longo de Dois Transectos Em Floresta Primária Ao Norte de Manaus (AM). In Pesquisas Florestais Para a Conservação da Floresta e Reabilitação de Áreas Degradadas da Amazônia; MCT-INPA/JICA, Ed.; INPA: Manaus, Brazil, 1998; pp. 109–143. [Google Scholar]
- De Almeida, A.F. Análise Fitossociológica Estrutural e Composição Florística da Área de Proteção Ambiental Margem Esquerda do Rio Negro. Master’s Thesis, Universidade Federal do Amazonas, Manaus, Brazil, 2012. [Google Scholar]
- Amaral, I.L.D.; Matos, F.D.A.; Lima, J. Composição Florística e Parâmetros Estruturais de Um Hectare de Floresta Densa de Terra Firme No Rio Uatumã, Amazônia, Brasil. Acta Amaz. 2000, 30, 377. [Google Scholar] [CrossRef]
- Woortmann, C.P.; Higuchi, N.; Dos Santos, J.; Da Silva, R.P. Allometric Equations for Total, above-and below-Ground Biomass and Carbon of the Amazonian Forest Type Known as Campinarana. Acta Amaz. 2018, 48, 85–92. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-Scale Geospatial Analysis for Everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Adams, J.B.; Sabol, D.E.; Kapos, V.; Almeida Filho, R.; Roberts, D.A.; Smith, M.O.; Gillespie, A.R. Classification of Multispectral Images Based on Fractions of Endmembers: Application to Land-Cover Change in the Brazilian Amazon. Remote Sens. Environ. 1995, 52, 137–154. [Google Scholar] [CrossRef]
- Shimabukuro, Y.E.; Smith, J.A. The Least-Squares Mixing Models to Generate Fraction Images Derived from Remote Sensing Multispectral Data. IEEE Trans. Geosci. Remote Sens. 1991, 29, 16–20. [Google Scholar] [CrossRef]
- Ponzoni, F.J.; Shimabukuro, Y.E.; Kuplich, T.M. (Eds.) Sensoriamento Remoto No Estudo Da Vegetação, 2nd ed.; Oficina de Textos: São Paulo, Brazil, 2012; ISBN 978-85-7975-053-3. [Google Scholar]
- Somers, B.; Asner, G.P.; Tits, L.; Coppin, P. Endmember Variability in Spectral Mixture Analysis: A Review. Remote Sens. Environ. 2011, 115, 1603–1616. [Google Scholar] [CrossRef]
- Environment for Visualizing Images: ENVI 5.3; Exelis Visual Solutions Information: Boulder, CO, USA, 2010.
- Green, A.A.; Berman, M.; Switzer, P.; Craig, M.D. A Transformation for Ordering Multispectral Data in Terms of Image Quality with Implications for Noise Removal. IEEE Trans. Geosci. Remote Sens. 1988, 26, 65–74. [Google Scholar] [CrossRef]
- Shimabukuro, Y.E.; Ponzoni, F.J. Mistura Espectral: Modelo Linear e Aplicações; Yosio Edemir Shimabukuro, F.J.P., Ed.; Oficina de Textos: São Paulo, Brasil, 2017; ISBN 978-85-7975-270-4. [Google Scholar]
- NV5. Environment for Visualizing Images; Geospatial ENVI: Broomfield, CO, USA, 2023. [Google Scholar]
- Uptike, T.; Comp, C. Radiometric Use of WorldView-2 Imagery. Available online: https://dg-cms-uploads-production.s3.amazonaws.com/uploads/document/file/104/Radiometric_Use_of_WorldView-2_Imagery.pdf (accessed on 11 May 2022).
- L3HARRIS Linear Spectral Unmixing. Available online: https://www.l3harrisgeospatial.com/docs/linearspectralunmixing.html (accessed on 19 January 2022).
- Nelson, B.W.; Kapos, V.; Adams, J.B.; Oliveira, W.J.; Braun, O.P.G.G. Forest Disturbance by Large Blowdowns in the Brazilian Amazon. Ecology 1994, 75, 853–858. [Google Scholar] [CrossRef]
- Roberts, D.A.; Smith, M.O.; Adams, J.B. Green Vegetation, Nonphotosynthetic Vegetation, and Soils in AVIRIS Data. Remote Sens. Environ. 1993, 44, 255–269. [Google Scholar] [CrossRef]
- Adams, J.B.; Smith, M.O.; Gillespie, A.R. Imaging Spectroscopy: Interpretation Based on Spectral Mixture Analysis. In Remote Geochemical Analysis: Elemental and Mineralogical Composition; Pieters, V.M., Englert, P., Eds.; Cambridge University Press: New York, NY, USA, 1993; pp. 145–166. [Google Scholar]
- Souza, C.M.; Roberts, D.A.; Cochrane, M.A. Combining Spectral and Spatial Information to Map Canopy Damage from Selective Logging and Forest Fires. Remote Sens. Environ. 2005, 98, 329–343. [Google Scholar] [CrossRef]
- Chambers, J.Q.; Asner, G.P.; Morton, D.C.; Anderson, L.O.; Saatchi, S.S.; Espírito-Santo, F.D.B.; Palace, M.; Souza, C. Regional Ecosystem Structure and Function: Ecological Insights from Remote Sensing of Tropical Forests. Trends Ecol. Evol. 2007, 22, 414–423. [Google Scholar] [CrossRef] [PubMed]
- QGIS Development Team. QGIS Geographic Information System; Open Source Geospatial Foundation Project: Beaverton, OR, USA, 2016. [Google Scholar]
- McCullagh, P.; Nelder, J.A. Generalized Linear Models, 2nd ed.; McCullagh, P., Nelder, J.A., Eds.; Taylor & Francis Group: Boca Raton, FL, USA, 1989; ISBN 0-412-31760-5. [Google Scholar]
- Hawkins, D.M. The Problem of Overfitting. J. Chem. Inf. Comput. Sci. 2004, 44, 1–12. [Google Scholar] [CrossRef]
- Murtaugh, P.A. In Defense of P Values. Ecology 2014, 95, 611–617. [Google Scholar] [CrossRef] [PubMed]
- Kullback, S. Information Theory and Statistics; Wiley, Ed.; Dover Publications: New York, NY, USA, 1997; ISBN 0-486-69684-7. [Google Scholar]
- Cameron, A.C.; Windmeijer, F.A.G. An R-Squared Measure of Goodness of Fit for Some Common Nonlinear Regression Models. J. Econom. 1997, 77, 329–342. [Google Scholar] [CrossRef]
- Gotelli, N.J.; Ellinson, A.M. A Primer of Ecological Statistics, 2nd ed.; Sinauer Associates: Sunderland, MA, USA, 2013; ISBN 9781605350646. [Google Scholar]
- Smith, T.J.; McKenna, C.M. A Comparison of Logistic Regression Pseudo R 2 Indices. Mult. Linear Regres. Viewp. 2013, 39, 17–26. [Google Scholar]
- Sheskin, D.J. Handbook of Parametric and Nonparametric Statistical Procedures, 3rd ed.; Chapman and Hall/CRC, Ed.; Chapman and Hall/CRC: New York, NY, USA, 2003; ISBN 9780429186165. [Google Scholar]
- Le Cam, L. The Central Limit Theorem around 1935. Stat. Sci. 1986, 1, 78–91. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2022. [Google Scholar]
- Goel, N.S.; Strebel, D.E.; Thompson, R.L. Inversion of Vegetation Canopy Reflectance Models for Estimating Agronomic Variables. II. Use of Angle Transforms and Error Analysis as Illustrated by Suits’ Model. Remote Sens. Environ. 1984, 14, 77–111. [Google Scholar] [CrossRef]
- Asner, G.P.; Palace, M.; Keller, M.; Pereira, R.; Silva, J.N.M.; Zweede, J.C. Estimating Canopy Structure in an Amazon Forest from Laser Range Finder and IKONOS Satellite Observations. Biotropica 2002, 34, 483–492. [Google Scholar] [CrossRef]
- Theiler, J.; Ziemann, A.; Matteoli, S.; Diani, M. Spectral Variability of Remotely Sensed Target Materials: Causes, Models, and Strategies for Mitigation and Robust Exploitation. IEEE Geosci. Remote Sens. Mag. 2019, 7, 8–30. [Google Scholar] [CrossRef]
- Peterson, C.J.; Ribeiro, G.; Negrón-Juárez, R.; Marra, D.M.; Chambers, J.Q.; Higuchi, N.; Lima, A.; Cannon, J.B. Critical Wind Speeds Suggest Wind Could Be an Important Disturbance Agent in Amazonian Forests. For. Int. J. For. Res. 2019, 92, 444–459. [Google Scholar] [CrossRef]
- Ribeiro, G.H.P.M.; Chambers, J.Q.; Peterson, C.J.; Trumbore, S.E.; Magnabosco Marra, D.; Wirth, C.; Cannon, J.B.; Négron-Juárez, R.I.; Lima, A.J.N.; de Paula, E.V.C.M.; et al. Mechanical Vulnerability and Resistance to Snapping and Uprooting for Central Amazon Tree Species. For. Ecol. Manag. 2016, 380, 1–10. [Google Scholar] [CrossRef]
- Strahler, A.H.; Woodcock, C.E.; Smith, J.A. On the Nature of Models in Remote Sensing. Remote Sens. Environ. 1986, 20, 121–139. [Google Scholar] [CrossRef]
- Dos Santos, L.T.; Marra, D.M.; Trumbore, S.; De Camargo, P.B.; Negrón-Juárez, R.I.; Lima, A.J.N.; Ribeiro, G.H.P.M.; Dos Santos, J.; Higuchi, N. Windthrows Increase Soil Carbon Stocks in a Central Amazon Forest. Biogeosciences 2016, 13, 1299–1308. [Google Scholar] [CrossRef]
- Viljur, M.; Abella, S.R.; Adámek, M.; Alencar, J.B.R.; Barber, N.A.; Beudert, B.; Burkle, L.A.; Cagnolo, L.; Campos, B.R.; Chao, A.; et al. The Effect of Natural Disturbances on Forest Biodiversity: An Ecological Synthesis. Biol. Rev. 2022, 97, 1930–1947. [Google Scholar] [CrossRef] [PubMed]
- Alencar, J.B.R.; da Fonseca, C.R.V.; Marra, D.M.; Baccaro, F.B. Windthrows Promote Higher Diversity of Saproxylic Beetles (Coleoptera: Passalidae) in a Central Amazon Forest. Insect Conserv. Divers. 2022, 15, 1–8. [Google Scholar] [CrossRef]
- Espirito-Santo, F.D.B.; Saatchi, S.; Keller, M. Detecting Tree-Fall Gap Disturbances in Tropical Rain Forests with Airborne Lidar. AGUFM 2017, 2017, B14C-01. [Google Scholar]
- Silvério, D.V.; Brando, P.M.; Bustamante, M.M.C.; Putz, F.E.; Marra, D.M.; Levick, S.R.; Trumbore, S.E. Fire, Fragmentation, and Windstorms: A Recipe for Tropical Forest Degradation. J. Ecol. 2019, 107, 656–667. [Google Scholar] [CrossRef]
- Planet Team. Available online: https://www.planet.com/products/ (accessed on 22 April 2022).
- Dial, G.; Bowen, H.; Gerlach, F.; Grodecki, J.; Oleszczuk, R. IKONOS Satellite, Imagery, and Products. Remote Sens. Environ. 2003, 88, 23–36. [Google Scholar] [CrossRef]
- Toutin, T. Review Article: Geometric Processing of Remote Sensing Images: Models, Algorithms and Methods. Int. J. Remote Sens. 2004, 25, 1893–1924. [Google Scholar] [CrossRef]
- Loveland, T.R.; Dwyer, J.L. Landsat: Building a Strong Future. Remote Sens. Environ. 2012, 122, 22–29. [Google Scholar]
- Storey, J.; Roy, D.P.; Masek, J.; Gascon, F.; Dwyer, J.; Choate, M. A Note on the Temporary Misregistration of Landsat-8 Operational Land Imager (OLI) and Sentinel-2 Multi Spectral Instrument (MSI) Imagery. Remote Sens. Environ. 2016, 186, 121–122. [Google Scholar] [CrossRef]
- Trémas, T.L.; Déchoz, C.; Lacherade, S.; Nosavan, J.; Petrucci, B. Sentinel-2: Presentation of the CAL/VAL Commissioning Phase. Image Signal Process. Remote Sens. XXI 2015, 9643, 94–106. [Google Scholar] [CrossRef]
- DigitalGlobe WorldView 2. Available online: http://www.engesat.com.br/imagem-de-satelite/world-view-2/ (accessed on 28 February 2021).
- Hand, D.J. Statistics: A Very Short Introduction, 1st ed.; Oxford University Press: New York, NY, USA, 2008; ISBN 9780199233564. [Google Scholar]
- Galvão, L.S.; dos Santos, J.R.; Roberts, D.A.; Breunig, F.M.; Toomey, M.; de Moura, Y.M. On Intra-Annual EVI Variability in the Dry Season of Tropical Forest: A Case Study with MODIS and Hyperspectral Data. Remote Sens. Environ. 2011, 115, 2350–2359. [Google Scholar] [CrossRef]
- Clark, M.L.; Roberts, D.A.; Clark, D.B. Hyperspectral Discrimination of Tropical Rain Forest Tree Species at Leaf to Crown Scales. Remote Sens. Environ. 2005, 96, 375–398. [Google Scholar] [CrossRef]
- Muller-Karger, F.E.; Hestir, E.; Ade, C.; Turpie, K.; Roberts, D.A.; Siegel, D.; Miller, R.J.; Humm, D.; Izenberg, N.; Keller, M.; et al. Satellite Sensor Requirements for Monitoring Essential Biodiversity Variables of Coastal Ecosystems. Ecol. Appl. 2018, 28, 749–760. [Google Scholar] [CrossRef]
- Denslow, J. Tropical Rainforest Gaps And Tree Species Diversity. Annu. Rev. Ecol. Syst. 1987, 18, 431–451. [Google Scholar] [CrossRef]
- Vitousek, P.M.; Denslow, J.S. Nitrogen and Phosphorus Availability in Treefall Gaps of a Lowland Tropical Rainforest. J. Ecol. 1986, 74, 1167. [Google Scholar] [CrossRef]
- USGS Landsat Science. Available online: https://landsat.gsfc.nasa.gov/satellites/landsat-8/ (accessed on 4 August 2022).
- European Space Agency. SENTINEL-2 User Handbook. Available online: https://sentinels.copernicus.eu/documents/247904/685211/Sentinel-2_User_Handbook.pdf/8869acdf-fd84-43ec-ae8c-3e80a436a16c?t=1438278087000 (accessed on 22 April 2021).
- European Space Agency. Sentinel 2 Level 2A. Available online: https://sentinel.https//sentinel.esa.int/web/sentinel/user-guides/sentinel-2-msi (accessed on 28 June 2021).
- Martins, V.S.; Novo, E.M.L.M.; Lyapustin, A.; Aragão, L.E.O.C.; Freitas, S.R.; Barbosa, C.C.F. Seasonal and Interannual Assessment of Cloud Cover and Atmospheric Constituents across the Amazon (2000–2015): Insights for Remote Sensing and Climate Analysis. ISPRS J. Photogramm. Remote Sens. 2018, 145, 309–327. [Google Scholar] [CrossRef]
- Williams, D.L.; Goward, S.; Arvidson, T. Landsat: Yesterday, Today, and Tomorrow. Photogramm. Eng. Remote Sens. 2006, 72, 1171–1178. [Google Scholar]
- Norway’s International Climate and Forest Initiative. Available online: https://www.nicfi.no/ (accessed on 22 April 2023).
- Roy, D.P.; Huang, H.; Houborg, R.; Martins, V.S. A Global Analysis of the Temporal Availability of PlanetScope High Spatial Resolution Multi-Spectral Imagery. Remote Sens. Environ. 2021, 264, 112586. [Google Scholar] [CrossRef]


| Model | Residual Deviance | AIC | Syx | RMSE | Sigma | R2KL | Coefficients | |
|---|---|---|---|---|---|---|---|---|
| a (Intercept) | b (Slope) | |||||||
| Landsat 8 | 125.33 | 183.37 | 0.2096 | 0.194 | 2.116 | 0.4342 | 9.08 | 0.9837 |
| Sentinel 2 | 136.51 | 194.55 | 0.2211 | 0.209 | 2.208 | 0.3837 | 11.21 | 0.9719 |
| WorldView 2 | 150.01 | 208.05 | 0.2234 | 0.219 | 2.315 | 0.3237 | 10.61 | 0.9977 |
| Subplot Type | Measure | Min | Max | Median | Q1 | Q3 | Iqr | Mean | SD | SE | CI |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Field | Field | 0.0 | 93.0 | 13.0 | 0.0 | 47.0 | 47.0 | 26.9 | 29.7 | 5.4 | 11.1 |
| Landsat 8 | 10.3 | 80.1 | 16.1 | 12.8 | 29.8 | 17.0 | 26.5 * | 22.5 | 4.1 | 8.4 | |
| Sentinel 2 | 11.4 | 75.0 | 16.3 | 14.0 | 22.8 | 8.8 | 26.5 * | 21.2 | 3.9 | 7.9 | |
| WorldView 2 | 12.6 | 80.8 | 18.0 | 15.4 | 22.3 | 6.9 | 26.5 * | 19.7 | 3.6 | 7.4 | |
| Virtual | Landsat 8 | 11.1 | 81.1 | 17.6 | 15.0 | 43.7 | 28.7 | 30.2 | 22.1 | 2.2 | 4.4 |
| Sentinel 2 | 11.7 | 80.2 | 19.5 | 16.2 | 40.9 | 24.7 | 30.3 | 19.5 | 1.9 | 3.9 | |
| WorldView 2 | 13.1 | 92.0 | 21.2 | 16.8 | 32.2 | 15.4 | 27.4 | 16.1 | 1.6 | 3.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Emmert, L.; Negrón-Juárez, R.I.; Chambers, J.Q.; Santos, J.d.; Lima, A.J.N.; Trumbore, S.; Marra, D.M. Sensitivity of Optical Satellites to Estimate Windthrow Tree-Mortality in a Central Amazon Forest. Remote Sens. 2023, 15, 4027. https://doi.org/10.3390/rs15164027
Emmert L, Negrón-Juárez RI, Chambers JQ, Santos Jd, Lima AJN, Trumbore S, Marra DM. Sensitivity of Optical Satellites to Estimate Windthrow Tree-Mortality in a Central Amazon Forest. Remote Sensing. 2023; 15(16):4027. https://doi.org/10.3390/rs15164027
Chicago/Turabian StyleEmmert, Luciano, Robinson Isaac Negrón-Juárez, Jeffrey Quintin Chambers, Joaquim dos Santos, Adriano José Nogueira Lima, Susan Trumbore, and Daniel Magnabosco Marra. 2023. "Sensitivity of Optical Satellites to Estimate Windthrow Tree-Mortality in a Central Amazon Forest" Remote Sensing 15, no. 16: 4027. https://doi.org/10.3390/rs15164027
APA StyleEmmert, L., Negrón-Juárez, R. I., Chambers, J. Q., Santos, J. d., Lima, A. J. N., Trumbore, S., & Marra, D. M. (2023). Sensitivity of Optical Satellites to Estimate Windthrow Tree-Mortality in a Central Amazon Forest. Remote Sensing, 15(16), 4027. https://doi.org/10.3390/rs15164027







