Abstract
This paper proposes an improved multi-frame coherent integration algorithm to improve the detection performance of weak targets in heterogeneous radar. In the detection of weak targets, integration within a single frame may fail to provide sufficient signal-to-noise ratio (SNR) gain. In this case, multi-frame coherent integration is an effective solution. However, radar parameters may be different across frames (i.e., heterogeneous radar) in some practical situations, leading to a mismatch of Doppler frequencies and the fixed phases, which poses difficulties to multi-frame coherent integration. To calibrate the ranges and Doppler frequencies of heterogenous multi-frame echoes, this paper firstly employs an improved Keystone Transform (KT). Compared to conventional KT, the improved KT aligns inter-frame carrier frequencies by applying varying degrees of slow-time rescaling based on the carrier frequencies of each frame, and aligns inter-frame Pulse Repetition Frequencies (PRF) through a unified global slow-time resampling. Secondly, this paper derives the explicit expressions of the fixed-phase terms and adopts a method based on fractional range bins, thus achieving explicit compensation for mismatched phases. Finally, heterogenous multi-frame coherent integration is achieved through slow-time fast Fourier transform. The effectiveness of the proposed algorithm is validated by simulation analyses. Compared to existing entropy-based methods, the proposed algorithm demonstrates higher robustness and lower computational complexity, making it more effective in detecting weak targets under low SNR conditions.
1. Introduction
The detection of weak targets is challenging in the radar field and has received much attention from researchers. Multi-frame coherent integration has become an effective approach to improve the detection probability of weak targets [1,2,3,4,5,6,7] (the term “frame” refers to the radar echo within a single coherent processing interval). The existing studies typically assume that the radar operates with constant working parameters throughout the integration but seldom consider that the working parameters differ across frames. However, the latter case aligns more closely with some practical scenarios and thus has potential research value. For example, phased array radars can dynamically adjust their working parameters across beams while scanning, enabling them to meet different target detection requirements in varying azimuths. When there are targets in the overlapping region of multiple beams, echoes from these targets will be captured in frames with different working parameters, as illustrated in Figure 1. Such a situation provides an opportunity to improve the detection performance of these targets through multi-frame coherent integration. For convenience, this paper uses the term “heterogeneous” to refer to the inter-frame variations in radar working parameters, where the working parameters include carrier frequency, bandwidth, pulse width, PRF and amplitude, etc.
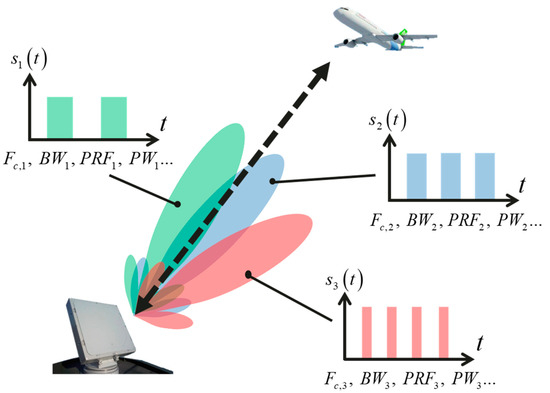
Figure 1.
An example of heterogeneous echoes. During a scanning task, a phased array radar sequentially generates transmission beams of linear frequency modulation pulses with varying working parameters in three azimuths. If a target appears in the overlapping region of these three beams, its echoes will be detected in multiple frames with distinct working parameters, thereby exhibiting heterogeneity. , , , and represent carrier frequency, bandwidth, pulse repetition frequency, and pulse width, respectively.
Assuming that the relative motion state of the target remains constant in the integration process, target motion may cause “range migration”, which refers to the variation in range to the target and can result in a loss of output SNR gain. Keystone transform (KT), with advantages such as not requiring knowledge of the target velocity and being insensitive to noise, is an effective method for range migration correction and has been widely used in long-time coherent integration [1,8,9,10,11,12,13]. For general cases, the target’s Doppler frequency remains constant. However, when considering the heterogeneity, it is necessary to further consider the Doppler shift and fixed-phase mismatches caused by inter-frame variations in carrier frequency and PRF, which will lead to difficulties for coherent integration. To align the inter-frame Doppler, references [14] calibrated inter-frame carrier frequency differences using the KT. References [13,15,16,17,18] discuss the coherent integration algorithms for multi-PRF radar, where [13] employs a unified global resampling-KT to eliminate the effects of non-uniform slow-time sampling. However, none of these references simultaneously consider both carrier frequency and PRF factors that would lead to Doppler shift. Reference [19] used an improved KT to calibrate carrier frequency and PRF differences between multiple sources during multi-band mutual-coherence processing, thereby correcting the Doppler shift. Though this method has a high reference value, the algorithm’s variable selection criteria given by this paper may cause aliasing in the Doppler spectrum, and other non-coherent phases besides the Doppler phase were not discussed in detail.
Early literature in the field of multi-band fusion [20] classified non-coherent phases between multi-band signals as linear phase and fixed phase, according to whether they are correlated with slow time. This classification can be applied to inter-frame non-coherent phases in the heterogeneous signal model discussed in this paper. The linear phase can be compensated by the improved KT. Existing studies on compensating fixed phases mainly include correlation-based methods [21,22,23], Prony model-based methods [20,24,25,26,27,28] and entropy-based methods [14,29,30,31,32]. The correlation-based methods and Prony model-based methods are sensitive to noise [29]. The entropy-based methods exhibit stronger robustness compared to these two categories of methods and are currently popular. They can compensate for fixed-phase mismatches caused by signal heterogeneity without the need to know the signal parameters. However, they require traverse search, and thus suffer from a drawback of high computational complexity, especially when the number of fixed phases increases. In practical applications, it is feasible to construct a prior information database of heterogeneous signal parameters. Thus, the explicit expressions of heterogeneity-caused fixed-phase terms can be derived, making explicit compensation possible. This paper proposes such a method and demonstrates its better robustness and lower computational complexity compared to existing entropy-based methods.
To overcome the difficulty of multi-frame coherent integration in heterogeneous echo, this paper first applies an improved KT [19] and provides a more reasonable criterion for selecting algorithm variables, thereby achieving correction of range migration and Doppler shift. Subsequently, the explicit expressions of the mismatched fixed-phase terms are derived and a method based on fractional range bins is adopted, thus achieving explicit compensation. Finally, multi-frame coherent integration is achieved through a slow-time Fourier transform. Simulation results indicate that compared to single-frame coherent integration, the method proposed in this paper effectively improves the output SNR and Doppler resolution of a point scatterer in heterogeneous echoes, and it exhibits stronger robustness and lower computational complexity compared to entropy-based methods under low input SNR conditions.
The rest of this paper is organized as follows. Section 2.1 presents the echo form of heterogeneous radar systems and analyzes the work needed to achieve coherent integration. Section 2.2 introduces the improved KT (including Doppler ambiguity correction). Section 2.3 points out two mismatched fixed-phase terms caused by heterogeneity and provides compensation methods separately. After these procedures, echoes can be considered inter-frame coherent within acceptable error bounds, and multi-frame coherent integration can be achieved by performing slow-time fast Fourier transform (FFT). Section 2.4 gives a criterion for selecting aligned carrier frequency and PRF as algorithm variables in the improved KT. In Section 2.5, the algorithm is summarized and the algorithm flowchart is given. Finally, in Section 3, the effectiveness of the proposed method is verified through simulation analyses.
2. Materials and Methods
2.1. Heterogeneous Signal Model
The radar echoes in the considered heterogeneous signal model are composed of N frames with different working parameters (carrier frequency, bandwidth, pulse width, PRF, amplitude, etc.). Let be the pulse waveform transmitted by the radar in the frame, where denotes the carrier frequency, and denotes the baseband signal with a bandwidth of , such as a linear-frequency-modulated waveform. Let be the range from the target at slow time , which is called the reference range. Assuming there is a point scatter that moves uniformly along the radar’s line-of-sight at a velocity of , the pulse will be received by the radar after a delay of and then demodulated to baseband, which can be expressed as
where denotes the slow-time timestamp of the pulse, denotes the total number of pulses within a frame, denotes the slow-time timestamp of the first pulse, and denotes the pulse-repetition interval. The noise is assumed to be Gaussian white noise and has not been explicitly incorporated into the formula derivation to maintain the conciseness of this paper.
To achieve range compression through matched filtering, the transfer function of the frame’s matched filter is given by
where denotes the fast-time frequency, denotes fast-time FFT, and the overline denotes the complex conjugate operation.
After range compression, the matched–filtered output in the frequency domain can be expressed as
Note that the initial phase information of the frame carried by has been eliminated in because each frame’s matched filter is uniquely constructed based on its respective reference signal . Without loss of generality, is assumed to be flat within the bandwidth ; therefore, it can be represented by a rectangular window in the frequency domain. After the inverse Fourier transform, the matched–filtered output in the time domain can be represented using a sinc function:
where amplitude factors do not need to be considered because the proposed method does not require inter-frame amplitude alignment.
Target motion causes the signal energy to migrate along the range. When this migration exceeds one range bin, it leads to smearing of the target Doppler signature in both range and Doppler domains, thereby declining the radar’s detection performance. In this case, motion compensation processing becomes crucial.
Moreover, the unambiguous Doppler interval of the frame is . If the target’s Doppler frequency exceeds this interval, it will result in Doppler ambiguity. Let be the target’s actual Doppler frequency within the frame. Then, the slow-time sampled Doppler frequency and the Doppler ambiguity number can be expressed as
The above equation indicates that heterogeneity can lead to distinct Doppler frequencies across frames for the same target, which poses challenges to multi-frame coherent integration. As a result, aligning the Doppler frequency across multiple frames becomes imperative.
2.2. Improved Keystone Transform
Considering that the improved KT operates in the fast-time frequency domain, the simplified form of matched–filtered output in the frequency domain is given by
There is a coupling with the fast-time frequency in the slow-time term , which causes range migration. Therefore, it is necessary to uncouple fast-time frequency and slow time. Moreover, the inter-frame differences between the carrier frequency and PRF in the slow-time term need to be eliminated in order to achieve Doppler alignment.
Considering the Doppler ambiguity, it is necessary to use the slow-time sampled Doppler frequency instead of the actual Doppler frequency when transforming the slow-time term from the discrete slow-time form to the continuous slow-time form. That is,
where a phase is added to ensure that the phase remains consistent before and after the transformation.
To align the Doppler frequencies across frames, the carrier frequency and PRF of each frame need to be aligned using the improved KT. For this purpose, a new slow-time variable is defined to rescale the slow-time axis as a function of the fast-time frequency according to the following equation:
where denotes the aligned carrier frequency.
Furthermore, in order to eliminate the inter-frame differences between PRF, the new discrete slow-time variable is defined as , where is the aligned PRF. The discrete form of the improved KT is given by
For a better understanding, the improved KT achieves carrier frequency alignment by applying slow-time scaling to the spectrum obtained from the conventional KT (given by and [33]), where a scaling factor of is employed for the frame, then achieves PRF alignment by a unified global slow-time resampling. Figure 2 provides an example to illustrate the above statement. By comparing Figure 2c with Figure 2b, it can be observed that the improved KT compresses the spectrums of frames with lower carrier frequencies along the slow time, while expands the spectrums of frames with higher carrier frequencies (as indicated by the red arrows in Figure 2c), thus achieving carrier-frequency alignment.
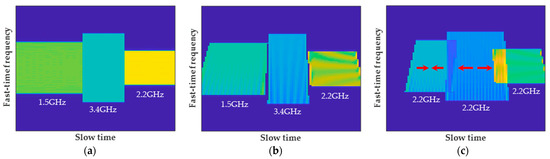
Figure 2.
An example of the fast-time frequency and slow-time spectrums before and after conventional KT or improved KT. The heterogeneous signal consists of 3 frames with carrier frequencies of 1.5 GHz, 3.4 GHz and 2.2 GHz, respectively. (a) The raw spectrum. (b) The spectrum after conventional KT which kept the carrier frequencies unchanged. (c) The spectrum after improved KT which aligned the carrier frequencies of each frame to 2.2 GHz.
The rescaling shown in Equation (9) will remove the fast–slow time coupling in the first slow-time phase term, but the coupling in the second phase term is left due to the Doppler ambiguity:
where corresponds to the slow-time rescaling transformation of Equation (9).
Therefore, using the new discrete slow-time variable , the Doppler ambiguity can be corrected by multiplying with
For heterogeneous signals, a single target may have multiple Doppler ambiguity numbers corresponding to multiple frames. Considering that the Doppler ambiguity numbers for a target are usually unknown in practical scenarios, they can be estimated by forming the corrected range–Doppler spectrum using several different combinations and choosing the one that produces the highest-amplitude peaks. Note that to avoid unnecessary computations, it only needs to try those potential combinations of ambiguity numbers as determined by radar parameters. That is, for an interested velocity bound , only those combinations of Doppler ambiguity numbers that satisfy the following equation need to be considered:
After the improved KT, the slow-time phase term is completely uncoupled from fast time, and the inter-frame Doppler shift is eliminated. The processed slow-time phase term can be expressed in discrete and continuous slow time as
2.3. Fixed-Phase Compensation
After the improved KT, the range–frequency and slow-time spectrum become
where contains a fixed phase that is related to Doppler ambiguity variation and non-uniform slow-time sampling (for simplicity, fixed phase A), and contains a fixed phase that is related to carrier frequency differences and reference range (for simplicity, fixed phase B). To achieve inter-frame coherence, this section will focus on the compensation methods for both fixed phases.
By setting to transform the continuous slow-time form shown in Equation (8) to the discrete slow-time form, we have
By equating the two expressions for shown in Equations (7) and (17), the explicit expression of the fixed phase A can be obtained.
The fixed phase A needs to be compensated by multiplying by
Due to the periodicity of slow-time sampling within the frame, the variable in Equation (19) can be replaced with .
After compensating for the fixed phase A, the signal can be expressed as
By applying an inverse FFT to range frequency, the fast-time and slow-time signal can be expressed as
Considering the fast-time sampling, the signal can be rewritten in terms of range bins and slow-time form.
where represents the fast-time sampling interval, corresponds to the reference range bin, and denotes the fixed phase B.
Since is unknown, it is not feasible to directly compensate for the fixed phase B, so a compensation in the form of can be performed along the slow time for each range bin instead. As may not be an integer, the range bin variable can be selected based on subdivided range bins, which are known as fractional range bins, to minimize compensation errors. The fractional range bins are defined based on a denominator factor , which means dividing an integer range bin into segments:
The signal value on a fractional range bin is defined as the signal value of the closest integer range bin:
Phase compensation is performed on the fractional range bins and slow-time signal:
The slow-time signal on the fractional range bin closest to exhibits the strongest coherence after the phase compensation. Thus, the range–Doppler spectrum obtained by performing a slow-time FFT on Equation (25) will exhibit a dominant peak at this fractional range bin. This fractional range bin is called the detection range bin , and it is given by . Then, the compensated slow-time signal on the detection range bin is
where is the residual phase term, and the maximum phase difference it may lead to between two frames is
As indicated by Equation (27), compared to the compensation based on integer range bins (when ), the compensation based on fractional range bins can reduce the residual phase by a factor of . Referring to Equation (27) and considering the practical system parameters to select an appropriate value for , the impact of the residual phase will be mitigated within an acceptable range at the cost of increased computational effort.
The diagram of compensating fixed phase B based on fractional range bins is shown in Figure 3a. Using the compensation method described in Equation (25), the phase coherence of the slow-time signal is approximately satisfied on the detection range bin, without prior knowledge of the target. However, the slow-time signals on other range bins exhibit non-coherence. This will cause multiple strong sidelobes in the range–Doppler spectrum, as shown in Figure 3b, thus increasing the false-alarm probability in the detection test.
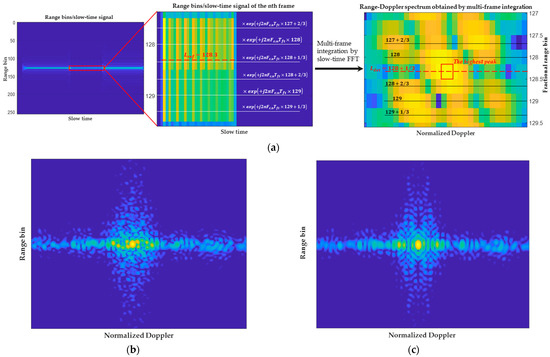
Figure 3.
The diagram and typical results of compensating fixed phase B based on fractional range bins. (a) The diagram of compensating fixed phase B using compensation term described in Equation (25). In this example, it is assumed that the target’s reference range bin is 128.3. Choosing the denominator factor , the strongest peak in multi-frame integrated result appears at the fractional range bin 128 + 1/3, which is called the detection range bin and serves as an estimation for . (b) The typical output of a point scatterer in the range–Doppler spectrum obtained with Equation (25). (c) The typical output of a point scatterer in the range–Doppler spectrum obtained with Equation (29).
Therefore, the range–Doppler spectrum shown in Figure 3b will not be directly used for detection. Instead, this spectrum is adopted to determine the detection range bin according to the range bin of the highest-amplitude peak. Then, the detection range bin is considered an estimate for the reference range bin to compensate for fixed phase B according to
The range–Doppler spectrum can be obtained through slow-time FFT on Equation (29). The dominant peak of the point target will appear at , and its shape is illustrated in Figure 3c, showing fewer and lower sidelobes compared with the result in Figure 3b.
Figure 4 provides an example of intermediate results of the fixed-phase compensations. Figure 4a,b demonstrate the phase variations along slow time with only compensating fixed phase A or B, respectively, revealing discontinuities in the slow-time phase across frames. Figure 4c demonstrates the phase variation after compensating both fixed phases A and B, and the inter-frame phase can be regarded as continuous within acceptable error bounds. Figure 4d compares the Doppler profiles of the range–Doppler spectrums obtained under different compensation conditions, indicating that non-coherent integration will lead to a loss in the SNR gain of the main lobe when not compensating both fixed phases simultaneously. This emphasizes the rationality and importance of fixed-phase compensation.
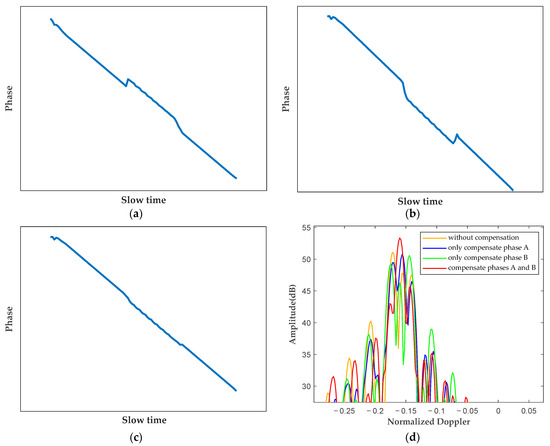
Figure 4.
An example of intermediate results of the compensations of fixed phases A and B. The heterogeneous signal consists of 3 frames. (a) The phase variation along slow time when only compensating fixed phase A. (b) The phase variation along slow time when only compensating fixed phase B. (c) The phase variation along slow time when compensating both fixed phases A and B. (d) The Doppler profiles of the range–Doppler spectrums obtained under four different compensation conditions.
2.4. Variable Selection Criteria
This section will focus on the selection criteria of input variables and in the improved KT. Although these variables may be chosen arbitrarily without causing errors, in reality, improper selection can cause the risk of Doppler spectrum aliasing. Thus, it is crucial to follow specific selection criteria to prevent this risk. The discrete form of the slow-time rescaling in Equation (11) can be rewritten as
It can be seen that, compared to the regular KT, the improved KT can be regarded as a slow-time resampling of the regular method’s output. In this resampling, the original frequency is , and the resampling frequency is .
The criterion outlined in reference [19] suggests selecting these variables based on the carrier frequency and PRF of a reference source with the largest PRF. However, the study failed to consider that if this reference source also has a high carrier frequency, it may lead to undersampling of slow time, resulting in Doppler spectrum aliasing.
Therefore, to avoid information loss, the selection of and should satisfy
Note that an excessively high sampling rate does not necessarily provide additional information. Therefore, this paper provides a selection criterion as
which minimizes computational complexity while avoiding the Doppler spectrum aliasing problem.
2.5. Algorithm Summary
The flowchart of the proposed algorithm is shown in Figure 5.
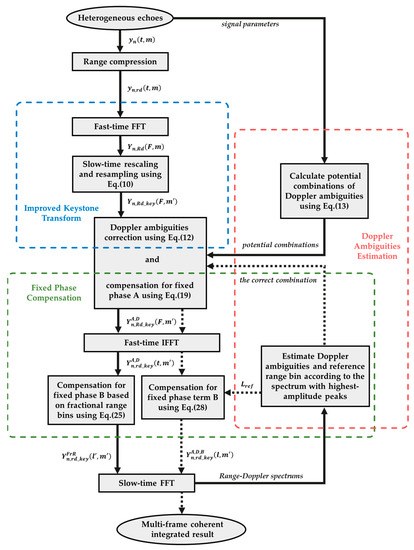
Figure 5.
The flowchart of the improved multi-frame coherent integration algorithm. The solid arrows represent the steps before the Doppler ambiguity estimation, while the dashed arrows represent the steps after the Doppler ambiguity estimation. Therefore, the latter steps need to be performed after the former steps. In the end, the desired multi-frame coherent integrated result is the range–Doppler spectrum obtained from the dashed arrows.
As shown in Figure 5, the proposed algorithm mainly consists of three modules: Improved Keystone Transform, Fixed-Phase Compensation, and Doppler-Ambiguity Estimation. The Improved Keystone Transform includes slow-time rescaling and Doppler-ambiguity correction. The Fixed-Phase Compensation includes the estimation of reference range and compensation for fixed phases A and B. Estimation of the reference range in the Fixed-Phase Compensation has been combined with the Doppler-Ambiguity Estimation to simplify the algorithm. That is, among the range–Doppler spectrums with potential Doppler ambiguity combinations, the correct combination is determined based on the one with the highest-amplitude peak, while the reference distance is estimated according to the range bin of this peak.
In heterogeneous radar systems, under the assumption of knowing the carrier frequency, PRF, and slow-time timestamp of each frame, the proposed algorithm can coherently integrate multiple frames of a point scatterer with an unknown velocity.
3. Simulation Results
In the simulation of heterogeneous signals, five frames of LFM signals are generated with the parameters listed in Table 1. It is assumed that a target moves at a constant velocity of 200 m/s along the radar’s line of sight, and the reference range bin is 128.7. There are different time intervals between the five frames, and the total number of pulses is 54.

Table 1.
The parameters of heterogeneous frames.
Figure 6 presents the range-compressed output, with the vertical axis and the horizontal axis representing the range bin and the pulse number, respectively. From this figure, it is evident that range migration occurs. Meanwhile, the inter-frame PRF differences result in inconsistent pulse-to-pulse range migration across frames. Furthermore, due to bandwidth differences, the number of range bins occupied by the target varies in different frames.
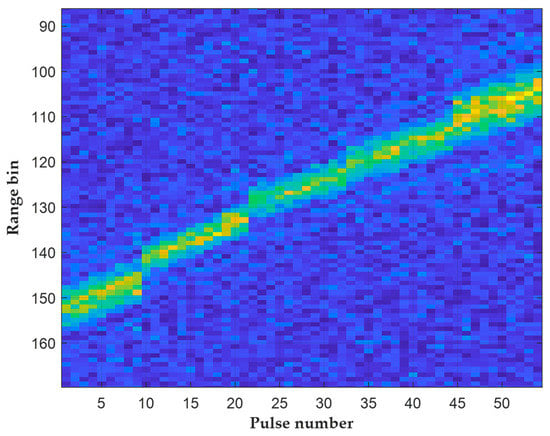
Figure 6.
The range-compressed output of heterogeneous echoes.
Figure 7 presents the range–Doppler spectrum obtained by the conventional KT on the original signal. This approach satisfies intra-frame coherence, but it fails to satisfy inter-frame coherence. Due to heterogeneity, the Doppler frequency of each frame is inconsistent, causing the spread of echo energy in the Doppler domain. This leads to a loss of output SNR and Doppler resolution in range, as shown in Figure 7.
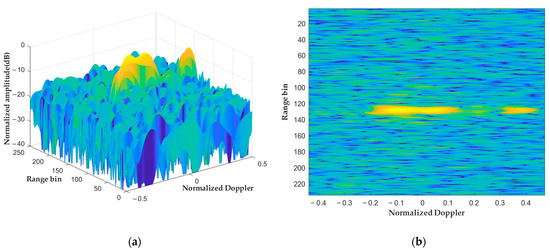
Figure 7.
The range–Doppler spectrum obtained by multi-frame non-coherent integration based on conventional KT. (a) The amplitude of the range–Doppler spectrum in dB scale. (b) The projection of figure (a).
Figure 8 illustrates the range bin and the slow-time spectrum obtained by applying the improved KT to the range-compressed signal. It can be seen that the proposed method successfully corrects the range migration across five frames.
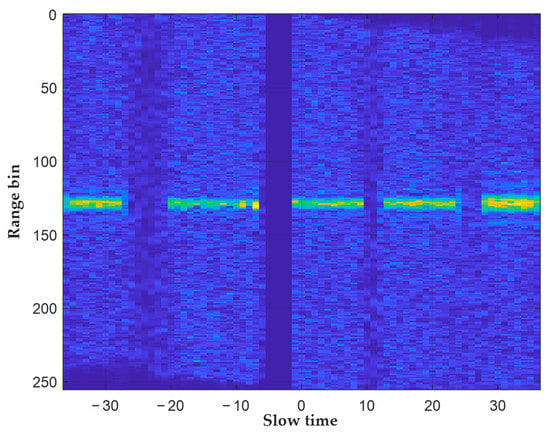
Figure 8.
The range bin and the slow-time spectrum obtained by the improved KT.
The range-migration-corrected signal is compensated for the fixed-phase terms and processed with a slow-time FFT to be integrated coherently across frames, resulting in the range–Doppler spectrum, as shown in Figure 9. By applying the proposed method, the echo energy from five frames is aligned to the same position in the range–Doppler spectrum, thereby generating a dominant peak with a higher resolution and output SNR.
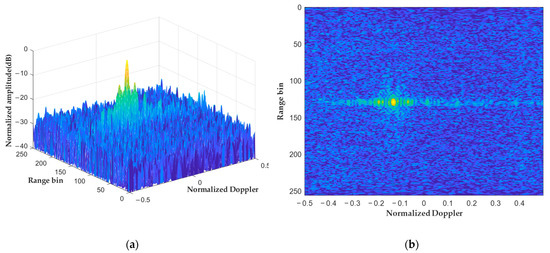
Figure 9.
The range–Doppler spectrum obtained from multi-frame coherent integration using the proposed algorithm. (a) The amplitude of the range–Doppler spectrum in dB scale. (b) The projection of figure (a).
To demonstrate the effectiveness of the proposed method more intuitively, Figure 10 and Figure 11, respectively, compare the Doppler profiles and range profiles of the dominant peaks in the range–Doppler spectrum obtained from three methods:
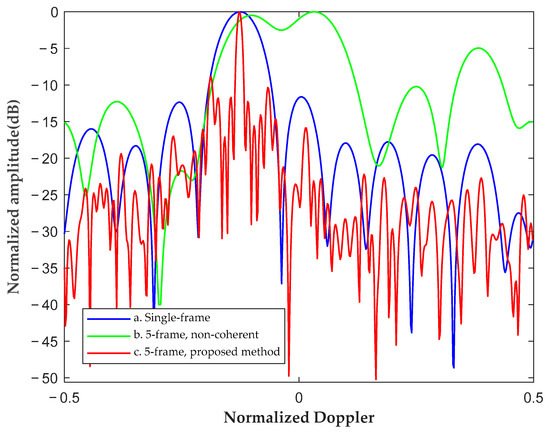
Figure 10.
Doppler profile comparison of the range–Doppler spectrums obtained from the conventional method and the proposed method.
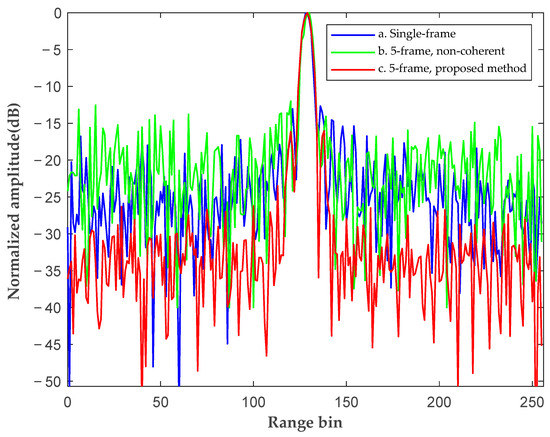
Figure 11.
Range profile comparison of the range–Doppler spectrums obtained from the conventional method and the proposed method.
- Single-frame coherent integration method based on conventional KT (parameters of the single frame are shown in Table 1 as the third frame);
- The intra-frame coherent and inter-frame non-coherent integration method based on conventional KT (parameters of five frames listed in Table 1, the same below);
- Multi-frame coherent integration using the proposed method.
The Doppler axis of the result obtained by Method a has already been calibrated with Method c for better comparison. As shown in Figure 10, the inter-frame Doppler shift caused by heterogeneity leads to poor Doppler resolution in the result obtained by the conventional method, even worse than the result obtained by single-frame integration. The proposed method achieves a higher Doppler resolution than the other two methods by aligning Doppler shift. Additionally, as shown in Figure 10 and Figure 11, it achieves higher output SNR than the other two methods. As a result, the proposed method is able to enhance the radar system’s target-detection probability and velocity-estimation accuracy.
To demonstrate the improvement in output SNR achieved by the proposed algorithm and compare the performance of the proposed fixed-phase compensation approach with that of the existing approach, the following four sets of simulation analyses were conducted:
- Single-frame coherent integration based on the conventional KT (the parameters of the single frame are shown in Table 1 as the third frame);
- Five-frame non-coherent integration based on the improved KT, without fixed-phase compensation (the parameters of the five frames are shown in Table 1, the same below);
- Five-frame coherent integration based on the improved KT, with the fixed-phase compensation method based on the minimum image entropy [14];
- Five-frame coherent integration using the proposed method.
Since entropy-based methods are popular in phase estimation, this paper selected a representative method from this category for comparison. Under different input SNR (calculated after range compression) conditions, Monte Carlo analyses were conducted to test the output SNR and detection probability of the integration results obtained by the above four methods. The results are presented in Figure 12.
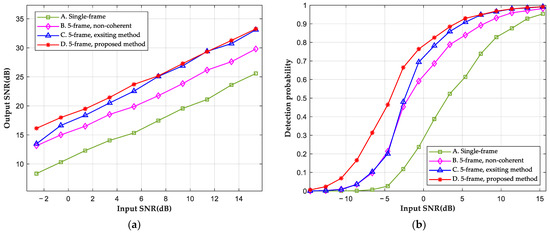
Figure 12.
The comparison of the detection performance of four methods. (a) Input SNR and output SNR curve. (b) Input SNR and detection probability curve, obtained from the cell-averaging constant false-alarm rate (CA-CFAR) thresholding with a false-alarm rate of 10−6.
By comparing the curves of Method A and Method D in Figure 12a, it can be seen that compared to single-frame coherent integration, five-frame coherent integration improves the output SNR greatly, with an SNR gain close to the theoretical gain of 7 dB. Figure 12 shows that the proposed method (Method D) achieves a similar output SNR to the minimum image entropy-based method (Method C) at a higher input SNR. This indicates that the proposed method yields results with the minimum entropy, further validating the algorithm’s coherence. At a lower input SNR (below 8dB), the estimation accuracy of Method C decreases, and its detection probability gradually approaches non-coherent results (Method B). Ultimately, Method B fails to perform effectively under low input SNR conditions (below −2 dB). However, the proposed method exhibits robustness under similar low SNR conditions, with a higher output SNR of approximately 3 dB compared to Method B. This is because entropy-based methods rely on the criterion that lower image entropies indicate sharper images, and when the image has the smallest entropy, it implies inter-frame phase alignment. This criterion works under high SNR conditions. However, taking into account that entropy is obtained through non-linear computations and is sensitive to overall noise, this criterion becomes less effective in indicating phase coherence under lower SNR conditions. In contrast, the proposed method explicitly compensates for fixed phase A, which remains unaffected by noise. Moreover, the compensation for fixed phase B is based on the maximum integrated amplitude, which is obtained through linear computations and is insensitive to noise. Thus, the proposed method is more robust than the entropy-based methods under lower SNR conditions.
Also, it is worth noting that entropy-based methods like Method C usually require traverse search, resulting in significantly increased computational complexity in the multi-frame model where multiple phases need to be compensated. Moreover, obtaining a more coherent result also demands larger computation. In contrast, the proposed method does not require traverse search, so its computational complexity is almost independent of the number of frames and the algorithm accuracy, making it more computationally efficient.
It should be noted that these advantages of the proposed method are related to its requirement for prior knowledge about signal parameters (carrier frequency, PRF, and slow-time timestamp of each frame).
4. Discussion
Several potential limitations or challenges in our work need to be indicated. Firstly, the proposed algorithm is designed for single-target detection. Considering practical scenarios, there may exist multiple targets with different Doppler ambiguities. However, the KT’s global rescaling operation is based on a specific Doppler ambiguity, so it poses a challenge when applying KT-based algorithms to handle multi-target detection. A potential solution is to adopt the CLEAN technique. In this technique, the strongest target is detected in a single-target detection and then removed from the scene. Subsequently, the next strongest target is detected and removed, and this process is iteratively repeated. The CLEAN technique can be combined with the proposed method to address the multi-target detection problem. Furthermore, the proposed method is based on a simple hypothesis that the target undergoes uniform motion during the observation time. This hypothesis is actually not strictly required, and in practical applications, certain levels of acceleration or higher-order motion can be tolerated. However, considering longer observation time or stronger target maneuverability, the Doppler shift caused by target motion becomes more severe and should not be ignored, which will result in loss of SNR gain. So, expanding the proposed algorithm to handle high-maneuvering target detection becomes one of our research interests.
Given the fast and flexible parameter adjustment capabilities of phased array radars, if the signal conforms to the heterogeneous assumption, the proposed method can be combined to exploit the existing data more effectively without increasing the hardware burden. It can improve the SNR, leading to enhanced detection probabilities of faint targets and extending the maximum detection range. Moreover, this algorithm also enhances the Doppler resolution, which improves the accuracy of velocity measurements. The proposed method has potential applications in vessel and aircraft monitoring. With improved SNR and Doppler resolution, it enhances the radar’s ability to effectively track and locate targets, which facilitates better decision making.
Meanwhile, though this paper focuses on active radars, the proposed method is also applicable to passive radar systems, as long as a prior database about the reference signal parameters is constructed. Considering the common issue of insufficient detection capability in passive radars, the joint utilization of signals from multiple operating modes of non-cooperative sources is a potential solution. This highlights the strong application potential of the proposed method in passive radar systems, such as a naval passive location system and urban drone surveillance system.
5. Conclusions
To improve the detection performance of radar systems for weak targets, a feasible approach is to improve the SNR through multi-frame coherent integration. However, inter-frame heterogeneous radar signals pose challenges to the coherent integration process, such as Doppler frequency and phase mismatches. In this paper, an improved multi-frame coherent integration algorithm is proposed to overcome these difficulties. Specifically, the proposed method applies the improved KT to align the range and Doppler frequencies of heterogeneous frames. Then, the explicit expressions of the mismatched fixed phases are derived and a method based on fractional range bins is adopted, thus achieving explicit compensation for mismatched phases. Finally, multi-frame coherent integration is achieved by using a slow-time Fourier transform.
In the simulation of five-frame integration, the proposed method improves the output SNR by about 7 dB compared to single-frame integration, where the improvement is close to the theoretical value. This result validates the coherence of the proposed method. The proposed method also achieves significant improvement in Doppler resolution compared to single-frame integration. Moreover, the proposed method demonstrates advantages over existing entropy-based multi-frame coherent integration methods. Under the simulated low input SNR conditions, the proposed method achieves an output SNR that is 3 dB higher than the method based on minimum image entropy, while also exhibiting lower computational complexity. Therefore, if carrier frequency, PRF, and the slow-time timestamp of each frame are known, the proposed method has been proven to be a better choice than the existing method.
Author Contributions
Conceptualization, Y.L., Q.D., X.L., X.W. and H.Z.; Investigation, Y.L., Q.D. and X.W.; Software, Y.L.; Writing—original draft preparation, Y.L. and Q.D.; Writing—review and editing, Y.L., Q.D., X.L. and H.Z.; Project administration, X.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data sharing not applicable.
Acknowledgments
The authors would like to thank the staff of the National Key Laboratory of Microwave Imaging Technology, Aerospace Information Research Institute, Chinese Academy of Sciences, for their valuable conversations and comments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Huang, P.; Liao, G.; Yang, Z.; Xia, X.; Ma, J.; Ma, J. Long-Time Coherent Integration for Weak Maneuvering Target Detection and High-Order Motion Parameter Estimation Based on Keystone Transform. IEEE Trans. Signal Process. 2016, 64, 4013–4026. [Google Scholar] [CrossRef]
- Yi, W.; Fang, Z.; Wen, M. An Efficient Coherent Multi-Frame Track-before-Detect Algorithm in Radar Systems. In Proceedings of the 2017 IEEE Radar Conference (RadarConf), Seattle, WA, USA, 8–12 May 2017; pp. 1521–1526. [Google Scholar]
- Huang, R.; Du, X.; Hu, W. Phase Compensation Based Multi-Frame Coherent Integration for Drone Detection with Radar. In Proceedings of the 2019 IEEE International Conference on Unmanned Systems (ICUS), Beijing, China, 17–19 October 2019; pp. 13–18. [Google Scholar]
- Li, X.; Yang, Y.; Sun, Z.; Cui, G.; Yeo, T.S. Multi-Frame Integration Method for Radar Detection of Weak Moving Target. IEEE Trans. Veh. Technol. 2021, 70, 3609–3624. [Google Scholar] [CrossRef]
- Gao, L.; Li, X.; Wang, M.; Chen, H.; Sun, Z.; Cui, G. Joint Intra-Frame and Inter-Frame Integration Method for High Speed Weak Target Detection. In Proceedings of the 2022 7th International Conference on Signal and Image Processing (ICSIP), Suzhou, China, 20–22 July 2022; pp. 290–294. [Google Scholar]
- Zhan, M.; Zhao, C.; Qin, K.; Huang, P.; Fang, M.; Zhao, C. Subaperture Keystone Transform Matched Filtering Algorithm and Its Application for Air Moving Target Detection in an SBEWR System. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 2262–2274. [Google Scholar] [CrossRef]
- Li, W.; Yi, W.; Teh, K.C. Greedy Integration Based Multi-Frame Detection Algorithm in Radar Systems. IEEE Trans. Veh. Technol. 2023, 72, 5877–5891. [Google Scholar] [CrossRef]
- Zhu, D.; Li, Y.; Zhu, Z. A Keystone Transform Without Interpolation for SAR Ground Moving-Target Imaging. IEEE Geosci. Remote Sensing Lett. 2007, 4, 18–22. [Google Scholar] [CrossRef]
- Perry, R.P.; DiPietro, R.C.; Fante, R.L. Coherent Integration With Range Migration Using Keystone Formatting. In Proceedings of the 2007 IEEE Radar Conference, Waltham, MA, USA, 17–20 April 2007; pp. 863–868. [Google Scholar]
- Li, G.; Xia, X.; Peng, Y. Doppler Keystone Transform: An Approach Suitable for Parallel Implementation of SAR Moving Target Imaging. IEEE Geosci. Remote Sensing Lett. 2008, 5, 573–577. [Google Scholar] [CrossRef]
- Kong, L.; Li, X.; Cui, G.; Yi, W.; Yang, Y. Coherent Integration Algorithm for a Maneuvering Target With High-Order Range Migration. IEEE Trans. Signal Process. 2015, 63, 4474–4486. [Google Scholar] [CrossRef]
- Tian, J.; Cui, W.; Xia, X.; Wu, S. Parameter Estimation of Ground Moving Targets Based on SKT-DLVT Processing. IEEE Trans. Comput. Imaging 2016, 2, 13–26. [Google Scholar] [CrossRef]
- Wang, C.; Jiu, B.; Liu, H. Maneuvering Target Detection in Random Pulse Repetition Interval Radar via Resampling-Keystone Transform. Signal Process. 2021, 181, 107899. [Google Scholar] [CrossRef]
- Hu, P.; Xu, S.; Wu, W.; Chen, Z. Sparse Subband ISAR Imaging Based on Autoregressive Model and Smoothed ℓ0 Algorithm. IEEE Sens. J. 2018, 18, 9315–9323. [Google Scholar] [CrossRef]
- Jia, X.; Xia, X.; Peng, S.; Yu, J.; Peng, Y.; Qian, L. Radar Maneuvering Target Motion Estimation Based on Generalized Radon-Fourier Transform. IEEE Trans. Signal Process. 2012, 60, 6190–6201. [Google Scholar] [CrossRef]
- Tian, J.; Xia, X.; Cui, W.; Yang, G.; Wu, S. A Coherent Integration Method via Radon-NUFrFT for Random PRI Radar. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 2101–2109. [Google Scholar] [CrossRef]
- Wen, M.; Yi, W.; Wang, Y. Track-Before-Detect Strategies for Multiple-PRF Radar System with Range and Doppler Ambiguities. In Proceedings of the 2018 21st International Conference on Information Fusion (FUSION), Cambridge, UK, 10–13 July 2018; pp. 295–301. [Google Scholar]
- Ma, J.; Huang, P.; Yu, J.; Liang, G.; Liao, G.; Sun, S.; Jiang, X. An Efficient Coherent Integration Method for Maneuvering Target Detection With Nonuniform Pulse Sampling Based on Filterbank Framework. IEEE Geosci. Remote Sens. Lett. 2020, 17, 2045–2049. [Google Scholar] [CrossRef]
- Wang, N.; Lv, X.; Li, M.; Liu, Z. P Multi-target Phase Compensation Method for Multi-band Mutual-coherence Processing. Syst. Eng. Electron. 2022, 44, 3083–3089. [Google Scholar] [CrossRef]
- Cuomo, K.M.; Pion, J.E.; Mayhan, J.T. Ultrawide-Band Coherent Processing. IEEE Trans. Antennas Propagat. 1999, 47, 1094–1107. [Google Scholar] [CrossRef]
- Fu, Y.; Zhang, C.; Li, X.; Zhuang, Z. One-Dimensional Super Resolution Multi-Band Radar Fusion Imaging Technology Research. Prog. Nat. Sci. 2006, 16, 1310–1316. [Google Scholar]
- Liu, C.; He, F.; Wei, X.; Gao, X. Research on Multiple Radar Fusion Imaging Coherence Compensation Based on Data Correlation. Syst. Eng. Electron. 2010, 32, 1266–1271. [Google Scholar]
- Tian, J.; Sun, J.; Wang, G.; Wang, Y.; Tan, W. Multiband Radar Signal Coherent Fusion Processing with IAA and ApFFT. IEEE Signal Process. Lett. 2013, 20, 463–466. [Google Scholar]
- Yu, Z.; Chen, Y.; Sun, Z.; Lu, Y. The Super-Resolution Range Imaging Based on Multiband Wideband Signal Fusion. In Proceedings of the 2nd Asian-Pacific Conference on Synthetic Aperture Radar, Xi’an, China, 26–30 October 2009; pp. 160–164. [Google Scholar]
- He, F.; Xu, X. High-Resolution Imaging Based on Coherent Processing for Distributed Multi-Band Radar Data. Prog. Electromagn. Res. 2013, 141, 383–401. [Google Scholar]
- Xu, X.; Li, J. Ultrawide-Band Radar Imagery from Multiple Incoherent Frequency Subband Measurements. J. Syst. Eng. Electron. 2011, 22, 398–404. [Google Scholar]
- Ye, F.; He, F.; Sun, Z. Radar Signal Level Fusion Imaging. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 7–11 July 2008; pp. 1288–1291. [Google Scholar]
- Tian, B.; Chen, Z.; Xu, S. Sparse Subband Fusion Imaging Based on Parameter Estimation of Geometrical Theory of Diffraction Model. IET Radar Sonar Navig. 2014, 8, 318–326. [Google Scholar]
- Zou, Y.; Gao, X.; Li, X. High Precision Coherent Compensation for Multiband Radar Data at Low SNR. Syst. Eng. Electron. 2015, 37, 48–54. [Google Scholar]
- Li, X.; Liu, G.; Ni, J. Autofocusing of ISAR images based on entropy minimization. IEEE Trans. Aerosp. Electron. Syst. 1999, 35, 1240–1252. [Google Scholar] [CrossRef]
- Pardini, M.; Papathanassiou, K.; Bianco, V.; Iodice, A. Phase calibration of multibaseline SAR data based on a minimum entropy criterion. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 5198–5201. [Google Scholar] [CrossRef]
- Fan, H.; Ren, L.; Mao, E.; Liu, Q. A High-Precision Method of Phase-Derived Velocity Measurement and Its Application in Motion Compensation of ISAR Imaging. IEEE Trans. Geosci. Remote Sens. 2018, 56, 60–77. [Google Scholar] [CrossRef]
- Richards, M.A. The Keystone Transformation for Correcting Range Migration in Range-Doppler Processing. Pulse 2014, 1000, 1. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).