Phenology-Based Maximum Light Use Efficiency for Modeling Gross Primary Production across Typical Terrestrial Ecosystems
Abstract
1. Introduction
2. Data and Preprocessing
2.1. FLUXNET Data
2.2. Phenology Camera Data
2.3. MODIS Data
3. Methodology
3.1. Phenology Extraction
3.1.1. Double Logistic Function
3.1.2. Hybrid Generalized Additive Model
3.2. Light Use Efficiency Model
3.2.1. Structure of the LUE Model
3.2.2. The Calculation of Maximum Light Use Efficiency (ε0)
3.2.3. The Calculation of FAPAR
3.3. Evaluation of Phenological Stages and GPP Estimation
4. Results
4.1. SOS and EOS Estimated from Vegetation Indices Based on DLF and HGAM at Flux Sites and Their Validation
4.2. Estimates of the Maximum LUE (ε0) during Phenological Stages
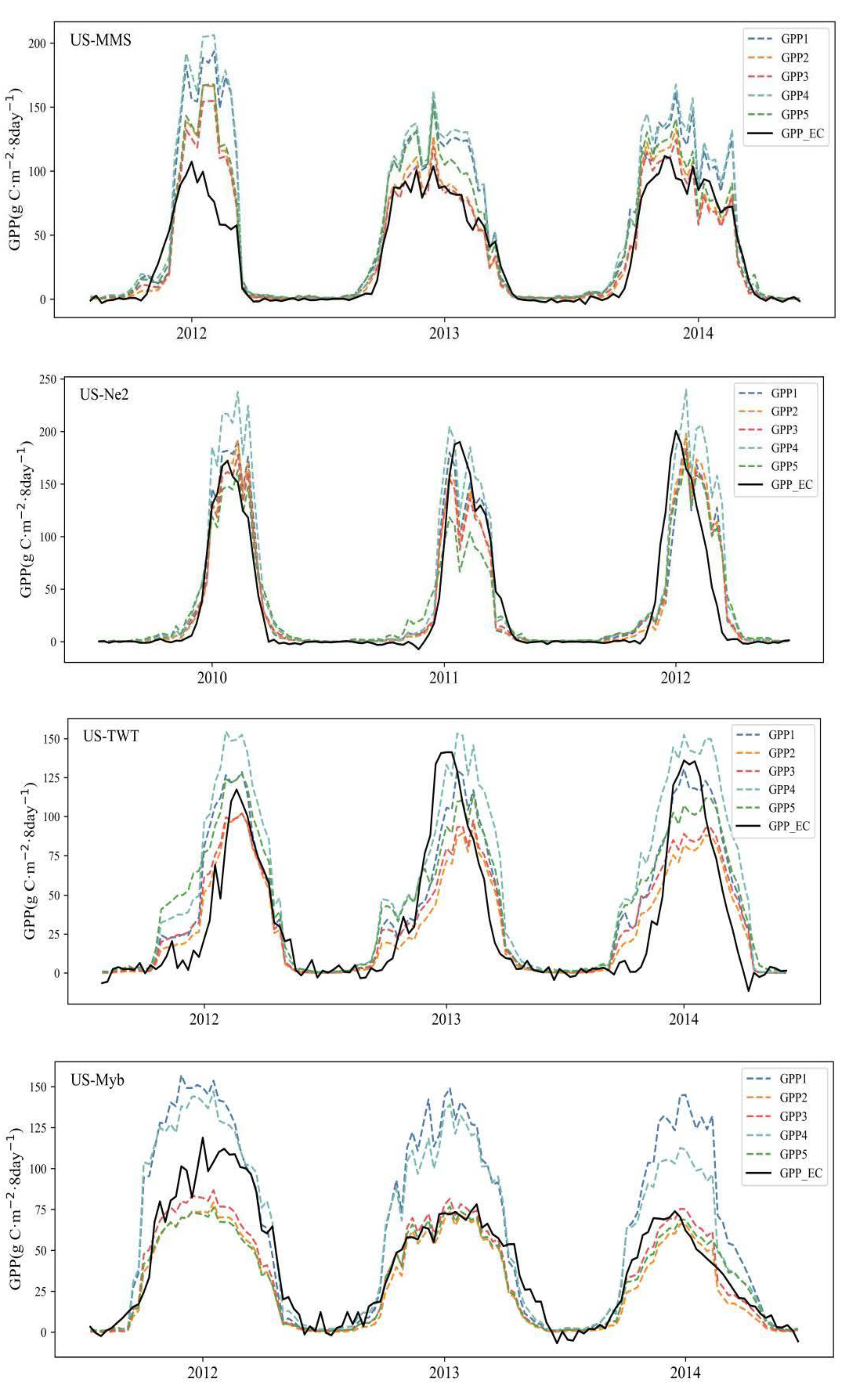
4.3. Comparison of GPP Estimates with Phenology-Regulated ε0 and Different FAPAR Proxies
5. Discussion
5.1. SOS/EOS Estimating Methods of Different PFTs
5.2. Phenology-Based ε0 of Different PFTs
5.3. Phenology-Based Methods in GPP Estimation with LUE Models—Strengths and Limitations
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LUE | light use efficiency |
| VPM | vegetation photosynthesis model |
| GPP | gross primary productivity |
| PFT | plant functional type |
| SOS | start of growing season |
| EOS | end of growing season |
| LOS | length of the growing season |
| HGAM | hybrid generalized additive model |
| DLF | double logistic function |
| EC | eddy covariance |
| ER | ecosystem respiration |
| APAR | absorbed photosynthetically active radiation |
| PAR | photosynthetically active radiation |
| FAPAR | fraction of absorbed photosynthetically active radiation |
| EVI | enhanced vegetation index |
| NDVI | normalized difference vegetation index |
| LAI | leaf area index |
| GCC | green chromatic coordinate |
| LSWI | land surface water index |
| SG | Savitzky–Golay |
| NEE | net ecosystem exchange |
| Re | ecosystem respiration |
| Tscalar | the scalars for the effects of temperature |
| Wscalar | the scalars for the effects of water |
| GEEmax | the maximum rate of ecosystem gross photosynthesis |
References
- Baldocchi, D.; Falge, E.; Gu, L.; Olson, R.; Hollinger, D.; Running, S.; Anthoni, P.; Bernhofer, C.; Davis, K.; Evans, R. FLUXNET: A new tool to study the temporal and spatial variability of ecosystem-scale carbon dioxide, water vapor, and energy flux densities. Bull. Am. Meteorol. Soc. 2001, 82, 2415–2434. [Google Scholar] [CrossRef]
- Pei, Y.; Dong, J.; Zhang, Y.; Yuan, W.; Doughty, R.; Yang, J.; Zhou, D.; Zhang, L.; Xiao, X. Evolution of light use efficiency models: Improvement, uncertainties, and implications. Agric. For. Meteorol. 2022, 317, 108905. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiao, X.; Wu, X.; Zhou, S.; Zhang, G.; Qin, Y.; Dong, J. A global moderate resolution dataset of gross primary production of vegetation for 2000–2016. Sci. Data 2017, 4, 170165. [Google Scholar] [CrossRef]
- Zheng, Y.; Xiao, Z.; Li, J.; Yang, H.; Song, J. Evaluation of Global Fraction of Absorbed Photosynthetically Active Radiation (FAPAR) Products at 500 m Spatial Resolution. Remote Sens. 2022, 14, 3304. [Google Scholar] [CrossRef]
- Veroustraete, F.; Sabbe, H.; Eerens, H. Estimation of carbon mass fluxes over Europe using the C-Fix model and Euroflux data. Remote Sens. Environ. 2002, 83, 376–399. [Google Scholar] [CrossRef]
- Yuan, W.P.; Liu, S.G.; Zhou, G.S.; Zhou, G.Y.; Tieszen, L.L.; Baldocchi, D.; Bernhofer, C.; Gholz, H.; Goldstein, A.H.; Goulden, M.L.; et al. Deriving a light use efficiency model from eddy covariance flux data for predicting daily gross primary production across biomes. Agric. Forest Meteorol. 2007, 143, 189207. [Google Scholar] [CrossRef]
- Running, S.W.; Nemani, R.R.; Heinsch, F.A.; Zhao, M.S.; Reeves, M.; Hashimoto, H. A Continuous Satellite-Derived Measure of Global Terrestrial Primary Production. Bioscience 2004, 54, 547–560. [Google Scholar] [CrossRef]
- Prince, S.D.; Goward, S.N. Global Primary Production: A Remote Sensing Approach. J. Biogeogr. 1995, 22, 815–835. [Google Scholar] [CrossRef]
- He, M.; Ju, W.; Zhou, Y.; Chen, J.; He, H.; Wang, S.; Wang, H.; Guan, D.; Yan, J.; Li, Y.; et al. Development of a two-leaf light use efficiency model for improving the calculation of terrestrial gross primary productivity. Agric. For. Meteorol. 2013, 173, 28–39. [Google Scholar] [CrossRef]
- Xie, Z.; Zhao, C.; Zhu, W.; Zhang, H.; Fu, Y.H. A Radiation-Regulated Dynamic Maximum Light Use Efficiency for Improving Gross Primary Productivity Estimation. Remote Sens. 2023, 15, 1176. [Google Scholar] [CrossRef]
- Huang, L.; Lin, X.; Jiang, S.; Liu, M.; Jiang, Y.; Li, Z.-L.; Tang, R. A two-stage light-use efficiency model for improving gross primary production estimation in agroecosystems. Environ. Res. Lett. 2022, 17, 104021. [Google Scholar] [CrossRef]
- Turner, D.; Ritts, W.; Styles, J.; Yang, Z.; Cohen, W.; Law, B.; Thornton, P. A diagnostic carbon flux model to monitor the effects of disturbance and interannual variation in climate on regional NEP. Tellus B Chem. Phys. Meteorol. 2006, 58, 476–490. [Google Scholar] [CrossRef]
- Dawson, T.P.; North, P.R.J.; Plummer, S.E.; Curran, P.J. Forest ecosystem chlorophyll content: Implications for remotely sensed estimates of net primary productivity. Int. J. Remote Sens. 2003, 24, 611–617. [Google Scholar] [CrossRef]
- Wang, S.; Huang, K.; Yan, H.; Yan, H.; Zhou, L.; Wang, H.; Zhang, J.; Yan, J.; Zhao, L.; Wang, Y.; et al. Improving the light use efficiency model for simulating terrestrial vegetation gross primary production by the inclusion of diffuse radiation across ecosystems in China. Ecol. Complex. 2015, 23, 1–13. [Google Scholar] [CrossRef]
- Wang, H.; Jia, G.; Fu, C.; Feng, J.; Zhao, T.; Ma, Z. Deriving maximal light use efficiency from coordinated flux measurements and satellite data for regional gross primary production modeling. Remote Sens. Environ. 2010, 114, 2248–2258. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiao, X.; Wolf, S.; Wu, J.; Wu, X.; Gioli, B.; Wohlfahrt, G.; Cescatti, A.; van der Tol, C.; Zhou, S.; et al. Spatio-Temporal Convergence of Maximum Daily Light-Use Efficiency Based on Radiation Absorption by Canopy Chlorophyll. Geophys. Res. Lett. 2018, 45, 3508–3519. [Google Scholar] [CrossRef]
- Huang, D.; Chi, H.; Xin, F.; Miyata, A.; Kang, M.; Liu, K.; Li, R.; Dang, H.; Qin, Y.; Xiao, X. Improved estimation of gross primary production of paddy rice cropland with changing model parameters over phenological transitions. Ecol. Model. 2021, 445, 109492. [Google Scholar] [CrossRef]
- Wu, C.; Peng, D.; Soudani, K.; Siebicke, L.; Gough, C.M.; Arain, M.A.; Bohrer, G.; Lafleur, P.M.; Peichl, M.; Gonsamo, A.; et al. Land surface phenology derived from normalized difference vegetation index (NDVI) at global FLUXNET sites. Agric. For. Meteorol. 2017, 233, 171–182. [Google Scholar] [CrossRef]
- Gonsamo, A.; Chen, J.M.; Ooi, Y.W. Peak season plant activity shift towards spring is reflected by increasing carbon uptake by extratropical ecosystems. Glob. Chang. Biol. 2017, 24, 2117–2128. [Google Scholar] [CrossRef]
- Yang, J.; Dong, J.; Xiao, X.; Dai, J.; Wu, C.; Xia, J.; Zhao, G.; Zhao, M.; Li, Z.; Zhang, Y.; et al. Divergent shifts in peak photosynthesis timing of temperate and alpine grasslands in China. Remote Sens. Environ. 2019, 233, 111395. [Google Scholar] [CrossRef]
- Wang, C.; Wu, Y.; Hu, Q.; Hu, J.; Chen, Y.; Lin, S.; Xie, Q. Comparison of Vegetation Phenology Derived from Solar-Induced Chlorophyll Fluorescence and Enhanced Vegetation Index, and Their Relationship with Climatic Limitations. Remote Sens. 2022, 14, 3018. [Google Scholar] [CrossRef]
- Richardson, A.D.; Braswell, B.H.; Hollinger, D.Y.; Jenkins, J.P.; Ollinger, S.V. Near-surface remote sensing of spatial and temporal variation in canopy phenology. Ecol. Appl. 2009, 19, 1417–1428. [Google Scholar] [CrossRef] [PubMed]
- Richardson, A.D.; Hufkens, K.; Milliman, T.; Aubrecht, D.M.; Chen, M.; Gray, J.M.; Johnston, M.R.; Keenan, T.F.; Klosterman, S.T.; Kosmala, M.; et al. Tracking vegetation phenology across diverse North American biomes using PhenoCam imagery. Sci. Data 2018, 5, 180028. [Google Scholar] [CrossRef] [PubMed]
- Burke, M.W.; Rundquist, B.C. Scaling Phenocam GCC, NDVI, and EVI2 with Harmonized Landsat-Sentinel using Gaussian Processes. Agric. For. Meteorol. 2021, 300, 108316. [Google Scholar] [CrossRef]
- Bórnez, K.; Richardson, A.D.; Verger, A.; Descals, A.; Peñuelas, J. Evaluation of Vegetation and PROBA-V Phenology Using PhenoCam and Eddy Covariance Data. Remote Sens. 2020, 12, 3077. [Google Scholar] [CrossRef]
- Zhang, X.; Jayavelu, S.; Liu, L.; Friedl, M.A.; Henebry, G.M.; Liu, Y.; Schaaf, C.B.; Richardson, A.D.; Gray, J. Evaluation of land surface phenology from VIIRS data using time series of PhenoCam imagery. Agric. For. Meteorol. 2018, 256–257, 137–149. [Google Scholar] [CrossRef]
- Tran, K.H.; Zhang, X.; Ketchpaw, A.R.; Wang, J.; Ye, Y.; Shen, Y. A novel algorithm for the generation of gap-free time series by fusing harmonized Landsat 8 and Sentinel-2 observations with PhenoCam time series for detecting land surface phenology. Remote Sens. Environ. 2022, 282, 113275. [Google Scholar] [CrossRef]
- Cao, M.; Sun, Y.; Jiang, X.; Li, Z.; Xin, Q. Identifying Leaf Phenology of Deciduous Broadleaf Forests from PhenoCam Images Using a Convolutional Neural Network Regression Method. Remote Sens. 2021, 13, 2331. [Google Scholar] [CrossRef]
- Melaas, E.K.; Friedl, M.A.; Richardson, A.D. Multiscale modeling of spring phenology across Deciduous Forests in the Eastern United States. Glob. Chang. Biol. 2016, 22, 792–805. [Google Scholar] [CrossRef]
- Pastorello, G.; Trotta, C.; Canfora, E.; Chu, H.; Christianson, D.; Cheah, Y.-W.; Poindexter, C.; Chen, J.; Elbashandy, A.; Humphrey, M. The FLUXNET2015 dataset and the ONEFlux processing pipeline for eddy covariance data. Sci. Data 2020, 7, 1–27. [Google Scholar] [CrossRef]
- Delwiche, K.B.; Knox, S.H.; Malhotra, A.; Fluet-Chouinard, E.; McNicol, G.; Feron, S.; Ouyang, Z.; Papale, D.; Trotta, C.; Canfora, E. FLUXNET-CH4: A global, multi-ecosystem dataset and analysis of methane seasonality from freshwater wetlands. Earth Syst. Sci. Data 2021, 13, 3607–3689. [Google Scholar] [CrossRef]
- Knox, S.H.; Jackson, R.B.; Poulter, B.; McNicol, G.; Fluet-Chouinard, E.; Zhang, Z.; Hugelius, G.; Bousquet, P.; Canadell, J.G.; Saunois, M. FLUXNET-CH 4 synthesis activity: Objectives, observations, and future directions. Bull. Am. Meteorol. Soc. 2019, 100, 2607–2632. [Google Scholar]
- Vuichard, N.; Papale, D. Filling the gaps in meteorological continuous data measured at FLUXNET sites with ERA-Interim reanalysis. Earth Syst. Sci. Data 2015, 7, 157–171. [Google Scholar] [CrossRef]
- Barr, A.; Richardson, A.; Hollinger, D.; Papale, D.; Arain, M.; Black, T.; Bohrer, G.; Dragoni, D.; Fischer, M.; Gu, L.; et al. Use of change-point detection for friction–velocity threshold evaluation in eddy-covariance studies. Agric. For. Meteorol. 2013, 171–172, 31–45. [Google Scholar] [CrossRef]
- Lasslop, G.; Reichstein, M.; Papale, D.; Richardson, A.D.; Arneth, A.; Barr, A.; Stoy, P.; Wohlfahrt, G. Separation of net ecosystem exchange into assimilation and respiration using a light response curve approach: Critical issues and global evaluation. Glob. Chang. Biol. 2010, 16, 187–208. [Google Scholar] [CrossRef]
- Savage, K.E.; Davidson, E.A. Interannual variation of soil respiration in two New England forests. Glob. Biogeochem. Cycles 2001, 15, 337–350. [Google Scholar] [CrossRef]
- Oliphant, A.J.; Grimmond, C.S.; Zutter, H.N.; Schmid, H.P.; Su, H.B.; Scott, S.L.; Offerle, B.J.; Randolph, J.C.; Ehman, J. Heat storage and energy balance fluxes for a temperate deciduous forest. Agric. For. Meteorol. 2004, 126, 185–201. [Google Scholar] [CrossRef]
- Chen, F.; Xu, X.; Barlage, M.; Rasmussen, R.; Shen, S.; Miao, S.; Zhou, G. Memory of irrigation effects on hydroclimate and its modeling challenge. Environ. Res. Lett. 2018, 13, 064009. [Google Scholar] [CrossRef]
- Xin, F.; Xiao, X.; Zhao, B.; Miyata, A.; Baldocchi, D.; Knox, S.; Kang, M.; Shim, K.-M.; Min, S.; Chen, B.; et al. Modeling gross primary production of paddy rice cropland through analyses of data from CO2 eddy flux tower sites and MODIS images. Remote Sens. Environ. 2016, 190, 42–55. [Google Scholar] [CrossRef]
- Oikawa, P.Y.; Jenerette, G.D.; Knox, S.H.; Sturtevant, C.; Verfaillie, J.; Dronova, I.; Poindexter, C.M.; Eichelmann, E.; Baldocchi, D.D. Evaluation of a hierarchy of models reveals importance of substrate limitation for predicting carbon dioxide and methane exchange in restored wetlands. J. Geophys. Res. Biogeosci. 2017, 122, 145–167. [Google Scholar] [CrossRef]
- Hemes, K.S.; Chamberlain, S.D.; Eichelmann, E.; Anthony, T.; Valach, A.; Kasak, K.; Szutu, D.; Verfaillie, J.; Silver, W.L.; Baldocchi, D.D. Assessing the carbon and climate benefit of restoring degraded agricultural peat soils to managed wetlands. Agric. For. Meteorol. 2019, 268, 202–214. [Google Scholar] [CrossRef]
- Miller, G.R.; Baldocchi, D.D.; Law, B.E.; Meyers, T. An analysis of soil moisture dynamics using multi-year data from a network of micrometeorological observation sites. Adv. Water Resour. 2007, 30, 1065–1081. [Google Scholar] [CrossRef]
- Richardson, A.D.; Hufkens, K.; Milliman, T.; Frolking, S. Intercomparison of phenological transition dates derived from the PhenoCam Dataset V1.0 and MODIS satellite remote sensing. Sci. Rep. 2018, 8, 5679. [Google Scholar] [CrossRef]
- Milliman, T.; Seyednasrollah, B.; Young, A.; Hufkens, K.; Friedl, M.; Frolking, S.; Richardson, A.; Abraha, M.; Allen, D.; Apple, M. PhenoCam Dataset v2.0: Digital Camera Imagery from the PhenoCam Network, 2000–2018; ORNL Distributed Active Archive Center: Oak Ridge, TN, USA, 2019. [Google Scholar]
- Knox, S.H.; Dronova, I.; Sturtevant, C.; Oikawa, P.Y.; Matthes, J.H.; Verfaillie, J.; Baldocchi, D. Using digital camera and Landsat imagery with eddy covariance data to model gross primary production in restored wetlands. Agric. For. Meteorol. 2017, 237–238, 233–245. [Google Scholar] [CrossRef]
- Zhou, X.; Wang, X.; Zhang, S.; Zhang, Y.; Bai, X. Combining Phenological Camera Photos and MODIS Reflectance Data to Predict GPP Daily Dynamics for Alpine Meadows on the Tibetan Plateau. Remote Sens. 2020, 12, 3735. [Google Scholar] [CrossRef]
- Seyednasrollah, B.; Young, A.; Hufkens, K.; Milliman, T.; Friedl, M.; Frolking, S.; Richardson, A.; Abraha, M.; Allen, D.; Apple, M. PhenoCam Dataset v2.0: Vegetation Phenology from Digital Camera Imagery, 2000–2018; ORNL Distributed Active Archive Center: Oak Ridge, TN, USA, 2019. [Google Scholar]
- Pelta, R.; Beeri, O.; Tarshish, R.; Shilo, T. Sentinel-1 to NDVI for Agricultural Fields Using Hyperlocal Dynamic Machine Learning Approach. Remote Sens. 2022, 14, 2600. [Google Scholar] [CrossRef]
- Zhang, Y.; He, Y.; Li, Y.; Jia, L. Spatiotemporal variation and driving forces of NDVI from 1982 to 2015 in the Qinba Mountains, China. Environ. Sci. Pollut. Res. 2022, 29, 52277–52288. [Google Scholar] [CrossRef] [PubMed]
- Christian, J.I.; Basara, J.B.; Lowman, L.E.; Xiao, X.; Mesheske, D.; Zhou, Y. Flash drought identification from satellite-based land surface water index. Remote Sens. Appl. Soc. Environ. 2022, 26, 100770. [Google Scholar] [CrossRef]
- Elmore, A.J.; Guinn, S.M.; Minsley, B.J.; Richardson, A.D. Landscape controls on the timing of spring, autumn, and growing season length in mid-Atlantic forests. Glob. Chang. Biol. 2012, 18, 656–674. [Google Scholar] [CrossRef]
- Raich, J.W.; Rastetter, E.B.; Melillo, J.M.; Kicklighter, D.W.; Steudler, P.A.; Peterson, B.J.; Grace, A.L.; Moore, B., 3rd; Vorosmarty, C.J. Potential Net Primary Productivity in South America: Application of a Global Model. Ecol. Appl. 1991, 1, 399–429. [Google Scholar] [CrossRef]
- Xiao, X.; Hollinger, D.; Aber, J.; Goltz, M.; Davidson, E.A.; Zhang, Q.; Moore, B. Satellite-based modeling of gross primary production in an evergreen needleleaf forest. Remote Sens. Environ. 2004, 89, 519–534. [Google Scholar] [CrossRef]
- Zhu, X.; Pei, Y.; Zheng, Z.; Dong, J.; Zhang, Y.; Wang, J.; Chen, L.; Doughty, R.B.; Zhang, G.; Xiao, X. Underestimates of Grassland Gross Primary Production in MODIS Standard Products. Remote Sens. 2018, 10, 1771. [Google Scholar] [CrossRef]
- Cheng, N.; Zhou, Y.; He, W.; Ju, W.; Zhu, T.; Liu, Y.; Song, P.; Bi, W.; Zhang, X.; Wei, X. Exploring light use efficiency models capacities in characterizing environmental impacts on paddy rice productivity. Int. J. Appl. Earth Obs. Geoinf. 2023, 117, 103179. [Google Scholar] [CrossRef]
- Yan, H.; Wang, S.-Q.; Billesbach, D.; Oechel, W.; Bohrer, G.; Meyers, T.; Martin, T.A.; Matamala, R.; Phillips, R.P.; Rahman, F.; et al. Improved global simulations of gross primary product based on a new definition of water stress factor and a separate treatment of C3 and C4 plants. Ecol. Model. 2015, 297, 42–59. [Google Scholar] [CrossRef]
- Liu, Z.; Wu, C.; Peng, D.; Wang, S.; Gonsamo, A.; Fang, B.; Yuan, W. Improved modeling of gross primary production from a better representation of photosynthetic components in vegetation canopy. Agric. For. Meteorol. 2017, 233, 222–234. [Google Scholar] [CrossRef]
- Wu, C.; Niu, Z.; Gao, S. The potential of the satellite derived green chlorophyll index for estimating midday light use efficiency in maize, coniferous forest and grassland. Ecol. Indic. 2012, 14, 66–73. [Google Scholar] [CrossRef]
- Cheng, S.J.; Steiner, A.L.; Hollinger, D.Y.; Bohrer, G.; Nadelhoffer, K.J. Using satellite-derived optical thickness to assess the influence of clouds on terrestrial carbon uptake. J. Geophys. Res. Biogeosci. 2016, 121, 1747–1761. [Google Scholar] [CrossRef]
- Fan, C.; Yang, J.; Zhao, G.; Dai, J.; Zhu, M.; Dong, J.; Liu, R.; Zhang, G. Mapping Phenology of Complicated Wetland Landscapes through Harmonizing Landsat and Sentinel-2 Imagery. Remote Sens. 2023, 15, 2413. [Google Scholar] [CrossRef]
- Larsen, K. GAM: The predictive modeling silver bullet. Multithreaded. Stitch Fix 2015, 30, 1–27. [Google Scholar]
- Wang, H.; Jia, G.; Epstein, H.E.; Zhao, H.; Zhang, A. Integrating a PhenoCam-derived vegetation index into a light use efficiency model to estimate daily gross primary production in a semi-arid grassland. Agric. For. Meteorol. 2020, 288, 107983. [Google Scholar] [CrossRef]
- Yang, L.; He, X.; Shen, F.; Zhou, C.; Zhu, A.-X.; Gao, B.; Chen, Z.; Li, M. Improving prediction of soil organic carbon content in croplands using phenological parameters extracted from NDVI time series data. Soil Tillage Res. 2020, 196, 104465. [Google Scholar] [CrossRef]
- Zhang, J.; Tong, X.; Zhang, J.; Meng, P.; Li, J.; Liu, P. Dynamics of phenology and its response to climatic variables in a warm-temperate mixed plantation. For. Ecol. Manag. 2021, 483, 118785. [Google Scholar] [CrossRef]
- Yu, H.; Yang, Y.; Wang, C.; Chen, R.; Xie, Q.; Liu, G.; Yin, G. Extracting Deciduous Forests Spring Phenology from Sentinel-1 Cross Ratio Index. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 2841–2850. [Google Scholar] [CrossRef]
- Wellington, M.J.; Kuhnert, P.; Renzullo, L.J.; Lawes, R. Modelling Within-Season Variation in Light Use Efficiency Enhances Productivity Estimates for Cropland. Remote Sens. 2022, 14, 1495. [Google Scholar] [CrossRef]
- Gan, R.; Zhang, L.; Yang, Y.; Wang, E.; Woodgate, W.; Zhang, Y.; Haverd, V.; Kong, D.; Fischer, T.; Chiew, F.H.S.; et al. Estimating ecosystem maximum light use efficiency based on the water use efficiency principle. Environ. Res. Lett. 2021, 16, 104032. [Google Scholar] [CrossRef]




| Site_ID | Site_Name | PFT | Latitude | Longitude | Data Availability | Tmin | Tmax | Topt |
|---|---|---|---|---|---|---|---|---|
| US-Ho1 | Howland Forest (main tower) | ENF | 45.204 | −68.740 | 2013–2015 | −20.64 | 25.66 | 18.87 |
| US-Ha1 | Harvard Forest EMS Tower (HFR1) | DBF | 42.537 | −72.171 | 2010–2012 | −15.83 | 27.52 | 20.13 |
| US-MMS | Morgan Monroe State Forest | DBF | 39.323 | −86.413 | 2012–2014 | −12.08 | 29.85 | 22.82 |
| US-Ne2 | Mead-irrigated maize–soybean rotation | CRO | 41.164 | −96.470 | 2010–2012 | −18.26 | 29.56 | 23.02 |
| US-Twt | Twitchell Island | CRO | 38.108 | −121.653 | 2012–2014 | 2.60 | 28.65 | 20.46 |
| US-Myb | Mayberry Wetland | WET | 38.049 | −121.765 | 2012–2014 | 4.14 | 27.27 | 20.02 |
| US-Var | Vaira Ranch, Ione | GRA | 38.413 | −120.950 | 2012–2014 | 3.45 | 31.58 | 23.73 |
| Site_ID | Year | NDVI_HGAM | EVI_HGAM | GCC_HGAM | NDVI_DLF | EVI_DLF | GCC_DLF |
|---|---|---|---|---|---|---|---|
| US-Ho1 | 2013 | 16.86 (36.86) | 17.58 (32.67) | 14.42 (39.06) | 17.46 (18.46) | 18.97 (29.41) | 9.57 (15.01) |
| 2014 | 6.72 (45.55) | 17.31 (31.72) | 15.77 (38.25) | 0.07 (3.90) | 19.91 (28.09) | −12.13 (16.17) | |
| 2015 | 17.80 (44.56) | 18.75 (32.22) | 15.32 (38.52) | 17.85 (39.06) | 19.21 (32.08) | 5.31 (13.90) | |
| US-Ha1 | 2010 | 14.02 (43.61) | 17.17 (34.78) | 14.92 (34.83) | 14.52 (35.12) | 16.67 (35.18) | −12.01 (14.12) |
| 2011 | 14.69 (37.85) | 17.58 (34.47) | 15.98 (36.42) | 16.16 (32.59) | 17.39 (34.55) | −48.10 (16.51) | |
| 2012 | 15.64 (38.61) | 17.53 (34.33) | 15.95 (34.87) | 16.59 (34.91) | 17.41 (34.38) | −15.79 (15.37) | |
| US-MMS | 2012 | 15.32 (36.68) | 15.95 (34.96) | 10.68 (35.73) | 14.80 (36.70) | 15.06 (35.39) | −63.56 (10.56) |
| 2013 | 14.74 (37.85) | 16.23 (34.69) | 13.12 (37.76) | 15.54 (41.16) | 15.05 (35.28) | 11.17 (232.91) | |
| 2014 | 14.65 (38.25) | 16.72 (35.10) | 14.78 (36.59) | 15.24 (37.29) | 15.74 (35.61) | −60.81 (14.74) | |
| US-Ne2 | 2010 | 21.32 (34.33) | 22.08 (32.98) | / | 20.41 (34.51) | 23.21 (29.20) | / |
| 2011 | 19.83 (33.66) | 21.14 (32.04) | / | 7.97 (18.55) | 22.60 (27.96) | / | |
| 2012 | 21.27 (34.06) | 21.95 (32.26) | / | 21.74 (32.89) | 21.86 (30.69) | / | |
| US-Twt | 2012 | 22.40 (37.98) | 22.89 (37.13) | 23.61 (37.94) | 23.95 (37.31) | 22.89 (37.23) | 25.36 (31.73) |
| 2013 | 21.90 (38.12) | 21.81 (37.17) | 16.99 (31.32) | 23.32 (37.01) | 21.18 (36.68) | 20.52 (28.36) | |
| 2014 | 18.88 (37.94) | 16.72 (37.62) | 19.38 (32.22) | 20.65 (32.71) | 16.94 (36.94) | 22.60 (29.71) | |
| US-Myb | 2012 | 12.44 (43.43) | 13.03 (42.13) | 11.14 (42.26) | −1.39 (8.39) | 13.33 (40.47) | 11.70 (50.75) |
| 2013 | 13.12 (41.95) | 13.48 (41.81) | 16.09 (43.43) | −0.53 (1.13) | 13.56 (40.20) | −11.49 (13.33) | |
| 2014 | 11.00 (36.50) | 13.12 (35.68) | 12.17 (29.69) | 11.52 (45.13) | 14.16 (34.77) | −12.58 (13.76) | |
| US-Var | 2012 | 6.27 (18.61) | 6.81 (18.79) | 8.97 (18.03) | 19.45 (21.74) | 8.07 (18.35) | −15.74 (15.22) |
| 2013 | 7.17 (17.71) | 7.76 (17.67) | 4.33 (16.72) | 9.71 (16.97) | 8.85 (17.32) | −12.19 (13.12) | |
| 2014 | 1.72 (17.31) | 4.83 (16.77) | 7.62 (17.13) | −1.31 (10.81) | 6.25 (16.17) | 12.34 (16.25) |
| Site_ID | Year | PS1 | PS2 | PS3 |
|---|---|---|---|---|
| US-Ho1 | 2013 | 0.032 | 0.035 | 0.049 |
| 2014 | 0.036 | 0.039 | 0.046 | |
| 2015 | 0.030 | 0.036 | 0.042 | |
| US-Ha1 | 2010 | 0.061 | 0.044 | 0.053 |
| 2011 | 0.037 | 0.040 | 0.053 | |
| 2012 | 0.041 | 0.045 | 0.062 | |
| US-MMS | 2012 | 0.031 | 0.040 | 0.022 |
| 2013 | 0.030 | 0.034 | 0.034 | |
| 2014 | 0.030 | 0.038 | 0.013 | |
| US-Ne2 | 2010 | 0.036 | 0.054 | 0.028 |
| 2011 | 0.020 | 0.065 | 0.030 | |
| 2012 | 0.045 | 0.050 | 0.026 | |
| US-Twt | 2012 | 0.024 | 0.040 | 0.020 |
| 2013 | 0.032 | 0.042 | 0.045 | |
| 2014 | 0.031 | 0.031 | 0.004 | |
| US-Myb | 2012 | 0.014 | 0.039 | 0.024 |
| 2013 | 0.035 | 0.037 | 0.015 | |
| 2014 | 0.033 | 0.038 | 0.035 | |
| US-Var | 2012 | 0.058 | 0.062 | 0.020 |
| 2013 | 0.035 | 0.042 | 0.028 | |
| 2014 | 0.010 | 0.084 | 0.029 |
| GPP | ε0 | FAPAR |
|---|---|---|
| GPP1 | Phenology-based ε0 | FAPARcanopy |
| GPP2 | Phenology-based ε0 | FAPARchl1 |
| GPP3 | Phenology-based ε0 | FAPARchl2 |
| GPP4 | Phenology-based ε0 | FAPARchl3 |
| GPP5 | Default ε0 | FAPARchl1 (default setting) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, Y.; Chi, H.; Shi, P.; Huang, D.; Gan, J.; Li, Y.; Gao, X.; Han, Y.; Chang, C.; Wan, J.; et al. Phenology-Based Maximum Light Use Efficiency for Modeling Gross Primary Production across Typical Terrestrial Ecosystems. Remote Sens. 2023, 15, 4002. https://doi.org/10.3390/rs15164002
Lv Y, Chi H, Shi P, Huang D, Gan J, Li Y, Gao X, Han Y, Chang C, Wan J, et al. Phenology-Based Maximum Light Use Efficiency for Modeling Gross Primary Production across Typical Terrestrial Ecosystems. Remote Sensing. 2023; 15(16):4002. https://doi.org/10.3390/rs15164002
Chicago/Turabian StyleLv, Yulong, Hong Chi, Peichen Shi, Duan Huang, Jialiang Gan, Yifan Li, Xinyi Gao, Yifei Han, Cun Chang, Jun Wan, and et al. 2023. "Phenology-Based Maximum Light Use Efficiency for Modeling Gross Primary Production across Typical Terrestrial Ecosystems" Remote Sensing 15, no. 16: 4002. https://doi.org/10.3390/rs15164002
APA StyleLv, Y., Chi, H., Shi, P., Huang, D., Gan, J., Li, Y., Gao, X., Han, Y., Chang, C., Wan, J., & Ling, F. (2023). Phenology-Based Maximum Light Use Efficiency for Modeling Gross Primary Production across Typical Terrestrial Ecosystems. Remote Sensing, 15(16), 4002. https://doi.org/10.3390/rs15164002











