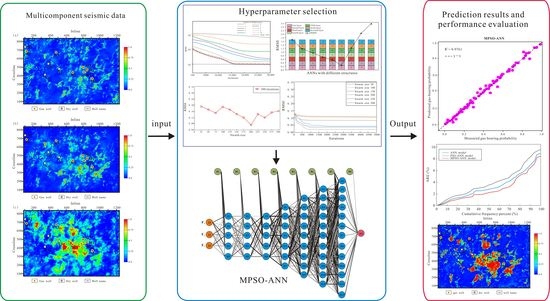
A Parametric Study of MPSO-ANN Techniques in Gas-Bearing Distribution Prediction Using Multicomponent Seismic Data
Abstract
1. Introduction
2. Materials and Methods
2.1. Artificial Neural Network
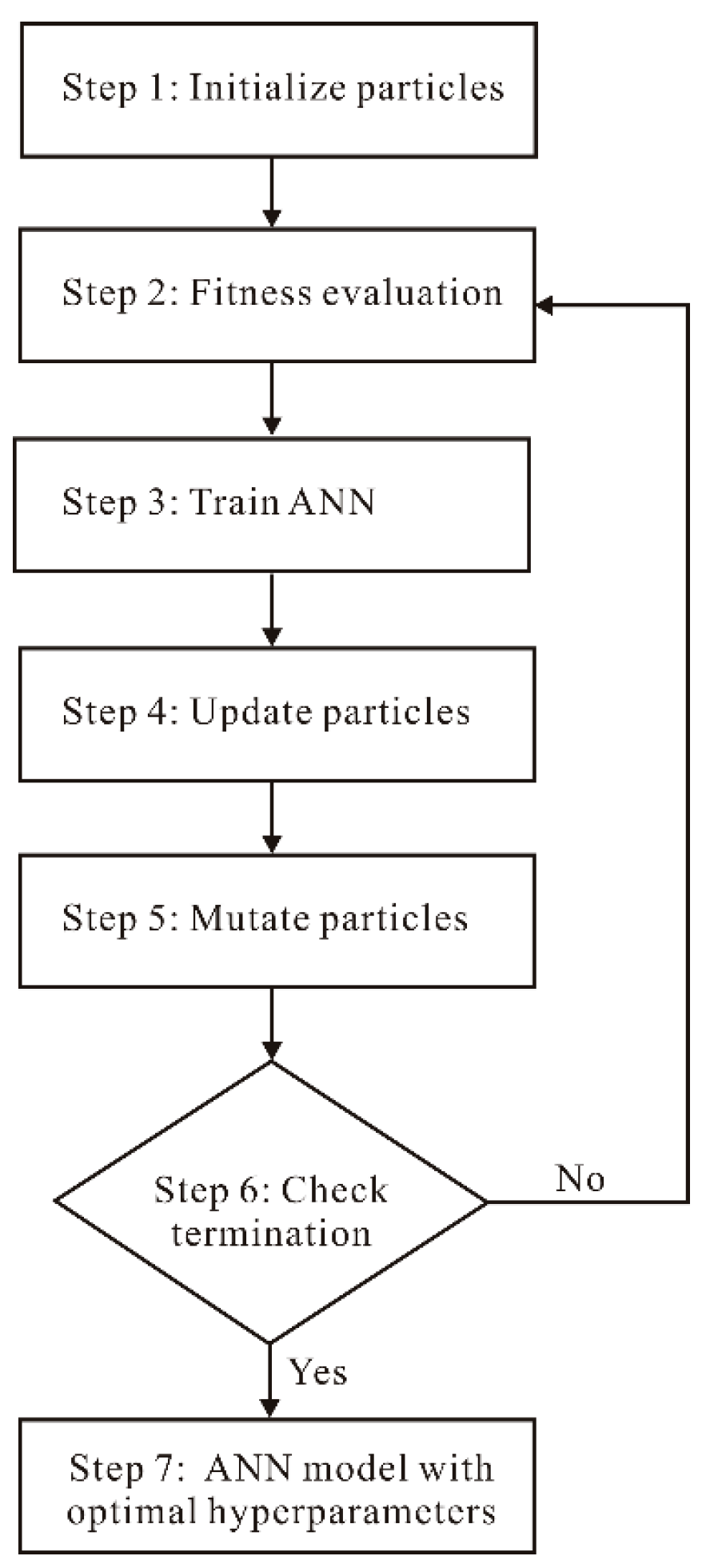
2.2. Mutation Particle Swarm Optimization
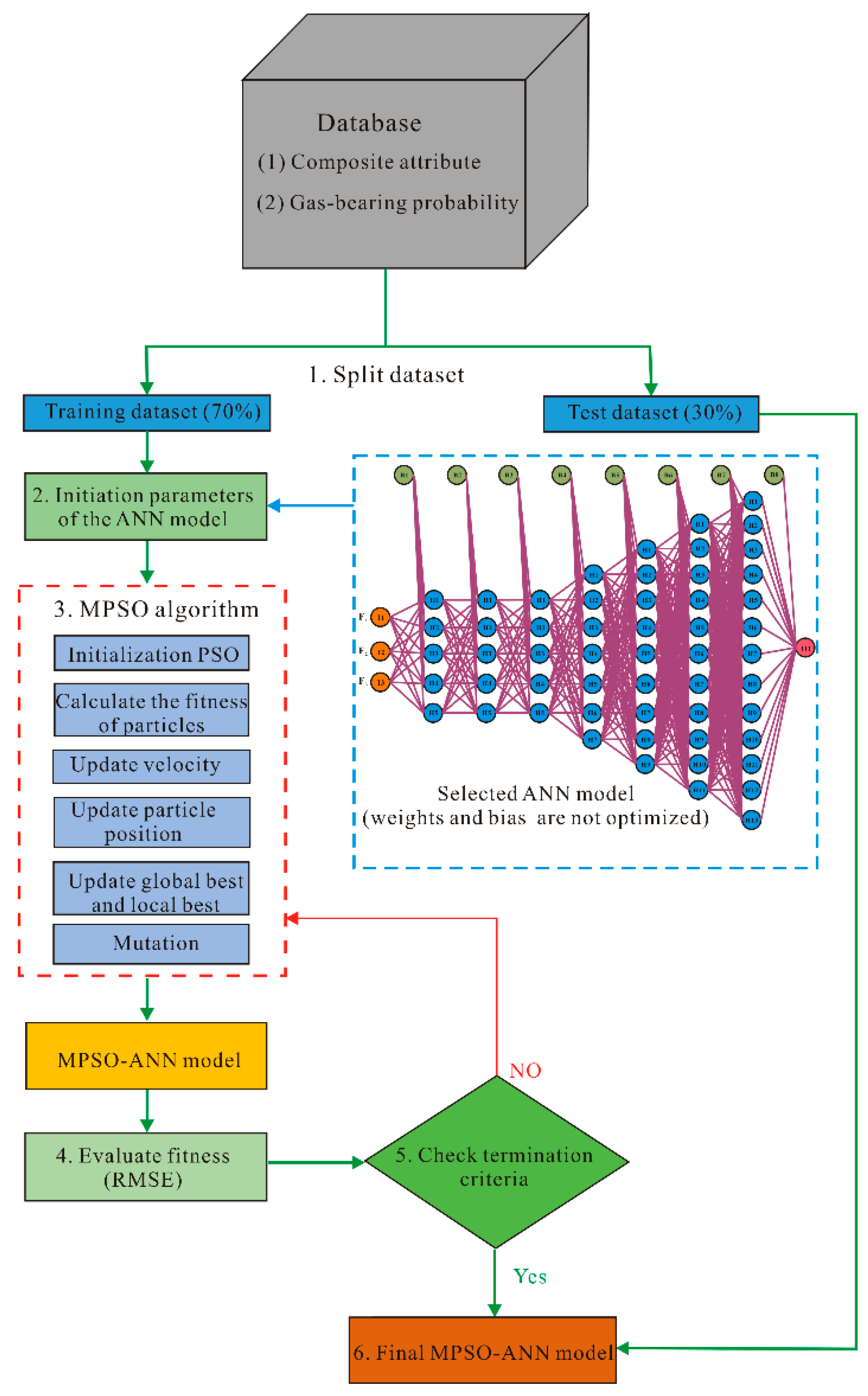
2.3. MPSO-ANN Framework
2.4. Performance Evaluation of the Model
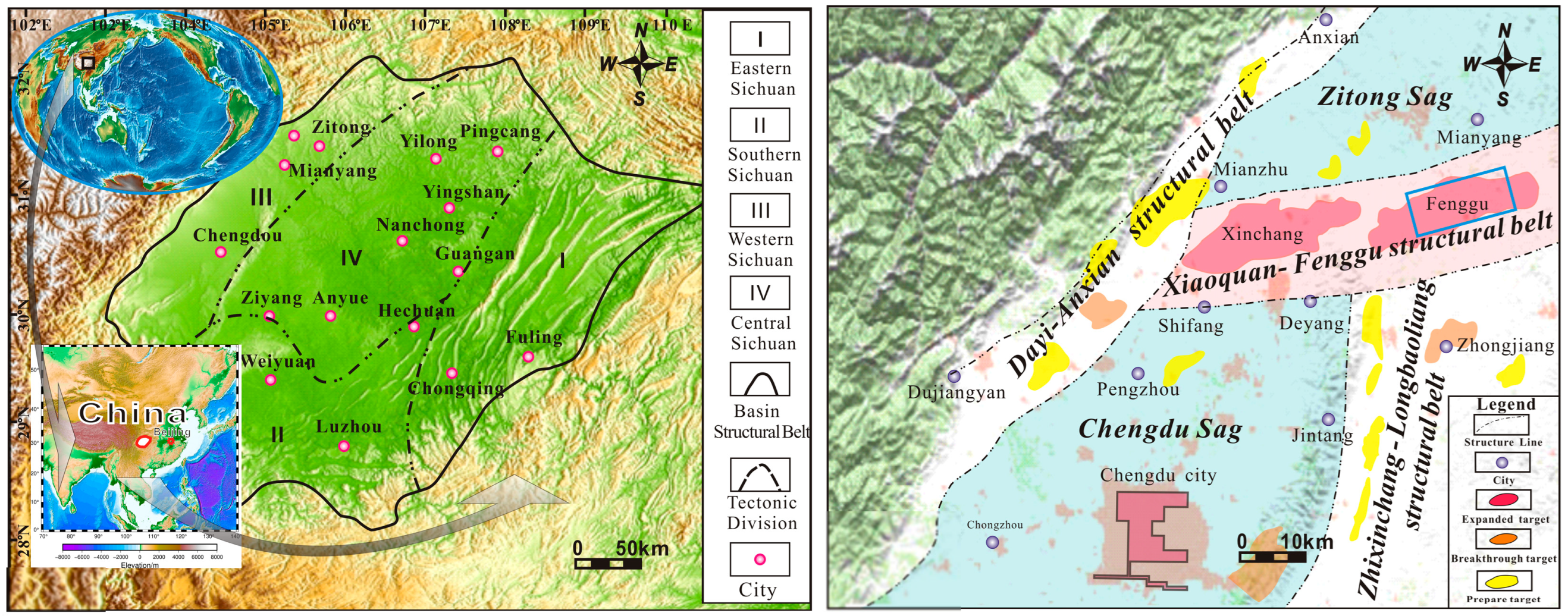
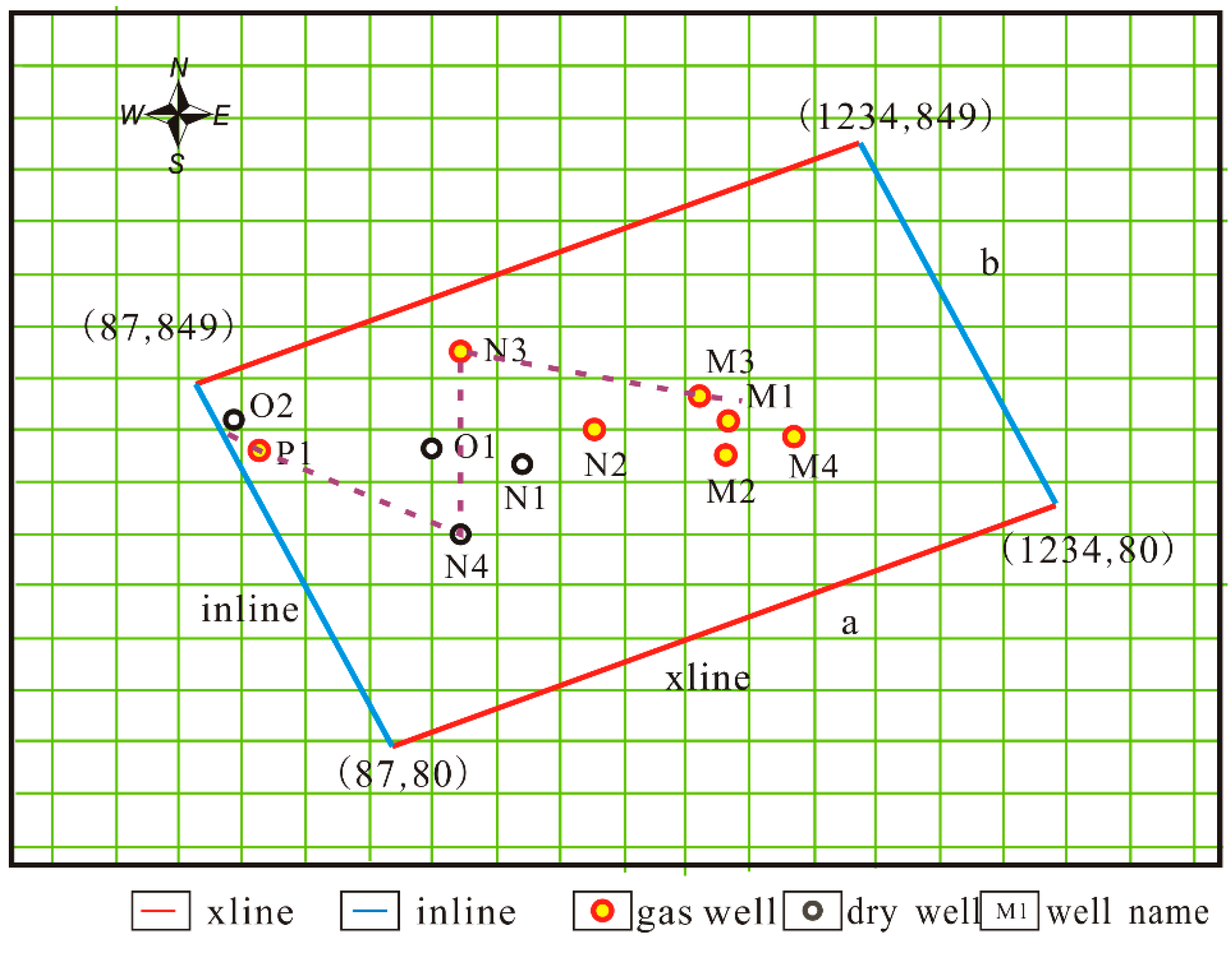
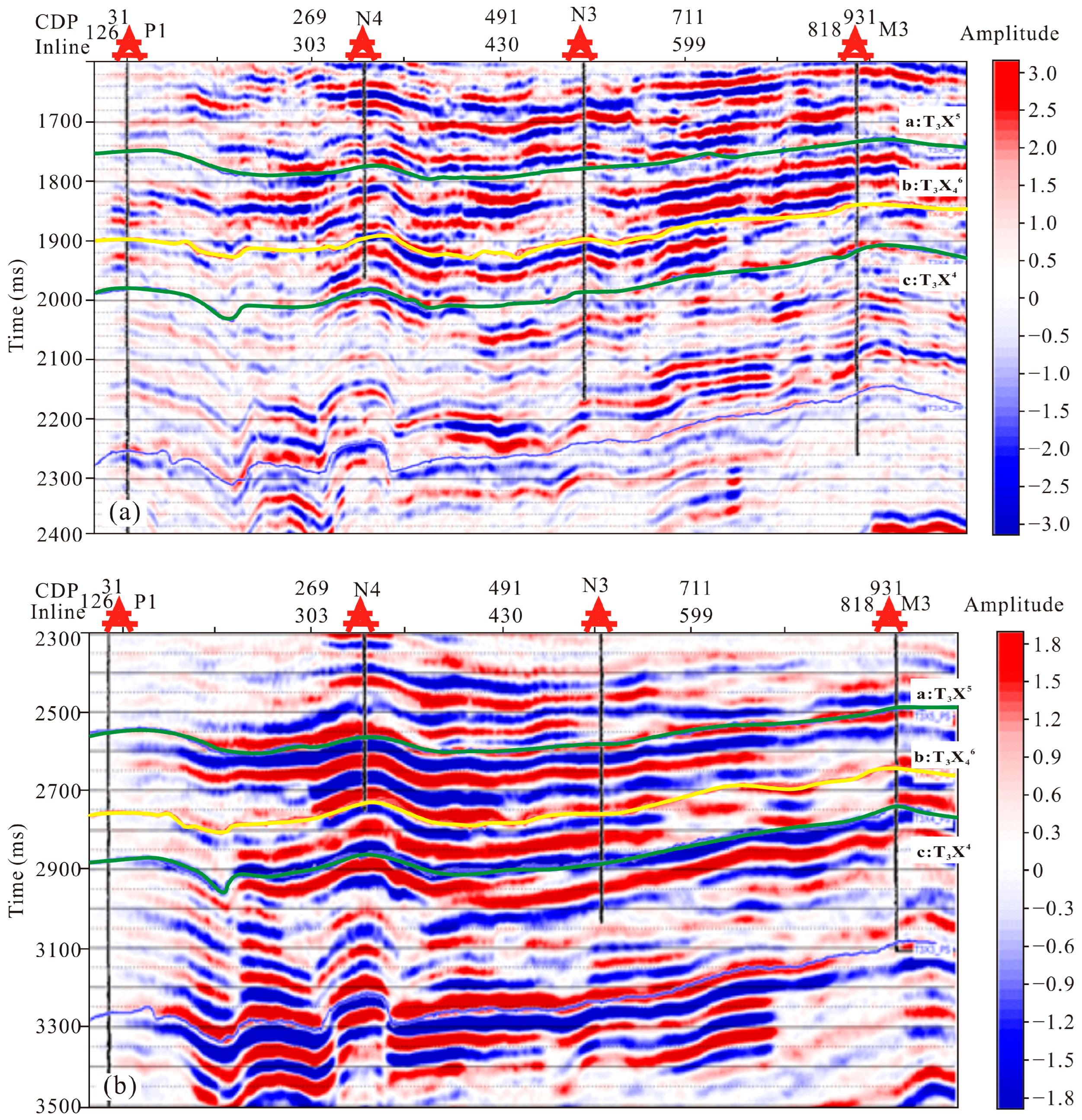
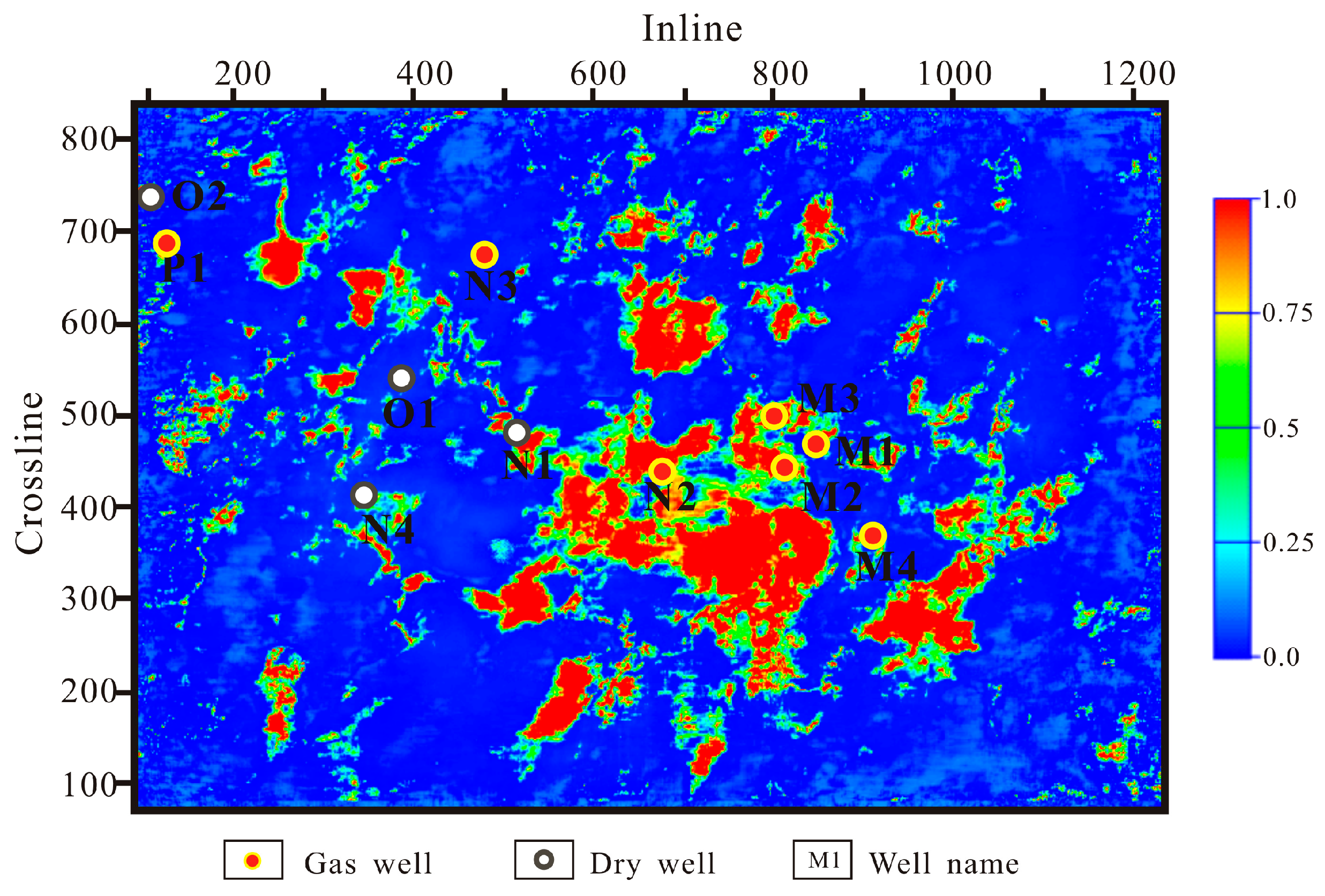
3. Study Area and Available Data
4. Analysis and Design of MPSO-ANN Model Parameters
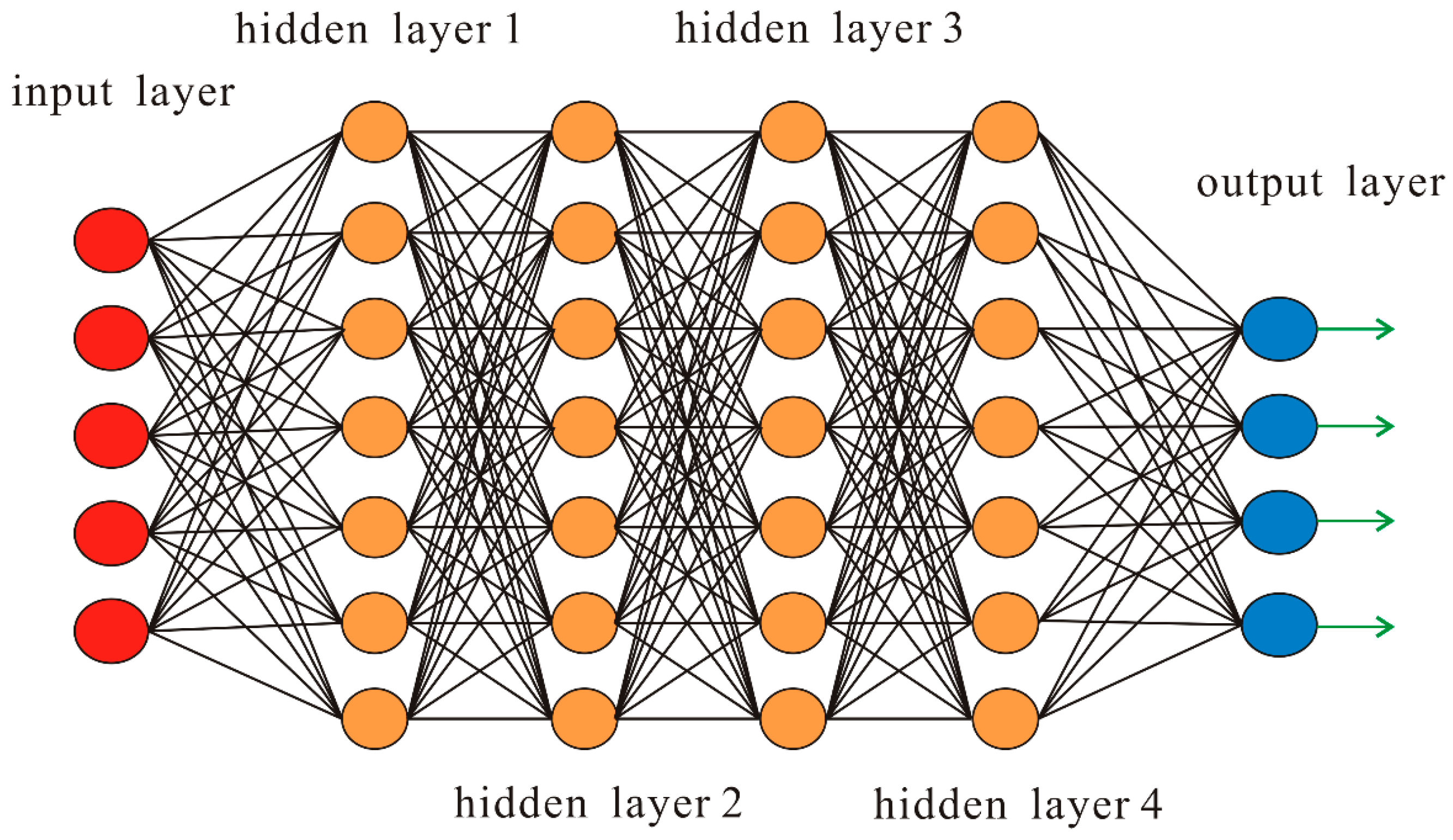
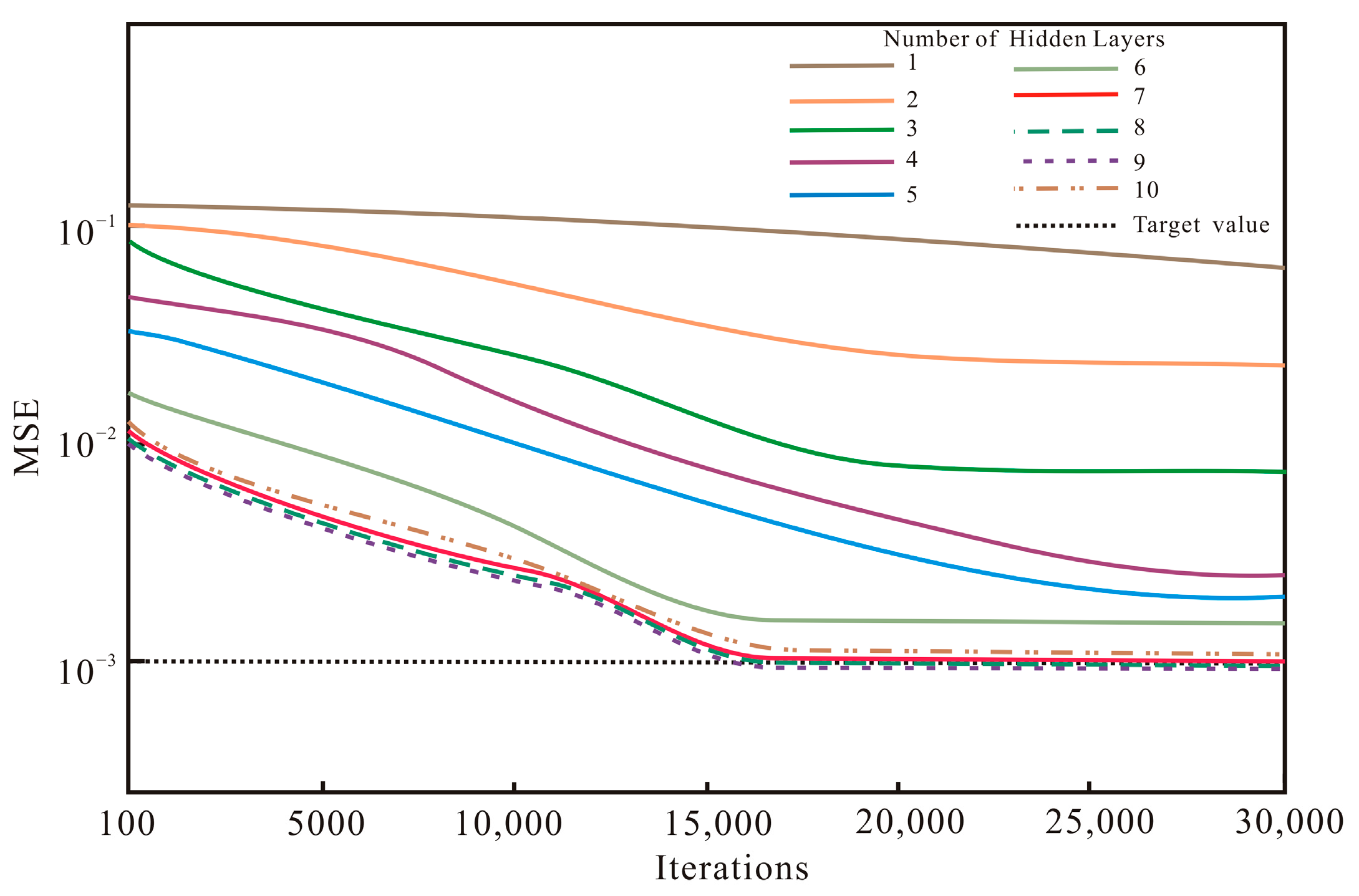
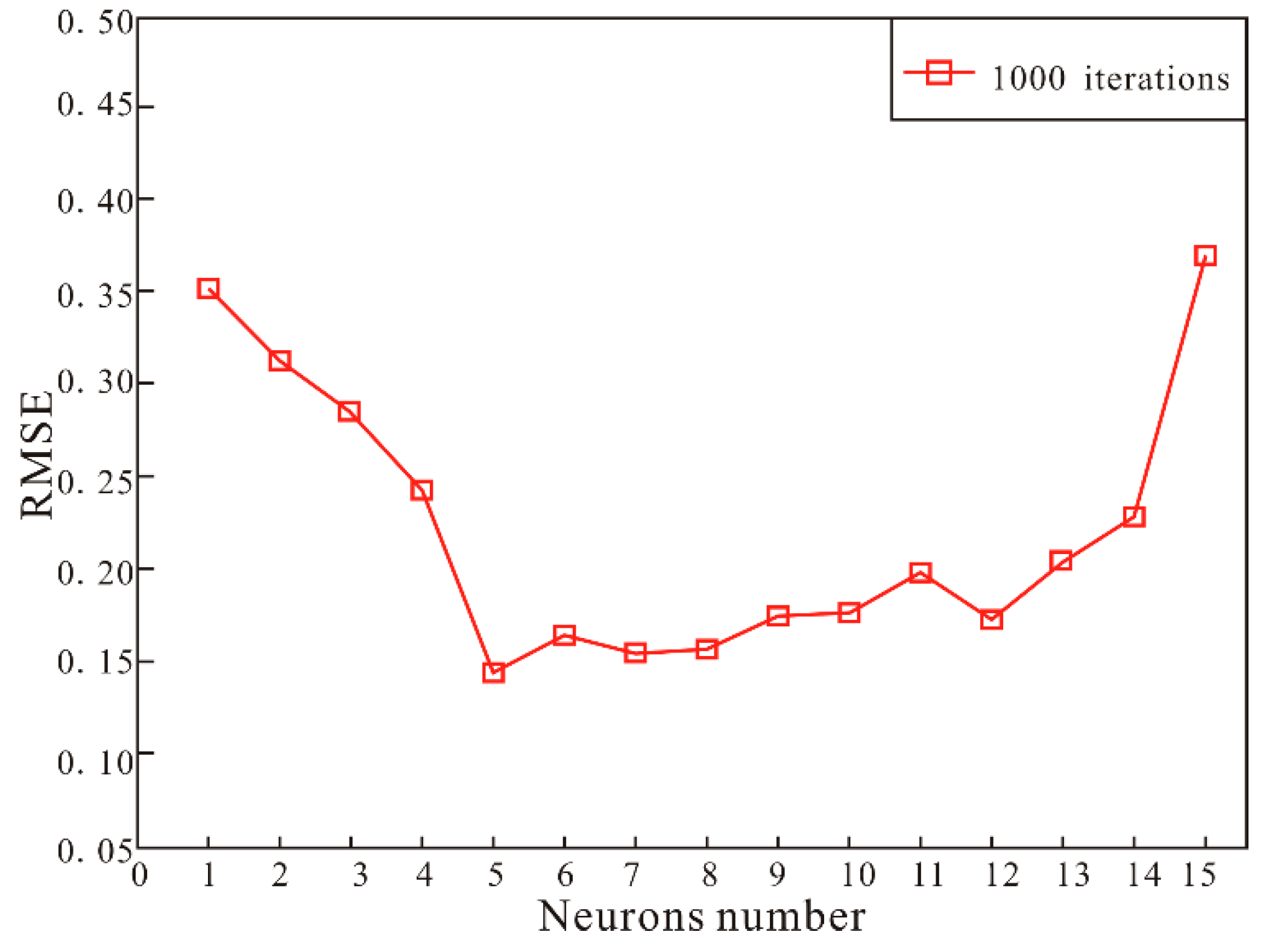
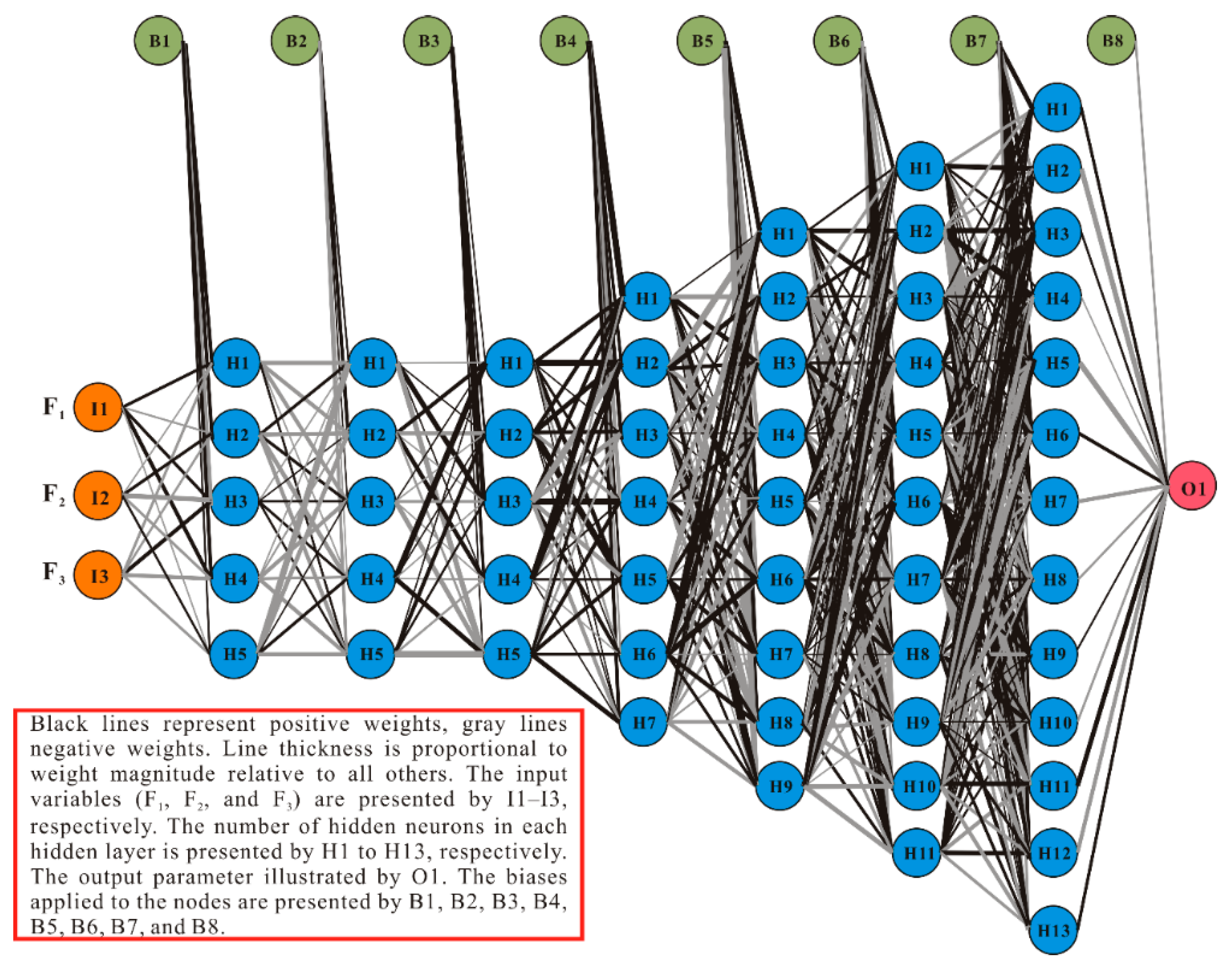
4.1. ANN Architecture
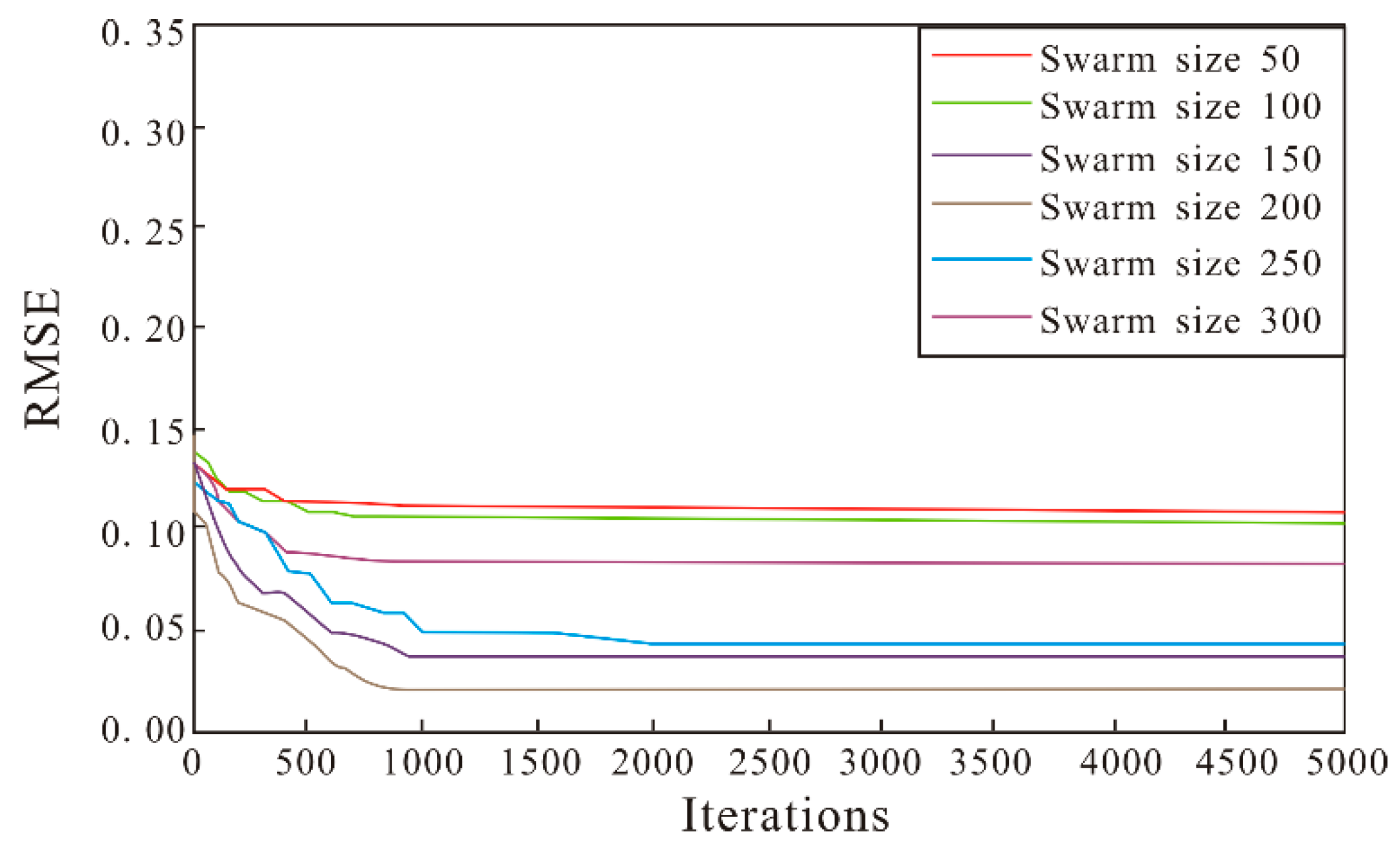
4.2. Design of MPSO Algorithm Parameters
4.3. Determining the MPSO-ANN Model
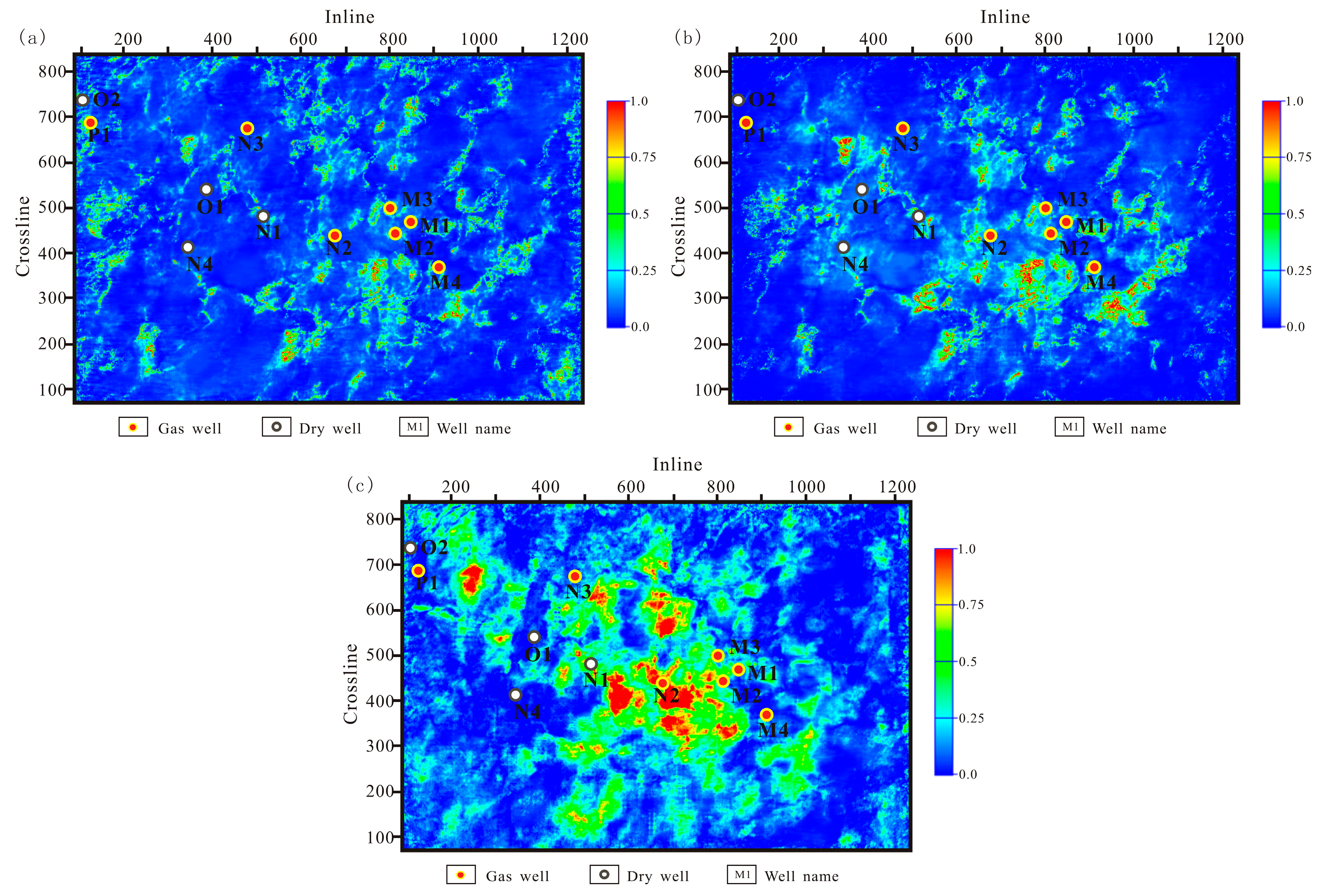
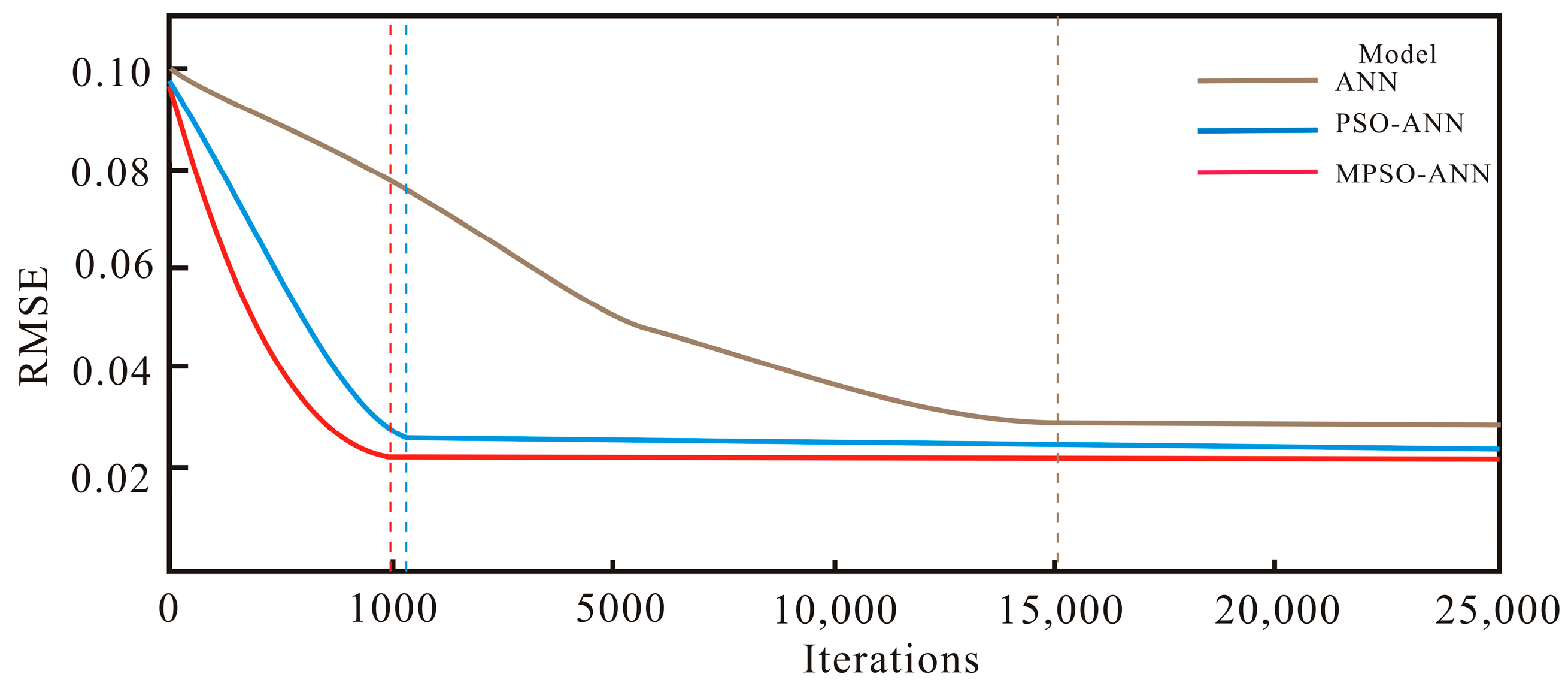
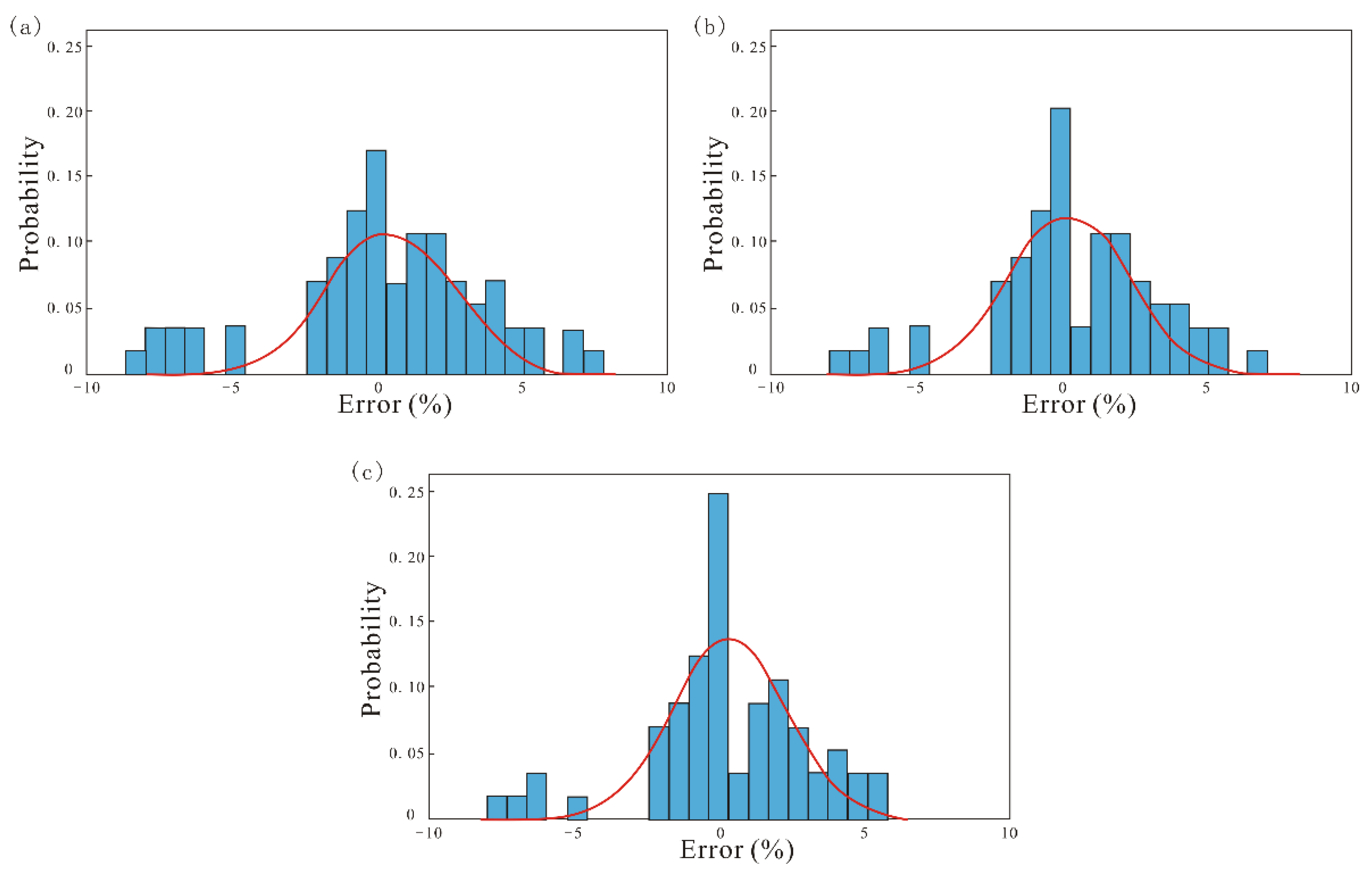
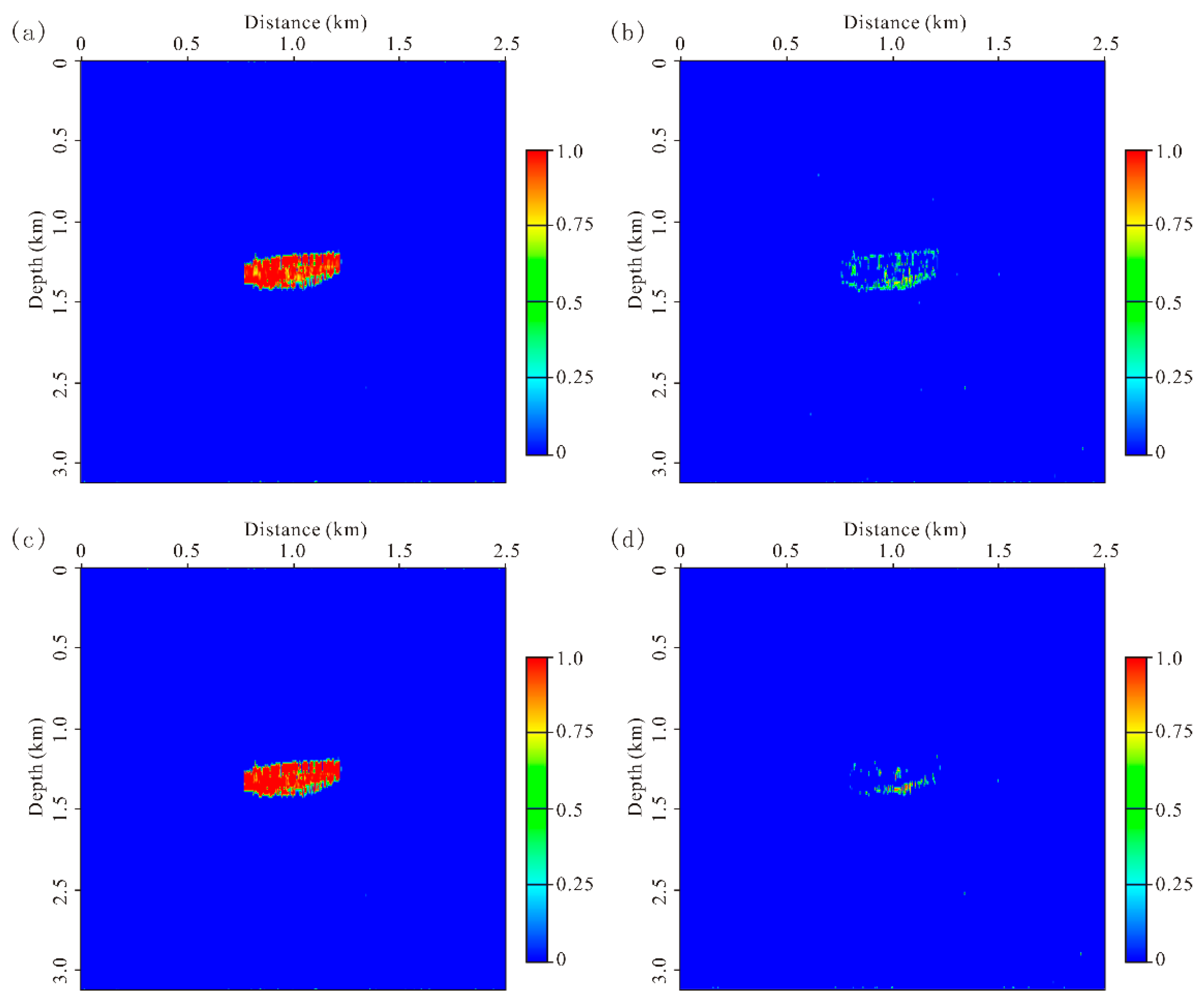
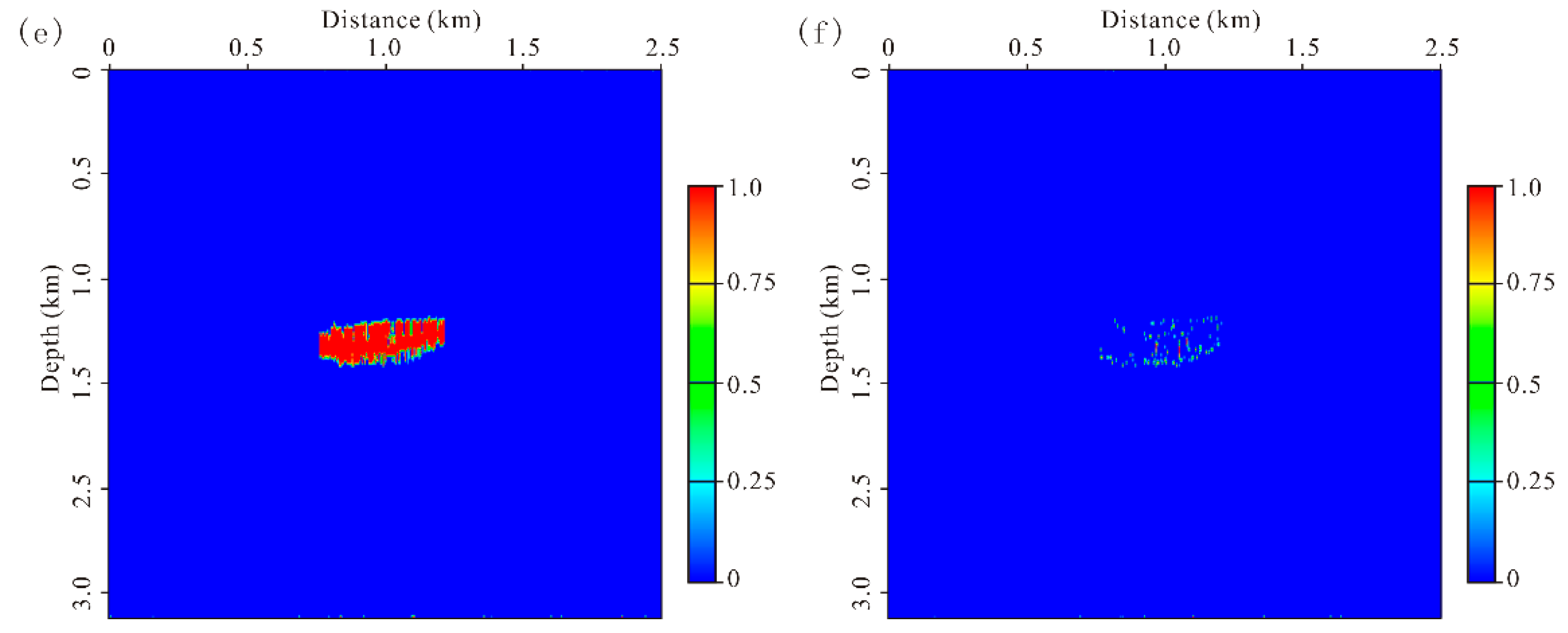
5. Results
6. Discussion
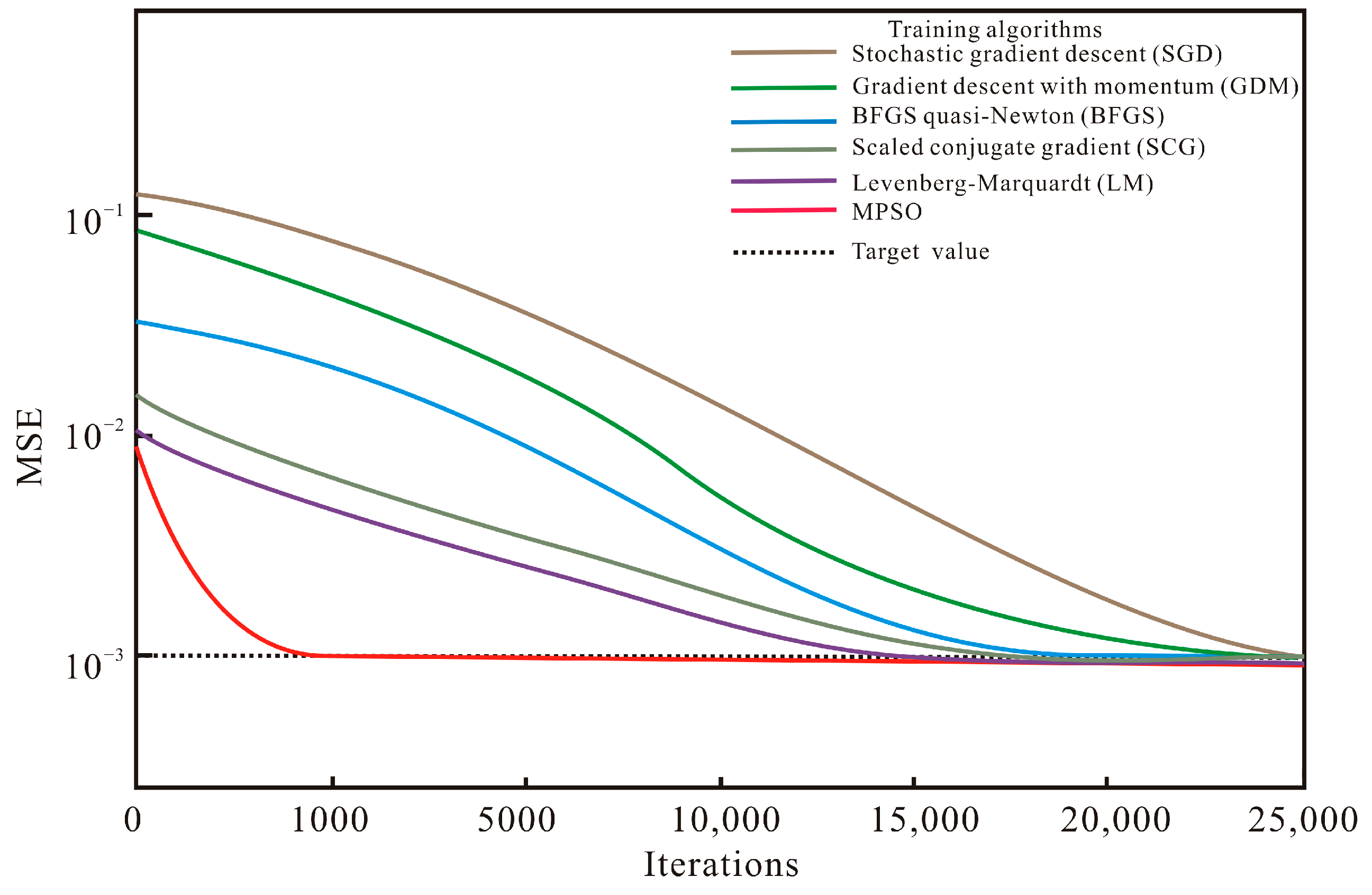
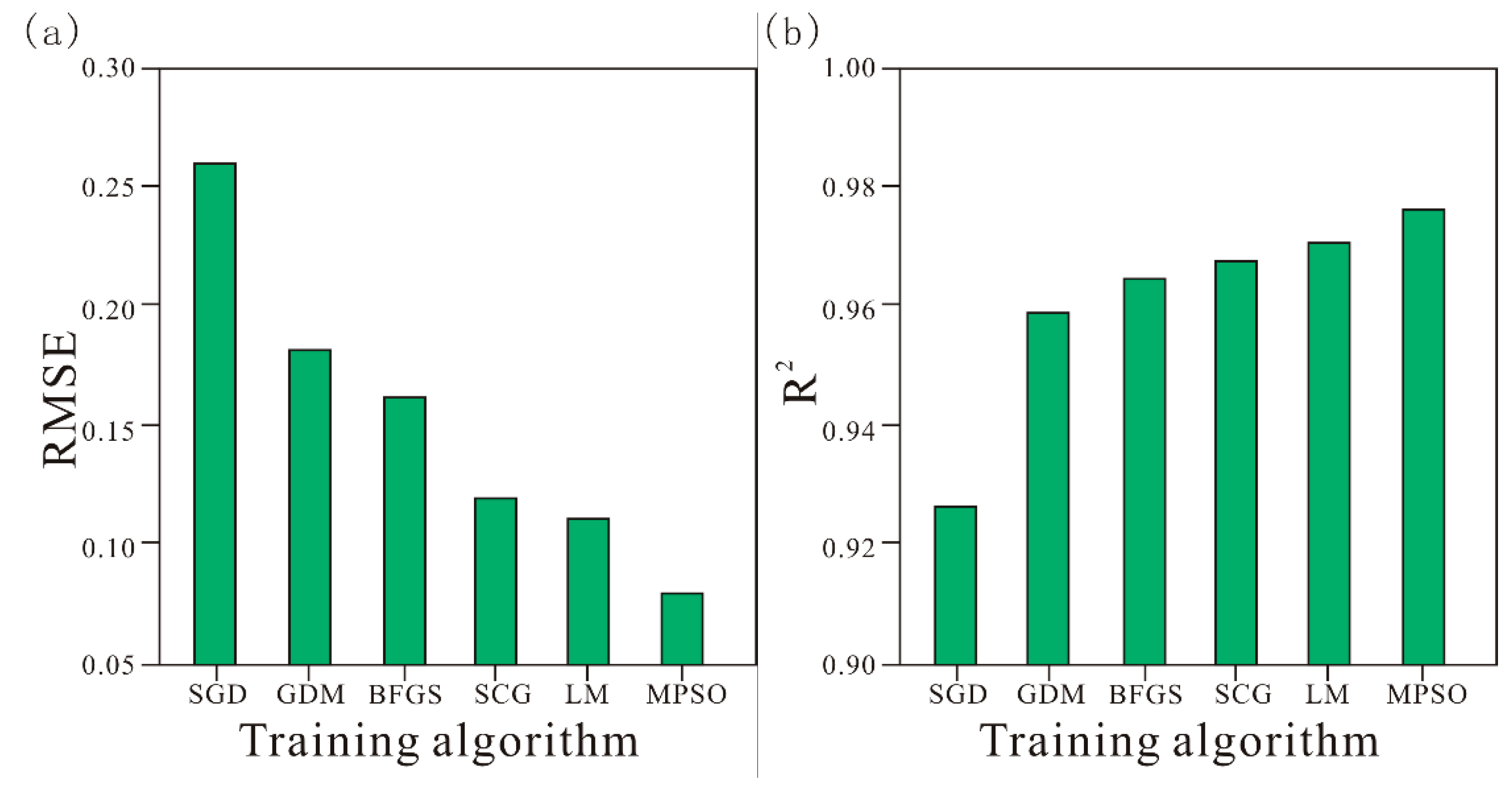
6.1. Comparison with ANN Training Algorithms
6.2. Comparison with Single-Component Seismic Data
6.3. Application to Other Datasets
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hui, G.; Chen, S.N.; He, Y.M.; Wang, H.; Gu, F. Machine learning-based production forecast for shale gas in unconventional reservoirs via integration of geological and operational factors. J. Nat. Gas Sci. Eng. 2021, 94, 104045. [Google Scholar] [CrossRef]
- Pan, Y.W.; Deng, L.C.; Zhou, P.; Lee, W.J. Laplacian Echo-State Networks for production analysis and forecasting in unconventional reservoirs. J. Pet. Sci. Eng. 2021, 207, 109068. [Google Scholar] [CrossRef]
- Yang, J.Q.; Lin, N.T.; Zhang, K.; Fu, C.; Cui, Y.; Li, G.H. An Improved Small-Sample Method Based on APSO-LSSVM for Gas-Bearing Probability Distribution Prediction From Multicomponent Seismic Data. IEEE Geosci. Remote S. 2023, 20, 7501705. [Google Scholar] [CrossRef]
- Park, J.; Datta-Gupta, A.; Singh, A.; Sankaran, S. Hybrid physics and data-driven modeling for unconventional field development and its application to US onshore basin. J. Pet. Sci. Eng. 2021, 15, 109008. [Google Scholar] [CrossRef]
- Cao, J.X.; Jiang, X.D.; Xue, Y.J.; Tian, R.F.; Xiang, T.; Cheng, M. The State-of-the-Art Techniques of Hydrocarbon Detection and Its Application in Ultra-Deep Carbonate Reservoir Characterization in the Sichuan Basin, China. Front. Earth Sci. 2022, 10, 851828. [Google Scholar] [CrossRef]
- Sun, J.; Innanen, K.A.; Huang, C. Physics-guided deep learning for seismic inversion with hybrid training and uncertainty analysis. Geophysics 2021, 86, R303–R317. [Google Scholar] [CrossRef]
- Sun, J.; Niu, Z.; Innanen, K.A.; Li, J.X.; Trad, D.O. A theory-guided deep-learning formulation and optimization of seismic waveform inversion. Geophysics 2020, 85, R87–R99. [Google Scholar] [CrossRef]
- Wang, H.; Chen, Z.; Chen, S.N.; Hui, G.; Kong, B. Production Forecast and Optimization for Parent-Child Well Pattern in Unconventional Reservoirs. J. Pet. Sci. Eng. 2021, 203, 108899. [Google Scholar] [CrossRef]
- Zargar, G.; Tanha, A.A.; Parizad, A.; Amouri, M.; Bagheri, H. Reservoir rock properties estimation based on conventional and NMR log data using ANN-Cuckoo: A case study in one of super fields in Iran southwest. Petroleum 2020, 6, 304–310. [Google Scholar] [CrossRef]
- Kalam, S.; Yousuf, U.; Abu-Khamsin, S.A.; Waheed, U.B.; Khan, R.A. An ANN model to predict oil recovery from a 5-spot waterflood of a heterogeneous reservoir. J. Pet. Sci. Eng. 2022, 210, 110012. [Google Scholar] [CrossRef]
- Baziar, S.; Shahripour, H.B.; Tadayoni, M.; Nabi-Bidhendi, M. Prediction of water saturation in a tight gas sandstone reservoir by using four intelligent methods: A comparative study. Neural Comput. Appl. 2018, 30, 1171–1185. [Google Scholar] [CrossRef]
- Jahan, L.N.; Munshi, T.A.; Sutradhor, S.S.; Hashan, M. A comparative study of empirical, statistical, and soft computing methods coupled with feature ranking for the prediction of water saturation in a heterogeneous oil reservoir. Acta Geophys. 2021, 69, 1697–1715. [Google Scholar] [CrossRef]
- Liu, J.J.; Liu, J.C. An intelligent approach for reservoir quality evaluation in tight sandstone reservoir using gradient boosting decision tree algorithm—A case study of the Yanchang Formation, mid-eastern Ordos Basin, China. Mar. Pet. Geol. 2021, 126, 104939. [Google Scholar] [CrossRef]
- Agbadze, O.K.; Cao, Q.; Ye, J.R. Acoustic impedance and lithology-based reservoir porosity analysis using predictive machine learning algorithms. J. Pet. Sci. Eng. 2022, 208, 109656. [Google Scholar] [CrossRef]
- Kang, B.; Choe, J. Uncertainty quantification of channel reservoirs assisted by cluster analysis and deep convolutional generative adversarial networks. J. Pet. Sci. Eng. 2020, 187, 106742. [Google Scholar] [CrossRef]
- Chen, L.F.; Guo, H.X.; Gong, P.S.; Yang, Y.Y.; Zuo, Z.L.; Gu, M.Y. Landslide susceptibility assessment using weights-of-evidence model and cluster analysis along the highways in the Hubei section of the Three Gorges Reservoir Area. Comput. Geosci. 2021, 156, 104899. [Google Scholar] [CrossRef]
- Fu, C.; Lin, N.T.; Zhang, D.; Wen, B.; Wei, Q.Q.; Zhang, K. Prediction of reservoirs using multi-component seismic data and the deep learning method. Chin. J. Geophys. 2018, 61, 293–303. [Google Scholar]
- Yasin, O.; Ding, Y.; Baklouti, S.; Boateng, C.D.; Du, Q.Z.; Golsanami, N. An integrated fracture parameter prediction and characterization method in deeply-buried carbonate reservoirs based on deep neural network. J. Pet. Sci. Eng. 2022, 208, 109346. [Google Scholar] [CrossRef]
- Saikia, P.; Baruah, R.D.; Singh, S.K.; Chaudhuri, P.K. Artificial neural networks in the domain of reservoir characterization: A review from shallow to deep models. Comput. Geosci. 2020, 135, 104357. [Google Scholar] [CrossRef]
- Luo, S.Y.; Xu, T.J.; Wei, S.J. Prediction method and application of shale reservoirs core gas content based on machine learning. J. Appl. Phys. 2022, 204, 104741. [Google Scholar] [CrossRef]
- Yang, J.Q.; Lin, N.T.; Zhang, K.; Ding, R.W.; Jin, Z.W.; Wang, D.Y. A data-driven workflow based on multisource transfer machine learning for gas-bearing probability distribution prediction: A case study. Geophysics 2023, 88, B163–B177. [Google Scholar] [CrossRef]
- Grana, D.; Azevedo, L.; Liu, M. A comparison of deep machine learning and Monte Carlo methods for facies classification from seismic data. Geophysics 2019, 85, WA41–WA52. [Google Scholar] [CrossRef]
- Wang, J.; Cao, J.X. Data-driven S-wave velocity prediction method via a deep-learning-based deep convolutional gated recurrent unit fusion network. Geophysics 2021, 86, M185–M196. [Google Scholar] [CrossRef]
- Yang, J.Q.; Lin, N.T.; Zhang, K.; Zhang, C.; Fu, C.; Tian, G.P.; Song, C.Y. Reservoir Characterization Using Multi-component Seismic Data in a Novel Hybrid Model Based on Clustering and Deep Neural Network. Nat. Resour. Res. 2021, 30, 3429–3454. [Google Scholar] [CrossRef]
- Song, Z.H.; Yuan, S.Y.; Li, Z.M.; Wang, S.X. KNN-based gas-bearing prediction using local waveform similarity gas-indication attribute—An application to a tight sandstone reservoir. Interpretation 2022, 10, SA25–SA33. [Google Scholar] [CrossRef]
- Wang, J.; Cao, J.X.; Yuan, S. Deep learning reservoir porosity prediction method based on a spatiotemporal convolution bi-directional long short-term memory neural network model. Geomech. Energy Environ. 2021, 32, 100282. [Google Scholar] [CrossRef]
- Zheng, D.Y.; Wu, S.X.; Hou, M.C. Fully connected deep network: An improved method to predict TOC of shale reservoirs from well logs. Mar. Petrol. Geol. 2021, 132, 105205. [Google Scholar] [CrossRef]
- Mohaghegh, S.; Arefi, R.; Ameri, S.; Rose, D. Design and development of an artificial neural network for estimation of formation permeability. SPE Comput. Appl. 1995, 7, 151–154. [Google Scholar] [CrossRef]
- Brantson, E.T.; Ju, B.S.; Ziggah, Y.Y.; Akwensi, P.H.; Sun, Y.; Wu, D.; Addo, B.J. Forecasting of Horizontal Gas Well Production Decline in Unconventional Reservoirs using Productivity, Soft Computing and Swarm Intelligence Models. Nat. Resour. Res. 2019, 28, 717–756. [Google Scholar] [CrossRef]
- Keyvani, F.; Amani, M.J.; Kalantariasl, A.; Vahdani, H. Assessment of Empirical Pressure–Volume–Temperature Correlations in Gas Condensate Reservoir Fluids: Case Studies. Nat. Resour. Res. 2020, 29, 1857–1874. [Google Scholar] [CrossRef]
- Saboori, M.; Homayouni, S.; Hosseini, R.S.; Zhang, Y. Optimum Feature and Classifier Selection for Accurate Urban Land Use/Cover Mapping from Very High Resolution Satellite Imagery. Remote Sens. 2022, 14, 2097. [Google Scholar] [CrossRef]
- Ebtehaj, I.; Bonakdari, H.; Zaji, A.H.; Gharabaghi, B. Evolutionary optimization of neural network to predict sediment transport without sedimentation. Complex Intell. Syst. 2021, 7, 401–416. [Google Scholar] [CrossRef]
- Mohamadi-Baghmolaei, M.; Sakhaei, Z.; Azin, R.; Osfouri, S.; Zendehboudim, S.; Shiri, H.; Duan, X.L. Modeling of well productivity enhancement in a gas-condensate reservoir through wettability alteration: A comparison between smart optimization strategies. J. Nat. Gas Sci. Eng. 2021, 94, 104059. [Google Scholar] [CrossRef]
- Sadowski, L.; Nikoo, M. Corrosion current density prediction in reinforced concrete by imperialist competitive algorithm. Neural Comput. Appl. 2014, 25, 1627–1638. [Google Scholar] [CrossRef] [PubMed]
- Amiri, M.; Ghiasi-Freez, J.; Golkar, B.; Hatampour, A. Improving water saturation estimation in a tight shaly sandstone reservoir using artificial neural network optimized by imperialist competitive algorithm—A case study. J. Pet. Sci. Eng. 2015, 127, 347–358. [Google Scholar] [CrossRef]
- Ouadfeul, S.A.; Aliouane, L. Total Organic Carbon Prediction in Shale Gas Reservoirs from Well Logs Data Using the Multilayer Perceptron Neural Network with Levenberg Marquardt Training Algorithm: Application to Barnett Shale. Arab. J. Sci. Eng. 2015, 40, 3345–3349. [Google Scholar] [CrossRef]
- Chanda, S.; Singh, R.P. Prediction of gas production potential and hydrological properties of a methane hydrate reservoir using ANN-GA based framework. Therm. Sci. Eng. Prog. 2019, 11, 380–391. [Google Scholar] [CrossRef]
- Mahmoodpour, S.; Kamari, E.; Esfahani, M.R.; Mehr, A.K. Prediction of cementation factor for low-permeability Iranian carbonate reservoirs using particle swarm optimization-artificial neural network model and genetic programming algorithm. J. Pet. Sci. Eng. 2021, 197, 108102. [Google Scholar] [CrossRef]
- Mcculloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biol. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Mehrjardi, R.T.; Emadi, M.; Cherati, A.; Heung, B.; Mosavi, A.; Scholten, T. Bio-Inspired Hybridization of Artificial Neural Networks: An Application for Mapping the Spatial Distribution of Soil Texture Fractions. Remote Sens. 2021, 13, 1025. [Google Scholar] [CrossRef]
- Othman, A.; Fathy, M.; Mohamed, I.A. Application of Artificial Neural Network in seismic reservoir characterization: A case study from Offshore Nile Delta. Earth Sci. Inform. 2021, 14, 669–676. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In MHS95, Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; IEEE: Piscataway, NJ, USA, 1995; pp. 39–43. [Google Scholar]
- Kalantar, B.; Ueda, N.; Saeidi, V.; Janizadeh, S.; Shabani, F.; Ahmadi, K.; Shabani, F. Deep Neural Network Utilizing Remote Sensing Datasets for Flood Hazard Susceptibility Mapping in Brisbane, Australia. Remote Sens. 2021, 13, 2638. [Google Scholar] [CrossRef]
- Lai, J.; Wang, G.W.; Fan, Z.Y.; Chen, J.; Wang, S.C.; Fan, X.Q. Sedimentary characterization of a braided delta using well logs: The Upper Triassic Xujiahe Formation in Central Sichuan Basin, China. J. Pet. Sci. Eng. 2017, 154, 172–193. [Google Scholar] [CrossRef]
- Zhang, G.Z.; Yang, R.; Zhou, Y.; Li, L.; Du, B.Y. Seismic fracture characterization in tight sand reservoirs: A case study of the Xujiahe Formation, Sichuan Basin, China. J. Appl. Phys. 2022, 203, 104690. [Google Scholar] [CrossRef]
- Zhang, K.; Lin, N.T.; Yang, J.Q.; Jin, Z.W.; Li, G.H.; Ding, R.W. Predicting gas bearing distribution using DNN based on multi-component seismic data: A reservoir quality evaluation using structural and fracture evaluation factors. Petrol. Sci. 2022, 19, 1566–1581. [Google Scholar] [CrossRef]
- Hossain, S. Application of seismic attribute analysis in fluvial seismic geomorphology. J. Pet. Explor, Prod. Technol. 2020, 10, 1009–1019. [Google Scholar] [CrossRef]
- Zhang, K.; Lin, N.T.; Yang, J.Q.; Zhang, D.; Cui, Y.; Jin, Z.W. An intelligent approach for gas reservoir identification and structural evaluation by ANN and Viterbi algorithm—A case study from the Xujiahe Formation, Western Sichuan Depression, China. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5904412. [Google Scholar] [CrossRef]
- Zhang, K.; Lin, N.T.; Fu, C.; Zhang, D.; Jin, X.; Zhang, C. Reservoir characterization method with multi-component seismic data by unsupervised learning and colour feature blending. Explor. Geophys. 2019, 50, 269–280. [Google Scholar] [CrossRef]
- Lin, N.T.; Zhang, D.; Zhang, K.; Wang, S.J.; Fu, C.; Zhang, J.B. Predicting distribution of hydrocarbon reservoirs with seismic data based on learning of the small-sample convolution neural network. Chin. J. Geophys. 2018, 61, 4110–4125. [Google Scholar]
- Gao, J.H.; Song, Z.H.; Gui, J.Y.; Yuan, S.Y. Gas-Bearing Prediction Using Transfer Learning and CNNs: An Application to a Deep Tight Dolomite Reservoir. IEEE Geosci. Remote Sens. Lett. 2020, 99, 1–5. [Google Scholar] [CrossRef]
- Yagiz, S.; Karahan, H. Prediction of hard rock TBM penetration rate using particle swarm optimization. Int. J. Rock Mech. Min. Sci. 2011, 48, 427–433. [Google Scholar] [CrossRef]
- Bishop, C.M. Neural Networks for Pattern Recognition; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Reynaldi, A.; Lukas, S.; Margaretha, H. Backpropagation and Levenberg–Marquardt algorithm for training finite element neural network. In Proceedings of the 2012 Sixth UKSim/AMSS European Symposium on Computer Modeling and Simulation (EMS), Valletta, Malta, 14–16 November 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 89–94. [Google Scholar]
- Martin, G.S.; Wiley, R.; Marfurt, K.J. Marmousi2: An elastic upgrade for Marmousi. Lead. Edge 2006, 25, 113–224. [Google Scholar] [CrossRef]
- Chen, W.; Chen, Y.Z.; Tsangaratos, P.; Ilia, I.; Wang, X.J. Combining Evolutionary Algorithms and Machine Learning Models in Landslide Susceptibility Assessments. Remote Sens. 2020, 12, 3854. [Google Scholar] [CrossRef]
- Wang, J.; Cao, J.X.; Yuan, S. Shear wave velocity prediction based on adaptive particle swarm optimization optimized recurrent neural network. J. Petrol. Sci. Eng. 2020, 194, 107466. [Google Scholar] [CrossRef]
- Qian, L.H.; Zang, S.Y.; Man, H.R.; Sun, L.; Wu, X.W. Determination of the Stability of a High and Steep Highway Slope in a Basalt Area Based on Iron Staining Anomalies. Remote Sens. 2023, 15, 3021. [Google Scholar] [CrossRef]
- Weitkamp, T.; Karimi, P. Evaluating the Effect of Training Data Size and Composition on the Accuracy of Smallholder Irrigated Agriculture Mapping in Mozambique Using Remote Sensing and Machine Learning Algorithms. Remote Sens. 2023, 15, 3017. [Google Scholar] [CrossRef]









| C1 | C2 | Combination of C1 and C2 | RMSE | Rank |
|---|---|---|---|---|
| 0.5 | 2.5 | 3 | 0.0686 | 6 |
| 1 | 2 | 3 | 0.7126 | 8 |
| 1.25 | 2.75 | 4 | 0.0642 | 3 |
| 1.5 | 2.5 | 4 | 0.0654 | 5 |
| 1.75 | 2.25 | 4 | 0.0606 | 1 |
| 2 | 2 | 4 | 0.0623 | 2 |
| 2 | 3 | 5 | 0.0692 | 7 |
| 2.5 | 2.5 | 5 | 0.0645 | 4 |
| Model | Performance Indicators | ||
|---|---|---|---|
| MSE | RMSE | R2 | |
| ANN | 0.0069 | 0.0833 | 0.9625 |
| PSO-ANN | 0.0062 | 0.0786 | 0.9713 |
| MPSO-ANN | 0.0058 | 0.0762 | 0.9761 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Lin, N.; Zhang, K.; Jia, L.; Zhang, D.; Li, G.; Zhang, J. A Parametric Study of MPSO-ANN Techniques in Gas-Bearing Distribution Prediction Using Multicomponent Seismic Data. Remote Sens. 2023, 15, 3987. https://doi.org/10.3390/rs15163987
Yang J, Lin N, Zhang K, Jia L, Zhang D, Li G, Zhang J. A Parametric Study of MPSO-ANN Techniques in Gas-Bearing Distribution Prediction Using Multicomponent Seismic Data. Remote Sensing. 2023; 15(16):3987. https://doi.org/10.3390/rs15163987
Chicago/Turabian StyleYang, Jiuqiang, Niantian Lin, Kai Zhang, Lingyun Jia, Dong Zhang, Guihua Li, and Jinwei Zhang. 2023. "A Parametric Study of MPSO-ANN Techniques in Gas-Bearing Distribution Prediction Using Multicomponent Seismic Data" Remote Sensing 15, no. 16: 3987. https://doi.org/10.3390/rs15163987
APA StyleYang, J., Lin, N., Zhang, K., Jia, L., Zhang, D., Li, G., & Zhang, J. (2023). A Parametric Study of MPSO-ANN Techniques in Gas-Bearing Distribution Prediction Using Multicomponent Seismic Data. Remote Sensing, 15(16), 3987. https://doi.org/10.3390/rs15163987