Simulation and Driving Factor Analysis of Satellite-Observed Terrestrial Water Storage Anomaly in the Pearl River Basin Using Deep Learning
Abstract
1. Introduction
2. Materials and Methods
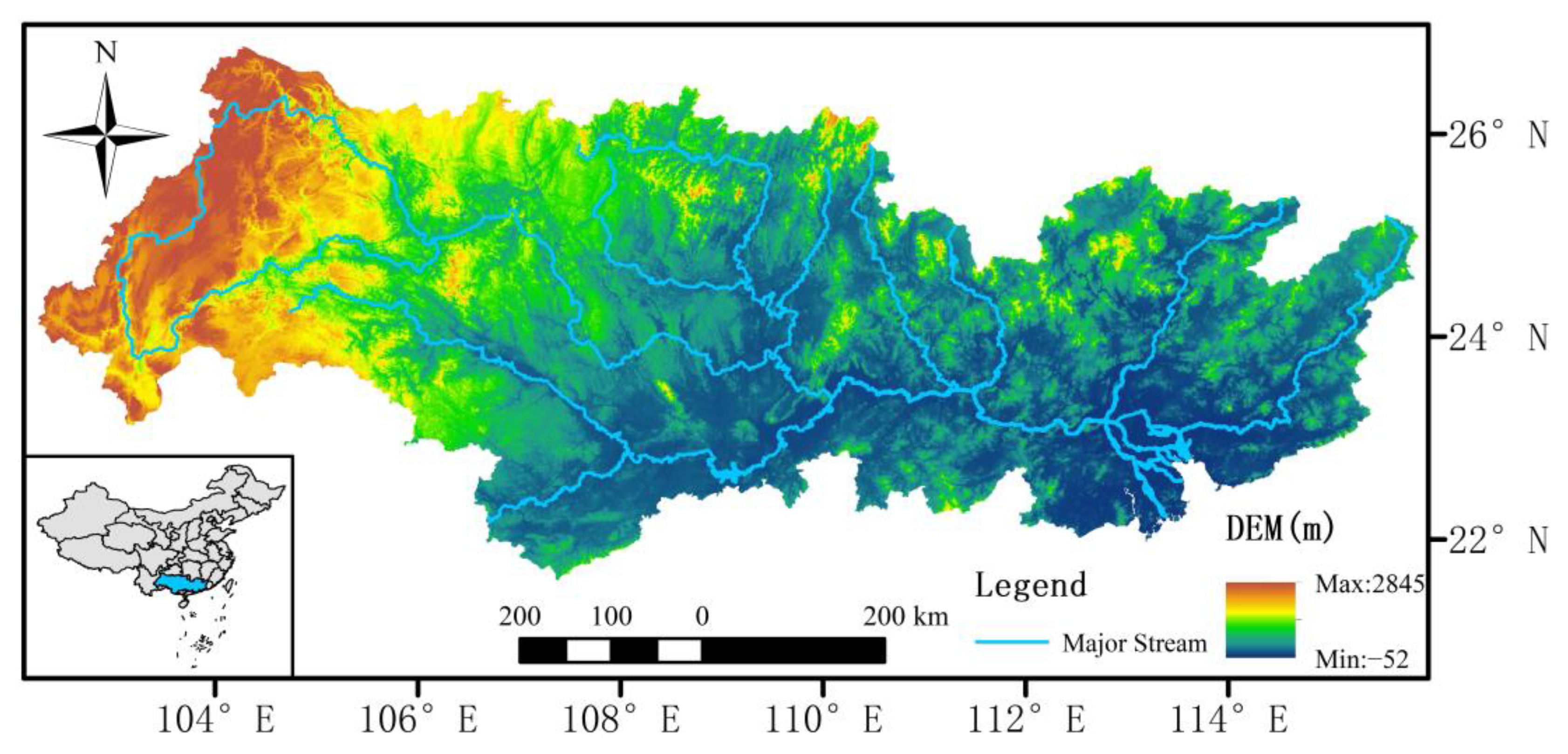
2.1. Study Area
2.2. Data Sources
2.2.1. GRACE Data
2.2.2. Input Data
2.3. Methods
2.3.1. LSTM Model
2.3.2. Model Evaluation Metrics
2.3.3. Interpretation Methods
3. Results
3.1. Performance of the LSTM Models
3.2. Correlation and Importance Analysis of TWSA Driving Factors Based on SHAP
3.3. Lead Time Analysis between GRACE TWSA and Driving Factors
4. Discussion
4.1. The Uncertainty of the LSTM Model
4.2. Analysis of Natural Driving Factors
4.3. Uncertainty of Explainable Machine Learning
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, F.P.; Kusche, J.; Chao, N.F.; Wang, Z.T.; Locher, A. Long-Term (1979–Present) Total Water Storage Anomalies Over the Global Land Derived by Reconstructing GRACE Data. Geophys. Res. Lett. 2021, 48, e2021GL093492. [Google Scholar] [CrossRef]
- Rodell, M.; Famiglietti, J.S.; Wiese, D.N.; Reager, J.T.; Beaudoing, H.K.; Landerer, F.W.; Lo, M.H. Emerging trends in global freshwater availability. Nature 2019, 565, E7. [Google Scholar] [CrossRef]
- Xie, X.M.; He, B.; Guo, L.L.; Miao, C.Y.; Zhang, Y.F. Detecting hotspots of interactions between vegetation greenness and terrestrial water storage using satellite observations. Remote Sens. Environ. 2019, 231, 111259. [Google Scholar] [CrossRef]
- Kusche, J.; Eicker, A.; Forootan, E.; Springer, A.; Longuevergne, L. Mapping probabilities of extreme continental water storage changes from space gravimetry. Geophys. Res. Lett. 2016, 43, 8026–8034. [Google Scholar] [CrossRef]
- Huang, Z.Y.; Jiao, J.J.; Luo, X.; Pan, Y.; Jin, T.Y. Drought and Flood Characterization and Connection to Climate Variability in the Pearl River Basin in Southern China Using Long-Term GRACE and Reanalysis Data. J. Clim. 2021, 34, 2053–2078. [Google Scholar] [CrossRef]
- Pokhrel, Y.; Felfelani, F.; Satoh, Y.; Boulange, J.; Burek, P.; Gadeke, A.; Gerten, D.; Gosling, S.N.; Grillakis, M.; Gudmundsson, L.; et al. Global terrestrial water storage and drought severity under climate change. Nat. Clim. Change 2021, 11, 226–233. [Google Scholar] [CrossRef]
- Luo, Z.; Yao, C.; Li, Q.; Huang, Z.J. Terrestrial water storage changes over the Pearl River Basin from GRACE and connections with Pacific climate variability. Geod. Geodyn. 2016, 7, 171–179. [Google Scholar] [CrossRef]
- Wahr, J.; Swenson, S.; Zlotnicki, V.; Velicogna, I. Time-variable gravity from GRACE: First results. Geophys. Res. Lett. 2004, 31, 11. [Google Scholar] [CrossRef]
- Deng, H.J.; Chen, Y.N.; Chen, X.W. Driving factors and changes in components of terrestrial water storage in the endorheic Tibetan Plateau. J. Hydrol. 2022, 612, 128225. [Google Scholar] [CrossRef]
- Guo, F.; Jiang, G.H.; Yuan, D.X.; Polk, J.S. Evolution of major environmental geological problems in karst areas of Southwestern China. Environ. Earth Sci. 2013, 69, 2427–2435. [Google Scholar] [CrossRef]
- Yao, C.L.; Luo, Z.C. Karstic water storage response to the recent droughts in Southwest China estimated from satellite gravimetry. Int. Conf. Intell. Earth Obs. Appl. 2015, 9808, 334–339. [Google Scholar]
- Sun, A.Y.; Scanlon, B.R. How can Big Data and machine learning benefit environment and water management: A survey of methods, applications, and future directions. Environ. Res. Lett. 2019, 14, 073001. [Google Scholar] [CrossRef]
- Hamshaw, S.D.; Dewoolkar, M.M.; Schroth, A.W.; Wemple, B.C.; Rizzo, D.M. A New Machine-Learning Approach for Classifying Hysteresis in Suspended-Sediment Discharge Relationships Using High-Frequency Monitoring Data. Water Resour. Res. 2018, 54, 4040–4058. [Google Scholar] [CrossRef]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N.; Prabhat. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef]
- Xue, M.; Hang, R.L.; Liu, Q.S.; Yuan, X.T.; Lu, X.Y. CNN-based near-real-time precipitation estimation from Fengyun-2 satellite over Xinjiang, China. Atmos. Res. 2021, 250, 105337. [Google Scholar] [CrossRef]
- Huang, X.; Gao, L.; Crosbie, R.S.; Zhang, N.; Fu, G.B.; Doble, R. Groundwater Recharge Prediction Using Linear Regression, Multi-Layer Perception Network, and Deep Learning. Water 2019, 11, 1879. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall-runoff modelling using Long Short-Term Memory (LSTM) networks. Hydrol. Earth Syst. Sci. 2018, 22, 6005–6022. [Google Scholar] [CrossRef]
- Long, D.; Shen, Y.J.; Sun, A.; Hong, Y.; Longuevergne, L.; Yang, Y.T.; Li, B.; Chen, L. Drought and flood monitoring for a large karst plateau in Southwest China using extended GRACE data. Remote Sens. Environ. 2014, 155, 145–160. [Google Scholar] [CrossRef]
- Qiu, R.J.; Wang, Y.K.; Rhoads, B.; Wang, D.; Qiu, W.J.; Tao, Y.W.; Wu, J.C. River water temperature forecasting using a deep learning method. J. Hydrol. 2021, 595, 126016. [Google Scholar] [CrossRef]
- Mo, S.X.; Zhong, Y.L.; Forootan, E.; Mehrnegar, N.; Yin, X.; Wu, J.C.; Feng, W.; Shi, X.Q. Bayesian convolutional neural networks for predicting the terrestrial water storage anomalies during GRACE and GRACE-FO gap. J. Hydrol. 2022, 604, 127244. [Google Scholar] [CrossRef]
- Fang, K.; Pan, M.; Shen, C.P. The Value of SMAP for Long-Term Soil Moisture Estimation With the Help of Deep Learning. IEEE Trans. Geosci. Remote Sens. 2019, 57, 2221–2233. [Google Scholar] [CrossRef]
- Cheng, S.J.; Cheng, L.; Qin, S.J.; Zhang, L.; Liu, P.; Liu, L.; Xu, Z.C.; Wang, Q.L. Improved Understanding of How Catchment Properties Control Hydrological Partitioning Through Machine Learning. Water Resour. Res. 2022, 58, e2021WR031412. [Google Scholar] [CrossRef]
- Li, L.Y.; Zeng, Z.Z.; Zhang, G.; Duan, K.; Liu, B.J.; Cai, X.T. Exploring the Individualized Effect of Climatic Drivers on MODIS Net Primary Productivity through an Explainable Machine Learning Framework. Remote Sens. 2022, 14, 4401. [Google Scholar] [CrossRef]
- Jiang, S.J.; Zheng, Y.; Wang, C.; Babovic, V. Uncovering Flooding Mechanisms Across the Contiguous United States Through Interpretive Deep Learning on Representative Catchments. Water Resour. Res. 2022, 58, e2021WR030185. [Google Scholar] [CrossRef]
- Kondylatos, S.; Prapas, I.; Ronco, M.; Papoutsis, I.; Camps-Valls, G.; Piles, M.; Fernandez-Torres, M.A.; Carvalhais, N. Wildfire Danger Prediction and Understanding With Deep Learning. Geophys. Res. Lett. 2022, 49, e2022GL099368. [Google Scholar] [CrossRef]
- Sihi, D.; Dari, B.; Kuruvila, A.P.; Jha, G.; Basu, K. Explainable Machine Learning Approach Quantified the Long-Term (1981–2015) Impact of Climate and Soil Properties on Yields of Major Agricultural Crops Across CONUS. Front. Sustain. Food Syst. 2022, 6, 847892. [Google Scholar] [CrossRef]
- Sonnewald, M.; Lguensat, R. Revealing the Impact of Global Heating on North Atlantic Circulation Using Transparent Machine Learning. J. Adv. Model. Earth Syst. 2021, 13, e2021MS002496. [Google Scholar] [CrossRef]
- Fan, M.; Zhang, L.J.; Liu, S.Y.; Yang, T.T.; Lu, D. Investigation of hydrometeorological influences on reservoir releases using explainable machine learning methods. Front. Water 2023, 5, 1112970. [Google Scholar] [CrossRef]
- Cai, X.; Li, L.; Fisher, J.B.; Zeng, Z.; Zhou, S.; Tan, X.; Liu, B.; Chen, X. The responses of ecosystem water use efficiency to CO2, nitrogen deposition, and climatic drivers across China. J. Hydrol. 2023, 622, 129696. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.I. A Unified Approach to Interpreting Model Predictions. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Lundberg, S.M.; Erion, G.G.; Lee, S.-I. Consistent individualized feature attribution for tree ensembles. arXiv 2018, arXiv:1802.03888. [Google Scholar]
- Sun, Z.L.; Long, D.; Yang, W.T.; Li, X.Y.; Pan, Y. Reconstruction of GRACE Data on Changes in Total Water Storage Over the Global Land Surface and 60 Basins. Water Resour. Res. 2020, 56, e2019WR026250. [Google Scholar] [CrossRef]
- Pearl River Water Resources Committee (PRWRC). The Zhujiang Archive; Guangdong Science and Technology Press: Guangzhou, China, 1991; Volume 1. (In Chinese) [Google Scholar]
- Lü-Liu, L.; Tong, J.; Jin-Ge, X.; Jian-Qing, Z.; Yong, L.J. Responses of hydrological processes to climate change in the Zhujiang River basin in the 21st century. Adv. Clim. Change Res. 2012, 3, 84–91. [Google Scholar] [CrossRef]
- Zhang, Q.; Xiao, M.Z.; Singh, V.P.; Li, J.F. Regionalization and spatial changing properties of droughts across the Pearl River basin, China. J. Hydrol. 2012, 472, 355–366. [Google Scholar] [CrossRef]
- Zhang, Q.; Singh, V.P.; Peng, J.T.; Chen, Y.D.; Li, J.F. Spatial-temporal changes of precipitation structure across the Pearl River basin, China. J. Hydrol. 2012, 440, 113–122. [Google Scholar] [CrossRef]
- Loomis, B.D.; Luthcke, S.B.; Sabaka, T.J. Regularization and error characterization of GRACE mascons. J. Geod. 2019, 93, 1381–1398. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Zhang, Z.Z.; Save, H.; Wiese, D.N.; Landerer, F.W.; Long, D.; Longuevergne, L.; Chen, J.L. Global evaluation of new GRACE mascon products for hydrologic applications. Water Resour. Res. 2016, 52, 9412–9429. [Google Scholar] [CrossRef]
- Murdoch, W.J.; Singh, C.; Kumbier, K.; Abbasi-Asl, R.; Yu, B. Definitions, methods, and applications in interpretable machine learning. Proc. Natl. Acad. Sci. USA 2019, 116, 22071–22080. [Google Scholar] [CrossRef] [PubMed]
- Harris, I.; Osborn, T.J.; Jones, P.; Lister, D. Version 4 of the CRU TS monthly high-resolution gridded multivariate climate dataset. Sci. Data 2020, 7, 109. [Google Scholar] [CrossRef] [PubMed]
- Martens, B.; Miralles, D.G.; Lievens, H.; van der Schalie, R.; de Jeu, R.A.M.; Fernandez-Prieto, D.; Beck, H.E.; Dorigo, W.A.; Verhoest, N.E.C. GLEAM v3: Satellite-based land evaporation and root-zone soil moisture. Geosci. Model Dev. 2017, 10, 1903–1925. [Google Scholar] [CrossRef]
- Miralles, D.G.; Holmes, T.R.H.; De Jeu, R.A.M.; Gash, J.H.; Meesters, A.G.C.A.; Dolman, A.J. Global land-surface evaporation estimated from satellite-based observations. Hydrol. Earth Syst. Sci. 2011, 15, 453–469. [Google Scholar] [CrossRef]
- Lin, W.Y.; Yuan, H.; Dong, W.Z.; Zhang, S.P.; Liu, S.F.; Wei, N.; Lu, X.J.; Wei, Z.W.; Hu, Y.; Dai, Y.J. Reprocessed MODIS Version 6.1 Leaf Area Index Dataset and Its Evaluation for Land Surface and Climate Modeling. Remote Sens. 2023, 15, 1780. [Google Scholar] [CrossRef]
- Yuan, H.; Dai, Y.J.; Xiao, Z.Q.; Ji, D.Y.; Shangguan, W. Reprocessing the MODIS Leaf Area Index products for land surface and climate modelling. Remote Sens. Environ. 2011, 115, 1171–1187. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Jing, W.L.; Zhao, X.D.; Yao, L.; Di, L.P.; Yang, J.; Li, Y.; Guo, L.Y.; Zhou, C.H. Can Terrestrial Water Storage Dynamics be Estimated From Climate Anomalies? Earth Space Sci. 2020, 7, e2019EA000959. [Google Scholar] [CrossRef]
- Chen, X.; Wang, S.; Gao, H.; Huang, J.; Shen, C.; Li, Q.; Qi, H.; Zheng, L.; Liu, M. Comparison of deep learning models and a typical process-based model in glacio-hydrology simulation. J. Hydrol. 2022, 615, 128562. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Strumbelj, E.; Kononenko, I. Explaining prediction models and individual predictions with feature contributions. Knowl. Inf. Syst. 2014, 41, 647–665. [Google Scholar] [CrossRef]
- Wang, F.; Chen, Y.N.; Li, Z.; Fang, G.H.; Li, Y.P.; Wang, X.X.; Zhang, X.Q.; Kayumba, P.M. Developing a Long Short-Term Memory (LSTM)-Based Model for Reconstructing Terrestrial Water Storage Variations from 1982 to 2016 in the Tarim River Basin, Northwest China. Remote Sens. 2021, 13, 889. [Google Scholar] [CrossRef]
- Wang, J.; Huang, Y.; Cao, Y.; Wang, Y. Spatial and temporal variation of water storage in recent seven years from GRACE in Yunnan Province. Water Sav. Irrig. 2012, 5, 1–5. [Google Scholar]
- Adadi, A.; Berrada, M. Peeking Inside the Black-Box: A Survey on Explainable Artificial Intelligence (XAI). IEEE Access 2018, 6, 52138–52160. [Google Scholar] [CrossRef]
- Sun, A.Y.; Scanlon, B.R.; Zhang, Z.; Walling, D.; Bhanja, S.N.; Mukherjee, A.; Zhong, Z. Combining Physically Based Modeling and Deep Learning for Fusing GRACE Satellite Data: Can We Learn From Mismatch? Water Resour. Res. 2019, 55, 1179–1195. [Google Scholar] [CrossRef]









| Data | Data Sources | Spatial Resolution (°) | Temporal Resolution | Date |
|---|---|---|---|---|
| Precipitation | CRU | 0.5 | Monthly | April 2002–December 2020 |
| Temperature | CRU | 0.5 | Monthly | April 2002–December 2020 |
| AET | GLEAM | 0.25 | Monthly | April 2002–December 2020 |
| Runoff | ERA5-Land | 0.25 | Monthly | April 2002–December 2020 |
| LAI | SYSU | 0.5 | Monthly | April 2002–December 2020 |
| TWSA | NASA GSFC | 0.5 | Monthly | April 2002–December 2020 |
| Group ID | Training Set | Testing Set |
|---|---|---|
| 1 | October 2005–December 2020 | April 2002–September 2005 |
| 2 | April 2002–September 2005, April 2009–December 2020 | October 2005–March 2009 |
| 3 | April 2002–March 2009, October 2012–December 2020 | April 2009–September 2012 |
| 4 | April 2002–September 2012, April 2016–December 2020 | October 2012–March 2016 |
| 5 | April 2002–March 2016 | April 2016–December 2020 |
| Group ID | Training Period | Testing Period | ||||||
|---|---|---|---|---|---|---|---|---|
| r | NRMSE | NSE | bias | r | NRMSE | NSE | bias | |
| 1 | 0.898 | 0.044 | 0.803 | −0.166 | 0.901 | 0.058 | 0.749 | −1.241 |
| 2 | 0.917 | 0.04 | 0.841 | −0.062 | 0.909 | 0.046 | 0.823 | 0.279 |
| 3 | 0.895 | 0.044 | 0.801 | −0.067 | 0.855 | 0.064 | 0.714 | −0.997 |
| 4 | 0.949 | 0.031 | 0.896 | 0.412 | 0.826 | 0.06 | 0.665 | −0.22 |
| 5 | 0.918 | 0.038 | 0.837 | 0.417 | 0.777 | 0.068 | 0.586 | −0.222 |
| Mean | 0.915 | 0.039 | 0.836 | 0.107 | 0.854 | 0.059 | 0.707 | −0.48 |
| Std | 0.022 | 0.005 | 0.039 | 0.284 | 0.055 | 0.008 | 0.089 | 0.624 |
| Group ID | Training Period | Testing Period | ||||||
|---|---|---|---|---|---|---|---|---|
| r | NRMSE | NSE | bias | r | NRMSE | NSE | bias | |
| 1 | 0.963 | 0.068 | 0.924 | 0.039 | 0.984 | 0.078 | 0.946 | −0.848 |
| 2 | 0.969 | 0.060 | 0.937 | −0.062 | 0.962 | 0.093 | 0.909 | 0.279 |
| 3 | 0.966 | 0.068 | 0.930 | 0.057 | 0.964 | 0.073 | 0.925 | −0.534 |
| 4 | 0.966 | 0.069 | 0.925 | −0.310 | 0.966 | 0.081 | 0.909 | −0.165 |
| 5 | 0.969 | 0.068 | 0.929 | −0.115 | 0.957 | 0.081 | 0.871 | −0.244 |
| Mean | 0.967 | 0.067 | 0.929 | −0.078 | 0.967 | 0.081 | 0.912 | −0.302 |
| Std | 0.003 | 0.004 | 0.005 | 0.148 | 0.010 | 0.007 | 0.027 | 0.422 |
| Group ID | Training Period | Testing Period | ||||||
|---|---|---|---|---|---|---|---|---|
| r | NRMSE | NSE | bias | r | NRMSE | NSE | bias | |
| 1 | 0.914 | 0.096 | 0.805 | −0.063 | 0.926 | 0.152 | 0.710 | −0.640 |
| 2 | 0.927 | 0.087 | 0.837 | −0.179 | 0.933 | 0.110 | 0.819 | 0.645 |
| 3 | 0.905 | 0.104 | 0.790 | 1.796 | 0.890 | 0.130 | 0.744 | 0.108 |
| 4 | 0.952 | 0.074 | 0.888 | 0.338 | 0.841 | 0.160 | 0.630 | −0.246 |
| 5 | 0.936 | 0.089 | 0.845 | 0.274 | 0.851 | 0.168 | 0.433 | 0.205 |
| Mean | 0.927 | 0.090 | 0.833 | 0.433 | 0.888 | 0.144 | 0.667 | 0.014 |
| Std | 0.018 | 0.011 | 0.038 | 0.793 | 0.042 | 0.024 | 0.147 | 0.484 |
| Variables | Unit | Rate of Change | Coincident Correlation Coefficient | Lag Time/Month | Lagged Correlation Coefficient |
|---|---|---|---|---|---|
| Precipitation | mm | 0.101 | 0.50 * | 2 | 0.79 * |
| Runoff | mm | 0 | 0.54 * | 2 | 0.76 * |
| AET | mm | 0.024 | 0.67 * | 1 | 0.77 * |
| Temperature | °C | 0.003 | 0.67 * | 1 | 0.75 * |
| LAI | - | 0.002 | 0.79 * | 0 | 0.79 * |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, H.; Feng, G.; Cao, Y.; Feng, G.; Dai, Z.; Tian, P.; Wei, J.; Cai, X. Simulation and Driving Factor Analysis of Satellite-Observed Terrestrial Water Storage Anomaly in the Pearl River Basin Using Deep Learning. Remote Sens. 2023, 15, 3983. https://doi.org/10.3390/rs15163983
Huang H, Feng G, Cao Y, Feng G, Dai Z, Tian P, Wei J, Cai X. Simulation and Driving Factor Analysis of Satellite-Observed Terrestrial Water Storage Anomaly in the Pearl River Basin Using Deep Learning. Remote Sensing. 2023; 15(16):3983. https://doi.org/10.3390/rs15163983
Chicago/Turabian StyleHuang, Haijun, Guanbin Feng, Yeer Cao, Guanning Feng, Zhikai Dai, Peizhi Tian, Juncheng Wei, and Xitian Cai. 2023. "Simulation and Driving Factor Analysis of Satellite-Observed Terrestrial Water Storage Anomaly in the Pearl River Basin Using Deep Learning" Remote Sensing 15, no. 16: 3983. https://doi.org/10.3390/rs15163983
APA StyleHuang, H., Feng, G., Cao, Y., Feng, G., Dai, Z., Tian, P., Wei, J., & Cai, X. (2023). Simulation and Driving Factor Analysis of Satellite-Observed Terrestrial Water Storage Anomaly in the Pearl River Basin Using Deep Learning. Remote Sensing, 15(16), 3983. https://doi.org/10.3390/rs15163983






