Joint Design of Complementary Sequence and Receiving Filter with High Doppler Tolerance for Simultaneously Polarimetric Radar
Abstract
:1. Introduction
- (1)
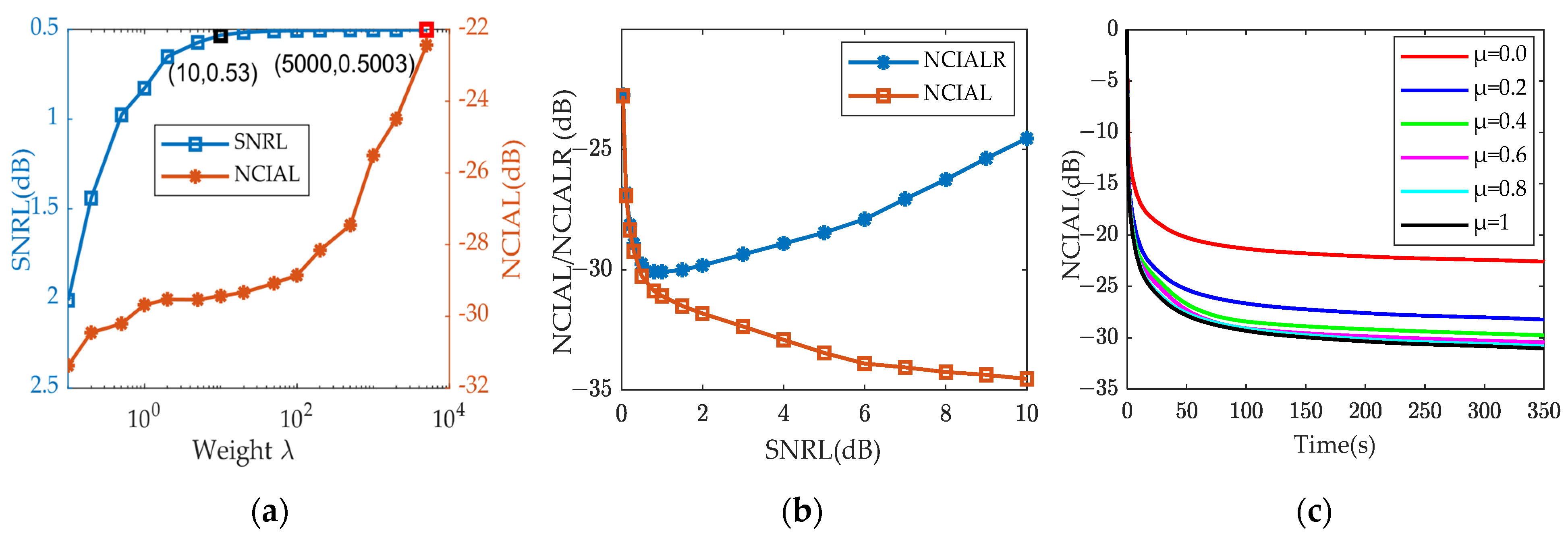
- Based on the AF, the joint design of unimodular orthogonal CCS (UOCCS) and receiving filter is proposed for SPR waveforms. Specifically, the complementary integrated sidelobe level (CISL) of Auto-AFs, the complementary integrated isolation level (CIIL) of Cross-AFs, and the mismatch constraint with controllable SNR loss are all considered simultaneously in the objective function formulated for optimization. By setting the predefined SNR loss, a trade-off between the suppression of CISL/CIIL and actual SNR loss can be achieved. In other words, the work in [41,42] was extended, i.e., the proposed scheme not only considers the low sidelobe of the pulse compression of CCS but also takes into account the orthogonality for all time delays within appropriate DFR.
- (2)
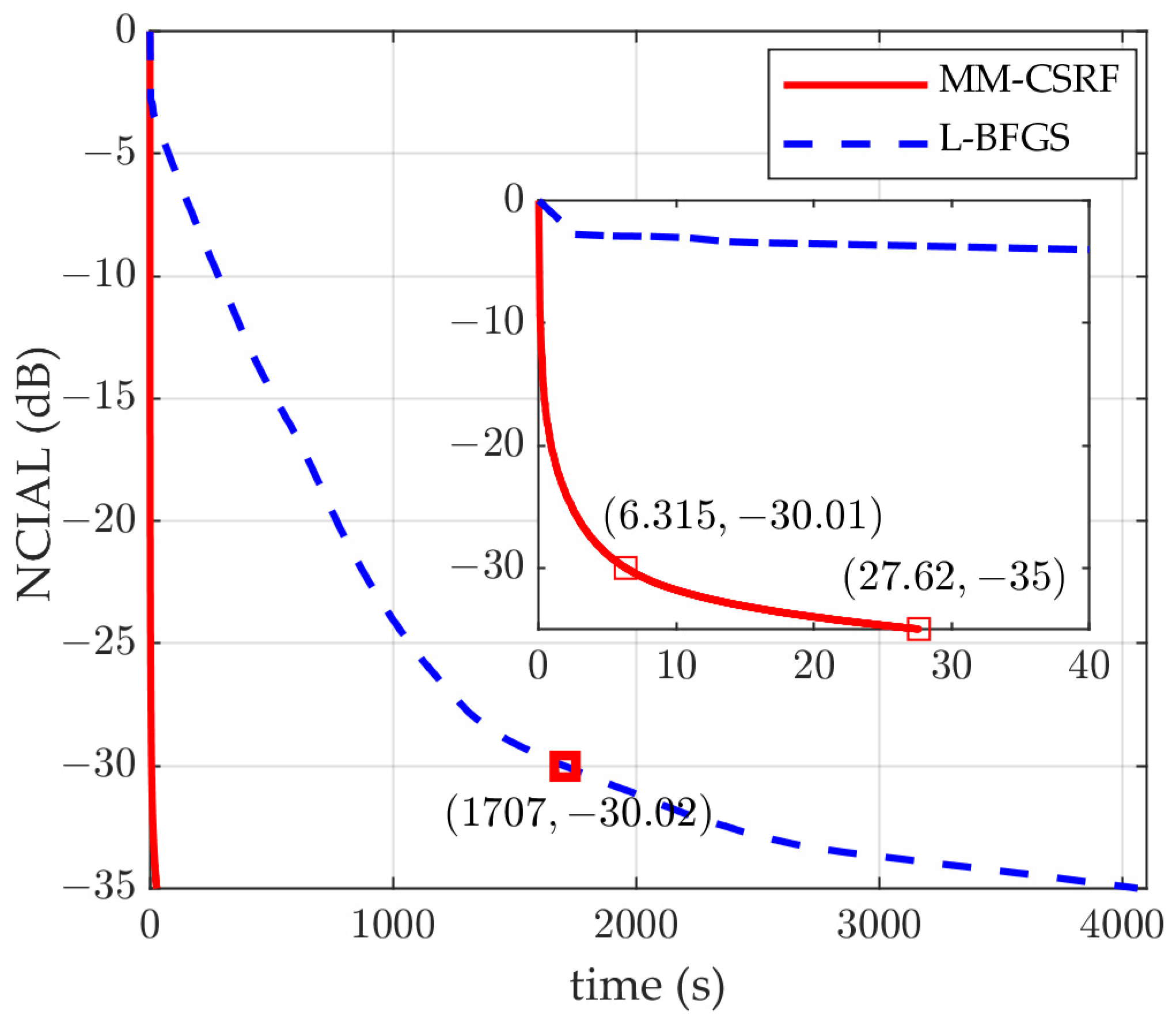
- The joint design problem is decomposed into subproblems of waveform design and receiving filter design via theoretical derivation, which is solved via an alternatively iterative approach. Concretely, the two subproblems are transformed into nonconvex quadratic terms containing the Hermitian matrix. The MM method is then applied to transforming these two nonconvex quadratic terms into linear programming problems with closed solutions. By utilizing the characteristics of Toeplitz matrix-vector multiplication, the main computation step can be completed via FFT. For further improvement, the convergence speed of the algorithm, an acceleration scheme of the squared iterative method (SQUAREM) is introduced. Compared with the representative and latest MM-CCS method [34] and the L-BFGS algorithm [35], better performance is achieved by the proposed algorithm, benefiting from both the joint design and the application of the MM framework.
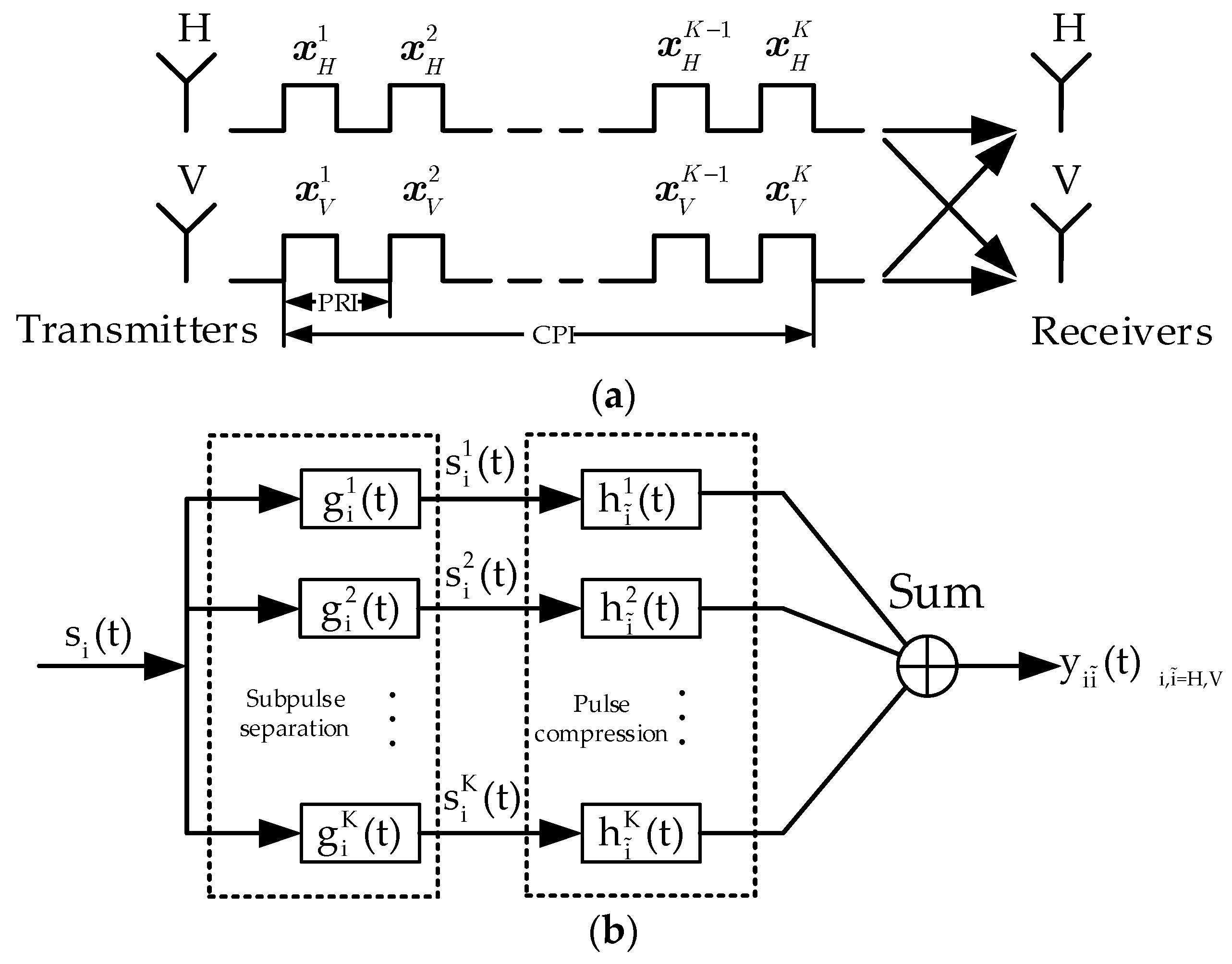
2. Problem Statement
3. Joint Design of UOCCS and Receiving Filters via MM Method
3.1. Reformulation of the Problem
3.2. Joint Optimization via the MM Method
| Algorithm 1. Joint Design CCSs and Receiving Filters with Expected AFs Shape Based on the MM Method via Alternately Iteration |
| Initialize: , pulse number , sequence and filter length , a predefine SNR loss , the DFR as . 1: Compute the predefined 2: Initialize , of length as (11) and (12) 3: compute by (28) 4: repeat 5: Compute by (34) with the designated 6: Update the receiving filters and by (35) 7: Compute by (40) with the designated 8: Update the CCSs and by (41) 9: ; 10: Output: CCS and receiving filter with expected AFs. |
3.3. Acceleration Scheme Using SQUAREM
| Algorithm 2. The Acceleration Scheme for Algorithm 1 using SQUAREM. |
| 1: Initialize: , 2: repeat 3: 4: 5: 6: 7: Compute the step-length 8: 9: while do 10: 11: 12: 13: 14: 15: until convergence. |
4. Simulations and Performance Analysis
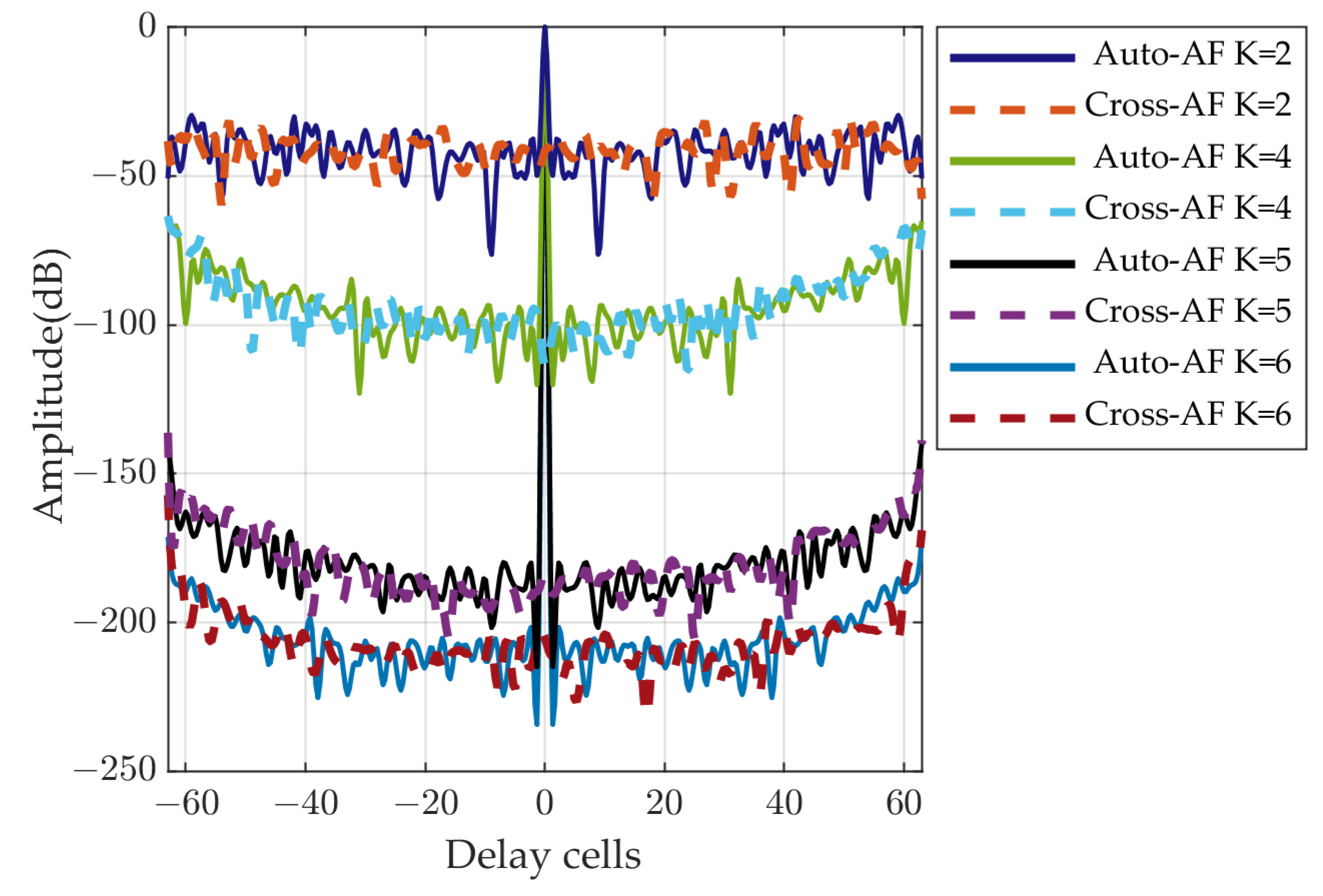
4.1. Performance of the Proposed Method
4.2. Doppler Effect Analysis
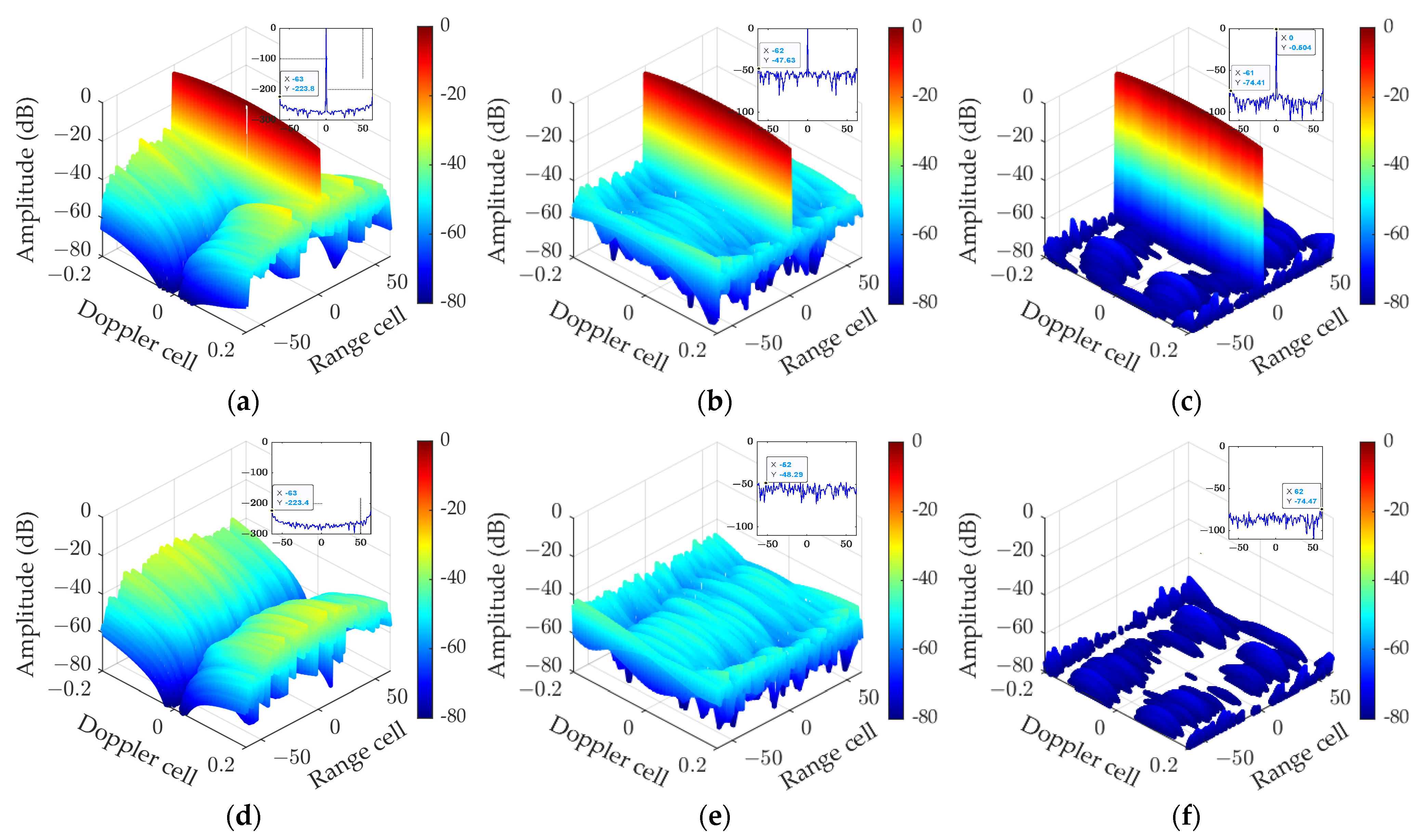
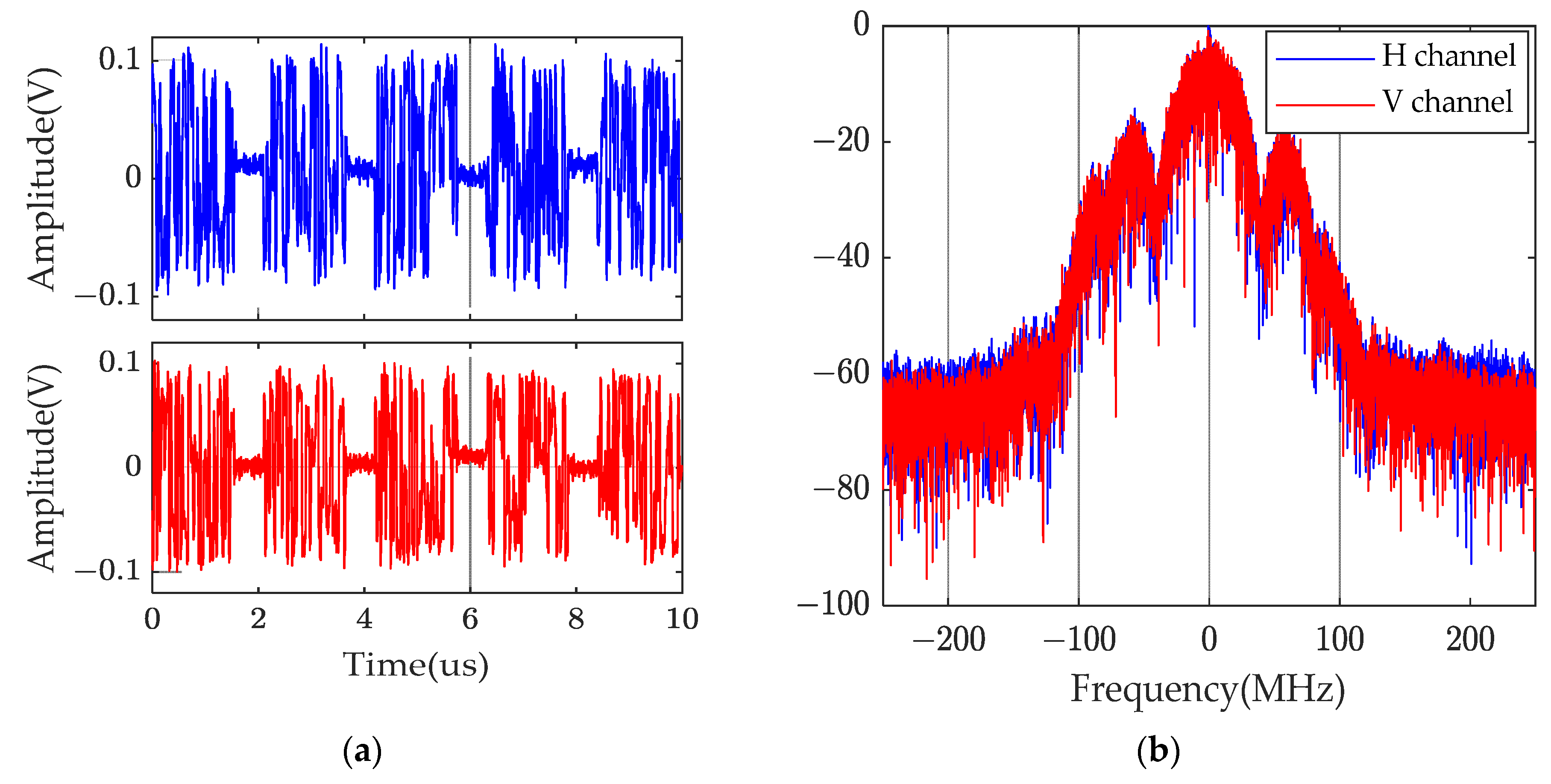
5. Experimental Validation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Lee, J.S.; Pottier, E. Polarimetric Radar Imaging: From Basics to Applications; CRC: Boca Raton, FL, USA, 2009. [Google Scholar]
- Hurtado, M.; Nehorai, A. Polarimetric detection of targets in heavy inhomogeneous clutter. IEEE Trans. Signal Process. 2008, 56, 1349–1361. [Google Scholar] [CrossRef]
- Liang, L.; Zhang, Y.; Li, D. A novel method for polarization orientation angle estimation over steep terrain and comparison of deorientation algorithms. IEEE Trans. Geosci. Remote Sens. 2020, 59, 4790–4801. [Google Scholar] [CrossRef]
- Liang, L.; Zhang, Y.; Li, D. Fast Huynen–Euler Decomposition and its Application in Disaster Monitoring. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 4231–4243. [Google Scholar] [CrossRef]
- Giuli, D.; Fossi, M.; Facheris, L. Radar target scattering matrix measurement through orthogonal signals. IEE Proc. F Radar Signal Process. 1993, 140, 233–242. [Google Scholar] [CrossRef]
- Li, C.; Li, Y.; Yang, Y.; Pang, C.; Wang, X. Moving target’s scattering matrix estimation with a polarimetric radar. IEEE Trans. Geosci. Remote Sens. 2020, 58, 5540–5551. [Google Scholar] [CrossRef]
- Wang, F.; Yin, J.; Pang, C.; Li, Y.; Wang, X. A unified framework of Doppler resilient sequences design for simultaneous polarimetric radars. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5109615. [Google Scholar] [CrossRef]
- Wang, X. Study on Wideband Polarization Information Processing. Ph.D. Thesis, Graduate School of National University of Defense Technology, Changsha, China, 1999. [Google Scholar]
- Wang, X.; Li, Y.; Dai, H.; Chang, Y.; Dai, D.; Ma, L.; Liu, Y. Research on instantaneous polarization radar system and external experiment. Chinese Sci. Bull. 2010, 55, 1560–1567. [Google Scholar] [CrossRef]
- Wang, F.; Pang, C.; Li, Y.; Wang, X. Algorithms for designing unimodular sequences with high Doppler tolerance for simultaneous fully polarimetric radar. Sensors 2018, 18, 905. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.; Liang, J.; Song, K.; Yang, Y.; Deng, X. On designing good doppler tolerance waveform with low PSL of ambiguity function. Signal Process. 2023, 210, 109075. [Google Scholar] [CrossRef]
- Hu, C.; Chen, Z.; Dong, X.; Cui, C. Multistatic geosynchronous SAR resolution analysis and grating lobe suppression based on array spatial ambiguity function. IEEE Trans. Geosci. Remote Sens. 2020, 58, 6020–6038. [Google Scholar] [CrossRef]
- Cui, G.; Fu, Y.; Yu, X.; Li, J. Local ambiguity function shaping via unimodular sequence design. IEEE Signal Process. Lett. 2017, 24, 977–981. [Google Scholar] [CrossRef]
- Ye, Z.; Zhou, Z.; Fan, P.; Liu, Z.; Lei, X.; Tang, X. Low ambiguity zone: Theoretical bounds and Doppler-resilient sequence design in integrated sensing and communication systems. IEEE J. Sel. Areas Commun. 2022, 40, 1809–1822. [Google Scholar] [CrossRef]
- He, H.; Stoica, P.; Li, J. Designing unimodular sequence sets with good correlations-Including an application to MIMO radar. IEEE Trans. Signal Process. 2009, 57, 4391–4405. [Google Scholar] [CrossRef]
- Li, C.; Yang, Y.; Li, Y.; Wang, X. Frequency calibration for the scattering matrix of the simultaneous polarimetric radar. IEEE Geosci. Remote Sens. Lett. 2018, 15, 429–433. [Google Scholar] [CrossRef]
- Zheng, Z.; Zhang, Y.; Peng, X.; Xie, H.; Chen, J.; Mo, J.; Sui, Y. MIMO Radar Waveform Design for Multipath Exploitation Using Deep Learning. Remote Sens. 2023, 15, 2747. [Google Scholar] [CrossRef]
- Li, C.; Yang, Y.; Pang, C.; Li, Y.; Wang, X. A simultaneous polarimetric measurement scheme using one amplitude modulation waveform. IEEE Geosci. Remote Sens. Lett. 2019, 17, 72–76. [Google Scholar] [CrossRef]
- Liu, B. Orthogonal discrete frequency-coding waveform set design with minimized autocorrelation sidelobes. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 1650–1657. [Google Scholar] [CrossRef]
- Yu, X.; Alhujaili, K.; Cui, G.; Monga, V. MIMO radar waveform design in the presence of multiple targets and practical constraints. IEEE Trans. Signal Process. 2020, 68, 1974–1989. [Google Scholar] [CrossRef]
- Zhang, Y.; Liao, G.; Xu, J.; Lan, L. Mainlobe Deceptive Jammer Suppression Based on Quadratic Phase Coding in FDA-MIMO Radar. Remote Sens. 2022, 14, 5831. [Google Scholar] [CrossRef]
- Liu, T.; Sun, J.; Wang, G.; Lu, Y. A Multi-Objective Quantum Genetic Algorithm for MIMO Radar Waveform Design. Remote Sens. 2022, 14, 2387. [Google Scholar] [CrossRef]
- Stoica, P.; He, H.; Li, J. New algorithms for designing unimodular sequences with good correlation properties. IEEE Trans. Signal Process. 2009, 57, 1415–1425. [Google Scholar] [CrossRef] [Green Version]
- Song, J.; Babu, P.; Palomar, D.P. Sequence design to minimize the weighted integrated and peak sidelobe levels. IEEE Trans. Signal Process. 2015, 64, 2051–2064. [Google Scholar] [CrossRef] [Green Version]
- Feng, X.; Zhao, Z.; Li, F.; Cui, W.; Zhao, Y. Radar Phase-Coded Waveform Design with Local Low Range Sidelobes Based on Particle Swarm-Assisted Projection Optimization. Remote Sens. 2022, 14, 4186. [Google Scholar] [CrossRef]
- He, H.; Stoica, P.; Li, J. On Aperiodic-Correlation Bounds. IEEE Signal Process. Lett. 2010, 17, 253–256. [Google Scholar] [CrossRef]
- Pezeshki, A.; Calderbank, A.R.; Moran, W.; Howard, S.D. Doppler Resilient Golay Complementary Waveforms. IEEE Trans. Inf. Theory 2008, 54, 4254–4266. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Liu, Y.; Liao, G.; Chen, Y. Joint Radar and Communications Waveform Design Based on Complementary Sequence Sets. Remote Sens. 2023, 15, 645. [Google Scholar] [CrossRef]
- Chen, H.H.; Yeh, Y.C.; Bi, Q.; Jamalipour, A. On a MIMO-based open wireless architecture: Space-time complementary coding. IEEE Commun. Mag. 2007, 45, 104–112. [Google Scholar] [CrossRef]
- Song, Y.; Wang, Y.; Xie, J.; Yang, Y.; Tian, B.; Xu, S. Ultra-Low Sidelobe Waveforms Design for LPI Radar Based on Joint Complementary Phase-Coding and Optimized Discrete Frequency-Coding. Remote Sens. 2022, 14, 2592. [Google Scholar] [CrossRef]
- Levanon, N.; Cohen, I.; Itkin, P. Complementary pair radar waveforms–evaluating and mitigating some drawbacks. IEEE Aerosp. Electron. Syst. Mag. 2017, 32, 40–50. [Google Scholar] [CrossRef]
- Aubry, A.; De Maio, A.; Jiang, B.; Zhang, S. Ambiguity function shaping for cognitive radar via complex quartic optimization. IEEE Trans. Signal Process. 2013, 61, 5603–5619. [Google Scholar] [CrossRef]
- Tang, J.; Zhang, N.; Ma, Z.; Tang, B. Construction of Doppler Resilient Complete Complementary Code in MIMO Radar. IEEE Trans. Signal Process. 2014, 62, 4704–4712. [Google Scholar] [CrossRef]
- Song, J.; Babu, P.; Palomar, D.P. Sequence set design with good correlation properties via majorization-minimization. IEEE Trans. Signal Process. 2016, 64, 2866–2879. [Google Scholar] [CrossRef] [Green Version]
- Wang, F.; Pang, C.; Wu, H.; Li, Y.; Wang, X. Designing Constant Modulus Complete Complementary Sequence With High Doppler Tolerance for Simultaneous Polarimetric Radar. IEEE Signal Process. Lett. 2019, 26, 1837–1841. [Google Scholar] [CrossRef]
- Xu, L.; Zhou, S.; Liu, H. Simultaneous optimization of radar waveform and mismatched filter with range and delay-Doppler sidelobes suppression. Digit. Signal Process. 2018, 83, 346–358. [Google Scholar] [CrossRef]
- Wang, Y.C.; Dong, L.; Xue, X.; Yi, K.-C. On the Design of Constant Modulus Sequences with Low Correlation Sidelobes Levels. IEEE Commun. Lett. 2012, 16, 462–465. [Google Scholar] [CrossRef]
- Wu, L.; Babu, P.; Palomar, D.P. Transmit waveform/receive filter design for MIMO radar with multiple waveform constraints. IEEE Trans. Signal Process. 2017, 66, 1526–1540. [Google Scholar] [CrossRef]
- Beauchamp, R.M.; Tanelli, S.; Peral, E.; Chandrasekar, V. Pulse compression waveform and filter optimization for spaceborne cloud and precipitation radar. IEEE Trans. Geosci. Remote Sens. 2016, 55, 915–931. [Google Scholar] [CrossRef]
- Wang, F.; Xia, X.-G.; Pang, C.; Cheng, X.; Li, Y.; Wang, X. Joint Design Methods of Unimodular Sequences and Receiving Filters with Good Correlation Properties and Doppler Tolerance. IEEE Trans. Geosci. Remote Sens. 2022, 61, 5100214. [Google Scholar] [CrossRef]
- Zhou, K.; Quan, S.; Li, D.; Liu, T.; He, F.; Su, Y. Waveform and filter joint design method for pulse compression sidelobe reduction. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5107615. [Google Scholar] [CrossRef]
- Wang, F.; Feng, S.; Yin, J.; Pang, C.; Li, Y.; Wang, X. Unimodular sequence and receiving filter design for local ambiguity function shaping. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5113012. [Google Scholar] [CrossRef]
- Xiong, W.; Hu, J.; Zhong, K.; Sun, Y.; Xiao, X.; Zhu, G. MIMO Radar Transmit Waveform Design for Beampattern Matching via Complex Circle Optimization. Remote Sens. 2023, 15, 633. [Google Scholar] [CrossRef]
- Zhou, K.; Li, D.; Quan, S.; Liu, T.; Su, Y.; He, F. SAR waveform and mismatched filter design for countering interrupted-sampling repeater jamming. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5214514. [Google Scholar] [CrossRef]
- Yang, J.; Zhou, J.; Liu, L.; Li, Y. A novel strategy of pareto-optimal solution searching in multi-objective particle swarm optimization (MOPSO). Comput. Math. Appl. 2009, 57, 1995–2000. [Google Scholar] [CrossRef] [Green Version]
- Everett, H. Generalized Lagrange multiplier method for solving problems of optimum allocation of resources. Oper. Res. 1963, 11, 399–417. [Google Scholar] [CrossRef]
- Raydan, M.; Svaiter, B.F. Relaxed steepest descent and Cauchy-Barzilai-Borwein method. Comput. Optim. Appl. 2002, 21, 155–167. [Google Scholar] [CrossRef]
- Varadhan, R.; Roland, C. Simple and globally convergent methods for accelerating the convergence of any EM algorithm. Scand. J. Stat. 2008, 35, 335–353. [Google Scholar] [CrossRef]
- Roughgarden, T. Beyond the Worst-Case Analysis of Algorithms; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- He, H.; Li, J.; Stoica, P. Waveform Design for Active Sensing Systems: A Computational Approach; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Chen, R.; Cantrell, B. Highly bandlimited radar signals. In Proceedings of the 2002 IEEE Radar Conference, Long Beach, CA, USA, 25 April 2002. [Google Scholar]
- Liu, J.; Zhang, Y.; Dong, X. Linear-FM random radar waveform compressed by dechirping method. IET Radar Sonar Navig. 2019, 13, 1107–1115. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, R.; Cheng, Y.; Li, J. Joint Design of Periodic Binary Probing Sequences and Receive Filters for PMCW Radar. IEEE Trans. Signal Process. 2022, 70, 5996–6010. [Google Scholar] [CrossRef]
- De Maio, A.; Huang, Y.; Piezzo, M.; Zhang, S.; Farina, A. Design of optimized radar codes with a peak to average power ratio constraint. IEEE Trans. Signal Process. 2011, 59, 2683–2697. [Google Scholar] [CrossRef]


| Notation | Meaning |
|---|---|
| the transposition of a vector/matrix | |
| the conjugate of a complex number/vector/matrix | |
| the conjugate transpose of a vector/matrix | |
| the modulus of a complex number | |
| the -norm of a vector | |
| the real part of a complex number | |
| the trace of a matrix | |
| the stacking vectorization of a matrix | |
| a diagonalized matrix of | |
| ⨀ | Hadamard product |
| an all-zero column vector with dimension N | |
| an all-one column vector with dimension N | |
| an all-zero matrix with dimension | |
| the identity matrix with dimension |
| Parameter | Quantity |
|---|---|
| Carrier Frequency | 13.58 GHz |
| Waveform bandwidth B | 40 MHz |
| Pulse duration | |
| Pulse PRI | |
| CPI | |
| Code length | 64 |
| Pulse number | 5 |
| A/D sampling rate | 500 MHz |
| ADC resolution | 12 bit |
| Waveform of [34] | Waveform of [35] | Our Waveform | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| HH | HV | VH | VV | HH | HV | VH | VV | HH | HV | VH | VV | ||
| Simulated 1 | −61.23 | −60.19 | −60.19 | −60.65 | −34.10 | −33.56 | −33.56 | −34.20 | −42.91 | −42.29 | −41.56 | −42.87 | |
| Simulated 2 | −40.81 | −39.85 | −41.02 | −40.96 | −32.17 | −33.20 | −32.28 | −32.98 | −38.11 | −38.46 | −39.29 | −38.68 | |
| Measured | −39.41 | −39.32 | −38.41 | −39.17 | −31.81 | −31.71 | −31.44 | −31.96 | −37.54 | −37.13 | −38.17 | −37.76 | |
| Simulated 1 | −38.83 | −37.74 | −38.06 | −38.31 | −32.66 | −32.70 | −32.78 | −32.73 | −42.04 | −41.72 | −40.10 | −43.17 | |
| Simulated 2 | −35.80 | −35.36 | −34.02 | −37.27 | −32.01 | −32.45 | −32.03 | −32.66 | −38.41 | −39.45 | −38.84 | −39.62 | |
| Measured | −34.17 | −35.55 | −33.78 | −36.34 | −31.01 | −30.88 | −31.76 | −32.05 | −37.90 | −38.13 | −36.88 | −38.73 | |
| Simulated 1 | −32.89 | −31.70 | −31.10 | −32.60 | −31.18 | −30.93 | −31.32 | −32.45 | −41.65 | −41.34 | −39.16 | −42.55 | |
| Simulated 2 | −32.19 | −30.56 | −29.72 | −33.04 | −30.90 | −30.47 | −30.36 | −32.29 | −38.61 | −38.73 | −37.59 | −37.53 | |
| Measured | −30.04 | −30.64 | −30.39 | −32.47 | −30.64 | −30.35 | −30.02 | −30.19 | −38.29 | −37.82 | −36.53 | −37.16 | |
| Simulated 1 | −29.58 | −28.37 | −27.80 | −29.25 | −30.00 | −30.11 | −30.2 | −33.25 | −41.27 | −40.39 | −38.28 | −41.13 | |
| Simulated 2 | −29.18 | −28.06 | −27.26 | −29.51 | −29.13 | −29.74 | −29.18 | −32.73 | −38.42 | −38.97 | −38.42 | −37.96 | |
| Measured | −27.90 | −28.0 | −27.19 | −29.47 | −29.54 | −29.33 | −29.42 | −30.43 | −37.36 | −36.73 | −37.33 | −36.81 | |
| Simulated 1 | −27.05 | −26.19 | −26.85 | −26.96 | −29.93 | −29.83 | −29.13 | −31.06 | −40.62 | −39.51 | −38.96 | −39.87 | |
| Simulated 2 | −26.84 | −26.30 | −25.56 | −27.12 | −28.98 | −29.56 | −28.65 | −30.91 | −38.35 | −38.54 | −38.59 | −37.49 | |
| Measured | −25.70 | −26.00 | −25.57 | −26.25 | −29.28 | −29.87 | −28.19 | −29.22 | −36.88 | −37.08 | −37.89 | −36.30 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Zhang, Y.; Li, D.; Yang, J. Joint Design of Complementary Sequence and Receiving Filter with High Doppler Tolerance for Simultaneously Polarimetric Radar. Remote Sens. 2023, 15, 3877. https://doi.org/10.3390/rs15153877
Chen Y, Zhang Y, Li D, Yang J. Joint Design of Complementary Sequence and Receiving Filter with High Doppler Tolerance for Simultaneously Polarimetric Radar. Remote Sensing. 2023; 15(15):3877. https://doi.org/10.3390/rs15153877
Chicago/Turabian StyleChen, Yun, Yunhua Zhang, Dong Li, and Jiefang Yang. 2023. "Joint Design of Complementary Sequence and Receiving Filter with High Doppler Tolerance for Simultaneously Polarimetric Radar" Remote Sensing 15, no. 15: 3877. https://doi.org/10.3390/rs15153877
APA StyleChen, Y., Zhang, Y., Li, D., & Yang, J. (2023). Joint Design of Complementary Sequence and Receiving Filter with High Doppler Tolerance for Simultaneously Polarimetric Radar. Remote Sensing, 15(15), 3877. https://doi.org/10.3390/rs15153877







