Improving the Accuracy of Vehicle Position in an Urban Environment Using the Outlier Mitigation Algorithm Based on GNSS Multi-Position Clustering
Abstract
:1. Introduction
- Generate position data for a receiving point based on a subset of observable satellites and calculate the position of the receiving point without relying on observation data. There is no need to take into account errors in position estimation caused by distortions in the observation data;
- In order to overcome the positioning error caused by observation data, we have utilized a density-based clustering technique, and also, by defining the initial input parameters for density-based clustering, we can effectively identify position data that are combined with LOS satellites. This approach not only addresses the drawback of processing speed commonly associated with clustering methods but also mitigates the inaccuracies resulting from observation data;
- To identify position data combined with LOS satellites from various clustered data points, we utilize the concept of nonholonomic constraints based on Doppler velocity measurements. This allows us to set a prediction range for improved position estimation. Furthermore, we incorporated weighted factors into the extracted clustering data and defined a probability density function based on exponential function.
2. Related Work
3. Positioning Method and Consistency Analysis Based on a Subset of Observable Satellites
3.1. Receiver Observation Model
- : pseudorange from the satellite to the receiver;
- : receiver position in the Earth-centered, Earth-fixed (ECEF) coordinate system;
- : satellite position in ECEF coordinates;
- : speed of light;
- : receiver clock bias;
- : error term associated with the -th propagation channel (ionospheric delay, tropospheric delay, satellite clock bias, satellite position uncertainty, and MP/NLOS error).
- , ;
- ;
- is an error term owing to the possible presence of MP affecting the pseudoranges (we assume that all errors except MP have been corrected);
- : number of selected satellites from at least four to ;
- , the Jacobian matrix associated with the linearized system.
3.2. Consistency Analysis of Position Data
- : position precision by the placement of satellites;
- : the i-th row and j-th column diagonal element of matrix ;
- : total error affecting a pseudorange from the user’s point of view; user equivalent range error.
- : pseudorange error value of the -th satellite computed at time ;
- : the number of visible satellites;
- : total number of epochs used to calculate the UERE.
- Position data consisting only of the LOS signal;
- Position data composed of signals with large MP/NLOS delays;
- Position data composed of signals with various error characteristics.
- : multiplication of the standard deviations for discrepancies between observation points in each direction.
- : number of selected satellites based on the subset;
- : number of MP/NLOS satellites; ;
- : -th satellite signal with a large MP/NLOS error.
4. Weighted Position Estimation Method through LOS Satellite-Based Position Data Clustering
4.1. DBSCAN Parameter Definition
- : maximum horizontal position error ≈ 6.1 m;
- : Low GNSS receiver horizontal position error (95% accuracy) ≈ 3.12 m.
4.2. Weighted Position Estimation Method
- : GNSS course angle at time , [] is the displacement vector of the vehicle in the north-east-down coordinate system;
- : estimated angle of the vehicle’s maximum turning radius;
- : turning radius of the vehicle;
- : distance traveled, calculated based on speed measurement.
- : samples for the mean positions in each cluster;
- : j-th selected clusters;
- : i-th clustered position of data.
- : j-th selected clusters;
- : speed-measurement based on doppler shift;
- : result of previously estimated position.
| Algorithm 1. Outlier mitigation algorithm based on multi-position clustering | ||
| Input: | Observation satellite info: PRN, SNR, , Ele | |
| Input: | Masking value of SNR, Ele: , | |
| Input: | masking value of HDOP for optimal clustering: | |
| Input: | Subset of observable satellites for each epoch: | |
| Input: | Define DBSCAN input parameter for Eps, Minpts: , Γ | |
| Output: | Estimated position: | |
| Output: | Set of utilized PRN satellites in selected position data: | |
| 1: | for t = 1: time | |
| 2: | for j = 1: | |
| 3: | if SNR & ELE & HDOP | |
| 4: | =Positioning() | |
| 5: | End | |
| 6: | position data = {, , , } | |
| 7: | End | |
| 8: | idx = dbscan(,Γ) | |
| 9: | ||
| 10: | for i = 1:k | |
| 11: | if <= | |
| 12: | Continue | |
| 13: | Else | |
| 14: | ||
| 15: | End | |
| 16: | End | |
| 17: | for M = 1:Max(idx) | |
| 18: | ||
| 19: | end | |
| 20: | ||
| 21: | = select() | |
| 22: | ||
| 23: | ||
| 24: | Else | |
| 25: | ||
| 26: | ||
| 27: | ||
| 28: | = idx() | |
| 29: | ||
| 30: | End | |
| 31: | End | |
5. Performance Verification
5.1. Algorithm Verification
5.2. Analysis of Result
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jiang, W.; Zhang, L. The impact of the transportation network companies on the taxi industry: Evidence from Beijing’s GPS taxi trajectory data. IEEE Access 2018, 6, 12438–12450. [Google Scholar] [CrossRef]
- Xu, Y.; Chen, D.; Zhang, X.; Tu, W.; Chen, Y.; Shen, Y.; Ratti, C. Unravel the landscape and pulses of cycling activities from a dockless bike-sharing system. Comput. Environ. Urban Syst. 2019, 75, 184–203. [Google Scholar] [CrossRef]
- Zhengxia, W.; Laisheng, X. Modern logistics monitoring platform based on the internet of things. In Proceedings of the 2010 International Conference on Intelligent Computation Technology and Automation, Changsha, China, 11–12 May 2010; Volume 2. [Google Scholar] [CrossRef]
- Bai, S.; Jiao, J. Dockless E-scooter usage patterns and urban built Environments: A comparison study of Austin, TX, and Minneapolis, MN. Travel Behav. Soc. 2020, 20, 264–272. [Google Scholar] [CrossRef]
- Ahmad, I.; Abd-Alhameed, R. New Trends in Location-Based Services Technology. In Proceedings of the 2nd International Multi-Disciplinary Conference Theme: Integrated Sciences and Technologies, IMDC-IST 2021, Sakarya, Turkey, 7–9 September 2021. [Google Scholar]
- Chen, D.; Gao, G.X. Probabilistic graphical fusion of LiDAR, GPS, and 3D building maps for urban UAV navigation. Navigation 2019, 66, 151–168. [Google Scholar] [CrossRef] [Green Version]
- Lesouple, J.; Robert, T.; Sahmoudi, M.; Tourneret, J.-Y.; Vigneau, W. Multipath mitigation for GNSS positioning in urban environment using sparse estimation. IEEE Trans. Intell. Transp. Syst. 2018, 20, 1316–1328. [Google Scholar] [CrossRef] [Green Version]
- Angrisano, A.; Gaglione, S. Smartphone GNSS Performance in an Urban Scenario with RAIM Application. Sensors 2022, 22, 786. [Google Scholar] [CrossRef]
- Xia, Y.; Pan, S.; Meng, X.; Gao, W.; Ye, F.; Zhao, Q.; Zhao, X. Anomaly detection for urban vehicle GNSS observation with a hybrid machine learning system. Remote Sens. 2020, 12, 971. [Google Scholar] [CrossRef] [Green Version]
- Ahad, S.A.; Fahmeen, S.; Sultana, Q. Analysis of GPS/GAGAN based Airborne Receiver Position Accuracy using RAIM Algorithms. In Proceedings of the 2020 IEEE-HYDCON, Hyderabad, India, 11–12 September 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Li, J.; Wu, M. The improvement of positioning accuracy with weighted least square based on SNR. In Proceedings of the 2009 5th International Conference on Wireless Communications, Networking and Mobile Computing, Beijing, China, 24–26 September 2009; pp. 1–4. [Google Scholar] [CrossRef]
- Tay, S.; Marais, J. Weighted models for GPS Pseudorange observations for land transportation in urban canyons. In Proceedings of the 6th European Workshop on GNSS Signals and Signal Processing, Munich, Germany, 5–6 December 2013; p. 4. Available online: https://hal.science/hal-00942180 (accessed on 11 April 2022).
- Xie, P.; Petovello, M.G. Measuring GNSS multipath distributions in urban canyon environments. IEEE Trans. Instrum. Meas. 2014, 64, 366–377. [Google Scholar] [CrossRef]
- Zhang, S.; Walter, T. GNSS multipath detection in urban environment using 3D building model. In Proceedings of the 2018 IEEE/ION Position, Location and Navigation Symposium (PLANS), Monterey, CA, USA, 23–26 April 2018; pp. 1053–1058. [Google Scholar] [CrossRef]
- Bauer, S.; Obst, M.; Wanielik, G. 3D environment modeling for GPS multipath detection in urban areas. In Proceedings of the International Multi-Conference on Systems, Signal & Devices, Chemnitz, Germany, 20–23 May 2012; pp. 1–5. [Google Scholar] [CrossRef]
- Miura, S.; Shoma, H.; Kamij, S. GPS positioning with multipath detection and rectification using 3D maps. Int. J. Automot. Eng. 2014, 5, 23–29. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ester, M.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. Kdd 1996, 96, 226–231. [Google Scholar]
- Yozevitch, R.; Ben Moshe, B.; Weissman, A. A robust GNSS los/nlos signal classifier. Navigation 2016, 63, 429–442. [Google Scholar] [CrossRef]
- Sun, R.; Wang, G.; Cheng, Q.; Fu, L.; Chiang, K.-W.; Hsu, L.-T.; Ochieng, W.Y. Improving GPS code phase positioning accuracy in urban environments using machine learning. IEEE Internet Things J. 2020, 8, 7065–7078. [Google Scholar] [CrossRef]
- Lyu, Z.; Gao, Y. An SVM Based Weighted Scheme for Improving Kinematic GNSS Positioning Accuracy with Los-Cost GNSS Receiver in Urban Environments. Sensors 2020, 20, 7265. [Google Scholar] [CrossRef]
- Zhang, J.; Hu, Q.; Li, J.; Ai, M. Learning for GPS trajectories of floating car for CNN-based urban road extraction with high-resolution satellite imagery. IEEE Trans. Geosci. Remote Sens. 2020, 59, 1836–1847. [Google Scholar] [CrossRef]
- Hartigan, J.A.; Wong, M.A. Algorithm AS 136: A k-means clustering algorithm. J. R. Stat. Soc. Ser. Appl. Stat. 1979, 28, 100–108. [Google Scholar] [CrossRef]
- Uaratanawong, V.; Satirapod, C.; Tsujii, T. Evaluation of multipath mitigation performance using signal-to-noise ratio (SNR) based signal selection methods. J. Appl. Geodesy 2020, 15, 75–85. [Google Scholar] [CrossRef]
- Shen, N.; Wang, B.; Gao, G.; Chen, L.; Chen, R. 3-D Displacement Detection Based on Enhanced Clustering from GNSS Positioning in a Kinematic Mode for Deformation Monitoring. IEEE Trans. Instrum. Meas. 2022, 72, 1–10. [Google Scholar] [CrossRef]
- Wang, H.; Pan, S.; Gao, W.; Xia, Y.; Ma, C. Multipath/NLOS Detection Based on K-Means Clustering for GNSS/INS Tightly Coupled System in Urban Area. Micromachines 2022, 13, 1128. [Google Scholar] [CrossRef] [PubMed]
- Luo, T.; Zheng, X.; Xu, G.; Fu, K.; Ren, W. An improved DBSCAN algorithm to detect stops in individual trajectories. ISPRS Int. J. Geo-Inf. 2017, 6, 63. [Google Scholar] [CrossRef]
- Mosavi, M.R. An effective method for GPS GDOP clustering using ant colony optimization algorithm. Asian J. Geoinform. 2012, 10, 1–7. [Google Scholar]
- Wang, J.; Rui, X.; Song, X.; Wang, C.; Tang, L.; Li, C.; Raghvan, V. A weighted clustering algorithm for clarifying vehicle GPS traces. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011; pp. 2949–2952. [Google Scholar] [CrossRef]
- Fu, Z.; Tian, Z.; Xu, Y.; Qiao, C. A two-step clustering approach to extract locations from individual GPS trajectory data. ISPRS Int. J. Geo-Inf. 2016, 5, 166. [Google Scholar] [CrossRef]
- Jang, S.; Lee, E. Map generation system with lightweight GPS trace data. In Proceedings of the 2010 12th International Conference on Advanced Communication Technology (ICACT), Gangwon-Do, Republic of Korea, 7–10 February 2010; Volume 2, pp. 1489–1493. [Google Scholar]
- Liang, T.; Yang, J.; Zhang, T. UAV aided vehicle positioning with imperfect data association. In Proceedings of the 2021 IEEE 93rd Vehicular Technology Conference (VTC2021-Spring), Helsinki, Finland, 25–28 April 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Granat, R.; Donnellan, A.; Heflin, M.; Lyzenga, G.; Glasscoe, M.; Parker, J.; Pierce, M.; Wang, J.; Rundle, J.; Ludwig, L.G. Clustering Analysis Methods for GNSS Observations: A Data-Driven Approach to identifying California’s Major Faults. Earth Space Sci. 2021, 8, 1680. [Google Scholar] [CrossRef]
- Comaniciu, D.; Meer, P. Mean shift: A robust approach toward feature space analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 603–619. [Google Scholar] [CrossRef] [Green Version]
- Hansen, L.P. Large sample properties of generalized method of moments estimators. Econometrica 1982, 50, 1029. [Google Scholar] [CrossRef]
- Parkinson, B.W.; Spilker, J.J. Progress in Astronautics and Aeronautics: Global Positioning System: Theory and Applications; AIAA: San Diego, CA, USA, 1996; Volume 164. [Google Scholar]
- Blewitt, G. Basic of the GPS technique: Observation equations. Geod. Appl. GPS 1997, 1, 46. [Google Scholar]
- Langley, R.B. Dilution of precision. GPS World 1999, 10, 52–59. [Google Scholar]
- ZED-F9P-04B u-Blox F9 High Precision GNSS Module. Data Sheet. 2021. Available online: https://www.u-blox.com/sites/default/files/ZED-F9P-04B_DataSheet_UBX-21044850.pdf (accessed on 11 April 2022).
- Tae, H.U.; Park, K.D.; Kim, M.S. Analysis of integrated GPS/GLONASS/BDS positioning accuracy using low-cost receiver. J. Korean Soc. Geospat. Inf. Syst. 2015, 23, 49–55. [Google Scholar] [CrossRef]
- Grubbs, F.E. Approach Circular and Non-circular offset Probability of Hitting. Oper. Res. 1964, 12, 51–62. Available online: https://www.jstor.org/stable/167752 (accessed on 11 April 2022). [CrossRef]
- Hwang, H.S. A Study on a Hit Probability Model for Polygonal Target. J. Mil. Oper. Res. Soc. Korea 1999, 25, 160–168. [Google Scholar]
- Pan, L.; Zhang, X.; Liu, J.; Li, X.; Li, X. Performance evaluation of single-frequency point positioning with GPS, GLONASS, BeiDou and Galileo. J. Navig. 2017, 70, 465–482. [Google Scholar] [CrossRef]
- Yuan, Y.; Shen, F.; Li, X. GPS multipath and NLOS mitigation for relative positioning in urban environments. Aerosp. Sci. Technol. 2020, 107, 106315. [Google Scholar] [CrossRef]
- Hsu, L.-T. Analysis and modeling GPS NLOS effect in highly urbanized area. GPS Solut. 2017, 22, 7. [Google Scholar] [CrossRef] [Green Version]
- Lee, H.; Pullen, S.; Lee, J.; Park, B.; Yoon, M.; Seo, J. Optimal parameter inflation to enhance the availability of single-frequency GBAS for intelligent air transportation. IEEE Trans. Intell. Transp. Syst. 2022, 23, 17801–17808. [Google Scholar] [CrossRef]
- Lee, Y.; Hwang, Y.; Ahn, J.Y.; Seo, J.; Park, B. Seamless Accurate Positioning in Deep Urban Area based on Mode Switching Between DGNSS and Multipath Mitigation Positioning. arXiv 2022, arXiv:2206.04457. [Google Scholar] [CrossRef]
- Lee, Y.; Park, B. Nonlinear Regression-Based GNSS Multipath Modeling in Deep Urban Area. Mathematics 2022, 10, 412. [Google Scholar] [CrossRef]
- Refan, M.H.; Mohammadi, K. Point averaging of the position components, before and after s/a is turned off. In Proceedings of the Asian GPS Conference, New Delhi, India, 29–30 October 2001. [Google Scholar]
- Wu, S.-C.; Melbourne, W. Melbourne. An optimal GPS data processing technique for precise positioning. IEEE Trans. Geosci. Remote Sens. 1993, 31, 146–152. [Google Scholar] [CrossRef]
- Tabatabaei, A.; Mosavi, M.R.; Khavari, A.; Shahhoseini, H.S. Reliable urban canyon navigation solution in GPS and GLONASS integrated receiver using improved Fuzzy weighted least-square method. Wirel. Pers. Commun. 2016, 94, 3181–3196. [Google Scholar] [CrossRef]
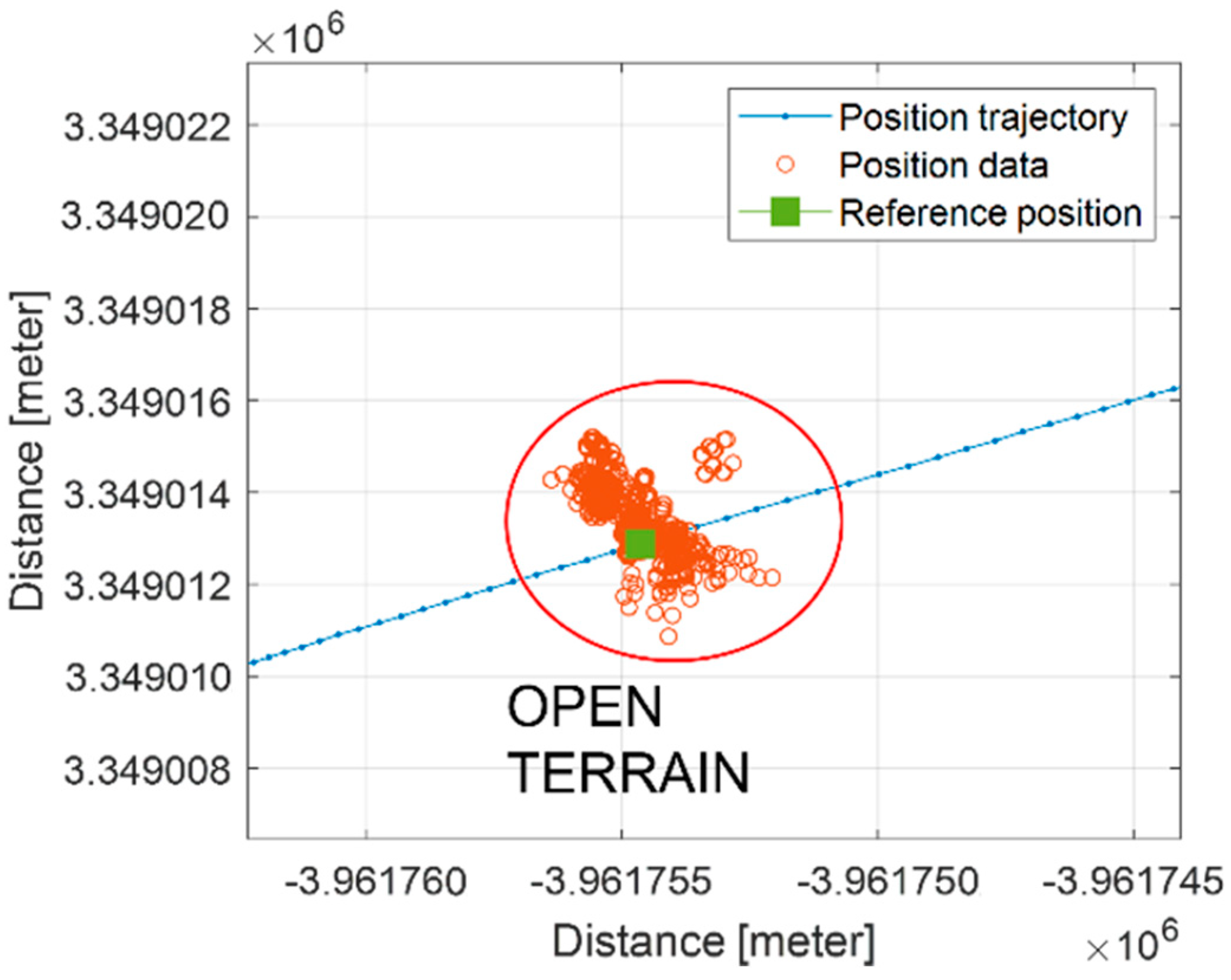

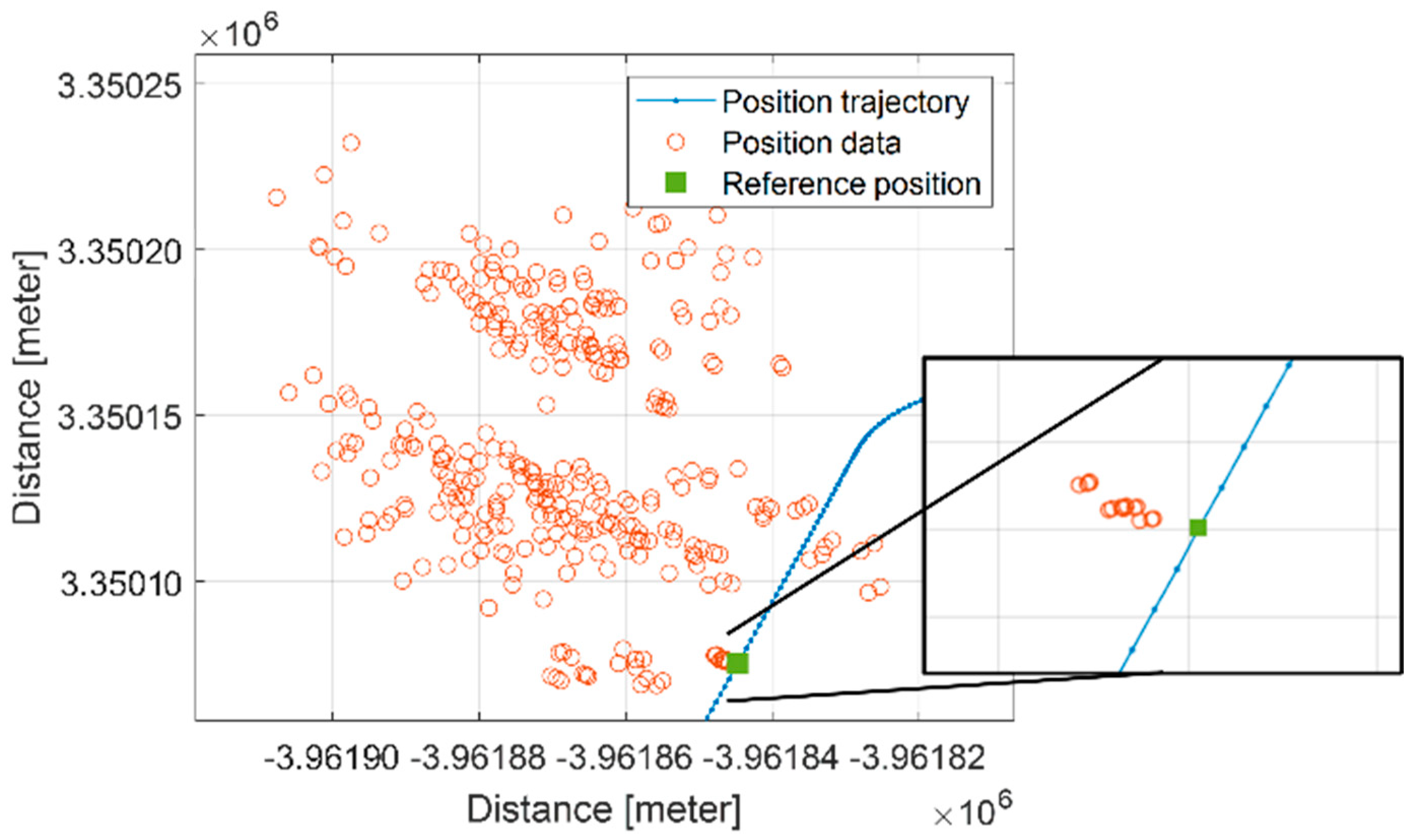














| Authors | Identification Technique | Contribution | Algorithm Verification | Note |
|---|---|---|---|---|
| Y. Xia et al. [9] | Chi-square and HDBSCAN | The authors present the HDBSCAN algorithm to label an offline dataset as normal based on observation data, effectively contributing to the estimation of position through a hybrid machine learning framework designed for GNSS anomaly detection. | Urban scenario | Need training set for labeling |
| R. Yozevitch et al. [18] | Decision tree and expectation maximization | The authors present the classification of LOS and NLOS scenarios using satellite signal strength. This classification is achieved through the application of both supervised and unsupervised learning technique. | Specific section and small scenario in an urban environment | Need training set for labeling |
| Uaratanawong et al. [23] | K-means | The authors focused on identifying LOS and NLOS signal using K-means based on SNR residual obtained through a classical noise model for carrier phase. | Specific points | Two location points: surrounded by buildings and rooftop of the building |
| Hao Wang et al. [25] | K-means | The authors considered different feature parameters derived from observation data to effectively classify GNSS signals: pseudorange, carrier phase, SNR, doppler frequency, etc. | Urban scenario | The author focused on multipath/NLOS detection |
| Luo et al. [26] | DBSCAN | The authors considered the problem by assigning a large weight to low mobility and overcoming the distortion of observation data based on the position trajectory without using observation data. | Stop section | MP/NLOS signals were not considered in an urban environment, and they focused only on the stop section. |
| M. R. Mosavi [27] | Ant colony optimization | The author present satellites geometry clustering for good navigation satellites subset selection. | Simulation |
| Number of Observable Satellites | Maximum Number of Position Data for all Combination of Satellites | Matrix H |
|---|---|---|
| 4 | 4C4 | H4 |
| 5 | 5C4 + 5C5 | H4, H5 |
| ⋮ | ⋮ | |
| N | NC4 + NC5 + + NCN | H4, H5, HN |
| Ublox-ZED-F9P-04B | |
|---|---|
| GNSS | GPS, QZSS |
| Number of observable satellites | |
| Frequency | 5 Hz |
| DOP | |
| Elevation angle | <15 |
| CEP | 1.5 (in case of DOP = 1) |
| Speed | Doppler shift |
| LOS→MP | ||||||
|---|---|---|---|---|---|---|
| 6 | 7 | 8 | 9 | 10 | 11 | |
| 1 | 72 | 65 | 60.74 | 57.33 | 54.95 | 53.3 |
| 2 | 95.45 | 90.62 | 68.50 | 83.25 | 80.79 | 78.96 |
| 3 | - | 98.44 | 83.86 | 94.24 | 82.45 | 91.02 |
| 4 | - | - | 99.39 | 98.69 | 87.41 | 96.48 |
| 5 | - | - | - | - | 99.29 | 98.79 |
| Time | WLSM [12] | Proposed Position Error (m) | Match Rate of Current and Previous PRN Data of Selected Cluster (%) | Speed Match Rate (%) |
|---|---|---|---|---|
| Trajectory | RMSE (m) | Max Error (m) General/Proposed Algorithm | |
|---|---|---|---|
| General Algorithm | Proposed Algorithm | ||
| Central building district 1 (low speed) | 36.6700 | 4.4640 | 128.3053/23.4324 |
| Central building district 2 (high speed) | 33.2654 | 3.8837 | 307.6143/14.5854 |
| Bridge | 3.6038 | 1.0857 | 7.5718/2.8457 |
| Narrow road (alley and intersection) | 18.9787 | 1.8719 | 80.3850/4.3433 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, H.J.; Kim, Y.H.; Lee, J.H.; Park, S.J.; Ko, B.S.; Song, J.W. Improving the Accuracy of Vehicle Position in an Urban Environment Using the Outlier Mitigation Algorithm Based on GNSS Multi-Position Clustering. Remote Sens. 2023, 15, 3791. https://doi.org/10.3390/rs15153791
Kim HJ, Kim YH, Lee JH, Park SJ, Ko BS, Song JW. Improving the Accuracy of Vehicle Position in an Urban Environment Using the Outlier Mitigation Algorithm Based on GNSS Multi-Position Clustering. Remote Sensing. 2023; 15(15):3791. https://doi.org/10.3390/rs15153791
Chicago/Turabian StyleKim, Hak Ju, Yong Hun Kim, Joo Han Lee, So Jin Park, Bo Sung Ko, and Jin Woo Song. 2023. "Improving the Accuracy of Vehicle Position in an Urban Environment Using the Outlier Mitigation Algorithm Based on GNSS Multi-Position Clustering" Remote Sensing 15, no. 15: 3791. https://doi.org/10.3390/rs15153791
APA StyleKim, H. J., Kim, Y. H., Lee, J. H., Park, S. J., Ko, B. S., & Song, J. W. (2023). Improving the Accuracy of Vehicle Position in an Urban Environment Using the Outlier Mitigation Algorithm Based on GNSS Multi-Position Clustering. Remote Sensing, 15(15), 3791. https://doi.org/10.3390/rs15153791





