Q-Compensated Gaussian Beam Migration under the Condition of Irregular Surface
Abstract
1. Introduction
2. Theory
2.1. Basic Principles of Gaussian Beam in Visco-Acoustic Media
2.2. Q-GBM under the Condition of Irregular Surfaces
3. Numerical Tests
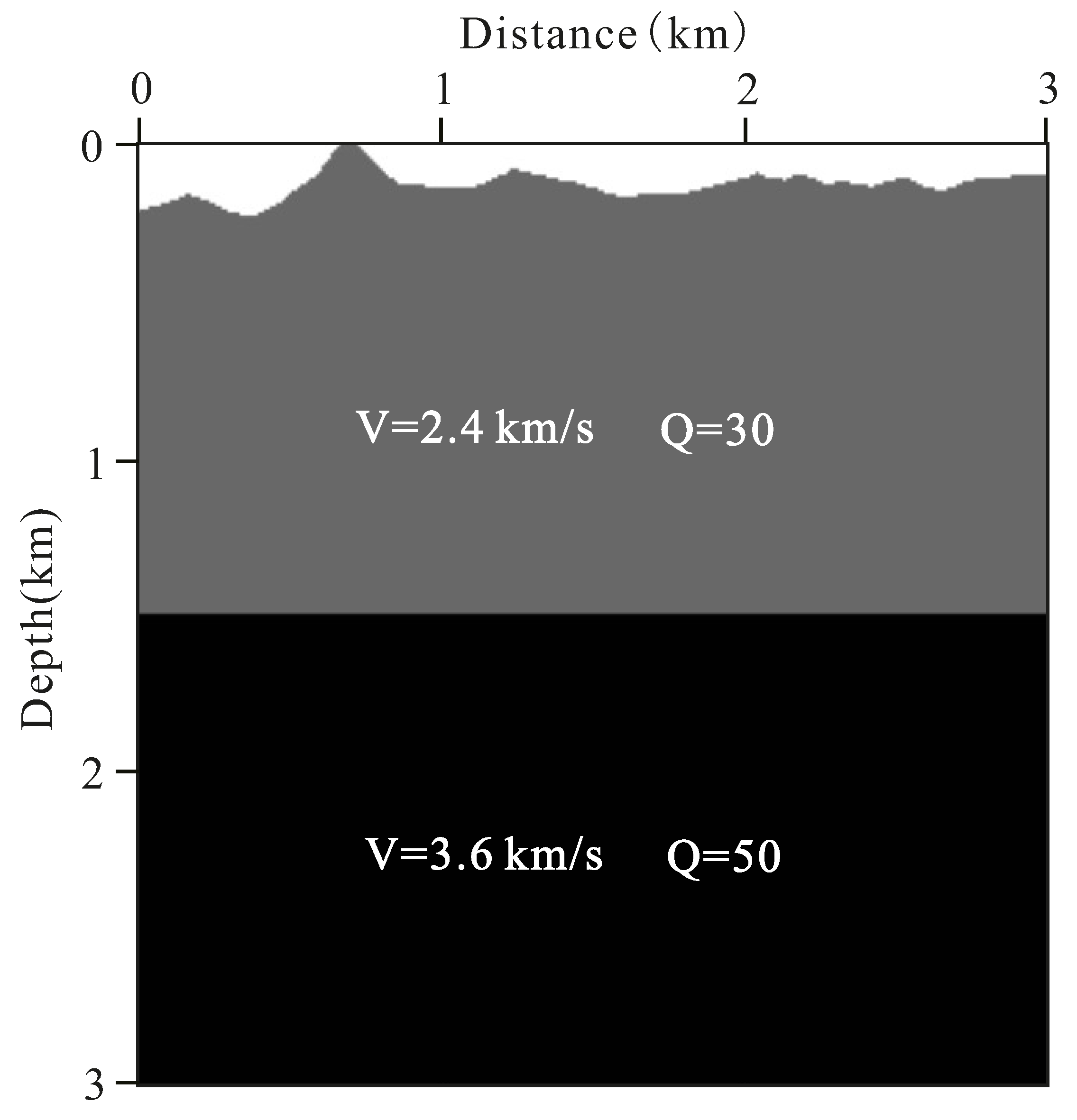
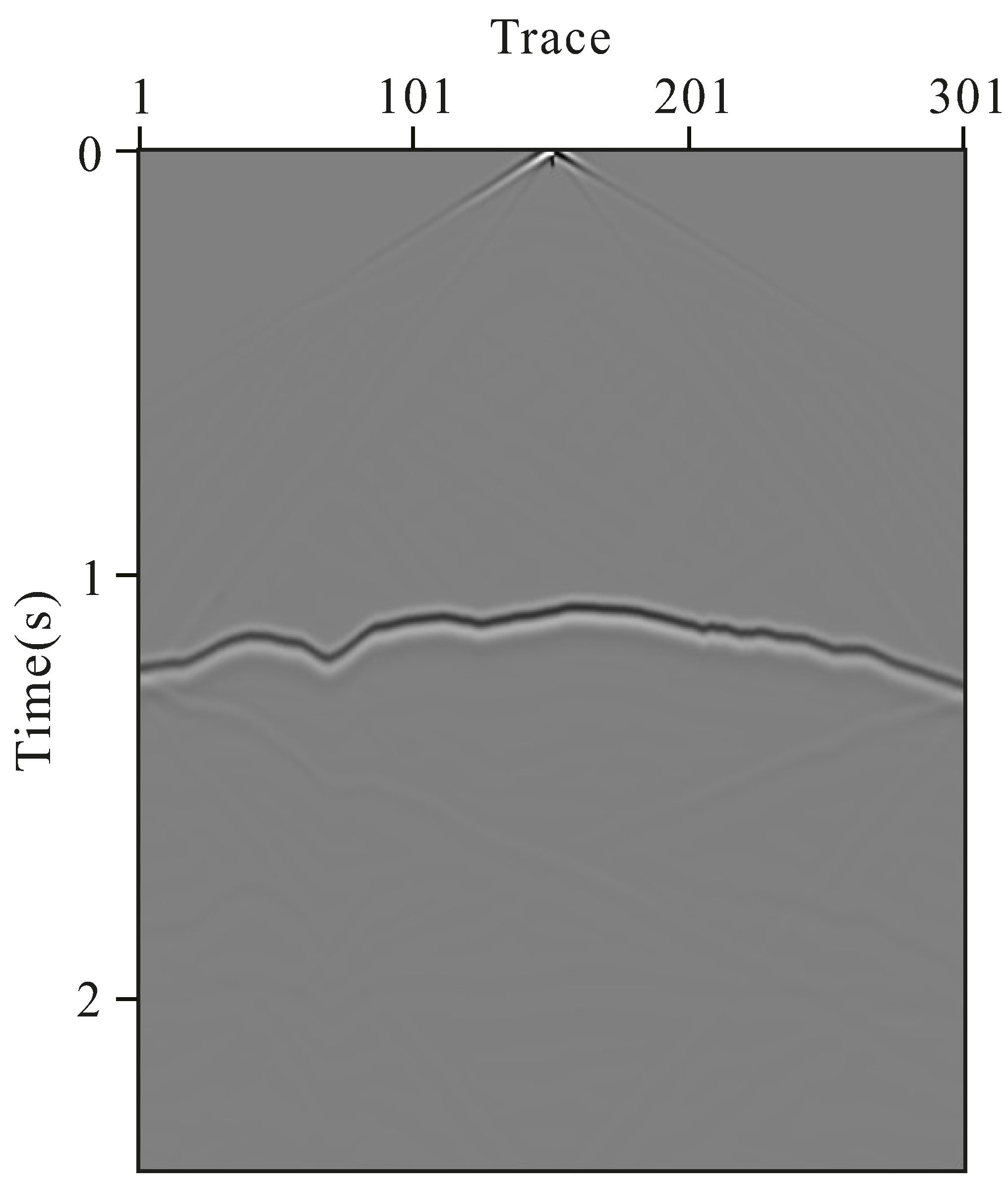
3.1. Single-Interface Model of the Visco-Acoustic Medium under the Condition of Irregular Surface
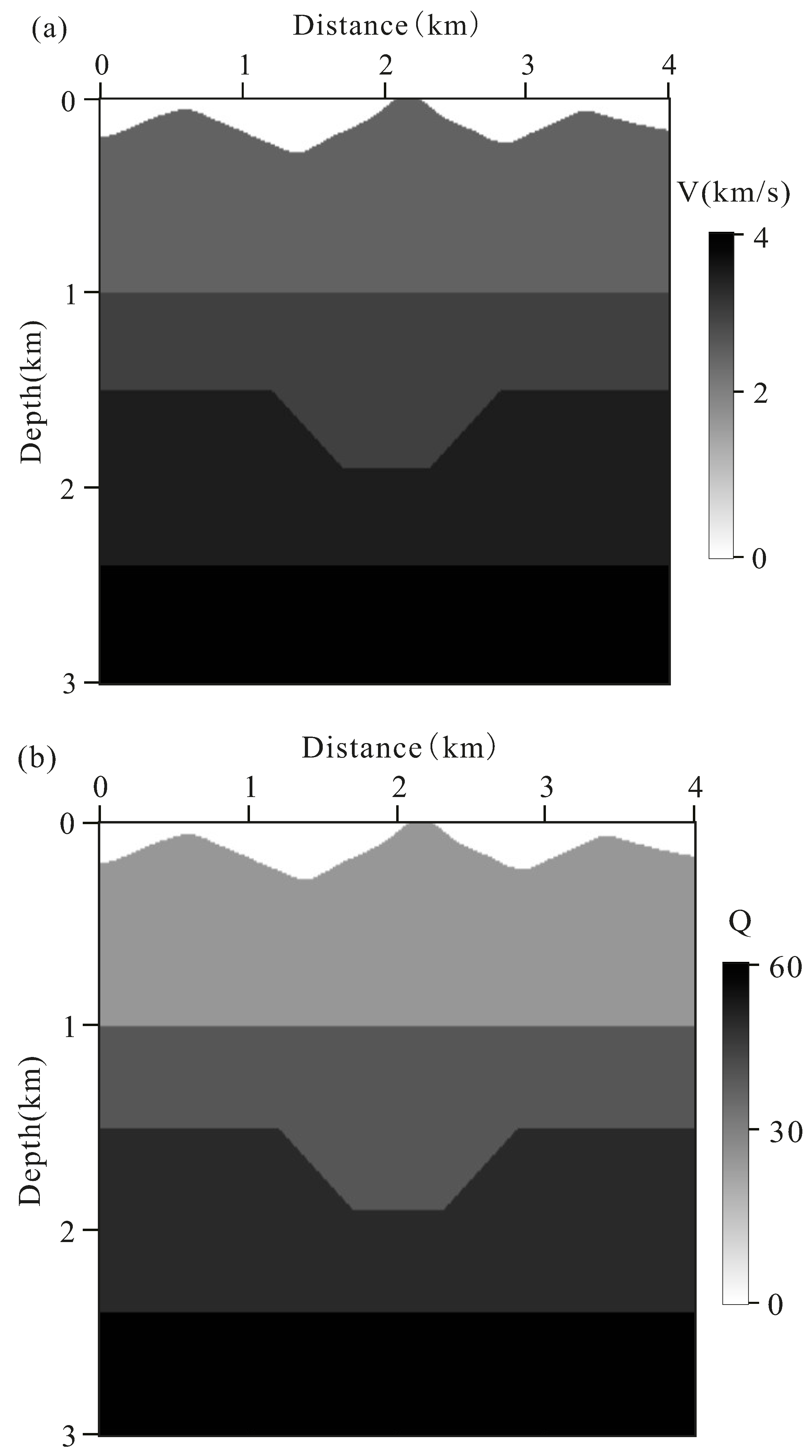
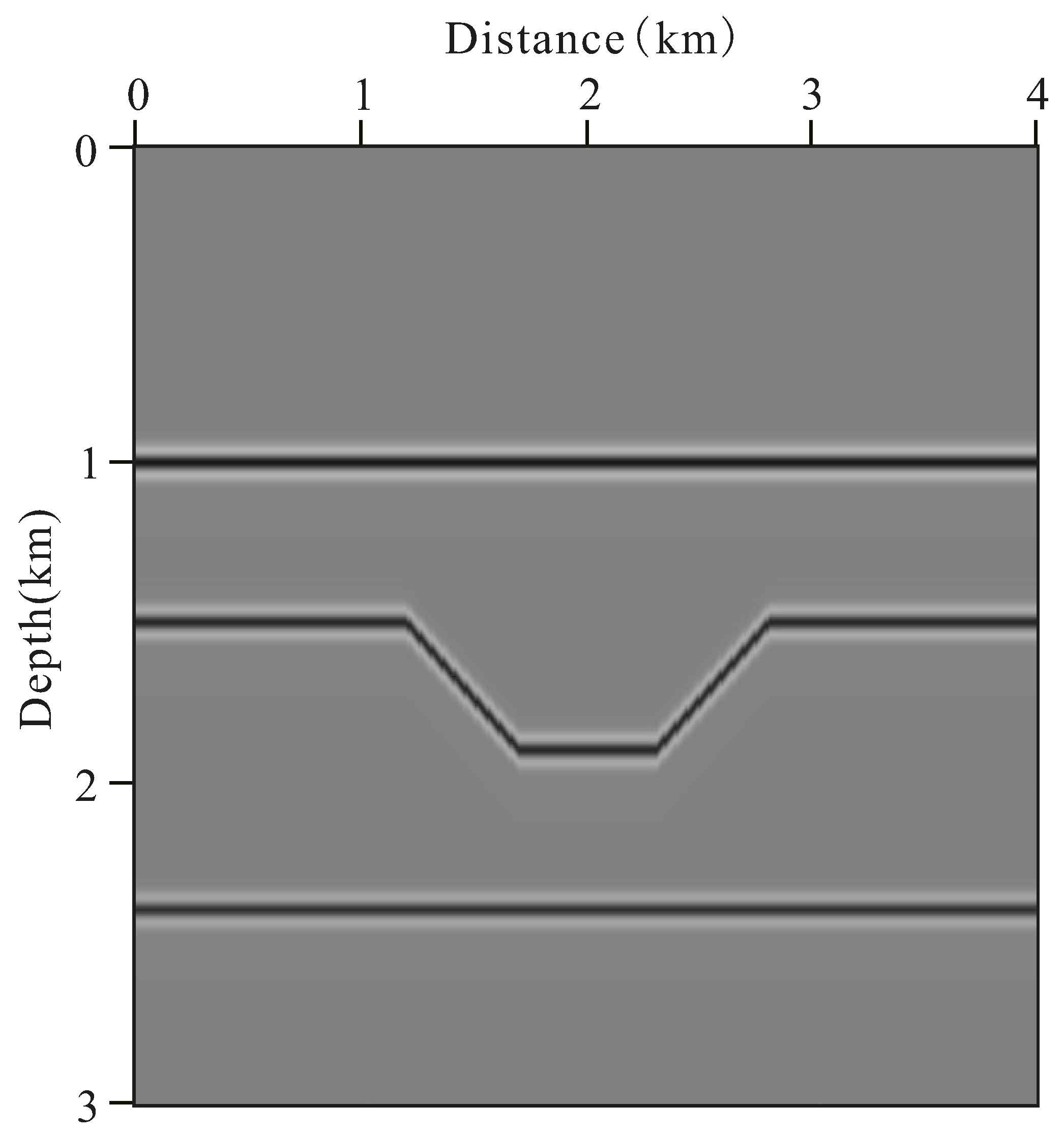
3.2. Sag Model of the Visco-Acoustic Medium under the Condition of Irregular Surfaces
3.3. Complex Fault Model of the Visco-Acoustic Medium under the Condition of Irregular Surfaces
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gu, B.L.; Zhang, S.S.; Huang, J.P.; Han, J.G. Q-compensated least-squares reverse time migration in TTI media using the visco-acoustic TTI wave equation based on the SLS model. J. Appl. Geophys. 2022, 203, 104682. [Google Scholar] [CrossRef]
- Wang, Y. A stable and efficient approach of inverse Q filtering. Geophysics 2002, 67, 657–663. [Google Scholar] [CrossRef]
- Traynin, P.; Liu, J.; Reilly, J. Amplitude and bandwidth recovery beneath gas zones using Kirchhoff prestack depth Q-migration. Proc. SEG Tech. Program Expanded Abstr. 2008, 2412–2416. [Google Scholar] [CrossRef]
- Xie, Y.; Xin, K.; Sun, J.; Notfors, C.; Biswal, A.K.; Balasubramaniam, M. 3D prestack depth migration with compensation for frequency dependent absorption and dispersion. Proc. SEG Tech. Program Expanded Abstr. 2009, 2919–2923. [Google Scholar] [CrossRef]
- Cavalca, M.; Fletcher, R.; Riedel, M. Q-compensation in complex media-Ray-based and wavefield extrapolation approaches. Proc. SEG Tech. Program Expanded Abstr. 2013, 2013, 3831–3835. [Google Scholar] [CrossRef]
- Xiao, X.; Hao, F.; Egger, C.; Wang, B.; Jiao, F.; Wang, X. Final Laser-Beam Q-Migration. Proc. SEG Tech. Program Expanded Abstr. 2014, 3872–3876. [Google Scholar] [CrossRef]
- Mittet, R. A simple design procedure for depth extrapolation operators that compensates for absorption and dispersion. Geophysics 2007, 72, S105–S112. [Google Scholar] [CrossRef]
- Zhu, T.; Harris, J.M.; Biondi, B. Q-compensated reverse-time migration. Geophysics 2014, 79, S77–S87. [Google Scholar] [CrossRef]
- Dutta, G.; Schuster, G.T. Attenuation compensation for least-squares reverse-time migration using the viscoacoustic-wave equation. Geophysics 2014, 79, S251–S262. [Google Scholar] [CrossRef]
- Zhao, Y.; Mao, N.; Ren, Z. A stable and efficient approach of Q reverse time migration. Geophysics 2018, 83, S557–S567. [Google Scholar]
- Yang, J.; Zhu, H. Viscoacoustic least-squares reverse time migration using a time-domain complex-valued wave equation. Geophysics 2019, 84, S479–S499. [Google Scholar]
- Fathalian, A.; Trad, D.O.; Innanen, K.A. Q-compensated reverse time migration in tilted transversely isotropic media. Geophysics 2021, 86, S73–S89. [Google Scholar]
- Yang, J.D.; Zhu, H.J.; Huang, J.P.; Li, Z.C. 2D isotropic elastic Gaussian-beam migration for common-shot multicomponent records. Geophysics 2018, 83, S127–S140. [Google Scholar]
- Hill, N.R. Gaussian beam migration. Geophysics 1990, 55, 1416–1428. [Google Scholar]
- Hill, N.R. Prestack Gaussian-beam depth migration. Geophysics 2001, 66, 1240–1250. [Google Scholar]
- Alkhalifah, T. Gaussian beam depth migration for anisotropic media. Geophysics 1995, 60, 1474–1484. [Google Scholar]
- Gray, S.H. Gaussian beam migration of common-shot records. Geophysics 2005, 70, S71–S77. [Google Scholar]
- Zhu, T.F.; Gray, S.H.; Wang, D.L. Prestack Gaussian-beam depth migration in anisotropic media. Geophysics 2007, 72, S133–S138. [Google Scholar]
- Popov, M.M.; Semtchenok, N.M.; Popov, P.M.; Verdel, A.R. Depth migration by the Gaussian beam summation method. Geophysics 2010, 75, S81–S93. [Google Scholar]
- Li, X.L.; Mao, W.J.; Shi, X.C.; Yue, Y.B. Elastic 3D PS converted-wave Gaussian beam migration. Geophysics 2018, 83, S213–S225. [Google Scholar]
- Yang, J.D.; Zhu, H.J. A practical data-driven optimization strategy for Gaussian beam migration. Geophysics 2018, 83, S81–S92. [Google Scholar]
- Han, J.G.; Lü, Q.T.; Gu, B.L.; Yan, J.Y.; Zhang, H. 2D anisotropic multicomponent Gaussian-beam migration under complex surface conditions. Geophysics 2020, 85, S89–S102. [Google Scholar] [CrossRef]
- Wu, J.; Chen, X.H.; Bai, M.; Liu, G.C. Attenuation compensation in multicomponent Gaussian beam prestack depth migration. Appl. Geophys. 2015, 12, 157–168. [Google Scholar] [CrossRef]
- Shi, X.C.; Mao, W.J.; Li, X.L. Viscoelastic Q-compensated Gaussian beam migration based on vector-wave imaging. Chin. J. Geophys. 2019, 64, 1480–1491. [Google Scholar]
- Al-Ali, M.N.; Verschuur, D.J. An integrated method for resolving the seismic complex near-surface problem. Geophys. Prospect. 2006, 54, 739–750. [Google Scholar]
- Liu, W.; Zhao, B.; Zhou, H.; He, Z.; Liu, H.; Du, Z. Wave-equation global datuming based on the double square root operator. Geophysics 2011, 76, U35–U43. [Google Scholar]
- Wiggins, J.W. Kirchhoff integral extrapolation and migration of nonplanar data. Geophysics 1984, 49, 1239–1248. [Google Scholar]
- Gray, S.H.; Marfurt, K.J. Migration from topography: Improving the near-surface image. Can. J. Explor. Geophys. 1995, 31, 18–24. [Google Scholar]
- Rajasekaran, S.; Mcmechan, G.A. Prestack processing of land data with complex topography. Geophysics 1995, 60, 1875–1886. [Google Scholar] [CrossRef]
- Lan, H.; Zhang, Z.; Chen, J.; Liu, Y. Reverse time migration from irregular surface by flattening surface topography. Tectonophysics 2014, 627, 26–37. [Google Scholar] [CrossRef]
- Keers, H.; Vasco, D.W.; Johnson, L.R. Viscoacoustic crosswell imaging using asymptotic waveforms. Geophysics 2001, 66, 861–870. [Google Scholar] [CrossRef]
- Han, J.G.; Lü, Q.T.; Gu, B.L.; Xing, Z.T. Gaussian beam summation migration of deep reflection seismic data: Numerical examples. IEEE Geosci. Remote Sens. Lett. 2022, 19, 8030805. [Google Scholar]
- Han, J.; Wang, Y.; Yu, C. Multiwave Gaussian beam prestack depth migration of exploration-scale seismic data with complex near-surface effects. Near Surf. Geophys. 2016, 14, 307–313. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, J.; Lü, Q.; Gu, B.; Yan, J. Q-Compensated Gaussian Beam Migration under the Condition of Irregular Surface. Remote Sens. 2023, 15, 3761. https://doi.org/10.3390/rs15153761
Han J, Lü Q, Gu B, Yan J. Q-Compensated Gaussian Beam Migration under the Condition of Irregular Surface. Remote Sensing. 2023; 15(15):3761. https://doi.org/10.3390/rs15153761
Chicago/Turabian StyleHan, Jianguang, Qingtian Lü, Bingluo Gu, and Jiayong Yan. 2023. "Q-Compensated Gaussian Beam Migration under the Condition of Irregular Surface" Remote Sensing 15, no. 15: 3761. https://doi.org/10.3390/rs15153761
APA StyleHan, J., Lü, Q., Gu, B., & Yan, J. (2023). Q-Compensated Gaussian Beam Migration under the Condition of Irregular Surface. Remote Sensing, 15(15), 3761. https://doi.org/10.3390/rs15153761






