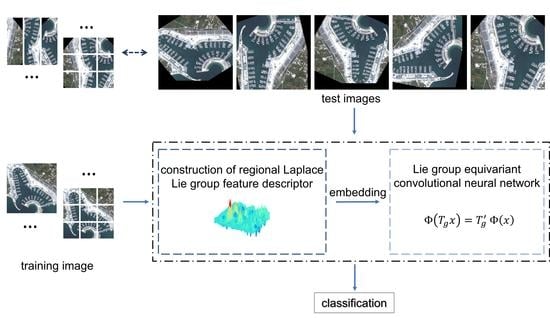
Lie Group Equivariant Convolutional Neural Network Based on Laplace Distribution
Abstract
:1. Introduction
- We leverage the Lie group of the Laplace distribution function space to construct the affine Lie group. This representation illustrates the relationship between different regions and features of the image, formulates the spatial information based on image decomposition, and preserves the geometric and algebraic structure of the pre- and post-mapping spaces, drawing upon Lie group theory.
- We achieve multifeature joint representation through the covariance and mean of the Laplace distribution. This approach integrates low- and mid-level features and reflects correlations among different features. Moreover, the affine Lie group resulting from mapping is a d-dimensional real symmetric matrix Lie group, possessing advantageous computational performance and noise resistance.
- The Lie group equivariant convolutional neural network, based on the Laplace distribution, offers excellent interpretability from a Lie group theory perspective, and significantly enhances data efficiency in terms of generalized symmetry. Its efficacy is apparent in practical remote sensing recognition experiments, positioning it as a lightweight neural network with wide-ranging application prospects.
2. Related Work
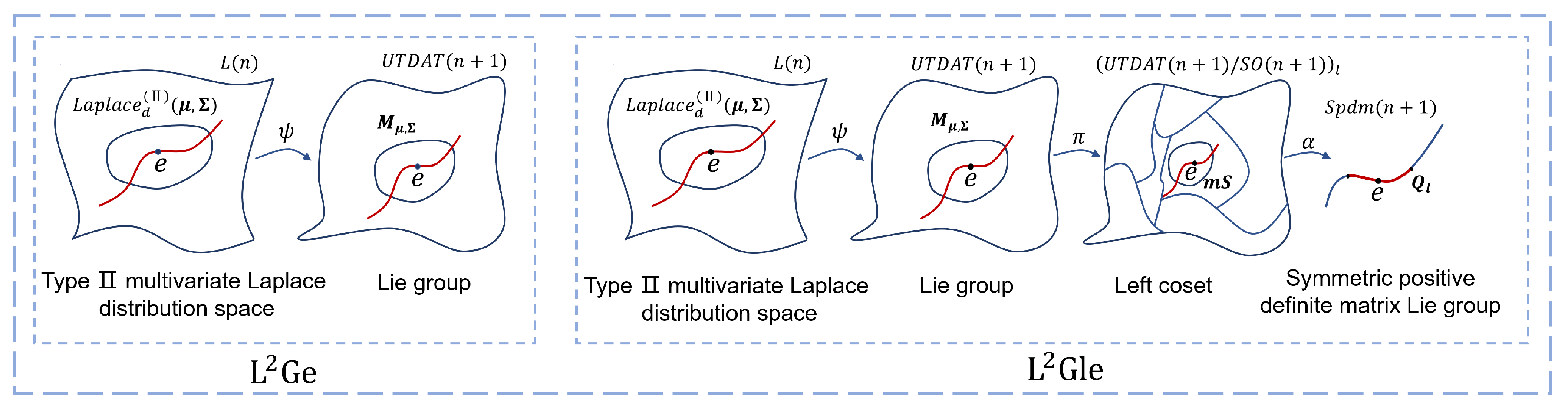
3. Lie Group Representation of Laplace Distribution
3.1. Construction of the Laplace Feature Map
3.2. Calculation of the Laplace Lie Group Feature Matrix
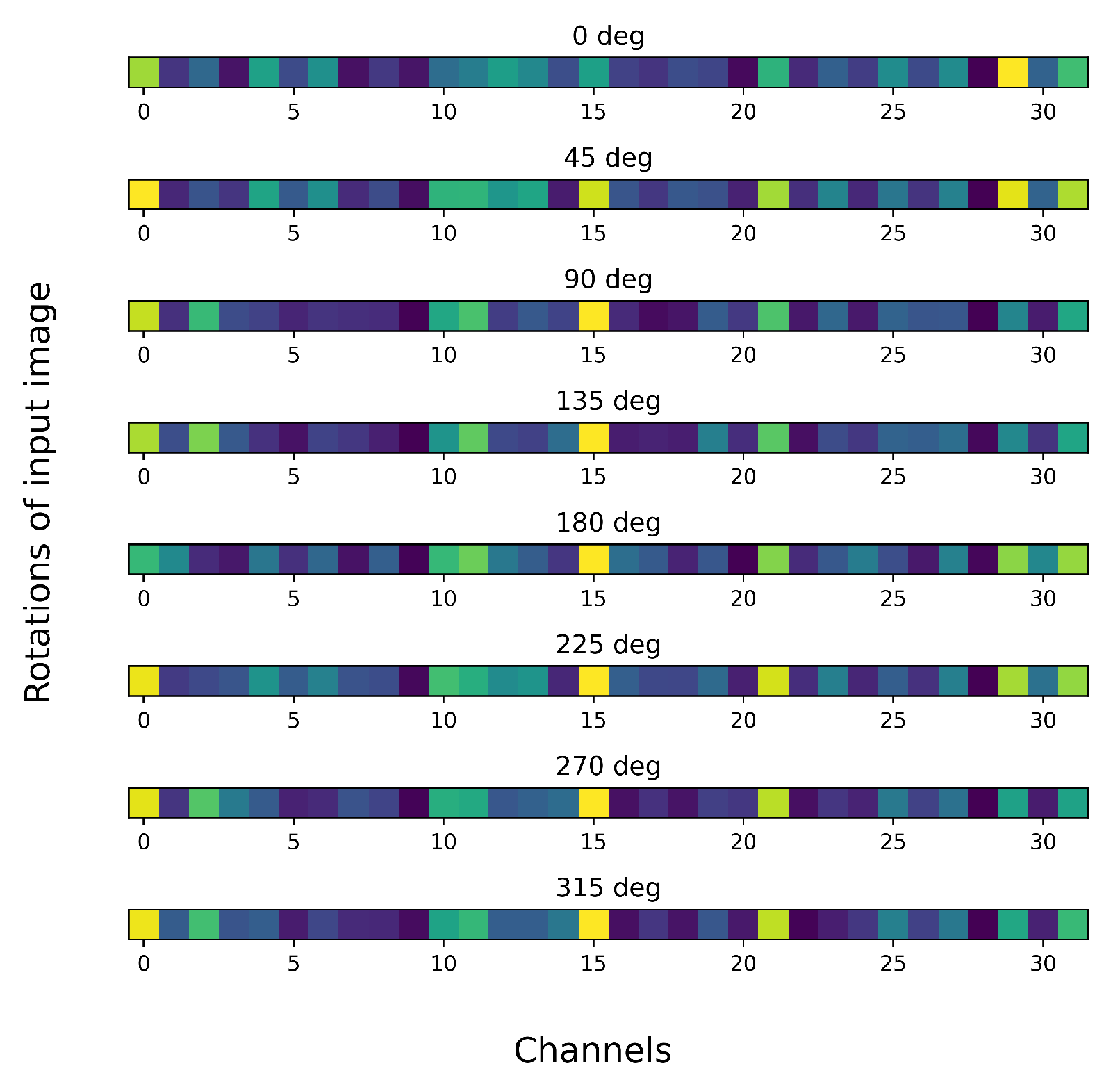
4. Lie Group Equivariant Convolutional Neural Network
4.1. Convolutional Layer of Lie Group
4.2. Activation Layer of Other Lie Groups
5. Experiment and Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kim, B.; Doshi-Velez, F. Interpretable machine learning: The fuss, the concrete and the questions. In Proceedings of the ICML: Tutorial on Interpretable Machine Learning, Sydney, NSW, Australia, 6–11 August 2017. [Google Scholar]
- Du, M.; Liu, N.; Hu, X. Techniques for interpretable machine learning. Commun. ACM 2019, 63, 68–77. [Google Scholar] [CrossRef] [Green Version]
- Arrieta, A.B.; Díaz-Rodríguez, N.; Del Ser, J.; Bennetot, A.; Tabik, S.; Barbado, A.; García, S.; Gil-López, S.; Molina, D.; Benjamins, R.; et al. Explainable Artificial Intelligence (XAI): Concepts, taxonomies, opportunities and challenges toward responsible AI. Inf. Fusion 2020, 58, 82–115. [Google Scholar] [CrossRef] [Green Version]
- Yao, H.; Jia, X.; Kumar, V.; Li, Z. Learning with Small Data. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, New York, NY, USA, 20 August 2020; KDD ’20. pp. 3539–3540. [Google Scholar] [CrossRef]
- Weiler, M.; Cesa, G. General E(2)-Equivariant Steerable CNNs. In Proceedings of the Conference on Neural Information Processing Systems (NeurIPS), Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Gidaris, S.; Singh, P.; Komodakis, N. Unsupervised Representation Learning by Predicting Image Rotations. arXiv 2018, arXiv:1803.07728. [Google Scholar]
- Feng, Z.; Xu, C.; Tao, D. Self-supervised representation learning by rotation feature decoupling. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 10364–10374. [Google Scholar]
- Hinton, G.E.; Krizhevsky, A.; Wang, S.D. Transforming auto-encoders. In Proceedings of the Artificial Neural Networks and Machine Learning–ICANN 2011: 21st International Conference on Artificial Neural Networks, Espoo, Finland, 14–17 June 2011; Proceedings, Part I 21. Springer: Berlin/Heidelberg, Germany, 2011; pp. 44–51. [Google Scholar]
- Cohen, T.; Welling, M. Group equivariant convolutional networks. In Proceedings of the International Conference on Machine Learning, PMLR, New York, NY, USA, 20–22 June 2016; pp. 2990–2999. [Google Scholar]
- Larocca, M.; Sauvage, F.; Sbahi, F.M.; Verdon, G.; Coles, P.J.; Cerezo, M. Group-invariant quantum machine learning. PRX Quantum 2022, 3, 030341. [Google Scholar] [CrossRef]
- Cohen, T.S.; Geiger, M.; Weiler, M. A general theory of equivariant cnns on homogeneous spaces. In Proceedings of the 33rd Conference on Neural Information Processing System, Vancouver, BC, Canada, 8–14 December 2019; p. 32. [Google Scholar]
- Cesa, G.; Lang, L.; Weiler, M. A Program to Build E(N)-Equivariant Steerable CNNs. In Proceedings of the International Conference on Learning Representations, Virtual Event, 25–29 April 2022. [Google Scholar]
- Xu, Y.; Lei, J.; Dobriban, E.; Daniilidis, K. Unified Fourier-based Kernel and Nonlinearity Design for Equivariant Networks on Homogeneous Spaces. In Proceedings of the International Conference on Machine Learning, PMLR, Baltimore, MD, USA, 17–23 July 2022; pp. 24596–24614. [Google Scholar]
- Cohen, T.S.; Geiger, M.; Köhler, J.; Welling, M. Spherical cnns. In Proceedings of the ICLR, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar] [CrossRef]
- Worrall, D.E.; Garbin, S.J.; Turmukhambetov, D.; Brostow, G.J. Harmonic networks: Deep translation and rotation equivariance. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 5028–5037. [Google Scholar]
- Weiler, M.; Geiger, M.; Welling, M.; Boomsma, W.; Cohen, T.S. 3d steerable cnns: Learning rotationally equivariant features in volumetric data. In Proceedings of the 2nd Conference on Neural Information Processing Systems 2018, Montreal, QC, Canada, 3–8 December 2018. [Google Scholar]
- Bekkers, E.J. B-spline cnns on lie groups. arXiv 2019, arXiv:1909.12057. [Google Scholar]
- MacDonald, L.E.; Ramasinghe, S.; Lucey, S. Enabling equivariance for arbitrary Lie groups. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 8183–8192. [Google Scholar]
- Feng, L.; Chen, S.; Zhang, C.; Zhang, Y.; He, Y. A comprehensive review on recent applications of unmanned aerial vehicle remote sensing with various sensors for high-throughput plant phenotyping. Comput. Electron. Agric. 2021, 182, 106033. [Google Scholar] [CrossRef]
- Xu, C.; Zhu, G.; Shu, J. A lightweight and robust lie group-convolutional neural networks joint representation for remote sensing scene classification. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5501415. [Google Scholar] [CrossRef]
- Gao, X.; Pan, Z.; Fan, G.; Zhang, X.; Yin, H. Local feature-based mutual complexity for pixel-value-ordering reversible data hiding. Signal Process. 2023, 204, 108833. [Google Scholar] [CrossRef]
- Zhang, X.; Gao, Z.; Jiao, L.; Zhou, H. Multifeature hyperspectral image classification with local and nonlocal spatial information via Markov random field in semantic space. IEEE Trans. Geosci. Remote Sens. 2017, 56, 1409–1424. [Google Scholar] [CrossRef] [Green Version]
- Zhou, D.; Jin, X.; Jiang, Q.; Cai, L.; Lee, S.J.; Yao, S. MCRD-Net: An unsupervised dense network with multi-scale convolutional block attention for multi-focus image fusion. IET Image Process. 2022, 16, 1558–1574. [Google Scholar] [CrossRef]
- Zhang, C.; Tang, M.; Li, T.; Sun, Y.; Tian, G. A new multivariate Laplace distribution based on the mixture of normal distributions. Sci. Sin. Math. 2020, 50, 711–728. [Google Scholar] [CrossRef]
- Tuzel, O.; Porikli, F.; Meer, P. Region covariance: A fast descriptor for detection and classification. In Proceedings of the Computer Vision–ECCV 2006: 9th European Conference on Computer Vision, Graz, Austria, 7–13 May 2006; Proceedings, Part II 9. Springer: Berlin/Heidelberg, Germany, 2006; pp. 589–600. [Google Scholar]
- Imani, M. Convolutional Kernel-based covariance descriptor for classification of polarimetric synthetic aperture radar images. IET Radar Sonar Navig. 2022, 16, 578–588. [Google Scholar] [CrossRef]
- Li, P.; Wang, Q.; Zeng, H.; Zhang, L. Local log-Euclidean multivariate Gaussian descriptor and its application to image classification. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 39, 803–817. [Google Scholar] [CrossRef]
- Chen, Y.; Tian, Y.; Pang, G.; Carneiro, G. Deep one-class classification via interpolated gaussian descriptor. In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; Volume 36, pp. 383–392. [Google Scholar]
- Sabour, S.; Frosst, N.; Hinton, G.E. Dynamic routing between capsules. In Proceedings of the Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Lenssen, J.E.; Fey, M.; Libuschewski, P. Group equivariant capsule networks. Adv. Neural Inf. Process. Syst. 2018, 31, 8858–8867. [Google Scholar]
- Finzi, M.; Stanton, S.; Izmailov, P.; Wilson, A.G. Generalizing convolutional neural networks for equivariance to lie groups on arbitrary continuous data. In Proceedings of the International Conference on Machine Learning, PMLR, Virtual, 13–18 July 2020; pp. 3165–3176. [Google Scholar]
- van der Ouderaa, T.F.; van der Wilk, M. Sparse Convolutions on Lie Groups. In Proceedings of the NeurIPS Workshop on Symmetry and Geometry in Neural Representations, PMLR, New Orleans, LA, USA, 3 December 2022; pp. 48–62. [Google Scholar]
- Gong, L.; Wang, T.; Liu, F. Shape of Gaussians as feature descriptors. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 2366–2371. [Google Scholar]
- Humphreys, J.E. Introduction to Lie Algebras and Representation Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 9. [Google Scholar]
- Suzuki, M. Group Theory II; Springer: Berlin/Heidelberg, Germany, 1986. [Google Scholar]
- Joshi, K.D. Foundations of Discrete Mathematics; New Age International: Dhaka, Bangladesh, 1989. [Google Scholar]
- Douglas, R.G. On majorization, factorization, and range inclusion of operators on Hilbert space. Proc. Am. Math. Soc. 1966, 17, 413–415. [Google Scholar] [CrossRef]
- Bouteldja, S.; Kourgli, A.; Belhadj Aissa, A. Efficient local-region approach for high-resolution remote-sensing image retrieval and classification. J. Appl. Remote Sens. 2019, 13, 016512. [Google Scholar] [CrossRef]
- Kondor, R.; Trivedi, S. On the generalization of equivariance and convolution in neural networks to the action of compact groups. In Proceedings of the International Conference on Machine Learning, PMLR, Stockholm, Sweden, 10–15 July 2018; pp. 2747–2755. [Google Scholar]
- Rossmann, W. Lie Groups: An Introduction through Linear Groups; Oxford University Press on Demand: Oxford, UK, 2006; Volume 5. [Google Scholar]
- Xia, G.S.; Hu, J.; Hu, F.; Shi, B.; Bai, X.; Zhong, Y.; Zhang, L.; Lu, X. AID: A benchmark data set for performance evaluation of aerial scene classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3965–3981. [Google Scholar] [CrossRef] [Green Version]
- Cheng, G.; Han, J.; Lu, X. Remote sensing image scene classification: Benchmark and state of the art. Proc. IEEE 2017, 105, 1865–1883. [Google Scholar] [CrossRef]
- Gallego, A.J.; Pertusa, A.; Gil, P. Automatic ship classification from optical aerial images with convolutional neural networks. Remote Sens. 2018, 10, 511. [Google Scholar] [CrossRef] [Green Version]




| Method | Training Rate | |
|---|---|---|
| 20% | 50% | |
| CNN-baseline [29] | 62.21 | 65.49 |
| CapsNet [29] | 72.56 | 75.55 |
| GE CapsNet [30] | 82.95 | 86.26 |
| Cov [20] + LGCNN | 88.32 | 90.22 |
| GDe [27] + LGCNN | 89.15 | 92.97 |
| -CNN | 90.60 | 92.45 |
| -CNN | 91.15 | 93.16 |
| Method | Training Rate | |
|---|---|---|
| 10% | 20% | |
| CNN-baseline [29] | 65.09 | 68.71 |
| CapsNet [29] | 71.95 | 74.95 |
| GE CapsNet [30] | 79.88 | 82.09 |
| Cov [20] + LGCNN | 83.32 | 86.03 |
| GDe [27] + LGCNN | 87.15 | 89.11 |
| -CNN | 87.60 | 89.47 |
| -CNN | 89.15 | 90.16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liao, D.; Liu, G. Lie Group Equivariant Convolutional Neural Network Based on Laplace Distribution. Remote Sens. 2023, 15, 3758. https://doi.org/10.3390/rs15153758
Liao D, Liu G. Lie Group Equivariant Convolutional Neural Network Based on Laplace Distribution. Remote Sensing. 2023; 15(15):3758. https://doi.org/10.3390/rs15153758
Chicago/Turabian StyleLiao, Dengfeng, and Guangzhong Liu. 2023. "Lie Group Equivariant Convolutional Neural Network Based on Laplace Distribution" Remote Sensing 15, no. 15: 3758. https://doi.org/10.3390/rs15153758
APA StyleLiao, D., & Liu, G. (2023). Lie Group Equivariant Convolutional Neural Network Based on Laplace Distribution. Remote Sensing, 15(15), 3758. https://doi.org/10.3390/rs15153758