1. Introduction
Evapotranspiration (ET) is a key component of the water cycle, while in rainfed ecosystems, it is the main consumer of available precipitation water [
1,
2,
3]. The anticipated climate trends suggest that the magnitude of ET will increase due to warming and changing precipitation patterns impacting the earth’s ecosystems [
4]. Due to its significance, accurate measurements or estimates of ET are crucial. However, direct ET measurement by methods such as lysimeters [
5] or eddy covariance [
6,
7] is difficult to obtain due to the high requirements of expensive equipment or application difficulties. The estimation of ET by common meteorological data is generally acceptable, since it is easier and in many cases produces reliable estimates.
The site-specific characteristics highly influence the ET magnitudes. Thus, numerous estimation models have been proposed worldwide with different approaches, whereas the substrate at each site highly influences the ET rates [
8]. In general, four major groups of methods can be defined to classify the empirical ET models: the mass-transfer-based methods, the temperature-based methods, the radiation-based methods and the combination methods. In all cases, the proposed equations aim to provide reliable estimates of the water demand driven by atmospheric conditions by minimizing the impact of plant species, vegetation stage or soil. To accomplish this, the estimates of ET are generally mentioned as potential (PET) or reference evapotranspiration, which are two different terms for expressing the water demand with different conceptual physical bases. The selection of the appropriate PET method is particularly important as it affects hydrometeorological and climatic variables that are linked to the sustainability of natural ecosystems [
9].
Raza et al. [
10] performed a comprehensive review on studies using several empirical evapotranspiration models and found that Thornthwaites’ 1948 and Hargreaves–Samani’s 1985 models were the most widely used among the temperature-based models, whereas Priestley 1972 and Ritchie 1972 were also the most often used among the radiation-based ones. However, the Penman–Monteith model is the most widely used in all categories.
The Penman–Monteith model is generally accepted as the most accurate method to estimate maximum ET as also suggested by the FAO (Food and Agriculture Organization of the United Nations) and WMO (World Meteorological Organization). In many studies, FAO56-PM is used as the standard method to compare and evaluate the performance of other methods in specific sites, areas or regions [
11,
12,
13,
14,
15,
16,
17]. The FAO adopted the concept of reference evapotranspiration in the FAO guidelines for crop water requirements by Doorenbos and Pruitt [
18,
19]. This approach to calculating crop evapotranspiration is widely accepted by engineers, agronomists and researchers in practice, design and research. The reference concept relates to a growing reference grass crop and is represented in FAO-24 by climate types calibrated with lysimeter data from various locations [
20]. However, many have pointed to weaknesses in the FAO-24 methodologies for implementation on a global scale. Researchers have tried to improve the evapotranspiration estimations for different locations and data availability through experimental and theoretical studies. First, the correlation of the calculated crop evapotranspiration with a reference crop proved difficult. The definition of a grass variety and its morphological characteristics have not been standardized for different climatic conditions. Furthermore, grass management varies from site to site and over time within the same site. Others have suggested alfalfa as a reference crop, but they have encountered similar variety and management problems [
11,
21,
22,
23,
24].
The FAO 56 Penman–Monteith equation incorporating standardized roughness and the bulk surface resistance parameters is recommended as the globally used equation to represent the new definition of reference evapotranspiration, replacing the Penman combination model. Thus, the reference grass evapotranspiration is redefined as the evapotranspiration from a clipped extended grass surface of 12 cm height with a total surface resistance equal to 70 s m−1. This change in definition and the choice of a specific calculation method is intended to help eliminate problems in measuring a true evapotranspiration rate and provide consistent estimates across regions of the globe. The use of the FAO Penman–Monteith equation overcomes the overestimation problems of the earlier FAO Penman combination method. A hypothetical calculation of reference evapotranspiration can be used to calibrate empirical evapotranspiration equations and be considered as the basis for determining crop coefficients where evapotranspiration cannot be measured simultaneously with specific crop evapotranspiration.
The need for new methods is generally imposed, because FAO56-PM produces accurate PET estimates, but for its application, a considerable number of meteorological parameters is required, which in many areas are not measured. Thus, the adjustment or calibration of simpler original method with fewer data requirements is very important to accurately estimate PET, particularly in regions where meteorological data are rare.
Solar radiation and air temperature are related parameters, considered as the most important for the determination of PET especially in summer [
25,
26], whereas relative humidity typically drives ET in winter [
25]. The impact of wind speed appears to be minor [
25]; however, there are studies [
27] indicating a strong wind dependence of PET. In all cases, the large spatial variability and the site-specific characteristics are considered as key factors for the formation of PET [
27,
28] along with seasonality [
25,
26].
Several methods have been proposed for PET estimation. The method of Hargreaves and Samani (1985) was extensively used in many applications due to the low data requirements as well as its simplicity in application. Similar approaches were proposed by many authors including Schendel [
29], Baier-Robertson [
30], and Trajkovic [
31]. Shirmohammadi-Aliakbarkhani and Saberali [
32] suggested that the Hargreaves–Samani method is a simple and reliable alternative for the estimation of ET in arid areas of Iran by assessing meteorological data from 13 sites in northeast Iran. The methods of Thornthwaite, Priestley and Taylor, Makkink and Abtew are recommended for humid climates, while this of Hargreaves and Samani is recommended for arid and semi-arid conditions, and those of Hamon and Linacre are recommended for all climates.
In general, simple empirical equations were evaluated for a variety of climates and regions worldwide, presenting different performances and imposing also the need for local calibration. Lang et al. [
16] investigated the performance of eight methods in southwestern China and found high variability between different regions. The authors found that Hargreaves–Samani, Priestley-Taylor and Abtew were overestimating and Makkink, Thornthwaite, Hammon, Linacre and Blaney-Criddle were underestimating ET, although they addressed the good performance of specific methods when applied to specific regions of southwestern China. Lang et al. [
16] also supported the overall better performance of the radiation-based methods compared to the temperature-based ones, proposing Makkink as the best radiation method and Hargreaves–Samani as the best temperature method for their study area.
Similarly, Makkink was reported to perform well in Malaysia [
33], but its performance was poor in the southeastern United States [
34], and this was attributed to the different climatic conditions and geographical environments [
16]. Priestley-Taylor was suggested by Wei and Menzel [
35] as the most suitable method for global application. Thornthwaite was found to perform worst in many regions [
16,
34,
36,
37], which was probably because it takes into consideration only temperature and because it was established in a valley’s humid climate. There are, however, many studies suggesting Thornthwaite as a well-performing method, e.g., in Malaysia [
38,
39].
Bourletsikas et al. [
14] evaluated the performance of 24 empirical PET models in a forest ecosystem in central Greece, using daily data for a 17-year time period and several statistical indices. They suggested the use of Copais and original Hargreaves methods for the daily PET estimation in forest environments, which were followed by Valiantzas (T, Rs) and Valiantzas (T, Rs, RH). The authors also proposed using the models of Turc, modified Hargreaves–Samani after Droogers and Allen (2002), the Sun Thermal Unit (STU), and Jensen-Haize, which also had a good performance. They also recommended local calibration for the use of all tested mass transfer-based methods (Albrecht, Mahringer, Penman, Romanenco, WMO), as well as Abtew, Caprio, de Bruin-Keijman, FAO24 Radiation, Hansen, Makkink, McGuiness-Brondne, Priestley-Taylor and modified Thornthwaite by Siegert and Schrodter.
In all cases, the characteristics of the surfaces, the prevailing local conditions and the number of input parameters in the empirical models affect the accuracy of the PET estimates. Bogawski and Bednorz [
40] reported on the decreasing performance of PET empirical methods with data availability.
Assessments of PET are typically performed in agricultural areas or on the larger scale of a basin. In the urban environment, PET is generally neglected, since the built-up cities covered by a variety of materials prevent the free movement of water or make it difficult to be studied. However, in urban green areas (i.e., parks), PET is of critical importance, determining the water requirements of the urban vegetation for its survival in the city’s unfavorable environment, which are characterized by increased temperatures and thermal stress as well as reduced water vapor content and decreased water quantities for irrigation, especially in Mediterranean and arid climates. In a recent study by Zhou et al. [
41], the authors describe the complex heat storage and shading effects in the urban environment, underlining also that only neglecting the shading effects leads to an overestimation of urban evapotranspiration of about 38.7%. In addition, the variable reflectance characteristics of the urban surfaces (even green ones) and surface temperatures in association with urban heat island and drought phenomena are highly affecting ET [
42,
43,
44] in the cities.
The aim of this study is to extend the existing knowledge and understanding about the impact of the built-up environment on the water requirements of urban vegetation, considering the significance of urban green spaces and their multiple socioeconomic and environmental benefits [
45,
46]. Toward this goal, 112 empirical PET methods were thoroughly evaluated against the benchmark FAO56-PM method in the Mediterranean environment of two Greek cities. Specifically, high-quality data from meteorological stations located above two urban green sites were used to test the performance of the methods including temperature-based, radiation-based, mass transfer and combination approaches, distinguishing the most suitable ones under different conditions and data availability schemes. In addition, locally adjusted mass transfer, temperature and radiation-based models are developed for enhancing the accuracy of PET estimations while maintaining low data requirements. Apart from the evaluation of a significantly high number of methods which have been rarely used in the literature, this study focuses on the research of micrometeorological aspects of urban green areas, which can provide crucial information for this vital resource for sustainable and quality life in the city under a changing climate.
3. Results
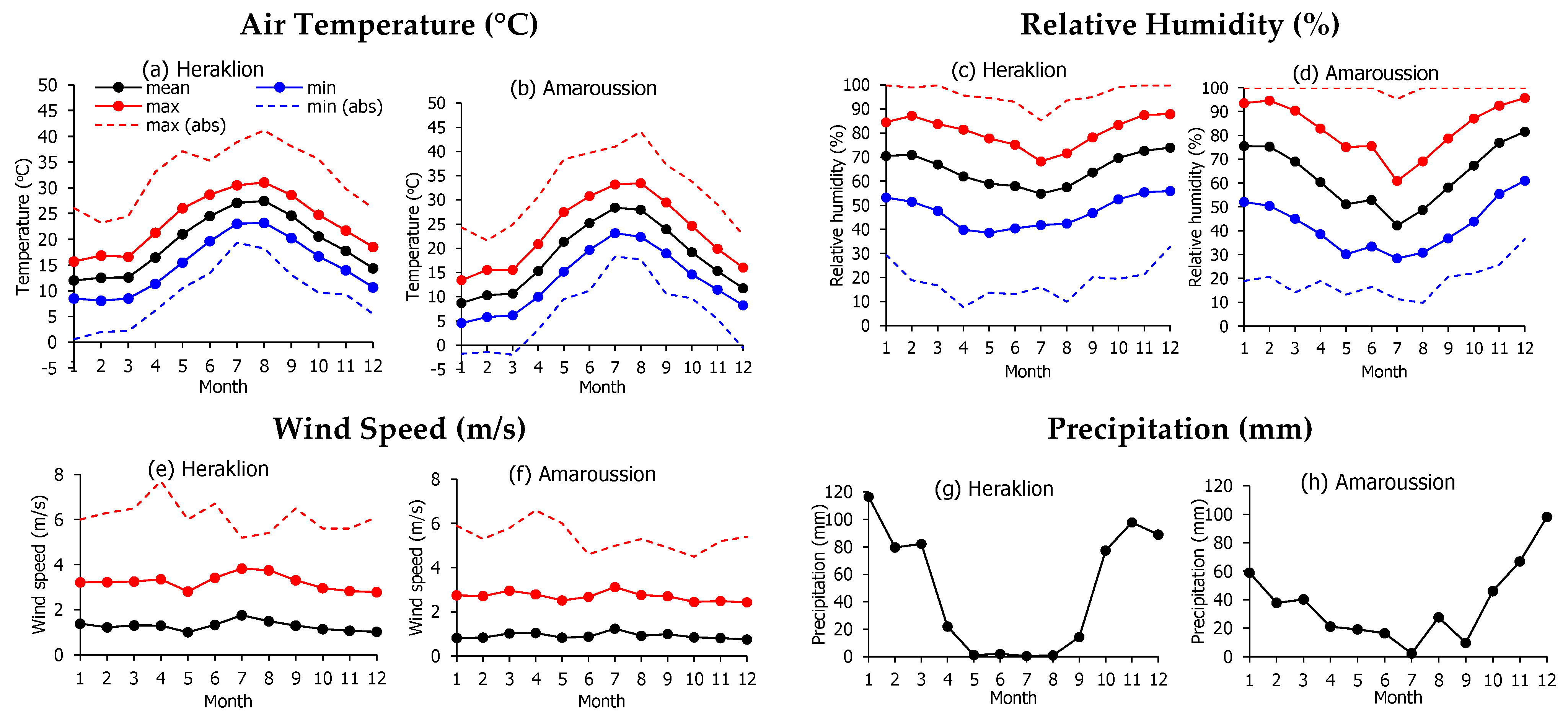
The micrometeorological stations of this study were installed above grass-covered irrigated surfaces inside the urban green spaces. Such surface characteristics allow the accurate estimation of PET by the application of the Penman–Monteith method considering that the measured meteorological parameters are highly affected by the substrate above which the measurements are taken [
8].
The PET estimates with the FAO56-PM method for the two cities present higher values for the southern site of Heraklion with an annual average of 3.37 ± 1.92 mm d
−1, which is slightly higher compared to the respective values of Amaroussion (3.10 ± 1.92 mm d
−1). Both sites present high seasonal variability with ET values ranging from 1.44 ± 0.49 mm d
−1 in winter to 5.87 ± 0.77 mm d
−1 in summer in Heraklion and from 1.05 ± 0.41 mm d
−1 in winter to 5.48 ± 1.00 mm d
−1 in summer in Amaroussion. The day-to-day and monthly values are even more variable, as depicted in
Figure 3.
The daily values of
Figure 3 were used as the basis for comparing PET with the respective estimates by the application of other methods. The results per method category follow.
3.1. Mass Transfer-Based Methods
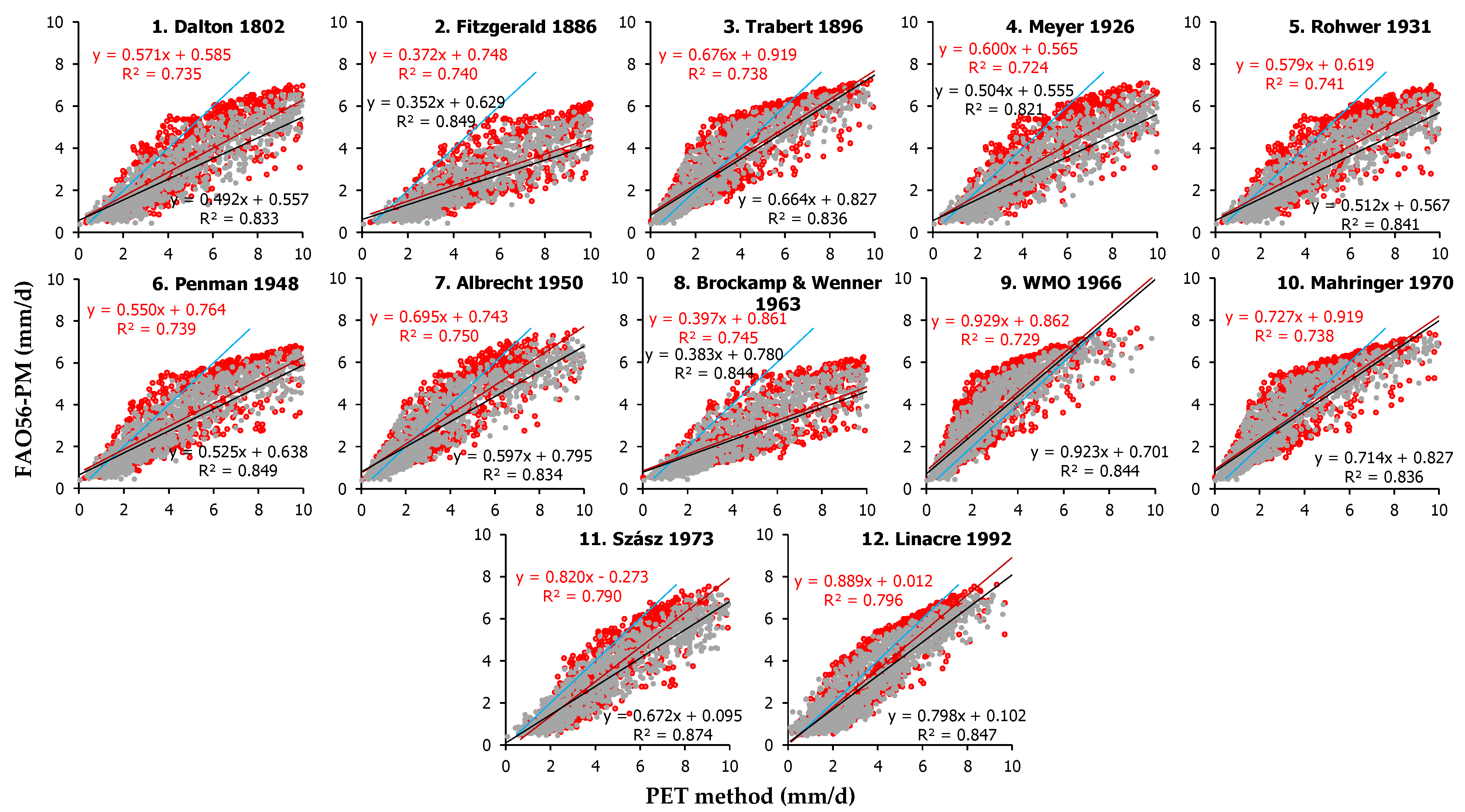
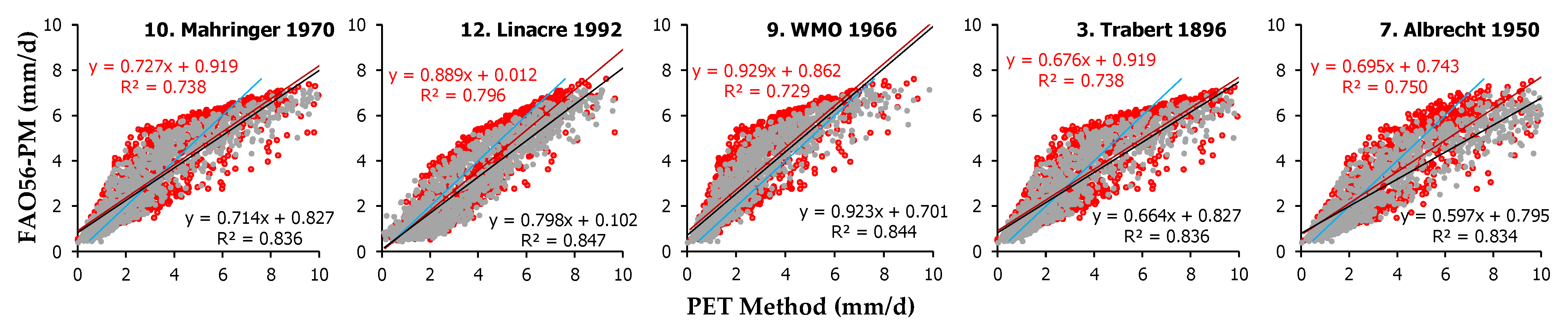
The comparative presentation of the PET estimates produced by the application of the 12 mass transfer methods (Equations (1)–(12)) against the PET values by the FAO56-PM method for the two urban green areas are presented in
Figure A1,
Appendix B, along with the regression line statistics. The values dispersion confirms the higher PET in Heraklion compared to Amaroussion. The combined assessment of
Figure A1 (
Appendix B) and
Table A1 (
Appendix C) indicates that in general, Mahringer 1970 (Equation (10)) followed by Trabert 1886 (Equation (3)) and Linacre 1992 (Equation (12)) are the best performing mass transfer-based methods in Heraklion, ranking 46th, 47th and 52nd among all 112 examined models with sRPI scores of 0.827, 0.825 and 0.813, respectively (
Table 5), whereas Fitzerald 1986 (Equation (2)) and Brockamp and Wenner 1963 (Equation (8)) are the worst (112th with sRPI = 0.177 and 111th with sRPI = 0.292, respectively, at the overall ranking). Mahringer 1970 (Equation (10)) produced the minimum MBE (−0.029 mm d
−1) and the best slope a value (1.015) compared to all other mass transfer methods, whereas its mean value (3.234 ± 2.264 mm d
−1) is quite close to FAO56-PM (3.266 ± 1.910 mm d
−1) and only underestimated by −0.98%. Trabert 1886 (Equation (3)) had the best d index (0.974) and Linacre 1992 (Equation (12)) had the smallest RMSE (0.977 mm d
−1), smallest MAE (0.801), smallest sd
2 (0.789 mm d
−1), and best R
2 (0.796) among all mass transfer-based method in Heraklion.
In the green space of Amaroussion, however, WMO 1966 (Equation (9)), Linacre 1992 (Equation (12)) and Mahringer 1970 (Equation (10)) were the best-performing mass transfer-based methods (
Table 5), ranking 40th, 44th and 50th, with sRPI scores of 0.853, 0.831 and 0.826, respectively. The worst methods were also Fitzerald 1986 (Equation (2)) and Brockamp and Wenner 1963 (Equation (8)), as in Heraklion, which were ranked 112th and 111th among all methods with sRPI values of 0.189 and 0.300, respectively. WMO 1966 (Equation (9)) produced the minimum MAE (0.693 mm d
−1), RMSE (0.923 mm d
−1) and the best sd
2 (0.592 mm d
−1) and d (0.982) values, but its average PET estimate (2.465 ± 1.905 mm d
−1) was −17% smaller compared to FAO56-PM (2.969 ± 1.904 mm d
−1). Linacre 1992 (Equation (12)) had the best slope a value (1.062).
The ranking scores for both sites (derived as averages of the sRPI) suggest that Mahgringer 1970 (Equation (10)) had the best performance among the mass transfer methods, followed by WMO 1966 (Equation (9)) and Linacre 1992 (Equation (12)), which ranked 45th, 47th and 49th among the 112 examined models with sRPI values of 0.827, 0.826 and 0.822, respectively. The correlations of the five best-performing models of this category are presented in
Figure 4.
3.2. Temperature-Based Methods
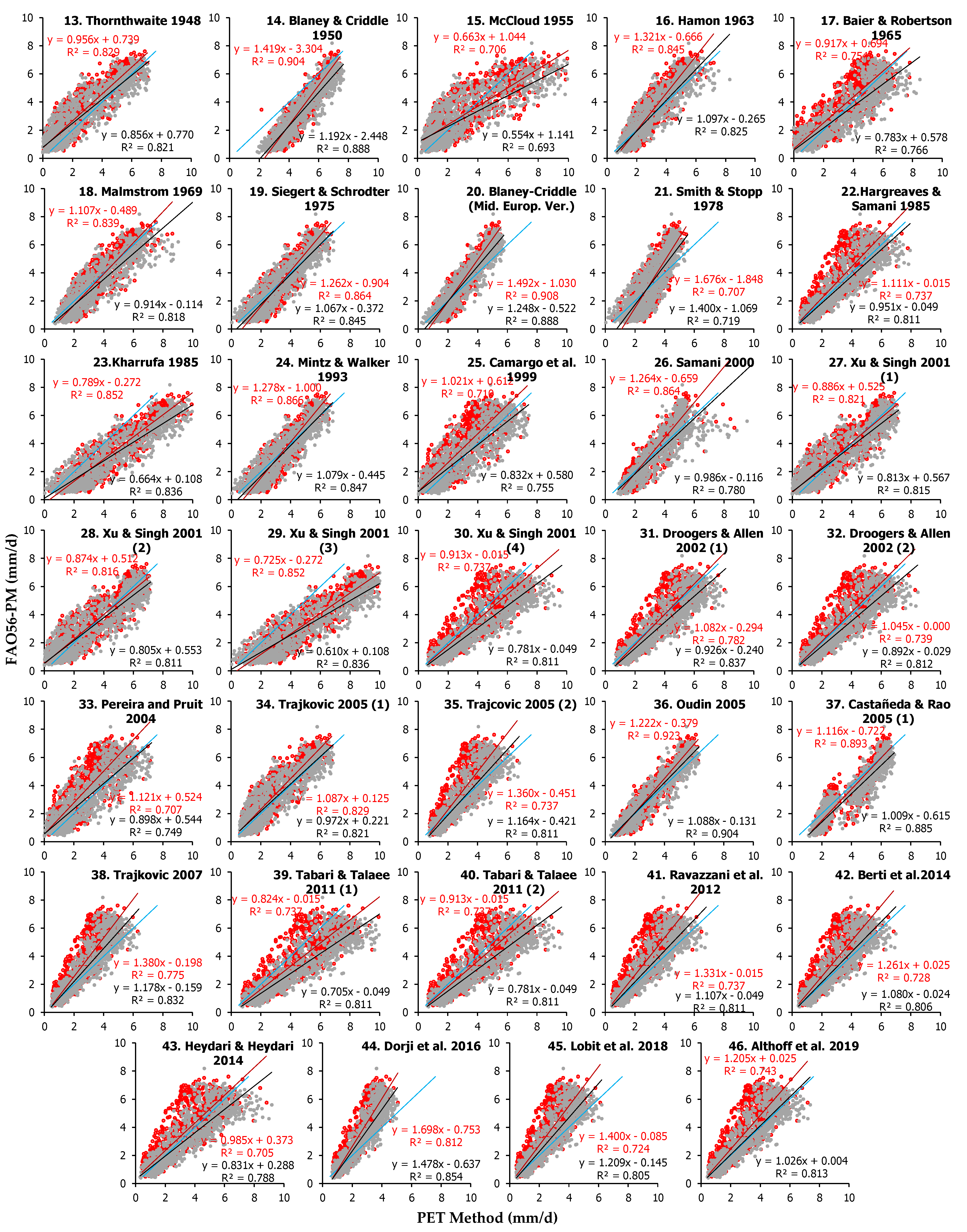
The PET estimates by the application of 48 temperature-based empirical models (Equations (13)–(60)) are presented against the respective daily values by FAO56-PM for the two sites in
Figure A2 and
Figure A3 (
Appendix B). The general patterns indicate generally higher estimates of the method of this category in Heraklion compared to the site in Amaroussion. The statistics from the comparisons for all methods in both sites are presented in
Table A2 (
Appendix C).
In Heraklion, Ahooghalaandari et al. 2016 (3) (Equation (58)) was the best temperature-based method, ranking 27th among all examined models with sRPI = 0.889, followed by Xu and Singh 2001 (2) (Equation (28)) and Xu and Singh 2001 (1) (Equation (27)), which ranked 34th and 37th, with sRPI values of 0.876 and 0.869, respectively. Ahooghalaandari et al. 2016 (3) (Equation (58)) had the minimum MAE (0.562 mm d−1) and the best d (0.966) values, and they produced an average PET (3.609 ± 2.451 mm d−1) +10% higher compared to FAO56-PM. The worst temperature-based methods for the site were by Antal 1968 (Equation (50)) and Smith and Stopp 1978 (Equation (21)), which ranked 109th and 108th among the 112 models.
Ahooghalaandari et al. 2016 (3) (Equation (58)) was also the best method for the site of Amaroussion, ranking 26th among the 112 tested models with a similar sRPI (0.887), which was followed by Oudin 2005 (Equation (36)) and Xu and Singh 2001 (2) (Equation (28)) ranking 27th (sRPI = 0.885) and 36th (sRPI = 0.861), respectively. The worst performing were the methods of Xu and Singh 2001 (5) (Equation (53)) and Antal 1968 (Equation (50)), which were ranked 110th and 109th with sRPI scores 0.407 and 0.489, respectively. The application of Ahooghalaandari et al. 2016 (3) (Equation (58)) produced an average PET of 3.607 ± 2.720 mm d−1, which was +21% higher compared to FAO56-PM.
The statistical indices and the ranking (among the 112 examined models) for the five best-performing temperature-based methods for each site are shown in
Table 6.
For both sites, Ahooghalaandari et al. 2016 (3) (Equation (58)), Oudin 2005 (Equation (36)) and Xu and Singh 2001 (2) (Equation (28)) are ranked higher among the temperature-based PET methods (27th, 31st and 35th, respectively, at the overall ranking) with sRPI scores of 0.888, 0.877 and 0.869, respectively. It is worth noting that all 48 temperature-based methods received sRPI scores ranging from 0.487 to 0.888, and 15 of them had sRPI values greater than 0.800, whereas 4 out of the 12 mass transfer-based methods had sRPIs greater than 0.800. The correlations of the daily value estimated by the five best-performing methods of this category against the FAO56-PM method are presented for both sites in
Figure 5.
3.3. Radiation-Based Methods
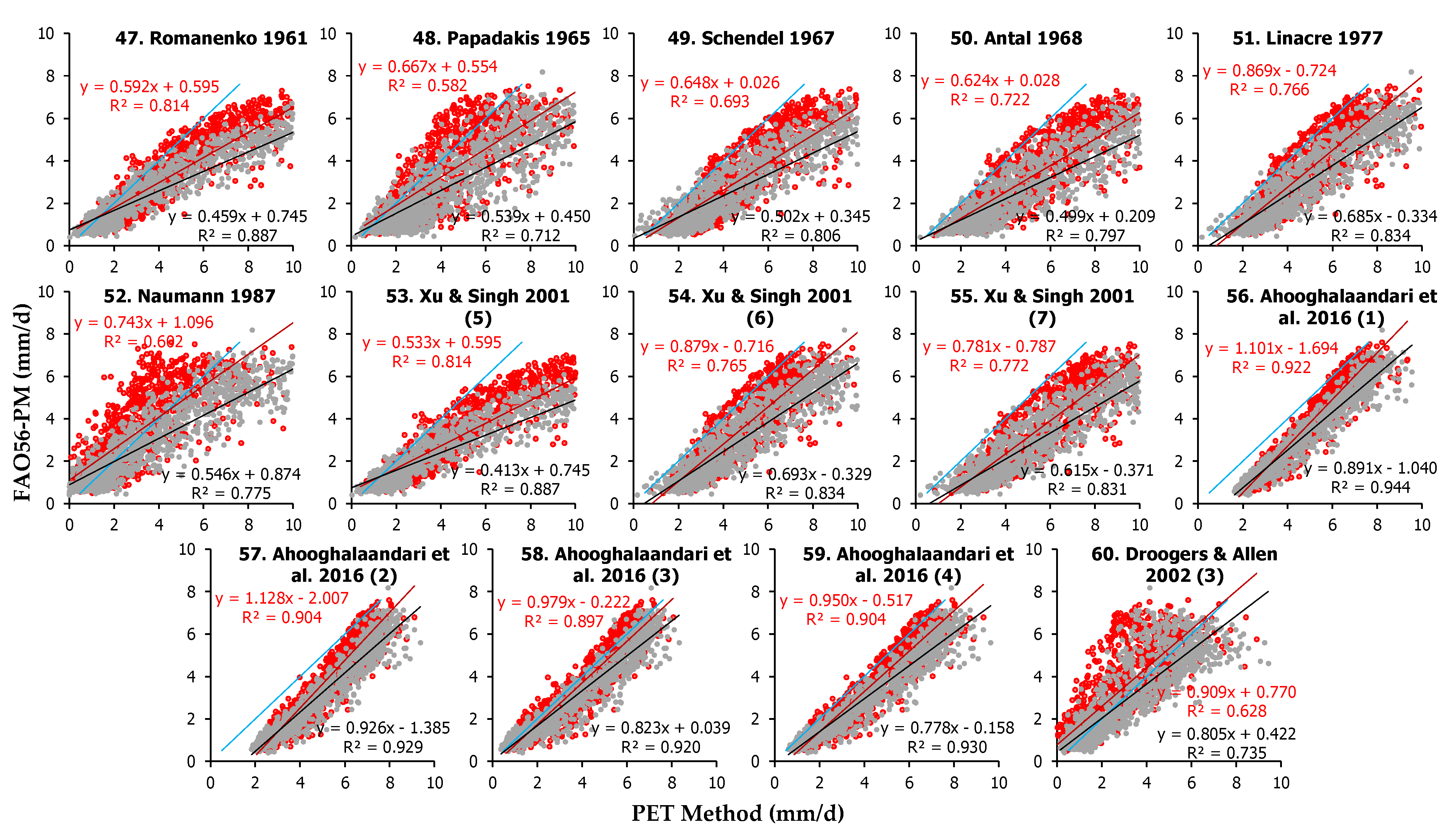
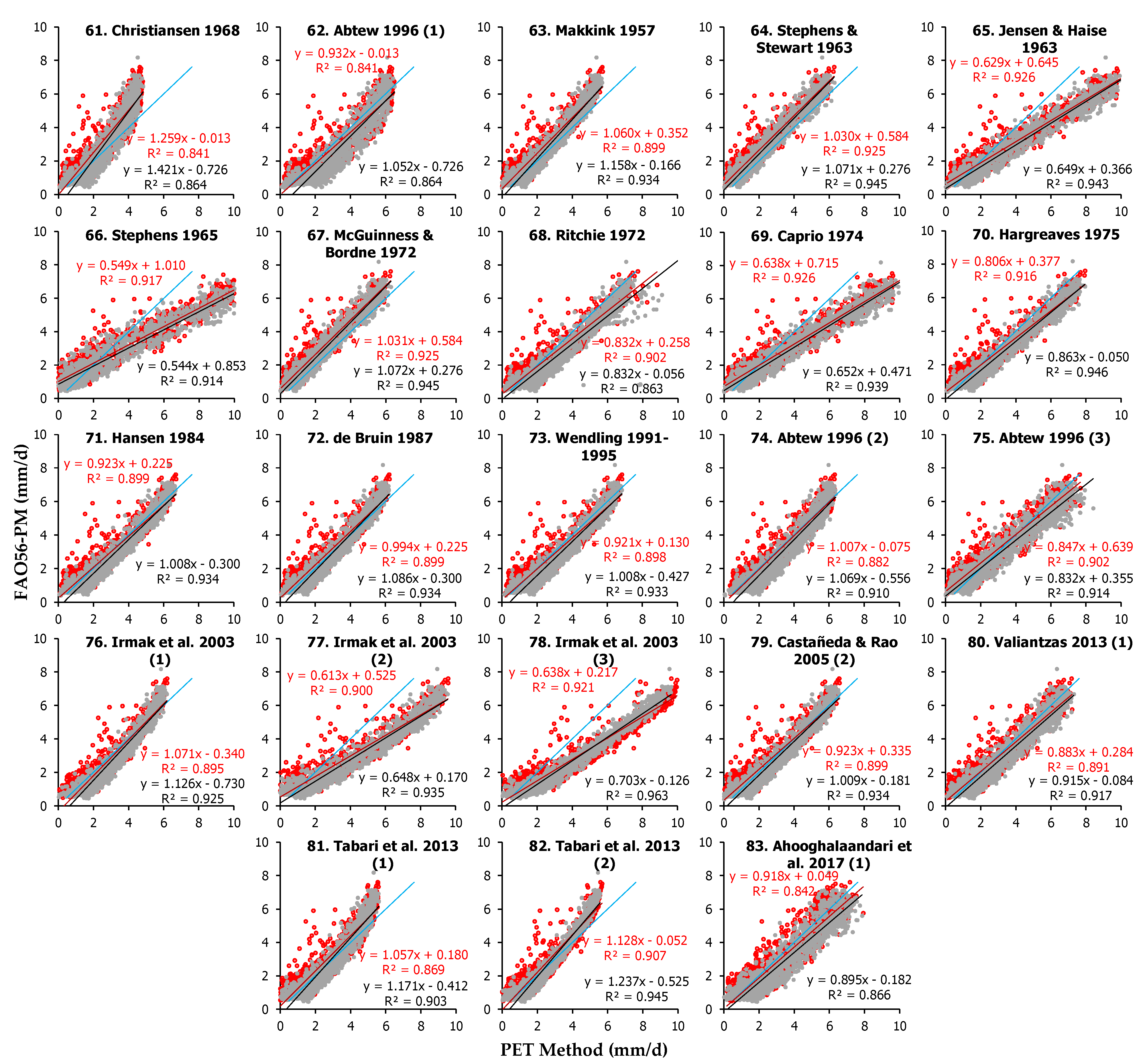
The 40 radiation-based methods (Equations (61)–(100)) examined in the two study sites produced daily estimates presented in conjunction with the FAO56-PM estimates in
Figure A4 and
Figure A5 (
Appendix B). The comparison between the values produced the statistics presented in
Table A3 (
Appendix C). The statistical indices for the five best-performing radiation-based methods in each site are presented in
Table 7.
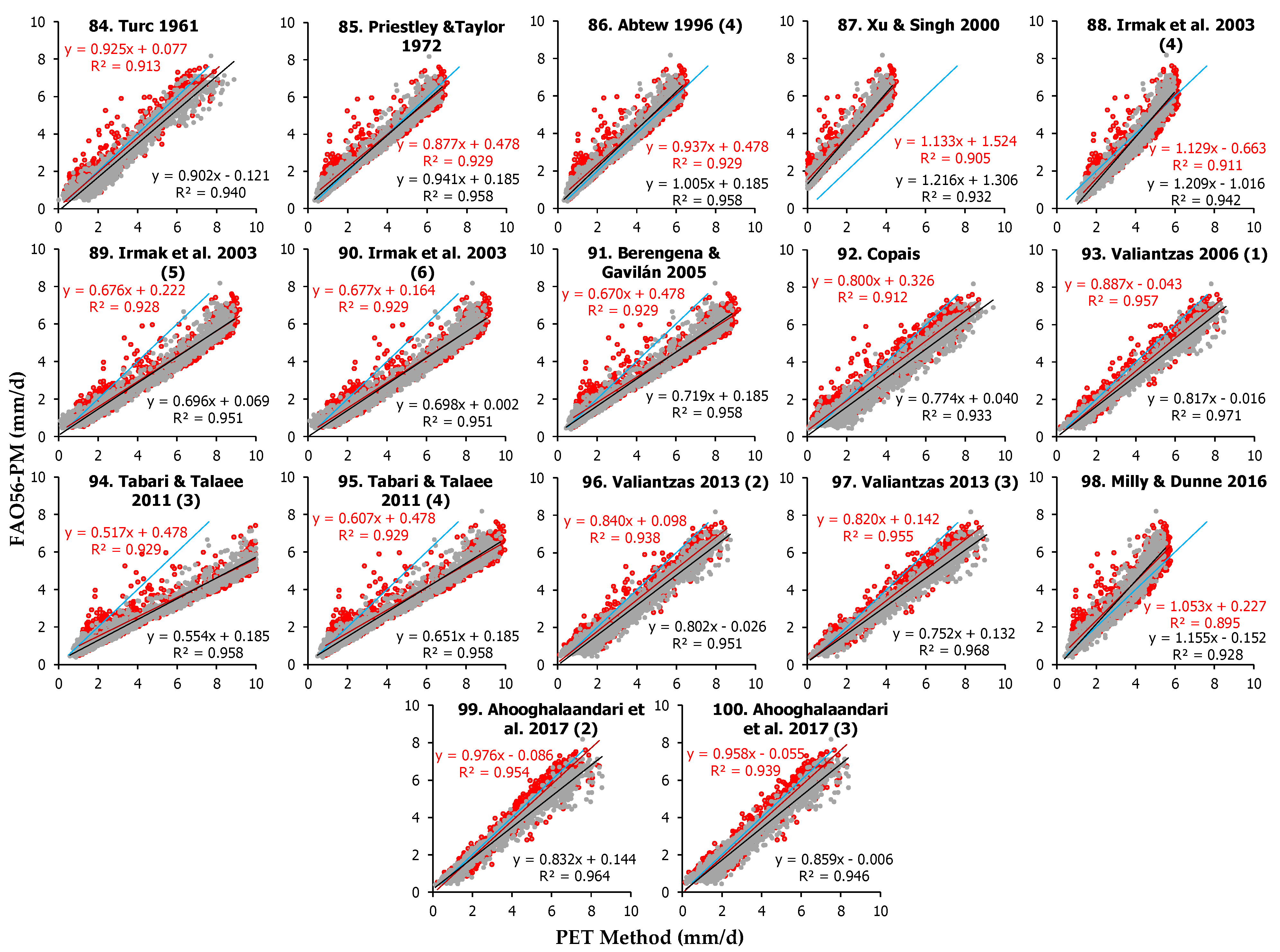
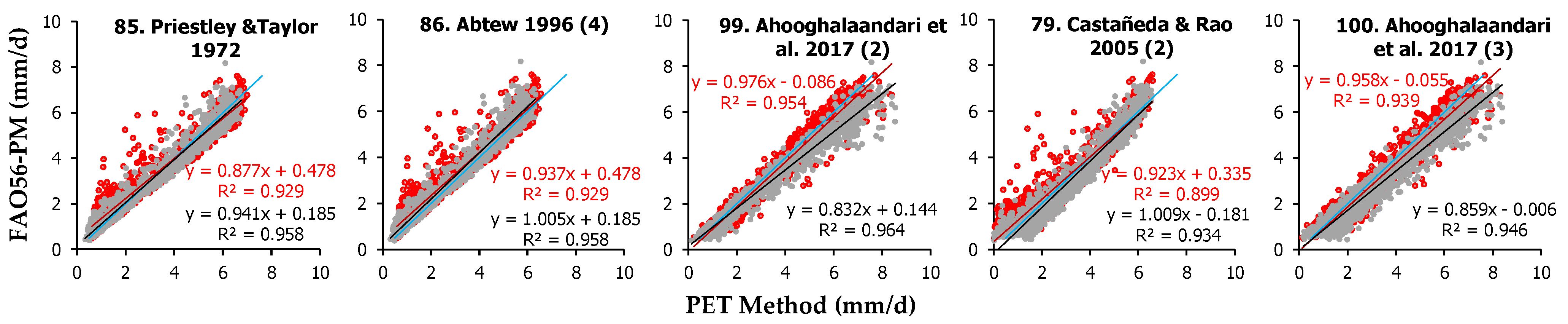
In Heraklion, the best-performing radiation-based methods were Ahooghalaandari et al. 2017 (2) (Equations (99)) followed by Castañeda and Rao 2005 (2) (Equation (79)) and Priestley and Taylor 1972 (Equation (85)), which were ranked 4th, 8th and 9th among all 112 models, with sRPI scores of 0.955, 0.943 and 0.941, and mean PET estimates +7.7%, −0.7% and −0.5% different compared to FAO56-PM, respectively. Ahooghalaandari et al. 2017 (2) (Equation (99)) presented minimum RMSE (0.534 mm d−1), MAE (0.416 mm d−1) and sd2 (0.178), whereas Castañeda and Rao 2005 (2) (Equation (79)) had the minimum offset b (−0.007 mm d−1) and Priestley and Taylor 1972 (Equation (85)) had the minimum MBE (−0.014 mm d−1) and the best d (0.986) among the radiation-based models. The worst methods of this category in Heraklion were Tabari and Talaee 2011 (3) (Equation (94)) ranking 110th sRPI = 0.495 and Xu and Singh 2000 (Equation (87)) ranking 103rd with sRPI = 0.603, producing PET means −30.7% and +67.6% different compared to FAO56-PM. In general, however, the radiation methods in Heraklion had a good performance in most cases, since the produced PET means were less than 10% different from FAO56-PM in 19 out of the 40 methods.
In Amaroussion, Priestley and Taylor 1972 (Equation (85)) was ranked first among the radiation-based methods (2nd among all 112 models, with sPRI = 0.972), followed by Abtew 1996 (4) (Equation (86)) and Ahooghalaandari et al. 2017 (2) (Equation (99)), which were ranked 6th (sPRI = 0.956) and 9th (sPRI = 0.933) among all examined models. These methods produced mean PET values +2.00%, −4.3% and +17% different compared to FAO56-PM, respectively. Priestley and Taylor 1972 (Equation (85)) showed the best MBE (−0.014 mm d−1), RMSE (0.486 mm d−1) and d (0.992) values, whereas Abtew 1996 (4) (Equation (86)) had the best MAE (0.374 mm d−1) and sd2 (0.229 mm d−1) and Ahooghalaandari et al. 2017 (2) (Equation (99)) presented the minimum offset b (−0.045 mm d−1) among all radiation-based methods. The worst models in Amaroussion were Tabari and Talaee 2011 (3) (Equation (94)) and Xu and Singh 2000 (Equation (87)), ranking 103rd and 99th, respectively, among all examined 112 methods, with sRPI values of 0.591 and 0.621. These methods’ mean PET values were +71.7% and −28.7% different compared to FAO56-PM. The overall performance of radiation-based methods in Amaroussion can be considered satisfactory, considering that 28 out of the 40 equations presented sRPI values higher than 0.800, whereas 15 of them had sRPI > 0.900.
The ranking derived from the statistics of both sites suggests that Priestley and Taylor 1972 (Equation (85)) ranking 5th with sRPI = 0.957, Abtew 1996 (4) (Equation (86)) ranking 7th with sRPI = 0.946 and Ahooghalaandari et al. 2017 (2) (Equation (99)) ranking 9th with sRPI = 0.944 between all 112 models were the best radiation-based methods, whereas Tabari and Talaee 2011 (3) (Equation (94)) ranking 107th and Xu and Singh 2000 (Equation (87)) ranking 102nd were the two worst methods with average sPRI values from both sites 0.543 and 0.612, respectively. The best five performing methods for both sites (according to the average sRPI scores) are depicted in
Figure 6.
3.4. Combination Methods
The PET estimates from the 12 combination methods (Equations (101)–(112)) assessed in this study are depicted against the PET daily values in
Figure A6 (
Appendix B), whereas the statistical indices values used for the ranking of the methods are presented in
Table A4 (
Appendix C). The graphs and the statistical results suggest that this category of models produces good PET estimates compared to all other categories.
The statistics for five best-performing methods of this PET model category are presented for both sites in
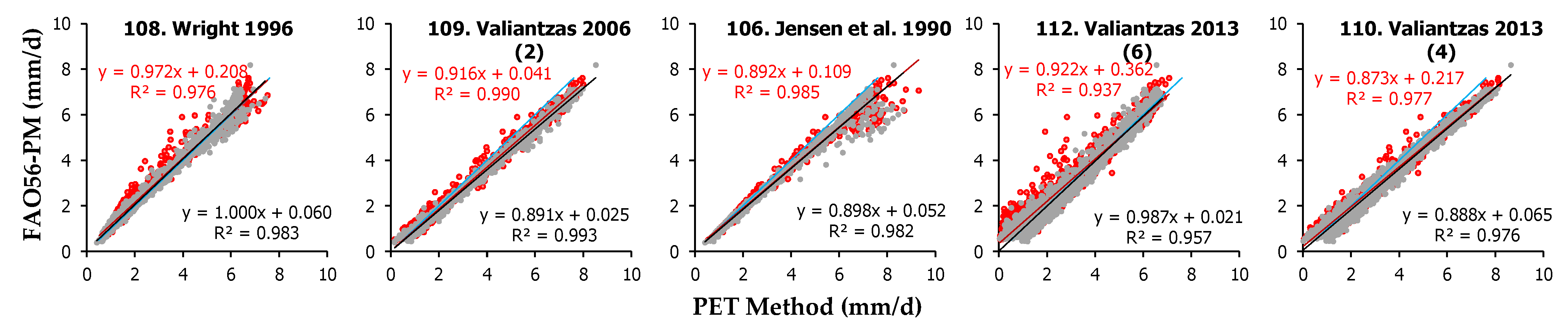
Table 8. The assessment of all combination methods statistics, presented also in
Table A4 (
Appendix C), indicates that Wright 1996 (Equation (108)) is the best-performing model in Heraklion, followed by Valiantzas 2006 (2) (Equation (109)) and Jensen et al. 1990 (Equation (106)). Wright 1996 (Equation (108)) is ranked 1st among all examined 112 models and had the best sRPI (0.987), whereas it produced an average PET that was only −0.8% lower compared to FAO56-PM. This method presented the minimum RMSE (0.446 mm d
−1) and MAE (0.315 mm d
−1) and also the best slope a (1.005) and d (0.989) values. Valiantzas 2006 (2) (Equation (109)) and Jensen et al. 1990 (Equation (106)) methods were ranked 2nd and 3rd, respectively, among all 112 examined models and had also high sRPI values (0.970 and 0.963). However, the produced mean PET values were about +11% higher compared to FAO56-PM. However, Valiantzas 2006 (2) (Equation (109)) presented the minimum offset b (−0.008 mm d
−1) and sd
2 (0.078 mm d
−1) in Heraklion not only among the combination but among all 112 methods. The worst-performing methods for the site were FAO24 Radiation (Equation (105)) followed by the modified Makkink by Doorenbos and Pruitt 1977 (Equation (103)), which were ranked 58th and 53rd with sRPI values of 0.792 and 0.813, respectively. The mean PET values of these methods were +25.3% and +20.4% higher compared to FAO56-PM.
In Amaroussion, Wright 1996 (Equation (108)) was the best-performing model ranked 1st with sRPI = 0.992 followed by Jensen et al. 1990 (Equation (106)), Valiantzas 2006 (2) (Equation (109)), and Valiantzas 2013 (6) (Equation (112)), which were ranked 3rd, 4th and 5th with similar sRPI values (0.963, 0.962 and 0.962). Wright 1996 (Equation (108)) showed the best slope a (0.984) and d (0.991) and the minimum RMSE (0.393 mm d−1), MAE (0.264 mm d−1) and sd2 (0.159 mm d−1) values, producing a mean PET estimate +0.97% higher compared to FAO56-PM. Also, in Amaroussion, Jensen et al. 1990 (Equation (106)) had the best offset b (0.003), but its mean PET was +12.3% higher compared to FAO56-PM. As in Heraklion, the worst combination methods for Amaroussion were also FAO24 Radiation (Equation (105)) followed by the modified Makkink by Doorenbos and Pruitt 1977 (Equation (103)), which ranked 54th and 49th, respectively, among the 112 models, presenting relatively low sRPI values (0.819 and 0.828) and also mean PET values +37.3% and +33.1% higher compared to FAO56-PM.
The combination methods ranking for both sites depicts Wright 1996 (Equation (108)) as the best combination model, followed by Valiantzas 2006 (2) (Equation (109)) and Jensen et al. 1990 (Equation (106)). These models were ranked 1st, 2nd and 3rd among all 112 investigated methods and received the highest sRPI scores (average sRPI scores from both sites: 0.990, 0.966 and 0.963, respectively). The daily PET estimates by the five best-performing combination methods against FAO56-PM are presented in
Figure 7. In all cases, however, the combination methods performed better compared than all other method categories, since they presented high sRPI scores (higher than 0.806), which is rather expected considering the higher number of input parameters required for the application of the combination equations.
3.5. Models Adjustment
The local calibration of the empirical models for the PET estimation is suggested in most research works and is also imposed by the results of the present study. In this work, an adjustment of the general forms of mass transfer, temperature and radiation-based equations was performed for local use in the territories of our study sites. Based on the daily data from both stations, 15 adjusted PET models were produced following the general forms of several widely used equations. For example, the mass transfer model proposed by Dalton 1802 (Equation (1)), Fitzgerald 1886 (Equation (2)), Meyer 1926 (Equation (4)), Rohwer 1931 (Equation (5)), Albrecht 1950 (Equation (7)) and WMO 1966 (Equation (9)) follow the general form of PET = (a + bu) (e
s – e
a). The adjusted values of a and b, based on the data from the two stations, are presented in
Table 9. Similarly, other widely used models were adjusted for local use, and the new models are also presented in
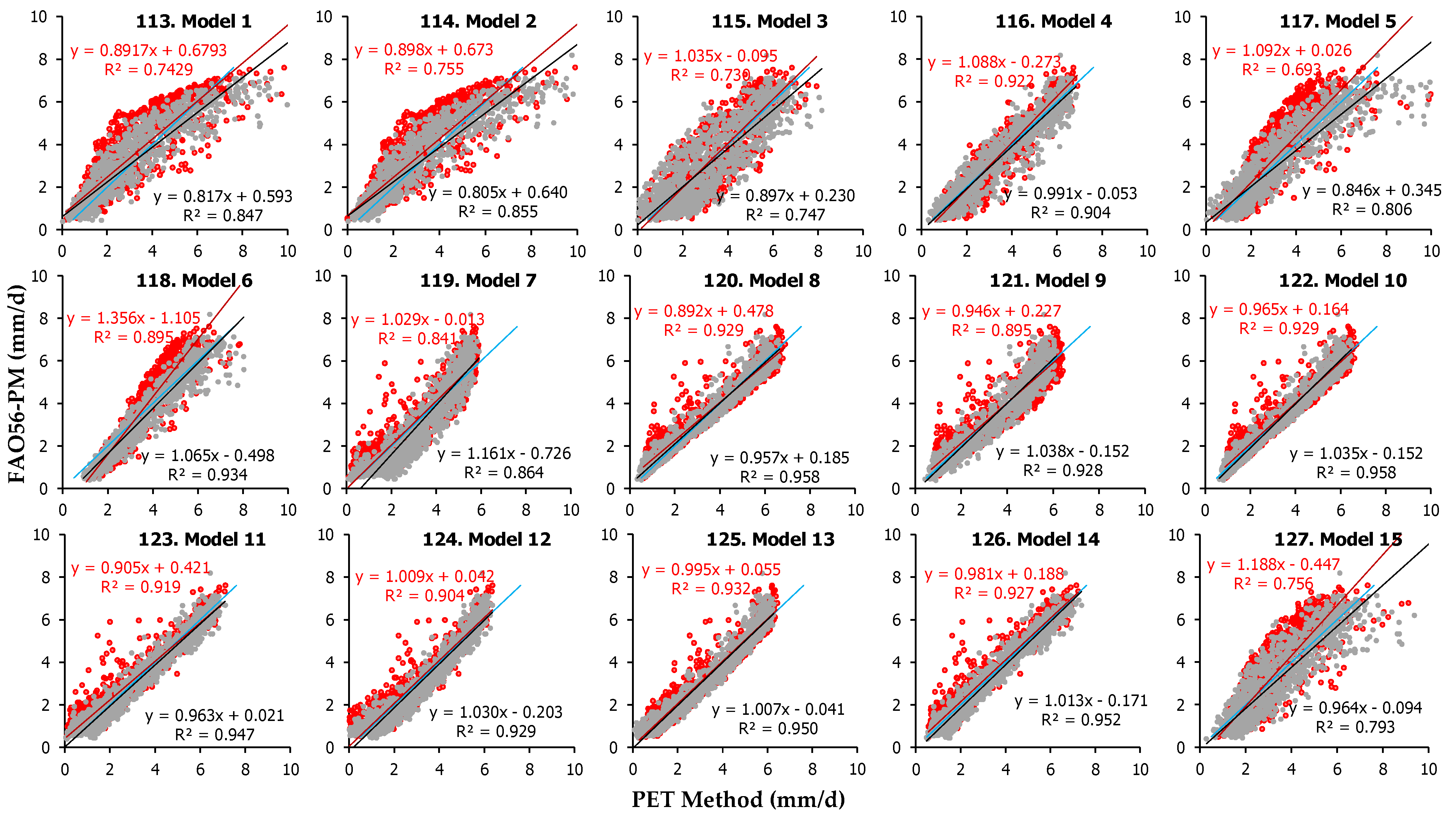
Table 9. The performance of the adjusted equations (Equations (113)–(127)) is evaluated following the estimation of statistical indices and ranking as above. The daily PET estimates for the new models are presented for the two sites along with the respective PET values by the FAO56-PM method in
Figure 8.
The daily PET dispersion of values depicted in
Figure 8 in association with the statistical indices of the new methods and the ranking with respect to all 127 models (112 original and 15 adjusted) in both sites that are presented in
Table 10 suggest that the adjusted models performed better compared to the original equations.
More specifically, the mass transfer models 1 (Equation (113)) and 2 (Equation (114)) were ranked 66th and 64th (with sRPI scores of 0.803 and 0.813), respectively, among all 127 models, in Heraklion, whereas in Amaroussion, they performed better (ranked 42nd and 44th, with similar sRPI scores of 0.867 and 0.866, respectively). Similarly, the adjusted temperature-based models 3, 4, 5, 6 and 15 (Equations (115)–(118) and (127)) were ranked between 26th and 97th with scores ranging from 0.701 to 0.916, in Heraklion, among which model 4 performed the best (Equation (116)), which is actually an adjustment of the Hargreaves and Samani method. The temperature-based adjusted models in Amaroussion presented also good performance, and they ranked between 21st and 84th among the 127 methods, with sRPI ranging from 0.783 to 0.913, among which model 4 performed the best (Equation (116)). Finally, the radiation-based adjusted models 7–14 (Equations (119)–(126)) produced in general accurate estimates. Their sRPI scores, in Heraklion, ranged from 0.851 to 0.960, resulting in ranks varying from 4th to 50th, among which model 10 performed the best (Equation (122)). In Amaroussion, model 8 had an excellent behavior, ranking 2nd among all 127 methods, with a high sRPI value (0.972), whereas the rest of the radiation-based adjusted models also received high sRPI scores ranging from 0.819 to 0.972, with ranks varying between 7th and 67th.
4. Discussion
The PET estimates of the examined 112 models in this work confirm the overall good performance of the combination methods against all other groups of methods in the environment of the two Mediterranean urban green sites, i.e., in Heraklion (S. Greece) and Amaroussion (c. Greece). The general ranking of the methods for both sites indicate that the method of Wright 1996 (Equation (108)) performed the best followed by Valiantzas 2006 (2) (Equation (109)), Jensen et al. 1990 (Equation (106)), Valiantzas 2013 (6) (Equation (112)), Priestley and Taylor 1972 (Equation (85)), Valiantzas 2013 (4) (Equation (110)), Abtew 1996 (4) (Equation (86)), Valiantzas 2013 (5) (Equation (111)), Ahooghalaandari et al. 2017 (2) (Equation (99)) and Castañeda and Rao 2005 (2) (Equation (79)). The above ten are the best-performing methods for both sites, producing the best statistics and the highest sRPI scores (higher than 0.936).
The worst-performing methods are mainly mass transfer and temperature-based with limited data requirements. Specifically, the ten worst-performing models were Fitzgerald 1886 (Equation (2)) followed by Brockamp and Wenner 1963 (Equation (8)), Xu and Singh 2001 (5) (Equation (53)), Antal 1968 (Equation (50)), Xu and Singh 2001 (7) (Equation (55)), Tabari and Talaee 2011 (3) (Equation (94)), Schendel 1967 (Equation (49)), Dalton 1802 (Equation (1)), Blaney and Criddle 1950 (Equation (14)), and Smith and Stopp 1978 (Equation (21)), which received the minimum sRPI scores (lower than 0.590).
Regarding each category of empirical methods, the best-performing mass transfer method for both sites was Mahringer 1970 (Equation (10)), which ranked 45th among all 112 models (sRPI = 0.827). Respectively, the best temperature-based model was Ahooghalaandari et al. 2016 (3) (Equation (58)) ranking 27th (sRPI = 0.888), and the best radiation-based method was Priestley and Taylor 1972 (Equation (85)) ranking 5th (sRPI = 0.957). As mentioned above, the best-performing combination model for the two sites was Wright 1996 (Equation (108)), which ranked also first among all 112 models.
Specifically in Heraklion, the ten best-performing methods in descending order were Wright 1996 (Equation (108)), Valiantzas 2006 (2) (Equation (109)), Jensen et al. 1990, (Equation (106)), Ahooghalaandari et al. 2017 (2) (Equation (99)), Valiantzas 2013 (6) (Equation (112)), Valiantzas 2013 (4) (Equation (110), Valiantzas 2013 (5) (Equation (111)), Castañeda and Rao 2005 (2) (Equation (79)), Priestley and Taylor 1972 (Equation (85)), and Ahooghalaandari et al. 2017 (3) (Equation (100)), with sRPI scores higher than 0.939. Similarly, in Amaroussion, the ten best methods were Wright 1996 (Equation (108)), Priestley and Taylor 1972 (Equation (85)), Jensen et al. 1990 (Equation (106)), Valiantzas 2013 (6) (Equation (112)), Valiantzas 2006 (2) (Equation (109)), Abtew 1996 (4) (Equation (86)), Valiantzas 2013 (4) (Equation (110)), Valiantzas 2013 (5) (Equation (111)), Ahooghalaandari et al. 2017 (2) (Equation (99)) and Castañeda and Rao 2005 (2) (Equation (79)), with sRPI scores higher than 0.930.
The above-mentioned results confirm the generally increasing performance of empirical PET estimation methods with the number of input parameters [
40] with the high data demanding combination methods to produce more accurate estimates. The performance of the radiation-based equations is adequate, and it ranked high among methods with limited data requirements. The better performance of the radiation methods compared to temperature-based is expected and has been confirmed also by Lang et al. [
16], who applied different empirical PET models in southwestern China, suggesting Makkink’s model as the best alternative. In the present work, Makking’s original equation was found to perform quite well, ranking 25th among the 112 examined models with an average, for both study sites, rank score of sRPI = 0.889, whereas its modified form proposed by Castañeda and Rao 2005 (2) (Equation (79)) was ranked among the 10 best-performing methods for both examined sites and received a high sRPI score of 0.936. The good performance of the Priestley and Taylor method in this study (rank 5th/112, sRPI = 0.957) is also in line with the findings by Wei and Menzel [
35], who suggested the specific method for global application.
It should be noted that the radiation-based methods requiring Rn radiation measurement are anticipated to perform better than those requiring Rs, since Rn is highly associated with the surface characteristics indicating the available energy stored in the natural surface and can be used for evapotranspiration. However, in this study, Rn is estimated from Rs [
11], and thus, its effect cannot be evaluated as in the case of real in situ Rn measurements. In all cases, the best two radiation methods (included also among the 10 best out of the 112 original models) require Rn, i.e., Priestley and Taylor 1972 (Equation (85)) and Abtew 1996 (4) (Equation (86)).
The limitation of input parameters and the local calibration of the examined models appear to affect their performance in the two sites. It should be also mentioned that almost all models were established in rural areas, and thus, their application in urban environments (even in green spaces) may result in overestimations or underestimations. This is also valid for the FAO56-PM method, which is highly affected by the aerodynamic characteristics of the surface. In all cases, the energy budget and the aerodynamic characteristics of the urban green spaces are considerably different compared to the open rural areas, and the built-up urban environment highly affects the energy exchanging processes, the energy budget of the green surfaces, and the wind flow above them, resulting in a complex environment that is difficult to be modeled. Multiple radiation scattering by the built-up environment surrounding the urban green areas and shadowing, as well as the use of artificial materials covering parts of the soil, can result in decreased ET fluxes and overestimation of the applied PET models [
41]. However, the estimation of PET by the empirical models remains a useful tool to assess plants’ water requirements, even at the urban environment.
The general ranking of the 127 methods (112 originals and 15 adjusted) after incorporating the scores for both sites are presented in
Table A5 (
Appendix C). The results suggest that many of the adjusted models performed better compared to the original equations. More specifically, the mass transfer models 1 (Equation (113)) and 2 (Equation (114)) were ranked 52nd and 51st (with sRPI scores of 0.835 and 0.839), respectively, among all 127 models, whereas the best original mass transfer method (Mahringer 1970 (Equation (10), sRPI = 0.827) is ranked 57th, WMO 1966 (Equation (9)) is ranked 59th, and all others were ranked much lower compared to the adjusted mass transfer models.
Among the adjusted temperature-based models 3, 4, 5, 6 and 15 (Equations (115)–(118) and (127)), model 4 (Equation (123)), which requires only temperature data and is actually the adjustment of the Hargreaves–Samani equation, presented better performance, ranking 22nd (sRPI = 0.915) among the 127 methods and first among all temperature-based models, which was followed by the best original method of Ahooghalaandari et al. 2016 (3) (Equation (58)), which ranked 35th/127 with sRPI = 0.888. It is worth noting the good performance of the adjusted Hargreaves–Samani Model 4 (Equation (116)) which is ranked 22nd/127, as mentioned, whereas its original form Hargreaves and Samani 1985 (Equation (22)) is ranked 86th/127 (sRPI = 0.751). It should be stated, though, that at the adjusted model 4, the power of the diurnal temperature range (DTR = Tmax − Tmin) is negative and small, suggesting a minor and negative effect of DTR on PET. Since DTR is considered to be related with atmospheric cloudiness and radiation factors that control plant photosynthesis [
138,
146,
147] and that clear sky conditions (higher DTR) can be associated with higher evapotranspiration rates [
148,
149], it is rather expected for there to be a positive DTR effect on PET. On the other hand, in our two sites, clear sky conditions typically persist; thus, DTR is expected to have an overall minor effect on PET.
The radiation-based adjusted models 7–14 (Equations (119)–(126)) had sufficient performance. Models 10 (Equation (122)) and 8 (Equation (120)), which are actually adjustments of the Priestley and Taylor method with (model 10) or without (model 8) interception, presented the best performances and ranked 4th and 6th, among the 127 models with sRPI values of 0.959 and 0.957, respectively. Also, models 13 (Equation (125)), 11 (Equation (123)) and 14 (Equation (126)) are among the ten best models ranking 8th, 9th and 10th, with quite similar sRPI values: 0.957, 0.952 and 0.951, respectively. It is worth noting that model 14 (Equation (126)), namely the adjustment of the original Copais (Equation (92), has significantly improved the performance of the original method, considering that the original equation is ranked 42nd/127 (sRPI = 0.871).
All adjusted models have reduced data requirements, allowing their local application in the two study sites. Nonetheless, it should be stressed that the models’ performance will benefit from further adjustments, incorporating a longer timeseries of data from the two stations. Their application in other regions and cities should be performed with caution, following a proper validation. Furthermore, additional adjustments may be applied by incorporating data from new stations with different geographical characteristics. In any case, the local calibration can significantly improve the performance of the PET empirical models and is highly suggested especially in regions with a limited availability of meteorological data. In summary, the best-performing methods with rank scores (sRPI) higher than 0.950 (derived as average values from both study sites) are depicted in
Table 11.
5. Conclusions
In the present work, the performance of 112 original empirical models for the estimation of potential evapotranspiration (PET) was investigated by comparing the models’ outputs with the PET estimates by the FAO56-PM standard method in two urban green sites in Greece (Heraklion, S. Greece and Amaroussion, c. Greece). Based on the general forms of the original mass transfer, temperature and radiation-based PET models, 15 adjusted equations were also produced and evaluated for application at the local level.
The results confirm that the accuracy of the model increases with the number of the input parameters included in the estimations. The combination methods produced in general more accurate PET estimates, which are followed by the radiation, temperature and mass transfer-based methods.
The combination model proposed by Wright 1996 (Equation (108) ranked 1st among the 112 original models) had the best performance, which was followed by Valiantzas 2006 (2) (Equation (109), ranked 2nd) and Jensen et al. 1990 (Equation (106), ranked 3rd), which are also combination methods. However, it is important to note that the combination methods require the same input parameters as FAO56-PM; thus, the standard method might be applied directly.
Priestley and Taylor (Equation (85), ranking 5th among the 112 original models) was the best radiation-based model and Ahooghalaandari et al. 2016 (3) (Equation (58), ranked 27th/112) was the best temperature-based one. Regardless of their high data requirements, the mass transfer methods had insufficient performance, even after adjustment. However, Mahringer 1970 (Equation (10), ranked 45th/112) was the best model of this category.
The adjusted PET models enhanced the performance of the original methods in all cases on the local level of the two study sites. The radiation-based model 10 (PET = f (Rs, T, RH)) was ranked 4th among all 127 models (112 original and 15 adjusted), presenting a high rank score. Also, models 8, 13, 11 and 14 (all radiation-based) produced accurate estimates in both sites, received high scores (>0.951) and ranked among the 10 best-performing methods. Their application in the two sites is recommended in the case of limited data availability; however, their applicability in other regions should be cautiously performed after proper validation and adjustment.
For wider application, it is proposed to test the methods in other cities around the world to evaluate the accuracy of the estimation of urban vegetation water requirements. It is essential though to underline the critical importance of the quality of measurements of the input parameters that should be obtained above irrigated, grass-covered surfaces, allowing the proper application of the FAO56-PM method. The findings of this study can be useful for the estimation of PET in Mediterranean cities and especially in areas with limited data availability. This can be particularly useful toward informed decision making for urban green infrastructure, including plant species selection, irrigation scheduling and water management as well as urban green management.
The findings from the present study, which is based on ground data, are a useful resource for determining the most appropriate method (especially at the local level) for estimating vegetation water requirements under the Mediterranean climate conditions. Based on the above principal information, using remote sensing—satellite data in the most appropriate PET methods identified in the two investigated sites, may produce more accurate local estimates. In future work, the performance of the PET methods can be evaluated by applying both satellite and ground data, and we can compare the methods performances. Further research is also required in order to validate the performance of the adjusted models by incorporating longer data series. In future work, the authors intend to investigate the performance of the original and adjusted models in other environments (urban or rural).