Research on an Intra-Pulse Orthogonal Waveform and Methods Resisting Interrupted-Sampling Repeater Jamming within the Same Frequency Band
Abstract
1. Introduction
- An intra-pulse orthogonal waveform based on a segmented chirp signal is proposed. The proposed orthogonal waveform makes full use of the quasi-orthogonal characteristics of the Up Chirp and Down Chirp signals. By comparing the target peak positions after the matched filtering of the Up Chirp and Down Chirp signals, most of the false target peak generated by ISRJ can be identified.
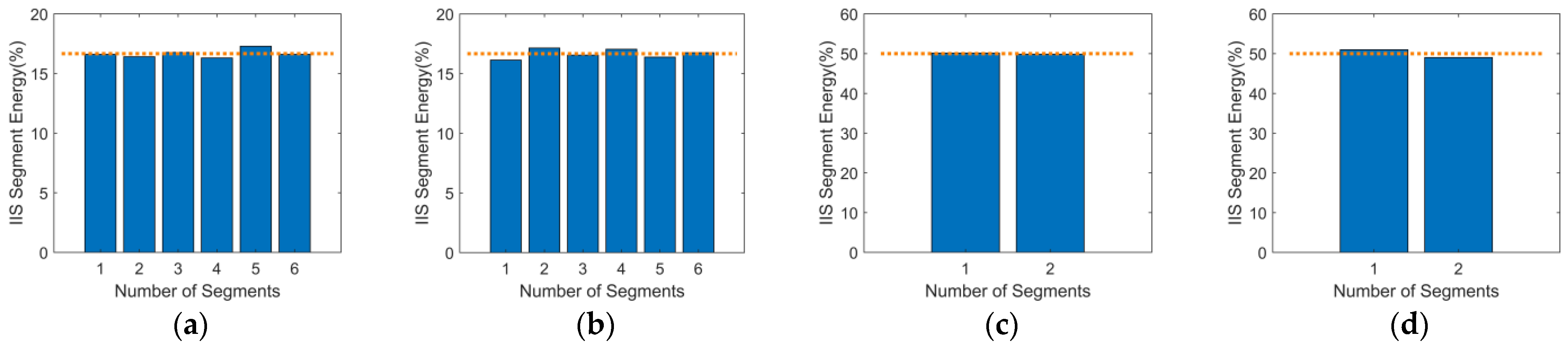
- An interference-identification algorithm based on an instantaneous energy integral is proposed. The proposed interference identification algorithm is applied to special scenarios such as ‘sample 1 turn 1′ and ‘sample 1 turn N’, which belong to direct forwarding interference mode. Based on the energy discontinuity of the interference signal in the time domain, the discrete sequence of the target peak in the time domain is transformed into the intrinsic integration sequence (IIS). To quantify the discontinuous information of the interference signal contained in IIS, a new piecewise cumulative method is proposed. This method divides the IIS into several segments and measures the fluctuation of energy distribution between segments by generating a variance. For the IIS of the real target, the energy distribution is uniform; while for the IIS of the ISRJ signal, the energy is only contained in some segments, and the others only contain noise. Therefore, the variance of the true target peak is small, while the variance of the false target peak caused by the interference signal is large, and the true and false target peaks can be identified clearly according to the variance.
2. Mechanism of Different Interrupted-Sampling Repeater Jamming Modes
3. Intra-Pulse Orthogonal Waveform
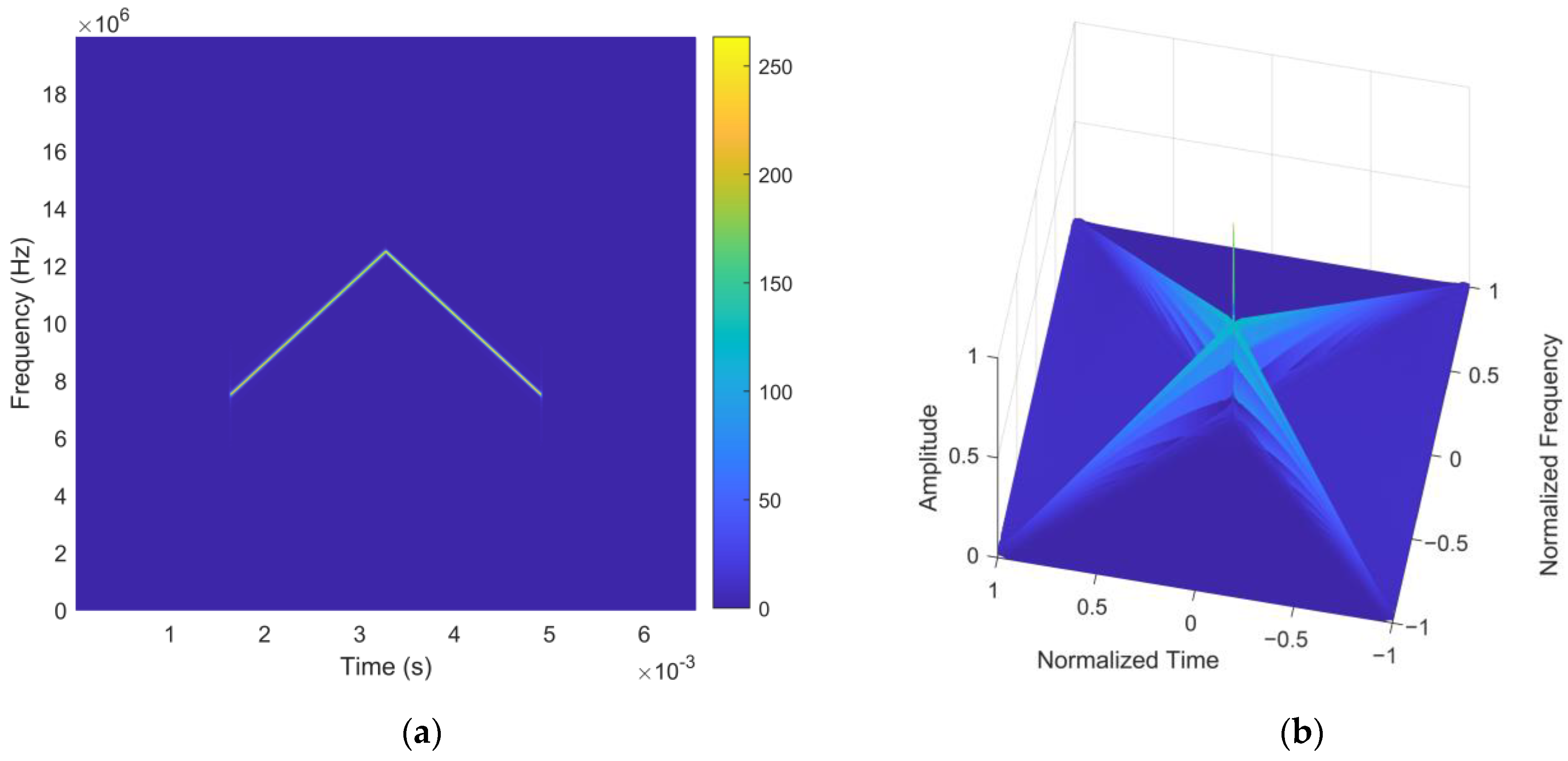
3.1. Waveform Design
3.2. Anti-Interference Principle of the Intra-Pulse Orthogonal Waveform
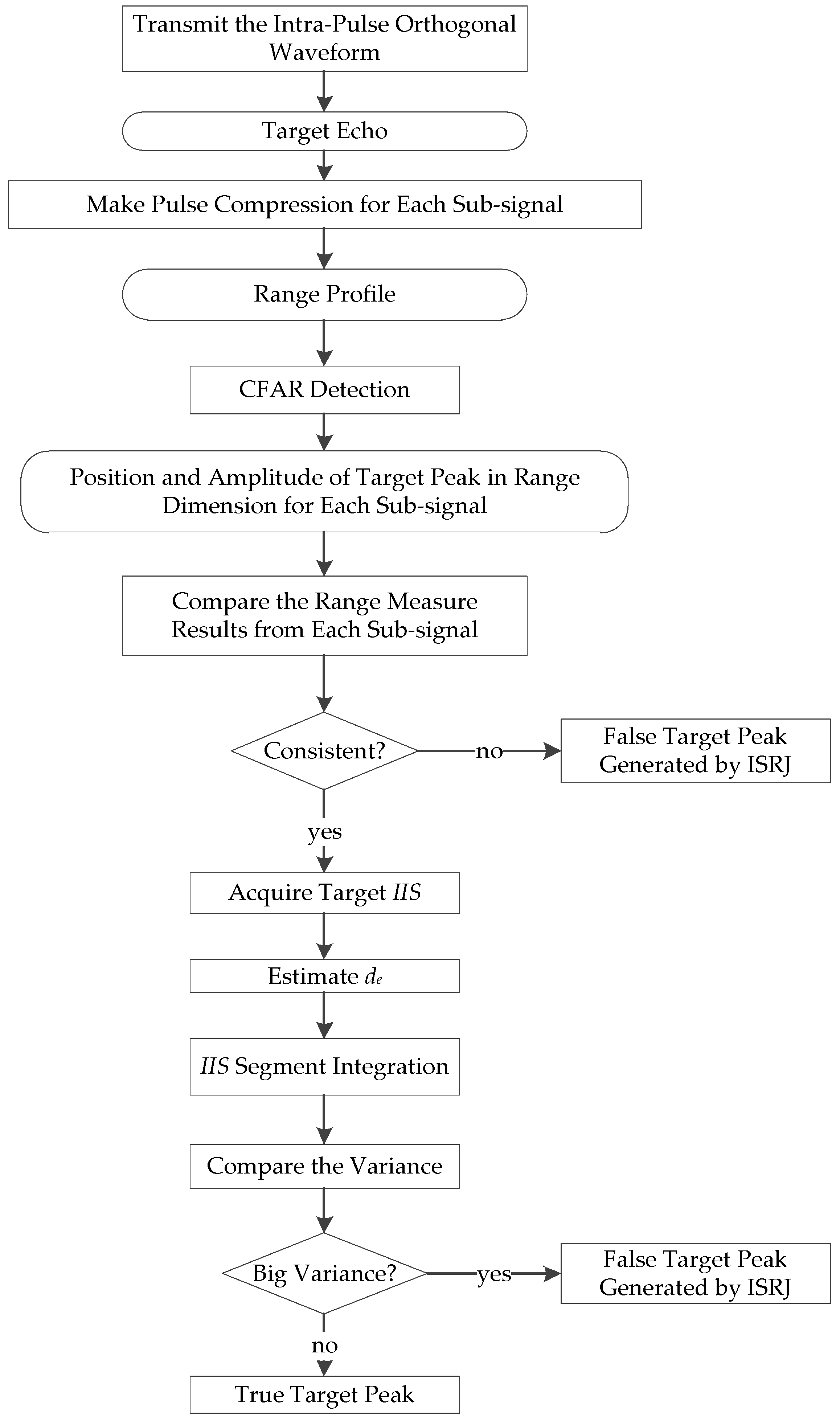
4. Interference Identification Algorithm based on Instantaneous Energy Integral
4.1. Interference Feature Extraction
4.2. Interference Feature Identification
- 1.
- Initialization. Obtain the values of with conventional linear fitting methods. ()
- 2.
- Recursion. Obtain the values of with the values of and . (, )
- 2.1
- Divide into two groups, and , where ;
- 2.2
- Obtain the values of and , and calculate the total error ;
- 2.3
- Calculate the optimal fitting error , and aquire the optimal segment point ;
- 2.4
- Calculate the values of . When , and when ,.
- 3.
- Termination. Output the values of and when .
5. Experiments
5.1. Anti-Interference Experiments of the Proposed Waveforms
5.2. Anti-Interference Experiments of the Interference-Identification Algorithm
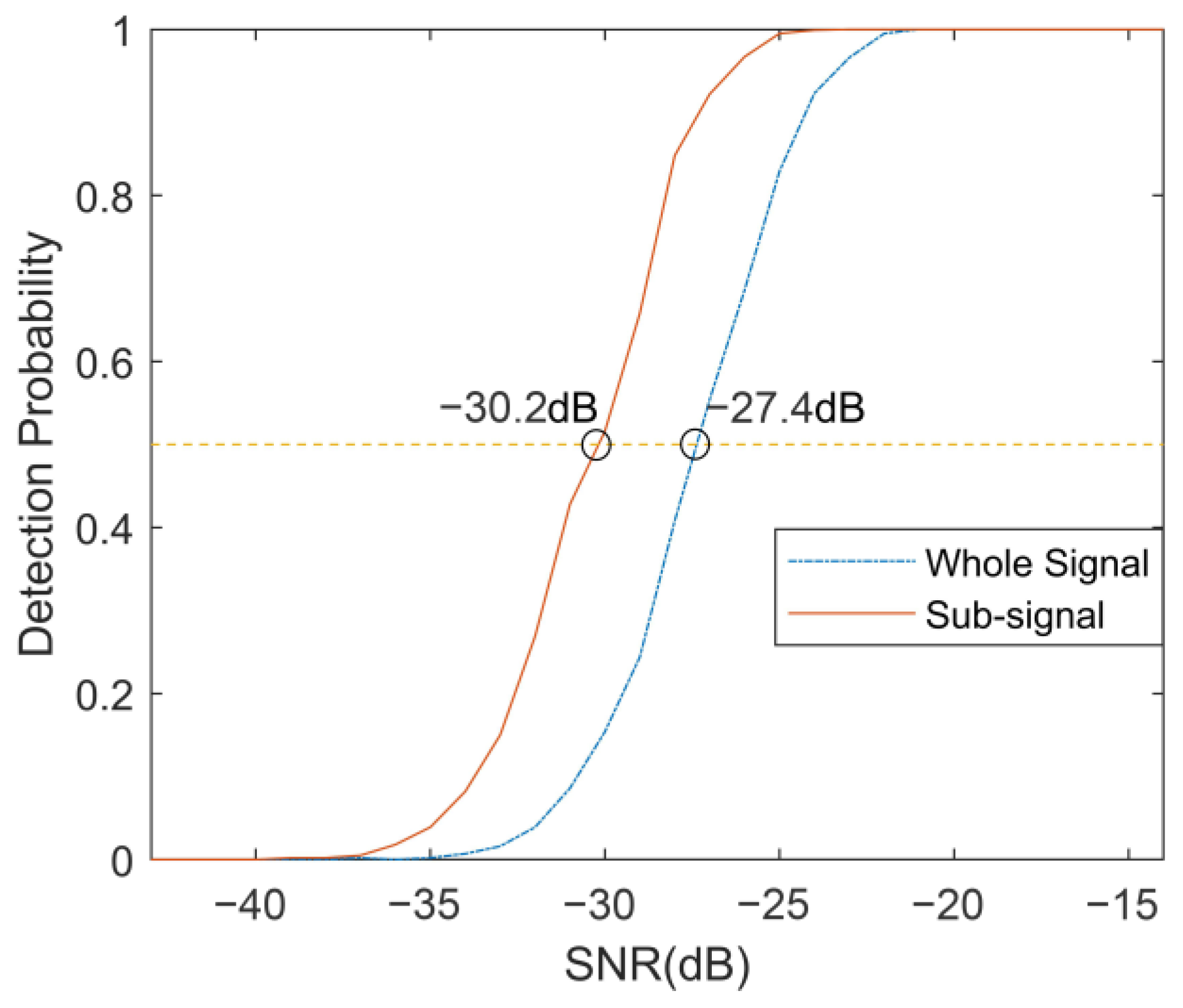
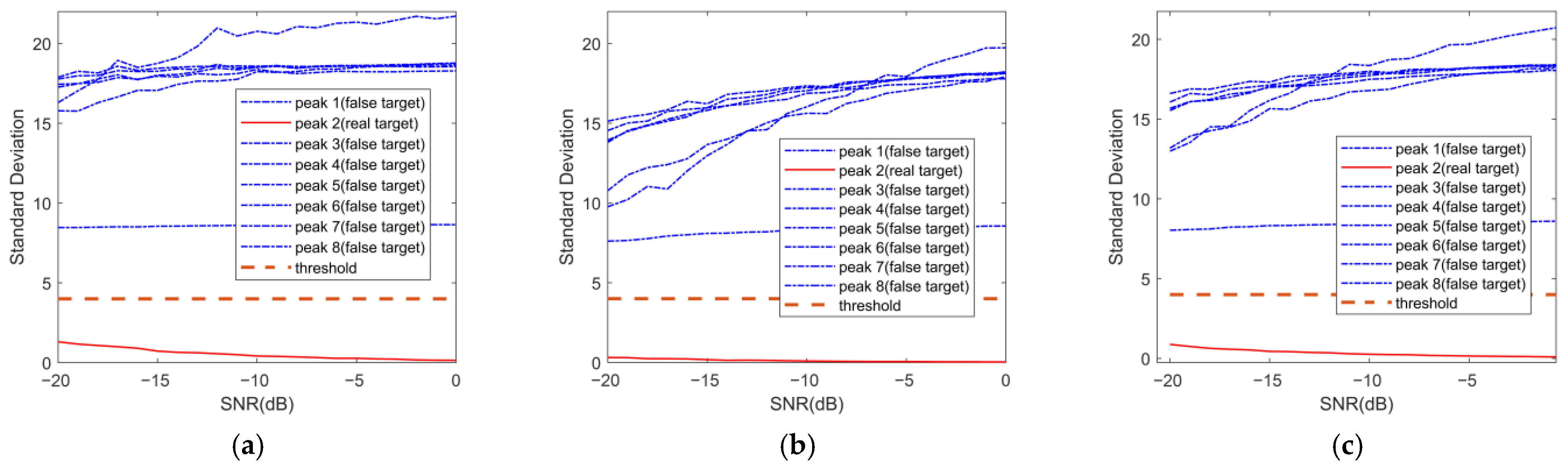
5.3. Robustness Analysis of the Proposed Orthogonal Waveform to Noise Interference
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, X.; Liu, J.; Zhang, W.; Fu, Q.; Liu, Z.; Xie, X. Mathematic principles of interrupted-sampling repeater jamming (ISRJ). Sci. China Ser. F Inf. Sci. 2007, 50, 113–123. [Google Scholar] [CrossRef]
- Xiao, J.; Wei, X.; Sun, J. Research on Interrupted Sampling Repeater Jamming Performance Based on Joint Frequency Shift/Phase Modulation. Sensors 2023, 23, 2812. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Duan, X.; Li, J.; Bai, P. Interrupted-Sampling and Non-Uniform Periodic Repeater Jamming against m DT-STAP System. Electronics 2022, 12, 152. [Google Scholar] [CrossRef]
- Gong, S.; Wei, X.; Li, X.; Ling, Y. Mathematic principle of active jamming against wideband LFM radar. J. Syst. Eng. Electron. 2015, 26, 50–60. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, B.; Zou, P. Jamming Performance Analysis of Interrupted Sampling Repeater Jamming to Phase Coded Radar. Shipboard Electron. Countermeas. 2021, 44, 45–49. [Google Scholar]
- Zhang, J.; Dai, D.; Xing, S.; Wang, X.; Xiao, S. Analysis of jamming effect on intermittent sampling repeater jamming to CRPJ-SAR. Syst. Eng. Electron. 2015, 37, 1030–1034. [Google Scholar]
- Yang, Y.; Wang, B.; Zeng, R. Analysis of the Performance of Intermittent Sampling Repeater Jamming to LFM Radar. Shipboard Electron. Countermeas. 2021, 44, 28–34. [Google Scholar]
- Hua, X.; Peng, L.; Liu, W.; Cheng, Y.; Wang, H.; Sun, H.; Wang, Z. LDA-MIG detectors for maritime targets in nonhomogeneous sea clutter. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–15. [Google Scholar] [CrossRef]
- Jiang, Y.; He, M.; Yu, C. Method of interrupted-sampling repeater jamming recognition based on box dimension. Mod. Def. Technol. 2016, 44, 157–164. [Google Scholar]
- Jiang, Y.; He, M.H.; Liu, H.B.; Yu, C.L. Recognition of interrupted-sampling repeater jamming based on resemblance coefficient. Mod. Radar 2016, 38, 72–76. [Google Scholar]
- Jiang, Y.; He, M.H.; Yu, C.; Wang, B.Q. A novel method of interrupted-sampling repeater jamming recognition based on correlation dimension. Fire Control. Command. Control. 2016, 41, 152–156. [Google Scholar]
- Gong, S.; Wei, X.; Li, X. ECCM scheme against interrupted sampling repeater jammer based on time-frequency analysis. J. Syst. Eng. Electron. 2014, 25, 996–1003. [Google Scholar] [CrossRef]
- Xiong, W.; Zhang, G.; Liu, W. Efficient filter design against interrupted sampling repeater jamming for wideband radar. EURASIP J. Adv. Signal Process. 2017, 2017, 9. [Google Scholar] [CrossRef]
- Yuan, H.; Wang, C.Y.; Li, X.; An, L. A method against interrupted-sampling repeater jamming based on energy function detection and band-pass filtering. Int. J. Antennas Propag. 2017, 2017, 6759169. [Google Scholar] [CrossRef]
- Chen, J.; Wu, W.; Xu, S.; Chen, Z.; Zou, J. Band pass filter design against interrupted-sampling repeater jamming based on time-frequency analysis. IET Radar Sonar Navig. 2019, 13, 1646–1654. [Google Scholar] [CrossRef]
- Chen, J.; Xu, S.; Zou, J.; Chen, Z. Interrupted-sampling repeater jamming suppression based on stacked bidirectional gated recurrent unit network and infinite training. IEEE Access 2019, 7, 107428–107437. [Google Scholar] [CrossRef]
- Li, F.; Li, G.; Nian, P. Radar signal deception jamming suppressing based on blind source separation. Journal of Naval Aeronautical and Astronautical University. J. Nav. Aeronaut. Astronaut. Univ. 2015, 30, 424–428. [Google Scholar]
- Zhou, C.; Liu, Q.H.; Zeng, T. Research on DRFM repeater jamming recognition. J. Signal Process. 2017, 33, 911–917. [Google Scholar]
- Zhou, C.; Tang, Z.; Zhu, Z.; Zhang, Y. Anti-interrupted sampling repeater jamming waveform design method. J. Electron. Inf. Technol. 2018, 40, 8. [Google Scholar]
- Xi, R.; Ma, D.; Liu, X.; Wang, L.; Liu, Y. Intra-Pulse Frequency Coding Design for a High-Resolution Radar against Smart Noise Jamming. Remote Sens. 2022, 14, 5149. [Google Scholar] [CrossRef]
- Xu, Z.; Xue, S.; Wang, Y. Incoherent interference detection and mitigation for millimeter-wave FMCW radars. Remote Sens. 2022, 14, 4817. [Google Scholar] [CrossRef]
- Zhou, C.; Tang, Z.; Dai, Y.; Li, X. Anti-intermittent sampling repeater jamming method based on intrapulse orthogonality. Syst. Eng. Electron. 2017, 39, 8. [Google Scholar]
- Wang, F.; Chen, P.; Yin, J.; Li, N.; Li, Y.; Wang, X. Joint design of doppler-tolerant complementary sequences and receiving filters against interrupted sampling repeater jamming. J. Radars 2022, 11, 11. [Google Scholar]
- Zhou, K.; Li, D.; Su, Y.; He, F.; Liu, T. Joint transmitted waveform and mismatched filter design against interrupted-sampling repeater jamming. J. Electron. Inf. Technol. 2021, 43, 8. [Google Scholar]
- Zhou, C.; Liu, Q.; Hu, C. Time-frequency analysis techniques for recognition and suppression of interrupted sampling repeater jamming. J. Radars 2019, 8, 100–106. [Google Scholar]
- Liu, J.; Liu, Z.; Wang, X.; Xiao, S.; Wang, G. Research on forward interference based on group delay. Prog. Nat. Sci. 2007, 17, 7. [Google Scholar]
- Jiang, Y. Study of Orthogonal Wave form Based on Phase-Coding Method. Master’s Thesis, University of Electronics Science and Technology of China, Chengdu, China, 2015. [Google Scholar]
- Gabor, D. Theory of communications. J. Inst. Electr. Eng. 1946, 93, 429–457. [Google Scholar] [CrossRef]
- Huang, S.; Lin, Z.; Yang, X.; Jiang, X.; Huang, Z. A binary orthogonal chirp signal modulation method with delay offset. Comput. Eng. 2017, 34, 6. [Google Scholar]
- Zhao, Y.; Chen, Z.; Zhang, Y.; Chen, J.; Yang, J.; Xiong, Y. Hybrid integration method for highly maneuvering radar target detection based on a Markov motion model. Chin. J. Aeronaut. 2020, 33, 1717. [Google Scholar] [CrossRef]
- Luong, D.; Young, A.; Balaji, B.; Rajan, S. Classifying Linear Frequency Modulated Radar Signals Using Matched Filters. In Proceedings of the 2022 IEEE Canadian Conference on Electrical and Computer Engineering (CCECE), Halifax, NS, Canada, 18–20 September 2022. [Google Scholar]
- Wu, W.; Zou, J.; Chen, J.; Xu, S.; Chen, Z. False-target recognition against interrupted-sampling repeater jamming based on integration decomposition. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 2979–2991. [Google Scholar] [CrossRef]









| Parameter | Value |
|---|---|
| Pulse width of the transmitted waveform (twice the sub-signal pulse width) | 3.28 ms |
| Bandwidth of the transmitted waveform | 5 MHz |
| Center frequency of the transmitted waveform | 1.2 GHz |
| SNR | −15 dB |
| Time duration of signal receiving | 6.56 ms |
| Complex sampling rate | 20 MHz |
| Pulse width of the interference signal | 273 μs |
| JSR | 5 dB, 10 dB |
| Frequency shift of the interference slices (partial interference signal) | 3.5 MHz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, H.; Zhao, Y.; Su, H.; Wang, Z.; Bao, Q.; Pan, J. Research on an Intra-Pulse Orthogonal Waveform and Methods Resisting Interrupted-Sampling Repeater Jamming within the Same Frequency Band. Remote Sens. 2023, 15, 3673. https://doi.org/10.3390/rs15143673
Dai H, Zhao Y, Su H, Wang Z, Bao Q, Pan J. Research on an Intra-Pulse Orthogonal Waveform and Methods Resisting Interrupted-Sampling Repeater Jamming within the Same Frequency Band. Remote Sensing. 2023; 15(14):3673. https://doi.org/10.3390/rs15143673
Chicago/Turabian StyleDai, Huahua, Yingxiao Zhao, Hanning Su, Zhuang Wang, Qinglong Bao, and Jiameng Pan. 2023. "Research on an Intra-Pulse Orthogonal Waveform and Methods Resisting Interrupted-Sampling Repeater Jamming within the Same Frequency Band" Remote Sensing 15, no. 14: 3673. https://doi.org/10.3390/rs15143673
APA StyleDai, H., Zhao, Y., Su, H., Wang, Z., Bao, Q., & Pan, J. (2023). Research on an Intra-Pulse Orthogonal Waveform and Methods Resisting Interrupted-Sampling Repeater Jamming within the Same Frequency Band. Remote Sensing, 15(14), 3673. https://doi.org/10.3390/rs15143673





