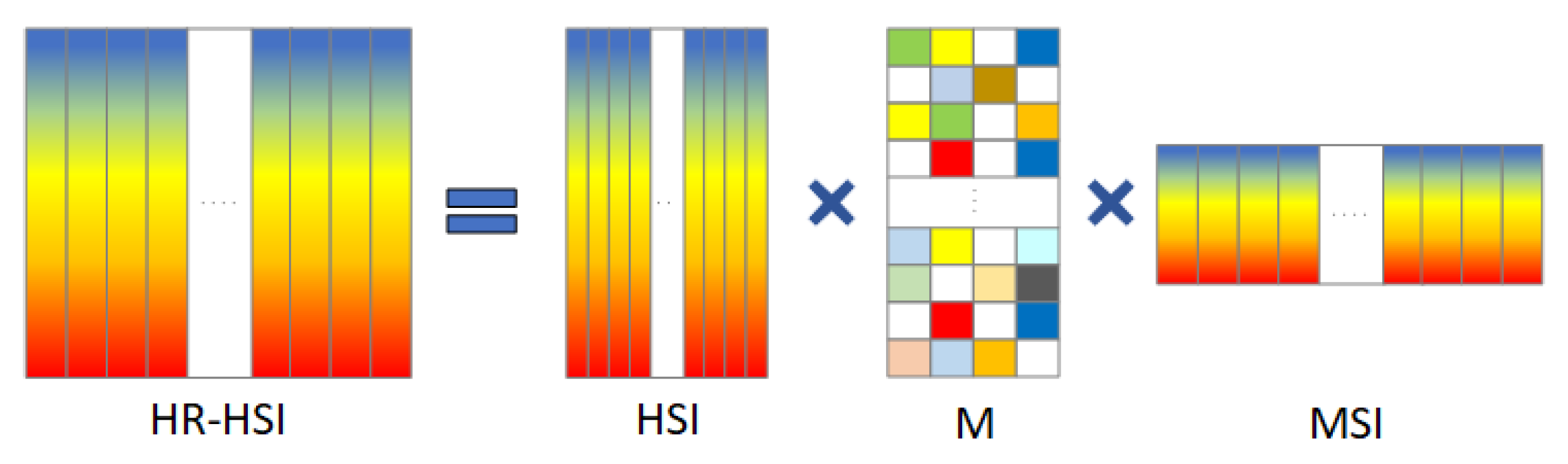
1. Introduction
Hyperspectral images have contributed significantly to various fields, including agriculture [
1,
2,
3,
4], environmental monitoring [
5,
6], image processing [
7,
8], mining [
9,
10,
11], and urban planning [
12,
13,
14]. Two commonly used imaging techniques in remote sensing are hyperspectral imaging and multispectral imaging. Hyperspectral imaging captures detailed information from hundreds of narrow and contiguous spectral bands, enabling a comprehensive material characterization based on spectral features [
15]; however, it often suffers from lower spatial resolution [
16]. On the other hand, multispectral imaging captures data in a broader range of spectral bands but with fewer spectral details, providing higher spatial resolution [
17]. Therefore, widespread research has focused on improving the spatial resolution of hyperspectral images by fusing hyperspectral and multispectral images [
18,
19]. The fused HR-HSI obtained combines the rich spectral information of HSI with the spatial information of MSI. This fusion technique has been widely applied in various tasks, including change detection [
20], anomaly detection [
21], and target classification [
22]. This indicates the significant application value of fusion techniques in remote sensing image processing.
However, the current methods used for hyperspectral and multispectral image fusion often prioritize fusion quality and overlook the requirement for fusion time, thereby limiting their feasibility in practical applications. Taking the work [
23] as an example, it assumes that HR-HSI consists of a spectral base and a corresponding coefficient matrix. The spectral base can be approximated by performing singular value decomposition on the HSI. Solving the coefficient matrix requires dividing the MSI into patches, performing clustering learning to obtain the corresponding coefficient matrix, and further optimizing the coefficient matrix. Although this method can achieve a high-quality HR-HSI, the fusion process is relatively time-consuming. The situation is even more pronounced for deep learning-based methods. Although deep learning-based methods require less prior information, the training time of the models is often excessively long, and the trained models are usually only applicable to specific datasets. They cannot be directly used for new datasets. When facing new datasets, retraining the models is typically necessary. Additionally, most fusion methods involve non-fixed parameters that must be adjusted based on different datasets. However, we often cannot obtain effective reference images like experiments to adjust these parameters in practical scenarios. The non-fixed parameters can result in inconsistent fusion performance when the downsampling factor varies within the same dataset or when dealing with different datasets. These two drawbacks significantly impact the effectiveness of these methods in practical scenarios.
In current fusion methods, it is common practice to extract spectral and spatial information from HSI and MSI and reconstruct them to obtain HR-HSI. The work [
24] above is a typical example of this approach. However, HSI and MSI already contain the spectral and spatial information required for reconstructing HR-HSI. Therefore, is it possible to use HSI and MSI directly without additional operations for the fusion step? In other words, can we combine HSI and MSI’s spectral and spatial information using a single matrix instead of complex information extraction processes? This strategy can reduce computational complexity and shorten the fusion time. Inspired by this, we propose a fusion method based on a correlation matrix. We assume the existence of a correlation matrix
that connects the spectral information of the hyperspectral image (HSI) and the spatial information of the multispectral image (MSI), enabling fast fusion through simple matrix operations with HSI and MSI.
Figure 1 provides an overview of this assumption. Since MSI and HSI are typically spectral and spatial downsampling of HR-HSI [
23], we derive the correlation matrix
that satisfies our assumption. Detailed theoretical derivations will be provided in subsequent sections.
The fusion method proposed in this paper can be divided into two stages. We first utilize the obtained correlation matrix
to fusion the HSI and MSI via simple matrix operations, as shown in
Figure 1. We name this stage CMF (correlation matrix-based fusion). CMF enables the rapid generation of high-quality HR-HSI without any parameters. As the fusion process only involves matrix operations, the fusion time required is short, addressing the issue of long fusion time. Additionally, no additional parameters are introduced in this stage.
We name the second stage CMF+, where we optimize the fusion result from the first stage using the Sylvester equation in this stage. We only introduce a fixed parameter for this stage. Since the solution of the Sylvester equation will take little time, this stage does not significantly increase the time overhead. Our method utilizes simple computations throughout the fusion process, and no parameters need to be adjusted. As a result, we can reconstruct HR-HSI quickly within a brief time.
The main contributions of this paper are as follows:
We give an assumption of the correlation matrix, which establishes the correlation between the spectral information of the hyperspectral image (HSI) and the spatial information of the multispectral image (MSI). Through this correlation matrix, we avoid complex computational processes, greatly simplify the fusion process, and reduce the fusion time.
The proposal of the correlation matrix assumption offers a novel method for future fusion processes, enabling efficient fusion through the solution of a matrix that fulfills the defined correlation matrix.
Based on the generative relationship among HSI, MSI, and HR-HSI, we derive a method to solve the correlation matrix and construct a new fusion model using this correlation matrix. We achieve the initial fusion by performing simple matrix operations on HSI, MSI, and the correlation matrix. We further optimize the preliminary fusion result using the Sylvester equation. The entire fusion process is more straightforward compared to common fusion methods, without the need for complex operations or parameter adjustments.
Experimental results on two simulated datasets and one real dataset validate the superiority of our proposed method over current state-of-the-art fusion methods. We can obtain high-quality fusion results while simplifying the fusion process and significantly improving fusion time.
We will organize the remaining sections of this paper according to the following structure.
Section 2 will introduce some classical literature and methods.
Section 3 will provide a detailed description of our proposed method.
Section 4 will present the experimental details.
Section 5 will showcase the experimental results and corresponding analysis. Finally,
Section 6 will provide a conclusion of our research.
2. Related Work
Hyperspectral and multispectral image fusion is an important research area that has gained significant attention and interest. Over the past few decades, numerous methods and techniques have been proposed to improve the fusion performance between hyperspectral and multispectral images. These methods can be broadly categorized into four groups, Bayesian-based, matrix factorization-based, tensor factorization-based, and deep learning-based.
Bayesian-based methods utilize Bayesian theory to model the relationship between spectral and spatial information and achieve fusion through statistical inference. These methods typically rely on prior knowledge and probability models for image fusion. The fusion method proposed in work [
25] utilizes a Bayesian non-parametric method with a Beta-Bernoulli process to learn dictionary elements and coefficient weights for achieving fusion between hyperspectral and multispectral images. Qi et al. [
24] transformed the fusion problem into a Bayesian estimation framework. It introduces a prior distribution based on the linear mixing model and employs a Gibbs sampling algorithm with a Hamiltonian Monte Carlo step to obtain the posterior distribution required for fusion.
Matrix factorization-based methods represent hyperspectral and multispectral images in matrix form and employ techniques like principal component analysis (PCA) and non-negative matrix factorization (NMF) to extract underlying features, facilitating fusion. These methods effectively reduce data redundancy and preserve crucial information through dimensionality reduction and feature extraction. A novel adaptive non-negative sparse representation model is proposed for fusion in work [
26]. Using a non-negative structured sparse representation model. The method begins with linear spectral unmixing to estimate the sparse coding of the spectral bases for HR-HSI from HSI and MSI. It generates a balance between sparsity and collaboration coefficients through adaptive sparse representation and performs alternating optimization on the spectral bases and coefficients. Ref. [
27] considers HR-HSI as a composition of a hyperspectral dictionary and sparse codes. The method proposes a non-negative dictionary learning approach based on block-coordinate descent optimization to learn the spectral dictionary from HSI. A clustering-based structured sparse coding method is introduced to solve the corresponding sparse codes. Huang et al. [
28] present the SASFM fusion model. Based on reasonable assumptions, this model first learns a spectral dictionary from the HSI data. Then, the learned spectral dictionary and known MSI are used to predict HR-HSI.
The tensor factorization-based methods utilize tensors to represent the relationships between hyperspectral and multispectral images and achieve fusion through tensor operations. These methods can leverage the high-dimensional structural information of the images more effectively, thus improving the fusion performance. Li et al. [
29] treat HR-HSI as composed of three sub-tensors and a sparse core tensor. This method proposes a fusion approach based on coupled sparse tensor representation, which achieves a high-quality fusion result through approximate alternating optimization. In ref. [
30], a low tensor-train rank prior is utilized to learn the correlations among the HR-HSI cube’s spatial, spectral, and non-local patterns. The HR-HSI is uniformly clustered based on the clustering structure in the MSI, and the LTTR (low tensor-train rank) constraint is imposed on each clustered block, effectively learning the spatial, spectral, and non-local similarities. The optimization is performed using alternating direction multiplication.
Methods based on deep learning utilize deep neural network models to learn the non-linear mapping relationship between hyperspectral and multispectral images. By training the network models, they can automatically extract and learn feature representations of the images, achieving high-quality image fusion.
A novel coupled unmixing network (CUCaNet) with a cross-attention mechanism is proposed by Yao et al. [
31]. The dual-stream convolutional auto-encoder framework serves as the backbone, and the MSI and HSI data are jointly decomposed into bases with spectral significance and corresponding coefficients for fusion. Work [
32] presents the CNN-Fus network, which achieves unsupervised fusion without training. Based on the high correlation between spectral bands, the HR-HSI is obtained by multiplying a low-dimensional subspace by coefficients. Subspace is learned from HSI using singular value decomposition, and coefficients are estimated using a CNN denoiser inserted into the alternating multiplier method algorithm. Liu et al. [
33] design a model-inspired deep network with an implicit auto-encoder network that treats each HR-HSI pixel as a separate sample. The non-negative matrix factorization (NMF) of the target HR-HSI is integrated into the auto-encoder network, consisting of spectral and spatial matrix NMF parts serving as decoder parameters and hidden outputs, respectively. Finally, a pixel-wise fusion model is proposed for fusion during the encoding stage.
In the above classification, methods based on Bayesian, matrix factorization, and tensor factorization are traditional fusion methods. This is primarily because they focus on constructing mathematical models and algorithms, utilizing traditional mathematical tools, such as statistics, matrix decomposition, and tensor decomposition to achieve image fusion. These methods typically emphasize modeling and analyzing the data to improve fusion performance and effectiveness.
In contrast, modern deep learning-based methods emphasize end-to-end feature learning and fusion using deep neural networks. They go beyond the limitations of traditional mathematical tools and techniques. These deep learning methods leverage the power of neural networks to learn hierarchical representations directly from the data and perform fusion in a more data-driven and automated manner.
3. Fusion Model
It is common to represent HSI, MSI, and HR-HSI using three-dimensional data. For clarity, in this paper, we define them using different symbols. We use the to denote the target HR-HSI, which has pixels and L spectral bands. The means the HSI, which comprises pixels and L spectral bands. Finally, the represents the MSI, with pixels and l bands. Since HSI contains more spectral information than MSI, we can express this relationship as . Similarly, and denote that the spatial resolution in MSI is larger than that in HSI.
The fusion method proposed in this paper is based on matrix operations. The basic principle is to use the hyperspectral image (HSI), multispectral image (MSI), and a correlation matrix to perform matrix multiplication for fusion. Therefore, we unfold the respective tensors along the spectral dimension and represent them as matrices, denoted as
,
, and
, corresponding to the tensors. Since
and
correspond to the spatial and spectral downsampling of
[
23], we can establish the following relationship
where the matrices
represents the convolution blur operation, and
denotes the spatial downsampling operation, both determined by the point spread function (PSF) of the hyperspectral camera sensor.
represents the spectral downsampling operation, determined by the multispectral camera’s spectral response function (SRF). In this paper, both PSF and SRF are known.
There is typically a high correlation among the spectral bands in HSI, and the spectral vectors often lie in a low-dimensional subspace [
34]. Therefore, in common fusion models, it is commonly assumed that
where
represents the spectral basis, and
represents the corresponding coefficient matrix. The reconstruction problem of the high spatial resolution hyperspectral image is thus transformed into a problem of solving for
and
. The essential purpose of
and
is to extract the spectral information from HSI and the spatial information from MSI and reasonably combine them to achieve fusion; however, obtaining a high-quality fusion result typically requires complex computations and iterative optimization for solving
and
. Therefore, we propose an assumption that there exists a matrix
satisfying the following expression
where
.
According to Equation (
4), we can perform fusion by matrix operations when
exists. The role of
is to associate the spectral information of HSI with the spatial information of MSI, which we call this matrix as the correlation matrix. Due to the use of matrix operations without the need for complex feature extraction or iterative optimization, this fusion process is efficient.
From Equation (
1), we can obtain that
where the
means the inverse matrix of
. It means that we can derive
once we have obtained
; however,
is typically a non-square matrix, meaning it does not have a corresponding inverse matrix
. To address this, we introduce a generalized inverse matrix to approximate
. In this case, we can obtain the following equation.
where the
is the generalized inverse matrix [
35] of
.
Limited by the large dimensionality of
, directly calculating the generalized inverse of
can be computationally demanding and require substantial hardware resources. To address this issue, we can explore Equation (
2) as an indirect alternative for solving the problem.
We apply the same spatial convolution blur and downsampling operations to
and obtain the
.
According to Equation (
7), we can indirectly obtain the generalized inverse matrix of
.
Since is obtained by spatially blurring and downsampling , its data dimension is significantly reduced, much smaller than the dimension of . Therefore, computing the generalized inverse matrix of does not require high hardware requirements and can be easily implemented.
Combining Equations (
6) and (
8), we can obtain the following relationship:
By comparing Equations (
4) and (
9), we can find that matrix
satisfies the requirements of matrix
. Therefore, once we can solve for
, we can easily achieve the fusion process through simple matrix operations. By substituting Equation (
1) into Equation (
9), we can mathematically demonstrate why this approach works.
At this point, by using Equation (
9), we can obtain a high-quality HR-HSI. To further enhance the fusion performance, we introduce a variable
and construct the optimization function as follows
where
means the Frobenius norm of
in this paper and
is a positive penalty parameter less than 1.
By minimizing Equation (
10) to make the gradient of
equal to zero, we obtain the following equation
where
is the identity matrix. The detailed derivation process from Equation (
10) to Equation (
11) is provided in
Appendix A.
We solve Equation (
11) using the Sylvester Equation [
36] and transform the problem as follows
where
For computational convenience, similar to work [
23], we assume that
satisfies a circulant–block–circulant (CBC) structure, which means that
can be diagonalized as
, where
represents the DFT matrix, and
represents the conjugate transpose of
. The diagonal matrix
contains the singular values of
.
The method proposed in this paper can be divided into two stages. The first stage is the fusion achieved using Equation (
9), where no constrained optimization conditions are introduced. We denote this stage as CMF. The second stage involves the fusion with the introduction of constrained optimization conditions, represented by Equation (
10). We denote this stage as CMF+. This is performed to facilitate comparing the two stages in the subsequent analysis. The detailed process of fusion is presented in Algorithm 1.
| Algorithm 1 The proposed method. |
| Require: , , , , |
| Obtain the from Equation (7) |
| Compute the generalized inverse matrix of to obtain . |
| Reconstruct the first stage HR-HSI using Equation (9). |
| Solve Equation (10) by substituting to obtain , , and in Equation (12). |
| Eigen-decomposition of : |
| |
| Eigen-decomposition of : |
| |
| for i = 1 to L do |
| |
| end for |
| Set |
| return |
In Algorithm 1, the and are vector, and their elements are all ones. denote l-th row of , that is, . is the elements in diagonal matrix and the s means the spatial downsampling factor.
5. Results and Analysis
5.1. Results on Simulated Dataset
Among the compared methods, MIAE and CUCaNet can perform image fusion without PSF and SRF information. In contrast, our proposed and other comparative methods perform fusion under the known PSF and SRF assumptions. The CUCaNet method can also be adapted to utilize PSF and SRF by modifying the source code. However, the MIAE method requires more extensive modifications to the source code to accommodate PSF and SRF. To minimize the impact of human factors on the experimental results, we retained the fusion results of the MIAE method without using PSF and SRF on the two simulated datasets. For the CUCaNet method, we made corresponding adjustments to enable fusion using PSF and SRF. The CMF and CMF+ show the different fusion results of the two stages in our proposed method.
The Harvard dataset has two categories of images, indoor and outdoor scenes. We selected representative images from each category for our experiments, namely “imgb2” for the outdoor image and “imgh7” for the indoor image. The corresponding fusion results are listed in
Table 2 and
Table 3, respectively. In the tables, the letter “
s” denotes the downsampling factor. For each evaluation metric, we have highlighted the optimal results using
bold font and indicated the second-best performance with an
underline, enabling easy comparison and identification of the fusion result.
Table 2 shows that when the downsampling factor is 16, the FLTMR method achieves the best performance in terms of PSNR and UIQI metrics, outperforming our proposed method; however, it is worth noting that the fusion results obtained by our CMF+ method are very close to FLTMR. The PSNR difference is only 1.134 dB, and other metrics also exhibit a high level of similarity. When the downsampling factor increases to 32, our method achieves the best or second-best results in most metrics, with only a slightly lower ERGAS metric performance than the CSTF method. Notably, the impact of changing the downsampling factor on our method is relatively small compared to the downsampling factor of 16. Specifically, the CMF experiences a decrease of only 0.081 dB in PSNR, while CMF+ shows a decrease of only 0.194 dB. In contrast, the LTMR method experiences a significant drop of 4.99 dB in this metric.
When the downsampling factor increases, the spatial information in HSI decreases, reducing available prior information for fusion. Therefore, as the downsampling factor increases, the fusion accuracy tends to decrease. The proposed method does not require additional feature extraction but operates based on the correlation matrix. When the downsampling factor changes, the correlation matrix is adjusted accordingly to adapt to the new HSI image, resulting in minimal changes. In contrast, the LTMR method assumes that the HR-HSI consists of a spectral base and corresponding coefficient matrix. The spectral base is obtained through singular value decomposition of the HSI, so changes in the downsampling factor directly affect the construction of the spectral base. Additionally, there are parameters in the fusion method that need to be adjusted to achieve optimal results; however, finding suitable references for parameter tuning in practical scenarios is challenging. As a result, the results of the LTMR method can vary significantly for different datasets and downsampling factors. FLTMR is an improvement upon LTMR, so it faces similar issues.
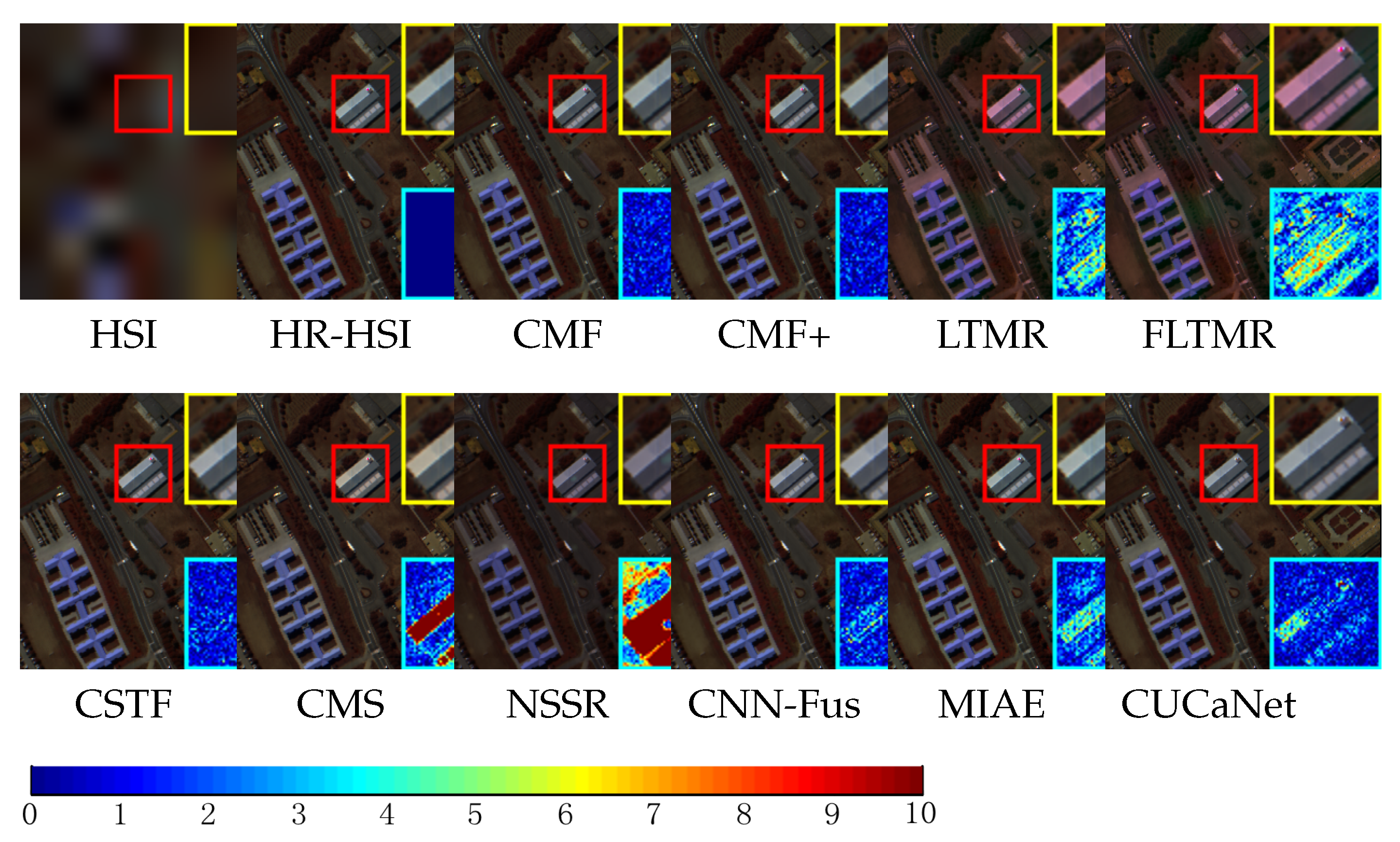
To provide a more intuitive display of the fusion results, we will show the false color images of the fusion results at a downsampling factor of 32.
Figure 2 illustrates the fusion results of various methods mentioned in
Table 2. The yellow box represents the image enlarged from the region marked by the red box, while the blue box represents the enlarged error image corresponding to that region.
Figure 2 shows that the fusion results of CMF, CMF+, and CNN-Fus methods are superior to the other methods.
According to the data in
Table 3, our method achieves optimal results in most indicators for the indoor image of the Harvard dataset at downsampling factors of 16 and 32. Although it may slightly lag behind other methods in individual indicators, our method still performs at a second-best level. Overall, our method outperforms other methods; however, it is worth noting that the CMS method in the table shows significant changes in fusion performance at a downsampling factor of 32. This is mainly because the parameters of the CMS method were not adjusted according to the downsampling factor. Moreover, in the corresponding fusion result
Figure 3, we can observe that CMF, CMF+, CNN-Fus, and MIAE methods exhibit significantly better fusion results than the others. These methods preserve image details and color accuracy, as evident from the enlarged regions and corresponding error images. The error images demonstrate their ability to reduce artifacts and distortions effectively.
According to the experimental results on the Pavia University dataset,
Table 4 presents the performance of various methods. We observed that, at a downsampling factor of 16, the CUCaNet method achieved the best experimental results, while our method obtained the second-best results. However, when the downsampling factor increased to 32, our method achieved the best results in terms of PSNR and ERGAS while obtaining the second-best results in terms of SAM and UIQI evaluation metrics. CUCaNet, MIAE, and CNN-Fus are deep learning-based methods, where the CNN-Fus method does not require extensive training and has relatively low requirements on the training set. However, MIAE and CUCaNet methods require repeated training, and their performance can vary significantly across different datasets. The parameter settings in these three methods also impose limitations on fusion performance. For the CNN-Fus method, the fusion results may not be satisfactory if we do not modify the spectral basic L. Indeed, from the fusion results in
Figure 4, it is evident that CMF, CMF+, and CSTF methods exhibit significant advantages in image fusion. They can better preserve image details and color consistency, producing more precise and natural fused images. In contrast, the fusion results of the NSSR method are relatively poorer, primarily because its parameters perform well only on specific datasets.
5.2. Results on Real Dataset
This section will test our proposed method on a real dataset. To better simulate real-world usage scenarios, the parameter settings for each method were kept the same setting as the experiment on the Pavia University dataset (
). The main reason for doing this is that it is often impossible to adjust the parameters based on reliable image pairs for optimal performance in real scenarios. As for our proposed and other methods, we employed the method in [
40] to generate PSF and SRF during the fusion process.
Figure 5 shows the fusion results of each method on the real dataset, where the yellow box highlights the effect of the region magnified three times compared to the red box region.
Based on the observations from the false color images, we found that the CMF, CMF+, MIAE, and CUCaNet methods are closer to the false color images of the HSI. Furthermore, upon closer examination of the magnified regions, the CMF method exhibits better detail preservation than the MSI. The CUCaNet and CMF+ methods also achieve relatively good results in preserving details. On the other hand, the MIAE method shows significant blurring. The fusion result of the CMF+ method is worse than CMF because CMF+ utilizes estimated PSF and SRF during the optimization process, which introduces additional errors. In contrast, the CMF method only employs PSF when generating and does not undergo further optimization, thus avoiding the introduction of additional errors.
5.3. Parameter Discussion
The proposed method in this paper involves only one parameter,
, in Equation (
10). This section will discuss the impact of
on the fusion results.
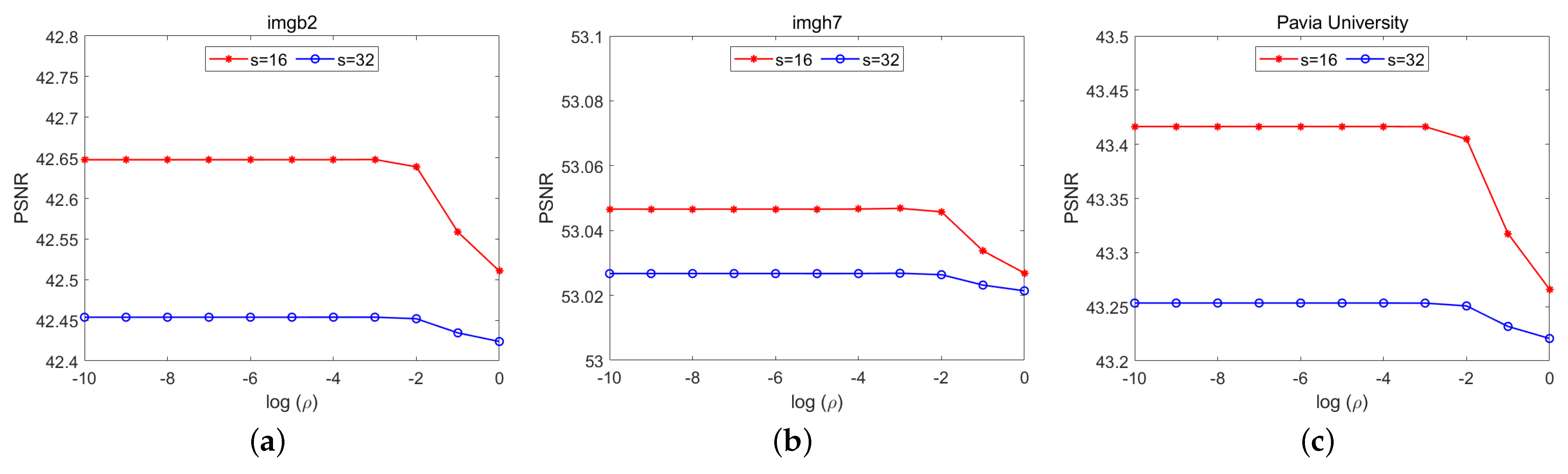
Figure 6 displays the variation of PSNR with different values of
(log is base 10) on the Harvard and Pavia University datasets. According to the variation of PSNR in
Figure 6, it can be observed that when the value of
is below −3, it has a minimal impact on the experimental results. Therefore, we set
as a fixed parameter in our proposed method, specifically 0.001.
Table 2,
Table 3 and
Table 4 show that the CMF stage alone can achieve decent fusion results even without introducing additional optimization processes. The optimization process further improves the fusion results based on the CMF stage. Although the variable
may influence the fusion results, it only improves the results obtained in the CMF stage when PSF and SRF are known. The parameter
constrains and optimizes the results without requiring iterative processes. Thus, its impact is limited. In contrast, parameters in other fusion methods are often related to selecting critical factors in the fusion process, directly affecting the fusion results. Moreover, these methods require iterative optimization, which may amplify the errors caused by parameters. Consequently, even in the case where both PSF and SRF are known, these methods often necessitate parameter adjustments for different datasets to achieve satisfactory fusion results, while our method does not have this concern. In the scenario where PSF and SRF are unknown, we can just use CMF for fusion, reducing the errors associated with the estimated PSF and SRF and eliminating the need for any parameter tuning.
5.4. Comparison between CMF and CMF+
When discussing the differences between CMF and CMF+, we must consider two scenarios: PSF and SRF are known; PSF and SRF are unknown. In
Section 3, we mentioned that CMF+ introduces the Sylvester equation to further optimize the results based on CMF. The downsampling factor and whether PSF and SRF are known largely influence the effect of the optimization.
When PSF and SRF are known, HSI contains more spatial information when the downsampling factor is low. In this case, the optimization equation can better adjust the fusion results, further improving the result of CMF. However, when the downsampling factor is high, the spatial information in HSI is significantly reduced, limiting the effect of the optimization equation. This observation is also evident in
Figure 7, where the effectiveness of the optimization equation decreases with increasing downsampling factor.
On the other hand, when PSF and SRF are unknown, as discussed in
Section 5.2, the iterative optimization process introduces and amplifies errors in PSF and SRF, resulting in inferior performance of CMF+ compared to CMF. Therefore, in this scenario, CMF outperforms CMF+ in terms of overall performance.
In conclusion, CMF and CMF+ all achieve good fusion results when PSF and SRF are known, where CMF+ performs better at lower downsampling factors. When the PSF and RSF are unknown, the fusion results of CMF combined with related estimation methods will have better fusion results than CMF+. We can make corresponding choices according to the actual requirements.
5.5. Computational Cost
To showcase the computational efficiency of our method and other comparative methods,
Table 5 displays the fusion time of each method on different datasets, and the average fusion time for all methods is calculated. Since MIAE and CUCaNet methods require an enormous amount of operating memory, we deployed them on a server configured with Intel(R) Xeon(R) Gold 5218 CPU @ 2.30 GHz and 125 GB RAM, along with NVIDIA TITAN RTX. The remaining methods were executed using Matlab 2021b on a local host with a 2.90 GHz 6-core Intel i5-9400F CPU and 8.0 GB DDR3 RAM.
Based on the data in
Table 5, we can observe that both CMF and CMF+ methods require a very short time to complete the fusion, showcasing excellent fusion time regardless of the dataset. In comparison to other methods, their fusion time is significantly shorter. It is worth noting that the time for CNN-Fus, MIAE, and CUCaNet in
Table 5 includes the training time, encompassing the entire process from training to fusion completion. Deep learning-based models often require retraining in practical scenarios to achieve satisfactory fusion results on new datasets.
Relative to the average fusion time of CMF, the average fusion time of CUCaNet is approximately 44,450 times longer. Even though the improved version of FLTMR shows significant improvement in average fusion time compared to LTMR, it is still around 298 times slower than CMF and nearly 32 times slower than CMF+. Additionally, we can infer from the objective metrics results in
Table 2,
Table 3 and
Table 4 that these comparative methods take longer than CMF and CMF+, but their overall fusion results do not show equivalent improvements. In fact, the fusion results of most methods are inferior to our proposed methods.
Therefore, considering both fusion quality and efficiency, the method proposed in this paper is significantly superior to other comparative methods.