Abstract
With global warming, Arctic sea ice, as one of the important factors regulating climate, has put forward new requirements for research. At present, the ground penetrating radar (GPR) is a powerful tool to obtain the structure of Arctic sea ice. Traditional offset imaging techniques no longer meet research requirements, and the two-parameter full waveform inversion (FWI) method has received widespread attention. To solve the high nonlinearity and ill-posed problem of FWI, the L-BFGS optimization algorithm and Wolfe criterion of inexact line search were used to update the model. The parameter scale factor, multiscale inversion strategy, and total variation (TV) regularization were introduced to optimize the inversion results. Finally, the inversion of anomalous bodies with different scales and different physical parameters is carried out, which verifies the reliability of the proposed method for dual-parameter imaging of Arctic sea ice and provides a powerful tool for the study of Arctic sea ice.
1. Introduction
The ice in the ocean, more broadly known as sea ice, consists of a mixture of freshwater ice crystals, “brine”, and bubbles containing salt. There are three types of sea ice based on how long it lasts: new ice, one-year ice, and multiyear ice, with multiyear ice being ice that has gone through at least one melting period. The Arctic Ocean is surrounded by continents and is less affected by atmospheric and ocean circulation than Antarctica. The multiyear ice presents a layered distribution, and part of the salt that has no time to flow away is surrounded in the form of brine in the space between the ice crystals to form a “salt bubble”. Arctic sea ice is an important factor regulating the global climate, and the Arctic temperature is rising twice as fast as the global average, resulting in a rapid decline in the Arctic sea ice area [1]. With the effect of global warming, research on Arctic sea ice has also put forward higher requirements.
GPR detects shallow media by transmitting and receiving high-frequency electromagnetic waves on the ground, and the cross-hole radar collects interlayer information between two boreholes, which has been successfully applied in archaeological investigations [2], road detection [3,4,5], polar investigations [6], and soil moisture measurements [7]. GPR has been successfully applied to the exploration of sea ice. Galley et al. [8] distinguished snow, sea ice, and freshwater ice by observing the characteristics of GPR. Annan et al. [9] used GPR to assess winter ice thickness to safely construct ice roads. Fantello et al. [10] used GPR to nondestructively quantify the amount of methane bubbles present in lake ice. Bradford et al. [11] developed a targeted GPR reflection waveform inversion algorithm to quantify the geometry of oil under sea ice and in sea ice spills.
In recent years, FWI methods have received wide attention from the geophysical academic community. GPR full waveform inversion can obtain the subsurface conductivity and permittivity to accurately describe the location and morphology of the target anomalous body. To accurately obtain the layered structure and internal media parameters of Arctic sea ice, FWI can obtain higher resolution than traditional migration imaging. FWI was proposed by Tarantola in the last century. It was initially applied to acoustic waves and elastic waves in seismic exploration and provided a theoretical framework in the time domain. The optimal solution was obtained by minimizing the observed and simulated data [12,13]. Pratt [14] applied FWI to the frequency domain and successfully obtained inversion results. The frequency domain is more suitable for large-scale inversion problems than the time domain. Sirgue et al. [15] developed mixed-domain FWI based on frequency-domain forward modeling combined with time-domain inversion. Pratt [16] and Shin [17] developed FWI for the Laplace domain and Laplace–Fourier domain, respectively. Among the time domain forward modeling methods, the time finite difference method is widely used, which has the advantages of direct time domain calculation, clear thinking, and simple programming.
When FWI was initially applied to GPR, the single-parameter inversion of the permittivity was realized [18]. At present, the requirement of radar FWI has been improved from single-parameter inversion to multiparameter inversion, but this will lead to a series inversion phenomenon, and the target parameters and morphology cannot be reconstructed. At the same time, the FWI of GPR has strong nonlinearity, which is mainly manifested by the phenomenon of cycle skipping. To improve the accuracy of dual-parameter inversion, Meles et al. [19] used a new vector algorithm to update the permittivity and conductivity distribution simultaneously by changing the step size during iteration. Ren [20] carried out a dual-parameter inversion based on the cross gradient and used the truncated Newton method to solve it. Gradient calculation is the core of full waveform inversion theory, and the adjoint state method is mainly used at present. Because GPR FWI is a highly nonlinear problem, the global optimization algorithm is difficult to apply, and the local optimization algorithm is often used to solve the problem. Hessian operator, as the second derivative of the objective function to the model parameters, has a crucial influence on the results of FWI. Métivier [21] used the truncated Newton method to realize FWI of P-wave velocity in the frequency domain. In the presence of multiple reflection waves, the inversion results of the truncated Newton method, L-BFGS method, and conjugate gradient method were compared, further verifying that the truncated Newton method could provide an accurate inverse estimation of the Hessian operator. In the frequency domain, forward modeling can be carried out due to the relatively small calculation amount, but in the time domain, forward modeling requires a lot of calculation, so it is impossible to carry out this method. The quasi-Newton method approximates the inverse of the Hessian operator by constructing a positive definite matrix with a certain number of models and gradient information of the objective function, among which the most representative method is the finite memory BFGS method (L-BFGS) [22]. Lavoué et al. [23] solved the inverse problem with a quasi-Newton optimization scheme, where the influence of the Hessian is approximated by the L-BFGS-B algorithm. Nilot et al. [24] applied the memory-free quasi-Newton (MLQN) method to conduct GPR inversion and obtained good results with low computing costs and small memory storage requirements.
Due to the pathological and strong nonlinear characteristics of the inversion problem itself, an initial model seriously deviating from the true solution will cause the problem of “cycle-skipping” during waveform matching [25], which will lead to the inversion process easily converging to the local minimum. Therefore, FWI is highly dependent on accurate initial models to ensure the correct convergence of the inversion process. The low-frequency component of radar data is not sensitive to local extreme values, and its objective function is relatively smooth, has fewer local extreme values, and is easy to converge to the global optimal solution, so the dependence on the initial model is low. Meles et al. [26] designed a frequency-time-domain combination method to achieve inversion, which allows the high-frequency component to be gradually increased from the low frequency to expand the frequency bandwidth of the data in the iterative process. Zhou et al. [27] applied the cosine angular difference identification method to GPR data to improve the onset model of cross-hole GPR FWI by amplifying the amplitude of low-frequency signals. Jin et al. [28] proposed a robust asymptotic migration learning method to derive low-frequency information from band-limited observation data, and the experimental results showed that the method converges quickly and with high accuracy in the case of a limited training set size. Fu et al. [29] utilized the integral wavefield transform to provide the low-frequency information of the data, fully utilized the low-frequency components hidden in the original data, and obtained the structure of the large-scale relative permittivity distribution, which reduced the instability of the full waveform inversion.
The essence of the regularization of geophysical inversion can be considered as changing the properties of the parameter matrix to make the solution of the inverse problem stable and achieve higher accuracy. The most commonly used regularization method is the Tikhonov regularization method [30], but the Tikhonov regularization method cannot obtain better inversion results due to excessive smoothness. In recent years, there have been some new regularization methods, such as total variation regularization, which can get better results in this case. Feng et al. [31] developed a new FWI method for ground penetrating radar data based on the total variation (TV) regularization L-BFGS algorithm, which can apply two-parameter prior information constraints to ensure the stability of inversion. Wang et al. [32] developed a 3-D FWI algorithm involving permittivity and conductivity for GPR in the frequency domain. In addition, a modified total variation regularization scheme is utilized for ensuring the stability of the inversion as well as identifying the abnormal body boundary more effectively.
For more new methods of FWI, Feng et al. [33] developed an efficient inversion algorithm independent of the source wavelet based on the convolution method to improve the efficiency of the algorithm for data inversion. Mozaffari et al. [34] introduced a novel 2.5D cross-hole GPR full waveform inversion, which carried out forward modeling in 3D and FWI in a 2D plane. Liu et al. [35] developed GPRInvNet software based on a deep learning algorithm, which can realize the inversion of the permittivity of tunnel lining radar data and effectively reconstruct the permittivity distribution of defects in complex tunnel lining. In the application of GPR FWI, Liu et al. [36] proposed a data inversion scheme for cross-hole GPR with low frequency missing and combined the envelope objective function with the method to effectively reduce the nonlinearity of the inversion and apply to the actual data. Liu et al. [37] used the global optimization SCE algorithm to estimate the radius of underground cylindrical objects. Feng et al. [38] adopted the wave field reconstruction inversion (WRI) strategy to conduct GPR data imaging and adopted the frequency weighting strategy and multiscale method to avoid the high-frequency component data dominating the optimization process, enhance the inversion stability, and apply to the actual data. Feng [39] proposed an FWI method involving dual-parameter attributes applied to common-offset GPR data from commercial antennas. The effectiveness of the optimized inversion is preliminarily verified through irregular trunk model tests, and the results present the precise characteristics of cracks, voids, and fading.
In this paper, the physical parameters, shapes, and exact positions of the ice cover and anomalous bodies of Arctic sea ice are obtained using dual-parameter full waveform inversion. To solve this problem in which FWI is highly nonlinear and ill-posed, multiscale inversion is adopted. Three center frequencies from low to high are selected to perform frequency-by-frequency inversion, which greatly improves the accuracy of inversion. At the same time, to obtain better inversion results, we used the total variation regularization constraint. Due to the difference between the sensitivity of the dual-parameter inversion conductivity and relative permittivity, we introduced a scale factor to control the proportion of conductivity inversion.
The framework of this paper is as follows: in the principle and methods section, the finite-difference forward modeling principle in the time domain of GPR and the objective function of FWI are briefly introduced, and the optimization algorithm formula and step size formula adopted in this paper are given. In this paper, multiscale inversion and TV regularization are used to optimize the inversion results. In the numerical examples, the comparison of multiscale inversion results and the comparison of results with different scale factors are given. In the numerical simulation, we use this method to simulate Arctic sea ice. Two sets of models are designed, which are inversion experiments of anomalous bodies with different scales and different physical parameters. Finally, we summarize the relevant conclusions of this method in the discussion and conclusion section, discuss the inversion results of Arctic sea ice, and point out the application prospects and limitations.
2. Methods
2.1. GPR Forward Modeling
In this paper, the finite difference time domain (FDTD) method is used to carry out grid subdivision of the electromagnetic field. For transverse electromagnetic waves (TMs), the difference form of the Maxwell curl equation is shown in the formulas
where and are the components of the magnetic field intensity in the x-axis and y-axis, respectively, and is the z-axis component of the electric field strength. The meaning of CA(m), CB(m), CP(m), and CQ(m) is as follows:
here, ε(m), σ(m), and μ(m) are the relative permittivity, conductivity, and permeability of point m, respectively, and is the time step.
In this paper, the Riker wavelet is selected as the excitation source. To eliminate the reflection of the boundary wave field, a convolution perfectly matched layer (CPML) is used to absorb the boundary.
2.2. Construction of FWI Misfit Function
The essence of GPR FWI is to reconstruct the distribution and structure closest to the real underground electrical parameters by using actual data, which is usually the permittivity and conductivity model. Algorithmically, by minimizing the observed data and simulated data, the optimal solution is gradually obtained in continuous iteration. The objective function is defined as
where N is the number of transmitting sources, M is the number of receiving points corresponding to each transmitting source, T is the time window length, is the spatial coordinate of the j-th receiver, is the observation data of the i-th source at , is the corresponding forward simulation data, and m is the model parameter:
Calculating the derivatives of the objective function with respect to the model parameters requires a large number of calculations, and to avoid the direct calculation of the Jacobi matrix, this paper adopts the first-order adjoint state method, which essentially uses the zero-delay intercorrelation of the forward and adjoint wave fields (the back-propagation of errors) to find the gradient. The gradient expression is given by
where is the adjoint wave field of .
Since FWI usually solves the problem of high dimensionality, it is difficult to apply the global optimization algorithm due to the large amount of calculation, so the local optimization method is usually adopted. Starting from the initial model , a new model is created by the local optimization algorithm. The model update is mainly divided into direction update and step update, among which the most critical problem lies in direction update. The model update expression is
where is the search step, is the search direction, and k is the number of iterations.
Local optimization methods are mainly divided into gradient-guided methods, Newton methods, and quasi-Newton methods. The Newton methods converge quickly and with high accuracy but need to calculate and store the Hessian matrix of the second derivative of the objective function. To avoid the direct calculation of the Hessian matrix, a quasi-Newton method is proposed, in which L-BFGS is considered to be a better coupled optimization algorithm in the quasi-Newton method, and its model updating quantity is
where is the approximation of the inverse Hessian matrix, and the updated formula of is
where , , , , is the initial inverse Hessian matrix, , and . After m recursions of Equation (11), the following can be obtained:
Therefore, it is only necessary to record the vector to construct according to the formula, in which m is 5.
After the direction is updated by the L-BFGS optimization algorithm, the step size also needs to be updated by line search. In this paper, the Wolfe criterion of imprecise line search is adopted, which needs to meet the following conditions:
where , = 10−4, and = 0.9.
Multiparameter inversion refers to the simultaneous inversion of two or more physical parameters, which can greatly improve the inversion efficiency. In GPR inversion, compared with the single inversion, the conductivity and permittivity are coupled with each other in dual-parameter inversion, and their values and dimensions are not uniform, which increases the difficulty of inversion. To ensure that the two are of the same order of magnitude, this paper adopts the conductivity unit as mS/m, and the method of Lavoué [23] is used to introduce dimensionless scaling factor β. β is a scale factor that can be adjusted according to the model to control the weight of conductivity in inversion, and a reasonable value can make the inversion quickly and statically obtain the optimal solution. In the inversion process, model parameter m is redefined as
2.3. Optimization Strategy
2.3.1. Multiscale Inversion Strategy
FWI is highly nonlinear and ill-posed. The nonlinearity is mainly manifested by the phenomenon of cycle skipping, which will occur when the synthesized recording time offset of the initial model is larger than half of the signal cycle. This phenomenon is more obvious in the high-frequency data. The low-frequency component of radar waves can construct large-scale background information and avoid the problem of cycle skipping in early inversion, while the high-frequency component describes the details of small structures. In this paper, a multiscale inversion strategy is adopted to improve the inversion accuracy. The inversion is carried out from low frequency to high frequency successively, and the inversion results of the previous frequency are used as the pilot model of the next frequency [40]. This multiscale inversion strategy can simultaneously use high and low frequencies to depict different scales and ensure the accuracy of inversion. Figure 1 shows the flow chart of the multiscale inversion strategy.
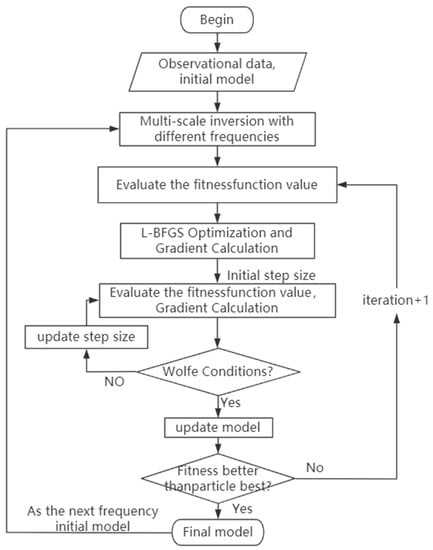
Figure 1.
Multiscale inversion strategy flow chart.
2.3.2. TV Regularization Inversion Strategy
For very large ill-conditioned systems, it is often impractical to directly implement regularization by filtering, since the representation requires the SVD of a large matrix. To further improve the inversion effect, TV regularization [30] constraint is used in the inversion, which can better improve the excessively smooth boundary than the common Tikhonov regularization method while preserving the edge information of the target [41]. After introducing TV regularization, a new objective function is obtained, and the expression is
where λ is the regularization factor, and TV is the TV regularization operator. Since the derivative of TV is not continuous, its differentiability can be guaranteed by the following formula approximation:
where Ω is the imaging region. The gradient of TV regularization is shown as follows:
The gradient expression of the new objective function is
where is the gradient of the data objective function, and is the objective function of the model parameters, which can be expressed as
3. Numerical Examples
3.1. Multiscale Inversion Strategy Experiment
To compare the inversion results caused by single-scale and multiscale strategies, a set of experiments were designed. The model is shown in Figure 2, with a length and width of 6 m × 6 m and a spatial step size of 0.05 m. The source function is a Ricker wavelet, the time step is 0.005 ns, and the time window length is 7.5 ns. The background is a homogeneous medium, whose relative permittivity is 4 and conductivity is 3 mS/m. Two crossover targets with different values are placed in the upper left corner and the lower right corner. The upper left corner target has a relative permittivity of 1 and a conductivity of 0 mS/m, while the lower right corner target has a relative permittivity of 8 and a conductivity of 10 mS/m. The distance between the observation system and the transceiver is shown in Figure 2, in which the distance between the sources is 1 m and the receivers is 0.2 m, uniformly arranged.

Figure 2.
Real model and collection setup: (a) relative permittivity model; (b) conductivity model. The red * represents the sources, and the black ◦ represents the receivers.
Three frequencies of 60 MHz, 100 MHz, and 200 MHz are selected for single-scale inversion. The initial model is a uniform background model with 50 iterations. The multiscale inversion uses the frequencies of multiple frequency bands, which are 60 MHz, 100 MHz, and 200 MHz successively from low to high. The initial model is a uniform background model, each frequency band is iterated 30 times, and the regularization factor λ = 1. There are two termination conditions for inversion, namely that the relative objective function k/0 is less than 1 × 10−4 or the step size is zero, and the termination conditions for subsequent experiments are the same.
The inversion results are shown in Figure 3 and Figure 4. It can be seen from the results that when single parameter inversion is adopted, the 60 MHz low-frequency single-scale inversion can depict the general background of the target body, but the detailed characterization is fuzzy, and the conductivity reconstruction is poor compared with the relative permittivity. The effect of 100 MHz frequency single-scale inversion is better than that of 60 MHz boundary remodeling, but there is still a certain gap with the original model, and the inversion boundary reconstruction is not accurate enough. It can be seen from the results of the 200 MHz high-frequency single-scale inversion that both the shape and value of the relative permittivity and conductivity are seriously deformed. The reconstruction of the upper left corner of the relative permittivity is good. However, due to the high frequency, it is more likely to produce the phenomenon of cycle skipping, so serious distortion occurs in the lower right corner of the relative permittivity, and the overall conductivity cannot be discernable. In the multiscale inversion results, we can see that both the shape and values of the relative permittivity are well reconstructed. Because the sensitivity of the physical property parameter of the conductivity is different from that of the relative permittivity, the inversion results show that the shape is roughly the same, but the boundary reconstruction is not sufficiently accurate.

Figure 3.
Inversion relative permittivity models of single frequencies and multiscale. (a) 60 MHz; (b) 100 MHz; (c) 200 MHz; (d) Multiscale inversion.

Figure 4.
Inversion conductivity models of single frequencies and multiscale. (a) 60 MHz; (b) 100 MHz; (c) 200 MHz; (d) Multiscale inversion.
3.2. The Influence of Regulatory Factor β
Due to the difference in the sensitivity of the permittivity and conductivity, the parametric adjustment factor β is introduced into the dual-parameter inversion to ensure stable convergence. The accuracy of dual-parameter inversion is affected by the difference in β values. To investigate the effect of β values on the results, a set of experiments are conducted. The values of β are 2, 2.5, 3, and 3.5. The real model is still selected in Figure 2, and the experimental data are the same as those in Section 3.1. The residual errors can be obtained as shown in Figure 5 and Figure 6. It can be seen from the figure that different values of β have little effect on the relative permittivity when the value is within the reasonable range. With increasing β, the conductivity continues to approach the true value. However, the value of beta has a certain range. When the value of beta is too large, the proportion of relative permittivity inversion decreases, which will lead to the shape and numerical distortion of the two physical parameters at the same time. Therefore, it is very important to select the appropriate value of beta.
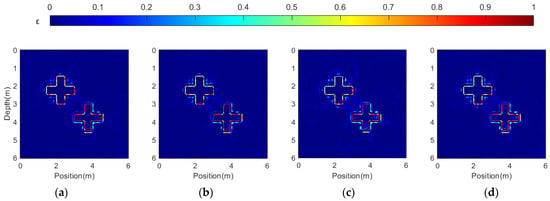
Figure 5.
Relative permittivity residual errors of different β values. (a) β = 2; (b) β = 2.5; (c) β = 3; (d) β = 3.5.

Figure 6.
Conductivity residual errors of different β values. (a) β = 2; (b) β = 2.5; (c) β = 3; (d) β = 3.5.
3.3. Sea Ice Inversion for Different Acquisition Setups
First, we need to model Arctic sea ice. Since most saltwater is expelled from the ice when it freezes, the conductivity of sea ice is generally approximately two orders of magnitude lower than that of the seawater that forms sea ice [42]. After a summer melt, the salt in the remaining ice will continue to drain out, resulting in lower conductivity with age [43] According to Archie’s law, the average conductivity of multiyear sea ice in the summer is 23 mS/m, while in the winter, it is 3 mS/m [44]. Based on the schematic diagram of the Arctic sea ice structure obtained by the 11th Chinese National Arctic Expedition [45], the research object of this paper is set as a three-layer structure. Generally, the longer the ice age is, the thicker the sea ice thickness is, and the more physical information it carries.
In a broad sense, sea ice is a mixture of freshwater ice crystals, “brine”, and bubbles containing salt, in which the size of the bubbles is different, and the proportion of air, ice crystals, and salt water is different, thus forming an abnormal body with different physical parameters. The abnormal body is the search object, and we set the abnormal body with different sizes and physical property parameters. The detection of these anomalies can be used for the study of sea ice dynamics, sea ice mass balance, sea ice stability, and subglacial environment.
In this paper, three acquisition setups are used to perform inversion tests on Arctic sea ice, which are provided as shown in Figure 7. To select the optimal acquisition setup, we placed anomalous bodies of three different scales in each layer of the three-layer sea ice model. The calculation area of the model is 5 m long and 2.4 m deep, in which the air layer is 0.2 m, the space grid used for forward modeling is 0.02 m, the time step is 0.003 ns, and the length of the time window is 9 ns. The distances between the sources and the receivers are 0.4 m and 0.08 m, and the center frequencies are 100 MHz, 200 MHz, and 400 MHz, respectively. The source function is a Ricker wavelet, and the observation mode is multi-offset measurement.

Figure 7.
Acquisition setup and true models: (a) relative permittivity model; (b) conductivity model. Acquisition setup ①: red * represents the sources, and black ◦ represents the receivers. Acquisition setup ②: yellow * represents the sources, and white ◦ represents the receivers. Acquisition setup ③ is the combination of setups ① and ②.
Considering the distance between sea ice and seawater, the relative permittivities of ice from top to bottom are 4, 5, and 6, and the conductivities are 3 mS/m, 4 mS/m, and 5 mS/m. The central burial depths of the anomalous body are 0.3 m, 1 m, and 1.7 m, and the radii from large to small are 0.14 m, 0.1 m, and 0.06 m. The relative permittivity is 15, and the conductivity is 12 mS/m. The real model and observation system are shown in Figure 7. A uniform background field with seawater is adopted as the initial model, with a relative permittivity value of 5 and conductivity value of 4 mS/m. The corresponding center frequency inversion iteration times are 50, 80, and 80, successively; the regularization factor is 1; and the β value is 5. In order to compare the effects of different acquisition setup, the reconstruction error calculation formula is defined as . From top to bottom, the relative permittivity reconstruction errors are 0.0574, 0.0982, and 0.00226, and conductivity is 0.8001, 0.8001, and 0.8, respectively.
The inversion results of different acquisition setups are shown in Figure 8, Figure 9 and Figure 10 and it is obvious from the figures that the relative permittivity inversion is better than the conductivity inversion. From Figure 8, the relative permittivity of the bottom layer cannot be reconstructed in the inversion result of acquisition setup ①, and the conductivity can show the location of the anomalies but cannot reconstruct the shape. In Figure 9, the relative permittivity of the middle layer in the inversion result of acquisition setup ② cannot be reconstructed, the anomalies are almost invisible in the conductivity inversion result, and there are many artifacts. Figure 10 shows the inversion results of acquisition setup ③. Compared with the first two inversion results, the shape and scale of the anomalies and the ice layer interface are clearly visible in the relative permittivity inversion results, and the structure and values are not much different from the real model, even though the smallest anomalies in the bottom layer can obtain clear inversion results. The structure of the top layer of conductivity is clear, and the values of the middle and bottom layers deviate with increasing depth but still reflect the shape and scale of the anomalies.

Figure 8.
Inversion models of acquisition setup ①. (a) Relative permittivity inversion diagram; (b) conductivity inversion diagram.

Figure 9.
Inversion models of acquisition setup ②. (a) Relative permittivity inversion diagram; (b) conductivity inversion diagram.

Figure 10.
Inversion models of acquisition setup ③. (a) Relative permittivity inversion diagram; (b) conductivity inversion diagram.
More comparative details can be found in the horizontal sections at depths of 0.3 m and 1 m in Figure 11, where slices of the anomalous body are captured at each level. It can be seen from the details of the three acquisition schemes that even if there is a deviation between the initial model and the real model, acquisition setup ③ has the best inversion result, while the other schemes all produce strong perturbations.
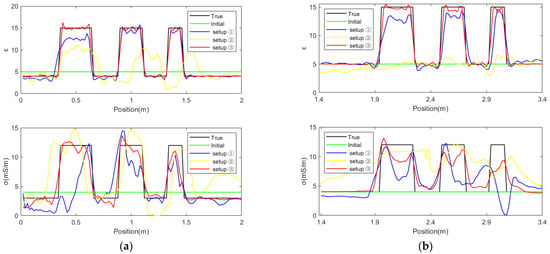
Figure 11.
Inversion relative permittivity and conductivity with different acquisition setups. (a) The top anomalous body section; (b) the middle anomalous body section.
Figure 12 shows the convergence curves of the normalized objective functions of different acquisition setups, selecting the parameters of the last 80 iterations of the multiscale inversion with a center frequency of 400 MHz. It can be seen from the figure that all setups converge to the real model as the number of iterations increases, with the fastest convergence in the first 10 iterations and then leveling off. The step size of acquisition setup ① is zero at the number of iterations of 57, the inversion ends early, and the final acquisition setup ③ is closest to the real model.

Figure 12.
Misfit curves of different acquisition setups.
3.4. Sea Ice Inversion for Different Materials
The calculation area of the model in this section is 2.4 m long and 2.4 m deep, the air layer is 0.2 m, the spatial grid used for the orthorectification is 0.02 m, the time step is 0.003 ns, and the length of the time window is 6 ns. The distances between the sources and the receivers are 0.4 m and 0.08 m, and the center frequencies are 100 MHz, 200 MHz, and 400 MHz. The surface acquisition is evenly distributed at the horizontal distance of 0.2–2.2 m, and the underground acquisition is evenly distributed at the depth of 0–1.8 m with horizontal positions of 0.2 m and 2.2 m. Relative permittivities from top to bottom are 4, 6, and 8, and conductivities are 3 mS/m, 4 mS/m, and 5 mS/m. The burial depths of the anomaly are 0.3 m, 1 m, and 1.7 m; the radius is 0.1 m; and the relative permittivity and conductivity from left to right are 1, 3, 9, 12, 15, and 0 mS/m, 2 mS/m, 6 mS/m, 10 mS/m, 15 mS/m. First of all, the abnormal body containing gas is the one with the lowest permittivity and conductivity, which mostly occurs when there is methane overflow from the sea floor while the ice surface is still freezing. At this time, the sea ice will trap and freeze the methane gas in the ice. By detecting the number and size of the abnormal body, we can provide a basis for the study of the methane in the sea floor. Secondly, when the interior of the ice body is not completely frozen, or partial melting occurs in the melting period, the abnormal body is produced. Because the proportion of freshwater ice crystals, brine, and bubbles in sea ice is different, their conductivity and permittivity values are often different. For example, saltwater channels exist in sea ice, which leads to the discharge of part of seawater outside the ice. At this time, the value of anomalous bodies containing bubbles will be lower than that of sea ice. When seawater is not discharged outside the ice but inside the ice, the value of different anomalous bodies in the proportion of seawater will also change, and the higher the proportion of seawater is, the greater the conductivity and permittivity value are. The real model is shown in Figure 13 and Figure 14, and we use a single physical parameter with seawater as the initial model, where the relative permittivity value is 6; the conductivity value is 4 mS/m; the number of inversion iterations is 30, 50, and 50, in that order; the regularization factor is 1; and the β value is 5.

Figure 13.
Realistic models of anomalous bodies with different relative permittivity. (a) The anomalous body model at the top level; (b) the anomalous body model at the middle level; (c) the anomalous body model at the bottom level.

Figure 14.
Realistic models of anomalous bodies with different conductivities. (a) The anomalous body model at the top level; (b) the anomalous body model at the middle level; (c) the anomalous body model at the bottom level.
The inversion results corresponding to different ice layers are shown in Figure 15 and Figure 16. From left to right, the relative permittivity reconstruction errors are 0.0186, 0.0189, and 0.0189, and the conductivity reconstruction errors are 0.0013, 0.0020, and 0.0021. In general, the inversion results of relative permittivity are superior to those of conductivity. Since the background field values of the initial model and the real model are different, more uncertainties will be brought to the inversion. However, in the inversion results of the relative permittivity, the values, and interfaces of the three layers of the ice layer are well reconstructed, and the values, shapes, and positions of abnormal bodies with different physical parameters in each layer are almost consistent with the real model. Conductivity inversion can generally distinguish the interface and value of each ice layer, but the resolution decreases with increasing depth, and artifacts appear in the underlying background.

Figure 15.
Inversion relative permittivity models. (a) The anomalous body model at the top level; (b) the anomalous body model at the middle level; (c) the anomalous body model at the bottom level.

Figure 16.
Inversion conductivity models. (a) The anomalous body model at the top level; (b) the anomalous body model at the middle level; (c) the anomalous body model at the bottom level.
In Figure 16, the inversion of the conductivity of the anomalous body in the top ice layer is optimal, and its shape and value are well reconstructed. However, as the electromagnetic wave energy weakens with increasing depth, the conductivity obtained by inversion begins to deviate. The inversion effect of the anomalous body is the worst in the bottom ice. In addition to the inaccuracy of the initial model and the weakening of the electromagnetic wave, the huge difference in parameters between the bottom seawater and the ice sheet also has some effects.
To better see the difference between the inversion results and real data from the details, we cut three horizontal sections from the center of abnormal bodies with different depths, as shown in Figure 17, where the black line is the real model, the green is the pilot model, and the blue is the inversion result. There are numerical differences between our initial model and the real model, and the full waveform inversion is extremely dependent on the accuracy of the initial model. However, it can be seen intuitively from the horizontal profile that the inversion results of the relative permittivity are basically consistent with the real model, and the inversion results can also be good when the relative permittivity of the abnormal body is similar to the background value. The conductivity inversion results deviate with increasing depth. When the anomalous body parameters are similar to the background values, they cannot be well identified. However, anomalous bodies with large numerical differences can still be identified. There are two peaks in the conductivity values on the left and right sides of the bottom inversion, which are caused by the inaccurate inversion values of the receiving point position.

Figure 17.
Section of different depth relative permittivity and conductivity at the center of the anomalous body. (a) The top anomalous body section; (b) the middle anomalous body section; (c) the bottom anomalous body section. The first layer is the relative permittivity value, and the second layer is the conductivity value.
4. Discussion
In this paper, the multiscale dual-parameter FWI of the cross model is first carried out to realize the simultaneous inversion of the conductivity and relative permittivity. The low-frequency to high-frequency multiscale inversion strategy is adopted, and the low-frequency inversion results are taken as the initial model, which can avoid the inversion falling into the local extreme value. At the same time, to solve the numerical difference between conductivity and relative permittivity, this paper introduces the parameter regulating factor β and conducts experiments. The results show that the regulating factor can directly affect the accuracy of conductivity, so it is very important to select the appropriate regulating factor.
Subsequently, different sea ice models were designed. To explore the impact of the acquisition setup on the inversion results, we conducted experiments on anomalous bodies with different scales at different depths. Three acquisition setups are used to collect data. It can be seen from the inversion results and the profile comparison diagram that the combined collection scheme has the best effect because it receives more information about the ice sheet. Subsequently, this paper uses a combination acquisition setup to perform inversion experiments on abnormal body models with different physical property parameters at different depths. The experimental results show that the proposed method can well identify anomalous bodies with different physical property parameters at different depths. The profile shows that the relative permittivity can well distinguish the anomalous body with little difference from the background field value, which verifies the rationality of the proposed method. However, the method in this paper still has some shortcomings. For example, when the logging distance is too far, the deep-depth information cannot be collected perfectly, resulting in a certain deviation of the conductivity value.
5. Conclusions
In this paper, the dual-parameter FWI of GPR is used to invert the Arctic sea ice model, and a parametric adjustment factor is introduced to realize the weight of synchronous inversion of relative permittivity and conductivity. The numerical simulation results show that the different parameter factors lead to different conductivity inversion results. The appropriate parameter regulating factor can obtain better conductivity results. To avoid the direct calculation of the Hessian matrix, the L-BFGS optimization algorithm is used to update the model, and the Wolfe criterion of inexact line search is used to update the step size. The FWI of GPR is highly inappropriate. In this paper, a multiscale inversion strategy is adopted, and three center frequencies from low to high are selected for inversion to avoid the local extreme value problem of inversion. The advantages of multiscale inversion can be seen from the inversion results. At the same time, the TV regularization constraint is used to further improve the inversion effect so that the inversion results are closer to the real model to achieve stable convergence.
Both the relative permittivity and conductivity are reconstructed well using the proposed method. It is worth noting that the proposed method has satisfactory fault tolerance performance for the initial model. This paper shows that in addition to the migration imaging method, FWI can provide more accurate values and shapes of subsurface anomalies and provide more reliable evidence for the study of Arctic sea ice.
Author Contributions
Conceptualization, M.L. and Y.L.; methodology, M.L. and Y.L.; software, Y.L.; validation, M.L. and Y.L.; writing—original draft preparation, M.L.; writing—review and editing, Y.L.; visualization, M.L.; supervision, Y.L., Y.Y. and J.X.; project administration, Y.L. and M.L.; funding acquisition, Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key R&D Program of China (2021YFC2801202, 2022YFC2808302), National Natural Science Foundation of China (42274104), and the Fundamental Research Funds for the Central Universities (202262012).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Serreze, M.C.; Barrett, A.P.; Stroeve, J.C.; Kindig, D.N.; Holland, M.M. The Emergence of Surface-Based Arctic Amplification. Cryosphere 2009, 3, 11–19. [Google Scholar] [CrossRef]
- Persico, R.; Colica, E.; Zappatore, T.; Giardino, C.; D’Amico, S. Ground-Penetrating Radar and Photogrammetric Investigation on Prehistoric Tumuli at Parabita (Lecce, Italy) Performed with an Unconventional Use of the Position Markers. Remote Sens. 2022, 14, 1280. [Google Scholar] [CrossRef]
- Liu, H.; Shi, Z.; Li, J.; Liu, C.; Meng, X.; Du, Y.; Chen, J. Detection of Road Cavities in Urban Cities by 3D Ground-Penetrating Radar. Geophysics 2021, 86, WA25–WA33. [Google Scholar] [CrossRef]
- Saarenketo, T.; Scullion, T. Road Evaluation with Ground Penetrating Radar. J. Appl. Geophys. 2000, 43, 119–138. [Google Scholar] [CrossRef]
- Solla, M.; González-Jorge, H.; Varela, M.; Lorenzo, H. Ground-Penetrating Radar for Inspection of In-Road Structures and Data Interpretation by Numerical Modeling. J. Constr. Eng. Manag. 2013, 139, 749–753. [Google Scholar] [CrossRef]
- Liu, Y.; Li, H.; Huang, M.; Chen, D.; Zhao, B. Ice Crevasse Detection with Ground Penetrating Radar Using Faster R-CNN. In Proceedings of the 2020 15th IEEE International Conference on Signal Processing (ICSP), Beijing, China, 6–9 December 2020; Volume 1, pp. 596–599. [Google Scholar] [CrossRef]
- Klotzsche, A.; Jonard, F.; Looms, M.C.; van der Kruk, J.; Huisman, J.A. Measuring Soil Water Content with Ground Penetrating Radar: A Decade of Progress. Vadose Zone J. 2018, 17, 1–9. [Google Scholar] [CrossRef]
- Galley, R.J.; Trachtenberg, M.; Langlois, A.; Barber, D.G.; Shafai, L. Observations of Geophysical and Dielectric Properties and Ground Penetrating Radar Signatures for Discrimination of Snow, Sea Ice and Freshwater Ice Thickness. Cold Reg. Sci. Technol. 2009, 57, 29–38. [Google Scholar] [CrossRef]
- Annan, A.P.; Diamanti, N.; Redman, J.D.; Jackson, S.R. Ground-Penetrating Radar for Assessing Winter Roads. Geophysics 2016, 81, WA101–WA109. [Google Scholar] [CrossRef]
- Fantello, N.; Parsekian, A.D.; Walter Anthony, K.M. Estimating Winter Ebullition Bubble Volume in Lake Ice Using Ground-Penetrating Radar. Geophysics 2018, 83, H13–H25. [Google Scholar] [CrossRef]
- Bradford, J.H.; Babcock, E.L.; Marshall, H.-P.; Dickins, D.F. Targeted Reflection-Waveform Inversion of Experimental Ground-Penetrating Radar Data for Quantification of Oil Spills under Sea Ice. Geophysics 2016, 81, WA59–WA70. [Google Scholar] [CrossRef]
- Cooke, D. Generalized Linear Inversion of Reflection Seismic Data. Geophysics 1983, 48, 665–676. [Google Scholar] [CrossRef]
- Tarantola, A. Inversion of Seismic Reflection Data in the Acoustic Approximation. Geophysics 1984, 49, 1259–1266. [Google Scholar] [CrossRef]
- Pratt, R.G. Inverse theory applied to multi-source cross-hole tomography: Part 2: Elastic wave-equation method1. Geophys. Prospect. 1990, 38, 311–329. [Google Scholar] [CrossRef]
- Sirgue, L.; Etgen, J.; Albertin, U. 3D Frequency Domain Waveform Inversion Using Time Domain Finite Difference Methods. In Proceedings of the 70th EAGE Conference and Exhibition incorporating SPE EUROPEC 2008, Rome, Italy, 9–12 June 2008. [Google Scholar] [CrossRef]
- Pratt, R.G. Seismic waveform inversion in the frequency domain, Part 1: Theory and verification in a physical scale model. Geophysics 1999, 64, 888–901. [Google Scholar] [CrossRef]
- Shin, C.; Cha, Y.H. Waveform Inversion in the Laplace Domain. Geophys. J. Int. 2008, 173, 922–931. [Google Scholar] [CrossRef]
- El Bouajaji, M.; Lanteri, S.; Yedlin, M. Discontinuous Galerkin Frequency Domain Forward Modelling for the Inversion of Electric Permittivity in the 2D Case. Geophys. Prospect. 2011, 59, 920–933. [Google Scholar] [CrossRef]
- Meles, G.A.; Van Der Kruk, J.; Greenhalgh, S.A.; Ernst, J.R.; Maurer, H.; Green, A.G. A New Vector Waveform Inversion Algorithm for Simultaneous Updating of Conductivity and Permittivity Parameters from Combination Crosshole/Borehole-to-Surface GPR Data. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3391–3407. [Google Scholar] [CrossRef]
- Ren, Q. Inverts Permittivity and Conductivity with Structural Constraint in GPR FWI Based on Truncated Newton Method. J. Appl. Geophys. 2018, 151, 186–193. [Google Scholar] [CrossRef]
- Métivier, L.; Bretaudeau, F.; Brossier, R.; Operto, S.; Virieux, J. Full Waveform Inversion and the Truncated Newton Method: Quantitative Imaging of Complex Subsurface Structures. Geophys. Prospect. 2014, 62, 1353–1375. [Google Scholar] [CrossRef]
- Jorge, N.; Stefen, W. Numerical Optimization; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Lavoué, F.; Brossier, R.; Métivier, L.; Garambois, S.; Virieux, J. Two-Dimensional Permittivity and Conductivity Imaging by Full Waveform Inversion of Multioffset GPR Data: A Frequency-Domain Quasi-Newton Approach. Geophys. J. Int. 2014, 197, 248–268. [Google Scholar] [CrossRef]
- Nilot, E.; Feng, X.; Zhang, Y.; Zhang, M.; Dong, Z.; Zhou, H.; Zhang, X. Multiparameter Full-Waveform Inversion of on-Ground GPR Using Memoryless Quasi-Newton (MLQN) Method. In Proceedings of the 2018 17th International Conference on Ground Penetrating Radar (GPR), Rapperswil, Switzerland, 18–21 June 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Virieux, J.; Operto, S. An Overview of Full-Waveform Inversion in Exploration Geophysics. Geophysics 2009, 74, WCC1–WCC26. [Google Scholar] [CrossRef]
- Meles, G.A.; Greenhalgh, S.; Maurer, H.R.; Green, A.G.; van der Kruk, J. GPR Full Waveform Sensitivity and Resolution Analysis Using an FDTD Adjoint Method. In Proceedings of the 2011 6th International Workshop on Advanced Ground Penetrating Radar (IWAGPR), Aachen, Germany, 22–24 June 2011; pp. 1–6. [Google Scholar] [CrossRef]
- Zhou, Z.; Klotzsche, A.; Hu, J.; Vereecken, H. Using Low-Wavenumber Information in Crosshole GPR FWI by Considering Angle Difference Identity with Cosine Approach: A Synthetic Study. In First International Meeting for Applied Geoscience & Energy Expanded Abstracts; Society of Exploration Geophysicists: Tulsa, OK, USA, 2021; pp. 553–557. [Google Scholar] [CrossRef]
- Jin, Y.; Zi, Y.; Wu, X.; Chen, J. An Enhanced GPR FWI Scheme with Low-Frequency Data Extrapolated by Progressive Transfer Learning. In Proceedings of the 2022 IEEE USNC-URSI Radio Science Meeting (Joint with AP-S Symposium), Denver, CO, USA, 10–15 July 2022; pp. 120–121. [Google Scholar] [CrossRef]
- Fu, C.; Jiang, Y.; Xie, Z.; Li, X.; Li, Y.; Li, K.; Zhao, Y.; Zhang, F.; Jiang, P. Full Waveform Inversion of Common-Offset Ground-Penetrating Radar Based on a Special Source Wavelet and Multiple Integral Wave-Field Transform. J. Appl. Geophys. 2022, 206, 104795. [Google Scholar] [CrossRef]
- Vogel, C.R. Computational Methods for Inverse Problems. In Computational Methods for Inverse Problems; Frontiers in Applied Mathematics; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2002; pp. 129–150. [Google Scholar] [CrossRef]
- Feng, D.; Wang, X.; Zhang, B. A Frequency-Domain Quasi-Newton-Based Biparameter Synchronous Imaging Scheme for Ground-Penetrating Radar with Applications in Full Waveform Inversion. IEEE Trans. Geosci. Remote Sens. 2021, 59, 1949–1966. [Google Scholar] [CrossRef]
- Wang, X.; Feng, D. Multiparameter Full-Waveform Inversion of 3-D On-Ground GPR with a Modified Total Variation Regularization Scheme. IEEE Geosci. Remote Sens. Lett. 2021, 18, 466–470. [Google Scholar] [CrossRef]
- Feng, D.; Liu, Y.; Wang, X.; Ding, S. Efficient Source-Independent Full Waveform Dual-Parameter Inversion of Common-Offset GPR Data. J. Appl. Geophys. 2023, 208, 104891. [Google Scholar] [CrossRef]
- Mozaffari, A.; Klotzsche, A.; Warren, C.; He, G.; Giannopoulos, A.; Vereecken, H.; van der Kruk, J. 2.5D Crosshole GPR Full-Waveform Inversion with Synthetic and Measured Data. Geophysics 2020, 85, H71–H82. [Google Scholar] [CrossRef]
- Liu, B.; Ren, Y.; Liu, H.; Xu, H.; Wang, Z.; Cohn, A.G.; Jiang, P. GPRInvNet: Deep Learning-Based Ground-Penetrating Radar Data Inversion for Tunnel Linings. IEEE Trans. Geosci. Remote Sens. 2021, 59, 8305–8325. [Google Scholar] [CrossRef]
- Liu, X.; Liu, S.; Luo, C.; Jiang, H.; Li, H.; Meng, X.; Feng, Z. Source-Independent Waveform Inversion Method for Ground Penetrating Radar Based on Envelope Objective Function. Remote Sens. 2022, 14, 4878. [Google Scholar] [CrossRef]
- Liu, T.; Klotzsche, A.; Pondkule, M.; Vereecken, H.; Su, Y.; Van Der Kruk, J. Radius Estimation of Subsurface Cylindrical Objects from Ground-Penetrating-Radar Data Using Full-Waveform Inversion. Geophysics 2018, 83, H43–H54. [Google Scholar] [CrossRef]
- Feng, D.; Ding, S.; Wang, X.; Su, X.; Liu, S.; Cao, C. Wavefield Reconstruction Inversion Based on the Multi-Scale Cumulative Frequency Strategy for Ground-Penetrating Radar Data: Application to Urban Underground Pipeline. Remote Sens. 2022, 14, 2162. [Google Scholar] [CrossRef]
- Feng, D.; Liu, Y.; Wang, X.; Zhang, B.; Ding, S.; Yu, T.; Li, B.; Feng, Z. Inspection and Imaging of Tree Trunk Defects Using GPR Multifrequency Full-Waveform Dual-Parameter Inversion. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5903715. [Google Scholar] [CrossRef]
- Meles, G.; Greenhalgh, S.; Der Kruk, J.V.; Green, A.; Maurer, H. Taming the Non-Linearity Problem in GPR Full-Waveform Inversion for High Contrast Media. J. Appl. Geophys. 2011, 73, 174–186. [Google Scholar] [CrossRef]
- Dai, Q.; Zhang, H.; Zhang, B. An Improved Particle Swarm Optimization Based on Total Variation Regularization and Projection Constraint with Applications in Ground-Penetrating Radar Inversion: A Model Simulation Study. Remote Sens. 2021, 13, 2514. [Google Scholar] [CrossRef]
- Pfaffling, A.; Haas, C.; Reid, J.E. Direct Helicopter EM—Sea-Ice Thickness Inversion Assessed with Synthetic and Field Data. Geophysics 2007, 72, F127–F137. [Google Scholar] [CrossRef]
- Rodriguez-Alvarez, N.; Holt, B.; Jaruwatanadilok, S.; Podest, E.; Cavanaugh, K.C. An Arctic Sea Ice Multi-Step Classification Based on GNSS-R Data from the TDS-1 Mission. Remote Sens. Environ. 2019, 230, 111202. [Google Scholar] [CrossRef]
- Haas, C.; Gerland, S.; Eicken, H.; Miller, H. Comparison of Sea-ice Thickness Measurements under Summer and Winter Conditions in the Arctic Using a Small Electromagnetic Induction Device. Geophysics 1997, 62, 749–757. [Google Scholar] [CrossRef]
- Xing, J.; Song, R.; Zhen, S.; Jiang, X. Construction of the Central Arctic Sea Ice Structure and Acoustic Velocity Model at the Short-Term Ice Station During N11 CHINARE. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5906307. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).