Estimation of Winter Wheat SPAD Values Based on UAV Multispectral Remote Sensing

Abstract

Unmanned aerial vehicle (UAV) multispectral imagery has been applied in the remote sensing of wheat SPAD (Soil and Plant Analyzer Development) values. However, existing research has yet to consider the influence of different growth stages and UAV flight altitudes on the accuracy of SPAD estimation. This study aims to optimize UAV flight strategies and incorporate multiple feature selection techniques and machine learning algorithms to enhance the accuracy of the SPAD value estimation of different wheat varieties across growth stages. This study sets two flight altitudes (20 and 40 m). Multispectral images were collected for four winter wheat varieties during the green-up and jointing stages. Three feature selection methods (Pearson, recursive feature elimination (RFE), and correlation-based feature selection (CFS)) and four machine learning regression models (elastic net, random forest (RF), backpropagation neural network (BPNN), and extreme gradient boosting (XGBoost)) were combined to construct SPAD value estimation models for individual growth stages as well as across growth stages. The CFS-RF (40 m) model achieved satisfactory results (green-up stage: R² = 0.7270, RPD = 2.0672, RMSE = 1.1835, RRMSE = 0.0259; jointing stage: R² = 0.8092, RPD = 2.3698, RMSE = 2.3650, RRMSE = 0.0487). For cross-growth stage modeling, the optimal prediction results for SPAD values were achieved at a flight altitude of 40 m using the Pearson-XGBoost model (R² = 0.8069, RPD = 2.3135, RMSE = 2.0911, RRMSE = 0.0442). These demonstrate that the flight altitude of UAVs significantly impacts the estimation accuracy, and the flight altitude of 40 m (with a spatial resolution of 2.12 cm) achieves better SPAD value estimation than that of 20 m (with a spatial resolution of 1.06 cm). This study also showed that the optimal combination of feature selection methods and machine learning algorithms can more accurately estimate winter wheat SPAD values. In addition, this study includes multiple winter wheat varieties, enhancing the generalizability of the research results and facilitating future real-time and rapid monitoring of winter wheat growth.

1. Introduction

Wheat is one of the most important cereal crops worldwide. Chlorophyll, as the primary pigment involved in photosynthesis, plays a crucial role in crop growth and nitrogen utilization efficiency by capturing sunlight energy. Chlorophyll content changes impact crops’ growth status and nitrogen utilization efficiency directly [1]. The green-up stage corresponds to Zadoks scale stages 25–30 [2], which is the second peak of tillering in wheat, during which the number of tillers increases by 30–40%. During this growth stage, the chlorophyll content plays a crucial role in determining wheat’s future growth rate and final yield [3]. The jointing stage corresponds to Zadoks scale stages 30–32 [2], when wheat enters a crucial phase of combined vegetative and reproductive growth and spike differentiation. This stage is highly sensitive to water and fertilizer conditions [4,5]. Therefore, the precise monitoring of chlorophyll content during the green-up and jointing stages of winter wheat is of significant practical importance.

Traditional methods of measuring crop chlorophyll content rely on chemical analysis, which is destructive, time consuming, costly, and prone to measurement inaccuracies due to the light degradation of extracted chlorophyll from plant leaves [6]. Using the SPAD-502Plus chlorophyll meter (Konica Minolta, Tokyo, Japan), plant leaves’ relative chlorophyll content (Soil and Plant Analyzer Development, SPAD) can be nondestructively measured in field conditions [7]. The SPAD values have a significant correlation with wheat leaf chlorophyll content and serve as a key indicator for assessing plant photosynthesis and nitrogen status [8,9,10]. The timely acquisition of SPAD values can provide the basis for a rapid fertilization diagnosis and play an important role in monitoring wheat growth and regulating water and nutrient management [11,12,13,14]. However, the SPAD-502Plus device can only work on a limited number of measurement points, making it difficult to achieve large-scale accurate measurements in space [15].

Satellite remote sensing enables large-scale, rapid, and nondestructive monitoring of crop SPAD values. However, its limitations include long revisiting periods and low spatial resolution [16]. In contrast, UAV-based remote sensing technology has gained increasing attention in crop monitoring and yield prediction due to its advantages of flexible image acquisition time, high spatial resolution, and low cost [17]. In particular, UAV platforms equipped with multispectral cameras have attracted considerable attention due to their low cost, ease of deployment, and high spectral and spatial resolution capabilities [18].

In recent years, many researchers have conducted studies on the estimation of chlorophyll content in wheat using unmanned aerial vehicle (UAV) multispectral imagery, and numerous studies have shown the promising application prospects of UAV multispectral remote sensing technology in wheat chlorophyll estimation. Wang et al. [19] utilized UAV to capture multispectral images of winter wheat during the overwintering stage, extracted the reflectance of five single spectral bands, calculated 31 spectral vegetation indices (VIs), and developed a winter wheat overwintering stage SPAD value estimation model based on the RF-SVR_sigmoid model, providing an effective method for variety screening of late-sown winter wheat. Han et al. [20] studied the potential application of UAV multispectral imagery in predicting winter wheat SPAD values, leaf area index (LAI), and yield under different water treatments (low, medium, and high water levels). They used VIs extracted from UAV multispectral images during the critical growth stages of winter wheat and compared the estimation performance of different models (linear regression, quadratic polynomial regression, exponential, and multiple linear regression models) based on VIs. They found that multiple linear regression could accurately estimate winter wheat SPAD, LAI, and yield under different water treatments. Wu et al. [10] collected multispectral images of wheat at different nitrogen application levels using the DJI P4M UAV (the DJI Phantom 4 Multispectral UAV) after the jointing stage and constructed 26 multispectral VIs. They used four machine learning algorithms to build SPAD estimation models at different time points during the heading stage. The results showed that the optimal SPAD estimation models varied for different growth stages of wheat. By selecting multiple vegetation indices as input variables and using the partial least squares algorithm, the accuracy of SPAD estimation can be significantly improved, especially 14 days after heading.

Although previous studies have demonstrated the powerful capabilities of UAV-based multispectral imagery combined with different vegetation indices, feature selection methods, and machine learning algorithms in predicting chlorophyll content [21,22], most of the existing research has focused on SPAD value estimation during individual growth stages. Compared to single-stage models, it is more practical to establish models that can estimate SPAD values across multiple growth stages in agricultural production. There is a pressing need to investigate the combination of different feature selection methods and machine learning regression algorithms to develop a comprehensive approach for SPAD value estimation applicable to different growth stages of crops.

Before conducting UAV remote sensing monitoring, it is necessary to optimize the flight parameters of the UAV. Currently, the setting of flight parameters mostly relies on empirical rules, especially when determining flight altitude, which is usually manually set to ensure flight safety, obstruction-free imaging, and minimal disturbance to crops caused by wind. However, this approach often fails to maximize the utilization efficiency of the sensing equipment, leading to increased experimental costs and resource consumption [23]. Furthermore, UAV images captured at different flight altitudes have varying spatial resolutions. Logically, acquiring multispectral images at higher altitudes may result in decreased image details, thus affecting the accuracy of information extraction from the images [24]. However, research has indicated that a higher image resolution is only sometimes beneficial for improving the accuracy of spectral information extraction. The resolution should match the ground samples, and the flight altitude affecting image resolution should be optimized to achieve better data fitting [25]. Existing studies have yet to consider the influence of UAV flight altitude on the accuracy of estimating crop parameters such as SPAD values.

In conclusion, it is crucial to investigate the effects of different growth stages of winter wheat and UAV flight altitudes on the accuracy of SPAD value estimation using UAV-based multispectral remote sensing. Therefore, this study hypothesizes that by optimizing UAV flight strategies and incorporating multiple feature selection techniques and machine learning algorithms, the accuracy of estimating winter wheat SPAD values using UAV-based multispectral remote sensing can be improved.

To test this hypothesis, this study focuses on winter wheat and selects two key growth stages, namely, the greening and jointing stages. Different flight altitudes are set to collect UAV multispectral imagery and ground measurements during the same period. Various feature selection methods are employed to determine the appropriate vegetation indices for SPAD value estimation in winter wheat. These indices are then combined with machine learning algorithms to construct and determine the optimal SPAD value estimation models suitable for both winter wheat’s single and multiple growth stages. Moreover, considering the limited research on crop-specific SPAD value estimation using remote sensing, especially for different winter wheat varieties, which significantly influence agricultural remote sensing models [26], this study includes multiple winter wheat varieties to enhance the universality of the research findings.

2. Materials and Methods

2.1. Experimental Site and Design

The experiment was conducted during the 2022–2023 winter wheat growing season at the Jiangyan District of Taizhou City in Jiangsu Province, China, specifically at the Jiangsu Modern Agricultural Science and Technology Comprehensive Demonstration Base (32°34’23.43”N, 120°5’25.80”E), as shown in Figure 1. The field for the experiment consisted of a total of 72 plots, with the first 48 plots designated for Experiment 1 and the remaining 24 plots for Experiment 2. Both experiments focused on the management of nitrogen fertilizer for winter wheat, but they differed in terms of the research subjects and design plans.

In Experiment 1, four different varieties of wheat (Yangmai 25, Yangmai 39, Ningmai 26, and Yangmai 22) were selected. As Yangmai 25 and Yangmai 39 are nitrogen-efficient varieties, while Yangmai 22 and Yangmai 26 are nitrogen-inefficient varieties, the relationship between canopy SPAD values and spectral variables is highly complex for these four winter wheat varieties at different growth stages. These will enhance the universality of the research findings. Four nitrogen fertilizer treatments were applied, including a control group with 0 kg/ha and treatment groups with pure nitrogen fertilizer rates of 150 kg/ha, 240 kg/ha, and 330 kg/ha. The experiment utilized a split-plot design, with nitrogen fertilizer treatments as the main plots and varieties as the subplots. The nitrogen fertilizer management followed a specific schedule: basal fertilizer, tillering fertilizer, jointing fertilizer, and heading fertilizer were applied at a ratio of 5:1:2:2. The basal fertilizer was applied before rotary tillage and sowing, the tillering fertilizer was applied at the three-leaf stage of wheat, and the jointing fertilizer was applied when the wheat had a leaf stage residue of 2.5. The heading fertilizer was applied when the wheat had a leaf stage residue of 0.8. The phosphorus and potassium fertilizers were applied as P₂O₅ and K₂O, respectively, with a pure phosphorus and potassium rate of 135 kg/ha for all treatments, applied as a one-time basal application. The wheat was sown in rows with a spacing of 25 cm using manual trenching. Each plot had an area of 12 m², and the experiment was replicated three times. A plant count was conducted at the two-leaf stage, with a target plant density of 240,000 plants/ha. Other field management measures followed standard practices.

In Experiment 2, two different varieties of wheat (Yangmai 39 and Yangmai 22) were selected. Four different nitrogen fertilizer application methods were used, including broadcast application, furrow application, and spaced furrow application. Two nitrogen fertilizers, urea and resin-coated urea, were used with a nitrogen application rate of 240 kg/ha. The experiment employed a split-plot design, with varieties as the main plots, fertilizer types as the subplots, and fertilizer application methods as the sub-subplots. The nitrogen fertilizer management, phosphorus and potassium fertilizer application, and plant count at the two-leaf stage followed the same procedures as in Experiment 1. The target plant density was set at 240,000 plants/ha. Other field management measures were consistent with standard practices. Wheat was sown in rows with a spacing of 25 cm using manual trenching. Each plot had an area of 12 m², and the experiment was replicated three times.

2.2. Data Collection and Processing

2.2.1. UAV Image Acquisition and Processing

In this study, the DJI P4M UAV (SZ DJI Technology Co.; Shenzhen, China) was utilized, equipped with five multispectral sensors corresponding to the blue (B), green (G), red (R), red edge (Rededge), and near-infrared (NIR) spectral regions. The data were collected between 9:00 a.m. and 11:00 a.m. under clear and windless conditions to avoid hotspot artifacts in the images. The UAV was launched from the same fixed position for every flight. Before each flight, two diffuse reflectance standard panels, representing 50% and 75% reflectance, were placed manually for radiometric calibration. The DJI Ground Station Pro application (https://www.dji.com/cn/ground-station-pro (accessed on 17 May 2023)) was used to plan the flight missions, considering the current solar azimuth angle to generate the flight paths automatically. The flight altitudes were set to 20 m (with a spatial resolution of 1.06 cm) and 40 m (with a spatial resolution of 2.12 cm), with a flight speed of 3 m/s. The overlap settings were 80% for both along-track and across-track directions. The settings of the UAV flight parameters can be found in

Table A1. Settings of UAV flight parameters.

Parameters	Setting 1	Setting 2
Flight altitude	20 m	40 m
Flight speed	3 m/s	3 m/s
Heading overlap rate	80%	80%
Sideways overlap	80%	80%
Resolution	1.06 cm	2.12 cm

in Appendix A. After completing the flights, DJI Terra software (https://enterprise.dji.com/cn/dji-terra (accessed on 22 May 2023)) was employed to perform two-dimensional multispectral synthesis and radiometric calibration on the acquired images, resulting in orthorectified single-band reflectance images.

2.2.2. In Situ Wheat SPAD Measurements

To establish a correlation between the UAV data and ground-truth measurements, immediately after the UAV image acquisition, field measurements of SPAD data were conducted in the 72 plots of the experimental field using a “five-point sampling method”. In each plot, ten randomly selected wheat plants were measured at the leaf tip, middle, and base of the second fully expanded leaf using a SPAD-502Plus handheld chlorophyll meter (Konica Minolta; Tokyo, Japan). The SPAD readings obtained from the selected wheat plants at each point represented the SPAD value of that particular point. The average of the five points was calculated as the SPAD value for each plot.

2.2.3. Background Removal

A thresholding method was employed to perform background removal in this study to reduce the influence of different growth stages and varying soil backgrounds, particularly during early stages with low vegetation cover. The background removal process used eCognition 9.0 object-oriented remote-sensing-processing software developed by Definiens (http://www.definiens.com (accessed on 19 May 2023)). Compared to pixel-based classification methods, object-oriented classification methods can avoid the “salt-and-pepper” effect that may occur during classification. The first step in object-oriented classification is to generate “objects,” and a frequently used approach in eCognition is the multiscale segmentation algorithm. This bottom-up region-merging algorithm merges pixels within a specified scale parameter, resulting in objects with the lowest pixel heterogeneity and containing only one land cover type. By analyzing the UAV remote sensing imagery, the images were prepared to be classified into three classes: soil, shadow, and vegetation. Corresponding vegetation indices were selected for each class (

Table 1. Equations related to background removal by a threshold method.

Type	Spectral Variable	Calculation Formula	Reference
Vegetation	NDVI	NDVI = (NIR − R)/(NIR + R)	[27]
Soil	NDWI	NDWI = (G − NIR)/(G + NIR)	[28]
Shade	OSAVI	OSAVI = ((1 + 0.16) ∗ (NIR − R))/(NIR + R + 0.16)	[29]

). The image classification was performed by setting appropriate threshold ranges, and similar objects were merged to generate vector boundaries for vegetation and nonvegetation classes. Masking operations were conducted in ArcMap to complete the background removal process. The segmentation accuracy for each stage can be found in

Table A2. Image segmentation accuracy for each growth stage.

Fertility	Overall Accuracy	Kappa
green-up stage	95.9%	0.85
jointing stage	97.3%	0.94

in Appendix A.

Overall accuracy reflects the probability of consistency between the classification results and the real ground results, and the Kappa coefficient serves as an index to judge whether the two images are consistent. According to Lillesand and Kiefer et al. [30], the minimum level of accuracy for results of a remote-sensing-based classified map to be considered valid is ≥85%, which the remote sensing community has widely accepted as a target in image classification. According to the Kappa coefficient, the performance of the model can be further classified into the following levels: ≤0 (poor), 0–0.2 (slight), 0.2–0.4 (fair), 0.4–0.6 (moderate), 0.6–0.8 (substantial), and 0.8–1 (almost perfect) [31]. According to Table A2, during the green-up stage and jointing stage, the overall accuracy achieved was 95.9% and 97.3%, respectively, with a Kappa value of 0.85 and 0.94. It can be observed that the background of the UAV images has been effectively removed.

2.2.4. Extraction and Construction of VIS

The partition statistics function in ENVI (ITT Exelis; Boulder, CO, USA) can be utilized to extract the canopy reflectance for each treatment plot and calculate the VI values in Table 2.

Due to the structural characteristics of leaves, canopy structure, and soil background, they can significantly influence the optical properties of leaves and canopies [32,33,34,35]. Furthermore, models with limited spectral variables are more prone to interference from background factors, leading to instability. VIs can partially mitigate these influences and provide more accurate information about leaf chlorophyll and canopy structure by using combinations of multiple VIs instead of relying on a single VI [36,37].

Table 2. The 22 spectral variables used in this study for SPAD estimation.

Spectral Variable	Calculation Formula	Reference
R	R	–
G	G	–
B	B	–
NIR	NIR	–
Rededge	Rededge	–
RVI	RVI = NIR/R	[38]
TVI	TVI = sqrt(120 ∗ (NIR − R)/(NIR + R) + 0.5)	[39]
RDVI	RDVI = (NIR − R)/sqrt(NIR + R)	[40]
MSAVI	MSAVI = 0.5 ∗ (2 ∗ (NIR + 1) − sqrt((2 ∗ NIR + 1)2 − 8 ∗ (NIR − R)))	[41]
GNDVI	GNDVI = (NIR − G)/(NIR + G)	[42]
EVI	EVI = 2.5 ∗ ((NIR − R)/(NIR + (G ∗ R) − (G ∗ B) + 0.1))	[43]
SAVI	SAVI = 1.5 ∗ (NIR − R))/(NIR + R + 0.5)	[44]
OSAVI	OSAVI = 1.16 ∗ (NIR − R))/(NIR + R + 0.16)	[29]
NDVI	NDVI = (NIR − R)/(NIR + R)	[27]
SR	SR = NIR/Rededge	[45]
MTVI	MTVI = 1.5 ∗ (1.2 ∗ (Rededge − G) − 2.1 ∗ (R − G)	[46]
CIgreen	CIgreen = (NIR/G) − 1	[47]
EVI2	EVI2 = 2.5 ∗ (NIR − R)/(NIR + 2.4 ∗ R + 1))	[48]
REV(NDRE)	REV = (NIR − Rededge)/(NIR + Rededge)	[49]
MCARI	MCARI = ((Rededge − R) − 0.2 ∗ (Rededge − G)) ∗ (RE/R)	[50]
MSR	MSR = (NIR/R − 1)/(NIR/R + 1)	[51]
CIre	CIre = (NIR/Rededge) − 1	[52]

Note: In the equations, B, G, R, Rededge, and NIR are the reflectance values at the blue (450 nm), green (560 nm), red (650 nm), red edge (730 nm), and near-infrared (840 nm) spectral bands, respectively.

Table 2. The 22 spectral variables used in this study for SPAD estimation.

Spectral Variable	Calculation Formula	Reference
R	R	–
G	G	–
B	B	–
NIR	NIR	–
Rededge	Rededge	–
RVI	RVI = NIR/R	[38]
TVI	TVI = sqrt(120 ∗ (NIR − R)/(NIR + R) + 0.5)	[39]
RDVI	RDVI = (NIR − R)/sqrt(NIR + R)	[40]
MSAVI	MSAVI = 0.5 ∗ (2 ∗ (NIR + 1) − sqrt((2 ∗ NIR + 1)2 − 8 ∗ (NIR − R)))	[41]
GNDVI	GNDVI = (NIR − G)/(NIR + G)	[42]
EVI	EVI = 2.5 ∗ ((NIR − R)/(NIR + (G ∗ R) − (G ∗ B) + 0.1))	[43]
SAVI	SAVI = 1.5 ∗ (NIR − R))/(NIR + R + 0.5)	[44]
OSAVI	OSAVI = 1.16 ∗ (NIR − R))/(NIR + R + 0.16)	[29]
NDVI	NDVI = (NIR − R)/(NIR + R)	[27]
SR	SR = NIR/Rededge	[45]
MTVI	MTVI = 1.5 ∗ (1.2 ∗ (Rededge − G) − 2.1 ∗ (R − G)	[46]
CIgreen	CIgreen = (NIR/G) − 1	[47]
EVI2	EVI2 = 2.5 ∗ (NIR − R)/(NIR + 2.4 ∗ R + 1))	[48]
REV(NDRE)	REV = (NIR − Rededge)/(NIR + Rededge)	[49]
MCARI	MCARI = ((Rededge − R) − 0.2 ∗ (Rededge − G)) ∗ (RE/R)	[50]
MSR	MSR = (NIR/R − 1)/(NIR/R + 1)	[51]
CIre	CIre = (NIR/Rededge) − 1	[52]

Note: In the equations, B, G, R, Rededge, and NIR are the reflectance values at the blue (450 nm), green (560 nm), red (650 nm), red edge (730 nm), and near-infrared (840 nm) spectral bands, respectively.

2.3. Feature Variable Screening

This study employed and compared three feature engineering methods, Pearson correlation coefficient, RFE, and CFS, to select the optimal spectral variables for subsequent modeling.

In the variable selection method utilizing the Pearson correlation coefficient, the coefficient (r) quantifies the linear association between predictor variables and the target variable, ranging from −1 to 1. Predictor variables exhibiting higher absolute values of r indicate more pronounced linear correlations with the target variable. Consequently, in this method, predictor variables with higher absolute r values are selected.

The RFE method starts by searching for a subset of variables from the training dataset and eliminates the least important variable [53]. The remaining variables are then used to rebuild the base model. This process is repeated until a specific number of variables are retained, and the elimination order of variables is based on their rankings. This study employed a cross-validated RFE approach, with the RF algorithm serving as the estimator.

The CFS algorithm is a filter algorithm based on correlation. The assessment of the correlation between features and categories, as well as between features themselves, was performed using the coefficient ${\mathrm{Merit}}_{\mathrm{S}}$ explicated in Equation (1), enabling data cleaning. The key aspect of CFS is the heuristic evaluation of the value of feature subsets, which is achieved by calculating symmetric uncertainty (SU) explicated in Equation (2) to measure the correlation within the feature subset [54].

$${\mathrm{Merit}}_{\mathrm{S}}=\frac{{\mathrm{kr}}_{\mathrm{cf}}^{-}}{\sqrt{\mathrm{k}+\mathrm{k}\left(\mathrm{k}-1\right){\mathrm{r}}_{\mathrm{ff}}^{-}}}$$

(1)

Theorem 1.

$Meri{t}_S$ is the evaluated value of a subset of features, containing K features, $r_{cf}^{-}$ is the average correlation between features and classes, and $r_{ff}^{-}$ is the average correlation between features and features.

$$\mathrm{SU}=2.0\ast \left[\frac{\mathrm{H}\left(\mathrm{X}\right)+\mathrm{H}\left(\mathrm{Y}\right)-\mathrm{H}\left(\mathrm{X},\mathrm{Y}\right)}{\mathrm{H}\left(\mathrm{X}\right)+\mathrm{H}\left(\mathrm{Y}\right)}\right]$$

(2)

The CFS algorithm operates on the initial feature space and performs a search for feature subspaces using forward selection or backward elimination. It constructs a feature subset T and utilizes a heuristic estimation method to evaluate the correlations between features within the feature subset and between features and the class. The CFS method can determine the number of selected subset features and ranks the feature subsets instead of individual features.

2.4. Machine Learning Regression Algorithms

Machine learning has been widely applied to spectral reflectance data based on simulation or field measurements. Machine learning techniques can retrieve vegetation parameters and demonstrate robustness and higher prediction accuracy by training on spectral reflectance data [55,56]. Linear regression (LR) is the most common regression algorithm used to establish the linear relationship between SPAD and VIs [57]. However, linear formulas may fail to capture nonlinear relationships in complex environmental conditions [58,59]. In this study, four machine learning algorithms, namely, elastic net, random forest (RF), backpropagation neural network (BPNN), and extreme gradient boosting (XGBoost), were employed for regression modeling. These algorithms offer the potential to capture nonlinear relationships and enhance the accuracy of vegetation parameter estimation.

Elastic net is a linear regression algorithm widely used for high-dimensional data regression problems. It effectively addresses the issues of overfitting and collinearity by simultaneously applying L1 regularization and L2 regularization [60].

RF [61] is an ensemble method that relies on decision trees as its base learners. It addresses the issue of overfitting by training multiple decision trees on different subsets of the same training dataset. The final prediction of the random forest model is obtained by averaging the predictions from these individual decision trees. There are three key hyperparameters associated with the random forest algorithm. First, the number of trees or base learners is determined by the hyperparameter “n_estimators”. Second, the hyperparameter “max_features” specifies the number of features to consider when searching for the best split at each tree node. In the case of RF, “max_features” is typically set to log2(n_features), where n_features represents the total number of predictor variables. This setting helps introduce attribute interference and enhances diversity among the base learners. Lastly, the “min_samples_leaf” hyperparameter sets the minimum number of samples required to form a leaf node in the decision trees of the random forest model.

BPNN is a feed-forward network that improves upon the coefficients and biases in the model compared to the multilayer perceptron. It has stronger mapping, adaptive, and generalization capabilities for nonlinear data. BP is a supervised learning algorithm that utilizes backpropagation to adjust the weights and thresholds of each neuron layer by layer. Its core idea is to compute the output values through forward propagation and propagate the error between the computed results and the true label values back through the network. It comprises an input layer, an output layer, and multiple hidden layers. Within each layer, neurons are interconnected with neurons in the subsequent layer to facilitate the transmission of information. The input values are linearly weighted within each neuron and then passed through an activation function to obtain the output values. Common activation functions include Sigmoid, Tanh, ReLU, etc. The output results are obtained through forward propagation, while the error is propagated backward through the network using the backpropagation method. The basic idea of backpropagation is to use the principle of gradient descent to adjust the network parameters by calculating the error between the output layer and the expected values. This minimizes the loss function of the neural network and reduces the error, making the predicted values closer to the true values [62].

XGBoost is also a tree-based ensemble learning algorithm that combines multiple weak classifiers to form a strong classifier, combining multiple decision trees to improve the model’s generalization performance. Its key feature is incorporating regularization terms in the loss function to prevent overfitting. XGBoost adopts a gradient-boosting strategy to iteratively fit the training data, ensuring that each iteration produces better results [63].

Parameter tuning is crucial for achieving optimal performance in machine learning models. This study employed a combination of grid search and cross-validation to find the best combination of parameters and hyperparameters.

2.5. Segmentation of Datasets and Model Evaluation

The dataset was randomly divided into a training dataset and test dataset using an 8:2 ratio. In order to further enhance the model’s performance and avoid overfitting, 5-fold cross-validation was employed during the training process, and the model’s performance was evaluated using the test dataset. In this approach, the original training set was divided into five subsets. The model was trained and evaluated five times, each time using a different subset as the validation set and the remaining four subsets as the training set. The results from these iterations were then averaged to reduce the training set’s error and improve the model’s generalization ability by avoiding the inclusion of test data during the training process.

The accuracy of the model was assessed using four metrics: R², RMSE, RRMSE, and RPD. Higher values of R² and lower values of RMSE and RRMSE indicate better model performance [64]. Additionally, this study calculated the ratio of performance to deviation (RPD) to evaluate the model’s predictive ability. RPD is determined by dividing the standard deviation of the measured values by the RMSE obtained from cross-validation [65]. According to Rossel et al. [66], RPD values can be categorized as follows: RPD < 1.4 indicates a very poor estimation, 1.4 ≤ RPD < 1.8 indicates a fair estimation, 1.8 ≤ RPD < 2.0 indicates a good estimation, 2.0 ≤ RPD < 2.5 indicates a very good estimation, and RPD ≥ 2.5 indicates an excellent estimation. The entire variable selection, modeling, cross-validation, and performance evaluation process was implemented using Scikit-learn, a Python library version 3.8 (https://scikit-learn.org (accessed on 15 May 2023)).

3. Results

3.1. Descriptive Statistics of SPAD Values in Winter Wheat Canopies

The statistical analysis of the ground-measured SPAD values for different growth stages of winter wheat in this study is presented in

Table 3. Descriptive statistics of measured wheat canopy SPAD values.

Fertility	n	Mean	Maximum	Maximum	S·D	C·V
green-up stage	72	45.50	39.05	51.15	2.063	4.53%
jointing stage	72	49.76	34.60	58.90	4.665	9.38%
cross-growth stage	144	47.63	34.60	58.90	4.189	8.79%

. The SPAD values during the green-up stage range from 39.05 to 51.15, with an average value of 45.50. The coefficient of variation for this dataset is 4.53%. For the jointing stage, the SPAD values range from 34.60 to 58.90, with an average value of 49.76 and a coefficient of variation of 9.38%. The combined SPAD values for the green-up and jointing stages range from 34.60 to 58.90, with an average value of 47.63 and a coefficient of variation of 8.79%.

The SPAD values of winter wheat increase gradually as the growth stages progress from green-up to jointing. The coefficient of variation reflects the variability of SPAD values among different treatments during the specific growth stage. A higher coefficient of variation is advantageous for the applicability and robustness of the models developed in later stages.

3.2. Spectral Index Screening

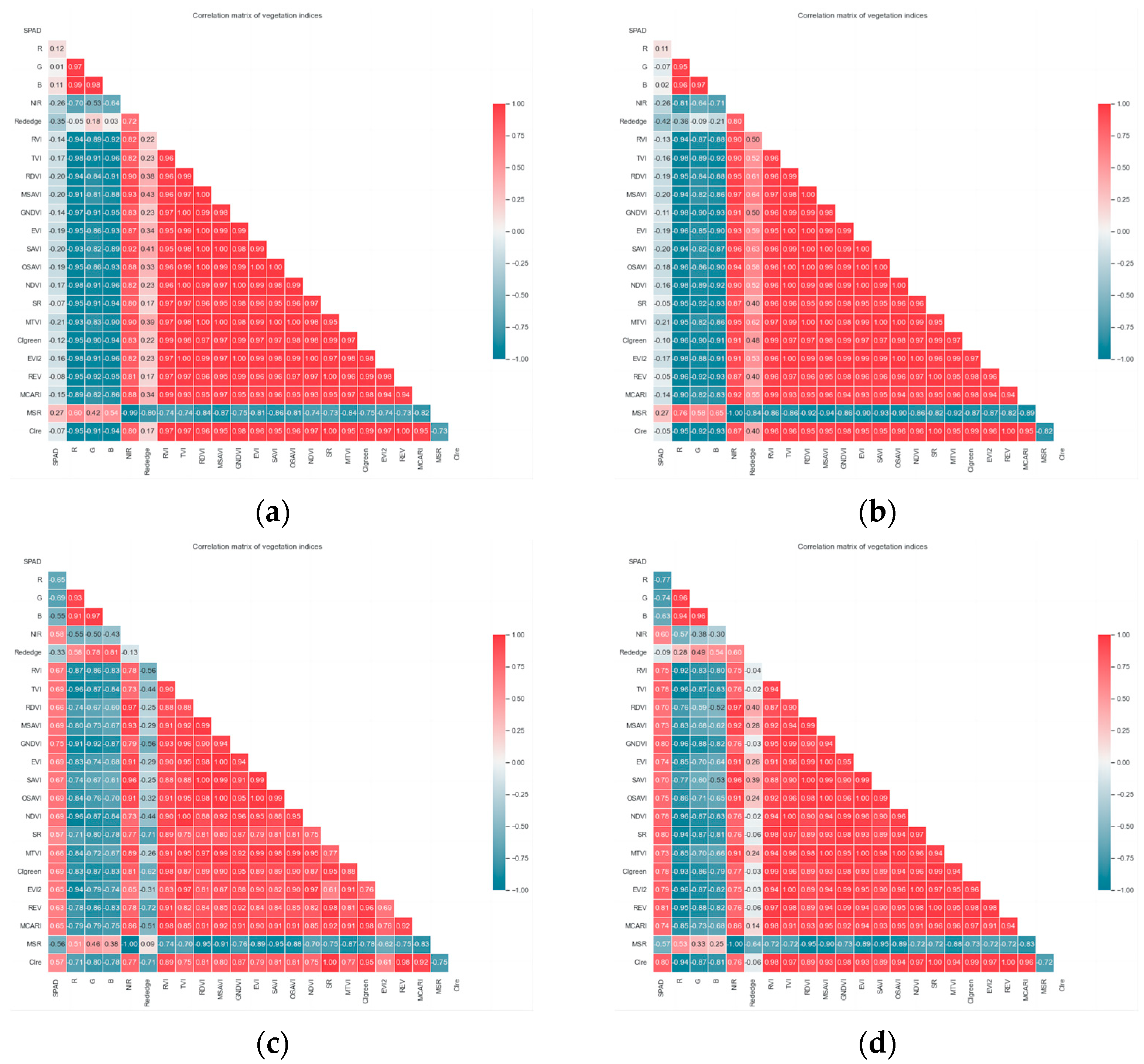
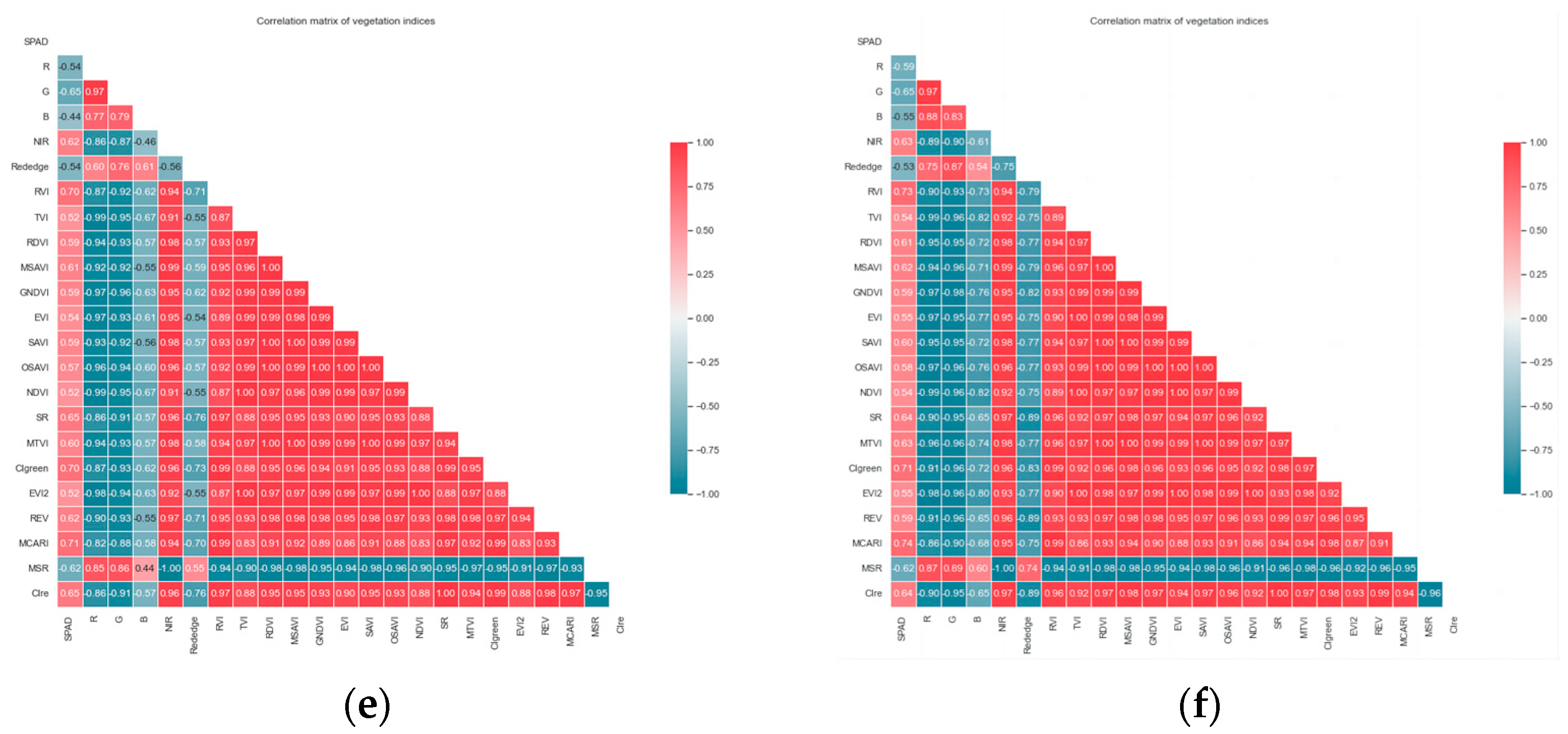
Correlation analysis was conducted between the measured SPAD values during the green-up stage, jointing stage, and combined growth stages, and the spectral variables extracted and calculated from the multispectral images obtained at two different UAV flight altitudes of 20 m and 40 m. Pearson correlation analysis was used to examine the correlation coefficients between the SPAD values and 22 spectral variables. The heat maps of correlation analysis can be found in Figure A1 in Appendix A.

Overall, there were distinct high-correlation regions for each growth stage. As the growth stages progressed from green-up to jointing, the correlation showed an increasing trend. The correlation coefficients between various indices for each growth stage and SPAD are presented in

Table 4. Correlation coefficients between winter wheat SPAD values and spectral variables.

Spectral Variable	Correlation Coefficient (r)
	Green-Up Stage		Jointing Stage		Cross-Growth Stage
	20 m	40 m	20 m	40 m	20 m	40 m
R	0.12	0.11	−0.65 **	−0.77 **	−0.54 **	−0.59 **
G	0.01	−0.07	−0.69 **	−0.74 **	−0.65 **	−0.65 **
B	0.11	0.02	−0.55 **	−0.63 **	−0.44 **	−0.55 **
NIR	−0.26 *	−0.26 *	0.58 **	0.60 **	0.62 **	0.63 **
Rededge	−0.35 **	−0.42 **	−0.33 **	−0.09	−0.54 **	−0.53 **
RVI	−0.14	−0.13	0.67 **	0.75 **	0.70 **	0.73 **
TVI	−0.17	−0.16	0.69 **	0.78 **	0.52 **	0.54 **
RDVI	−0.20	−0.19	0.66 **	0.70 **	0.59 **	0.61 **
MSAVI	−0.20	−0.20	0.69 **	0.73 **	0.61 **	0.62 **
GNDVI	−0.14	−0.11	0.75 **	0.80 **	0.59 **	0.59 **
EVI	−0.19	−0.19	0.69 **	0.74 **	0.54 **	0.55 **
SAVI	−0.20	−0.20	0.67 **	0.70 **	0.59 **	0.60 **
OSAVI	−0.19	−0.18	0.69 **	0.75 **	0.57 **	0.58 **
NDVI	−0.17	−0.16	0.69 **	0.78 **	0.52 **	0.54 **
SR	−0.07	−0.05	0.57 **	0.80 **	0.65 **	0.64 **
MTVI	−0.21	−0.21	0.66 **	0.73 **	0.60 **	0.63 **
CIgreen	−0.12	−0.10	0.69 **	0.78 **	0.70 **	0.71 **
EVI2	−0.16	−0.17	0.65 **	0.79 **	0.52 **	0.55 **
REV	−0.08	−0.05	0.63 **	0.81 **	0.62 **	0.59 **
MCARI	−0.15	−0.14	0.65 **	0.74 **	0.71 **	0.74 **
MSR	0.27*	0.27 *	−0.56 **	−0.57 **	−0.62 **	−0.62 **
CIre	−0.07	−0.05	0.57 **	0.80 **	0.65 **	0.64 **

Note: * and ** indicate significant differences at the levels of p < 0.05 and p < 0.01, respectively.

.

During the green-up stage, most spectral indices showed similar response patterns to the SPAD values of winter wheat at both the 20 m and 40 m flight altitudes. The Rededge index exhibited the strongest correlation with SPAD values, with correlation coefficients of −0.35 and −0.42, respectively. The MSR and NIR indices ranked second and third in correlation coefficients. The MSR index had a correlation coefficient of 0.27, while the NIR index had a correlation coefficient of −0.26 for both flight altitudes.

During the jointing stage, we found that the spectral variables at the 40 m flight altitude exhibited a stronger correlation with SPAD values compared to the 20 m flight altitude. Most spectral variables showed higher correlation coefficients, with REV reaching a correlation coefficient of 0.81. Conversely, at 20 m, the correlation between most spectral indices and SPAD values significantly decreased, with GNDVI having the highest correlation coefficient of 0.75. Through significance testing, all spectral variables at different flight altitudes, except for Rededge at the 40 m flight altitude, showed a highly significant correlation with SPAD values at a significance level of p < 0.01.

During the cross-growth stage, the spectral variables at both 20 m and 40 m flight altitudes exhibited the strongest correlation with SPAD values. The top three variables with the highest correlation coefficients were MCARI, CIgreen, and RVI. MCARI had the highest correlation coefficient, reaching 0.71 and 0.74, respectively, at the two flight altitudes. Overall, the correlation between spectral variables and wheat SPAD values during the cross-growth stage showed a significant improvement compared to the green-up stage, although slightly lower than the jointing stage.

For the CFS feature selection, a global best-first algorithm was employed as the search strategy for the heuristic search to perform feature preselection and eliminate irrelevant variables. CFS is a feature selection method that can determine the number of selected subset features. It estimates feature subsets and ranks them based on the subsets rather than individual features. After CFS selection, during the green-up stage, there were nine spectral variables (20 m) and seven spectral variables (40 m), respectively. During the jointing stage, both at 20 m and 40 m flight altitudes, there were eight spectral variables. During the cross-growth stage, after CFS selection, there were eight spectral variables (20 m) and seven spectral variables (40 m), respectively. The results are presented in

Table 5. Results of CFS feature selection.

Fertility	Altitude	Feature Set	k	${\mathbf{M}\mathbf{e}\mathbf{r}\mathbf{i}\mathbf{t}}_{\mathbf{S}}$
green-up stage	20 m	B, CIre, SR, REV, R, GNDVI, RVI	7	0.2611
	40 m	G, REV, CIre, SR, CIgreen, R, B, GNDVI, NIR	9	0.2943
jointing stage	20 m	NIR, RDVI, MSAVI, GNDVI, SAVI, MTVI, CIgreen, MSR	8	0.3865
	40 m	R, RVI, OSAVI, SR, REV, MTVI, MCARI, CIre	8	0.4046
cross-growth stage	20 m	MSAVI, MTVI, GNDVI, CIgreen, RDVI, SAVI, OSAVI, NIR, MCARI	9	0.3573
	40 m	CIgreen, MCARI, RVI, CIre, SR, G, MTVI, GNDVI	8	0.3459

.

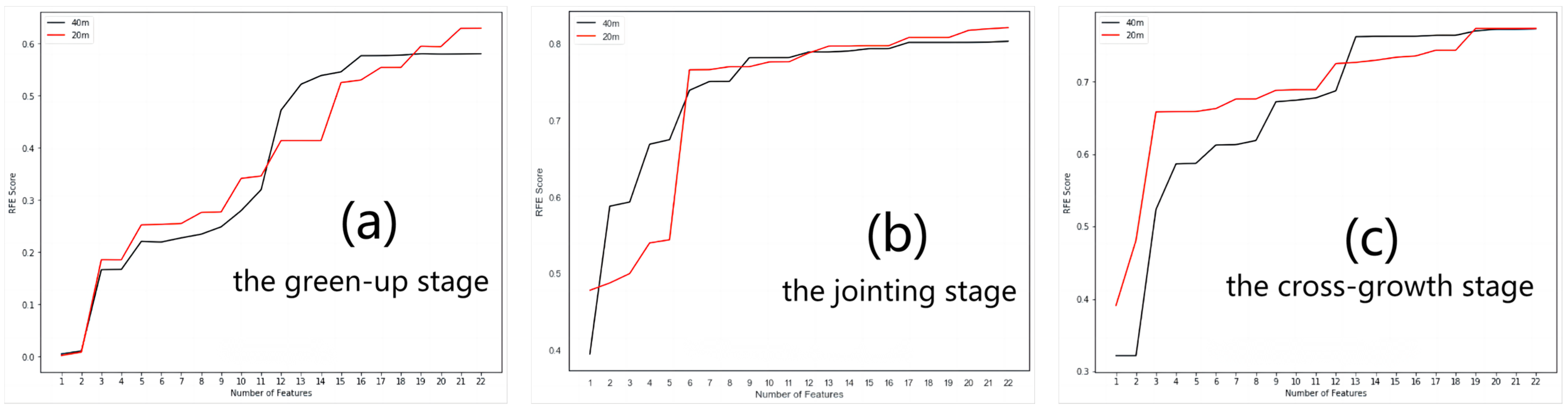
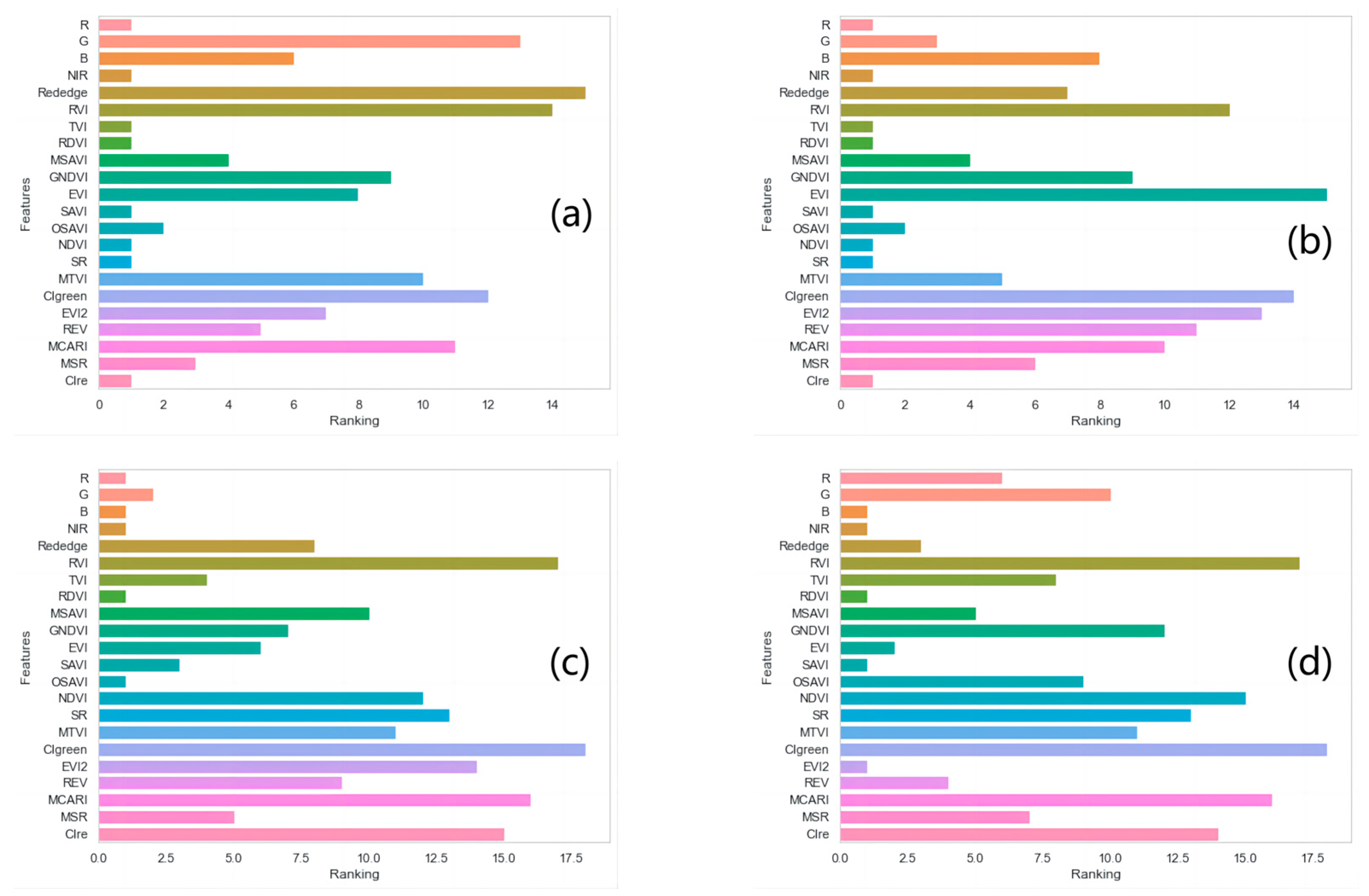
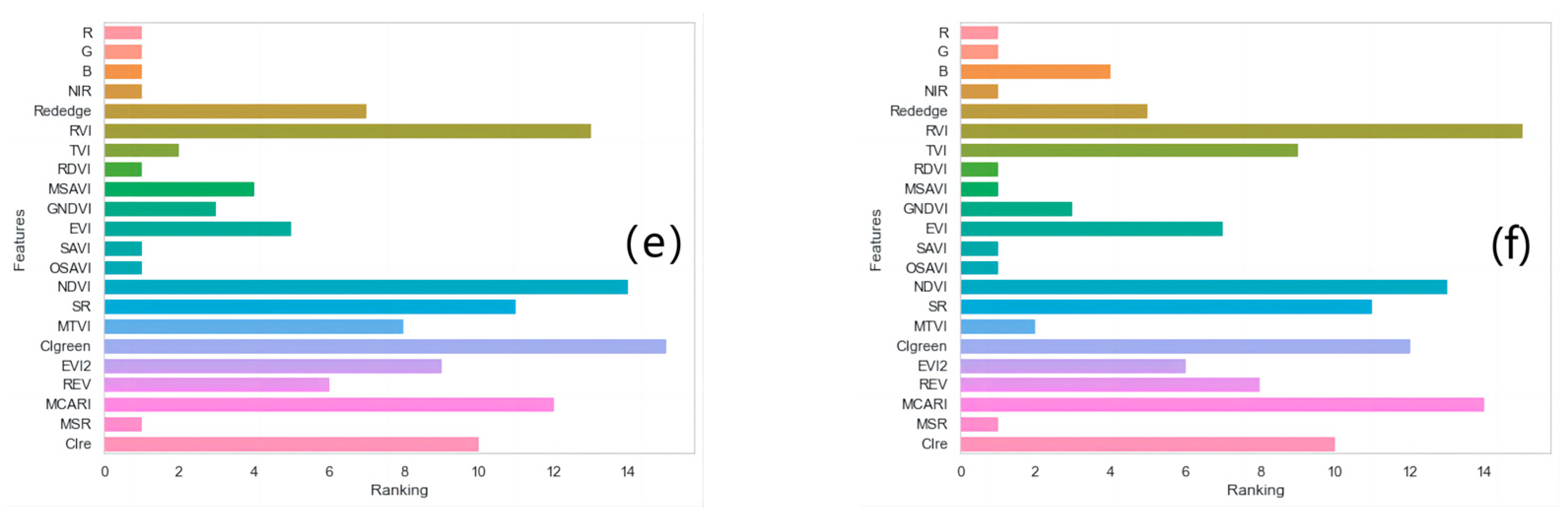
In the RFE feature selection based on cross-validation, the RF was chosen as the estimator. The learning curve (Figure 2) obtained from RFE feature selection was used to determine the optimal number of spectral variables, and the feature importance ranking (Figure 3) from RFE was used to select the optimal spectral indices.

Taking into account the limited number of spectral features and the optimal model performance, during the green-up stage modeling, the selected number of optimal features was 19 (20 m) and 16 (40 m) for the different flight altitudes. During the jointing stage modeling, the selected number of optimal features was eight for both flight altitudes. During the cross-growth stage modeling, the selected number of optimal features was 19 (20 m) and 13 (40 m), respectively, indicating excellent model performance.

In the Pearson feature selection, as well as the CFS feature selection, the selection is based on feature correlations. The difference is that Pearson considers the correlation between the feature variables and the measured SPAD values, while CFS considers the correlation among the feature variables themselves. To avoid the influence of different numbers of independent variables on the final prediction results, in this study, the same number of spectral variables as selected by the CFS feature selection was chosen for the subsequent modeling in each case.

After applying the Pearson, RFE, and CFS feature selection methods, the selected spectral variables in this study are presented in

Table 6. The results of variable selection.

Spectral Variable	Green-Up Stage						Jointing Stage						Cross-Growth Stage
	20 m			40 m			20 m			40 m			20 m			40 m
	Pearson	RFE	CFS	Pearson	RFE	CFS	Pearson	RFE	CFS	Pearson	RFE	CFS	Pearson	RFE	CFS	Pearson	RFE	CFS
R		√	√		√	√		√				√		√			√
G					√	√	√	√					√	√		√	√	√
B		√	√		√	√		√			√			√			√
NIR	√	√		√	√	√		√	√		√		√	√	√	√	√
Rededge	√			√	√						√			√			√
RVI			√									√	√			√		√
TVI		√			√		√	√		√				√
RDVI	√	√		√	√			√	√		√			√	√		√
MSAVI	√	√		√	√		√		√		√		√	√	√		√
GNDVI		√	√		√	√	√		√	√				√	√		√	√
EVI		√		√			√							√
SAVI	√	√		√	√			√	√		√			√	√		√
OSAVI		√		√	√		√	√				√		√	√		√
NDVI		√			√		√			√
SR		√	√		√	√				√		√	√	√		√		√
MTVI	√	√		√	√				√			√		√	√	√	√	√
CIgreen		√	√			√	√		√	√			√		√	√		√
EVI2		√								√	√			√			√
REV		√	√			√				√	√	√	√	√
MCARI		√										√		√	√	√		√
MSR	√	√		√	√				√				√	√			√
CIre		√	√		√	√				√		√	√	√		√		√

. It can be observed that the optimal spectral indices selected by these three different feature selection methods cover all the mentioned spectral variables in this study.

Furthermore, significant variations exist in the selected spectral indices among different altitudes and feature selection methods. For example, during the jointing stage, Rededge was selected as the optimal variable only at a flight altitude of 40 m through the RFE feature selection. This also emphasizes the importance of comparing different feature selection methods.

3.3. Selection of the Best Model for Estimating SPAD Values in Winter Wheat Canopies

3.3.1. Selection of the Optimal Estimation Model for Winter Wheat Canopy SPAD Values during the Green-Up Stage

In this study, models for estimating winter wheat canopy SPAD values were conducted separately for individual growth stages (green-up stage and jointing stage) and the cross-growth stage (green-up stage + jointing stage). For each single stage, model construction was performed at both 20 m and 40 m flight altitudes, utilizing three feature selection methods and four machine learning algorithms in a 3 × 4 combination. This resulted in 24 regression models for estimating canopy SPAD values during the jointing stage of wheat. Grid search combined with 5-fold cross-validation was employed to select the optimal hyperparameters based on the goodness of fit as the evaluation criterion.

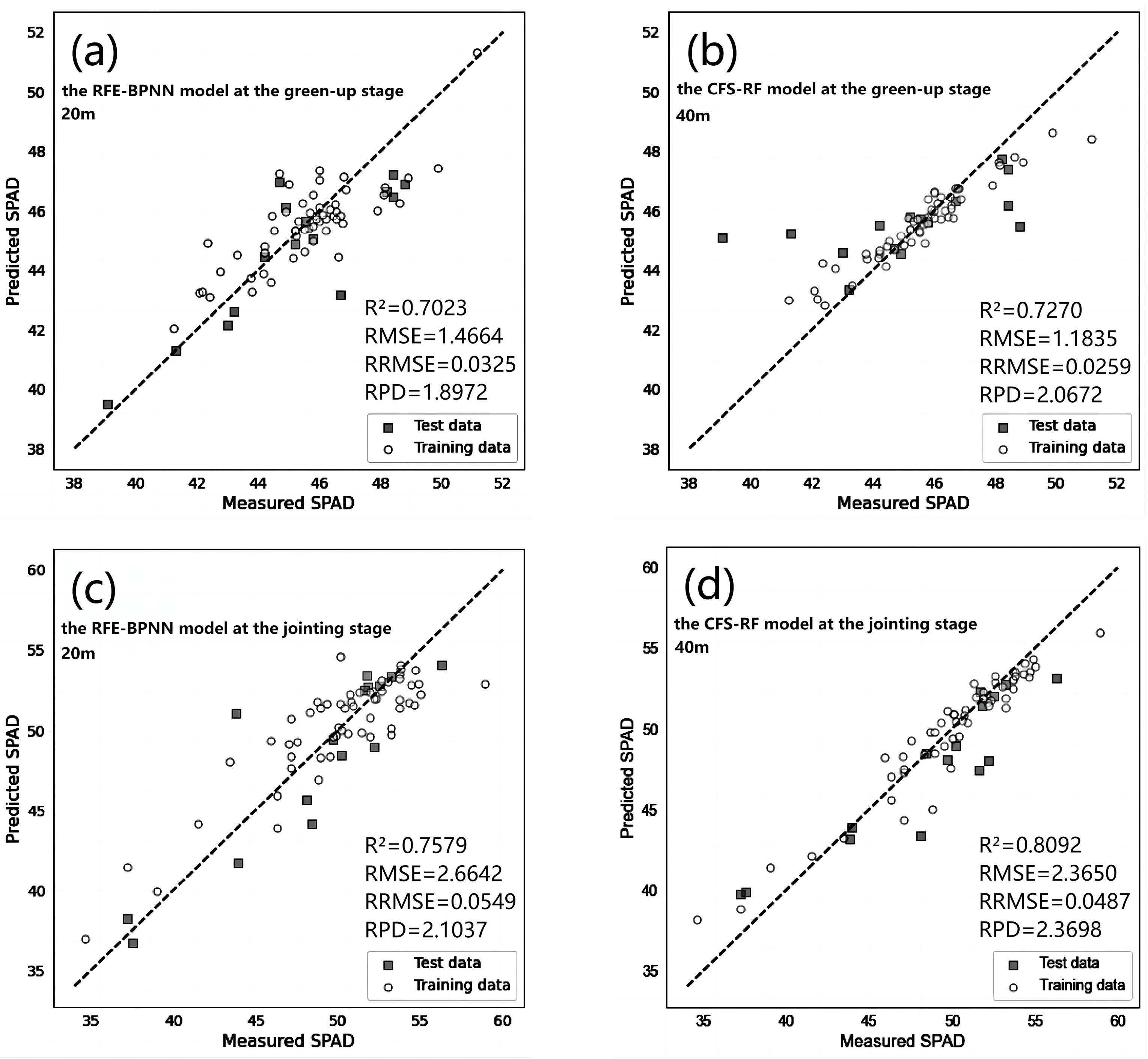
As shown in

Table 7. Comparison of winter wheat SPAD value estimation models at the green-up stage.

Green-Up Stage		Model	Train				Test
			R2	RMSE	RRMSE	RPD	R2	RMSE	RRMSE	RPD
20 m	Pearson	Elastic Net	0.3308	1.5165	0.0333	1.2333	0.1739	2.1275	0.0466	1.1388
		RF	0.6154	1.1497	0.0252	1.6268	0.2226	2.3698	0.0525	1.1740
		BPNN	0.6818	1.0458	0.0229	1.7884	0.4441	2.0039	0.0444	1.3884
		XGboost	0.7336	0.9568	0.0210	1.9548	0.1063	2.5409	0.0563	1.0949
	RFE	Elastic Net	0.2529	2.3232	0.0514	1.1975	0.1435	1.7157	0.0376	1.0901
		RF	0.7459	1.0280	0.0226	1.9991	0.5900	1.4504	0.0317	1.6868
		BPNN	0.7514	0.9881	0.0217	2.0234	0.7023	1.4664	0.0325	1.8972
		XGboost	0.7037	1.0090	0.0221	1.8535	0.1117	2.5331	0.0561	1.0983
	CFS	Elastic Net	0.2811	1.5718	0.0345	1.1899	0.2633	2.3070	0.0511	1.2059
		RF	0.7884	0.9381	0.0206	2.1906	0.5326	1.5485	0.0339	1.5799
		BPNN	0.5927	1.1831	0.0259	1.5809	0.5329	1.8368	0.0407	1.5146
		XGboost	0.4844	1.4230	0.0313	1.4050	0.1739	2.1275	0.04660	1.1388
40 m	Pearson	Elastic Net	0.2827	1.5700	0.0344	1.1913	0.2474	2.3317	0.0516	1.1931
		RF	0.5909	1.1857	0.0260	1.5774	0.2700	2.2964	0.0508	1.2115
		BPNN	0.5973	1.1765	0.0258	1.5898	0.2488	2.3295	0.0516	1.1943
		XGboost	0.8232	0.7795	0.0171	2.3994	0.1666	2.4537	0.0543	1.1339
	RFE	Elastic Net	0.2419	2.3402	0.0518	1.1888	0.2236	1.6335	0.0358	1.1450
		RF	0.8167	0.7936	0.0174	2.3567	0.4154	2.0551	0.0455	1.3538
		BPNN	0.7585	0.9110	0.0200	2.0531	0.6214	1.6537	0.0366	1.6823
		XGboost	0.8366	0.7495	0.0164	2.4955	0.3336	2.1942	0.0486	1.2680
	CFS	Elastic Net	0.3501	0.2508	0.0328	1.2515	0.2508	2.3264	0.0515	1.1959
		RF	0.8859	0.6888	0.0151	2.9834	0.7270	1.1835	0.0259	2.0672
		BPNN	0.6636	1.0752	0.0236	1.7395	0.6633	1.5596	0.0345	1.7839
		XGboost	0.8137	0.8002	0.0176	2.3372	0.2172	2.3781	0.0527	1.1699

Note: the best results are in bold.

, at a flight altitude of 20 m, the regression model for estimating winter wheat canopy SPAD values during the green-up stage constructed using RFE feature selection and the BPNN algorithm (RFE-BPNN) achieves the best estimation accuracy. Specifically, the model exhibits the following performance metrics: R² value of 0.7514 and RPD value of 2.0234 for the training set, with an RMSE value of 0.9881 and RRMSE value of 0.0217. For the test set, the model achieves an R² value of 0.7023, RPD value of 1.8972, RMSE value of 1.4664, and RRMSE value of 0.0325.

On the other hand, at a flight altitude of 40 m, the regression model for estimating winter wheat canopy SPAD values during the green-up stage constructed using CFS feature selection and the RF algorithm (CFS-RF) achieves the best estimation accuracy. The specific performance metrics are as follows: an R² value of 0.8859, an RPD value of 2.9834, an RMSE value of 0.6888, and an RRMSE value of 0.0151 for the training set. For the test set, the model achieves an R² value of 0.7270, RPD value of 2.0672, RMSE value of 1.1835, and RRMSE value of 0.0259.

Therefore, the CFS-RF model (40 m) is considered the optimal model for estimating winter wheat canopy SPAD values during the green-up stage.

3.3.2. Selection of the Optimal Estimation Model for Winter Wheat Canopy SPAD Values during the Jointing Stage

As shown in

Table 8. Comparison of winter wheat SPAD value estimation models at the jointing stage.

Jointing Stage		Model	Train				Test
			R2	RMSE	RRMSE	RPD	R2	RMSE	RRMSE	RPD
20 m	Pearson	Elastic Net	0.7437	2.7411	0.0565	2.0447	0.5967	2.7884	0.0557	1.5887
		RF	0.8409	1.7513	0.0350	2.5294	0.7235	2.8471	0.0587	1.9686
		BPNN	0.7417	2.6856	0.0567	2.0368	0.6259	2.6856	0.0536	1.6494
		XGboost	0.7398	2.7620	0.0569	2.0292	0.5985	2.7821	0.0556	1.5923
	RFE	Elastic Net	0.8784	1.8879	0.0389	2.9688	0.6966	2.4184	0.0483	1.8317
		RF	0.8910	1.4496	0.0289	3.0559	0.6241	3.3198	0.0684	1.6883
		BPNN	0.7599	2.1516	0.0430	2.0588	0.7579	2.6642	0.0549	2.1037
		XGboost	0.8917	1.7821	0.0367	3.1449	0.7052	2.3839	0.0476	1.8582
	CFS	Elastic Net	0.7520	2.6967	0.0556	2.0784	0.5380	2.9843	0.0596	1.4843
		RF	0.9001	0.6231	0.0277	3.1923	0.6231	3.3243	0.0685	1.6860
		BPNN	0.7802	2.0585	0.0411	2.1520	0.7487	2.7142	0.0559	2.0649
		XGboost	0.7230	2.8499	0.0587	1.9667	0.5853	2.8275	0.0565	1.5667
40 m	Pearson	Elastic Net	0.9201	1.5304	0.0315	3.6621	0.7000	2.4051	0.0480	1.8418
		RF	0.8835	1.4984	0.0299	2.9564	0.6811	3.0576	0.0630	1.8330
		BPNN	0.8272	2.2506	0.0464	2.4903	0.7412	2.2336	0.0446	1.9833
		XGboost	0.7127	2.3533	0.0470	1.8823	0.5478	3.6409	0.0750	1.5394
	RFE	Elastic Net	0.6201	3.3375	0.0688	1.6793	0.4899	3.1360	0.0626	1.4126
		RF	0.9186	1.2527	0.0250	3.5362	0.7610	2.6471	0.0545	2.1173
		BPNN	0.8486	1.7084	0.0341	2.5930	0.3404	4.3975	0.0906	1.2745
		XGboost	0.8825	1.8564	0.0382	3.0192	0.6688	2.5268	0.0505	1.7531
	CFS	Elastic Net	0.7030	2.9507	0.0608	1.8995	0.5559	2.9262	0.0584	1.5139
		RF	0.9176	1.2602	0.0252	3.5151	0.8092	2.3650	0.0487	2.3698
		BPNN	0.7424	2.2285	0.0445	1.9877	0.7156	2.8877	0.0595	1.9409
		XGboost	0.7202	2.3226	0.0464	1.9072	0.5903	3.4657	0.0714	1.6172

Note: the best results are in bold.

, at a flight altitude of 20 m, the regression model for estimating winter wheat canopy SPAD values during the jointing stage constructed using RFE feature selection and the BPNN algorithm (RFE-BPNN) achieves the best estimation accuracy. Specifically, the model exhibits the following performance metrics: an R² value of 0.7599 and an RPD value of 2.0588 for the training set, with an RMSE value of 2.1516 and an RRMSE value of 0.0430. For the test set, the model achieves an R² value of 0.7579, RPD value of 2.1037, RMSE value of 2.6642, and RRMSE value of 0.0549.

On the other hand, at a flight altitude of 40 m, the regression model for estimating winter wheat canopy SPAD values during the jointing stage constructed using CFS feature selection and the random forest algorithm (CFS-RF) achieves the best estimation accuracy. The specific performance metrics are as follows: an R² value of 0.9176, an RPD value of 3.5151, an RMSE value of 1.2602, and an RRMSE value of 0.0252 for the training set. For the test set, the model achieves an R² value of 0.8092, an RPD value of 2.3698, an RMSE value of 2.3650, and an RRMSE value of 0.0487.

Therefore, the CFS-RF model (40 m) is considered the optimal model for estimating winter wheat canopy SPAD values during the jointing stage.

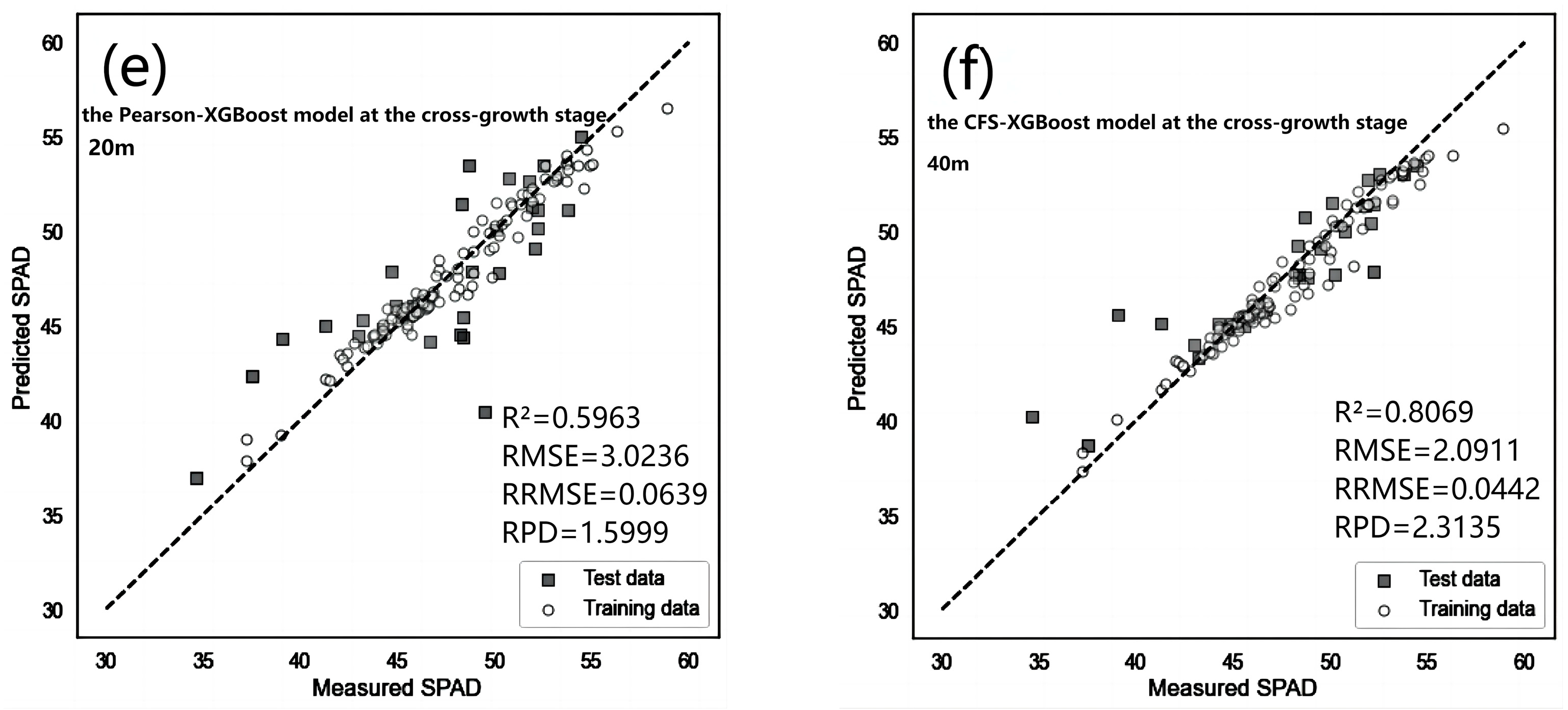
3.3.3. Selection of the Optimal Estimation Model for Winter Wheat Canopy SPAD Values during the Cross-Growth Stage

As shown in

Table 9. Comparison of winter wheat SPAD value estimation models across the two growth stages.

Cross-Growth Stage		Model	Train				Test
			R2	RMSE	RRMSE	RPD	R2	RMSE	RRMSE	RPD
20 m	Pearson	Elastic Net	0.6605	2.3390	0.0490	1.7240	0.4552	3.5127	0.0742	1.3772
		RF	0.9204	1.1329	0.0237	3.5593	0.4555	3.5118	0.0742	1.3775
		BPNN	0.7645	1.9481	0.0408	2.0699	0.3517	3.8319	0.0809	2.0699
		XGboost	0.9422	0.9648	0.0202	4.1797	0.3945	3.7033	0.0782	1.3063
	RFE	Elastic Net	0.5931	2.5608	0.0537	1.5747	0.5728	3.1104	0.0657	1.5553
		RF	0.9180	1.1498	0.0241	3.5072	0.4565	3.5085	0.0741	1.3788
		BPNN	0.7449	2.0275	0.0425	1.9888	0.5446	3.2117	0.0678	1.5063
		XGboost	0.9254	1.0966	0.0230	3.6771	0.4580	3.5034	0.0740	1.3808
	CFS	Elastic Net	0.5688	2.6362	0.0553	1.5296	0.4748	3.4487	0.0728	1.4027
		RF	0.9268	1.0860	0.0228	3.7132	0.5220	3.2902	0.0695	1.4703
		BPNN	0.5932	2.5605	0.0537	1.5749	0.5118	3.3252	0.0702	1.4548
		XGboost	0.9584	0.8188	0.0172	4.9245	0.5963	3.0236	0.0639	1.5999
40 m	Pearson	Elastic Net	0.6948	2.2180	0.0465	1.8181	0.3782	3.7527	0.0793	1.2891
		RF	0.9359	1.0167	0.0213	3.9661	0.7168	2.5327	0.0535	1.9101
		BPNN	0.7284	2.0921	0.0439	1.9274	0.7196	2.5202	0.0532	1.9196
		XGboost	0.9492	0.9048	0.0190	4.4566	0.8069	2.0911	0.0442	2.3135
	RFE	Elastic Net	0.6390	2.4122	0.0506	1.6717	0.6275	2.9043	0.0613	1.6657
		RF	0.9378	1.0011	0.0210	4.0278	0.6491	2.8189	0.0595	1.7162
		BPNN	0.7166	2.1372	0.0448	1.8868	0.7056	2.5821	0.0545	1.8736
		XGboost	0.9666	0.7336	0.0154	5.4968	0.6000	3.0098	0.0636	1.6073
	CFS	Elastic Net	0.6928	2.2252	0.0466	1.8122	0.4244	3.6106	0.0763	1.3399
		RF	0.9344	1.0281	0.0215	3.9224	0.7002	2.6056	0.0550	1.8567
		BP	0.7367	2.0599	0.0432	1.9576	0.7310	2.4682	0.0521	1.9600
		XGboost	0.9640	0.7618	0.0160	5.2936	0.7077	2.5731	0.0543	1.8801

Note: the best results are in bold.

, at a flight altitude of 20 m, the regression model for estimating winter wheat canopy SPAD values during the cross-growth stage constructed using CFS feature selection and the XGBoost algorithm (CFS-XGBoost) achieves the best estimation accuracy. The model exhibits the following performance metrics: an R² value of 0.9584 and an RPD value of 4.9245 for the training set, with an RMSE value of 0.8188 and an RRMSE value of 0.0172. For the test set, the model achieves an R² value of 0.5963, RPD value of 1.5999, RMSE value of 3.0236, and RRMSE value of 0.0639.

On the other hand, at a flight altitude of 40 m, the regression model for estimating winter wheat canopy SPAD values during the cross-growth stage constructed using Pearson feature selection and the XGBoost algorithm (Pearson-XGBoost) achieves the best estimation accuracy. The specific performance metrics are as follows: an R2 value of 0.9492, an RPD value of 4.4566, an RMSE value of 0.9048, and an RRMSE value of 0.0190 for the training set. For the test set, the model achieves an R2 value of 0.8069, RPD value of 2.3135, RMSE value of 2.0911, and RRMSE value of 0.0442.

Therefore, the Pearson-XGBoost model (40 m) is considered the optimal model for estimating the SPAD values of winter wheat during the cross-growth stage.

To further analyze the modeling accuracy, Figure 4 presents a scatter plot of measured SPAD values versus predicted SPAD values for all optimal models. From the graph, it can be observed that most data points are clustered around the 1:1 diagonal line, indicating a good agreement between the measured and predicted SPAD values. The small errors between the predicted results and actual values demonstrate the model’s capability to accurately estimate the canopy SPAD values of wheat.

4. Discussion

4.1. The Optimal Inversion Models

This study involved wheat nitrogen management experiments in 72 plots, including four wheat varieties, four nitrogen application rates, and five nitrogen application methods. This led to a complex relationship between wheat canopy SPAD values and spectral variables. Machine learning algorithms have been widely used in crop quantitative remote sensing because they can accurately capture the dynamic relationship between variables and input–output mappings. Therefore, in this study, four machine learning algorithms (elastic net model, RF model, BPNN model, and XGBoost model) were constructed based on three different feature selection methods at 40 m and 20 m flight altitudes, and cross-validation and comparisons were performed.

This study found that the newly developed models work well for the cross-growth stage (the green-up stage and the jointing stage). Hence, the models are capable of handling dynamic changes during the two growth stages.

According to Viscarra Rossel et al. [66], the RPD values of the above optimal inversion models are all greater than 2.0, indicating excellent estimation. So, machine learning can accurately estimate SPAD values based on the inversion results of winter wheat SPAD values.

Compared to the linear model elastic net, nonlinear models such as RF, BPNN, and XGBoost are more favorable for revealing the changing patterns of complex intrinsic parameters such as vegetation chlorophyll. This is consistent with Tang et al. [67], in which they predicted field winter wheat yield using fewer parameters at the middle growth stage by linear regression and the BP neural network method, and they found that the BPNN model achieved the highest accuracy in predicting field wheat yield. However, the present study also found that the accuracy of the linear model elastic net in predicting wheat SPAD values was not consistently lower than the three nonlinear models, revealing that not all nonparametric models perform worse than parametric models in predicting wheat SPAD values.

In addition, previous studies have often focused on the estimation of SPAD values during the individual growth stages of crops. Compared to single-stage models, models capable of cross-growth stage estimation have higher practicality in agricultural production [68,69]. Surprisingly, the model established for wheat during the cross-growth stage achieved higher accuracy than the best model established during the green-up stage, although slightly lower than the best model established during the jointing stage. Cross-growth stage models can integrate data from different growth stages, enabling a comprehensive understanding of patterns and trends learned from multiple stages. This allows for a more accurate prediction of the overall trend and variations in wheat SPAD values, enhancing its generalization capability. This has significant implications for the large-scale field monitoring of crops, as it saves time and resources.

4.2. Effect of Different Flight Altitudes on the Estimation of SPAD Values

The impact of different flight altitudes on estimating SPAD values has been largely overlooked in previous studies. To investigate the response of the accuracy of the multispectral UAV-based model for estimating winter wheat SPAD values to different spatial resolutions, this study employed two flight altitudes, 20 m and 40 m, corresponding to spatial resolutions of 1.06 cm and 2.12 cm, respectively.

The results of winter wheat SPAD value estimation showed significant differences in the predictive and estimation accuracy of SPAD values when using four different models at the 20 m and 40 m flight altitudes. At the 40 m flight altitude, the spectral variables exhibited strong estimation capabilities for SPAD values, with good prediction accuracy and stability. However, at the 20 m flight altitude, the estimation capability for SPAD values was relatively limited compared to the 40 m altitude.

This implies that a higher image resolution does not necessarily lead to improved accuracy in SPAD value estimation. The spatial resolution of 2.12 cm provided a more precise match with the SPAD values measured using the SPAD-502Plus device. This finding is consistent with the conclusions of Guo et al. [70], who considered the scale effect on calculating vegetation indices and the influence it has on the estimation of corn SPAD values using machine learning algorithms; different flight altitudes (25 m, 50 m, 75 m, 100 m, and 125 m) were applied to capture aerial RGB images using UAVs. The results indicated that a flight altitude of 50 m (with a spatial resolution of 0.018 m) was the optimal choice for estimating corn SPAD values. It exhibited precise matching with ground samples of chlorophyll content measured using the SPAD-502Plus device.

The battery life of UAVs limits the geographical coverage achievable in a single flight, making UAVs less suitable for large-scale agricultural applications [71]. Higher flight altitudes are advantageous for remote sensing monitoring over larger geographic areas. Additionally, higher flight altitudes can reduce flight time, minimizing the negative impact of changing illumination conditions on quantitative remote sensing [20]. Importantly, this study found that compared to a flight altitude of 20 m, a higher altitude of 40 m improved accuracy in estimating winter wheat SPAD values. Therefore, determining the appropriate flight altitude for UAVs is crucial for enhancing the accuracy and efficiency of remote sensing estimation of winter wheat SPAD values.

4.3. The Influence of Different Variable Selection Methods on Machine Learning Algorithm Models

The estimation results of spectral variables can vary significantly on different remote sensing data [72], posing a challenge in selecting appropriate spectral variables for estimating SPAD values of winter wheat at different growth stages and under different flight altitudes of unmanned aerial vehicles (UAVs). However, the application of variable selection in vegetation-chlorophyll-content remote sensing research based on machine learning is limited.

Through the three variable selection methods, Pearson, RFE, and CFS, optimal spectral variables for modeling were selected. According to Table 8, regardless of the growth stage, flight altitude, and selection method, NIR, RDVI, MSAVI, GNDVI, SAVI, SR, MTVI, and CIgreen were frequently selected as the spectral variables involved in the modeling. Among them, NIR was the most frequently selected spectral variable, and the other selected spectral variables were combinations of NIR with other bands. This finding is consistent with the conclusion of Zhang et al. [73] that using visible and NIR spectral sensors for predicting SPAD values of winter wheat can achieve good accuracy and precision.

In the limited studies that have applied variable selection techniques in vegetation-chlorophyll-content remote sensing, most of them have only considered the relationship between spectral variables and SPAD values, without considering the relationships among spectral variables themselves. For instance, Wang et al. [19] reported that the RF and SVR_linear models using the RFE variable selection method provided overall higher R2 and more robust results for estimating winter wheat canopy SPAD values compared to the RF or r variable selection methods with RF and SVR_linear models. In this study, the modeling results for the green-up stage and jointing stage both showed that the combination of the CFS feature selection method and RF algorithm yielded the best SPAD estimation capability at a flight altitude of 40 m. At a flight altitude of 20 m, the combination of the RFE feature selection method and BPNN algorithm produced the best SPAD estimation capability, followed by the combination of the CFS feature selection method and BPNN algorithm. During the cross-growth stage modeling, the CFS-BPNN combination still demonstrated high model accuracy. Overall, the combination of the CFS feature selection method and BPNN algorithm provided higher R² values and more robust results compared to the combinations of Pearson and RFE variable selection methods with the BPNN algorithm.

The advantage of the CFS variable selection method, compared to Pearson and RFE, lies in considering the correlations among features during variable selection. Therefore, the CFS method can comprehensively consider the interactions among features, thus improving the prediction accuracy of the model.

4.4. Limitations and Future Research Perspectives

This study only collected multiscale spectral data at two UAV flight altitudes of 20 m and 40 m. In the future, higher flight altitudes will be explored to investigate further the influence of UAV multispectral imagery spatial resolution on the extraction of winter wheat SPAD values and other vegetation parameters.

Furthermore, this study used data from two key growth stages (green-up and jointing stages) of four different winter wheat varieties and 72 plots. Future research can collect data from multiple stages of different winter wheat varieties, use larger-scale datasets, and establish models that can span the entire growth period to better adapt to different growth stages and improve the applicability and reliability of the models.

In future research, we will consider collecting data over multiple years to evaluate the consistency and repeatability of our results. Additionally, we will broaden our research scope to include other crops or plants to further validate and generalize our findings. We also aim to integrate our research outcomes with precision agriculture tools and technologies to optimize fertilization and irrigation practices.

5. Conclusions

This study focuses on the estimation accuracies of winter wheat canopy SPAD values at different growth stages and UAV flight altitudes. The results of this study indicate that UAV flight altitude significantly impacts the estimation accuracy of crop SPAD values and other vegetation parameters. Compared to the 20 m flight altitude (with a spatial resolution of 1.06 cm), the multispectral imagery obtained by the UAV at a flight altitude of 40 m (with a spatial resolution of 2.12 cm) showed stronger estimation capabilities for SPAD values, with better predictive accuracy and stability. Furthermore, the combination of different feature selection methods and machine learning algorithms also considerably impacts the estimation accuracy. The optimal combination of feature selection methods and machine learning algorithms can more accurately estimate winter wheat SPAD values.

In the modeling of single growth stages (the green-up stage or the jointing stage), the optimal prediction results for SPAD values were achieved under the 40 m altitude condition, using the CFS variable selection method combined with the RF algorithm to construct the CFS-RF (40 m) model. In the modeling of cross-growth stages, the optimal prediction result for SPAD values was obtained under the 40 m altitude condition, using the Pearson variable selection method combined with the XGBoost algorithm to construct the Pearson-XGBoost (40 m) model.

This study improves the accuracy of the optimal models for estimating winter wheat SPAD values by optimizing UAV flight strategies and combining various feature selection methods and machine learning algorithms. This study also establishes high-accuracy models that can span multiple growth stages and include various winter wheat varieties, enhancing the research findings’ universality and providing a practical application for actual production settings.