Abstract
With the advent of deep learning, significant progress has been made in low-light image enhancement methods. However, deep learning requires enormous paired training data, which is challenging to capture in real-world scenarios. To address this limitation, this paper presents a novel unsupervised low-light image enhancement method, which first introduces the frequency-domain features of images in low-light image enhancement tasks. Our work is inspired by imagining a digital image as a spatially varying metaphoric “field of light”, then subjecting the influence of physical processes such as diffraction and coherent detection back onto the original image space via a frequency-domain to spatial-domain transformation (inverse Fourier transform). However, the mathematical model created by this physical process still requires complex manual tuning of the parameters for different scene conditions to achieve the best adjustment. Therefore, we proposed a dual-branch convolution network to estimate pixel-wise and high-order spatial interactions for dynamic range adjustment of the frequency feature of the given low-light image. Guided by the frequency feature from the “field of light” and parameter estimation networks, our method enables dynamic enhancement of low-light images. Extensive experiments have shown that our method performs well compared to state-of-the-art unsupervised methods, and its performance approximates the level of the state-of-the-art supervised methods qualitatively and quantitatively. At the same time, the light network structure design allows the proposed method to have extremely fast inference speed (near 150 FPS on an NVIDIA 3090 Ti GPU for an image of size ). Furthermore, the potential benefits of our method to object detection in the dark are discussed.
1. Introduction
Image capturing in suboptimal lighting conditions is a common occurrence, leading to images with low brightness, poor contrast, and color distortion, which consequently hinder computer vision tasks, including object detection and image segmentation. To combat these issues, low-light image enhancement has emerged as an essential research topic in computer vision, particularly for improving the visual fidelity of suboptimal photos. However, suboptimal lighting conditions necessitate a comprehensive approach rather than simply amplifying brightness to enhance the contrast, as this may inversely impact the overall quality of the image. Therefore, addressing the fundamental causes of low-light imaging is crucial to produce high-quality images that meet the needs of various tasks in computer vision and image analysis.
Various traditional methods have been proposed to further mitigate the degradation caused by low-light conditions. These methods are divided into two main categories. Some of the methods depended on the Retinex Theory [1,2] and the others based on histogram equalization [3,4]. The Retinex-based method involves the decomposition of images into reflection and illumination components. The first component contains information about the scene’s inherent attributes such as texture, edge details, and color. Meanwhile, the second component contains distribution information on contours and lighting. On the other hand, the main idea behind histogram equalization methods is to increase the dynamic range of the gray values in an image by adjusting its gray distribution. It is achieved by rearranging the pixels of the image to improve its overall dynamic range. These proposed methods use image-specific curve mapping instead of randomly changing the histogram distribution or relying on inaccurate physical models, resulting in natural enhancement without creating unrealistic artifacts. However, previous methods may still have limitations, particularly concerning their processing of high-noise pictures and their potential to cause insufficient local brightness enhancement and loss of details.
In recent years, deep Convolutional Neural Networks (CNNs) have established the state of the art [5,6,7] in low-light image enhancement due to their ability to learn superior feature representation. Advanced techniques have emerged for image enhancement, such as end-to-end learning methods, methods based on learning the components of illumination, and unsupervised and semi-supervised learning methods. In the context of low-light image enhancement, CNN models are designed to learn the mapping between a dark input image and its enhanced counterpart. This mapping can be formulated as a regression problem, where the network is trained to predict the enhanced image given the dark input as the input. To achieve this, CNN models make use of multiple convolutional layers, which extract local patterns and features from the input image. Moreover, some state-of-the-art models integrate different CNN architectures [7,8] with attention mechanisms [8] to selectively enhance image details while preserving the overall image content. However, most CNN-based methods necessitate paired training data, which is challenging to acquire for the same scene with both low-light and normal-light images. To address this, unsupervised deep learning-based methods have been proposed. One of the most representative models is the Generative Adversarial Network (GAN) [9,10,11] for low-light image enhancement. GANs consist of two main components: a generator and a discriminator. The generator network generates enhanced images, while the discriminator network evaluates the realism of these generated images. The training process involves a competitive game between the generator and discriminator. The generator aims to generate images that can deceive the discriminator, while the discriminator aims to accurately classify real and generated images. Through this adversarial training process, the generator learns to produce visually pleasing and realistic enhancements. Some of the state-of-art methods have also tried to integrate attention mechanisms in the generator to generate finer enhanced images However, since these methods lack ground-truth data to guild the network training, they often rely on carefully selected training data and may produce artifacts or unrealistic enhancements in the generated images. Moreover, GAN models, usually with complex architectures, can require significant computational resources and training time than the CNN-based methods. Furthermore, deep neural networks may pose challenges for practical applications, mainly due to their high memory footprint and long inference time. Thus, the need arises for deep models with low computational cost and fast inference speed for deployment on resource-limited and real-time devices, such as mobile platforms.
Through a brief survey of the model-based and data-driven methods, it is not difficult to find that three significant challenges in low-light image enhancement still exist, which are listed below.
- (1)
- Model-based methods aim to build an explicit model to enhance low-light images, but suboptimal lighting conditions dramatically increase model complexity. Therefore, these methods require the complex manual tuning of parameters and even the idealization of some mathematical processes, making it challenging to achieve dynamic adjustment and even more difficult to achieve optimal enhancement results;
- (2)
- Data-driven methods typically employ a limited size of convolutional kernels to extract image features, which have a limited receptive field to obtain global illumination information for adaptive image enhancement. Consequently, bright areas in the original image may become over-exposed after enhancement processing, leading to poor overall visibility. Furthermore, a natural concern for data-driven methods is the necessity to acquire large amounts of high-quality data, which is very costly and difficult, especially when these data have to be acquired under real-world illumination conditions for the same scenarios;
- (3)
- Moreover, although deep neural networks have shown impressive performance in image enhancement and restoration, their massive parameter leads to large memory requirements and long inference time, making them unsuitable for resource-limited and real-time devices. To address these issues, designing deep neural networks with optimized network structures and reduced parameters is crucial for practical engineering and real-time device applications, where a low computational cost and fast inference speed of deep models are highly desired.
Considering the issues above and inspired by previous works [6,7,12], this paper explores the integration of physical-based reasoning into the data-driven method of low-light enhancement. Therefore, aiming at the above situation, we propose a novel end-to-end neural network named the Unsupervised Low-Light Image Enhancement via Virtual Diffraction in Frequency Domain (ULEFD). The main contributions are summarized below.
- (1)
- Inspired by previous work [12], we proposed a novel low-light image enhancement method that mapped the physics occurring from the frequency domain into a deep neural network architecture to build a more efficient image enhancement algorithm. The proposed method can balance broad applications and performance of the model-based and data-driven based method, as well as data efficiency and a large requirement of training data;
- (2)
- Considering strong feature consistency in images under varying lighting conditions, this paper designed an unsupervised learning network based on the recursive-based gated convolution block to obtain the global illumination information from the low-light image. Furthermore, the unsupervised network is independent of paired and unpaired training data. Through this process, the network is able to extract higher-order, consistent illumination features in images, thus providing support for the global adaptive image enhancement task without the large amounts of high-quality data;
- (3)
- In this paper, the superiority of the proposed unsupervised algorithm is verified by comparative experiments with the state-of-the-art unsupervised algorithms based on the different low-light public datasets. Furthermore, the expansion experiment demonstrated that the ULEFD can be accelerated in both physical modeling and network structure levels while still keeping impressive image enhancement performance, which has great potential for deployment on resource-limited devices for real-time image enhancement.
The rest of this work is structured as follows: Section 2 concerns related work, describing current related approaches to low-light image enhancement and the existing problems. In Section 3, the proposed image enhancement method ULEFD is described in detail. Section 4 provides the experimental results and discussion. Meanwhile, the expansion experiments for our method and the comparison methods are also provided in Section 4. Finally, conclusions and future work are drawn in Section 5.
2. Related Work
For decades, low-light image enhancement has received significant attention in computer version tasks. As mentioned above, the mainstream methods for low-light image enhancement can be roughly categorized as model-based and data-driven methods. This section briefly reviews these related works and discusses the inspiration from these methods.
2.1. Model-Based Methods
Low-light image enhancement is a critical area for image processing, with a range of classical and more recent algorithms developed to improve image quality in low-light conditions [5]. Model-based methods include Gamma Correction [13,14], Histogram Equalization [15,16,17,18,19], and Retinex Theory [1,20,21,22], each with its strengths and weaknesses. Gamma Correction edits the gamma curve of the image to improve contrast by detecting dark and light segments of the image but struggles with complex global parameter selection and local over-exposure [23]. Histogram Equalization stretches the dynamic range of the image by equally distributing pixel values but can lead to artifacts and unexpected local over-exposure as well [6]. However, Histogram Equalization methods are still widely relied on, despite their tendency to suffer from color distortion and other image artifacts. The Retinex Theory decomposes images into reflectance and illumination maps to estimate and enhance illumination in non-uniform lighting conditions. However, these methods can lead to unrealistic or partially over-enhanced images without carefully accounting for noise and other factors [8]. More recent methods abandon these approaches to employ image-specific curve mapping for light enhancement, which enables broader dynamic range adjustment and avoids creating unrealistic artifacts. In addition, several other model-based approaches, including frequency-based [12] and image fusion [9], are also commonly used to enhance images in low-light conditions. These methods expand the research avenues of low-light image enhancement methods from different perspectives. However, these types of methods also suffer from the inability to achieve adaptive adjustment for low-light images. In general, model-driven methods rely on mathematical models or assumptions about the underlying image formation process. These methods typically involve handcrafted image processing algorithms that explicitly capture the characteristics of low-light image degradation and aim to restore the image based on these assumptions. These methods have better interpretability, which can provide insights into the physical processes underlying low-light image degradation. However, model-driven methods heavily depend on the accuracy of the assumed degradation models. If the real-world degradation deviates significantly from the assumptions made by the model, the performance of these methods may be limited. Moreover, low-light image degradation can be caused by various factors, such as noise, blur, and non-uniform illumination. Designing a model-driven approach that accurately captures all these complexities becomes challenging, and the performance can suffer accordingly.
2.2. Data-Driven Methods
Data-driven methods typically rely on either Convolutional Neural Network (CNN)-based or Generative Adversarial Network (GAN)-based approaches. Most CNN-based methods require paired data for supervised training [8,24,25,26,27], which can be resource-intensive to obtain. It often involves collecting data through automated light degradation and altering camera settings during image acquisition or retouching. To improve the weakness, some CNN-based methods, such as LL-Net [28] and MBLLEN [29], generate synthetic data through gamma correction or photosensitivity changes, while datasets such as LOL [24] and MIT-Adobe FiveK [30] collect paired low-/normal-light images. Retinex-based deep models [25,31,32,33] are also trained on paired data. Frequency-based decomposition-and-enhancement models, such as [34], use real low-light datasets for training. Nonetheless, these methods are constrained by the amount of paired data required and often yield poor generalization capabilities. In contrast, unsupervised GAN-based [10,11,35] methods such as EnlightenGAN [11] and semi-supervised models such as [36] learn to enhance images without paired data, although a careful selection of unpaired data is needed. While such methods eliminate paired data’s drawbacks, generalization and overfitting are still challenges. Overall, the data-based method can effectively learn complex relationships between low-light and enhanced images without relying on explicit assumptions or constraints. This adaptability allows them to handle a wide range of low-light conditions and variations. In addition, these methods enable end-to-end learning, where the model learns to automatically optimize the enhancement process based on the provided training data. This holistic approach can lead to improved overall performance, as the model learns to address various low-light challenges concurrently. However, it is worth noting that neural networks used in data-driven methods are often considered black boxes, making it challenging to interpret the learned representations or understand the underlying enhancement process. On the other hand, although reference images or any prior knowledge about the image formation process are not required to guide learning, the Zero-DCE++ [6] still relies on large-scale training data, which may suffer if the available data do not cover the entire range of low-light scenarios or if it contains biases that affect model generalization. Ultimately, data-driven methods are a promising and constantly evolving field, with ongoing research (such as integrating different neural network architectures [7,8,35] with attention mechanisms [8]) into overcoming these challenges and improving low-light image enhancement. Furthermore, these improvements also come at a cost; for most of the data-driven methods, a complex and large-scale network is introduced for image enhancement, and the massive number of parameters makes these methods time-consuming. When applied in real-time applications, significant delays may occur. Table 1 summarizes the main properties of the different types of methods.

Table 1.
The main properties of model-based methods and data-driven based methods.
In summary, model-based methods, which aim to build an explicit model to enhance low-light images, possess resource-friendly properties and impressive data efficiency due to their universal underlying physical rules. However, when applied in different scenarios, these methods must converge to a good enough local optimum through carefully designed handcrafted priors or specific statistical models. In contrast, data-driven methods can improve the ability of model-based methods to understand and analyze data by incorporating a larger number of parameters. This allows for an implicit representation of enhancement modeling, resulting in a high-quality local optimum when the model is adequately trained. However, it is important to note that these methods require large amounts of carefully selected paired or unpaired data, which are often difficult to obtain. Additionally, these implicit models restrict the scope of their application due to the lack of general model-based reasoning and may suffer from overfitting. On the other hand, some data-driven methods, thanks to their larger number of parameters, are able to dynamically adjust to low-light image enhancement tasks. Nevertheless, this also brings higher computational costs.
3. Materials and Methods
Figure 1 illustrates the detailed structure of ULEFD, which comprises two primary modules: the Brightness Adjustment in Frequency-Domain (BAFD) component and the Global Enhancement Net (GEN) component. The BAFD component takes the L channel as an input and transforms the L channel from the spatial domain to the frequency domain. Inspired by the [12], the digital image can be reimaged as a spatially varying metaphoric “field of light”. After transferring this “field of light” to the frequency domain, it can provide image brightness adjustment information from physical processes such as diffraction and coherence detection. In addition, to overcome the problem, the original physical brightness adjustment model requires complex manual tuning of parameters in various scenes, and the adjustment effect can only converge to suboptimal results. We used a lightweight network architecture to extract the L channel feature to achieve dynamic adjustment of the turning of paraments.
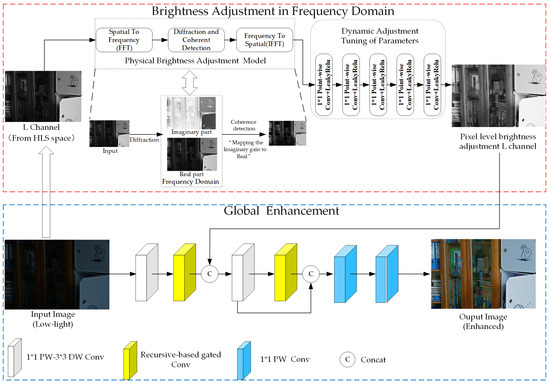
Figure 1.
The detailed structure of the proposed method.
The GEN component takes the low-light image and the dynamic brightness adjustment proposal as inputs and enhances the image with some carefully designed loss functions. It consists of different types of convolutional layers, especially the recursive-based convolution block block with a variable receptive field to capture local and global image information and generate high-order spatial information interaction for better performance of the low-light enhancement.
3.1. Brightness Adjustment in Frequency-Domain Component
3.1.1. Physical Brightness Adjustment
In [12], the authors demonstrate that introducing the concepts of virtual light field to use the frequency-domain information of images as low-light image enhancement has significant effects. Specifically, let be the original spatial domain digital image. The virtual “field of light” of can be represented as:
where represents the spatial spectrum of the virtual “field of light” and represents the signal(pixel coordinates) in the frequency domain. Then, the brightness gain can be obtained by transforming the spatial signal to the frequency domain, and this gain can be represented as a spectral phase: , the brightness adjustment can be defined as:
In the end, the brightness gain in the frequency domain needs to be mapped back to the image in the normal spatial domain as:
where refers to the inverse Fourier transform, and now contains frequency-dependent brightness gain entirely described by the phase function .
As known, digital images have three bands corresponding to the three fundamental color channels (RGB). However, when performing low-light image enhancement, it is necessary to adjust the image brightness range while preserving the original color saturation information of the image. This requires separating the color information from the luminance information to the greatest extent possible. Therefore, we tried different color space conversion methods to keep the image color saturation information as much as possible and adjust only the image brightness information. As shown in Figure 2, through experiments, we found that brightness adjustment of the image in HLS space [37] has the best effect on preserving the original color saturation information of the image.

Figure 2.
Ablation study of the advantage of HLS color space.
3.1.2. Mathematical Modeling
Given our focus on digital images, we transition from a continuous-valued in the spatial domain to a pixelated waveform . In the frequency domain, the discrete waveform is expressed as a sum of complex exponential waves with different frequencies:
where N is the number of pixels in each dimension, j is the imaginary unit, and is the discrete Fourier transform (DFT) of defined as:
Similarly, we shift from continuous to discrete momentum .
Therefore, the Gaussian function with zero mean and variance T can be used for the phase function transformation as:
Resulting in a spectral brightness adjustment operator,
where S is a parameter that maps the loss or gain of spectral brightness adjustment.
Following the spectral intensity adjustment and inverse Fourier transform operation, coherent detection generates the real and imaginary parts of the optical field. The combined processes of diffraction with the low pass spectral phase and coherent detection produce the output of the physical brightness adjustment model:
where denotes the Fourier transform operation, and processes the computation of the phase from a complex-valued function of its argument.
In summary, in order to use the interference information obtained in the frequency-domain space at different phases as the brightness adjustment gain of the digital input image, we first add a small constant bias term b to the light field corresponding to the input image to make the numerical calculation more stable and to achieve the effect of noise reduction. Then, the input image in the spatial domain is transformed to the frequency domain by the FFT and subsequently multiplied with the complex exponential elements, the parameters of which define the frequency-dependent phase. The inverse Fourier transform (IFFT) is then used to return a complex signal in the spatial domain. Mathematically, the inverse tangent operation in phase detection behaves like an activation function. Before calculating the phase, the signal is multiplied by a parameter called the phase activation gain G. The output phase is normalized to match the image formatting convention [0–255]. This output is then injected into the original image as a new L channel in HSL color space (for low-light enhancement). Thus, the output of the physical brightness adjustment model can be represented as:
where and is the imaginary and real component of , and is used for calculating the phase gain of the diffraction in frequency domain.
3.1.3. Dynamic Adjustment Tuning
The established brightness adjustment model contains three adjustable parameters: the mapping parameter S, bias term b, and phase gain parameter G. The parameters mentioned earlier need manual adjustment to enhance low-light images under varied conditions. Inspired by previous work [6], we propose to extract global information from the L channel of the low-light image and use a five-layer multi-layer perceptron, which consists of five layers of 3*3 point-by-point convolution to learn the parameters as mentioned earlier from the sufficient dataset. This processing can be represented as:
where represents the L channel of the low-light image I in the HLS color space, and represents the processing of learning these parameters via the five-layer multi-layer perceptron.
After obtaining the pixel brightness adjustment proposal in the L channel, it will be concatenated with the middle layer of GEN and fed into the GEN for further enhancement. The entire ULEFD is trained end-to-end, which means that all the components are trained jointly to optimize the overall performance of the network.
3.2. Global Enhancement Net
When utilizing traditional convolutional kernels for image feature extraction, the limited perceptual fields make it challenging for the network to comprehensively understand the image. Moreover, the enhanced image is exceptionally vulnerable to noise as there is a lack of information in the low-illumination image. To address these issues, this paper proposes a Global Light Enhancement Net containing three different convolution structures.
As Figure 1 shows, firstly, the point-wise ( kernel size) and Depth-wise ( kernel size) convolution block is used to extract the input low-light image feature. More specifically, point-wise convolution is applied to aggregate pixel-level cross-channel context, then depth-wise convolution to encode channel-level spatial context. This convolution structure has been applied in state-of-the-art image restoration methods [38,39], proving its effectiveness in image noise reduction.
The essential operation in CNN is “convolution”, which provides local connectivity and translation equivariance, features that bring efficiency and versatility to CNNs. However, while enhancing low-light images, the consistency of the original images in terms of color, contrast, and other image information should be ensured. The small size of conventional convolutional kernels limits their field of perception and thus cannot model long-range pixel correlations, making it difficult to retain consistent information about the global image. To address this challenge, this paper introduces a recursive gated depth convolutional neural network [40], which focuses on using the recursive gated convolution for higher-order interaction of image information and long-distance image information modeling. Specifically, the gating mechanism can selectively combine information from the different kernel sizes of the convolution based on the importance of features. By assigning different weights to the features, the model can prioritize important details while suppressing noise and artifacts. At the same time, it allows for the hierarchical representation of images, capturing both local and global structure information. Thus, the gating mechanism helps to ensure that the restored image remains consistent with the original image. Moreover, the recursive architecture design helps to build high-order spatial interactions of image information to preserve the consistency of the image throughout the image enhancement process. The use of residual connections allows the GEN component to learn residual information directly. By learning the difference between input and output images, the network can focus on modeling the enhancement details rather than attempting to reconstruct the entire image. This residual learning enhances the network’s capacity for image enhancement and preserves image consistency. Benefiting from these abilities, the network is able to avoid severe noise distortion and color degradation when enhancing the dark regions on the input low-light images.
3.3. Loss Function
Due to the lack of absolute supervision information to guide the training process, it is tough to recover these two components from low-light images. The only way is to use relative information in loss function designing, which reduces the assumption of the existence of absolute ground-truth data. Previous unsupervised methods have proposed some useful loss functions, such as normalized gradient loss [41], spatial consistency loss [6,7], and perception loss [11]. However, only some achieve impressive results, mainly due to the ineffective use of more specific constraint information in designing these loss functions. Therefore, in this paper, we design each loss function of the algorithm for the image feature information in different components.
3.3.1. Loss for Brightness Adjustment in Frequency-Domain Component
First, for the component of brightness adjustment in the frequency domain, Low-light degradation causes changes in pixel intensity and color distribution of images. Therefore, we adopt the image color histogram prior to constraining the dynamic brightness adjustment. Specifically, we define an MSE loss inspired by [23,42]. The main idea of this loss function design is that the color histogram prior information contains not only the input low-light image’s color distribution information but also the image’s structural and semantic information at the higher level, which can be extracted from this color distribution information. The kernel density estimation has been used to keep the loss differentiable:
where N represents the batch size of the input, represents the input low-light image, represents the enhanced image, and represents the obtained color histogram prior.
In addition, the image maintains its natural and explicit detail content to make the brightness adjustment, and the smooth illumination loss function is designed. The main idea is to make the model more focused on image edges and textures by processing the gradient information of the low-light and enhanced images. More specifically, the loss function consists of two different components. The first component is the gradient loss calculation along the x and y directions.
where represents the normalization of the gradient of the pixel on the low-illumination image, represents the normalization of the gradient of the piexl on the image after enhancement, and H and W represent the height and weight of the image. Moreover, ReLU represents the rectified linear unit function.
The other component of is:
where represents the absolute value of the difference between the gradient of the enhanced image and the low-light image, p represents the parametric number (e.g., L1-norm or L2-norm), is a very small constant (e.g., 1 × 10−4), C is the number of the image channel, and H and W are the height and weight of the image. In summary, the total loss function is:
3.3.2. Loss for Global Enhancement Component
From the two aspects of maintaining image color and contrast consistency, two loss functions are applied in this paper for global light enhancement. The first loss function is color constancy loss. The main idea is to calculate the mean channel value for both the enhanced image and the input low-light image to obtain the average pixel values of the enhanced image and the input low-light image . The processing can be defined as follows:
where c represents the picture channel (red, green, blue), and H and W are the height and width of the image. Then, the ratio difference between the three different color channels is calculated as follows:
where represent the pixel values of the r, g, and b channels of the enhanced image, respectively. Correspondingly, represent the pixel values of the r, g, and b channels of the original image. The final color consistency loss is obtained by summing the above three ratio differences and taking the mean value of the results:
where N is the number of images.
To preserve the contrast consistency, we add a gradient consistency loss. The main idea is to extract the gradients of each channel and calculate the gradient consistency loss by comparing the similarity of the corresponding gradients in the original and enhanced images. The gradient consistency loss can be represented as:
where and represent the gradients of the enhanced and original image, respectively; i represents the number of images; and c represents the color channel of the images.
In the end, we use an exposure control loss () to control the exposure level and avoid under-/over-exposed regions. This loss function quantifies the difference between the average intensity value of a local region and the desired level of well-exposedness (E). The calculation of this loss function consists of the following main steps. First, the enhanced image is fed into the function, which performs an averaging pooling operation and calculates its grayscale value, obtained by averaging the pixel values of the red, green, and blue channels.
where r represents the window size of the pooling operation, and represent the color channel of the image. Then, calculate the difference between the average grayscale value and the given threshold, take the absolute value, and then average to obtain the exposure control loss as follows:
where n represents the number of windows for pooling operation, represents the average value of the pooling window, and E is the given threshold. The range of values is 5–7, and in our experiments the value is . Specifically, if you want the exposure adjustment to be dramatic, choose a larger value in this range if possible, and vice versa, choose a smaller value. Beyond the range, the image will be over-exposed or underexposed.
In summary, the total loss function for the proposed method can be expressed as follows:
where the weights are used for balancing the scales of different losses. According to the effect of the the model training convergence, the values of are taken as (0.1, 1, 1, 0.5, 1), respectively.
4. Experiment and Results
In this section, we present the implementation details of our proposed low-light image enhancement method. Afterward, we perform both qualitative and quantitative comparisons with state-of-the-art supervised and unsupervised methods, utilizing traditional metrics such as Peak Signal-to-Noise Ratio (PSNR), Structural Similarity Index (SSIM) [43], and Natural Image Quality Evaluator (NIQE) [44]. In addition, we conduct ablation studies to demonstrate the effectiveness of each component or loss in the proposed method. Finally, we investigate the performance of our method to improve the efficiency of downstream tasks, such as face detection in the dark.
4.1. Implementation Details
The framework is implemented with PyTorch on an NVIDIA 3090 Ti GPU with 24 GB memory. The batch size used for training is 64. We use the Adam optimizer to train the network with an initial learning rate of 1 × 10−4 and a decay rate of 0.5 every 50 epochs. We mainly use two datasets for training and comparisons: the LOL dataset [24] and VE-LOL dataset [45].
4.2. Quantitative Evaluation
In this section, we compare our method with several state-of-the-art low-light image enhancement methods. These methods include one conventional method (Vevid [12]), three supervised methods(KinD++ [26], Restormer [38], LACN [8]), and four unsupervised methods (Zero-DCE++ [6], Reference-freeLLIE [46], EnlightGAN [11], LE-GAN [35]). To demonstrate the robustness of our proposed method, we give more experiments on cross-datasets. We have fine-tuned all the above methods on the train sets of LOL and VE-LOL datasets and then evaluated them on their test sets. From Table 2, our method achieves significantly better results among all unsupervised methods, and its performance approximates the level of the state-of-the-art supervised methods. It is obvious that the proposed ULEFD can achieve better PSNR than other unsupervised methods and some supervised methods, whether trained on the LOL or VE-LOL dataset. Regarding SSIM, the proposed method achieved results close to the supervised methods KinD++ [26] and Restormer [38], which do not require any reference images for training. However, the proposed method has fewer parameters (only 70 K parameters) and costs less running time during testing.

Table 2.
Quantitative comparison results on (LOL [24] and VE-LOL [45]) datasets. Red, blue, and green indicate the best and the second-best and third-best results, respectively. Where ↑ means bigger values are better, and ↓ means smaller values are better.
To further demonstrate the generalization ability of the proposed method, we have tested the proposed method on some real-world low-light image sets, including DICM [18] (64 images), LIME [21] (10 images), VV1 (24 images), LCDP [47], and SCIE [48] (select 100 low-light images from the datasets). In the expanding experiments, we use unpaired public datasets and the NIQE (Naturalness and Image Quality Evaluator) and BRISQUE (Blind/Referenceless Image Spatial Quality Evaluator) metrics to compare the proposed method quantitatively with state-of-the-art methods that assess natural image restoration without requiring ground truth. Table 3 contains the NIQE scores for five different public datasets that were previously used in relevant studies. In summary, these experimental results show the effectiveness of our proposed method.

Table 3.
NIQE and BRISQUE scores on low-light image sets (DICM [18], LIME [21], VV 1, LCDP [47], SCIE [48]). The best result is in red, whereas the second-best results are in blue, and the third best results are in green, respectively. Smaller NIQE scores indicate a better quality of perceptual tendency.
4.3. Qualitative Evaluation
Figure 3 shows some representative results for visual comparison from the LOL dataset. We have zoomed in on the details inside the red and green bounding boxes to further investigate the differences between these comparison methods. The enhanced results show that the conventional method LIME [21] enhances the images by directly estimating the illumination map but has some external noises. For unsupervised methods, Zero-DCE++ [6] produces under-enhanced and noisy results, respectively. Meanwhile, the KIND++ [26] has apparent noise and weak illumination. EnlightenGAN [11] suffers from under-enhanced and over-smoothing. The LE-GAN [35] performs better than the EnlightenGAN but is still under-enhanced in some local details. Benefiting from the introduction of the normal illumination reference image, the image enhancement effect of the Restormer [38] is closest to the ground truth. In contrast, Figure 3 shows that our method can well preserve the structural and textural image details without reference images to guide the network. It demonstrates that our proposed method achieves more satisfactory visualization results than the unsupervised learning methods for comparison, especially in the exposure level, structure description, and color saturation.

Figure 3.
Qualitative results on LOL test dataset.
Figure 4 shows some representative results for visual comparison from the VE-LOL dataset. This dataset further expands the scenario based on the LOL dataset. The enhanced results show that the LIME [21] has severe contrast and noise issues. For unsupervised methods, the results of Zero-DCE++ [6] also suffer from extreme contrast and noise issue. KIND++ [26] has weak illumination. EnlightenGAN [11] still suffers from under-enhanced and over-smoothing. Regarding the LE-GAN [35], the global enhancement effect is better than the above methods, but there are some issues of color distortion in a few details. In terms of global and local effects of image enhancement, the proposed method in this paper, especially the model trained on the VE-LOL training set, is able to obtain almost the same enhancement results as the Restormer [38], which is the supervised learning method, achieving visual quality close to the ground truth.

Figure 4.
Qualitative results on VE-LOL test dataset.
Figure 5 shows the image enhancement effect of the algorithm in this paper and other comparison algorithms in real low-light scenarios, respectively. Zero-DCE++ [6] fail to suppress noise when the background of the scenarios is extremely dark in the DICM [18] and LIME [21] datasets. Meanwhile, EnlightenGAN [11] provides limited image enhancement in the above scenarios. KIND++ [26] suffer from blurring artifacts in the LIME [21] dataset. As for the LCDP [47] datasets, Zero-DCE++ [6] and LE-GAN [35] easily lead to over-exposure artifacts and blurriness, which make the results distorted and glaring with information loss. LIME [21] retains the contrast information of images in all of the datasets relatively well, but the overall enhancement effect is weak. In contrast, our proposed method in all datasets tends to generate the same performance as the state-of-the-art supervised method Restormer [38], with proper color contrast, sufficient detailed information, and acceptable and controllable noise.
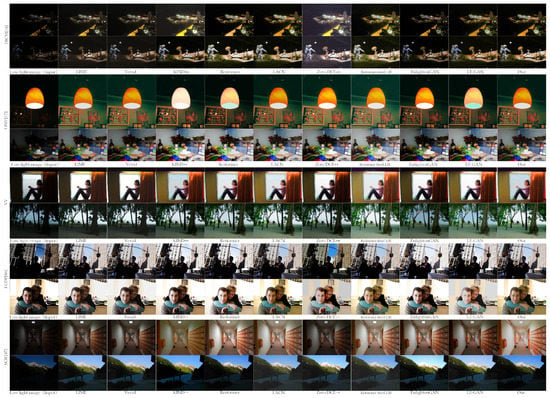
Figure 5.
Qualitative results on DICM [18], LIME [21], VV 1, LCDP [47], and SCIE [48] datasets, respectively.
4.4. Ablation Study
4.4.1. Contribution of BAFD Component
In this ablation study, the network only has the GEN component, and the three associated loss functions , , and are considered as the baseline model. The effects of adding the BAFD component and losses proposed in this paper were compared and studied. The results are presented in Table 4.

Table 4.
The influence of BAFD component and loss functions based on relative information. During training. Relative losses represent .
From Table 4, it can be observed that when we add the other losses proposed in this paper or the BAFD component to the baseline model, both PSNR and SSIM show improvement. This proves the effectiveness of the BAFD component and the loss functions designed with relative information. The BAFD component can adjust the global brightness information and integrate it into the enhancement process with few parameters, which can effectively improve the PSNR by 2.87 dB and the SSIM value by 0.02 (PSNR: , SSIM: ).
4.4.2. Contribution of Each Loss
In this ablation study, we present the results of ULEFD trained by various combinations of losses. As shown in Table 5, the performance of the proposed ULEFD steadily increases with the addition of five loss functions, and the effectiveness of our hybrid loss function is proved. As shown in Figure 6, the result without the BAFD component has limited brightness adjustment than the full result. The result of smooth illumination loss has a relatively lower color contrast than the full result. Severe color casts emerge when histogram prior loss to is discarded.

Table 5.
The influence of different training losses.

Figure 6.
Ablation study of the contribution of BAFD component and each loss (histogram prior loss , smooth illumination loss , color constancy loss , gradient consistency loss exposure control loss ). Red boxes indicate the obvious differences and amplified details.
Meanwhile, it hampers the correlations between neighboring regions leading to apparent artifacts. Removing the color constancy loss fails to recover the color contrast of the image. Removing the gradient consistency loss hampers the correlations between neighboring regions leading to apparent artifacts. Finally, Removing the exposure control loss fails to brighten the image compared with the full result. Such results demonstrate that the BAFD component and each loss used in the proposed method play a significant role in achieving the final visually pleasing results.
4.5. Pedestrian Detection in the Dark
In this section, we aim to evaluate the effectiveness of low-light image enhancement methods for the pedestrian detection task in low-light conditions. We utilized the DARK FACE dataset [49], which consists of 10,000 images captured in low-light conditions. Since the label of the test set is not accessible to the public, we opt to evaluate the proposed method on the training and validation sets comprising 6000 images. We adopted the public deep face detector, Dual Shot Face Detector (DSFD) [50], which pre-trained on the WIDER FACE dataset [51], to serve as our baseline model. The results of various low-light image enhancement methods were fed to the DSFD [50] for analysis. We utilized the evaluation tool from the DARK FACE dataset [49] to compare the average precision (AP) at various IoU thresholds, including 0.5, 0.7, and 0.9. Table 6 shows the detailed AP results of our evaluation.

Table 6.
The average precision (AP) for face detection in the dark under different IoU thresholds (0.5, 0.7, 0.9). The best result is in red whereas the second best one is in blue under each case.
Based on the results presented in Table 6, it is evident that all the methods’ AP scores decrease as the IoU thresholds increase. At an IoU threshold of 0.9, all the approaches perform exceptionally poorly. However, under IoU thresholds of 0.5 and 0.7, the proposed method achieves similar AP scores that are only slightly lower than Restormer’s [38] superior performance. Moreover, our method achieves balanced subject enhancement performance, application performance, and computational cost without using paired training data. The proposed method effectively lights up facial features in dark areas while preserving features in well-light areas, ultimately improving pedestrian detection in low-light conditions. Figure 7 shows examples of object detection using the Dual Shot Face Detector (DSFD) on low-light images and enhanced images with the proposed method.

Figure 7.
Impact of VEViD pre-processing on pedestrian detection in the dark.
5. Discussion
- Deep-learning-based methods have recently attracted significant attention in the image processing field. Due to the powerful feature representation ability of the data, data-driven methods can learn more general visual features. This property means these methods can be used to relieve some challenges for image enhancement, such as poor illumination conditions. Our research aims to combine the physical brightness adjustment model based on frequency information with a data-driven-based low-light image enhancement method to improve the performance of the dynamic enhancement for low-light images. Moreover, the proposed method is based on a lightweight network design, offering it the advantages of a flexible generalization capability and real-time inference speed. The quantitative results in Table 2 and Table 3 show that the data-driven methods have better image enhancement results on all the test sets than the conventional method when the training data is sufficient. It is due to the fact that the data-driven approach relies on the powerful feature extraction capability of the deep learning network to adjust the brightness of each pixel in the image dynamically. As for data-driven methods, supervised learning usually has better image enhancement results because it can rely on normally exposed images to guide network learning. However, collecting pairs of images in natural environments is very time-consuming. The data dependence of supervised learning also causes a lack of generalization ability of the model. Specifically, the model degrades in scenarios with significant differences from the training data. In contrast, unsupervised learning reduces the reliance on paired data and performs better generalization. The result of our method shows that the method in this paper outperforms all unsupervised learning methods in key metrics and surpasses some of the supervised learning methods, with a small gap compared to the state-of-the-art supervised learning methods. In general, its performance is based on each branch of the network. Firstly, the physical brightness via the frequency-domain model in the BAFD component is able to improve the performance of the algorithm by providing interpretability for algorithm optimization, even with the limited amount of training datasets. Moreover, the integrated physics modeling procedure represents greater robustness than other methods for enhanced images with scenario changes. Furthermore, it also significantly reduces the complexity of designing the network architecture, which leads to the proposed method only having 70K parameters. Secondly, the design of the GEN component architecture, which is inspired by image restoration methods and the variable effective receptive field of the recursive gated deep convolution, keeps the high-order features and the detail information (such as texture) from the image to preserve the original structural information of the image and suppress noise generated by enhanced processing.
- Through ablation experiments, this paper analyzes the reasons for the performance improvement of the algorithm from two aspects. First, the ablation experiments demonstrate that this paper uses the two-branch network structure, and the one-way network introduces the channel characterizing the image brightness with the frequency-domain feature model under the assumption of the virtual light field, which can effectively achieve the brightness adjustment. Moreover, a lightweight parameter estimation network can achieve dynamic brightness adjustment. Meanwhile, the other network relies on acquiring global image information to preserve the original image structure, color contrast, and other critical information while enhancing the image so that the enhanced image noise can be better suppressed. On the other hand, the contribution of the loss function of constrained unsupervised learning is analyzed in this paper through ablation experiments. Through the structure of the ablation experiment, it is easy to find that for the brightness adjustment branch, the histogram prior information loss function used in this paper can effectively preserve the original distribution of image information while brightness adjustment, thus making it possible to adjust the brightness without losing the original image semantic structure features. On the other hand, the illumination smoothing loss function allows the network to reduce the impact of noise on the overall image enhancement results during the brightness adjustment learning. For the global enhancement branch, this paper constrains the network to retain the high-level image feature information from two aspects: color gradient consistency and image gradient change consistency so that the enhanced images achieve significant improvement in both the quantitative and qualitative evaluation (in Table 2 and Table 3 and Figure 3 and Figure 4). Meanwhile, the exposure consistency loss further enhances the intuitive image enhancement effect.
- To analyze the potential of the algorithms in this paper for real-time applications, the paper first compares the parametric quantities and inference implementations of the various algorithms in Table 2. It can be seen that the number of parameters of the proposed method in this paper is better than most of the comparison methods, and the inference speed is only slightly slower than Zero-DCE++ [6], which is significantly lightweight and fast for practical applications.
6. Conclusions
In this work, we propose an unsupervised dual-branch network for low-light image enhancement. One network branch uses the frequency-domain information of low-light images to achieve dynamic brightness adjustment of images. At the same time, the other focuses on the global image information to dynamically adjust the overall brightness of images while preserving the high-level structural features of low-light images themselves, guiding the network to suppress noise effectively, color contrast differences, and other problems that exist when enhancing low-light images while enhancing images. Moreover, the loss functions designed in this paper can effectively guide the network to make dynamic adjustments while preserving the structural information of low-illumination images. It further enhances the low-light image enhancement effect and can support the performance improvement of downstream tasks. Finally, the lightweight network structure design reduces the number of network parameters and computational complexity. It improves the inference speed of this paper, which gives the proposed method the potential to be used in computing platforms with limited computing power.
Restricted by the imaging principle, when the illumination changes, different objects in the scene due to their material, surface texture, and other differences in the degree of reflection of light, resulting in the imaging results and image enhancement results there are large differences. Specifically, objects with strong reflectivity (such as smooth walls) may be over-exposed after image enhancement, while objects with poor reflectivity (such as dark carpets) may still be underexposed. Including the proposed method, most existing methods improve low-light images by global and uniform approaches without considering the semantic information of different regions. Therefore, using semantic information to guide the network training may enable the network to focus more on the differences between different regions in low-illumination images and produce richer image texture information, and color distribution. Ultimately, more naturally enhanced images are obtained. Therefore, in the future, we plan to explore a useful approach to obtain the semantic information and integrate the semantic information into image sequence enhancement.
Author Contributions
Conceptualization, X.Z. and Y.Y.; methodology, X.Z.; software, X.Z. and G.W.; validation, X.Z. and G.W.; formal analysis, X.Z.; investigation, Y.Y.; resources, H.Q.; data curation, X.Y.; writing—original draft preparation, X.Z.; writing—review and editing, X.Z. and S.Y.; visualization, X.Z.; supervision, Y.Y.; project administration, H.Q.; funding acquisition, H.Q. All authors have read and agreed to the published version of the manuscript.
Funding
The National Natural Science Foundation of China (62174128); the Ningbo Natural Science Foundation (2022J185); the Xian City Science and Technology Plan Project (Nos. 21JBGSZ-OCY9-0004, 22JBGS-QCY4-0006).
Data Availability Statement
Data sharing is not applicable to this article.
Acknowledgments
The authors wish to thank the editors and the reviewers for their valuable suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CNN | Convolutional Neural Networks |
| ULEFD | Unsupervised Low-light Image Enhancement via Virtual Diffraction |
| in Frequency Domain | |
| BAFD | Bright Adjustment in Frequency Domain |
| GEN | Global Enhancement Net |
| FT | Fourier Transform |
| FFT | Fast Fourier Transform |
| IFFT | Inverse Fourier Transform |
| MLP | Multi-Layer Perception |
| MSE | Mean-Square Error |
References
- Wang, S.; Zheng, J.; Hu, H.M.; Li, B. Naturalness preserved enhancement algorithm for non-uniform illumination images. IEEE Trans. Image Process. 2013, 22, 3538–3548. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Xiao, L.; Liu, H.; Wei, Z. Variational Bayesian method for retinex. IEEE Trans. Image Process. 2014, 23, 3381–3396. [Google Scholar] [CrossRef]
- Pisano, E.D.; Zong, S.; Hemminger, B.M.; DeLuca, M.; Johnston, R.E.; Muller, K.; Braeuning, M.P.; Pizer, S.M. Contrast limited adaptive histogram equalization image processing to improve the detection of simulated spiculations in dense mammograms. J. Digit. Imaging 1998, 11, 193–200. [Google Scholar] [CrossRef]
- Pizer, S.M.; Johnston, R.E.; Ericksen, J.P.; Yankaskas, B.C.; Muller, K.E. Contrast-limited adaptive histogram equalization: Speed and effectiveness. In Proceedings of the First Conference on Visualization in Biomedical Computing, Atlanta, GA, USA, 22–25 May 1990; Volume 337, p. 1. [Google Scholar]
- Li, C.; Guo, C.; Han, L.; Jiang, J.; Cheng, M.M.; Gu, J.; Loy, C.C. Low-light image and video enhancement using deep learning: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 9396–9416. [Google Scholar] [CrossRef]
- Li, C.; Guo, C.; Loy, C.C. Learning to enhance low-light image via zero-reference deep curve estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 4225–4238. [Google Scholar] [CrossRef]
- Quan, Y.; Fu, D.; Chang, Y.; Wang, C. 3D Convolutional Neural Network for Low-Light Image Sequence Enhancement in SLAM. Remote Sens. 2022, 14, 3985. [Google Scholar] [CrossRef]
- Fan, S.; Liang, W.; Ding, D.; Yu, H. LACN: A lightweight attention-guided ConvNeXt network for low-light image enhancement. Eng. Appl. Artif. Intell. 2023, 117, 105632. [Google Scholar] [CrossRef]
- Ying, Z.; Li, G.; Ren, Y.; Wang, R.; Wang, W. A new image contrast enhancement algorithm using exposure fusion framework. In Proceedings of the Computer Analysis of Images and Patterns: 17th International Conference, CAIP 2017, Ystad, Sweden, 22–24 August 2017; Proceedings, Part II 17. Springer: Berlin/Heidelberg, Germany, 2017; pp. 36–46. [Google Scholar]
- Chen, Y.S.; Wang, Y.C.; Kao, M.H.; Chuang, Y.Y. Deep photo enhancer: Unpaired learning for image enhancement from photographs with gans. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 6306–6314. [Google Scholar]
- Jiang, Y.; Gong, X.; Liu, D.; Cheng, Y.; Fang, C.; Shen, X.; Yang, J.; Zhou, P.; Wang, Z. Enlightengan: Deep light enhancement without paired supervision. IEEE Trans. Image Process. 2021, 30, 2340–2349. [Google Scholar] [CrossRef]
- Jalali, B.; MacPhee, C. VEViD: Vision Enhancement via Virtual diffraction and coherent Detection. eLight 2022, 2, 24. [Google Scholar]
- Farid, H. Blind inverse gamma correction. IEEE Trans. Image Process. 2001, 10, 1428–1433. [Google Scholar] [CrossRef] [PubMed]
- Lee, Y.; Zhang, S.; Li, M.; He, X. Blind inverse gamma correction with maximized differential entropy. Signal Process. 2022, 193, 108427. [Google Scholar]
- Coltuc, D.; Bolon, P.; Chassery, J.M. Exact histogram specification. IEEE Trans. Image Process. 2006, 15, 1143–1152. [Google Scholar] [CrossRef]
- Ibrahim, H.; Kong, N.S.P. Brightness preserving dynamic histogram equalization for image contrast enhancement. IEEE Trans. Consum. Electron. 2007, 53, 1752–1758. [Google Scholar] [CrossRef]
- Stark, J.A. Adaptive image contrast enhancement using generalizations of histogram equalization. IEEE Trans. Image Process. 2000, 9, 889–896. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.; Lee, C.; Kim, C.S. Contrast enhancement based on layered difference representation of 2D histograms. IEEE Trans. Image Process. 2013, 22, 5372–5384. [Google Scholar] [CrossRef] [PubMed]
- Singh, K.; Kapoor, R. Image enhancement using exposure based sub image histogram equalization. Pattern Recognit. Lett. 2014, 36, 10–14. [Google Scholar] [CrossRef]
- Fu, X.; Zeng, D.; Huang, Y.; Zhang, X.P.; Ding, X. A weighted variational model for simultaneous reflectance and illumination estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2782–2790. [Google Scholar]
- Guo, X.; Li, Y.; Ling, H. LIME: Low-light image enhancement via illumination map estimation. IEEE Trans. Image Process. 2016, 26, 982–993. [Google Scholar] [CrossRef]
- Li, M.; Liu, J.; Yang, W.; Sun, X.; Guo, Z. Structure-revealing low-light image enhancement via robust retinex model. IEEE Trans. Image Process. 2018, 27, 2828–2841. [Google Scholar] [CrossRef]
- Zhang, F.; Shao, Y.; Sun, Y.; Zhu, K.; Gao, C.; Sang, N. Unsupervised low-light image enhancement via histogram equalization prior. arXiv 2021, arXiv:2112.01766. [Google Scholar]
- Wei, C.; Wang, W.; Yang, W.; Liu, J. Deep retinex decomposition for low-light enhancement. arXiv 2018, arXiv:1808.04560. [Google Scholar]
- Zhang, Y.; Zhang, J.; Guo, X. Kindling the darkness: A practical low-light image enhancer. In Proceedings of the 27th ACM International Conference on Multimedia, Nice, France, 21–25 October 2019; pp. 1632–1640. [Google Scholar]
- Zhang, Y.; Guo, X.; Ma, J.; Liu, W.; Zhang, J. Beyond brightening low-light images. Int. J. Comput. Vis. 2021, 129, 1013–1037. [Google Scholar]
- Jiang, N.; Lin, J.; Zhang, T.; Zheng, H.; Zhao, T. Low-Light Image Enhancement via Stage-Transformer-Guided Network. In IEEE Transactions on Circuits and Systems for Video Technology; IEEE: Piscataway Township, NJ, USA, 2023. [Google Scholar]
- Lore, K.G.; Akintayo, A.; Sarkar, S. LLNet: A deep autoencoder approach to natural low-light image enhancement. Pattern Recognit. 2017, 61, 650–662. [Google Scholar] [CrossRef]
- Lv, F.; Lu, F.; Wu, J.; Lim, C. MBLLEN: Low-Light Image/Video Enhancement Using CNNs. In Proceedings of the BMVC, Newcastle, UK, 3–6 September 2018; Volume 220, p. 4. [Google Scholar]
- Bychkovsky, V.; Paris, S.; Chan, E.; Durand, F. Learning photographic global tonal adjustment with a database of input/output image pairs. In Proceedings of the CVPR 2011, Colorado Springs, CO, USA, 20–25 June 2011; IEEE: Piscataway Township, NJ, USA, 2011; pp. 97–104. [Google Scholar]
- Wang, R.; Zhang, Q.; Fu, C.W.; Shen, X.; Zheng, W.S.; Jia, J. Underexposed photo enhancement using deep illumination estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 6849–6857. [Google Scholar]
- Ren, W.; Liu, S.; Ma, L.; Xu, Q.; Xu, X.; Cao, X.; Du, J.; Yang, M.H. Low-light image enhancement via a deep hybrid network. IEEE Trans. Image Process. 2019, 28, 4364–4375. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.; Weng, J.; Zhang, P.; Wang, X.; Yang, W.; Jiang, J. Uretinex-net: Retinex-based deep unfolding network for low-light image enhancement. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19–20 June 2022; pp. 5901–5910. [Google Scholar]
- Xu, K.; Yang, X.; Yin, B.; Lau, R.W. Learning to restore low-light images via decomposition-and-enhancement. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 2281–2290. [Google Scholar]
- Fu, Y.; Hong, Y.; Chen, L.; You, S. LE-GAN: Unsupervised low-light image enhancement network using attention module and identity invariant loss. Knowl.-Based Syst. 2022, 240, 108010. [Google Scholar] [CrossRef]
- Yang, W.; Wang, S.; Fang, Y.; Wang, Y.; Liu, J. From fidelity to perceptual quality: A semi-supervised approach for low-light image enhancement. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 3063–3072. [Google Scholar]
- Saravanan, G.; Yamuna, G.; Nandhini, S. Real time implementation of RGB to HSV/HSI/HSL and its reverse color space models. In Proceedings of the 2016 International Conference on Communication and Signal Processing (ICCSP), Melmaruvathur, India, 6–8 April 2016; IEEE: Piscataway Township, NJ, USA, 2016; pp. 0462–0466. [Google Scholar]
- Zamir, S.W.; Arora, A.; Khan, S.; Hayat, M.; Khan, F.S.; Yang, M.H. Restormer: Efficient transformer for high-resolution image restoration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19–20 June 2022; pp. 5728–5739. [Google Scholar]
- Chen, L.; Chu, X.; Zhang, X.; Sun, J. Simple baselines for image restoration. In Proceedings of the Computer Vision–ECCV 2022: 17th European Conference, Tel Aviv, Israel, 23–27 October 2022; Proceedings, Part VII. Springer: Berlin/Heidelberg, Germany, 2022; pp. 17–33. [Google Scholar]
- Rao, Y.; Zhao, W.; Tang, Y.; Zhou, J.; Lim, S.N.; Lu, J. Hornet: Efficient high-order spatial interactions with recursive gated convolutions. Adv. Neural Inf. Process. Syst. 2022, 35, 10353–10366. [Google Scholar]
- Zhang, Y.; Di, X.; Zhang, B.; Li, Q.; Yan, S.; Wang, C. Self-supervised low light image enhancement and denoising. arXiv 2021, arXiv:2103.00832. [Google Scholar]
- Johnson, J.; Alahi, A.; Fei-Fei, L. Perceptual losses for real-time style transfer and super-resolution. In Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Proceedings, Part II 14. Springer: Berlin/Heidelberg, Germany, 2016; pp. 694–711. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Mittal, A.; Soundararajan, R.; Bovik, A.C. Making a “completely blind” image quality analyzer. IEEE Signal Process. Lett. 2012, 20, 209–212. [Google Scholar] [CrossRef]
- Liu, J.; Xu, D.; Yang, W.; Fan, M.; Huang, H. Benchmarking low-light image enhancement and beyond. Int. J. Comput. Vis. 2021, 129, 1153–1184. [Google Scholar]
- Yang, X.; Gong, J.; Wu, L.; Yang, Z.; Shi, Y.; Nie, F. Reference-free low-light image enhancement by associating hierarchical wavelet representations. Expert Syst. Appl. 2023, 213, 118920. [Google Scholar]
- Haoyuan Wang, K.X.; Lau, R.W. Local Color Distributions Prior for Image Enhancement. In Proceedings of the European Conference on Computer Vision (ECCV), Tel Aviv, Israel, 23–27 October 2022. [Google Scholar]
- Cai, J.; Gu, S.; Zhang, L. Learning a deep single image contrast enhancer from multi-exposure images. IEEE Trans. Image Process. 2018, 27, 2049–2062. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Y.; Yang, W.; Ren, W.; Liu, J.; Scheirer, W.J.; Wang, Z. UG 2+ Track 2: A Collective Benchmark Effort for Evaluating and Advancing Image Understanding in Poor Visibility Environments. arXiv 2019, arXiv:1904.04474. [Google Scholar]
- Li, J.; Wang, Y.; Wang, C.; Tai, Y.; Qian, J.; Yang, J.; Wang, C.; Li, J.; Huang, F. DSFD: Dual shot face detector. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 5060–5069. [Google Scholar]
- Yang, S.; Luo, P.; Loy, C.C.; Tang, X. Wider face: A face detection benchmark. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 5525–5533. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).