Improving the Accuracy of TanDEM-X Digital Elevation Model Using Least Squares Collocation Method
Abstract
1. Introduction
2. Study Area and Data
2.1. Study Area
2.2. Study Datasets
2.2.1. TanDEM-X/TerraSAR-X (TDX/TSX) Data
2.2.2. ICESat-2 Data
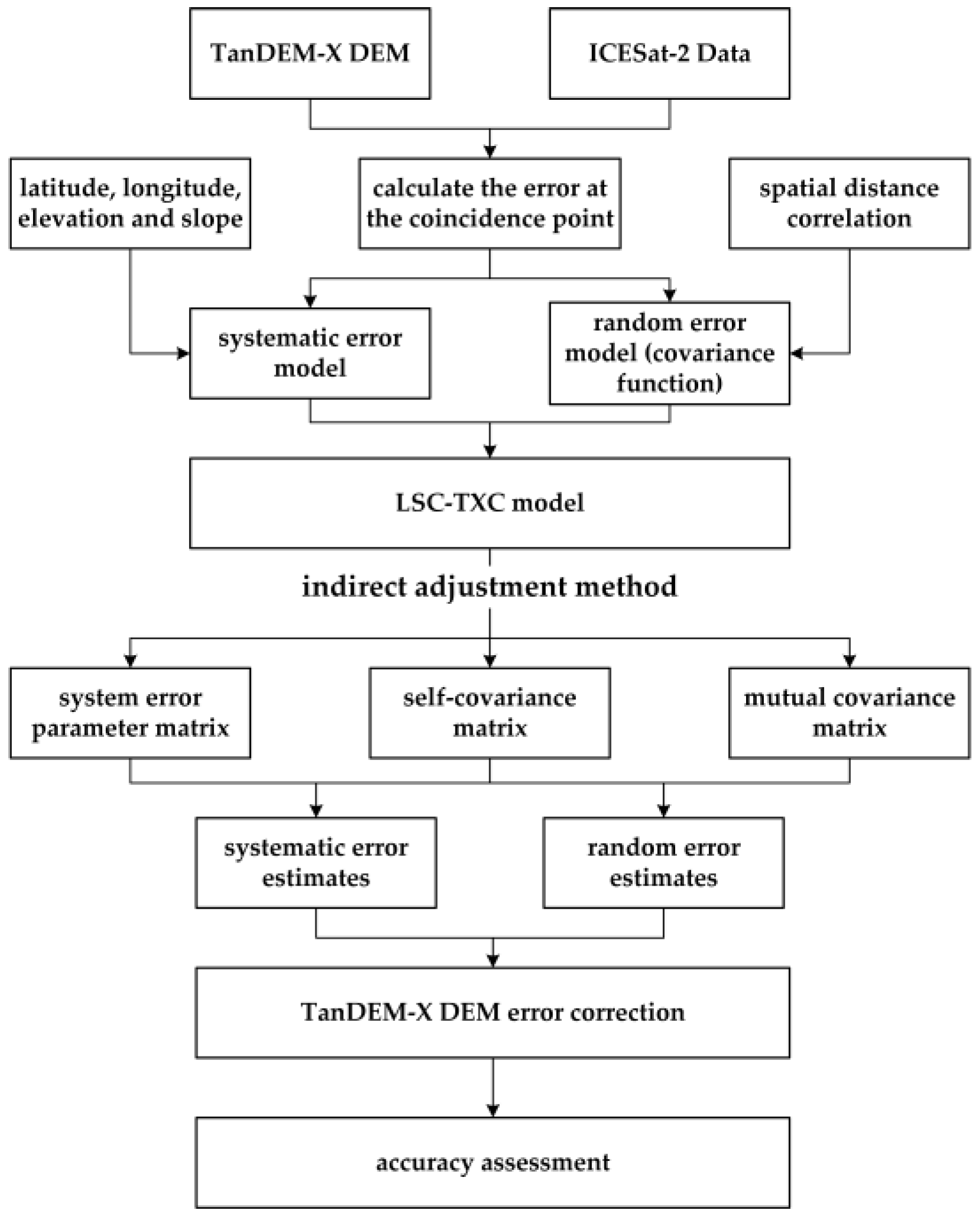
3. Methods
3.1. Overview of TDX/TSX DEM Generation
3.2. Error Analysis on TanDEM-X DEM
3.3. LSC-TXC Algorithm for TanDEM-X DEM Error Correction
3.3.1. Observation Equation System
3.3.2. Error Correction of TanDEM-X DEM
4. Results
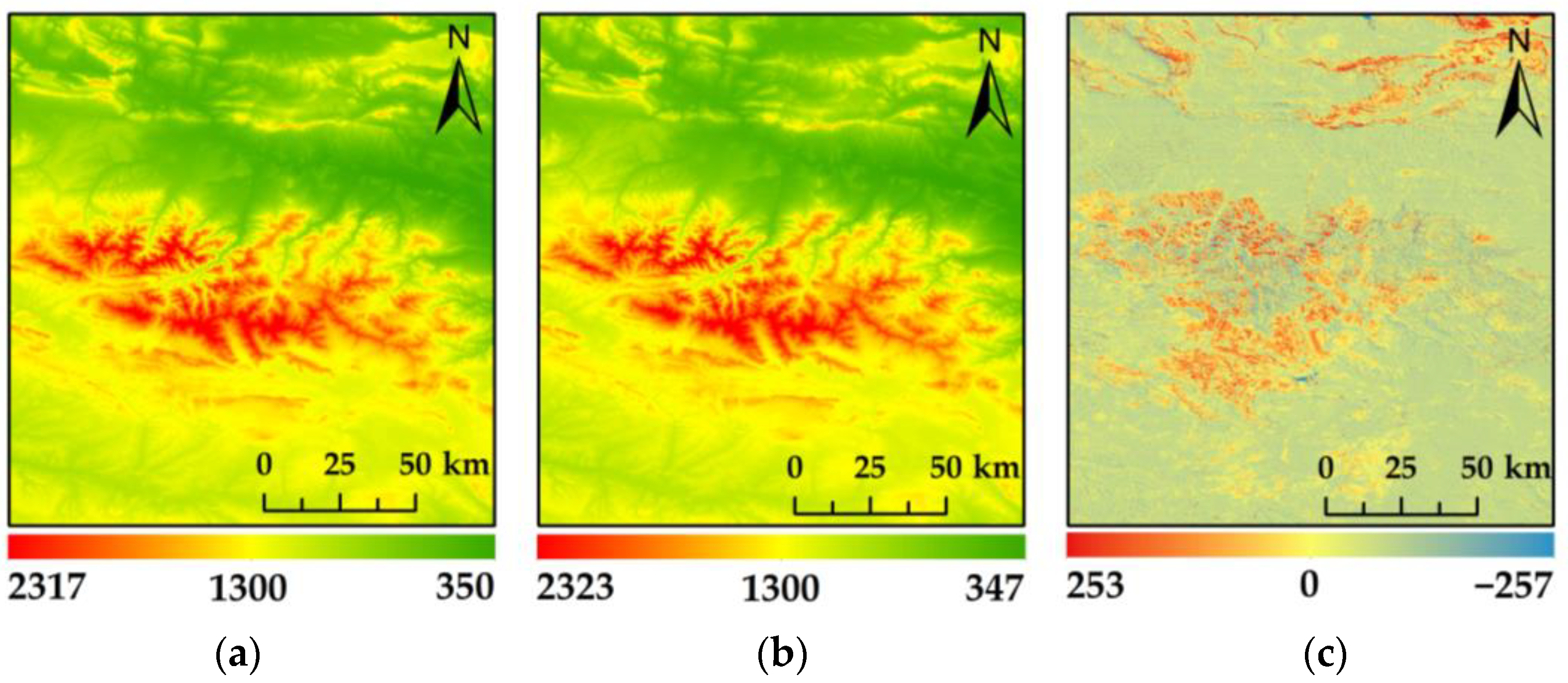
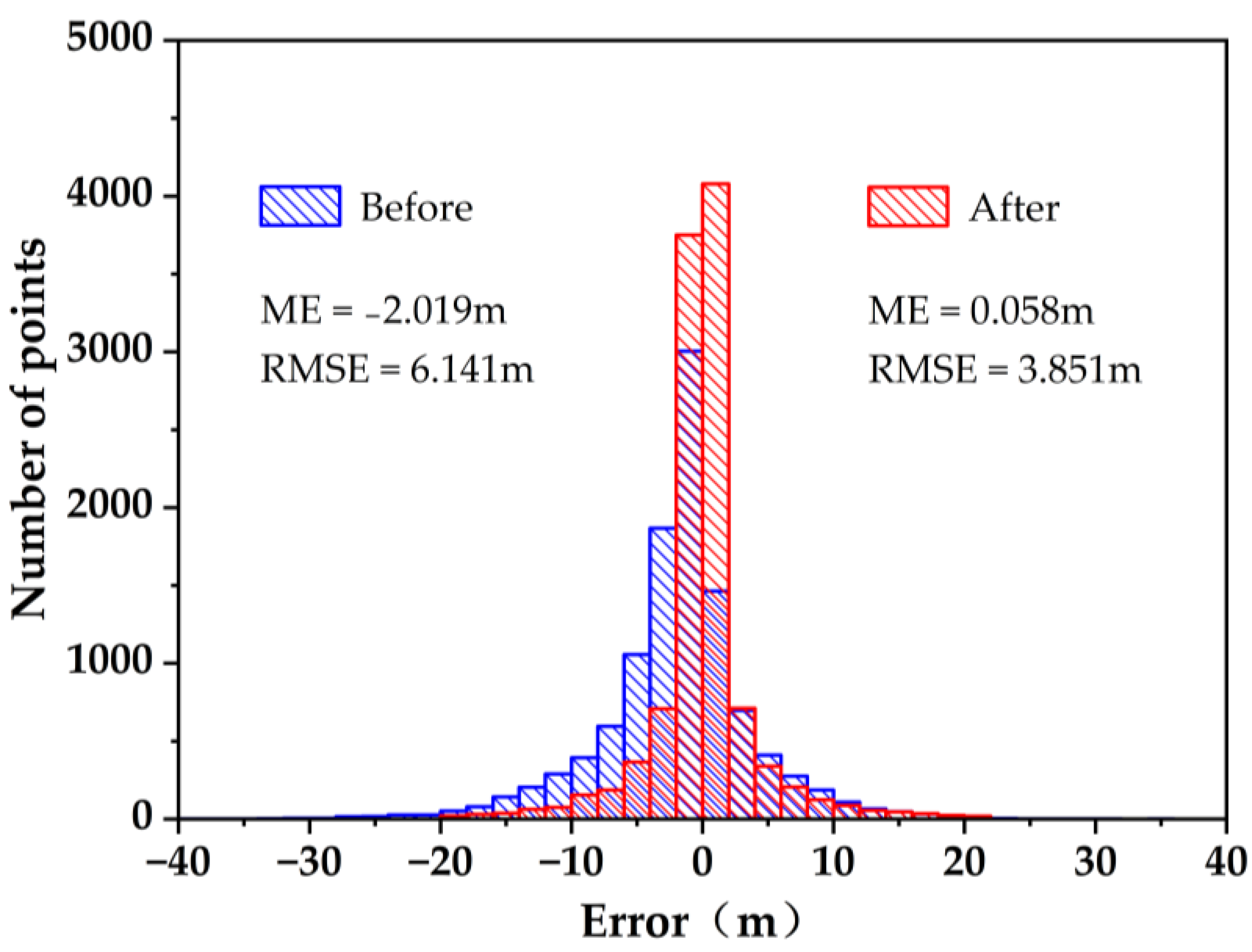
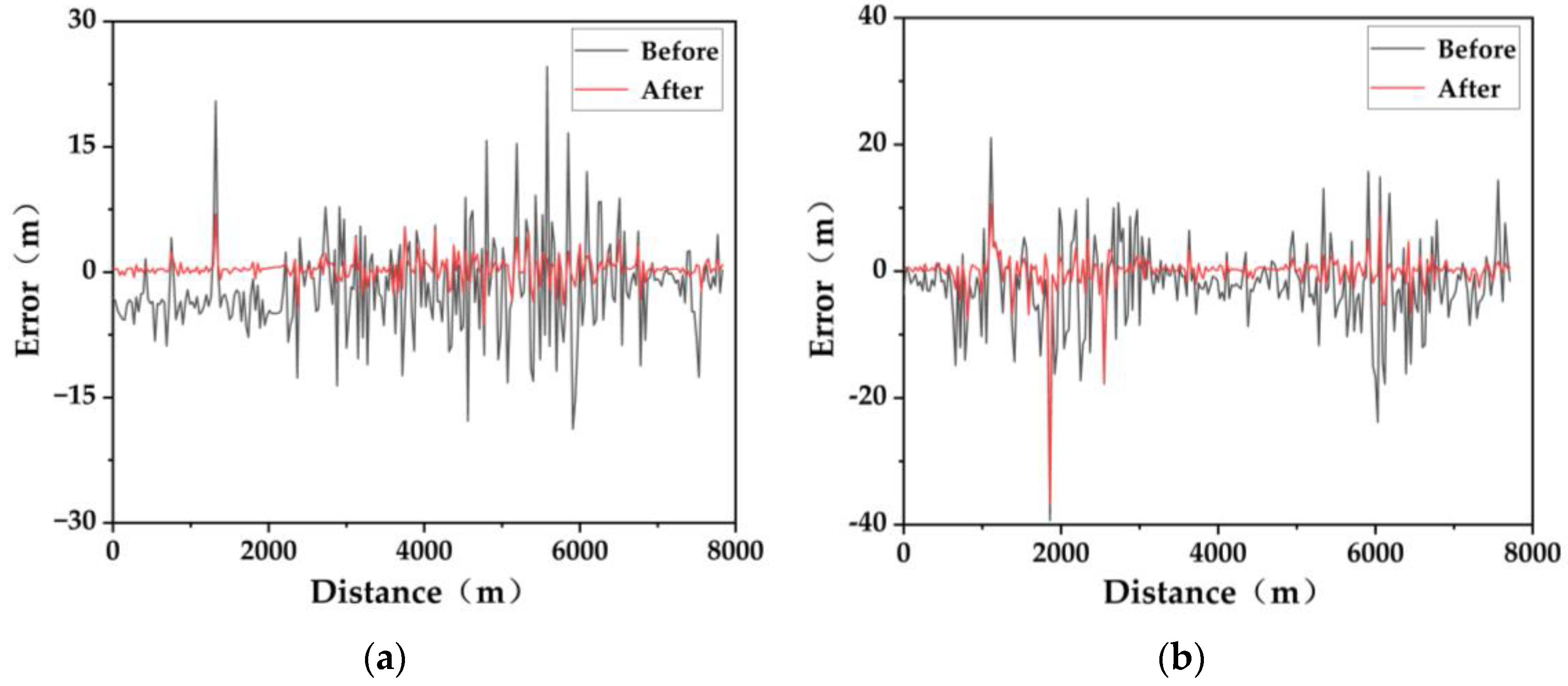
4.1. TanDEM-X DEM Correction Results
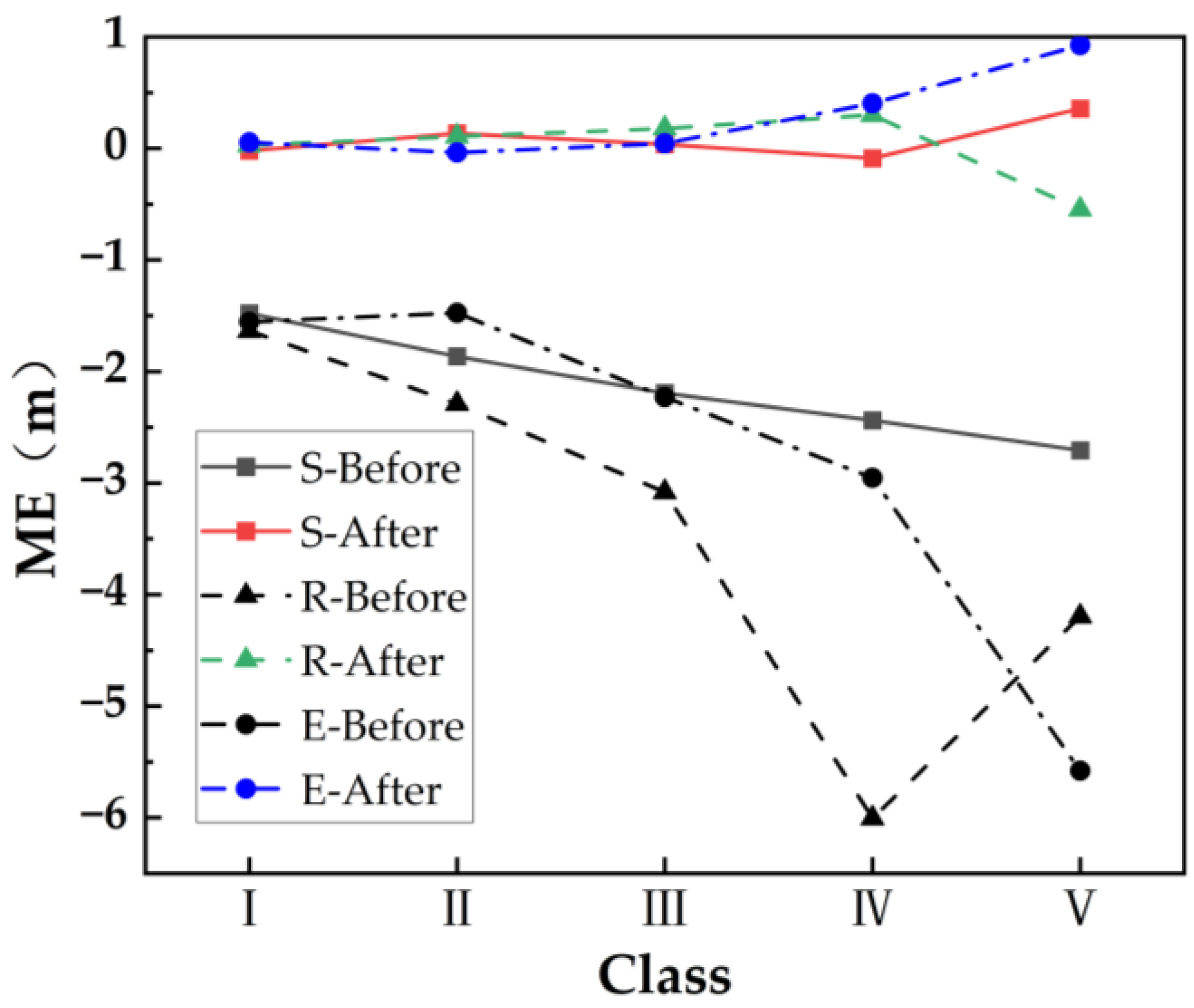
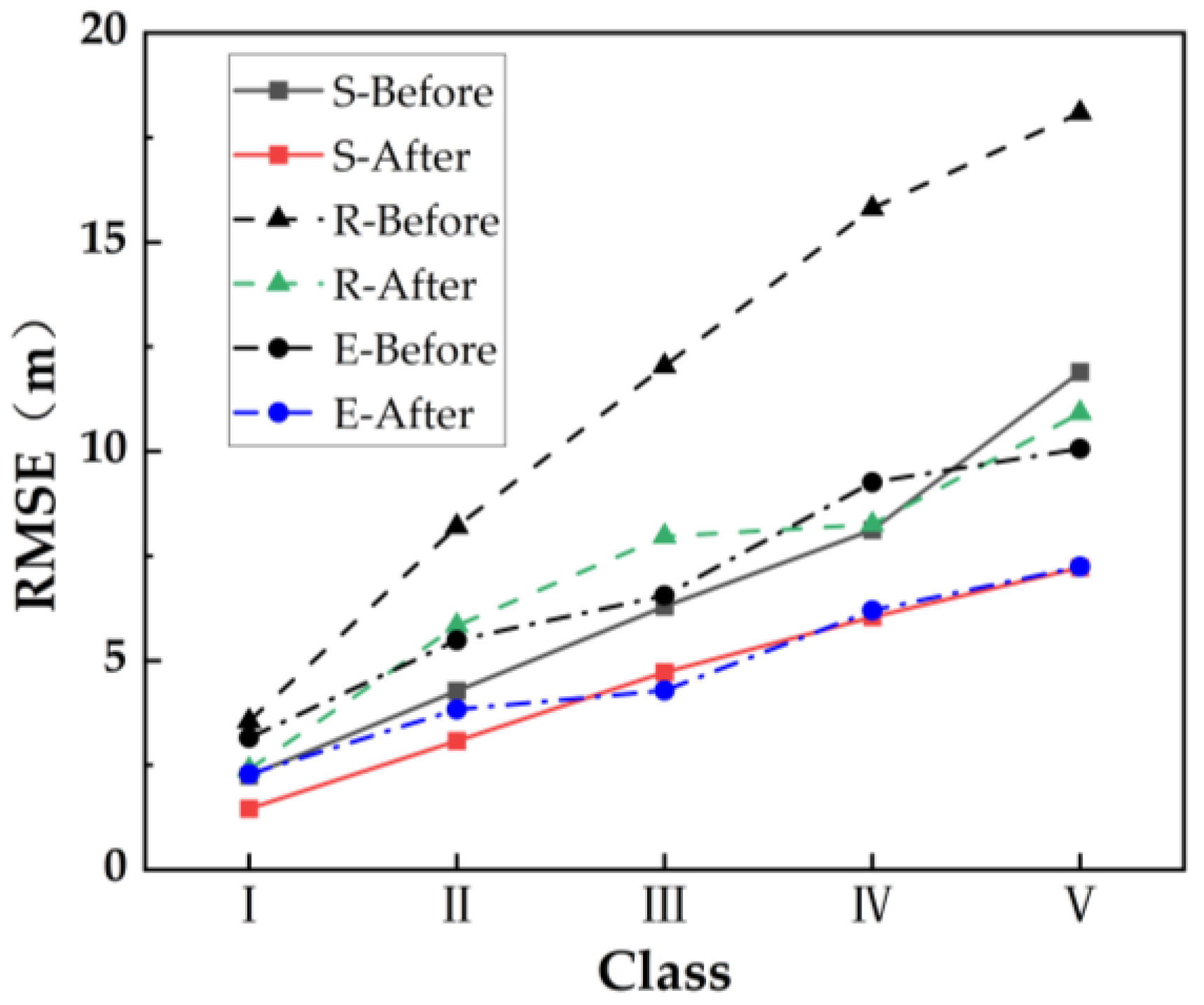
4.2. Influence of Terrain Factors on TanDEM-X DEM Correction Results
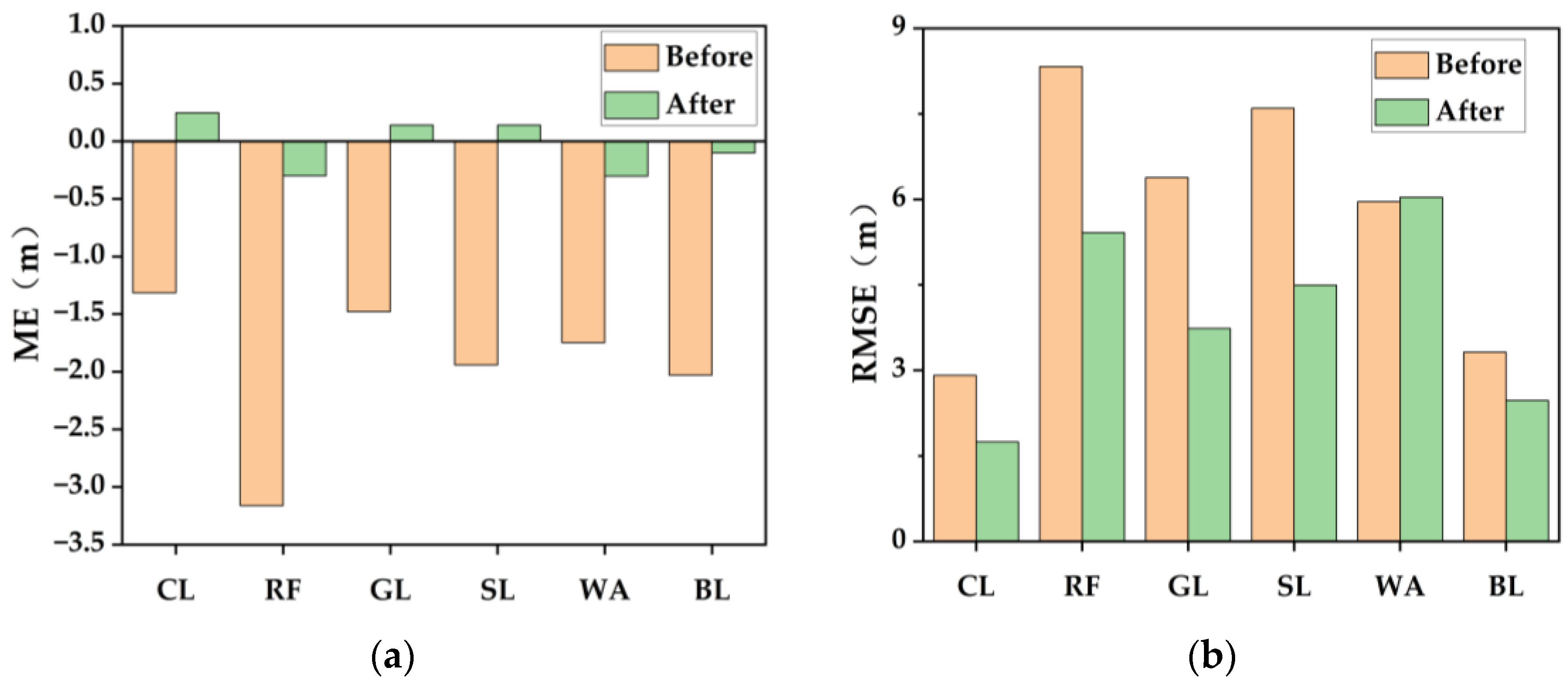
4.3. Influence of Land Use on TanDEM-X DEM Correction Results
4.4. Model Performance Comparison
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tang, G. Research progress of digital elevation model and digital terrain analysis in China. Acta Geogr. Sin. 2014, 69, 1305–1325. [Google Scholar]
- Zhou, C.; Zhang, G.; Yang, Z.; Ao, M.; Liu, Z.; Zhu, J. An adaptive terrain-dependent method for SRTM DEM correction over mountainous areas. IEEE Access 2020, 8, 130878–130887. [Google Scholar] [CrossRef]
- Lee, H.; Hahn, M. KOMPSAT-3 digital elevation model correction based on point-to-surface matching. Remote Sens. 2019, 11, 2340. [Google Scholar] [CrossRef]
- Li, X.; Shen, H.; Feng, R.; Li, J.; Zhang, L. DEM generation from contours and a low-resolution DEM. ISPRS J. Photogramm. Remote Sens. 2017, 134, 135–147. [Google Scholar] [CrossRef]
- Fujita, K.; Suzuki, R.; Nuimura, T.; Sakai, A. Performance of ASTER and SRTM DEMs, and their potential for assessing glacial lakes in the Lunana region, Bhutan Himalaya. J. Glaciol. 2008, 54, 220–228. [Google Scholar] [CrossRef]
- Tadono, T.; Takaku, J.; Tsutsui, K.; Oda, F.; Nagai, H. Status of “ALOS World 3D (AW3D)” global DSM generation. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 3822–3825. [Google Scholar]
- Zhao, S.; Liu, J.; Cheng, W.; Zhou, C. Fusion Scheme and Implementation Based on SRTM1, ASTER GDEM V3, and AW3D30. ISPRS Int. J. Geo-Inf. 2022, 11, 207. [Google Scholar] [CrossRef]
- Rizzoli, P.; Martone, M.; Gonzalez, C.; Wecklich, C.; Tridon, D.B.; Bräutigam, B.; Bachmann, M.; Schulze, D.; Fritz, T.; Huber, M.; et al. Generation and performance assessment of the global TanDEM-X digital elevation model. ISPRS J. Photogramm. Remote Sens. 2017, 132, 119–139. [Google Scholar] [CrossRef]
- Chen, N. Influence of Resolutions of DEM on the Error of Slope. Geomat. Inf. Sci. Wuhan Univ. 2013, 38, 594–598. [Google Scholar]
- Florinsky, I.V.; Skrypitsyna, T.N.; Luschikova, O.S. Comparative accuracy of the AW3D30 DSM, ASTER GDEM, and SRTM1 DEM: A case study on the Zaoksky testing ground, Central European Russia. Remote Sens. Lett. 2018, 9, 706–714. [Google Scholar] [CrossRef]
- Girohi, P.; Bhardwaj, A. InSAR-Based Digital Elevation Model (DEM) Improvement Using Data Fusion Technique with Neural Networks on Diverse Topographic Indian Regions. Authorea Prepr. 2022, 4, 625–646. [Google Scholar]
- Girohi, P.; Bhardwaj, A. A Neural Network-Based Fusion Approach for Improvement of SAR Interferometry-Based Digital Elevation Models in Plain and Hilly Regions of India. AI 2022, 3, 820–843. [Google Scholar] [CrossRef]
- Qin, X.; Zhang, H.; Heng, Z.; Yu, W.; Huayou, L. A High Precision DEM Generation Method Based on Ascending and Descending Pass TerraSAR-X/TanDEM-X BiSAR Data. J. Radars 2018, 7, 487–497. [Google Scholar]
- Podgórski, J.; Kinnard, C.; Pętlicki, M.; Urrutia, R. Performance Assessment of TanDEM-X DEM for Mountain Glacier Elevation Change Detection. Remote Sens. 2019, 11, 187. [Google Scholar] [CrossRef]
- Ke, L.; Song, C.; Yong, B.; Lei, Y.; Ding, X. Which heterogeneous glacier melting patterns can be robustly observed from space? A multi-scale assessment in southeastern Tibetan Plateau. Remote Sens. Environ. 2020, 242, 111777. [Google Scholar] [CrossRef]
- Wu, Q.; Song, C.; Liu, K.; Ke, L. Integration of TanDEM-X and SRTM DEMs and spectral imagery to improve the large-scale detection of opencast mining areas. Remote Sens. 2020, 12, 1451. [Google Scholar] [CrossRef]
- Vanthof, V.; Kelly, R. Water storage estimation in ungauged small reservoirs with the TanDEM-X DEM and multi-source satellite observations. Remote Sens. Environ. 2019, 235, 111437. [Google Scholar] [CrossRef]
- Li, W.; Wang, C.; Zhu, W. Error spatial distribution characteristics of TanDEM-X 90m DEM over China. J. Geo-Inf. Sci. 2020, 22, 2277–2288. [Google Scholar]
- Apeh, O.I.; Uzodinma, V.N.; Ebinne, E.S.; Moka, E.C.; Onah, E.U. Accuracy Assessment of Alos W3d30, Aster Gdem and Srtm30 Dem: A Case Study of Nigeria, West Africa. J. Geogr. Inf. Syst. 2019, 11, 111–123. [Google Scholar] [CrossRef][Green Version]
- Kim, D.E.; Liong, S.Y.; Gourbesville, P.; Andres, L.; Liu, J. Simple-yet-effective SRTM DEM improvement scheme for dense urban cities using ANN and remote sensing data: Application to flood modeling. Water 2020, 12, 816. [Google Scholar] [CrossRef]
- Elshambaky, H.T. Using direct transformation approach as an alternative technique to fuse global digital elevation models with GPS/levelling measurements in Egypt. J. Appl. Geod. 2019, 13, 159–177. [Google Scholar] [CrossRef]
- Yue, G.; Liu, Y.; Zheng, C. Study on DEM Fusion Methods Based on InSAR Technology in Complex Terrain Areas. Geomat. Spat. Inf. Technol. 2021, 44, 205–209+214. [Google Scholar]
- Mason, D.C.; Trigg, M.; Garcia-Pintado, J.; Cloke, H.L.; Neal, J.C.; Bates, P.D. Improving the TanDEM-X Digital Elevation Model for flood modelling using flood extents from Synthetic Aperture Radar images. Remote Sens. Environ. 2016, 173, 15–28. [Google Scholar] [CrossRef]
- Kim, D.E.; Liu, J.; Liong, S.Y.; Gourbesville, P.; Strunz, G. Satellite DEM improvement using multispectral imagery and an artificial neural network. Water 2021, 13, 1551. [Google Scholar] [CrossRef]
- Guo, C.; Nie, J.; Tian, J. Vertical deformation analysis of adaptive fusion of GNSS level elevation change. Geomat. Inf. Sci. Wuhan Univ. 2020, 45, 7–12. [Google Scholar]
- Trojanowicz, M.; Osada, E.; Karsznia, K. Precise local quasigeoid modelling using GNSS/levelling height anomalies and gravity data. Surv. Rev. 2020, 52, 76–83. [Google Scholar] [CrossRef]
- Lü, J.; Zhang, Z.; Zhang, X.; Liu, Z. Application of combination model of quadric surfaces and least squares collocation in GPS height anomaly fitting. Bull. Surv. Mapp. 2020, 5, 127–129. [Google Scholar]
- Rehman, K.; Fareed, N.; Chu, H.-J. NASA ICESat-2: Space-Borne LiDAR for Geological Education and Field Mapping of Aeolian Sand Dune Environments. Remote Sens. 2023, 15, 2882. [Google Scholar] [CrossRef]
- Jin, G.; Xu, Q.; Zhang, H. Synthetic Aperture Radar Interferometry; National Defense Industry Press: Beijing, China, 2014. [Google Scholar]
- Du, Y.; Fu, H.; Liu, L.; Feng, G.; Peng, X.; Wen, D. Orbit error removal in InSAR/MTInSAR with a patch-based polynomial model. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102438. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, J.; Yue, D. Modern Measurement Data Processing and Application; Surveying and Mapping Press: Beijing, China, 2011. [Google Scholar]
- Du, Y.; Feng, G.; Li, Z.; Zhu, J.; Peng, X. Generation of high precision DEM from TerraSAR-X/TanDEM-X. Chin. J. Geophys. 2015, 58, 3089–3102. [Google Scholar]
- Gruber, A.; Wessel, B.; Huber, M.; Roth, A. Operational TanDEM-X DEM calibration and first validation results. ISPRS J. Photogramm. Remote Sens. 2012, 73, 39–49. [Google Scholar] [CrossRef]
- Zhang, W.; Zhu, W.; Tian, X.; Zhang, Q.; Zhao, C.; Niu, Y.; Wang, C. Improved DEM reconstruction method based on multibaseline InSAR. IEEE Geosci. Remote Sens. Lett. 2021, 19, 4011505. [Google Scholar] [CrossRef]
- Helmut, M. Least-squares collocation. Rev. Geophys. 1978, 16, 421–430. [Google Scholar]
- Xu, L.; Shao, D.; Wu, X.; Niu, T. Study on deformation and strain characteristics of Yunnan region based on least squares configuration. Sci. Surv. Mapp. 2021, 46, 16–23. [Google Scholar]
- Deng, W.; Lan, M.; Wang, H. Dynamic analysis of crust deformation in Xinjiang under least squares configuration. Chin. J. Geol. 2022, 57, 958–974. [Google Scholar]
- Ruan, M.; Chen, S.; Han, J. Regional gravity field model constructed by the Least squares collocation. Acta Seismol. Sin. 2020, 42, 53–65. [Google Scholar]
- Jarmołowski, W.; Mieczysław, B. Two covariance models in Least Squares Collocation (LSC) tested in interpolation of local topography. Contrib. Geophys. Geod. 2013, 43, 1–19. [Google Scholar] [CrossRef][Green Version]
- Gdulová, K.; Marešová, J.; Moudrý, V. Accuracy assessment of the global TanDEM-X digital elevation model in a mountain environment. Remote Sens. Environ. 2020, 241, 111724. [Google Scholar] [CrossRef]
- Yu, J.; Liu, K.; Zhang, B.; Huang, Y.; Fan, C.; Song, C.; Tang, G. Vertical accuracy assessment and applicability analysis of TanDEM-X 90 m DEM in China. J. Geo-Inf. Sci. 2021, 23, 646–657. [Google Scholar]
- Chen, C.; Yang, S.; Li, Y. Accuracy assessment and correction of SRTM DEM using ICESat/GLAS data under data coregistration. Remote Sens. 2020, 12, 3435. [Google Scholar] [CrossRef]
- Shen, H.; Liu, L.; Yue, L.; Li, X.; Zhang, L. A Multi-source DEM Fusion Method Based on Elevation Difference Fitting Neural Network. Acta Geod. Et Cartogr. Sin. 2018, 47, 854–863. [Google Scholar]
- Tang, X.; Feng, D.; Li, K.Q.; Liu, J.; Song, J.; Sheng, V.S. An Improved BPNN Prediction Method Based on Multi-Strategy Sparrow Search Algorithm. Comput. Mater. Contin. 2023, 74, 2789–2802. [Google Scholar] [CrossRef]
- Zhao, W.; Wu, H.; Yin, G.; Duan, S.B. Normalization of the temporal effect on the MODIS land surface temperature product using random forest regression. ISPRS J. Photogramm. Remote Sens. 2019, 152, 109–118. [Google Scholar] [CrossRef]

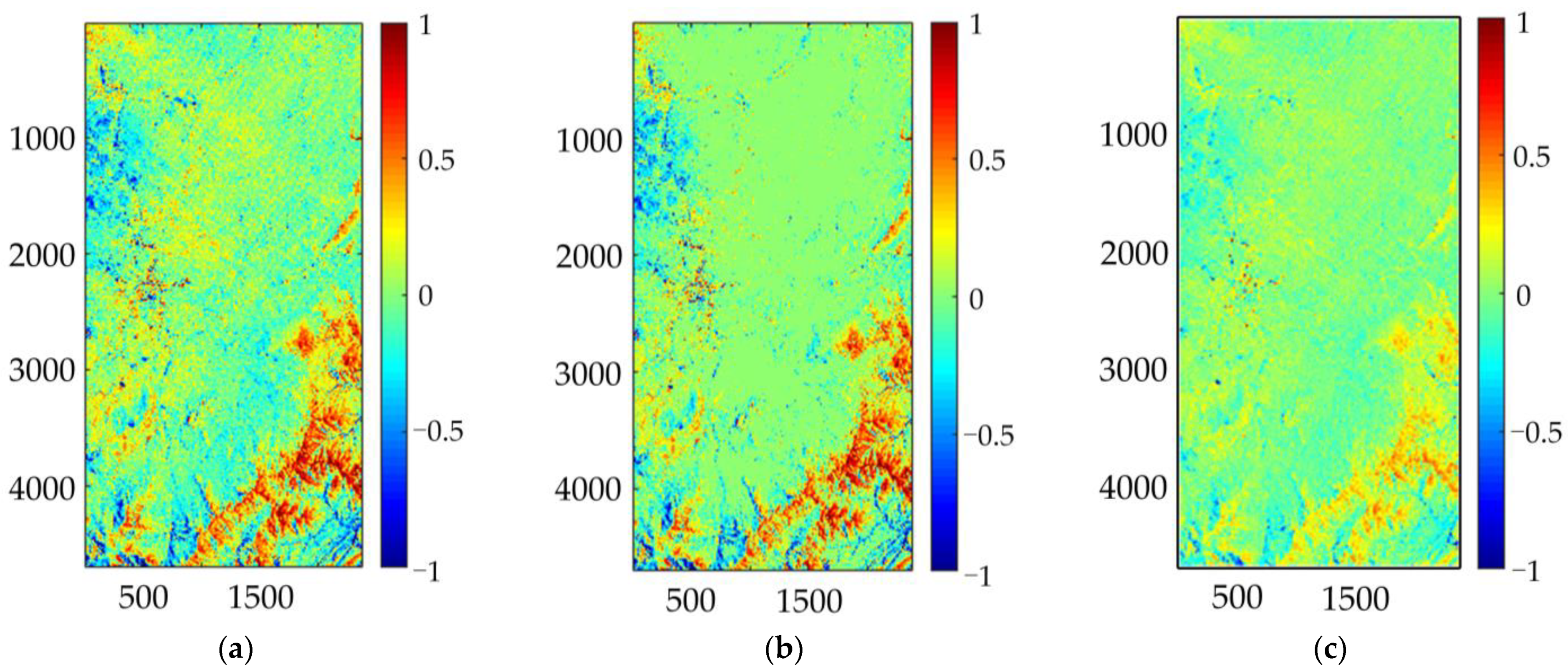

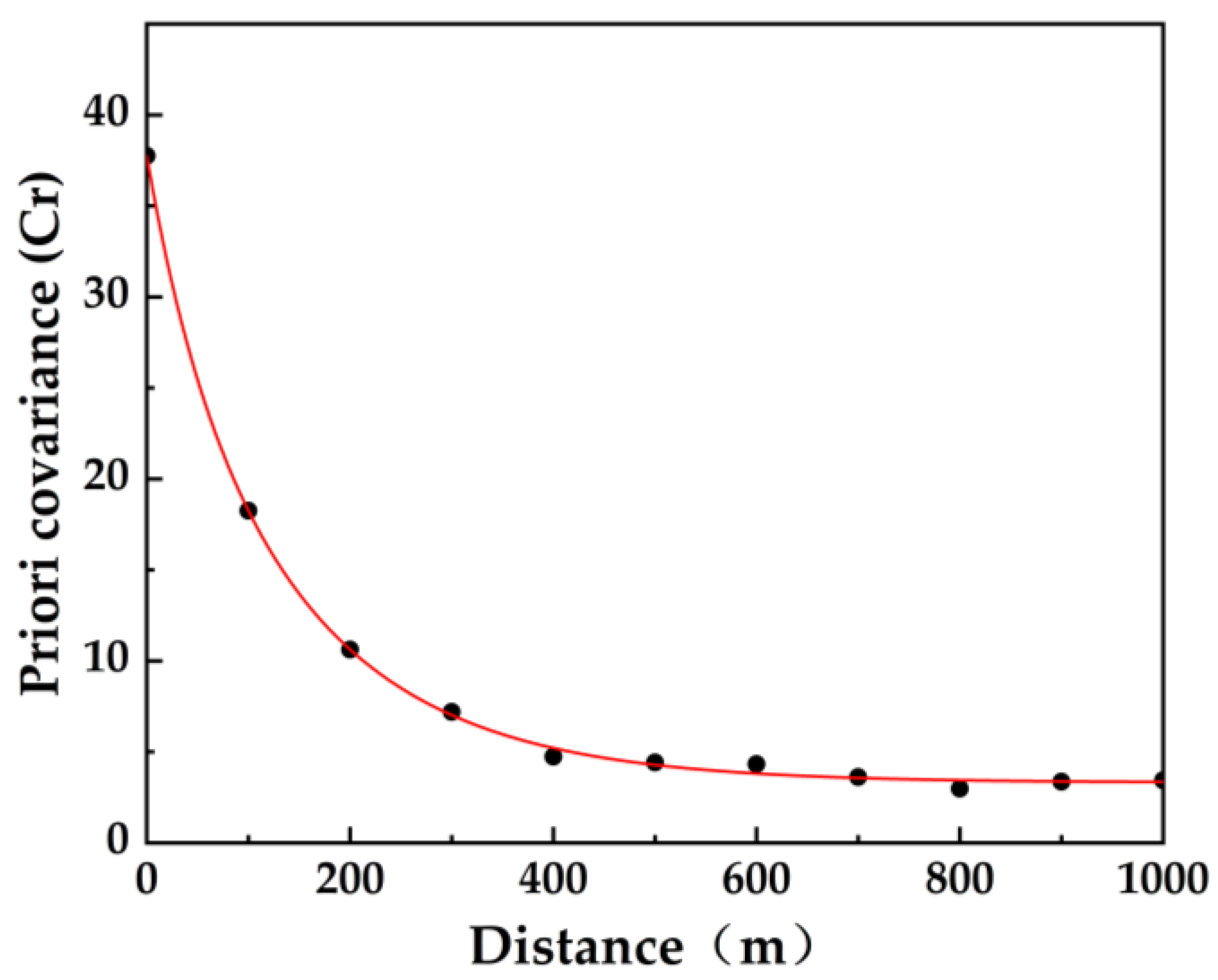

| Influence Factors | Classes | ME (m) | RMSE (m) | |||
|---|---|---|---|---|---|---|
| Grade | Interval | Before | After | Before | After | |
| Slope (°) | I | 0–5 | −1.478 | −0.021 | 2.246 | 1.462 |
| II | 5–10 | −1.866 | 0.134 | 4.271 | 3.079 | |
| III | 10–15 | −2.195 | 0.037 | 6.295 | 4.721 | |
| IV | 15–20 | −2.438 | −0.088 | 8.121 | 6.036 | |
| V | >20 | −2.708 | 0.357 | 11.895 | 7.223 | |
| Relief (m) | I | 0–30 | −1.636 | 0.029 | 3.549 | 2.392 |
| II | 30–60 | −2.290 | 0.107 | 8.198 | 5.834 | |
| III | 60–90 | −3.081 | 0.178 | 12.037 | 7.967 | |
| IV | 90–120 | −6.006 | 0.299 | 15.809 | 8.250 | |
| V | >120 | −4.196 | −0.548 | 18.088 | 10.918 | |
| Elevation (m) | I | 300–700 | −1.555 | 0.054 | 3.154 | 2.287 |
| II | 700–1100 | −1.475 | −0.038 | 5.482 | 3.831 | |
| III | 1100–1500 | −2.230 | 0.045 | 6.554 | 4.284 | |
| IV | 1500–1900 | −2.954 | 0.403 | 9.259 | 6.198 | |
| V | >1900 | −5.580 | 0.925 | 10.063 | 7.242 | |
| Land use | Croplands | −1.403 | 0.023 | 2.860 | 1.977 | |
| Forests | −2.559 | 0.124 | 7.718 | 5.128 | ||
| Grasslands | −2.191 | −0.296 | 6.416 | 4.448 | ||
| Shrublands | −1.882 | 0.057 | 7.508 | 5.049 | ||
| Water area | −1.256 | −0.488 | 4.178 | 4.486 | ||
| Built-up lands | −2.099 | −0.222 | 3.079 | 1.880 | ||
| Models | ME (m) | RMSE (m) |
|---|---|---|
| TanDEM-X DEM | −2.019 | 6.141 |
| LSC-TXC | 0.058 | 3.851 |
| RF | −0.033 | 4.252 |
| HDFNN | 0.123 | 4.317 |
| BPNN | −0.288 | 4.965 |
| Spatial Distances (m) | RMSE (m) |
|---|---|
| 200 | 4.973 |
| 300 | 4.327 |
| 400 | 3.851 |
| 500 | 3.989 |
| 600 | 4575 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, X.; Zhou, C.; Zhu, J. Improving the Accuracy of TanDEM-X Digital Elevation Model Using Least Squares Collocation Method. Remote Sens. 2023, 15, 3695. https://doi.org/10.3390/rs15143695
Shen X, Zhou C, Zhu J. Improving the Accuracy of TanDEM-X Digital Elevation Model Using Least Squares Collocation Method. Remote Sensing. 2023; 15(14):3695. https://doi.org/10.3390/rs15143695
Chicago/Turabian StyleShen, Xingdong, Cui Zhou, and Jianjun Zhu. 2023. "Improving the Accuracy of TanDEM-X Digital Elevation Model Using Least Squares Collocation Method" Remote Sensing 15, no. 14: 3695. https://doi.org/10.3390/rs15143695
APA StyleShen, X., Zhou, C., & Zhu, J. (2023). Improving the Accuracy of TanDEM-X Digital Elevation Model Using Least Squares Collocation Method. Remote Sensing, 15(14), 3695. https://doi.org/10.3390/rs15143695






