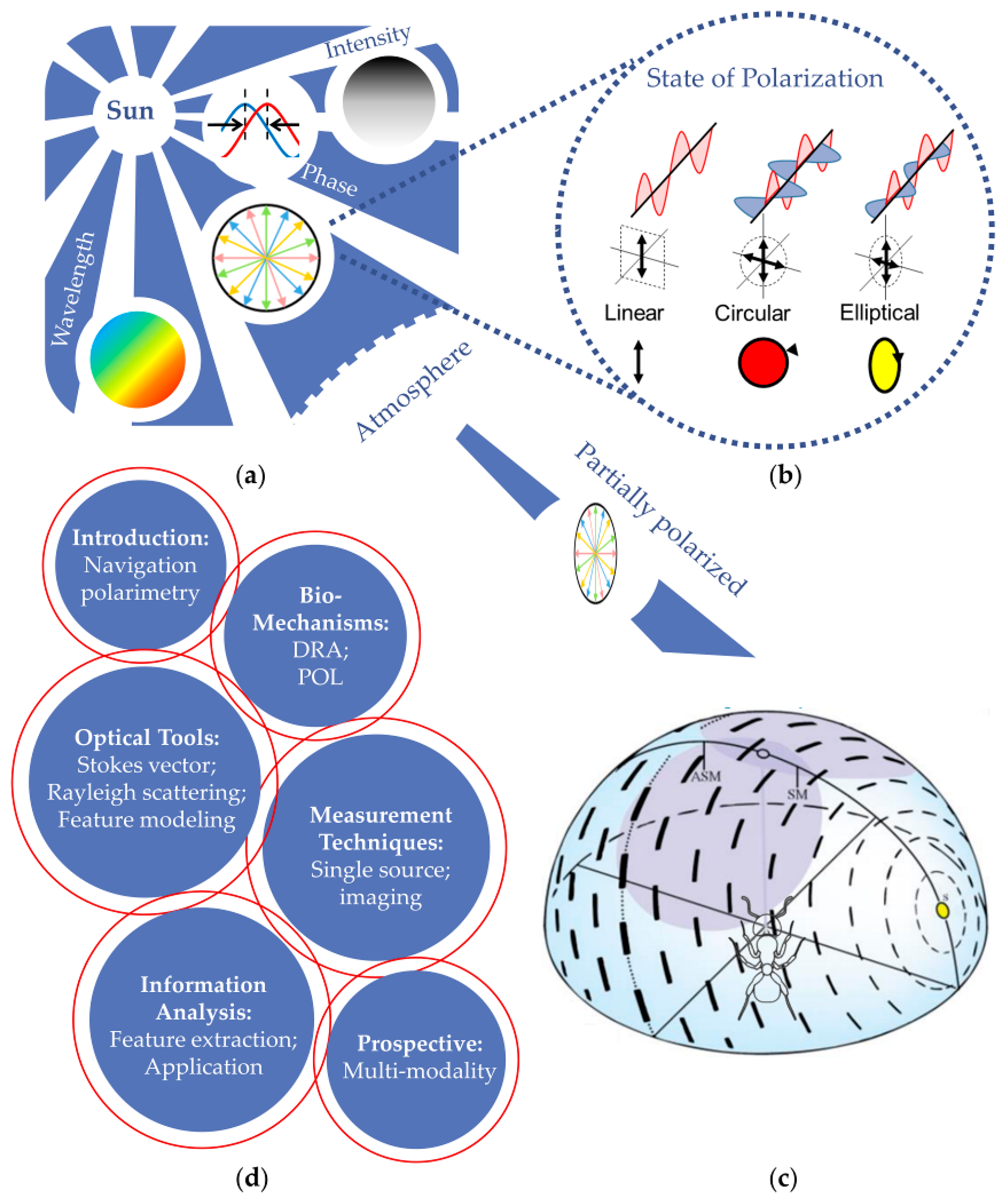
Polarimetry for Bionic Geolocation and Navigation Applications: A Review
Abstract
1. Introduction
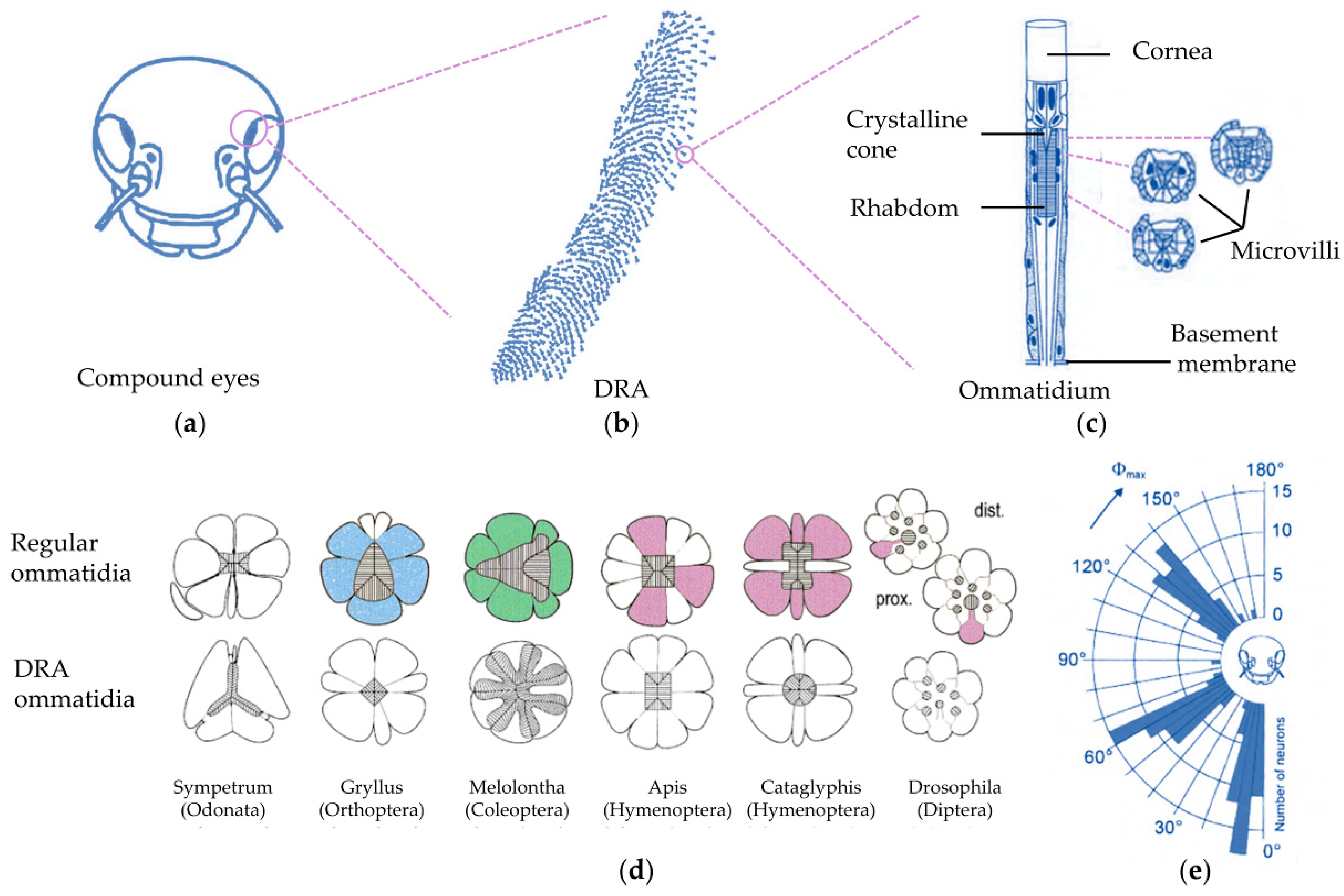
2. Biological Inspirations for Polarization Geolocation
3. Vectorial Characterization and Modeling for Bionic Geolocation Applications
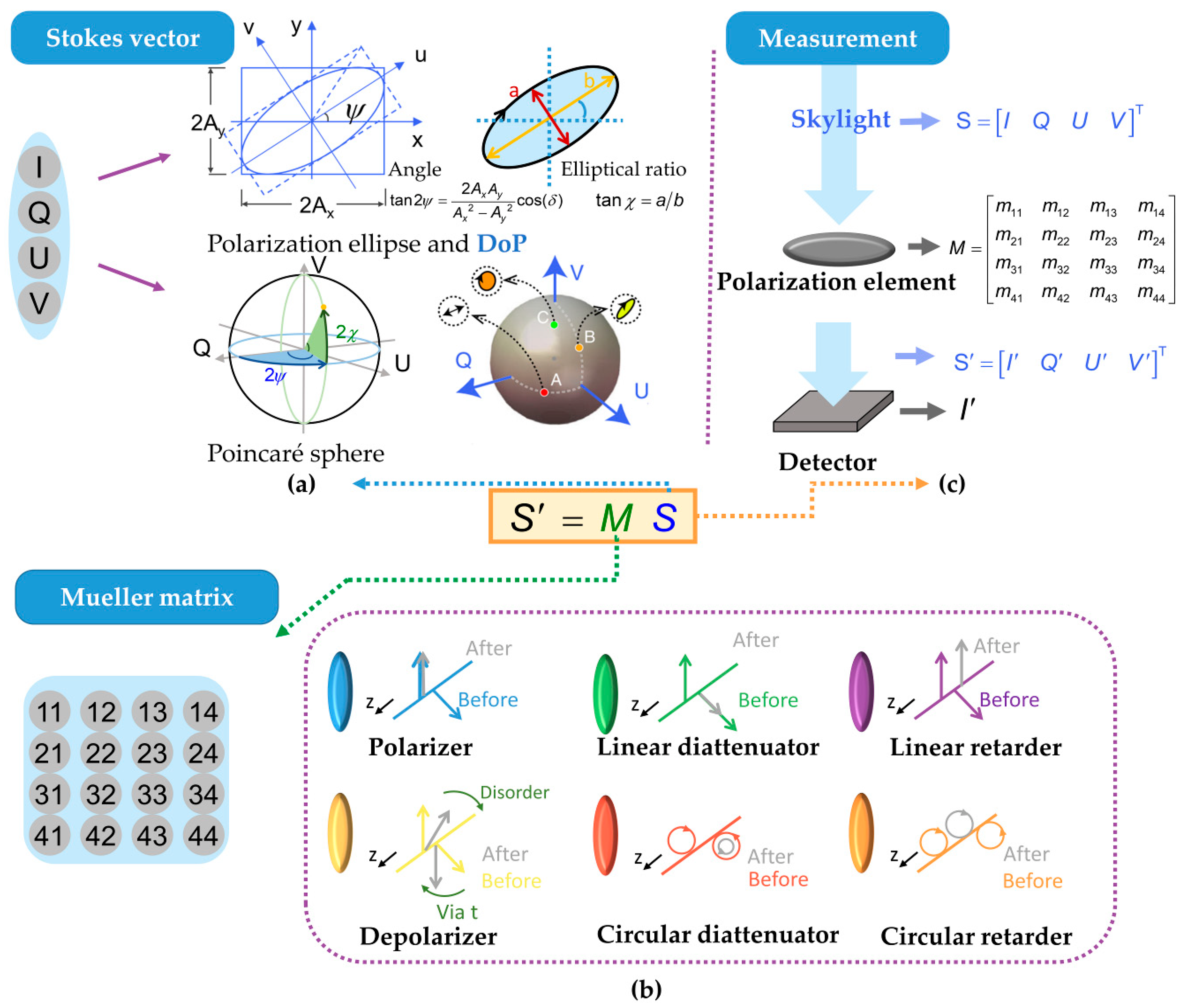
3.1. Stokes–Mueller Formalism
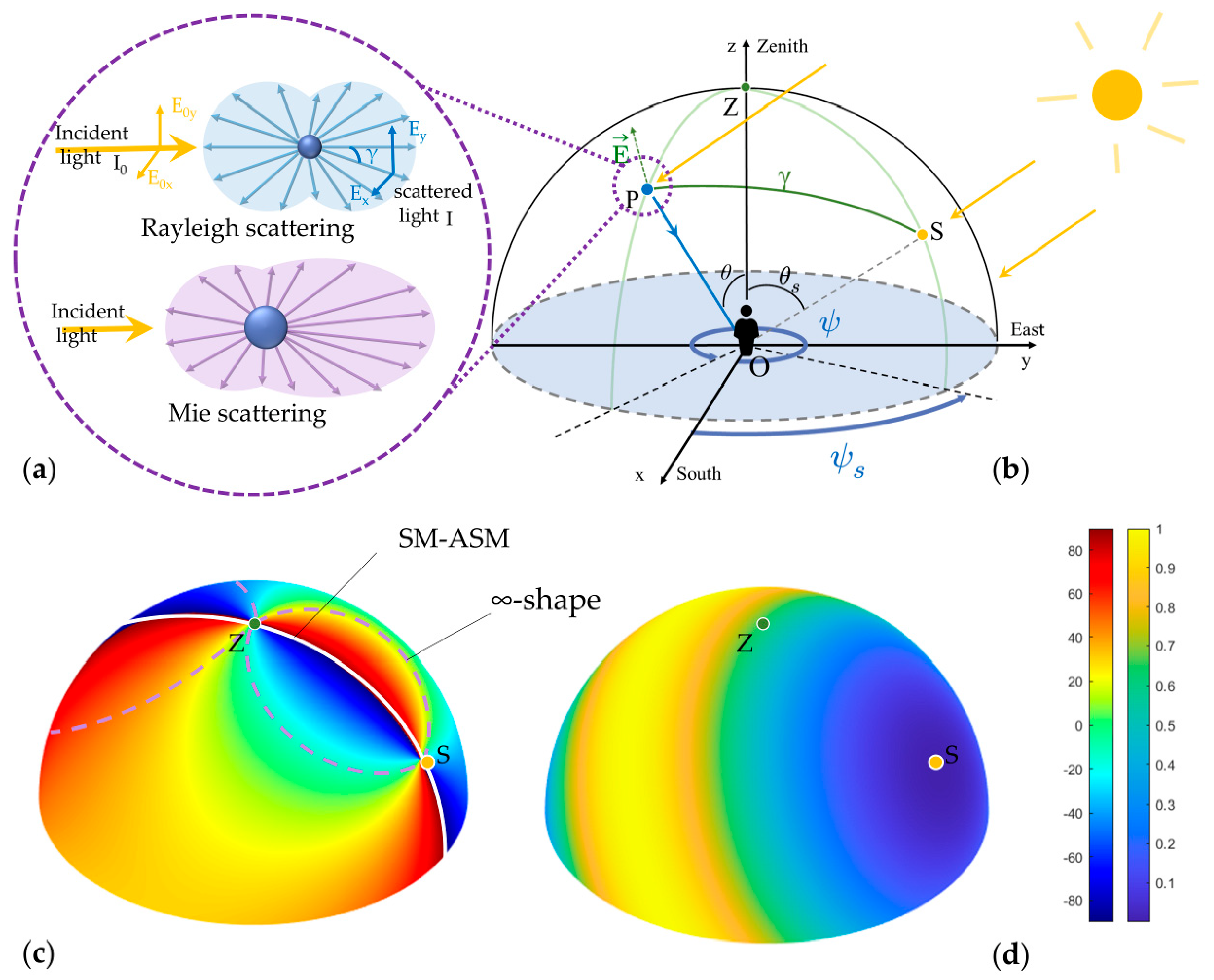
3.2. Atmospheric Polarized Light Field Modeling
4. Vectorial Information Measurement for Bionic Geolocation Applications
4.1. Point-Source Measurement
4.2. Imaging Measurement
4.2.1. Division-of-Time Polarimeters
4.2.2. Division-of-Channel Polarimeters
4.2.3. Division-of-Focal-Plane Polarimeters
5. Vectorial Information Analysis for Bionic Geolocation Applications
5.1. Vectorial Feature Extraction
5.2. Vectorial Information Analysis Adapted to Specific Conditions
5.2.1. Atmospheric and Weather Conditions
5.2.2. Environmental Conditions of the Observation Site
6. Development Directions for Polarization Geolocation and Future Prospects
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ronchi, V.; Barocas, V. The Nature of Light: An Historical Survey; Harvard University Press: Cambridge, MA, USA, 1970; ISBN 100674605268. [Google Scholar]
- Huard, S. Polarization of Light; Wiley-VCH: Hoboken, NJ, USA, 1997; ISBN 0471965367. [Google Scholar]
- Zhan, Q. Cylindrical Vector Beams: From Mathematical Concepts to Applications. Adv. Opt. Photonics 2009, 1, 1–57. [Google Scholar]
- Ndagano, B.; Perez-Garcia, B.; Roux, F.S.; McLaren, M.; Rosales-Guzman, C.; Zhang, Y.; Mouane, O.; Hernandez-Aranda, R.I.; Konrad, T.; Forbes, A. Characterizing Quantum Channels with Non-Separable States of Classical Light. Nat. Phys. 2017, 13, 397–402. [Google Scholar]
- Wang, J.; Castellucci, F.; Franke-Arnold, S. Vectorial Light–Matter Interaction: Exploring Spatially Structured Complex Light Fields. AVS Quantum Sci. 2020, 2, 031702. [Google Scholar] [CrossRef]
- Schulz, M.; Zablocki, J.; Abdullaeva, O.S.; Brück, S.; Balzer, F.; Lützen, A.; Arteaga, O.; Schiek, M. Giant Intrinsic Circular Dichroism of Prolinol-Derived Squaraine Thin Films. Nat. Commun. 2018, 9, 2413. [Google Scholar]
- Ghosh, N.; Vitkin, A.I. Tissue Polarimetry: Concepts, Challenges, Applications, and Outlook. J. Biomed. Opt. 2011, 16, 110801. [Google Scholar]
- He, C.; He, H.; Chang, J.; Chen, B.; Ma, H.; Booth, M.J. Polarisation Optics for Biomedical and Clinical Applications: A Review. Light Sci. Appl. 2021, 10, 194. [Google Scholar] [CrossRef]
- Boerner, W.M.; Mott, H.; Lueneburg, E. Polarimetry in Remote Sensing: Basic and Applied Concepts. Int. Geosci. Remote Sens. Symp. 1997, 3, 1401–1403. [Google Scholar] [CrossRef]
- Cloude, S. Polarisation: Applications in Remote Sensing; OUP Oxford: Oxford, UK, 2009; ISBN 0191580384. [Google Scholar]
- Powell, S.B.; Garnett, R.; Marshall, J.; Rizk, C.; Gruev, V. Bioinspired Polarization Vision Enables Underwater Geolocalization. Sci. Adv. 2018, 4, eaao6841. [Google Scholar] [CrossRef]
- Karman, S.B.; Diah, S.Z.M.; Gebeshuber, I.C. Bio-Inspired Polarized Skylight-Based Navigation Sensors: A Review. Sensors 2012, 12, 14232–14261. [Google Scholar] [CrossRef]
- Zhang, X.; Wan, Y.; Li, L. Bio-Inspired Polarized Skylight Navigation: A Review. MIPPR 2015: Remote Sensing Image Processing, Geographic Information Systems, and Other Applications, Enshi, China, 30 October–1 November 2015; 2015; Volume 9815, pp. 274–281. [Google Scholar] [CrossRef]
- Vowles, D.M. Sensitivity of Ants to Polarized Light. Nature 1950, 165, 282–283. [Google Scholar]
- Rossel, S.; Wehner, R. Polarization Vision in Bees. Nature 1986, 323, 128–131. [Google Scholar]
- Reppert, S.M.; Zhu, H.; White, R.H. Polarized Light Helps Monarch Butterflies Navigate. Curr. Biol. 2004, 14, 155–158. [Google Scholar] [CrossRef]
- Weir, P.T.; Dickinson, M.H. Flying Drosophila Orient to Sky Polarization. Curr. Biol. 2012, 22, 21–27. [Google Scholar]
- Liou, K.-N. An Introduction to Atmospheric Radiation; Elsevier: Amsterdam, The Netherlands, 2002; Volume 84, ISBN 0080491677. [Google Scholar]
- Coulson, K. Polarization and Intensity of Light in the Atmosphere; A. Deepak Pub.: Hampton, VA, USA, 1988. [Google Scholar]
- Brines, M.L.; Gould, J.L. Skylight Polarization Patterns and Animal Orientation. J. Exp. Biol. 1982, 96, 69–91. [Google Scholar] [CrossRef]
- Brines, M.L. Dynamic Patterns of Skylight Polarization as Clock and Compass. J. Theor. Biol. 1980, 86, 507–512. [Google Scholar]
- Schinz, R.H. Structural Specialization in the Dorsal Retina of the Bee, Apis Mellifera. Cell Tissue Res. 1975, 162, 23–34. [Google Scholar]
- Wehner, R.; Bernard, G.D.; Geiger, E. Twisted and Non-Twisted Rhabdoms and Their Significance for Polarization Detection in the Bee. J. Comp. Physiol. 1975, 104, 225–245. [Google Scholar]
- Labhart, T.; Petzold, J.; Helbling, H. Spatial Integration in Polarization-Sensitive Interneurones of Crickets: A Survey of Evidence, Mechanisms and Benefits. J. Exp. Biol. 2001, 204, 2423–2430. [Google Scholar]
- Lambrinos, D.; Kobayashi, H.; Pfeifer, R.; Maris, M.; Labhart, T.; Wehner, R. An Autonomous Agent Navigating with a Polarized Light Compass. Adapt. Behav. 1997, 6, 131–161. [Google Scholar] [CrossRef]
- Bohren, C.F.; Clothiaux, E.E. Fundamentals of Atmospheric Radiation: An Introduction with 400 Problems; John Wiley & Sons: Hoboken, NJ, USA, 2006; ISBN 3527608370. [Google Scholar]
- Kimball, H.H. The Effect of the Atmospheric Turbidity of 1912 on Solar Radiation Intensities and Skylight Polarization. Bull. Mt. Weather Obs. 1913, 5, 295–312. [Google Scholar]
- Coulson, K.L. Characteristics of Skylight at the Zenith during Twilight as Indicators of Atmospheric Turbidity. 1: Degree of Polarization. Appl. Opt. 1980, 19, 3469–3480. [Google Scholar]
- Oates, T.W.H.; Wormeester, H.; Arwin, H. Characterization of Plasmonic Effects in Thin Films and Metamaterials Using Spectroscopic Ellipsometry. Prog. Surf. Sci. 2011, 86, 328–376. [Google Scholar] [CrossRef]
- Arteaga, O.; Kahr, B. Mueller Matrix Polarimetry of Bianisotropic Materials. J. Opt. Soc. Am. B Opt. Phys. 2019, 36, F72–F83. [Google Scholar] [CrossRef]
- Yoo, S.; Park, Q.H. Spectroscopic Ellipsometry for Low-Dimensional Materials and Heterostructures. Nanophotonics 2022, 11, 2811–2825. [Google Scholar] [CrossRef]
- Chen, X.G.; Gu, H.G.; Liu, J.M.; Chen, C.; Liu, S.Y. Advanced Mueller Matrix Ellipsometry: Instrumentation and Emerging Applications. Sci. China Technol. Sci. 2022, 65, 2007–2030. [Google Scholar] [CrossRef]
- Tuchin, V. V Polarized Light Interaction with Tissues. J. Biomed. Opt. 2016, 21, 071114. [Google Scholar] [CrossRef]
- Ramella-Roman, J.C.; Saytashev, I.; Piccini, M. A Review of Polarization-Based Imaging Technologies for Clinical and Preclinical Applications. J. Opt. 2020, 22, 123001. [Google Scholar] [CrossRef]
- Migliaccio, M.; Nunziata, F.; Buono, A. SAR Polarimetry for Sea Oil Slick Observation. Int. J. Remote Sens. 2015, 36, 3243–3273. [Google Scholar] [CrossRef]
- Touzi, R.; Boerner, W.M.; Lee, J.S.; Lueneburg, E. A Review of Polarimetry in the Context of Synthetic Aperture Radar: Concepts and Information Extraction. Can. J. Remote Sens. 2004, 30, 380–407. [Google Scholar] [CrossRef]
- Tyo, J.S.; Goldstein, D.L.; Chenault, D.B.; Shaw, J.A. Review of Passive Imaging Polarimetry for Remote Sensing Applications. Appl. Opt. 2006, 45, 5453–5469. [Google Scholar] [CrossRef]
- Yan, L.; Li, Y.; Chandrasekar, V.; Mortimer, H.; Peltoniemi, J.; Lin, Y. General Review of Optical Polarization Remote Sensing. Int. J. Remote Sens. 2020, 41, 4853–4864. [Google Scholar] [CrossRef]
- Wehner, R. On the Brink of Introducing Sensory Ecology: Felix Santschi (1872–1940)—Tabib-En-Neml. Behav. Ecol. Sociobiol. 1990, 27, 295–306. [Google Scholar]
- Horváth, G.; Lerner, A.; Shashar, N. Polarized Light and Polarization Vision in Animal Sciences; Springer: Berlin/Heidelberg, Germany, 2014; Volume 2, ISBN 3642547184. [Google Scholar]
- Carthy, J.D. The Orientation of Two Allied Species of British Ant, II. Odour Trail Laying and Following in Acanthomyops (Lasius) Fuliginosus. Behaviour 1951, 3, 304–318. [Google Scholar]
- Wellington, W.G. Motor Responses Evoked by the Dorsal Ocelli of Sarcophaga Aldrichi Parker, and the Orientation of the Fly to Plane Polarized Light. Nature 1953, 172, 1177–1179. [Google Scholar]
- Papi, F. Orientamento Astronomico in Alcuni Carabidi. Atti. Soc. Toscana Sci. Nat. Mem. B 1955, 62, 83–97. [Google Scholar]
- Labhart, T.; Hodel, B.; Valenzuela, I. The Physiology of the Cricket’s Compound Eye with Particular Reference to the Anatomically Specialized Dorsal Rim Area. J. Comp. Physiol. A 1984, 155, 289–296. [Google Scholar]
- Homberg, U. Sky Compass Orientation in Desert Locusts—Evidence from Field and Laboratory Studies. Front. Behav. Neurosci. 2015, 9, 346. [Google Scholar]
- Bech, M.; Homberg, U.; Pfeiffer, K. Receptive Fields of Locust Brain Neurons Are Matched to Polarization Patterns of the Sky. Curr. Biol. 2014, 24, 2124–2129. [Google Scholar] [CrossRef]
- Mouritsen, H.; Frost, B.J. Virtual Migration in Tethered Flying Monarch Butterflies Reveals Their Orientation Mechanisms. Proc. Natl. Acad. Sci. USA 2002, 99, 10162–10166. [Google Scholar]
- Muheim, R. Behavioural and Physiological Mechanisms of Polarized Light Sensitivity in Birds. Philos. Trans. R. Soc. B Biol. Sci. 2011, 366, 763–771. [Google Scholar]
- Adler, K. Extraocular Photoreception in Amphibians. Photochem. Photobiol. 1976, 23, 275–298. [Google Scholar]
- Freake, M.J. Evidence for Orientation Using the E-Vector Direction of Polarised Light in the Sleepy Lizard Tiliqua Rugosa. J. Exp. Biol. 1999, 202, 1159–1166. [Google Scholar]
- Greif, S.; Borissov, I.; Yovel, Y.; Holland, R.A. A Functional Role of the Sky’s Polarization Pattern for Orientation in the Greater Mouse-Eared Bat. Nat. Commun. 2014, 5, 4488. [Google Scholar]
- Waterman, T.H. Reviving a Neglected Celestial Underwater Polarization Compass for Aquatic Animals. Biol. Rev. 2006, 81, 111–115. [Google Scholar]
- Garcia, M.; Edmiston, C.; Marinov, R.; Vail, A.; Gruev, V. Bio-Inspired Color-Polarization Imager for Real-Time in Situ Imaging. Optica 2017, 4, 1263. [Google Scholar] [CrossRef]
- Homberg, U.; Paech, A. Ultrastructure and Orientation of Ommatidia in the Dorsal Rim Area of the Locust Compound Eye. Arthropod Struct. Dev. 2002, 30, 271–280. [Google Scholar] [CrossRef]
- Labhart, T.; Meyer, E.P. Detectors for Polarized Skylight in Insects: A Survey of Ommatidial Specializations in the Dorsal Rim Area of the Compound Eye. Microsc. Res. Tech. 1999, 47, 368–379. [Google Scholar]
- Labhart, T. Polarization-Opponent Interneurons in the Insect Visual System. Nature 1988, 331, 435–437. [Google Scholar]
- Labhart, T. Polarization-Sensitive Interneurons in the Optic Lobe of the Desert Ant Cataglyphis Bicolor. Naturwissenschaften 2000, 87, 133–136. [Google Scholar]
- Henze, M.J.; Labhart, T. Haze, Clouds and Limited Sky Visibility: Polarotactic Orientation of Crickets under Difficult Stimulus Conditions. J. Exp. Biol. 2007, 210, 3266–3276. [Google Scholar]
- Labhart, T. How Polarization-Sensitive Interneurones of Crickets Perform at Low Degrees of Polarization. J. Exp. Biol. 1996, 199, 1467–1475. [Google Scholar]
- Wehner, R.; Srinivasan, M.V. Path Integration in Insects. Neurobiol. Spat. Behav. 2003, 1, 9–30. [Google Scholar]
- Mittelstaedt, H.; Mittelstaedt, M.-L. Homing by Path Integration. In Avian Navigation; Springer: Berlin/Heidelberg, Germany, 1982; pp. 290–297. [Google Scholar]
- Wittlinger, M.; Wehner, R.; Wolf, H. The Desert Ant Odometer: A Stride Integrator That Accounts for Stride Length and Walking Speed. J. Exp. Biol. 2007, 210, 198–207. [Google Scholar]
- Wohlgemuth, S.; Ronacher, B.; Wehner, R. Ant Odometry in the Third Dimension. Nature 2001, 411, 795–798. [Google Scholar]
- Sakura, M.; Lambrinos, D.; Labhart, T. Polarized Skylight Navigation in Insects: Model and Electrophysiology of e-Vector Coding by Neurons in the Central Complex. J. Neurophysiol. 2008, 99, 667–682. [Google Scholar]
- El Jundi, B.; Pfeiffer, K.; Heinze, S.; Homberg, U. Integration of Polarization and Chromatic Cues in the Insect Sky Compass. J. Comp. Physiol. A 2014, 200, 575–589. [Google Scholar]
- Fujiwara, H. Spectroscopic Ellipsometry: Principles and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2007; ISBN 0470060182. [Google Scholar]
- Azzam, R.; Bashara, N.M.; Ballard, S. Ellipsometry and Polarized Light. Phys. Today 1978, 31, 72. [Google Scholar] [CrossRef]
- Jones, R.C. A New Calculus for the Treatment of Optical Systemsi. Description and Discussion of the Calculus. Josa 1941, 31, 488–493. [Google Scholar]
- Schurcliff, W.A. Polarized Light: Production and Use; Harvard University: Cambridge, MA, USA, 1962. [Google Scholar]
- Horváth, G.; Bernáth, B.; Suhai, B.; Barta, A.; Wehner, R. First Observation of the Fourth Neutral Polarization Point in the Atmosphere. Josa A 2002, 19, 2085–2099. [Google Scholar]
- Dahlberg, A.R.; Pust, N.J.; Shaw, J.A. Effects of Surface Reflectance on Skylight Polarization Measurements at the Mauna Loa Observatory. Opt. Express 2011, 19, 16008. [Google Scholar] [CrossRef]
- Pezzaniti, J.L.; Chipman, R.A. Mueller Matrix Imaging Polarimetry. Opt. Eng. 1995, 34, 1558–1568. [Google Scholar]
- Azzam, R. Stokes-Vector and Mueller-Matrix Polarimetry. J. Opt. Soc. Am. A 2016, 33, 1396. [Google Scholar] [CrossRef]
- York, T.; Powell, S.B.; Gao, S.; Kahan, L.; Charanya, T.; Saha, D.; Roberts, N.W.; Cronin, T.W.; Marshall, J.; Achilefu, S.; et al. Bioinspired Polarization Imaging Sensors: From Circuits and Optics to Signal Processing Algorithms and Biomedical Applications. Proc. IEEE 2014, 102, 1450–1469. [Google Scholar] [CrossRef]
- Laude-Boulesteix, B.; De Martino, A.; Drévillon, B.; Schwartz, L. Mueller Polarimetric Imaging System with Liquid Crystals. Appl. Opt. 2004, 43, 2824–2832. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light; Elsevier: Amsterdam, The Netherlands, 2013; ISBN 148310320X. [Google Scholar]
- Brosseau, C. Fundamentals of Polarized Light: A Statistical Optics Approach; Wiley-Interscience: Hoboken, HJ, USA, 1998; ISBN 0471143022. [Google Scholar]
- Stokes, G.G. On the Composition and Resolution of Streams of Polarized Light from Different Sources. Trans. Camb. Philos. Soc. 1851, 9, 399. [Google Scholar]
- Poincaré, H. Théorie Mathématique de La Lumière II.: Nouvelles Études Sur La Diffraction.—Théorie de La Dispersion de Helmholtz. Leçons Professées Pendant Le Premier Semestre 1891–1892; G. Carré: Paris, France, 1889; Volume 1. [Google Scholar]
- McMaster, W. Polarization and the Stokes Parameters. Am. J. Phys. 1954, 22, 351–362. [Google Scholar] [CrossRef]
- Mayer, B. Radiative Transfer in the Cloudy Atmosphere. In EPJ Web of Conferences; EDP Sciences: Les Ulis, France, 2009; Volume 1, pp. 75–99. [Google Scholar]
- Kisselev, V.B.; Roberti, L.; Perona, G. Finite-Element Algorithm for Radiative Transfer in Vertically Inhomogeneous Media: Numerical Scheme and Applications. Appl. Opt. 1995, 34, 8460–8471. [Google Scholar]
- Collins, D.G.; Blättner, W.G.; Wells, M.B.; Horak, H.G. Backward Monte Carlo Calculations of the Polarization Characteristics of the Radiation Emerging from Spherical-Shell Atmospheres. Appl. Opt. 1972, 11, 2684–2696. [Google Scholar]
- de Haan, J.F.; Bosma, P.B.; Hovenier, J.W. The Adding Method for Multiple Scattering Calculations of Polarized Light. Astron. Astrophys. 1987, 183, 371–391. [Google Scholar]
- Stamnes, K.; Conklin, P. A New Multi-Layer Discrete Ordinate Approach to Radiative Transfer in Vertically Inhomogeneous Atmospheres. J. Quant. Spectrosc. Radiat. Transf. 1984, 31, 273–282. [Google Scholar]
- Karp, A.H.; Greenstadt, J.; Fillmore, J.A. Radiative Transfer through an Arbitrarily Thick, Scattering Atmosphere. J. Quant. Spectrosc. Radiat. Transf. 1980, 24, 391–406. [Google Scholar]
- Irvine, W.M. Multiple Scattering in Planetary Atmospheres. Icarus 1975, 25, 175–204. [Google Scholar]
- Bucholtz, A. Rayleigh-Scattering Calculations for the Terrestrial Atmosphere. Appl. Opt. 1995, 34, 2765–2773. [Google Scholar]
- Rayleigh, L.X. On the Electromagnetic Theory of Light. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1881, 12, 81–101. [Google Scholar]
- Perez, R.; Seals, R.; Michalsky, J. All-Weather Model for Sky Luminance Distribution-Preliminary Configuration and Validation. Sol. Energy 1993, 50, 235–245. [Google Scholar] [CrossRef]
- Zufall, F.; Menzel, M.S. Spectral and Polarized Light Sensitivity of Photoreceptors in the Compound Eye of the Cricket (Gryllus Bimaculatus). J. Comp. Physiol. A Neuroethol. Behav. Physiol. 1989, 164, 597–608. [Google Scholar]
- Wilkie, A.; Ulbricht, C.; Tobler, R.F.; Zotti, G.; Purgathofer, W. An Analytical Model for Skylight Polarisation. In Rendering Techniques; CRC Press: Boca Raton, FL, USA, 2004; pp. 387–398. [Google Scholar]
- Nishita, T.; Dobashi, Y.; Nakamae, E. Display of Clouds Taking into Account Multiple Anisotropic Scattering and Sky Light. In Proceedings of the 23rd Annual Conference on Computer Graphics and Interactive Techniques, New Orleans, LA, USA, 4–9 August 1996. [Google Scholar]
- Wang, X.; Gao, J.; Fan, Z.; Roberts, N.W. An Analytical Model for the Celestial Distribution of Polarized Light, Accounting for Polarization Singularities, Wavelength and Atmospheric Turbidity. J. Opt. 2016, 18, 65601. [Google Scholar]
- Horváth, G.; Gál, J.; Pomozi, I.; Wehner, R. Polarization Portrait of the Arago Point: Video-Polarimetric Imaging of the Neutral Points of Skylight Polarization. Naturwissenschaften 1998, 85, 333–339. [Google Scholar] [CrossRef]
- Fan, Z.; Wang, X.; Jin, H.; Wang, C.; Pan, N.; Hua, D. Neutral Point Detection Using the AOP of Polarized Skylight Patterns. Opt. Express 2021, 29, 5665. [Google Scholar] [CrossRef]
- Eshelman, L.M.; Jan Tauc, M.; Hashimoto, T.; Gillis, K.; Weiss, W.; Stanley, B.; Hooser, P.; Shaw, G.E.; Shaw, J.A. Digital All-Sky Polarization Imaging of the Total Solar Eclipse on 21 August 2017 in Rexburg, Idaho, USA. Appl. Opt. 2020, 59, F41–F52. [Google Scholar] [CrossRef]
- Berry, M.V.; Dennis, M.R.; Lee, R.L. Polarization Singularities in the Clear Sky. New J. Phys. 2004, 6, 162. [Google Scholar] [CrossRef]
- Hannay, J.H. Polarization of Sky Light from a Canopy Atmosphere. New J. Phys. 2004, 6, 197. [Google Scholar]
- Mie, G. Beiträge Zur Optik Trüber Medien, Speziell Kolloidaler Metallösungen. Ann. Phys. 1908, 330, 377–445. [Google Scholar]
- Pust, N.J.; Shaw, J.A. Digital All-Sky Polarization Imaging of Partly Cloudy Skies. Appl. Opt. 2008, 47, H190–H198. [Google Scholar] [CrossRef]
- Lambrinos, D.; Möller, R.; Labhart, T.; Pfeifer, R.; Wehner, R. Mobile Robot Employing Insect Strategies for Navigation. Rob. Auton. Syst. 2000, 30, 39–64. [Google Scholar] [CrossRef]
- Labhart, T. How Polarization-Sensitive Interneurones of Crickets See the Polarization Pattern of the Sky: A Field Study with an Optoelectronic Model Neurone. J. Exp. Biol. 1999, 202, 757–770. [Google Scholar] [CrossRef]
- Jinkui, C.; Kaichun, Z.; Qiang, Z.; Tichang, W. Construction and Performance Test of a Novel Polarization Sensor for Navigation. Sens. Actuators A Phys. 2008, 148, 75–82. [Google Scholar] [CrossRef]
- Gál, J.; Horváth, G.; Meyer-Rochow, V.B.; Wehner, R. Polarization Patterns of the Summer Sky and Its Neutral Points Measured by Full-Sky Imaging Polarimetry in Finnish Lapland North of the Arctic Circle. Proc. R. Soc. A Math. Phys. Eng. Sci. 2001, 457, 1385–1399. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, X.; Lian, J.; Zhang, L.; Xian, Z.; Ma, T. Design of a Device for Sky Light Polarization Measurements. Sensors 2014, 14, 14916–14931. [Google Scholar] [CrossRef]
- Lu, H.; Zhao, K.; You, Z.; Huang, K. Angle Algorithm Based on Hough Transform for Imaging Polarization Navigation Sensor. Opt. Express 2015, 23, 7248. [Google Scholar] [CrossRef]
- Fan, C.; Hu, X.; He, X.; Zhang, L.; Wang, Y. Multicamera Polarized Vision for the Orientation with the Skylight Polarization Patterns. Opt. Eng. 2018, 57, 1. [Google Scholar] [CrossRef]
- Horváth, G.; Barta, A.; Gál, J.; Suhai, B.; Haiman, O. Ground-Based Full-Sky Imaging Polarimetry of Rapidly Changing Skies and Its Use for Polarimetric Cloud Detection. Appl. Opt. 2002, 41, 543. [Google Scholar] [CrossRef]
- Zhi, W.; Chu, J.; Li, J.; Wang, Y. A Novel Attitude Determination System Aided by Polarization Sensor. Sensors 2018, 18, 158. [Google Scholar] [CrossRef]
- Sarkar, M.; Bello, D.S.S.; Van Hoof, C.; Theuwissen, A. Integrated Polarization Analyzing Cmos Image Sensor for Autonomus Navigation Using Polarized Light. In Proceedings of the 2010 5th IEEE International Conference Intelligent Systems, London, UK, 7–9 July 2010; pp. 224–229. [Google Scholar] [CrossRef]
- Higashi, Y.; Tokuami, H.; Kimura, H. Robot Navigation Using Polarized Light Sensor without Crossed-Analyzer. In Proceedings of the 6th International Symposium on Advanced Science and Technology in Experimental Mechanics, Osaka, Japan, 3–5 November 2011; pp. 3–5. [Google Scholar]
- Chahl, J.; Mizutani, A. Biomimetic Attitude and Orientation Sensors. IEEE Sens. J. 2012, 12, 289–297. [Google Scholar] [CrossRef]
- Chahl, J.; Mizutani, A. Integration and Flight Test of a Biomimetic Heading Sensor. In Bioinspiration, Biomimetics, Bioreplication 2013; SPIE: Bellingham, WA, USA, 2013; Volume 8686. [Google Scholar] [CrossRef]
- Coulson, K.L.; Whitehead, V.S.; Campbell, C. Polarized Views of the Earth from Orbital Altitude. In Ocean Optics VIII; SPIE: Bellingham, WA, USA, 1986; Volume 637, pp. 35–41. [Google Scholar]
- Stürzl, W.; Carey, N. A Fisheye Camera System for Polarisation Detection on UAVs. In Computer Vision–ECCV 2012. Workshops and Demonstrations: Florence, Italy, 7–13 October 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 431–440. [Google Scholar] [CrossRef]
- Walraven, R. Polarization Imagery. In Proceedings of the Optical Polarimetry: Instrumentation and Applications, International Society for Optics and Photonics, San Diego, CA, USA, 23–24 August 1977; Volume 112, pp. 164–167. [Google Scholar]
- Egan, W.G.; Johnson, W.R.; Whitehead, V.S. Terrestrial Polarization Imagery Obtained from the Space Shuttle: Characterization and Interpretation. Appl. Opt. 1991, 30, 435–442. [Google Scholar]
- Wu, L.; Gao, J.; Fan, Z.; Zhang, J. Measurements of Skylight Polarization: A Case Study in Urban Region with High-Loading Aerosol. Appl. Opt. 2015, 54, B256. [Google Scholar] [CrossRef]
- Voss, K.J.; Liu, Y. Polarized Radiance Distribution Measurements of Skylight I System Description and Characterization. Appl. Opt. 1997, 36, 6083. [Google Scholar] [CrossRef]
- Liu, Y.; Voss, K. Polarized Radiance Distribution Measurement of Skylight II Experiment and Data. Appl. Opt. 1997, 36, 8753. [Google Scholar] [CrossRef]
- Lu, H.; Zhao, K.; Wang, X.; You, Z.; Huang, K. Real-Time Imaging Orientation Determination System to Verify Imaging Polarization Navigation Algorithm. Sensors 2016, 16, 144. [Google Scholar] [CrossRef]
- Lu, H.; Zhao, K.; You, Z.; Huang, K. Real-Time Polarization Imaging Algorithm for Camera-Based Polarization Navigation Sensors. Appl. Opt. 2017, 56, 3199. [Google Scholar] [CrossRef]
- Guan, L.; Li, S.; Zhai, L.; Liu, S.; Liu, H.; Lin, W.; Cui, Y.; Chu, J.; Xie, H. Study on Skylight Polarization Patterns over the Ocean for Polarized Light Navigation Application. Appl. Opt. 2018, 57, 6243. [Google Scholar] [CrossRef]
- Giudicotti, L.; Brombin, M. Data Analysis for a Rotating Quarter-Wave, Far-Infrared Stokes Polarimeter. Appl. Opt. 2007, 46, 2638–2648. [Google Scholar] [CrossRef]
- Gál, J.; Horváth, G.; Meyer-Rochow, V.B. Measurement of the Reflection—Polarization Pattern of the Flat Water Surface under a Clear Sky at Sunset. Remote Sens. Environ. 2001, 76, 103–111. [Google Scholar] [CrossRef]
- Gál, J.; Horváth, G.; Barta, A.; Wehner, R. Polarization of the Moonlit Clear Night Sky Measured by Full-Sky Imaging Polarimetry at Full Moon: Comparison of the Polarization of Moonlit and Sunlit Skies. J. Geophys. Res. Atmos. 2001, 106, 22647–22653. [Google Scholar] [CrossRef]
- Pomozi, I.; Horváth, G.; Wehner, R. How the Clear-Sky Angle of Polarization Pattern Continues underneath Clouds: Full-Sky Measurements and Implications for Animal Orientation. J. Exp. Biol. 2001, 204, 2933–2942. [Google Scholar]
- Pomozi, I.; Gál, J.; Horvath, G.; Wehner, R. Fine Structure of the Celestial Polarization Pattern and Its Temporal Change during the Total Solar Eclipse of 11 August 1999. Remote Sens. Environ. 2001, 76, 181–201. [Google Scholar]
- Lu, H.; Zhao, K.-C.; Ma, Q.; You, Z. Design and Implementation of Detection System for Skylight Polarized Pattern Using Continuously Spinning Polarization Analyzer. J. Astronaut. 2014, 35, 1087–1094. [Google Scholar] [CrossRef]
- Han, Y.; Zhao, K.-C.; You, Z. Developement of Rapid Rotary Polarization Imaging Detection Devices. Optics Precis. Eng. 2018, 26, 2345–2354. [Google Scholar] [CrossRef]
- Gerhart, G.R. Rapid 4-Stokes Parameter Determination Using a Motorized Rotating Retarder. Opt. Eng. 2006, 45, 098002. [Google Scholar] [CrossRef]
- Liang, Y.; Qu, Z.; Zhong, Y.; Song, Z.; Li, S. Analysis of Errors in Polarimetry Using a Rotating Waveplate. Appl. Opt. 2019, 58, 9883–9895. [Google Scholar] [CrossRef]
- Pust, N.J.; Shaw, J.A. Dual-Field Imaging Polarimeter Using Liquid Crystal Variable Retarders. Appl. Opt. 2006, 45, 5470–5478. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, H.; Song, P.; Shi, S.; Xu, W.; Liang, X. Ground-Based Full-Sky Imaging Polarimeter Based on Liquid Crystal Variable Retarders. Opt. Express 2014, 22, 8749. [Google Scholar] [CrossRef]
- Zhao, H.; Xu, W.; Zhang, Y.; Li, X.; Zhang, H.; Xuan, J.; Jia, B. Polarization Patterns under Different Sky Conditions and a Navigation Method Based on the Symmetry of the AOP Map of Skylight. Opt. Express 2018, 26, 28589. [Google Scholar] [CrossRef]
- Sornsin, E.A.; Chipman, R.A. Mueller Matrix Polarimetry of Electro-Optic PLZT Spatial Light Modulators. In International Symposium on Polarization Analysis and Applications to Device Technology; SPIE: Bellingham, WA, USA, 1996; Volume 2873, pp. 196–201. [Google Scholar]
- Gendre, L.; Foulonneau, A.; Bigué, L. Full Stokes Polarimetric Imaging Using a Single Ferroelectric Liquid Crystal Device. Opt. Eng. 2011, 50, 81209. [Google Scholar] [CrossRef]
- Jaulin, A. High-Speed Degree-of-Polarization Imaging with a Ferroelectric Liquid-Crystal Modulator. Opt. Eng. 2008, 47, 033201. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, H.; Li, N. Polarization Calibration with Large Apertures in Full Field of View for a Full Stokes Imaging Polarimeter Based on Liquid-Crystal Variable Retarders. Appl. Opt. 2013, 52, 1284–1292. [Google Scholar] [CrossRef]
- North, J.A.; Duggin, M.J. Stokes Vector Imaging of the Polarized Sky-Dome. Appl. Opt. 1997, 36, 723–730. [Google Scholar]
- Wang, D.; Liang, H.; Zhu, H.; Zhang, S. A Bionic Camera-Based Polarization Navigation Sensor. Sensors 2014, 14, 13006–13023. [Google Scholar] [CrossRef]
- Tang, J.; Zhang, N.; Li, D.; Wang, F.; Zhang, B.; Wang, C.; Shen, C.; Ren, J.; Xue, C.; Liu, J. Novel Robust Skylight Compass Method Based on Full-Sky Polarization Imaging under Harsh Conditions. Opt. Express 2016, 24, 15834. [Google Scholar] [CrossRef]
- Fan, C.; Hu, X.; He, X.; Zhang, L.; Lian, J. Integrated Polarized Skylight Sensor and MIMU with a Metric Map for Urban Ground Navigation. IEEE Sens. J. 2018, 18, 1714–1722. [Google Scholar] [CrossRef]
- Zhang, Z. A Flexible New Technique for Camera Calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar]
- Kannala, J.; Brandt, S.S. A Generic Camera Model and Calibration Method for Conventional. Pattern Anal. Mach. Intell. 2006, 28, 1335–1340. [Google Scholar]
- Svoboda, T.; Martinec, D.; Pajdla, T. A Convenient Multicamera Self-Calibration for Virtual Environments. Presence Teleoperators Virtual Environ. 2005, 14, 407–422. [Google Scholar] [CrossRef]
- Brückner, M.; Bajramovic, F.; Denzler, J. Intrinsic and Extrinsic Active Self-Calibration of Multi-Camera Systems. Mach. Vis. Appl. 2014, 25, 389–403. [Google Scholar]
- Sun, Q.; Xu, D. Self-Calibration of Multi-Camera Networks without Feature Correspondence between Different Cameras. Optik 2014, 125, 3331–3336. [Google Scholar]
- Fan, C.; Hu, X.; Lian, J.; Zhang, L.; He, X. Design and Calibration of a Novel Camera-Based Bio-Inspired Polarization Navigation Sensor. IEEE Sens. J. 2016, 16, 3640–3648. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, X.; Lian, J.; Zhang, L.; He, X.; Fan, C. Geometric Calibration Algorithm of Polarization Camera Using Planar Patterns. J. Shanghai Jiaotong Univ. 2017, 22, 55–59. [Google Scholar] [CrossRef]
- Beekman, D.W.; Van Anda, J. Polarization Sensitive QWIP Thermal Imager. Infrared Phys. Technol. 2001, 42, 323–328. [Google Scholar] [CrossRef]
- Garlick, G.F.J.; Steigmann, G.A.; Lamb, W.E. Differential Optical Polarization Detectors. U.S. Patent No. 3,992,571, 16 November 1976. [Google Scholar]
- Farlow, C.A.; Chenault, D.B.; Pezzaniti, J.L.; Spradley, K.D.; Gulley, M.G. Imaging Polarimeter Development and Applications. Polariz. Anal. Meas. IV 2002, 4481, 118. [Google Scholar] [CrossRef]
- Azzam, R.M.A. Arrangement of Four Photodetectors for Measuring the State of Polarization of Light. Opt. Lett. 1985, 10, 309–311. [Google Scholar]
- Liang, H.; Bai, H.; Liu, N.; Sui, X. Polarized Skylight Compass Based on a Soft-Margin Support Vector Machine Working in Cloudy Conditions. Appl. Opt. 2020, 59, 1271. [Google Scholar] [CrossRef]
- Pezzaniti, J.L.; Chenault, D.B. A Division of Aperture MWIR Imaging Polarimeter. In Polarization Science and Remote Sensing II; SPIE: Bellingham, WA, USA, 2005; Volume 5888, pp. 239–250. [Google Scholar]
- Wei, X.; Cui, C.; Wang, G.; Wan, X. Autonomous Positioning Utilizing Star Sensor and Inclinometer. Meas. J. Int. Meas. Confed. 2019, 131, 132–142. [Google Scholar] [CrossRef]
- Sarkar, M.; Bello, D.S.S.; Van Hoof, C.; Theuwissen, A. Integrated Polarization-Analyzing CMOS Image Sensor. In Proceedings of the 2010 IEEE International Symposium on Circuits and Systems, Paris, France, 30 May–2 June 2010; Volume 60, pp. 621–624. [Google Scholar] [CrossRef]
- Gruev, V.; Perkins, R.; York, T. CCD Polarization Imaging Sensor with Aluminum Nanowire Optical Filters. Opt. Express 2010, 18, 19087. [Google Scholar] [CrossRef]
- Garcia, M.; Davis, T.; Blair, S.; Cui, N.; Gruev, V. Bioinspired Polarization Imager with High Dynamic Range. Optica 2018, 5, 1240. [Google Scholar] [CrossRef]
- Li, Q.; Hu, Y.; Zhang, S.; Cao, J.; Hao, Q. Calibration and Image Processing Method for Polarized Skylight Sensor. In Optoelectronic Imaging and Multimedia Technology VII; Dai, Q., Shimura, T., Zheng, Z., Eds.; SPIE: Bellingham, WA, USA, 2020; Volume 11550, pp. 75–83. [Google Scholar]
- Li, Q.; Hu, Y.; Hao, Q.; Cao, J.; Cheng, Y.; Dong, L.; Huang, X. Skylight Polarization Patterns under Urban Obscurations and a Navigation Method Adapted to Urban Environments. Opt. Express 2021, 29, 42090. [Google Scholar] [CrossRef]
- Zhao, F.; Wu, R.; Feng, B.; Cheng, X.; Dong, Y.; Zhang, J. Pixel Response Model for a Division of Focal Plane Polarimeter. Appl. Opt. 2019, 58, 8109. [Google Scholar] [CrossRef]
- Powell, S.B.; Gruev, V. Calibration Methods for Division-of-Focal-Plane Polarimeters. Opt. Express 2013, 21, 21039. [Google Scholar] [CrossRef]
- Zhang, J.; Luo, H.; Hui, B.; Chang, Z. Non-Uniformity Correction for Division of Focal Plane Polarimeters with a Calibration Method. Appl. Opt. 2016, 55, 7236. [Google Scholar] [CrossRef]
- Fei, H.; Li, F.-M.; Chen, W.-C.; Zhang, R.; Chen, C.-S. Calibration Method for Division of Focal Plane Polarimeters. Appl. Opt. 2018, 57, 4992. [Google Scholar] [CrossRef]
- Yang, J.; Qiu, S.; Jin, W.; Xue, F. Temporal and Spatial Error Model for Estimating the Measurement Precision of the Division of Focal Plane Polarimeters. Opt. Express 2021, 29, 20808. [Google Scholar] [CrossRef]
- Ratliff, B.M.; LaCasse, C.F.; Scott Tyo, J. Interpolation Strategies for Reducing IFOV Artifacts in Microgrid Polarimeter Imagery. Opt. Express 2009, 17, 9112. [Google Scholar] [CrossRef]
- Gao, S.; Gruev, V. Image Interpolation Methods Evaluation for Division of Focal Plane Polarimeters. In Infrared Technology and Applications XXXVII; SPIE: Bellingham, WA, USA, 2011; Volume 8012. [Google Scholar] [CrossRef]
- Gao, S.; Gruev, V. Gradient-Based Interpolation Method for Division-of-Focal-Plane Polarimeters. Opt. Express 2013, 21, 1137. [Google Scholar] [CrossRef]
- Zhang, J.; Luo, H.; Hui, B.; Chang, Z. Image Interpolation for Division of Focal Plane Polarimeters with Intensity Correlation. Opt. Express 2016, 24, 20799. [Google Scholar] [CrossRef]
- Cheng, Z.; Mei, T.; Liang, H. Positioning Algorithm Based on Skylight Polarization Navigation; IFAC: New York, NY, USA, 2013; Volume 8, ISBN 9783902823366. [Google Scholar]
- Hamaoui, M. Polarized Skylight Navigation. Appl. Opt. 2017, 56, B37. [Google Scholar] [CrossRef]
- Liu, B.; Fan, Z.; Wang, X. Solar Position Acquisition Method for Polarized Light Navigation Based on ∞ Characteristic Model of Polarized Skylight Pattern. IEEE Access 2020, 8, 56720–56729. [Google Scholar] [CrossRef]
- Pan, N.; Fan, Z.; Jin, H.; Liu, B. Solar Position Acquisition Method by Structural Similarity Characteristics of Skylight Polarized Pattern Images. In Proceedings of the 2022 3rd International Conference on Computer Vision, Image and Deep Learning & International Conference on Computer Engineering and Applications (CVIDL & ICCEA), Changchun, China, 20–22 May 2022. [Google Scholar]
- Ma, T.; Hu, X.; Zhang, L.; Lian, J.; He, X.; Wang, Y.; Xian, Z. An Evaluation of Skylight Polarization Patterns for Navigation. Sensors 2015, 15, 5895–5913. [Google Scholar] [CrossRef]
- Guan, L.; Liu, S.; Chu, J.; Zhang, R.; Chen, Y.; Li, S.; Zhai, L.; Li, Y.; Xie, H. A Novel Algorithm for Estimating the Relative Rotation Angle of Solar Azimuth through Single-Pixel Rings from Polar Coordinate Transformation for Imaging Polarization Navigation Sensors. Optik 2019, 178, 868–878. [Google Scholar] [CrossRef]
- Arago, F.J.D. Oeuvres de François Arago; Gide: Paris, France, 1862; Volume 17. [Google Scholar]
- Babinet, J. Sur Un Nouveau Point Neutre Dans l’atmosphere. CR Acad. Sci. Paris 1840, 11, 618–620. [Google Scholar]
- Brewster, D. LXVIII. On the Polarization of the Atmosphere. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1847, 31, 444–454. [Google Scholar]
- Brewster, D. XXL.—Observations on the Polarisation of the Atmosphere, Made at St Andrews in 1841, 1842, 1843, 1844, and 1845. Trans. R. Soc. Edinb. 1863, 23, 211–239. [Google Scholar] [CrossRef]
- Horváth, G.; Pomozi, I.; Gál, J. Neutral Points of Skylight Polarization Observed during the Total Eclipse on 11 August 1999. Appl. Opt. 2003, 42, 465. [Google Scholar] [CrossRef]
- Barta, A.; Farkas, A.; Száz, D.; Egri, Á.; Barta, P.; Kovács, J.; Csák, B.; Jankovics, I.; Szabó, G.; Horváth, G. Polarization Transition between Sunlit and Moonlit Skies with Possible Implications for Animal Orientation and Viking Navigation: Anomalous Celestial Twilight Polarization at Partial Moon. Appl. Opt. 2014, 53, 5193. [Google Scholar] [CrossRef]
- Wang, Z.; Fan, Z.; Jin, H.; Zhang, X. Neutral Points Recognition Based on the Atmospheric Polarization Pattern’s Global Characteristics. Acta Opt. Sin. 2014, 34, 0701001. [Google Scholar] [CrossRef]
- Kyba, C.C.M.; Ruhtz, T.; Fischer, J.; Hölker, F. Lunar Skylight Polarization Signal Polluted by Urban Lighting. J. Geophys. Res. Atmos. 2011, 116, D24106. [Google Scholar]
- Konnen, G.P.; Können, G.P. Polarized Light in Nature; CUP Archive: Cambridge, UK, 1985; ISBN 0521258626. [Google Scholar]
- Ugolnikov, O.S.; Postylyakov, O.V.; Maslov, I.A. Effects of Multiple Scattering and Atmospheric Aerosol on the Polarization of the Twilight Sky. J. Quant. Spectrosc. Radiat. Transf. 2004, 88, 233–241. [Google Scholar]
- Ugolnikov, O.S.; Maslov, I.A. Studies of the Stratosphere Aerosol Layer Based on Polarization Measurements of the Twilight Sky. Cosm. Res. 2009, 47, 198–207. [Google Scholar]
- Hegedüs, R.; Åkesson, S.; Horváth, G. Polarization Patterns of Thick Clouds: Overcast Skies Have Distribution of the Angle of Polarization Similar to That of Clear Skies. J. Opt. Soc. Am. A 2007, 24, 2347. [Google Scholar] [CrossRef]
- Miyazaki, D.; Ammar, M.; Kawakami, R.; Ikeuchi, K. Estimating Sunlight Polarization Using a Fish-Eye Lens. IPSJ Trans. Comput. Vis. Appl. 2009, 1, 288–300. [Google Scholar] [CrossRef]
- Dacke, M.; Nilsson, D.-E.; Scholtz, C.H.; Byrne, M.; Warrant, E.J. Insect Orientation to Polarized Moonlight. Nature 2003, 424, 33. [Google Scholar]
- Dacke, M.; Byrne, M.J.; Scholtz, C.H.; Warrant, E.J. Lunar Orientation in a Beetle. Proc. R. Soc. London. Ser. B Biol. Sci. 2004, 271, 361–365. [Google Scholar]
- Chu, J.; Guan, L.; Li, S.; Zhang, R.; Jin, R.; Cui, Y.; Wang, L. Atmospheric Polarization Field Pattern Distribution and Polarization Navigation Technology. J. Remote Sens. 2018, 22, 969–979. [Google Scholar] [CrossRef]
- Jensen, H.W.; Durand, F.; Dorsey, J.; Stark, M.M.; Shirley, P.; Premože, S. A Physically-Based Night Sky Model. In Proceedings of the 28th Annual Conference on Computer Graphics and Interactive Techniques, New York, NY, USA, 1 August 2001; pp. 399–408. [Google Scholar]
- Snik, F.; Bos, S.P.; Brackenhoff, S.A.; Doelman, D.S.; Por, E.H.; Bettonvil, F.; Rodenhuis, M.; Vorobiev, D.; Eshelman, L.M.; Shaw, J.A. Detection of Polarization Neutral Points in Observations of the Combined Corona and Sky during the 21 August 2017 Total Solar Eclipse. Appl. Opt. 2020, 59, F71–F77. [Google Scholar] [CrossRef]
- Hegedüs, R.; Barta, A.; Bernáth, B.; Meyer-Rochow, V.B.; Horváth, G. Imaging Polarimetry of Forest Canopies: How the Azimuth Direction of the Sun, Occluded by Vegetation, Can Be Assessed from the Polarization Pattern of the Sunlit Foliage. Appl. Opt. 2007, 46, 6019–6032. [Google Scholar]
- Hegedüs, R.; Åkesson, S.; Wehner, R.; Horváth, G. Could Vikings Have Navigated under Foggy and Cloudy Conditions by Skylight Polarization? On the Atmospheric Optical Prerequisites of Polarimetric Viking Navigation under Foggy and Cloudy Skies. Proc. R. Soc. A Math. Phys. Eng. Sci. 2007, 463, 1081–1095. [Google Scholar]
- Cui, Y.; Zhao, J.; Guan, L.; Chu, J.; Zhang, X.; Liu, H. Simulation and Measurement of Skylight Polarization Distributionin in Yellow Sea. Acta Opt. Sin. 2017, 37, 1001004. [Google Scholar] [CrossRef]
- Liu, Q.; Chu, J.; Wang, J.; Guan, L. Research and Simulation Analysis of Atmospheric Polarization Properties under Water Cloud Condition. Acta Opt. Sin. 2014, 34, 0301004. [Google Scholar] [CrossRef]
- Zhou, G.; Xu, W.; Niu, C.; Zhao, H. The Polarization Patterns of Skylight Reflected off Wave Water Surface. Opt. Express 2013, 21, 32549. [Google Scholar] [CrossRef]
- Barta, A.; Horváth, G.; Horváth, Á.; Egri, Á.; Blahó, M.; Barta, P.; Bumke, K.; Macke, A. Testing a Polarimetric Cloud Imager Aboard Research Vessel Polarstern: Comparison of Color-Based and Polarimetric Cloud Detection Algorithms. Appl. Opt. 2015, 54, 1065–1077. [Google Scholar]
- Hofmann-Wellenhof, B.; Lichtenegger, H.; Wasle, E. GNSS–Global Navigation Satellite Systems: GPS, GLONASS, Galileo, and More; Springer Science & Business Media: Berlin, Germany, 2007; ISBN 3211730176. [Google Scholar]
- Goldenberg, F. Geomagnetic Navigation beyond the Magnetic Compass. In Proceedings of the IEEE/ION PLANS, San Diego, CA, USA, 25–27 April 2006; pp. 684–694. [Google Scholar]
- Greenspan, R.L. Inertial Navigation Technology from 1970–1995. Navigation 1995, 42, 165–185. [Google Scholar]
- Hensgen, R.; Zittrell, F.; Pfeiffer, K.; Homberg, U. Performance of Polarization-Sensitive Neurons of the Locust Central Complex at Different Degrees of Polarization. J. Comp. Physiol. A Neuroethol. Sens. Neural Behav. Physiol. 2022, 208, 387–403. [Google Scholar] [CrossRef]
- Patel, R.N.; Cronin, T.W. Mantis Shrimp Navigate Home Using Celestial and Idiothetic Path Integration. Curr. Biol. 2020, 30, 1981. [Google Scholar] [CrossRef]
- Le Moel, F.; Wystrach, A. Opponent Processes in Visual Memories: A Model of Attraction and Repulsion in Navigating Insects’ Mushroom Bodies. PLOS Comput. Biol. 2020, 16, e1007631. [Google Scholar] [CrossRef]
- Wang, X.; Gao, J.; Roberts, N.W. Bio-Inspired Orientation Using the Polarization Pattern in the Sky Based on Artificial Neural Networks. Opt. Express 2019, 27, 13681–13693. [Google Scholar]
- Liang, H.; Bai, H.; Li, Z.; Cao, Y. Polarized Light Sun Position Determination Artificial Neural Network. Appl. Opt. 2020, 61, 1456–1463. [Google Scholar]
- Liang, H.; Bai, H.; Hu, K.; Lv, X. Bioinspired Polarized Skylight Orientation Determination Artificial Neural Network. J. Bionic Eng. 2022, 20, 1141–1152. [Google Scholar] [CrossRef]
- Rubin, N.A.; D’Aversa, G.; Chevalier, P.; Shi, Z.; Chen, W.T.; Capasso, F. Matrix Fourier Optics Enables a Compact Full-Stokes Polarization Camera. Science 2019, 365, eaax1839. [Google Scholar]
- Miyata, M.; Nakajima, M.; Hashimoto, T. Compound-Eye Metasurface Optics Enabling a High-Sensitivity, Ultra-Thin Polarization Camera. Opt. Express 2020, 28, 9996–10014. [Google Scholar]
- Du, T.; Shi, S.; Zeng, Y.; Yang, J.; Guo, L. An Integrated INS/Lidar Odometry/Polarized Camera Pose Estimation via Factor Graph Optimization for Sparse Environment. IEEE Trans. Instrum. Meas. 2022, 71, 1–11. [Google Scholar]
- Li, S.; Zhao, D.; Yu, H.; Jin, T.; Wang, C.; Tang, J.; Shen, C.; Liu, J.; Wu, Y.; Yang, H. Three-Dimensional Attitude Determination Strategy for Fused Polarized Light and Geomagnetism. Appl. Opt. 2022, 61, 765–774. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Dong, L.; Hu, Y.; Hao, Q.; Wang, W.; Cao, J.; Cheng, Y. Polarimetry for Bionic Geolocation and Navigation Applications: A Review. Remote Sens. 2023, 15, 3518. https://doi.org/10.3390/rs15143518
Li Q, Dong L, Hu Y, Hao Q, Wang W, Cao J, Cheng Y. Polarimetry for Bionic Geolocation and Navigation Applications: A Review. Remote Sensing. 2023; 15(14):3518. https://doi.org/10.3390/rs15143518
Chicago/Turabian StyleLi, Qianhui, Liquan Dong, Yao Hu, Qun Hao, Wenli Wang, Jie Cao, and Yang Cheng. 2023. "Polarimetry for Bionic Geolocation and Navigation Applications: A Review" Remote Sensing 15, no. 14: 3518. https://doi.org/10.3390/rs15143518
APA StyleLi, Q., Dong, L., Hu, Y., Hao, Q., Wang, W., Cao, J., & Cheng, Y. (2023). Polarimetry for Bionic Geolocation and Navigation Applications: A Review. Remote Sensing, 15(14), 3518. https://doi.org/10.3390/rs15143518










