High-Accuracy Filtering of Forest Scenes Based on Full-Waveform LiDAR Data and Hyperspectral Images
Abstract
1. Introduction
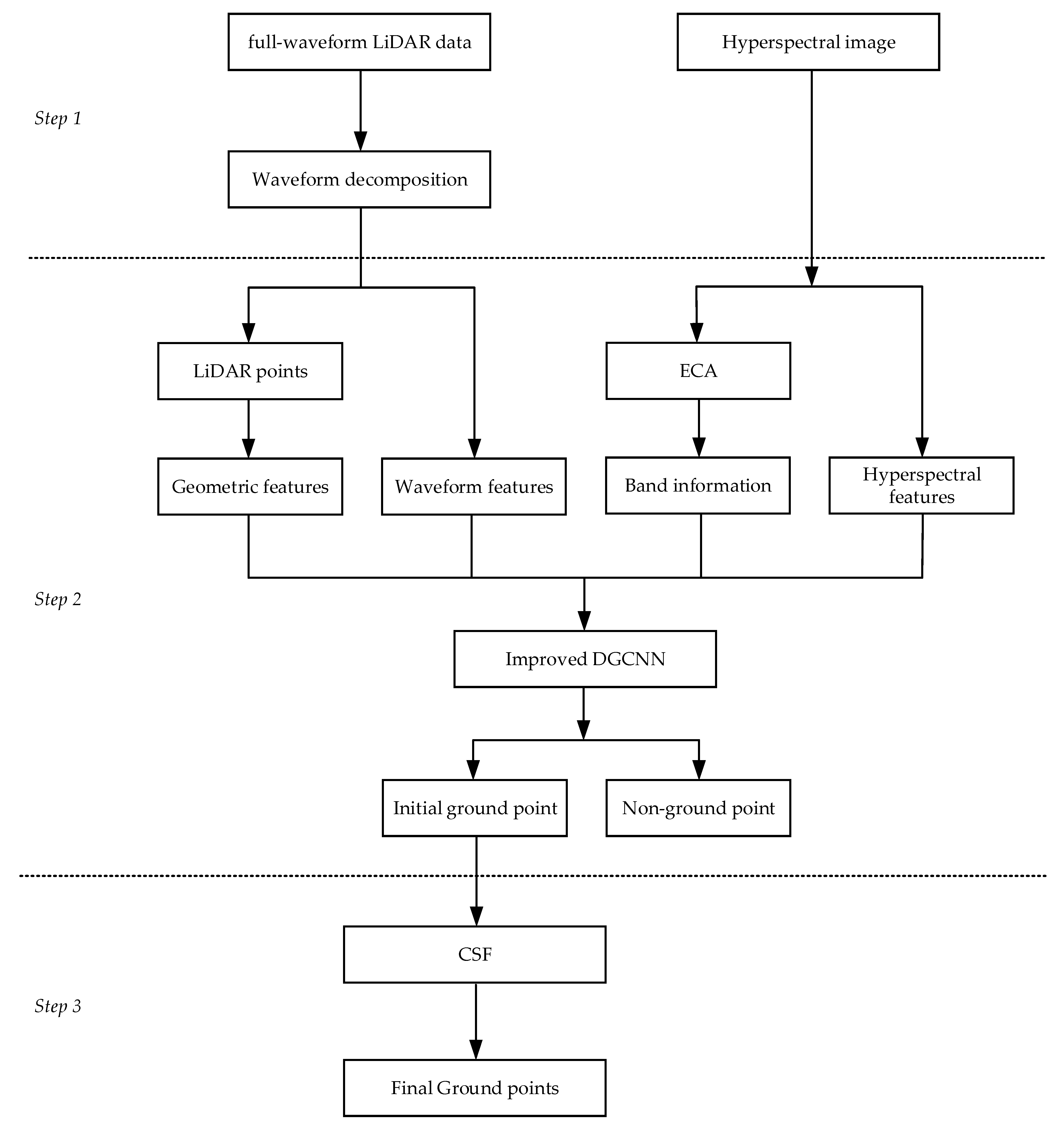
- We introduce a deep learning algorithm to implement the automatic filtering of point clouds. Aiming at the difficulty of the traditional DGCNN algorithm establishing correlations between multiple related inputs, we added a self-attention layer to enhance the connections between different types of features to improve the filtering accuracy of the DGCNN algorithm and its adaptability to the multiple features used in this paper. At the same time, in order to reduce the classification error of point clouds processed with the improved DGCNN algorithm, we also added a post-processing operation based on the cloth filter algorithm.
- Considering the sparseness of ground point clouds in forest scenes, this paper uses airborne full-waveform LiDAR data as one of the data sources and uses a waveform decomposition algorithm to decompose the airborne full-waveform LiDAR data to increase the densities of point clouds. This paper also uses hyperspectral data on the sampled area and discusses the filtering effect of multi-source data composed of hyperspectral images and full-waveform LiDAR data on forest scenes.
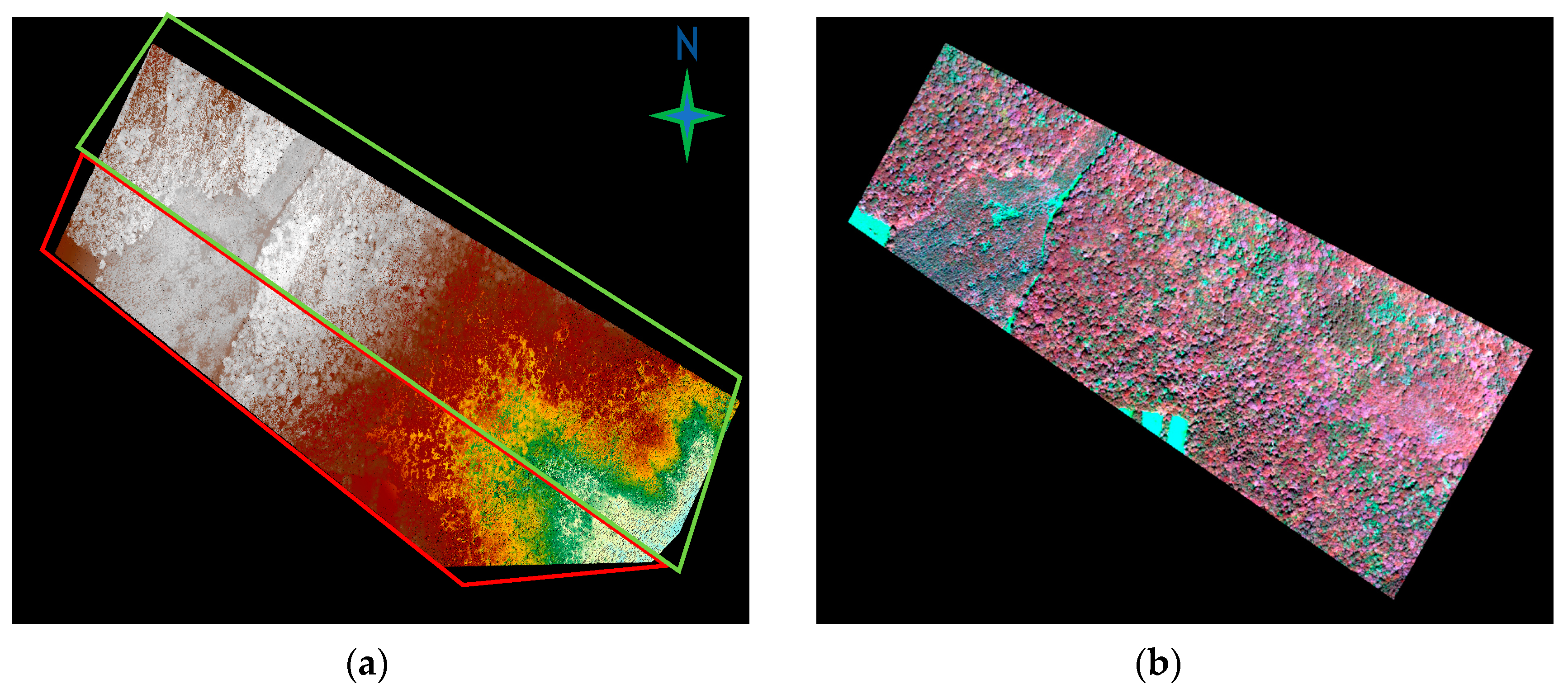
2. Study Area and Datasets
3. Methodology
3.1. Workflow Overview
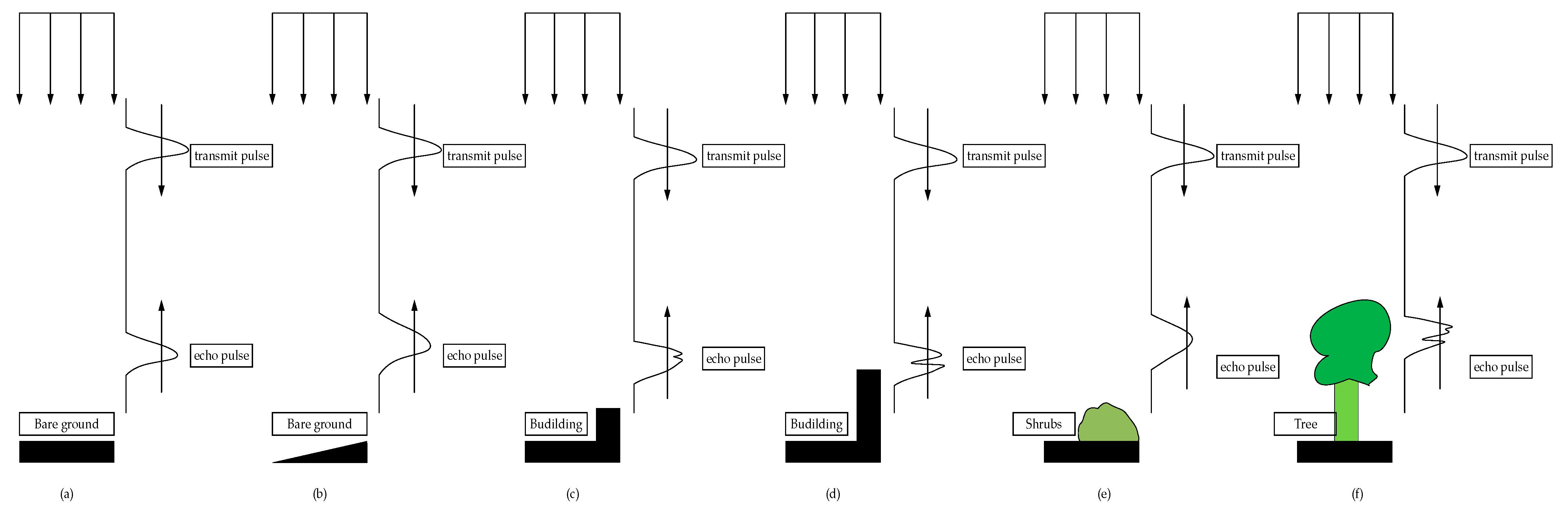
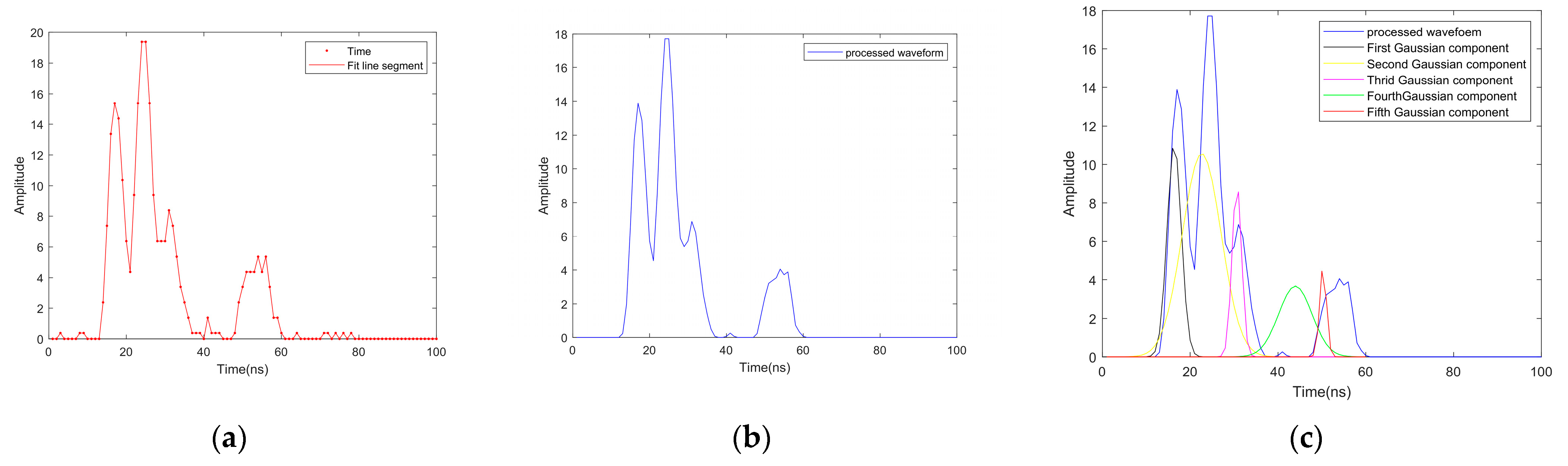
3.2. Waveform Decomposition
3.3. Feature Generation
3.3.1. Geometric Feature Generation from Point Cloud
3.3.2. Band Selection from Hyperspectral Image
- (1)
- When n ≤ 10, select 75% of the features;
- (2)
- When 10 < n ≤ 75, select 40% of the features;
- (3)
- When 75 < n ≤ 100, select 10% of the features;
- (4)
- When n > 100, select 3% of the features.
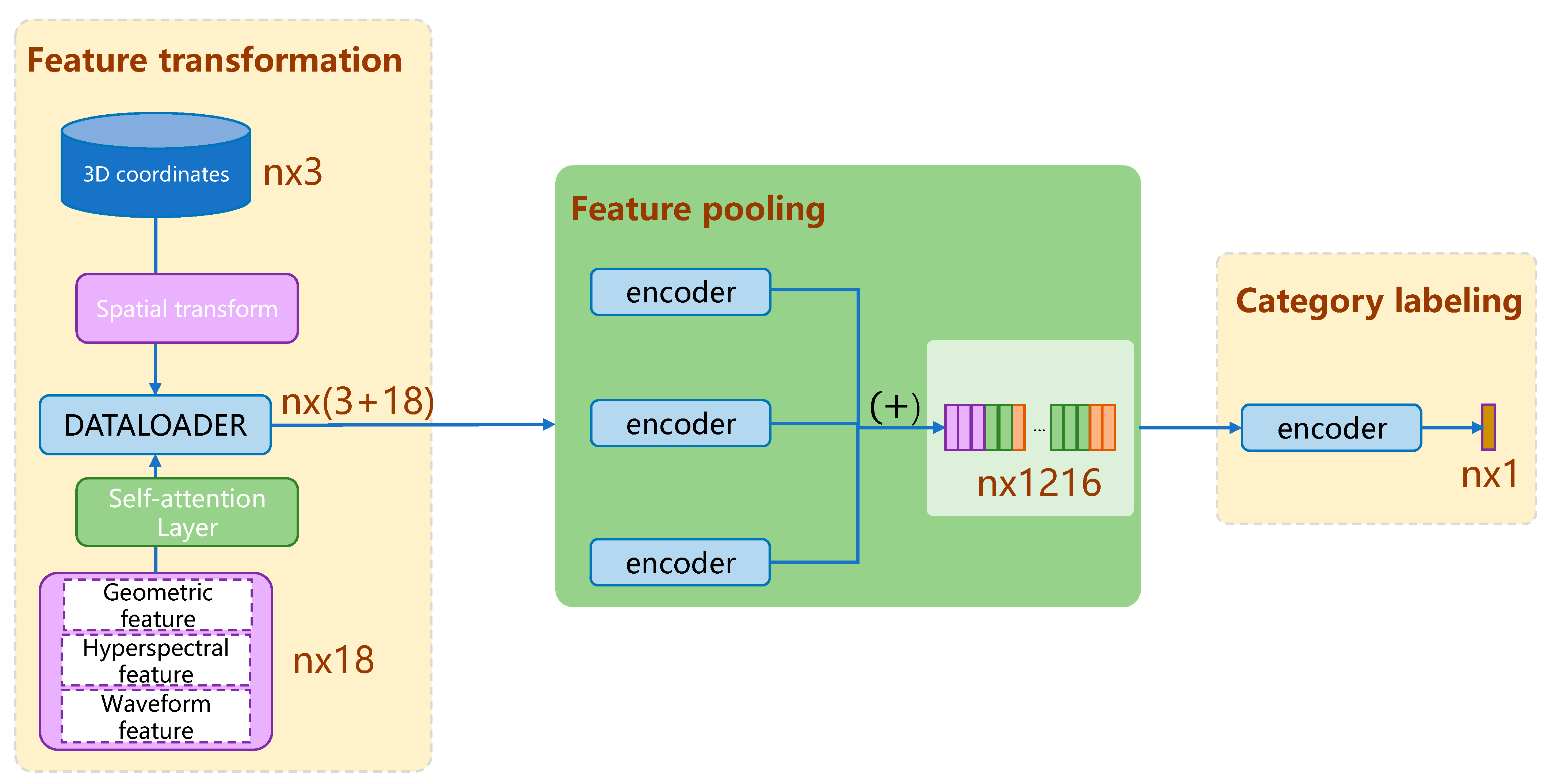
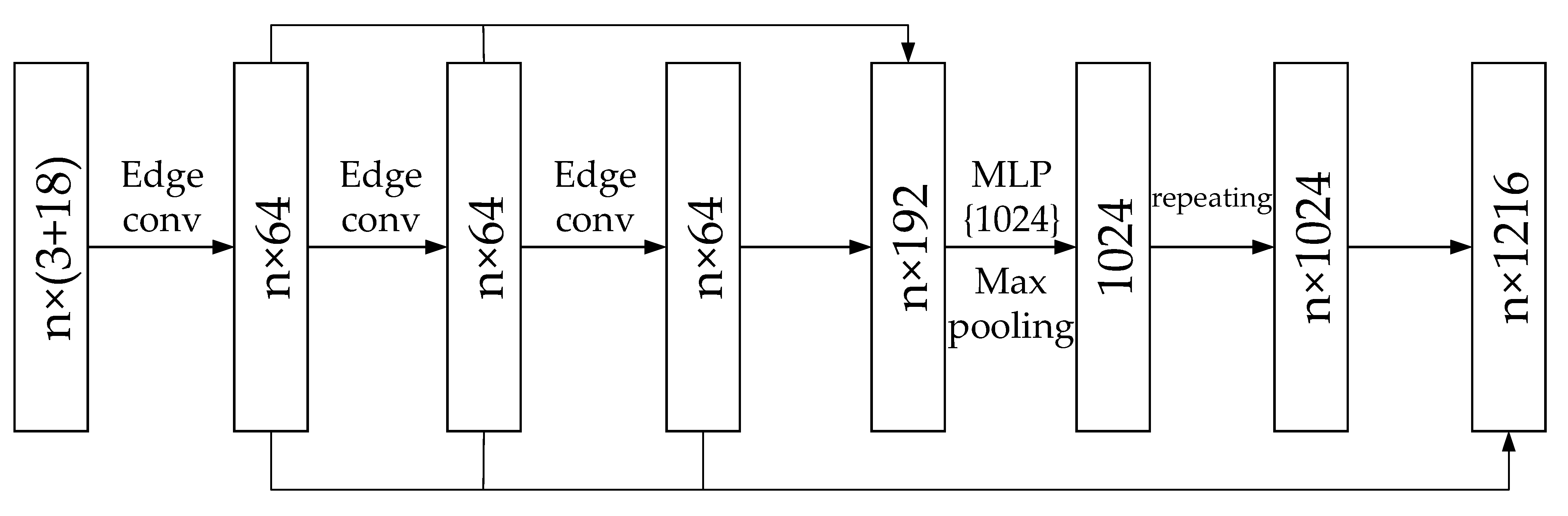
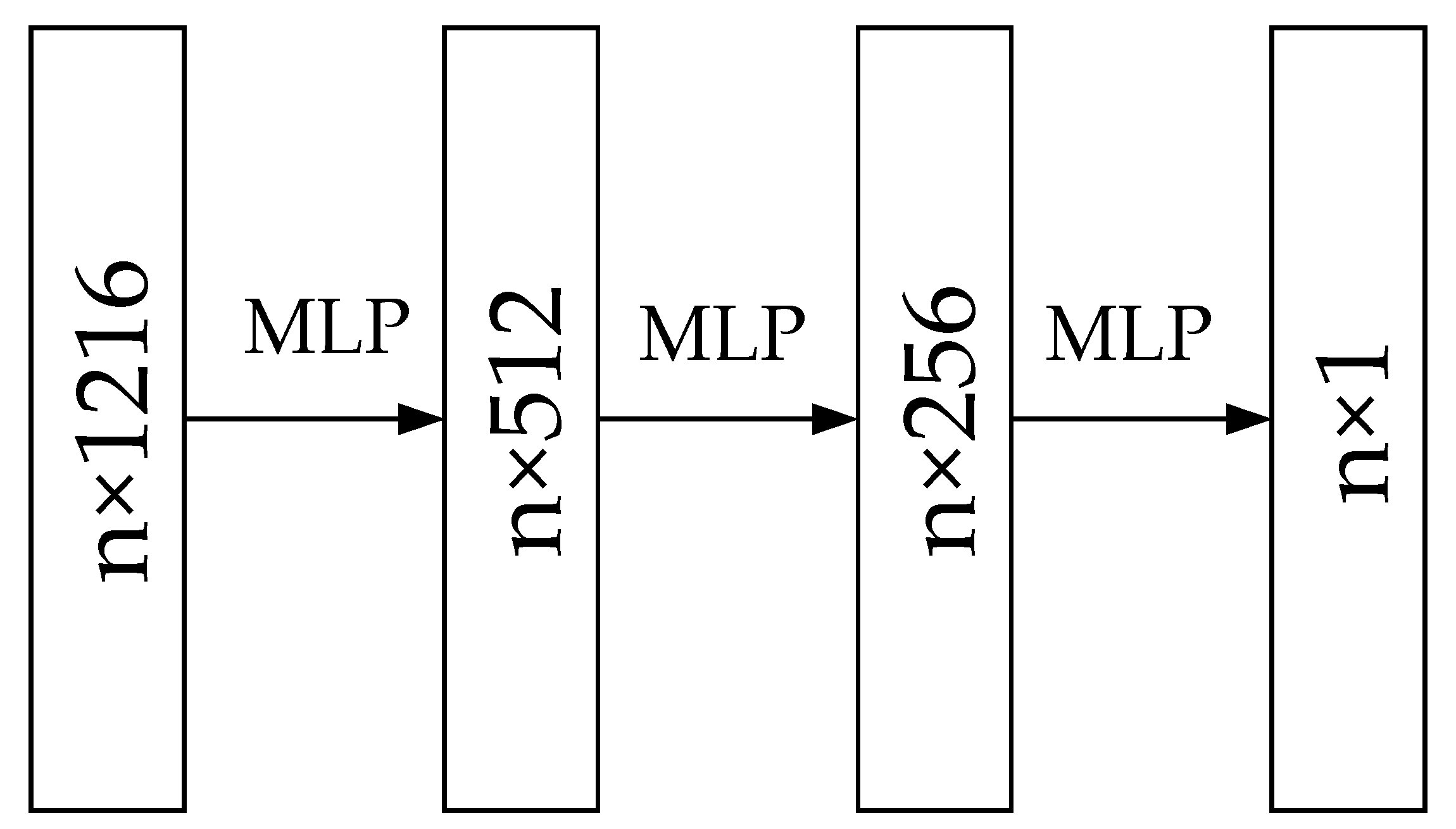
3.4. Improved DGCNN Algorithm
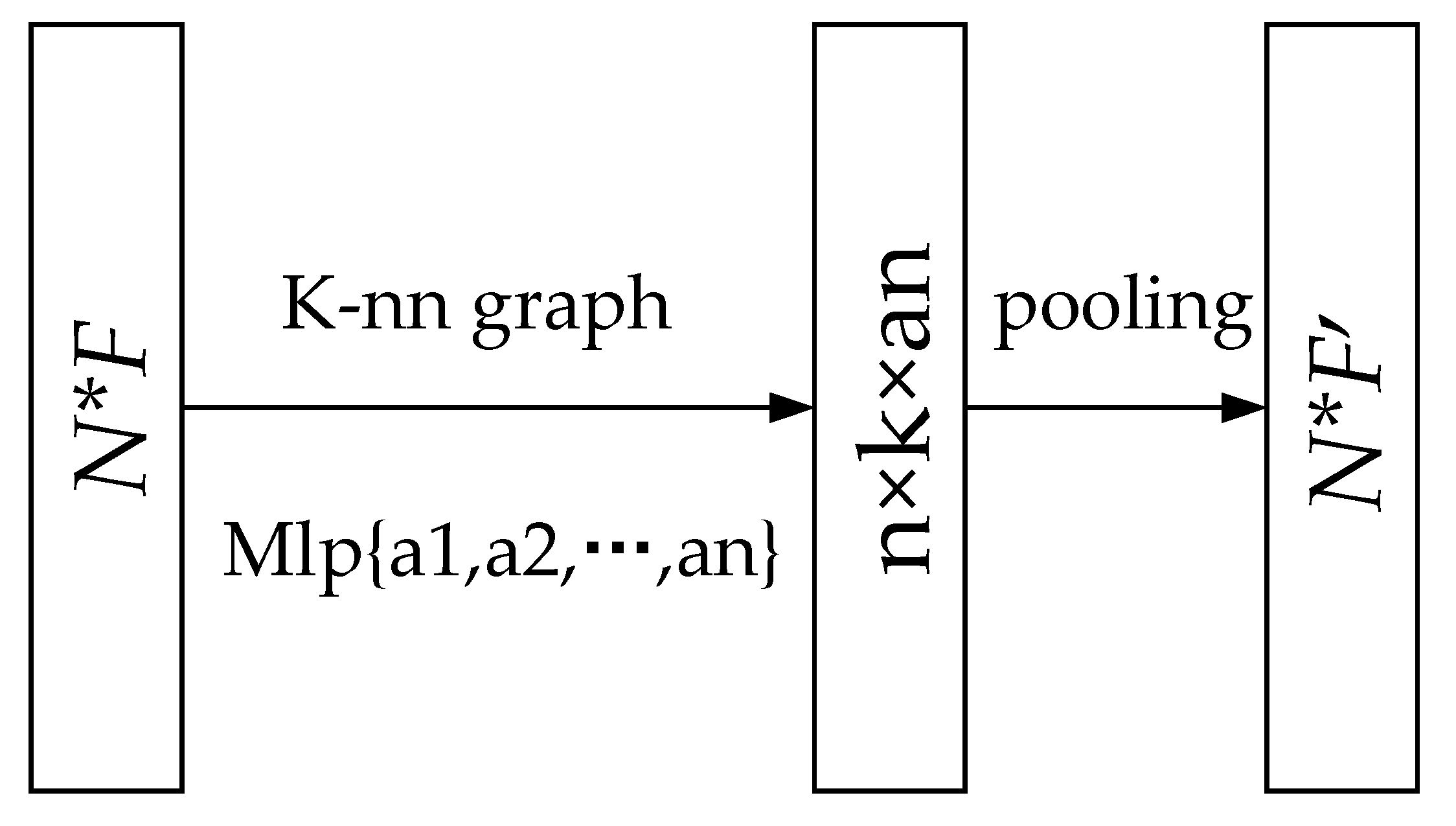
3.4.1. Self-Attention Layer
3.4.2. Network Architecture
3.4.3. EdgeConv Convolution
3.5. Refinement with CSF Algorithm
4. Experimental Results
4.1. Experimental Results of Waveform Decomposition
4.2. Experimental Results of IDGCNN Labeling
- (1)
- In general, the decreasing order of the three features’ impacts on the filtering was WF > HF > LF.
- (2)
- The addition of geometric features to 3C slightly increased (by approximately 0.5%) the overall accuracy while decreasing the type-II and total errors. This may be because most of the geometric features were generated based on the 3D spatial coordinates of the point cloud, while few of them were generated by considering the spatial structure embedded in the dataset, such as the number of steps, which improves the classification accuracy of non-ground points.
- (3)
- The hyperspectral features outweigh the geometric features in terms of the classification accuracy measured with all five parameters in Table 2. This is predictable because a point cloud lacks spectral information, so some objects such as bare soil and grass are difficult to distinguish via the point cloud alone, but they can be differentiated using NDVI.
- (4)
- The waveform features, namely, the HWHM and the backscatter coefficient, allowed for the most significant improvement compared with the geometric and hyperspectral features. In the scenario of an airborne LiDAR signal, the HWHM describes the target distribution along the laser beam traveling path or in the spot area formed by the laser beam hitting the ground, as shown in Figure 3. The backscatter coefficient is a normalized measure of the reflectance of a target, which depends on the material and the size of the target as well as the incident and reflected angles. Combining these two features not only describes the structural characteristics of the targets but also indicates the differences in their material compositions. This explains why the addition of the waveform features achieved the greatest improvement in classification accuracy.
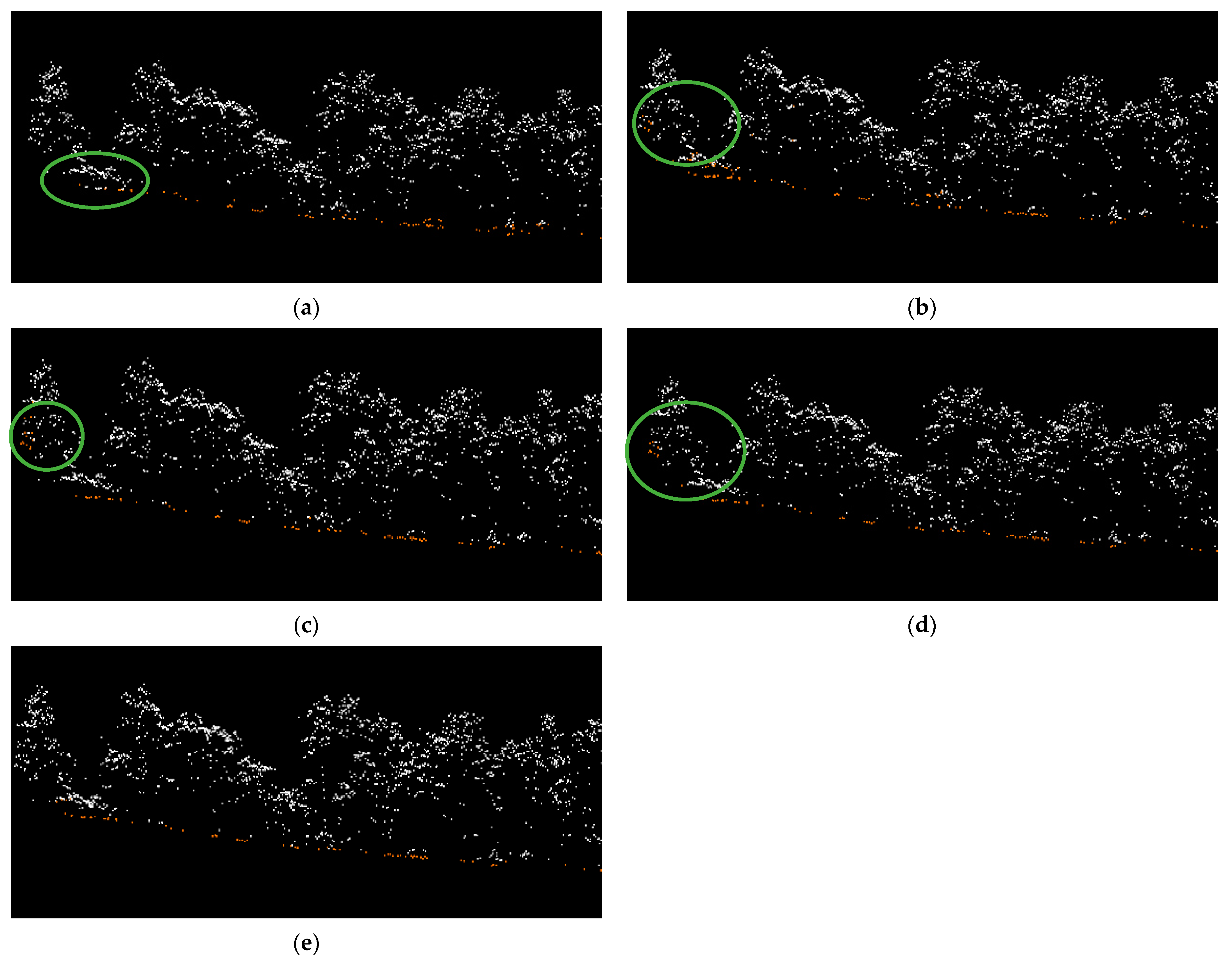
4.3. Refinement of Ground Points
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Van Genderen, J.L. Airborne and terrestrial laser scanning. Int. J. Digit. Earth 2011, 4, 183–184. [Google Scholar] [CrossRef]
- Reutebuch, S.E.; Hans-Erik, A.; Mcgaughey, R.J. Light Detection and Ranging (LIDAR): An Emerging Tool for Multiple Resource Inventory. J. For. 2005, 103, 286–292. [Google Scholar]
- Hyypp, J.; Hyypp, H.; Leckie, D.; Gougeon, F.; Yu, X.; Maltamo, M. Review of methods of small-footprint airborne laser scanning for extracting forest inventory data in boreal forests. Remote Sens. 2008, 29, 1339–1366. [Google Scholar] [CrossRef]
- Andersen, H.E.; Strunk, J.; Temesgen, H. Using Airborne Light Detection and Ranging as a Sampling Tool for Estimating Forest Biomass Resources in the Upper Tanana Valley of Interior Alaska. West. J. Appl. For. 2011, 26, 157–164. [Google Scholar] [CrossRef]
- Zhu, X.; Skidmore, A.K.; Darvishzadeh, R.; Olaf Niemann, K.; Jing, L.; Shi, Y.; Wang, T. Foliar and woody materials discriminated using terrestrial LiDAR in a mixed natural forest. Int. J. Appl. Earth Obs. Geoinf. 2018, 64, 43–50. [Google Scholar] [CrossRef]
- Mongus, D.; Zalik, B. Parameter-free ground filtering of LiDAR data for automatic DTM generation. ISPRS J. Photogramm. Remote Sens. 2012, 67, 1–12. [Google Scholar] [CrossRef]
- Anderson, E.S.; Thompson, J.A.; Crouse, D.A.; Austin, R.E. Horizontal resolution and data density effects on remotely sensed LIDAR-based DEM. Geoderma 2006, 132, 406–415. [Google Scholar] [CrossRef]
- Hui, Z.; Jin, S.; Cheng, P.; Ziggah, Y.Y.; Wang, L.; Wang, Y.; Hu, H.; Hu, Y. An Active Learning Method for DEM Extraction from Airborne LiDAR Point Clouds. IEEE Access 2019, 7, 89366–89378. [Google Scholar] [CrossRef]
- Meng, X.; Currit, N.; Zhao, K. Ground Filtering Algorithms for Airborne LiDAR Data: A Review of Critical Issues. Remote Sens. 2010, 2, 833–860. [Google Scholar] [CrossRef]
- Montealegre, A.L.; Lamelas, M.T.; Juan, D. A Comparison of Open-Source LiDAR Filtering Algorithms in a Mediterranean Forest Environment. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4072–4085. [Google Scholar] [CrossRef]
- Hyyppä, H.; Yu, X.; Hyyppä, J.; Kaartinen, H.; Kaasalainen, S.; Honkavaara, E.; Rönnholm, P. Factors affecting the quality of DTM generation in forested areas. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2005, 36, 85–90. [Google Scholar]
- Zhao, X.; Su, Y.; Li, W.K.; Hu, T.; Liu, J.; Guo, Q. A comparison of LiDAR filtering algorithms in vegetated mountain areas. Can. J. Remote Sens. 2018, 44, 287–298. [Google Scholar] [CrossRef]
- Evans, J.S.; Hudak, A.T. A multiscale curvature algorithm for classifying discrete return LiDAR in forested environments. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1029–1038. [Google Scholar] [CrossRef]
- Véga, C.; Durrieu, S.; Morel, J.; Allouis, T. A sequential iterative dual-filter for Lidar terrain modeling optimized for complex forested environments. Comput. Geosci. 2012, 44, 31–41. [Google Scholar] [CrossRef]
- Maguya, A.S.; Junttila, V.; Kauranne, T. Adaptive algorithm for large scale DTM interpolation from LiDAR data for forestry applications in steep forested terrain. ISPRS J. Photogramm. Remote Sens. 2013, 85, 74–83. [Google Scholar] [CrossRef]
- Zhao, X.; Guo, Q.; Su, Y.; Xue, B. Improved progressive TIN densification filtering algorithm for airborne LiDAR data in forested areas. ISPRS J. Photogramm. Remote Sens. 2016, 117, 79–91. [Google Scholar] [CrossRef]
- Chen, C.; Wang, M.; Chang, B.; Li, Y. Multi-level interpolation-based filter for airborne LiDAR point clouds in forested areas. IEEE Access 2020, 8, 41000–41012. [Google Scholar] [CrossRef]
- Maguya, A.S.; Junttila, V.; Kauranne, T. Algorithm for extracting digital terrain models under forest canopy from airborne LiDAR data. Remote Sens. 2014, 6, 6524–6548. [Google Scholar] [CrossRef]
- Bigdeli, B.; Amirkolaee, H.A.; Pahlavani, P. DTM extraction under forest canopy using LiDAR data and a modified invasive weed optimization algorithm. Remote Sens. Environ. 2018, 216, 289–300. [Google Scholar] [CrossRef]
- Liu, L.; Lim, S. A voxel-based multiscale morphological airborne lidar filtering algorithm for digital elevation models for forest regions. Measurement 2018, 123, 135–144. [Google Scholar] [CrossRef]
- Hui, Z.; Jin, S.; Xia, Y.; Nie, Y.; Xie, X.; Li, N. A mean shift segmentation morphological filter for airborne LiDAR DTM extraction under forest canopy. Opt. Laser Technol. 2021, 136, 106728. [Google Scholar] [CrossRef]
- Durbha, S.S.; King, R.L.; Younan, N.H. Support vector machines regression for retrieval of leaf area index from multiangle imaging spectroradiometer. Remote Sens. Environ. 2007, 107, 348–361. [Google Scholar] [CrossRef]
- Zhao, K.; Popescu, S.; Zhang, X. Bayesian learning with Gaussian processes for supervised classification of hyperspectral data. Photogramm. Eng. Remote Sens. 2008, 74, 1223–1234. [Google Scholar] [CrossRef]
- Nourzad, S.H.H.; Pradhan, A. Ensemble methods for binary classifications of airborne LiDAR data. J. Comput. Civ. Eng. 2014, 28, 04014021. [Google Scholar] [CrossRef]
- Shi, W.; Zheng, S.; Tian, Y. Adaptive mapped least squares SVM-based smooth fitting method for DSM generation of LIDAR data. Int. J. Remote Sens. 2009, 30, 5669–5683. [Google Scholar] [CrossRef]
- Ma, H.; Cai, Z.; Zhang, L. Comparison of the filtering models for airborne LiDAR data by three classifiers with exploration on model transfer. J. Appl. Remote Sens. 2018, 12, 016021. [Google Scholar] [CrossRef]
- Jahromi, A.B.; Zoej MJ, V.; Mohammadzadeh, A.; Sadeghian, S. A novel filtering algorithm for bare-earth extraction from airborne laser scanning data using an artificial neural network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2011, 4, 836–843. [Google Scholar] [CrossRef]
- Hu, X.; Yuan, Y. Deep-learning-based classification for DTM extraction from ALS point cloud. Remote Sens. 2016, 8, 730. [Google Scholar] [CrossRef]
- Rizaldy, A.; Persello, C.; Gevaert, C.; Elberink, S.O.; Vosselman, G. Ground and multi-class classification of airborne laser scanner point clouds using fully convolutional networks. Remote Sens. 2018, 10, 1723. [Google Scholar] [CrossRef]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. PointNet: Deep learning on point sets for 3D classification and segmentation. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 77–85. [Google Scholar] [CrossRef]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. Pointnet++: Deep hierarchical feature learning on point sets in a metric space. Adv. Neural Inf. Process. Syst. 2017, 30, 5105–5114. [Google Scholar] [CrossRef]
- Hu, Q.; Yang, B.; Xie, L.; Rosa, S.; Guo, Y.; Wang, Z.; Trigoni, N.; Markham, A. Randla-net: Efficient semantic segmentation of large-scale point clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11108–11117. [Google Scholar] [CrossRef]
- Xiao, A.; Yang, X.; Lu, S.; Guan, D.; Huang, J. FPS-Net: A convolutional fusion network for large-scale LiDAR point cloud segmentation. ISPRS J. Photogramm. Remote Sens. 2021, 176, 237–249. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, Y.; Liu, Z.; Sarma, S.E.; Bronstein, M.M.; Solomon, J.M. Dynamic graph cnn for learning on point clouds. Acm. Trans. Graph. (Tog) 2019, 38, 1–12. [Google Scholar] [CrossRef]
- Mao, Y.; Chen, K.; Diao, W.; Sun, X.; Lu, X.; Fu, K.; Weinmann, M. Beyond single receptive field: A receptive field fusion-and-stratification network for airborne laser scanning point cloud classification. ISPRS J. Photogramm. Remote Sens. 2022, 188, 45–61. [Google Scholar] [CrossRef]
- Mallet, C.; Bretar, F. Full-waveform topographic lidar: State-of-the-art. ISPRS J. Photogramm. Remote Sens. 2009, 64, 1–16. [Google Scholar] [CrossRef]
- Wulder, M.A.; White, J.C.; Nelson, R.F.; Næsset, E.; Ørka, H.O.; Coops, N.C.; Hilker, T.; Bater, C.W.; Gobakken, T. LiDAR sampling for large-area forest characterization: A review. Remote Sens. Environ. 2012, 121, 196–209. [Google Scholar] [CrossRef]
- Doneus, M.; Briese, C. Digital terrain modelling for archaeological interpretation within forested areas using full-waveform laserscanning. In Proceedings of the 7th International Conference on Virtual Reality, Archaeology and Intelligent Cultural Heritage, Nicosia, Cyprus, 30 October–4 November 2006; pp. 155–162. [Google Scholar] [CrossRef]
- Wagner, W.; Hollaus, M.; Briese, C.; Ducic, V. 3D vegetation mapping using small-footprint full-waveform airborne laser scanners. Int. J. Remote Sens. 2008, 29, 1433–1452. [Google Scholar] [CrossRef]
- Lin, Y.C.; Mills, J.P. Integration of full-waveform information into the airborne laser scanning data filtering process. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2009, 36, 224–229. [Google Scholar]
- Hu, B.; Gumerov, D.; Wang, J.; Zhang, W. An integrated approach to generating accurate DTM from airborne full-waveform LiDAR data. Remote Sens. 2017, 9, 871. [Google Scholar] [CrossRef]
- Xing, S.; Li, P.; Xu, Q.; Wang, D.; Li, P. Surface Fitting Filtering of LiDAR Point Cloud with Waveform Information. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 4, 179–184. [Google Scholar] [CrossRef]
- Ma, H.; Zhou, W.; Zhang, L. DEM refinement by low vegetation removal based on the combination of full waveform data and progressive TIN densification. ISPRS J. Photogramm. Remote Sens. 2018, 146, 260–271. [Google Scholar] [CrossRef]
- Pirotti, F. Analysis of full-waveform LiDAR data for forestry applications: A review of investigations and methods. Iforest-Biogeosciences For. 2011, 4, 100. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, Z.; Zhao, X.; Hong, D.; Li, W.; Cai, W.; Zhan, Y. AF2GNN: Graph convolution with adaptive filters and aggregator fusion for hyperspectral image classification. Inf. Sci. 2022, 602, 201–219. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, Z.; Zhao, X.; Cai, W.; Yang, N.; Hu, H.; Huang, X.; Cao, Y.; Cai, W. Unsupervised self-correlated learning smoothy enhanced locality preserving graph convolution embedding clustering for hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar] [CrossRef]
- Zhang, Z.; Ding, Y.; Zhao, X.; Siye, L.; Yang, N.; Cai, Y.; Zhan, Y. Multireceptive field: An adaptive path aggregation graph neural framework for hyperspectral image classification. Expert Syst. Appl. 2023, 217, 119508. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, Z.; Zhao, X.; Hong, D.; Cai, W.; Yang, N.; Wang, B. Multi-scale receptive fields: Graph attention neural network for hyperspectral image classification. Expert Syst. Appl. 2023, 223, 119858. [Google Scholar] [CrossRef]
- Dalponte, M.; Bruzzone, L.; Gianelle, D. Fusion of hyperspectral and LIDAR remote sensing data for classification of complex forest areas. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1416–1427. [Google Scholar] [CrossRef]
- Wang, H.; Glennie, C. Fusion of waveform LiDAR data and hyperspectral imagery for land cover classification. ISPRS J. Photogramm. Remote Sens. 2015, 108, 1–11. [Google Scholar] [CrossRef]
- Chu, H.J.; Wang, C.K.; Kong, S.J.; Chen, K.C. Integration of full-waveform LiDAR and hyperspectral data to enhance tea and areca classification. GIScience Remote Sens. 2016, 53, 542–559. [Google Scholar] [CrossRef]
- Wagner, W.; Ullrich, A.; Ducic, V.; Melzer, T.; Studnicka, N. Gaussian decomposition and calibration of a novel small-footprint full-waveform digitising airborne laser scanner. ISPRS J. Photogramm. Remote Sens. 2006, 60, 100–112. [Google Scholar] [CrossRef]
- Hofton, M.A.; Minster, J.B.; Blair, J.B. Decomposition of laser altimeter waveforms. IEEE Trans. Geosci. Remote Sens. 2000, 38, 1989–1996. [Google Scholar] [CrossRef]
- Sun, K.; Geng, X.; Ji, L. Exemplar component analysis: A fast band selection method for hyperspectral imagery. IEEE Geosci. Remote Sens. Lett. 2014, 12, 998–1002. [Google Scholar] [CrossRef]
- Bolón-Canedo, V.; Sánchez-Maroño, N.; Alonso-Betanzos, A. Feature selection for high-dimensional data. Prog. Artif. Intell. 2016, 5, 65–75. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 3–9 December 2017; Volume 30, p. 3058. [Google Scholar] [CrossRef]
- Zhang, W.; Qi, J.; Wan, P.; Wang, H.; Xie, D.; Wang, X.; Yan, G. An easy-to-use airborne LiDAR data filtering method based on cloth simulation. Remote Sens. 2016, 8, 501. [Google Scholar] [CrossRef]







| ID | Author Name | Algorithm Name |
|---|---|---|
| 1 | Evans and Hudak | Multiscale curvature classification (MCC) [13] |
| 2 | Vega et al. | Sequential iterative dual-filter [14] |
| 3 | Almasi et al. | Ground-fitting- and residual-filtering-based filter [15] |
| 4 | Zhao et al. | Improved progressive TIN densification (IPTD) [16] |
| 5 | Chen et al. | Multi-level-interpolation-based filter [17] |
| 6 | Almasi et al. | Fitting-based algorithm [18] |
| 7 | Behnaz et al. | Fused-morphology-based and slope-based filter [19] |
| 8 | Li et al. | Voxels-based morphological filter [20] |
| 9 | Hui et al. | Mean-shift segmentation morphological filter [21] |
| OA (%) | Kappa (%) | Type I (%) | Type II (%) | Total (%) | |
|---|---|---|---|---|---|
| 3C | 97.90 | 84.42 | 7.29 | 1.63 | 2.10 |
| 3C + LF | 98.47 | 89.94 | 5.53 | 1.18 | 1.53 |
| 3C + HF | 98.76 | 91.68 | 4.03 | 1.00 | 1.24 |
| 3C + WF | 99.05 | 94.24 | 3.85 | 0.61 | 0.95 |
| ALL | 99.38 | 95.95 | 2.92 | 0.41 | 0.62 |
| OA (%) | Kappa (%) | Type I (%) | Type II (%) | Total (%) | |
|---|---|---|---|---|---|
| DGCNN | 98.33 | 89.27 | 7.74 | 1.11 | 1.67 |
| PointNet++ | 98.20 | 88.20 | 10.08 | 1.05 | 1.80 |
| RandLA-Net | 98.73 | 91.68 | 6.75 | 0.78 | 1.27 |
| RFFS-Net | 97.82 | 86.36 | 7.04 | 1.74 | 2.18 |
| IDGCNN | 99.38 | 95.95 | 2.92 | 0.41 | 0.62 |
| Median Error (m) | Maximum Error (m) | Average Error (m) | |
|---|---|---|---|
| IDCGNN | 0.45 | 1.01 | 0.35 |
| CSF | 0.68 | 2.09 | 0.42 |
| IDGCNN + CSF | 0.41 | 0.75 | 0.33 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, W.; Ma, H.; Yuan, J.; Zhang, L.; Ma, H.; Cai, Z.; Zhou, W. High-Accuracy Filtering of Forest Scenes Based on Full-Waveform LiDAR Data and Hyperspectral Images. Remote Sens. 2023, 15, 3499. https://doi.org/10.3390/rs15143499
Luo W, Ma H, Yuan J, Zhang L, Ma H, Cai Z, Zhou W. High-Accuracy Filtering of Forest Scenes Based on Full-Waveform LiDAR Data and Hyperspectral Images. Remote Sensing. 2023; 15(14):3499. https://doi.org/10.3390/rs15143499
Chicago/Turabian StyleLuo, Wenjun, Hongchao Ma, Jialin Yuan, Liang Zhang, Haichi Ma, Zhan Cai, and Weiwei Zhou. 2023. "High-Accuracy Filtering of Forest Scenes Based on Full-Waveform LiDAR Data and Hyperspectral Images" Remote Sensing 15, no. 14: 3499. https://doi.org/10.3390/rs15143499
APA StyleLuo, W., Ma, H., Yuan, J., Zhang, L., Ma, H., Cai, Z., & Zhou, W. (2023). High-Accuracy Filtering of Forest Scenes Based on Full-Waveform LiDAR Data and Hyperspectral Images. Remote Sensing, 15(14), 3499. https://doi.org/10.3390/rs15143499








