A Space-Time Partial Differential Equation Based Physics-Guided Neural Network for Sea Surface Temperature Prediction
Abstract
1. Introduction
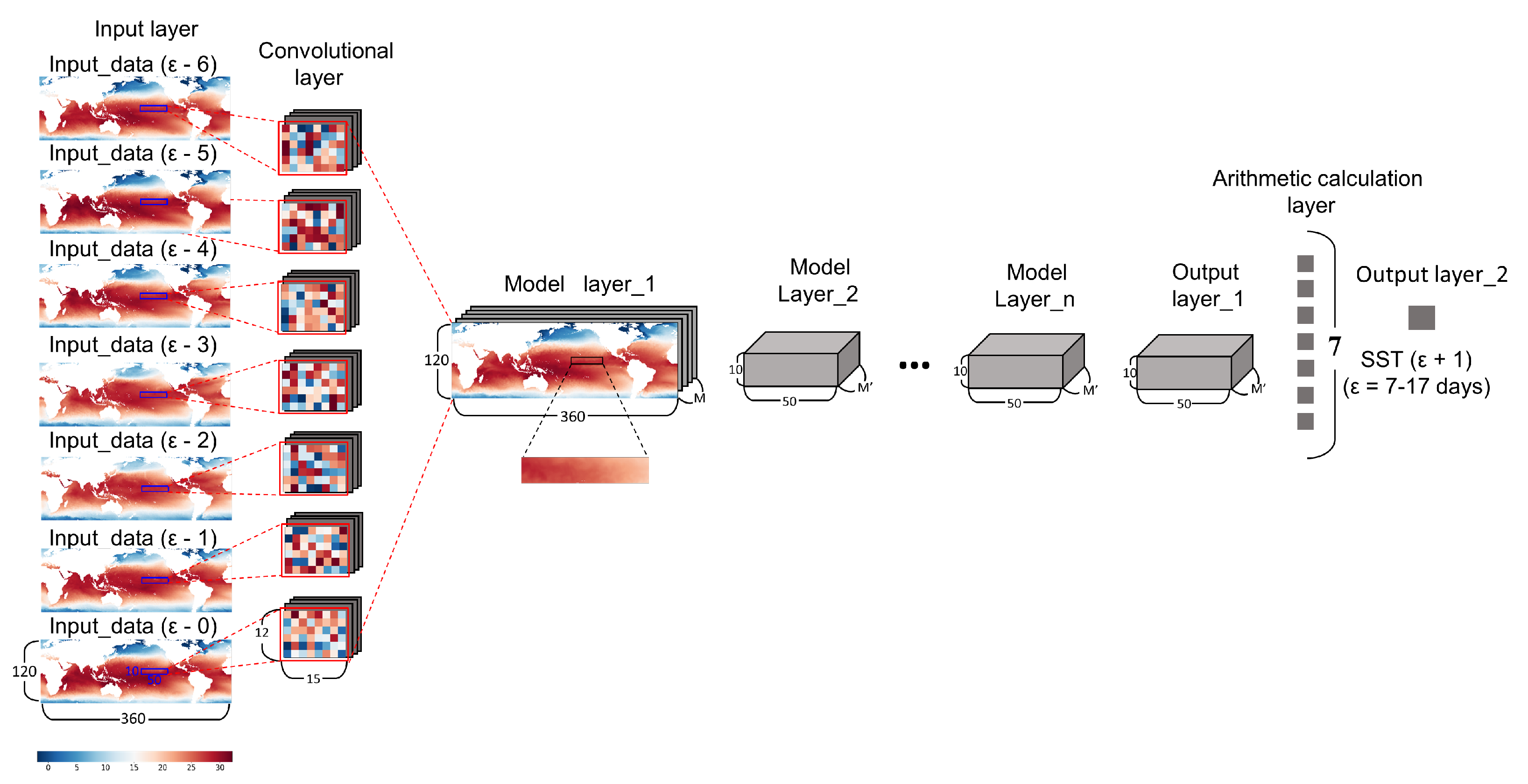
2. Data
3. Methodology
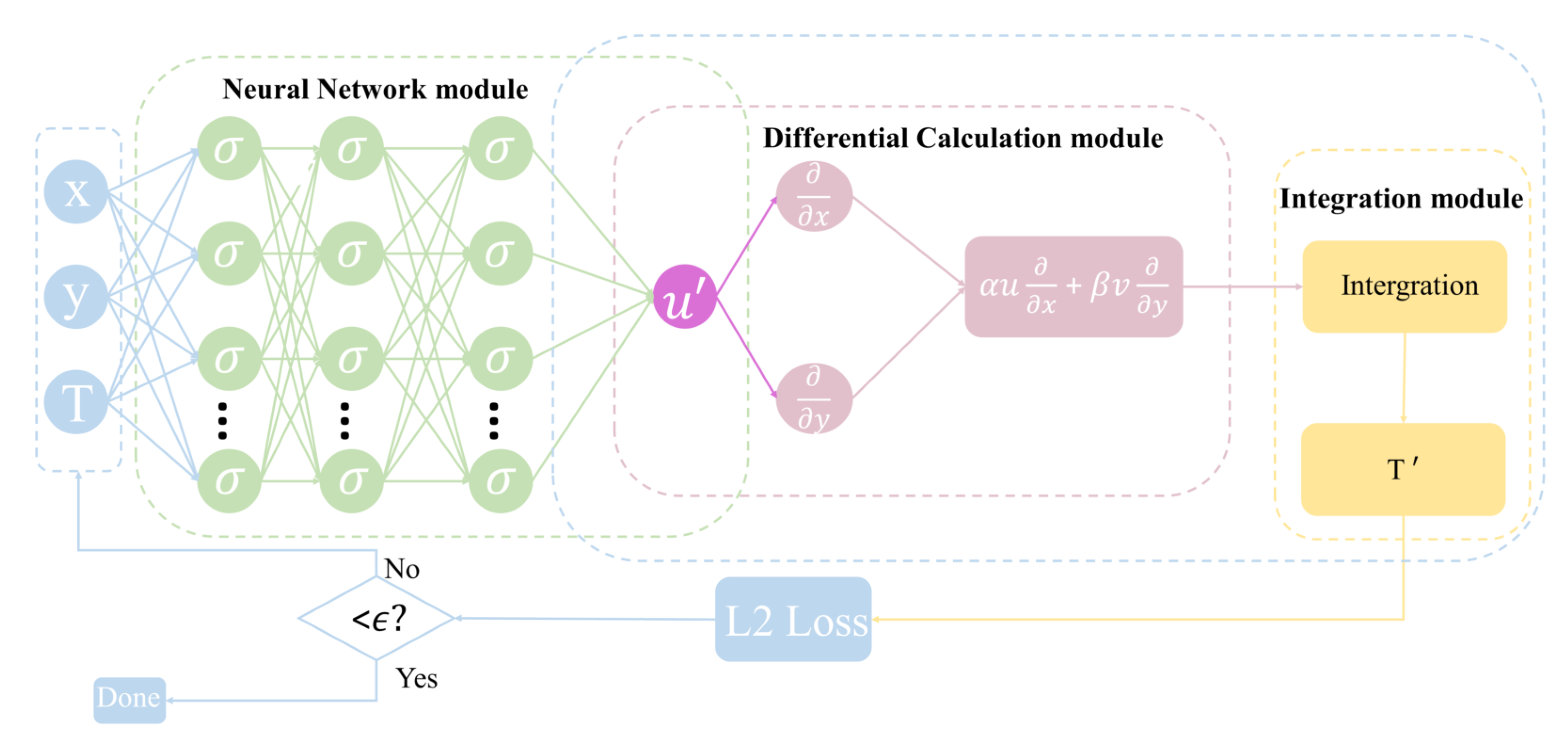
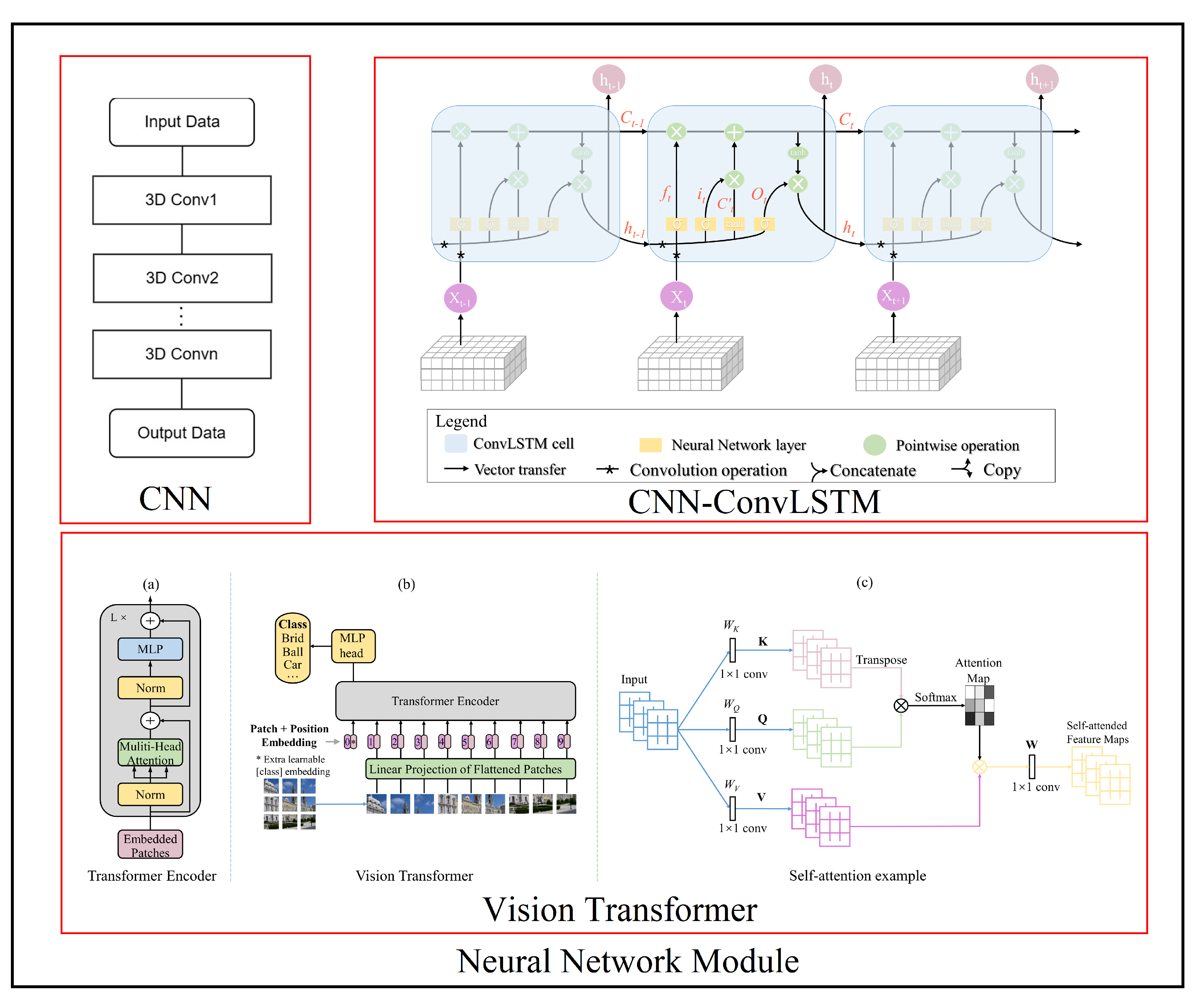
3.1. Architecture
3.2. Differential Calculation Module
3.3. Model Training Strategy
3.4. Mixed-Layer Heat Budget Equation
| Algorithm 1: Training procedure of the STPDE-NET for SST prediction. |
 |
3.5. Extract Knowledge from Data and Optimize Equations
4. Results
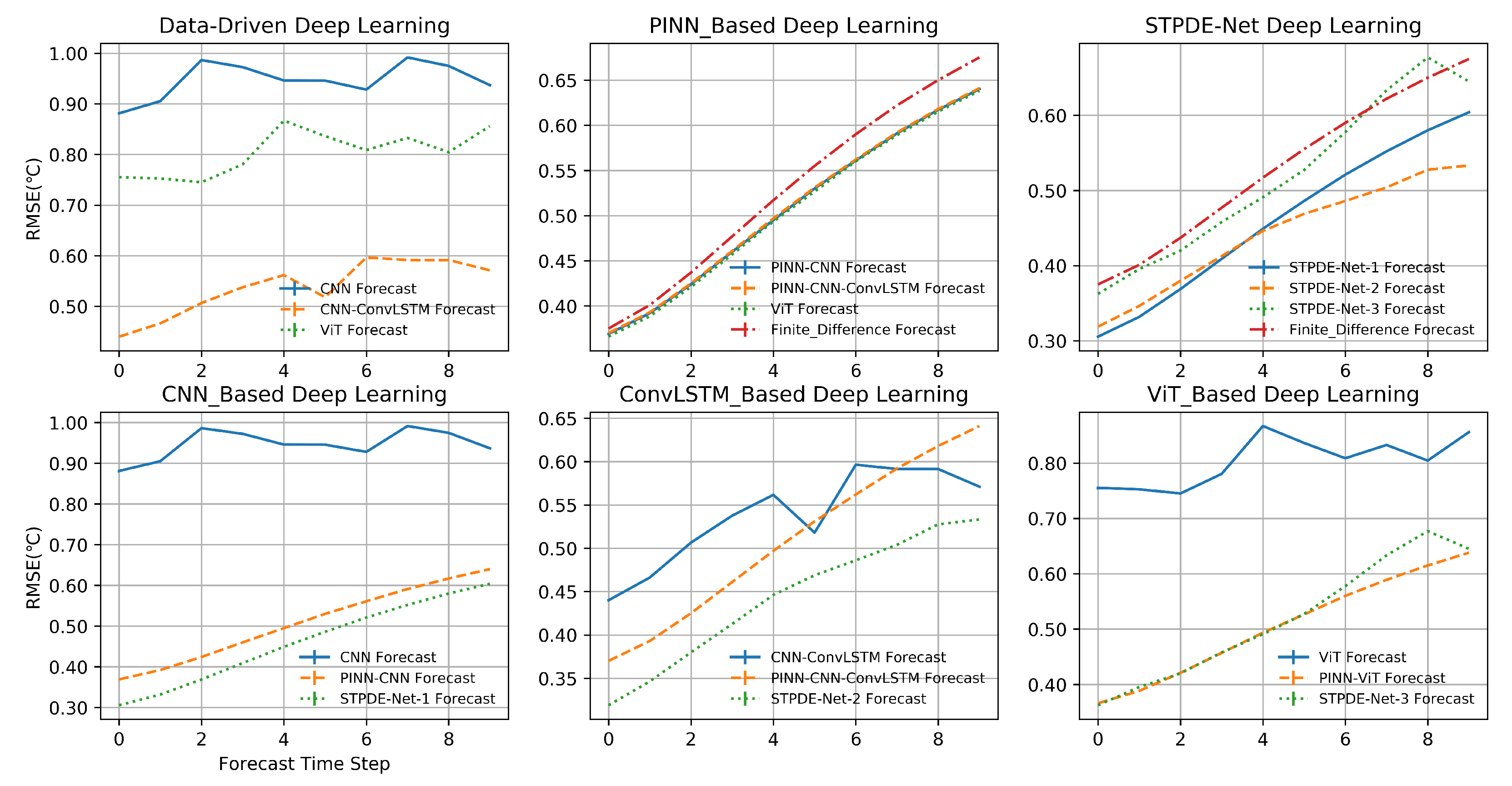
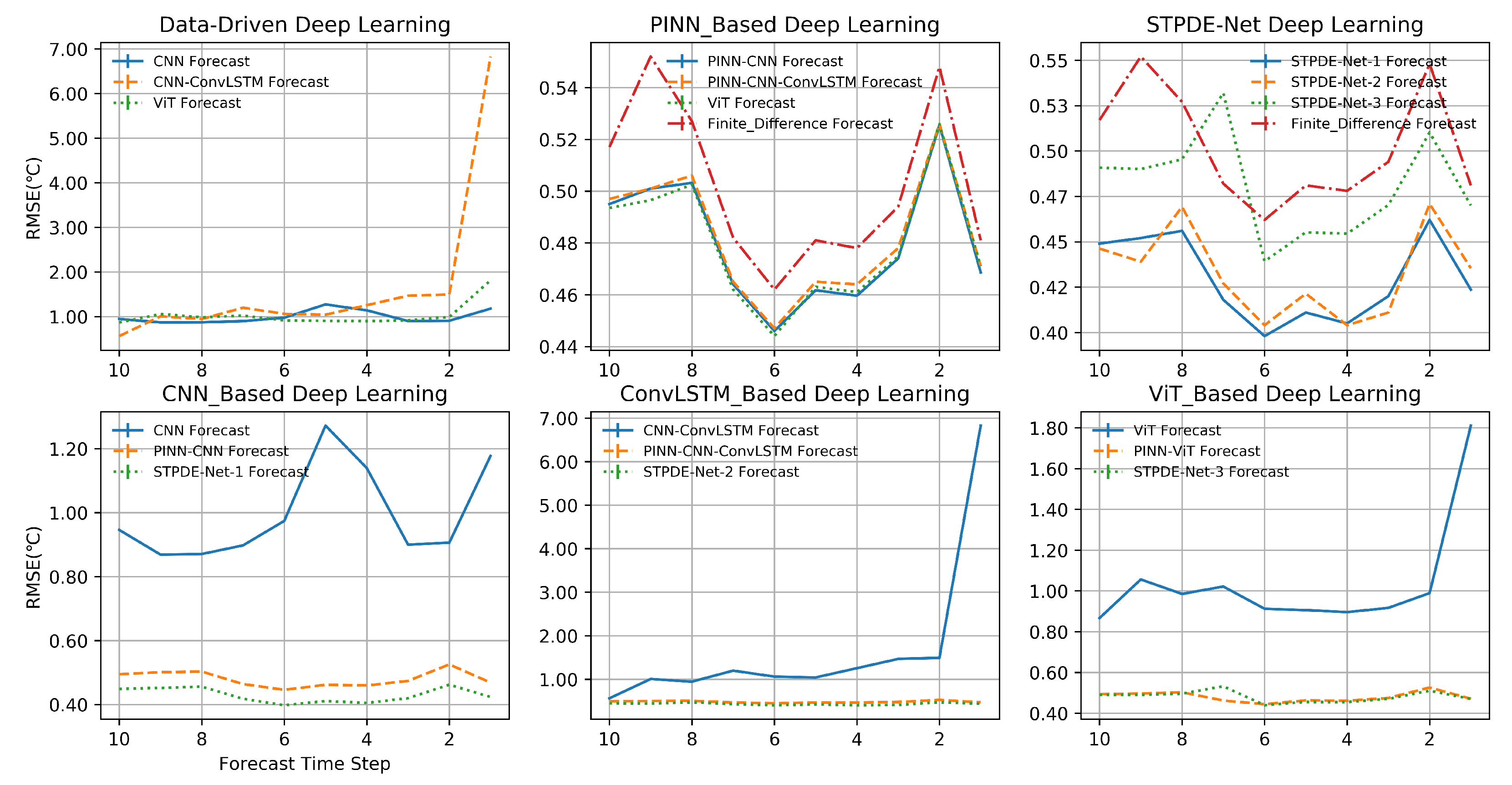
4.1. Comprehensive Evaluation of the General Prediction Capabilities of Various Models through Multiple Error Statistical Analyses Based on Spatiotemporal Evolution Characteristics
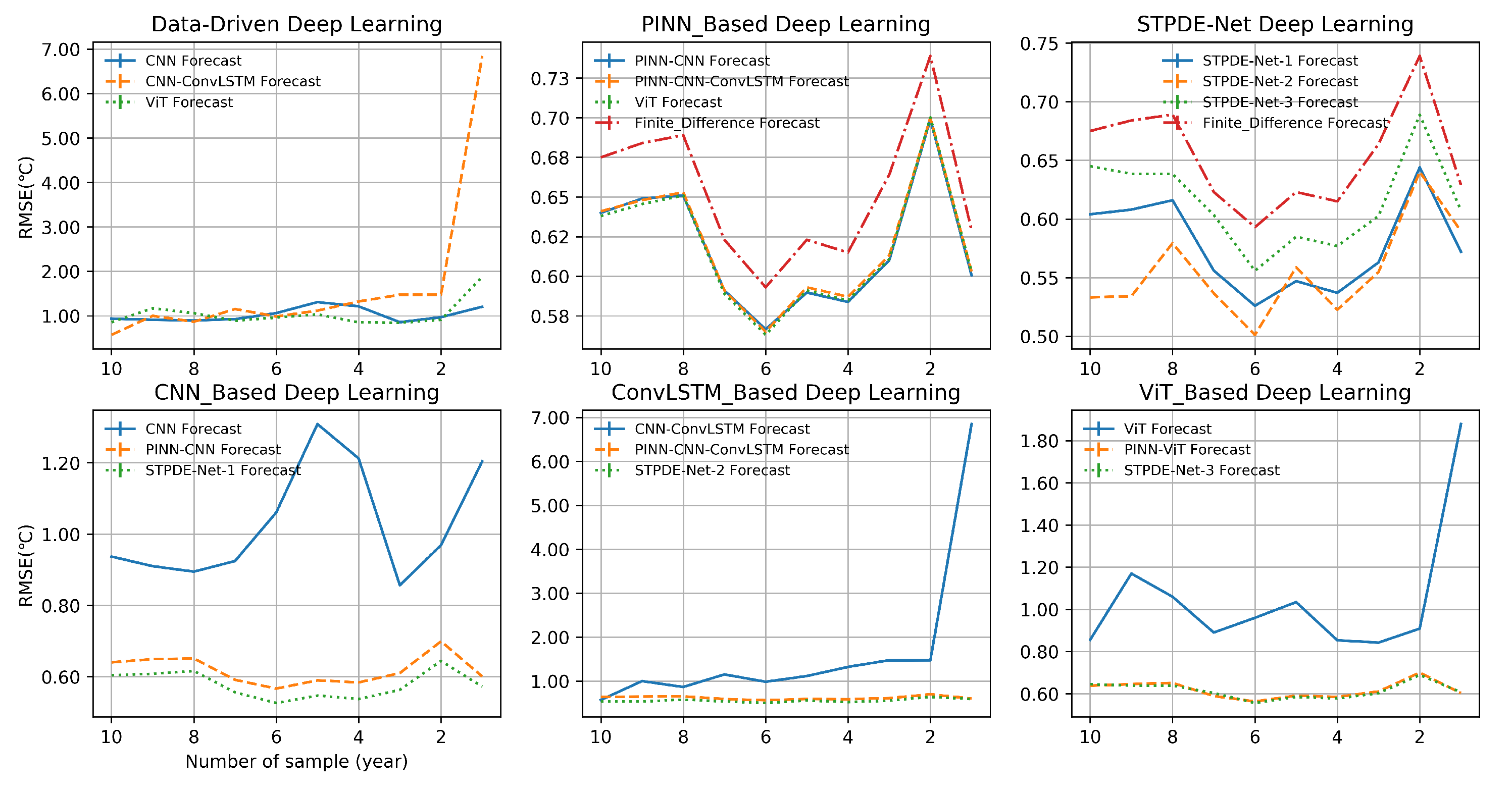
4.2. Sensitivity Experiments Performed for Robustness
4.3. Limitation Analysis of Pure Data-Driven Deep Learning Methods
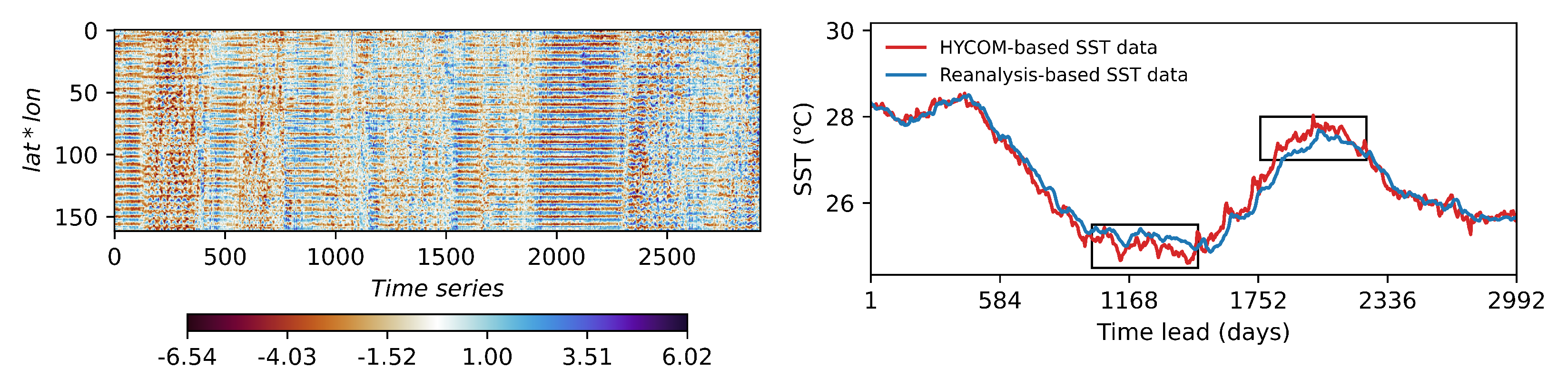
4.4. Evaluating the Accuracy of Oceanic Models with Reanalysis SST Data
4.5. Empirical Analyses Showing PINN Failure Modes
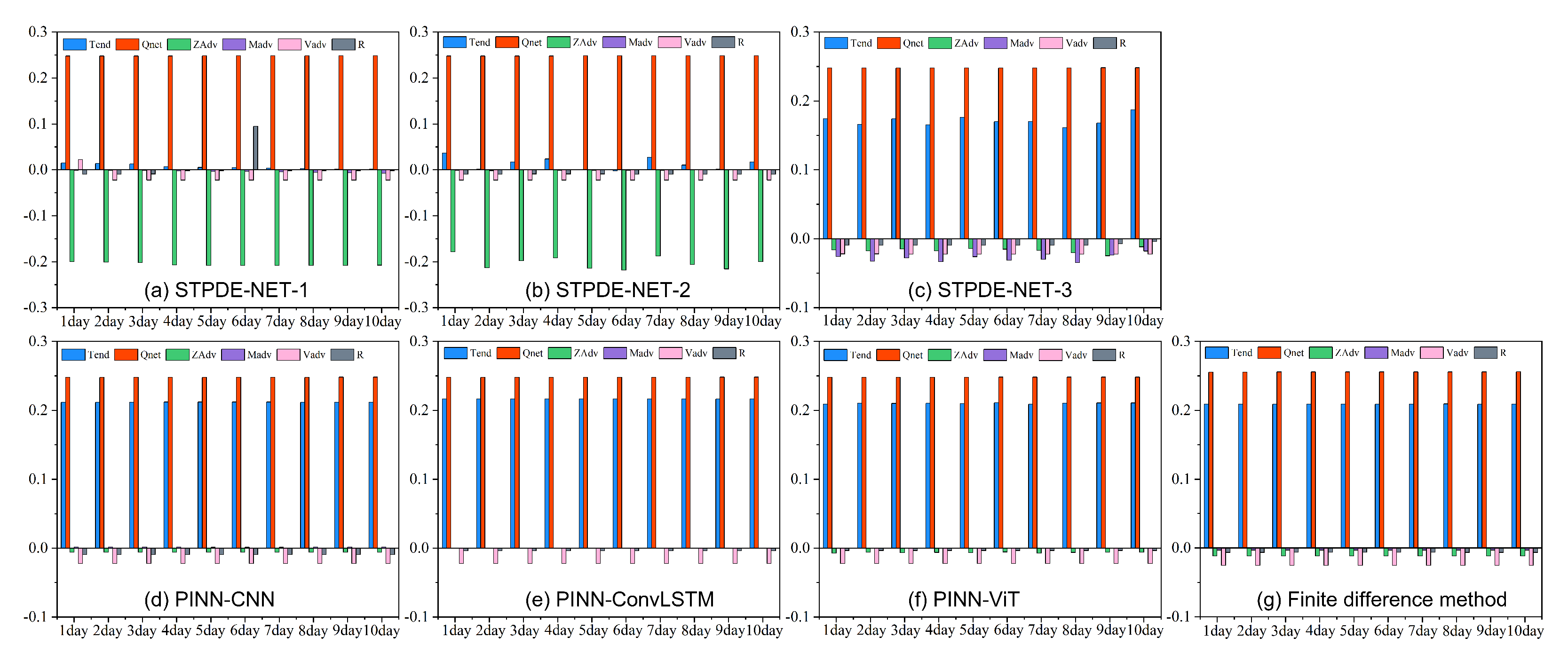
4.6. Possible Mechanism Analysis for Interpretability
5. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SST | Sea Surface Temperature |
| HYCOM | Hybrid Coordinate Ocean Mode |
| ROMs | Regional Ocean Modeling System |
| POM | Princeton Ocean Model |
| CNN | Convolutional Neural Network |
| RNN | Recurrent Neural Network |
| VIT | Vision Transformer |
| PINN | Physics-informed deep learning |
| STPDE-NET | Space-Time Partial Differential Equation-Neural Network |
| PDE | Partial Differential Equation |
References
- Sun, C.; Kucharski, F.; Kang, I.S.; Wang, C.; Ding, R.; Xie, F. Recent Acceleration of Arabian Sea Warming Induced by the Atlantic-Western Pacific Trans-basin Multidecadal Variability. Geophys. Res. Lett. 2019, 46, 123–456. [Google Scholar] [CrossRef]
- Ren, H.H.; Dudhia, J.; Li, H. Large-Eddy Simulation of Idealized Hurricanes at Different Sea Surface Temperatures. J. Adv. Model. Earth Syst. 2020, 12, 1–9. [Google Scholar] [CrossRef]
- Stuart-Menteth, A.C.; Robinson, I.S.; Challenor, P.G. A global study of diurnal warming using satellite-derived sea surface temperature. J. Geophys. Res. Part C Oceans 2003, 108, 3155. [Google Scholar] [CrossRef]
- L’Heureux, M.L.; Tippett, M.K.; Wang, W.Q. Prediction Challenges From Errors in Tropical Pacific Sea Surface Temperature Trends. Front. Clim. 2022, 4, 837483. [Google Scholar] [CrossRef]
- Borgne, P.L.; Roquet, H.; Merchant, C.J. Estimation of Sea Surface Temperature from the Spinning Enhanced Visible and Infrared Imager, improved using numerical weather prediction. Remote Sens. Environ. 2011, 4, 55–65. [Google Scholar] [CrossRef]
- Minnett, P.J.; Azcárate, A.A.; Corlett, T.M.; Cuervo, J.V. Half a century of satellite remote sensing of sea-surface temperature. Remote Sens. Environ. 2019, 233, 111366. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Y.; Frery, A.C.; Ren, P. Sea Surface Temperature Prediction with Memory Graph Convolutional Networks. IEEE Geosci. Remote Sens. Lett. 2022, 19, 8017105. [Google Scholar] [CrossRef]
- Chassignet, E.P.; Hurlburt, H.E.; Smedstad, O.M.; Halliwell, G.R.; Hogan, P.J.; Wallcraft, A.J.; Baraille, R.; Bleck, R. The HYCOM (HYbrid Coordinate Ocean Model) data assimilative system. J. Mar. Syst. 2007, 65, 60–83. [Google Scholar] [CrossRef]
- Shchepetkin, A.F.; Mcwilliams, J.C. The regional oceanic modeling system (ROMS): A split-explicit, free-surface, topography-following-coordinate oceanic model. Ocean. Model. 2005, 9, 347–404. [Google Scholar] [CrossRef]
- Mellor, G.L.; Blumberg, A.F. Modeling Vertical and Horizontal Diffusivities with the Sigma Coordinate System. Mon. Weather Rev. 2003, 113, 1379–1383. [Google Scholar] [CrossRef]
- Chen, X.W.; Lin, X.T. Big Data Deep Learning: Challenges and Perspectives. IEEE Access 2014, 2, 514–525. [Google Scholar] [CrossRef]
- Ogut, M.; Bpsch-Liuis, X.; Reising, S.C. A Deep Learning Approach for Microwave and Millimeter-Wave Radiometer Calibration. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5344–5355. [Google Scholar] [CrossRef]
- He, K.M.; Zhang, X.Y.; Ren, S.Q.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]
- Daniel, W.O.; Julian, R.M.; Jugal, K.K. A Survey of the Usages of Deep Learning for Natural Language Processing. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 604–624. [Google Scholar]
- Wang, X.; Iwabuchi, H.; Yamashita, T. Cloud identification and property retrieval from Himawari-8 infrared measurements via a deep neural network. Remote Sens. Environ. 2022, 275, 113026. [Google Scholar] [CrossRef]
- Liu, J.; Tang, Y.M.; Wu, Y.L.; Li, T.; Wang, Q.; Chen, D.K. Forecasting the Indian Ocean Dipole With Deep Learning Techniques. Geophys. Res. Lett. 2021, 48, e2021GL094407. [Google Scholar] [CrossRef]
- Ghorbani, A.; Ouyang, D.; Abid, A.; He, B.; Chen, J.H.; Harrington, R.A.; Liang, D.H.; Ashley, E.A.; Zou, J.Y. Deep learning interpretation of echocardiograms. NPJ Digit. Med. 2020, 3, 10. [Google Scholar] [CrossRef]
- Iravani, S.; Conrad, T.O.F. An Interpretable Deep Learning Approach for Biomarker Detection in LC-MS Proteomics Data. IEEE/ACM Trans. Comput. Biol. Bioinform. 2022, 20, 151–161. [Google Scholar] [CrossRef]
- Kong, X.; Ge, Z. Deep PLS: A Lightweight Deep Learning Model for Interpretable and Efficient Data Analytics. IEEE Trans. Geosci. Remote Sens. 2022, 3154090. [Google Scholar] [CrossRef]
- Meng, Y.X.; Rigall, E.; Chen, X.E.; Gao, F.; Dong, J.Y.; Chen, S. Physics-Guided Generative Adversarial Networks for Sea Subsurface Temperature Prediction. IEEE Trans. Neural Netw. Learn. Syst. 2022, 1–14. [Google Scholar] [CrossRef]
- Daw, A.; Karpatne, A.; Watkins, W.; Read, J.; Kumar, V. Physics-guided Neural Networks (PGNN): An Application in Lake Temperature Modeling. arXiv 2017, arXiv:1710.11431. [Google Scholar]
- Yadav, A.; Vishwakarma, D.K. Sentiment analysis using deep learning architectures: A review. Artif. Intell. Rev. 2020, 53, 4335–4385. [Google Scholar] [CrossRef]
- Chattopadhyay, A.; Mustafa, M.; Hassanzadeh, P.; Bach, E.; Kashinath, K. Towards physics-inspired data-driven weather forecasting: Integrating data assimilation with a deep spatial-transformer-based U-NET in a case study with ERA5. Geosci. Model Dev. 2022, 15, 2221–2237. [Google Scholar] [CrossRef]
- Yann, L.C.; Bengio, Y.S.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar]
- Raghu, M.; Schmidt, E. A Survey of Deep Learning for Scientific Discovery. arXiv 2020, arXiv:2003.11755. [Google Scholar]
- Ham, Y.G.; Kim, J.H.; Luo, J.J. Deep learning for multi-year ENSO forecasts. Nature 2020, 573, 568–572. [Google Scholar] [CrossRef]
- Xiao, C.J.; Chen, N.C.; Hu, C.L.; Wang, K.; Gong, J.Y.; Chen, Z.Q. Short and mid-term sea surface temperature prediction using time-series satellite data and LSTM-AdaBoost combination approach. Remote Sens. Environ. 2019, 233, 111358. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Paramar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. In Proceedings of the 31st Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 6000–6010. [Google Scholar]
- Alexey, D.; Lucas, B.; Alexander, K.; Dirk, W.; Zhai, X.H.; Thom, U.; Mostafa, D.; Matthias, M.; Georg, H.; Sylvain, G.; et al. An Image Is Worth 16 × 16 Words: Transformers for Image Recognition at Scale. In Proceedings of the 2021 IEEE International Conference on Learning Representations (ICLR), Vitural, 3–7 May 2021; pp. 1–22. [Google Scholar]
- Zhou, L.; Zhang, R.H. A self-attention–based neural network for three-dimensional multivariate modeling and its skillful ENSO predictions. Sci. Adv. 2023, 9, eadf2827. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Nguyen, T.N.K.; Dairay, T.; Meunier, R.; Mougeot, M. Physics-informed neural networks for non-Newtonian fluid thermo-mechanical problems: An application to rubber calendering process. Eng. Appl. Artif. Intell. 2022, 114, 105176. [Google Scholar] [CrossRef]
- Bihlo, A.; Popovych, R.O. Physics-informed neural networks for the shallow-water equations on the sphere. J. Comput. Phys. 2022, 456, 111024. [Google Scholar] [CrossRef]
- Yuan, T.K.; Zhu, J.X.; Ren, K.J.; Wang, W.X.; Wang, X.; Li, X.Y. Neural Network Driven by Space-time Partial Differential Equation for Predicting Sea Surface Temperature. In Proceedings of the 2022 IEEE International Conference on Data Mining, Orlando, FL, USA, 28 November–1 December 2022; pp. 656–665. [Google Scholar]
- Zhang, X.P.; Cai, Y.Z.; Wang, J.; Ju, L.L.; Qian, Y.Z.; Ye, M.; Yang, J.Z. GW-PINN: A deep learning algorithm for solving groundwater flow equations. Adv. Water Resour. 2022, 165, 104243. [Google Scholar] [CrossRef]
- Tu, J.Z.; Liu, C.; Qi, P. Physics-informed Neural Network Integrating PointNet-based Adaptive Refinement for Investigating Crack Propagation in Industrial Applications. IEEE Trans. Ind. Inform. 2022, 19, 2210–2218. [Google Scholar] [CrossRef]
- Sarabian, M.; Babaee, H.; Laksari, K. Physics-informed neural networks for brain hemodynamic predictions using medical imaging. IEEE Trans. Med. Imaging 2022, 41, 2285–2303. [Google Scholar] [CrossRef] [PubMed]
- Raj, A.; Bresler, Y.; Li, B. Improving Robustness of Deep-Learning-Based Image Reconstruction. In Proceedings of the 37th International Conference on Machine Learning, PMLR, Online, 13–18 July 2020; Volume 119, pp. 7932–7942. [Google Scholar]
- Cronin, M.F.; Pell, N.A.; Emerson, S.R.; Crawford, W.R. Estimating diffusivity from the mixed layer heat and salt balances in the North Pacific. J. Geophys. Res. Ocean. 2015, 120, 7346–7362. [Google Scholar] [CrossRef]
- Oliver, E.C.J.; Benthuysen, J.A.; Darmaraki, S.; Donat, M.G.; Hobday, A.J.; Holbrook, N.J.; Schlegel, R.W.; Gupta, A.S. Marine Heatwaves. Annu. Rev. Mar. Sci. 2020, 13, 313–342. [Google Scholar] [CrossRef]
- Deser, C.; Alexander, M.A.; Xie, S.P.; Phillips, A.S. Sea Surface Temperature Variability: Patterns and Mechanisms. Annu. Rev. Mar. Sci. 2010, 2, 115–143. [Google Scholar] [CrossRef]
- Vecchi, G.A.; Soden, B.J. Effect of remote sea surface temperature change on tropical cyclone potential intensity. Nature 2007, 13, 313–342. [Google Scholar] [CrossRef]
- Wunsch, C. What Is the Thermohaline Circulation? Science 2002, 298, 1179–1181. [Google Scholar] [CrossRef]
- Lou, Q.; Meng, X.H.; Karniadakis, G.E. Physics-informed neural networks for solving forward and inverse flow problems via the Boltzmann-GKG formulation. J. Comput. Phys. 2021, 445, 110676. [Google Scholar] [CrossRef]
- Huang, Y.H.; Xu, Z.; Qian, C.; Liu, L. Solving free-surface problems for non-shallow water using boundary and initial conditions-free physics-informed neural network (bif-PINN). J. Comput. Phys. 2023, 479, 112003. [Google Scholar] [CrossRef]
- Sarker, S. Fundamentals of Climatology for Engineers: Lecture Note. Engineering 2022, 3, 573–595. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Shi, X.J.; Chen, Z.R.; Wang, H.; Yeung, D.Y.; Wong, W.K.; Woo, W.C. Convolutional LSTM Network: A machine learning approach for precipitation nowcasting. In Proceedings of the 28th International Conference on Neural Information Processing System, Montreal, QC, Canada, 7–12 December 2015; Volume 1, pp. 802–810. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenbom, D.; Zhai, X.H.; Unterthiner, T.; Dehghanni, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image is Worth 16 × 16 Words: Transformers for Image Recognition at Scale (ViT). In Proceedings of the International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar]
- Sarker, S. A short review on computational hydraulics in the context of water resources engineering. Open J. Model. Simul. 2021, 10, 1–31. [Google Scholar] [CrossRef]
- Sarker, S. Essence of mike 21c (fdm numerical scheme): Application on the river morphology of bangladesh. Open J. Model. Simul. 2022, 10, 88–117. [Google Scholar] [CrossRef]
| Input Variables | Data Source | |
|---|---|---|
| 1 | Downward Longwave Radiation (in ) | ERA5 |
| 2 | Upward Longwave Radiation (in ) | ERA5 |
| 3 | Downward Shortwave Radiation (in ) | ERA5 |
| 4 | Upward Shortwave Radiation (in ) | ERA5 |
| 5 | Latent Heat (in ) | ERA5 |
| 6 | Sensible Heat (in ) | ERA5 |
| 7 | Sea Surface Temperature (in ) | NOAA and CMEMS |
| 8 | Sea Surface Temperature at 108 m (in ) | CMEMS |
| 9 | Momentum Flux-u-Component (in ) | CMEMS |
| 10 | Momentum Flux-v-Component (in ) | CMEMS |
| 11 | Vertical Ocean Current Velocity at 108 m (in ) | CMEMS |
| 12 | Mixed Layer Thickness (in ) | CMEMS |
| 13 | Longitude (-) | all data source |
| 14 | Latitude (-) | all data source |
| Models | 1 Day | 5 Day | 10 Day |
|---|---|---|---|
| Number of sample: 10 year | |||
| STPDE-NET-1 | 18.56 ± 0.15% | 13.15 ± 0.12% | 10.52 ± 0.08% |
| STPDE-NET-2 | 14.99 ± 1.60% | 13.69 ± 1.47% | 21.01 ± 1.39% |
| STPDE-NET-3 | 3.36% ± 2.40% | 5.07% ± 1.80% | 4.44% ± 2.51% |
| Number of sample: 9 year | |||
| STPDE-NET-1 | 18.88 ± 0.85% | 18.12% ± 0.28% | 11.11 ± 0.14% |
| STPDE-NET-2 | 15.27 ± 3.04% | 20.47 ± 1.78% | 21.90 ± 2.40% |
| STPDE-NET-3 | 3.83 ± 1.25% | 11.23 ± 0.46% | 6.67 ± 1.30% |
| Number of sample: 8 year | |||
| STPDE-NET-1 | 18.42 ± 0.00% | 13.47 ± 0.60% | 10.60% ± 0.40% |
| STPDE-NET-2 | 9.26 ± 2.29% | 10.97 ± 3.09% | 15.91 ± 2.44% |
| STPDE-NET-3 | 5.21 ± 0.73% | 6.00 ± 0.82% | 7.34 ± 0.84% |
| Number of sample: 7 year | |||
| STPDE-NET-1 | 18.23 ± 0.19% | 13.28 ± 0.00% | 10.75 ± 0.00% |
| STPDE-NET-2 | 14.70 ± 0.84% | 11.41 ± 0.85% | 13.87% ± 2.74% |
| STPDE-NET-3 | 2.15 ± 2.19% | −10.4 ± 12.39% | 3.15 ± 3.47% |
| Number of sample: 6 year | |||
| STPDE-NET-1 | 18.87 ± 1.27% | 13.85 ± 0.30% | 11.30% ± 0.35% |
| STPDE-NET-2 | 17.52 ± 1.44% | 12.55 ± 1.80% | 15.48 ± 2.92% |
| STPDE-NET-3 | 3.72 ± 2.92% | 4.94 ± 1.01% | 6.27 ± 2.36% |
| Number of sample: 5 year | |||
| STPDE-NET-1 | 18.78 ± 1.16% | 14.55 ± 0.84% | 12.20 ± 0.51% |
| STPDE-NET-2 | 16.41 ± 4.11% | 12.39 ± 2.96% | 10.31 ± 2.16% |
| STPDE-NET-3 | 3.76 ± 0.61% | 5.36 ± 0.37% | 6.13 ± 0.07% |
| Number of sample: 4 year | |||
| STPDE-NET-1 | 20.22 ± 1.18% | 15.27 ± 0.69% | 12.68 ± 0.49% |
| STPDE-NET-2 | 18.47 ± 1.44% | 15.48 ± 0.61% | 15.02 ± 3.08% |
| STPDE-NET-3 | 3.83 ± 2.89% | 4.94 ± 0.70% | 6.18 ± 0.62% |
| Number of sample: 3 year | |||
| STPDE-NET-1 | 20.54 ± 1.08% | 14.98 ± 0.66% | 12.58 ± 0.51% |
| STPDE-NET-2 | 21.46 ± 0.97% | 16.80 ± 0.55% | 13.85 ± 5.31% |
| STPDE-NET-3 | 4.87 ± 0.54% | 4.82 ± 1.07% | 6.43 ± 0.46% |
| Number of sample: 2 year | |||
| STPDE-NET-1 | 19.53 ± 0.19% | 15.69 ± 0.13% | 12.86 ± 0.00% |
| STPDE-NET-2 | 13.77 ± 7.79% | 14.09 ± 2.86% | 13.37 ± 3.81% |
| STPDE-NET-3 | 6.33 ± 1.59% | 6.90 ± 0.66% | 6.79 ± 0.11% |
| Number of sample: 1 year | |||
| STPDE-NET-1 | 17.88 ± 0.11% | 11.93 ± 0.14% | 9.06 ± 0.00% |
| STPDE-NET-2 | 13.97 ± 8.19% | 9.48 ± 1.07% | 6.26 ± 1.30% |
| STPDE-NET-3 | 1.31 ± 0.35% | 2.29 ± 0.51% | 3.47 ± 0.38% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, T.; Zhu, J.; Wang, W.; Lu, J.; Wang, X.; Li, X.; Ren, K. A Space-Time Partial Differential Equation Based Physics-Guided Neural Network for Sea Surface Temperature Prediction. Remote Sens. 2023, 15, 3498. https://doi.org/10.3390/rs15143498
Yuan T, Zhu J, Wang W, Lu J, Wang X, Li X, Ren K. A Space-Time Partial Differential Equation Based Physics-Guided Neural Network for Sea Surface Temperature Prediction. Remote Sensing. 2023; 15(14):3498. https://doi.org/10.3390/rs15143498
Chicago/Turabian StyleYuan, Taikang, Junxing Zhu, Wuxin Wang, Jingze Lu, Xiang Wang, Xiaoyong Li, and Kaijun Ren. 2023. "A Space-Time Partial Differential Equation Based Physics-Guided Neural Network for Sea Surface Temperature Prediction" Remote Sensing 15, no. 14: 3498. https://doi.org/10.3390/rs15143498
APA StyleYuan, T., Zhu, J., Wang, W., Lu, J., Wang, X., Li, X., & Ren, K. (2023). A Space-Time Partial Differential Equation Based Physics-Guided Neural Network for Sea Surface Temperature Prediction. Remote Sensing, 15(14), 3498. https://doi.org/10.3390/rs15143498






