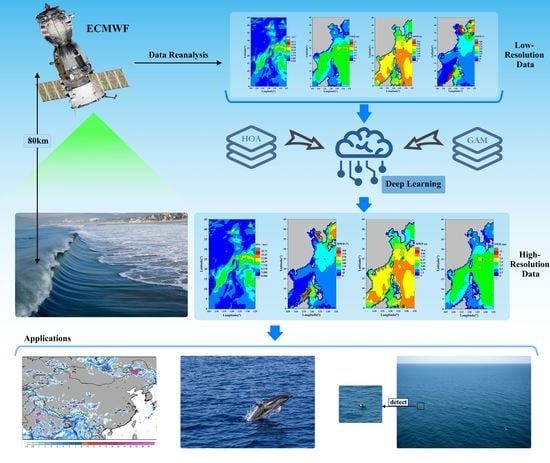
Research on High-Resolution Reconstruction of Marine Environmental Parameters Using Deep Learning Model
Abstract
1. Introduction
2. Methodology
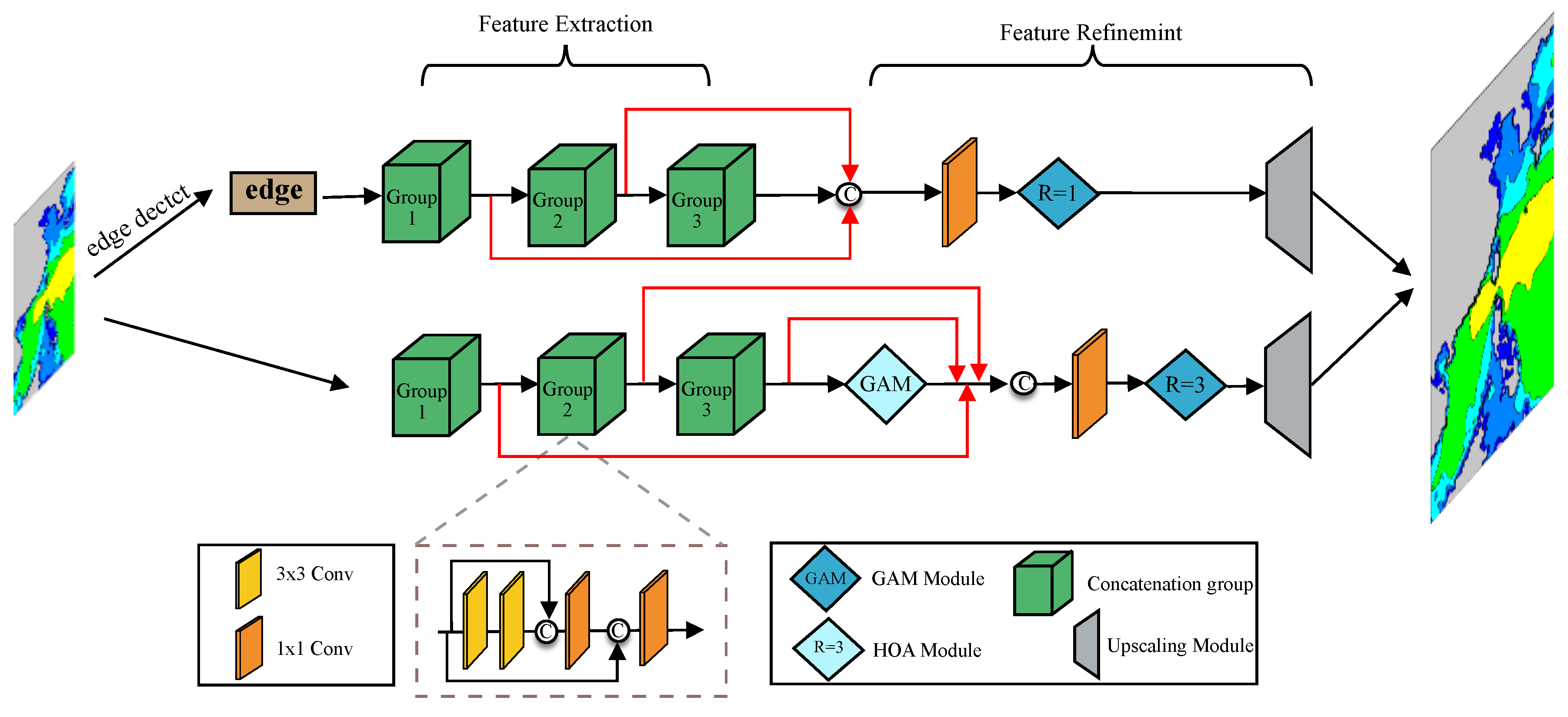
2.1. Network Structure
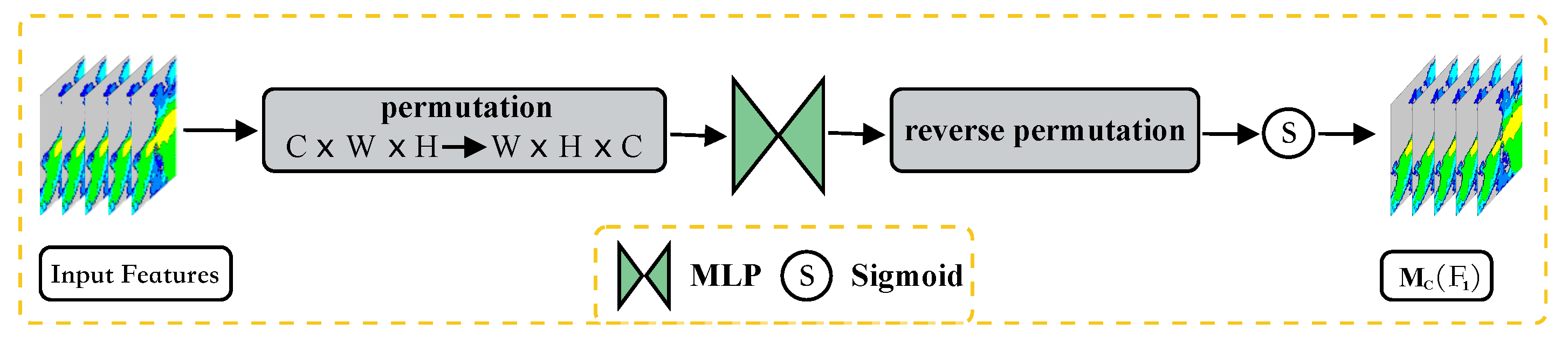
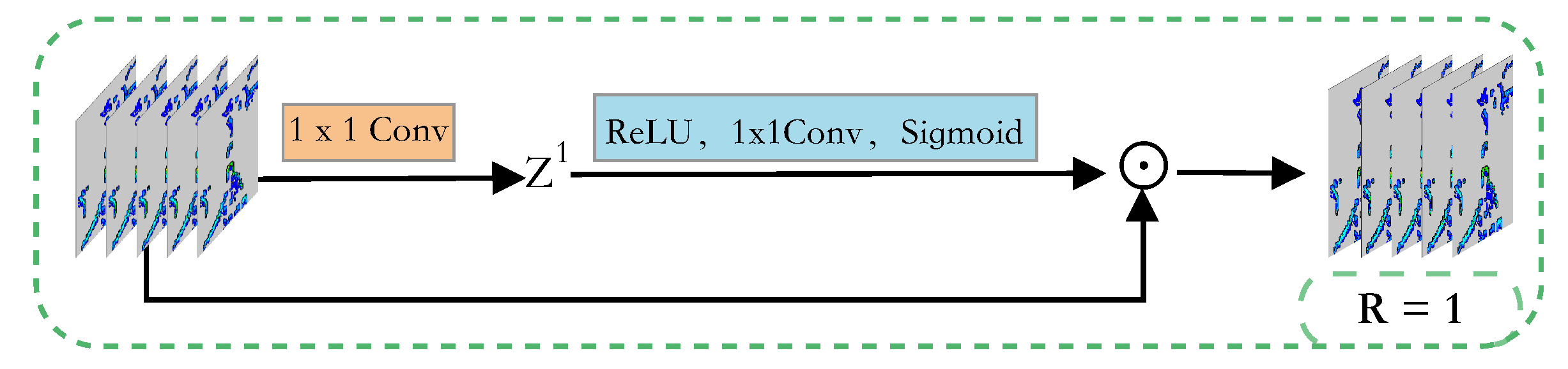
2.2. Attentional Mechanisms
2.2.1. GAM Module
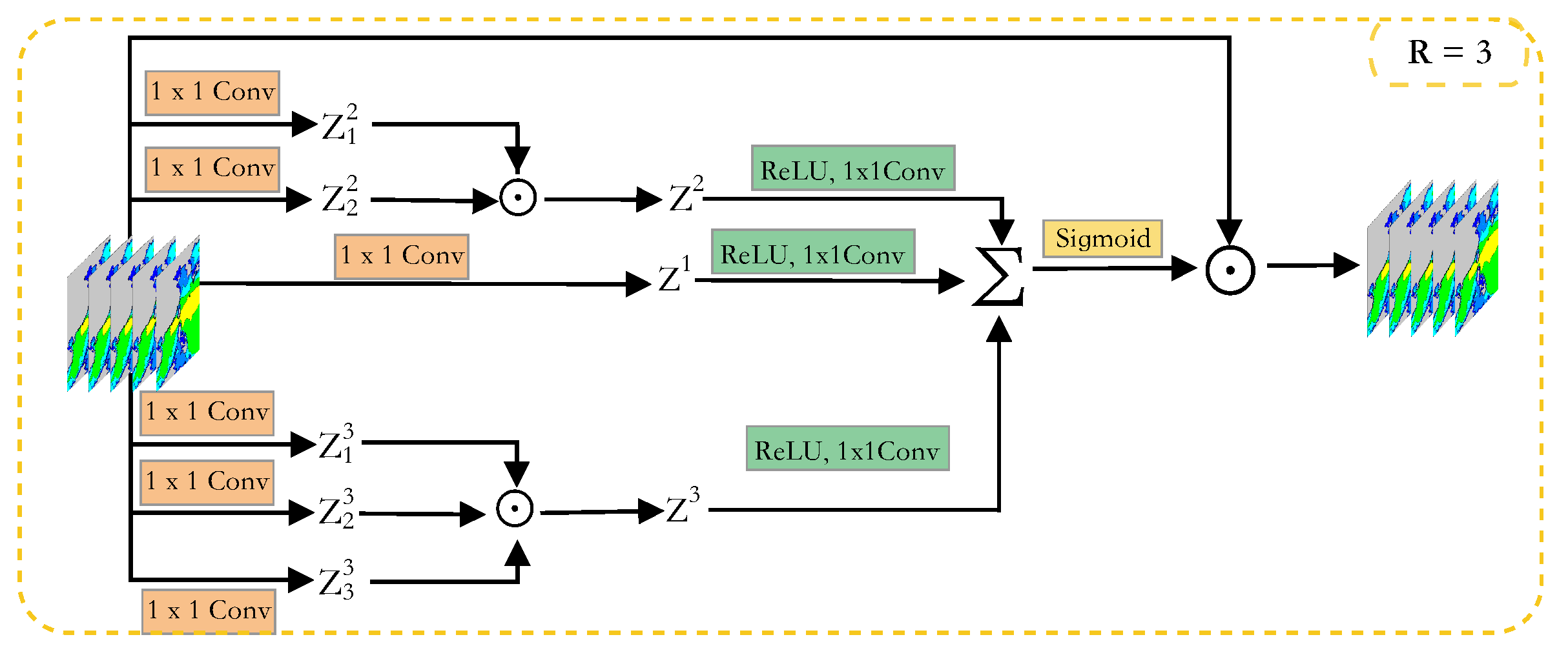
2.2.2. HOA Module
3. Experiments
3.1. Settings
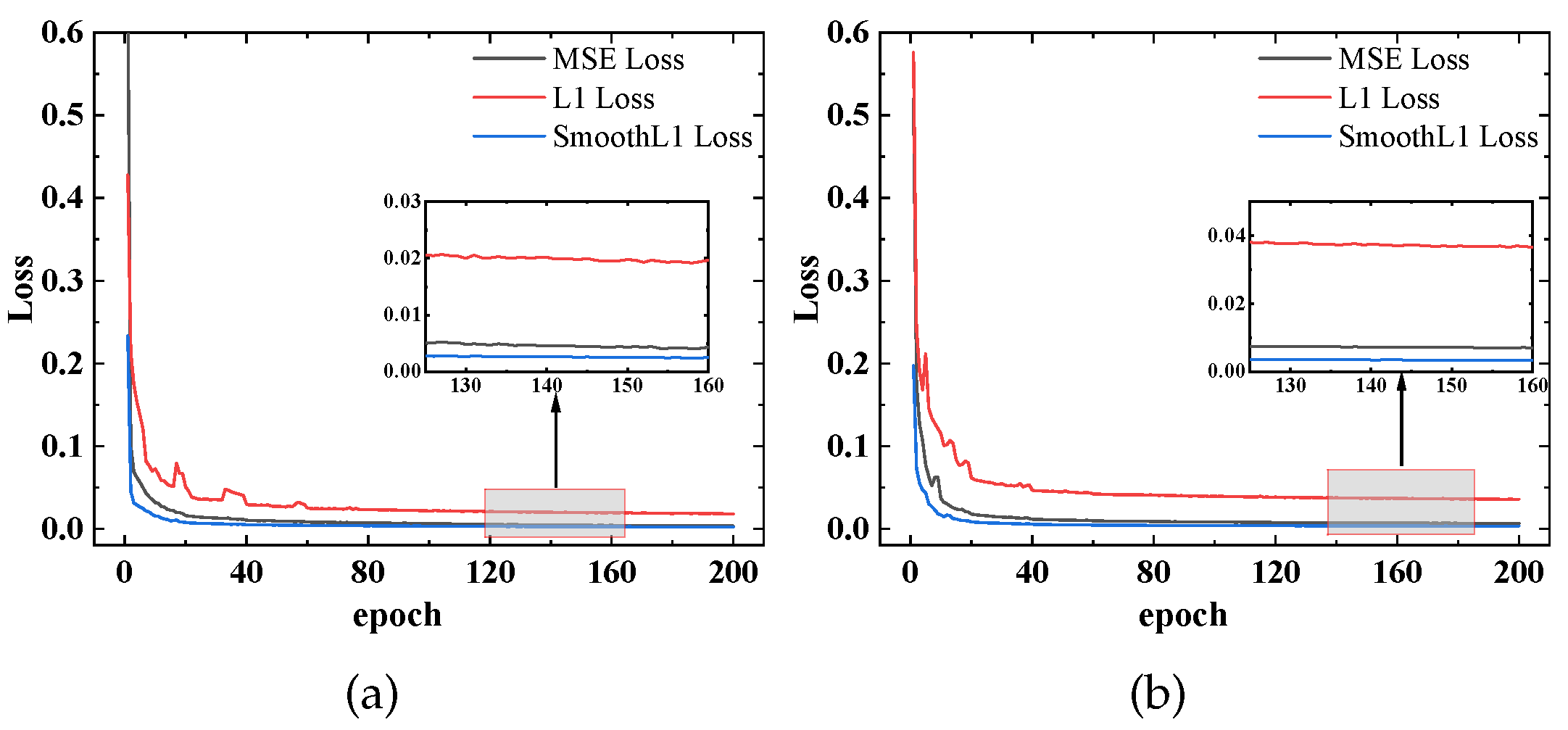
3.2. Loss Function
- MSE loss function [44]. Given the same input data x, the MSE loss function can be formulated aswhere N is the total training data, is the true output of the input data x, and is the predicted output of the input data x.
- SmoothL1 loss function [46]. Given the same input data x, the SmoothL1 loss function can be formulated as
3.3. Evaluation Criteria
- The MSE measures the average squared difference between the estimated values and the actual value. Given an actual value and predicted value , the MSE value is
- The PSNR is an objective criterion for evaluating images and is used to measure the difference between two images. Given an actual value Y and predicted value , the PSNR value isThe max value is the maximum possible pixel value of the given value, usually 255. The higher the PSNR value, the better the reconstruction effect of the estimated image and the higher the similarity to the actual image.
- The SSIM is used to measure the similarity between two images. Given an actual value Y and predicted values , the PSNR value iswhere () represents the pixel sample mean of Y (), () represents the variance of Y (), and is the covariance between Y and . Compared with the MSE and PSNR, the SSIM is closer to the human visual system. The higher the SSIM value, the higher the similarity between the two images.
3.4. Traditional Method
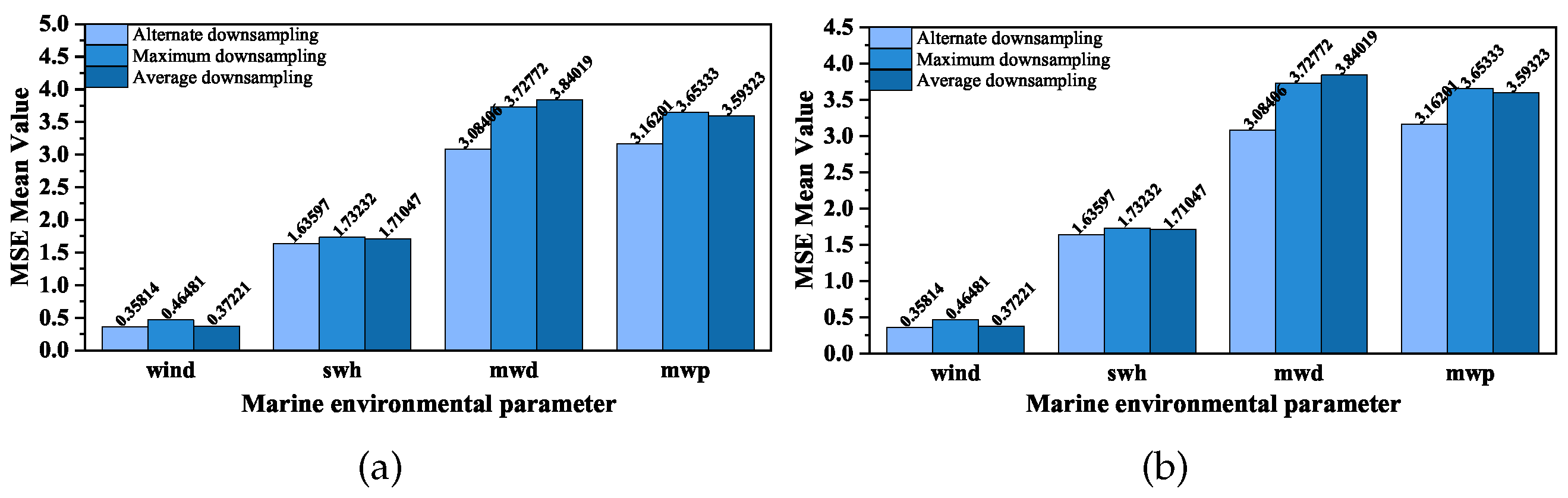
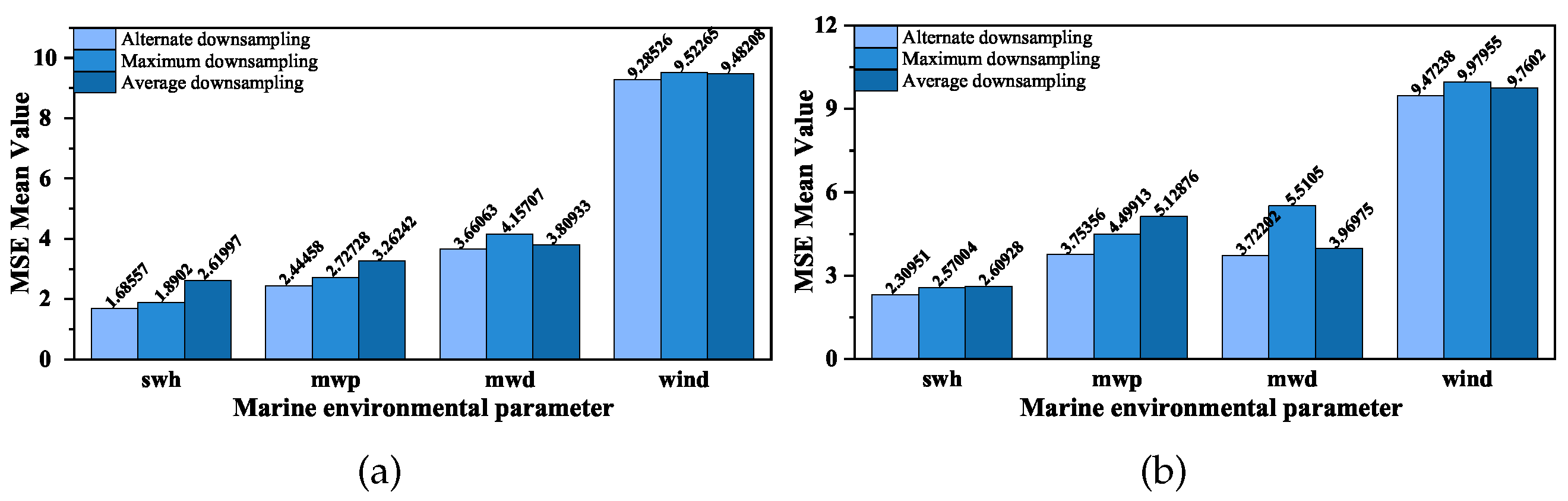
3.5. Downsampling Method
3.6. Ablation Study
4. Comparison
4.1. Assessment in Terms of Different Metrics
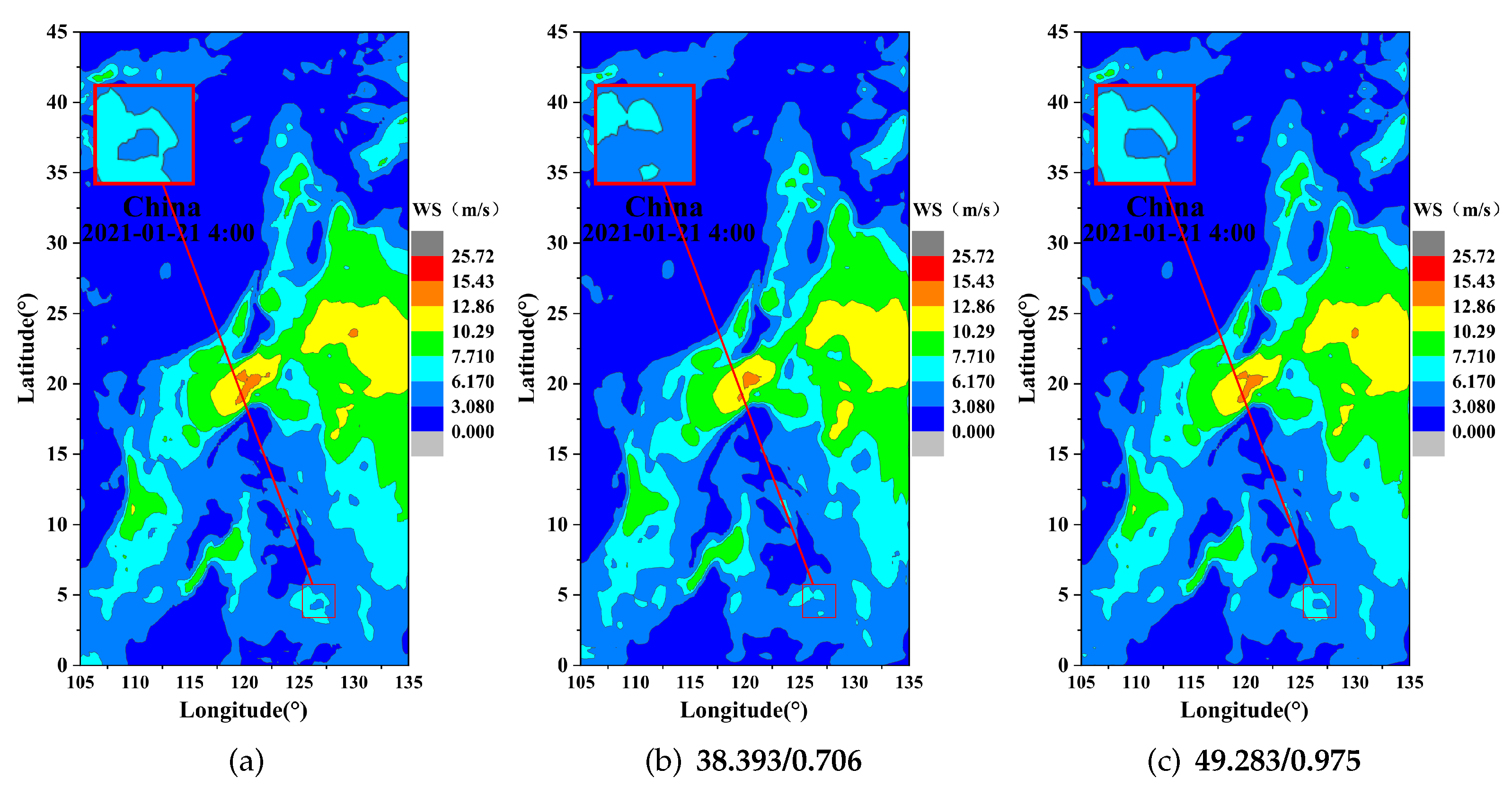
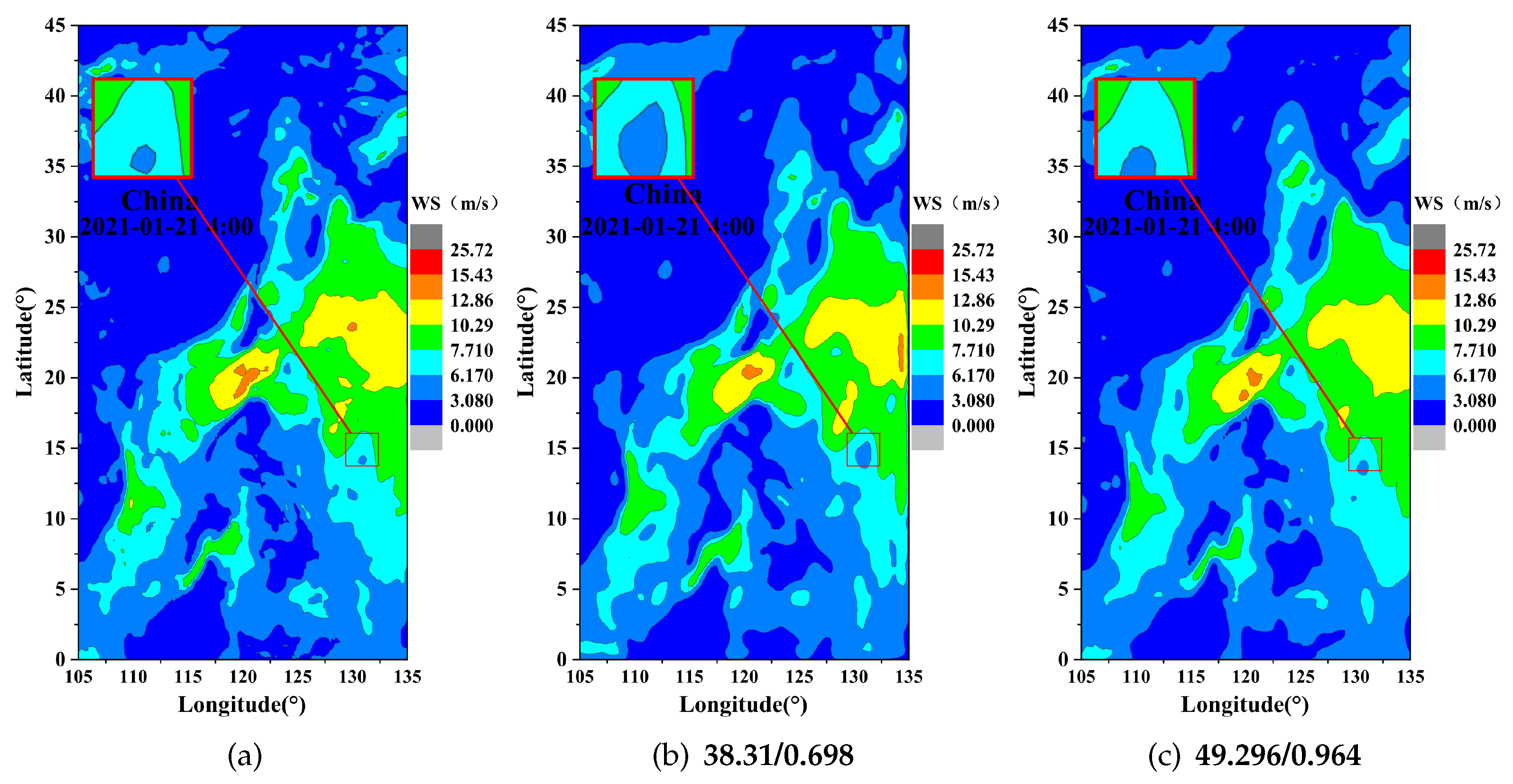
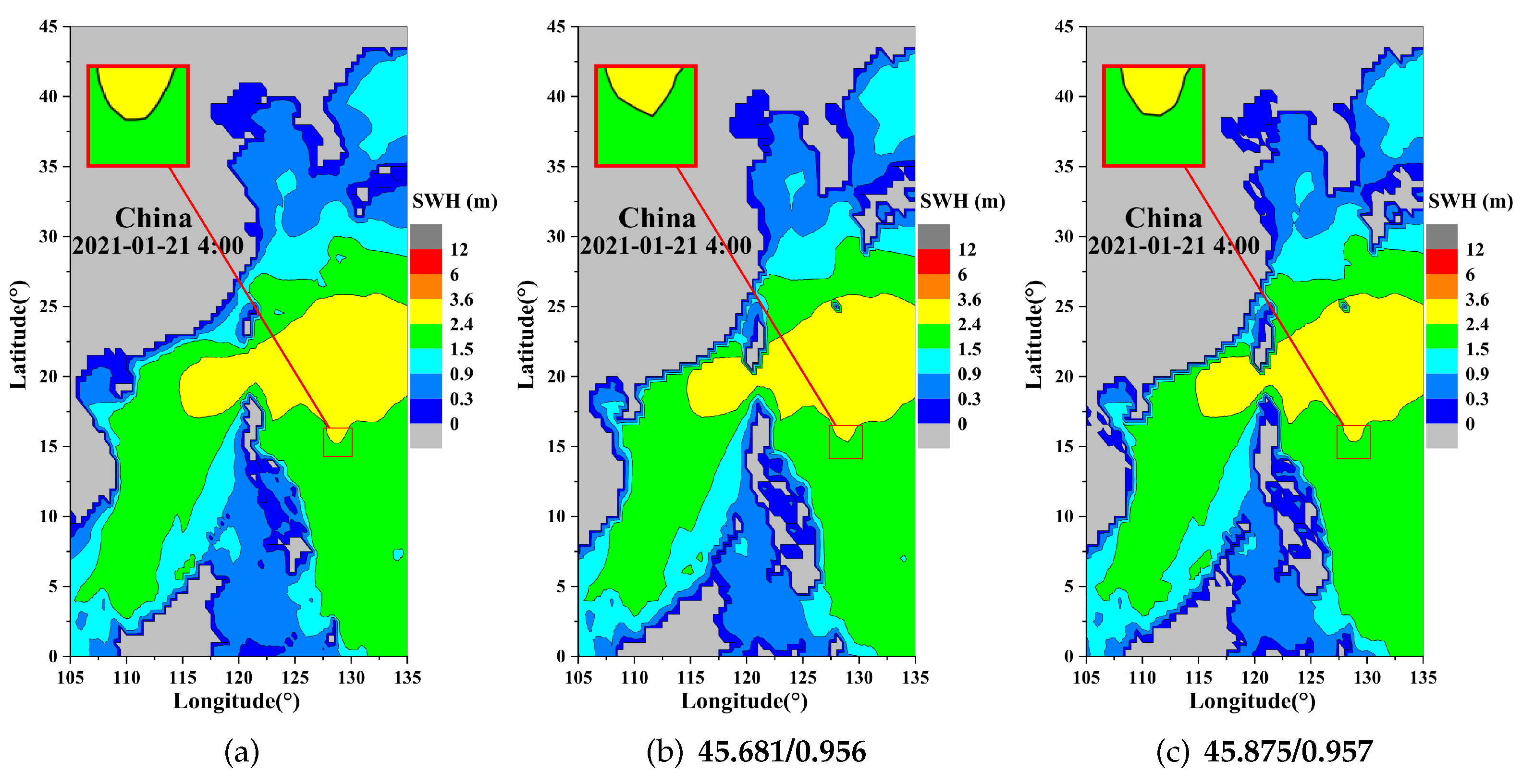
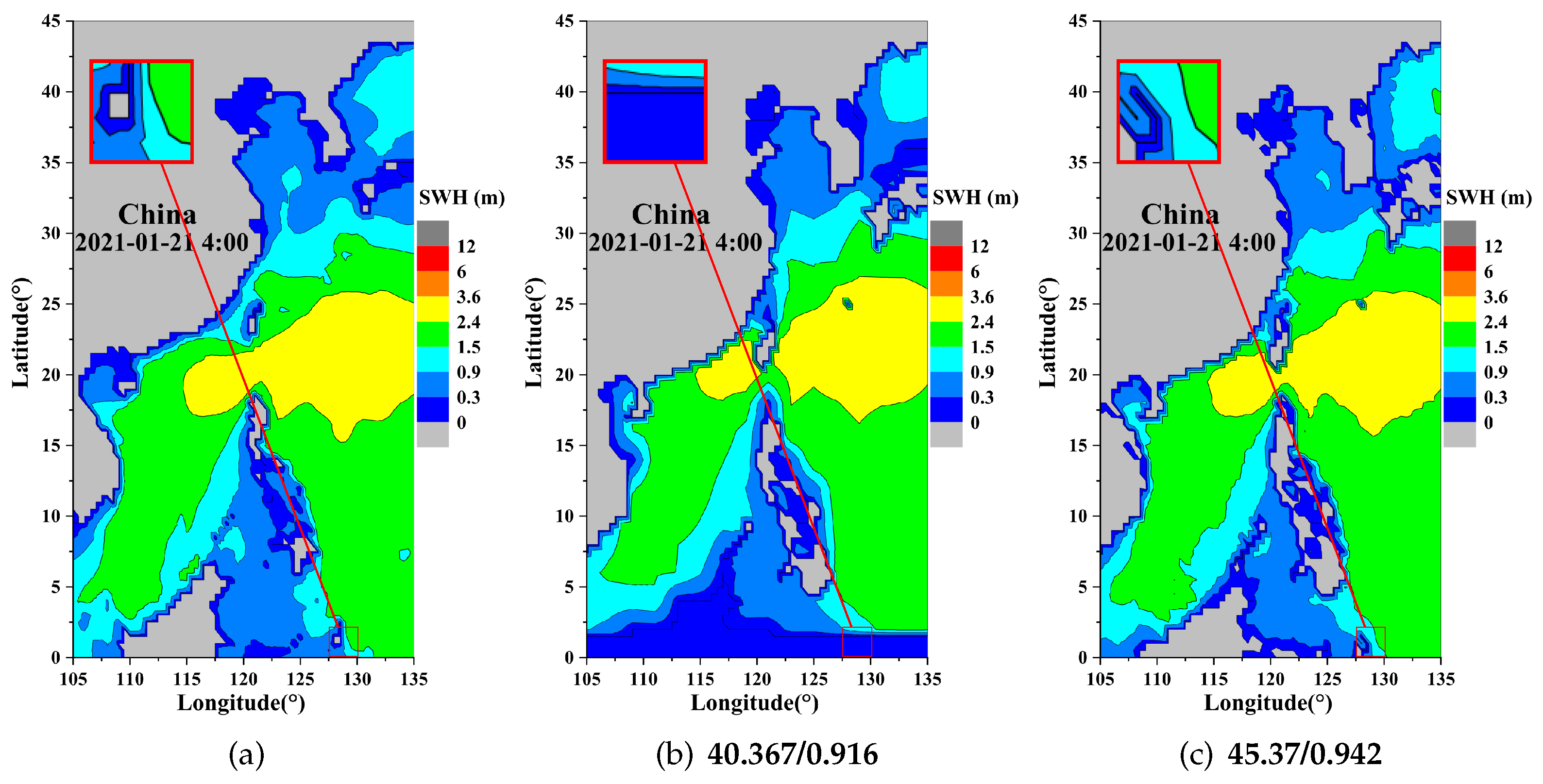
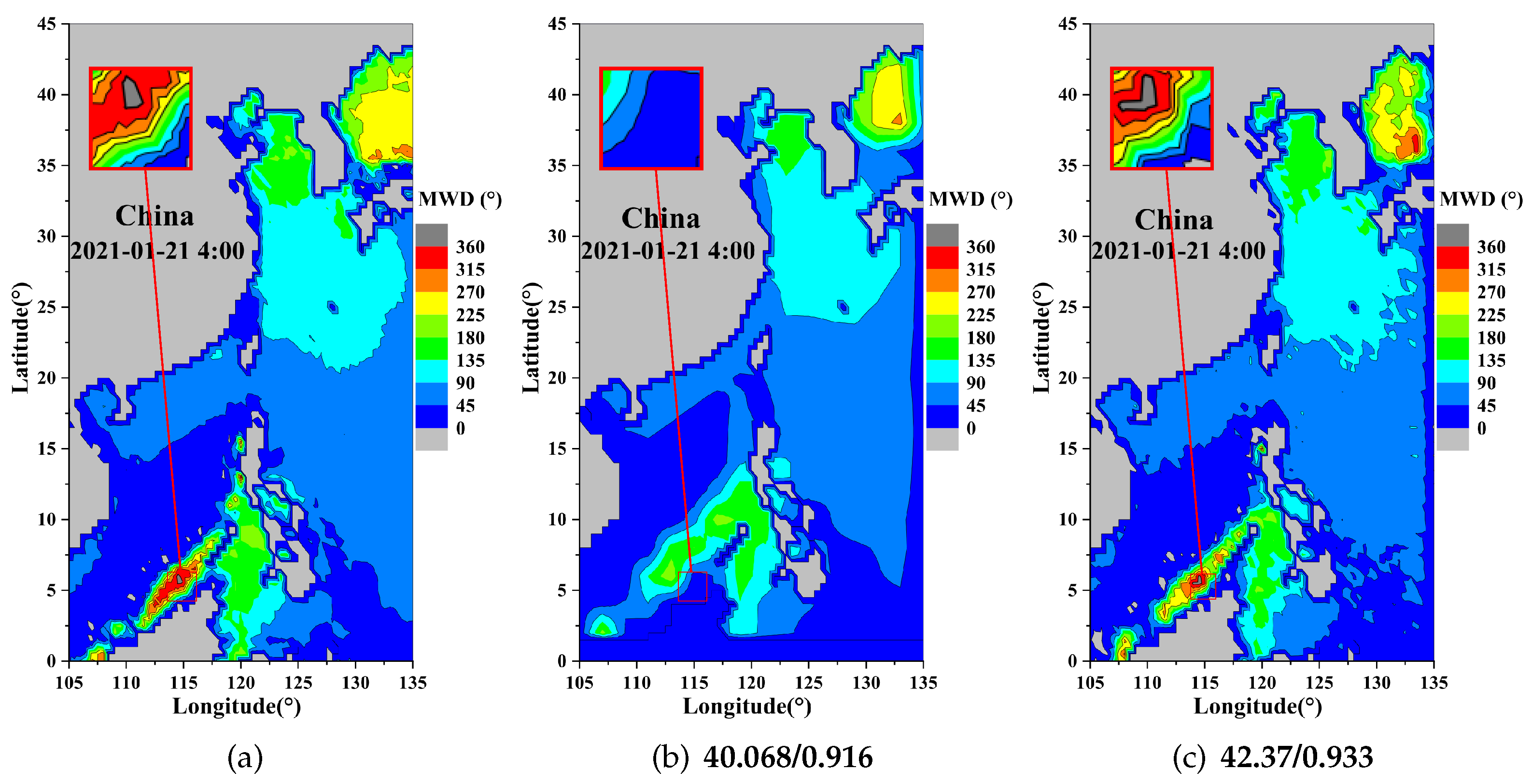
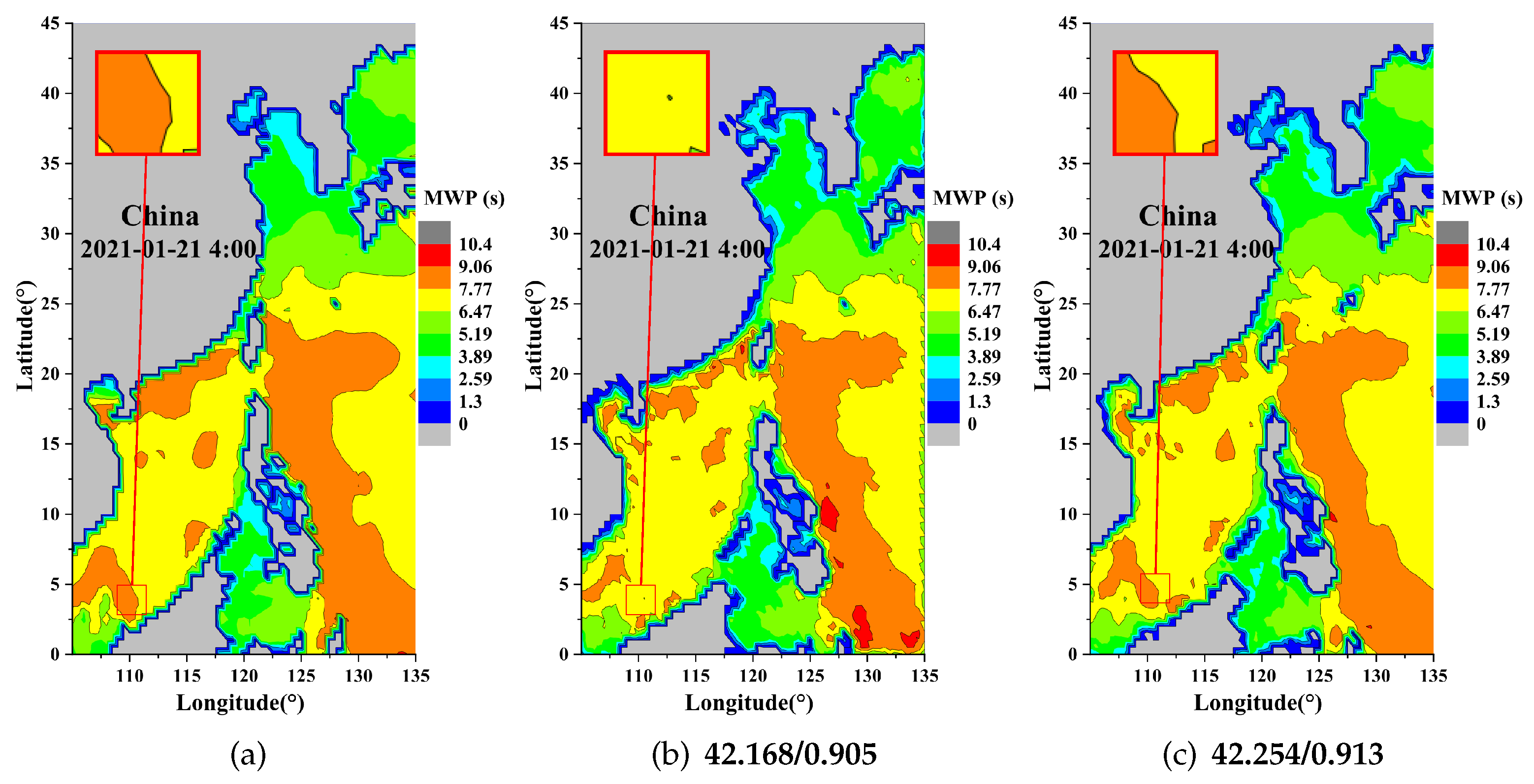
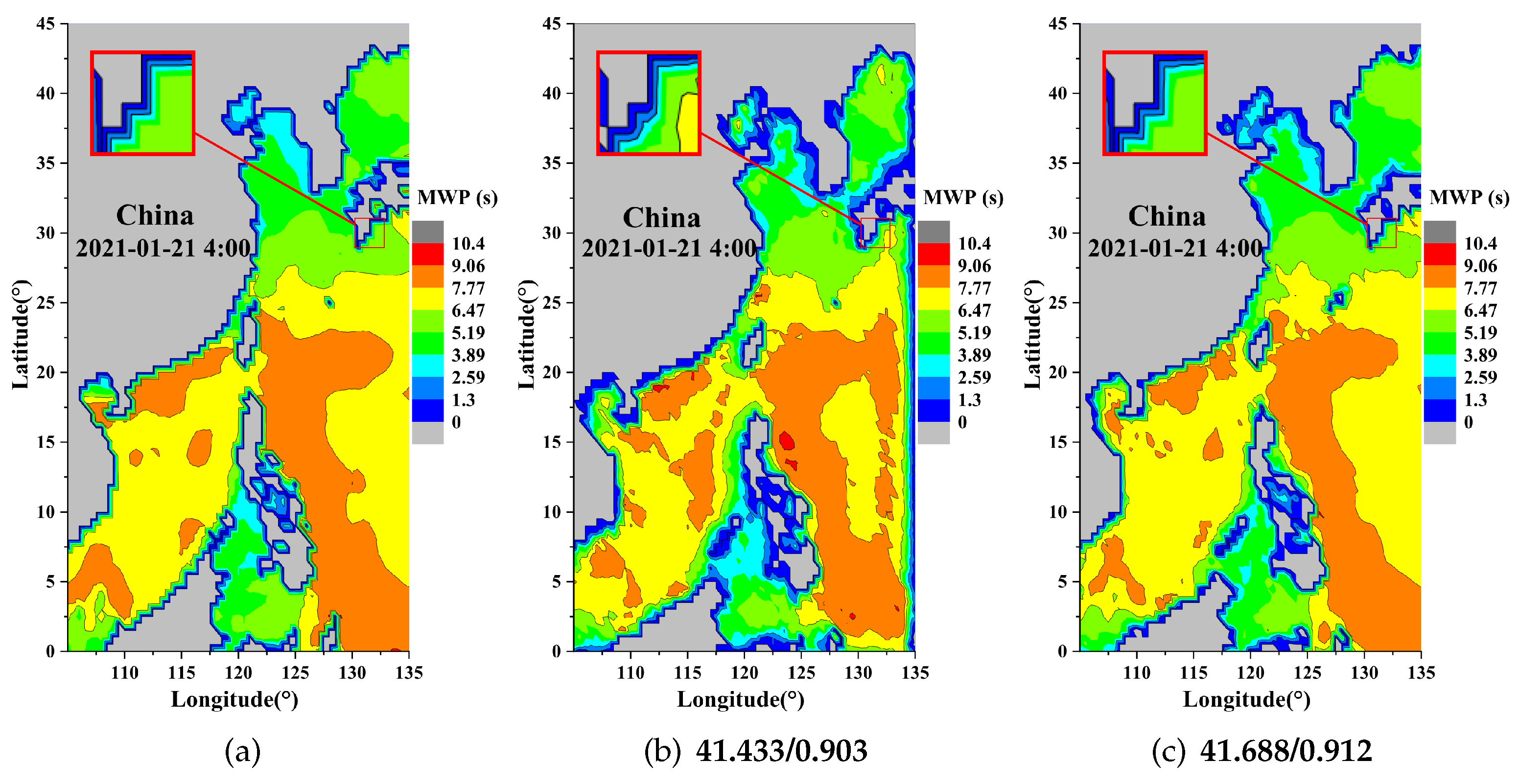
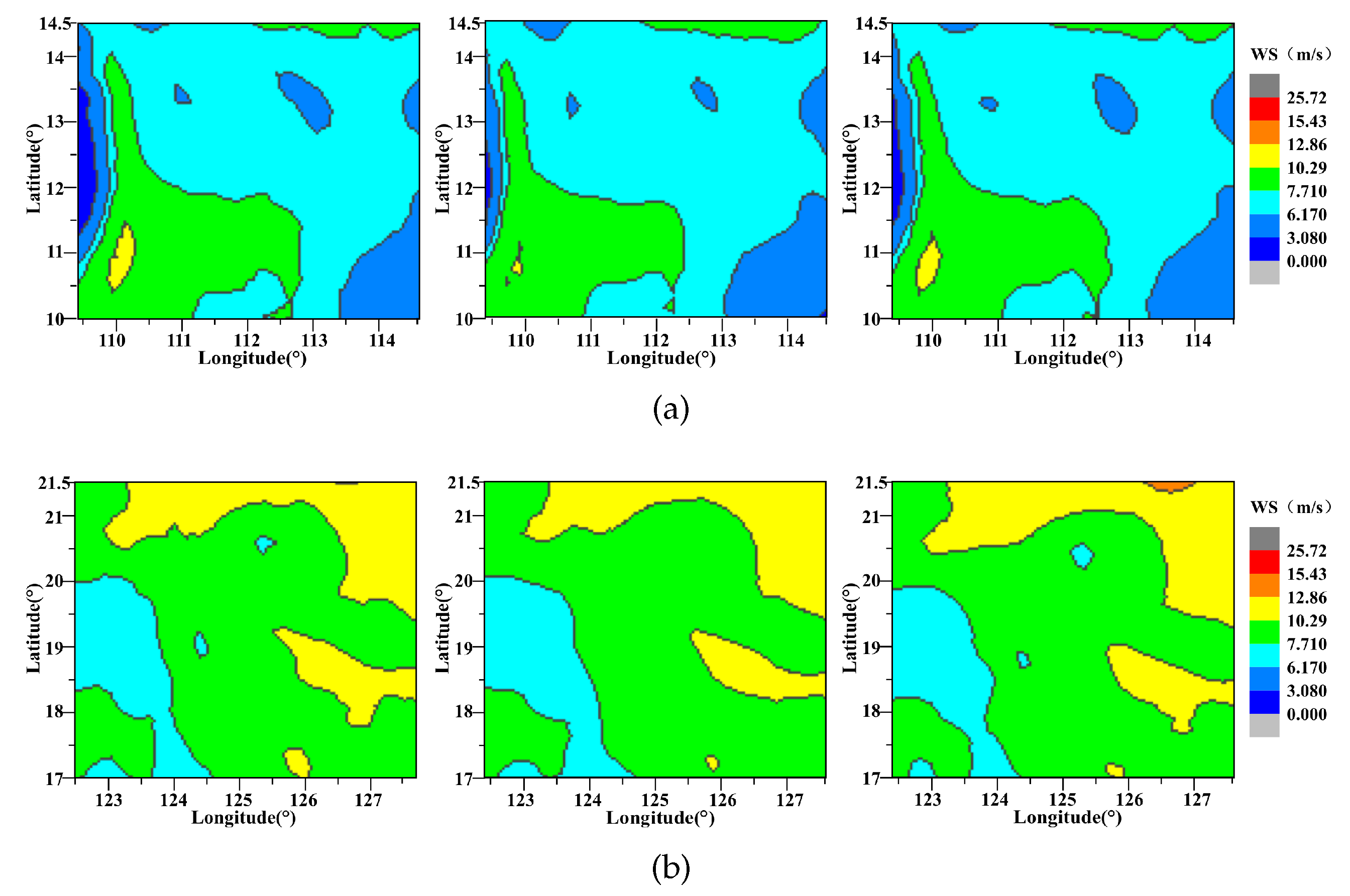
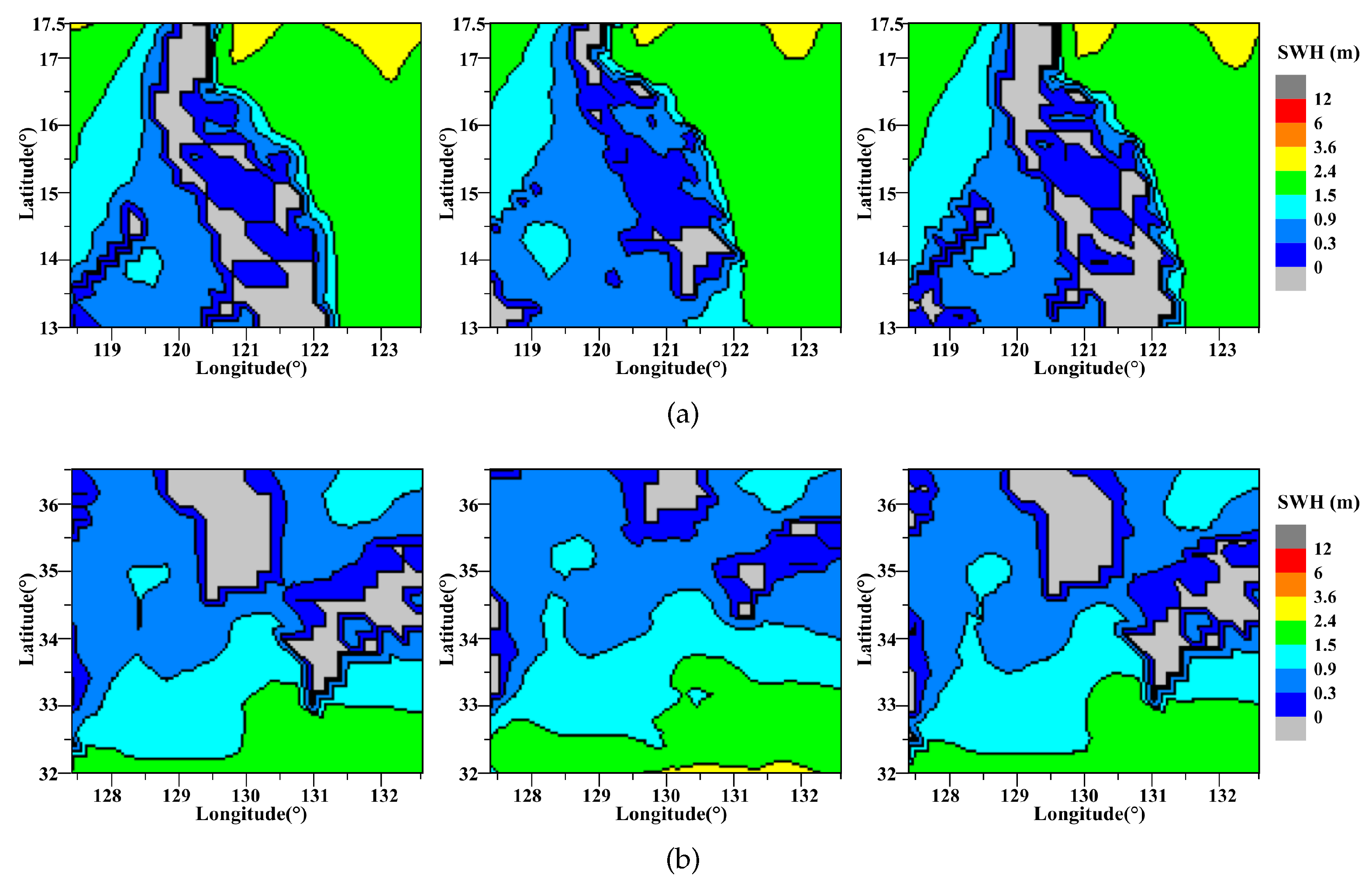
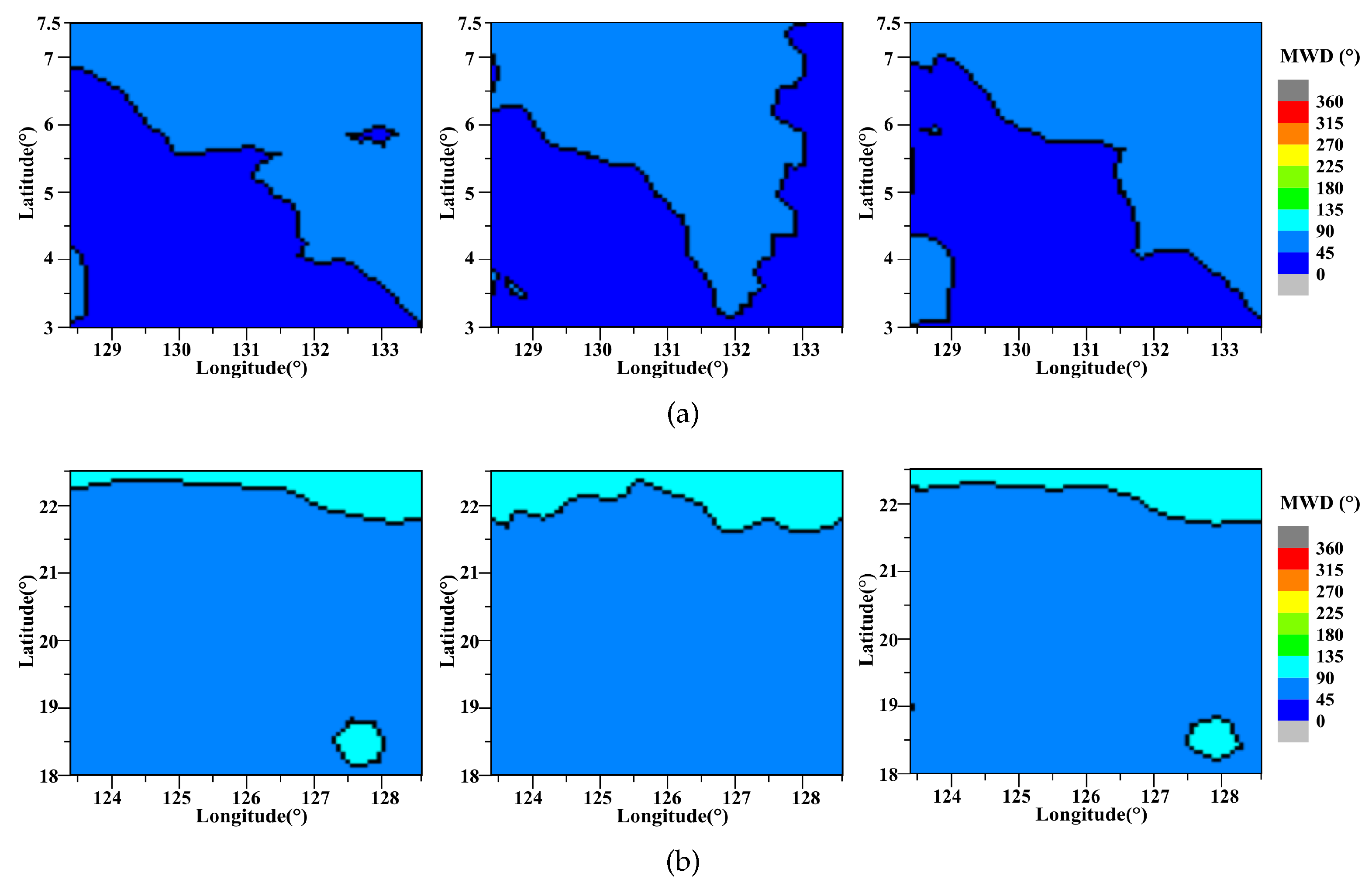
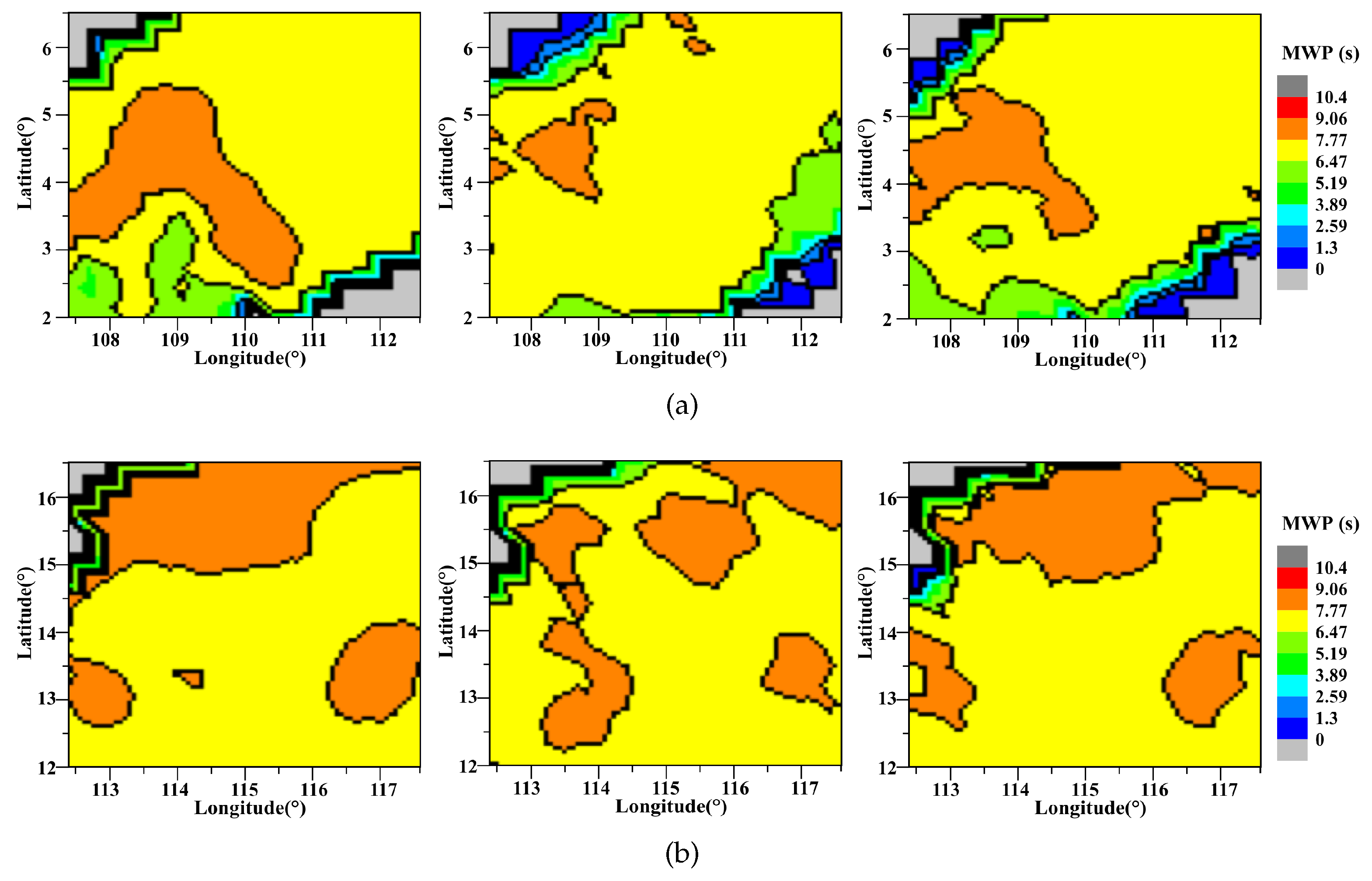
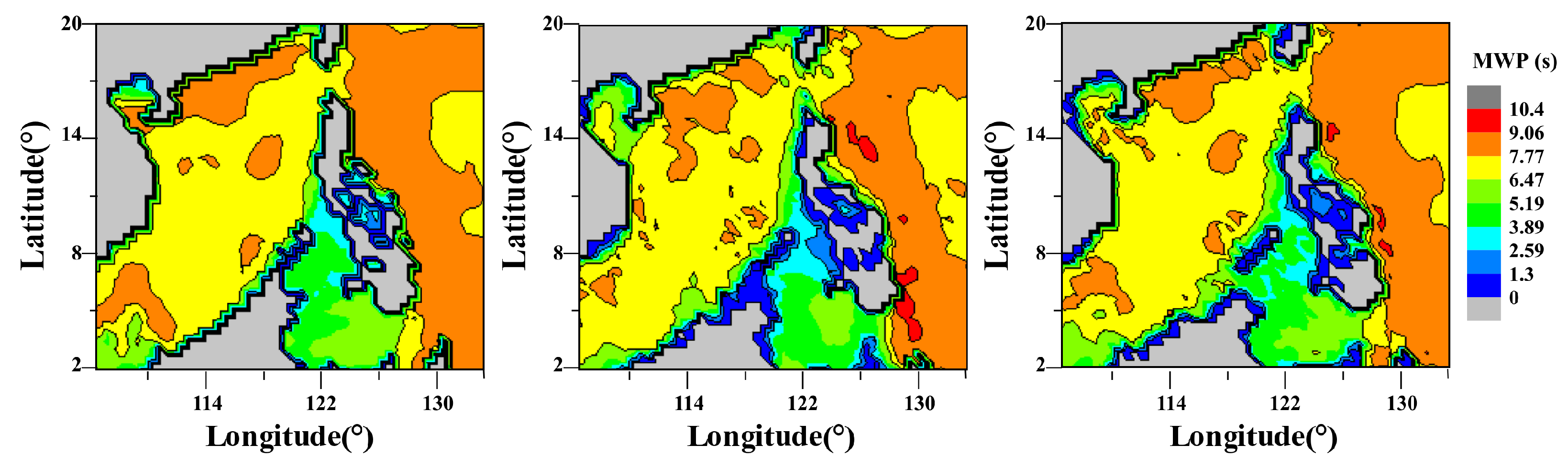
4.2. Visual Results
5. Discussion
- (1)
- More marine environmental parameters and data sources can be combined to conduct further feature analysis of the data, achieving more comprehensive and multidimensional reconstruction results;
- (2)
- Enhancement of attention modules to enhance the extraction and refinement of important fine-grained features;
- (3)
- Optimization and improvement of network architecture can be studied to enhance reconstruction accuracy and efficiency.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xingwei, J.L.; Lin, M.; Jia, Y. Past, Present and Future Marine Microwave Satellite Missions in China. Remote Sens. 2022, 14, 1330. [Google Scholar]
- Meng, L.; Yan, C.; Zhuang, W.; Zhang, W.; Geng, X.; Yan, X.-H. Reconstructing High-Resolution Ocean Subsurface and Interior Temperature and Salinity Anomalies From Satellite Observations. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Biswas, S.; Sinha, M. Performances of Deep Learning Models for Indian Ocean Wind Speed Prediction. Model. Earth Syst. Environ. 2021, 7, 809–831. [Google Scholar] [CrossRef]
- Luo, Z.; Li, Z.; Zhang, C.; Deng, J.; Qin, T. Low Observable Radar Target Detection Method within Sea Clutter Based on Correlation Estimation. Remote Sens. 2022, 14, 2233. [Google Scholar] [CrossRef]
- Reddy, G.T.; Priya, R.; Parimala, M.; Chowdhary, C.L.; Reddy, M.S.K.; Hakak, S.; Khan, W.Z. A Deep Neural Networks Based Model for Uninterrupted Marine Environment Monitoring. Comput. Commun. 2020, 157, 64–75. [Google Scholar]
- Ma, L.; Wu, J.; Zhang, J.; Wu, Z.; Jeon, G.; Zhang, Y.; Wu, T. Research on Sea Clutter Reflectivity Using Deep Learning Model in Industry 4.0. IEEE Trans. Ind. Inform. 2020, 16, 5929–5937. [Google Scholar] [CrossRef]
- Hao, D.; Ningbo, L.I.U.; Yunlong, D.; Xiaolong, C.; Jian, G. Overview and Prospects of Radar Sea Clutter Measurement Experiments. J. Radars 2019, 8, 281–302. [Google Scholar]
- Klemas, V.; Yan, X.-H. Subsurface and Deeper Ocean Remote Sensing from Satellites: An Overview and New Results. Prog. Oceanogr. 2014, 122, 1–9. [Google Scholar] [CrossRef]
- Cruz, H.; Véstias, M.; Monteiro, J.; Neto, H.; Duarte, R.P. A Review of Synthetic-Aperture Radar Image Formation Algorithms and Implementations: A Computational Perspective. Remote Sens. 2022, 14, 1258. [Google Scholar] [CrossRef]
- Woods, A. Medium-Range Weather Prediction, 1st ed.; Springer: New York, NY, USA, 2005; pp. 23–47. [Google Scholar]
- Linghu, L.; Wu, J.; Wu, Z.; Jeon, G.; Wang, X. GPU-Accelerated Computation of Time-Evolving Electromagnetic Backscattering Field From Large Dynamic Sea Surfaces. IEEE Trans. Ind. Inform. 2020, 16, 3187–3197. [Google Scholar] [CrossRef]
- Linghu, L.; Wu, J.; Wu, Z.; Jeon, G.; Wu, T. GPU-Accelerated Computation of EM Scattering of a Time-Evolving Oceanic Surface Model II: EM Scattering of Actual Oceanic Surface. Remote Sens. 2022, 14, 2727. [Google Scholar] [CrossRef]
- Bounaceur, H.; Khenchaf, A.; Le Caillec, J.-M. Analysis of Small Sea-Surface Targets Detection Performance According to Airborne Radar Parameters in Abnormal Weather Environments. Sensors 2022, 22, 3263. [Google Scholar] [CrossRef] [PubMed]
- Xing, Y.; Song, Q.; Cheng, G. Benefit of Interpolation in Nearest Neighbor Algorithms. SIAM J. Math. Data Sci. 2022, 4, 935–956. [Google Scholar] [CrossRef]
- Meijering, E. A Chronology of Interpolation: From Ancient Astronomy to Modern Signal and Image Processing. Proc. IEEE 2002, 90, 319–342. [Google Scholar] [CrossRef]
- Redondi, A.E.C. Radio Map Interpolation Using Graph Signal Processing. IEEE Commun. Lett. 2018, 22, 153–156. [Google Scholar] [CrossRef]
- Yongchun, L.; Qiang, W. New Solution of Cubic Spline Interpolation Function. Pure Math. 2013, 3, 362–367. [Google Scholar]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Learning a Deep Convolutional Network for Image Super-Resolution. In Proceedings of the Computer Vision—ECCV, Zurich, Switzerland, 6–12 September 2014; pp. 184–199. [Google Scholar]
- Kim, J.; Lee, J.K.; Lee, K.M. Accurate Image Super-Resolution Using Very Deep Convolutional Networks. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1646–1654. [Google Scholar]
- Lim, B.; Son, S.; Kim, H.; Nah, S.; Lee, K.M. Enhanced Deep Residual Networks for Single Image Super-Resolution. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Honolulu, HI, USA, 21–26 July 2017; pp. 1132–1140. [Google Scholar]
- Li, J.; Fang, F.; Li, J.; Mei, K.; Zhang, G. MDCN: Multi-Scale Dense Cross Network for Image Super-Resolution. IEEE Trans. Circuits Syst. Video Technol. 2021, 31, 2547–2561. [Google Scholar] [CrossRef]
- Ducournau, A.; Fablet, R. Deep Learning for Ocean Remote Sensing: An Application of Convolutional Neural Networks for Super-Resolution on Satellite-Derived SST Data. In Proceedings of the 2016 9th IAPR Workshop on Pattern Recogniton in Remote Sensing (PRRS), Cancun, Mexico, 4 December 2016; pp. 1–6. [Google Scholar]
- Wang, Z.; Wang, G.; Guo, X.; Hu, J.; Dai, M. Reconstruction of High-Resolution Sea Surface Salinity over 2003–2020 in the South China Sea Using the Machine Learning Algorithm LightGBM Model. Remote Sens. 2022, 14, 6147. [Google Scholar] [CrossRef]
- Su, H.; Wang, A.; Zhang, T.; Qin, T.; Du, X.; Yan, X.-H. Super-Resolution of Subsurface Temperature Field from Remote Sensing Observations Based on Machine Learning. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102440. [Google Scholar] [CrossRef]
- Gao, L.; Li, X.; Song, J.; Shen, H.T. Hierarchical LSTMs with Adaptive Attention for Visual Captioning. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 1112–1131. [Google Scholar] [CrossRef]
- Fu, J.; Liu, J.; Tian, H.; Li, Y.; Bao, Y.; Fang, Z.; Lu, H. Dual Attention Network for Scene Segmentation. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 3141–3149. [Google Scholar]
- Zhong, Z.; Lin, Z.; Bidart, R.; Hu, X.; Ben Daya, I.; Li, Z.; Zheng, W.-S.; Li, J.; Wong, A. Squeeze-and-Attention Networks for Semantic Segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 13065–13074. [Google Scholar]
- Luong, T.; Pham, H.; Manning, C.D. Effective Approaches to Attention-Based Neural Machine Translation. In Proceedings of the 2015 Conference on Empirical Methods in Natural Language Processing, Lisbon, Portugal, 17–21 September 2015. [Google Scholar]
- Yin, W.; Schütze, H.; Xiang, B.; Zhou, B. ABCNN: Attention-Based Convolutional Neural Network for Modeling Sentence Pairs. Trans. Assoc. Comput. Linguist. 2016, 4, 259–272. [Google Scholar] [CrossRef]
- Serrano, S.; Smith, N.A. Is Attention Interpretable? In Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, Florence, Italy, 28 July–2 August 2019; pp. 2931–2951. [Google Scholar]
- Chan, W.; Jaitly, N.; Le, Q.; Vinyals, O. Listen, Attend and Spell: A Neural Network for Large Vocabulary Conversational Speech Recognition. In Proceedings of the 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20–25 March 2016; pp. 4960–4964. [Google Scholar]
- Tran, D.T.; Iosifidis, A.; Kanniainen, J.; Gabbouj, M. Temporal Attention-Augmented Bilinear Network for Financial Time-Series Data Analysis. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 1407–1418. [Google Scholar] [CrossRef]
- Chaudhari, S.; Mithal, V.; Polatkan, G.; Ramanath, R. An Attentive Survey of Attention Models. ACM Trans. Intell. Syst. Technol. 2021, 12, 1–32. [Google Scholar] [CrossRef]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-Excitation Networks. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.-Y.; Kweon, I.S. CBAM: Convolutional Block Attention Module. In Proceedings of the Computer Vision—ECCV, Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- Misra, D.; Nalamada, T.; Arasanipalai, A.U.; Hou, Q. Rotate to Attend: Convolutional Triplet Attention Module. In Proceedings of the 2021 IEEE Winter Conference on Applications of Computer Vision (WACV), Virtual, 3–8 January 2021; pp. 3138–3147. [Google Scholar]
- Liu, Y.; Shao, Z.; Hoffmann, N. Global Attention Mechanism: Retain Information to Enhance Channel-Spatial Interactions. arXiv 2021, arXiv:2112.05561. [Google Scholar]
- Chen, B.; Deng, W.; Hu, J. Mixed High-Order Attention Network for Person Re-Identification. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 371–381. [Google Scholar]
- Zhang, Y.; Li, K.; Li, K.; Wang, L.; Zhong, B.; Fu, Y. Image Super-Resolution Using Very Deep Residual Channel Attention Networks. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018; pp. 286–301. [Google Scholar]
- Park, J.; Woo, S.; Lee, J.-Y.; Kweon, I.S. BAM: Bottleneck Attention Module. In Proceedings of the British Machine Vision Conference, Newcastle, UK, 3–6 September 2018. [Google Scholar]
- Zhang, X.; Zhou, X.; Lin, M.; Sun, J. ShuffleNet: An Extremely Efficient Convolutional Neural Network for Mobile Devices. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 6848–6856. [Google Scholar]
- Hu, Y.; Li, J.; Huang, Y.; Gao, X. Channel-Wise and Spatial Feature Modulation Network for Single Image Super-Resolution. IEEE Trans. Circuits Syst. Video Technol. 2018, 30, 3911–3927. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Picking Loss Functions—A Comparison between MSE, Cross Entropy, and Hinge Loss. Available online: https://rohanvarma.me/Loss-Functions/ (accessed on 14 May 2023).
- Differences between L1 and L2 as Loss Function and Regularization. Available online: http://www.chioka.in/differences-between-l1-and-l2-as-loss-function-and-regularization/ (accessed on 14 May 2023).
- Girshick, R. Fast R-CNN. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 1440–1448. [Google Scholar]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. (Eds.) Linear Model Selection and Regularization. In An Introduction to Statistical Learning: With Applications in R; Springer Texts in Statistics; Springer: New York, NY, USA, 2013; pp. 203–264. [Google Scholar]
- Erfurt, J.; Helmrich, C.R.; Bosse, S.; Schwarz, H.; Marpe, D.; Wiegand, T. A Study of the Perceptually Weighted Peak Signal-To-Noise Ratio (WPSNR) for Image Compression. In Proceedings of the 2019 IEEE International Conference on Image Processing (ICIP), Taipei, Taiwan, 22–25 September 2019; pp. 2339–2343. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image Quality Assessment: From Error Visibility to Structural Similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]


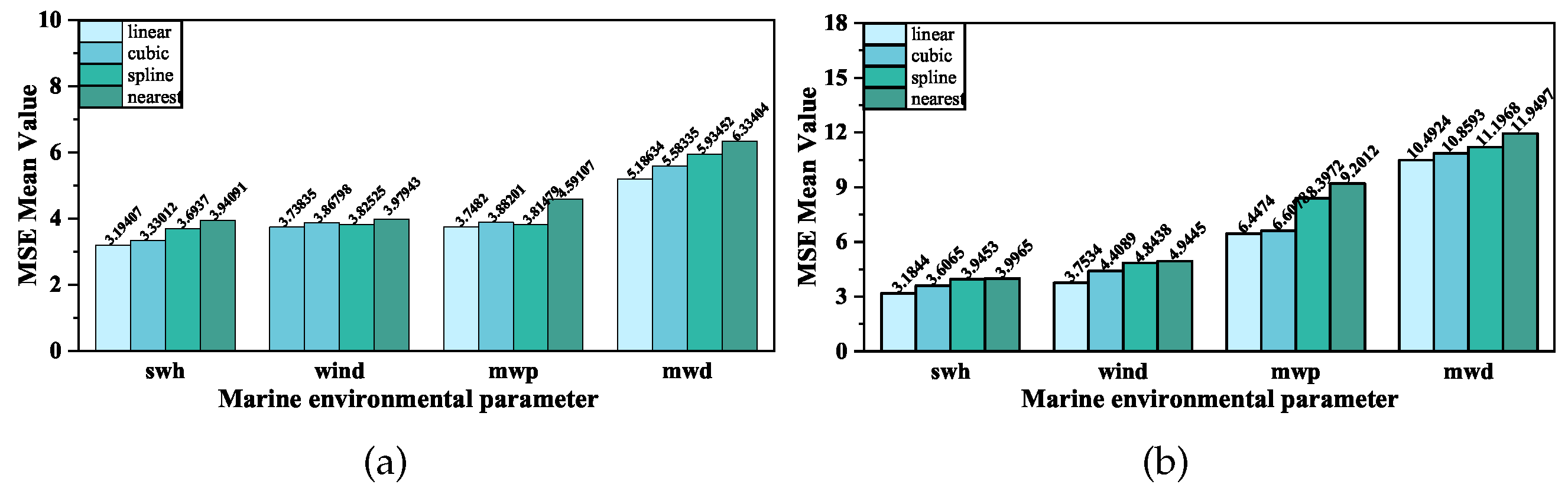

| Marine Environmental Parameter | Number | Resolution | Data Size |
|---|---|---|---|
| wind | 8186 | 0.25° | |
| swh | 8186 | 0.5° | |
| mwd | 8186 | 0.5° | |
| mwp | 8186 | 0.5° |
| Marine Environmental Parameter | Number | Resolution | Data Size with a Downsampling Factor of 2 | Data Size with a Downsampling Factor of 4 |
|---|---|---|---|---|
| wind | 8186 | 0.25° | ||
| swh | 8186 | 0.5° | ||
| mwd | 8186 | 0.5° | ||
| mwp | 8186 | 0.5° |
| Model | MSE | PSNR | SSIM |
|---|---|---|---|
| Baseline model | 4.575 | 41.527 | 0.915 |
| Model with GAM Module | 3.467 | 42.723 | 0.932 |
| to (HOA Modules) | 3.512 | 42.675 | 0.927 |
| to (HOA Modules) | 3.438 | 42.767 | 0.928 |
| (HOA Module) | 3.478 | 42.718 | 0.944 |
| (HOA Module) | 3.268 | 42.988 | 0.947 |
| (HOA Module) | 2.978 | 43.391 | 0.929 |
| Our model (GAM and HOA Module) | 2.299 | 44.515 | 0.934 |
| Data | Scale Factor | Evaluation Criteria | Traditional Method | Our Method | |
|---|---|---|---|---|---|
| Linear Interpolation | Alternate Downsampling | Average Downsampling | |||
| WS | 2× | MSE | 9.285 | 0.713 | 0.734 |
| PSNR | 38.453 | 49.598 | 49.471 | ||
| SSIM | 0.711 | 0.981 | 0.977 | ||
| 4× | MSE | 9.472 | 0.755 | 0.817 | |
| PSNR | 38.367 | 49.362 | 49.015 | ||
| SSIM | 0.703 | 0.961 | 0.957 | ||
| SWH | 2× | MSE | 1.711 | 1.339 | 1.319 |
| PSNR | 45.798 | 46.864 | 46.928 | ||
| SSIM | 0.948 | 0.957 | 0.957 | ||
| 4× | MSE | 2.31 | 1.894 | 1.883 | |
| PSNR | 44.5 | 45.358 | 45.386 | ||
| SSIM | 0.926 | 0.942 | 0.942 | ||
| MWD | 2× | MSE | 3.661 | 3.035 | 3.693 |
| PSNR | 42.501 | 43.309 | 42.457 | ||
| SSIM | 0.910 | 0.930 | 0.921 | ||
| 4× | MSE | 3.798 | 3.715 | 3.222 | |
| PSNR | 42.335 | 42.431 | 43.049 | ||
| SSIM | 0.909 | 0.918 | 0.913 | ||
| MWP | 2× | MSE | 3.862 | 3.162 | 2.299 |
| PSNR | 42.263 | 43.148 | 44.515 | ||
| SSIM | 0.93 | 0.940 | 0.934 | ||
| 4× | MSE | 3.951 | 3.741 | 3.645 | |
| PSNR | 42.172 | 42.401 | 42.513 | ||
| SSIM | 0.939 | 0.936 | 0.944 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Y.; Ma, L.; Zhang, Y.; Wu, Z.; Wu, J.; Zhang, J.; Zhang, X. Research on High-Resolution Reconstruction of Marine Environmental Parameters Using Deep Learning Model. Remote Sens. 2023, 15, 3419. https://doi.org/10.3390/rs15133419
Hu Y, Ma L, Zhang Y, Wu Z, Wu J, Zhang J, Zhang X. Research on High-Resolution Reconstruction of Marine Environmental Parameters Using Deep Learning Model. Remote Sensing. 2023; 15(13):3419. https://doi.org/10.3390/rs15133419
Chicago/Turabian StyleHu, Yaning, Liwen Ma, Yushi Zhang, Zhensen Wu, Jiaji Wu, Jinpeng Zhang, and Xiaoxiao Zhang. 2023. "Research on High-Resolution Reconstruction of Marine Environmental Parameters Using Deep Learning Model" Remote Sensing 15, no. 13: 3419. https://doi.org/10.3390/rs15133419
APA StyleHu, Y., Ma, L., Zhang, Y., Wu, Z., Wu, J., Zhang, J., & Zhang, X. (2023). Research on High-Resolution Reconstruction of Marine Environmental Parameters Using Deep Learning Model. Remote Sensing, 15(13), 3419. https://doi.org/10.3390/rs15133419