Hierarchical Refined Composite Multi-Scale Fractal Dimension and Its Application in Feature Extraction of Ship-Radiated Noise
Abstract
1. Introduction
2. Methodology
2.1. Fractal Dimension
2.2. Refined Composite Multi-Scale Fractal Dimension
- (1)
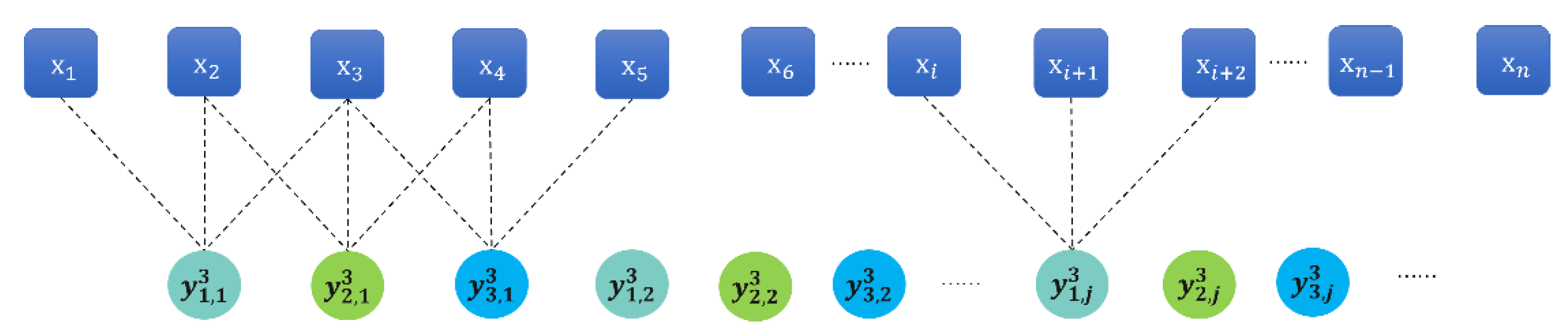
- For a given a time series , convert it to coarse-grained sequence as follows:where represents the scale factor, is the integer of representing the length of the coarse-grained series, is the - element of the - subsequence.
- (2)
- For each subsequence , the value is calculated according to the steps in Section 2.1.
- (3)
- The average value of FD of all coarse-grained series is taken as the result of RCMFD:where represents the original time series, and represents the scale factor. Taking as an example, a schematic diagram of the coarse granulation process is given in Figure 2, and Figure 3 presents the flow calculation chart of RCMFD.
2.3. Hierarchical Refined Composite Multi-Scale Fractal Dimension
- (1)
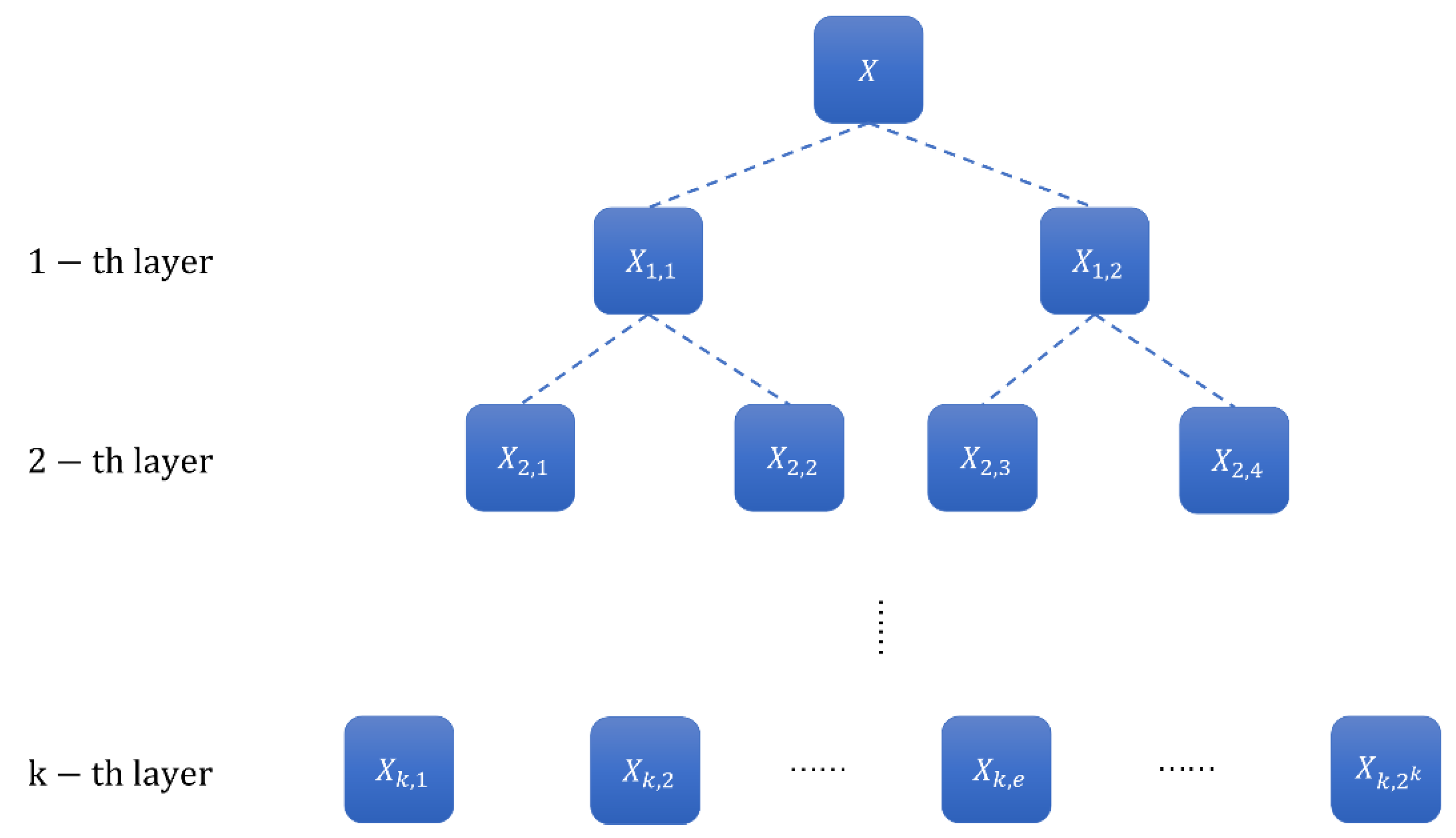
- For a given time series , the average operator and difference operator are, respectively, defined as:where is the positive integer, and and denote the low-frequency and high-frequency components of the original time series in the first level decomposition, respectively.
- (2)
- Construct an n-dimensional vector [] and an integer value , where {} represents the average operator or difference operator of the - layer. Therefore, the hierarchical component of the - node of the - layer can be expressed as:
- (3)
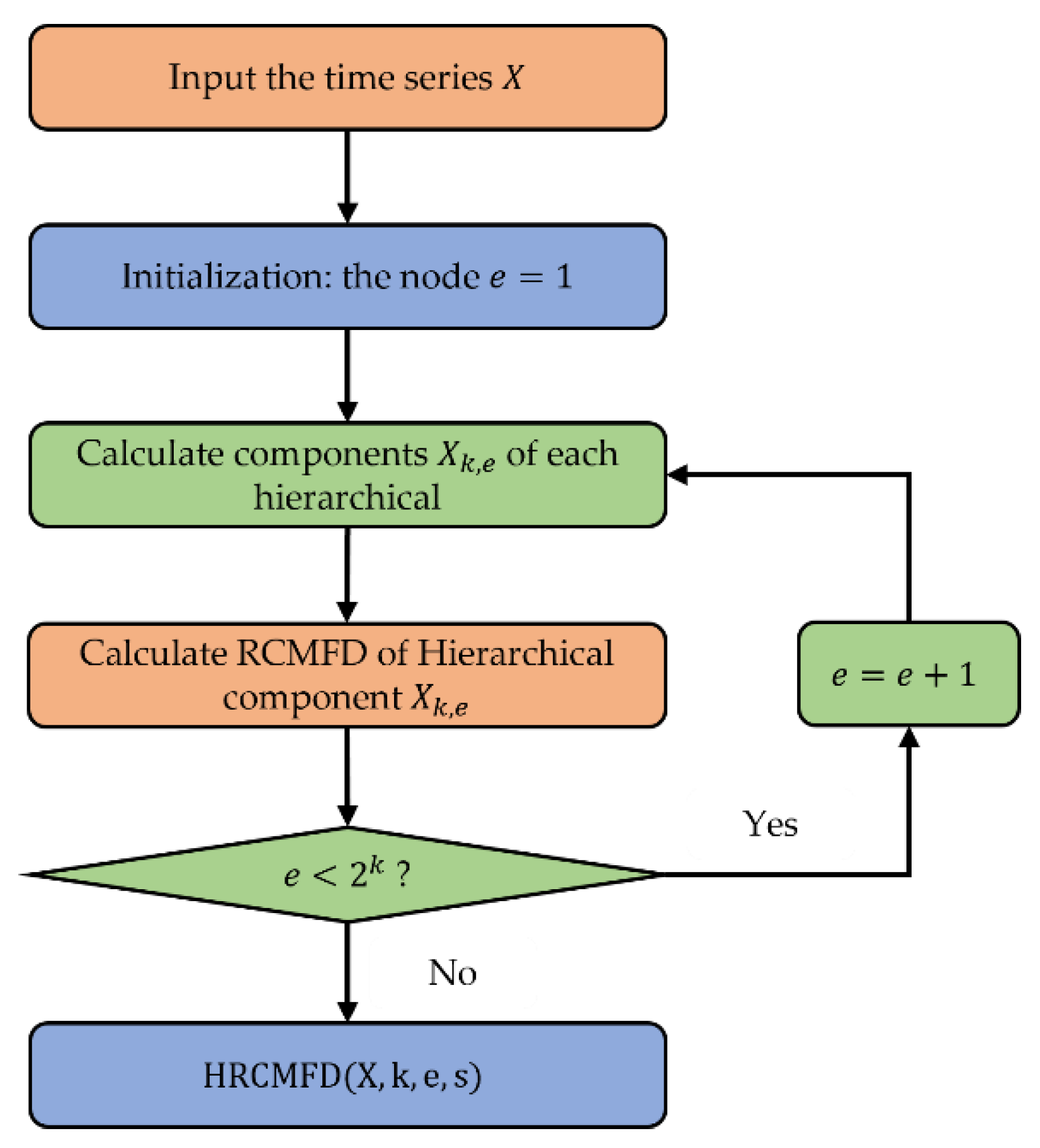
- According to the definition of RCMFD, calculate the RCMFD of each improved coarse grain series , so the final HRCMFD can be obtained by the following:where is the original time series, is the decomposition layers, is the node, and is the scale factor. Figure 4 displays a schematic chart of hierarchical decomposition, and the flow calculation chart of HRCMFD is given in Figure 5.
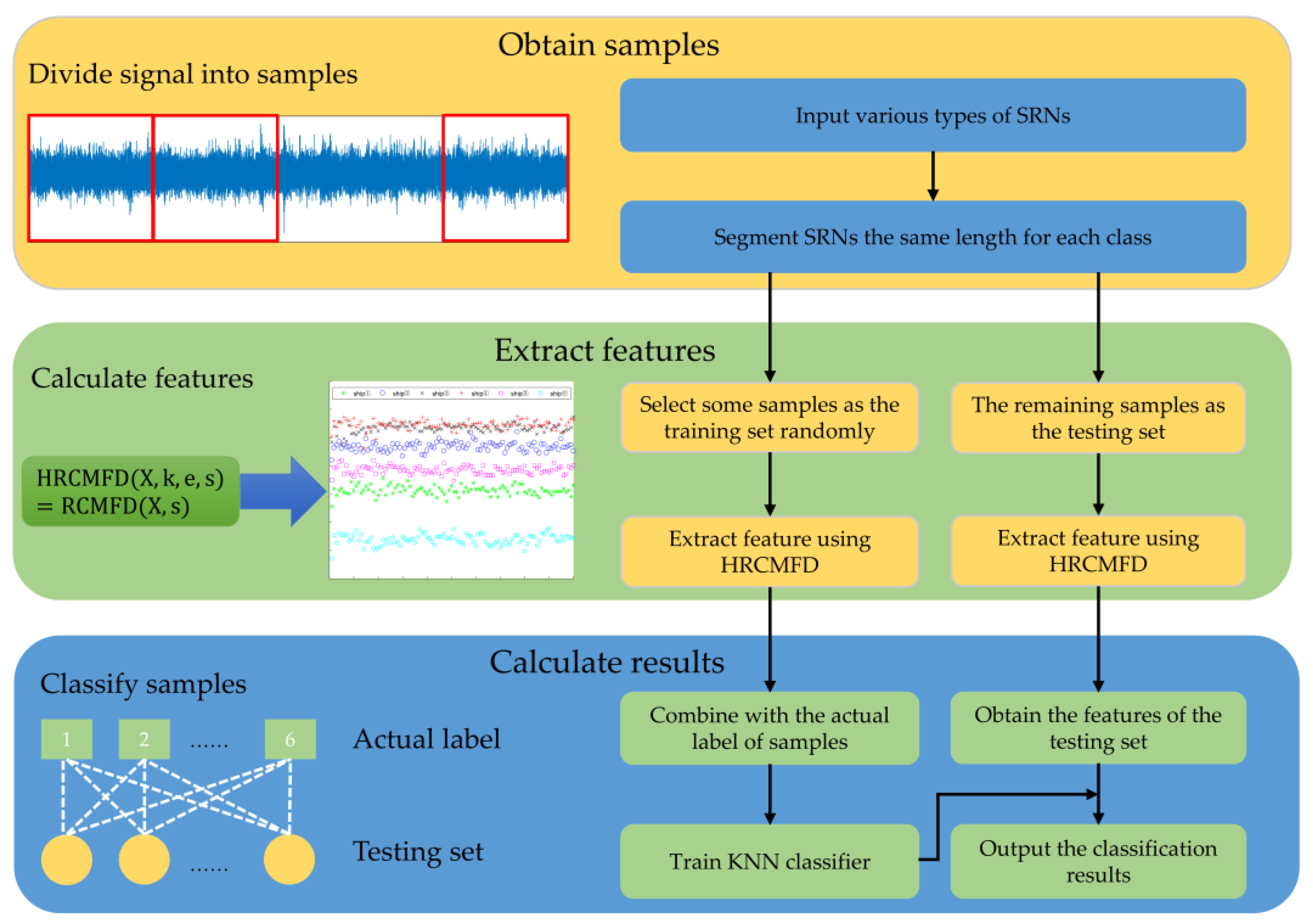
3. Feature Extraction Method for SRN
4. Analysis of Simulated Signals
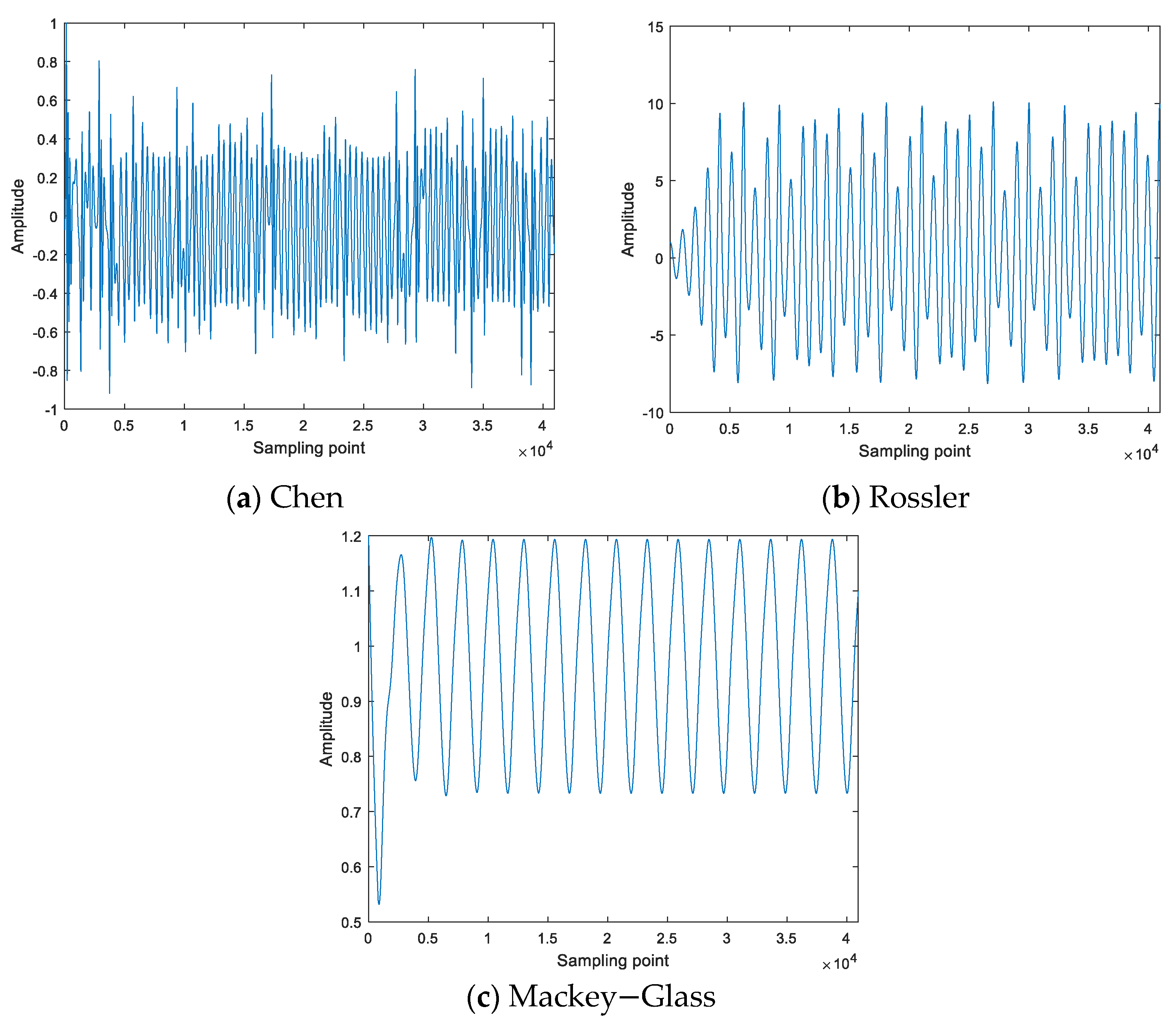
4.1. Three Types of Simulated Signals
- (1)
- Chen signal
- (2)
- Rossler signal
- (3)
- Mackey–Glass signal
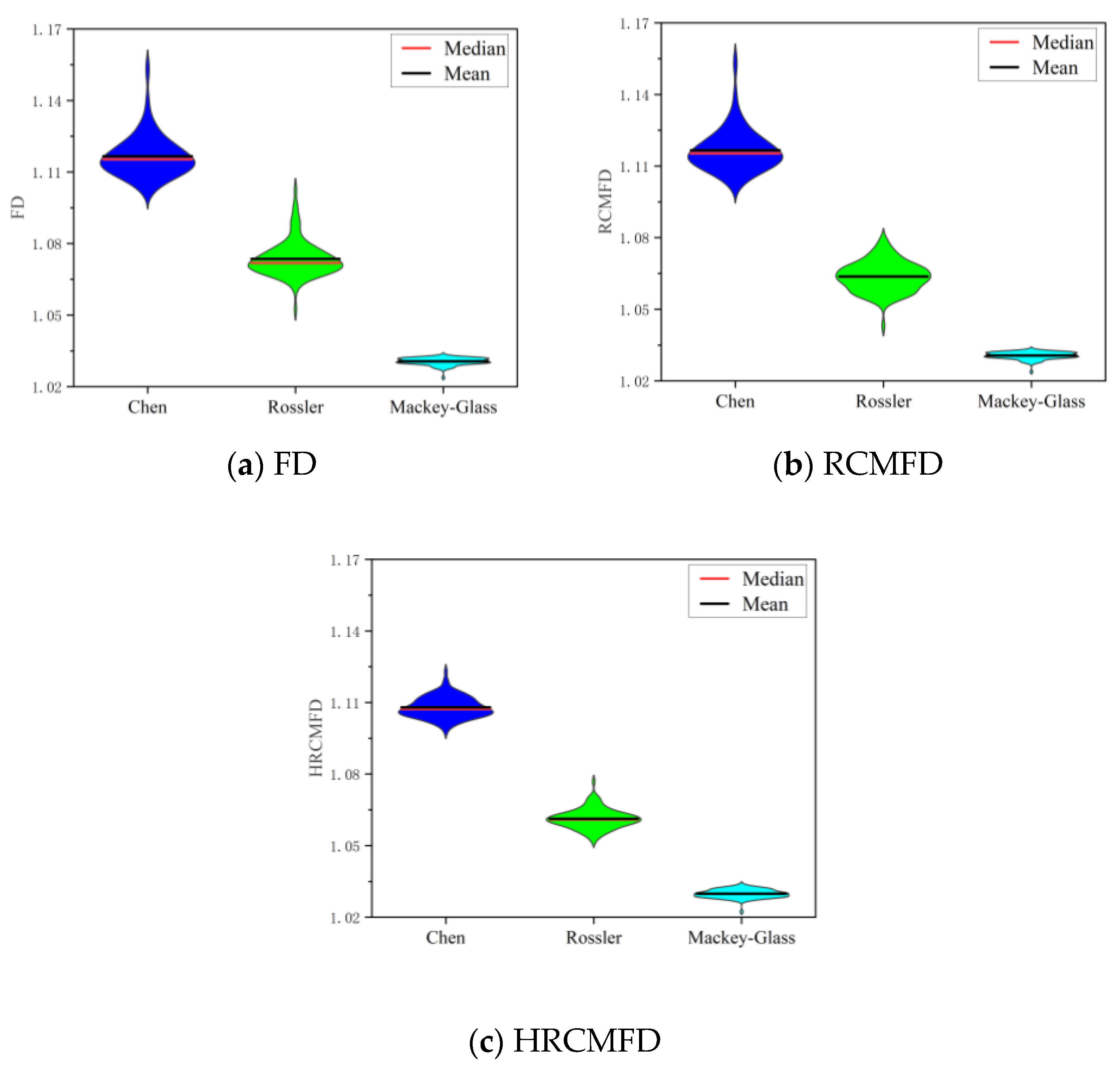
4.2. Single Feature Characterization of Simulated Signals
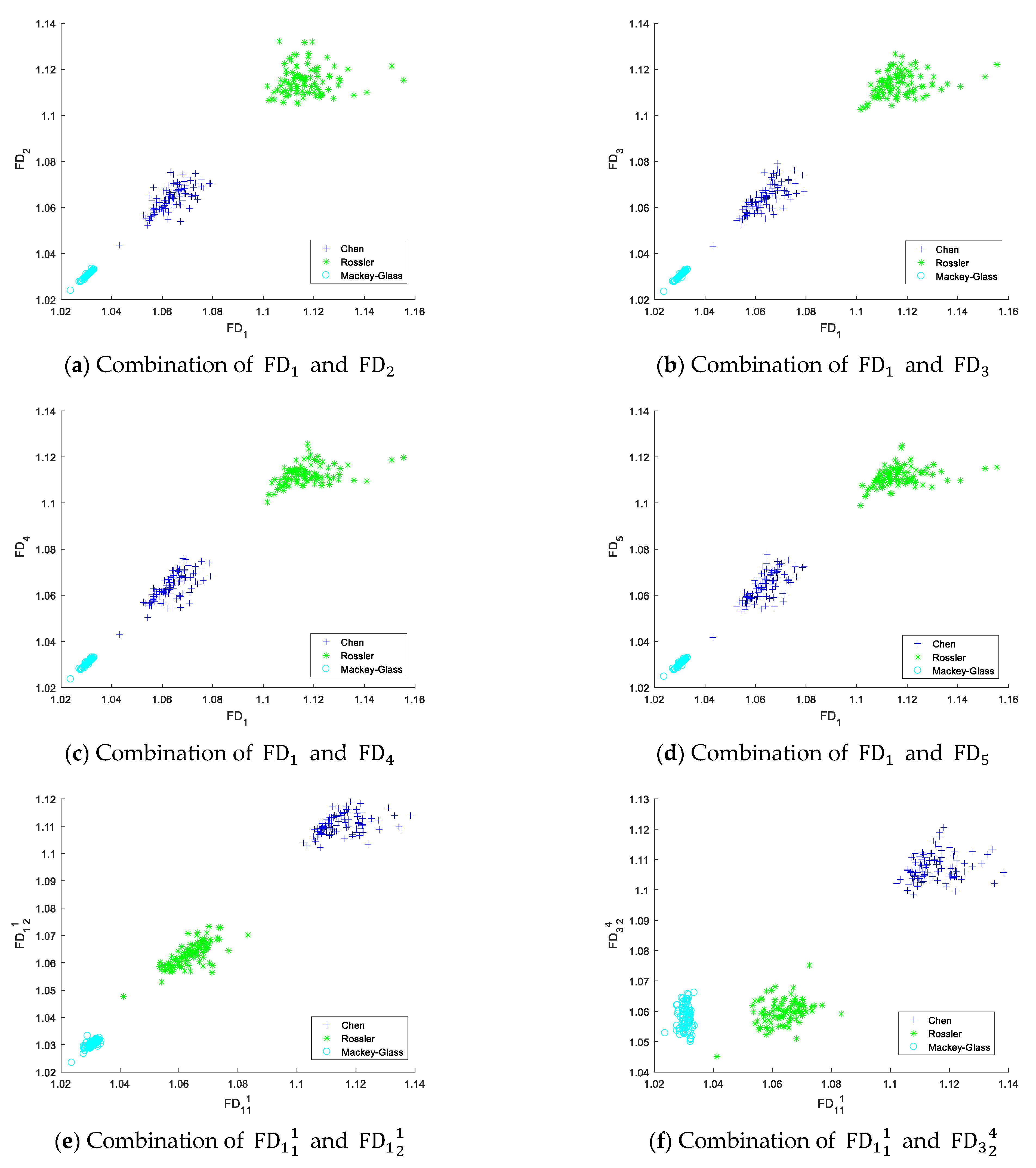
4.3. Multi-Feature Characterization of Simulated Signals
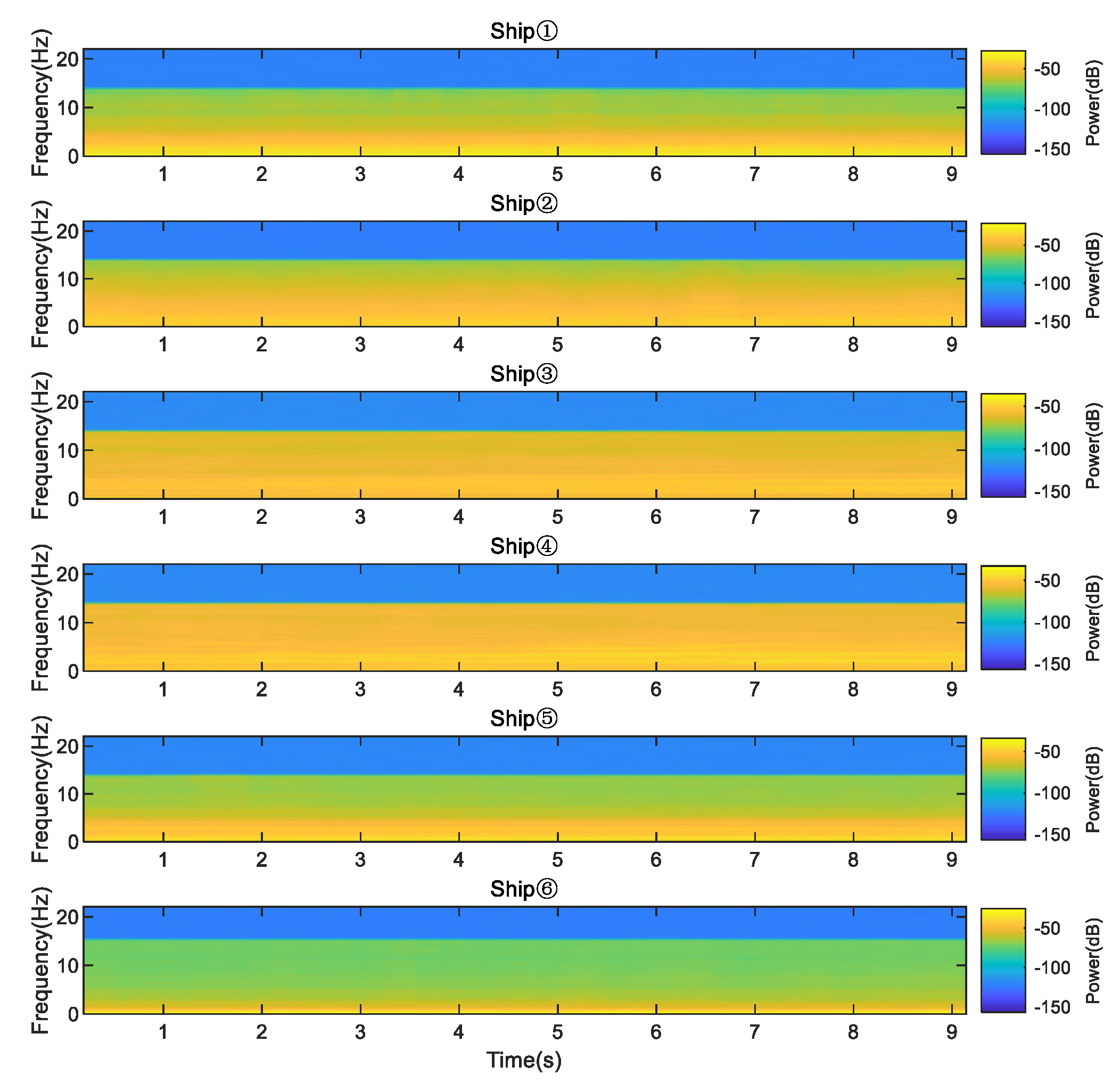
5. Feature Extraction of SRN
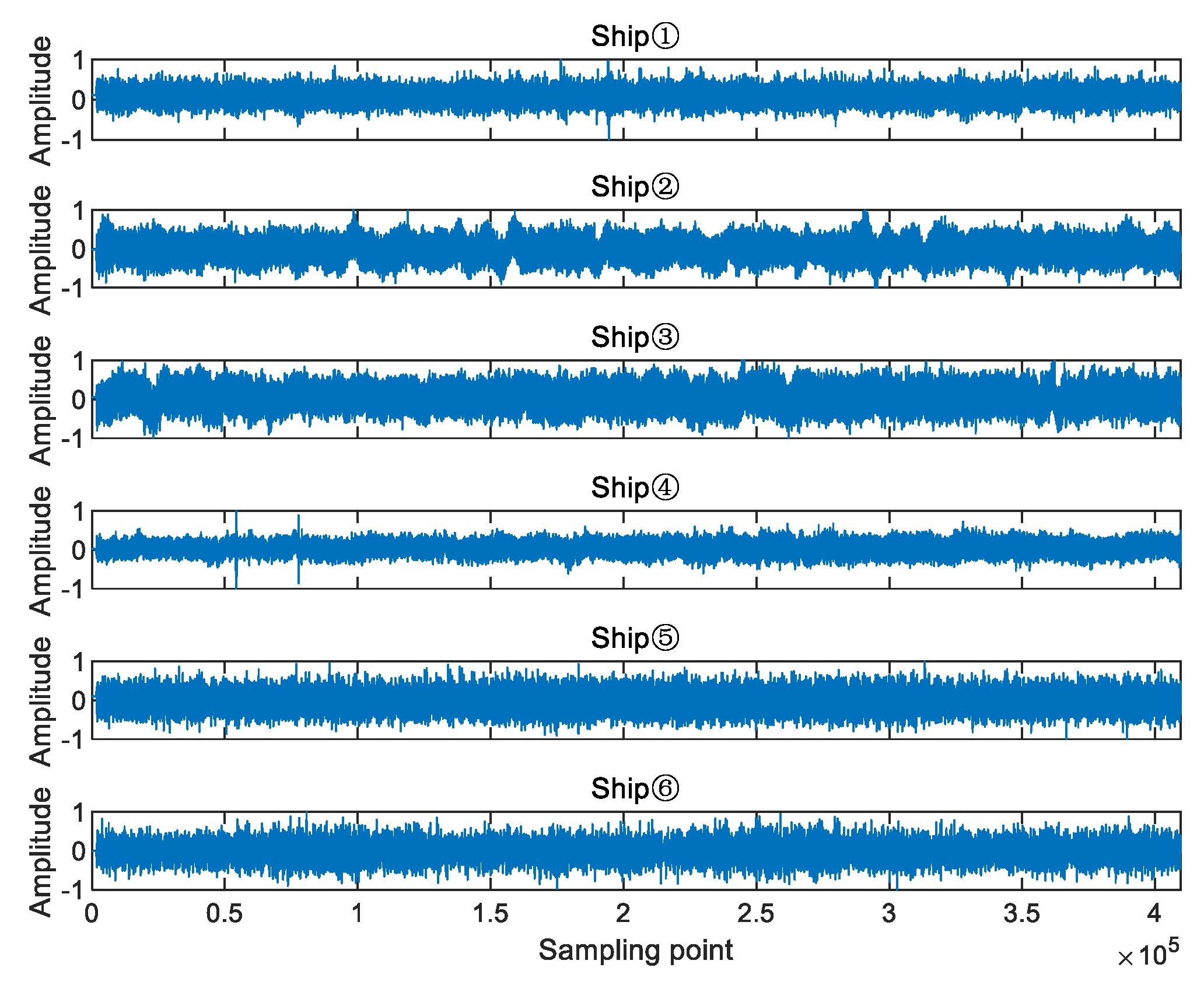
5.1. Data Sources of SRNs and Parameter Settings of Nonlinear Dynamic Indexes
5.2. Feature Extraction Using Indexes Based on RCMP
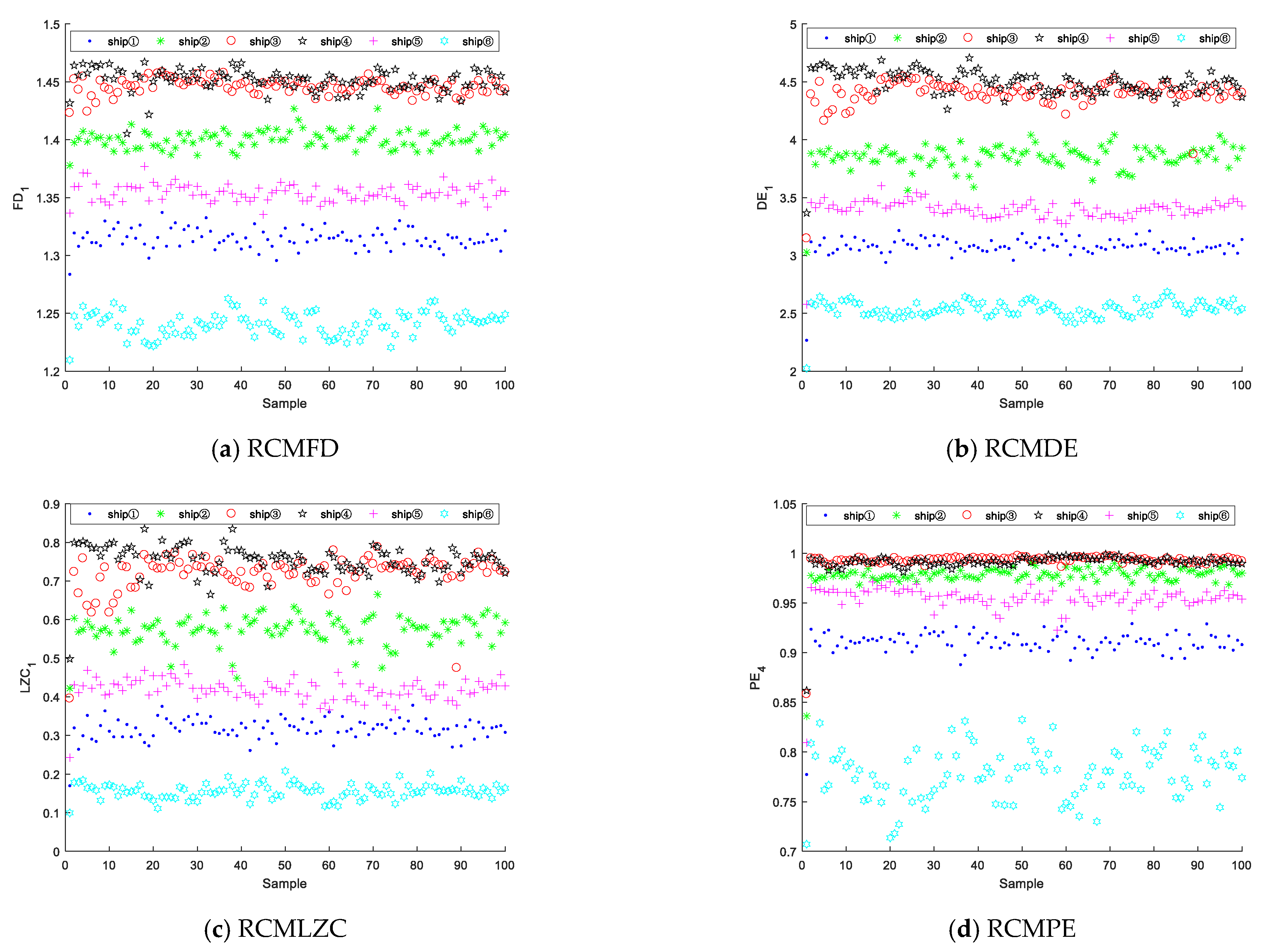
5.2.1. Single Feature Extraction and Classification
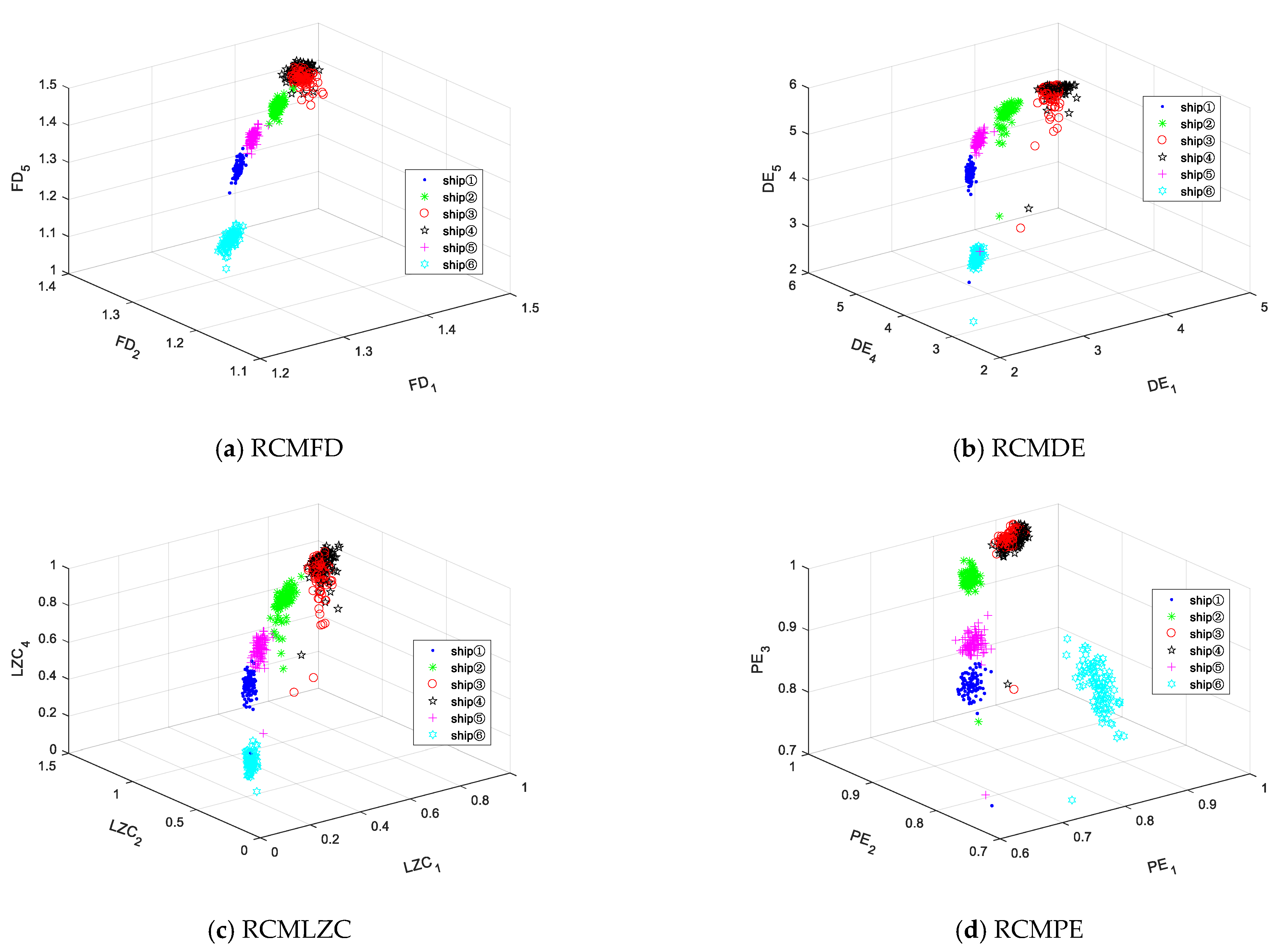
5.2.2. Double-Feature Extraction and Classification
5.2.3. Multi-Feature Extraction and Classification
5.3. Feature Extraction Using Indexes Based on HRCMP
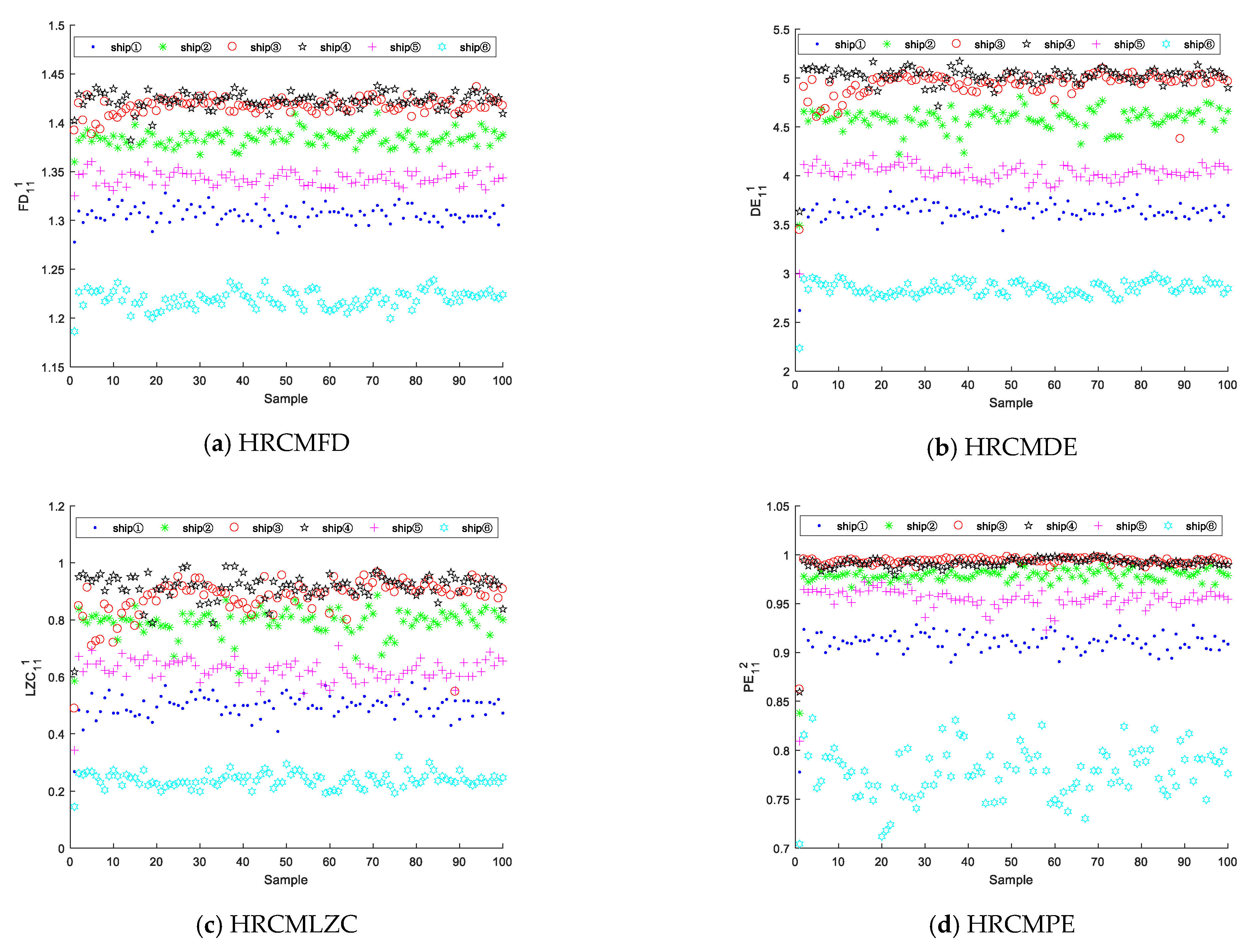
5.3.1. Single-Feature Extraction and Classification
5.3.2. Double-Feature Extraction and Classification
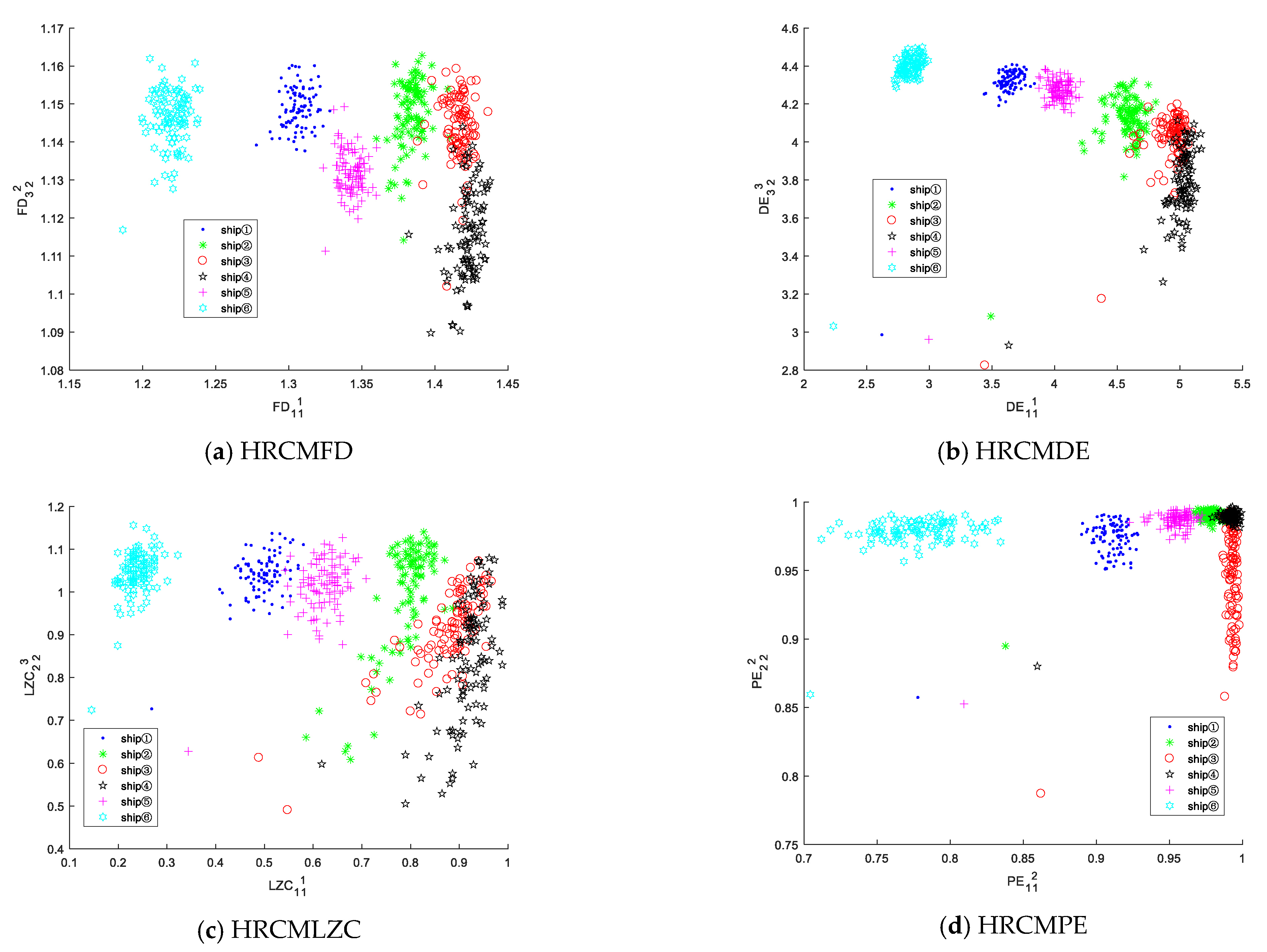
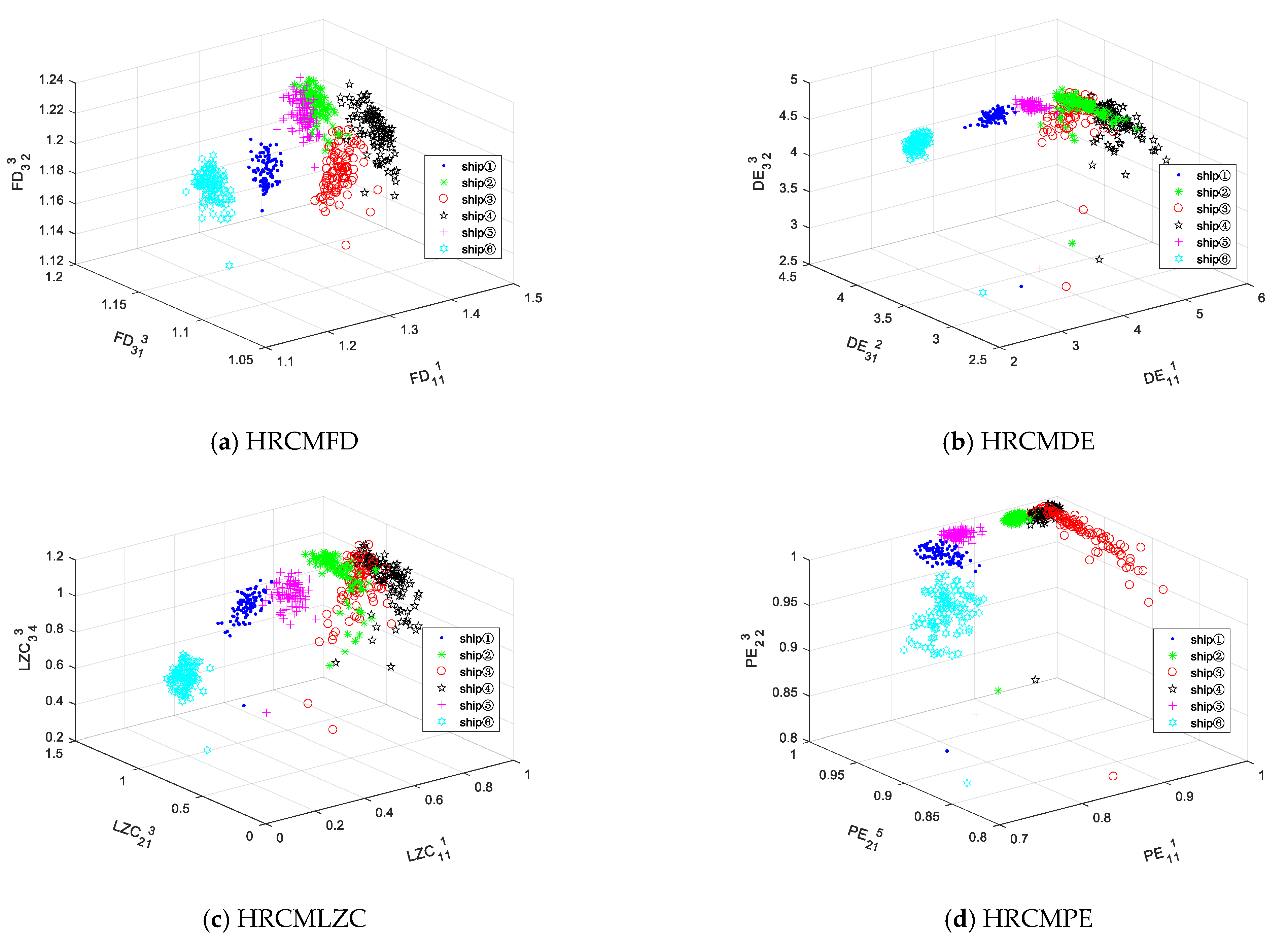
5.3.3. Multi-Feature Extraction and Classification
6. Discussion
7. Conclusions
- (1)
- RCMFD and HRCMFD are proposed as two new nonlinear dynamic indexes which enhance the signal characterization ability of FD from the scale and frequency. The simulation results also prove their superiority in identifying simulated signals;
- (2)
- The multi-feature extraction method based on RCMFD is proposed, which can reflect SRN information at multi-scales and extract features of SRNs more effectively. The experimental results show that the proposed feature-extraction method is superior to the other three methods based on RCMDE, RCMLZC, and RCMPE;
- (3)
- We propose a multi-feature extraction method based on HRCMFD for SRNs, which can extract multi-scale SRN features in each sub-frequency band and reflect SRN information more comprehensively. The experimental results indicate that the HARR of the proposed feature-extraction method for six SRNs is higher than that of the other seven methods, and the recognition rate is close to 100% when taking the number of five features.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bernardini, M.; Fredianelli, L.; Fidecaro, F.; Gagliardi, P.; Nastasi, M.; Licitra, G. Noise Assessment of Small Vessels for Action Planning in Canal Cities. Environments 2019, 6, 31. [Google Scholar] [CrossRef]
- Fredianelli, L.; Nastasi, M.; Bernardini, M.; Fidecaro, F.; Licitra, G. Pass-by characterization of noise emitted by different categories of seagoing ships in ports. Sustainability 2020, 12, 1740. [Google Scholar] [CrossRef]
- Fredianelli, L.; Bolognese, M.; Fidecaro, F.; Licitra, G. Classification of noise sources for port area noise mapping. Environments 2021, 8, 12. [Google Scholar] [CrossRef]
- Li, Y.; Tang, B.; Jiao, S. SO-slope entropy coupled with SVMD: A novel adaptive feature extraction method for ship-radiated noise. Ocean Eng. 2023, 280, 114677. [Google Scholar] [CrossRef]
- Li, Y.; Tang, B.; Yi, Y. A novel complexity-based mode feature representation for feature extraction of ship-radiated noise using VMD and slope entropy. Appl. Acoust. 2022, 196, 108899. [Google Scholar] [CrossRef]
- Yuan, F.; Ke, X.; Cheng, E. Joint Representation and Recognition for Ship-Radiated Noise Based on Multimodal Deep Learning. J. Mar. Sci. Eng. 2019, 7, 380. [Google Scholar] [CrossRef]
- Wang, S.; Zeng, X. Robust underwater noise targets classification using auditory inspired time–frequency analysis. Appl. Acoust. 2014, 78, 68–76. [Google Scholar] [CrossRef]
- Gassmann, M.; Wiggins, S.M.; Hildebrand, J.A. Deep-water measurements of container ship-radiated noise signatures and di-rectionality. J. Acoust. Soc. Am. 2017, 142, 1563. [Google Scholar] [CrossRef]
- Yan, J.; Sun, H.; Chen, H.; Junejo, N.U.R.; Cheng, E. Resonance-Based Time-Frequency Manifold for Feature Extraction of Ship-Radiated Noise. Sensors 2018, 18, 936. [Google Scholar] [CrossRef]
- Lin, L.; Chu, F. Feature extraction of AE characteristics in offshore structure model using Hilbert–Huang transform. Measurement 2011, 44, 46–54. [Google Scholar] [CrossRef]
- Bracewell, R.N. The Fourier Transform and Its Applications; McGraw-Hill: New York, NY, USA, 1986. [Google Scholar]
- Hu, Q.; Li, Y.; Sun, X.; Chen, M.; Bu, Q.; Gong, B. Integrating test device and method for creep failure and ultrasonic response of methane hydrate-bearing sediments. Rev. Sci. Instrum. 2023, 94, 025105. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Li, Y.; Chen, J. Prediction of underwater acoustic signal based on neural network. Microprocessors 2006, 27, 47–48. [Google Scholar]
- Liu, S.; Fu, X.; Xu, H.; Zhang, J.; Zhang, A.; Zhou, Q.; Zhang, H. A Fine-Grained Ship-Radiated Noise Recognition System Using Deep Hybrid Neural Networks with Multi-Scale Features. Remote. Sens. 2023, 15, 2068. [Google Scholar] [CrossRef]
- Xie, D.; Hong, S.; Yao, C. Optimized Variational Mode Decomposition and Permutation Entropy with Their Application in Feature Extraction of Ship-Radiated Noise. Entropy 2021, 23, 503. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Geng, B.; Jiao, S. Dispersion entropy-based Lempel-Ziv complexity: A new metric for signal analysis. Chaos Solitons Fractals 2022, 161, 112400. [Google Scholar] [CrossRef]
- Li, Y.; Geng, B.; Tang, B. Simplified coded dispersion entropy: A nonlinear metric for signal analysis. Nonlinear Dyn. 2023, 111, 9327–9344. [Google Scholar] [CrossRef]
- Li, Y.; Gao, P.; Tang, B.; Yi, Y.; Zhang, J. Double Feature Extraction Method of Ship-Radiated Noise Signal Based on Slope Entropy and Permutation Entropy. Entropy 2021, 24, 22. [Google Scholar] [CrossRef]
- Li, Y.; Li, Y.; Chen, Z.; Chen, X. Feature Extraction of Ship-Radiated Noise Based on Permutation Entropy of the Intrinsic Mode Function with the Highest Energy. Entropy 2016, 18, 393. [Google Scholar] [CrossRef]
- Rostaghi, M.; Azami, H. Dispersion Entropy: A Measure for Time-Series Analysis. IEEE Signal Process. Lett. 2016, 23, 610–614. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef]
- Lempel, A.; Ziv, J. On the complexity of finite sequences, Inform. IEEE Trans. Inf. Theory 1976, 22, 75–81. [Google Scholar] [CrossRef]
- Giorgilli, A.; Casati, D.; Sironi, L.; Galgani, L. An efficient procedure to compute fractal dimensions by box counting. Phys. Lett. A 1986, 115, 202–206. [Google Scholar] [CrossRef]
- Li, Y.; Yang, Y.; Li, G.; Xu, M.; Huang, W. A fault diagnosis scheme for planetary gearboxes using modified multi-scale symbolic dynamic entropy and mRMR feature selection. Mech. Syst. Signal Process. 2017, 91, 295–312. [Google Scholar] [CrossRef]
- Li, Y.; Tang, B.; Geng, B.; Jiao, S. Fractional Order Fuzzy Dispersion Entropy and Its Application in Bearing Fault Diagnosis. Fractal Fract. 2022, 6, 544. [Google Scholar] [CrossRef]
- Yeh, C.; Shi, W. Generalized multi-scale Lempel–Ziv complexity of cyclic alternating pattern during sleep. Nonlinear Dyn. 2018, 93, 1899–1910. [Google Scholar] [CrossRef]
- Li, Z.; Li, Y.; Zhang, K.; Guo, J. A Novel Improved Feature Extraction Technique for Ship-Radiated Noise Based on IITD and MDE. Entropy 2019, 21, 1215. [Google Scholar] [CrossRef]
- Mao, X.; Shang, P.; Xu, M. Measuring time series based on multi-scale dispersion Lempel-Ziv complexity and dispersion entropy plane. Chaos Solitons Fractals 2020, 137, 109868. [Google Scholar] [CrossRef]
- Li, Y.; Liu, F.; Wang, S. Multi-scale symbolic Lempel–Ziv: An effective feature extraction approach for fault diagnosis of railway vehicle systems. IEEE Trans. Ind. Inf. 2021, 17, 199–208. [Google Scholar] [CrossRef]
- Ibáñez-Molina, A.; Iglesias-Parro, S.; Soriano, M.; Aznarte, J. Multi-scale Lempel-Ziv complexity for EEG measures. Clin. Neu-Rophysiology 2015, 126, 541–548. [Google Scholar] [CrossRef]
- Humeau, H.; Wu, C.; Wu, S. Refined Composite Multi-scale Permutation Entropy to Overcome Multi-scale Permutation Entropy Length Dependence. IEEE Signal Process. Lett. 2015, 22, 2364–2367. [Google Scholar] [CrossRef]
- Azami, H.; Rostaghi, M.; Abásolo, D.; Escudero, J. Refined Composite Multi-scale Dispersion Entropy and its Application to Biomedical Signals. IEEE Trans. Biomed. Eng. 2017, 64, 2872–2879. [Google Scholar] [PubMed]
- Li, Y.; Wang, S.; Deng, Z. Intelligent fault identification of rotary machinery using refined composite multi-scale Lempel–Ziv complexity. J. Manuf. Syst. 2020, 61, 725–735. [Google Scholar] [CrossRef]
- Li, Y.; Jiao, S.; Geng, B. Refined composite multi-scale fluctuation-based dispersion Lempel–Ziv complexity for signal analysis. ISA Trans. 2023, 133, 273–284. [Google Scholar] [CrossRef]
- Jiang, Y.; Peng, C.-K.; Xu, Y. Hierarchical entropy analysis for biological signals. J. Comput. Appl. Math. 2011, 236, 728–742. [Google Scholar] [CrossRef]
- Zhu, K.; Li, H. A rolling element bearing fault diagnosis approach based on hierarchical fuzzy entropy and support vec-tor machine. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2015, 230, 2314–2322. [Google Scholar] [CrossRef]
- Li, Y.; Xu, M.; Zhao, H.; Huang, W. Hierarchical fuzzy entropy and improved support vector machine based binary tree ap-proach for rolling bearing fault diagnosis. Mech. Mach. Theory 2016, 98, 114–132. [Google Scholar] [CrossRef]
- Yilmaz, A.; Unal, G. Multi-scale Higuchi’s fractal dimension method. Nonlinear. Dyn. 2020, 101, 1441–1455. [Google Scholar] [CrossRef]
- Tian, Y.; Wang, Z.; Lu, C.; Wang, Z. Bearing diagnostics: A method based on differential geometry. Mech. Syst. Signal Process. 2016, 80, 377–391. [Google Scholar] [CrossRef]
- Jin, Q.; Zhang, H.; Zhang, Y.; Cai, W.; Chi, M. An improved parallel MDBN with AVMD for nonlinear system modeling. IEEE Access 2020, 8, 18408–18419. [Google Scholar] [CrossRef]
- Godó, B.; Nagy, Á. Characterization of Rössler and Duffing maps with Rényi entropy and generalized complexity measures. J. Physics Conf. Ser. 2013, 410, 12090. [Google Scholar] [CrossRef]
- National Park Service. Available online: https://www.nps.gov/glba/learn/nature/soundclips (accessed on 8 May 2023).



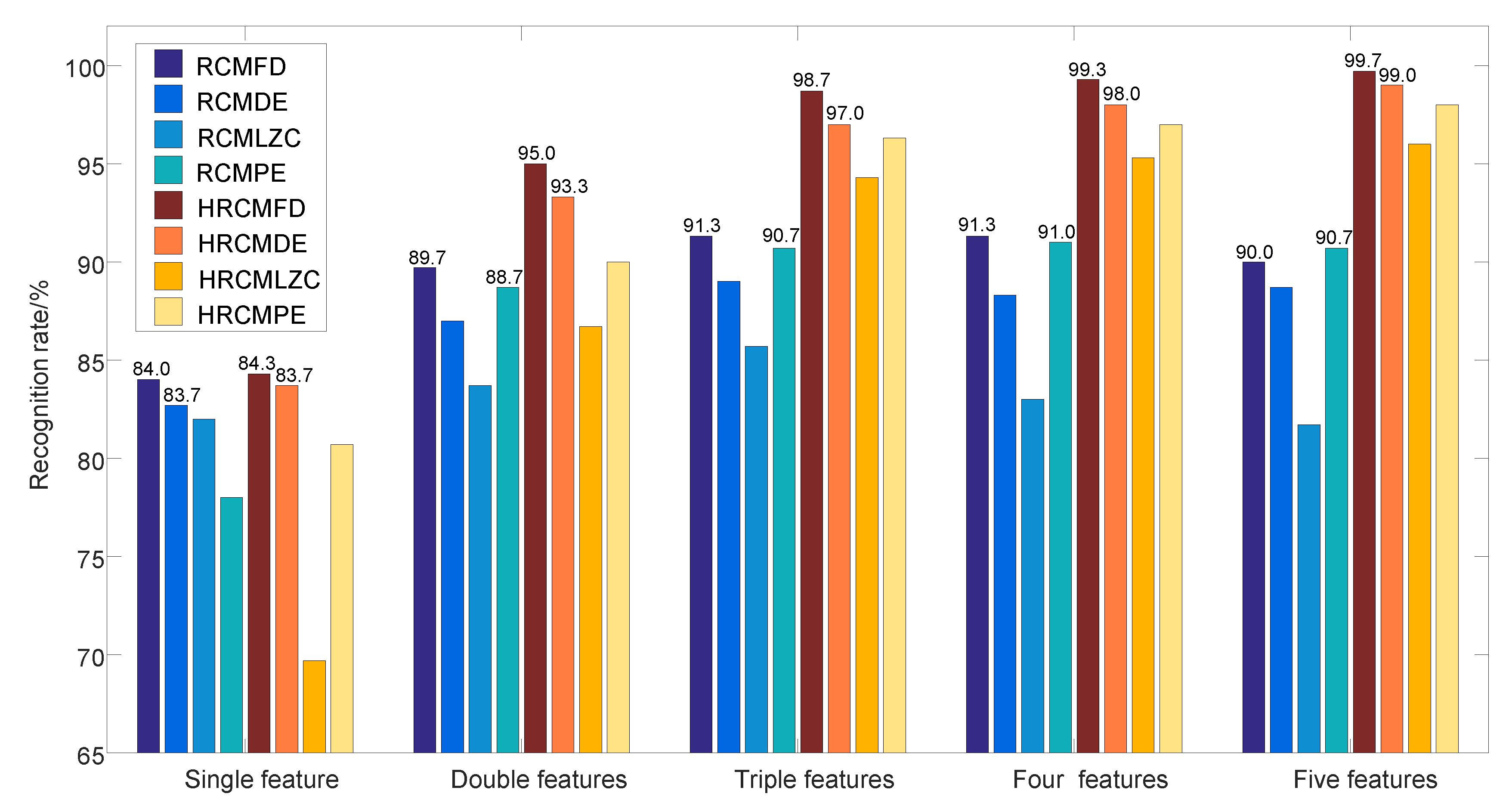
| Nonlinear Dynamic Index | Embedding Dimension | Time Delay | Category Number | Scale Factor | Decomposition Level |
|---|---|---|---|---|---|
| RCMFD | - | - | - | 5 | 3 |
| RCMDE | 3 | 1 | 6 | 5 | 3 |
| RCMLZC | - | - | - | 5 | 3 |
| RCMPE | 3 | 1 | - | 5 | 3 |
| HRCMFD | - | - | - | 5 | 3 |
| HRCMDE | 3 | 1 | 6 | 5 | 3 |
| HRCMLZC | - | - | - | 5 | 3 |
| HRCMPE | 3 | 1 | - | 5 | 3 |
| Nonlinear Dynamic Index | SF | Six Types of SRNs | HARR | |||||
|---|---|---|---|---|---|---|---|---|
| Ship① | Ship② | Ship③ | Ship④ | Ship⑤ | Ship⑥ | |||
| RCMFD | 100% | 92% | 54% | 62% | 96% | 100% | 84.0% | |
| RCMDE | 98% | 98% | 54% | 48% | 98% | 100% | 82.7% | |
| RCMLZC | 96% | 92% | 64% | 46% | 94% | 100% | 82.0% | |
| RCMPE | 98% | 76% | 60% | 38% | 96% | 100% | 78.0% | |
| Nonlinear Dynamic Index | SF | Six Types of SRNs | HARR | |||||
|---|---|---|---|---|---|---|---|---|
| Ship① | Ship② | Ship③ | Ship④ | Ship⑤ | Ship⑥ | |||
| RCMFD | & | 100% | 94% | 64% | 84% | 96% | 100% | 89.7% |
| RCMDE | & | 98% | 98% | 62% | 70% | 94% | 100% | 87.0% |
| RCMLZC | & | 96% | 96% | 56% | 58% | 96% | 100% | 83.7% |
| RCMPE | & | 100% | 98% | 80% | 60% | 96% | 98% | 88.7% |
| Nonlinear Dynamic Index | HARR/SF | Number of Extracted Features | ||
|---|---|---|---|---|
| Three | Four | Five | ||
| RCMFD | HARR | 91.3% | 91.3% | 90.0% |
| SF combination | & & | && | && | |
| RCMDE | HARR | 89.0% | 88.3% | 88.7% |
| SF combination | & & | && & | && & | |
| RCMLZC | HARR | 85.7% | 83.0% | 81.7% |
| SF combination | & & | &,& & | && && | |
| RCMPE | HARR | 90.7% | 91.0% | 90.7% |
| SF combination | & & | && & | && && | |
| Nonlinear Dynamic Index | Chosen Feature | Six Types of SRNs | HARR | |||||
|---|---|---|---|---|---|---|---|---|
| Ship① | Ship② | Ship③ | Ship④ | Ship⑤ | Ship⑥ | |||
| HRCMFD | 96% | 98% | 64% | 48% | 100% | 100% | 84.3% | |
| HRCMDE | 98% | 92% | 52% | 62% | 98% | 100% | 83.7% | |
| HRCMLZC | 88% | 94% | 48% | 14% | 66% | 100% | 69..7% | |
| HRCMPE | 98% | 96% | 60% | 42% | 88% | 100% | 80.7% | |
| Nonlinear Dynamic Index | Chosen Features | Six Types of SRNs | HARR | |||||
|---|---|---|---|---|---|---|---|---|
| Ship① | Ship② | Ship③ | Ship④ | Ship⑤ | Ship⑥ | |||
| HRCMFD | & | 100% | 98% | 92% | 90% | 100% | 100% | 95.0% |
| HRCMDE | & | 96% | 94% | 92% | 80% | 98% | 100% | 93.3% |
| HRCMLZC | & | 88% | 98% | 66% | 72% | 96% | 100% | 86.7% |
| HRCMPE | & | 94% | 98% | 92% | 64% | 92% | 100% | 90.0% |
| Nonlinear Dynamic Index | HARR/Chosen Features | Number of Extracted Features | ||
|---|---|---|---|---|
| Three | Four | Five | ||
| HRCMFD | HARR | 98.7% | 99.3% | 99.7% |
| Chosen features | & & | && & | && && | |
| HRCMDE | HARR | 97.0% | 98.0% | 99.0% |
| Chosen features | & & | && & | && && | |
| HRCMLZC | HARR | 94.3% | 95.3% | 96.0% |
| Chosen features | & & | &&& | && && | |
| HRCMPE | HARR | 96.3% | 97.0% | 98.0% |
| Chosen features | && | && & | & && | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Liang, L.; Zhang, S. Hierarchical Refined Composite Multi-Scale Fractal Dimension and Its Application in Feature Extraction of Ship-Radiated Noise. Remote Sens. 2023, 15, 3406. https://doi.org/10.3390/rs15133406
Li Y, Liang L, Zhang S. Hierarchical Refined Composite Multi-Scale Fractal Dimension and Its Application in Feature Extraction of Ship-Radiated Noise. Remote Sensing. 2023; 15(13):3406. https://doi.org/10.3390/rs15133406
Chicago/Turabian StyleLi, Yuxing, Lili Liang, and Shuai Zhang. 2023. "Hierarchical Refined Composite Multi-Scale Fractal Dimension and Its Application in Feature Extraction of Ship-Radiated Noise" Remote Sensing 15, no. 13: 3406. https://doi.org/10.3390/rs15133406
APA StyleLi, Y., Liang, L., & Zhang, S. (2023). Hierarchical Refined Composite Multi-Scale Fractal Dimension and Its Application in Feature Extraction of Ship-Radiated Noise. Remote Sensing, 15(13), 3406. https://doi.org/10.3390/rs15133406








