A Novel Technique for High-Precision Ionospheric VTEC Estimation and Prediction at the Equatorial Ionization Anomaly Region: A Case Study over Haikou Station
Abstract
1. Introduction
2. Materials and Methods
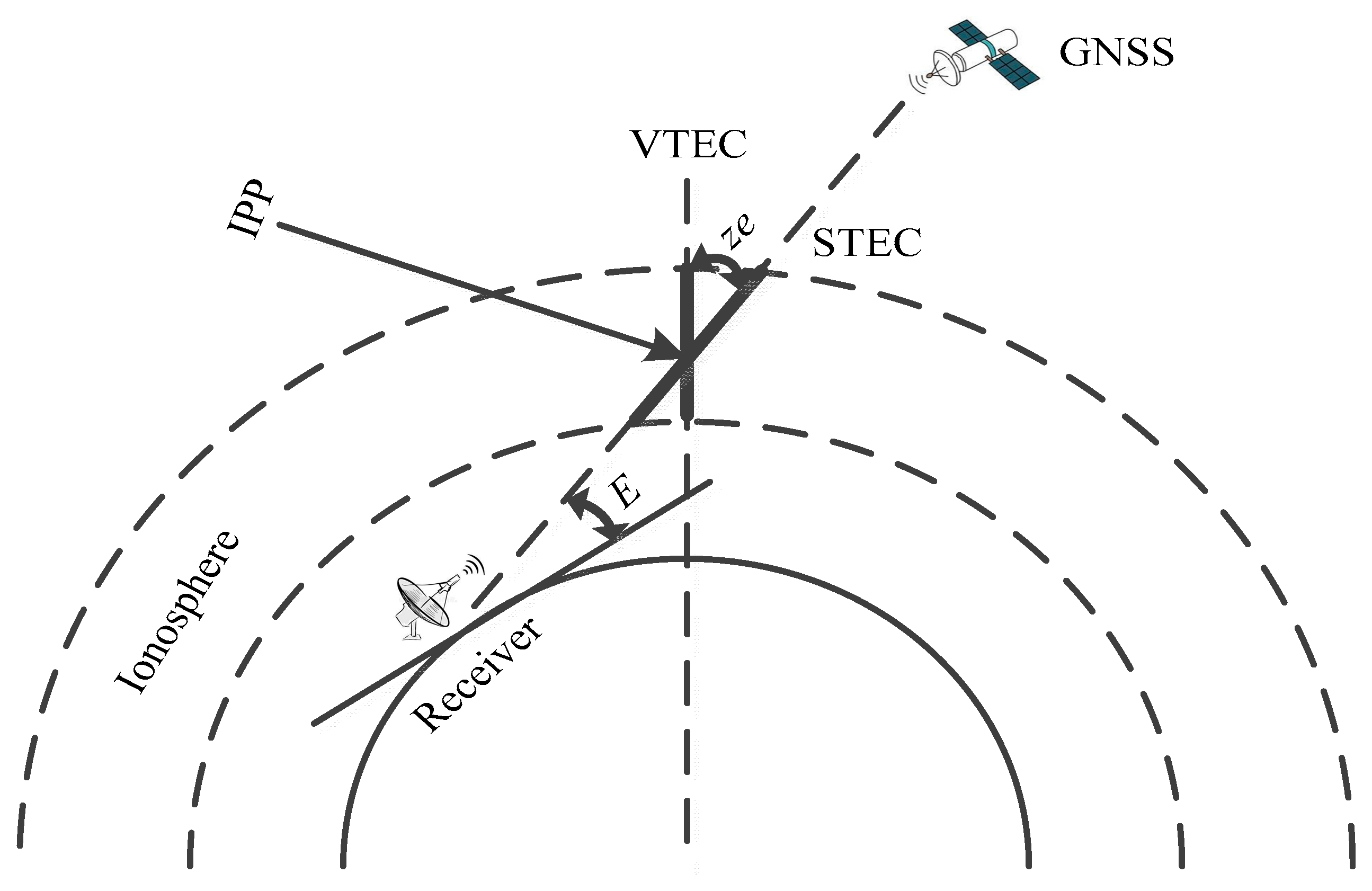
2.1. Ionospheric VTEC Estimation Method
2.2. Ionospheric VTEC Prediction Method
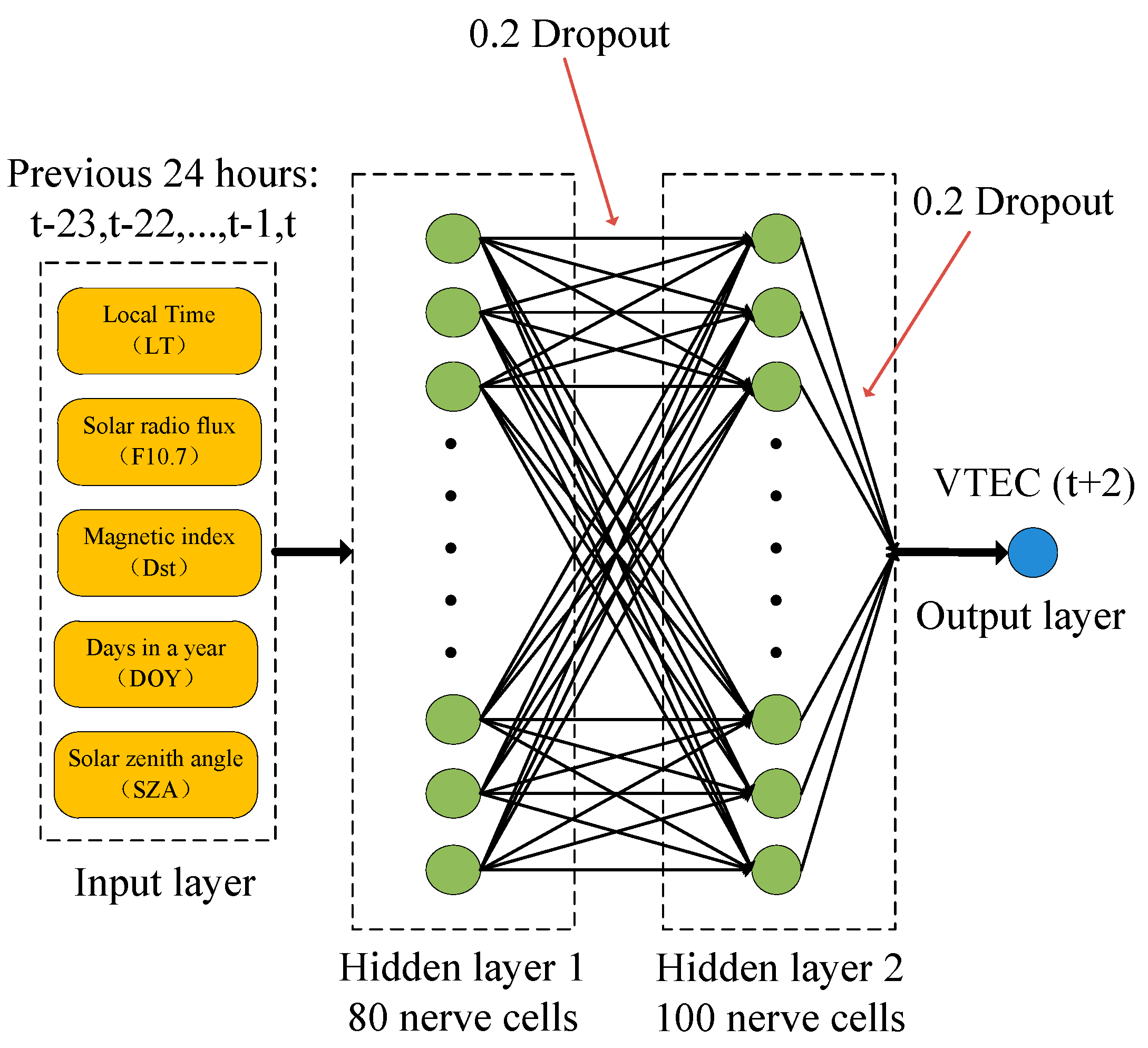
2.2.1. NN Model
2.2.2. LSTM Model
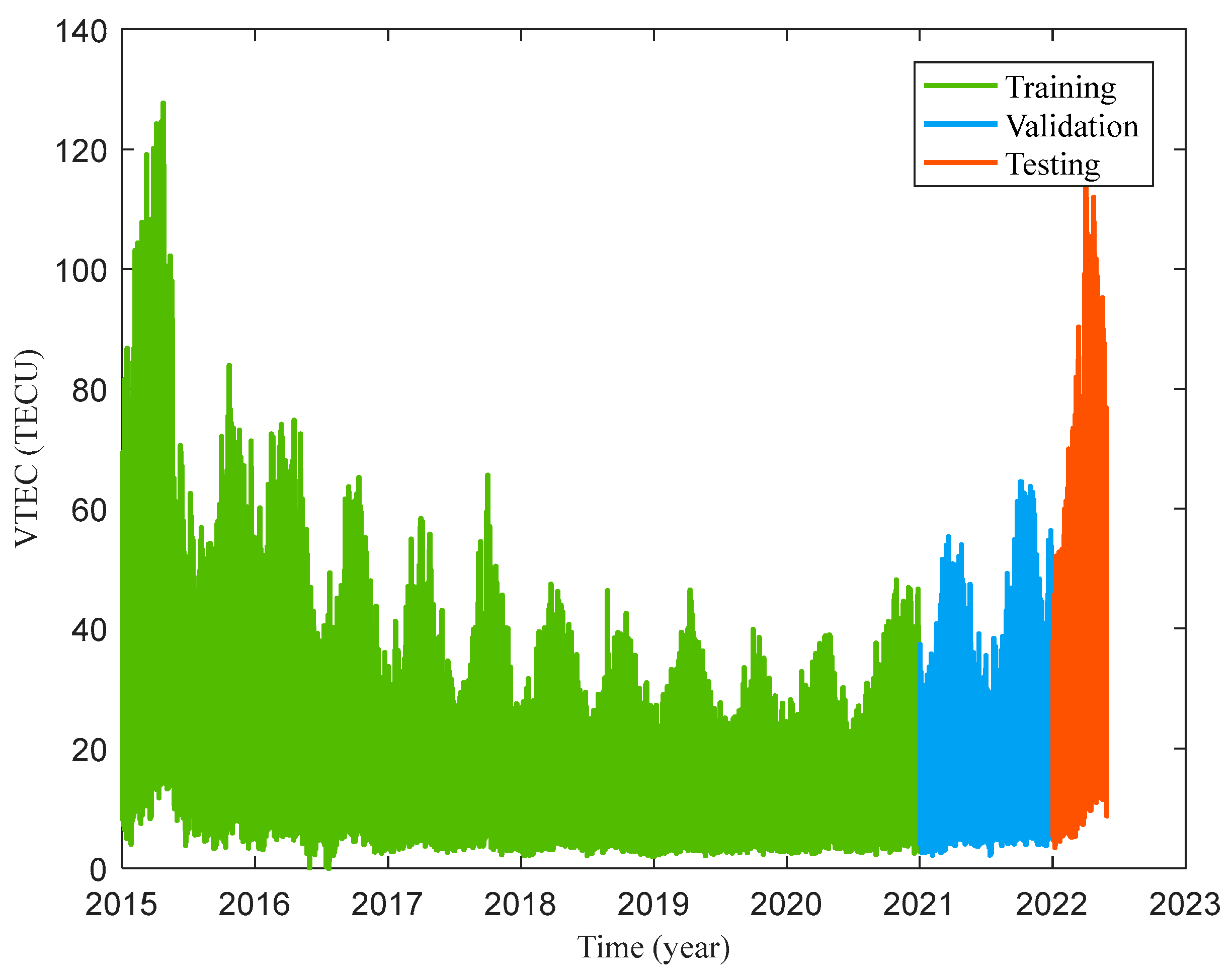
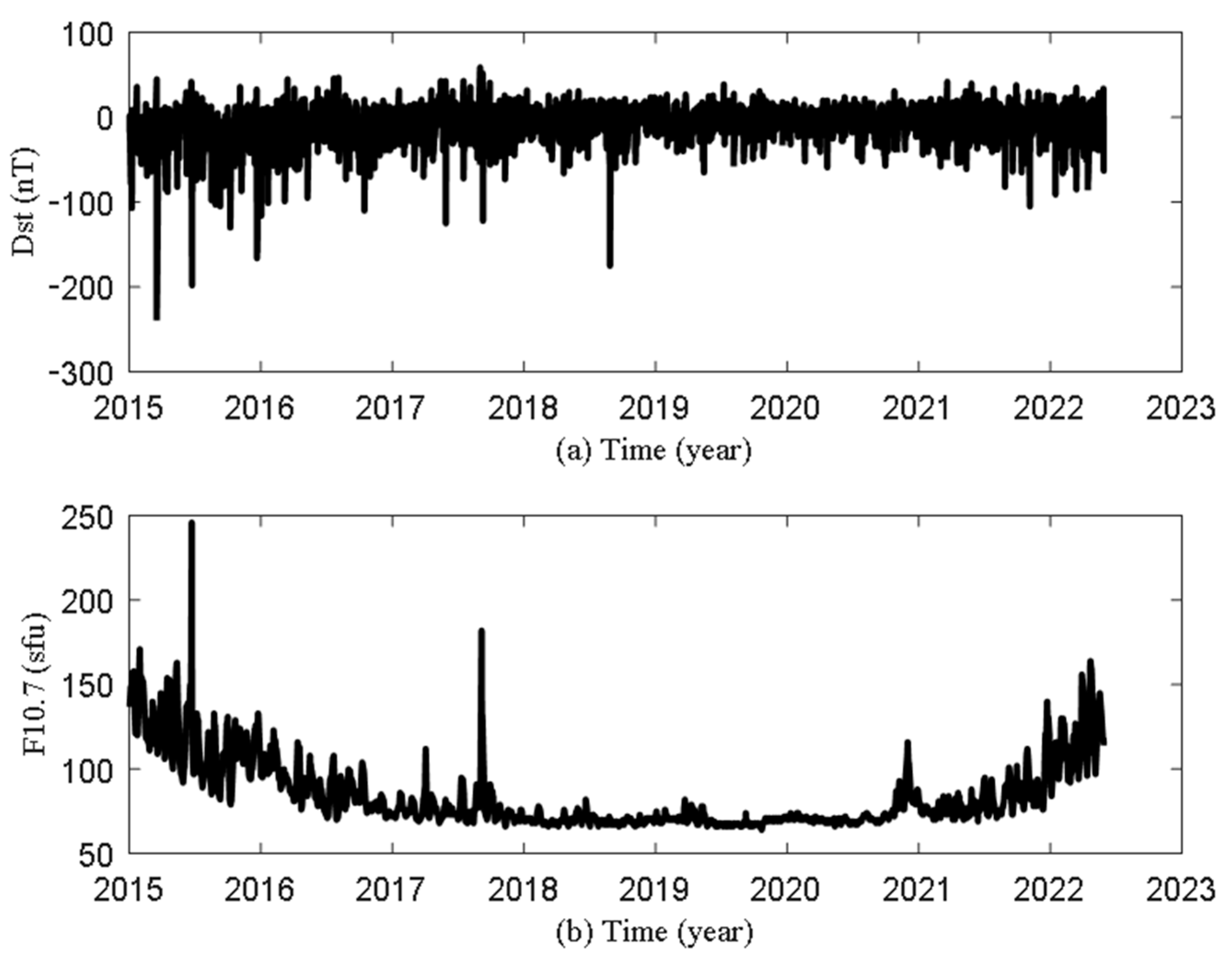
2.2.3. Database
2.3. Accuracy Evaluation
3. Results
3.1. Ionospheric VTEC Estimation Experiment
3.1.1. Site Observation Test in Non-Equatorial Anomaly Area
3.1.2. Observation Experiment in Equatorial Anomaly Area
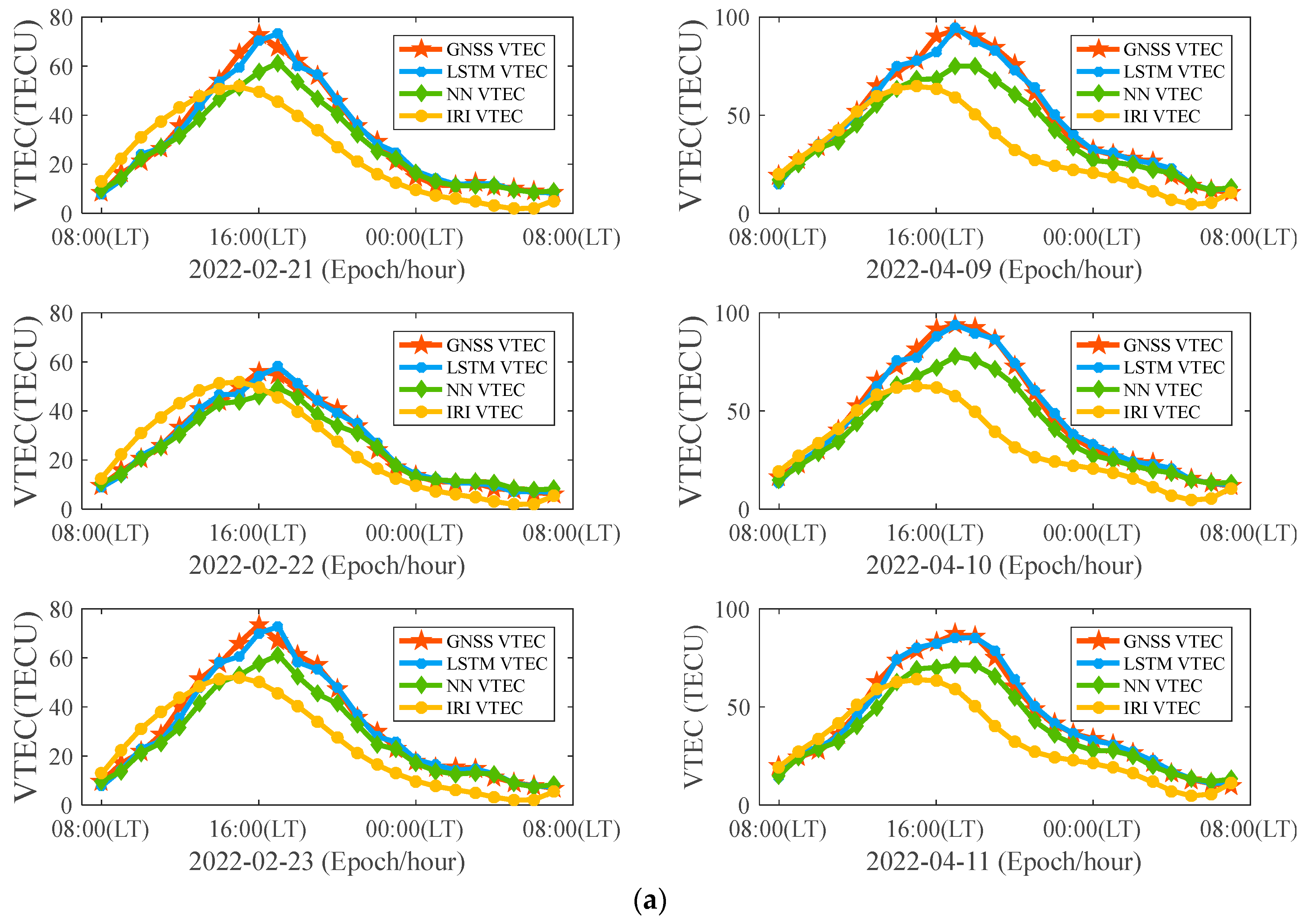
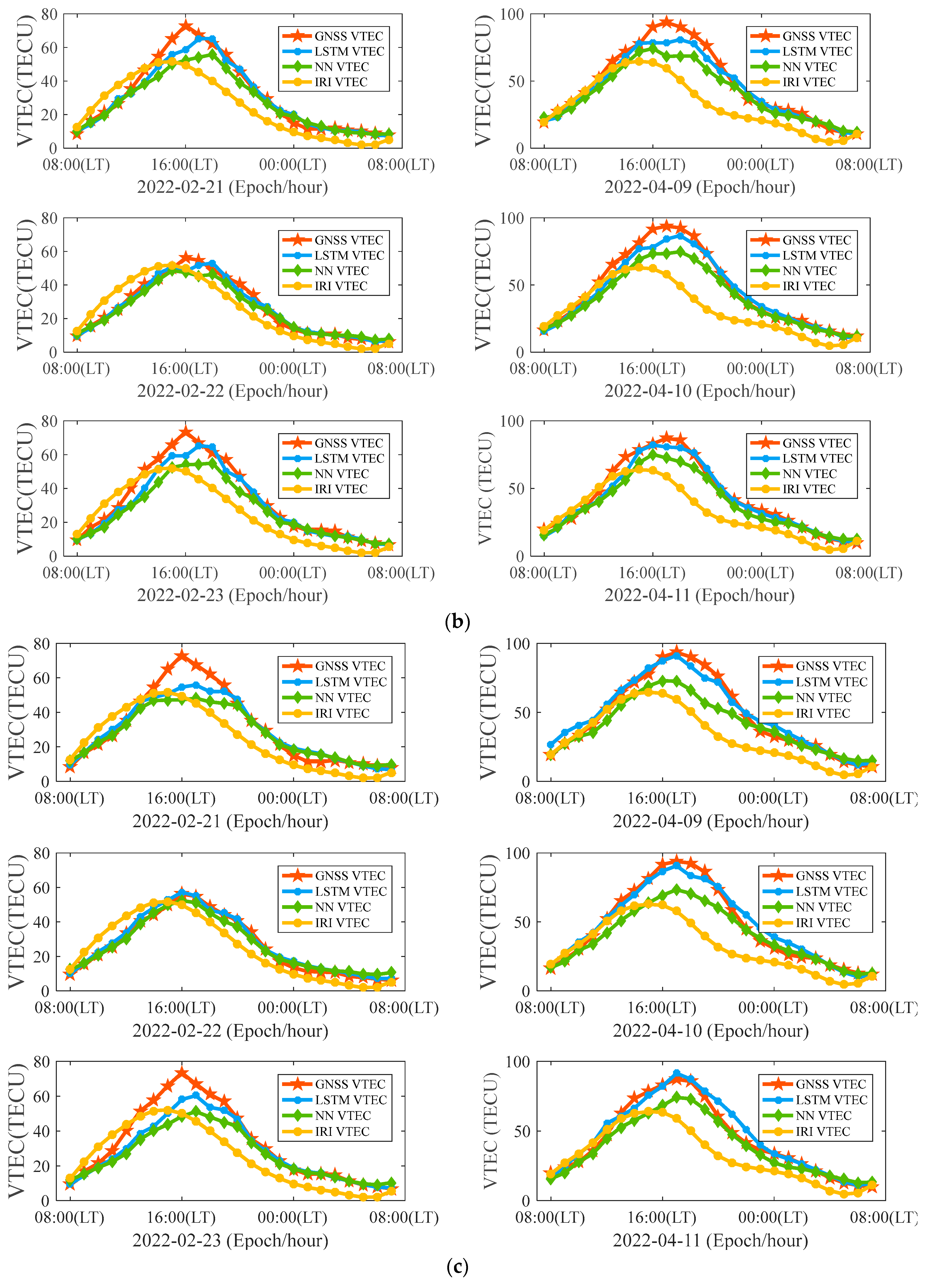
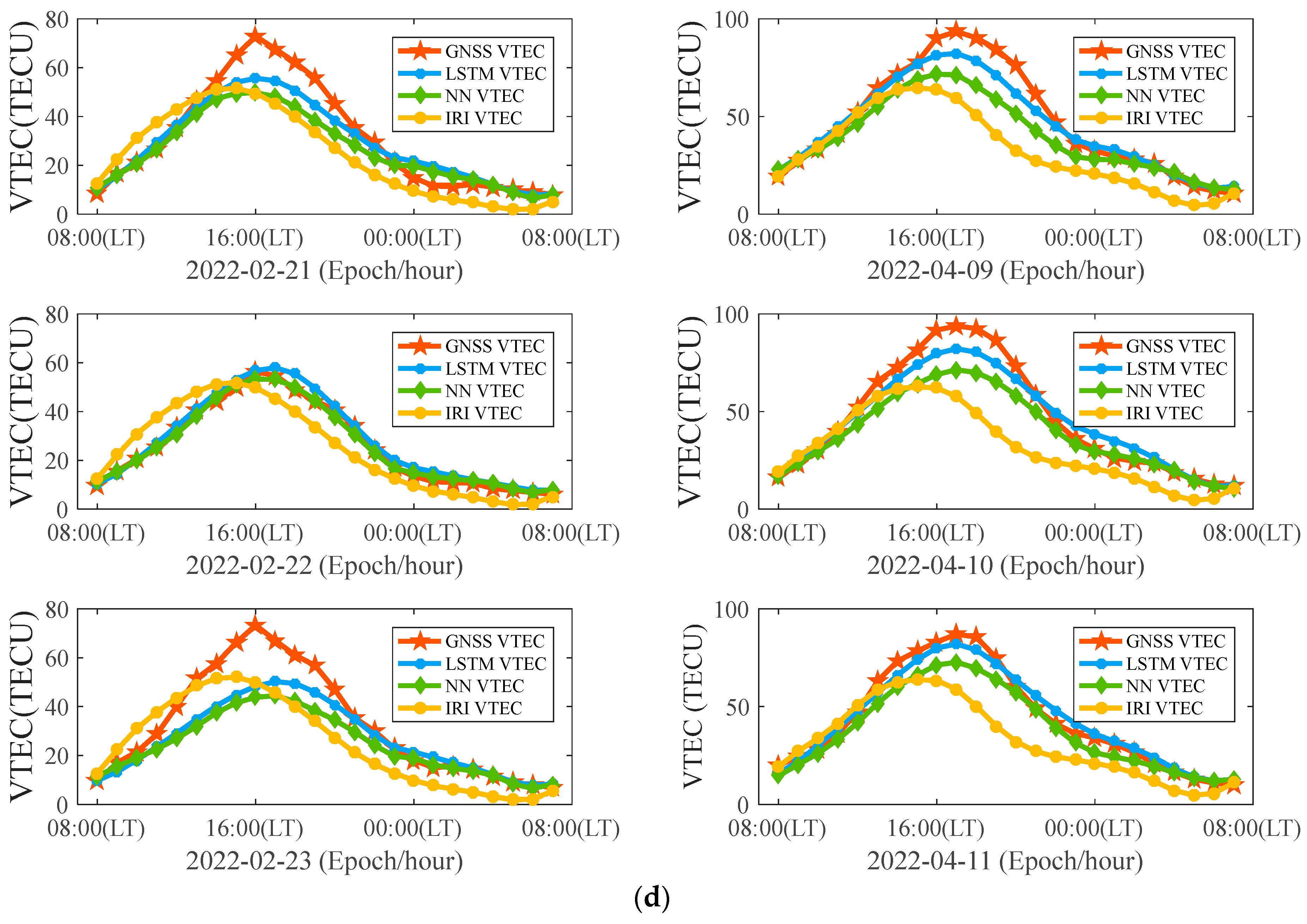
3.2. Ionospheric VTEC Prediction Experiment
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jin, S.; Jin, R.; Li, D. GPS detection of ionospheric Rayleigh wave and its source following the 2012 Haida Gwaii earthquake. J. Geophys. Res. Space Phys. 2017, 122, 1360–1372. [Google Scholar] [CrossRef]
- Jin, S. Two-Mode Ionospheric Disturbances Following the 2005 Northern California Offshore Earthquake from GPS Measurements. J. Geophys. Res. Space Phys. 2018, 123, 8587–8598. [Google Scholar] [CrossRef]
- Goodman, J.M. Operational communication systems and relationships to the ionosphere and space weather. Adv. Space Res. 2005, 36, 2241–2252. [Google Scholar] [CrossRef]
- Ritchie, S.E.; Honary, F. Storm sudden commencement and its effect on high-latitude HF communication links. Space Weather 2009, 7, S06005. [Google Scholar] [CrossRef]
- Deng, Y.; Ridley, A.J. The Global Ionosphere-Thermosphere Model and the Nonhydrostatic Processes. Geophys. Monogr. Ser. 2014, 201, 85–100. [Google Scholar] [CrossRef]
- Chetia, B.; Barman, M.K.; Devi, M.; Barbara, A.K. Study of Physical and Dynamical Processes in the Ionosphere at Equatorial Anomaly Crest Region during Magnetic Storm for High and Low Solar Activity Period. In Geostatistical and Geospatial Approaches for the Characterization of Natural Resources in the Environment; Springer: Berlin/Heidelberg, Germany, 2016; pp. 861–866. [Google Scholar] [CrossRef]
- Kouris, S.S.; Xenos, T.D.; Polimeris, K.V.; Stergiou, D. TEC and foF2 variations: Preliminary results. Ann. Geophys. 2009, 47, 1325–1332. [Google Scholar] [CrossRef]
- Gowtam, V.S.; Ram, S.T. Ionospheric annual anomaly-New insights to the physical mechanisms. J. Geophys. Res. Space Phys. 2017, 122, 8816–8830. [Google Scholar] [CrossRef]
- Balan, N.; Liu, L.; Le, H. A brief review of equatorial ionization anomaly and ionospheric irregularities. Earth Planet. Phys. 2018, 2, 257–275. [Google Scholar] [CrossRef]
- Gan, Q.; Wang, W.; Yue, J.; Liu, H.; Chang, L.C.; Zhang, S.; Burns, A.; Du, J. Numerical simulation of the 6 day wave effects on the ionosphere: Dynamo modulation. J. Geophys. Res. Space Phys. 2016, 121, 10103–10116. [Google Scholar] [CrossRef]
- Ferdousi, B.; Raeder, J. Signal propagation time from the magnetotail to the ionosphere: OpenGGCM simulation. J. Geophys. Res. Space Phys. 2016, 121, 6549–6561. [Google Scholar] [CrossRef]
- Ridley, A.J.; Deng, Y.; Tóth, G. The global ionosphere–thermosphere model. J. Atmos. So-Lar-Terr. Phys. 2006, 68, 839–864. [Google Scholar] [CrossRef]
- Bilitza, D.; Altadill, D.; Truhlik, V.; Shubin, V.; Galkin, I.; Reinisch, B.; Huang, X. International Reference Ionosphere 2016: From ionospheric climate to real-time weather predictions. Space Weather 2017, 15, 418–429. [Google Scholar] [CrossRef]
- Wang, N.; Li, Z.; Yuan, Y.; Li, M.; Huo, X.; Yuan, C. Ionospheric correction using GPS Klobuchar coefficients with an empirical night-time delay model. Adv. Space Res. 2018, 63, 886–896. [Google Scholar] [CrossRef]
- Jiang, H.; Liu, J.; Wang, Z.; An, J.; Ou, J.; Liu, S.; Wang, N. Assessment of spatial and temporal TEC variations derived from ionospheric models over the polar regions. J. Geod. 2019, 93, 455–471. [Google Scholar] [CrossRef]
- Sardón, E.; Rius, A.; Zarraoa, N. Estimation of the transmitter and receiver differential biases and the ionospheric total electron content from Global Positioning System observations. Radio Sci. 1994, 29, 577–586. [Google Scholar] [CrossRef]
- Ma, G.; Gao, W.; Li, J.; Chen, Y.; Shen, H. Estimation of GPS instrumental biases from small scale network. Adv. Space Res. 2014, 54, 871–882. [Google Scholar] [CrossRef]
- Chen, L.; Yi, W.; Song, W.; Shi, C.; Lou, Y.; Cao, C. Evaluation of three ionospheric delay computation methods for ground-based GNSS receivers. GPS Solut. 2018, 22, 125. [Google Scholar] [CrossRef]
- Lu, W.; Ma, G.; Wang, X.; Wan, Q.; Li, J. Evaluation of ionospheric height assumption for single station GPS-TEC der-ivation. Adv. Space Res. 2017, 60, 286–294. [Google Scholar] [CrossRef]
- Cai, H.; Wang, Q. Resolving the Regional Ionospheric Grid Model by Applying Kalman Filter. China Satell. Navig. Conf. 2016, 390, 425–434. [Google Scholar] [CrossRef]
- Prasad, R.; Kumar, S.; Jayachandran, P. Receiver DCB estimation and GPS vTEC study at a low latitude station in the South Pacific. J. Atmos. Sol. -Terr. Phys. 2016, 149, 120–130. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhao, Q.L. Evaluation and analysis of the global ionosphere maps from Wuhan University IGS Ionosphere Associate Analysis Center. Chin. J. Geophys. 2019, 62, 4493–4505. (In Chinese) [Google Scholar]
- Tulunay, E.; Senalp, E.T.; Radicella, S.M.; Tulunay, Y. Forecasting total electron content maps by neural network technique. Radio Sci. 2006, 41, RS4016. [Google Scholar] [CrossRef]
- Dabbakuti, J.K.; Ratnam, D.V. Performance evaluation of linear time-series ionospheric Total Electron Content model over low latitude Indian GPS stations. Adv. Space Res. 2017, 60, 1777–1786. [Google Scholar] [CrossRef]
- Li, W.; Zhao, D.; Shen, Y.; Zhang, K. Modeling Australian TEC Maps Using Long-Term Observations of Australian Regional GPS Network by Artificial Neural Network-Aided Spherical Cap Harmonic Analysis Approach. Remote Sens. 2020, 12, 3851. [Google Scholar] [CrossRef]
- Adolfs, M.; Hoque, M.M. A Neural Network-Based TEC Model Capable of Reproducing Nighttime Winter Anomaly. Remote Sens. 2021, 13, 4559. [Google Scholar] [CrossRef]
- Adolfs, M.; Hoque, M.M.; Shprits, Y.Y. Storm-Time Relative Total Electron Content Modelling Using Machine Learning Techniques. Remote Sens. 2022, 14, 6155. [Google Scholar] [CrossRef]
- Lin, X.; Wang, H.; Zhang, Q.; Yao, C.; Chen, C.; Cheng, L.; Li, Z. A Spatiotemporal Network Model for Global Ionospheric TEC Forecasting. Remote Sens. 2022, 14, 1717. [Google Scholar] [CrossRef]
- Tang, J.; Li, Y.; Ding, M.; Liu, H.; Yang, D.; Wu, X. An Ionospheric TEC Forecasting Model Based on a CNN-LSTM-Attention Mechanism Neural Network. Remote Sens. 2022, 14, 2433. [Google Scholar] [CrossRef]
- Kim, J.-H. Potential of Regional Ionosphere Prediction Using a Long Short-Term Memory Deep-Learning. Space Weather 2021, 19, e2021SW002741. [Google Scholar] [CrossRef]
- Ren, X.; Yang, P.; Liu, H.; Chen, J.; Liu, W. Deep Learning for Global Ionospheric TEC Forecasting: Different Approaches and Validation. Space Weather 2022, 20, e2021SW003011. [Google Scholar] [CrossRef]
- Ulukavak, M. Deep learning for ionospheric TEC forecasting at mid-latitude stations in Turkey. Acta Geophys. 2021, 69, 589–606. [Google Scholar] [CrossRef]
- Oliver, M.A.; Webster, R. Kriging: A method of interpolation for geographical information systems. Int. J. Geogr. Inf. Syst. 1990, 4, 313–332. [Google Scholar] [CrossRef]
- Cortesi, A.F.; Jannoun, G.; Congedo, P.M. Kriging-sparse Polynomial Dimensional Decomposition surrogate model with adaptive refinement. J. Comput. Phys. 2018, 380, 212–242. [Google Scholar] [CrossRef]
- Imran, M.; Stein, A.; Zurita-Milla, R. Using geographically weighted regression kriging for crop yield mapping in West Africa. Int. J. Geogr. Inf. Sci. 2014, 29, 234–257. [Google Scholar] [CrossRef]
- Liu, C.; Liu, C.; Feng, X.; Quan, W. Quality Evaluation of IGS GIMs Based on the Statistical Characteristics of VTEC/RMS Eigenvalues: A Macro Perspective. Radio Sci. 2018, 53, 790–803. [Google Scholar] [CrossRef]
- Jee, G.; Lee, H.-B.; Kim, Y.H.; Chung, J.-K.; Cho, J. Assessment of GPS global ionosphere maps (GIM) by comparison between CODE GIM and TOPEX/Jason TEC data: Ionospheric perspective. J. Geophys. Res. Space Phys. 2010, 115, A10319. [Google Scholar] [CrossRef]



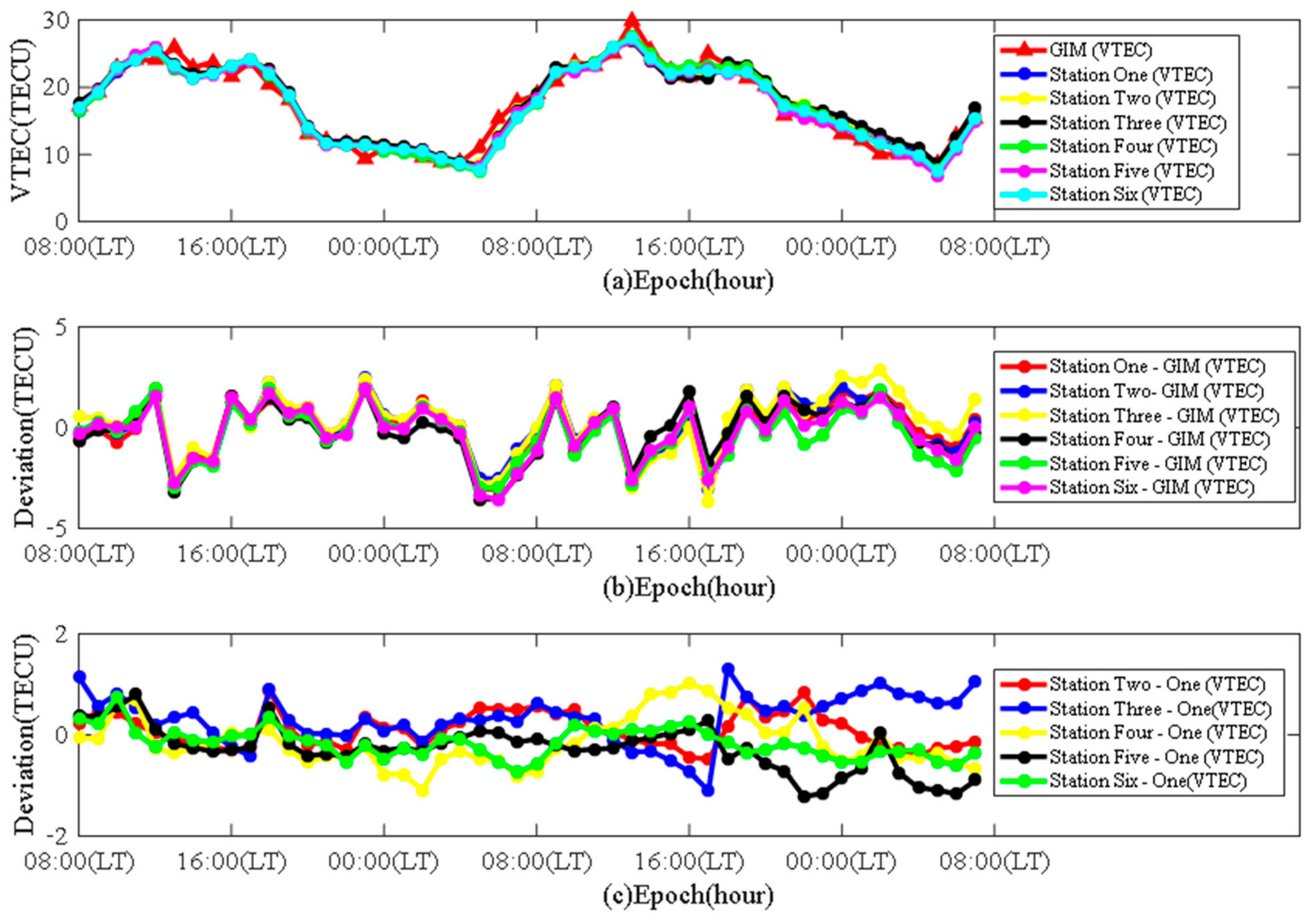

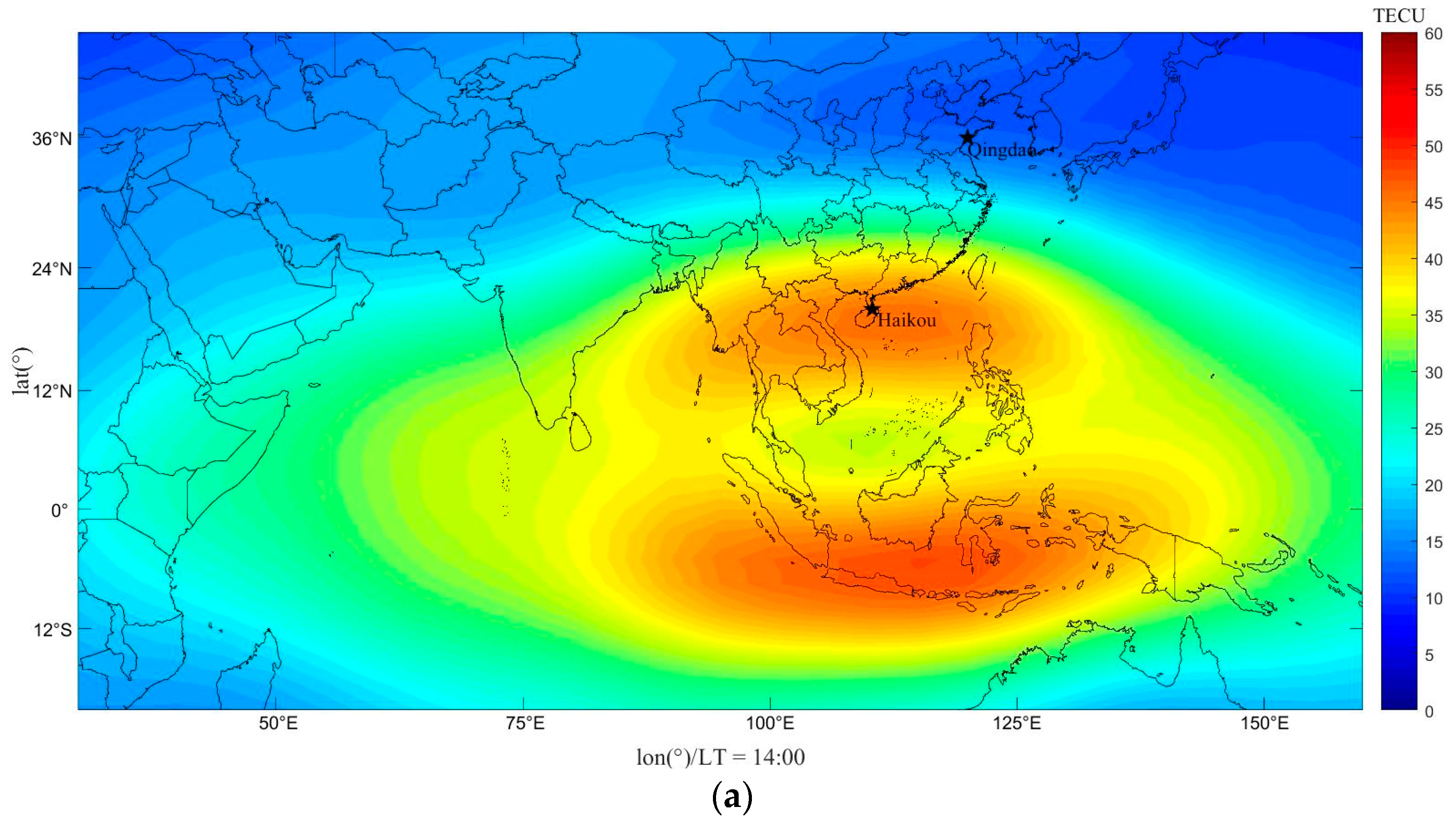
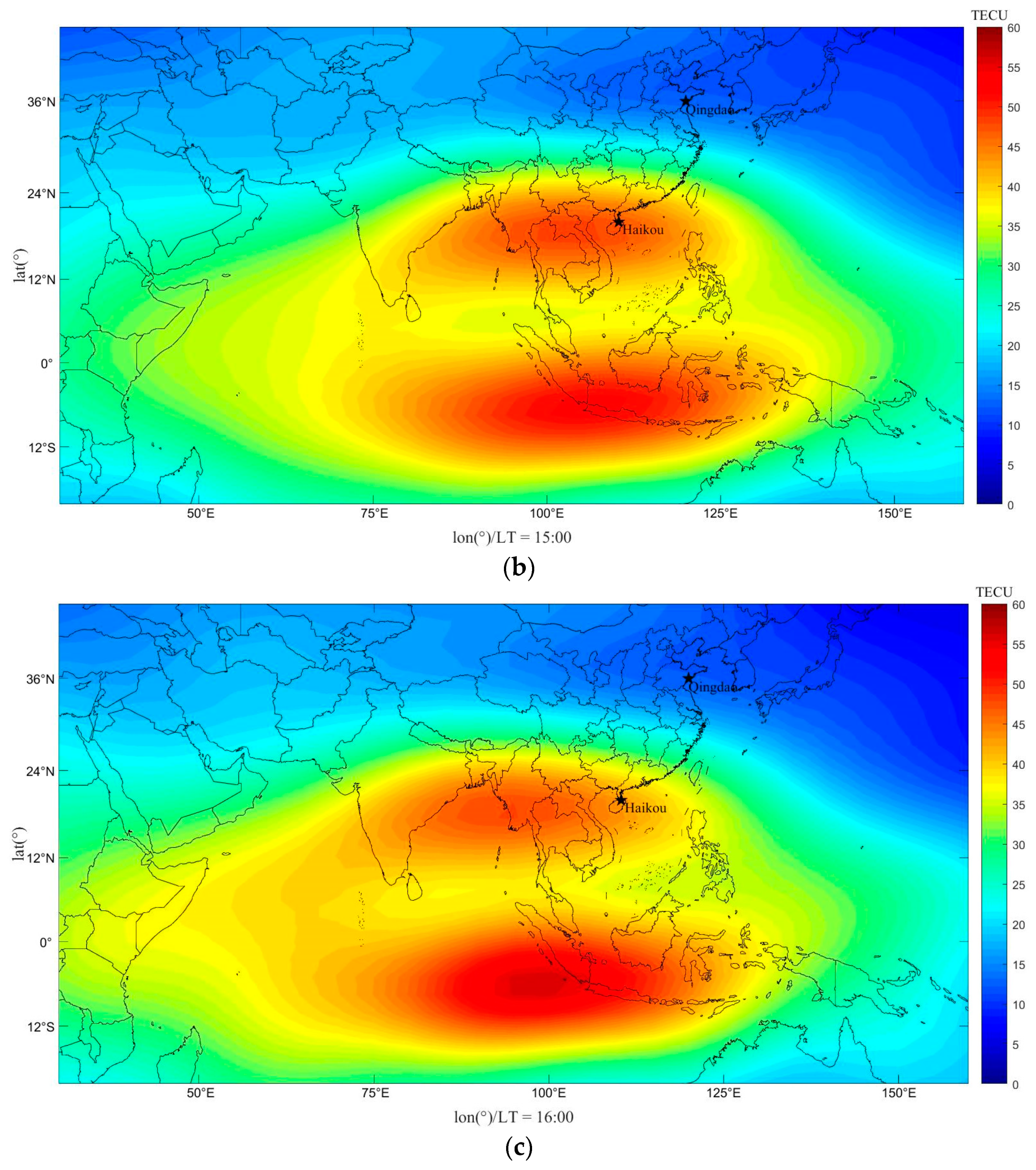
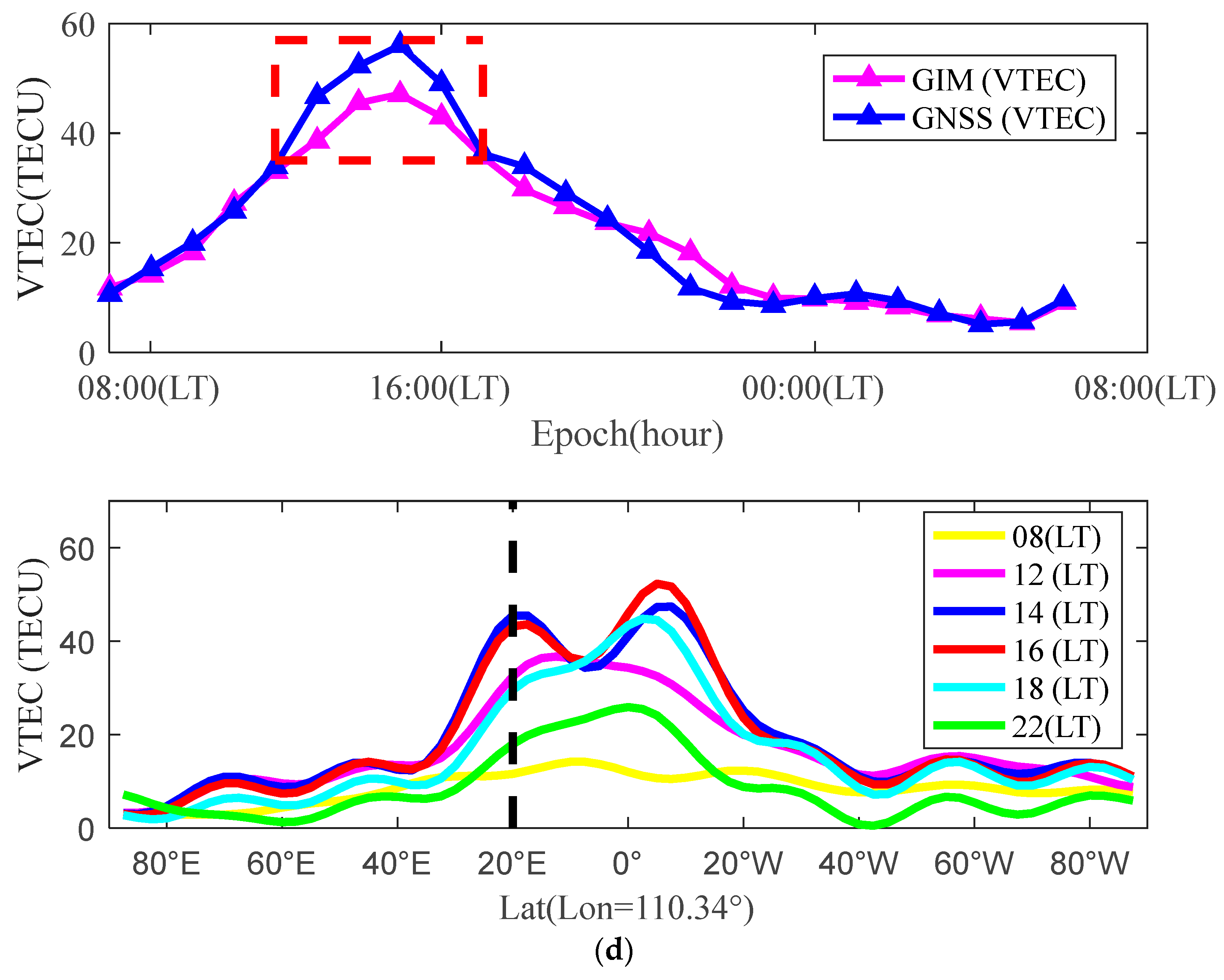

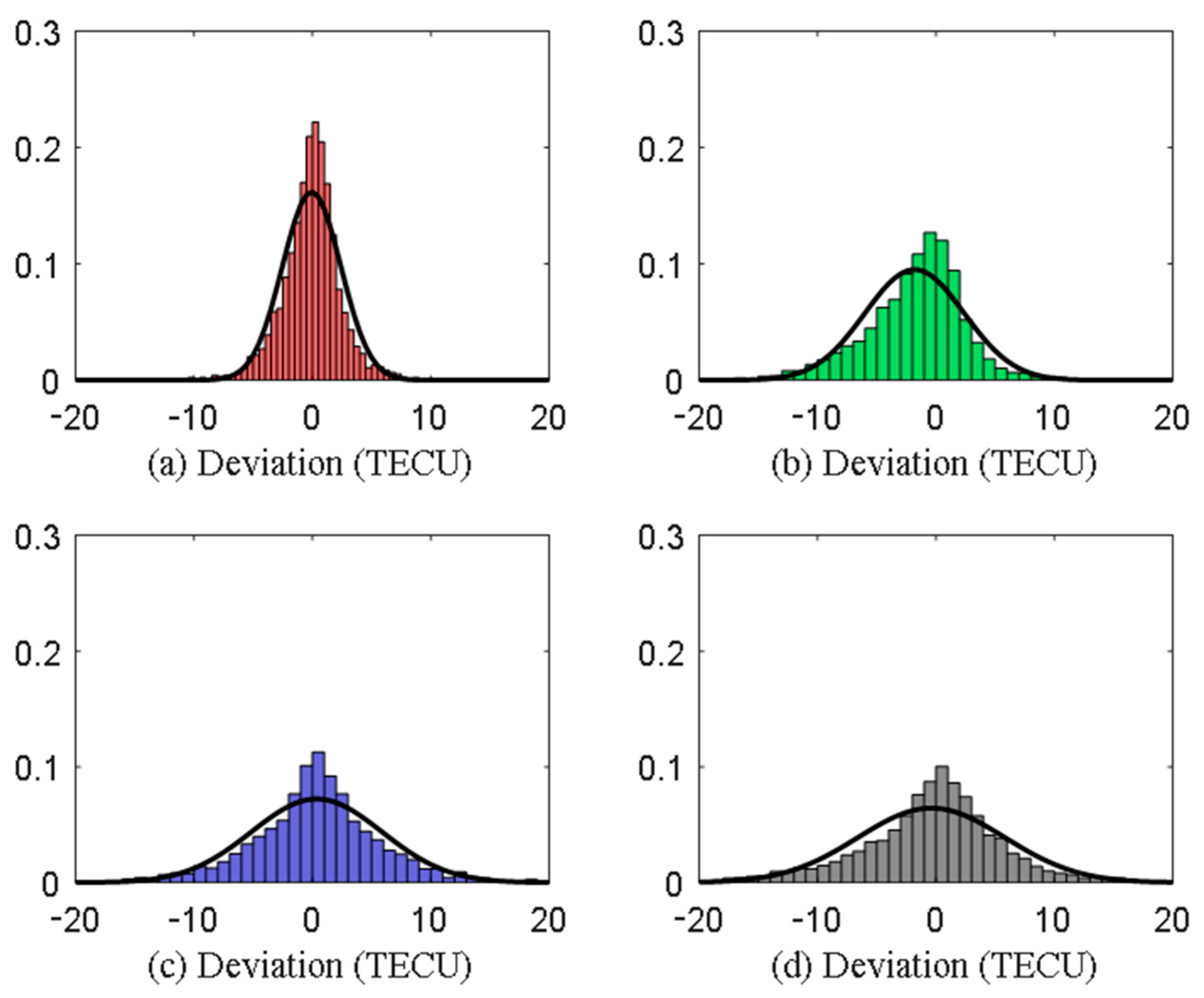
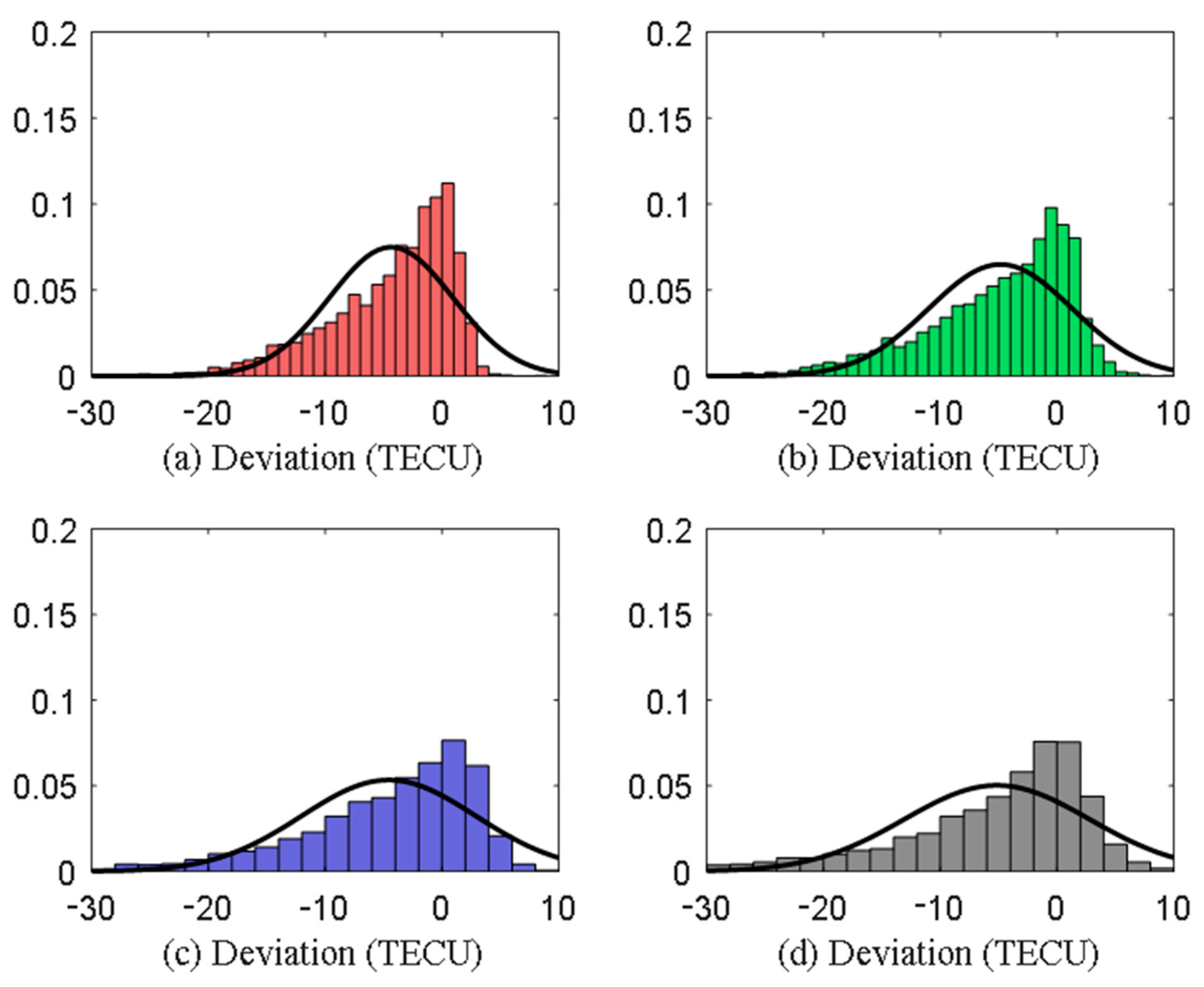

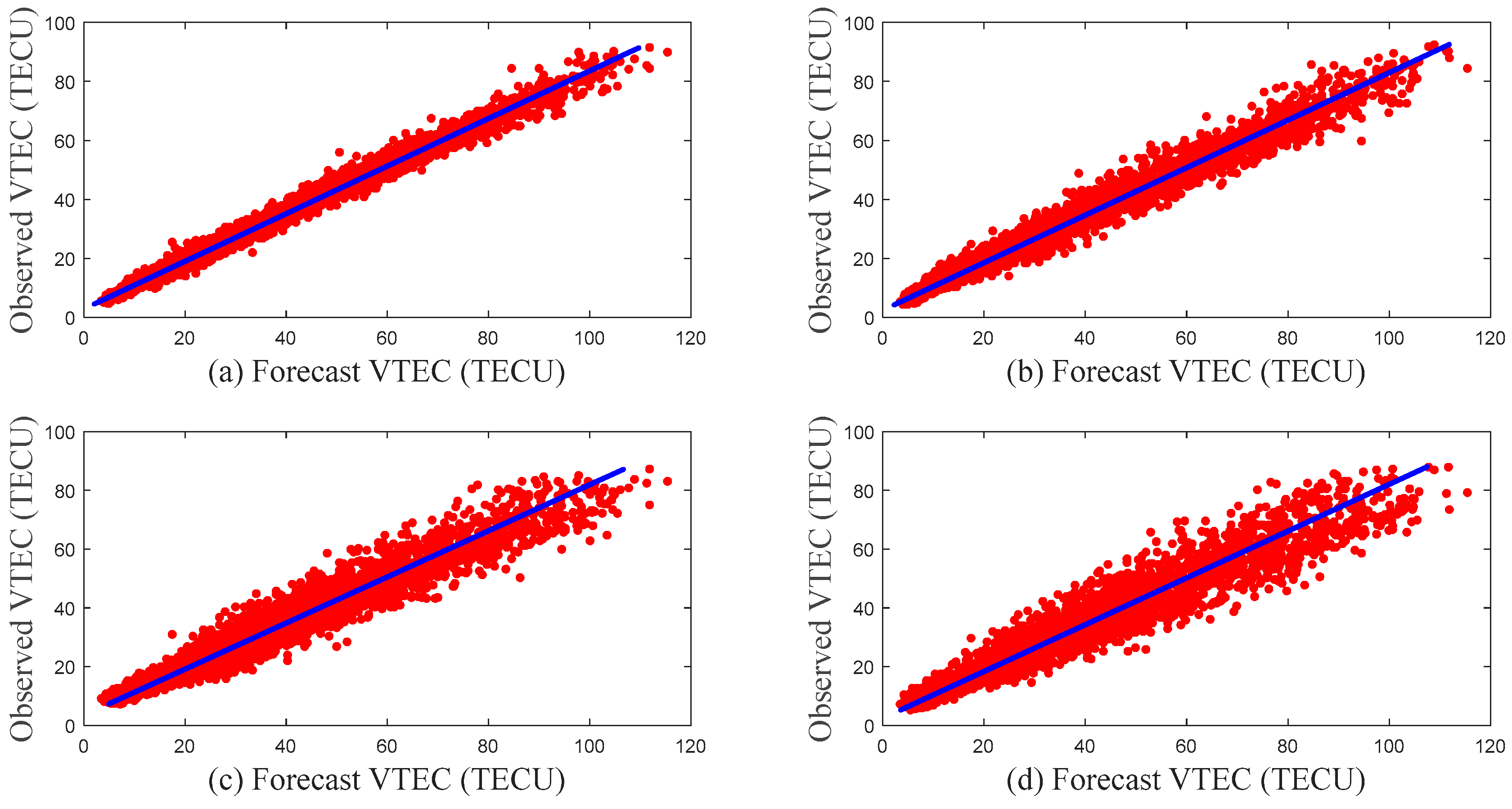
| Station Numbers | RMSE (TECU) | MAE (TECU) | R |
|---|---|---|---|
| Two–One | 0.3641 | 0.3015 | 0.9981 |
| Three–One | 0.5903 | 0.4917 | 0.9964 |
| Four–One | 0.5116 | 0.4248 | 0.9980 |
| Five–One | 0.5284 | 0.4079 | 0.9974 |
| Six–One | 0.3347 | 0.2681 | 0.9991 |
| Statistics | 0.4658 | 0.3788 | 0.9978 |
| Station Number | RMSE (TECU) | MAE (TECU) | R |
|---|---|---|---|
| One | 1.3577 | 1.0966 | 0.9731 |
| Two | 1.4211 | 1.1495 | 0.9705 |
| Three | 1.5612 | 1.2429 | 0.9659 |
| Four | 1.4021 | 1.1016 | 0.9721 |
| Five | 1.3803 | 1.1040 | 0.9733 |
| Six | 1.3731 | 1.0605 | 0.9728 |
| Statistics | 1.4159 | 1.1259 | 0.9713 |
| Deviation | RMSE (TECU) | MAE (TECU) | R |
|---|---|---|---|
| GNSS (VTEC)-GIM (VTEC) | 3.7713 | 2.7388 | 0.9870 |
| GNSS (VTEC)-BDS GEO3 (VTEC) | 1.9204 | 1.5553 | 0.9942 |
| Forecast Duration (h) | LSTM Model | NN Model | ||||
|---|---|---|---|---|---|---|
| RMSE (TECU) | MAE (TECU) | R | RMSE (TECU) | MAE (TECU) | R | |
| 1 | 2.4636 | 1.7886 | 0.9948 | 6.8740 | 4.8839 | 0.9940 |
| 2 | 4.5672 | 3.3162 | 0.9862 | 7.8217 | 5.5972 | 0.9859 |
| 4 | 5.5284 | 4.0286 | 0.9737 | 8.7482 | 6.1541 | 0.9738 |
| >8 | 6.2093 | 4.4957 | 0.9666 | 9.4552 | 6.5320 | 0.9648 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.-N.; Zhu, Q.-L.; Dong, X.; Sheng, D.-S.; Zhi, Y.-F.; Zhou, C.; Xu, B. A Novel Technique for High-Precision Ionospheric VTEC Estimation and Prediction at the Equatorial Ionization Anomaly Region: A Case Study over Haikou Station. Remote Sens. 2023, 15, 3394. https://doi.org/10.3390/rs15133394
Wang H-N, Zhu Q-L, Dong X, Sheng D-S, Zhi Y-F, Zhou C, Xu B. A Novel Technique for High-Precision Ionospheric VTEC Estimation and Prediction at the Equatorial Ionization Anomaly Region: A Case Study over Haikou Station. Remote Sensing. 2023; 15(13):3394. https://doi.org/10.3390/rs15133394
Chicago/Turabian StyleWang, Hai-Ning, Qing-Lin Zhu, Xiang Dong, Dong-Sheng Sheng, Yong-Feng Zhi, Chen Zhou, and Bin Xu. 2023. "A Novel Technique for High-Precision Ionospheric VTEC Estimation and Prediction at the Equatorial Ionization Anomaly Region: A Case Study over Haikou Station" Remote Sensing 15, no. 13: 3394. https://doi.org/10.3390/rs15133394
APA StyleWang, H.-N., Zhu, Q.-L., Dong, X., Sheng, D.-S., Zhi, Y.-F., Zhou, C., & Xu, B. (2023). A Novel Technique for High-Precision Ionospheric VTEC Estimation and Prediction at the Equatorial Ionization Anomaly Region: A Case Study over Haikou Station. Remote Sensing, 15(13), 3394. https://doi.org/10.3390/rs15133394







