Choice of Solar Spectral Irradiance Model for Current and Future Remote Sensing Satellite Missions
Abstract
1. Introduction
2. Methods
2.1. Model Evaluation Using Landsat 8 and 9 Solar Spectrum Observations
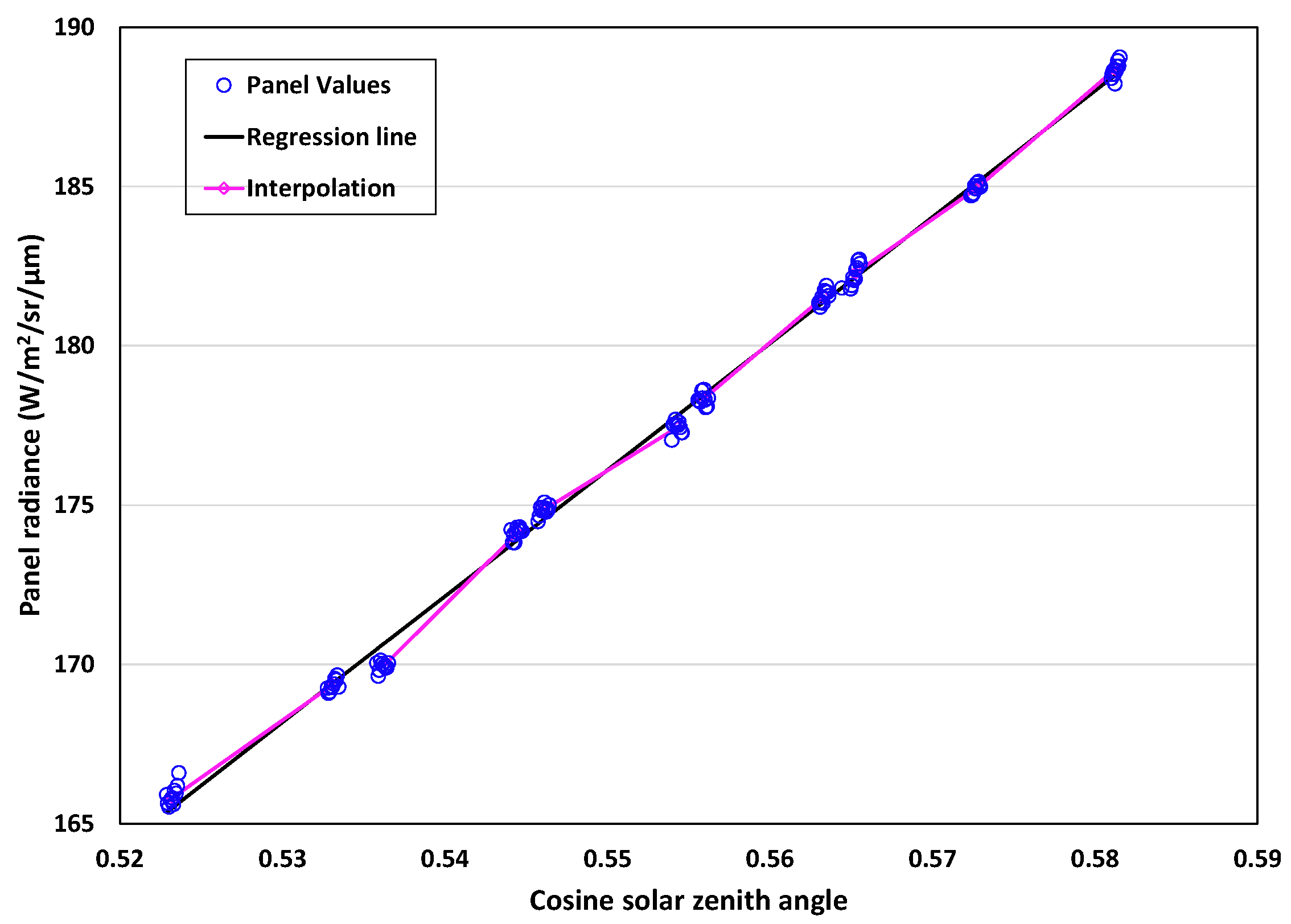
2.2. Model Evaluation Using Inversion of Measured Surface Irradiance Data
3. Data and Pre-Processing
3.1. Pre-Processing Solar Spectrum Data
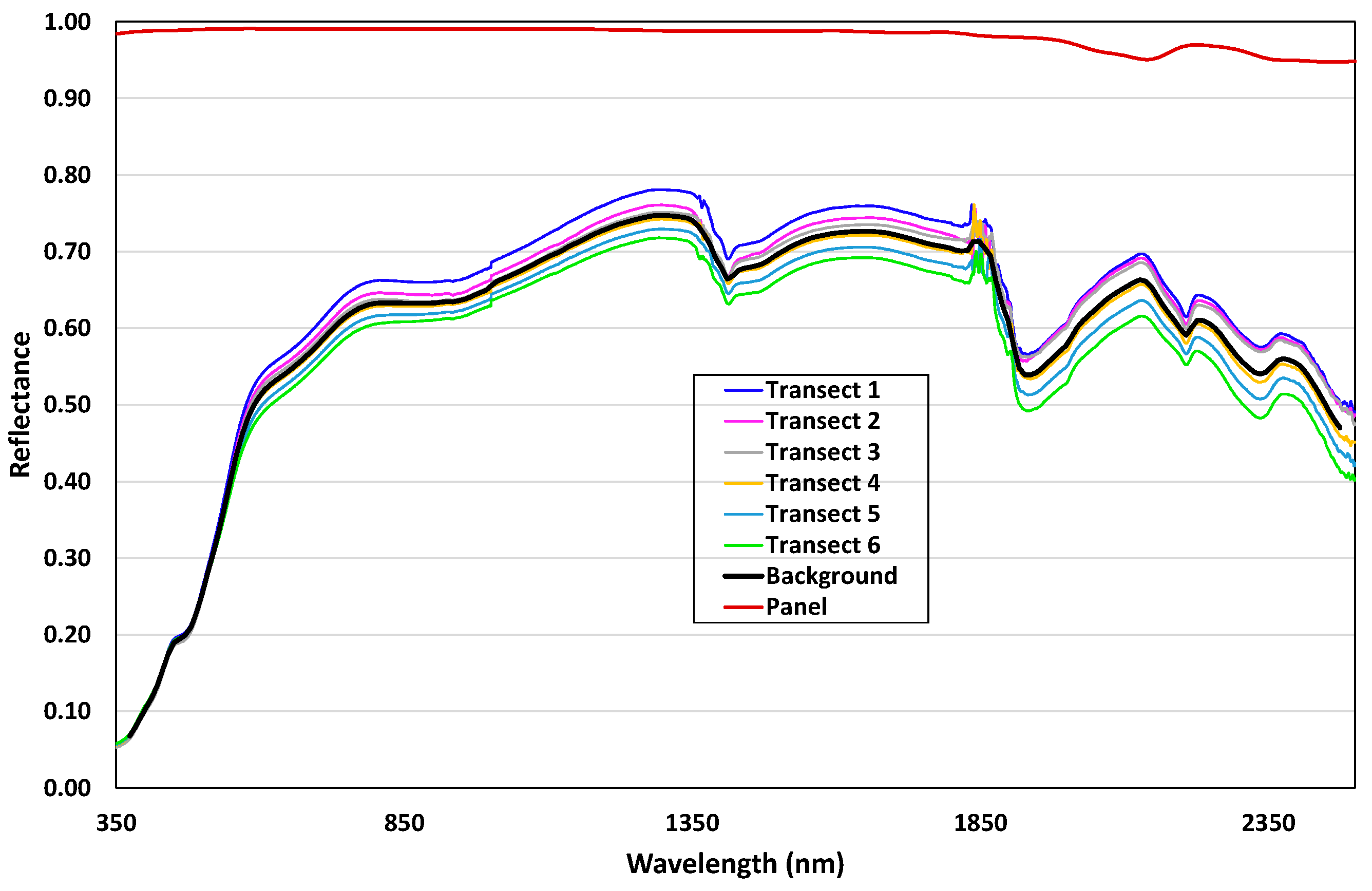
3.2. Field Site and Data Preparation
4. Results
4.1. Model Evaluation Results from Landsat 8 and 9 Broadband Solar Spectrum Observations
| (a) | |||||||||
| Model | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| Band | cwl (nm) | ||||||||
| 1 | 442.98 | 0.05849 | −0.00576 | 0.02621 | 0.04045 | 0.00631 | 0.01627 | 0.03115 | 0.02095 |
| 2 | 482.59 | −0.00447 | −0.01812 | −0.00638 | 0.00750 | −0.00619 | 0.00454 | 0.00125 | 0.00190 |
| 3 | 561.33 | −0.01052 | −0.01356 | 0.00808 | 0.02220 | −0.00160 | 0.00427 | −0.00326 | 0.00988 |
| 4 | 654.61 | 0.00380 | −0.00454 | −0.00125 | 0.01280 | 0.00760 | −0.00074 | 0.00284 | −0.00448 |
| 5 | 864.57 | 0.00915 | 0.00065 | −0.03946 | 0.00910 | 0.01281 | −0.01271 | 0.01236 | −0.02456 |
| 6 | 1609.10 | −0.02077 | −0.01451 | −0.01475 | −0.03525 | −0.00253 | −0.01512 | 0.00044 | −0.00544 |
| 7 | 2201.20 | −0.01816 | −0.02399 | −0.02411 | −0.05809 | −0.01214 | −0.02460 | −0.01131 | 0.00561 |
| 8 | 591.67 | 0.00523 | 0.00081 | 0.01604 | 0.03030 | 0.01297 | 0.01499 | 0.01037 | 0.01744 |
| Mean | 0.00284 | −0.00988 | −0.00445 | 0.00363 | 0.00215 | −0.00164 | 0.00548 | 0.00266 | |
| STD | 0.02499 | 0.00904 | 0.02154 | 0.03351 | 0.00916 | 0.01465 | 0.01275 | 0.01450 | |
| RMS | 0.02516 | 0.01339 | 0.02200 | 0.03371 | 0.00941 | 0.01474 | 0.01388 | 0.01474 | |
| (b) | |||||||||
| Model | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| Band | cwl (nm) | ||||||||
| 1 | 442.76 | 0.05274 | −0.01172 | 0.02056 | 0.03476 | 0.00031 | 0.01007 | 0.02537 | 0.01515 |
| 2 | 482.30 | 0.01074 | −0.00311 | 0.00866 | 0.02279 | 0.00900 | 0.01984 | 0.01660 | 0.01721 |
| 3 | 560.92 | 0.01190 | 0.00890 | 0.03118 | 0.04561 | 0.02112 | 0.02718 | 0.01948 | 0.03302 |
| 4 | 654.30 | 0.01182 | 0.00355 | 0.00681 | 0.02090 | 0.01572 | 0.00745 | 0.01092 | 0.00361 |
| 5 | 864.61 | −0.00310 | −0.01152 | −0.05090 | −0.00318 | 0.00047 | −0.02482 | 0.00004 | −0.03656 |
| 6 | 1608.40 | −0.01298 | −0.00680 | −0.00709 | −0.02783 | 0.00526 | −0.00741 | 0.00828 | 0.00220 |
| 7 | 2201.10 | 0.00317 | −0.00278 | −0.00290 | −0.03775 | 0.00933 | −0.00340 | 0.01021 | 0.02749 |
| 8 | 593.95 | 0.00858 | 0.00402 | 0.01889 | 0.03318 | 0.01626 | 0.01778 | 0.01347 | 0.01988 |
| Mean | 0.010360 | −0.002433 | 0.003150 | 0.011058 | 0.009684 | 0.005833 | 0.013049 | 0.010253 | |
| STD | 0.019206 | 0.007506 | 0.025193 | 0.030651 | 0.007591 | 0.016968 | 0.007658 | 0.021650 | |
| RMS | 0.021822 | 0.007890 | 0.025389 | 0.032585 | 0.012305 | 0.017943 | 0.015130 | 0.023955 | |
| (c) | |||||||||
| Model | RMS | % | Max% | ||||||
| Model 5 | 0.00820 | 0.82 | 1.2 | ||||||
| Model 2 | 0.00832 | 0.83 | 1.3 | ||||||
| Model 7 | 0.01257 | 1.26 | 2.9 | ||||||
| Model 6 | 0.01473 | 1.47 | 1.9 | ||||||
| Model 8 | 0.01850 | 1.85 | 3.0 | ||||||
| Model 1 | 0.02242 | 2.24 | 5.6 | ||||||
| Model 3 | 0.02264 | 2.26 | 4.5 | ||||||
| Model 4 | 0.03236 | 3.24 | 4.8 | ||||||
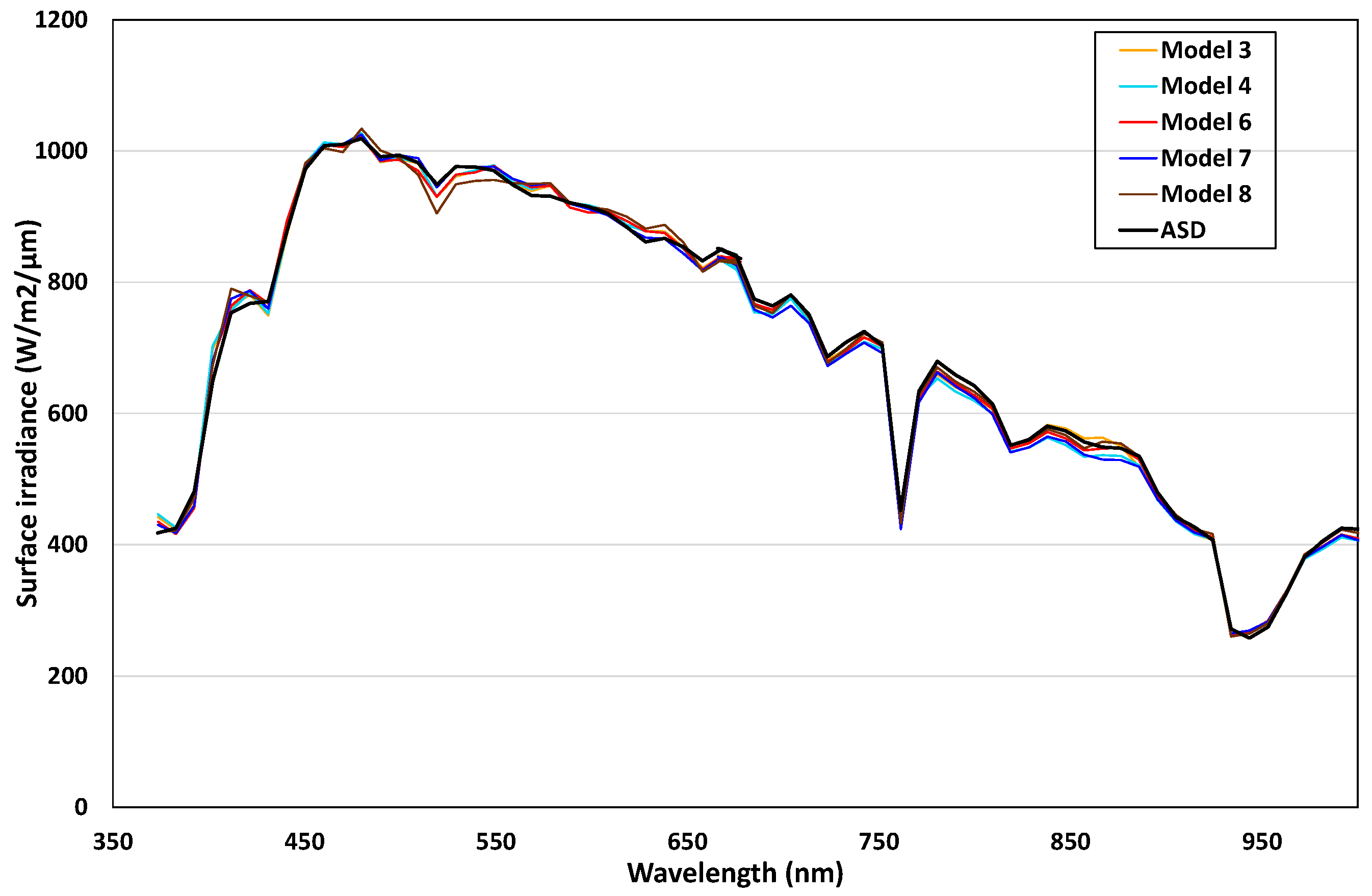
4.2. Analysis of the Solar Spectra at 10 nm Resolution
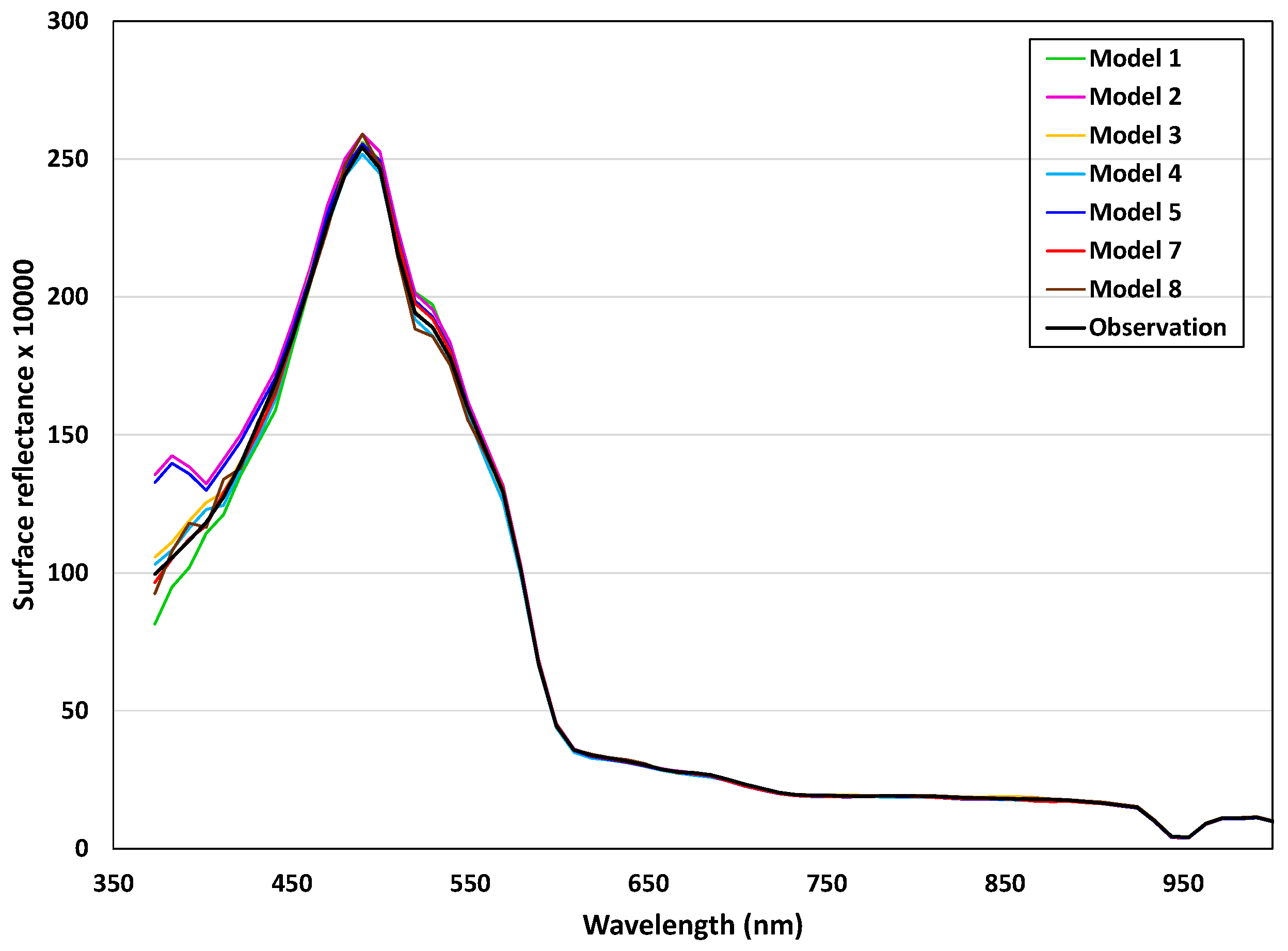
4.3. Model Evaluation Results Based on Inversion of Surface Irradiance Observations
4.4. Potential Change in Estimated Surface Reflectance with Change in Solar Spectrum
5. Discussion
5.1. Scale of Comparison
5.2. Ancillary Information
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Thome, K.J.; Biggar, S.F.; Slater, P.N. Effects of assumed solar spectral irradiance on intercomparisons of Earth-observing sensors. Proc. SPIE 2001, 4540, 260–269. [Google Scholar] [CrossRef]
- Fröhlich, C. Solar irradiance variability. In Solar Variability and Its Effects on Climate; Geophysical Monograph 141; AGU: Washington, DC, USA, 2004; pp. 97–110. [Google Scholar]
- Li, F.; Jupp, D.L.B.; Sagar, S.; Schroeder, T. The Impact of Choice of Solar Spectral Irradiance Model on Atmospheric Correction of Landsat 8 OLI Satellite Data. IEEE Trans. Geosci. Remote Sens. 2021, 59, 4094–4104, Erratum in IEEE Trans. Geosci. Remote Sens. 2021, 59, 5388–5388. [Google Scholar] [CrossRef]
- Markham, B.; Barsi, J.; Kvaran, G.; Ong, L.; Kaita, E.; Biggar, S.; Czapla-Myers, J.; Mishra, N.; Helder, D. Landsat-8 Operational Land Imager radiometric calibration and stability. Remote Sens. 2014, 6, 12275–12308. [Google Scholar] [CrossRef]
- Chance, K.; Kurucz, R.L. An improved high-resolution solar reference spectrum for Earth’s atmosphere measurements in the ultraviolet visible and near infrared. J. Quant. Spectrosc. Radiat. Transf. 2010, 111, 1289–1295. [Google Scholar] [CrossRef]
- Kurucz, R. High Resolution Irradiance Spectrum from 300 to 1000 nm. Available online: https://arxiv.org/pdf/astro-ph/0605029.pdf (accessed on 1 August 2019).
- Meftah, M.; Damé, L.; Bolsée, D.; Pereira, N.; Snow, M.; Weber, M.; Bramstedt, K.; Hilbig, T.; Cessateur, G.; Boudjella, M.-Y.; et al. A New Version of the SOLAR-ISS Spectrum Covering the 165–3000 nm Spectral Region. Sol. Phys. 2020, 295, 14. [Google Scholar] [CrossRef]
- Coddington, O.M.; Richard, E.C.; Harber, D.; Pilewskie, P.; Woods, T.N.; Chance, K.; Liu, X.; Sun, K. The TSIS-1 Hybrid Solar Reference Spectrum. Geophys. Res. Lett. 2021, 48, e2020GL091709. [Google Scholar] [CrossRef]
- Thuillier, G.; Herse, M.; Labs, D.; Foujols, T.; Peetermans, W.; Gillotay, D.; Simon, P.C.; Mandel, H. The solar spectral irradiance from 200 to 2400 nm as measured by SOLSPEC Spectrometer from the ATLAS and EURECA missions. Sol. Phys. 2003, 214, 1–22. [Google Scholar] [CrossRef]
- Green, R. (Ed.) HyspIRI Final Report, HyspIRI Mission Concept Team. NASA & JPL. 2018. Available online: https://hyspiri.jpl.nasa.gov/ (accessed on 1 February 2021).
- Loizzo, R.; Guarini, R.; Longo, F.; Scopa, T.; Formaro, R.; Facchinetti, C.; Varacalli, G.N. Prisma: The Italian Hyperspectral Mission. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 175–178. [Google Scholar] [CrossRef]
- ENMAP. Environmental Mapping and Analysis Program, DLR, Germany. Available online: https://www.enmap.org/ (accessed on 1 October 2022).
- Senese, S.; Thiel, M.; König, B.; Sornig, M.; Fischer, S.; Bergander, A.; Brunner, S.; Müller, S.; Schmidt, T.; Zajac, K. Full aperture diffuser assembly, fully redundant and high reliable optic mechanism for ENMAP mission. In Proceedings of the ‘ESMATS 2017’, Hatfield, UK, 20–22 September 2017; Available online: https://esmats.eu/esmatspapers/pastpapers/pdfs/2017/senese.pdf (accessed on 1 October 2022).
- EMIT. Earth Surface Mineral Dust Source Investigation. NASA EOS. Available online: https://eospso.gsfc.nasa.gov/missions/earth-surface-mineral-dust-source-investigation-evi-4 (accessed on 1 October 2022).
- Kopp, G.; Lawrence, G.; Rottman, G. The Total Irradiance Monitor (TIM): Science results. Sol. Phys. 2005, 230, 129–139. [Google Scholar] [CrossRef]
- Lean, J.L.; Coddington, O.; Marchenko, S.V.; Machol, J.; DeLand, M.T.; Kopp, G. Solar Irradiance Variability: Modeling the Measurements. Earth Space Sci. 2020, 7, e2019EA000645. [Google Scholar] [CrossRef]
- Rochford, P.A.; Acharya, P.K.; Adler-Golden, S.M.; Berk, A.; Bernstein, L.S.; Matthew, M.W.; Richtsmeier, S.C.; Gulick, S.; Slusser, J. Validation and Refinement of Hyperspectral/Multispectral Atmospheric Compensation using Shadowband Radiometers. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2898–2907. [Google Scholar] [CrossRef]
- Byrne, G.; Walsh, A.; Thankappan, M.; Broomhall, M.; Hay, E. DEA Analysis Ready Data: Phase 1 Validation Project Report; Data Summary; Geoscience Australia: Canberra, Australia, 2022. [Google Scholar] [CrossRef]
- Jupp, D.L.B.; Li, F.; Byrne, G.; Ong, C.; Lau, I.; Malthus, T.; Thankappan, M.; Fearns, P. Using Irr_Inv, MODTRAN and Spectral Irradiance data to Estimate Atmospheric Parameters; CSIRO Report EP2022-3491; CSIRO: Canberra, Australia, 2022. [CrossRef]
- Berk, A.; van den Bosch, J.; Hawes, F.; Perkins, T.; Conforti, P.F.; Acharya, P.K.; Anderson, G.P.; Kennett, R.G. MODTRAN 6.0 User’s Manual. 2019. Available online: http://MODTRAN.spectral.com/ (accessed on 1 January 2020).
- Thompson, D.R.; Gao, B.C.; Green, R.O.; Roberts, D.A.; Dennison, P.E.; Lundeen, S.R. Atmospheric correction for global mapping spectroscopy: ATREM advances for the HyspIRI preparatory campaign. Remote Sens. Environ. 2015, 167, 64–77. [Google Scholar] [CrossRef]
- Pearlman, J.S.; Crawford, M.; Jupp, D.L.B.; Ungar, S. Foreword to the earth observing 1 special issue. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1147–1148. [Google Scholar] [CrossRef]
- Green, R.O.; Mahowald, N.; Ung, C.; Thompson, D.R.; Bator, L.; Bennet, M.; Bernas, M.; Blackway, N.; Bradley, C.; Cha, J.; et al. The Earth Surface Mineral Dust Source Investigation: An Earth Science Imaging Spectroscopy Mission. In Proceedings of the 2020 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2020; pp. 1–15. [Google Scholar]
- Ångström, A. The parameters of atmospheric turbidity. Tellus 1964, 16, 64–75. [Google Scholar] [CrossRef]
- Fontenla, J.M.; Harder, J.; Livingston, W.; Snow, M.; Woods, T. High-resolution solar spectral irradiance from extreme ultraviolet to far infrared. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
- CEOS. Recommended Solar Irradiance Spectrum for Use in Earth Observation Applications. 2006. Available online: https://eocalibration.wordpress.com/2006/12/ (accessed on 1 August 2019).
- Gross, G.; Helder, D.; Begeman, C.; Leigh, L.; Kaewmanee, M.; Shah, R. Initial cross-calibration of Landsat 8 and Landsat 9 using the simultaneous underfly event. Remote Sens. 2022, 14, 2418. [Google Scholar] [CrossRef]
- Morfitt, R.; Barsi, J.; Levy, R.; Markham, B.; Micijevic, E.; Ong, L.; Scaramuzza, P.; Vanderwerff, K. Landsat-8 Operational Land Imager (OLI) Radiometric Performance On-Orbit. Remote Sens. 2015, 7, 2208–2237. [Google Scholar] [CrossRef]
- Markham, B.; Barsi, J.; (NASA Biospheric Sciences Laboratory, Greenbelt, MD, USA). Personal communication, 2022.
- Patrick, H.; Zarobila, C.; Germer, T. The NIST Robotic Optical Scatter Instrument (ROSI) and its Application to BRDF Measurements of Diffuse Reflectance Standards for Remote Sensing. Proc. SPIE 2013, 8866, 886615. [Google Scholar] [CrossRef]
- Ong, C.; Caccetta, M.; Lau, I.C.; Ong, L.; Middleton, E. Compositional characterisation of the pinnacles vicarious calibration site. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 3059–3062. [Google Scholar] [CrossRef]
- ASD. Fieldspec® 4 User Manual. ASD Document 600540 Rev. J. 2016. Available online: https://www.malvernpanalytical.com/en/products/product-range/asd-range/fieldspec-range (accessed on 1 May 2021).
- Malthus, T.; Ong, C.; Lau, I.; Fearns, P.; Byrne, G.; Thankappan, M.; Chisholm, L.; Suarez Barranco, L.; Clarke, K.; Scarth, P.; et al. A Community Approach to the Standardised Validation of Surface Reflectance Data—A Technical Handbook to Support the Collection of Field Reflectance Data; CSIRO Report EP183233; CSIRO Centre for Earth Observation: Brisbane, Australia, 2019. [CrossRef]
- Lau, I.C.; Thapar, N. Laboratory Spectroscopy Calibration Procedures, Version 2.0; CSIRO Report EP147766; CSIRO: Kensington, Australia, 2015. [CrossRef]
- Ruddick, K.G.; Voss, K.; Banks, A.C.; Boss, E.; Castagna, A.; Frouin, R.; Hieronymi, M.; Jamet, C.; Johnson, B.C.; Kuusk, J.; et al. A Review of Protocols for Fiducial Reference Measurements of Downwelling Irradiance for the Validation of Satellite Remote Sensing Data over Water. Remote Sens. 2019, 11, 1742. [Google Scholar] [CrossRef]
- Morys, M.; Mims, F.M.; Hagerup, S.; Anderson, S.E.; Baker, A.; Kia, J.; Walkup, T. Design, calibration, and performance of MICROTOPS II handheld ozone monitor and Sun photometer. J. Geophys. Res. Atmos. 2001, 106, 14573–14582. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, D.P.; et al. The ERA-Interim Reanalysis: Configuration and Performance of the Data Assimilation System. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Li, F.; Jupp, D.L.B.; Thankappan, M.; Wang, L.W.; Sixsmith, J.; Lewis, A.; Held, A. Land surface brightness temperature retrieved from Landsat data. In Proceedings of the 21st International Congress on Modelling and Simulation, Gold Coast, Australia, 29 November–4 December 2015. [Google Scholar]
- Mitchell, R.M.; Forgan, B.W.; Campbell, S.K. The climatology of Australian aerosol. Atmos. Chem. Phys. 2017, 17, 5131–5154. [Google Scholar] [CrossRef]
- Qin, Y.; Mitchell, R.; Forgan, B.W. Characterizing the Aerosol and Surface Reflectance Over Australia Using AATSR. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6163–6182. [Google Scholar] [CrossRef]
- Geoscience Australia 2022. Available online: https://cmi.ga.gov.au/data-products/dea/365/dea-surface-reflectance-landsat-8-oli-tirs (accessed on 17 February 2022).
- Holben, B.; Eck, T.; Slutsker, I.; Tanré, D.; Buis, J.; Setzer, A.; Vermote, E.; Reagan, J.; Kaufman, Y.; Nakajima, T.; et al. AERONET—A Federated Instrument Network and Data Archive for Aerosol Characterization. Remote Sens. Environ. 1998, 66, 1–16. [Google Scholar] [CrossRef]
- Holben, B.N.; Tanré, D.; Smirnov, A.; Eck, T.F.; Slutsker, I.; Abuhassan, N.; Newcomb, W.W.; Schafer, J.S.; Chatenet, B.; Lavenu, F.; et al. An emerging ground-based aerosol climatology: Aerosol optical depth from AERONET. J. Geophys. Res. Space Phys. 2001, 106, 12067–12097. [Google Scholar] [CrossRef]
- Mitchell, R.M.; Forgan, B.W. Aerosol measurements in the Australian Outback: Intercomparison of sun photometers. J. Atmos. Ocean. Technol. 2003, 20, 54–66. [Google Scholar] [CrossRef]
- Mitchell, R.M.; Campbell, S.K.; Qin, Y.; Gras, J. Performance characteristics of integrating nephelometers in the Australian Outback. J. Atmos. Ocean. Technol. 2009, 26, 984–995. [Google Scholar] [CrossRef]

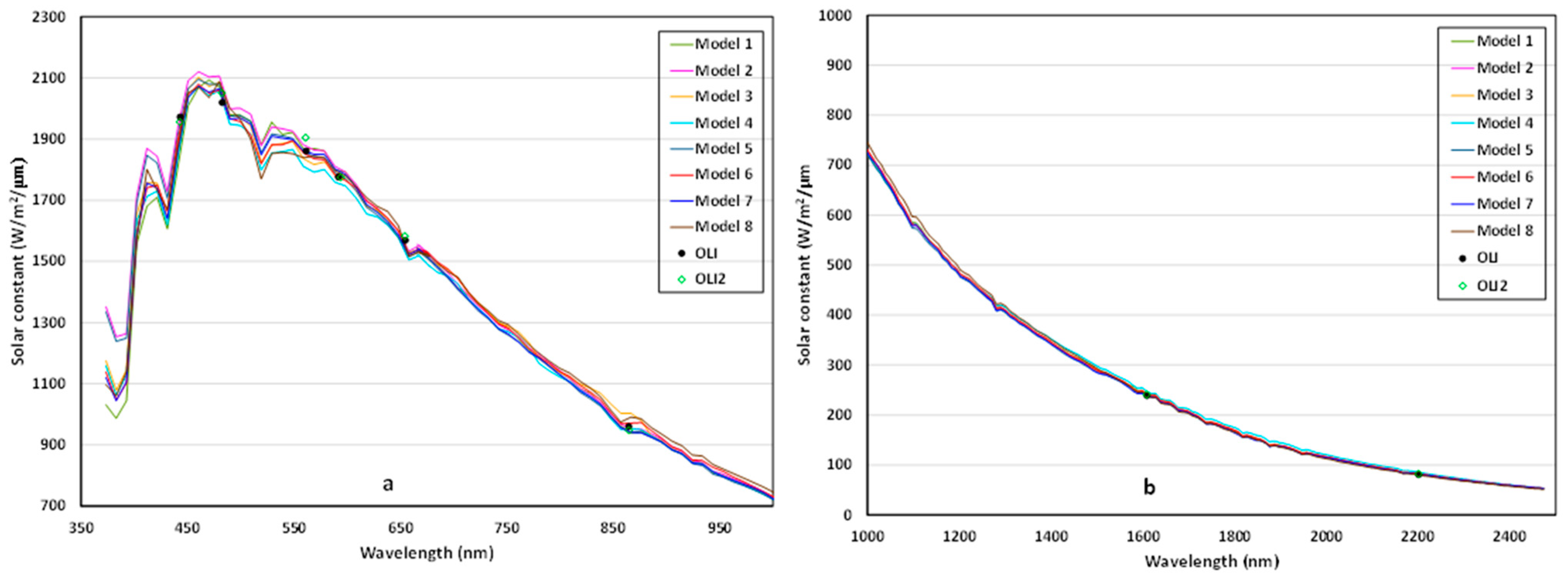

| Model | Solar Spectrum Model |
|---|---|
| 1 | MODTRAN 6 default. Based on [20,25] |
| 2 | MODTRAN 6 LSUNFL 1 based on [6,20] |
| 3 | MODTRAN 6 Thuillier LSUNFL 4 (Thuillier and Kurucz composite) [20] |
| 4 | CEOS recommendation CEOS (2006) [26] based on [9] |
| 5 | Bias-adjusted version of Model 2 [3] |
| 6 | Chance and Kurucz (2010) SA2010 spectrum [5] |
| 7 | Coddington et al. (2021) TSIS-1 spectrum [8] |
| 8 | Meftah et al. (2020) SOLAR-ISS spectrum [7] |
| (a) | ||||||||||
| Model | OLI | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| Band | cwl (nm) | |||||||||
| 1 | 442.98 | 1972.28 | 1863.30 | 1983.70 | 1921.90 | 1895.60 | 1959.90 | 1940.70 | 1912.70 | 1931.80 |
| 2 | 482.59 | 2019.63 | 2028.70 | 2056.90 | 2032.60 | 2004.60 | 2032.20 | 2010.50 | 2017.10 | 2015.80 |
| 3 | 561.33 | 1861.11 | 1880.90 | 1886.70 | 1846.20 | 1820.70 | 1864.10 | 1853.20 | 1867.20 | 1842.90 |
| 4 | 654.61 | 1569.34 | 1563.40 | 1576.50 | 1571.30 | 1549.50 | 1557.50 | 1570.50 | 1564.90 | 1576.40 |
| 5 | 864.57 | 960.37 | 951.66 | 959.74 | 999.82 | 951.71 | 948.22 | 972.73 | 948.64 | 984.55 |
| 6 | 1609.10 | 238.83 | 243.90 | 242.35 | 242.41 | 247.56 | 239.44 | 242.50 | 238.73 | 240.14 |
| 7 | 2201.20 | 80.50 | 81.99 | 82.48 | 82.49 | 85.46 | 81.49 | 82.53 | 81.42 | 80.05 |
| 8 | 591.67 | 1776.14 | 1766.90 | 1774.70 | 1748.10 | 1723.90 | 1753.40 | 1749.90 | 1757.90 | 1745.70 |
| 9 | 1373.50 | 375.33 | 360.24 | 361.05 | 361.11 | 366.98 | 356.72 | 361.28 | 358.56 | 366.76 |
| (b) | ||||||||||
| Model | OLI2 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| Band | cwl (nm) | |||||||||
| 1 | 442.76 | 1956.00 | 1858.00 | 1979.20 | 1916.60 | 1890.30 | 1955.40 | 1936.50 | 1907.60 | 1926.80 |
| 2 | 482.30 | 2051.00 | 2029.20 | 2057.40 | 2033.40 | 2005.30 | 2032.70 | 2011.10 | 2017.50 | 2016.30 |
| 3 | 560.92 | 1905.00 | 1882.60 | 1888.20 | 1847.40 | 1821.90 | 1865.60 | 1854.60 | 1868.60 | 1844.10 |
| 4 | 654.30 | 1583.00 | 1564.50 | 1577.40 | 1572.30 | 1550.60 | 1558.50 | 1571.30 | 1565.90 | 1577.30 |
| 5 | 864.61 | 948.70 | 951.65 | 959.76 | 999.58 | 951.73 | 948.25 | 972.85 | 948.66 | 984.70 |
| 6 | 1608.40 | 241.00 | 244.17 | 242.65 | 242.72 | 247.90 | 239.74 | 242.82 | 239.02 | 240.47 |
| 7 | 2201.10 | 82.29 | 82.03 | 82.52 | 82.53 | 85.52 | 81.53 | 82.57 | 81.46 | 80.09 |
| 8 | 593.95 | 1775.00 | 1759.90 | 1767.90 | 1742.10 | 1718.00 | 1746.60 | 1744.00 | 1751.40 | 1740.40 |
| 9 | 1374.00 | 401.00 | 359.92 | 360.74 | 360.80 | 366.66 | 356.41 | 360.97 | 358.26 | 366.45 |
| Time | Results | Model | Average | CV | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||||
| t1 | RMS | 7.239 | 8.468 | 6.247 | 7.130 | 9.663 | 5.793 | 6.219 | 7.1075 | 7.233 | 17.74 |
| AOD550 | 0.0593 | 0.1890 | 0.1144 | 0.0755 | 0.1588 | 0.0903 | 0.0812 | 0.0889 | 0.107 | 41.73 | |
| n | 1.450 | 1.450 | 1.450 | 1.4500 | 1.450 | 1.450 | 1.450 | 1.450 | 1.450 | 0.00 | |
| W | 0.5065 | 0.4859 | 0.5065 | 0.5057 | 0.4581 | 0.5217 | 0.4863 | 0.5465 | 0.502 | 5.24 | |
| Uoz | 0.3546 | 0.2130 | 0.2257 | 0.1900 | 0.1803 | 0.2672 | 0.2980 | 0.2601 | 0.249 | 23.57 | |
| t2 | RMS | 7.999 | 9.389 | 6.742 | 8.026 | 10.798 | 6.296 | 7.150 | 7.3101 | 7.964 | 18.64 |
| AOD550 | 0.0525 | 0.1895 | 0.1105 | 0.0702 | 0.1583 | 0.0853 | 0.0760 | 0.084 | 0.103 | 45.74 | |
| n | 1.450 | 1.450 | 1.450 | 1.450 | 1.450 | 1.450 | 1.450 | 1.45 | 1.450 | 0.00 | |
| W | 0.4808 | 0.4622 | 0.4810 | 0.4805 | 0.4354 | 0.4954 | 0.4616 | 0.5192 | 0.477 | 5.23 | |
| Uoz | 0.3504 | 0.2045 | 0.2170 | 0.1784 | 0.1693 | 0.2598 | 0.2913 | 0.2528 | 0.240 | 25.33 | |
| t3 | RMS | 9.093 | 10.761 | 7.659 | 9.322 | 12.390 | 7.222 | 8.498 | 7.8808 | 9.103 | 19.07 |
| AOD550 | 0.0391 | 0.1846 | 0.1004 | 0.0585 | 0.1521 | 0.0738 | 0.0645 | 0.0728 | 0.093 | 53.82 | |
| n | 1.450 | 1.450 | 1.450 | 1.450 | 1.450 | 1.450 | 1.450 | 1.45 | 1.450 | 0.00 | |
| W | 0.4716 | 0.4546 | 0.4722 | 0.4717 | 0.4279 | 0.4861 | 0.4529 | 0.5096 | 0.468 | 5.18 | |
| Uoz | 0.3310 | 0.1806 | 0.1928 | 0.1508 | 0.1427 | 0.2369 | 0.2690 | 0.23 | 0.217 | 29.22 | |
| Mean | RMS | 8.110 | 9.539 | 6.883 | 8.159 | 10.950 | 6.437 | 7.289 | 7.433 | 8.100 | 18.40 |
| AOD550 | 0.0503 | 0.1877 | 0.1084 | 0.0681 | 0.1564 | 0.0831 | 0.0739 | 0.0819 | 0.101 | 46.81 | |
| N | 1.450 | 1.450 | 1.450 | 1.450 | 1.450 | 1.450 | 1.450 | 1.450 | 1.450 | 0.00 | |
| W | 0.4863 | 0.4676 | 0.4866 | 0.4860 | 0.4405 | 0.5011 | 0.4669 | 0.5251 | 0.482 | 5.22 | |
| Uoz | 0.3453 | 0.1994 | 0.2118 | 0.1731 | 0.1641 | 0.2546 | 0.2861 | 0.2476 | 0.235 | 25.90 | |
| Models 2, 5 | Models 3, 4, 6, 7, 8 | Model 1 | |
|---|---|---|---|
| RMS | 10.24 | 7.24 | 8.11 |
| AOD550 | 0.1721 | 0.0831 | 0.0503 |
| W | 0.4540 | 0.4931 | 0.4863 |
| Uoz | 0.1817 | 0.2347 | 0.3453 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, F.; Jupp, D.L.B.; Markham, B.L.; Lau, I.C.; Ong, C.; Byrne, G.; Thankappan, M.; Oliver, S.; Malthus, T.; Fearns, P. Choice of Solar Spectral Irradiance Model for Current and Future Remote Sensing Satellite Missions. Remote Sens. 2023, 15, 3391. https://doi.org/10.3390/rs15133391
Li F, Jupp DLB, Markham BL, Lau IC, Ong C, Byrne G, Thankappan M, Oliver S, Malthus T, Fearns P. Choice of Solar Spectral Irradiance Model for Current and Future Remote Sensing Satellite Missions. Remote Sensing. 2023; 15(13):3391. https://doi.org/10.3390/rs15133391
Chicago/Turabian StyleLi, Fuqin, David L. B. Jupp, Brian L. Markham, Ian C. Lau, Cindy Ong, Guy Byrne, Medhavy Thankappan, Simon Oliver, Tim Malthus, and Peter Fearns. 2023. "Choice of Solar Spectral Irradiance Model for Current and Future Remote Sensing Satellite Missions" Remote Sensing 15, no. 13: 3391. https://doi.org/10.3390/rs15133391
APA StyleLi, F., Jupp, D. L. B., Markham, B. L., Lau, I. C., Ong, C., Byrne, G., Thankappan, M., Oliver, S., Malthus, T., & Fearns, P. (2023). Choice of Solar Spectral Irradiance Model for Current and Future Remote Sensing Satellite Missions. Remote Sensing, 15(13), 3391. https://doi.org/10.3390/rs15133391










