Collaborative Trajectory Planning and Resource Allocation for Multi-Target Tracking in Airborne Radar Networks under Spectral Coexistence
Abstract
1. Introduction
1.1. Literature Review and Motivation
1.2. Our Contributions
- A closed-form expression for the Bayesian Cramér–Rao lower bound (BCRLB) with the consideration of spectral coexistence is theoretically calculated and employed as the performance metric to quantify the precision of target state estimates. As stated previously, it is incorrect to adopt the traditional BCRLB in an ideal situation to evaluate MTT performance for radar systems with spectral coexistence. In the current study, we analytically derive the BCRLB for airborne radar networks with spectral coexistence in terms of the kinematic velocity, course angle, radar selection, illumination power, dwell time, and signal effective bandwidth of multiple airborne radars. In contrast to the target tracking performance metric computed in [29,30,31], we extend the BCRLB from the power domain of the static radar networks to the multi-domain of airborne radar networks, where the computational complexity of BCRLB grows exponentially with the number of radar nodes and available resources.
- The problem of CTPRA for MTT in airborne radar networks with the consideration of spectral coexistence is formulated as a mathematical optimization model under the constraints of the predetermined tolerable level of interference energy, platform kinematic limitations, and several illumination resource budgets. Previously, most of the resource allocation studies were based on ideal detection or clutter scenarios, whereas the resource-aware management problem for MTT in airborne radar networks under the consideration of spectral coexistence has not been investigated yet. In such a case, these transmit resource allocation schemes are no longer applicable. Thus, we need to establish a suitable resource management mechanism and coordinate appropriate working parameters to track multiple targets with certain resource budgets in a spectral coexistence environment. To be more specific, the ultimate goal of the CTPRA strategy is to enhance the tracking accuracies of multiple targets of the underlying system under the spectral coexistence environment by collaboratively adapting the kinematic velocity, course angle, radar assignment, transmit power, dwell time, and signal effective bandwidth of each airborne radar node while satisfying the given constraint conditions.
- In order to tackle the resulting mixed-integer programming, non-linear, non-convex optimization problem, we design an iterative and efficient four-stage solution algorithm, which incorporates the SDP, PSO, and cyclic minimization algorithm. In the CTPRA problem, the intractability originates from the following: (i) the target-to-radar assignment is a binary parameter, whereas the kinematic velocity, course angle, transmit power, dwell time, and signal effective bandwidth of each airborne radar are continuous parameters, respectively, and (ii) the six adaptable parameters are highly coupled regarding the objective function and constraints. Hence, it is challenging and rather difficult to solve the original problem and determine its optimal solutions in real time. To realize this, we develop the following four-stage solution algorithm to obtain one of its feasible solutions, which significantly lowers the computational complexity when compared with that of the exhaustive-search-based technique.
- A resource-aware closed-loop feedback processing framework for MTT in airborne radar networks under spectral coexistence is established. Owing to the non-linear characteristics of the measurement model and the convergence speed demand, the extended Kalman filtering (EKF) approach is used to estimate the multi-target states. The multi-target state estimates collected by all the individual airborne radars are directly sent to the fusion center for further processing to obtain the optimal MTT accuracy. Next, the MTT results for the next time interval are utilized to calculate the criterion function for the MTT task. After solving the CTPRA problem, the flight trajectory and resource optimization results are sent back to local airborne platforms to implement the MTT operation for the next round of transmission.
1.3. Organization of the Article
2. System Model
2.1. Target Dynamic Model
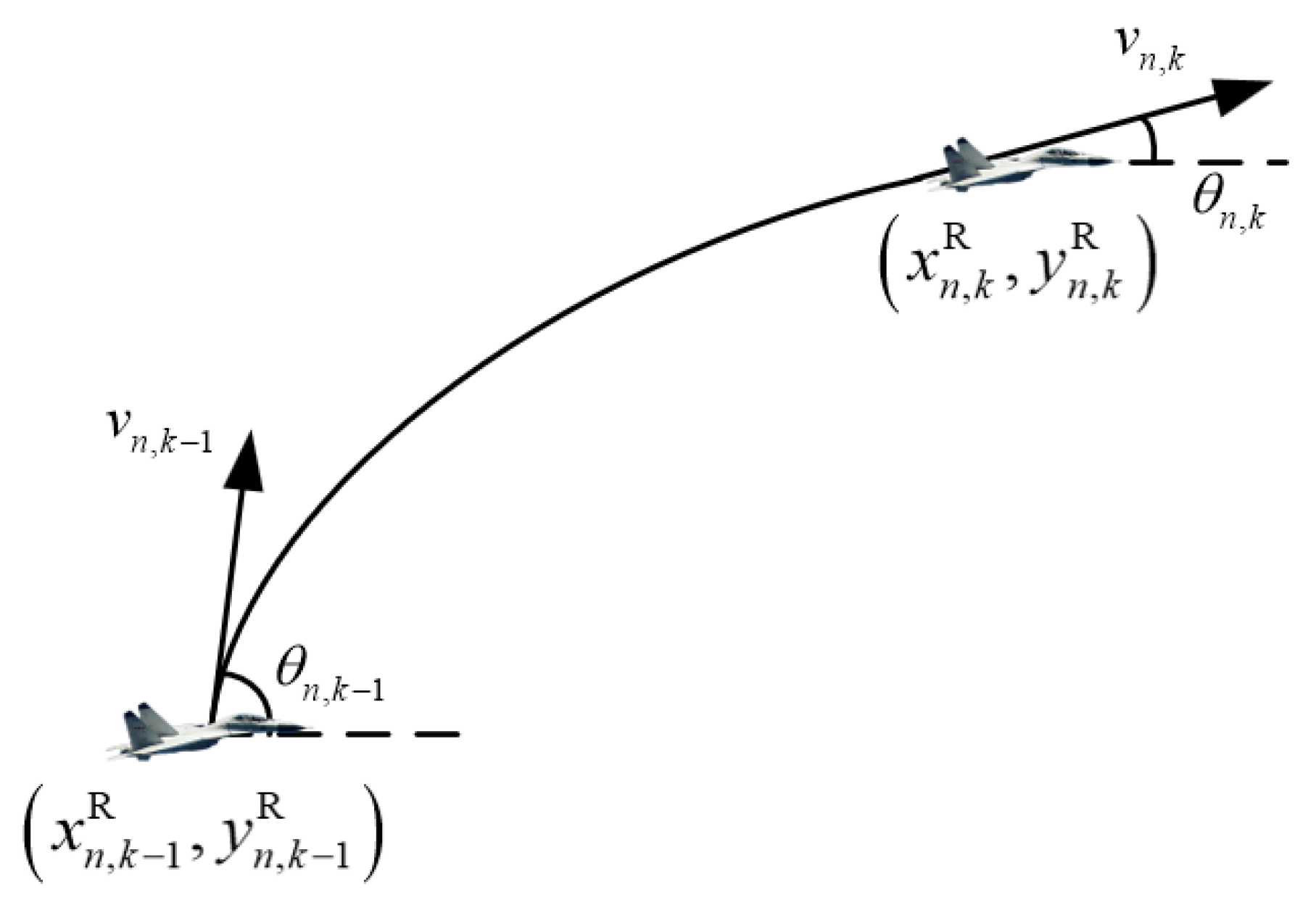
2.2. Airborne Radar Kinematic Model
2.3. Measurement Model
3. Proposed CTPRA Strategy for MTT
3.1. Basis of the Technique
3.2. MTT Performance Metric under Spectral Coexistence
3.3. Problem Formulation
3.4. Solution Technique
| Algorithm 1: The Detailed Steps of the PSO Method for Trajectory Planning in Airborne Radar Networks |
 |
3.5. Resource-Aware Closed-Loop Signal Processing Framework for MTT
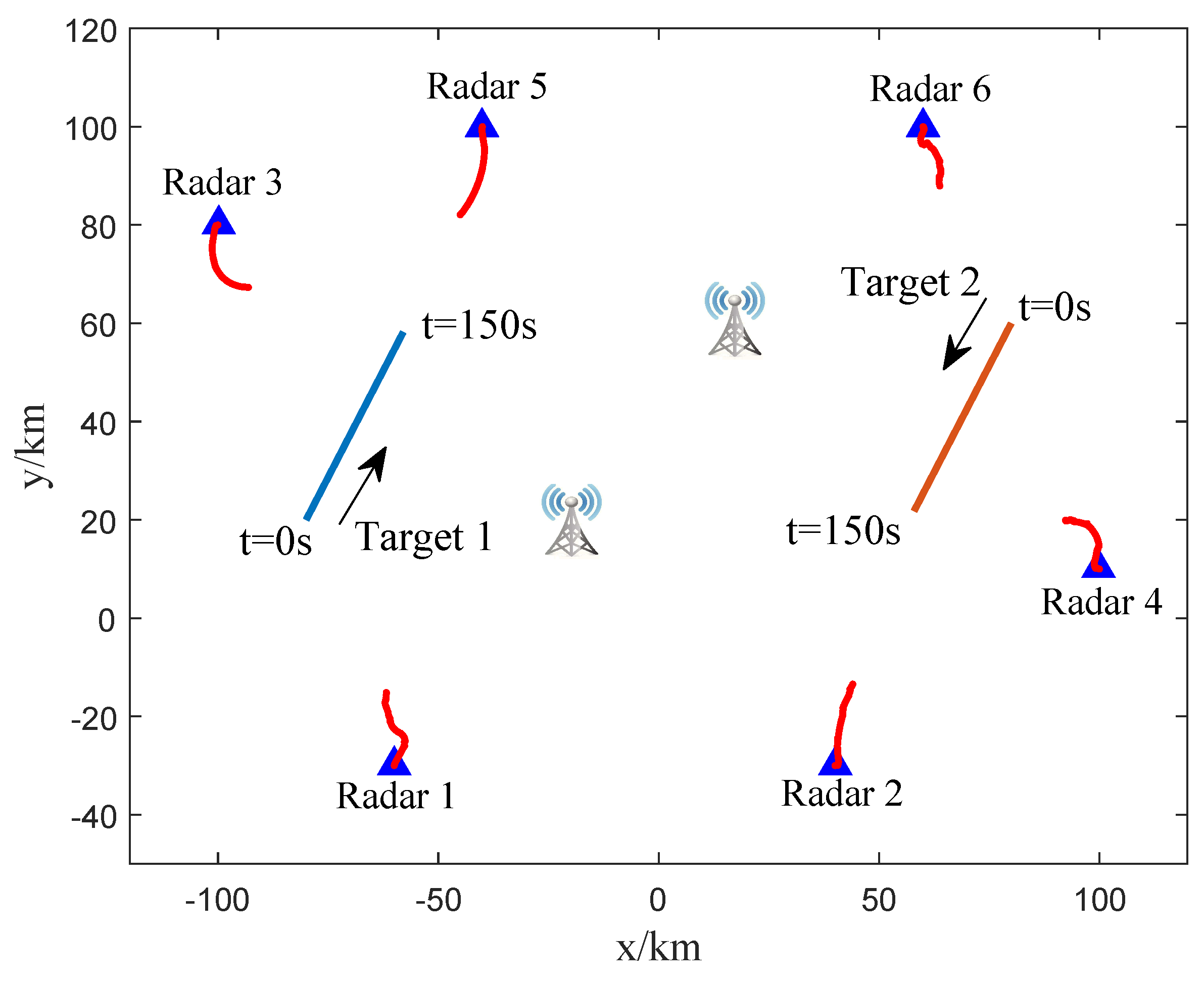
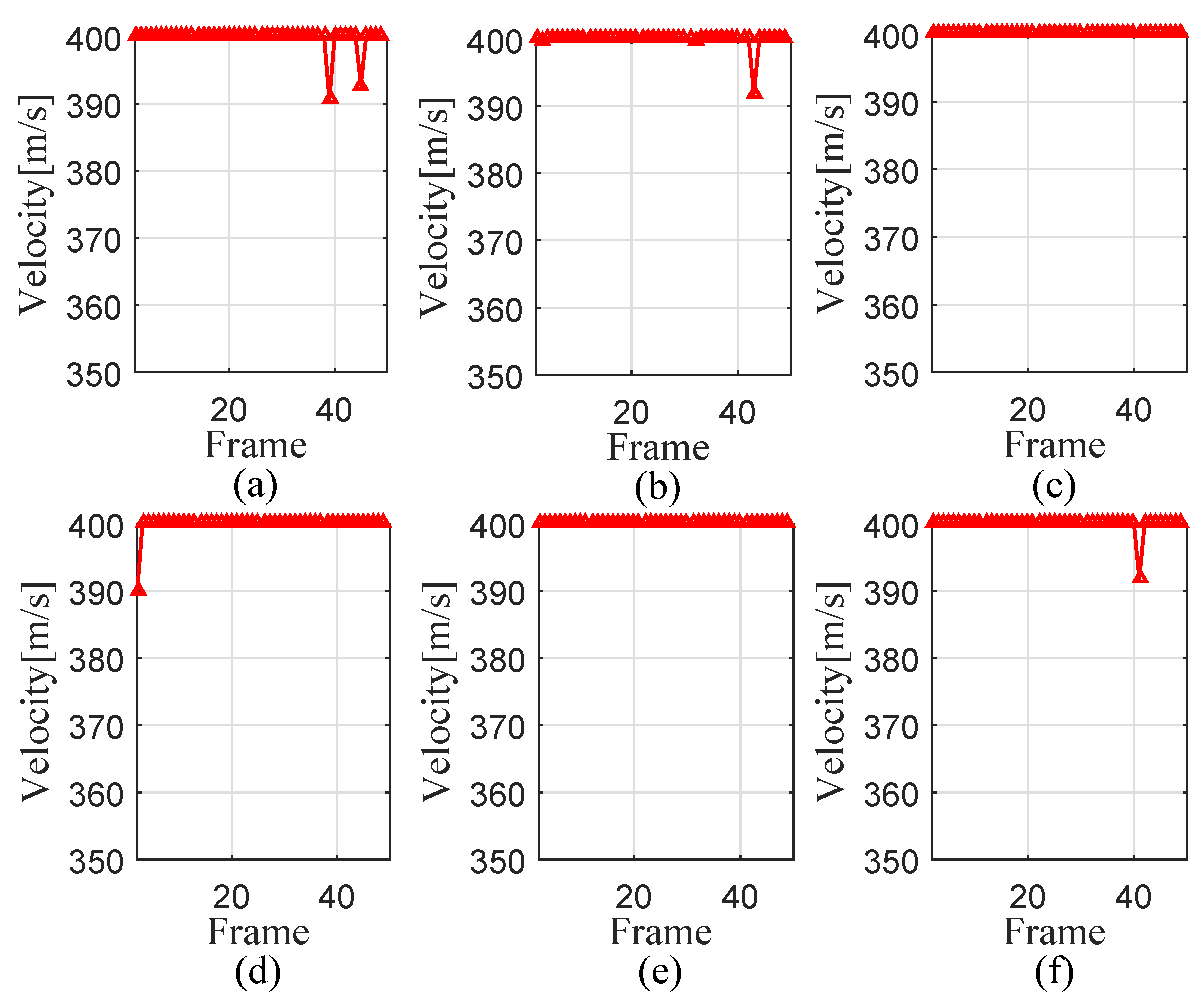
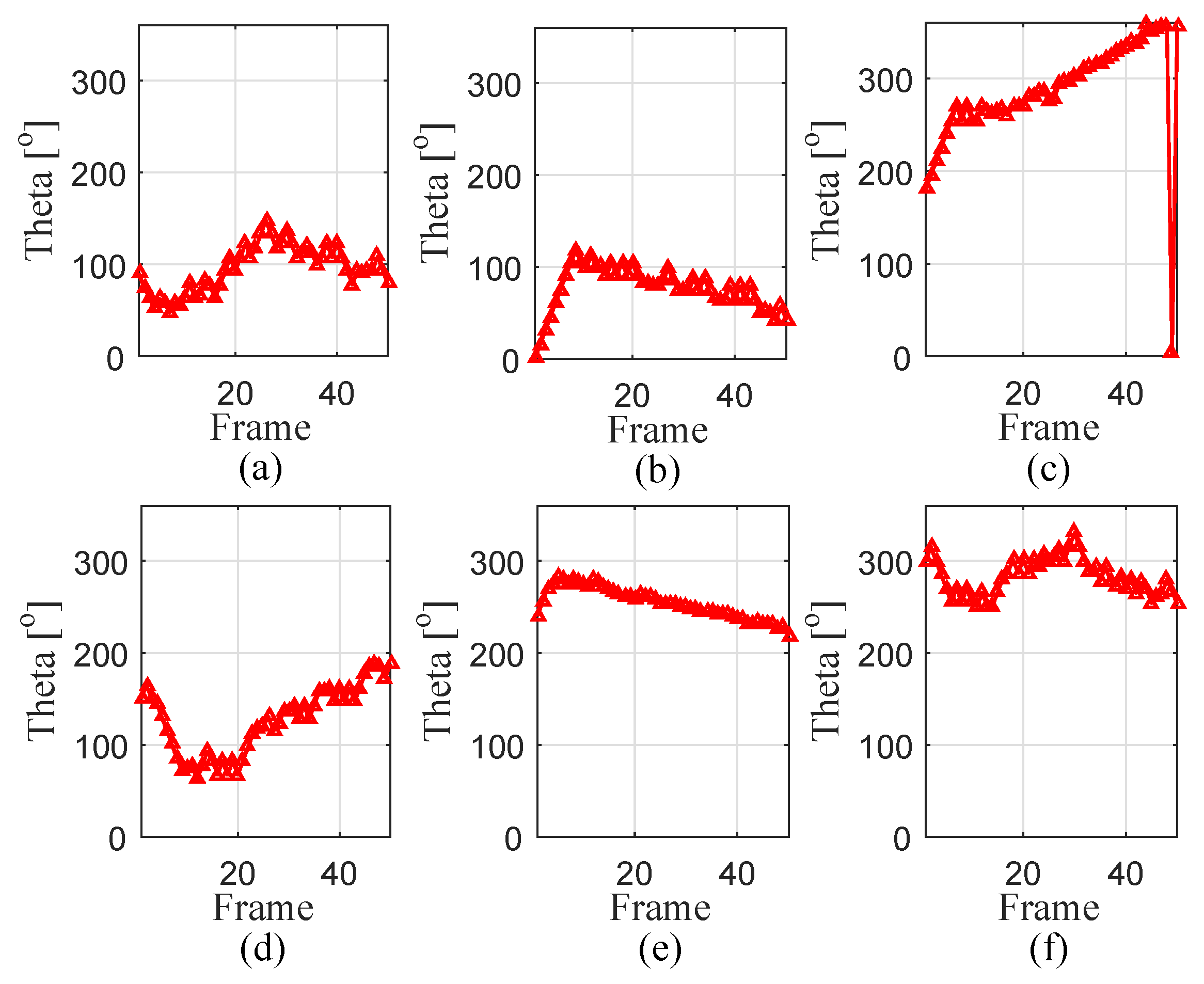
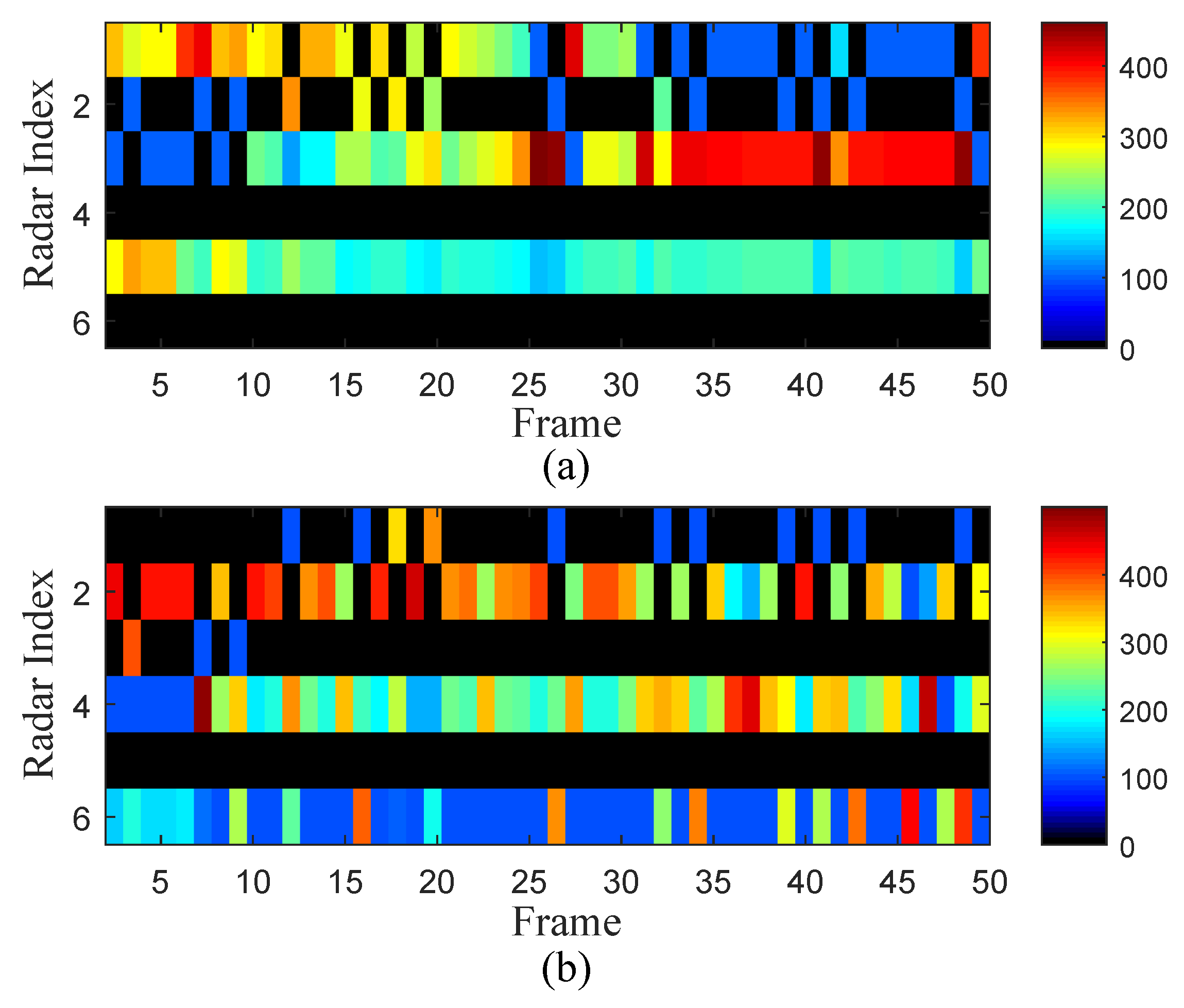
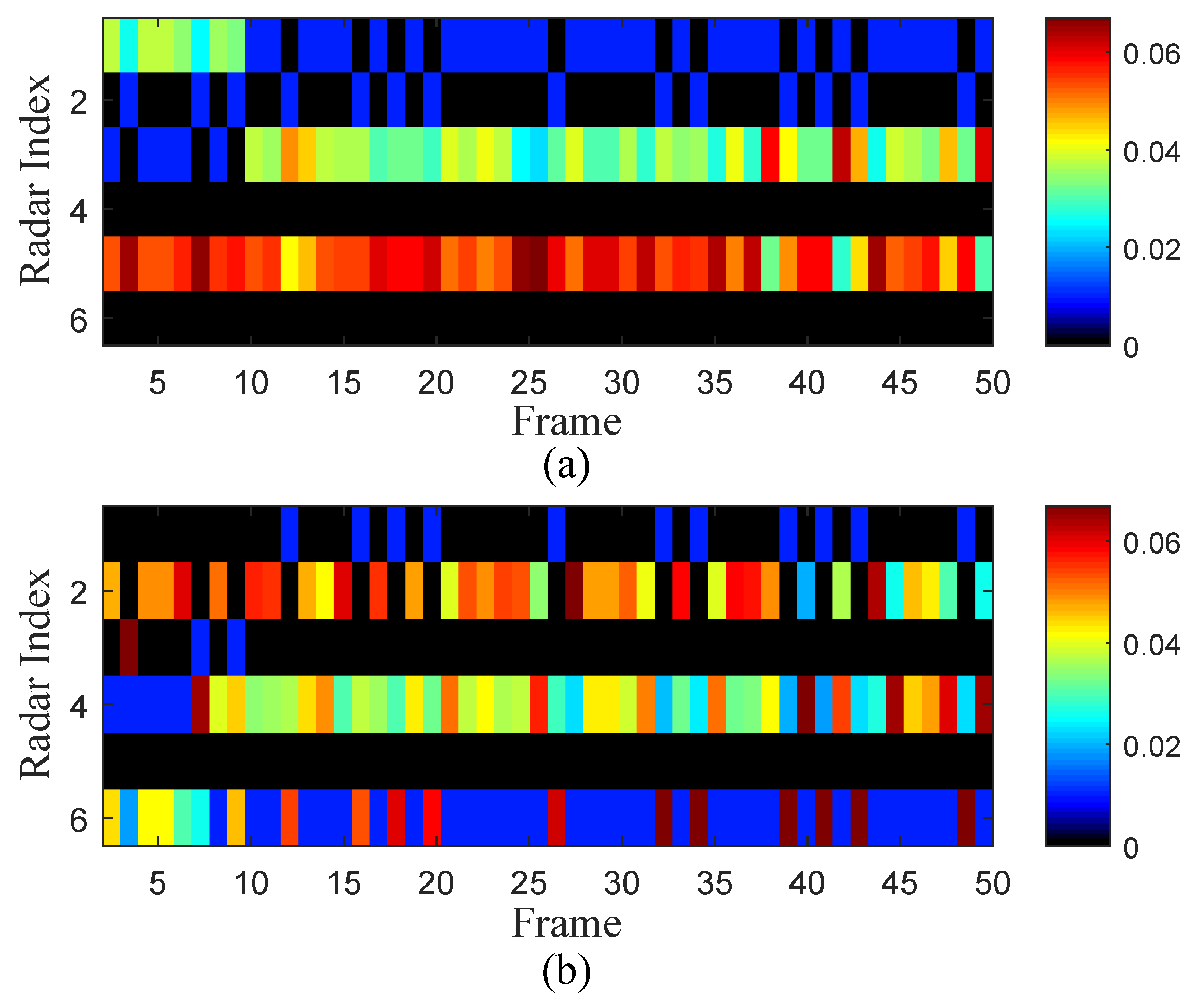
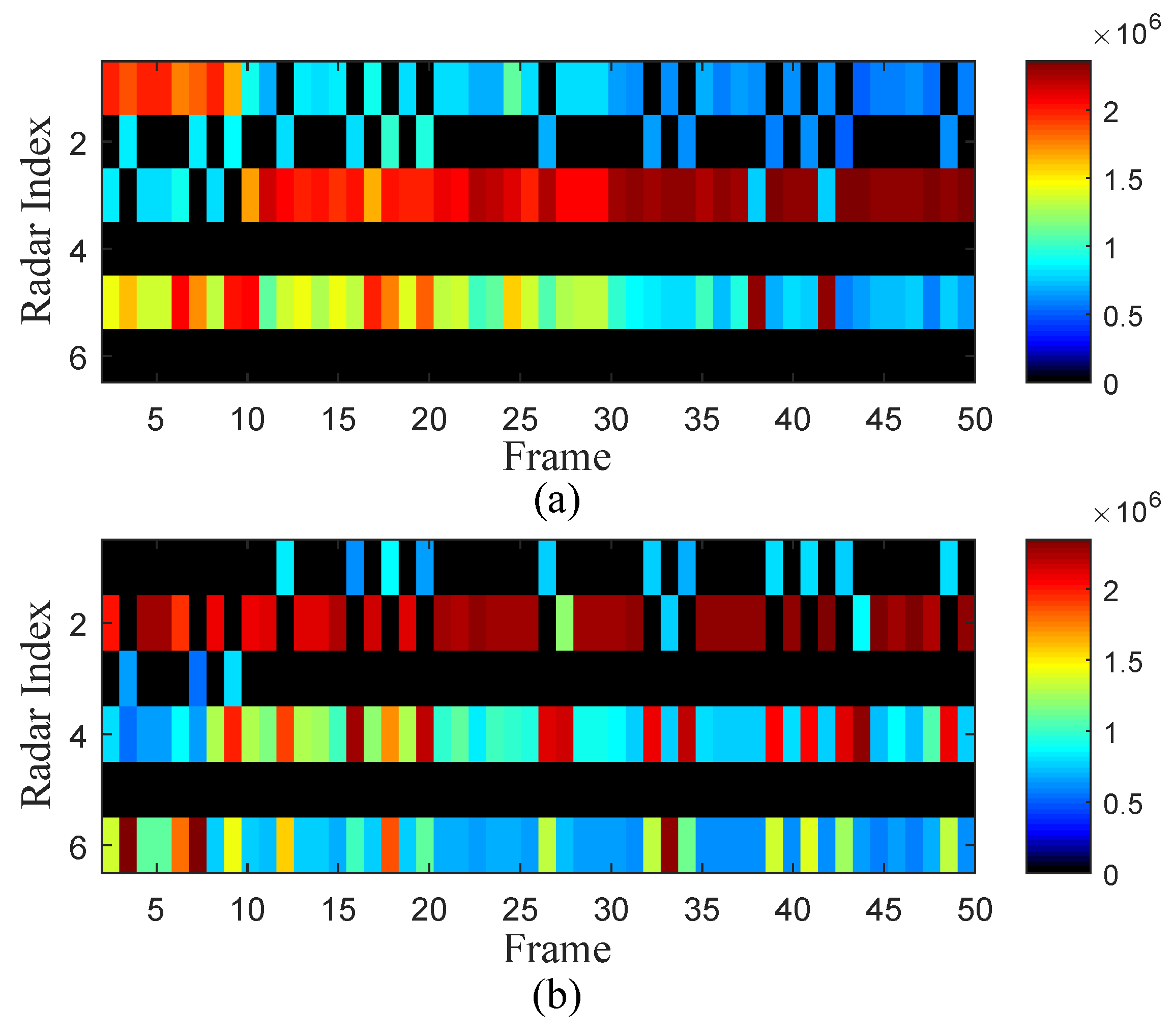
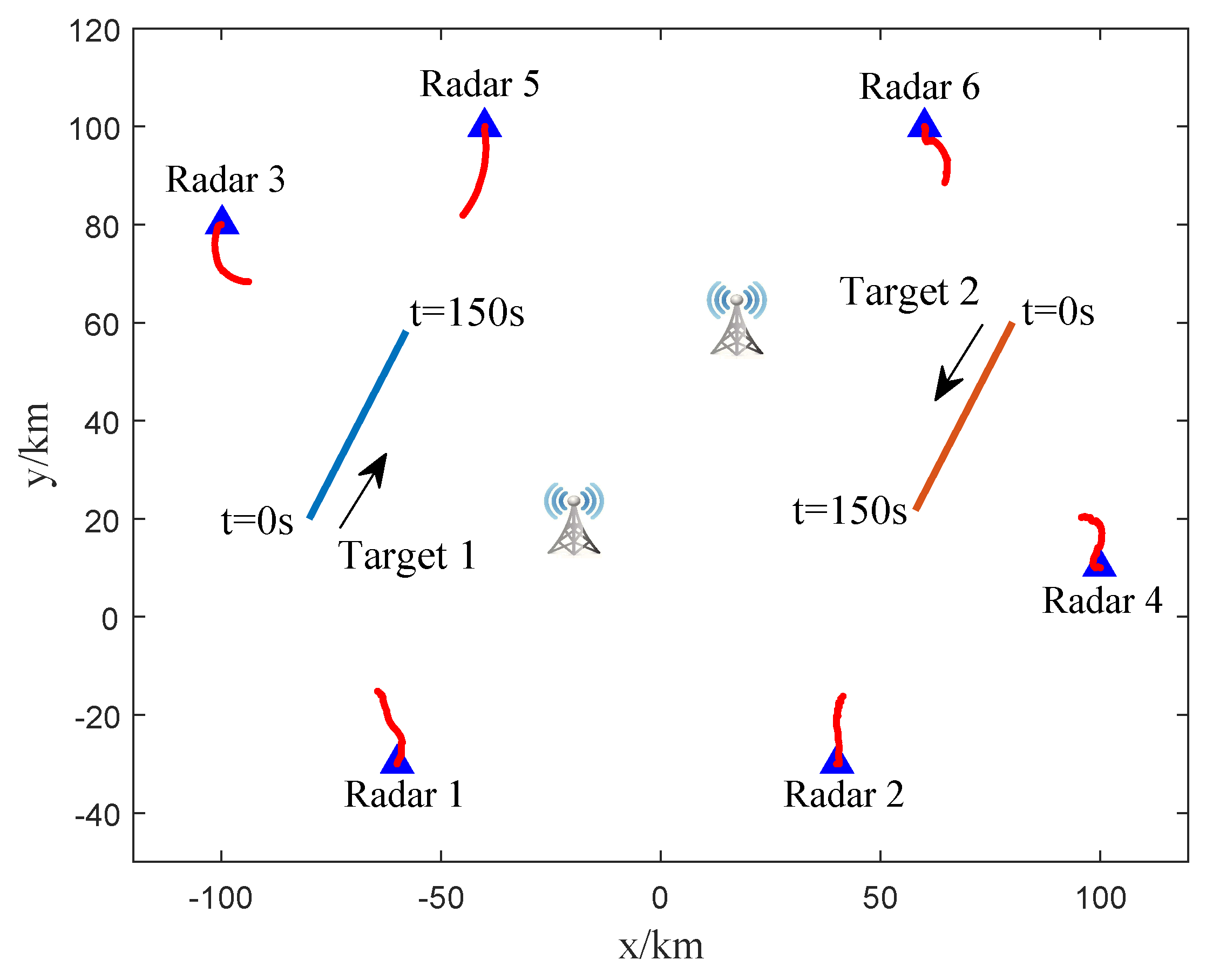
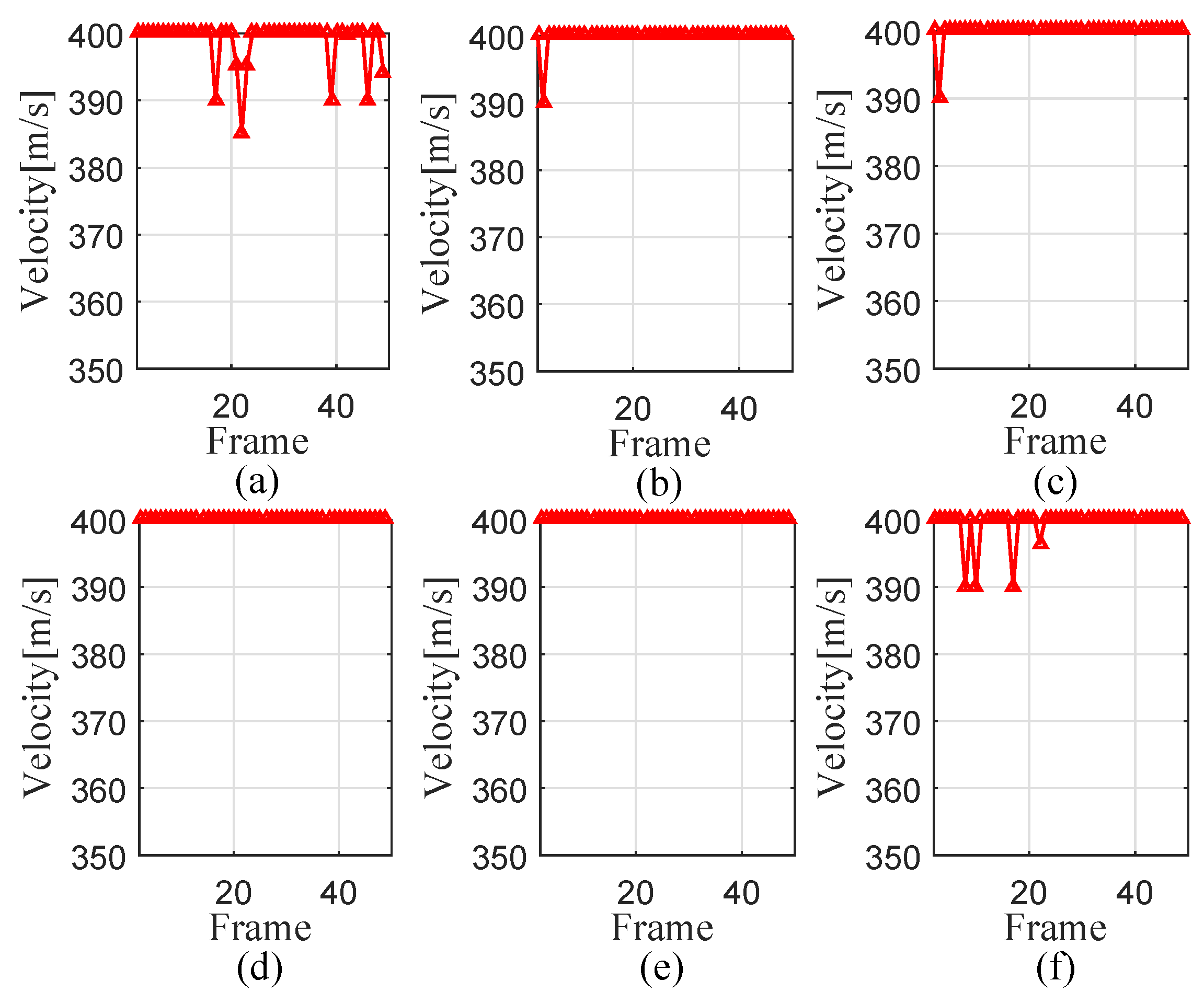
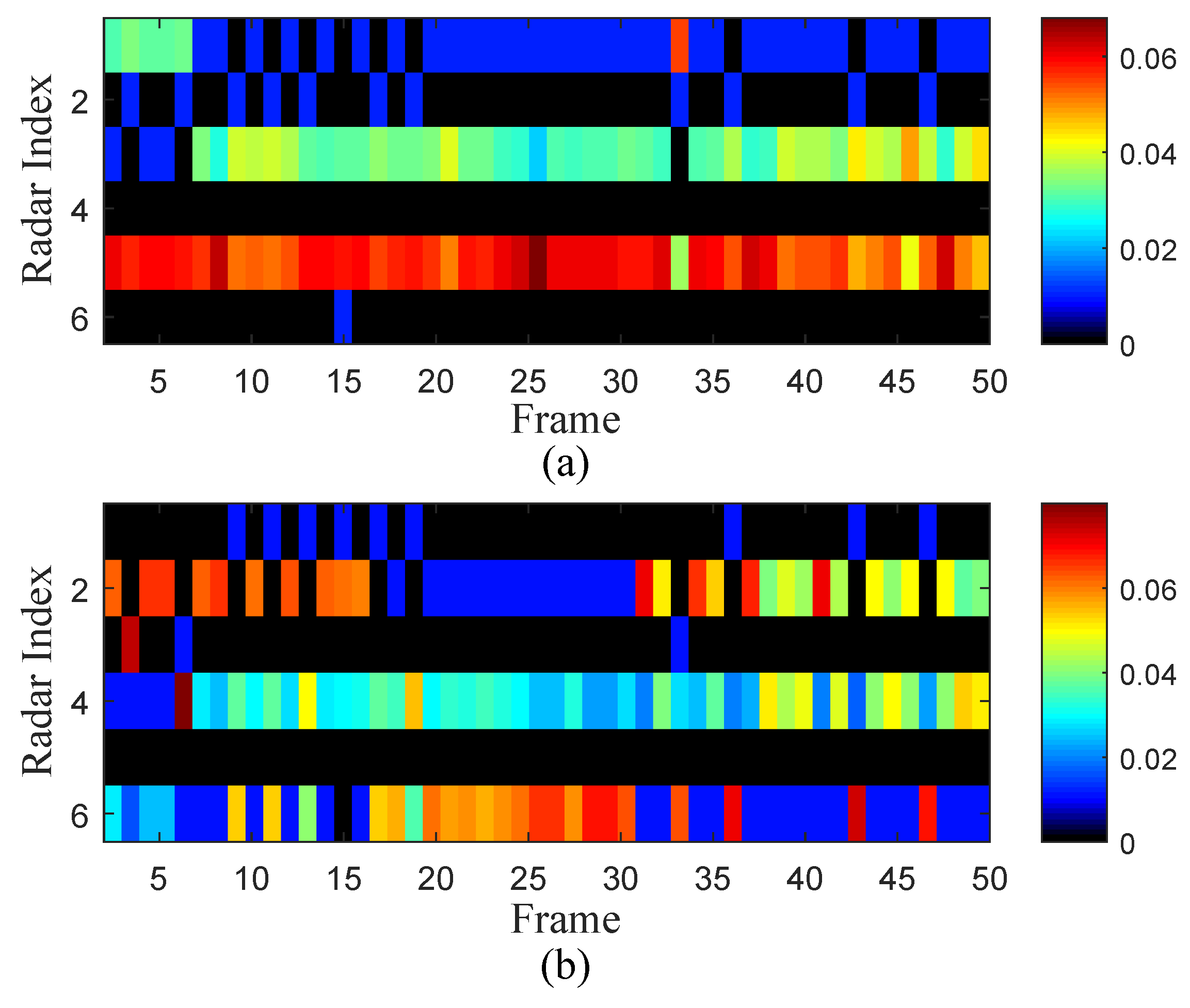
4. Numerical Results
4.1. Parameter Designation
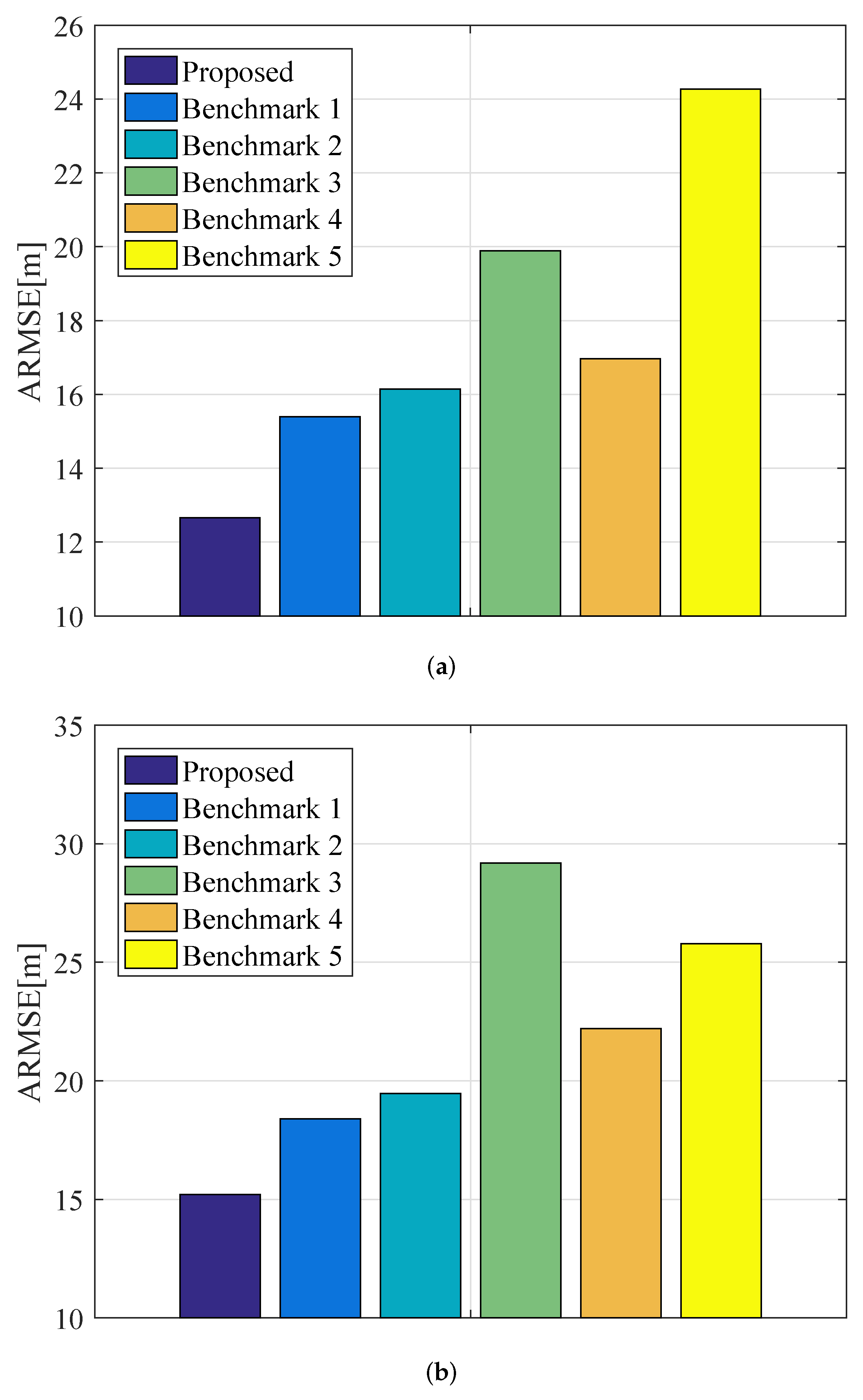
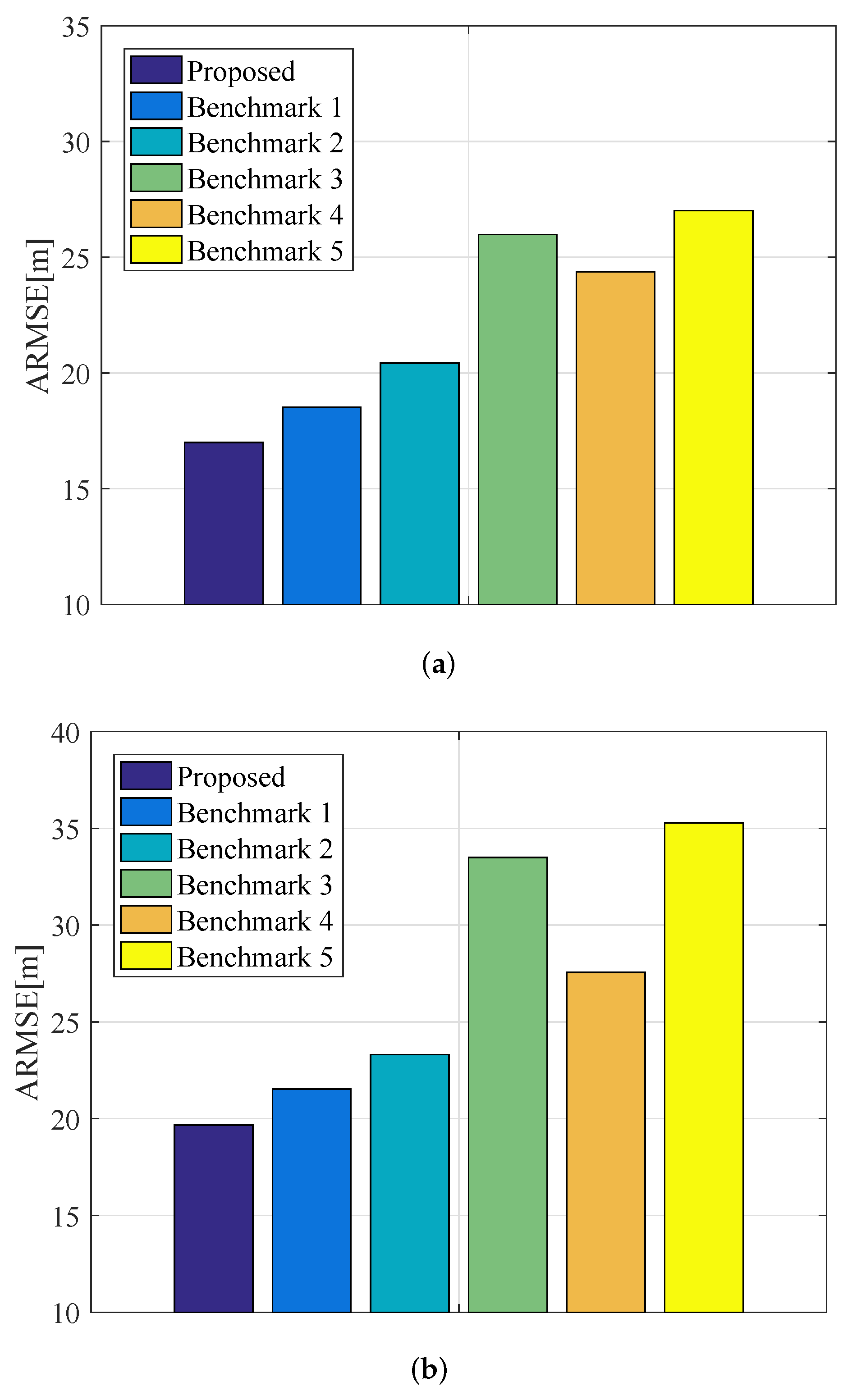
4.2. Experiment 1
- Benchmark 1: This benchmark jointly optimizes the kinematic velocity, course angle, radar assignment, transmit power, and dwell time of each airborne radar node by utilizing the developed four-stage-based solution technique, whereas the signal effective bandwidth of multiple airborne radars is uniformly allocated [17].
- Benchmark 2: This benchmark adopts the developed four-stage-based solution algorithm to collaboratively coordinate the kinematic velocity, course angle, radar assignment, and transmit power of each airborne radar node, while the dwell time and signal effective bandwidth of multiple airborne radars are uniformly distributed [2].
- Benchmark 3: In this benchmark, only the kinematic velocity, course angle, and radar assignment of each airborne platform are jointly optimized, whereas the other illumination resources are uniformly allocated to the chosen airborne radar nodes.
- Benchmark 5: This benchmark randomly assigns the airborne radars to multiple targets. For the selected radar nodes with respect to the corresponding targets, the flight trajectory and illumination resource are optimally designed by solving the problem in (21) with the four-stage-based solution approach.Figure 9. Comparison of the achievable ARMSE by employing various algorithms for different targets in Experiment 1: (a) target 1; (b) target 2.Figure 9. Comparison of the achievable ARMSE by employing various algorithms for different targets in Experiment 1: (a) target 1; (b) target 2.
4.3. Experiment 2
4.4. Experiment 3
5. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, W.W.; Shi, C.G.; Zhou, J.J.; Lv, R.G. Joint aperture and transmit resource allocation strategy for multitarget localization in the phased array radar network. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 1551–1565. [Google Scholar]
- Zhang, Y.S.; Pan, M.H.; Han, Q.H.; Long, W.J.; Yang, S.W. Joint power allocation and route planning scheme for multitarget tracking in airborne radar network under multiuncertainty. IEEE Sens. J. 2023, 23, 7705–7718. [Google Scholar] [CrossRef]
- Xie, M.C.; Yi, W.; Kirubarajan, T.; Kong, L.J. Joint node selection and power allocation strategy for multitarget tracking in decentralized radar networks. IEEE Trans. Signal Process. 2018, 66, 729–743. [Google Scholar] [CrossRef]
- Zhang, H.W.; Liu, W.J.; Shi, J.P.; Fei, T.Y.; Zong, B.F. Joint detection threshold optimization and illumination time allocation strategy for cognitive tracking in a networked radar system. IEEE Trans. Signal Process. 2022, 70, 5833–5847. [Google Scholar] [CrossRef]
- Yi, W.; Yuan, Y.; Kirubarajan, T.; Kong, L.J. Resource scheduling for distributed multi-target tracking in netted colocated MIMO radar systems. IEEE Trans. Signal Process. 2020, 68, 1602–1617. [Google Scholar] [CrossRef]
- Sun, H.; Li, M.; Zuo, L.; Zhang, P. Joint radar scheduling and beampattern design for multitarget tracking in netted colocated MIMO radar systems. IEEE Signal Process. Lett. 2021, 28, 1863–1867. [Google Scholar] [CrossRef]
- Dai, J.H.; Yan, J.K.; Lv, J.D.; Ma, L.; Pu, W.Q.; Liu, H.W.; Greco, M. Composed resource optimization for multitarget tracking in active and passive radar network. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Du, Y.; Liao, K.F.; Ouyang, S.; Li, J.J.; Huang, G.J. Time and aperture resource allocation strategy for multitarget ISAR imaging in a radar network. IEEE Sens. J. 2020, 20, 3196–3206. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, Q.; Luo, Y.; Liu, X.W.; Ni, J.C.; Su, L.H. Joint optimization of time and aperture resource allocation strategy for multi-target ISAR imaging in radar sensor network. IEEE Sens. J. 2021, 21, 19570–19581. [Google Scholar] [CrossRef]
- Su, Y.; Cheng, T.; He, Z.S. Joint resource and detection threshold optimization for maneuvering targets tracking in colocated MIMO radar network. IEEE Trans. Aerosp. Electron. Syst. 2023. [Google Scholar] [CrossRef]
- Yan, J.K.; Pu, W.Q.; Zhou, S.H.; Liu, H.W.; Bao, Z. Collaborative detection and power allocation framework for target tracking in multiple radar system. Inf. Fusion 2020, 55, 173–183. [Google Scholar] [CrossRef]
- Li, X.; Cheng, T.; Su, Y.; Peng, H. Joint time-space resource allocation and waveform selection for the collocated MIMO radar in multiple targets tracking. Signal Process. 2020, 176, 107650. [Google Scholar] [CrossRef]
- Lawrence, D.E. Low probability of intercept antenna array beamforming. IEEE Trans. Antennas Propag. 2010, 58, 2858–2865. [Google Scholar] [CrossRef]
- Govoni, M.A.; Li, H.B.; Kosinski, J.A. Low probability of intercept of an advanced noise radar waveform with linear-FM. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 1351–1356. [Google Scholar]
- Shi, C.G.; Wang, F.; Sellathurai, M.; Zhou, J.J.; Salous, S. Power minimization-based robust OFDM radar waveform design for radar and communication systems in coexistence. IEEE Trans. Signal Process. 2018, 66, 1316–1330. [Google Scholar] [CrossRef]
- Zhou, C.W.; Gu, Y.J.; He, S.B.; Shi, Z.G. A robust and efficient algorithm for coprime array adaptive beamforming. IEEE Trans. Veh. Technol. 2018, 67, 1099–1112. [Google Scholar] [CrossRef]
- Shi, C.G.; Dai, X.R.; Wang, Y.J.; Zhou, J.J.; Salous, S. Joint route optimization and multidimensional resource management scheme for airborne radar network in target tracking application. IEEE Syst. J. 2022, 16, 6669–6680. [Google Scholar] [CrossRef]
- Yuan, Y.; Yi, W.; Hoseinnezhad, R.; Varshney, P.K. Robust power allocation for resource-aware multi-target tracking with colocated MIMO radars. IEEE Trans. Signal Process. 2021, 69, 443–458. [Google Scholar] [CrossRef]
- Shi, C.G.; Wang, Y.J.; Salous, S.; Zhou, J.J.; Yan, J.K. Joint transmit resource management and waveform selection strategy for target tracking in distributed phased array radar network. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 2762–2778. [Google Scholar] [CrossRef]
- Su, Y.; Cheng, T.; He, Z.S.; Li, X. Joint waveform control and resource optimization for maneuvering targets tracking in netted colocated MIMO radar systems. IEEE Syst. J. 2022, 16, 3960–3971. [Google Scholar] [CrossRef]
- Shi, Y.C.; Jiu, B.; Yan, J.K.; Liu, H.W.; Li, K. Data-driven simultaneous multibeam power allocation: When multiple targets tracking meets deep reinforcement learning. IEEE Syst. J. 2021, 15, 1264–1274. [Google Scholar] [CrossRef]
- Deligiannis, A.; Panoui, A.; Lambotharan, S.; Chambers, J.A. Game-theoretic power allocation and the Nash equilibrium analysis for a multistatic MIMO radar network. IEEE Trans. Signal Process. 2017, 65, 6397–6408. [Google Scholar] [CrossRef]
- Yan, J.K.; Pu, W.Q.; Liu, H.W.; Jiu, B.; Bao, Z. Robust chance constrained power allocation scheme for multiple target localization in colocated MIMO radar system. IEEE Trans. Signal Process. 2018, 66, 3946–3957. [Google Scholar] [CrossRef]
- Shi, C.G.; Ding, L.T.; Wang, F.; Salous, S.; Zhou, J.J. Joint target assignment and resource optimization framework for multitarget tracking in phased array radar network. IEEE Syst. J. 2021, 15, 4379–4390. [Google Scholar] [CrossRef]
- Qian, J.H.; Lops, M.; Zheng, L.; Wang, X.D.; He, Z.S. Joint system design for coexistence of MIMO radar and communication. IEEE Trans. Signal Process. 2018, 66, 3504–3519. [Google Scholar] [CrossRef]
- Qian, J.H.; Venturino, L.; Lops, M.; Wang, X.D. Radar and communication spectral coexistence in range-dependent interference. IEEE Trans. Signal Process. 2021, 69, 5891–5906. [Google Scholar] [CrossRef]
- Bica, M.; Koivunen, V. Radar waveform optimization for target parameter estimation in cooperative radar-communications systems. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 2314–2326. [Google Scholar] [CrossRef]
- Wang, F.Z.; Li, H.B. Power allocation for coexisting multicarrier radar and communication systems in cluttered environment. IEEE Trans. Signal Process. 2021, 69, 1603–1613. [Google Scholar] [CrossRef]
- Lu, Y.X.; He, Z.S.; Liu, S.L.; Sun, G.H. Communication-awareness joint beams and power allocation scheme of radar network for manoeuvring targets tracking. IET Radar Sonar Navig. 2020, 14, 207–215. [Google Scholar] [CrossRef]
- Su, Y.; Cheng, Z.Y.; He, Z.S.; Deng, M.L. Communication-awareness adaptive resource scheduling strategy for multiple target tracking in a multiple radar system. IET Signal Process. 2022, 16, 750–761. [Google Scholar] [CrossRef]
- Wu, L.L.; Mishra, K.V.; Shankar, M.R.B.; Ottersten, B. Resource allocation in heterogeneously-distributed joint radar-communication under asynchronous Bayesian tracking framework. IEEE J. Sel. Areas Commun. 2022, 40, 2026–2042. [Google Scholar] [CrossRef]
- Boyd, S.P.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]

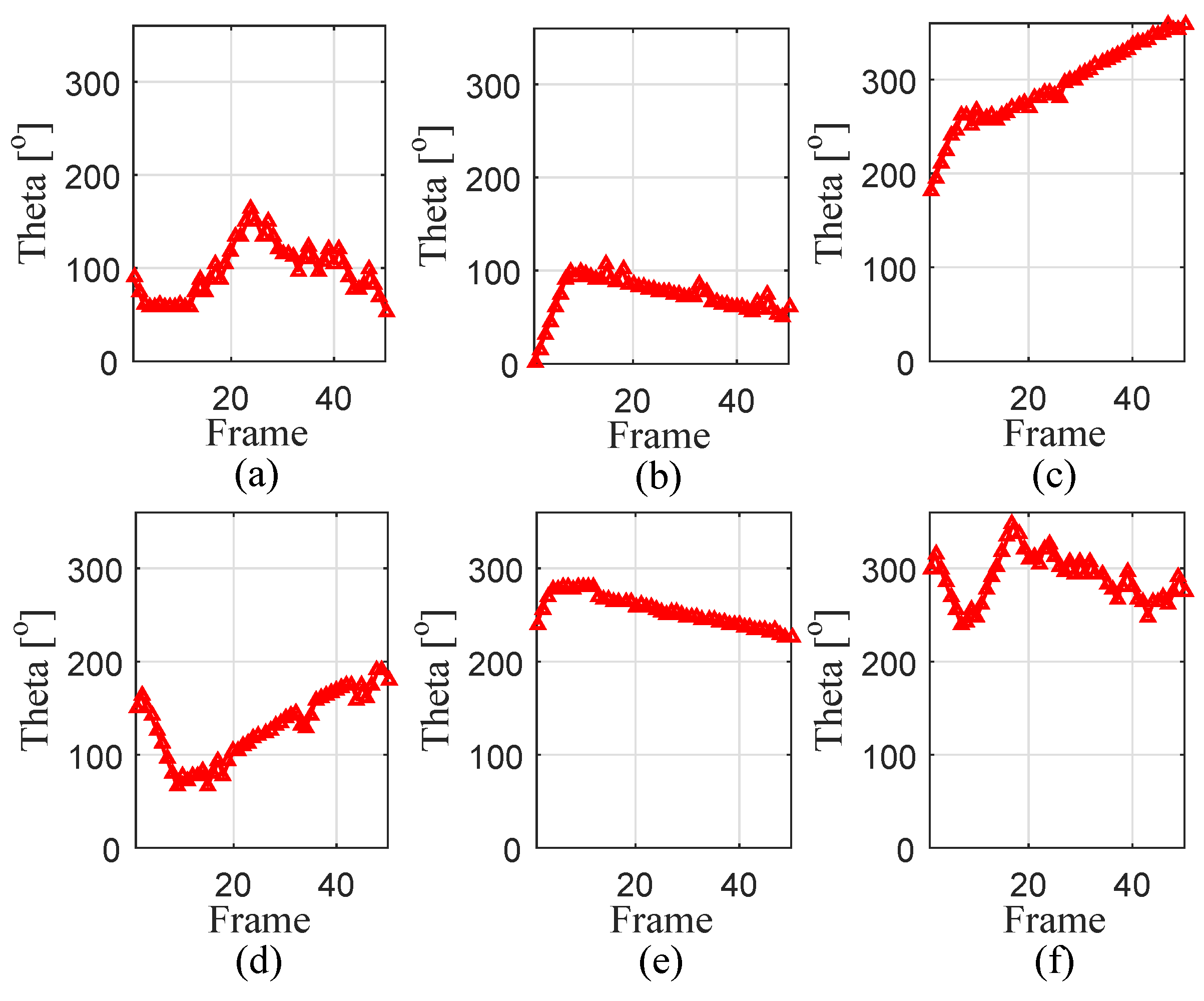
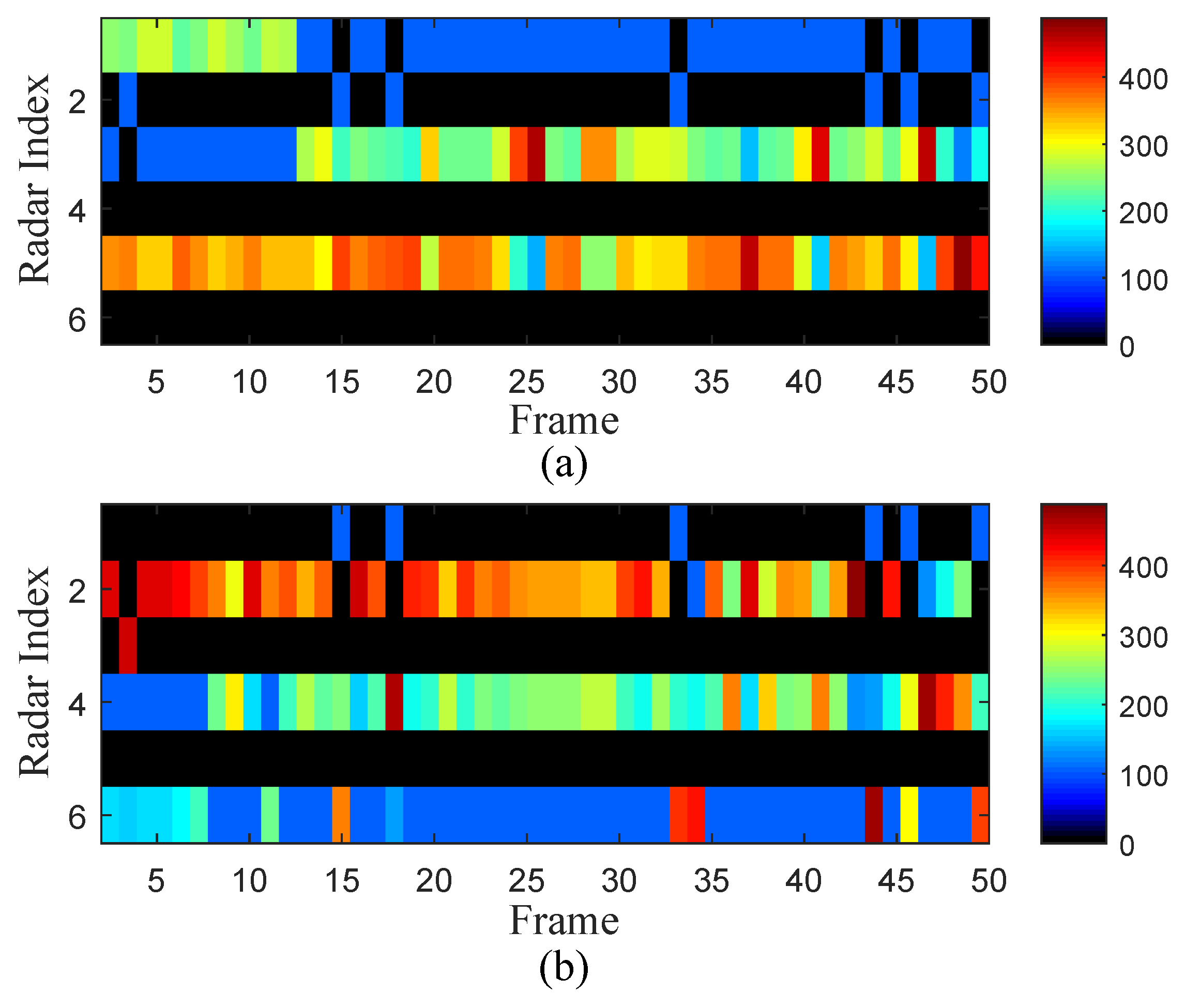


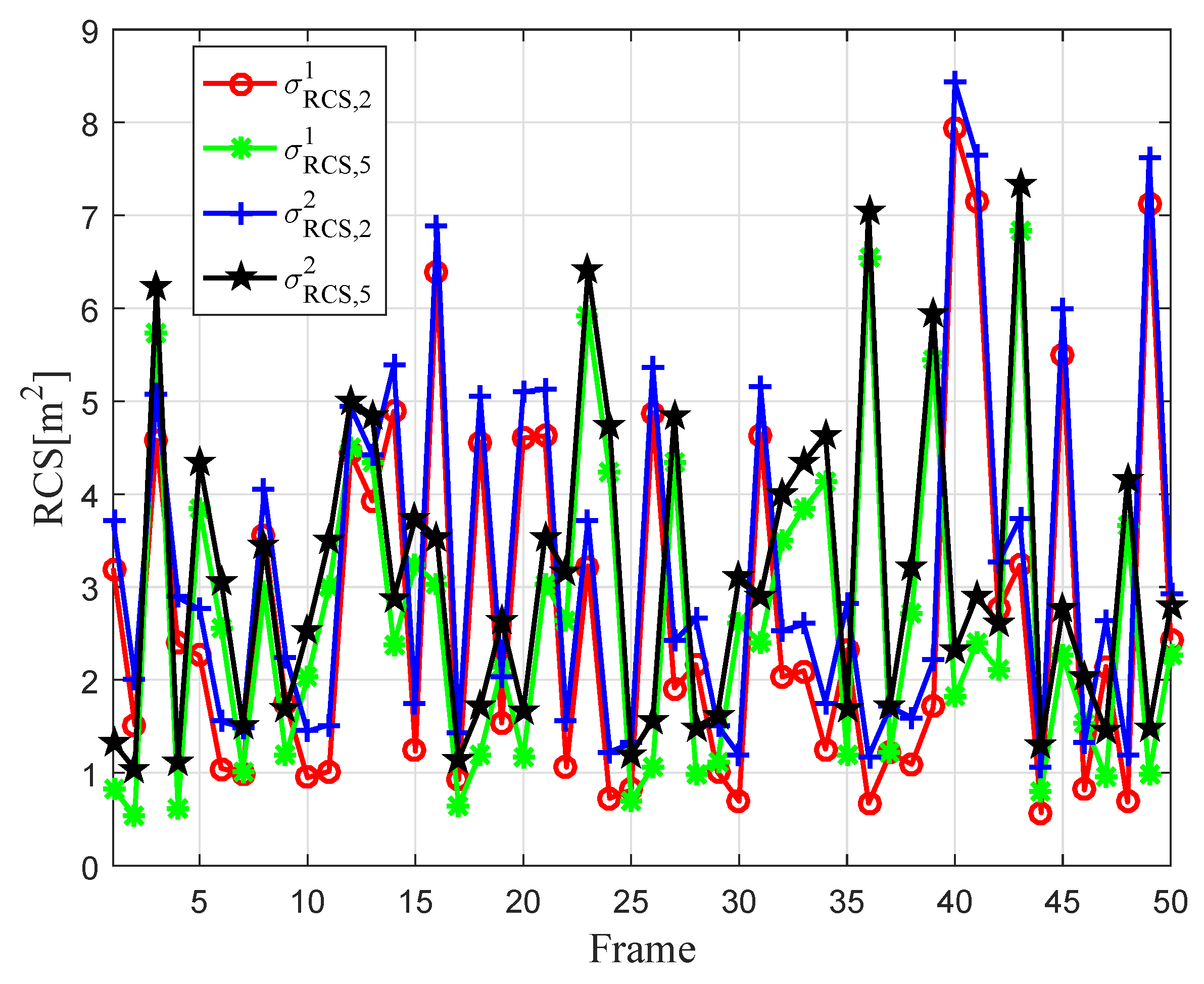
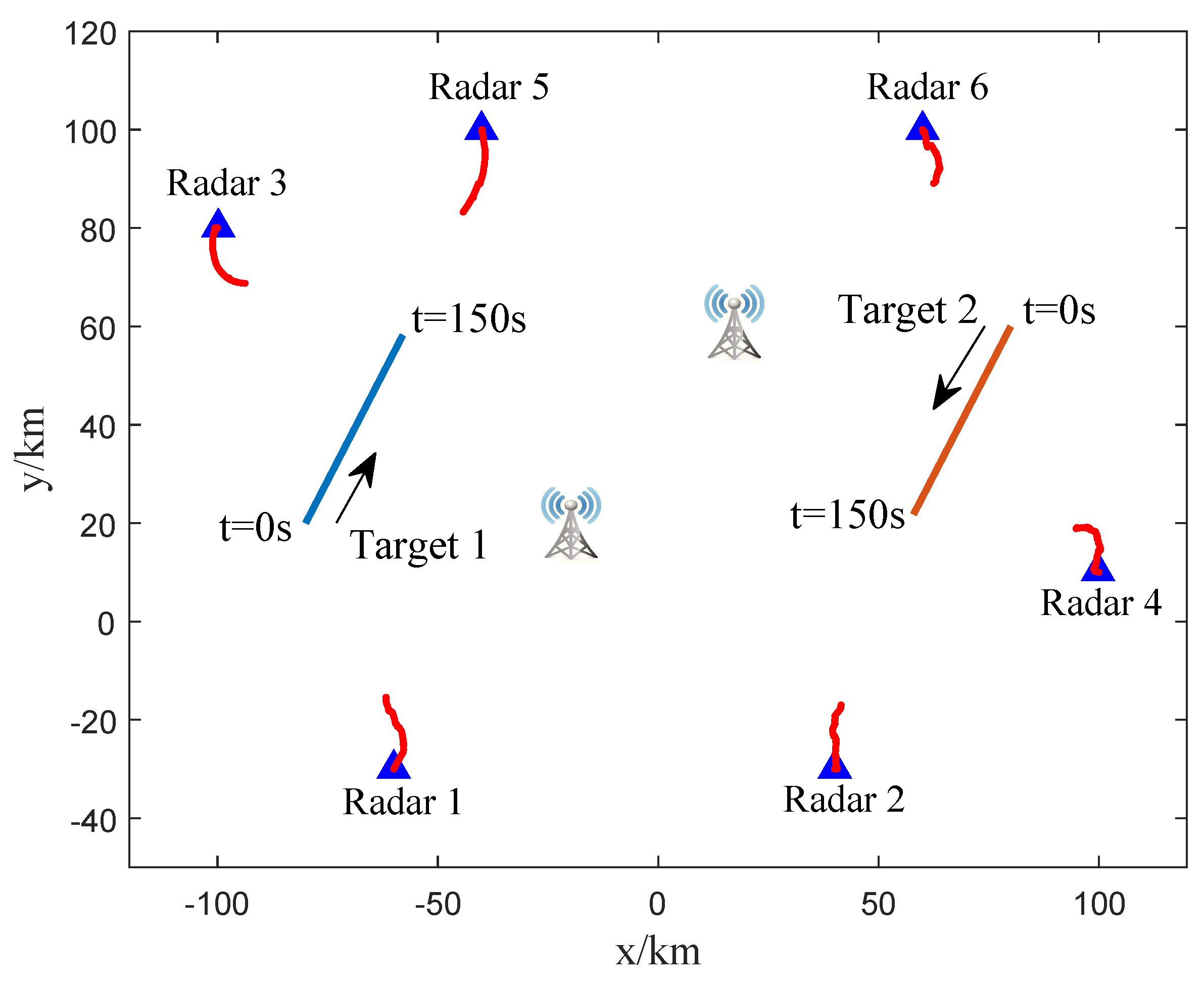



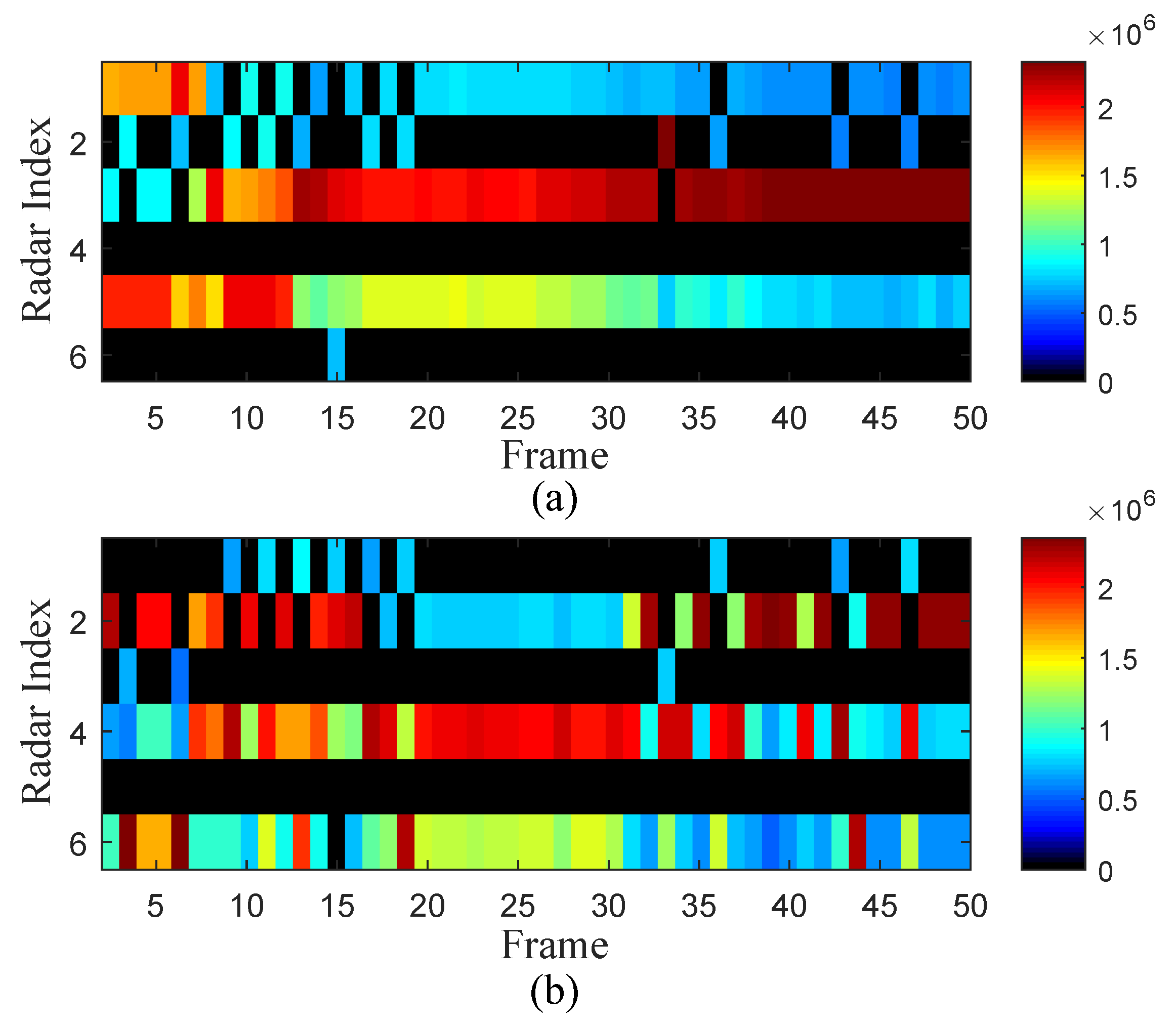
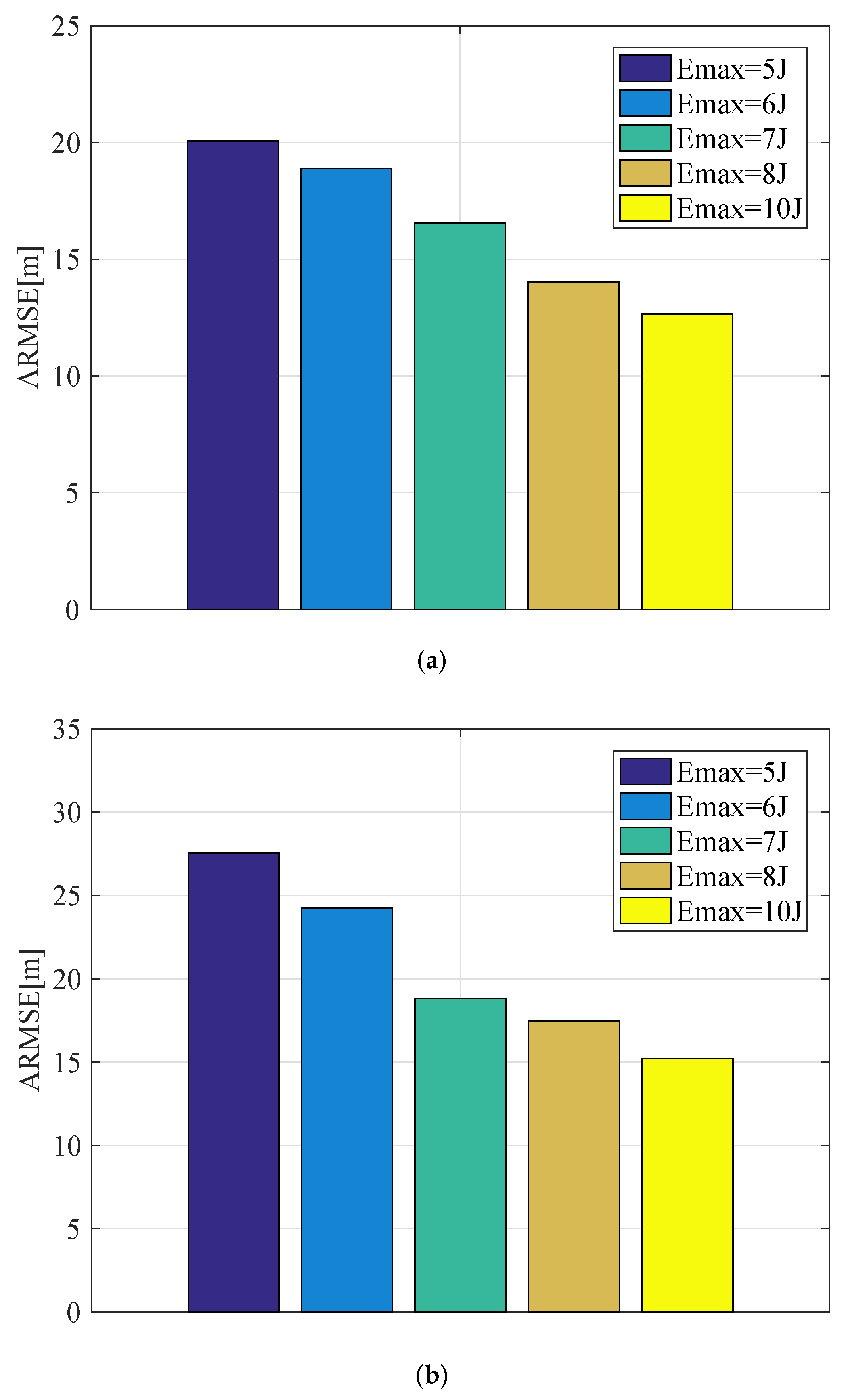
| Index | Initial Position | Initial Velocity |
|---|---|---|
| 1 | ||
| 2 |
| Symbol | Value | Symbol | Value |
|---|---|---|---|
| 3 | |||
| Index | Initial Position | Initial Velocity | Initial Course Angle |
|---|---|---|---|
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
| 5 | |||
| 6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, C.; Dong, J.; Salous, S.; Wang, Z.; Zhou, J. Collaborative Trajectory Planning and Resource Allocation for Multi-Target Tracking in Airborne Radar Networks under Spectral Coexistence. Remote Sens. 2023, 15, 3386. https://doi.org/10.3390/rs15133386
Shi C, Dong J, Salous S, Wang Z, Zhou J. Collaborative Trajectory Planning and Resource Allocation for Multi-Target Tracking in Airborne Radar Networks under Spectral Coexistence. Remote Sensing. 2023; 15(13):3386. https://doi.org/10.3390/rs15133386
Chicago/Turabian StyleShi, Chenguang, Jing Dong, Sana Salous, Ziwei Wang, and Jianjiang Zhou. 2023. "Collaborative Trajectory Planning and Resource Allocation for Multi-Target Tracking in Airborne Radar Networks under Spectral Coexistence" Remote Sensing 15, no. 13: 3386. https://doi.org/10.3390/rs15133386
APA StyleShi, C., Dong, J., Salous, S., Wang, Z., & Zhou, J. (2023). Collaborative Trajectory Planning and Resource Allocation for Multi-Target Tracking in Airborne Radar Networks under Spectral Coexistence. Remote Sensing, 15(13), 3386. https://doi.org/10.3390/rs15133386