A Software-Defined Radar for Low-Altitude Slow-Moving Small Targets Detection Using Transmit Beam Control
Abstract
1. Introduction
- 1.
- We developed a novel two-dimensional electronic scanning active phased array radar implemented in a software-defined radar architecture, providing an adaptive LSS target monitoring capability under various complex environments.
- 2.
- We proposed a transmit beam control algorithm based on the low peak-to-average ratio (PAPR) constraint that can significantly improve the LSS detection performance under strong ground clutter and inference.
- 3.
- We devised a flexible arbitrary radar waveform generator that can generate various complex waveforms depending on the feedback of the environmental sensing module.
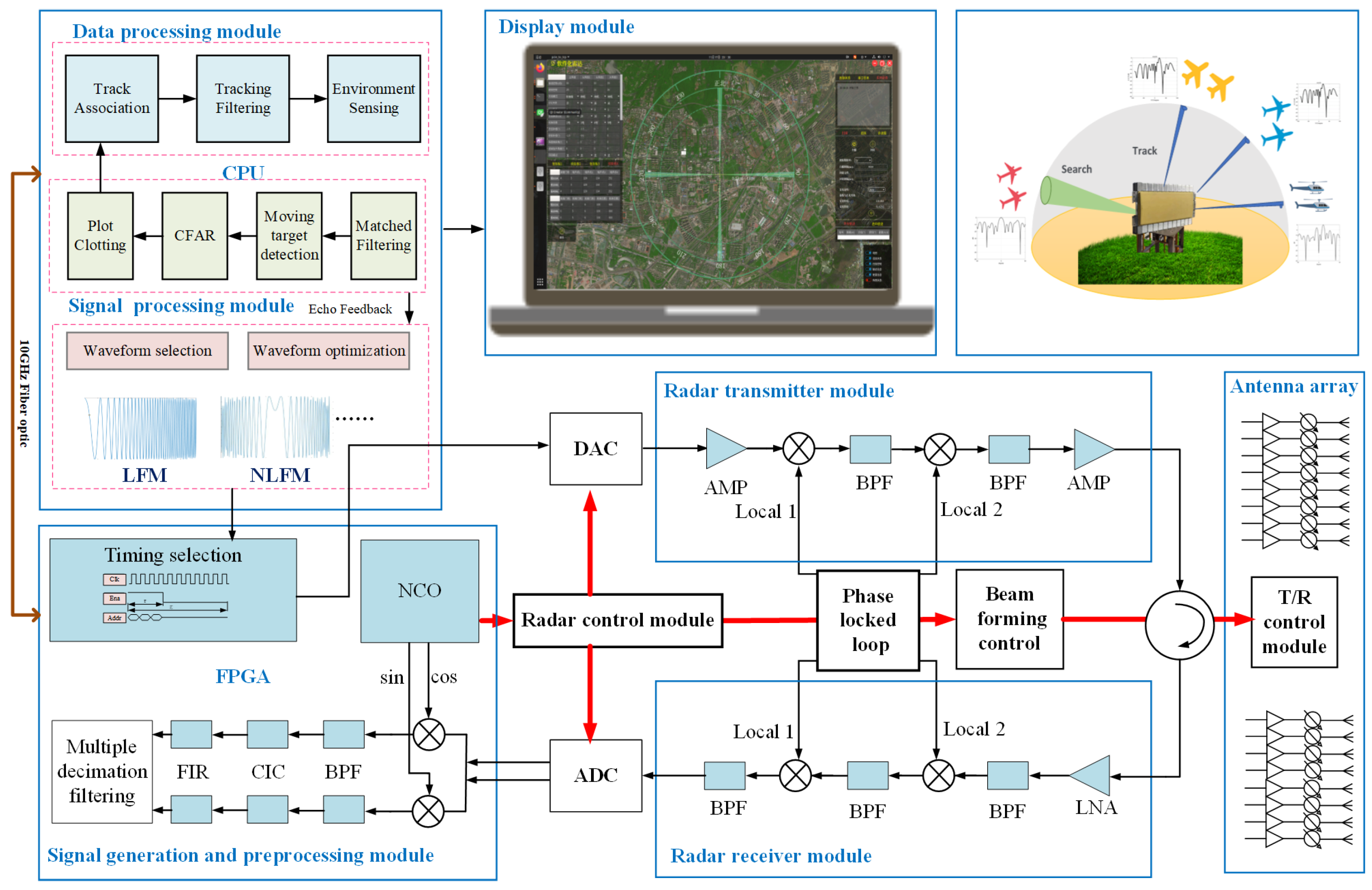
2. System Overview
2.1. Specification
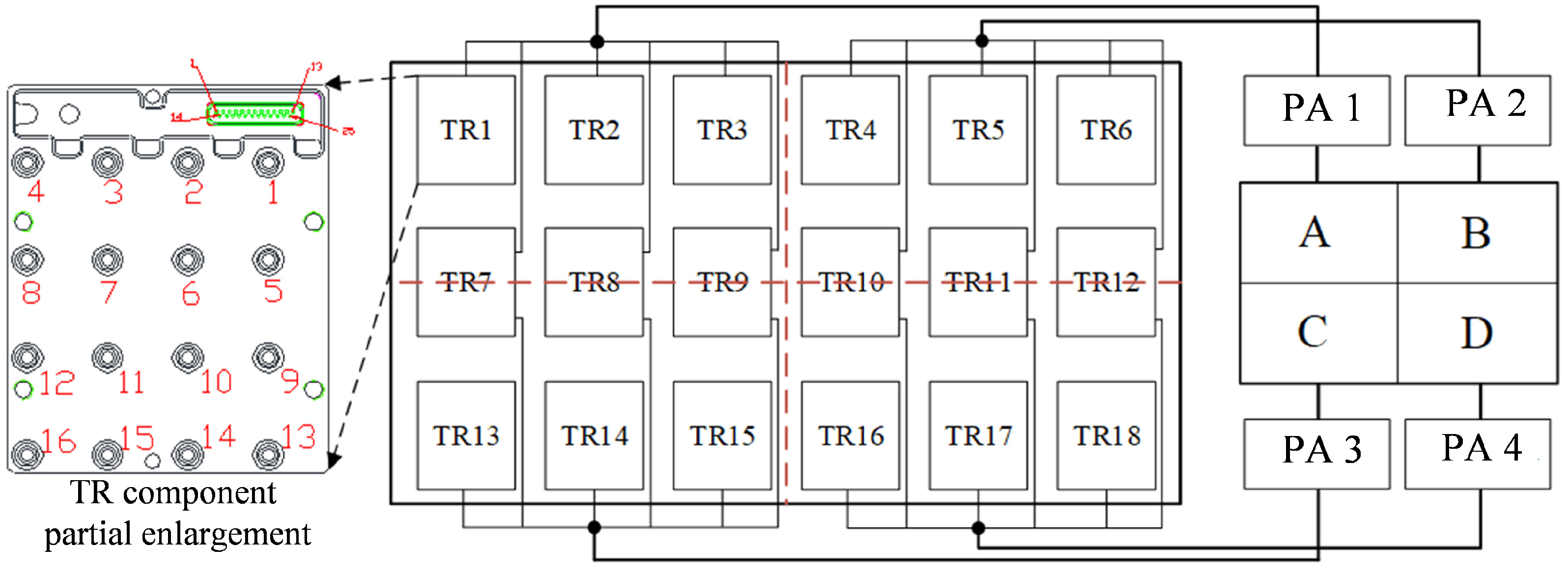
2.2. Antenna Module
2.3. Transmitter and Receiver Module
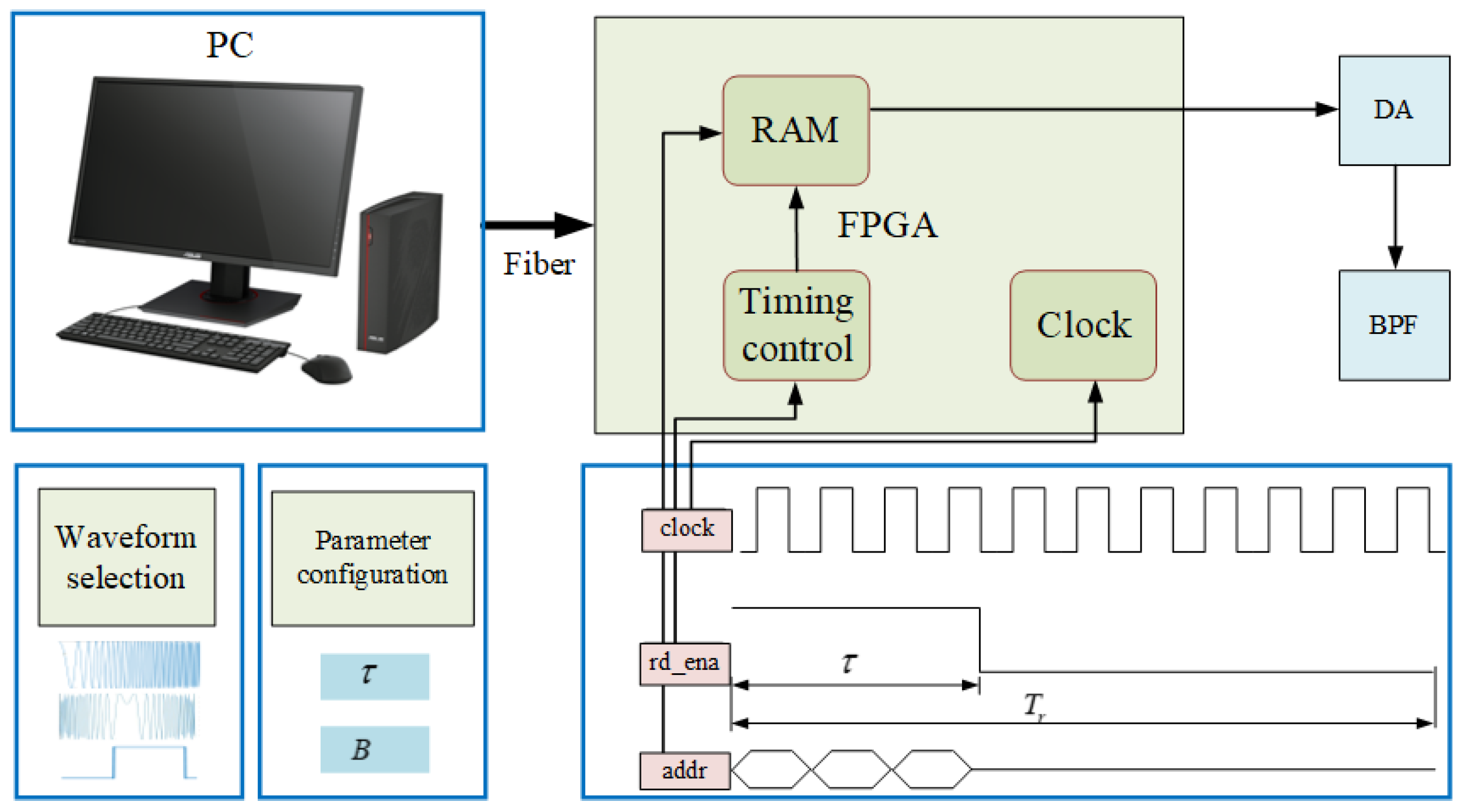
2.4. Signal Generation and Preprocessing Module
2.5. Signal and Data Processing Module
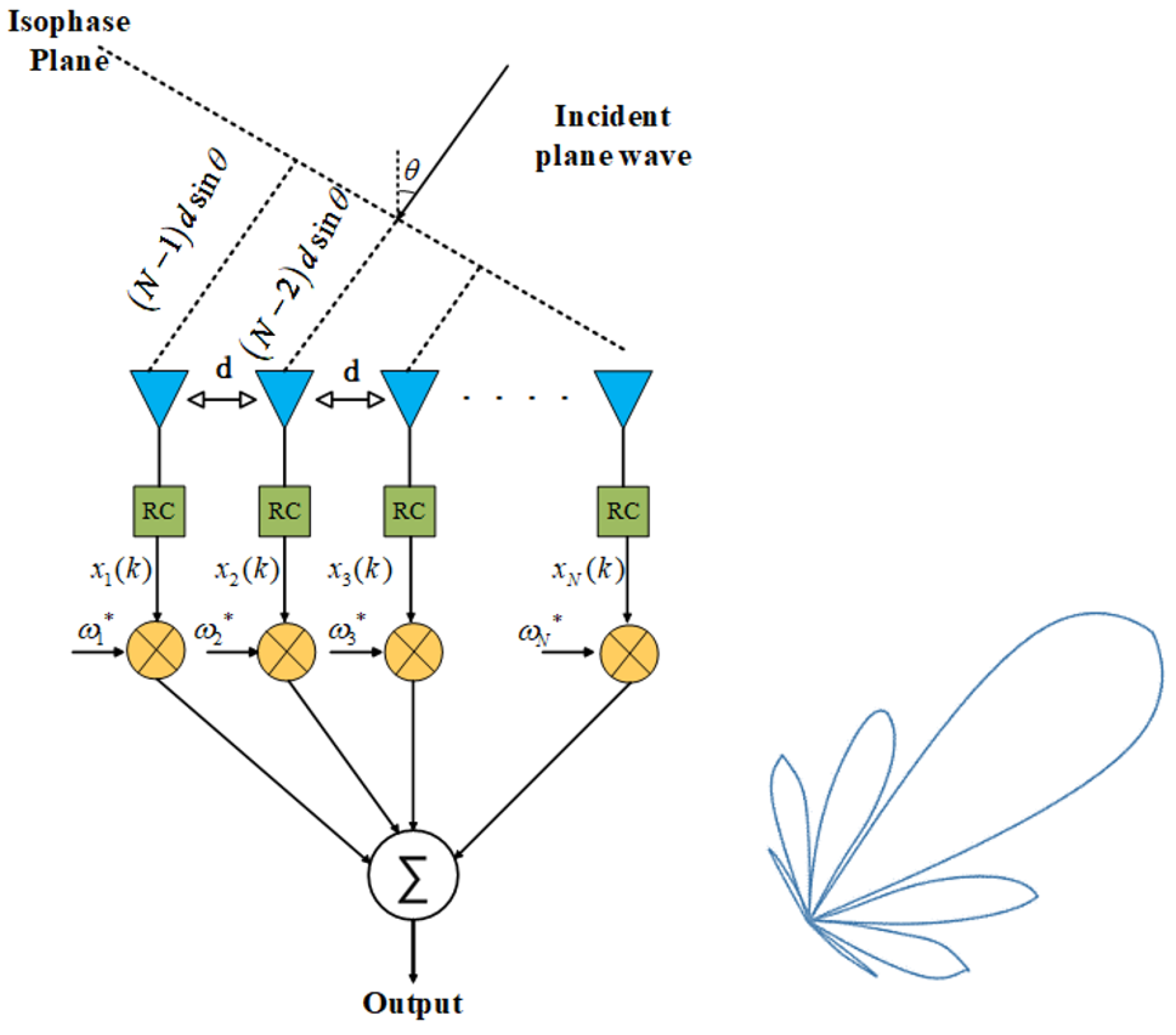
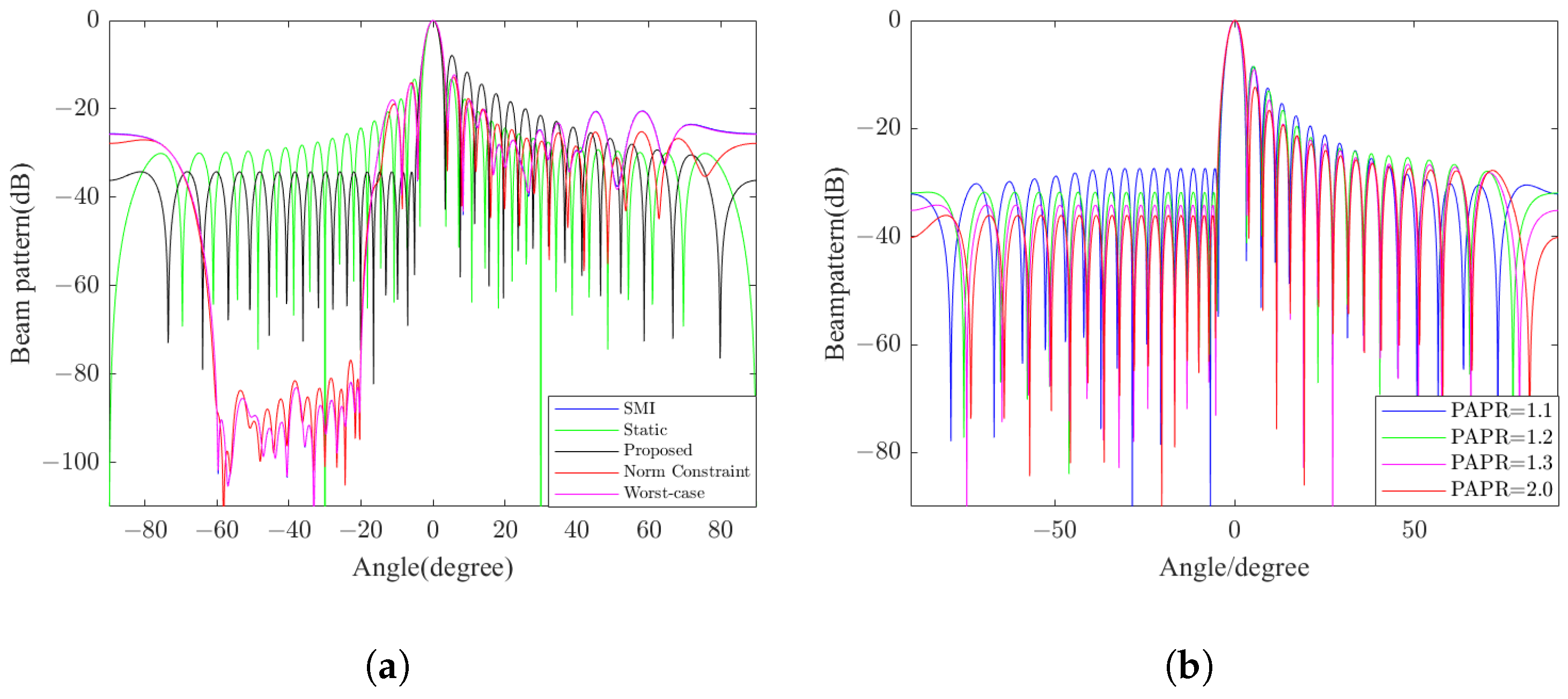
3. Transmit Beam Control
4. Scalable Arbitrary Wave Generator and Signal Processing
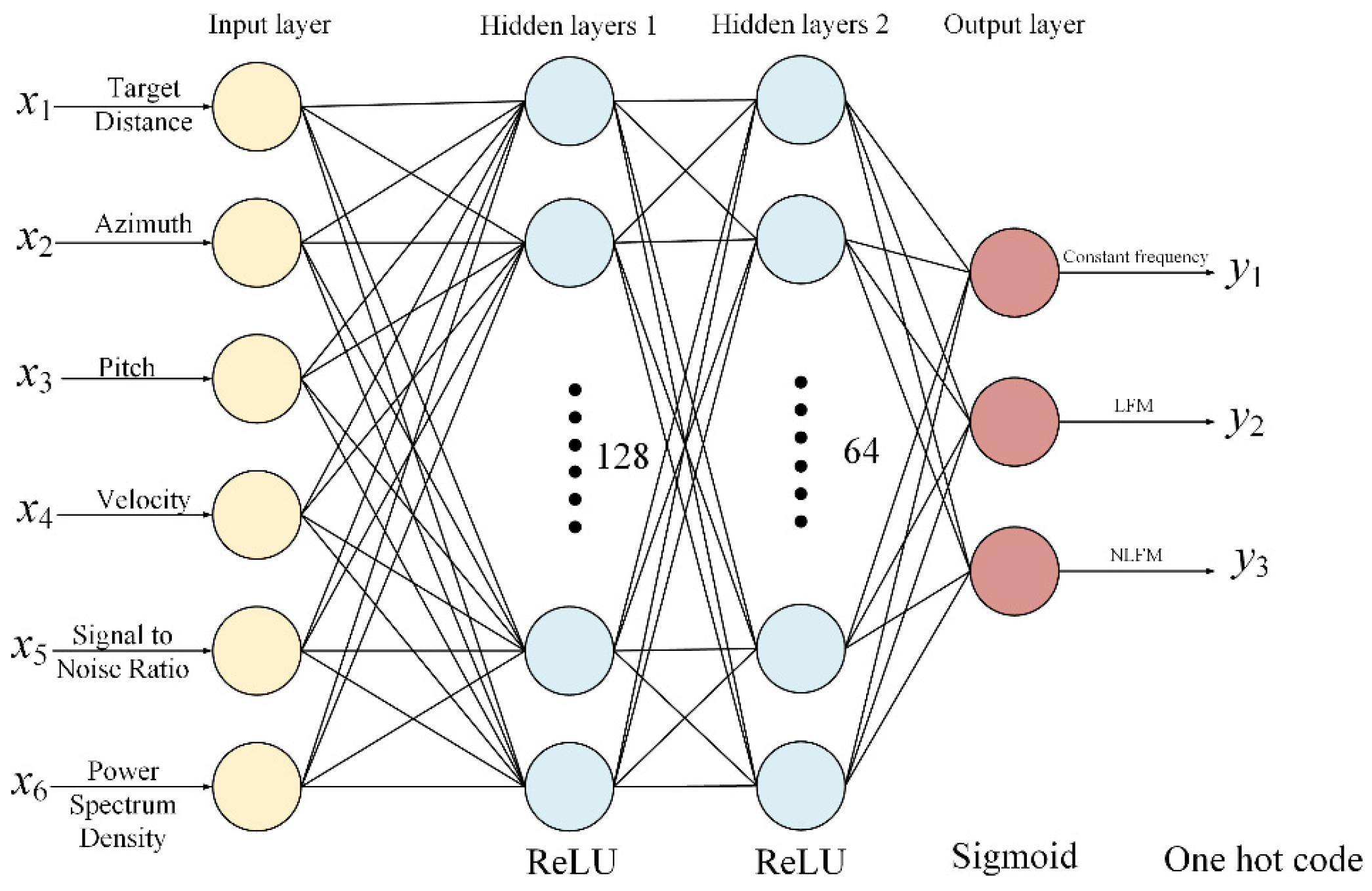
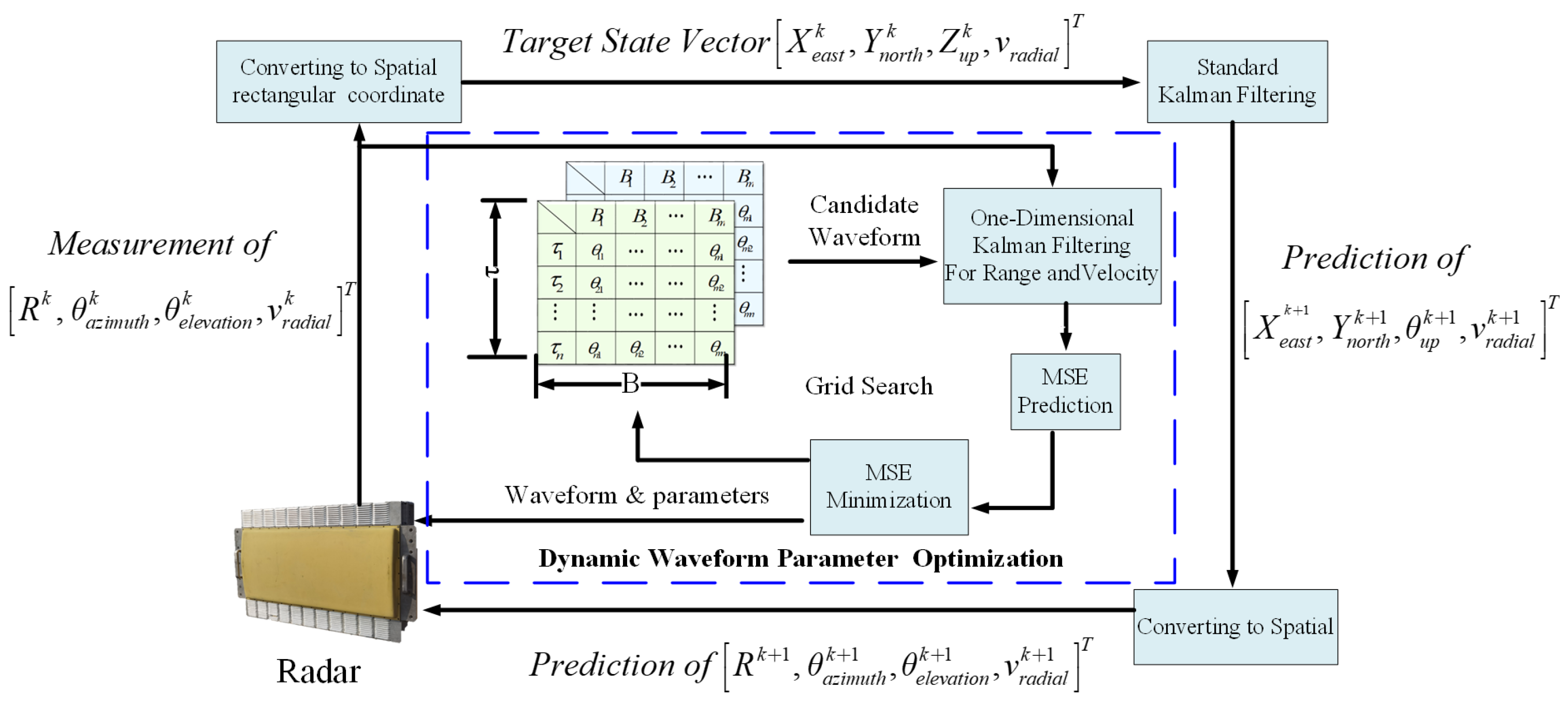
4.1. Adaptive Waveform Optimization Strategy for Target Tracking
4.2. Software-Defined Arbitrary Waveform Generation and Processing
5. Experiments and Analysis
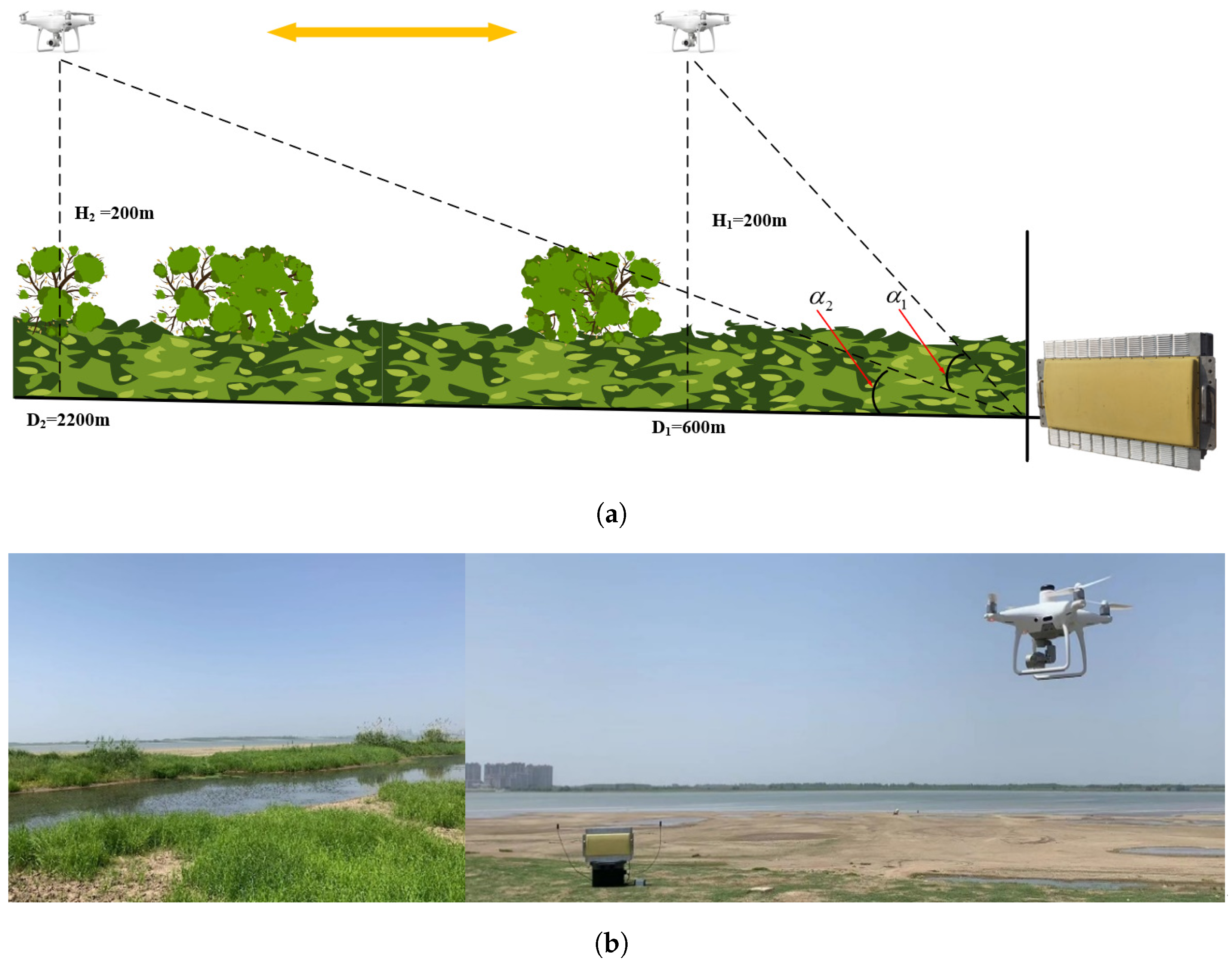
5.1. Experimental Setup
5.2. Performance Evaluation of the Developed Radar System
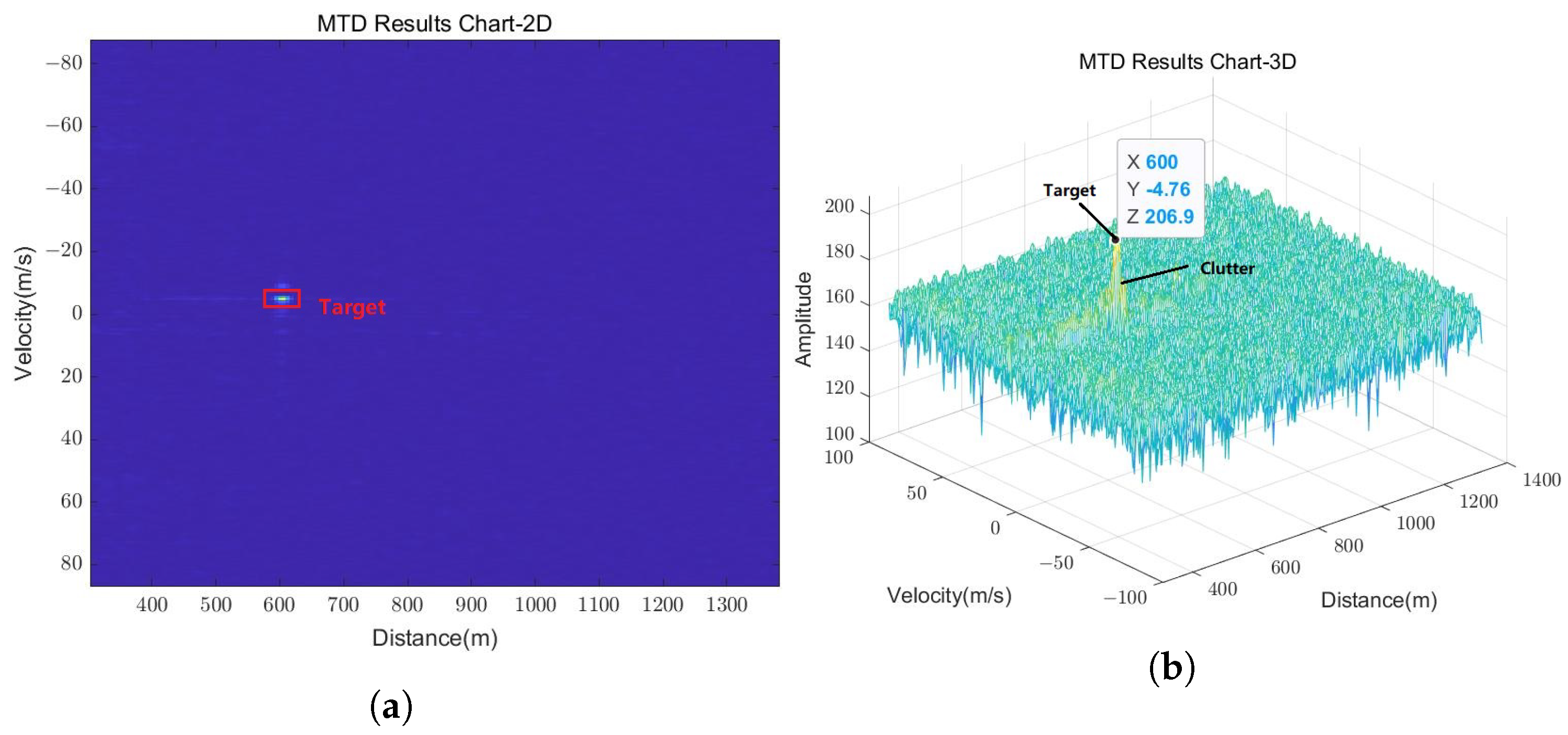
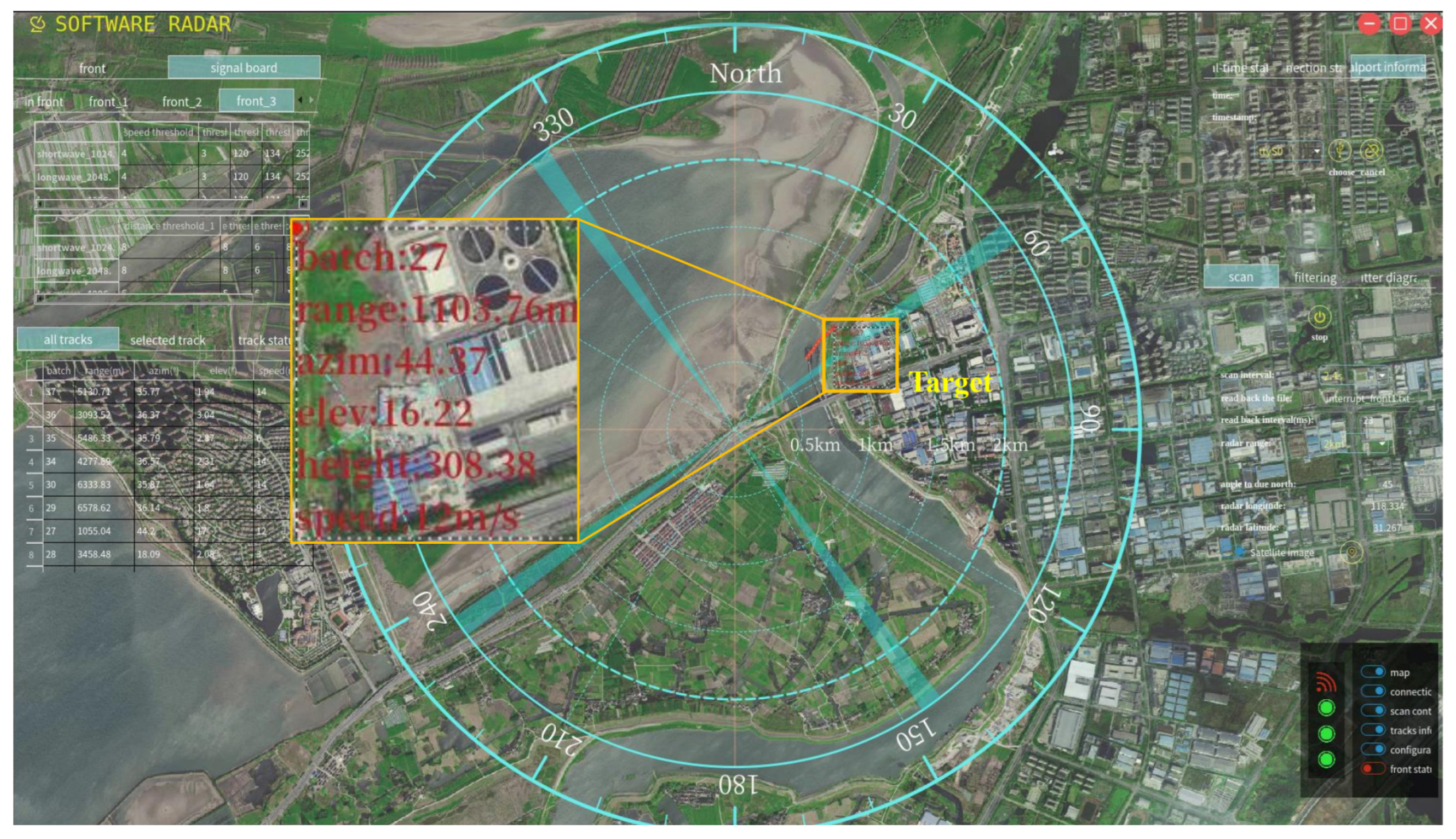
5.2.1. Detection and Tracking
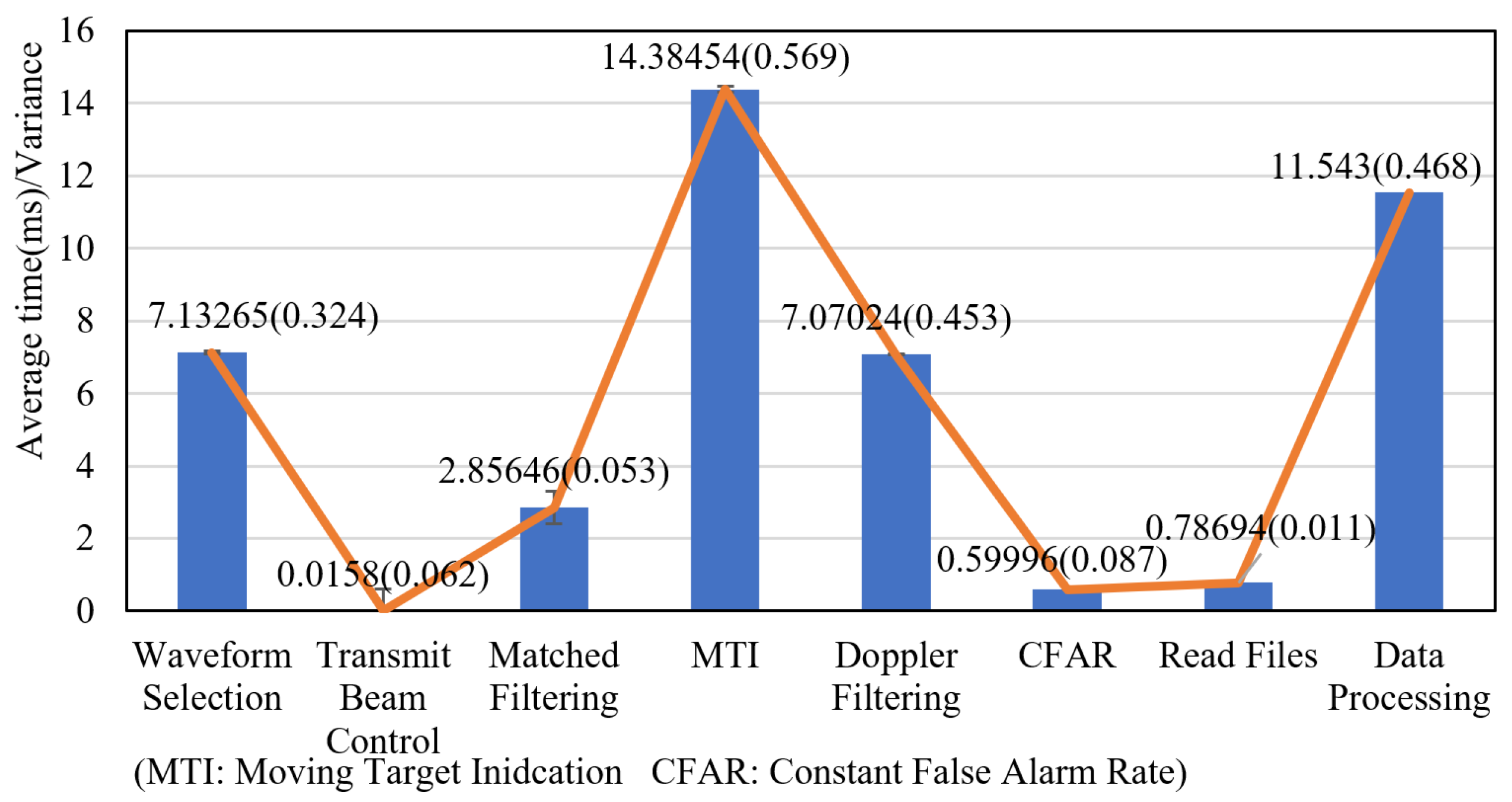
5.2.2. Real-Time Analysis
5.3. Ablation Experiments and Analysis
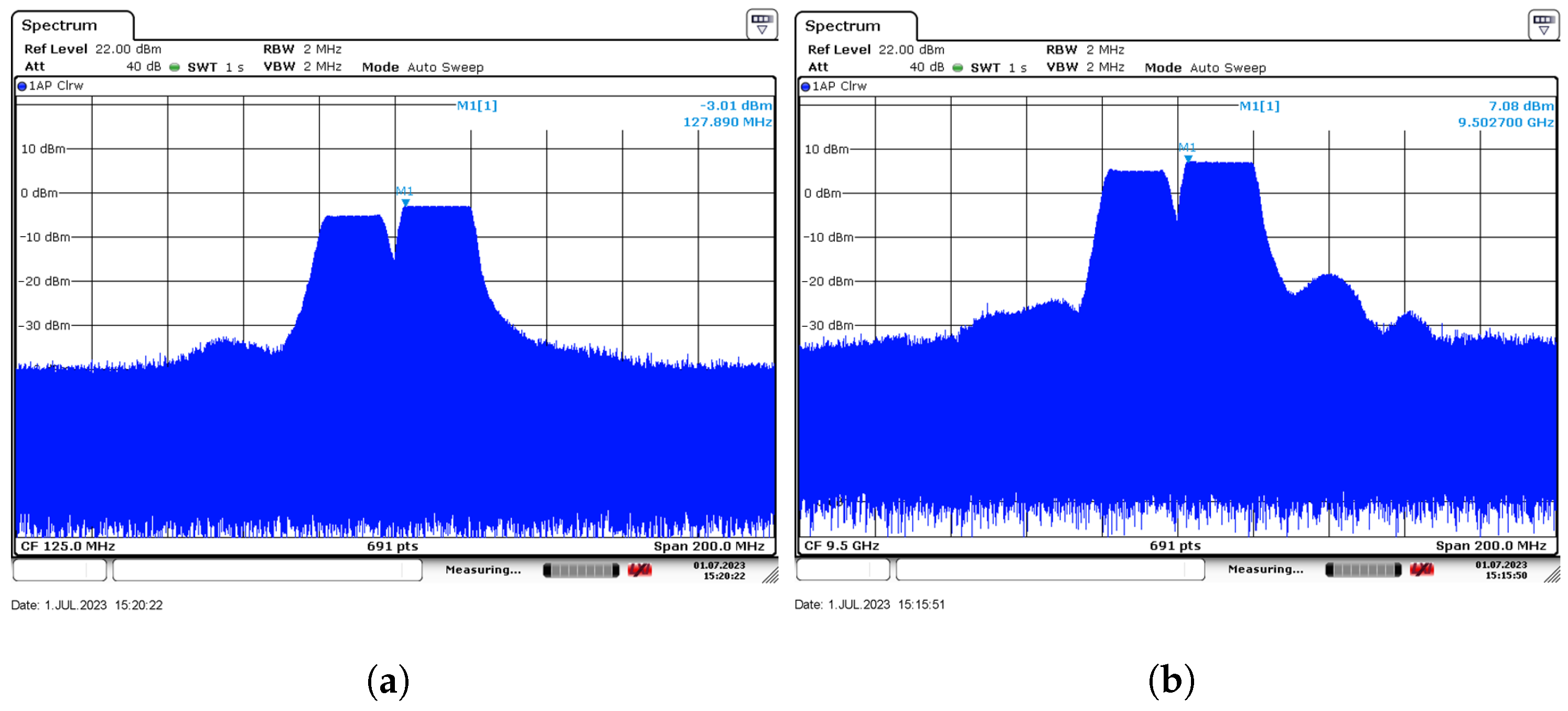
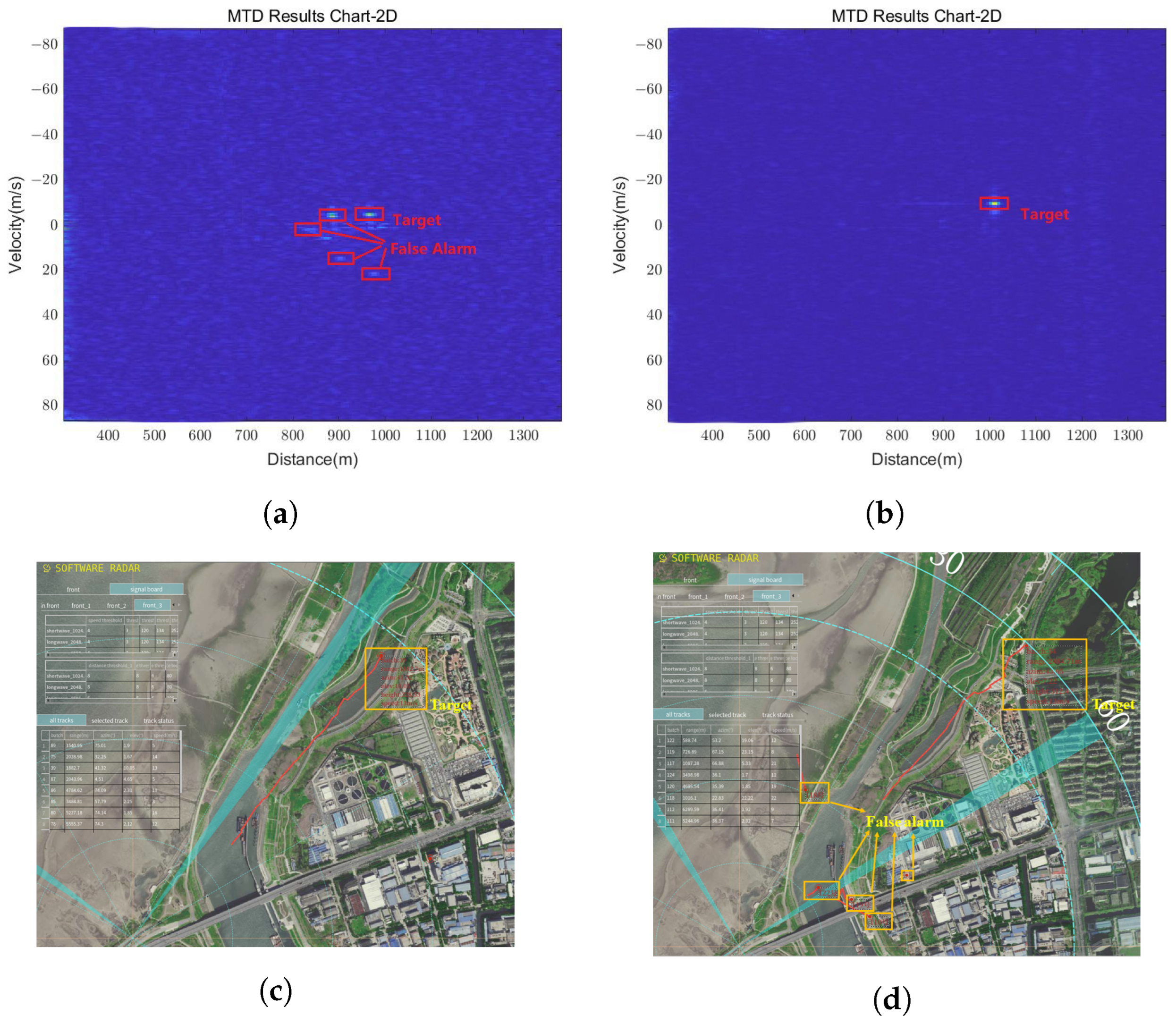
5.3.1. Validation of the Transmit Beam Control
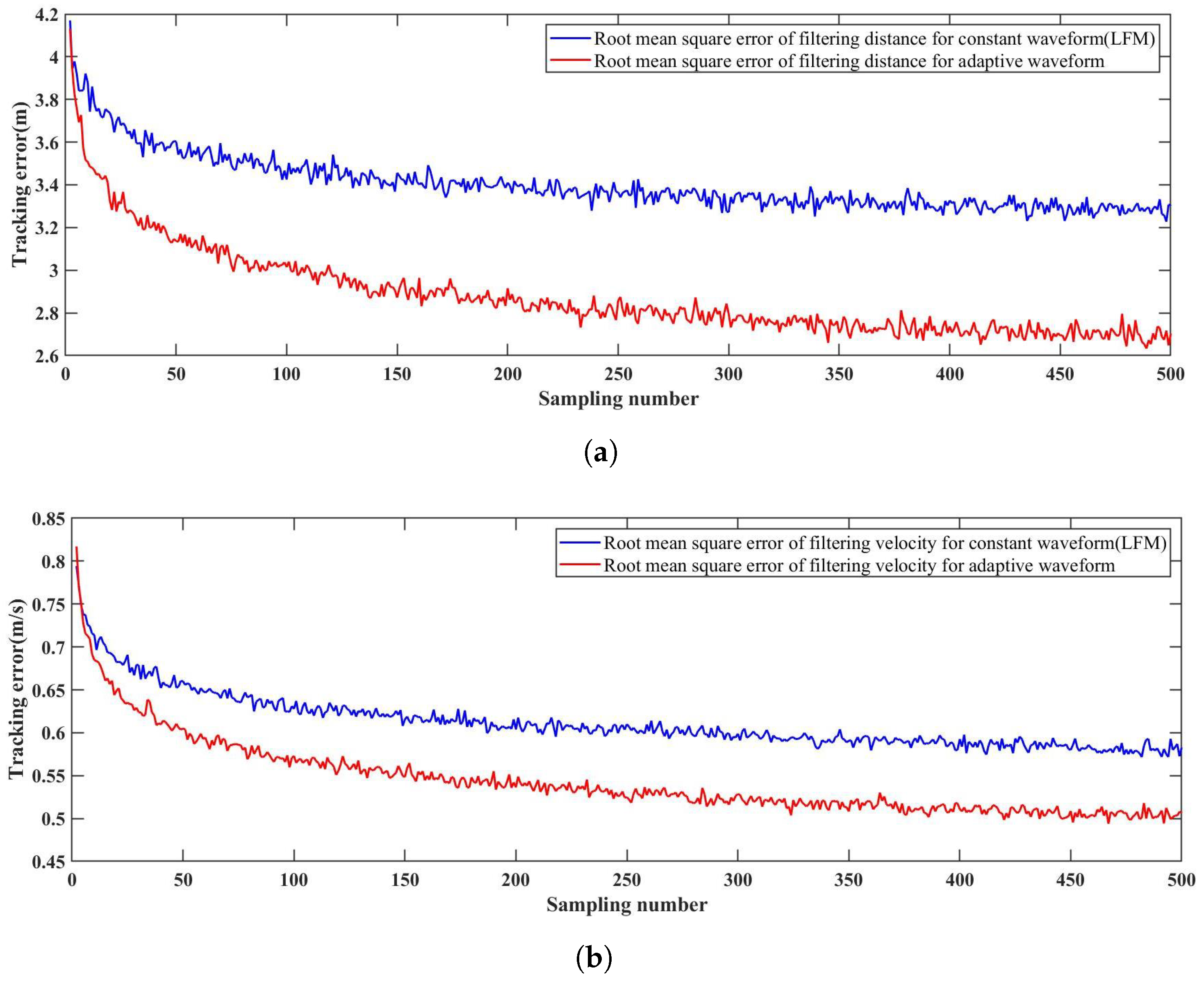
5.3.2. Validation of the Adaptive Waveform Optimization and Generation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, C.; Jin, S.; Ding, Z.; Kuang, Q.; Zhuang, S.; Li, H. Transmit beam control in low-altitude slow-moving small targets detection. In Proceedings of the 2022 7th International Conference on Intelligent Computing and Signal Processing (ICSP), Xi’an, China, 15–17 April 2022; pp. 470–473. [Google Scholar]
- Chen, X.; Chen, W.; Rao, Y.; Huang, Y.; Guan, J.; Dong, Y. Progress and prospects of radar target detection and recognition technology for flying birds and unmanned aerial vehicles. J. Radars 2020, 9, 803–827. [Google Scholar]
- Zhang, X.; Feng, J.; Li, Z. Application of acoustic detection technology in opening low altitude airspace. Electroacoust. Technol. 2015, 39, 264–270. [Google Scholar]
- Omologo, M.; Svaizer, P. Acoustic source location in noisy and reverberant environment using CSP analysis. In Proceedings of the 1996 IEEE International Conference on Acoustics, Speech, and Signal Processing Conference Proceedings, Atlanta, GA, USA, 9 May 1996; Volume 2, pp. 921–924. [Google Scholar]
- Dang, C.; Li, Z.; Hao, C.; Xiao, Q. Infrared small marine target detection based on spatiotemporal dynamics analysis. Remote Sens. 2023, 15, 1258. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhang, Y.; Ding, R.; Ma, C.; Li, X. Fast and robust infrared small target detection using weighted local difference variance measure. Sensors 2023, 23, 2630. [Google Scholar] [CrossRef]
- Yang, F.; Guo, J.; Zhu, R.; Le Kernec, J.; Liu, Q.; Zeng, T. Ground clutter mitigation for slow-time MIMO radar using independent component analysis. Remote Sens. 2022, 14, 6098. [Google Scholar] [CrossRef]
- Wu, Q.; Chen, J.; Lu, Y.; Zhang, Y. A complete automatic target recognition system of low altitude, small rcs and slow speed (LSS) targets based on multi-dimensional feature fusion. Sensors 2019, 19, 5048. [Google Scholar] [CrossRef]
- Aldowesh, A.; Alnuaim, T.; Alzogaiby, A. Slow-moving micro-UAV detection with a small scale digital array radar. In Proceedings of the 2019 IEEE Radar Conference (RadarConf), Boston, MA, USA, 22–26 April 2019; pp. 1–5. [Google Scholar]
- Mu, J.; Rao, J.; Chen, R.; Li, F. Low-altitude infrared slow-moving small target detection via spatial-temporal features measure. Sensors 2022, 22, 5136. [Google Scholar] [CrossRef] [PubMed]
- Li, K.; Zhang, Y.; Zhang, Y.; Chen, Y.; Zhao, C. Infrared detection of small-moving targets using spatial local vector difference and temporal sample consensus measures. IEEE Access 2022, 10, 113865–113874. [Google Scholar] [CrossRef]
- Huang, X.; Wang, Z.; Peng, Q.; Xu, H.; He, Z. LSS UAV target intelligent detection in urban complex environment. In Proceedings of the 2021 IEEE 3rd International Conference on Civil Aviation Safety and Information Technology (ICCASIT), Changsha, China, 20–22 October 2021; pp. 648–650. [Google Scholar]
- Sun, H.; Liu, Q.; Wang, J.; Ren, J.; Wu, Y.; Zhao, H.; Li, H. Fusion of infrared and visible images for remote detection of low-altitude slow-speed small targets. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 2971–2983. [Google Scholar] [CrossRef]
- Xu, D.; Zhang, H. Overview of radar LSS target detection technology. Mod. Def. Technol. 2018, 46, 148. [Google Scholar]
- Zhang, H.; Xu, D.; Ma, J.; Ran, H. Radar detection method for low-altitude slow and small target based on radon transform. Mod. Def. Technol. 2018, 46, 105–111. [Google Scholar]
- Chen, X.; Guan, J.; Huang, Y.; Yu, X.; Dong, Y.; Liu, N.; He, Y. Radar refinement of low-observable moving targets and applications. Sci. Technol. Rev. 2017, 35, 19–27. [Google Scholar]
- Zhang, Y. Analysis of detection system for “low, slow and small ” target based on multi living-agent. Guangxi Commun. Technol. 2012, 2, 35–37. [Google Scholar]
- Wang, Y.; Tao, R.; Li, B. Research on complex information systems based on multi-active agents. Sci. China (Ser. E Inf. Sci.) 2008, 38, 2020–2037. [Google Scholar]
- Wang, D.; Qin, J.; Ma, X. Clutter-whitening-based low-speed weak target detection over the sea. Mod. Radar 2003, 25, 15–18. [Google Scholar]
- Zhang, H.; Hao, C.; Song, W.; Jiang, B.; Li, B. Adaptive slicing-aided hyper inference for small object detection in high-resolution remote sensing images. Remote Sens. 2023, 15, 1249. [Google Scholar] [CrossRef]
- Li, H.; Ding, Z.; Tian, S.; Jin, S. Transmit beam control in low-altitude slow-moving small targets detection based on peak to average power ratio constraint. Electronics 2022, 11, 3456. [Google Scholar] [CrossRef]
- Wan, F.; Xu, J.; Zhang, Z. Robust Beamforming Based on Covariance Matrix Reconstruction in FDA-MIMO Radar to Suppress Deceptive Jamming. Sensors 2022, 22, 1479. [Google Scholar] [CrossRef]
- Liu, X.; Huang, T.; Shlezinger, N.; Liu, Y.; Zhou, J.; Eldar, Y.C. Joint transmit beamforming for multiuser MIMO communications and MIMO radar. IEEE Trans. Signal Process. 2020, 68, 3929–3944. [Google Scholar] [CrossRef]
- Hassanien, A.; Amin, M.G.; Zhang, Y.D.; Ahmad, F. Dual-function radar-communications: Information embedding using sidelobe control and waveform diversity. IEEE Trans. Signal Process. 2016, 64, 2168–2181. [Google Scholar] [CrossRef]
- McCormick, P.M.; Blunt, S.D.; Metcalf, J.G. Simultaneous radar and communications emissions from a common aperture, Part I: Theory. In Proceedings of the 2017 IEEE Radar Conference (RadarConf), Seattle, WA, USA, 8–12 May 2017; pp. 1685–1690. [Google Scholar]
- McCormick, P.M.; Ravenscroft, B.; Blunt, S.D.; Duly, A.J.; Metcalf, J.G. Simultaneous radar and communication emissions from a common aperture, Part II: Experimentation. In Proceedings of the 2017 IEEE Radar Conference (RadarConf), Seattle, WA, USA, 8–12 May 2017; pp. 1697–1702. [Google Scholar]
- Brüggenwirth, S.; Warnke, M.; Wagner, S.; Barth, K. Cognitive radar for classification. IEEE Aerosp. Electron. Syst. Mag. 2019, 34, 30–38. [Google Scholar] [CrossRef]
- Yang, F.; Xu, F.; Yang, X.; Liu, Q. DDMA MIMO radar system for low, slow, and small target detection. J. Eng. 2019, 2019, 5932–5935. [Google Scholar] [CrossRef]
- Fangbao, L. Research on antenna reconfigured software defined radar architecture. Mod. Navig. 2018, 9, 352–356. [Google Scholar]
- Baskar, S.; Ertin, E. A software defined radar platform for waveform adaptive MIMO radar research. In Proceedings of the 2015 IEEE Radar Conference (RadarCon), Arlington, VA, USA, 10–15 May 2015; pp. 1590–1594. [Google Scholar]
- Hiari, O.; Mesleh, R. A reconfigurable SDR transmitter platform architecture for space modulation MIMO techniques. IEEE Access 2017, 5, 24214–24228. [Google Scholar] [CrossRef]
- Wu, Y.M.; Chou, H.C.; Ke, C.Y.; Wang, C.C.; Li, C.T.; Chang, L.H.; Su, B.; Chu, T.S.; Wang, Y.J. An X-Band CMOS digital phased array radar from hardware to software. Sensors 2021, 21, 7382. [Google Scholar] [CrossRef] [PubMed]
- Feng, W.; Luo, X.; Kong, F. A minimal software integrated processor design based on DBF radar system. J. China Acad. Electron. Inf. Technol. 2021, 16, 576–581. [Google Scholar]
- Choi, B. Creating an ubuntu server virtual machine. In Introduction to Python Network Automation: The First Journey; Springer: Berlin/Heidelberg, Germany, 2021; pp. 169–222. [Google Scholar]
- Li, H.; Ding, Z.; Tian, S.; Jin, S. Robust adaptive transmit beamforming under the constraint of low peak-to-average ratio. Sensors 2022, 22, 7278. [Google Scholar] [CrossRef]
- Bassily, R.; Feldman, V.; Talwar, K.; Guha Thakurta, A. Private stochastic convex optimization with optimal rates. Adv. Neural Inf. Process. Syst. 2019, 32, 1–10. [Google Scholar]
- Kershaw, D.; Evans, R. Optimal waveform selection for tracking systems. IEEE Trans. Inf. Theory 1994, 40, 1536–1550. [Google Scholar] [CrossRef]
- Trees, H.L.V. Detection, Estimation, and Modulation Theory, Part III; John Wiley & Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- Förstner, W.; Wrobel, B.P. Photogrammetric Computer Vision; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]








| Parameter | Value |
|---|---|
| Frequency | X-band |
| Instantaneous Bandwidth | ≤40 MHz |
| Signal Form | Constant frequency, linear frequency modulation, non-linear frequency modulation |
| Pulse Repetition Period | 84–100 s |
| Pulse Width | 2–20 s |
| Transmit Power | ≤250 W |
| Detection Range | 300∼6000 m@0.01 |
| Maximum Detection Velocity | 98 m/s |
| Range Resolution | ≤10 m |
| Velocity Resolution | ≤0.734 m/s |
| Short Distance Blind Region | ≤300 m |
| Azimuth: 90° | |
| Search Range | Elevation: 0°∼30° |
| Range: 0.3∼10 km@0.05 | |
| Azimuth: ∼45° | |
| Electrical Scanning Range | Elevation: ∼15° |
| Azimuth: ≤ | |
| Measurement Accuracy | Elevation: ≤0.5° |
| Range: ≤4 m | |
| Size | Antenna size: 384 × 240 mm |
| Single array size: ≤600 × 400 × 150 mm | |
| Number of Array Elements | 288 |
| Interval of Array Elements | Azimuth: 16 mm |
| Elevation: 20 mm |
| Name | Description | Parameters | Plot |
|---|---|---|---|
| CF |  | ||
| LFM |  | ||
| NLFM | 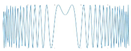 |
| Waveform Type | Root Mean Square Error in Filtering Distance (m) | Root Mean Square Error in Filtering Velocity (m/s) |
|---|---|---|
| Constant waveform (LFM) | 3.24 | 0.574 |
| Adaptive waveform | 2.65 | 0.473 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, L.; Qian, H.; Xing, L.; Zou, Y.; Qiu, L.; Liu, Z.; Tian, S.; Li, H. A Software-Defined Radar for Low-Altitude Slow-Moving Small Targets Detection Using Transmit Beam Control. Remote Sens. 2023, 15, 3371. https://doi.org/10.3390/rs15133371
Cai L, Qian H, Xing L, Zou Y, Qiu L, Liu Z, Tian S, Li H. A Software-Defined Radar for Low-Altitude Slow-Moving Small Targets Detection Using Transmit Beam Control. Remote Sensing. 2023; 15(13):3371. https://doi.org/10.3390/rs15133371
Chicago/Turabian StyleCai, Lingping, Haonan Qian, Linger Xing, Yang Zou, Linkang Qiu, Zihan Liu, Sirui Tian, and Hongtao Li. 2023. "A Software-Defined Radar for Low-Altitude Slow-Moving Small Targets Detection Using Transmit Beam Control" Remote Sensing 15, no. 13: 3371. https://doi.org/10.3390/rs15133371
APA StyleCai, L., Qian, H., Xing, L., Zou, Y., Qiu, L., Liu, Z., Tian, S., & Li, H. (2023). A Software-Defined Radar for Low-Altitude Slow-Moving Small Targets Detection Using Transmit Beam Control. Remote Sensing, 15(13), 3371. https://doi.org/10.3390/rs15133371






