Abstract
Near-surface structure investigation plays an important role in studying shallow active faults and has various engineering applications. Therefore, we developed a near-surface structure investigation method using ambient noise in a water environment. This newly developed seismic acquisition technology, fiber-optic distributed acoustic sensing (DAS), was used to acquire ambient noise from the Yangtze River. The recorded data were processed to reconstruct surface waves based on the theory of seismic interferometry. The fundamental-mode dispersion curves were extracted and inverted to obtain a shear-wave velocity model below the DAS line. We compared the inverted velocity model with the subsurface geological information from near the study area. The results from the inverted model were consistent with the prior geological information. Therefore, ambient noise in the water environment can be combined with DAS technology to effectively investigate near-surface structures.
1. Introduction
In recent years, ambient noise tomography has been widely used in many fields, such as seismology, ultrasonics, and underwater acoustics, to obtain subsurface structures [1,2,3,4]. In contrast to active seismic methods, ambient noise tomography is a passive seismic method that obtains subsurface structures using data from ambient noise caused by natural and anthropogenic activities. Therefore, ambient noise sources are readily available and less damaging to the environment than active sources such as an explosive source. These advantages make it a powerful tool for near-surface structure investigation, especially in areas with challenging terrains for active source data acquisition.
The ambient noise tomography method is based on seismic interferometry. It extracts seismic surface waves or body waves at one receiver from a virtual source at another receiver by cross-correlation and the summation of the ambient noise between the two receivers. In recent years, ambient noise from anthropogenic activities has been extensively studied and used in subsurface structure investigation [5,6]. Traffic noise from vehicles or trains in urban areas is one of the most widely used sources. Quiros et al. recovered body and surface waves from train-generated noise and further inverted the geological structure beneath a railway using the recovered wavefields [7]. The results confirmed that trains are practical sources for obtaining high-resolution subsurface structures. Zhang et al. investigated near-surface structures using vehicle-generated noise in an urban city and demonstrated that a short acquisition time of 15 min was sufficient to obtain accurate and stable results [8]. Brenguier et al. showed that train-generated ambient noise is a powerful source for active fault monitoring [9].
The water environment has abundant ambient noise from various sources, such as shipping and wind-generated, river-current-generated, and biological noise [10,11]. When acquiring data near a main ship channel, shipping noise is the primary source of ambient noise in the water environment, particularly with the increased shipping activities caused by globalization and global cargo flows [12]. Shipping noise originates from multiple mechanisms, including propeller, auxiliary, and hull movements through the water. These sources are located near the surface and are distributed along shipping channels. Shipping noise can travel tens or hundreds of kilometers and ranges from frequencies as low as a few hertz to as high as several kilohertz, depending on the ship size and speed. Therefore, shipping noise is a powerful source for subsurface structure investigation in the water environment. Li et al. inverted sound speed profiles in shallow water based on wavefields extracted from ambient noise, including shipping noise [13]. Tan et al. demonstrated the feasibility of seafloor characterization using ambient and shipping noises in shallow water [14]. Their method first calculated the cross-correlation of noise data to extract an effective wavefield. Then, a time-warping transform was applied to the extracted wavefield to obtain the dispersion curves. Finally, the sediment layer thickness and speed of sound were inverted from the measured dispersion curves. Most recent studies acquired shipping noise data using hydrophones that are typically moored in the water. The positions of hydrophones are unstable owing to mooring motion, which can reduce the coherence of the extracted wavefields via cross-correlations [15]. In addition, data are usually acquired by using a limited number of hydrophones with large spatial sampling intervals, making it impossible to reliably resolve subsurface structures.
The newly developed fiber-optic distributed acoustic sensing (DAS) technology uses an optical fiber cable as a sensor and measures vibrations along the entire cable. Compared to traditional hydrophones, DAS is a promising tool because of its low cost, real-time operation, and dense sampling. Most DAS systems are built based on the principle of coherent optical time-domain reflectometry (COTDR) [16,17]. Laser light is pulsed into the optical fiber from the interrogation units. When the optical probe pulse travels through the optical fiber, some of it is backscattered due to microscopic imperfections in the fiber. After all the backscattered light generated from the previous optical probe pulse is received by the interrogator, the system calculates the stretches of the optical fiber caused by external vibrations by comparing the measurements between the two pulses. The potential of DAS was tested and verified in oil and gas exploration [18,19], seismological research [20], microseismic monitoring [21,22], and ambient noise-based seismic monitoring [23,24,25].
This study investigated the feasibility of near-surface structure investigation using ambient noise in a water environment recorded using DAS. First, we introduced the DAS data acquisition and analyzed the characteristics of the raw ambient noise data. Subsequently, the surface waves were reconstructed from the acquired ambient noise data, from which the fundamental-mode dispersion curves were extracted. Finally, the shear-wave velocity model was inverted based on the dispersion curves. The velocity model obtained was consistent with the prior information from near the study area. Our results confirm the effectiveness of near-surface structure investigation using ambient noise in a water environment recorded using DAS.
2. Method
2.1. Surface Waves Reconstruction Using Seismic Interferometry
Surface waves were reconstructed from ambient noise in a water environment based on the theory of seismic interferometry. The noise at the two receivers was cross-correlated and summed to calculate a virtual wavefield recorded at one receiver with the virtual source at the other receiver. The governing equation for seismic interferometry [26,27] in the frequency-space domain is as follows:
where is the ship channel, is the DAS cable, and is the boundary at infinity. and denote the Green’s functions received at and with a source excited at , respectively. denotes the angular frequency. is the complex conjugate, and is the normal direction. All the sources in Equation (1) are assumed to come from the ship channel. Since the ship channel is parallel to the DAS cable, the stationary points in the ship channel lie far away from the receivers and , as shown in Figure 1. The geometry in Figure 1 is similar to the field case described in this study. A linear DAS array records noises originating from a parallel ship channel. The stationary regions are indicated by the grey area for the two receiving locations, and in this context. When considering the far-field approximation, Equation (1) is simplified as follows:
where denotes the wavenumber, and c denotes the propagation velocity.
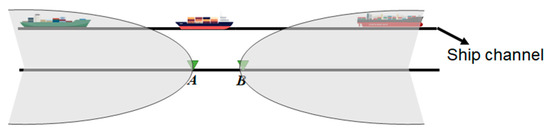
Figure 1.
Stationary regions for the linear geometry. The grey area indicates the stationary regions for two receiving locations and .
We defined the noise source at as . The noise sources at all different locations were assumed to be uncorrelated, such that
where denotes the spatial ensemble average, and is the power spectrum of the source wavelet. The observed noise wavefields at and in the frequency domain are
According to Equations (3)–(5), the cross-correlation of the noise wavefield, and , is shown as follows:
Combining Equation (6) with Equation (2) gives
Finally, Equation (7) is transformed into the time-space domain as follows:
where is the causal wavefield received at with a source excited at . is the noncausal wavefield received at with a source excited at . As shown in Equation (8), a virtual trace is obtained by cross-correlating the traces recorded at and . This process was repeated until a virtual shot gather was determined for each recording location in the DAS array.
2.2. Shear-Wave Velocity Inversion Using the Multichannel Analysis of Surface Waves
Surface waves are the main components of ambient noise and have dispersion properties. Different frequency components of surface waves travel at different velocities. The dispersion of surface waves is usually used for near-surface characterization. Therefore, the dispersion curves, describing the relationship between velocity and frequency, need to be extracted first. They were then inverted to obtain the near-surface shear-wave velocity. This study used the multichannel analysis of the surface waves (MASW) method [28], extracting a dispersion curve from a multichannel record using different methods such as the phase-shift [29], frequency-wavenumber transform [30], and slowness frequency methods [31]. We used the phase-shift method because of its robustness and computational efficiency.
The virtual shot gather by seismic interferometry is represented by , where is the total number of traces in the shot gather. The expression for the virtual trace, , is given in the left-hand side of Equation (8). According to the phase-shift method, each trace in the multichannel record was first transformed into the frequency domain using the Fourier transform. The transformed record, , can be expressed by multiplying the amplitude, , and the phase spectrum, . For example,
where is related to the real phase velocity, , to be determined from the virtual shot gathers. The transformed record was then normalized to remove the effects of geometrical spreading and attenuation on the amplitude. Finally, the dispersion image, , was calculated by summing the traces at different offsets after applying a phase-shift, , determined by an assumed phase velocity, .
When the assumed phase velocity, , was equal to the real phase velocity, , constructive superposition occurred, and a maximum was observed in the dispersion image. Otherwise, the summation process generated a destructive superposition. After calculating the dispersion image, the dispersion curve was extracted by picking the maximum at each frequency.
The shear-wave velocity was inverted by iteratively comparing the theoretical dispersion curve with the observed curve. The theoretical dispersion curve was calculated using the stiffness matrix method [32], which assumed a layered subsurface medium model. The Bayesian Markov chain Monte Carlo inversion method [33] was applied to solve the inversion problem. According to the Bayesian theory, the posterior distribution for the shear velocity model, , is computed from the prior probability density, , and the likelihood function, :
where represents the model to be inverted, and is composed of the shear-wave velocity, , and thickness, , for each layer. represents the extracted dispersion curve.
The prior probability density, , in Equation (11) describes the prior knowledge of the shear-wave velocity model. Assuming that the shear-wave velocity model is uniformly distributed over a fixed range, the prior probability density is expressed as follows:
where and denote the upper and lower boundaries, respectively, of the model . The likelihood function, , in Equation (11) is related to the misfit between the forward and observed dispersion curves and is defined as follows:
where is the theoretical dispersion curve. After the posterior probability density was calculated by Equations (11)–(13), the Markov chain Monte Carlo algorithm was used to solve the shear-wave velocity model.The inversion algorithm is performed for each virtual shot gathers. The inverted velocities from all the virtual shot gathers are assembled to obtain the pseudo 2D velocity profile. Finally, the inversion result at each location are linearly interpolated at an interval less than the trace interval. A Gaussian filter was applied to the interpolated data for lateral smoothing.
where is standard deviation. The value of is in grid points. The half width of gaussian filter is three times the sigma. The filter parameter is set in a trial-and-error way to smooth out the unrealistic discontinuities between the different locations while maintaining as many characteristics as possible at each position. Figure 2 shows a Gaussian filter with the sigma of 6. The half width of gaussian filter is three times the sigma, i.e., 18 grid points. When the interval between grid points is 0.2 m, the smoothing width of the gaussian filter is 7.2 m:3.6 m to the left and 3.6 m to the right of the current data point.
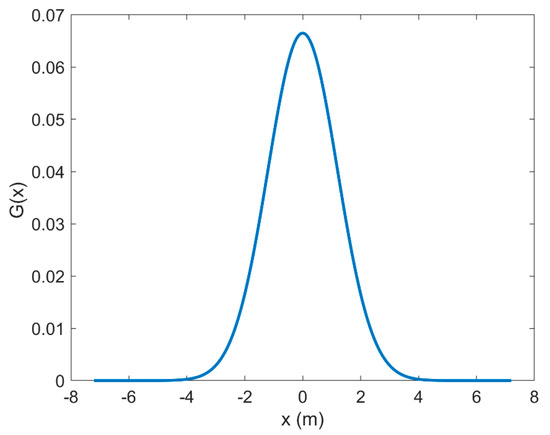
Figure 2.
The Gaussian filter for lateral smoothing.
3. Data and Results
3.1. DAS Data Acquisition and Analysis
The experiment was conducted along a floodplain in the lower reaches of the Yangtze River in China, as shown in Figure 3. Business shipping channels were used for cargo transportation at the study site. Many ships travel daily through these shipping channels. Therefore, the acquired ambient noise data were significantly affected by traveling ships and contained much shipping noise. The DAS instrument was placed on a floating dock. A common underground communication optical fiber cable was deployed along the riverside, parallel to the shipping channels, as shown in Figure 4. The optical fiber cable was buried at a depth of approximately 10 cm to ensure good coupling between the cable and the ground. The distance between the DAS line and the shipping lane nearest to the riverside was approximately 100 m. The DAS line was 210 m long. Data were recorded at a trace interval of 1 m and a temporal sampling interval of 1 ms. The gauge length was set to 10 m.
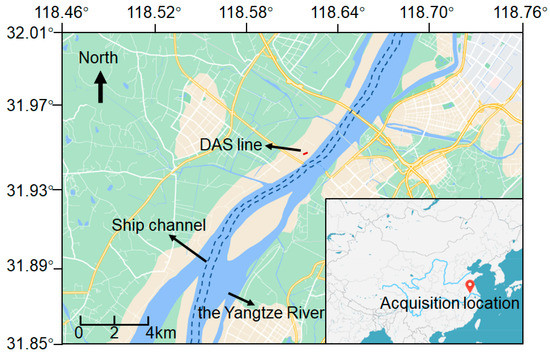
Figure 3.
Location of the DAS data acquisition.
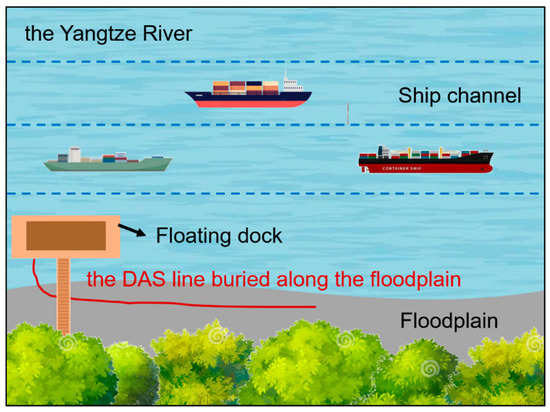
Figure 4.
The layout of the DAS line.
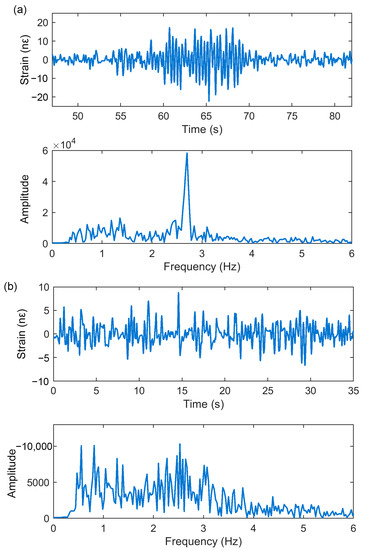
Since the raw DAS data were contaminated by abnormal optical noise, a bandpass filter with cut-off frequencies of 0.5 Hz and 25 Hz was applied to the raw data to remove the noise and clearly show the ship-related data. Figure 5a shows the filtered DAS data of two minutes, during which one ship passed through the DAS line. The horizontal axis represents the distance along the optical fiber cable. The black arrow indicates a linear event, when the ship passed through the DAS line. As seen from the zoom-in view in Figure 5b, the ship was traveling from left to right. The FK spectrum of the DAS data in Figure 5a is shown in Figure 5c. Figure 6 shows the waveform and its amplitude spectrum when a ship passed through and was far from the DAS line. Figure 6a shows the waveform indicated by the yellow line in Figure 5a and the corresponding amplitude spectrum. Figure 6a shows the strong amplitude vibrations when the ship passed through the DAS line. The amplitude spectrum was distributed in a frequency ranging from 0.5 to 6 Hz. A significant component of the signal was observed at frequencies near 2.7 Hz. On the other hand, the data from the period in the vicinity of the passage of the ship (indicated by the green line in Figure 5a) had weak energy, as shown in Figure 6b. However, they showed a frequency band (0.5–6 Hz) similar to that of the ship-related data.
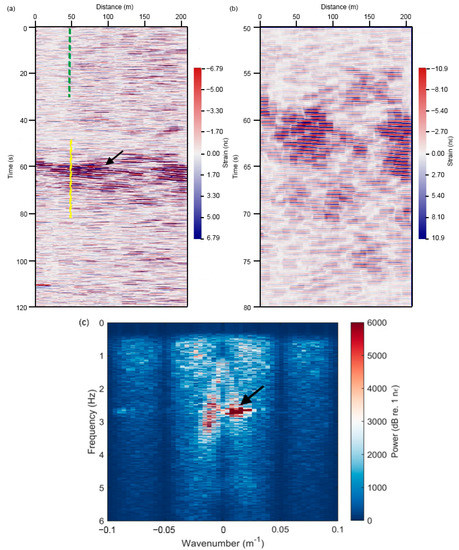
Figure 5.
(a) The raw DAS data of two minutes, (b) The zoom-in view of ship-related data in (a). (c) FK analysis of data in (a). The black arrows indicate the signal generated by a ship.
3.2. Surface Waves Reconstruction and Inversion
The DAS data were processed according to the workflow shown in Figure 7. Various preprocessing methods [34] were first applied to the raw noise data before the surface wave reconstruction. One hour of continuous data was cut to a length of one minute. Since there was heavy shipping traffic in the study area, one hour of data was enough to obtain a good virtual shot gather. Since ambient noise was distributed below 6 Hz, the data were bandpass-filtered to 0.5–6 Hz. Finally, time-domain one-bit normalization and spectral whitening were applied to remove the interference of the transient signal. After several preprocessing steps, seismic interferometry was performed to reconstruct the virtual shot gathers. Cross-correlation was first performed for each minute of data. The cross-correlated data were then stacked using the phase-weighted stacking (PWS) method [35]. Compared with the commonly used linear stacking method, the PWS method can improve the signal-to-noise (SNR) ratio of a virtual shot gather by using the phase coherence among the stacked signals. In addition, the causal and noncausal parts of the virtual shot gather were stacked to further improve the signal. Figure 8 shows the final virtual shot gathers at different locations. As shown in Figure 8, coherent surface wave signals were clearly reconstructed from the noise record.
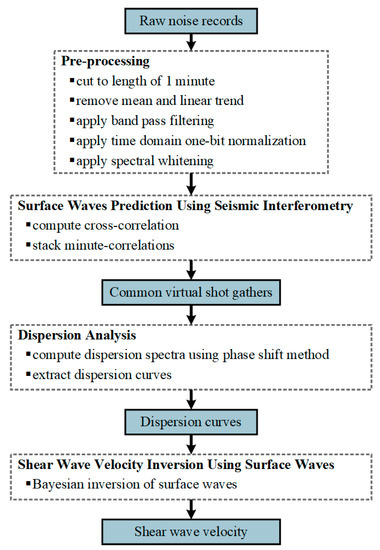
Figure 7.
Workflow of shear-wave velocity inversion using ambient noise in shallow water.
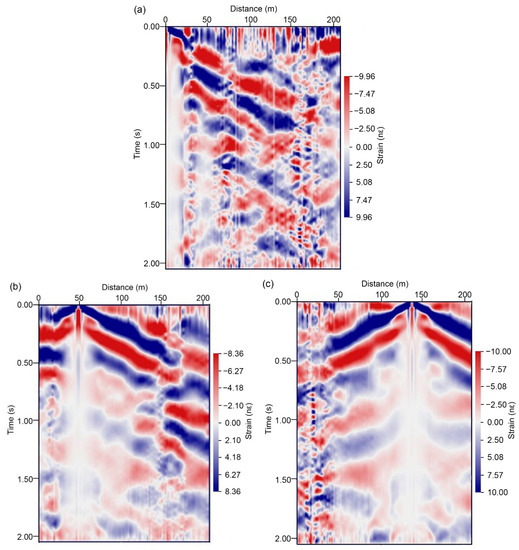
Figure 8.
The virtual shot gathers with a virtual source at (a) 0 m, (b) 50 m, and (c) 140 m. The horizontal axis represents the distance along the optical fiber cable.
As shown in Figure 8, the SNR at the far offset was low. Therefore, the dispersion image was calculated from the data at the near offset (a maximum offset of 100 m from the shot point). The fundamental-mode dispersion curves were obtained from the reconstructed surface waves, as indicated by the black open circles in Figure 9. The dispersion curves picked from the virtual shot gathers at different locations had similar shapes, which effectively verified the correctness of the identified surface waves. The 1D shear-wave velocities were then inverted from the selected dispersion curves, as shown in Figure 10. During the inversion process, the number of layers was set to seven according to the prior information from near the study area. The velocity and thickness ranges for each layer were set wide enough. The upper and lower velocity boundaries of each layer were 50 m/s and 500 m/s, respectively. The upper and lower thickness boundaries of each layer were 0 m and 5 m, respectively. The red dashed line in Figure 10 indicates the initial shear-wave velocity model. The blue lines indicate the inverted velocities when the corresponding dispersion curves deviate by less than 1% from the synthetic curves. The red solid line indicates the final inverted velocity at which the corresponding dispersion curve best fits the synthetic curve. Figure 11 shows the fitting of the observed dispersion curve to the synthetic curve using the final inverted velocity (solid red line in Figure 10). However, Figure 11 does not prove the inversion results. The inverted velocities from all the virtual shot gathers were assembled to obtain the pseudo 2D velocity profile. Finally, the inversion result at an interval of 1 m was linearly interpolated at an interval of 0.2 m. A Gaussian filter was applied to the interpolated data for lateral smoothing. The filter is shown in Figure 2. The final inversion result is shown in Figure 12.
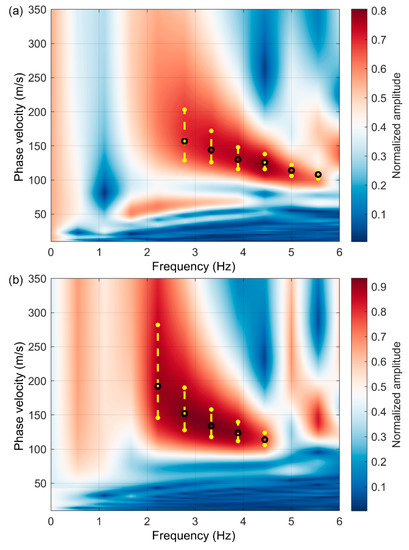
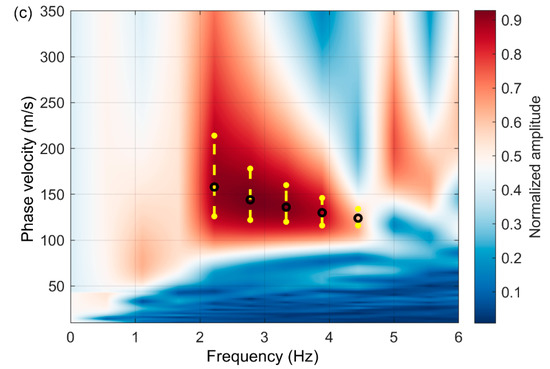
Figure 9.
(a–c) Dispersion spectra and dispersion curves extracted from data in Figure 8a–c. The black open circles indicate the picked fundamental-mode dispersion curves. The yellow dots and lines indicate the uncertainty of dispersion curves picking.
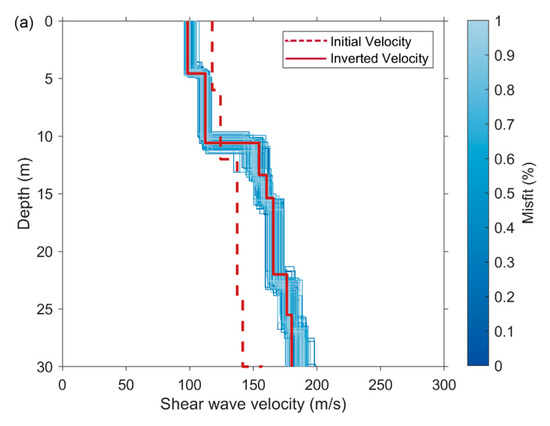
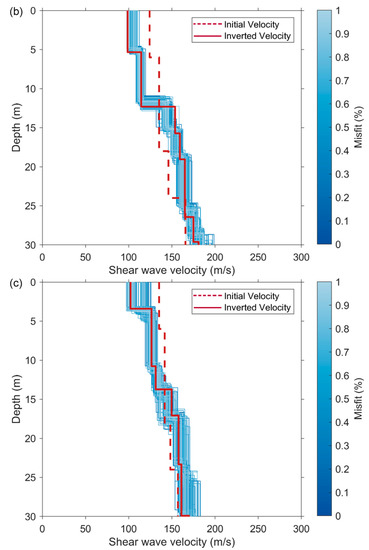
Figure 10.
(a–c) The inverted 1D shear-wave velocities using the fundamental-mode dispersion curves in Figure 9a–c.
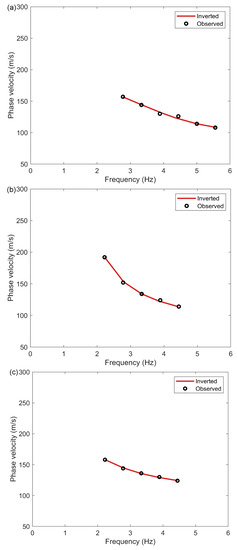
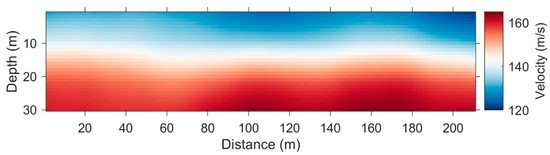
Figure 12.
The inverted 2D shear-wave velocity profile along the DAS line.
To validate the shear-wave velocity model inverted from the ambient noise data, we compared the obtained results with the prior information from near the study area. A previous study [36] showed that silted floodplains are widespread at the study site, where the stratigraphy is composed of thinly bedded deposits of clay, silty clay, silty sand, and sand. Holocene sediments consist of silty clay and mucky silty clay within a depth range of approximately 0–12m. Holocene sediments at a depth of approximately 12–30 m consist of silty sand and silty clay, which is consistent with the results shown in Figure 12, where an evident velocity variation occurred at a depth of approximately 12 m.
4. Discussion
We have verified the feasibility of near-surface structure investigation using ambient noise in a water environment. Surface waves were first reconstructed from ambient noise data based on the theory of seismic interferometry. Then, the fundamental-mode dispersion curves were extracted and inverted for the shear-wave velocity model. The quality of the reconstructed surface wave data is crucial for accurate shear-wave velocity inversion. In fact, the distribution of ambient noise sources affects the quality of reconstructed surface waves. Seismic interferometry requires that the noise sources are equally distributed in azimuth or are all aligned to the receiver array [37,38]. When a strongly directional source appears, the accuracy of the reconstructed surface waves decreases, thus leading to incorrected inversion results. In addition, DAS has limited sensitivity toward particle motion direction compared to a geophone. It is the most sensitive to waves propagating along the fiber. Therefore, the directionality of ambient source and the directional sensitivity of DAS both have an effect on the reconstructed surface waves.
In this study, the ambient sources were assumed to come from the ship channel. A linear DAS array was deployed parallel to the ship channel. We used a linear array because of its simplicity and the field site limitations. In this context, distant noise sources (ships) are almost aligned to the DAS array and can contribute to the proper reconstruction of surface waves [39]. Channel-parallel DAS can receive a wave from a variety of azimuths [25]. This is demonstrated by the FK spectrum shown in Figure 5c, where the spread-out spectral energy is distributed in both positive and negative wavenumbers. The noise propagating along the fiber axis is preferred for the seismic interferometry with a linear array. The noise propagating in other directions decreases the SNR of the reconstructed surface waves. Since only data with a high SNR are used to calculate the dispersion curve, these low SNR data in the virtual gathers do not greatly affect the final inversion result.
5. Conclusions
This study introduces a near-surface structure investigation method using ambient noise in a water environment recorded using fiber-optic distributed acoustic sensing (DAS). The DAS line was deployed along the Yangtze River floodplain in China. Large amounts of water traffic were present in the study area. The ambient noise data acquired in the water environment were concentrated in the frequency band ranging from 0.5 to 6 Hz. Based on the theory of seismic interferometry, the surface waves were reconstructed from the ambient noise data. Finally, the shear-wave velocity along the DAS line was obtained by inverting the fundamental-mode dispersion curves extracted from the surface waves. The calculated shear-wave velocity was consistent with the geological information from near the study area. These results demonstrate that ambient noise in the water environment can provide useful information for near-surface structure investigations. In addition, the use of DAS provides a low-cost, high-efficiency, and high-density field acquisition compared to that of conventional hydrophones, making it a promising tool for near-surface investigations in the future.
Author Contributions
Conceptualization, J.S. and Y.W.; methodology, J.S. and Y.W.; software, J.S. and Y.W.; validation, J.S. and Y.W.; data curation, C.Z., X.Z. and Y.Z.; writing—original draft preparation, J.S. and Y.W.; writing—review and editing, J.S., Y.W., C.Z., X.Z. and Y.Z.; project administration, Y.W.; funding acquisition, Y.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the CAS Project for Young Scientists in Basic Research, grant number YSBR-020; the National Natural Science Foundation of China (NSFC), grant numbers U2001601 and 62175100; and the Fundamental Research Funds for the Central Universities, grant number 0213-14380202.
Data Availability Statement
Not applicable.
Acknowledgments
The authors gratefully acknowledge the supports of various foundations. The authors are grateful to the editor and anonymous reviewers. Their comments have greatly contributed to improving the quality of this study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Siderius, M.; Harrison, C.H.; Porter, M.B. A passive fathometer technique for imaging seabed layering using ambient noise. J. Acoust. Soc. Am. 2006, 120, 1315–1323. [Google Scholar] [CrossRef]
- Draganov, D.; Campman, X.; Thorbecke, J.; Verdel, A.; Wapenaar, K. Seismic exploration-scale velocities and structure from ambient seismic noise (>1 Hz). J. Geophys. Res. Solid Earth 2013, 118, 4345–4360. [Google Scholar] [CrossRef]
- Lu, Y.; Stehly, L.; Brossier, R.; Paul, A.; AlpArray Working Group. Imaging Alpine crust using ambient noise wave-equation tomography. Geophys. J. Int. 2020, 222, 69–85. [Google Scholar] [CrossRef]
- Mohamadian Sarvandani, M.; Kästle, E.; Boschi, L.; Leroy, S.; Cannat, M. Seismic Ambient Noise Imaging of a Quasi-Amagmatic Ultra-Slow Spreading Ridge. Remote Sens. 2021, 13, 2811. [Google Scholar] [CrossRef]
- Albert, D.G.; Decato, S.N. Acoustic and seismic ambient noise measurements in urban and rural areas. Appl. Acoust. 2017, 119, 135–143. [Google Scholar] [CrossRef]
- Dean, T.; Hasani, M.A.A. Seismic noise in an urban environment. Lead. Edge 2020, 39, 639–645. [Google Scholar] [CrossRef]
- Quiros, D.A.; Brown, L.D.; Kim, D. Seismic interferometry of railroad induced ground motions: Body and surface wave imaging. Geophys. J. Int. 2016, 205, 301–313. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Y.E.; Zhang, H.; Ku, T. Near-surface site investigation by seismic interferometry using urban traffic noise in Singapore. Geophysics 2019, 84, B169–B180. [Google Scholar] [CrossRef]
- Brenguier, F.; Boué, P.; Ben-Zion, Y.; Vernon, F.; Johnson, C.W.; Mordret, A.; Coutant, O.; Share, P.E.; Beaucé, E.; Hollis, D.; et al. Train traffic as a powerful noise source for monitoring active faults with seismic interferometry. Geophys. Res. Lett. 2019, 46, 9529–9536. [Google Scholar] [CrossRef]
- Zakarauskas, P. Ambient noise in shallow water: A literature review. Can. Acoust. 1986, 14, 3–17. [Google Scholar]
- Olofsson, B. Marine ambient seismic noise in the frequency range 1–10 Hz. Lead. Edge 2010, 29, 418–435. [Google Scholar] [CrossRef]
- Hermannsen, L.; Beedholm, K.; Tougaard, J.; Madsen, P.T. High frequency components of ship noise in shallow water with a discussion of implications for harbor porpoises (Phocoena phocoena). J. Acoust. Soc. Am. 2014, 136, 1640–1653. [Google Scholar] [CrossRef]
- Li, F.; Yang, X.; Zhang, Y.; Luo, W.; Gan, W. Passive ocean acoustic tomography in shallow water. J. Acoust. Soc. Am. 2019, 145, 2823–2830. [Google Scholar] [CrossRef]
- Tan, T.W.; Godin, O.A.; Katsnelson, B.G.; Yarina, M. Passive geoacoustic inversion in the Mid-Atlantic Bight in the presence of strong water column variability. J. Acoust. Soc. Am. 2020, 147, EL453–EL459. [Google Scholar] [CrossRef]
- Skarsoulis, E.K.; Cornuelle, B.D. Cross-correlation of shipping noise: Refraction and receiver-motion effects. J. Acoust. Soc. Am. 2019, 145, 3003–3010. [Google Scholar] [CrossRef]
- He, Z.; Liu, Q. Optical fiber distributed acoustic sensors: A review. J. Light. Technol. 2021, 39, 3671–3686. [Google Scholar] [CrossRef]
- Bakulin, A.; Silvestrov, I.; Pevzner, R. Surface seismics with DAS: An emerging alternative to modern point-sensor acquisition. Lead. Edge 2020, 39, 808–818. [Google Scholar] [CrossRef]
- Harris, K.; White, D.; Samson, C. Imaging the Aquistore reservoir after 36 kilotonnes of CO2 injection using distributed acoustic sensingAquistore CO2-injection VSP results. Geophysics 2017, 82, M81–M96. [Google Scholar] [CrossRef]
- Ellmauthaler, A.; LeBlanc, M.; Bush, J.; Willis, M.E.; Maida, J.L.; Wilson, G.A. Real-time DAS VSP acquisition and processing on single-and multi-mode fibers. IEEE Sens. J. 2020, 21, 14847–14852. [Google Scholar] [CrossRef]
- Lindsey, N.J.; Martin, E.R.; Dreger, D.S.; Freifeld, B.; Cole, S.; James, S.R.; Biondi, B.L.; Ajo-Franklin, J.B. Fiber-optic network observations of earthquake wavefields. Geophys. Res. Lett. 2017, 44, 11–792. [Google Scholar] [CrossRef]
- Walter, F.; Gräff, D.; Lindner, F.; Paitz, P.; Köpfli, M.; Chmiel, M.; Fichtner, A. Distributed acoustic sensing of microseismic sources and wave propagation in glaciated terrain. Nat. Commun. 2020, 11, 2436. [Google Scholar] [CrossRef] [PubMed]
- Luo, B.; Jin, G.; Stanek, F. Near-field strain in distributed acoustic sensing-based microseismic observation. Geophysics 2021, 86, P49–P60. [Google Scholar] [CrossRef]
- Song, Z.; Zeng, X.; Thurber, C.H. Surface-wave dispersion spectrum inversion method applied to Love and Rayleigh waves recorded by distributed acoustic sensing. Geophysics 2021, 86, EN1–EN12. [Google Scholar] [CrossRef]
- Song, Z.; Zeng, X.; Xie, J.; Bao, F.; Zhang, G. Sensing shallow structure and traffic noise with fiber-optic internet cables in an urban area. Surv. Geophys. 2021, 42, 1401–1423. [Google Scholar] [CrossRef]
- Dou, S.; Lindsey, N.; Wagner, A.M.; Daley, T.M.; Freifeld, B.; Robertson, M.; Peterson, J.; Ulrich, C.; Martin, E.R.; Ajo-Franklin, J.B. Distributed acoustic sensing for seismic monitoring of the near surface: A traffic-noise interferometry case study. Sci. Rep. 2017, 7, 11620. [Google Scholar] [CrossRef]
- Wapenaar, K. Retrieving the elastodynamic Green’s function of an arbitrary inhomogeneous medium by cross correlation. Phys. Rev. Lett. 2004, 93, 254301. [Google Scholar] [CrossRef]
- Wang, Y.; Luo, Y.; Schuster, G.T. Interferometric interpolation of missing seismic data. Geophysics 2009, 74, SI37–SI45. [Google Scholar] [CrossRef]
- Park, C.B.; Miller, R.D.; Xia, J. Multichannel analysis of surface waves. Geophysics 1999, 64, 800–808. [Google Scholar] [CrossRef]
- Park, C.B.; Miller, R.D.; Xia, J. Imaging dispersion curves of surface waves on multi-channel record. In SEG Technical Program Expanded Abstracts of the Society of Exploration Geophysicists (SEG) International Exposition and 68th Annual Meeting, New Orleans, LA, USA, 13–18 September 1998; Society of Exploration Geophysicists: Tulsa, OK, USA, 1998; pp. 1377–1380. [Google Scholar]
- Yilmaz, Ö. Seismic Data Processing; Society of Exploration Geophysicists: Tulsa, OK, USA, 1987. [Google Scholar]
- McMechan, G.A.; Yedlin, M.J. Analysis of dispersive waves by wave field transformation. Geophysics 1981, 46, 869–874. [Google Scholar] [CrossRef]
- Kausel, E.; Roesset, J.M. Stiffness matrices for layered soils. Bull. Seismol. Soc. Am. 1981, 71, 1743–1761. [Google Scholar] [CrossRef]
- Socco, L.V.; Boiero, D. Improved Monte Carlo inversion of surface wave data. Geophys. Prospect. 2008, 56, 357–371. [Google Scholar] [CrossRef]
- Bensen, G.D.; Ritzwoller, M.H.; Barmin, M.P.; Levshin, A.L.; Lin, F.; Moschetti, M.P.; Shapiro, N.M.; Yang, Y. Processing seismic ambient noise data to obtain reliable broad-band surface wave dispersion measurements. Geophys. J. Int. 2007, 169, 1239–1260. [Google Scholar] [CrossRef]
- Schimmel, M.; Paulssen, H. Noise reduction and detection of weak, coherent signals through phase-weighted stacks. Geophys. J. Int. 1997, 130, 497–505. [Google Scholar] [CrossRef]
- Tong, L.; Che, H.; Zhang, M.; Li, H. Review of shear-wave velocity prediction equations based on piezocone penetration test data: Example from Yangtze River floodplain deposits at Nanjing, Jiangsu Province, China. Q. J. Eng. Geol. Hydrogeol. 2018, 51, 229–246. [Google Scholar] [CrossRef]
- Strobbia, C.; Boaga, J.; Cassiani, G. Double-array refraction microtremors. J. Appl. Geophys. 2015, 121, 31–41. [Google Scholar] [CrossRef]
- Strobbia, C.; Cassiani, G. Refraction microtremors (ReMi): Data analysis and diagnostics of key hypotheses. Geophysics 2011, 76, MA11–MA20. [Google Scholar] [CrossRef]
- Le Feuvre, M.; Joubert, A.; Leparoux, D.; Côte, P. Passive multi-channel analysis of surface waves with cross-correlations and beamforming. Application to a sea dike. J. Appl. Geophys. 2015, 114, 36–51. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).