Improved Dempster–Shafer Evidence Theory for Tunnel Water Inrush Risk Analysis Based on Fuzzy Identification Factors of Multi-Source Geophysical Data
Abstract
1. Introduction
- (1)
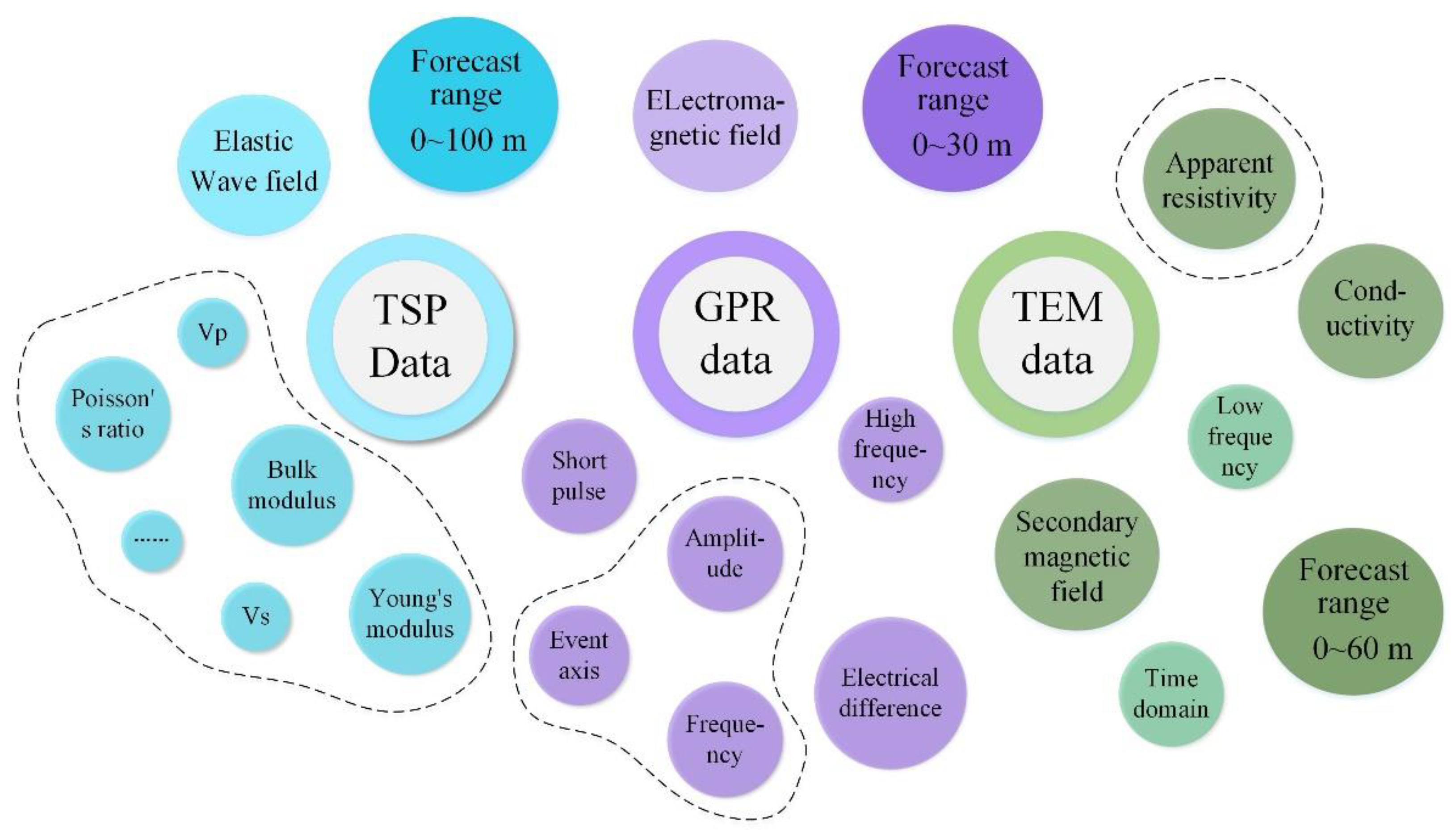
- Heterogeneity of the multi-source geophysical data. Different advanced geological prediction methods have been implemented for the same tunnel face to detect the water outlet of the tunnel. The TSP data store the attenuation parameters of seismic waves propagating in the tunnel, including longitudinal wave velocity, shear wave velocity, Poisson’s ratio of rock, Young’s modulus, and positive and negative reflection interfaces of seismic waves. The GPR data store the distribution of the amplitude, frequency, event axis, and energy of the electromagnetic wave signal propagation in the tunnel’s surrounding rock. Additionally, the TEM data measure the resistivity distribution of the surrounding rock. In addition, these parameters are presented in different formats (tables, images). Based on the generation method of the data field, the propagation characteristics of the wave, signal processing method, and characteristic parameters are all different. Therefore, we require a complementary method of fusing multi-source geophysical data to extract more valuable information.
- (2)
- Complex correlation characteristics of multi-source geophysical data. Although the detection objects of different data are all water output conditions of the same tunnel mileage section, it is difficult to have a unified method to correlate these data. In one case, the water-rich region deduced from the change in the physical property parameters of the TSP data reflect the absence of water in the electromagnetic waveform attenuation characteristics of the GPR data or high resistance to the resistivity value of the TEM data. Therefore, there may be contradictions in the performance results of these data in water-rich areas and there is no way to determine the internal relationship between the characteristics of these data. This was determined by the multi-source heterogeneity of the data. Nevertheless, the characteristics of these data are closely related to the water outflow in this area, and it is difficult to make full use of the interpreted results of these geophysical data to establish a unified water inrush risk analysis model.
2. Data and Methods
2.1. Multi-Source Geophysical Data
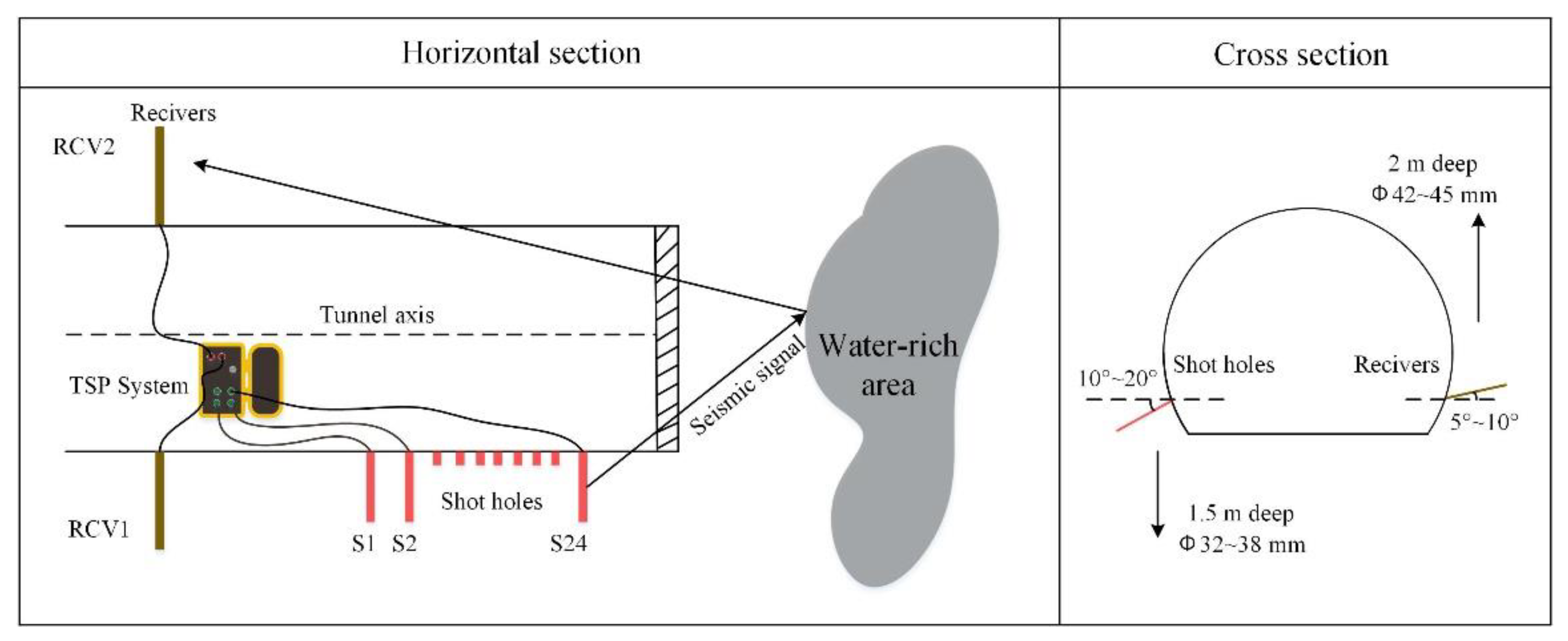
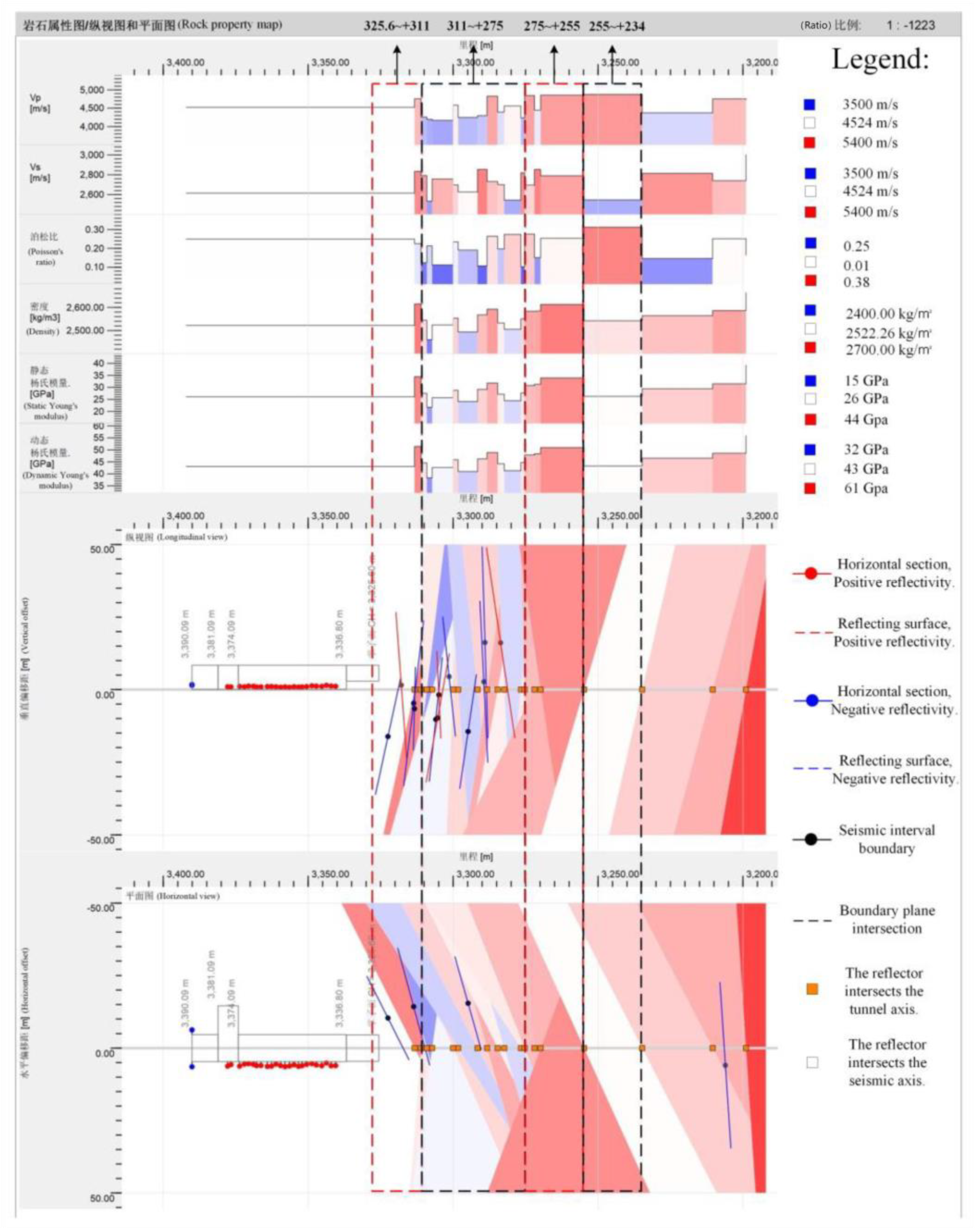
2.1.1. TSP Data
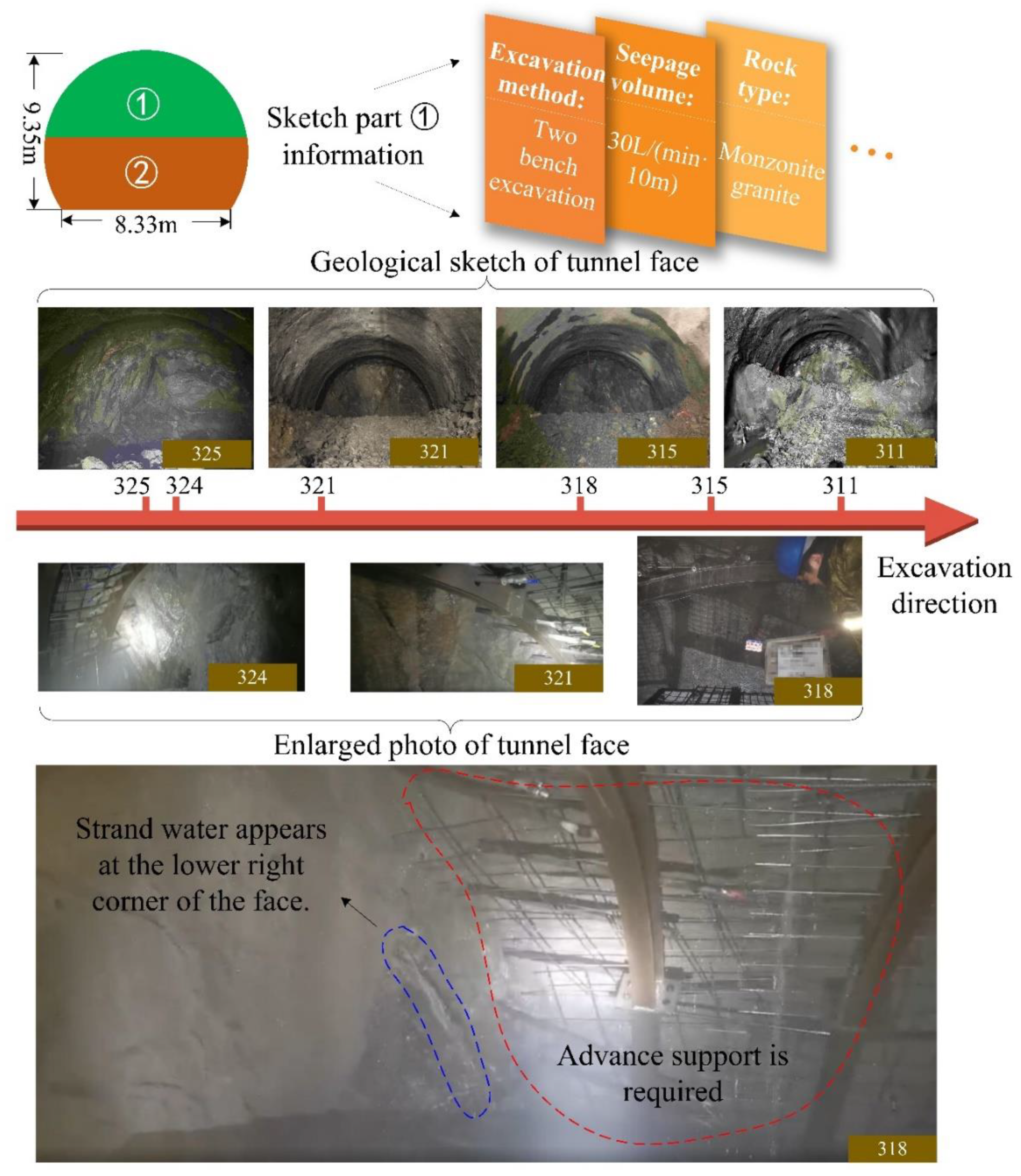
- Range 325.6~+ 311 m: The surrounding rock is basically the same as the current face, partially broken, with more developed joints, containing water (mainly linear and strand-shaped water).
- Range 311~+ 275 m: The surrounding rock is mainly fragmented, partially fragmented, with developed joints, and densely developed fissures, containing water (increased local water volume), and there is a risk of water inrush locally. Sufficient attention must be paid during the construction process.
- Range 275~+ 255 m: the surrounding rock is relatively broken, with relatively developed joints, and contains water (mainly linear and strand-shaped water).
- Range 255~+ 234 m: the surrounding rock is relatively broken, with relatively developed joints and fissures, and contains water (the local water volume increases).
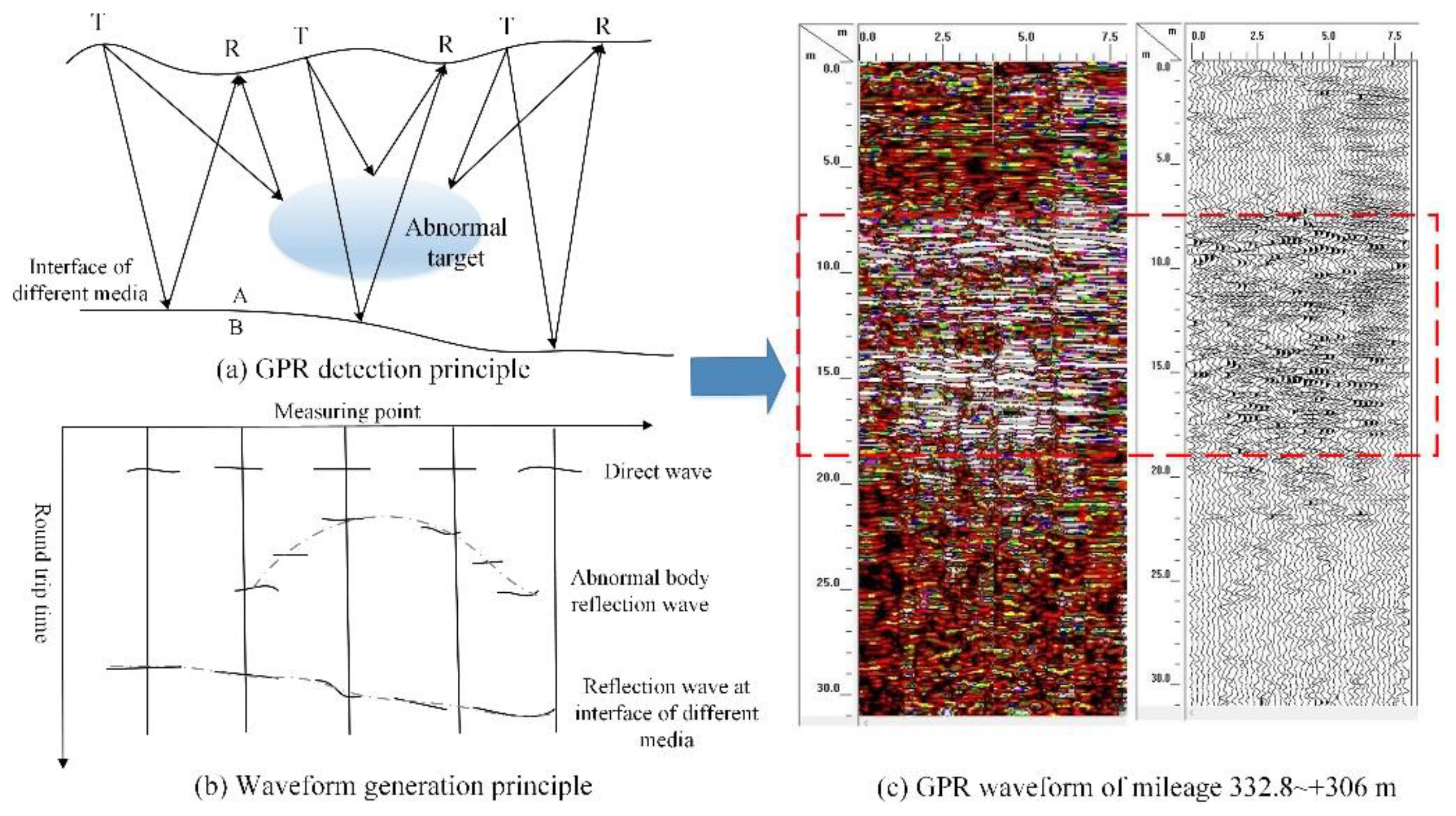
2.1.2. GPR Data
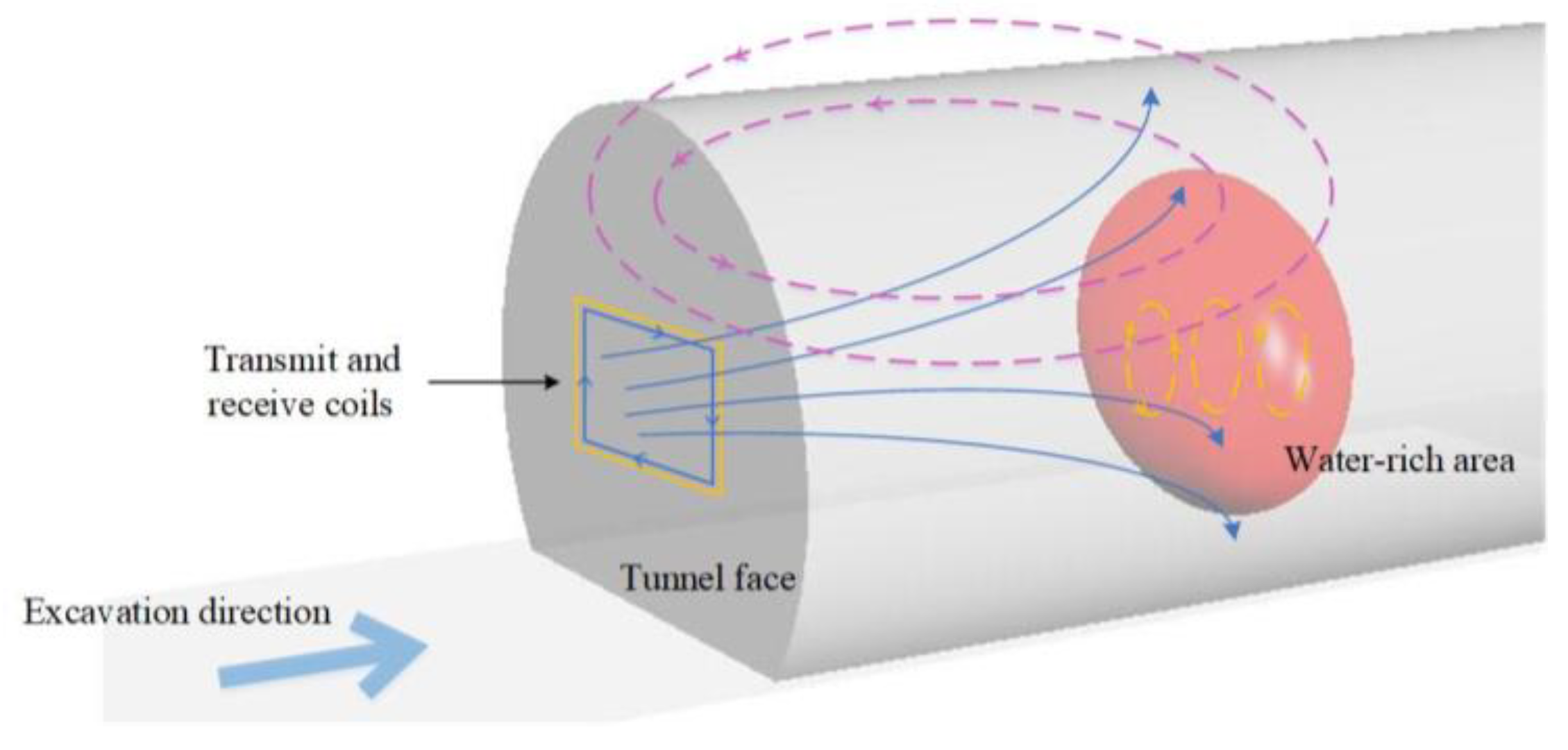
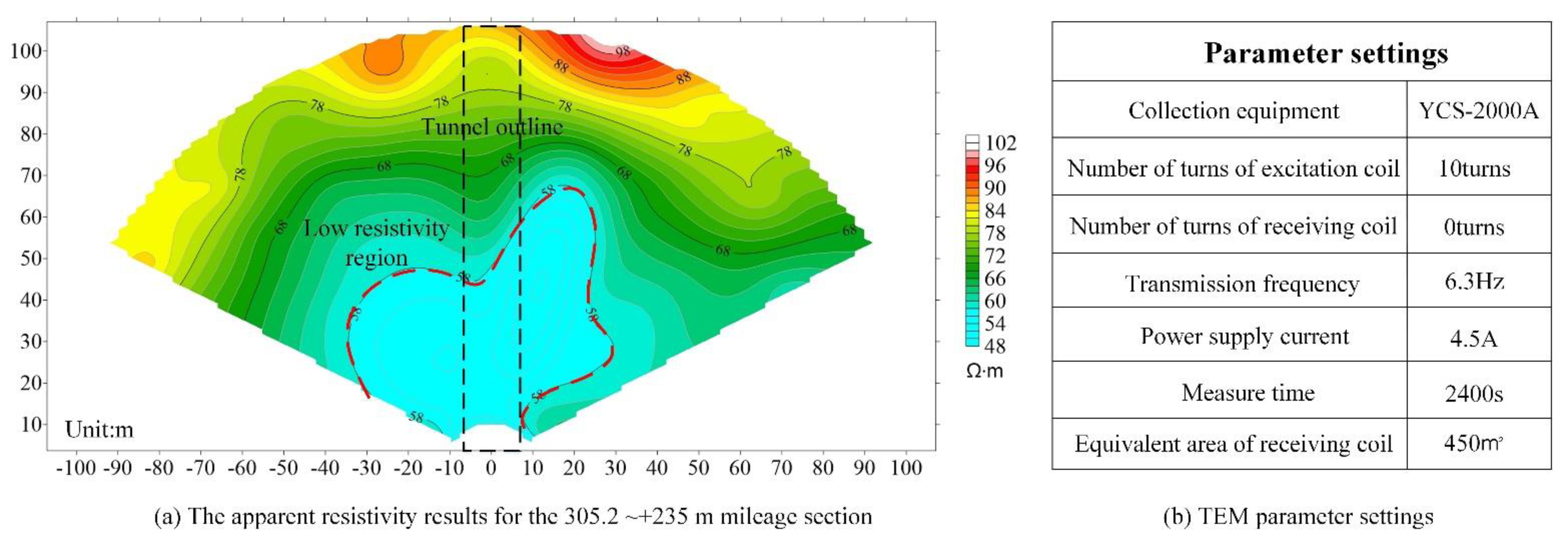
2.1.3. TEM Data
2.1.4. Fuzzy Identification Factors
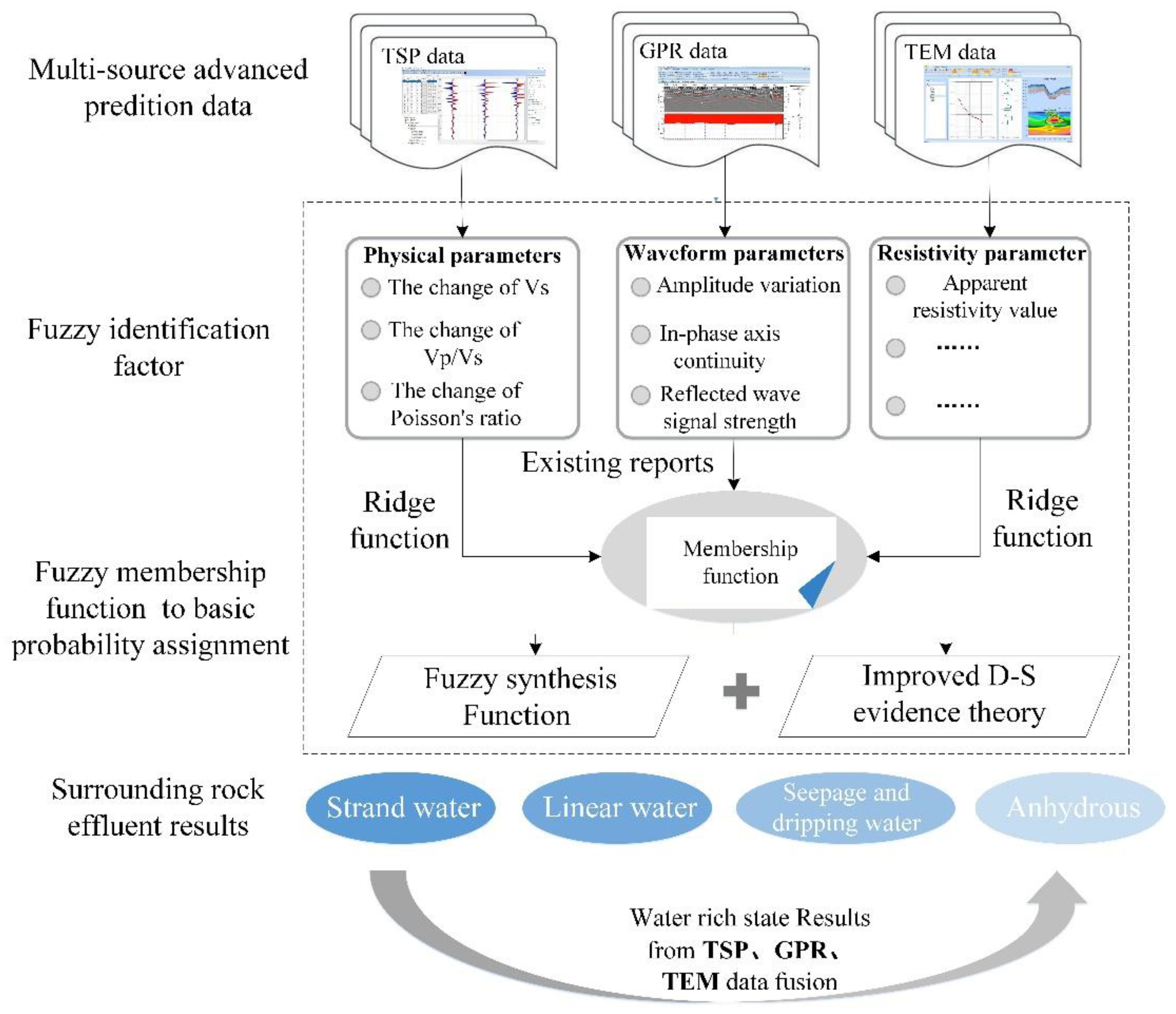
2.2. Fusion Methods
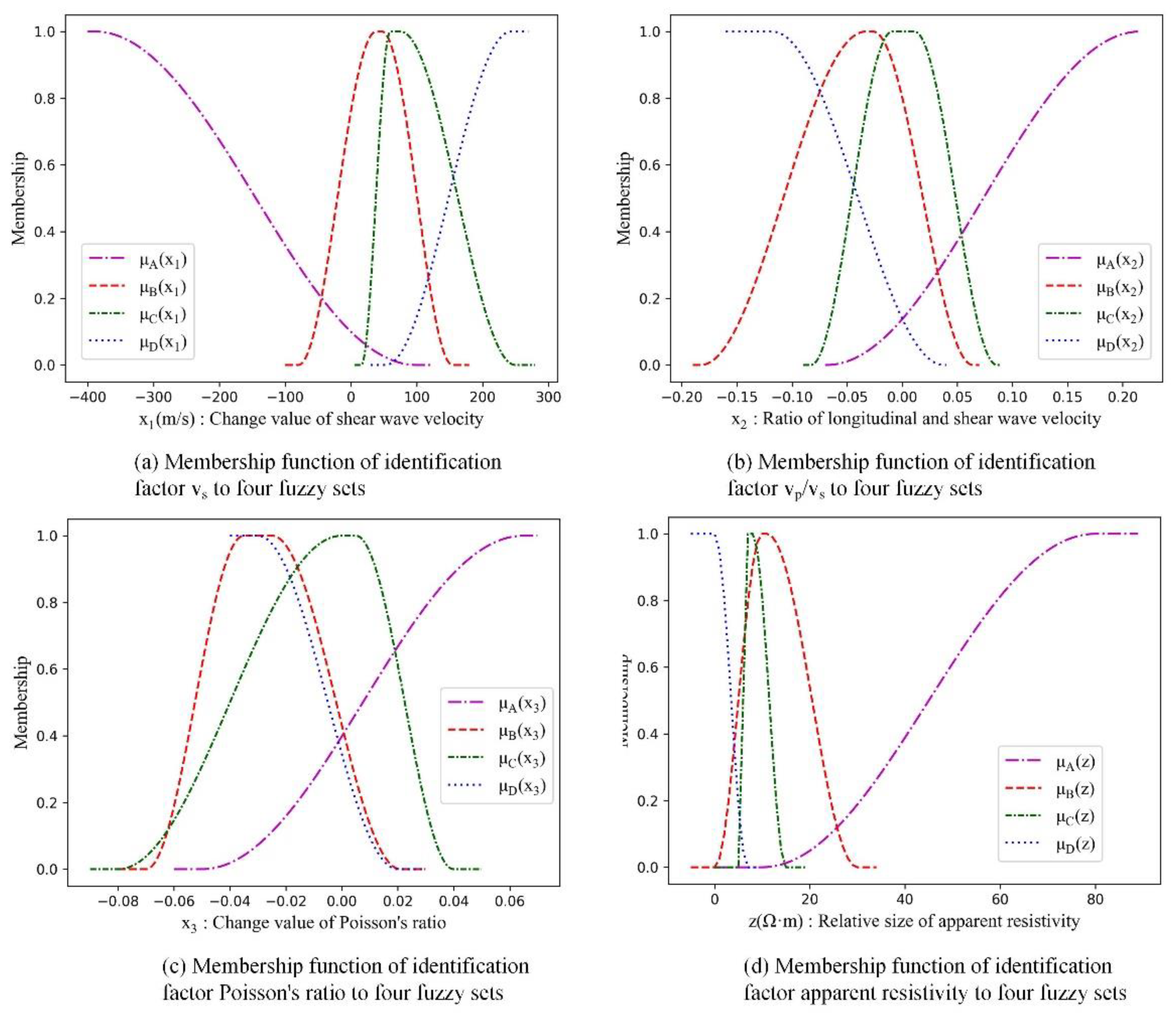
2.2.1. Membership Functions of Different Identification Factors
2.2.2. BPA Based on the Degree of Membership for the Improved D-S Theory
3. Results and Analysis
3.1. Study Area
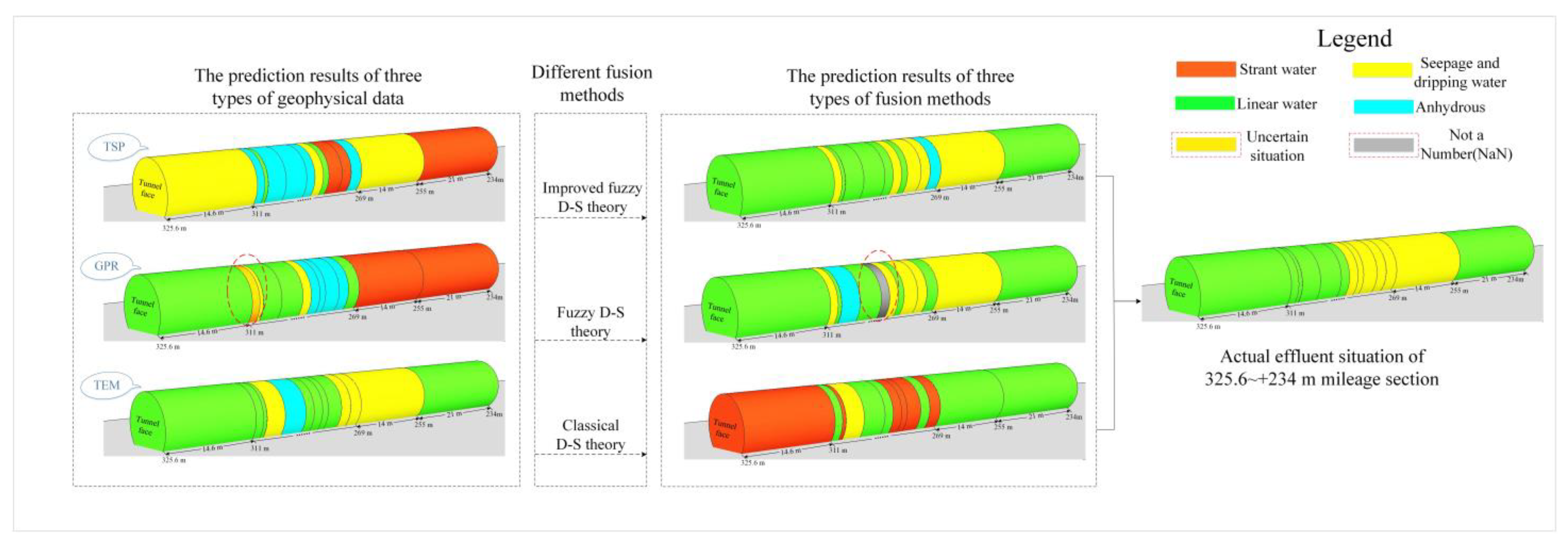
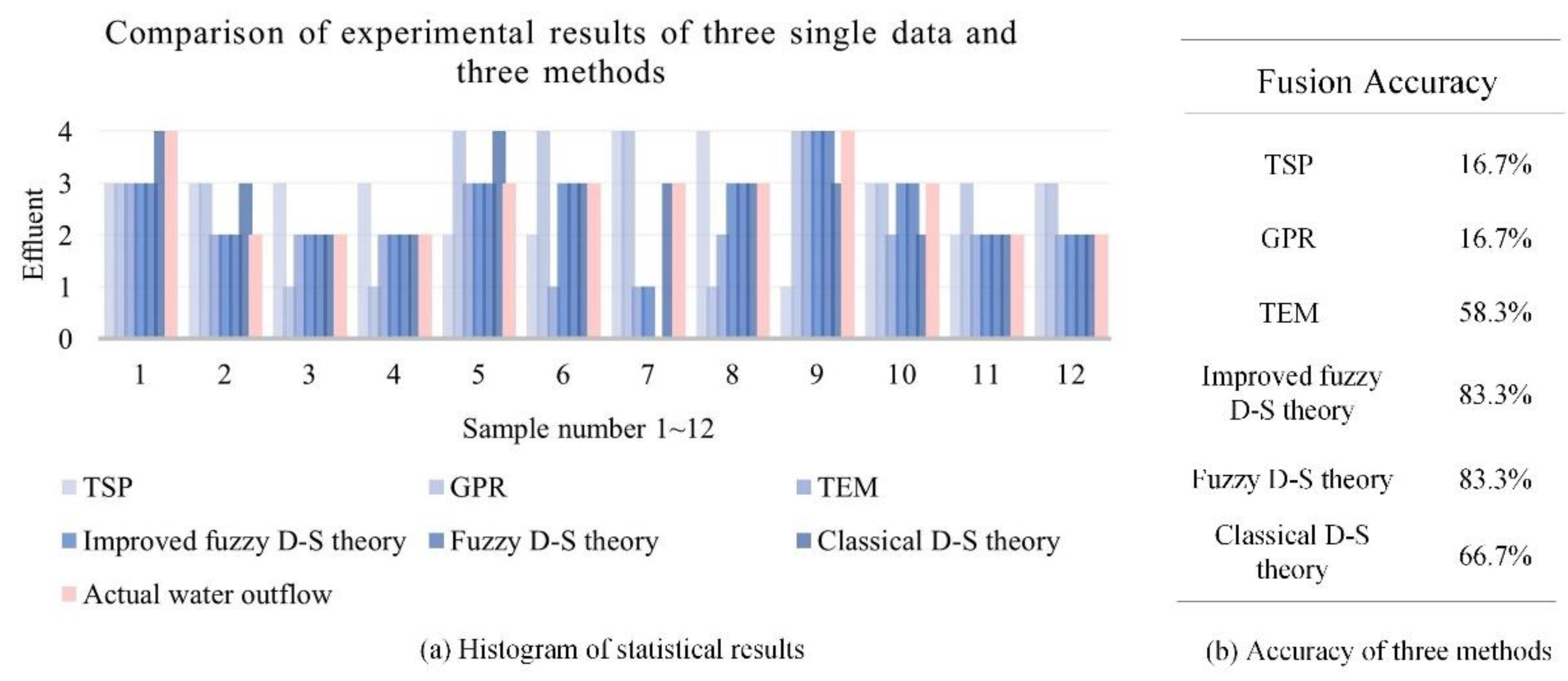
3.2. Result of Effluent Condition
4. Discussion
5. Conclusions
- The model improves the automation of geophysical data interpretation and can reduce the number of interpreters used in tunnel construction, thus reducing cost.
- The results of this study can also be used as auxiliary reference information for interpreters, prompting the careful examination of problems when the conclusions of the model are inconsistent with those of interpreters.
- The prediction results of the water effluent obtained by the model in this study have high accuracy, robustness, and important reference values for practical engineering applications.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, X.-S.; Xu, Z.-H.; Bao, X.-H.; Wang, W.-T.; Fu, Y.-B. Challenges and technological breakthroughs in tunnel construction in China. China J. Highw. Transp. 2020, 33, 1. [Google Scholar]
- Qian, Q.; Lin, P. Safety risk management of underground engineering in China: Progress, challenges and strategies. J. Rock Mech. Geotech. Eng. 2016, 8, 423–442. [Google Scholar] [CrossRef]
- Sun, W.; Liang, Q.; Qin, S.; Yuan, Y.; Zhang, T. Evaluation of groundwater effects on tunnel engineering in loess. Bull. Eng. Geol. Environ. 2021, 80, 1947–1962. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhou, J.; Zhang, B.; Wang, H.; Huang, M. Statistical analysis of major tunnel construction accidents in China from 2010 to 2020. Tunn. Undergr. Space Technol. 2022, 124, 104460. [Google Scholar] [CrossRef]
- Li, S.; Liu, B.; Xu, X.; Nie, L.; Liu, Z.; Song, J.; Sun, H.; Chen, L.; Fan, K. An overview of ahead geological prospecting in tunneling. Tunn. Undergr. Space Technol. 2017, 63, 69–94. [Google Scholar] [CrossRef]
- Xu, L.; Zhang, J.-q.; Qi, Z.-f. Comparison research on comprehensive advanced geological prediction of hydraulic tunnels. Prog. Geophys. 2018, 33, 411–417. [Google Scholar]
- Shi, S.; Xie, X.; Tian, S.; Wen, Z.; Bu, L.; Zhou, Z.; Song, S.; Zhao, R. Advanced geological prediction. In Tunnel Engineering-Selected Topics; IntechOpen: London, UK, 2019. [Google Scholar]
- Chalikakis, K.; Plagnes, V.; Guerin, R.; Valois, R.; Bosch, F.P. Contribution of geophysical methods to karst-system exploration: An overview. Hydrogeol. J. 2011, 19, 1169–1180. [Google Scholar] [CrossRef]
- Chen, Y.-l.; Gan, F.-p.; Lu, C.-j.; Wei, J.-y.; Zhao, W. The study of underground river course detection by integrated geophysical methods in bare karst area. Prog. Geophys. 2013, 28, 1608–1616. [Google Scholar]
- Xue, G.-q.; Pan, D.-m.; Yu, J.-c. Review the applications of geophysical methods for mapping coal-mine voids. Prog. Geophys. 2018, 33, 2187–2192. [Google Scholar]
- Lu, T.; Liu, S.-d.; Wang, B. Application of integrated mining geophysical method in detection of water-bearing faults. Prog. Geophys. 2015, 30, 1371–1375. [Google Scholar]
- Lu, T.; Liu, S.; Wang, B.; Wu, R.; Hu, X. A review of geophysical exploration technology for mine water disaster in China: Applications and trends. Mine Water Environ. 2017, 36, 331–340. [Google Scholar] [CrossRef]
- Pugin, A.J.M.; Pullan, S.E.; Hunter, J.A.; Oldenborger, G.A. Hydrogeological prospecting using P-and S-wave landstreamer seismic reflection methods. Near Surf. Geophys. 2009, 7, 315–328. [Google Scholar] [CrossRef]
- Brossier, R.; Operto, S.; Virieux, J. Velocity model building from seismic reflection data by full-waveform inversion. Geophys. Prospect. 2015, 63, 354–367. [Google Scholar] [CrossRef]
- Choudary, K.; Dickmann, T. 3D-TSP–Advanced geological prediction during construction of hydro tunnels in the Himalayas. In Proceedings of the Indo-Rock Conference, Mumbai, India, 17–18 June 2016. [Google Scholar]
- Annan, A. Electromagnetic principles of ground penetrating radar. Ground Penetrating Radar Theory Appl. 2009, 1, 1–37. [Google Scholar]
- Xue, G.; Li, H.; He, Y.; Xue, J.; Wu, X. Development of the inversion method for transient electromagnetic data. IEEE Access 2020, 8, 146172–146181. [Google Scholar] [CrossRef]
- Shi, S.; Bu, L.; Li, S.; Xiong, Z.; Xie, X.; Li, L.; Zhou, Z.; Xu, Z.; Ma, D. Application of comprehensive prediction method of water inrush hazards induced by unfavourable geological body in high risk karst tunnel: A case study. Geomat. Nat. Hazards Risk 2017, 8, 1407–1423. [Google Scholar] [CrossRef]
- Bu, L.; Li, S.; Shi, S.; Li, L.; Zhao, Y.; Zhou, Z.; Nie, L.; Sun, H. Application of the comprehensive forecast system for water-bearing structures in a karst tunnel: A case study. Bull. Eng. Geol. Environ. 2019, 78, 357–373. [Google Scholar] [CrossRef]
- Huang, C.-f.; Zhang, S.-l.; Wu, S.-c.; Gao, Y.-t. Research and application of a comprehensive forecasting system for tunnels in water-bearing fault fracture zones: A case study. Arab. J. Geosci. 2022, 15, 171. [Google Scholar] [CrossRef]
- Kuang, Y.; Li, L. Speech emotion recognition of decision fusion based on DS evidence theory. In Proceedings of the 2013 IEEE 4th International Conference on Software Engineering and Service Science, Beijing, China, 23–25 May 2013; pp. 795–798. [Google Scholar]
- Yan, R.; Li, G.; Liu, B. Knowledge fusion based on DS theory and its application on Expert System for software fault diagnosis. In Proceedings of the 2015 Prognostics and System Health Management Conference (PHM), Beijing, China, 21–23 October 2015; pp. 1–5. [Google Scholar]
- Li, Y.; Chen, J.; Ye, F.; Liu, D. The improvement of DS evidence theory and its application in IR/MMW target recognition. J. Sens. 2016, 2016, 1903792. [Google Scholar] [CrossRef]
- Chen, Y.; Wen, G.; Dong, X.; Zhang, Z. Research on rotor condition monitoring based on DS evidence theory. In Proceedings of the 2016 13th International Conference on Ubiquitous Robots and Ambient Intelligence (URAI), Xi’an, China, 19–22 August 2016; pp. 848–853. [Google Scholar]
- Wang, H.; Guo, L.; Dou, Z.; Lin, Y. A new method of cognitive signal recognition based on hybrid information entropy and DS evidence theory. Mob. Netw. Appl. 2018, 23, 677–685. [Google Scholar] [CrossRef]
- Gong, Y.; Su, X.; Qian, H.; Yang, N. Research on fault diagnosis methods for the reactor coolant system of nuclear power plant based on DS evidence theory. Ann. Nucl. Energy 2018, 112, 395–399. [Google Scholar] [CrossRef]
- Jiang, W.; Yang, Y.; Luo, Y.; Qin, X. Determining basic probability assignment based on the improved similarity measures of generalized fuzzy numbers. Int. J. Comput. Commun. Control 2015, 10, 333–347. [Google Scholar] [CrossRef]
- Tang, Y.; Wu, D.; Liu, Z. A new approach for generation of generalized basic probability assignment in the evidence theory. Pattern Anal. Appl. 2021, 24, 1007–1023. [Google Scholar] [CrossRef]
- Rasol, M.; Pérez-Gracia, V.; Fernandes, F.M.; Pais, J.C.; Santos-Assunçao, S.; Roberts, J.S. Ground Penetrating Radar System: Principles. Handb. Cult. Herit. Anal. 2022, 25, 705–738. [Google Scholar]
- Liu, B.; Zhang, F.; Li, S.; Li, Y.; Xu, S.; Nie, L.; Zhang, C.; Zhang, Q. Forward modelling and imaging of ground-penetrating radar in tunnel ahead geological prospecting. Geophys. Prospect. 2018, 66, 784–797. [Google Scholar] [CrossRef]
- Li, R.; Hu, X.; Xu, D.; Liu, Y.; Yu, N. Characterizing the 3D hydrogeological structure of a debris landslide using the transient electromagnetic method. J. Appl. Geophys. 2020, 175, 103991. [Google Scholar] [CrossRef]
- Yu, C.; Liu, X.; Liu, J.; Li, E.; Yue, P.; Yan, S. Application of transient electromagnetic method for investigating the water-enriched mined-out area. Appl. Sci. 2018, 8, 1800. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Jones, A.; Kaufmann, A.; Zimmermann, H.-J. Fuzzy Sets Theory and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 177. [Google Scholar]
- Liu, N.; Zou, S.; Huang, B. Research on optimal maintenance cycle model of nuclear equipment based on left and right fuzzy sorting method. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Raipur, India, 25–26 February 2022; p. 012095. [Google Scholar]
- Li, H.; Wang, P. Fuzzy Mathematics; National Defence Industry Press: Beijing, China, 1994. [Google Scholar]
- Shafer, G. Dempster-shafer theory. Encycl. Artif. Intell. 1992, 1, 330–331. [Google Scholar]
- Sentz, K.; Ferson, S. Combination of Evidence in Dempster-Shafer Theory, Sandia Report No: SAND2002-0835; Sandia National Laboratories: Albuquerque, NH, USA, 2002.
- Qi, X.-M.; Zhang, S.-C. Application of seismic multi-attribute fusion method based on DS evidence theory in prediction of CBM-enriched area. Appl. Geophys. 2012, 9, 80–86. [Google Scholar] [CrossRef]
- Ye, F.; Chen, J.; Li, Y.; Kang, J. Decision-making algorithm for multisensor fusion based on grey relation and DS evidence theory. J. Sens. 2016, 2016, 3954573. [Google Scholar] [CrossRef]
- Sun, Q.; Ye, X.-Q.; Gu, W.-k. A new combination rules of evidence theory. Acta Electonica Sin. 2000, 28, 117. [Google Scholar]
- Qiu, W.; Jian, L.; Cheng, Y.; Bai, H. Three-Dimensional Reconstruction of Tunnel Face Based on Multiple Images. Adv. Civ. Eng. 2021, 2021, 8837309. [Google Scholar] [CrossRef]
- Yusoff, I.N.; Ismail, M.A.M.; Tobe, H.; Date, K.; Yokota, Y. Quantitative granitic weathering assessment for rock mass classification optimization of tunnel face using image analysis technique. Ain Shams Eng. J. 2022, 14, 101814. [Google Scholar] [CrossRef]

| Discriminating Factor | Degree | Strand Water (A) | Linear Water (B) | Seepage and Dripping Water (C) | Anhydrous (D) |
|---|---|---|---|---|---|
| Amplitude changes of the reflected wave signal | Fairly obvious | 0.2 | 0.1 | 0.4 | 0.8 |
| Quite obvious | 0.6 | 0.9 | 0.6 | 0.2 | |
| Very obvious | 0.9 | 0.7 | 0.6 | 0.4 | |
| The continuity of the event axis | Poor | 0.9 | 0.6 | 0.3 | 0.4 |
| Quite poor | 0.8 | 0.9 | 0.7 | 0.6 | |
| Quite continuous | 0.3 | 0.2 | 0.8 | 0.8 | |
| Continuous | 0.1 | 0.1 | 0.1 | 0.6 | |
| Reflected wave signal strength | Strong | 0.9 | 0.5 | 0.1 | 0.1 |
| Relatively strong | 0.7 | 0.9 | 0.6 | 0.5 | |
| Normal | 0.3 | 0.3 | 0.6 | 0.9 |
| Mileage Section | Discriminating Factor | Strand Water (A) | Linear Water (B) | Seepage and Dripping Water (C) | Anhydrous (D) |
|---|---|---|---|---|---|
| 325~+ 311 m | () | 0.000 | 0.180 | 0.815 | 0.312 |
| 0.086 | 0.960 | 0.984 | 0.257 | ||
| Poisson’s ratio () | 0.212 | 0.888 | 0.916 | 0.794 |
| Mileage Section | Discriminating Factor | Strand Water (A) | Linear Water (B) | Seepage and Drip-Ping Water (C) | Anhydrous(D) |
|---|---|---|---|---|---|
| 325~+ 311 m | Amplitude change in reflected wave signal () | 0.600 | 0.900 | 0.600 | 0.200 |
| In-phase axis continuity () | 0.800 | 0.900 | 0.700 | 0.600 | |
| Reflected wave signal strength () | 0.700 | 0.900 | 0.600 | 0.500 |
| Mileage Section | Discriminating Factor | Strand Water (A) | Linear Water (B) | Seepage and Drip-Ping Water (C) | Anhydrous (D) |
|---|---|---|---|---|---|
| 325~+ 311 m | Apparent resistivity (z) | 0.000 | 0.655 | 0.500 | 0.050 |
| Geophysical Data | Water Abundance | |||
|---|---|---|---|---|
| Strand Water (A) | Linear Water (B) | Seepage and Drip-Ping Water (C) | Anhydrous (D) | |
| TSP | 0.099 | 0.676 | 0.905 | 0.454 |
| GPR | 0.700 | 0.900 | 0.633 | 0.433 |
| TEM | 0.000 | 0.655 | 0.500 | 0.050 |
| Fusion Method | Water Abundance Fusion Results | ||||
|---|---|---|---|---|---|
| Strand Water (A) | Linear Water (B) | Seepage and Drip-Ping Water (C) | Anhydrous (D) | Unknown Proposition (X) | |
| Classical D-S theory | 0.505 | 0.393 | 0.100 | 0.002 | / |
| Fuzzy D-S theory | 0.000 | 0.574 | 0.412 | 0.014 | / |
| Improved fuzzy D-S theory | 0.046 | 0.236 | 0.202 | 0.063 | 0.448 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, Y.; Yang, B.; Xu, G.; Wang, X. Improved Dempster–Shafer Evidence Theory for Tunnel Water Inrush Risk Analysis Based on Fuzzy Identification Factors of Multi-Source Geophysical Data. Remote Sens. 2022, 14, 6178. https://doi.org/10.3390/rs14236178
Ding Y, Yang B, Xu G, Wang X. Improved Dempster–Shafer Evidence Theory for Tunnel Water Inrush Risk Analysis Based on Fuzzy Identification Factors of Multi-Source Geophysical Data. Remote Sensing. 2022; 14(23):6178. https://doi.org/10.3390/rs14236178
Chicago/Turabian StyleDing, Yulin, Binru Yang, Guangchun Xu, and Xiaoyong Wang. 2022. "Improved Dempster–Shafer Evidence Theory for Tunnel Water Inrush Risk Analysis Based on Fuzzy Identification Factors of Multi-Source Geophysical Data" Remote Sensing 14, no. 23: 6178. https://doi.org/10.3390/rs14236178
APA StyleDing, Y., Yang, B., Xu, G., & Wang, X. (2022). Improved Dempster–Shafer Evidence Theory for Tunnel Water Inrush Risk Analysis Based on Fuzzy Identification Factors of Multi-Source Geophysical Data. Remote Sensing, 14(23), 6178. https://doi.org/10.3390/rs14236178




