Energy-Efficient and QoS-Aware Computation Offloading in GEO/LEO Hybrid Satellite Networks

Abstract

Benefiting from advanced satellite payload technologies, edge computing servers can be deployed on satellites to achieve orbital computing and reduce the mission processing delay. However, geostationary Earth orbit (GEO) satellites are hindered by long-distance communication, whereas low Earth orbit (LEO) satellites are restricted by time windows. Relying solely on GEO or LEO satellites cannot meet the strict quality of service (QoS) requirements of on-board missions while conserving energy consumption. In this paper, we propose a computation offloading strategy for GEO/LEO hybrid satellite networks that minimizes total energy consumption while guaranteeing the QoS requirements of multiple missions. We first innovatively transform the on-board partial computation offloading problem, which is a mixed-integer nonlinear programming (MINLP) problem, into a minimum cost maximum flow (MCMF) problem. Then, the successive shortest path-based computation offloading (SSPCO) method is introduced to obtain the offloading decision in polynomial time. To evaluate the effectiveness and performance of SSPCO, we conduct a series of numerical experiments and compare SSPCO with other offloading methods. The experimental results demonstrate that our proposed SSPCO outperforms the reference methods in terms of total energy consumption, QoS violation degree, and algorithm running time.

1. Introduction

With the rapid advancements in aerospace and space networking technologies, satellite networks offer ubiquitous internet services to various users in the sea, land, and air with the advantages of wide coverage and small geographical impact [1,2]. For instance, the US company SpaceX’s Starlink constellation is expected to deploy approximately 12,000 satellites by 2027, providing high-speed and low-cost internet services for billions of users worldwide, including those in remote areas such as deserts and mountains [3]. Benefiting from the development of on-board processing technology, orbital edge computing (OEC) has emerged as a focal point of interest for both academic and industrial communities and is being recognized as a key area of research for the implementation of future network infrastructures [4,5]. However, due to the limited computing resources and energy, in OEC, a fundamental problem is designing an efficient computation offloading strategy to coordinate the satellite computing capabilities, thus meeting the processing delay and energy consumption requirements of multiple missions [6,7].

1.1. Related Works

In recent years, computation offloading has received widespread attention [8,9,10,11]. Offloading approaches in terrestrial networks utilize nearby edge servers or the cloud center to offload computation tasks, which can effectively reduce the task processing delay and energy consumption of end users [12]. Satellites, due to their ability to provide coverage in special natural spaces such as airspace, land, and sea, are considered promising supplements to enhance the terrestrial networks. Therefore, the increasing demand for real-time and reliable applications has led to the development of OEC technology, which deploys multi-access edge computing (MEC) servers on satellite constellations [6,13]. Mao et al. [14] proposed a satellite-UAV-served Internet of Things (IoT) system, which utilized satellites to offload tasks to UAV-based edge servers or remote cloud servers for providing seamless coverage to IoT devices in remote areas. Considering the computing power of satellites, Tang et al. [7] presented a hybrid cloud and LEO satellite computation architecture and proposed an offloading algorithm based on the alternating direction method of multipliers to minimize the total energy consumption of users. However, the time window problem of LEO satellites significantly limits the satellites’ computing power and mission processing delay [15]. Therefore, GEO/LEO hybrid satellite networks have been a growing interest in recent years due to the advantage of the always-on connectivity of GEO satellites [16,17,18]. Jia et al. [19] proposed a collaborative satellite–terrestrial edge computing (STEC) network architecture based on multi-agent collaboration, where GEO satellites serve as the manager covering LEO satellites and connecting to ground cloud servers, while LEO satellites primarily provide in-orbit computing services. To exploit the capability of in-orbit computing fully, Fang et al. [20] developed a satellite network edge computing scenario utilizing a double-layer network topology consisting of LEO and GEO satellites. The offloading decision problem was formulated as a two-sided matching game problem with LEO and GEO satellites as participants. Based on previous works, in this paper, we focus on the latest GEO/LEO hybrid satellite networks and investigate the computation offloading problem in OEC.

Table 1. Comparison between related works.

Works	GEO	LEO	Processing Delay	Energy Consumption	QoS	Role of Satellites
[6]		✓	✓	✓		computing
[7]		✓	✓	✓		computing
[13]		✓	✓			computing
[14]		✓	✓			communication
[17]	✓	✓	✓			computing
[18]	✓	✓	✓			communication, computing
[19]	✓	✓	✓	✓		communication, computing
[20]	✓	✓	✓	✓		computing
Our work	✓	✓	✓	✓	✓	computing

shows the comparison results of our work and other works. The detailed motivations and contributions will be discussed below.

1.2. Motivations

Although the above efforts have achieved effective computation offloading in OEC, there still remain some problems.

Role of satellites: in most studies, satellites still mainly play the role as communication relays and the computing capabilities of satellites carrying edge servers are often overlooked, which ignores the potential benefits of in-orbit computing [3,19].

Limitations of single-tier satellite network: due to the time window problem of LEO satellites and the long communication delay of GEO satellites, relying solely on LEO or GEO satellites for in-orbit computing has significant limitations. Therefore, the GEO/LEO hybrid satellite networks that integrate LEO and GEO satellites can fully utilize the advantages of both layers to achieve more efficient in-orbit computing.

Objective: overly emphasizing the minimization of processing delay may lead to excessive allocation of resources and an increase in total energy consumption [21,22,23]. Under the premise of ensuring QoS, an appropriate increase in mission processing delay can lead to lower energy consumption, which is more suitable for energy-sensitive in-orbit computing.

Offloading granularity: most existing research adopts binary offloading modeling, which leads to suboptimal energy consumption when coordinating the offloading of multiple missions. As indicated in [20,24], partial offloading, which allows missions to be partially processed on both LEO and GEO satellites, is more appropriate for missions with stringent QoS requirements.

1.3. Novelty and Contributions

Motivated by the aforementioned issues, this paper proposes a partial offloading strategy for the GEO/LEO hybrid satellite networks scenario. To avoid the problem of excessive energy consumption caused by too much pursuit of minimizing mission processing delay, the goal of this paper is to minimize the total energy consumption of the satellite networks while ensuring missions QoS constraints. Specifically, we first construct a framework for GEO/LEO hybrid satellite networks and formulate the mission processing delay and energy consumption in detail, modeling the computation offloading problem as a mixed-integer nonlinear programming (MINLP) problem. Then, we transform the above MINLP problem into the minimum cost maximum flow (MCMF) problem and propose the successive shortest path-based computation offloading (SSPCO) method, which can obtain the offloading decision in polynomial time. Simulation experiments verify the effectiveness of the proposed SSPCO method. The main contributions are as follows:

• Constructing a partial offloading model for GEO/LEO hybrid satellite networks, which aims to minimize the total energy consumption of the networks while guaranteeing QoS constraints of satellite missions.
• Transforming the partial computation offloading problem into the MCMF problem and proposing the SSPCO method to obtain the computation offloading decision in polynomial time.
• Performing extensive numerical experiments to demonstrate the effectiveness of the proposed SSPCO method. The results show that SSPCO achieves significant performance superiority compared with other benchmark strategies in the total energy consumption of the satellite networks, QoS violation degree, and algorithm running time.

2. Materials and Methods

2.1. System Model

In this section, we first introduce the computation offloading framework for GEO/LEO hybrid satellite networks. Then, the time model and energy consumption model are formulated to quantify the mission processing delay and energy consumption. Finally, based on the above models, an energy-aware constrained optimization model with QoS constraints is constructed.

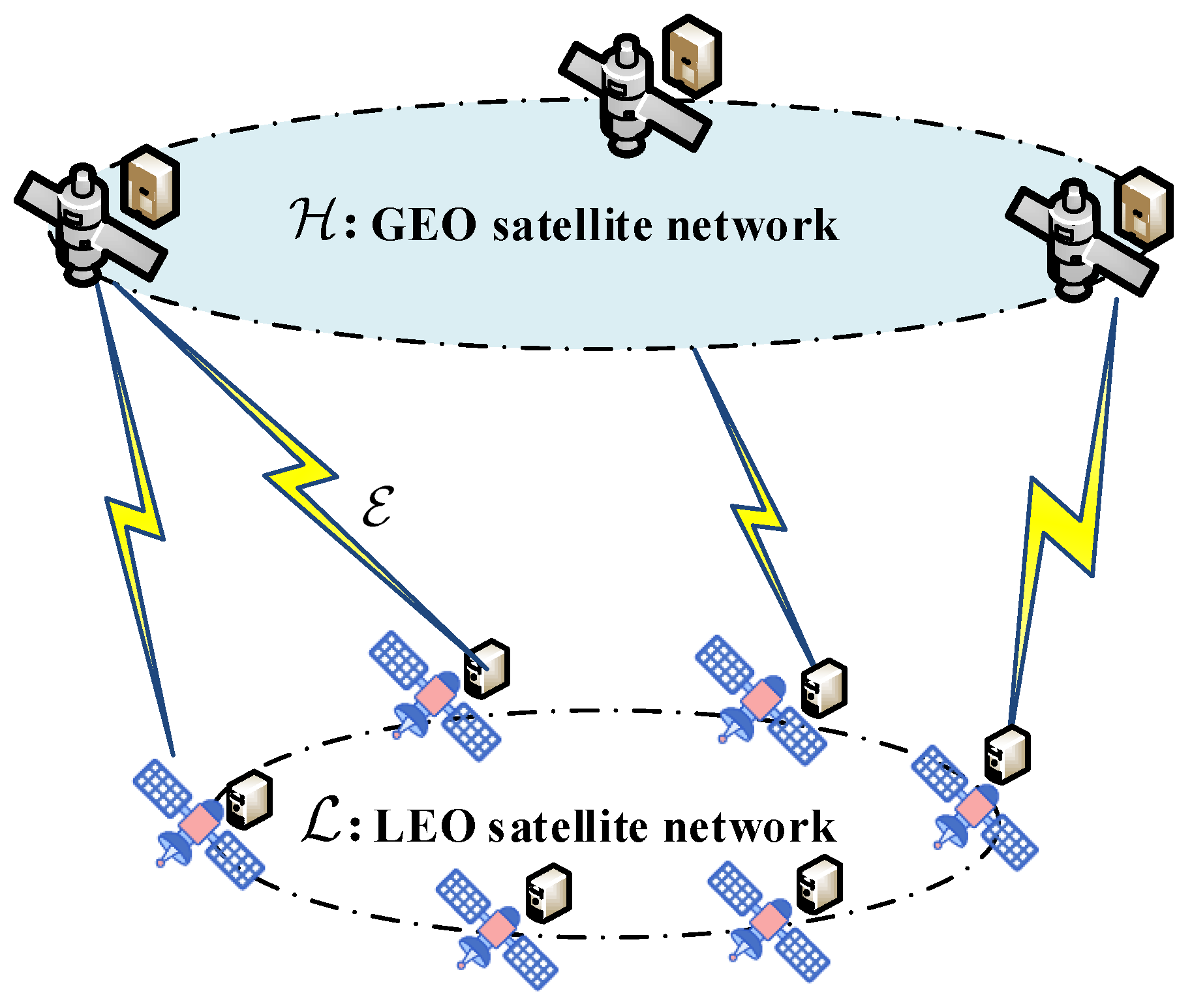
2.1.1. Offloading Framework

The computation offloading framework for GEO/LEO hybrid satellite networks is shown in Figure 1. The scenario consists of the GEO satellite network and the LEO satellite network. The on-board missions are generated by LEO satellite observations and are decided by the GEO satellites whether to offload or not, the allocated resources, and the offloading ratios. To guarantee QoS constraints for on-board missions, each LEO satellite can offload the missions entirely or partially to the GEO satellite for processing through inter-satellite links, while the remaining missions are processed on the LEO satellite. It should be clarified that we focus on the scenario of in-orbit mission processing within the framework of the GEO/LEO hybrid satellite networks. All missions in this paper are generated by LEO satellites and processed exclusively using the collaborative computational capabilities of GEO and LEO satellites. Therefore, we only consider the GEO and LEO satellite networks, with missions generated on satellites and not involving terrestrial terminals, and neither are they offloaded to terrestrial networks for processing.

2.1.2. Time Model

As shown in Figure 1, the GEO/LEO hybrid satellite networks can be denoted as $HSN=\{\mathcal{L}\cup \mathcal{H},\mathcal{E}\}$, where $\mathcal{L}=\{1,2,\dots ,L\}$ denotes the set of LEO satellites, $\mathcal{H}=\{1,2,\dots ,H\}$ denotes the set of GEO satellites, and $\mathcal{E}$ denotes the set of inter-satellite links. In addition, we use ${\mathcal{N}}_i=\{1,2,\dots ,N_i\}$ to describe the set of missions on LEO satellite i. $\left|L\right|$, $\left|H\right|$, and $|N_i|$ denote the number of LEO satellites, GEO satellites, and missions on LEO satellite i, respectively. The mission on LEO satellite i can be represented by a triplet $T_{n,i}\triangleq (B_{n,i},{\tau }_{n,i},m_{n,i})$, where $B_{n,i}$ denotes the data size of the mission, ${\tau }_{n,i}$ denotes the QoS constraint of the mission, and $m_{n,i}$ denotes the processing density (in CPU $cycles/bit$).

In this paper, we are concerned with partial offloading and define ${\lambda }_{n,i}$ as the ratio of $T_{n,i}$ data volume offloaded to the GEO satellite ($0\le {\lambda }_{n,i}\le 1$). Thus, for $T_{n,i}$, there is ${\lambda }_{n,i}{B}_{n,i}$ amount of data that will be offloaded to the GEO satellite, while the amount of data that will be processed by the LEO satellite is $(1-{\lambda }_{n,i})B_{n,i}$.

Computation delay: we define $f_{n,i}^{leo}$ as the processing capacity provided to mission $T_{n,i}$ by LEO satellite i, then the LEO satellite processing time of mission $T_{n,i}$ can be expressed as

$$D_{n,i}^{leo}=\frac{m_{n,i}(1-{\lambda }_{n,i})B_{n,i}}{f_{n,i}^{leo}}$$

(1)

where $0\le f_{n,i}^{leo}\le f_i^{LEO}$ and $f_i^{LEO}$ denotes the maximum processing capacity of LEO satellite i.

The GEO satellite j processing time of mission $T_{n,i}$ can be calculated by

$$D_{n,i}^{j,geo}=\frac{m_{n,i}{\lambda }_{n,i}{B}_{n,i}}{f_{n,i}^{j,geo}}$$

(2)

where $f_{n,i}^{j,geo}$ ($0\le f_{n,i}^{j,geo}\le f_j^{GEO}$) denotes the processing capacity provided to mission $T_{n,i}$ by GEO satellite j and $f_j^{GEO}$ denotes the maximum processing capacity of GEO satellite j.

Transmission delay: usually, the data size of the results is much smaller than the original data size, so we ignore the time of receiving the result of offloading missions [25]. According to the Shannon–Hartley theorem, the maximum uplink transmission rate, $R_{n,i}^j$, for transmitting mission $T_{n,i}$ from LEO satellite i to GEO satellite j can be obtained by

$$R_{n,i}^j={\omega }_{n,i}^{j}lo{g}_2(1+\frac{p_i{h}_{i,j}}{{\sum }_{u\in \mathcal{L}}{p}_u{h}_{u,j}+N_0})$$

(3)

where ${\omega }_{n,i}^j$ denotes the radio channel bandwidth for transmitting mission $T_{n,i}$ from LEO satellite i to GEO satellite j, $p_i$ denotes the transmit power of LEO satellite i, and $h_{i,j}$ denotes the channel gain between LEO satellite i and GEO satellite j. The interference term in the denominator ${\sum }_{u\in \mathcal{L}}{p}_u{h}_{u,j}$ denotes the total interference signal power from other LEO satellites and $N_0$ denotes the Gaussian noise power.

Then, the uplink transmission delay of mission $T_{n,i}$ on LEO satellite i is calculated by

$$D_{n,i}^{j,tra}=\frac{{\lambda }_{n,i}{B}_{n,i}}{R_{n,i}^j}$$

(4)

Propagation delay: we define $R_{light}$ as the speed of light in a vacuum, $h_{n,i}^{leo}$ as the altitude of LEO satellite i, and $h_{n,i}^{j,geo}$ as the altitude of GEO satellite j. Then, the propagation delay from LEO satellite i to GEO satellite j can be expressed as

$$D_{n,i}^{j,prop}=\frac{h_{n,i}^{j,geo}-h_{n,i}^{leo}}{R_{light}}$$

(5)

2.1.3. Energy Consumption Model

The energy consumption of GEO/LEO hybrid satellite networks during the mission offloading process is mainly divided into two aspects: on the one hand, the computational energy consumption generated during the computation processing, and, on the other hand, the transmission energy consumption during the data transmission process.

Computational energy consumption: in this paper, we use $E_{n,i}^{leo}$ and $E_{n,i}^{j,geo}$ to denote the energy consumption of the processing mission on LEO satellite i and the processing offloaded mission on GEO satellite j, respectively. In addition, we use $p_{n,i}^{leo}$ to denote the computational power of LEO satellite i for processing mission $T_{n,i}$. Since the processing power of the device directly affects the processing energy consumption [26], $p_{n,i}^{leo}$ is given by

$$p_{n,i}^{leo}={\kappa }^{leo}{\left(f_{n,i}^{leo}\right)}^3$$

(6)

where ${\kappa }^{leo}$ denotes the effective switching capacitance constant determined by the chip integration architecture [26].

Similarly, the computational power of the GEO satellite j for processing mission $T_{n,i}$ can be expressed as

$$p_{n,j}^{geo}={\kappa }^{geo}{\left(f_{n,i}^{j,geo}\right)}^3$$

(7)

Thus, the computational energy consumption of processing mission $T_{n,i}$ on LEO satellite i can be obtained by

$$\begin{array}{cc}\hfill E_{n,i}^{leo}& =p_{n,i}^{leo}{D}_{n,i}^{leo}\hfill \\ \hfill & ={\kappa }^{leo}{\left(f_{n,i}^{leo}\right)}^2(1-{\lambda }_{n,i})B_{n,i}{m}_{n,i}\hfill \end{array}$$

(8)

The computational energy consumption of processing the offloaded mission on GEO satellite j can be expressed as

$$\begin{array}{cc}\hfill E_{n,i}^{j,geo}& =p_{n,j}^{geo}{D}_{n,i}^{j,geo}\hfill \\ \hfill & ={\kappa }^{geo}{\left(f_{n,i}^{j,geo}\right)}^2{\lambda }_{n,i}{B}_{n,i}{m}_{n,i}\hfill \end{array}$$

(9)

Transmission energy consumption: in this paper, we use $E_{n,i}^{j,tra}$ to denote the energy consumption of communication resources generated by the LEO satellite i uploading $T_{n,i}$ to the GEO satellite j. Thus, the transmission energy consumption can be expressed as

$$\begin{array}{cc}\hfill E_{n,i}^{j,tra}& =p_i{D}_{n,i}^{j,tra}\hfill \\ \hfill & =\frac{p_i{\lambda }_{n,i}{B}_{n,i}}{{\omega }_{n,i}^{j}lo{g}_2(1+\frac{p_i{h}_{i,j}}{{\sum }_{u\in \mathcal{L}}{p}_u{h}_{u,j}+N_0})}\hfill \end{array}$$

(10)

2.1.4. Problem Formulation

According to the time model constructed by Section 2.1.2, the processing delay, $D_{n,i}$ of $T_{n,i}$, includes the satellite computation part, the mission data transmission part, and the propagation part. Specifically, $D_{n,i}$ is determined by the maximum value of the sum of the transmission delay, $D_{n,i}^{j,tra}$, of LEO satellite i, the propagation delay, $D_{n,i}^{j,prop}$, from LEO satellite i to GEO satellite j, and the computation delay, $D_{n,i}^{j,geo}$, of GEO satellite j and the remaining mission processing time, $D_{n,i}^{leo}$, on LEO satellite i, which is denoted as

$$\begin{array}{cc}\hfill D_{n,i}& =max\left(D_{n,i}^{j,tra}+D_{n,i}^{j,prop}+D_{n,i}^{j,geo},D_{n,i}^{leo}\right)\hfill \\ \hfill & =max\left(\frac{{\lambda }_{n,i}{B}_{n,i}}{R_{n,i}^j}+\frac{h_{n,i}^{j,geo}-h_{n,i}^{leo}}{R_{light}}+\frac{m_{n,i}{\lambda }_{n,i}{B}_{n,i}}{f_{n,i}^{j,geo}},\frac{m_{n,i}(1-{\lambda }_{n,i})B_{n,i}}{f_{n,i}^{leo}}\right)\hfill \end{array}$$

(11)

According to the energy consumption model constructed by Section 2.1.3, the total energy consumption, $E_{n,i}$, includes the computational energy consumption of LEO satellites and GEO satellites and the transmission energy consumption, which is calculated by

$$\begin{array}{cc}\hfill E_{n,i}& =E_{n,i}^{leo}+E_{n,i}^{j,geo}+E_{n,i}^{j,tra}\hfill \\ \hfill & ={\kappa }^{leo}{(f_{n,i}^{leo})}^2(1-{\lambda }_{n,i})B_{n,i}{m}_{n,i}+{\kappa }^{geo}{(f_{n,i}^{j,geo})}^2{\lambda }_{n,i}{B}_{n,i}{m}_{n,i}\hfill \\ \hfill & +\frac{p_i{\lambda }_{n,i}{B}_{n,i}}{{\omega }_{n,i}^{j}lo{g}_2(1+\frac{p_i{h}_{i,j}}{{\sum }_{u\in \mathcal{L}}{p}_u{h}_{u,j}+N_0})}\hfill \end{array}$$

(12)

As mentioned above, the objective of this paper is to minimize the total energy consumption of GEO/LEO hybrid satellite networks without violating the QoS constraints of on-board missions, and the final constrained optimization model can be formulated as follows:

$$\begin{array}{cc}\hfill min& \left(\sum _{i=1}^{\left|L\right|}\sum _{n=1}^{|N_i|}{E}_{n,i}\right)\hfill \end{array}$$

(13)

$$\begin{array}{ccc}\hfill s.t.& 0\le {\lambda }_{n,i}\le 1,\hfill & \hfill \forall n\in {\mathcal{N}}_i,\forall i\in \mathcal{L}\end{array}$$

(14)

$$\begin{array}{ccc}\hfill & D_{n,i}\le {\tau }_{n,i},\hfill & \hfill \forall n\in {\mathcal{N}}_i,\forall i\in \mathcal{L}\end{array}$$

(15)

$$\begin{array}{ccc}\hfill & 0\le f_{n,i}^{j,geo}\le f_j^{GEO},\hfill & \hfill \forall j\in \mathcal{H}\end{array}$$

(16)

$$\begin{array}{ccc}\hfill & \sum _{i=1}^{\left|L\right|}\sum _{n=1}^{|N_i|}{f}_{n,i}^{j,geo}\le f_j^{GEO},\hfill & \hfill \forall j\in \mathcal{H}\end{array}$$

(17)

$$\begin{array}{ccc}\hfill & \sum _{j=1}^{\left|H\right|}\lceil {\lambda }_{n,i}^j\rceil \le 1,\hfill & \hfill \forall n\in {\mathcal{N}}_i,\forall i\in \mathcal{L}\end{array}$$

(18)

where Equation (13) shows that the optimization objective of this paper is to minimize the total energy consumption; Equation (14) denotes the offloading decision variable constraint of any mission; Equation (15) denotes that the total processing delay of any mission cannot exceed its own QoS constraint; Equations (16) and (17) ensure that the computational resources allocated to a mission cannot exceed the processing capacity of GEO satellites; and Equation (18) denotes that any mission can only be offloaded to the GEO satellite covering it for processing, and $\lceil ·\rceil$ denotes rounding up, since ${\sum }_{j=1}^{\left|H\right|}\lceil {\lambda }_{n,i}^j\rceil \le 1$ indicates that there will not be two different GEO satellites j and $j^{\prime }$ such that both ${\lambda }_{n,i}^j$ and ${\lambda }_{n,i}^{j^{\prime }}$ are greater than 0.

2.2. Computation Offloading Method Based on Minimum Cost Maximum Flow

According to the computation offloading model constructed in Section 2, the proposed problem is a MINLP problem [27]. The main methods for solving MINLP problems are deterministic and stochastic methods. However, the large computational cost of deterministic methods such as branch and bound methods will cause high delay. Stochastic methods such as genetic algorithms may have a time-consuming search process and are easy to get trapped in local optimal solutions. None of the above methods are applicable to resource-constrained GEO/LEO hybrid satellite networks that have high real-time requirements. In this paper, we transform the computation offloading problem in GEO/LEO hybrid satellite networks into the MCMF problem and propose the SSPCO method based on the successive shortest path algorithm to solve it in polynomial time.

2.2.1. Overview of MCMF

The MCMF problem is the optimization problem of traffic delivery among nodes of a directed graph, which aims at finding the minimum cost way to deliver the maximum flow, $f_{max}$, from the source node, S, to the sink node, T.

Figure 2 illustrates a case of a minimum cost maximum flow network where each edge, $e(u,v)$, has two weights, i.e., capacity, $c(u,v)$, which denotes the maximum amount of flow shipped on $e(u,v)$, and unit cost, $w(u,v)$, of shipping flow from node u to node v on $e(u,v)$. We use $f(u,v)$ to denote the flow amount shipped on $e(u,v)$. Then, the cost of sending a flow of $f(u,v)$ units on $e(u,v)$ is equal to $f(u,v)\times w(u,v)$. As shown in Figure 2, the minimum cost maximum flow network has 6 nodes and 9 edges. The flow is sent from the source node, S, to the sink node, T. Take $e(v_1,v_2)$ for example, the maximum capacity of this edge is 6 and the unit cost of this edge is 9. We assume the current amount of flow through this edge is 2. Then, the cost of this edge is equal to $2\times 9=18$. Given such a flow network of $G=(V,\mathcal{E})$, finding a maximum flow that minimizes the total cost of the flow can be expressed as

$$\begin{array}{cc}\hfill min& \left(\sum _{e(u,v)\in E}f(u,v)w(u,v)\right)\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill s.t.& 0\le f(u,v)\le c(u,v),\forall e(u,v)\in \mathcal{E}\hfill \\ \hfill & \sum _{e(u,v)\in \mathcal{E}}f(u,v)-\sum _{e(v,u)\in \mathcal{E}}f(v,u)\hfill \end{array}$$

(20)

$$\begin{array}{cc}& =\left\{\begin{array}{cc}{f}_{max},\hfill & \hfill u=S\\ -f_{max},\hfill & \hfill u=T\\ 0,\hfill & \hfill u\ne S,T\end{array}\right.\hfill \end{array}$$

(21)

where $f_{max}$ represents the maximum flow obtained by solving the problem and Equation (20) denotes that the amount of flow shipped on the edge cannot exceed its capacity. From Equation (21), it can be seen that the outflow from the source node is equal to the inflow at the sink node, and, for all intermediate nodes except the source and sink node, the outflow is equal to the inflow.

The objective of our work is to find an offloading decision (mapping between the on-board missions and the satellites) that minimizes the total energy consumption, since MCMF problems have been extensively researched over the years and several algorithms have been proposed to solve the problems efficiently in polynomial time [28]. By transforming the computation offloading problem of on-board missions into the MCMF problem using a flow network, it is also possible to solve the computation offloading problem in polynomial time. This is because a solution of MCMF can be extracted as a mapping between the nodes in the flow network. By setting the corresponding capacity and unit cost on the edges in the flow network, MCMF algorithms can find the offloading decision (mapping) that minimizes the total energy consumption for GEO/LEO hybrid satellite networks. Therefore, we focus on how to transform the computation offloading problem into an MCMF problem and how to solve it.

2.2.2. Transformation of Computation Offloading Problem into Minimum Cost Maximum Flow Problem

Construction of flow network: to map the partial computation offloading problem of on-board missions into the MCMF problem, we formulate the problem using a specific structure of the flow network. Figure 3 shows a natural idea to construct a flow network, which corresponds to an instantaneous status of GEO/LEO hybrid satellite networks, while encoding a set of LEO satellites and GEO satellites. The flow network can be described as follows.

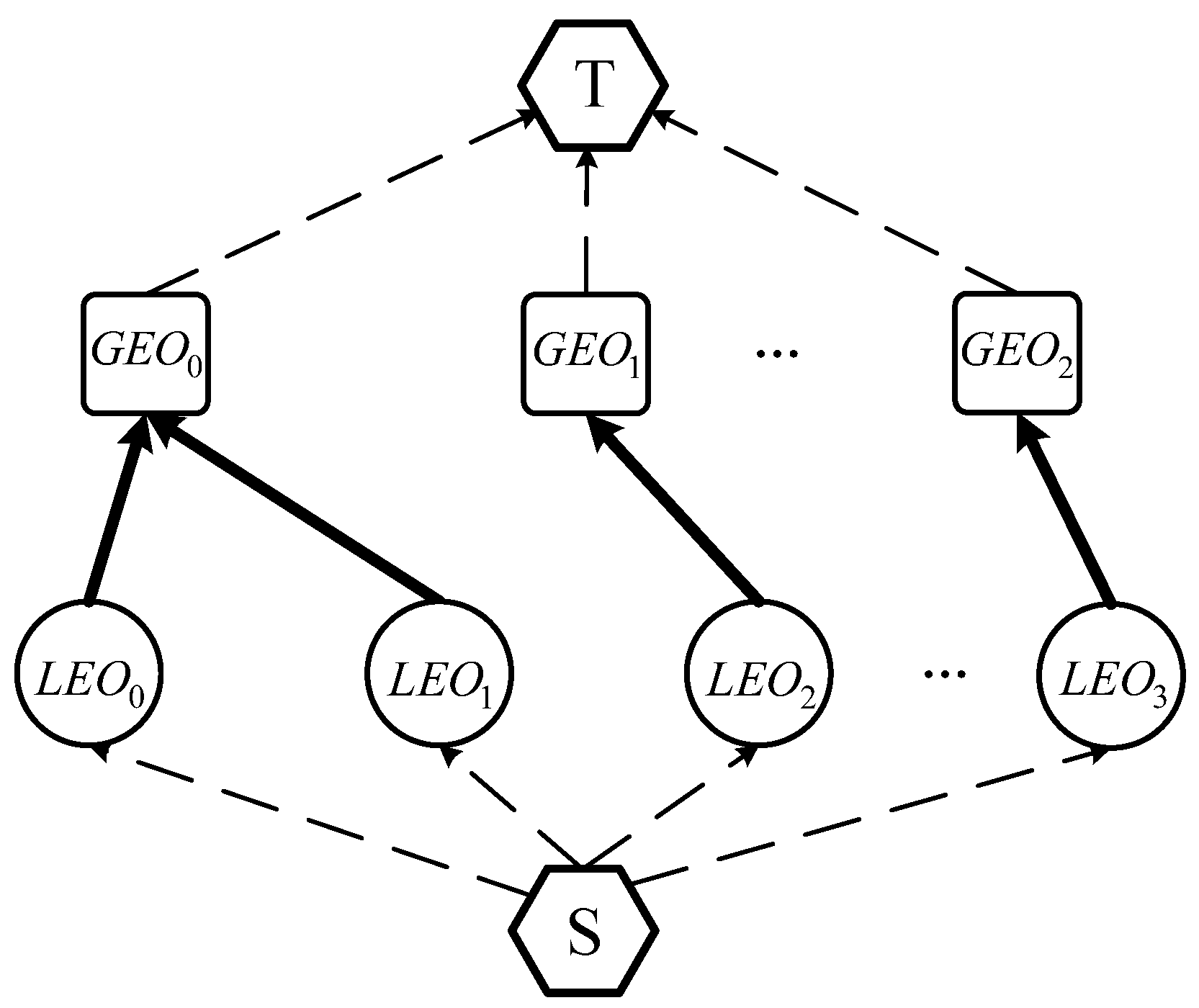
• Source node: the source node (S) is a virtual node that can satisfy the single-source single-sink condition in solving the MCMF problems.
• LEO node: the LEO node ($LEO\_Node$) denotes the LEO satellite in GEO/LEO hybrid satellite networks.
• GEO node: the GEO node ($GEO\_Node$) denotes the GEO satellite in GEO/LEO hybrid satellite networks. Each node has an edge from the LEO node in its coverage area, and the amount of the flow on the edge indicates the amount of mission data offloaded from the LEO satellite to the GEO satellite.
• Sink node: the sink node (T) is a virtual node that is introduced to satisfy the single-source single-sink requirement when solving the MCMF problem.

A path of one MCMF solution must first connect to an LEO node from the source node and then reach the sink node through a GEO node. Thus, if a path goes through a GEO node, it represents an offloading for the missions on an LEO satellite. For instance, the solution as shown in Figure 3 corresponds to an offloading decision: missions on $LE{O}_0$ and $LE{O}_1$ are offloaded to $GE{O}_0$; missions on $LE{O}_2$ are offloaded to $GE{O}_1$; and missions on $LE{O}_{\left|L\right|}$ are offloaded to $GE{O}_{\left|H\right|}$.

However, in the multiple satellites and multiple missions scenario, the flow network shown in Figure 3 has the following problems:

• Since there may be several missions in LEO satellites, the satellite-level granularity modeling shown in Figure 3 cannot generate mission-level offloading decisions;
• The network shown in Figure 3 can only represent the process of missions offloaded to GEO satellites and cannot represent the process of missions processed on LEO satellites;
• Due to the limited computing and storage resources of LEO and GEO satellites, the offloading of several missions may fail. However, the network shown in Figure 3 cannot indicate mission offloading failures.

To address the above issues, we propose an improved flow network, as shown in Figure 4a. Based on the initial flow network, as shown in Figure 3, we add three types of nodes, which can be described as follows.

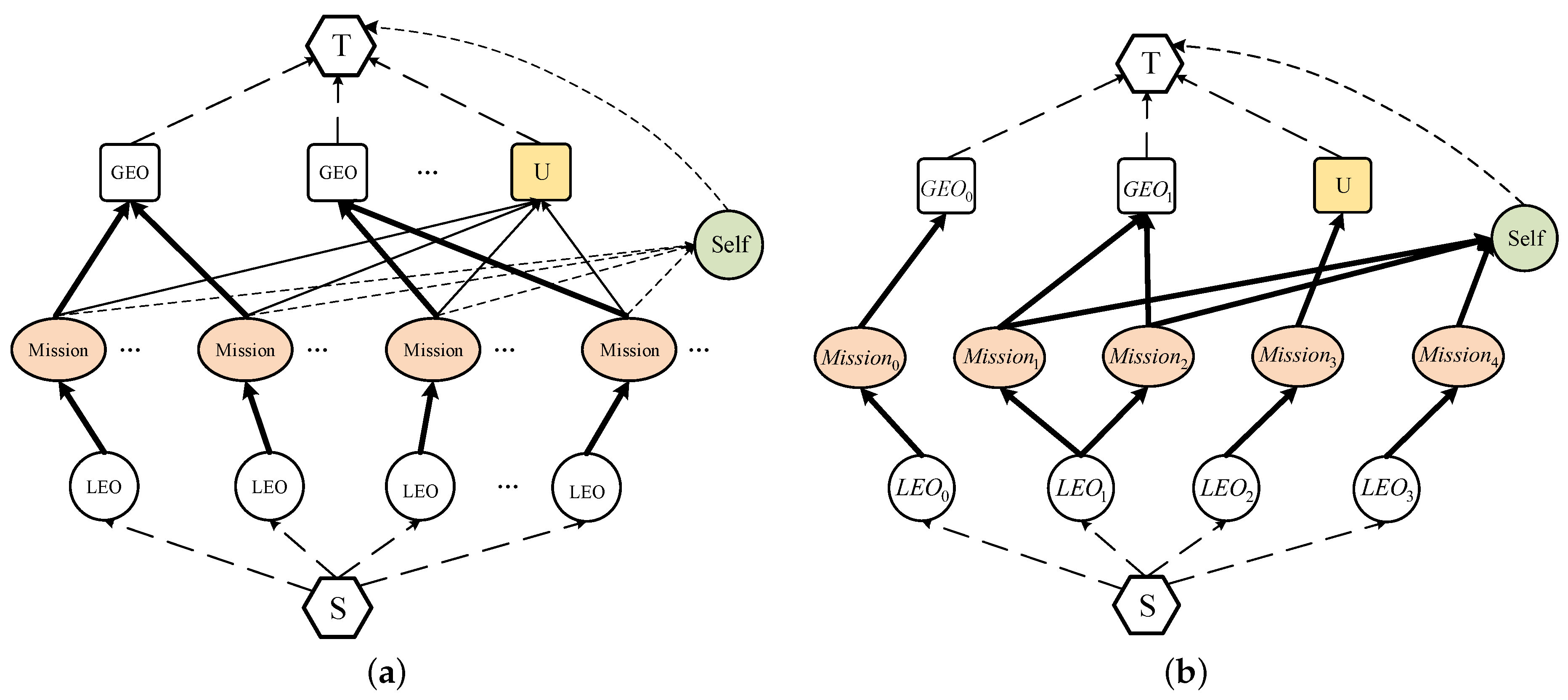
• Mission node: the mission node ($Mission\_Node$) represents the missions generated on or accessed from LEO satellites and different LEO nodes have different numbers of mission nodes. By adding mission nodes, finer-grained mission-level offloading decisions can be generated.
• Self node: the self node ($Self$) indicates the process of missions processed on LEO satellites, and all mission nodes are connected to the self node.
• U node: when there is a flow passing through the edge connecting a certain mission node and the U node (U), it means that the processing time of the mission is greater than its QoS constraint, indicating that the offloading has failed.

A path of one MCMF solution must first connect to an LEO node from the source node and then pass through the mission node and finally reach the sink node through a GEO node or the U node or the self node. Thus, if a path only goes through a GEO node, it represents a full offloading for a mission on an LEO satellite. In addition, if a path only goes through the self node, it represents that the mission is fully processed on the LEO satellite where the mission is generated, and, if a path goes through both a GEO node and self node, it represents a partial offloading for the mission on an LEO satellite. Otherwise, if a path goes through the U node, it represents that the offloading has failed. For instance, all bold edges can be one possible solution obtained by MCMF algorithms, as shown in Figure 4b. The figure corresponds to an offloading decision: $missio{n}_0$ on $LE{O}_0$ is fully offloaded to $GE{O}_0$; $missio{n}_1$ and $missio{n}_2$ on $LE{O}_1$ are partially offloaded to $GE{O}_1$ and the remaining parts are processed on $LE{O}_1$ simultaneously; $missio{n}_3$ on $LE{O}_2$ is failed; and $missio{n}_4$ on $LE{O}_3$ is fully processed on $LE{O}_3$.

Capacity and unit cost: as indicated in Section 2.2.1, the capacity and the unit cost are the key factors in solving MCMF problems. Thus, based on Figure 4a, the capacity and the unit cost of different types of edges will be defined to transform this partial computation offloading problem into an MCMF problem. Let $e(u,v)$ denote the edges from node u to node v, and $\mathcal{E}$ denote the set of all edges. We use $c(u,v)$ and $w(u,v)$ to represent the capacity and the unit cost of $e(u,v)$, respectively. Next, we present the capacity and unit cost of different types of edge in $\mathcal{E}$.

• $\mathbf{e}(\mathbf{S},\mathbf{LEO}\_\mathbf{Node})$: we set the capacity to be the sum of the amount of data of all missions on the LEO node. Since there is no actual consumption, the unit cost is set to zero, which can be given by

  $$\begin{array}{cc}c(u,v)=\sum _{n=1}^{|N_v|}{B}_{n,v},\hfill & \hfill u=S,\forall v\in \mathcal{L}\end{array}$$

  (22)

  $$\begin{array}{cc}w(u,v)=0,\hfill & \hfill u=S,\forall v\in \mathcal{L}\end{array}$$

  (23)
• $\mathbf{e}(\mathbf{LEO}\_\mathbf{Node},\mathbf{Mission}\_\mathbf{Node})$: we set the capacity to the amount of data of the mission node v. And the unit cost is set to zero as there is no actual consumption, which can be expressed as

  $$\begin{array}{cc}c(u,v)=B_{v,u},\hfill & \hfill \forall u\in \mathcal{L},\forall v\in {\mathcal{N}}_u\end{array}$$

  (24)

  $$\begin{array}{cc}w(u,v)=0,\hfill & \hfill \forall u\in \mathcal{L},\forall v\in {\mathcal{N}}_u\end{array}$$

  (25)
• $\mathbf{e}(\mathbf{Mission}\_\mathbf{Node},\mathbf{GEO}\_\mathbf{Node})$: the maximum amount of mission data that can be offloaded to the GEO satellite is calculated based on the QoS constraint and the processing density, and the capacity is set to this calculated value. We also set the unit cost to the sum of the unit transmission energy consumption and the unit computational energy consumed by the GEO satellite, as shown in Equation (26).

  $$\begin{array}{ccc}\hfill c(u,v)& =\frac{f_{u,i}^{v,geo}{\tau }_{u,i}{R}_{u,i}^v}{f_{u,i}^{v,geo}+R_{u,i}^v{m}_{u,i}},\hfill & \hfill \forall i\in \mathcal{L},\forall u\in {\mathcal{N}}_i,\forall v\in \mathcal{H}\\ \hfill w(u,v)& =\frac{E_{u,i}^{v,geo}+E_{u,i}^{v,tra}}{{\lambda }_{u,i}{B}_{u,i}}\hfill \end{array}$$

  (26)

  $$\begin{array}{ccc}\hfill & ={\kappa }^{geo}{\left(f_{u,i}^{v,geo}\right)}^2{m}_{u,i}+\frac{p_i}{R_{u,i}^v},\hfill & \hfill \forall i\in \mathcal{L},\forall u\in {\mathcal{N}}_i,\forall v\in \mathcal{H}\end{array}$$

  (27)
• $\mathbf{e}(\mathbf{Mission}\_\mathbf{Node},\mathbf{Self})$: we calculate the maximum amount of mission data that can be processed on the LEO satellite based on the QoS constraint and the processing density, and set the capacity to this calculated value. The unit computational energy consumed by the LEO satellite is mapped to the unit cost, as shown in Equation (28).

  $$\begin{array}{ccc}\hfill c(u,v)& =\frac{f_{u,v}^{leo}{\tau }_{u,v}}{m_{u,v}},\hfill & \hfill \forall u\in {\mathcal{N}}_i,v=Self\end{array}$$

  (28)

  $$\begin{array}{ccc}\hfill w(u,v)& =\frac{E_{u,v}^{leo}}{(1-{\lambda }_{u,v})B_{u,v}}\hfill & \hfill \\ \hfill & ={\kappa }^{leo}{\left(f_{u,v}^{leo}\right)}^2{m}_{u,v},\hfill & \hfill \forall u\in {\mathcal{N}}_i,v=Self\end{array}$$

  (29)
• $\mathbf{e}(\mathbf{Mission}\_\mathbf{Node},\mathbf{U})$: the capacity of this edge is set to Y, and Y needs to be greater than the total sum of the amount of the mission data, which is to ensure that failed missions can successfully flow to the sink node, T. In addition, the unit cost is set to K, and K is greater than the unit energy consumption of all offloaded missions. This is because the proposed SSPCO method selects the path with the minimum cost while finding the shortest augmenting path. If the unit cost of $e(Mission\_Node,U)$ is small, SSPCO will give up offloading missions to GEO satellite nodes or self nodes and offload to U nodes instead, which leads to offloading failure. The equation is as follows

  $$\begin{array}{cc}c(u,v)=Y,\hfill & \hfill \forall i\in \mathcal{L},\forall u\in {\mathcal{N}}_i,v=U\end{array}$$

  (30)

  $$\begin{array}{cc}w(u,v)=K,\hfill & \hfill \forall i\in \mathcal{L},\forall u\in {\mathcal{N}}_i,v=U.\end{array}$$

  (31)
• $\mathbf{e}(\mathbf{GEO}\_\mathbf{Node},\mathbf{T})$: we set the capacity to a larger value, Z, to ensure that the missions can be successfully offloaded to the sink node, T. Since the mission processing result is much smaller than the original amount of data, we neglect the energy consumed by the result return and set the unit cost to zero. Thus, we can obtain Equation (32).

  $$\begin{array}{cc}c(u,v)=Z,\hfill & \hfill \forall u\in \mathcal{H},v=T\end{array}$$

  (32)

  $$\begin{array}{cc}w(u,v)=0,\hfill & \hfill \forall u\in \mathcal{H},v=T.\end{array}$$

  (33)
• $\mathbf{e}(\mathbf{Self},\mathbf{T})$: we set the capacity to X to guarantee that the missions processed on LEO satellites can successfully flow to the sink node, T, and the unit cost is set to zero since there is no additional consumption. Thus, we can obtain Equation (34).

  $$\begin{array}{cc}c(u,v)=X,\hfill & \hfill u=Self,v=T\end{array}$$

  (34)

  $$\begin{array}{cc}w(u,v)=0,\hfill & \hfill u=Self,v=T.\end{array}$$

  (35)
• $\mathbf{e}(\mathbf{U},\mathbf{T})$: similar to the capacity definition of $e(Mission\_Node,U)$, the capacity of this edge is set to $MAX$, which is also carried out to ensure that the failed missions can successfully flow to the sink node, T, and the unit cost is set to zero since there is no actual consumption, so that Equation (36) can be obtained.

  $$\begin{array}{cc}c(u,v)=MAX,\hfill & \hfill u=U,v=T\end{array}$$

  (36)

  $$\begin{array}{cc}w(u,v)=0,\hfill & \hfill u=U,v=T.\end{array}$$

  (37)

Formulation of MCMF for computation offloading: based on the above mentioned, the partial computation offloading problem for on-board missions can be transformed into the MCMF problem, as shown in Equation (38). The minimum value of ${\sum }_{e(u,v)\in \mathcal{E}}f(u,v)w(u,v)$ corresponds to our optimization objective, i.e., total energy consumption, and the offloading decision can be obtained from the solved MCMF.

$$\begin{array}{cc}\hfill min& \left(\sum _{e(u,v)\in \mathcal{E}}f(u,v)w(u,v)\right)\hfill \end{array}$$

(38)

$$\begin{array}{cc}\hfill s.t.& 0\le f(u,v)\le c(u,v),\forall e(u,v)\in \mathcal{E}\hfill \\ \hfill & \sum _{e(u,v)\in \mathcal{E}}f(u,v)-\sum _{e(v,u)\in \mathcal{E}}f(v,u)\hfill \end{array}$$

(39)

$$\begin{array}{cc}& =\left\{\begin{array}{cc}\sum _{i=1}^{\left|L\right|}\sum _{n=1}^{|N_i|}{B}_{n,i},\hfill & \hfill u=S\\ -\sum _{i=1}^{\left|L\right|}\sum _{n=1}^{|N_i|}{B}_{n,i},\hfill & \hfill u=T\\ 0,\hfill & \hfill u\ne S,T\end{array}\right.\hfill \end{array}$$

(40)

where Equation (39) denotes that the amount of flow passing through an edge cannot exceed its capacity. Since in our improved flow network, as shown in Figure 4a, the U node can guarantee that the data volume of all missions flows out of the source node, S, and into the sink node, T, so the maximum flow, $f_{max}$, in Equation (21) is equal to ${\sum }_{i=1}^{\left|L\right|}{\sum }_{n=1}^{|N_i|}{B}_{n,i}$, and for all intermediate nodes except the source and sink node the outflow must be equal to the inflow.

For the convenience of readers, based on Equations (22)–(37), we denote the unit cost of different types of edges by Equation (41), and the capacity of different types of edges can be expressed as Equation (42).

$$\begin{array}{c}\hfill \begin{array}{c}\hfill w(u,v)=\left\{\begin{array}{cc}0,\hfill & \hfill u=S,\forall v\in \mathcal{L}\\ 0,\hfill & \hfill \forall u\in \mathcal{L},\forall v\in {\mathcal{N}}_u\\ {\kappa }^{geo}{\left(f_{u,i}^{v,geo}\right)}^2{m}_{u,i}+\frac{p_i}{R_{u,i}^v},\hfill & \hfill \forall i\in \mathcal{L},\forall u\in {\mathcal{N}}_i,\forall v\in \mathcal{H}\\ {\kappa }^{leo}{\left(f_{u,v}^{leo}\right)}^2{m}_{u,v},\hfill & \hfill \forall u\in {\mathcal{N}}_i,v=Self\\ K,\hfill & \hfill \forall i\in \mathcal{L},\forall u\in {\mathcal{N}}_i,v=U\\ 0,\hfill & \hfill \forall u\in \mathcal{H}\cup Self\cup U,v=T\end{array}\right.\end{array}\end{array}$$

(41)

$$\begin{array}{c}\hfill \begin{array}{c}\hfill c(u,v)=\left\{\begin{array}{cc}\sum _{n=1}^{|N_v|}{B}_{n,v},\hfill & \hfill u=S,\forall v\in \mathcal{L}\\ B_{v,u},\hfill & \hfill \forall u\in \mathcal{L},\forall v\in {\mathcal{N}}_u\\ \frac{f_{u,i}^{v,geo}{\tau }_{u,i}{R}_{u,i}^v}{f_{u,i}^{v,geo}+R_{u,i}^v{m}_{u,i}},\hfill & \hfill \forall i\in \mathcal{L},\forall u\in {\mathcal{N}}_i,\forall v\in \mathcal{H}\\ \frac{f_{u,v}^{leo}{\tau }_{u,v}}{m_{u,v}},\hfill & \hfill \forall u\in {\mathcal{N}}_i,v=Self\\ Y,\hfill & \hfill \forall i\in \mathcal{L},\forall u\in {\mathcal{N}}_i,v=U\\ Z,\hfill & \hfill \forall u\in \mathcal{H},v=T\\ X,\hfill & \hfill u=Self,v=T\\ MAX,\hfill & \hfill u=U,v=T\end{array}\right.\end{array}\end{array}$$

(42)

2.2.3. Successive Shortest Path-Based Computation Method

There are two main methods to solve the MCMF problems: one is the cycle-canceling algorithm (CCA). CCA first uses the method of solving the maximum flow problems to establish a feasible flow, f, and then, in the process of eliminating negative cycles, the total cost is gradually reduced while ensuring the feasibility of f until there is no negative cycle [29]. The other is the successive shortest path algorithm (SSPA). SSPA generally takes zero flow as the initial flow, finds an augmenting path from the source node, S, to the sink node, T, on the residual network, augments the flow on this path to the current flow, and then iteratively finds the augmenting path until it increases to the maximum flow. While finding the augmenting path, SSPA gives preference to the augmenting path with the minimum cost, thus ensuring that the augmented flow costs the minimum among the current feasible flows [30]. Next, the time complexity of these two algorithms is analyzed for the computation offloading problem studied in this paper.

For CCA, the Dinic’s algorithm can be used to obtain the maximum flow with a time complexity of $O\left(V^{2}E\right)$, where V denotes the number of nodes and E denotes the number of edges. Assuming that each elimination of negative cost cycles can reduce the cost by at least 1 unit, and C denotes the maximum capacity of all edges, then there are, at most, $ECM$ times to find negative cost cycles and increase/decrease flow operations, where M denotes the maximum unit cost among all edges. In addition, the Bellman–Ford algorithm can be used to find negative cost cycles. Then, the time complexity of CCA is $O(V^{2}E+V{E}^{2}CM)$ and, since $V{E}^{2}CM$ is much larger than $V^{2}E$, the final time complexity is $O\left(V{E}^{2}CM\right)$. For SSPA, the Bellman–Ford algorithm with time complexity of $O\left(VE\right)$ is used in finding the minimum cost path. Then SSPA augments, at most, $O\left(VC\right)$ times. The time complexity of SSPA is $O\left(V^{2}CE\right)$.

In this paper, we study the partial computation offloading problem in GEO/LEO hybrid satellite networks, where the situation is $C>M>E>V$. The time complexity analysis of the above two algorithms shows that the time complexity of SSPA is better than that of CCA ($O\left(V^{2}CE\right)<O\left(V{E}^{2}CM\right)$) for our problem. Therefore, we propose the successive shortest path-based computation offloading (SSPCO) algorithm, as shown in Algorithm 1. SSPCO uses the shortest path fast algorithm to search for the shortest path with unit cost as weight from the source node, S, to the sink node, T. Specifically, the flow network, G, is first constructed based on the input set of on-board missions, GEO/LEO satellite processing capacity, channel bandwidth, and channel gain (line 1), and then the corresponding residual network, $G^R$, is constructed based on G, and the flows and unit costs of the edges on $G^R$ are initialized (lines 2–7); the shortest augmenting path from the source node to the sink node is continuously searched for and augmented in residual network, $G^R$, until there is no augmenting path, p, in $G^R$ (lines 8–18); finally, the MCMF is transformed into the offloading decision: if there is flow from the mission node to the U node, it is considered as the mission offloading failure, otherwise the offloading ratio can be calculated by the flow on the edges from the mission node to the GEO satellite node and the self node (lines 19–27).

Algorithm 1 Successive shortest path-based computation offloading algorithm

input: the set of on-board missions, GEO/LEO satellite processing capacity, channel bandwidth, and channel gain; output: offloading decision for on-board missions;   1: According to the input information, construct the flow network G;   2: Construct the residual network $G^R$ based on G: $f(a,b),f(b,a),w(a,b),w(b,a)$;   3: for $e(a,b)\in G^R$ do   4:     $w(b,a)\leftarrow -w(a,b)$;   5:     $f(a,b)\leftarrow 0$;   6:     $f(b,a)\leftarrow 0$;   7: end for   8: while TRUE do   9:     Use shortest path fast algorithm in the residual network $G^R$ to find the augmenting path p from the source node S to the sink node T with an increase of $\delta$;  10:     if there is no augmenting path p in $G^R$ then  11:         break;  12:     end if  13:     Augment the flow in $G^R$ along the augmenting path p;  14:     for $e(a,b)\in p$ do  15:         Update $f(a,b)$ based on $\delta$;  16:         Update $f(b,a)$ based on $\delta$;  17:     end for  18: end while  19: for $e(a,b)\in G$ do  20:     for $e(a,b),a\in Mission\_Node,b=U$ do  21:         if $f(a,b)=0$ then  22:            Obtain the offloading decision for this mission, which can be expressed as ${\lambda }_a=\frac{f(a,c)}{B_a},c=GEO\_Node$;  23:         else  24:            Record this mission in the mission failure collection;  25:         end if  26:     end for  27: end for

3. Results

3.1. Experiment Setup

For simplicity without loss of generality, the GEO/LEO hybrid satellite networks considered in this paper consist of five LEO satellites and three GEO satellites. It is assumed that each LEO satellite has one or more missions to be processed and the data size of each mission is randomly distributed between 0.5 and 2.5 Gb. The processing density is randomly selected from the set $\{10,15,20\}$ and the QoS constraints are randomly generated in the $[650,5000]$ ms. We use containers to process the missions and each offloaded mission can be assigned a maximum processing capacity of $6\times {10}^{10}$ cycles/s on GEO satellites and $2\times {10}^9$ cycles/s on LEO satellites.

Table 2. Parameters in numerical analysis.

Parameter	Meaning	Value
${\omega }_{n,i}^j$	Radio channel bandwidth for transmitting mission $T_{n,i}$ from LEO satellite i to GEO satellite j	100 MHZ
$p_i$	Transmit power of LEO satellite i	90 W
$h_{i,j}$	Channel gain between LEO satellite i and GEO satellite j	2
$N_0$	Gaussian noise power	$-100$ dBm
$m_{n,i}$	Processing density of mission $T_{n,i}$	$\{10,15,20\}$ cycles/bit
$B_{n,i}$	Amount of mission $T_{n,i}$ data	0.5∼2.5 Gb
$h_{n,i}^{leo}$	Altitude of LEO satellite i	1200 km
$h_{n,i}^{j,geo}$	Altitude of GEO satellite j	$35,786$ km
$R_{light}$	Speed of light in a vacuum	$299,792$ km/s
${\kappa }^{leo},{\kappa }^{geo}$	Effective switching capacitance constant determined by the chip	${10}^{-28},{10}^{-29}$
${\tau }_{n,i}$	QoS constraints of mission $T_{n,i}$	650∼5000 ms
$f^{LEO}$	Maximum LEO satellite processing capacity	$2\times {10}^{10}$ cycles/s
$f^{GEO}$	Maximum GEO satellite processing capacity	$6\times {10}^{11}$ cycles/s

shows the parameters set in this paper [1,17,18]. All the experiments were conducted on the same computer with an Intel Xeon Silver 4110 CPU with 32 GB of RAM, using Python 3.8.15 with source code.

In addition, we compare the proposed SSPCO with four benchmark methods to evaluate the effectiveness of SSPCO.

• GEO offloading computing (GOC): all missions are offloaded to GEO satellites for processing;
• LEO offloading computing (LOC): all missions are processed on LEO satellites;
• Genetic algorithm-based computation offloading (GACO) method [31]. GACO is an optimization method inspired by biological evolution mechanisms. It simulates processes such as biological inheritance, mutation, and selection to perform iterative searches for the optimal solution. In GACO, the fitness of individuals is evaluated in each iteration according to a fitness function (identical to our objective function), with superior individuals having a higher chance of being selected to generate the next generation.
• Particle swarm optimization-based computation offloading (PSOCO) method [32]. PSOCO is a swarm intelligence optimization algorithm that simulates the foraging behavior of bird flocks. In PSOCO, each solution in the search space is considered a ’particle’, and all particles move iteratively in the search space to find the optimal solution. The velocity and direction of each particle’s movement are influenced by its individual best experience and the overall best experience of the swarm. Like GACO, the fitness function of PSOCO is identical to our objective function.

The experimental results first show the energy consumption and processing delay consumed by each mission of the five different computation offloading methods, as shown in Figure 5 and Figure 6. Then, the effects of the number of missions obtained by different methods are analyzed, as shown in Figure 7 and Figure 8. Finally, Figure 9 and Figure 10 plot the effects of QoS constraints.

3.2. Experiment Result

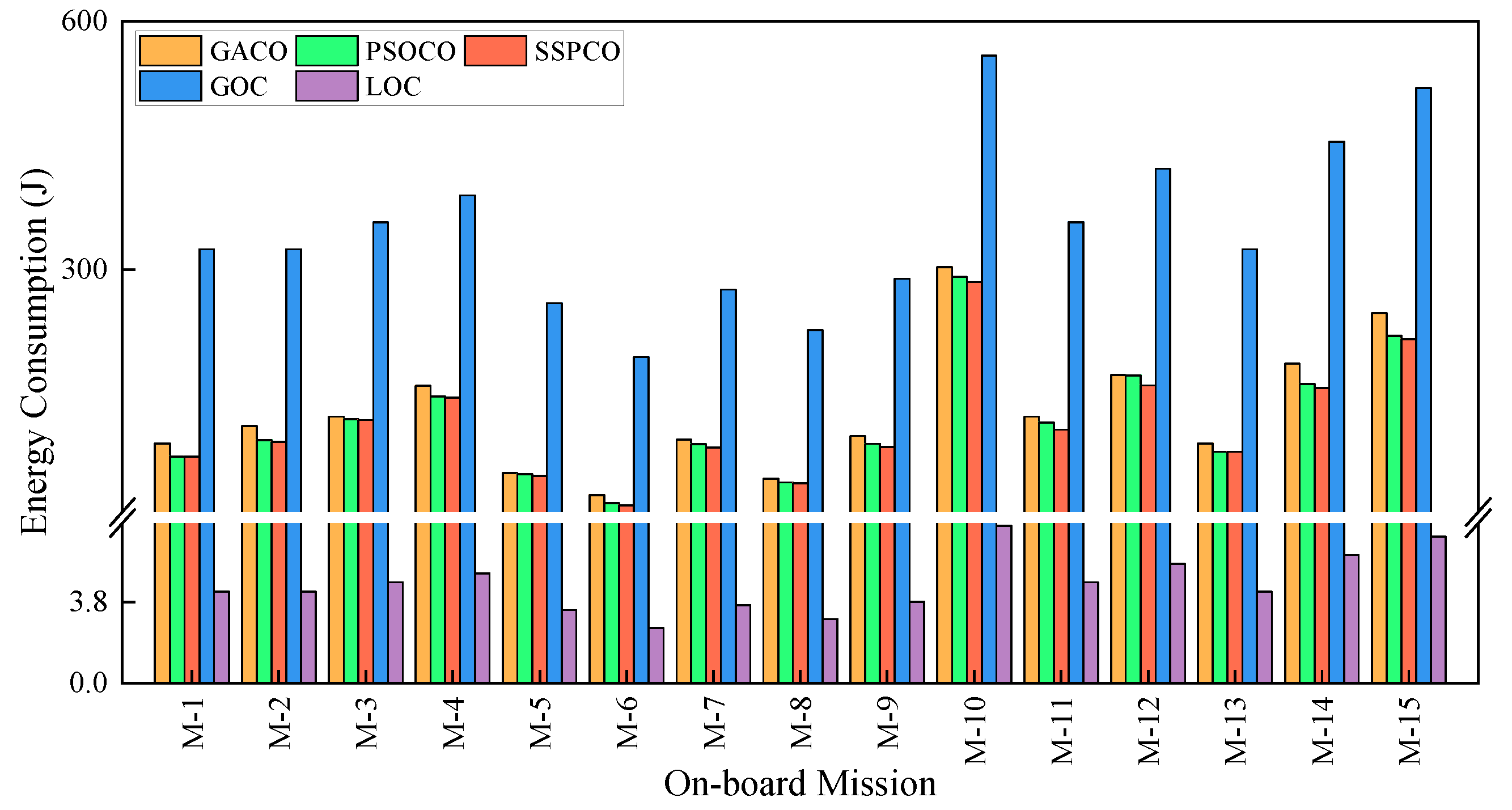
3.2.1. Energy Consumption and Processing Delay

Figure 5 and Figure 6 show the satellite energy consumed by each mission and the processing delay of each mission when the number of on-board missions is set to 15.

In Figure 5, we can see that LOC achieves the lowest energy consumption because it does not utilize any GEO satellite resources. However, it is undesirable because LOC violates the QoS constraints. GOC achieves the highest energy consumption by completely offloading missions to GEO satellites for processing. SSPCO achieves a lower energy consumption for all on-board missions because it coordinates the computing power of LEO and GEO satellites to save satellite energy as much as possible while guaranteeing the QoS requirements of on-board missions.

From Figure 6, it can be seen that the processing delay of each mission of LOC is much larger than other methods. This is due to the limited computing power of LEO satellites, and processing missions entirely on LEO satellites leads to a huge delay. GOC obtains the lowest processing delay by completely offloading the missions to GEO satellites with high computing power. GACO and PSOCO have lower processing delays compared with SSPCO. This is due to the fact that SSPCO takes into account the time cost of LEO satellite computation, GEO satellite computation, and mission transmission, and prioritizes the QoS constraints of on-board missions rather than simply pursuing the minimization of mission processing delay.

3.2.2. Influence of Number of On-Board Missions

Since LOC cannot guarantee QoS constraints for all on-board missions, comparison experiments are conducted for GACO, PSOCO, GOC, and SSPCO.

From Figure 7, it can be seen that the total energy consumption of the four methods increases with the increase of the number of on-board missions. The reason is that, when the number of missions increases, both LEO and GEO satellites process more missions, thus increasing the total energy consumption of the four methods. SSPCO achieves the lowest total energy consumption compared with the others because it does not overly pursue the minimization of processing delay, but makes full use of the computing power of LEO and GEO satellites to minimize the total energy consumption instead. Moreover, GOC has the highest total energy consumption due to the fact that all submitted missions are completely offloaded to GEO satellites for processing.

Furthermore, when the total energy consumption is the same for the computation offloading strategies, it does not mean that their offloading decisions are the same. This is because the number of successfully offloaded missions may be different for different strategies. Therefore, we propose the average energy consumption performance index (AEC), thus adding the number of successfully offloaded missions to the evaluation of energy consumption. Specifically, AEC is defined as shown in Equation (43). As the number of successfully offloaded missions increases and the total energy consumption decreases, the average energy consumption decreases, and this leads to better offloading decisions.

$$AEC=\frac{\mathrm{total} \mathrm{energy} \mathrm{consumption}}{\mathrm{the} \mathrm{number} \mathrm{of} \mathrm{successfully} \mathrm{offloaded} \mathrm{missions}}$$

(43)

From Figure 8, it can be seen that the proposed SSPCO still obtains the lowest average energy consumption as the number of on-board missions increases. This is because SSPCO can help LEO satellites choose the best offloading ratio to process onboard missions under the QoS constraints to ensure the maximum number of successfully offloaded missions and thus achieve the best average energy consumption. Experimental results show that SSPCO can reduce the energy by 19.45% and 7.73% on average compared with GACO and PSOCO, respectively. In addition, it can save 56.43% of energy compared with GOC.

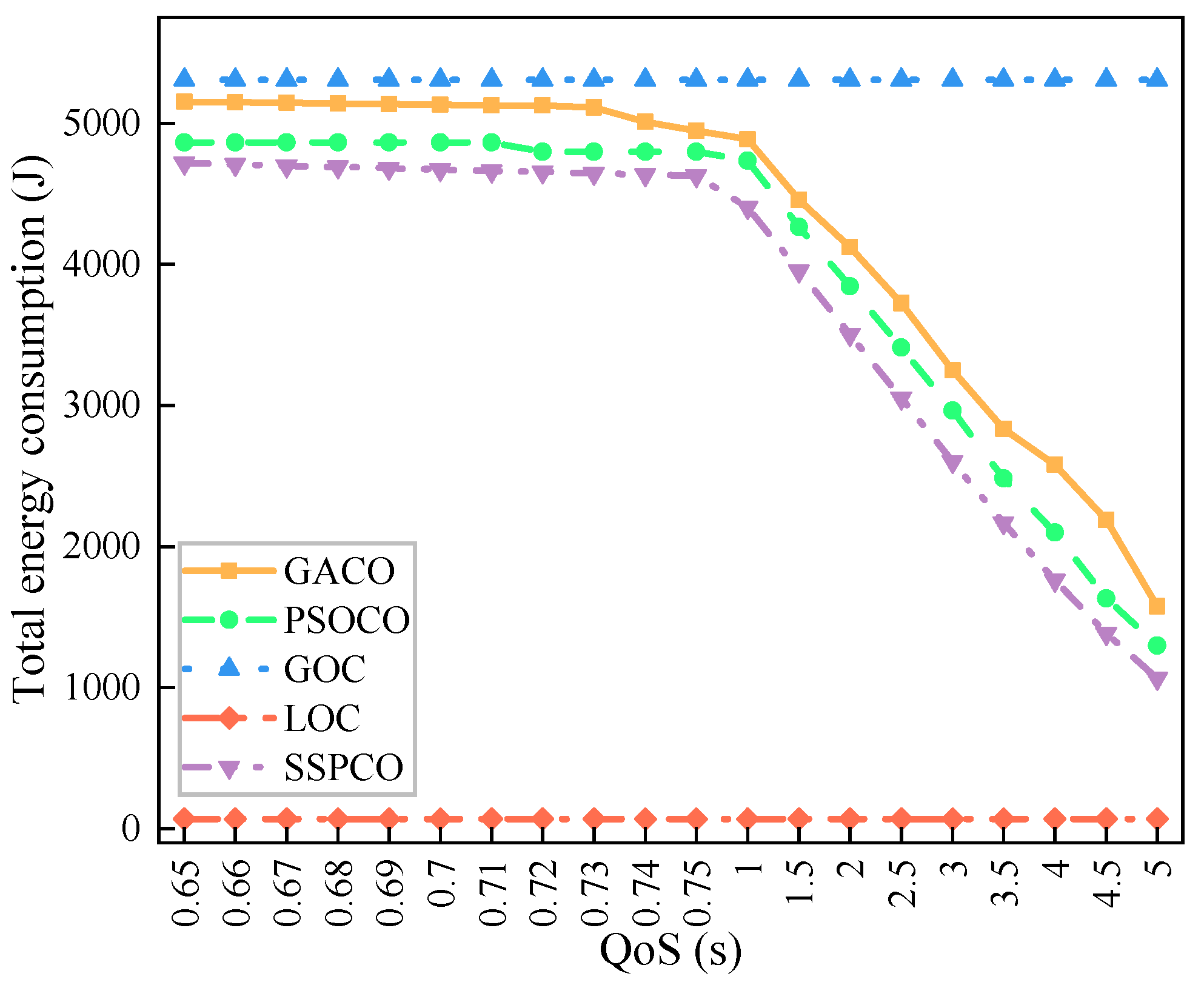
3.2.3. Influence of QoS

The degree of QoS violation of one on-board mission can be measured by the difference between the processing delay and its QoS constraint, which can be expressed by Equation (44).

$$vi{o}_{n,i}=\left\{\begin{array}{cc}\frac{D_{n,i}-{\tau }_{n,i}}{{\tau }_{n,i}},\hfill & D_{n,i}>{\tau }_{n,i},\hfill \\ 0,\hfill & otherwise.\hfill \end{array}\right.$$

(44)

Then, the overall degree of QoS violation for all on-board missions can be expressed as

$$vio=\sum _{i=1}^{\left|L\right|}\sum _{n=1}^{|N_i|}vi{o}_{n,i}$$

(45)

A higher $vio$ indicates that the current offloading decision does not satisfy the QoS constraints of missions.

From Figure 9, it can be seen that $vio$ of different computation offloading methods is decreasing as the QoS constraint gradually becomes loose. We notice that $vio$ of LOC is the highest under each QoS constraint. This is because of the limited processing capacity of LEO satellites, which leads to long processing delays, making it easy to violate QoS constraints. When the QoS constraint is set to $0.65$ s, $vio$ of SSPCO is 0 and stays at 0. When the QoS constraint is relaxed to $0.68$ s, $vio$ of GACO decreases to 0, and when the QoS constraint is relaxed to $0.69$ s, $vio$ of PSOCO decreases to 0. In addition, $vio$ of GOC decreases to 0 when the QoS constraint is relaxed to $0.7$ s. That is, SSPCO can satisfy more stringent QoS constraints for on-board missions than other methods.

Figure 10 plots the total energy consumption with QoS constraints for different computation offloading methods. Since the offloading ratios of GOC and LOC are fixed, their total energy consumption is constant under different QoS constraints. From Figure 10, it can be seen that the total energy consumption of GACO, PSOCO, and SSPCO increases as QoS constraints become tighter. This is because these methods offload more missions to GEO satellites to ensure the QoS requirements are met, resulting in reduced processing delays but higher energy consumption. Obviously, the total energy consumption of SSPCO is always better than the other methods under different QoS constraints because SSPCO adjusts the offloading ratio to utilize the computational resources of LEO and GEO satellites fully, thus reducing the total energy consumption.

4. Discussion

In this section, we first discuss the impact of increasing the satellite number of GACO, PSOCO, and the proposed SSPCO. Then, we discuss the limitations of the proposed method.

4.1. Impact of Increasing Satellite Number

In order to validate the efficacy of the algorithm proposed in this study further under conditions of large-scale satellite deployment, we conduct additional comparisons on energy consumption and algorithm running time across various quantities of LEO satellites. In these experiments, each LEO satellite is assumed to contain an average of three missions.

As depicted in Figure 11a, the total energy consumption under each strategy increases correspondingly with the rising number of satellites. This is to be expected as more satellites invariably lead to more missions. Notably, the energy consumption under the SSPCO strategy consistently remains lower than that under other strategies, affirming the superior energy-saving capabilities of the SSPCO method.

Moreover, Figure 11b demonstrates the inevitable increase in the algorithm’s running time resulting from the growth in satellite quantity, as a larger number of satellites engenders an expanded solution space. Remarkably, the running time of SSPCO is significantly shorter than that of PSOCO and GACO. This is due to the design of SSPCO, which constructs an improved flow network, thereby avoiding extensive ineffective searching like other algorithms and effectively reducing the runtime.

The combined results of Figure 11 clearly exhibit the effectiveness and superiority of the proposed SSPCO when applied to a large-scale satellite deployment.

4.2. Limitations and Future Works

The partial computation offloading problem discussed in this paper only considers that missions can be decomposed. In future work, we will pay attention to the partial computation offloading problem in GEO/LEO hybrid satellite networks considering the interdependencies among missions. Moreover, the selection of mission offloading nodes can be further enriched. In the future, consideration can be given to the terrestrial networks and offloading missions of LEO satellites to their adjacent and idle LEO satellites to enhance the computing capabilities for GEO/LEO hybrid satellite networks.

5. Conclusions

In this paper, we design a computation offloading framework for GEO/LEO hybrid satellite networks and construct the energy-efficient and QoS-aware constrained optimization model. After that, we transform the computation offloading problem into an MCMF problem and propose a successive shortest path algorithm-based solution method to obtain the offloading decision in polynomial time. Finally, a set of numerical experiments are conducted to demonstrate the effectiveness of the proposed SSPCO. The results show that SSPCO can effectively reduce the total energy consumption of the satellite networks while guaranteeing the QoS constraints of the on-board missions.