Self-Supervised Monocular Depth Estimation Using Global and Local Mixed Multi-Scale Feature Enhancement Network for Low-Altitude UAV Remote Sensing

Abstract

Estimating depth from a single low-altitude aerial image captured by an Unmanned Aerial System (UAS) has become a recent research focus. This method has a wide range of applications in 3D modeling, digital terrain models, and target detection. Traditional 3D reconstruction requires multiple images, while UAV depth estimation can complete the task with just one image, thus having higher efficiency and lower cost. This study aims to use deep learning to estimate depth from a single UAS low-altitude remote sensing image. We propose a novel global and local mixed multi-scale feature enhancement network for monocular depth estimation in low-altitude remote sensing scenes, which exchanges information between feature maps of different scales during the forward process through convolutional operations while maintaining the maximum scale feature map. At the same time, we propose a Global Scene Attention (GSA) module in the decoder part of the depth network, which can better focus on object edges, distinguish foreground and background in the UAV field of view, and ultimately demonstrate excellent performance. Finally, we design several loss functions for the low-altitude remote sensing field to constrain the network to reach its optimal state. We conducted extensive experiments on public dataset UAVid 2020, and the results show that our method outperforms state-of-the-art methods.

1. Introduction

Low-altitude remote sensing is a technique that employs Unmanned Aerial Vehicles (UAVs) or other airborne devices equipped with sensors to acquire ground features and environmental information. This technology has wide-ranging applications in areas such as map making [1], resource monitoring [2], and urban planning [3]. In low-altitude remote sensing, accurate depth information is critical for achieving these tasks.

In recent years, with the development of deep learning techniques, it has become possible to obtain depth information from low-altitude remote sensing images using depth estimation methods, without the need for traditional depth sensors. However, depth estimation in the field of low-altitude remote sensing still faces several challenges. On the one hand, traditional depth estimation methods require a large amount of labeled data for training [4], and obtaining labeled data in low-altitude remote sensing is difficult and costly. On the other hand, the complexity and uncertainty of low-altitude remote sensing scenes pose challenges to the accuracy and robustness of depth estimation.

As an alternative approach, unsupervised monocular depth estimation has become a highly sought-after research direction. Compared to traditional depth estimation methods [5,6,7,8,9], unsupervised monocular depth estimation methods do not require labeled data for training, making them more efficient in handling depth estimation problems in low-altitude remote sensing.

Self-supervised monocular depth estimation is a deep learning method that does not require manual annotation of depth labels, and its basic principle is to use self-supervised signals between image frames for learning. Specifically, this method uses a sequence of monocular images to estimate the relative pose and depth information between adjacent frames, thereby learning the geometric information of the scene. The key to using monocular image sequences for self-supervision is that pseudo-depth labels can be generated by using properties such as temporal consistency and motion continuity, which can replace manually annotated depth labels and reduce data annotation costs.

Currently, there are many unsupervised monocular depth estimation methods [10,11,12,13,14,15] available for autonomous driving scenarios. Zhou et al. [10] is one of the earliest works on unsupervised monocular depth estimation using self-supervised learning. The method proposed by Godard et al. [16] is based on deep convolutional neural networks (CNNs) and predicts depth by reconstructing the input image. Yin et al. [17] proposed an unsupervised deep learning model called GeoNet, which can simultaneously learn the depth, optical flow, and camera pose of an image. Godard et al. [18] introduced the minimum reprojection loss and automask to address moving objects and occlusion, making it the most classic unsupervised monocular depth estimation framework. Casser et al. [19] used pre-defined segmentation masks to segment object categories in the known field of view to help deal with moving objects.

These depth estimation methods have shown promise in the field of autonomous driving, but they cannot be directly applied to low-altitude remote sensing due to the following challenges: in low-altitude remote sensing scenes, the non-uniformity of depth distribution can affect the measurement of depth. Unlike the uniform distribution of depth in autonomous driving scenes, depth in low-altitude remote sensing scenes can be concentrated in the foreground or background, such as on roofs and walls. There are also scale variations and occlusion problems in low-altitude remote sensing scenes. Traditional training methods based on photometric consistency are suitable for autonomous driving scenes, but, in low-altitude scenes, scale variations can occur quickly and there may be large areas of occlusion. This makes it difficult for the network to quickly capture these differences.

As far as we know, there are currently very few depth estimation studies that focus specifically on low-altitude remote sensing with a wide field of view. Mou et al. [20] trained the network using aerial imagery and corresponding DSM generated through semi-global matching. Hermann et al. [21] used a similar architecture to Monodepth [16] and trained it on monocular drone videos to jointly estimate depth and pose. Madhuanand et al. [22] proposed a state-of-the-art method that uses a dual encoder with a 3D decoder to estimate the depth information of a scene.

Previous studies have successfully demonstrated the possibility of using monocular depth estimation algorithms on UAVs. Our work focuses on the research of unsupervised monocular depth estimation algorithms in low-altitude remote sensing scenes, enhancing the applicability and robustness of depth estimation in this type of scenario.

The main contributions of this work are as follows:

• We propose a global and local mixed multi-scale feature enhancement network for depth estimation in low-altitude remote sensing scenarios. It parallelizes the input image into lateral branches of different scales, where the same branch maintains the same size throughout the process, and different branches exchange feature information at the intersection nodes, reducing information loss during convolution to obtain a more refined depth estimation result.
• We propose a Global Scene Attention (GSA) module for the decoder part of the depth network, which aims to establish long-distance semantic connections in the global context of the input feature map and integrate this contextual information into the channel representation of the feature map. This helps to improve the model’s understanding and reasoning ability for the overall scene, thereby enhancing the performance of the task.

Our method achieves depth estimation of ground objects in low-altitude remote sensing scenes through end-to-end self-supervised training. We compared our method with other existing methods on public dataset UAVid 2020. The experimental results show that our method can obtain higher depth estimation accuracy and stronger robustness, providing an effective and practical solution for depth estimation in the low-altitude remote sensing field.

The structure of this article is as follows. Section 2 provides an overview of the related work to our research. In Section 3, we describe in detail our proposed method and introduce each component. Section 4 describes the datasets used in our experiments and the qualitative and quantitative results. The final section is a summary of our work and an outlook for future research.

2. Related Work

In this section, we will provide a detailed overview of two research areas related to our study: self-supervised monocular depth estimation and monocular depth estimation for aerial images.

2.1. Self-Supervised Monocular Depth Estimation

Self-supervised monocular depth estimation is a hot research topic in the field of computer vision. Monocular depth estimation starts from traditional methods that relied on manually designed image features and depth mapping. These features mainly include shadows [23], vanishing points [24], focus/defocus cues [25], etc., to construct mathematical models. However, due to the additional assumptions made, the robustness of these models is relatively poor. With the rise and development of deep learning, supervised depth estimation has gained widespread attention. However, this training method requires paired depth and image data for training, but this method is costly, data-scarce, and difficult to collect. Therefore, self-supervised depth estimation has become an alternative method. Unlike supervised deep learning, self-supervised depth estimation only requires video sequences or adjacent image frames as input, and trains neural networks to estimate the depth of objects in a single image.

It is inspired by the classic computer vision algorithm Structure from Motion (SfM), a groundbreaking work that proposed a basic framework consisting of a depth network and pose network, trained simultaneously with consecutive video frames. Subsequently, many research works further developed this idea and made improvements in model architecture or loss function, including [10,17,18,19,26,27,28,29]. Among them, the most classic is Monodepth2 [18], where Godard et al. introduced the minimum reprojection loss and auto-masking to enhance the robustness of the algorithm in handling occluded scenes and to ignore pixels in training that violate the camera motion assumption, reducing the number of wrongly projected points in training.

2.2. Monocular Depth Estimation for Aerial Images

Videos captured by low-altitude drones are easier to obtain than creating actual depth labels, but single-image depth estimation models in aerial scenes require additional complexity to estimate both depth and position compared to those in autonomous driving scenes. Currently, research on using videos for self-supervised single-image depth estimation is mainly focused on ground images, and there are few studies that specifically focus on low-altitude remote sensing scenes. In the following, we will discuss some important research related to our study.

The diverse pitch angles present in drone video scenes yield a considerable range of depths within scenes, coupled with a wider field of view, thereby intensifying training difficulties. Hermann et al. [21] devised a self-supervised training strategy for training on drone-captured videos and extended this methodology to a monocular depth estimation task performed in naturalistic settings. Madhuanand et al. [22] proposed a network architecture that employed a dual-branch ResNet [30] encoder connected to a 3D decoder, similar to PackNet [27], for joint depth and pose learning to predict depth. The architecture adopted the classic self-supervised learning paradigm proposed by [10,16,18]; i.e., the supervision signal came from adjusting the reference image to reconstruct the target image by calculating the pose change between the reference and target images. They applied the reprojection loss, edge-aware smoothness loss, and the contrastive loss to constrain the network training. Finally, they evaluated the model performance on public dataset UAVid 2020 [31].

We have implemented a high-performance model for low-altitude remote sensing depth estimation. Our model utilizes a global and local mixed multi-scale feature enhancement network that can estimate the depth of targets in real-time within the field of view of UAVs. The encoder of the depth network extracts multi-scale feature information and divides it into multiple streams for processing. During the convolution process, the feature map scale of each stream remains unchanged, and the information is fused at intersection nodes of different streams to achieve complementary information. In the decoder, we designed a GSA module to better distinguish between the foreground and background of objects, resulting in excellent monocular depth estimation results.

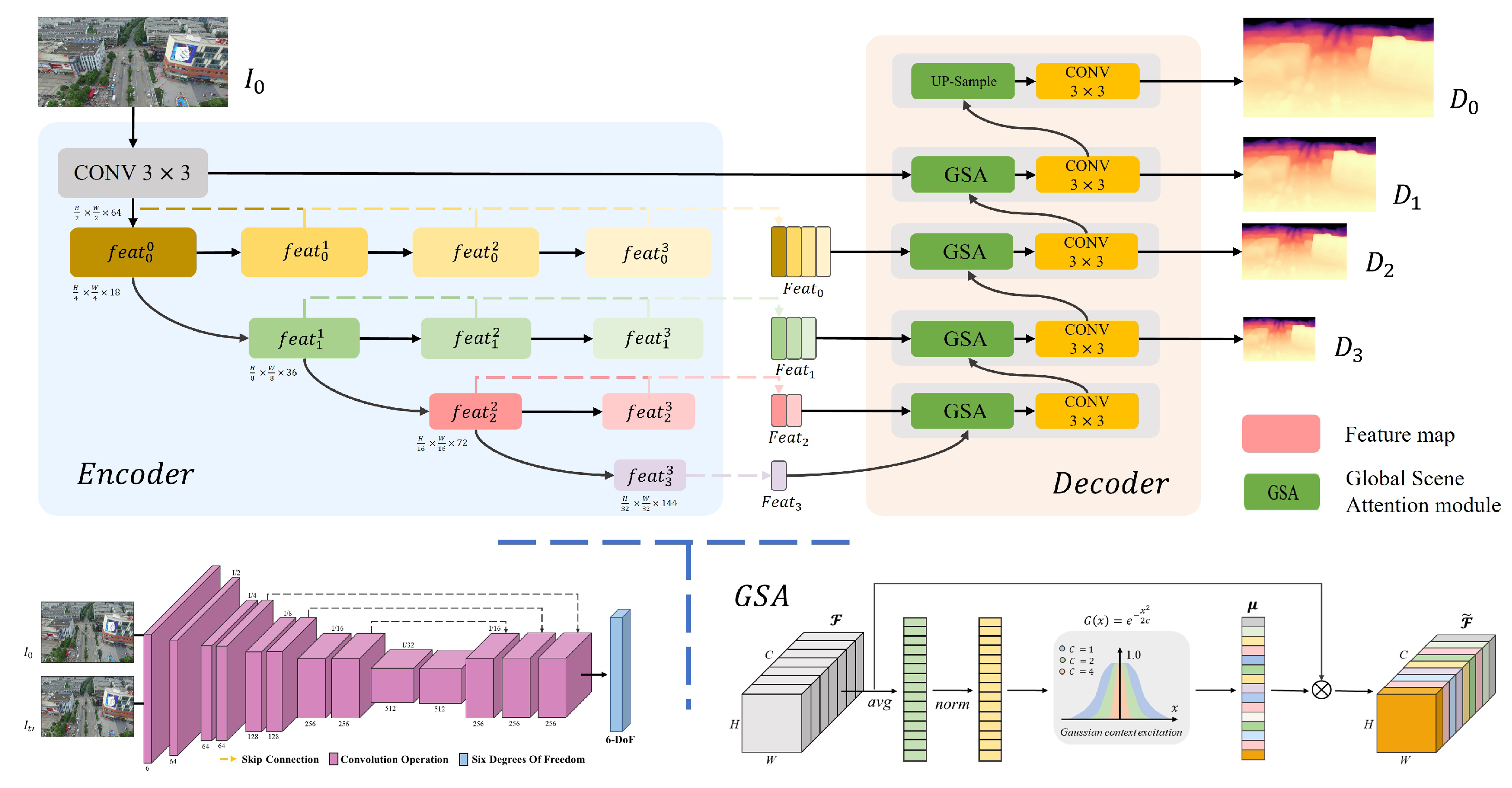
3. Materials and Methods

In the following content, we propose a self-supervised monocular depth estimation algorithm for low-altitude remote sensing. This method is divided into four sub-parts, including model inputs, overall network architecture, combination of different loss functions, and network inference process.

3.1. Model Inputs

During the training phase, the input data for the depth network and pose network consist of three consecutive RGB frames, denoted as $I_t\in {\mathbb{R}}_{H\times W\times 3}$, where $t\in \{-1,0,1\}$. These frames are extracted from manually captured drone videos. The input images contain sufficient scene information and show the variation in drone perspective. The three consecutive frames are split into two groups as input to the network, and we apply the internal parameters obtained from the calibrated drone to the pose network. The accuracy of depth estimation increases with the resolution of the input images, but it also increases the computational and memory usage. Therefore, after studying, we adjust the resolution of the input images for the network to 352 × 640. The pose network takes the target frame $I_0$ and two source frames $I_{t^{\prime }}$ ($t^{\prime }\in \{-1,1\}$) as input and passes them to the encoder.

During the evaluation of depth estimation, the model takes a single low-altitude remote sensing image $I_0$ as input and attempts to predict the depth value of each pixel to generate a depth map.

3.2. Network Architecture

The overall structure, as depicted in Figure 1, consists of two networks: DepthNet and PoseNet. Each of these networks is trained in a self-supervised manner using three consecutive RGB frame sequences, $I_t$, $t\in \{-1,0,1\}$. The input of the DepthNet is an RGB image $I_0$, and the resulting depth map $D_0$ is generated through the encoder–decoder, represented by Equation $D_0=DepthNet\left(I_0\right)$. The input of the PoseNet is two pairs of consecutive frames, and its output is a six-degree of freedom (6-DoF) vector, divided into translation and rotation vectors, represented by Equation $T_{0\to t^{\prime }}=PoseNet(I_0,I_{t^{\prime }})$, $t^{\prime }\in \{-1,1\}$.

3.2.1. Depth Network

Many existing depth estimation methods [18,22,27,29] are based on ResNet [30], where the network encodes the image into low-resolution feature maps during the convolution process. In contrast, we propose a novel encoder–decoder architecture that includes a multi-scale feature enhancement encoder and a decoder based on Global Scene Attention modules, which can fuse semantic-rich and spatial features during the encoding process. The encoder processes the input image in parallel streams of different scales, where each feature map in each stream has the same resolution, and nodes with different resolutions in each stage exchange information. Each stream contains many intermediate nodes to aggregate features. Based on the assumption that the level of semantic information contained in the feature maps increases with the number of channels, we set the network feature map node $fea{t}_s^r$ to represent the output of encoder node $fea{t}_s^r$, where s represents different stream sequence along the encoder forward propagation, and r represents the intermediate node number along the skip-connection direction. The stack computation of feature mapping is as follows:

$$fea{t}_s^r=\left\{\begin{array}{c}\begin{array}{cc}\epsilon \left(\mathrm{conv}\right(I\left)\right),\hfill & \hfill r=s=0\\ \epsilon \left(fea{t}_{s-1}^{r-1}\right),\hfill & \hfill r=s\ne 0\\ \psi (\left[fea{t}_s^{r-1}\right],\mathcal{D}\left[fea{t}_{s-1}^{r-1}\right],\mathcal{U}\left[fea{t}_{s+1}^{r-1}\right]),\hfill & \hfill others\end{array}\end{array}\right.$$

(1)

where $\epsilon (·)$ represents the feature extraction block, $\psi (·)$ represents the feature fusion block composed of convolution operation and activation function, $\mathcal{U}(·)$ and $\mathcal{D}(·)$ represent the up-sampling block and down-sampling block composed of convolution and bilinear interpolation operations, respectively.

The overall network architecture is shown in Figure 1. The number of channels in different intermediate nodes within the same stream remains unchanged, whereas the number of channels in feature maps from different streams doubles as the resolution decreases. The connection feature maps of the intersecting stages of the same stream are input into the decoder part of the deep network by skipping the connection, as shown in Equation (2). In ablation experiments, we report performance gains using our designed network.

$$Fea{t}_s=concat(fea{t}_s^r,...,fea{t}_s^3),r\in \{s...3\},s\in \{0...3\}$$

(2)

where $concat(·)$ denotes the concatenate operation, r represents the nodes of different stages on the same tributary, s denotes the index of different tributary.

The decoder part of the depth network receives four different scales of feature maps through skip connections. These feature maps are first input into the GSA module to generate attention maps with different importance and then restored to different scales of depth maps through $3\times 3$ convolutional operations. During the training process, these depth maps are combined with pose transformation matrices to reconstruct the target image $I_0$.

Convolutional neural networks (CNNs) have achieved great success in computer vision. However, the local context awareness of convolutional kernels makes it difficult for CNNs to effectively capture global contextual information in images. To address this issue, many recent works [22,29,32] have incorporated attention mechanisms into the network. Inspired by SENet [33], we use a Gaussian function that represents pre-set negative correlation to directly map global attention to an attention map. The basic structure of this module is shown in Figure 1. Given a feature map $\mathcal{F}\in {\mathbb{R}}_{C\times H\times W}$ as input to this module, the GSA module first normalizes the channel vector through the GAP operation, using $avg(·)$ and $norm(·)$ operations to stabilize the distribution of global context. Then, a Gaussian function, as shown in Equation (3), is used to perform activation on the normalized global context to obtain the attention map.

$$g=G\left(x\right)=e^{\frac{x^2}{2c^2}}$$

(3)

where g represents the activated values of attention, which can be multiplied by the original feature map to obtain the attention enhanced feature map. c represents the standard deviation of the Gaussian function $G\left(x\right)$, controlling the diversity of the channel attention maps. A larger standard deviation leads to less diversity in the activated values between channels.

3.2.2. Pose Network

Following Monodepth2 [18], we also use a Pose network to estimate the changes in camera pose between consecutive frames. Given the target image $I_0$ and the source image $I_{t^{\prime }},t^{\prime }\in \{$−$1,1\}$, the network predicts the relative pose $T_{0\to t^{\prime }}$ between the source image $I_{t^{\prime }}$ and the target image $I_0$, where the output of the network is a six-degree of freedom (6-DoF) feature vector representing the rotation and translation vectors from the source image to the target image. The output of the network is then fed into a depth network that reconstructs the target image $I_{t^{\prime }\to 0}$ using ResNet-18 [30] as the pose encoder and a decoder with upsampling operations and $3\times 3$ convolutional layers, as shown in Figure 1. To achieve optimal initial performance, the pose network is pretrained on ImageNet dataset [34].

3.3. Loss Functions

Usually, self-supervised training for autonomous driving assumes photometric consistency, meaning that objects in the field of view are static and have correct reflectance. However, it cannot be directly applied to low-altitude remote sensing scenes. We introduce several loss terms into the network framework to constrain the training of the network in low-altitude remote sensing scenes. Using the predicted depth map $D_0$, the reconstructed view $I_{t^{\prime }\to 0}$, and the corresponding target frame $I_0$, we build a supervisory signal consisting of three items. The total loss function is defined as Equation (4),

$${\mathcal{L}}_{total}={\mathcal{L}}_{GD}+{\mathcal{L}}_{PM}+{\mathcal{L}}_G$$

(4)

where ${\mathcal{L}}_{GD}$ represents the gradient discrimination loss, ${\mathcal{L}}_{PM}$ represents the photometric loss, and ${\mathcal{L}}_G$ represents the minimization of the photometric loss. We will discuss the importance of different loss terms in ablation experiments.

3.3.1. Gradient Discrimination Loss (${\mathcal{L}}_{GD}$)

Due to the Edge Smoothness Loss function [18], i.e., Equation (5), designed for autonomous driving scenarios using first-order gradient ${\nabla }^1$, it is not applicable to low-altitude remote sensing scenes with large areas of low texture.

$$\begin{array}{cc}\hfill {\mathcal{L}}_{ES}(D\left(p\right),I\left(p\right))=& \frac{1}{T}(\sum _p\sum _{d\in x,y}\left|{\nabla }_d^{1}D\left(p\right)\right|e^{-|{\nabla }_d^{1}I\left(p\right)|})\hfill \end{array}$$

(5)

Therefore, we follow the previous works [15,35] and introduce second-order gradient ${\nabla }^2$ discrimination to increase the differentiation of low-texture areas, improving the model’s estimation performance in low-texture areas, such as roofs and ground. The calculation method is shown in Equation (6).

$$\begin{array}{cc}\hfill {\mathcal{L}}_{GD}(D\left(p\right),I\left(p\right))=& \frac{1}{T}(\sum _p\sum _{d\in x,y}\left|{\nabla }_d^{1}D\left(p\right)\right|e^{-|{\nabla }_d^{1}I\left(p\right)|}+\hfill \\ \hfill & \sum _p\sum _{d\in x,y}|{\nabla }_d^{2}D\left(p\right)\left|e^{-|{\nabla }_d^{2}I\left(p\right)|}\right)\hfill \end{array}$$

(6)

3.3.2. Photometric Loss (${\mathcal{L}}_{PM}$)

The photometric loss function ${\mathcal{L}}_{PM}$ is used to calculate the difference between $I_0$ and $I_{t^{\prime }\to 0}$. Following [14,18,22,29], we also use the structural similarity (SSIM) [36] index to evaluate the similarity between the reconstructed frame $I_{t^{\prime }\to 0}$ and the target frame $I_0$. By combining the SSIM index with the ${\mathcal{L}}_1$ norm, the final photometric loss function is defined as Equation (7), where $\phi =0.85$.

$$\begin{array}{c}\hfill {\mathcal{L}}_{PM}(I_0\left(p\right),I_{t^{\prime }\to 0}\left(p\right))=(1-\phi ){\mathcal{L}}_1(I_0\left(p\right),I_{t^{\prime }\to 0}\left(p\right))+\\ \hfill \frac{1}{T}\sum _p\left(\frac{\phi }{2}(1-SSIM(I_0\left(p\right),I_{t^{\prime }\to 0}\left(p\right)))\right)\end{array}$$

(7)

3.3.3. Minimization of the Photometric Loss (${\mathcal{L}}_G$)

To address occlusion issues, we also employed the minimum photometric loss and automatic masking strategy introduced in Monodepth2 [18]. The final loss function is calculated as follows:

$$\begin{array}{c}\hfill {\mathcal{L}}_G=Min({\mathcal{L}}_{PM}(I_0\left(p\right),I_{t^{\prime }\to 0}\left(p\right))<{\mathcal{L}}_{PM}(I_0\left(p\right),I_{t^{\prime }}\left(p\right)))\end{array}$$

(8)

where $I_{t^{\prime }\to 0}$ denotes the reprojected target image, $I_0$ represents the target image, $I_{t^{\prime }}$ represents the source images from the previous and subsequent frames, and ${\mathcal{L}}_{PM}$ represents the Photometric Loss.

3.4. Inference

During the inference stage, we perform depth estimation on a single input image. As the attitude transformation information is only used during training, we do not estimate the rotation and translation vectors here.

In the encoder of our depth network, we use a multi-scale feature enhancement network to extract low-altitude remote sensing feature information at different scales. These feature maps are concatenated after exchanging information at certain nodes and then input into the scene texture attention module of the decoder in our depth network via skip connections. Under the guidance of Hermann et al. [21], we use the reference depth information created by COLMAP software [37], which uses traditional Structure from Motion (SfM) techniques for multi-view reconstruction of scenes, to compare our proposed method with different state-of-the-art depth estimation models. In the following section, we will introduce the public dataset we used and the results of the qualitative and quantitative evaluations conducted on it.

4. Results

In this section, we describe the dataset used and provide implementation details of our proposed method. We then compare our method with current state-of-the-art model architectures through qualitative and quantitative analysis, demonstrating superior performance on the UAVid 2020 [31] benchmark test compared to previously published methods. We validate that our proposed network is capable of outputting depth maps with semantic richness and spatial accuracy. Our research holds important implications for fields such as the UAV industry, virtual reality, and beyond.

4.1. Dateset

The UAVid 2020 [31] dataset is a widely used collection of drone videos for training and evaluating computer vision and machine learning algorithms. The dataset includes a total of 42 video sequences, each with a length of 45 s. The drone flies at a height of 50–100 m, with a speed of 10 meters per second, capturing video frames at a rate of 20 frames per s, at a 45-degree angle; some of the images are shown in Figure 2. The image resolution is 4096 × 2160 or 3840 × 2160, and the video sequences contain stable, moving, and non-stationary camera views. The UAVid 2020 dataset also includes various common object categories, such as vehicles, humans, buildings, and more. After conducting a detailed study of the dataset, we extracted and adjusted the frames to 0.2 s per frame, using the preceding and following five frames as supervisory signals during training. Through this frame extraction method, we obtained 6666 training images, 539 testing images, and 209 validation images. During the evaluation process, we used the median ground truth scaling of each image in the validation set to report the results.

4.2. Implementation Details

Our model was trained and tested on a single NVIDIA RTX 3090 GPU using PyTorch framework [38]. We used the Adam [39] optimizer with default beta values of 0.9 and 0.999 for training. The batch size was set to 8, and the input and output resolutions were 640 × 352. We employed stepLR optimization strategy, with an initial learning rate of $1\times {10}^{-4}$, which decayed to 0.1 times the original rate (i.e., $1\times {10}^{-5}$) after the 15th epoch. Similar to the optimization function combination used in Monodepth2 [18], we used a weighted combination of photometric loss, minimum reprojection loss, and edge-aware smoothness to train the depth network. Specifically, we set the weight of the photometric loss to $1\times {10}^{-3}$ and the SSIM [36] weight to 0.85. Additionally, we applied edge-aware smoothness regularization to the depth map, with a weight of $1\times {10}^{-3}$.

Depth Network. For the depth network, we employed our proposed architecture, which is a modified version of HRNet [26]. The encoder consists of multiple convolutional layers and residual blocks, which divide the input image into horizontally aligned parallel streams and fuse information at the intersection nodes of different streams, thereby complementing global structural information and local detail information. Finally, the feature maps of different nodes are concatenated and inputted to the decoder part of the depth network through skip connections. We used pre-trained encoder weights on the ImageNet dataset [34] to initialize the model. We also incorporated a Global Scene Attention module into the decoder to better capture the spatial information of the depth map.

Pose Network. Regarding the pose network, we adopted the structure proposed in [18], which is based on ResNet-18 [30]. The pose network takes the current frame and the previous frame as input and outputs the relative transformation pose 6-DOF between them, where the first three represent the translation vector and the last three represent the rotation vector. We attempted to use different pre-trained encoders, such as ResNet-50 [30] and HRNet [26], but ultimately decided to use ResNet-18 as it performed the best.

4.3. Evaluation Metrics

To evaluate the performance of the model, we use a set of metrics that are also employed in [18,22,27,29]. These include absolute relative difference (Abs Rel), as shown in Equation (9), which calculates the average difference between the reference and corresponding pixel position of the predicted depth by the method. Squared relative difference (Sq Rel) is provided in Equation (10) and represents the squared difference between the reference and method predicted depth. Root mean squared error (RMSE) is provided in Equation (11). Root mean squared logarithmic error (RMSE${}_{log}$) uses a logarithmic function to reduce the effect of large errors on distance, as shown in Equation (12), and accuracy, as provided in Equation (13), which are also used as evaluation metrics.

$$\mathrm{Abs}\mathrm{Rel}=\frac{1}{T}\sum _{i=1}^T\frac{\left|D\left(x_i\right)-D^{\prime }\left(x_i\right)\right|}{D\left(x_i\right)}$$

(9)

$$\mathrm{Sq}\mathrm{Rel}=\frac{1}{T}\sum _{i=1}^T\frac{{\left|D\left(x_i\right)-D^{\prime }\left(x_i\right)\right|}^2}{D\left(x_i\right)}$$

(10)

$$\mathrm{RMSE}=\sqrt{\frac{1}{T}\sum _{i=1}^T{\left|D\left(x_i\right)-D^{\prime }\left(x_i\right)\right|}^2}$$

(11)

$${\mathrm{RMSE}}_{log}=\sqrt{\frac{1}{T}\sum _{i=1}^T{\left|\log D\left(x_i\right)-\log D^{\prime }\left(x_i\right)\right|}^2}$$

(12)

$$\begin{array}{c}\hfill \mathrm{Accuracy}=\%\mathrm{of}D\left(x_i\right)\mathrm{s}.\mathrm{t}.\mathrm{Max}(\frac{D\left(x_i\right)}{D^{\prime }\left(x_i\right)},\frac{D^{\prime }\left(x_i\right)}{D\left(x_i\right)})<\theta ,\mathrm{where}\theta =1.25,1.{25}^2,1.{25}^3\end{array}$$

(13)

These equations calculate the accuracy of the predicted depth values at each pixel position, where $D\left(x_i\right)$ represents the ground truth depth and $D^{\prime }\left(x_i\right)$ represents the predicted depth using the selected method. T is the total number of valid pixels in the ground truth. The accuracy is determined by measuring the percentage of pixels whose absolute difference between predicted and ground truth depths is within a specific threshold $\theta$. To comply with the standard evaluation benchmarks of KITTI [4], we set the threshold values to 5%, 15%, and 25%.

4.4. Comparison Methods

We qualitatively and quantitatively evaluated the performance of our model and compared it with current state-of-the-art monocular depth estimation methods, namely Monodepth2 [18], Madhuanand et al. [22], and CADepth [29]. Monodepth2 introduced posenet and depthnet, which estimate the depth information of monocular images through self-supervised training. Madhuanand et al. focused on the field of low-altitude remote sensing and used a dual encoder and a 3D decoder to estimate the depth information from a drone’s perspective. CADepth proposed a channel-enhanced depth estimation model that focuses on feature map channel information and achieved impressive results. The final results were obtained by comparing the depth maps generated by these models with the reference depth provided by COLMAP [37].

4.5. Qualitative Results in UAVid 2020

We conducted a qualitative analysis of various models on the UAVid 2020 dataset [31], and their results and reference depths are shown in Figure 3. The performance of different models in depth estimation varies, and all models can accurately estimate the depth information of objects in the scene. However, our method performs better when dealing with complex scenes. For example, in urban street scenes, our model can accurately estimate the depth information of objects such as buildings and roads. Our method also outperforms others in handling small objects, such as fences and power poles. In the last two rows of Figure 3, we have highlighted in red boxes the regions of elongated objects on the road, which occupy only a few pixels (pixels <=10) in a given direction and can easily lose information through convolution. The method of Monodepth2 [18] is susceptible to factors such as changes in lighting and shadows, resulting in less accurate estimates. Our experimental results demonstrate that our model performs exceptionally well in low-altitude remote sensing depth estimation, especially in complex scenes and depth estimation of small objects. In contrast, traditional methods based on convolutional feature extraction perform better in processing simple scenes and single-object detection but are inferior to our proposed model in handling complex scenes.

4.6. Quantitative Results in UAVid 2020

We also conducted a quantitative analysis on the uavid 2020 dataset to compare the performance of different models in depth estimation. We used the metrics mentioned in Section 4.3 as evaluation metrics. The results of the quantitative analysis are shown in

Table 1. Quantitative results on the UAVid 2020 dataset. Without additional datasets or online refinement. Best results are in bold. For Abs Rel, Sq Rel, RMSE, and RMSE${}_{log}$, lower is better, and, for $\delta <1.25$, $\delta <1.{25}^2$, and $\delta <1.{25}^3$, higher is better. The values represent the mean score over all the images in the corresponding test dataset.

Method	Dataset	Abs Rel	Sq Rel	RMSE	RMSE${}_{\mathit{log}}$	$\mathit{\delta }<1.25$	$\mathit{\delta }<1.{25}^2$	$\mathit{\delta }<1.{25}^3$
Godard et al. [18]	UAVid 2020	0.1389	1.7943	4.5913	0.2130	0.8781	0.9537	0.9795
Yan et al. [29]	UAVid 2020	0.1297	3.2008	4.4344	0.1964	0.9177	0.9620	0.9782
Madhuanand et al. [22]	UAVid 2020	0.1383	3.2538	4.7721	0.2052	0.9054	0.9621	0.9792
Our model	UAVid 2020	0.0955	1.3705	3.3753	0.1724	0.9341	0.9730	0.9856

.

From Table 1, it can be seen that our model has the best performance among all models on the uavid 2020 dataset [31], with an average AbsRel and RMSE of 0.0955 and 3.3753, respectively. Our model performs best in urban street and mountain scenes. In contrast, other models’ depth estimation performance in complex scenes is not as good, which may be because objects in complex scenes are usually smaller and denser, such as cars on the road, making it difficult to accurately estimate their depth information. Additionally, our model performs well in handling small objects, low-texture regions, and lighting changes, such as the roofs of buildings and trees.

Overall, our model performs exceptionally well on the uavid 2020 dataset, especially in handling complex scenes and depth estimation of small objects. These results demonstrate the high practicality and application value of our proposed method in practical applications.

4.7. Ablation Study

In addition, we conducted several ablation experiments to verify the performance improvements resulting from our contribution. We used Monodepth2 [18] as a baseline.

Table 2. Ablation experiments using different attention modules in the decoder part of the depth network. N/A: without attention module. Best results are in bold, For Abs Rel, Sq Rel, RMSE, and RMSE${}_{log}$, lower is better, and, for $\delta <1.25$, $\delta <1.{25}^2$, and $\delta <1.{25}^3$, higher is better. The values represent the mean score over all the images in the corresponding test dataset.

Method	Dataset	Abs Rel	Sq Rel	RMSE	RMSE${}_{\mathit{log}}$	$\mathit{\delta }<1.25$	$\mathit{\delta }<1.{25}^2$	$\mathit{\delta }<1.{25}^3$
N/A	UAVid 2020	0.1210	1.7066	4.4226	0.1993	0.9033	0.9626	0.9817
CAM [40]	UAVid 2020	0.1487	3.3558	5.5283	0.2189	0.8918	0.9499	0.9722
SAM [40]	UAVid 2020	0.1341	3.2246	4.4733	0.2078	0.9091	0.9677	0.9799
Coordinate [41]	UAVid 2020	0.1060	1.2173	3.5873	0.1832	0.9190	0.9671	0.9845
GSA	UAVid 2020	0.0955	1.3705	3.3753	0.1724	0.9341	0.9730	0.9856

and

Table 3. Quantitative results of different loss functions on the UAVid 2020 dataset. All methods in this table were trained on the UAVid 2020 dataset [31]; the best results are in bold. We used Monodepth2 [18] as the baseline. For Abs Rel, Sq Rel, RMSE, and RMSE${}_{log}$, lower is better, and, for $\delta$ < 1.25, $\delta$ < $1.{25}^2$, and $\delta$ < $1.{25}^3$, higher is better. The values represent the mean score over all the images in the corresponding test dataset.

Method	Pre- Train	Loss Function	Abs Rel	Sq Rel	RMSE	RMSE${}_{\mathit{log}}$	$\mathit{\delta }<1.25$	$\mathit{\delta }<1.{25}^2$	$\mathit{\delta }<1.{25}^3$
Baseline	✗	${\mathcal{L}}_{PM}$	0.1797	3.8392	6.6307	0.2540	0.8377	0.9292	0.9622
Baseline	✓	${\mathcal{L}}_{PM}$	0.1250	1.1581	3.7793	0.1987	0.8908	0.9605	0.9854
Our model	✗	${\mathcal{L}}_{PM}$	0.1543	3.2377	4.7649	0.2374	0.8577	0.9439	0.9725
Our model	✓	${\mathcal{L}}_{PM}$	0.1253	2.3697	3.9955	0.1949	0.9142	0.9658	0.9828
Our model	✓	${\mathcal{L}}_{PM}+{\mathcal{L}}_G$	0.1203	2.1244	3.4125	0.1891	0.9212	0.9693	0.9831
Our model	✓	${\mathcal{L}}_{PM}+{\mathcal{L}}_G+{\mathcal{L}}_{ES}$	0.1081	1.8056	3.3994	0.1809	0.9302	0.9715	0.9854
Our model	✓	${\mathcal{L}}_{PM}+{\mathcal{L}}_G+{\mathcal{L}}_{GD}$	0.0955	1.3705	3.3753	0.1724	0.9341	0.9730	0.9856

show the results of the ablation experiments, including pretraining on ImageNet, adding the GSA module, and adding the gradient discrimination loss function. Table 2 shows the quantitative comparison of the effects of including different attention mechanisms in the decoder part of the depth network. From the analytical results, we observed that using a multi-scale feature enhancement network can improve the performance of the model. The GSA module can pay more attention to small objects and increase their importance in the decoder recovery stage compared to other attention mechanisms.

We consider that the depth information distribution of salient objects in the scene is related to the shape of the objects. Finally, we combined our multiple modules to achieve the optimal state of the entire network architecture.

5. Discussion

This study proposes a novel approach for estimating depth information of low-altitude remote sensing monocular videos in complex scenes based on a global and local mixed multi-scale feature enhancement network, aimed at improving the accuracy of monocular depth estimation in complex scenes. Our method calculates depth by using the pixel coordinate relationship between frames. The input image extracts image information through the encoder part of the depth network using multiple different scales of convolution. The feature map size is not changed during the processing of each stream, and information exchange occurs at the partially intersecting nodes of different streams. Supervisory signals are created using the reprojection method for training, without requiring additional supervision information, making it easier to obtain and more accurate. In the decoder part of the depth network, we propose using a Global Scene Attention module to enhance the recovery of image information, avoiding the degradation of detail information during decoding and better distinguishing foreground and background in low-altitude remote sensing images. Finally, we use a combination of different loss functions to constrain the training of the network architecture to support our proposed structure. We conducted comprehensive experiments on the UAVid 2020 dataset, comparing our method with several state-of-the-art methods for monocular depth estimation designed for autonomous driving scenarios and low-altitude remote sensing. The experimental results show that our method can estimate more accurate scene texture details for low-altitude remote sensing images and works well in complex environments.

In future work, we will further explore depth estimation methods for low-altitude remote sensing videos in complex scenes, improve the accuracy of depth estimation for dynamic objects, and further study the accuracy of target localization using monocular depth estimation algorithms.