Abstract
The inversion method based on the reflection loss-grazing angle curve is an effective tool to obtain local underwater acoustic parameters. Because geoacoustic parameters vary in sensitivity to grazing angle, it is difficult to get accurate results in geoacoustic parameter inversion based on small-grazing-angle data in shallow water. In addition, the normal-mode model commonly used in geoacoustic parameter inversion fails to meet the needs of accurate local sound field simulation as the influence of the secant integral is ignored. To solve these problems, an acoustic data acquisition scheme was rationally designed based on a sparker source, a fixed vertical array, and ship drifting with the swell, which could balance the trade-off among signal transmission efficiency and signal stability, and the actual local acoustic data at low-to-mid frequencies were acquired at wide grazing angles in the South Yellow Sea area. Furthermore, the bottom reflection coefficients (bottom reflection losses) corresponding to different grazing angles were calculated based on the wavenumber integration method. The local seafloor sediment parameters were then estimated using the genetic algorithm and the bottom reflection loss curve with wide grazing angles, obtaining more accurate local acoustic information. The seafloor acoustic velocity inverted is and the sound attenuation is in the South Yellow Sea. Relevant experimental results indicate that the method described in this study is feasible for local inversion of geoacoustic parameters for seafloor sediments. Compared with conventional large-scale inversion methods, in areas where there are significant changes in the seabed sediment level, this method can obtain more accurate local acoustic features within small-scale areas.
1. Introduction
With the continuous development of maritime engineering, submarine resource exploration, coastal defense infrastructure, and other marine programs, the geoacoustic parameters of seafloor sediments, as an important part of seafloor characterization, have gradually become the main research object of marine acoustic exploration [,,,]. In terms of acquisition methods for seafloor geoacoustic parameters, the telemetry of seafloor parameters based on acoustic signals (i.e., geoacoustic parameter inversion) has the advantages of low cost, usability, and wide detection range compared with direct measurement methods such as sampling and drilling [,,,], making geoacoustic parameter inversion a popular subject of current research in the field of seafloor exploration.
Geoacoustic parameters [,,] are important in describing the inherent characteristics of the seafloor sediments, but they differ obviously with sediment type. In areas in which seafloor sediments change dramatically in the horizontal direction, it is difficult for the conventional long-distance inversion method to represent accurately the seafloor geoacoustic parameters. This objective has to be achieved by using a local geoacoustic inversion method [,], in which the method based on reflection coefficients and loss is an effective tool to obtain local seafloor parameters in shallow water. Holland et al. [] used a time–frequency hybrid algorithm to enable the inversion of the speed, density, and attenuation coefficient of the seafloor, and then they used the Bayesian inversion approach to enable the inversion of density and sound velocity gradients with the frequency band of 300–1600 Hz []. Spofford [] proposed a method to estimate sound speed gradient and attenuation using bottom-loss versus grazing-angle data, which addressed the problem of the inability to separate gradient and attenuation for inversion in thick sediments areas. Yang et al. [] proposed a high-resolution inversion method using sub-bottom reflection, but the horizontal range between the acoustic source and the receiving array was kept constant in the field experimental data of the study and the corresponding grazing angle range was too narrow to meet the inversion requirement. Chapman [] provided a method of Bayesian inference for estimation of geoacoustic model parameters based on ocean bottom reflection coefficient data. In the inversion by using the reflection coefficient–loss method, the larger the range of the grazing angle, the more advantageous it is for the inversion of different parameters, as geoacoustic parameters differ in sensitivity to incident grazing angles within 0–90°. However, in existing studies, it is difficult to acquire high-quality data at wide grazing angles, as the ratio of the vertical scale to the horizontal scale in shallow-water environments is too small.
At the same time, exact acoustic field simulation is an important foundation for realizing local geoacoustic parameter inversion. Currently, the geoacoustic inversion algorithms are mostly implemented based on normal-mode models []. Rubano [] proposed a four-layer fluid normal-mode acoustic propagation model, describing accurately the acoustic propagation characteristics in shallow water over a low-velocity bottom. Based on the normal-mode model, Zhou et al. [,] enabled the inversion of the P-wave velocity and attenuation by changing the model parameters to make the model calculation results consistent with the actual data. Based on the same model, Becker et al. [] proposed a P-wave velocity inversion method in the horizontal wavenumber domain. Potty et al. [] discussed the influences of changes in the spatial distribution and depth profile of sediments on the dispersion characteristics of acoustic waves and then used the relationship among arriving times in different normal modes to invert the P-wave velocity. In a shallow-sea environment, Guo et al. [] used a warping transform to perform effective normal-mode separation between the signals generated by two broadband explosion sound sources at different distances propagating in the waveguide, and inverted the bottom sound velocity and attenuation based on modal dispersion arrival time difference and propagation loss. Although the normal-mode method is widely applied in long distance geoacoustic inversion, the contribution of the secant integral is ignored in the calculation of the conventional normal-mode model. However, the normal mode corresponding to the secant integral has a non-negligible influence on the near field; therefore, the normal-mode model fails to meet the needs of exact local acoustic field simulation and local geoacoustic parameters have to be inverted by using other acoustic field computing methods, such as the wavenumber integration method employed in this study. Compared with the normal-mode algorithm, the wavenumber integration method uses a direct numerical method to calculate the integral, which can effectively eliminate the problem of modal loss, enabling a more accurate acoustic field calculation in the near field. Therefore, proactively studying geoacoustic inversion techniques related to the wavenumber integration method is conducive to acquisition of near-field seafloor sediment parameters.
At present, in the fields of underwater acoustic communication, seafloor sediment structure detection, seafloor buried target detection, and anti-submarine sonar application, most of the operating frequencies are in the low-to-mid frequency bands (<10 kHz). Consequently, it is necessary to study seafloor geoacoustic parameter inversion methods at low-to-mid frequencies, which is vital to the acquisition of geoacoustic parameters in a specific area and the implementation of relevant research and applications such as accurate forecasting of ocean acoustic fields, detection of seafloor targets, ensuring marine environmental safety, and exploration of ocean engineering []. To enable acoustic property detection for seafloor sediment, the acoustic signal carrying characteristic information of the sediments has to be obtained. The sound sources and receivers are essential devices for the acoustic signal data acquisition in offshore experiments. In seafloor geoacoustic parameter inversion experiments, many types of sound sources are used, among which explosive sound sources and air guns are often used at present [,,]. Explosive sound sources are most extensively applied, but they have a huge impact on the ambient surroundings and do not meet the requirements of environmental protection. Compared with explosive sound sources, air guns are highly advantageous because of their low frequency, high power, and long lifetime [,], yet they are costly and have large launch intervals leading to low efficiency of launch repetition rate. In addition, transducer sound sources are common in geoacoustic experiments []. With their wide bandwidth and ability to accurately control the frequency of the signal, transducers are very advantageous for research on the relationships between acoustic parameters and frequency, but the sound source levels are often low, making it difficult to meet the need of actual data acquisition.
Owing to functional limitations of acoustic equipment and the need of a source level, it is difficult to acquire high-quality experimental data during conventional local low-to-mid frequency geoacoustic experiments. Sparkers are a kind of typical nonexplosive source used for seismic surveying; they are safe and environmentally friendly and have relatively less impact on the surrounding environment [,]. They emit acoustic waves in the low-to-mid frequency range, which can meet the needs of geoacoustic experiments. Having small volumes and high energy, they are suitable for offshore operations. From the perspective of the above characteristics, sparkers have huge potential in local geoacoustic inversion experiments. Using a sparker as a signal transmitting device can enable continuous acquisition of local low-to-mid frequency acoustic signals.
The composition of the receiving array will also affect the accuracy of the inversion results. Generally, a vertical receiving array (composed of multiple hydrophones) is often used in underwater acoustic detection because of its high spatial resolution, especially in ocean acoustic tomography and in research on geoacoustic parameters [,]. Qiu [] found that, for the same array length, an inclined array is comparable to a vertical array and better than a horizontal array in the inversion of parameters such as sound source distance, depth, and seawater depth. There is a significantly smaller relative error for the vertical array than the other two arrays in inversion of sedimentary layer parameters. In addition, reasonable deployment of shooting and receiving devices in actual offshore operations, for instance, choosing a vertical array moored to the seafloor to reduce sea surface noise [,], is also an important assurance for acquisition of high signal-to-noise ratio acoustic signal and improvement of inversion accuracy.
To acquire local seafloor geoacoustic parameters, the current status of and advances in research on geoacoustic inversion were considered, forward modeling of bottom reflection loss versus grazing angle based on the wavenumber integration method was studied, and geoacoustic parameters based on wide-grazing-angle reflection loss were inverted by using the genetic algorithm. Based on a sparker source and a fixed vertical array, a data acquisition method for actual local offshore acoustic detection was designed and studied. The local bottom reflection data in a wide-grazing-angle range in the South Yellow Sea were acquired, and an effective signal was extracted by using a filtering method based on the wavelet transform. The bottom reflection signal was recognized by an eigenray extraction method based on ray tracing. Finally, the data were used to invert the geoacoustic parameters of the oceanic sediment based on the bottom reflection loss curve and the parameters were verified by using a posteriori probability distribution. This study was performed to help provide a feasible data acquisition and processing scheme for the inversion of local seafloor geoacoustic parameters.
2. Numerical Calculation of Shallow Water Local Acoustic Field Based on the Wavenumber Integration Method
2.1. Solution of Depth-Separated Wave Equation Based on the Wavenumber Integration Method
It is the wavenumber integration method that can involve contribution of the branch cut integral to the total field, which means accurate calculation of each mode is possible, providing a precise description of the near field and helping to carry out local inversion studies of the geoacoustic parameters.
The total field solution is expressed as a spectral integration of solution to the depth-separated wave equation. The normal-mode approach and wavenumber integration technique employ different approaches to estimate the integral. Instead of applying the residue theorem to simplify the integral expression, it is the direct numerical quadrature that the wavenumber integration approach employs. The principle of the wave number integration method will be briefly discussed below.
The wavenumber integration method is suitable for horizontally layered or range-independent environments, as illustrated in Figure 1. The interfaces between layers are flat and parallel, with layer properties being solely depth-dependent.
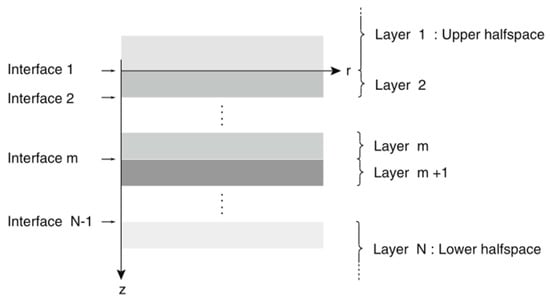
Figure 1.
Horizontally stratified environment.
A cylindrical coordinate system is established. Without considering submarine stratification, for water layer with sound source, the Helmholtz equation satisfied by field is
for sedimentary layer without source, the field is required to fulfill the homogeneous Helmholtz equation,
where is the source function, is the medium wavenumber for layer , subscript 0 stands for water layer, and 1 for sedimentary layer.
Using the zeroth-order Bessel function, the forward Hankel transform [] is performed on Equations (1) and (2), with the depth-separated wave equation derived as follows
The solution is given by the sum of a particular solution to Equation (3) and arbitrary linear combination of the two independent solution, denoted by and , to Equation (2).
Therefore, the complete solution to describe the depth-dependent field can be expressed as follows:
where and represent arbitrary coefficients determined by the boundary conditions at the layered interface. Calculating the undetermined coefficients for the entire global system of equations, the set of coefficients to be determined can be used to determine the integral expression for the sound field in each layer exactly. Then, the total sound field at the angular frequency can be obtained at any distance via the inverse Hankel transform [].
It can be seen that the core of the shallow-water acoustic field calculation based on wavenumber integration method can be divided into two main components: Green’s function with depth obtained at discrete horizontal wavenumbers for selected receiver depths and sound field as a function of distance and depth found by numerically evaluating the expression for sound field integration. In the realization, the direct global matrix method is used to solve the linear equations with undetermined coefficients, and the fast field method used to calculate the acoustic field integral expression [].
2.2. Calculation of Bottom Reflection Loss in Shallow Water
The wavenumber integration method is based on splitting the overall wave field into plane waves in the case of propagation in a planar geometry. The grazing angle and the horizontal wavenumber satisfy the following relationship:
where is medium wavenumber. It is evident that the grazing angle is a real angle only when .
In the direct global matrix approach, an infinite half-space is used instead of the layer above the interface, then the field of acoustic source will be a plane wave incident at an angle with an amplitude on the interface. Solving the system of equations for this new stratification problem by the approach mentioned above calculating the depth separated wave equation, it will directly yield the complex amplitude of the reflected plane wave, denoted by , and the reflection coefficient can be simply expressed as
Notedly, the above is the reflection coefficient for true plane waves.
In geoacoustic inversion, a reflection coefficient is usually transformed into a bottom reflection loss curve by using the relationship between the reflection coefficient and reflection loss:
3. Data Acquisition for a Marine Geoacoustic Experiment
Although the reflection characteristics indicate the inherent properties of the seafloor, there are obvious differences in the seabed between different sea areas and types of sediments. Therefore, in response to different actual requirements, it is necessary to systematically study the reflection characteristics of the seafloor in a specific sea area. Taking the clayey sandy seafloor sediment area of the South Yellow Sea, for example, we elaborate upon the data acquisition for a seafloor reflection signal measurement experiment.
3.1. Experiment Description
The study area was selected in the sea area roughly within the central South Yellow Sea shelf ~210 km to the southeast of Qingdao, China. The experimental data were acquired at station S1 (Figure 2), where the sediment type is clayey sand, the water depths are ~40–50 m, and the seafloor is relatively flat, deepening slightly in the NW–SE direction. Before measurement of the seafloor reflection data, the seafloor sediment samples were obtained at the survey station and the sound velocity profile of seawater as well.
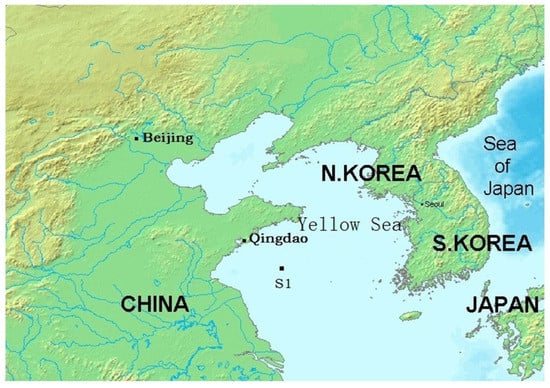
Figure 2.
Map of the area around the survey station. S1 is the location of the survey station.
From the perspective of the seawater acoustic velocity profile obtained from the experiment shown in Figure 3, the sound velocities were very uniform (within 1502–1503 m/s).
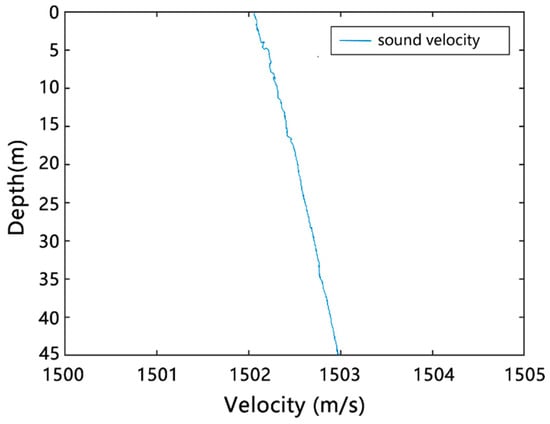
Figure 3.
Sound velocity profile (the blue line) at the survey station.
3.2. Acoustic Data Acquisition in the Study Area
3.2.1. Experimental Scheme
In the operation area, the water depth at the workstation was ~45 m. A 17.1m-long vertical receiving array was laid into the water. The array consisted of 96 elements, set 18 cm apart. The survey ship, Xiangyanghong 81, carried a sound source to complete the horizontal movement and the source was sunk at a depth of 30 m. The experimental devices were configured as shown in Figure 4.
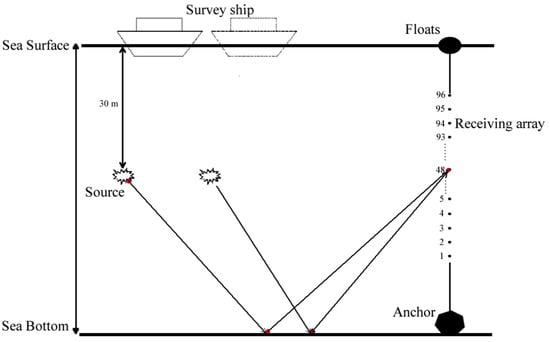
Figure 4.
Configuration schematic of the marine experimental devices.
To obtain seafloor reflection data, the sparker emitted the acoustic signal. According to the geometric relationship between the source and receivers shown in Figure 5, the horizontal-l distance between the source and the vertical receiving array is , the height of the sound source relative to the seafloor is , and the height of a certain element in the vertical linear array relative to the seafloor is . Single-channel experimental data were processed; that is, for a set of fixed values of , , and , the seabed reflection loss at the corresponding graze angle was calculated. According to the configuration of the experimental devices shown in Figure 5, when both and were constant, the survey ship carrying the sound source was moved to vary the distance between the source and the vertical receiving array such that the sound source emitted acoustic signals at different horizontal positions, which were then received by the vertical receiving array to enable calculation of the bottom reflection losses within a given range of grazing angle. Signals emitted and received at multiple horizontal distances yield a wider range of grazing angle to meet the inversion requirement.
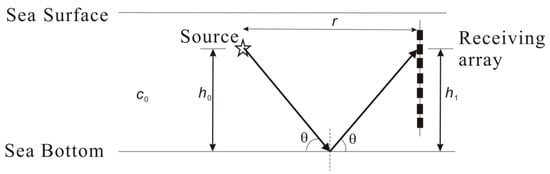
Figure 5.
Schematic of the geometric relationship between the source and receivers.
3.2.2. Experimental Procedure
In this experiment, movement of the survey ship was driven by the swells.
- After the ship sailed to the target experimental station, the data acquisition devices such as the sparker and receivers were connected, and the self-contained inclinometer and the bathythermograph were mounted onto the vertical linear array. After commissioning of the devices, the vertical linear array was put into the water, and the sound velocity profiler (CTD48M, Sea-Sun-Tech, Trappenkamp, Germany) was used to measure the acoustic velocity profile data in the sea area.
- At the stern, the sparker source was sunk via frame A to a depth of 30 m. When the ship traveled to the vicinity of the vertical linear array, the main engine was turned off to reduce the noise of the vessel. While the ship was drifting, the sound source continuously emitted sharp pulse signals in intervals of 3 s for a duration of 20 min.
- The data acquisition was done after step (2) was repeated three times. The sparker source was reclaimed, the survey ship engine was turned on, and the ship returned to the vertical array, and the acoustic releaser released the vertical array and the acquisition device. These were then salvaged after they floated to the water surface.
- The experimental data were exported and backed up.
4. Geoacoustic Parameter Inversion Based on Bottom Reflection Loss within the Wide-Grazing-Angle Range
4.1. Curves of Bottom Reflection Loss versus Grazing Angle for Different Seafloor Parameters
Figure 6 shows the graph of bottom reflection loss versus grazing angle for different seafloor acoustic velocities under the assumption of a liquid half-space hypersonic seafloor model. The simulation model parameters were as listed below: seawater sound velocity = 1500 m/s; seawater density = 1.0 g/cm3; seafloor sound velocities = 1600, 1800, and 2000 m/s; seafloor density = 2.0 g/cm3; and computing frequency = 2000 Hz.
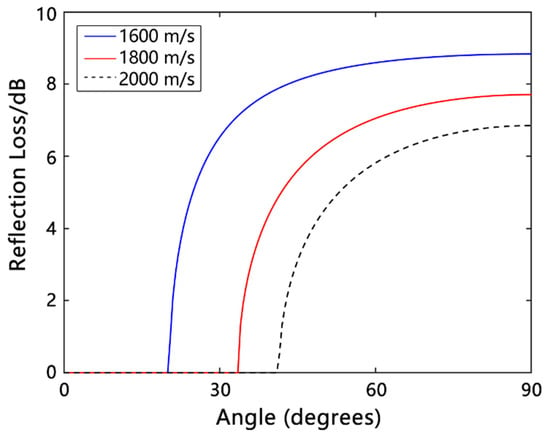
Figure 6.
Curves of bottom reflection loss versus grazing angle for different seafloor acoustic velocities.
Figure 7 shows the graph of bottom reflection loss versus grazing angle for different seafloor acoustic attenuation values based on the liquid half-space seafloor model. The simulation parameters of the model were as listed below: seawater sound velocity = 1500 m/s; seawater density = 1.0 g/cm3; seafloor sound velocity = 1800 m/s; seafloor sound attenuation values = 0, 0.1, and 0.2; seafloor density = 2.0 g/cm3; and computing frequency = 1000 Hz.
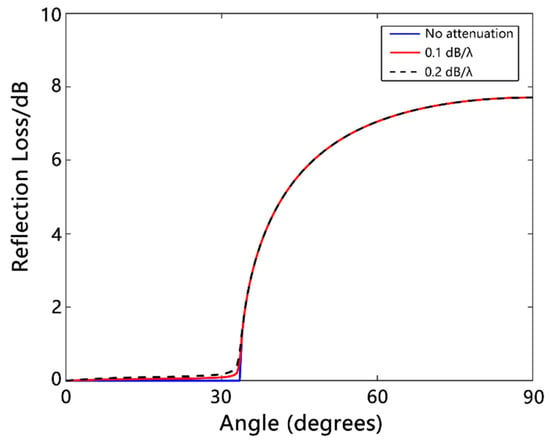
Figure 7.
Curves of bottom reflection loss versus grazing angle for different seafloor acoustic attenuation values.
It can be observed from the two figures above that the reflection loss within a wide grazing angle range can effectively distinguish different geoacoustic parameters, enabling inversion of multiple geoacoustic parameters.
4.2. Simulation Experiment Based on the Theoretical Model
Figure 8 shows a theoretical model of a Pekeris waveguide with a seafloor interface. In the numerical example, the seawater layer and the sediment layer are assumed to be uniform and isotropic. The source frequency was 50 Hz. The seawater acoustic velocity and density were 1500 m/s and 1000 kg/m3, respectively. The seafloor acoustic velocity and density were 2000 m/s and 1600 kg/m3, respectively. The seafloor acoustic attenuation was .

Figure 8.
Schematic of the marine environment used for inversion.
According to the above environmental information, substituting the parameters into the wavenumber integration model yielded the bottom reflection coefficient curve shown in Figure 9.
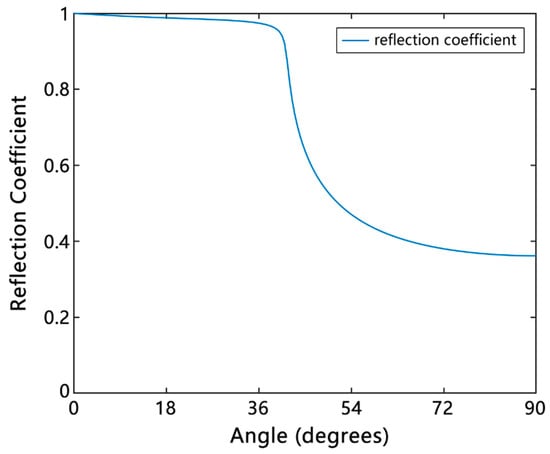
Figure 9.
Theoretical reflection coefficient curve (the blue line) for the marine environment.
The inversion process of sediment geoacoustic parameters based on bottom reflection loss is given here according to the computing steps of the genetic algorithm [,]. In this modeling example, the parameters to be inverted were acoustic velocity and the attenuation of seafloor sediments. In the experiment, the range of acoustic velocity was to be 1450–3500 m/s, with the number of individuals in this range to be 1001. The acoustic attenuation was determined to range from 0.1 to 0.6 and the number of individuals in this range was 1001. Each model parameter to be inverted was represented as a 20-bit chromosome string based on the character set . The values (i.e., individual phenotypes) of the original acoustic velocity and attenuation were encoded into a series of binary character strings (i.e., individual genotypes). The binary-to-decimal character conversion enabled the conversion of an individual genotype into an individual phenotype. Substituting different individual phenotypes into the forward model yielded a number of bottom reflection coefficients within a wide-grazing-angle range, which were then converted into reflection losses according to . Because it is very difficult to obtain the reflection loss at the minimum angle and that at the maximum angle in the actual operation at sea, the data in the range of 10–60° were taken as an example for the inversion calculation, as shown in Figure 10.
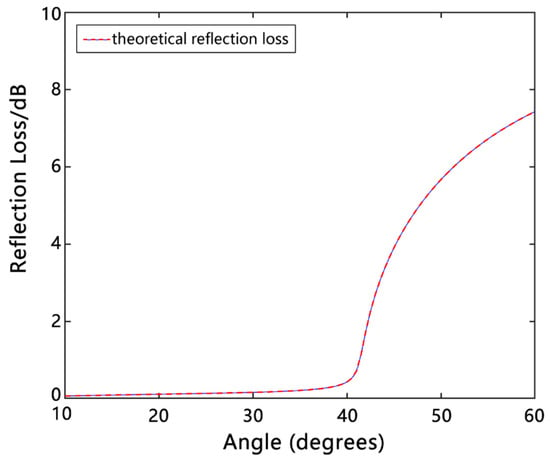
Figure 10.
Theoretical reflection loss curve (the dashed line) for the marine environment.
It is evident from Figure 10 that the reflection losses at small angles differed from those at large angles by several orders of magnitude. To reduce the dynamic range, a further logarithm operation is required, i.e., , to obtain the reflection loss curve after the dynamic range adjustment.
The sum of squared errors of calculated from the theoretical model data and of the inversion model data calculated by substituting different individual phenotypes in the population into the forward model served as the objective function. According to the implementation of the genetic algorithm [], in this inversion, the population size was set to 64, the selection ratio was 0.8, with a crossover probability of 0.5 and a mutation probability of 0.05. For the sake of computing the probability distribution, the number of replicate population runs was set to 50 and the maximum number of inversion iterations for each population was set to 2000.
As shown in Figure 11, after 2000 iterations, the bottom reflection loss–grazing angle curve obtained by inversion (the red asterisks in the figure) and that obtained by theoretical calculation (the green solid line in the figure) are basically consistent. At this time, the corresponding P-wave velocity of the seafloor sediment was 2000.016 m/s and the sound attenuation was 0.4, in agreement with the maximum probability density of the a posteriori probability distribution (as shown in Figure 12).
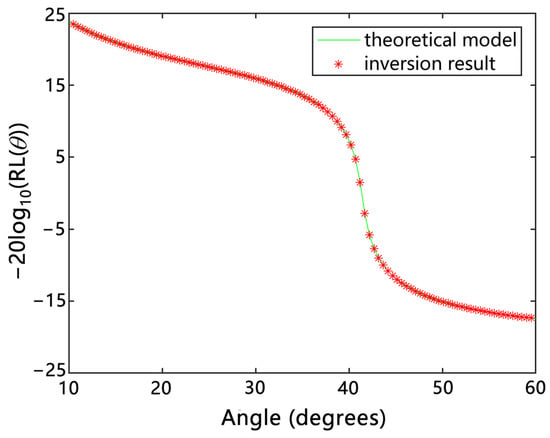
Figure 11.
Comparison between the inversion results (red asterisks) and the theoretical modeling results (green solid line).
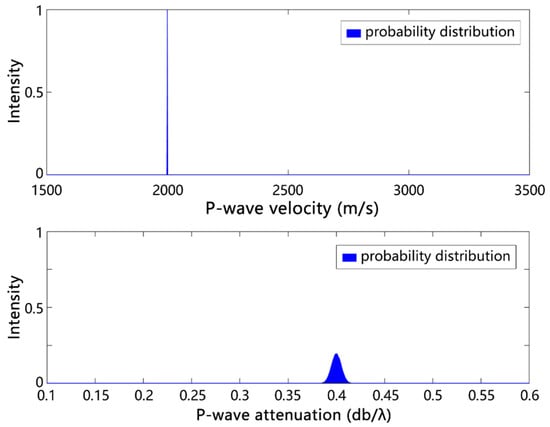
Figure 12.
Schematics of the posteriori probability distributions of inverted acoustic P-wave velocity and sound attenuation.
4.3. Actual Data Inversion
In this section, the detailed data preprocessing process is described and a local geoacoustic parameter optimization algorithm based on the bottom reflection loss within a wide-grazing-angle range is used to enable the inversion of the bottom sediment parameters.
4.3.1. Data Preprocessing
The data receiving device used in this marine experiment was a 96-channel self-contained collector, in which every 24 channels of data were continuously recorded on a data card. Therefore, there were four data cards: Card1, Card2, Card3, and Card4. The data have to be preprocessed to distinguish the bottom reflection signals from different shots. Figure 13 shows some of the valid received acoustic signals in channel 1 on Card1.
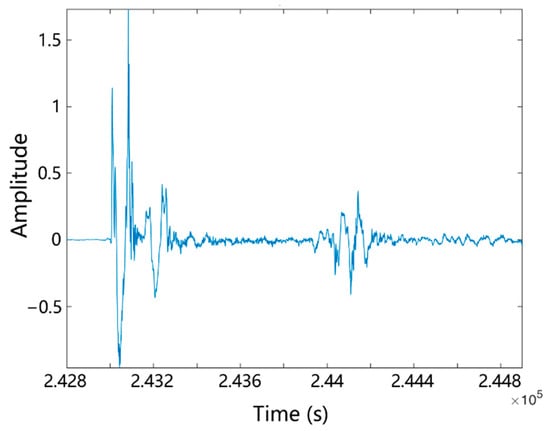
Figure 13.
Some of the valid signals in channel 1 on Card1.
4.3.2. Extraction of Acoustic Signals Based on the Wavelet Transform
The processing of raw data shown in Figure 13 is taken as an example. It is clear that obvious signal noise was present, most of which was high-frequency noise. Therefore, the wavelet transform was considered to filter the high-frequency signal. Based on the wden function in MATLAB software, the “sym8” wavelet was used to decompose the signal. On layer 5 of the decomposition, the heuristic “heursure” threshold selection method was used to low-pass filter and denoise. The denoising results are shown in Figure 14. From the filtered spectrum, it is evident that the high-frequency noise was eliminated and the acoustic signal was well preserved. The frequency band of the effective signal is about 100 to 2000 Hz, which is in the low-to-mid frequency range.
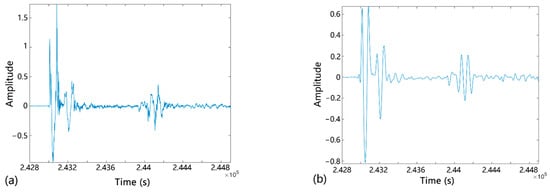
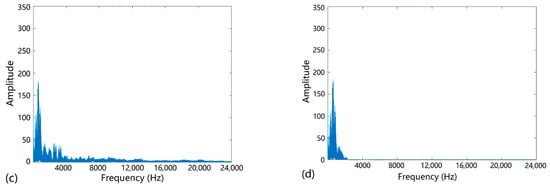
Figure 14.
Comparison among the results of filtering based on the wavelet transform: (a) original signal; (b) low-pass-filtered signal based on the wavelet transform; (c) spectrum of the original signal; (d) spectrum of the low-pass-filtered signal based on the wavelet transform.
4.3.3. Inversion Process
To invert geoacoustic parameters based on the reflection loss from the seafloor within wide grazing angles, it is necessary to extract the direct wave and bottom reflection signal from the signal filtered by the wavelet transform in the previous section. By taking a hydrophone at a receiving point at a depth of 30 m and a horizontal distance of 100 m, for example, the sound ray trace and response times calculated using the ray model [] are presented in Figure 15 and Figure 16, respectively. Evidently, depending on the travel time of arriving at the receiving point, it is possible to distinguish direct waves, seafloor reflection waves, and sea surface reflection waves in the signal, thereby enabling the pickup of direct waves and seafloor reflection waves.
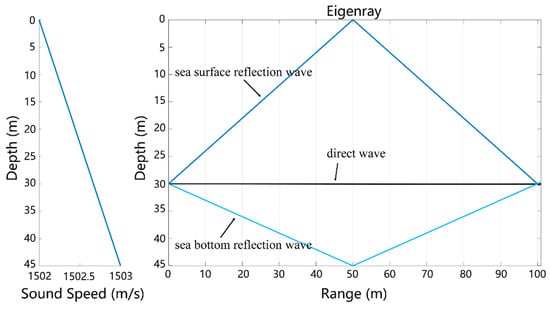
Figure 15.
Calculating eigenrays based on the ray model (horizontal distance = 100 m; depth of the receiving point = 30 m).
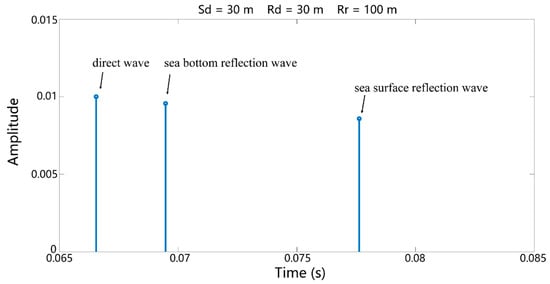
Figure 16.
Calculating response times of eigenray signals based on the ray model (horizontal distance = 100 m; depth of the receiving point = 30 m).
For each shot signal received, the propagation distance was calculated from the depth of the sound source, depth of the receiving point, and travel time. The grazing angle of the seabed reflected wave was obtained according to Figure 5, and the intensity of the bottom reflected signal and the direct signal, denoted by and , were determined in turn. The direct wave is used as the incident wave and the reflected wave is represented by the actual reflected signal. Performing correction to offset expansion losses, the reflection coefficient was then calculated using
where and represent the path lengths of the reflected wave and the direct wave, respectively.
After a series of data-processing operations, the seafloor reflection coefficients at grazing angles of to were obtained, as shown in Figure 17. The reflection coefficient data were further converted into the variables of the objective function of inversion (i.e., reflection losses) by using , as shown in Figure 18.
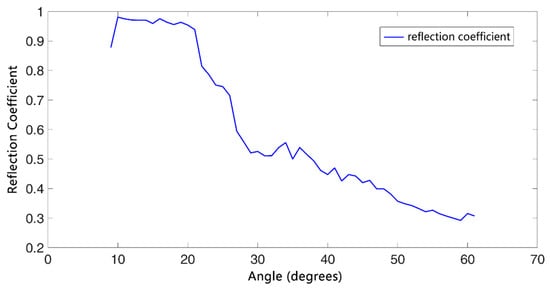
Figure 17.
Actual reflection coefficients.
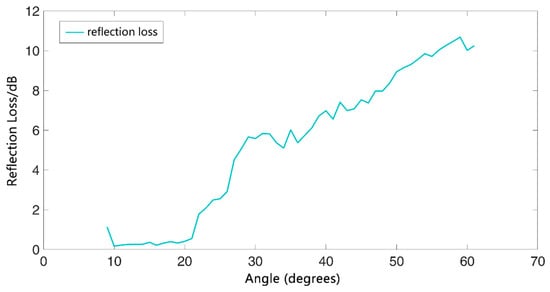
Figure 18.
Actual reflection losses.
It is assumed that the inversion model is a horizontal seafloor because of the flat seafloor in the study area. The known marine environmental parameters in the inversion were set up based on information such as the sound velocity profile of the seawater and the density measured after sediment sampling. The main frequency of the sound source was ~600 Hz. The acoustic velocity in the seawater was defined by the sound velocity profile. The density of the seawater was 1000 kg/m3 and the density of seafloor sediments was 1900 kg/m3. The parameters to be inverted were the acoustic P-wave velocity and acoustic attenuation of the seafloor sediments. Based on existing experience and data, the range of acoustic velocity to be inverted was set to 1400–2000 m/s and the number of individuals in this range was 1001; the range of acoustic attenuation to be inverted was set to 0.01–1.0 and the number of individuals in this range was 1001.
Based on the implementation of the genetic algorithm mentioned above, the population size was set to 64 in the inversion, the selection ratio was 0.8, with a crossover probability of 0.8 and a mutation probability of 0.05, and the maximum number of inversion iterations was 2000. For the sake of computing the probability distribution, the number of replicate population runs was equal to 50. Inversion based on the above parameters yielded the reflection loss curve shown in Figure 19, where the blue one represents the inverted reflection loss while the green one represents the actual reflection loss.
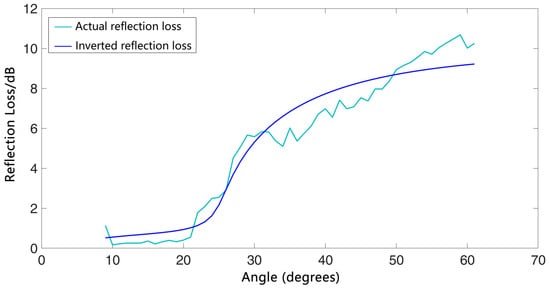
Figure 19.
Inverted reflection loss curve and actual reflection loss curve.
In this inversion, the optimal seafloor acoustic velocity was and the sound attenuation was . To assess the reliability of the inversion process, a posteriori probability distribution calculation on the inversion results was conducted as shown in Figure 20. It can be seen that the peak regions of the posteriori probability distribution were consistent with the inversion results.
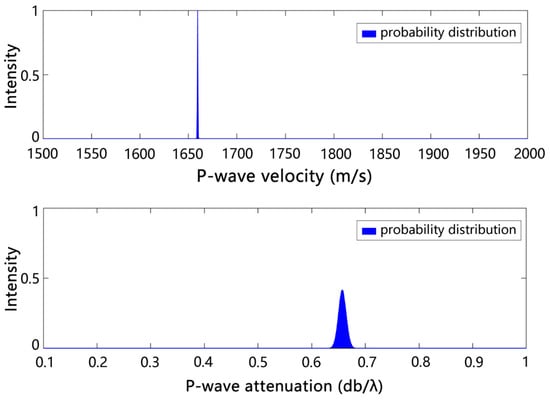
Figure 20.
Posterior probability distributions of inversion parameters.
5. Discussion
From the two curves of bottom reflection loss obtained in Section 4.1, it can be seen that, when the grazing angle range covered by the extracted bottom reflection loss is large, different geoacoustic parameters can be effectively distinguished to enable the inversion of the seafloor geoacoustic parameters. Therefore, in actual data acquisition in this study, the sound sources were placed at different distances and a vertical linear array was used for signal reception. The main purpose was to make the seafloor reflected signal cover a wider grazing-angle range to enhance the accuracy of the inversion.
By means of the numerical model test example, we give the process of inversion of acoustic parameters of submarine sediments based on seafloor reflection loss. The results indicate that the inversion of the bottom acoustic P-wave velocity and acoustic attenuation can be achieved by using the wavenumber integration method for the forward simulation of the bottom reflection loss under wide-grazing-angle conditions and iterative calculation with a genetic algorithm.
At the end, we carried out an actual marine local geoacoustic parameters inversion experiment. The experimental results reveal the following: (1) The experimental scheme enables effective acquisition of bottom reflection signals within a wide-grazing-angle range and the range of grazing angle for actual valid data was –. (2) With the seafloor acoustic velocity and sound attenuation as parameters to be inverted, the inversion based on the wavenumber integration method and genetic algorithm yielded the following sediment parameters for the clayey sandy area of the South Yellow Sea: acoustic velocity and sound attenuation . Furthermore, the reliability of the inversion results was verified through posterior probability distribution. We compared the locally inverted results based on reflection losses with the measurements conducted by other scholars in the same sea area [,]. The results obtained in this study are consistent with previous studies and more specific.
6. Conclusions
The geoacoustic inversion method is currently an important object of research in detection of seafloor sediment characteristics. To address the accuracy problem existing in acoustic field simulation of local geoacoustic inversion, a method of calculating the bottom reflection loss within a wide-grazing-angle range based on the wavenumber integration method was studied. At the same time, by using the genetic algorithm, the seafloor reflection-signal-based local geoacoustic parameters were inverted. Furthermore, a local acoustic detection data acquisition method based on a sparker source and a fixed vertical array was investigated. The above methods were then used to acquire the local acoustic data within a wide-grazing-angle range in the South Yellow Sea and invert the seafloor geoacoustic parameters.
The method proposed in this study presents three primary advantages over existing geoacoustic inversion techniques. (1) During the data collection process, the vessel’s engine remains off, allowing for data to be gathered passively via drifting. This approach minimizes the interference of vessel noise in experimental results. Furthermore, it facilitates the acquisition of the seafloor’s reflection loss over a broad range of grazing angles, thereby providing adequate raw data for geoacoustic inversion. (2) Our research employs the wavenumber integration method for sound field modeling. This approach delivers a more accurate computation of local sound propagation and establishes a more precise sound field model compared to the normal-mode method. (3) The utilization of the genetic algorithm for inversion is well-suited to optimizing multi-parameter non-linear problems, leading to higher computational efficiency and accuracy in geoacoustic inversion.
This study introduces a novel, accurate, and efficient approach to geoacoustic inversion. The proposed method is particularly well-suited for addressing geoacoustic inversion challenges within localized areas of shallow seas. Both the modeling experiment results and actual data-processing results demonstrate the feasibility of estimating geoacoustic parameters of seafloor sediments using the wide-grazing-angle bottom reflection loss curve. In addition, related actual inversion results for clayey sandy sediment in the South Yellow Sea show that the seafloor acoustic velocity was and the sound attenuation was . The inversion results closely align with prior inversion results derived from empirical formulas applied in the same region. Furthermore, the peak regions of the posteriori probability distribution were also consistent with the inversion results. These two aspects prove the effectiveness of the geoacoustic inversion method proposed in this study.
Author Contributions
Conceptualization, X.Z. (Xiaobo Zhang) and Z.W.; methodology, X.Z. (Xinghua Zhou) and Y.M.; software, Z.W.; validation, Y.M.; formal analysis, Z.W.; investigation, Y.M.; resources, G.K. and B.L.; data curation, G.K. and B.L.; writing—original draft preparation, Z.W.; writing—review and editing, Y.M. and Z.W.; visualization, Y.M. and Z.W.; supervision, Y.M.; project administration, X.Z. (Xiaobo Zhang); funding acquisition, X.Z. (Xiaobo Zhang). All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Shandong Provincial Natural Science Foundation (No. ZR2020QD071), the National Natural Science Foundation of China (No. 42106072).
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
Sincere thanks are owed to all the workers on the ship Xiangyanghong 81 for their help during the experiment.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ingenito, F. Measurement of mode attenuation coefficients in shallow water. J. Acoust. Soc. Am. 1973, 53, 858–863. [Google Scholar] [CrossRef]
- Rajan, S.D. Waveform inversion for the geoacoustic parameters of the ocean bottom. J. Acoust. Soc. Am. 1992, 91, 3228–3241. [Google Scholar] [CrossRef]
- Yang, K.D. A Study on Matched Field Processing of Underwater Acoustic Signals. Ph.D. Thesis, Northwestern Polytechnical University, Xi’an, China, 2003. [Google Scholar]
- Ren, Q.Y. Research on Techniques of Bottom Parameters Acquirement in Shallow Water. Master’s Thesis, Harbin Engineering University, Harbin, China, 2009. [Google Scholar]
- Collins, M.D.; Kuperman, N.A.; Schmidt, H. Nonlinear inversion for ocean-bottom properties. J. Acoust. Soc. Am. 1992, 92, 2770–2883. [Google Scholar]
- Li, F.H.; Zhang, R.H. Bottom sound speed and attenuation inverted by using pulsed waveform and transmission loss. Acta Acust. 2000, 25, 297–302. [Google Scholar]
- Li, Z.L.; Yan, J.; Li, F.H.; Guo, L.H. Inversion for the sea bottom acoustic parameters by using the group time delays and amplitude of normal mode. Acta Acust. 2002, 27, 487–491. [Google Scholar]
- Shi, J.J.; Dosso, S.E.; Sun, D.J.; Liu, Q.Y. Geoacoustic inversion of the acoustic-pressure vertical phase gradient from a single vector sensor. J. Acoust. Soc. Am. 2019, 146, 3159–3173. [Google Scholar] [CrossRef]
- Dosso, S.E.; Jan, D. Bayesian matched-field geoacoustic inversion. Can. Acoust. 2007, 35, 178–179. [Google Scholar]
- Holland, C.W.; Osler, J. High-resolution geoacoustic inversion in shallow water: A joint time-and frequency-domain technique. J. Acoust. Soc. Am. 2000, 107, 1263–1279. [Google Scholar] [CrossRef]
- Koch, R.A.; David, P.K. Geoacoustic inversion with ships as sources. J. Acoust. Soc. Am. 2005, 117, 626–637. [Google Scholar]
- Potty, G.P.; Miller, J.H. Tomographic inversion for sediment parameters in shallow water. J. Acoust. Soc. Am. 2000, 108, 973–986. [Google Scholar]
- Potty, G.R.; Miller, J.H.; Dahl, P.H.; Lazauski, C.J. Geoacoustic inversion results from the ASIAEX East China Sea experiment. IEEE J. Oceanic Eng. 2004, 29, 1000–1010. [Google Scholar]
- Holland, C.W.; Dettmer, J.; Dosso, S.E. Remote sensing of sediment density and velocity gradients in the transition layer. J. Acoust. Soc. Am. 2005, 118, 163–177. [Google Scholar]
- Spofford, C.W. Inference of geo-acoustic parameters from bottom loss data. In Bottom-Interacting Ocean Acoustics; William, A.K., Finn, B.J., Eds.; Springer: New York, NY, USA, 1980; pp. 159–171. [Google Scholar]
- Yang, K.D.; Ma, Y.L. A geoacoustic inversion method based on bottom reflection signals. Acta Phys. Sin. 2009, 58, 1798–1805. [Google Scholar] [CrossRef]
- Chapman, N.R. Perspectives on geoacoustic inversion of ocean bottom reflectivity data. J. Mar. Sci. Eng. 2016, 4, 61. [Google Scholar] [CrossRef]
- Liu, H.; Yang, K.D.; Ma, Y.L. Synchrosqueezing transform for geoacoustic inversion with air-gun source in the East China Sea. Appl. Acoust. 2020, 169, 107460. [Google Scholar]
- Rubano, L.A. Acoustic propagation in shallow water over a low velocity bottom. J. Acoust. Soc. Am. 1980, 67, 1608–1613. [Google Scholar]
- Zhou, J.X. Normal mode measurements and remote sensing of sea-bottom sound velocity and attenuation in shallow water. J. Acoust. Soc. Am. 1985, 78, 1003–1009. [Google Scholar]
- Zhou, J.X.; Zhang, X.Z.; Rogers, P.H.; Jarzynski, J. Geoacoustic parameters in a stratified sea bottom from shallow water acoustic propagation. J. Acoust. Soc. Am. 1987, 82, 2068–2074. [Google Scholar] [CrossRef]
- Becker, K.M.; Rajan, S.D.; Frisk, G.V. Results from the geoacoustic inversion techniques workshop using modal inverse methods. IEEE J. Oceanic Eng. 2003, 28, 331–341. [Google Scholar]
- Potty, G.P.; Miller, J.H. Dispersion of broadband acoustic normal modes in the context of long range sediment tomography. In Acoustic Sensing Techniques for the Shallow Water Environment; Caiti, A., Chapman, N.R., Hermand, J.P., Jesus, S.M., Eds.; Springer: New York, NY, USA, 2006; pp. 57–72. [Google Scholar]
- Guo, X.L.; Yang, K.D.; Ma, Y.L. A far distance wideband geoacoustic parameter inversion method based on a modal dispersion curve. Acta Phys. Sin. 2015, 64, 174–302. [Google Scholar]
- Yang, J.; Jackson, D.R.; Tang, D.J. Mid-frequency geoacoustic inversion using bottom loss data from the Shallow Water 2006 Experiment. J. Acoust. Soc. Am. 2012, 131, 711–1721. [Google Scholar] [CrossRef]
- Tolstoy, A. Using matched field processing to estimate shallow-water bottom properties from shot data in the Mediterranean Sea. IEEE J. Oceanic Eng. 1996, 21, 471–479. [Google Scholar]
- Tolstoy, A.; Chapman, N.R.; Brooke, G. Workshop ‘97: Benchmarking for geoacoustic inversion in shallow water. J. Comput. Acoust. 1998, 6, 1–28. [Google Scholar] [CrossRef]
- Tan, B.A.; Gerstoft, P.; Yardim, C.; Hodgkiss, W.S. Broadband synthetic aperture geoacoustic inversion. J. Acoust. Soc. Am. 2013, 134, 312–322. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.T. Inversion of Sea Bottom Geoacoustic Parameters Using Underwater Explosion at Fixed Sea Depth. Master’s Thesis, Third Institute of Oceanography, MNR, Xiamen, China, 2015. [Google Scholar]
- Heaney, K.D. Rapid geoacoustic characterization using a surface ship of opportunity. IEEE J. Oceanic Eng. 2004, 29, 88–99. [Google Scholar] [CrossRef]
- Ohta, K.; Okabe, K.; Morishita, I.; Frisk, G.V.; Turgut, A. Modal inversion analysis for geoacoustic properties of the New Jersey continental shelf in the SWAT experiments. IEEE J. Oceanic Eng. 2009, 34, 526–538. [Google Scholar]
- Li, Y.; Sun, Y.; Liu, Y. Electrohydraulic Effect and Sparker Source: Current Situation and Prospects. High Volt. Eng. 2021, 47, 753–765. [Google Scholar]
- Schaefer, R.B.; Flynn, D. The development of a sonobuoy using sparker acoustic sources as an alternative to explosive SUS devices. In Proceedings of the Oceans ‘99. MTS/IEEE. Riding the Crest into the 21st Century. Conference and Exhibition, Seattle, WA, USA, 13 September 1999. [Google Scholar]
- Tollefsen, D.; Wilmut, M.J.; Chapman, R. Inversions of horizontal and vertical line array data for the estimation of geoacoustic model parameters. In Acoustic Sensing Techniques for the Shallow Water Environment; Caiti, A., Chapman, N.R., Hermand, J., Jesus, S.M., Eds.; Springer: New York, NY, USA, 2006; pp. 309–320. [Google Scholar]
- Tollefsen, D.; Dosso, S.E.; Knobles, D.P. Ship-of-opportunity noise inversions for geoacoustic profiles of a layered mud-sand seabed. IEEE J. Oceanic Eng. 2019, 45, 189–200. [Google Scholar] [CrossRef]
- Qiu, H.B.; Yang, K.D. Performance of the geoacoustic inversion results for differential array shape. Tech. Acoust. 2009, 28, 151–152. [Google Scholar]
- Holland, C.W. Seabed reflection measurement uncertainty. J. Acoust. Soc. Am. 2003, 114, 1861–1873. [Google Scholar] [CrossRef]
- Dettmer, J.; Dosso, S.E.; Holland, C.W. Full wave-field reflection coefficient inversion. J. Acoust. Soc. Am. 2007, 122, 3327–3337. [Google Scholar]
- Luo, W.Y.; Yu, X.L.; Yang, X.F.; Zhang, R.H. Analytical solution based on the wavenumber integration method for the acoustic field in a Pekeris waveguide. Chinese Phys. B 2016, 25, 044302. [Google Scholar] [CrossRef]
- Quijano, J.E.; Dosso, S.E.; Dettmer, J. Bayesian geoacoustic inversion using wind-driven ambient noise. J. Acoust. Soc. Am. 2012, 131, 2658–2667. [Google Scholar]
- Gerstoft, P. Inversion of Seismoacoustic Data using genetic algorithms and a posteriori probability distributions. J. Acoust. Soc. Am. 1994, 95, 770–782. [Google Scholar] [CrossRef]
- Gerstoft, P. Inversion of acoustic data using a combination of genetic algorithms and the Gauss-Newton approach. J. Acoust. Soc. Am. 1995, 97, 2181–2190. [Google Scholar] [CrossRef]
- Jiang, Y.; Chapman, N.R.; DeFerrari, H.A. Geoacoustic inversion of broadband data by matched beam processing. J. Acoust. Soc. Am. 2006, 119, 3707–3716. [Google Scholar]
- Zhou, J.X.; Zhang, X.Z.; Knobles, D.P. Low-frequency geoacoustic model for the effective properties of sandy seabottoms. J. Acoust. Soc. Am. 2009, 125, 2847–2866. [Google Scholar]
- Lu, B.; Li, G. The comparing of seabed sediment acoustic-physical properties in the Yellow Sea, the East China Sea and northern the South China Sea. Ocean. Technol. 2005, 24, 28–33. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).