Abstract
When construction materials are exposed to the atmospheric environment, they are subject to deterioration, which varies according to the time period of exposure and the location. A tool named Dose–Response Functions (DRFs) has been developed to estimate this deterioration. DRFs use specific air pollutants and climatic parameters as input data. Existing DRFs in the literature use only ground-based measurements as input data. This fact constitutes a limitation for the application of this tool because it is too expensive to establish and maintain such a large network of ground-based stations for pollution monitoring. In this study, we present the development of new DRFs using only satellite data as an input named Satellite Sensed Data Dose-Response Functions (SSD-DRFs). Due to the global coverage provided by satellites, this new tool for monitoring the corrosion/soiling of materials overcomes the previous limitation because it can be applied to any area of interest. To develop SSD-DRFs, we used measurements from MODIS (Moderate Resolution Imaging Spectroradiometer) and AIRS (Atmospheric Infrared Sounder) on board Aqua and OMI (Ozone Monitoring Instrument) on Aura. According to the obtained results, SSD-DRFs were developed for the case of carbon steel, zinc, limestone and modern glass materials. SSD-DRFs are shown to produce more reliable corrosion/soiling estimates than “traditional” DRFs using ground-based data. Furthermore, research into the development of the SSD-DRFs revealed that the different corrosion mechanisms taking place on the surface of a material do not act additively with each other but rather synergistically.
1. Introduction
When various materials are exposed to the air we breathe, they suffer wear and tear from both air quality and the wind depending on the time of exposure and location. To deal with this problem, maintenance procedures are used, which constitute 4–5% of the global GDP (gross domestic product) [1]. The role of air pollution, in relation to climatic conditions, in the deterioration of construction materials exposed outdoors has already been recognized in the literature [2,3,4,5,6]. To model this deterioration, a tool named Dose–Response Function (DRF) has been developed. Firstly, this tool was developed after laboratory deterioration experiments in a controlled environment. Before the 2000s, it was found that the main air pollutant dominating the corrosion/soiling effect was SO2. So, the main research focused on the effect of SO2 on different materials. The presence of additional contaminants in the atmospheric environment has led to the study of their participation in the corrosion/soiling effect on materials such as SO2. After several studies, it was shown that NO2 and O3 contribute to corrosion/the soiling effect. The difference is that there is no direct chemical reaction with materials, but their presence on the surface of the material has a catalytic reaction with the presence of SO2. After the 2000s, with the desulfurization of the atmosphere, it was seen that the corrosion/soiling problem was a multi-factorial effect [7,8,9,10,11,12,13,14,15,16,17,18,19]. Nowadays, DRFs quantify the corrosion/soiling effect on materials using the concentration of specific air pollutants, such as SO2, NO2, O3, HNO3, PM10 (particulate matter with an aerodynamic diameter equal to or less than 10 µm) and meteorological parameters such as temperature, relative humidity and precipitation [20,21,22,23,24,25,26,27].
Over the years, several projects have been carried out with exposure campaigns to develop new DRFs or improve existing ones. One of these projects with a significant contribution to this effort is called the “International Co-operative Programme on Effects on Materials including Historic and Cultural Monuments (ICP Materials)”. In this study, we use some of the DRFs developed in the framework of ICP Materials, specifically for the materials carbon steel, zinc, limestone and modern glass [23,28]. The common characteristic of all existing DRFs in the literature is that they use ground-based measurements of air pollutants and meteorological parameters. This feature limits their application to cases where the necessary ground-based data are available.
This research attempts to overcome this limitation by developing new deterioration modeling tools that make use of satellite data that have the advantage of near-global coverage. Such satellite data are recorded by remote sensing instruments on environmental satellites. All these available satellite data can be used in material deterioration modeling.
This study presents the development of these new deterioration modeling tools that use satellite data to quantify corrosion/soiling in structural materials. To identify these new DRFs, the term Satellite-Sensed Data Dose–Response Functions or SSD-DRFs is proposed.
2. Materials and Methods
2.1. Object of Study
The materials studied in this research are the following:
- Carbon steel;
- Zinc;
- Limestone;
- Modern glass.
These materials were chosen because they are widely used in modern constructions. Additionally, limestone and zinc are the basic materials in cultural heritage monuments. Within the framework of the ICP Materials and MULTI-ASSESS (model for multi-pollutant impact and assessment of threshold levels for cultural heritage) projects, DRFs were developed for each material. These DRFs are presented below ([23] Equations (1)–(3); [28] Equation (4)):
DRFs.
Carbon steels
Zinc
Limestone
Modern glass
where
ML = mass loss (the difference in the specimen’s initial mass minus the remaining mass after removing its corroded part), g m−2;
R = surface recession, µm (absolute values);
H = haze, %;
t = exposure time, in days;
Rh = relative humidity, %—annual average;
Rh60 = Rh − 60 when Rh > 60, 0 otherwise;
T = mean annual temperature, °C;
[SO2] = mean annual concentration, µg m−3;
[NO2] = mean annual concentration, µg m−3;
[HNO3] = mean annual concentration, µg m−3;
Rain = precipitation amount, mm year−1—total rain amount in one year;
PM10 = mean annual concentration, µg m−3;
[H+] = mean annual concentration, mg L−1. The unit for [H+] is not the normal one (mol L−1) used for this denomination and the relationship between pH and [H+] is therefore [H+] = 1007.97 × 10−pH ≈ 103−pH here.
In the case of [HNO3], if in situ measurements are unavailable, then the concentration is estimated by Equation (5) [22].
where
[O3] = mean annual concentration, µg m−3.
In the above DRFs, and all other available DRFs in the literature, it is clearly shown that they rely solely on the availability of ground-based data to provide deterioration estimates of the different materials. This is a major limitation of the utility of these models because, among other things, it is difficult and expensive to deploy the necessary network of ground-based stations at all sites of interest. The authors believe that the solution to this may be the development of SSD-DRFs. Nowadays, the multitude of different satellite data enables us to develop new techniques and approaches.
2.2. Satellite Remote Sensing Data
Satellite air quality data from the Ozone Monitoring Instrument (OMI), the Atmospheric Infrared Sounder (AIRS) and the Moderate Resolution Imaging Spectroradiometer (MODIS) were used for this purpose. Specifically, concentration data for O3, NO2 and SO2 were collected by OMI [29,30,31], air temperature (Temp) data were collected by AIRS [32] and Aerosol Optical Depth (AOD) data were collected by MODIS [33]. In the case of relative humidity (RH), reanalysis data from the European Centre for Medium-Range Weather Forecasts (ECMWF) were used. This fact was deemed necessary since satellite-derived relative humidity data show little correlation with ground-based data.
Data were collected for the same time periods and sites as the ICP Materials exposure campaigns. Table 1 shows the time periods of the exposure campaigns, and all the cities where the campaigns took place are shown in Table 2.

Table 1.
Time periods of ICP Materials exposure campaigns.

Table 2.
ICP Materials exposure sites for time periods (2005–2006, 2008–2009, 2011–2012, 2014–2015, 2017–2018) [34,35,36,37,38].
In addition to satellite and reanalysis data, corrosion/soiling results from the above-mentioned exposure campaigns were collected for the needs of the SSD-DRFs being developed. The corrosion/soiling results were used to develop and test the new SSD-DRFs [39,40,41,42,43,44,45,46].
3. Results
Multiple regression analysis, a supervised machine learning technique, was performed to develop the SSD-DRFs. Due to the non-linearity of the corrosion/soiling effect, and the complexity that presents such problems from a study point of view, an attempt was made to convert the non-linear problem into a linear one. As mentioned earlier, the corrosion/soiling effect is a multi-factorial effect. If we consider that observed deterioration results from the synergistic effect of all meteorological and air pollution parameters, we can consider that the non-linear Equation (6) describes the relationship between them.
where
D = deterioration;
[Xi]j = corrosion/soiling parameters, where i denotes different parameters or products of parameters and j denotes the exponent of the i term.
If we calculate the logarithm of Equation (6), then the following relationship is obtained:
When trying to model the response using a single predictor or more variables, Pearson’s correlation is used to estimate a linear correlation coefficient between the predictors and the target. In our case, the meteorological parameters and air pollutants mentioned above are the predictive factors and the target is the corrosion/soiling of the material. One of the first sources of non-linearity is due to different interactions between predictors. For instance, the synergistic effects on corrosion between NO2, O3 and SO2, combined with the relative humidity, affect the amount and form of water available on a material’s surface. To examine the linear relationship of the interaction between parameters and corrosion, the interaction terms must be multiplied by themselves.
In addition, in this study, an attempt was made to insert SSD-DRFs, a term for pollutants’ diffusivity, on the material surfaces, as it is known that atmospheric corrosion can occur either in a dry environment (low humidity) or in a wet environment (high humidity). In the case of high humidity, a thin film of water forms on the material’s surface (Figure 1). Air pollutants can diffuse into this water film, resulting in an acceleration of the corrosion effect [47]. This mechanism is modelled in the SSD-DRFs by incorporating the diffusion coefficient parameter into them.
Figure 1.
Thin film of water formation on the material’s surface.
As has been shown, the diffusion coefficient, D, in a single diffusion mode obeys an Arrhenius-like behavior, as seen in Equation (8):
where the activation energy E and the pre-exponential factor D0 are essentially temperature independent, and KB is the Boltzmann constant. From Equation (8), it is possible to calculate the values of the activation energy E through the slope of the plot of lnD vs. 1/T [48]. In the following years, many experimental studies were carried out using infrared laser resonant desorption (LRD) techniques to calculate diffusion coefficients in ice film [49,50,51,52,53,54,55]. The results from these studies confirmed the linear relationship between lnD and 1/T [56]. This result clearly suggests that Equation (8) can be used to estimate the diffusion coefficient at any temperature when the diffusion coefficient at two different temperatures is known.
Varotsos and Zellner [56] used the above studies [53,54] and found a significant result, namely that there is a linear relationship between the natural logarithm of the pre-exponential factor D0 and the activation energy E (i.e., lnD0 vs. E). Summarizing all the above studies, it is concluded that it is possible to estimate the diffusion coefficients of other important species in ice. Based on the same theory, it is possible to calculate the diffusion coefficient of any important species we want in the thin film of water on the material’s surface. Thus, if the diffusion coefficient is known at two different temperatures, from the slope of the lnD vs. 1/T plot, it is possible to calculate the diffusion coefficient at any temperature. The diffusion coefficients of O3 [57], NO2 [58] and SO2 [59] in water, at different temperatures, are available from laboratory experiments that are presented in the literature. The resulting equations for the diffusion coefficients are the following (Equations (9)–(11)):
The resulting diffusion coefficients from Equations (9)–(11) for each site in the exposure campaigns were multiplied by the corresponding atmospheric pollutant concentration, as derived from satellite data. After multiplications between all parameters, 36 products were calculated. These products were used to investigate the correlation of each of them with the corrosion/soiling experimental results of each material by calculating the Pearson’s correlation coefficient. According to the obtained results, different parameters showed a linear correlation with the corrosion/soiling in each material. The parameters that correlate well with the corrosion/soiling of each material have been used in SSD-DRFs development.
Table 3, Table 4, Table 5 and Table 6 present the results of Pearson’s correlation coefficient calculations between environmental parameters and corrosion/soiling estimates. For the case of carbon steel, Table 3, it is evident that this material presents the highest correlation coefficients with relative humidity (RH), parameters, the product of RH with NO2 and AOD (Aerosol Optical Depth) concentrations, as well as the product of RH2, NO2 and SO2 concentrations. The asterisks denote the statistical significance level of the obtained correlation coefficients. The parameter N in the following tables denotes the number of samples of experimental corrosion/soiling values used in each case.

Table 3.
Chosen parameters for carbon steel mass loss SSD-DRF.

Table 4.
Chosen parameters for zinc mass loss SSD-DRF.

Table 5.
Chosen parameters for limestone mass loss SSD-DRF.

Table 6.
Chosen parameters for modern glass soiling SSD-DRF.
For the case of zinc (Table 4), it is evident that this material presents the highest correlation coefficients with the parameters of RH and the product of RH with the concentrations of O3 and SO2.
For the case of limestone (Table 5), it is obvious that this material, in all cases, presents low values of correlation coefficients; however, we have considered the highest of them, i.e., RH and the product of RH with O3 concentration. Both are statistically significant at the 0.05 level. Analyzing the obtained results, it was evident that these two parameters could not adequately model the limestone’s corrosion, so it was decided that the product of RH with SO2 concentration should also be used, which, according to the literature [4], is an air pollutant that affects limestone’s corrosion.
For the case of modern glass (Table 6), it was found that this material presents the highest correlation coefficients with the climatic parameter of temperature (Temp), the air quality parameter of AOD and the products of the SO2, NO2 and O3 concentrations with their diffusion coefficients, respectively.
After selecting the parameters to be used to develop SSD-DRFs, linear regression analysis was applied using the Sklearn library in python. To apply this tool, the entire data set was split into train and test sets in a ratio of 80–20% and with the help of a loop we run regression analysis 10,000 times for each material. Each run resulted in 10,000 different sets of constants and coefficients for the parameters. In the next step, we kept only the results where all parameters were positive, because a negative parameter would mean a decrease in corrosion with increasing pollutant concentration, which is contrary to current knowledge. In the end, from the remaining results, we selected the set of a coefficient and constant value which showed similar accuracy in train/test sets and the whole data set.
The following list gives the mathematical formulation of the SSD-DRF of each material (Equations (12)–(15)):
Carbon steel
Zinc
Limestone
Modern glass
These functions were then used to calculate the corrosion/soiling estimates of the different materials at each different site during all exposure periods. Table 7 gives the Pearson’s correlation coefficient obtained by investigating the linear correlation between the SSD-DRFs corrosion/soiling estimates and the experimental data. The size of the paired samples used for each material is given in the second line of Table 7.

Table 7.
Pearson correlation coefficients between SSD-DRFs estimates and experimental data.
Table 8 shows the Pearson’s correlation coefficients between G-DRFs and experimental data as well as SSD-DRFs and experimental data, where the name G-DRFs refers to the existing DRFs, Equations (1)–(4), which use ground-based data as inputs. The size of the paired samples used for each material is given in the third line of Table 8.

Table 8.
Pearson correlation coefficients between G-DRFs and experimental data, SSD-DRFs and experimental data.
Figure 2, Figure 3, Figure 4 and Figure 5 show the observed experimentally (OBS) corrosion/soiling values estimated using SSD-DRFs (SSD-DRFs) and estimated using G-DRFs (G-DRF) for the case of carbon steel, zinc, limestone and modern glass, respectively, at the indicated sites.
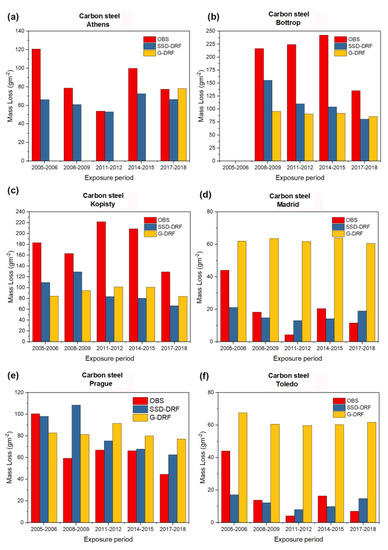
Figure 2.
The experimentally observed mass loss of carbon steel (red bars), the estimated mass loss of carbon steel using SSD-DRF (blue bars) and the estimated mass loss of carbon steel using G-DRF (yellow bars) for case (a) Athens, (b) Bottrop, (c) Kopisty, (d) Madrid, (e) Prague and (f) Toledo after five different one-year exposure periods (2005–2006, 2008–2009, 2011–2012, 2014–2015, 2017–2018). The missing yellow bars in the case of Athens are due to the lack of the necessary ground-based data necessary for the application of G-DRF.
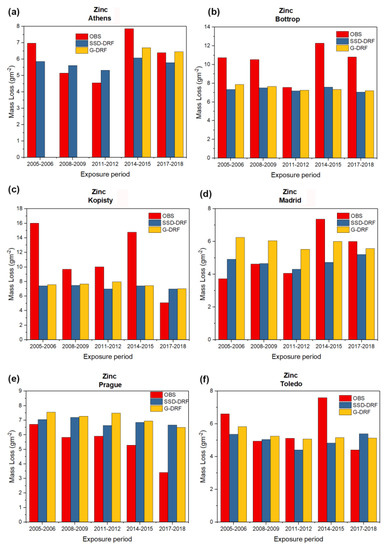
Figure 3.
As in Figure 2, but for the case of zinc. (a) Athens, (b) Bottrop, (c) Kopisty, (d) Madrid, (e) Prague and (f) Toledo.
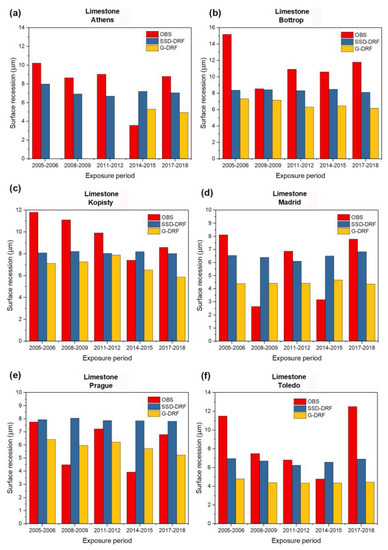
Figure 4.
As in Figure 2, but for the case of Limestone. (a) Athens, (b) Bottrop, (c) Kopisty, (d) Madrid, (e) Prague and (f) Toledo.
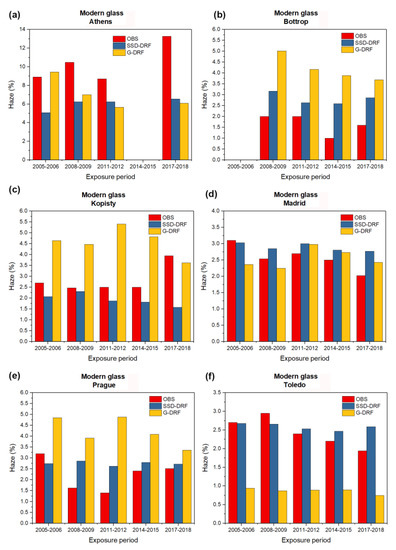
Figure 5.
As in Figure 2, but for the case of modern glass haze. (a) Athens, (b) Bottrop, (c) Kopisty, (d) Madrid, (e) Prague and (f) Toledo. The gaps at Athens and Bottrop at the exposure periods of 2005–2006 and 2008–2009, respectively, are due to a lack of experimental data.
Figure 6 presents, in the form of box plots, the statistics of the relative differences between SSD-DRFs and G-DRF estimates in experimentally obtained corrosion/soiling values.
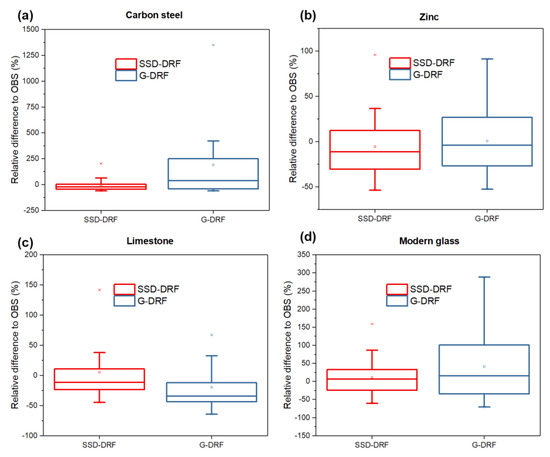
Figure 6.
The relative differences between corrosion/soiling estimates calculated using SSD-DRFs and G-DRFs and experimentally obtained data for the case of (a) carbon steel mass loss, (b) zinc mass loss, (c) limestone recession and (d) modern glass haze.
4. Discussion and Conclusions
According to Table 8, the corrosion/soiling estimates produced by SSD-DRFs show a better correlation with the experimental results than the estimates produced by G-DRFs for all materials studied. This means that the SSD-DRFs developed using only satellite data improve the corrosion/soiling estimation results compared to the already available G-DRFs, which use only ground-based data. This conclusion is also supported by the box plots presented in Figure 6. According to these results, the populations with relative differences between the corrosion/soiling estimates, calculated using SSD-DRFs, and experimentally obtained data have a smaller range, excluding the extreme values, and in most cases their medians are closer to zero than the same results estimated using G-DRFs.
Another remark is related to data availability. According to Table 7, the sizes of the available sample pairs of carbon steel, zinc, limestone and modern glass are 110, 112, 105 and 97, respectively. As for G-DRFs, their usability is limited by the availability of ground-based data. Due to the lack of necessary data, the sizes of the available sample pairs given in Table 8 are 55, 73, 55 and 71 for carbon steel, zinc, limestone and modern glass, respectively. This means that the applicability of SSD-DRFs increases for the various materials by about 200%, 150%, 190% and 135%, respectively. This is confirmed by the graphs plotted in Figure 2, Figure 3 and Figure 4 for the case of Athens. Yellow bars indicating G-DRFs estimates of carbon steel, zinc and limestone corrosion are missing for the exposure periods 2005–2006, 2008–2009 and 2011–2012 (and 2014–2015 carbon steel only) due to a lack of some necessary ground-based data. In contrast, the availability of satellite data meets the data needs of SSD-DRFs to enable continuous monitoring of the corrosion/soiling.
It should be mentioned that satellite data also offer an almost global coverage, which means that the proposed SSD-DRFs can be directly applied to almost any part of the globe according to user needs (e.g., cultural heritage managers, stakeholders, policy makers, etc.). In addition, this new tool offers the potential to produce continuous large-scale corrosion/soiling mapping, without the need for ground-based meteorological and pollution networks. Thus, the SSD-DRFs tool could act as a global corrosion/soiling monitoring system capable of identifying “hot spots” across the planet and/or providing warnings about sensitive areas at an early stage, offering valuable time to address any type of problematic status.
Although we have historical air pollution data, more work needs to be carried out to improve the knowledge and accuracy of corrosion/soiling estimation obtained with satellite data to contribute, inter alia, to the achievement of the Sustainable Development Goals—UN 2030 Agenda [60,61].
Author Contributions
Conceptualization, J.C. and G.K.; methodology, J.C. and G.K.; software, G.K.; validation, G.K., Y.X. and J.C.; formal analysis, G.K.; investigation, G.K.; data curation, G.K. and Y.X.; writing—original draft preparation, G.K. and J.C.; writing—review and editing, Y.X. and C.V.; supervision, C.V.; project administration, C.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here: https://www.ri.se/en/icp-materials/documents/icp-materials-reports.
Acknowledgments
A large part of this research was carried out in the frame of the Dragon Project “Air quality over China” and ICP Materials.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bhaskaran, R.; Palaniswamy, N.; Rengaswamy, N.; Jayachandran, M. Global Cost of Corrosion—A Historical Review. In ASM Handbook Volume 13B, Corrosion: Materials; ASM International: Detroit, MI, USA, 2005; Volume 13, p. 704. ISBN 978-0-87170-707-9. [Google Scholar]
- Ebel, A.; Davitashvili, T. Air, Water and Soil Quality Modelling for Risk and Impact Assessment; NATO Security through Science Series C; Springer: Dordrecht, The Netherlands, 2007; ISBN 978-1-4020-5875-2. [Google Scholar]
- Varotsos, C.; Tzanis, C.; Cracknell, A. The Enhanced Deterioration of the Cultural Heritage Monuments Due to Air Pollution. Environ. Sci. Pollut. Res. 2009, 16, 590–592. [Google Scholar] [CrossRef] [PubMed]
- Tidblad, J.; Kucera, V.; Ferm, M.; Kreislova, K.; Brüggerhoff, S.; Doytchinov, S.; Screpanti, A.; Grøntoft, T.; Yates, T.; De La Fuente, D.; et al. Effects of Air Pollution on Materials and Cultural Heritage: ICP Materials Celebrates 25 Years of Research. Int. J. Corros. 2012, 2012, 496321. [Google Scholar] [CrossRef]
- Tzanis, C.; Varotsos, C.; Ferm, M.; Christodoulakis, J.; Assimakopoulos, M.N.; Efthymiou, C. Nitric Acid and Particulate Matter Measurements at Athens, Greece, in Connection with Corrosion Studies. Atmos. Chem. Phys. 2009, 9, 8309–8316. [Google Scholar] [CrossRef]
- Tzanis, C.; Varotsos, C.; Christodoulakis, J.; Tidblad, J.; Ferm, M.; Ionescu, A.; Lefevre, R.-A.; Theodorakopoulou, K.; Kreislova, K. On the Corrosion and Soiling Effects on Materials by Air Pollution in Athens, Greece. Atmos. Chem. Phys. 2011, 11, 12039–12048. [Google Scholar] [CrossRef]
- Hudson, J.C.; Stanners, J.F. The Effect of Climate and Atmospheric Pollution on Corrosion. J. Appl. Chem. 2007, 3, 86–96. [Google Scholar] [CrossRef]
- Vernon, W.H.J. A Laboratory Study of the Atmospheric Corrosion of Metals. Part I.—The Corrosion of Copper in Certain Synthetic Atmospheres, with Particular Reference to the Influence of Sulphur Dioxide in Air of Various Relative Humidities. Trans. Faraday Soc. 1931, 27, 255–277. [Google Scholar] [CrossRef]
- Vernon, W.H.J. A Laboratory Study of the Atmospheric Corrosion of Metals. Part II.—Iron: The Primary Oxide Film. Part III.—The Secondary Product or Rust (Influence of Sulphur Dioxide, Carbon Dioxide, and Suspended Particles on the Rusting of Iron). Trans. Faraday Soc. 1935, 31, 1668–1700. [Google Scholar] [CrossRef]
- Johansson, L.-G. Synergistic Effects of Air Pollutants on the Atmospheric Corrosion of Metals and Calcareous Stones. Mar. Chem. 1990, 30, 113–122. [Google Scholar] [CrossRef]
- Eriksson, P.; Johansson, L.-G.; Strandberg, H. Initial Stages of Copper Corrosion in Humid Air Containing SO2 and NO2. J. Electrochem. Soc. 1993, 140, 53–59. [Google Scholar] [CrossRef]
- Zakipour, S.; Tidblad, J.; Leygraf, C. Atmospheric Corrosion Effects of SO2 and O3 on Laboratory-Exposed Copper. J. Electrochem. Soc. 1995, 142, 757. [Google Scholar] [CrossRef]
- Strandberg, H.; Johansson, L. Role of O3 in the Atmospheric Corrosion of Copper in the Presence of SO2. J. Electrochem. Soc. 1997, 144, 2334. [Google Scholar] [CrossRef]
- Feliu, S.; Mariaca, L.; Simancas, J.; González, J.A.; Morcillo, M. Effect of NO2 and/or SO2 Atmospheric Contaminants and Relative Humidity on Copper Corrosion. Rev. Metal. 2003, 39, 279–288. [Google Scholar] [CrossRef]
- Mariaca, L.; de la Fuente, D.; Feliu, S.; Simancas, J.; González, J.A.; Morcillo, M. Interaction of Copper and NO2: Effect of Joint Presence of SO2, Relative Humidity and Temperature. J. Phys. Chem. Solids 2008, 69, 895–904. [Google Scholar] [CrossRef]
- Svensson, J.-E.; Johansson, L.-G. A Laboratory Study of the Effect of Ozone, Nitrogen Dioxide, and Sulfur Dioxide on the Atmospheric Corrosion of Zinc. J. Electrochem. Soc. 1993, 140, 2210. [Google Scholar] [CrossRef]
- Castaño, J.G.; de la Fuente, D.; Morcillo, M. A Laboratory Study of the Effect of NO2 on the Atmospheric Corrosion of Zinc. Atmos. Environ. 2007, 41, 8681–8696. [Google Scholar] [CrossRef]
- Allen, G.C.; El-Turki, A.; Hallam, K.R.; McLaughlin, D.; Stacey, M. Role of NO2 and SO2 in Degradation of Limestone. Br. Corros. J. 2000, 35, 35–38. [Google Scholar] [CrossRef]
- Mangio, R.; Johansson, L. The Influence of Ozone on the Atmospheric Corrosion of Carrara Marble in Humid Atmospheres Containing Sulfur Dioxide, Deposition Studies of SO2 on Marble. In Proceedings of the 11th Scandinavian Corrosion Congress, Stavanger, Norway, 1–6 October 1989. [Google Scholar]
- Ferm, M.; De Santis, F.; Varotsos, C. Nitric Acid Measurements in Connection with Corrosion Studies. Atmos. Environ. 2005, 39, 6664–6672. [Google Scholar] [CrossRef]
- Ferm, M.; Watt, J.; O’Hanlon, S.; De Santis, F.; Varotsos, C. Deposition Measurement of Particulate Matter in Connection with Corrosion Studies. Anal. Bioanal. Chem. 2006, 384, 1320–1330. [Google Scholar] [CrossRef]
- Kucera, V.; Tidblad, J.; Samie, F.; Schreiner, M.; Melcher, M.; Kreislova, K.; Lefevre, R.-A.; Ionescu, A.; Snethlage, R.; Varotsos, C.; et al. Model for Multi-Pollutant Impact and Assessment of Threshold Levels for Cultural Heritage Publishable Final Report; Swedish Corrosion Institute (SCI): Stockholm, Sweden, 2005; p. 52. [Google Scholar]
- Kucera, V.; Tidblad, J.; Kreislova, K.; Knotkova, D.; Faller, M.; Reiss, D.; Snethlage, R.; Yates, T.; Henriksen, J.; Schreiner, M.; et al. UN/ECE ICP Materials Dose-Response Functions for the Multi-Pollutant Situation. Water Air Soil Pollut. Focus 2007, 7, 249–258. [Google Scholar] [CrossRef]
- Gil, H.; Buitrago, C.P.; Calderón, J.A. Atmospheric Corrosion of Copper and Silver Influenced by Particulate Matter. J. Solid State Electrochem. 2017, 21, 1111–1119. [Google Scholar] [CrossRef]
- Samie, F.; Tidblad, J.; Kucera, V.; Leygraf, C. Atmospheric Corrosion Effects of HNO3: A Comparison of Laboratory and Field Exposed Copper, Zinc, and Carbon Steel. J. Electrochem. Soc. 2007, 154, C249. [Google Scholar] [CrossRef]
- Samie, F.; Tidblad, J.; Kučera, V.; Leygraf, C. Atmospheric Corrosion Effects of HNO3—Influence of Temperature and Relative Humidity on Laboratory-Exposed Copper. Atmos. Environ. 2007, 41, 1374–1382. [Google Scholar] [CrossRef]
- Samie, F.; Tidblad, J. Influence of Nitric Acid on Atmospheric Corrosion of Copper, Zinc and Carbon Steels. Corros. Eng. Sci. Technol. 2008, 43, 117–122. [Google Scholar] [CrossRef]
- Verney-Carron, A.; Lombardo, T. UN/ECE International Cooperative Programme on Effects on Materials, Including Historic and Cultural Monuments, Report No 74: Results of the Exposure of Modern Glass 2008–2012 and Soiling Dose-Response Functions; Laboratoire Interuniversitaire des Systèmes Atmosphérique (LISA): Paris, France, 2013. [Google Scholar]
- Bhartia, P.K. OMI/Aura TOMS-Like Ozone and Radiative Cloud Fraction L3 1 Day 0.25 Degree x 0.25 Degree V3; NASA Goddard Space Flight Center, Goddard Earth Sciences Data and Information Services Center: Greenbelt, MD, USA, 2012.
- Krotkov, N.A.; Lamsal, L.N.; Marchenko, S.V.; Celarier, E.A.; Bucsela, E.J.; Swartz, W.H.; Joiner, J. The OMI Core Team OMI/Aura NO2 Cloud-Screened Total and Tropospheric Column L3 Global Gridded 0.25 Degree x 0.25 Degree V3; NASA Goddard Space Flight Center, Goddard Earth Sciences Data and Information Services Center: Greenbelt, MD, USA, 2019.
- Li, J.; Yang, H.; Liu, X.; Yu, N.; Tian, Y.; Zhou, X.; Zhang, P.; Wang, K. Aircraft Emission Inventory and Characteristics of the Airport Cluster in the Guangdong–Hong Kong–Macao Greater Bay Area, China. Atmosphere 2020, 11, 323. [Google Scholar] [CrossRef]
- AIRS Science Team; Teixeira, J. AIRS/Aqua L3 Daily Standard Physical Retrieval (AIRS-Only) 1 Degree x 1 Degree V006; NASA Goddard Space Flight Center, Goddard Earth Sciences Data and Information Services Center: Greenbelt, MD, USA, 2013.
- Levy, R.; Hsu, C. MODIS Atmosphere L2 Aerosol Product; Goddard Space Flight Center: Greenbelt, MD, USA, 2015.
- Tidblad, J.; Kucera, V. Report No 51: Technical Manual for the Trend Exposure Programme 2005–2006; UN/ECE International co-Operative Programme on Effects on Materials, including Historic and Cultural Monuments: Stockholm, Sweden, 2006; p. 26. [Google Scholar]
- Tidblad, J. Report No 58: Technical Manual for the Trend Exposure Programme 2008–2009; UN/ECE International Co-Operative Programme on Effects on Materials, including Historic and Cultural Monuments: Stockholm, Sweden, 2009; p. 62. [Google Scholar]
- Tidblad, J.; Gordon, A. Report No 69: Technical Manual for the Trend Exposure Programme 2011–2012; UN/ECE International Co-Operative Programme on Effects on Materials, including Historic and Cultural Monuments: Stockholm, Sweden, 2012; p. 71. [Google Scholar]
- Tidblad, J. Report No 79: Technical Manual for the Trend Exposure Programme 2011–2015; UN/ECE International Co-Operative Programme on Effects on Materials, including Historic and Cultural Monuments: Stockholm, Sweden, 2016; p. 29. [Google Scholar]
- Tidblad, J. Report No 84: Technical Manual for the Trend Exposure Programme 2017–2018; UN/ECE International Co-Operative Programme on Effects on Materials, including Historic and Cultural Monuments: Stockholm, Sweden, 2018; p. 32. [Google Scholar]
- Kreislova, K.; Knotkova, D.; Kvapil, J.; Divisova, H. Report No. 53: Results from the Multi-Pollutant Programme Corrosion Attack on Carbon Steel after 1 Year of Exposure (2005–2006); UN/ECE International Co-Operative Programme on effects on Materials, including Historic and Cultural Monuments: Prague, The Czech Republic, 2008; p. 26. [Google Scholar]
- Reiss, D.; Faller, M. Report 54: Results from the 2005–2006 Trend Exposure Programm. Corrosion Attack of Zinc after 1 Year of Exposure; UN/ECE International Co-Operative Programme on Effects on Materials, including Historic and Cultural Monuments: Dübendorf, Switzerland, 2007; p. 16. [Google Scholar]
- Yates, T. Report 55: Results from the 2005–2006 Trend Exposure Programm. Corrosion Attack of Limestone after 1 Year of Exposure; UN/ECE International Co-Operative Programme on Effects on Materials, including Historic and Cultural Monuments: Watford, UK, 2007; p. 9. [Google Scholar]
- Lombardo, T.; Ionescu, A. Report No 59: Soiling of Exposed Materials and Dose-Response Functions for Modern Glass; UN/ECE International Co-Operative Programme on Effects on Materials, including Historic and Cultural Monuments: Paris, France, 2009; p. 39. [Google Scholar]
- Tidblad, J.; Kreislova, K.; Faller, M.; Yates, T.; Lombardo, T.; Grøntoft, T. Report No 62: Results of Corrosion and Soiling from the 2008–2009 Exposure Programme for Trend Analysis; UN/ECE International Co-Operative Programme on Effects on Materials, including Historic and Cultural Monuments: Stockholm, Sweden, 2010; p. 18. [Google Scholar]
- Tidblad, J.; Gordon, A.; Kreislova, K.; Faller, M.; De La Fuente, D.; Yates, T.; Verney-Carron, A. Report No 72: Results of Corrosion and Soiling from the 2011–2012 Exposure Programme for Trend Analysis; UN/ECE International Co-Operative Programme on Effects on Materials, including Historic and Cultural Monuments: Stockholm, Sweden, 2013; p. 24. [Google Scholar]
- Tidblad, J.; Kreislova, K.; Faller, M.; De La Fuente, D.; Yates, T.; Verney-Carron, A. Report No 78: Results of Corrosion and Soiling from the 2011–2015 Exposure Programme for Trend Analysis; UN/ECE International Co-Operative Programme on Effects on Materials, including Historic and Cultural Monuments: Stockholm, Sweden, 2016; p. 35. [Google Scholar]
- Tidblad, J.; Kreislova, K.; Faller, M.; De La Fuente, D.; Yates, T.; Verney-Carron, A.; Vuorio, T. Report No 85: Results of Corrosion and Soiling from the 2017–2018 Exposure Programme for Trend Analysis; UN/ECE International Co-Operative Programme on Effects on Materials, including Historic and Cultural Monuments: Stockholm, Sweden, 2019; p. 21. [Google Scholar]
- Roberge, P.R. Handbook of Corrosion Engineering, 2nd ed.; McGraw-Hill Education: New York, NY, USA, 2012; ISBN 978-0-07-175037-0. [Google Scholar]
- Varotsos, P.A.; Alexopoulos, K.D. Thermodynamics of Point Defects and Their Relation with Bulk Properties; Defects in Solids: North Holland, The Netherlands, 1986; Volume 14. [Google Scholar]
- Livingston, F.E.; George, S.M. Effect of HNO3 and HCl on HDO Diffusion on Crystalline D2O Ice Multilayers. J. Phys. Chem. B 1999, 103, 4366–4376. [Google Scholar] [CrossRef]
- Livingston, F.E.; George, S.M. Diffusion Kinetics of HCl Hydrates in Ice Measured Using Infrared Laser Resonant Desorption Depth-Profiling. J. Phys. Chem. A 2001, 105, 5155–5164. [Google Scholar] [CrossRef]
- Livingston, F.E.; Whipple, G.C.; George, S.M. Diffusion of HDO into Single-Crystal H216O Ice Multilayers: Comparison with H218O. J. Phys. Chem. B 1997, 101, 6127–6131. [Google Scholar] [CrossRef]
- Livingston, F.E.; Whipple, G.C.; George, S.M. Surface and Bulk Diffusion of HDO on Ultrathin Single-Crystal Ice Multilayers on Ru(001). J. Chem. Phys. 1998, 108, 2197–2207. [Google Scholar] [CrossRef]
- Livingston, F.E.; Smith, J.A.; George, S.M. Depth-Profiling and Diffusion Measurements in Ice Films Using Infrared Laser Resonant Desorption. Anal. Chem. 2000, 72, 5590–5599. [Google Scholar] [CrossRef] [PubMed]
- Livingston, F.E.; Smith, J.A.; George, S.M. General Trends for Bulk Diffusion in Ice and Surface Diffusion on Ice. J. Phys. Chem. A 2002, 106, 6309–6318. [Google Scholar] [CrossRef]
- Krasnopoler, A.; George, S.M. Infrared Resonant Desorption of H2O from Ice Multilayers. J. Phys. Chem. B 1998, 102, 788–794. [Google Scholar] [CrossRef]
- Varotsos, C.A.; Zellner, R. A New Modeling Tool for the Diffusion of Gases in Ice or Amorphous Binary Mixture in the Polar Stratosphere and the Upper Troposphere. Atmos. Chem. Phys. 2010, 10, 3099–3105. [Google Scholar] [CrossRef]
- Johnson, P.N.; Davis, R.A. Diffusivity of Ozone in Water. J. Chem. Eng. Data 1996, 41, 1485–1487. [Google Scholar] [CrossRef]
- Cheung, J.L.; Li, Y.Q.; Boniface, J.; Shi, Q.; Davidovits, P.; Worsnop, D.R.; Jayne, J.T.; Kolb, C.E. Heterogeneous Interactions of NO2 with Aqueous Surfaces. J. Phys. Chem. A 2000, 104, 2655–2662. [Google Scholar] [CrossRef]
- Diaz, M.; Vega, A.; Coca, J. Correlation for the Estimation of Gas-Liquid Diffusivity. Chem. Eng. Commun. 1987, 52, 271–281. [Google Scholar] [CrossRef]
- Varotsos, C.A.; Cracknell, A.P. Remote Sensing Letters Contribution to the Success of the Sustainable Development Goals—UN 2030 Agenda. Remote Sens. Lett. 2020, 11, 715–719. [Google Scholar] [CrossRef]
- Varotsos, C.; Cartalis, C. Re-evaluation of surface ozone over Athens, Greece, for the period 1901–1940. Atmos. Res. 1991, 26, 303–310. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).