Abstract
This comparative study evaluates the performance of three popular deep learning architectures, AlexNet, VGG-16, and VGG-19, on a custom-made dataset of GPR C-scans collected from several archaeological sites. The introduced dataset has 15,000 training images and 3750 test images assigned to three classes: Anomaly, Noise, and Structure. The aim is to assess the performance of the selected architectures applied to the custom dataset and examine the potential gains of using deeper and more complex architectures. Further, this study aims to improve the training dataset using augmentation techniques. For the comparisons, learning curves, confusion matrices, precision, recall, and f1-score metrics are employed. The Grad-CAM technique is also used to gain insights into the models’ learning. The results suggest that using more convolutional layers improves overall performance. Further, augmentation techniques can also be used to increase the dataset volume without causing overfitting. In more detail, the best-obtained model was trained using VGG-19 architecture and the modified dataset, where the training samples were raised to 60,000 images through augmentation techniques. This model reached a classification accuracy of 94.12% on an evaluation set with 170 unseen data.
1. Introduction
Ground penetrating radar (GPR) is an electromagnetic geophysical technique widely used in archaeological prospection, as it can detect detailed buried foundations and other archaeological remains on the near-surface when proper soil conditions are met [1,2,3]. The information obtained from GPR systems can efficiently guide excavation projects, avoiding unnecessary work. Moreover, it can enrich the insights of an archaeological site in the case the excavation is not feasible. Further, hardware improvements in GPR systems have led to faster and more detailed data acquisition, making them applicable in larger-scale surveys, resulting in larger data volumes per survey. Consequently, data interpretation, which was already challenging [4,5], has become more demanding. The main reason is that the archaeological sites’ subsurface is usually disturbed and causes complex patterns and noise in GPR data that are often difficult to distinguish from the archaeological material. Hence, GPR practitioners are called to study and cross-correlate hundreds, or even thousands, of images per site to fully understand the recorded signals. Therefore, developing and establishing methodologies to assist and guide data interpretation in more automatic ways, which are currently lacking, is of great importance in the archaeological prospection using GPR.
Convolutional neural networks (CNNs) and deep learning (DL) architectures are up-and-coming in developing such methodologies for GPR data interpretation. They have shown remarkable performance and capabilities in various domains related to computer vision tasks such as classification, segmentation, and object detection. A few examples are medical diagnosis [6], autonomous driving [7], face recognition [8], and plant disease diagnosis [9]. In recent years, there has been a notable surge in studies involving CNNs in the field of GPR for automatic target detection. Most of the studies are applicable in civil engineering tasks such as tunnel lining and rebar detection, showing promising results [10,11,12]. Regarding archaeological prospection, CNNs, and DL architectures have not yet been explored to the same extent. However, the few studies in the literature show great potential for automatic data interpretation and are encouraging further investigations [13,14]. The limited availability of annotated datasets suitable for training CNNs has been identified as a primary factor contributing to the existing literature gap due to the lack of open databases and the rare GPR data of buried ancient structures. In addressing this, a custom and multiclass dataset using GPR data collected from several archaeological sites was constructed and presented in our previous studies [4,15]. In these studies, AlexNet was trained to classify patterns in the data identified as ancient structures, noise, and patterns from the subsurface unrelated to the archaeological remains. These provide some initial insights on performing image classification using a DL architecture. However, despite the good performance, the generalization to unseen data was under question due to the small dataset used for training.
This study aims to take a few steps further to improve the custom-made dataset and exploit other popular and well-established DL architectures to evaluate the overall performance and use the results as a reference to navigate future improvements. In more detail, the architectures VGG-16 and VGG-19 are trained and compared to AlexNet to examine whether deeper and more complex architectures, originally designed for large datasets such as ImageNet, may positively impact the generalization and model’s learning in the case of a small training dataset. Furthermore, data augmentation techniques are employed to improve the training dataset and are used in two ways. The first is to produce more training samples to increase the dataset volume, and the other is to apply the selected techniques to replace training samples without affecting the dataset volume. Several classification metrics are used to gain more insights into the comparisons and better assess the models’ performance. Last, the Gradient-weighted Class Activation Mapping technique (GradCAM) is also employed to visually explain what each trained model has learned to make the predictions. More details are given in the Methodology section, and then the comparative results are presented and discussed.
2. Methodology
This section describes the methods and tools used in this comparative study. These include details on the raw data and preprocessing used to construct the training dataset, a general description of the DL architectures under evaluation, the training overview, and a brief description of the chosen metrics and Grad-CAM technique.
2.1. Dataset Description
In supervised learning, a well-defined annotated dataset is crucial to efficiently train models that can classify or predict new unseen data [16]. Such a dataset for detecting ancient buried structures in GPR data is currently missing or is not publicly available. This constraint has led to a limited exploration and utilization of CNNs in the field of GPR for archaeological purposes. For this reason, a training dataset was made from scratch to perform image classification. This dataset underwent initial testing in our previous studies [4,15]. To better describe the complexity of the GPR C-scans that are collected from archaeological surveys, three classes were defined that, from experience, are being used the most when interpreting such data:
- Anomaly: a generic class that represents strong reflections from the subsurface identified either as stratigraphic layers, bedrock, buried metallic objects, or buried objects not related to the archaeological context. Their shape and size vary, from small and circular (i.e., metallic object) to large and irregular or with some linearity (i.e., stratigraphic layer)
- Noise: in linear form, created either by the rough terrain (i.e., plowing lines) or residual noise when the background noise removal correction is applied.
- Structure: patterns of identified buried foundations and walls of residential and public complexes that are linear, forming corners and rectangles. The structural remains included in this dataset are from the Neolithic, Minoan, Hellenistic, Roman, and early Byzantine Periods. They were all detected in the range of 0.5–1.5 m deep. The identified walls in the dataset exhibit a thickness in the range of ~0.3 to ~1.5 m. The material of most structures is limestone. Further, linear patterns delining ancient roads of the Hellenistic period were also included.
Gathering samples for the Structure class was challenging as GPR C-scans featuring structures were limited to a few hundred. Therefore, training a DL architecture such as AlexNet was not possible due to underfitting. Further, the feature classes mentioned above usually coexist in the GPR C-scans. Hence, selected C-scans were cropped into sub-images using an overlapping sliding window corresponding to 10 m × 10 m. This window size was found adequate to describe the feature of interest well enough and, simultaneously, to increase the number of images per class to be used for training. In this study, the dataset is reworked, where some images were replaced while new ones were added, aiming for performance improvements. Details are given in the following subsections.
2.1.1. C-scans Processing and Preprocessing
As mentioned, the dataset is entirely made from GPR C-scans, the most common data representation in archaeological investigations. C-scans are extracted when collecting GPR data using survey grids, which allows producing a pseudo 3D of the subsurface. They are 2D images of the pseudo 3D showing the instantaneous envelope calculated by Hilbert Transform at different time instances, which can be later converted to depth if the travel velocity of the E/M waves in the subsurface is estimated. This approach usually reveals buried objects that exhibit higher reflectivity than the surrounding medium.
All the data used for the training dataset are collected through various geophysical surveys in different archaeological sites, mainly in Greece. The surveys were guided by the Laboratory of Geophysical—Satellite Remote Sensing and Archaeo-Environment (GeoSa ReSeArch), Institute for Mediterranean Studies—Foundation and Research and Technology Hellas (IMS—FORTH), Rethymno, Greece. All data were collected using NOGGIN GPR equipped with a 250 MHz antenna, a line spacing of 0.5 m or 0.25 m, and a sampling interval of 0.05 m or 0.025 m. For this study, GPR data from 6 more archaeological sites having 17 survey grids in total were included. Hence, the updated version of the dataset used for training and evaluating the models take into account C-scans from 58 different archaeological sites that were extracted from 487 survey grids.
The data were processed in MATLAB to extract C-scans using standard methods and techniques, as it was presented in Figure 2 in our previous study in [4]. C-scans were then selected, and the sliding crop window was applied to extract patches of the input C-scan that were saved as 256 × 256 images. Finally, examples that better describe the three feature classes were selected from those images.
Further, additional augmentation techniques were applied in the images of the training set to further increase its volume and examine whether the generalization can be improved in this way. The applied transformations are a random combination of image rotation, horizontal and vertical flips, zoom, and brightness adjustments. In addition, the parameters of each transformation were adjusted to achieve realism and avoid distortions. Image augmentation techniques were applied thrice for each image in the training set.
2.1.2. Training Datasets
The preprocessing step previously described resulted in two training datasets. The first, named dataset-1, is the reworked version of the training dataset used in our previous studies and has 5000 images for training and 1250 for testing per class that were randomly split using the 80–20% rule. Random 100 samples of the training set are presented in Figure 1 (top row). Further, to increase the diversity, some images were replaced with less similar ones while retaining the number of images. Dataset-1 is used to compare different DL architectures and examine the benefits, if any, of deeper architectures in cases of small datasets. Further, image augmentation without increasing the volume is also examined using this dataset.

Figure 1.
Random training set samples for the classes Anomaly, Noise, and Structure. On the top row are 100 samples from dataset-1 per class, while on the bottom row are 100 samples from dataset-2, where the volume is increased using data augmentation techniques to produce synthetic data.
In an attempt to further increase the volume and the multiplicity of the training set without adding new data, the random image transforms were applied thrice for each training sample. The produced images were added to the training set, resulting in 20,000 images per class for training. This dataset, named dataset-2, has the same test set as dataset-1. A small sample of 100 images per class of this modified training set is presented in Figure 1 (bottom row). Similar to dataset-1, dataset-2 is used to compare the performance of different architectures for a larger training set and to examine whether using image augmentation to produce synthetic C-scans for training can lead to a better generalization.
2.1.3. Evaluation Set
The preprocessing step of the overlapping sliding crop window to increase the samples used for the training and the test set was mandatory to overcome underfitting; however, the test set is not expected to represent how well a trained model can generalize to new data. For this reason, in our previous studies, an evaluation set with 100 images entirely excluded from the training process was defined to make predictions and evaluate the generalization of the trained models. The evaluation set is also reworked for this study, and data recently collected were added. The final count is 170 images, where 42 examples are anomalies, 52 are noise, and 76 are structures.
2.2. Deep Learning Architectures
The DL architectures that are the focus of this study are feedforward convolutional neural networks (CNNs) of multiple layers designed for image classification. These CNN architectures are characterized by four main layers: the convolutional layer, the pooling layer, the flattening layer, and the fully connected or dense layer. The convolutional and pooling layers are primarily responsible for feature detection. The convolutional layer applies filters to the input image, producing an equivalent number of feature maps highlighting certain features. Usually, a pooling layer succeeds the convolutional layer, reducing the spatial dimensions of the input feature maps while retaining the most important features. The flattened output from the convolutional and pooling layers is then passed to the dense layers, which are fully connected and responsible for classifying the learned features and making predictions [17]. The main differences lay in the number and sequence of the convolutional and pooling layers during the feature detection stage.
It is acknowledged in the DL community that increasing the number of layers in a CNN can enable the network to learn more complex features from the input data. This concept is often referred to as the “depth” of the network [18]. By adding more layers to a CNN, the network can capture and represent hierarchical patterns and features at various levels of abstraction. As the depth increases, the network can progressively learn more complex combinations of features, enabling it to capture intricate relationships and representations within the data. This increased depth can be beneficial when dealing with large, more complex, and diverse datasets (i.e., ImageNet), as it gives the network a greater capacity to learn and distinguish between subtle patterns and variations. However, excessively deep networks may encounter challenges such as vanishing gradients and overfitting [18]. Similar considerations apply when training deep architectures with smaller datasets, as they may struggle to generalize effectively due to limited training instances.
This study investigates the achievable performance gains of deeper architectures by implementing and comparing three CNN architectures: AlexNet, VGG-16, and VGG-19. AlexNet, which has shown promising results in our previous study, serves as a reference point for evaluating the improvements, if any, achieved by the deeper VGG architectures. These architectures were selected as a baseline for the classification of GPR-C scans in archaeological prospection, as no previous comparison has been conducted in this context. Both AlexNet and VGG architectures have established their performance in image classification and have been extensively studied in the deep learning community. Moreover, they are known for their ease of understanding and implementation. The results of this study are expected to provide valuable insights into the effectiveness of these architectures with GPR C-scans, allowing for informed decision-making and potential advancements in future studies. An overview of the three architectures is presented in Figure 2, while a more detailed description is given in the following paragraphs.

Figure 2.
Schematic description of AlexNet, VGG-16, and VGG-19 architectures as they were implemented for the purposes of the study. The filter size, filter number, stride, and pad size are given on each convolutional layer. Similarly, the kernel size, stride, and pad size are given on the pooling layers. A pad of 1 indicates no changes in dimension, while a pad of 2 indicates dimensionality reduction. On the bottom right of each layer, the output dimensions are noted. Last, the feature extraction and classification stages are pointed out in each architecture.
2.2.1. AlexNet
AlexNet, introduced in [19], is a deep CNN architecture and is considered a significant milestone in the performance improvements of CNNs. The input is a color image of 227 × 227 × 3 and has eight layers. The first five are convolutional (Conv) layers, with the Conv1, Conv2, and Conv5 being succeeded by overlapping max-pooling layers. The remaining three layers are fully connected (FC), with the last one (FC3) being the output. Rectified linear unit (ReLU) activation functions are applied after every Conv layer and after FC1 and FC2 layers. Based on the findings of our previous study, batch normalization (BN) [20] and dropout [21] enhance the overall performance, with the former having a greater impact [15]. Therefore, BN is applied after every Conv layer and prior to ReLU, while dropout is used after FC1 and FC2 and prior to ReLU. Last, the softmax activation function is applied for the last FC layer, which produces a distribution over the total number of the class labels defined by the dataset used for training. AlexNet was retrained and used as a reference for monitoring improvements in overall performance.
2.2.2. VGG-16 and VGG-19
VGG-16 and VGG-19 were introduced in [22] as very deep CNN architectures and were developed by the Visual Geometry Group (VGG) at the University of Oxford. The input of both architectures is a color image of 224 × 224 × 3, and while they have similar structures, they differ in the number of layers, with VGG-19 being deeper.
VGG-16 has a total of 16 layers, including 13 convolutional (Conv) layers and 3 fully connected (FC) layers. The architecture is divided into convolutional blocks where each block has a stack of convolutional layers, succeeded by a max-pooling layer. The first two blocks have two convolutional layers each, while the remaining three blocks have three convolutional layers each. All convolutional layers use small 3 × 3 filters, increasing their number as the network goes deeper. ReLU activation functions are applied after every Conv and FC layer. BN was also used after every convolutional layer and prior to ReLU. Dropout was not used in this case.
VGG-19 has a total of 19 layers, including 16 Conv layers and 3 FC layers. It has a similar structure to VGG-16 but with an additional Conv layer in block3, block4, and block5. Like VGG-16, all the Conv layers use 3 × 3 filters, and ReLU activation functions are applied after every Conv and FC layer. BN was also used in the same manner as VGG-16, while dropout was not employed.
Both VGG-16 and VGG-19 have been shown to achieve state-of-the-art performance on various image classification tasks, particularly in the ImageNet Large Scale Visual Recognition Challenge (ILSVRC) competition, and inspired other popular architecture such as ResNet [23]. However, they are more computationally and memory-demanding.
2.3. Training Overview
The models were implemented and trained in Google Colab using the Tensorflow [24] and Keras [25] libraries with GPU acceleration. Each architecture was trained for three different trials using the different versions of the training dataset combined with the image augmentation techniques as previously described. More precisely:
- The first trial uses dataset-1, which consists of 15,000 training samples. The resulting models for each architecture are named AlexNet-1, VGG-16-1, and VGG-19-1.
- The second trial uses dataset-2, which is produced from image augmentation techniques and has 60,000 training samples. The resulting models for each architecture were named AlexNet-2, VGG-16-2, and VGG-19-2.
- The third trial uses dataset-1, and image augmentation techniques are applied to replace training samples without affecting the volume. The resulting models for each architecture were named AlexNet-3, VGG-16-3, and VGG-19-3.
Each model was trained for 50 epochs using the stochastic gradient descent (SGD) optimizer with a momentum of 0.9. The learning rate was set to 0.001. The choice of the optimizer and the learning rate was based on the findings of our previous study, where SGD with momentum outperformed Adam optimizer when training AlexNet [15]. During training, the model weights were saved each time the validation loss was improved. The weights that exhibited the lower loss were chosen as the best model for each architecture and were used to evaluate and compare the generalization. These models were later used to compare the generalization on unseen data.
2.4. Metrics and Performance Evaluation
In this study, several metrics are being employed to better highlight the differences and benefits that each model exhibits over the other and navigate future improvements. The metrics used here are divided into those that measure the training performance and those that measure the classification performance. In addition to the metrics, the gradient-weighted class activation mapping (Grad-CAM) technique is used to gain better insights and visualize how each model makes predictions on new data. More details are given in the following paragraphs.
2.4.1. Training Performance Metrics
For training performance, Keras library metrics such as accuracy, loss, validation accuracy, and validation loss were used to assess how well the models were learning during the training process. These metrics are calculated after a training epoch is completed. Briefly:
- The loss represents the error between the predicted output and the true output for the images of the training set. It is a measure of how well the model is able to fit the training data.
- Validation loss measures the error for the images on the test set that were not used during training.
- Accuracy expresses the fraction of correctly classified images out of the total number of images. In other words, it measures the percentage of predictions that the model got right in the training set. A higher accuracy value indicates better performance of the model.
- Validation accuracy is the accuracy of the model calculated on the test set.
These metrics are used to plot learning curves, giving valuable insights into the training process and revealing whether learning problems such as overfitting exist. In terms of loss and validation loss, the signs of overfitting can be observed when the model’s training loss decreases while the validation loss increases or remains stagnant. In terms of accuracy and validation, high accuracy and low validation accuracy may indicate overfitting.
2.4.2. Classification Metrics
To evaluate and compare the classification performance of the trained models, the following metrics were used and calculated from predictions made in the evaluation and test set [26,27]:
- Confusion matrix: the matrix that is calculated from true positives (TPs), false positives (FPs), false negatives (FNs), and true negatives (TNs). In other words, it shows the number of correct and incorrect predictions made by the model in each class and helps to assess the performance of a classification model.
- Precision: a metric that measures the proportion of TPs among the predicted positives. In other words, it measures the model’s ability to identify TPs without including FPs. A high precision indicates a low FPs rate.
- Recall: a metric that measures the proportion of TPs among the actual positives. In other words, it measures the model’s ability to identify all positives. A high recall indicates a low FN rate.
- F1 score: the harmonic mean of precision and recall. It delivers a balance between precision and recall and is a good metric for evaluating the overall performance of a classification model.
TP refers to the number of samples that are actually positive and correctly predicted as positive. TN refers to the number of samples that are actually negative and correctly predicted as negative. FP refers to the number of samples that are actually negative but incorrectly predicted as positive. FN refers to the number of samples that are actually positive but incorrectly predicted as negative. These metrics and confusion matrix were calculated for each class individually using the SciKit-Learn library [28].
2.4.3. Grad-CAM
Grad-CAM is a technique used to highlight important regions of an image that contributed the most to a neural network’s prediction. This is achieved by generating a heatmap showing each feature map’s contribution to the final prediction. The weights are calculated by taking the gradient of the predicted class score with respect to the feature maps of the last convolutional layer of the CNN. The resulting weighted feature maps are averaged to produce a 2D map, and ReLU activation is applied to highlight only the positive values. The map is then upsampled to match the input image dimensions, and a colormap is applied to produce the final heatmap, which is overlaid on the input image for better visualization.
This study uses Grad-CAM to gain insights into how each of the 9 trained models made their predictions on the evaluation dataset. To generate heatmaps, the last convolutional layer of each architecture was utilized, i.e., Conv5 for the models trained with AlexNet, Conv13 for the models trained with VGG-16, and Conv16 for the models trained with VGG-19 (as shown in Figure 2). The softmax layer was removed as the unnormalized scores were found to produce more representative heatmaps.
The produced heatmaps are also used to compare the trained models and examine whether deeper architectures can lead to better learning, but also test the quality of learning when incorporating training set images generated by image augmentation techniques.
3. Results
This section presents and briefly describes the obtained results of this study. It begins with comparisons of the training performance by observing the learning curves of all 9 models on the train and test set, then moves to the generalization by comparing the classification metrics calculated on the evaluation set, and finalizes by comparing the heatmaps produced by the Grad-Cam. For the latter, representative samples of the evaluation set are presented.
3.1. Training Performance
Training models with DL architectures is a resource-intensive process that demands significant time and computational power. Since VGG16 and VGG19 have much more parameters than the AlexNet architecture, the time and memory requirements are increased much more. Moreover, these requirements were further amplified when trained on the larger dataset-2 (i.e., 60,000 training samples). Table 1 summarizes the average time of an epoch completion in Google Colab using a GPU backend, along with the model’s parameters and the models’ size in the disk. For the latter, only the weights were saved.

Table 1.
Comparative table showing the average time an epoch required to be completed on Google Colab using GPU backend, the total model’s parameter, and the model’s size. For the latter, only the weights of the model were saved.
VGG19-2 model has the longest average epoch time, while AlexNet-1 has the shortest average time suggesting faster training. The average training time is significantly affected by the increase in convolutional layers. For instance, compared to the average epoch time of AlexNet-1, the VGG16-1 model is approximately 357.1% larger, while VGG19-1 is 458.3% larger. Moreover, VGG19-1, which has three additional convolutional layers than VGG16-1, takes 22.2% more time on average. The epoch times are further increased when using dataset-2, with VGG16-2 and VGG19-2 taking longer times by 461.5% and 603.5% over AlexNet-2, respectively. In this case, the addition of three more convolutional layers in VGG19-2 over VGG16-2 further increases the epoch time by 25.3%. Lastly, the increase in training set volume resulted in an average time increase of 212.5% for AlexNet-2, 283.9% for VGG16-2, and 293.7% for VGG19-2.
The accuracy and loss learning curves are summarized in the left and right columns, respectively, in Figure 3. Starting with AlexNet architecture, the validation curves show significant fluctuations in both accuracy and loss. Some important observations are:
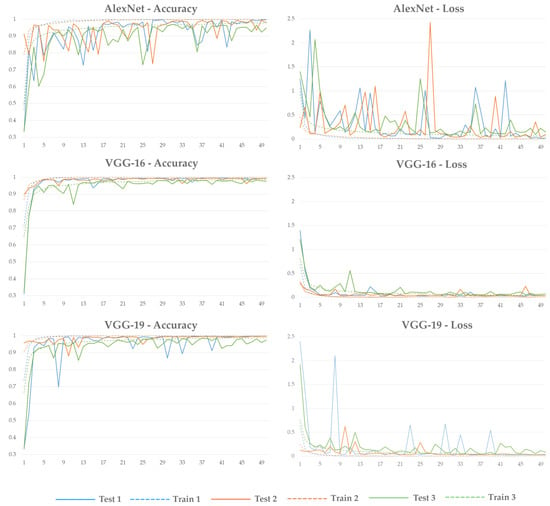
Figure 3.
The resulting loss and accuracy learning curves for all 9 models grouped by the architecture. Blue color represents the results obtained from models AlexNet-1, VGG16-1, and VGG19-1 that were trained with dataset-1 (~15,000 training samples) and orange represents the results obtained from models AlexNet-2, VGG16-2, and VGG19-2 trained with dataset-2 (~60,000 training samples), while green color represents the results obtained from AlexNet-3, VGG-16-3, and VGG19-3 trained with dataset-1 using image augmentation techniques to replace training samples. The dashed line indicates the accuracy and loss calculated on the training set, while the solid line is the validation accuracy and validation loss calculated on the test set for each dataset.
- AlexNet-1 appears to be more stable towards the end of training. In contrast to validation, the training curves are smooth with model AlexNet-1 to present the fastest convergence to 1, followed closely by model AlexNet-2. Among the three models, AlexNet-3 performed the worst, having very noisy validation curves, while training curves of accuracy and loss do not converge to 1 and 0, respectively. Convergence to 1 and 0 for accuracy and loss are important indices expressing how effectively a model learns during training. Hence, a faster convergence suggests faster learning.
- The models trained by VGG-16 architecture demonstrate overall better training performance. Fluctuations are still present in the validation curves but are more limited compared to AlexNet models. Models VGG16-1 and VGG16-2 performed similarly, with VGG16-1 being slightly more stable toward the end of the training. All three models exhibit smooth training curves, with VGG16-2 having faster convergence, followed closely by VGG16-1. VGG16-3 has a poorer performance exhibiting more noisy validation curves and slower convergence in the training curves.
- The behavior of VGG-19 models is mixed in comparison to VGG-16 models. Models VGG19-1 and VGG19-3 have worse performance than VGG16-1 and VGG16-3, respectively, with more fluctuations in the validation curves. However, towards the end of the training, VGG19-1 also stabilizes its performance. On the other hand, the model VGG19-2 performed the best and better than VGG16-2, exhibiting much smoother and more stable validation curves. The training curves also show good behavior with the accuracy to converge to 1 and loss to converge to 0.
3.2. Generalization
To compare the generalization, the models’ sets of weights exhibiting the lowest validation loss were chosen from the learning curves presented in Figure 3. Specifically, AlexNet-1 was epoch 29, AlexNet-2 was epoch 36, AlexNet-3 was epoch 31, VGG16-1 was epoch 44, VGG16-2 was epoch 27, VGG16-3 was epoch 35, VGG19-1 was epoch 32, VGG19-2 was epoch 38, and, lastly, VGG19-3 was epoch 40. These models were used to make predictions on the 170 unseen samples of the evaluation set. The confusion matrices and classification accuracy are presented in Figure 4. Overall, the resulting models perform well, with the VGG19 architecture models exhibiting the highest and lowest accuracies. More specifically, VGG19-2 has the highest accuracy of 94.12%, while VGG19-1 and VGG19-3 have the lowest of 87.65%.
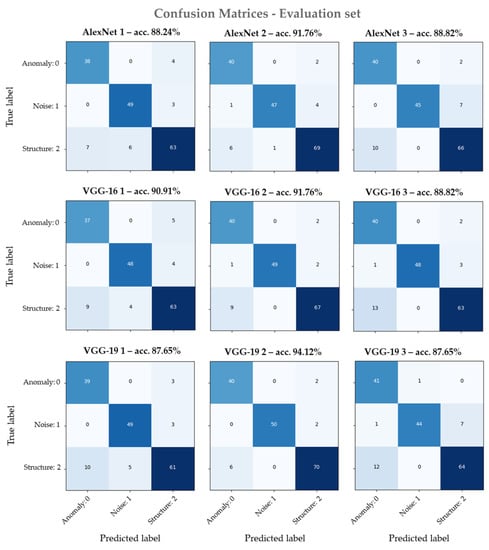
Figure 4.
The confusion matrices were calculated on the evaluation set for all 9 models. On top of each matrix, the total accuracy score is presented.
The diagonal elements of the matrices represent the TPs for each class, while the rest are the misclassified elements. For the Anomaly class, VGG19-3, despite the lower classification accuracy, has the most TPs. It correctly predicted 41 out of 42 samples, while 1 sample was wrongly classified as Noise. The next best models for the Anomaly class are VGG19-2, VGG16-2, and AlexNet-2, counting 40 TPs. For all three models, the 2 samples are misclassified as a Structure. The model with the fewer TPs is VGG16-1, having predicted 37 out of 42 samples correctly, while the rest are misclassified as a Structure.
For the Noise class, VGG19-2 has the most TPs, having predicted correctly 50 out of 52 samples, while the remaining 2 samples are misclassified as a Structure. The next best performance for the Noise class is observed in models VGG19-1, VGG16-2, and AlexNet-1, counting 49 TPs each. VGG19-1 and AlexNet misclassified three samples as a Structure, while VGG16-2 wrongly classified one sample as an Anomaly and two as a Structure. The worst performance for this class is observed by model VGG16-3, having 44 TPs and 8 misclassified samples, where 7 of these were identified as a Structure and 1 as an Anomaly.
Last, VGG19-2 performed the best for the Structure class, correctly classifying 70 out of 76 samples, while the remaining 6 were misclassified as an Anomaly. The next best-performing models are AlexNet-1, having 69 TPs and 7 misclassified samples. Out of them, one is identified as Noise, while the rest are misclassified as an Anomaly. Finally, the worst performance is observed by VGG19-1, having predicted 61 samples correctly. Of the 15 misclassified samples, 5 were identified as Noise and 10 as Anomaly.
Table 2 summarizes the metrics of precision, recall, and f1-score for each model and each class. For comparison reasons, red is used to highlight the lowest score, while blue is used to highlight the highest. Some observations are:

Table 2.
Classification metrics results for the 9 models. Precision, recall, and f1-score calculated for each model are presented. Bold blue indicates the highest score per class for each metric, while bold red shows the lowest score per class for each metric.
- For the Anomaly class, most models have precision ranging from 0.8 to 0.87. Exceptions are the models VGG16-3 and VGG19-3, which have relatively low precision of 0.74 and 0.76, respectively. The highest precision of 0.87 is scored by model VGG19-2, having a recall of 0.95. The f1-score ranges from 0.84 to 0.91, with VGG19-2 having the highest and VGG16-3 the lowest. Overall, the model with the best performance for the anomaly class is VGG19-2.
- The Noise class’s precision is very high and ranges from 0.89 to 1.00, with model AlexNet-1 scoring the lowest and models AlexNet-3, VGG16-2, VGG16-3, and VGG19-2 scoring the highest. The recall metric ranges from 0.85 to 0.96, with model VGG19-3 scoring lower and VGG19-2 scoring higher. Finally, the f1-score is very high, ranging from 0.91 to 0.98, with model VGG19-3 scoring the lowest and VGG19-2 scoring the highest. In this case, the model with the best performance is VGG19-2, while VGG19-3 performs the worst.
Structure class also has a high precision ranging from 0.88 to 0.95, with models VGG16-1 and AlexNet-3 scoring the lowest, while model VGG19-2 scored the highest. As for the recall, the range is from 0.80 to 0.92, with VGG19-1 performing the worst and VGG19-2 performing the best. The f1-score ranges from 0.85 to 0.93, where model VGG19-1 scored the lowest and VGG19-2 the highest. Model VGG19-2 performed the best also for the Structure class.
Further, the Anomaly class has better recall scores and worse precision scores compared to the other classes. On the other hand, the Noise class has a better precision score and f1-score. The Structure class has lower recall scores; however, the f1-score was better than the Anomaly class. So overall, the prediction made for the Anomaly class were more accurate. According to these observations on the classification metrics, it can be seen that some models performed better than others on the three classes, while model VGG19-2 has the overall best performance and achieved better generalization.
3.3. Grad-CAM Results
In this section, the heatmaps generated by the Grad-CAMs are overlaid on selective and representative samples of the evaluation set and presented. These heatmaps show the part of the C-scan that each model identifies as the output class. Figure 5a summarizes the results of correctly predicted examples for the Anomaly class, Figure 5b for the Noise class, and Figure 5c for the Structure class.

Figure 5.
Selective Grad-CAM results of the evaluation set for correct predictions under the Anomaly class (a), the Noise class (b), and the Structure class (c). For all three cases, the first column is the input to trained models, and the following columns are the generated heatmaps for each model overlaid on the input image. Warm colors indicate the most important regions for each model’s correct prediction, while cooler colors suggest little to no contribution to the classification prediction.
Starting with the Anomaly class and Figure 5a, the selected samples exhibit buried small metallic objects (sample no. 5), scatter anomalies identified as a rocky layer (sample no. 9), linear anomalies of the stratigraphic layer (samples no. 13 and no. 24), and anomalies of irregular shapes identified as stratigraphic layers (samples no. 27, no. 34, and no. 39). The produced heatmaps showed the regions of the image that affected the correct prediction the most. For sample no. 5, it is revealed that not all the targets were identified as an Anomaly, and not much correlation exists for all 9 models. For sample no. 9, most of the models were affected by the upper part of the image. For samples no. 13, no. 24, no. 27, no. 34, and no. 39, the VGG16 and VGG19 models have an overall higher correlation to the targets than AlexNet models, with VGG16-2, VGG19-1, VGG19-2, and VGG19-3 standing out.
For the Noise class (Figure 5b), the selected samples are weak striping noise in the background (sample no. 44) and linear noise in different amplitude intensities caused by background removal (samples no. 47, no. 52, no. 61, no. 69, and no. 88). Lastly, sample no. 68 is horizontal linear noise caused by plowing lines. Aside from sample no. 47, no. 52, and no. 61, where most models describe the target noise well, the rest of the heatmaps show variations in the areas upon which the predictions were made. The horizontal noise in sample no. 68 is best described by AlexNet-1 and VGG16-3, while the rest of the VGG models are affected by more extensive areas of the image. Similar behavior is presented for the vertical noise of sample no. 69, with AlexNet-1 having the best correlation. As for the attenuated noise in sample no. 44 and no. 88, AlexNet models were affected almost by the whole image, while VGG models were affected by image segments of different shapes and sizes. In addition, some of the models were affected by points in the image, such as the cases of VGG19-1 and VGG19-2 for input sample no. 88, which have no correlation with the target. Lastly, AlexNet3 has produced zero heatmaps for sample no. 47, no. 52, no. 61, no. 68, no. 69, and no. 88, showing no correlation to the targets but having made a correct prediction.
Representative results for correctly classified samples under the Structure class are summarized in Figure 5c. The selected samples include well-defined segments of structures forming corners and rectangles. Samples no. 102 and no. 121 derive from the ancient Halos site [29], with the former having more attenuated amplitudes compared to the other samples. Sample no. 126 derives from the Sissi archaeological site and is ground truth [30]. The rest of the samples were collected near the ancient Roman road of Egnatia in northern Greece. Overall, the VGG models describe the targets the best for all samples, all showing good correlations with slight differences. Sample no. 102 is best described by VGG19-1; sample no. 121 by VGG16-2; sample no. 126 by VGG16-3, VGG19-2, and VGG19-3; sample no. 136 by VGG16-1; sample no. 144 by VGG16-3, VGG19-2, and VGG19-3; sample no. 161 by VGG16-3, VGG19-1, and VGG19-2; and, lastly, sample no. 169 by VGG16-2, VGG16-3, and VGG19-1.
To gain more insights, a selection of samples wrongly classified by the majority of the models is presented in Figure 6. These include one sample of the Anomaly class and nine samples of the Structure class. The bottom of each sample also displays the prediction scores for the two highest-ranking classes. In this visual representation, incorrect predictions are highlighted in red, while the correct class for each input sample is indicated in blue.
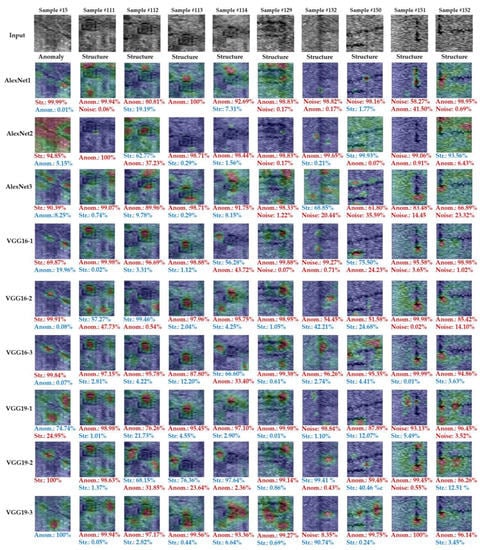
Figure 6.
Compilation of Grad-CAM results for the samples where models made the most mistakes. On the top row are the inputs, where each class is mentioned at the bottom. The generated heatmaps for all 9 models are overlaid on each input. Warm colors indicate the highest impact, while cooler colors indicate little to no impact on the classification prediction. The classification prediction of the highest two percentages is presented at the bottom of each sample, with the first one being the classification outcome. Red indicates the wrong class, while blue indicates the correct class.
Sample no. 13 is a linear stratigraphic layer that was mistaken by most models as a Structure, with VGG9-1 and VGG19-3 being exceptions. VGG19-1 predicted sample no. 13 by 74.74% as Anomaly and 24.96% as a Structure, while VGG19-3 predicted it as a 100% Anomaly. However, the heatmap showed little correlation with the target and was affected the most by the background. The rest of the models classify this sample as a Structure. In these predictions, AlexNet models have the lowest correlation to the target, with AlexNet2 being the worst, while VGG16-1, VGG16-2, VGG16-3, and VGG19-2 perform better.
Samples no. 111, no. 112, and no. 113 are different images of the same structural pattern collected at the ancient Halos site. Most of the models classified it as a Structure. More precisely, sample no. 111 was wrongly classified by all models, while sample no. 112 was correctly predicted as a Structure by models AlexNet2 (by 62.77%), VGG16-2 (by 99.46%), and VGG19-2 (by 68.15%). The heatmaps showed some correlation for VGG16-2 and VGG19-2; however, the main target did not affect the correct prediction. For the same sample, AlexNet-2 was affected by most parts of the image, emphasizing three smaller regions. Similarly, sample no. 113 was also misclassified as an Anomaly by most models, and only VGG19-2 classified it correctly as a Structure by 76.36%. Likewise, the heatmap shows no correlation to the main structural pattern despite being classified correctly. Sample no. 114 is the same structure shown in no. 111, no. 112, and no. 113 but from a deeper C-scan, where it is not well described. This sample was also classified as an Anomaly by most models, with VGG16-1 (56.28% structure), VGG16-3 (66.6% structure), and VGG19-2 (97.64% structure) being exceptions. The heatmaps in all these examples are partially correlated to the target.
Sample no. 129 is part of a structure close to the ancient Egnatia road that is not well preserved. All models predicted this sample as an Anomaly. For this case, the heatmaps for most models show that small parts of the target have led to wrong prediction, while AlexNet-1 and AlexNet-3 were affected by the most part of the image. Sample no. 132 is also collected at the ancient Egnatia road and is a structure from deeper levels that exhibits attenuated amplitudes. Models AlexNet-1, VGG16-1, VGG19-1, and VGG19-3 classified it as Noise, while models AlexNet-2, VGG16-2, and VGG16-3 classified it as an Anomaly. Only VGG19-2 classified this sample as a Structure by 99.41%. However, the heatmap shows only a small correlation with the target.
Samples no. 150, no. 151, and no. 152 are linear structures partially preserved and also collected from the ancient Egnatia road. Sample no. 150 was wrongly classified as an Anomaly by models AlexNet-3, VGG16-2, VGG16-3, VGG19-1, VGG19-2, and VGG19-3, while AlexNet-1 classified it as Noise. The AlexNet-2 and VGG16-1 correctly classified this sample as a Structure with 99.93% and 75.50%, respectively. The heatmaps of AlexNet-2 showed that the prediction was affected by the whole image, while VGG16-1 has a partial correlation to this structural pattern. Similarly, Sample no. 151 was mistaken as Noise by models AlexNet-1, AlexNet-2, and VGG19-1, while it was classified as an Anomaly by the rest models. With the exception of AlexNet-1, which has a good correlation to the target, the generated heatmaps for the rest models do not clearly show what contributed to the wrong prediction. Last, sample no. 152 was misclassified as an Anomaly by most models. Only AlexNet-2 classified it correctly as a Structure by 93.56%, but the heatmap, once again, does not show much correlation with the target.
4. Discussion
The results presented in the previous section provide intriguing and informative comparisons among the 9 evaluated DL models. These comparisons between AlexNet and VGG offer valuable insights into the potential impact of deeper DL architectures on learning, particularly when the training dataset is limited in size. It also encourages further investigation using more recent and state-of-the-art architectures. Furthermore, the results shed light on the efficacy of augmentation techniques for generating additional training samples and the impact of training dataset volume on model performance. Notably, the study also demonstrates the significant potential of DL for automatically interpreting GPR C-scans images from archaeological sites. In the following subsections, the key findings of this study are discussed in greater detail.
4.1. Training Performance Comparisons
As shown in the learning curves of Figure 3, all the models trained with AlexNet architectures produced smooth training curves, while the validation curves have significant fluctuations. This is one of the signs indicating overfitting, where the training accuracy is high but the validation accuracy drops. This inconsistent behavior could also show an insufficient training dataset. However, no improvements were shown when producing more data with augmentation techniques (i.e., model AlexNet-2) and by applying random augmentation techniques to the training samples (i.e., model AlexNet-3).
With the AlexNet models’ learning curves as a reference, VGG-16 models brought significant improvements. The validation curves have limited fluctuations and show a more consistent training behavior. It seems that the additional and succeeded convolutional layers of small kernel size helped limit overfitting. However, the increment of data volume using augmentation techniques did not seem to have any particular gains, as VGG16-1 and VGG16-2 models performed very similarly. Next, the additional layers of VGG19 did not improve the performance further for the case of VGG19-1 and VGG19-3, where dataset-1 was used, but on the contrary, it produced more fluctuation in the validation curves. On the other hand, VGG19-2 trained with dataset-2 showed the best overall performance. The validation curves become stable after epoch 29, converging to 1 and 0 for accuracy and loss, respectively. This suggests that producing more training samples through augmentation techniques and using a deeper architecture can lead to great performance gains and limited overfitting, even when the initial training set is small. This observation suggests exploiting deeper architectures but can also be used for future improvement on the training dataset to increase the training samples. On the other hand, image augmentation techniques, when applied randomly to the training samples, worsen both training and validation performance for all the architectures tested in this study. This might suggest that the chosen techniques and parameters are inappropriate and further testing is required.
However, all this performance improvement comes at a cost. As it was shown in Table 1, using the deeper architectures, VGG-16 and VGG-19 over AlexNet significantly increased the average epoch time, which amplifies when using a larger dataset. Therefore, any potential improvements in performance using these architectures come at the expense of longer training times. Despite this, the results of this study suggest that the trade-off is worthwhile.
4.2. Classification Results Comparisons
The generalization comparison was performed on 170 unseen data, and predictions were made using the models’ set of weights for each architecture that showed the lowest validation loss. The validation loss was preferred to validation accuracy to avoid overfitting. In addition, several popular metrics were used to better evaluate and gain more insights, including the accuracy, classification matrix, recall, precision, and f1-score.
Starting with the accuracy (Figure 4), the model VGG19-2 scored the highest at 94.12%, while VGG19-1 and VGG19-3 had the lowest at 87.65% each. The next best-performing models are AlexNet-2 and VGG16-2, scoring both 91.76%. The same accuracies observed here are due to the small size of the evaluation set. The accuracy metric suggests that increasing the volume of the training set with data augmentation techniques improved the generalization for all the architectures; however, when trained with the deeper VGG19 architecture, the obtained best model, VGG19-2, outperformed the others.
The confusion matrices (Figure 4) were helpful in seeing each model’s TPs and misclassified samples and better showing their differences. For example, the best-acquired model VGG19-2 was the most accurate in the predictions for the Noise and Structure classes; however, it was the second most precise model for the Anomaly class. The confusion matrix observations become clearer when comparing the precision, recall, and f1-score metrics summarized in Table 2. Based on the f1-score, VGG19-2 performed the best for all classes and was the highest for the Noise class (0.98), followed by the Structure class (0.93) and then the Anomaly class (0.93). It is also shown that the models trained with dataset-2 scores have higher f1-scores, showing improved generalization. This is important as it suggests more training data can be produced with image augmentation without leading to overfitting, regardless of the architecture.
Focusing on the best-obtained model, the anomaly class shows a higher recall value (0.95) and a lower precision (0.87). This suggests that the model tends to classify samples of other classes as an anomaly. This is validated by the confusion matrix, where most of the misclassified samples were identified as an Anomaly. On the other hand, the Noise class has the perfect score in precision (1.00) and a slightly lower recall value (0.96). This means that all the samples classified as Noise were a correct prediction, but some noise samples were mistaken as an Anomaly or a Structure by the model. Likewise, the Structure class also has a lower recall value (0.92) and a higher precision (0.95), meaning that more samples were misclassified. This is expected since the evaluation set is imbalanced, having more samples under the Structure class.
4.3. Grad-CAM Results Comparison
The grad-CAM technique was used to give more insights into how the models make predictions, what they have learned, and whether differences are observed. In contrast with the other metrics, the heatmap did not reveal “the best model” but rather differences in how each model behaves, which can be used to navigate future work for improvements. For example, the produced heatmaps for the correctly predicted samples (Figure 5) showed that each model was affected by different parts of the targets. For most cases, the heatmaps of VGG models tend to have a better correlation to the target than AlexNet models, suggesting improvement in using deeper architecture. In addition, using augmentation techniques in the two ways tested in this study seems to improve the heatmaps’ correlation to the target when using VGG architectures. In a similar way, the heatmaps produced for the misclassified samples (Figure 6) were also interesting as the images’ regions that confused the models were highlighted, giving more useful insights.
Additionally, it was revealed for many samples that despite the correct prediction, there was no correlation to the target. These cases might suggest that more training samples are needed to better describe the patterns of interest. A good example is the structure of sample no. 112, no. 113, and no. 114 of Figure 6. Even though the best model according to the classification metrics, VGG19-2, was one of the few to make correct predictions, the produced heatmaps show no correlation to the target. Another possible explanation is that the most important features were learned in the previous convolutional layers, so the last layer did not affect the prediction much. In any case, more research is required on this matter, including generating heatmaps of the previous layers and using alternatives or variations of Grad-CAMs such as guided backpropagation [31] and Grad-CAMs++ [32].
5. Conclusions
This study evaluated and compared the performances of AlexNet architecture with the deeper VGG-16 and VGG-19 on a custom-made dataset of GPR C-scans collected from various archaeological sites. These are widely used and well-studied architectures in image classification, never tested before for this study’s context, and were chosen to serve as a baseline to monitor future improvements and assist decision-making. The main goal was to examine whether adding more layers in a CNN network can improve the generalization in unseen data or would lead to overfitting due to the small size of the custom dataset. The dataset of interest has a training set of 15,000 images and 3750 images as a test set, belonging to three classes, Anomaly, Noise, and Structure. Acknowledging the small size of the dataset can be a limitation in improving the generalization, augmentation techniques were employed in two ways. The first way was to produce more training samples, resulting in raising the original dataset to 60,000 images. The second way was to apply a random combination of the selected techniques to the training samples without affecting the volume of the dataset. Therefore, 9 models were trained in total and compared. Finally, the generalization was tested on the evaluation set, with 170 samples entirely excluded from the training process.
For the comparisons, several metrics were used. The accuracy and loss calculated on the training and test set and the respective learning curves were produced to evaluate the training performance. The metrics used to compare the generalization on the new data were the classification matrix, accuracy, precision, recall, and f1-score. These metrics were calculated on the evaluation set. Additionally, to gain more insights into what the models have learned, the Grad-CAM technique was used to generate heatmaps highlighting the regions of the input images of the evaluation set that affected the final prediction the most.
The comparison of the results showed that using DL architectures has overall benefits in both training performance and generalization over the AlexNet models. The best model, however, was obtained by VGG-19 when trained in the dataset of 60,000 images. It exhibited less overfitting, and the learning curves had little fluctuations compared to the other models. Further, it scored the highest accuracy of 94.12% and showed the best generalization, based on the f1-score, for all classes. The heatmaps calculated by the Grad-CAM also showed some improvement of the VGG-trained models over AlexNet models, as the correct prediction had a higher correlation to the target. This observation suggests that deeper DL architectures might positively impact the model’s learning. However, there were also instances, even by the best-obtained model, where the prediction was correct but there was no or little correlation to the target. For this, further research is required, including using alternatives to the Grad-CAM technique to better understand and improve the training dataset. Further, this study’s results showed the importance of generating a visual explanation of the classification results besides classification metrics. Lastly, the results showed the potential of DL architectures toward an automated data interpretation of the GPR C-scans collected from archaeological sites.
In conclusion, the findings of this study offer valuable insights into the adaptation of DL architectures for classifying GPR C-scans in archaeological prospection, bridging a gap in the existing literature. The study highlights the potential of DL in facilitating an efficient and automated interpretation scheme for GPR C-scans, emphasizing the importance of utilizing larger and more diverse annotated datasets and leveraging the advantages of deeper DL architectures. These results underscore the need for further investigations in this area, promoting continued exploration and advancements.
Author Contributions
Conceptualization, M.M.; methodology, M.M.; software, M.M.; validation, M.M., formal analysis, M.M.; investigation, M.M.; resources, M.M. and N.P.; data curation, M.M.; writing—original draft preparation, M.M.; writing—review and editing, N.P., N.S. and A.D.I.; visualization, M.M.; supervision, M.M.; project administration, N.S. and A.D.I.; funding acquisition, A.D.I. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the European Union through two projects: ERA4CH (Earthquake Risk Platform For European Cities Cultural Heritage Protection—grant agreement No. 101086280) and EYE (Economy bY spacE—grand agreement No. 10100763), both part of the Horizon 2020 research and innovation programme.
Acknowledgments
We sincerely acknowledge the students, researchers, and professors who collaborated with the Laboratory of Geophysical Satellite Remote Sensing and Archaeoenvironment (GeoSat ReSeArch Lab), Institute for Mediterranean Studies (IMS), Foundation for Research and Technology Hellas (FORTH) in conducting all the fieldworks and collecting the GPR data. Their contributions were vital to constructing the dataset used in this study. We also extend our thanks to the GeoSat ReSeArch Lab personnel for their support and provision of resources, which greatly facilitated the research process.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Conyers, L.B. Ground-Penetrating Radar for Archaeology; AltaMira Press: Walnut Creek, CA, USA, 2004. [Google Scholar]
- Goodman, D. GPR methods for archaeology. In Seeing the Unseen. Geophysics and Landscape Archaeology; Taylor & Francis: Abingdon, UK, 2009; pp. 229–244. [Google Scholar]
- Manataki, M.; Sarris, A.; Donati, J.C.; Cuenca Garcia, C.; Kalayci, T. GPR: Theory and Practice in Archaeological Prospection. In Best Practices of Geoinformatic Technologies for the Mapping of Archaeolandscapes; Archaeopress Archaeology: Oxford, UK, 2015; pp. 13–24. [Google Scholar]
- Manataki, M.; Vafidis, A.; Sarris, A. GPR Data Interpretation Approaches in Archaeological Prospection. Appl. Sci. 2021, 11, 7531. [Google Scholar] [CrossRef]
- Küçükdemirci, M.; Sarris, A. GPR Data Processing and Interpretation Based on Artificial Intelligence Approaches: Future Perspectives for Archaeological Prospection. Remote Sens. 2022, 14, 3377. [Google Scholar] [CrossRef]
- Shen, D.; Wu, G.; Suk, H.-I. Deep Learning in Medical Image Analysis. Annu. Rev. Biomed. Eng. 2017, 19, 221–248. [Google Scholar] [CrossRef]
- Grigorescu, S.; Trasnea, B.; Cocias, T.; Macesanu, G. A survey of deep learning techniques for autonomous driving. J. Field Robot. 2020, 37, 362–386. [Google Scholar] [CrossRef]
- Guo, G.; Zhang, N. A survey on deep learning based face recognition. Comput. Vis. Image Underst. 2019, 189, 102805. [Google Scholar] [CrossRef]
- Li, L.; Zhang, S.; Wang, B. Plant Disease Detection and Classification by Deep Learning—A Review. IEEE Access 2021, 9, 56683–56698. [Google Scholar] [CrossRef]
- Huang, J.; Yang, X.; Zhou, F.; Li, X.; Zhou, B.; Lu, S.; Ivashov, S.; Giannakis, I.; Kong, F.; Slob, E. A deep learning framework based on improved self-supervised learning for ground-penetrating radar tunnel lining inspection. Comput. Aided Civ. Infrastruct. Eng. 2023; early view. [Google Scholar] [CrossRef]
- Li, X.; Liu, H.; Zhou, F.; Chen, Z.; Giannakis, I.; Slob, E. Deep learning–based nondestructive evaluation of reinforcement bars using ground-penetrating radar and electromagnetic induction data. Comput. Aided Civ. Infrastruct. Eng. 2022, 37, 1834–1853. [Google Scholar] [CrossRef]
- Elghaish, F.; Matarneh, S.T.; Talebi, S.; Abu-Samra, S.; Salimi, G.; Rausch, C. Deep learning for detecting distresses in buildings and pavements: A critical gap analysis. Constr. Innov. 2021, 22, 554–579. [Google Scholar] [CrossRef]
- Küçükdemirci, M.; Sarris, A. Deep learning based automated analysis of archaeo-geophysical images. Archaeol. Prospect. 2020, 27, 107–118. [Google Scholar] [CrossRef]
- Wunderlich, T.; Wilken, D.; Majchczack, B.S.; Segschneider, M.; Rabbel, W. Hyperbola Detection with RetinaNet and Comparison of Hyperbola Fitting Methods in GPR Data from an Archaeological Site. Remote Sens. 2022, 14, 3665. [Google Scholar] [CrossRef]
- Manataki, M.; Vafidis, A.; Sarris, A. Comparing Adam and SGD optimizers to train AlexNet for classifying GPR C-scans featuring ancient structures. In Proceedings of the 2021 11th International Workshop on Advanced Ground Penetrating Radar (IWAGPR), Valletta, Malta, 1–4 December 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Abu-Mostafa, Y.S.; Magdon-Ismail, M.; Lin, H.-T. Learning from Data; AMLBook: New York, NY, USA, 2012; Volume 4. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; The MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; Curran Associates, Inc.: Red Hook, NY, USA, 2012. Available online: https://papers.nips.cc/paper_files/paper/2012/hash/c399862d3b9d6b76c8436e924a68c45b-Abstract.html (accessed on 29 April 2023).
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. arXiv 2015, arXiv:1502.03167. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2015, arXiv:1409.1556. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Distributed Systems. arXiv 2016, arXiv:1603.04467. [Google Scholar] [CrossRef]
- Chollet, F.; Keras. Keras: Deep Learning for Humans. 2015. Available online: https://keras.io/ (accessed on 8 May 2023).
- Hossin, M.; Sulaiman, M.N. A review on evaluation metrics for data classification evaluations. Int. J. Data Min. Knowl. Manag. Process 2015, 5, 1. [Google Scholar]
- Lever, J. Classification evaluation: It is important to understand both what a classification metric expresses and what it hides. Nat. Methods 2016, 13, 603–605. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Donati, J.C.; Sarris, A.; Papadopoulos, N.; Kalaycı, T.; Simon, F.-X.; Manataki, M.; Moffat, I.; Cuenca-García, C. A regional approach to ancient urban studies in Greece through multi-settlement geophysical survey. J. Field Archaeol. 2017, 42, 450–467. [Google Scholar] [CrossRef]
- Driessen, J.; Sarris, A. Archaeology and Geophysics in Tandem on Crete. J. Field Archaeol. 2020, 45, 571–587. [Google Scholar] [CrossRef]
- Springenberg, J.T.; Dosovitskiy, A.; Brox, T.; Riedmiller, M. Striving for simplicity: The all convolutional net. arXiv 2014, arXiv:1412.6806. [Google Scholar]
- Chattopadhay, A.; Sarkar, A.; Howlader, P.; Balasubramanian, V.N. Grad-CAM++: Generalized Gradient-Based Visual Explanations for Deep Convolutional Networks. In Proceedings of the 2018 IEEE Winter Conference on Applications of Computer Vision (WACV), Lake Tahoe, NV, USA, 12–15 March 2018; pp. 839–847. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).