Deep Graph-Convolutional Generative Adversarial Network for Semi-Supervised Learning on Graphs
Abstract
1. Introduction
- We use the topological structure and attribute information of the graph to perform symmetric normalized Laplace transform, map the graph data into a highly nonlinear space, and obtain the hidden variables and the features of each node.
- The bicubic structured interpolation (BI) is used for each sample to transform the node features into regular structured data, which is sent to the discriminator as a positive sample.
- The feature-enhanced (FE) module is introduced to selectively enhance the the typicality and discriminability of node characteristics and extract richer and more representative feature information, which is in favor of facilitating accurate classification.
- We expand the sample size of the model and add additional constraints to the network model by incorporating DCGAN, thus enhancing the robustness of the model. We perform four benchmark datasets to confirm the validity and evaluate the properties of DGCGAN through a comprehensive comparison with state-of-the-art methods.
2. Preliminary and Related Work
2.1. Graph Convolutional Networks
2.2. Spectral GCN and Spatial GCN
2.3. Deep Convolutional Generative Adversarial Network
2.4. Semi-Supervised Learning on Graphs
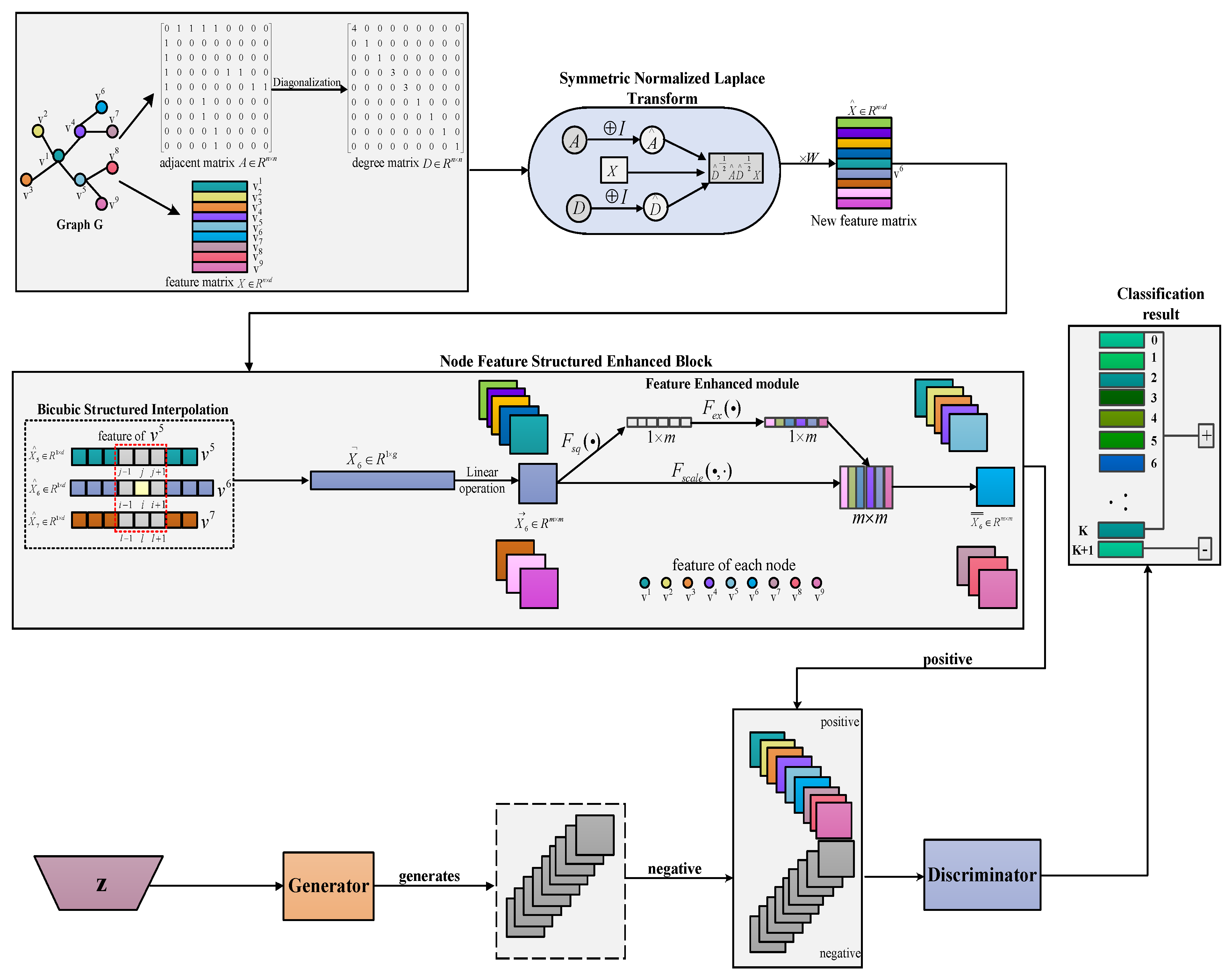
3. Deep Graph Convolutional Generative Adversarial Networks
3.1. The Overall Architecture
| Algorithm 1: The framework of DGCGAN. |
Input: Graph structure G containing adjacency matrix and feature matrix Output: dimensional vector R 1 for do (n is the number of nodes) Initialize the , 2 Symmetric normalized Laplace transformation (3) to calculate the feature matrix 3 According to the i-th node feature to obtain by bicubic structured interpolation, obtaining by reshape operation. to calculate 5 Input random noise to the generator to obtain 6 for to T do (T is the total number of iterations) Taking two positive samples from the set and taking two negative samples from the set 7 discriminator generator 8 According to Equation (11), calculate unsupervised loss function 9 The discriminator performs supervised learning to obtain dimensional vector R and updates the full supervised loss function 10 end for 11 end for 12 return the classification results R |
3.2. Symmetric Normalized Laplace Transform
3.3. Node Feature-Structured Enhanced Block
3.3.1. Bicubic Structured Interpolation
3.3.2. Feature-Enhanced Module
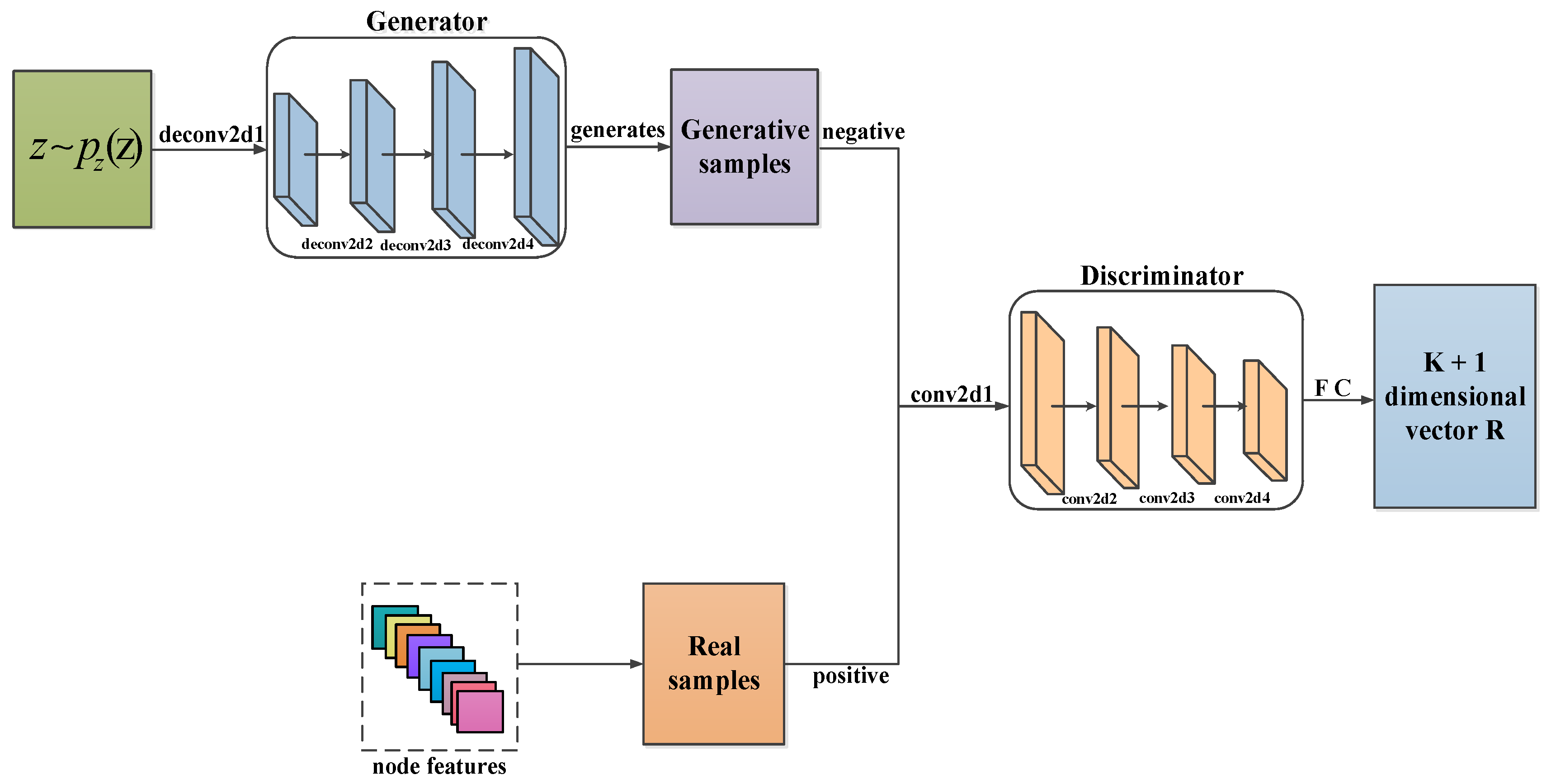
3.4. Deep Convolutional Generative Adversarial Networks
3.4.1. Generator
3.4.2. Discriminator
3.5. Loss Function
3.6. Complexity Analysis
4. Experiments and Analysis
4.1. Datasets
4.2. Baselines
4.3. Performance Comparison
4.3.1. Node Classification
4.3.2. Node Clustering
4.3.3. Remote Sensing Scene Classification
4.4. Ablation Study
4.4.1. The Effectiveness of Symmetric Normalized Laplace Transform
4.4.2. The Effectiveness of BI and SE
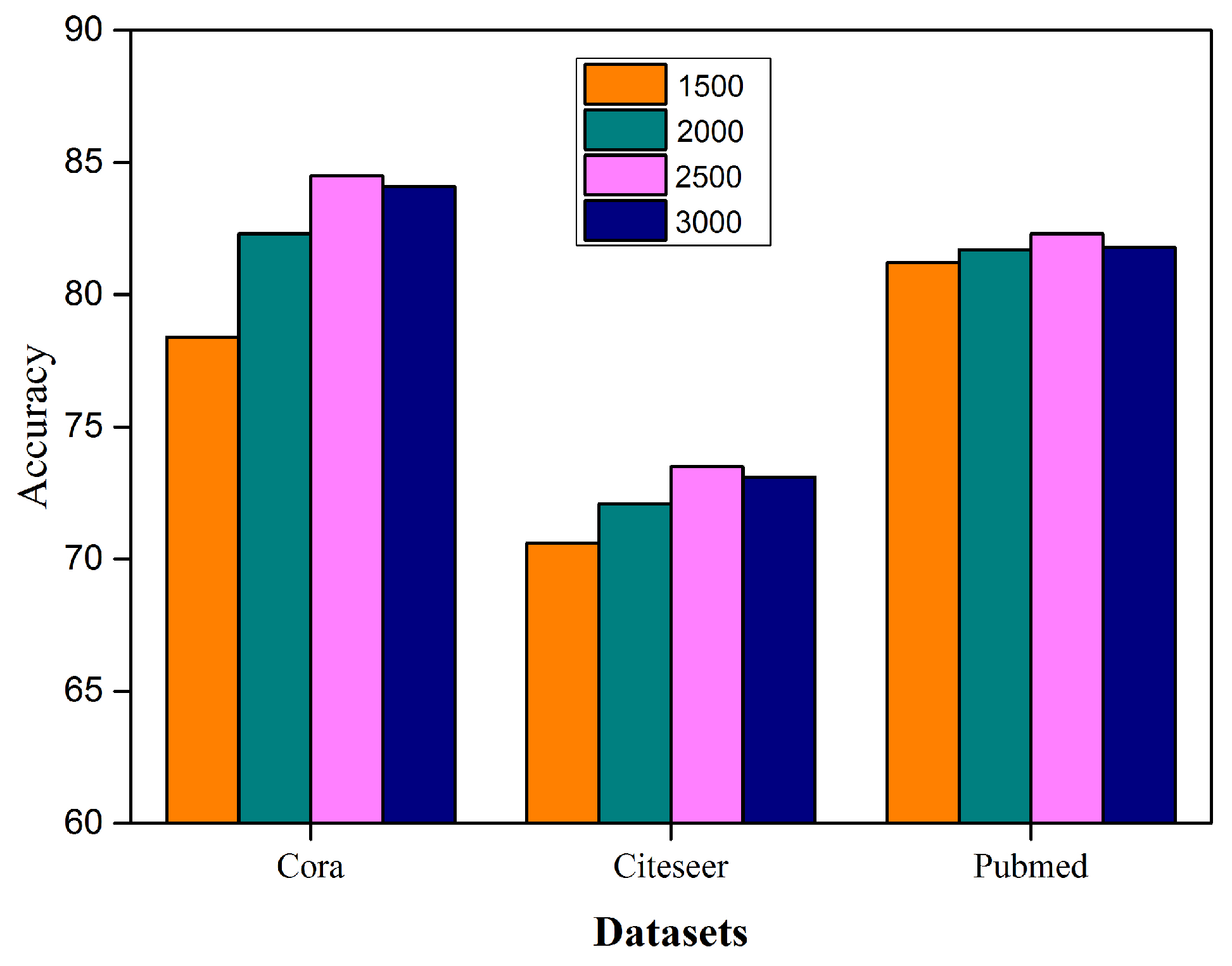
4.4.3. Sample Augment Analysis
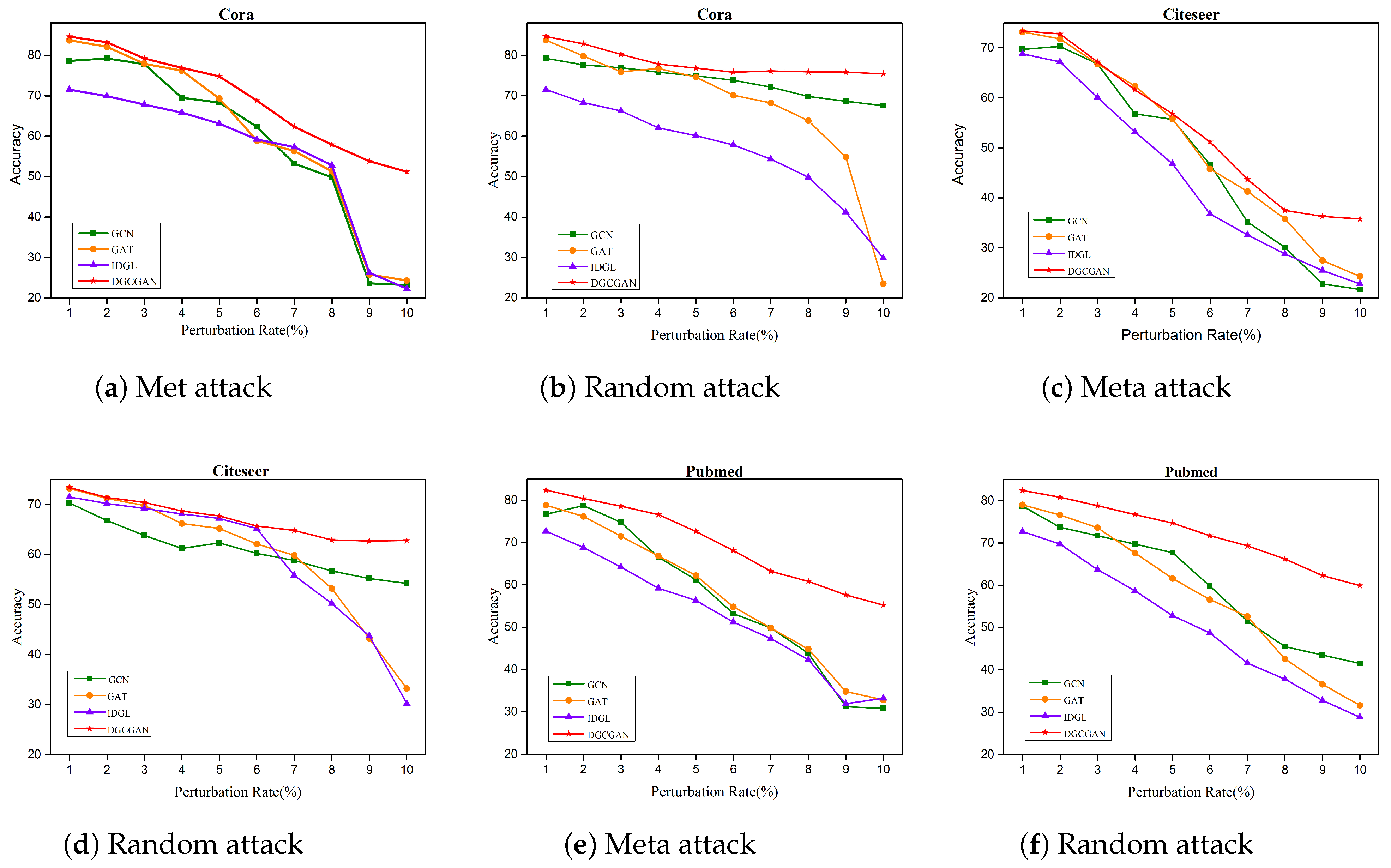
4.4.4. Robustness Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kipf, T.N.; Welling, M. Variational Graph Auto-Encoders. Neural Inf. Process. Syst. Workshop 2016, 3, 1–3. [Google Scholar]
- Peng, Z.; Huang, W.; Luo, M.; Zheng, Q.; Rong, Y.; Xu, T.; Huang, J. Graph representation learning via graphical mutual information maximization. Proc. Web Conf. 2020, 2, 259–270. [Google Scholar]
- Liu, Y.; Li, Z.; Pan, S.; Gong, C.; Zhou, C.; Karypis, G. Anomaly Detection on Attributed Networks via Contrastive Self-Supervised Learning. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 2378–2392. [Google Scholar] [CrossRef]
- Abu-El-Haija, S.; Perozzi, B.; Kapoor, A.; Alipourfard, N.; Lerman, K.; Harutyunyan, H.; Ver Steeg, G.; Galstyan, A. Mixhop: Higher-order graph convolution architectures via sparsified neighborhood mixing. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019. [Google Scholar]
- Jin, W.; Ma, Y.; Liu, X.; Tang, X.; Wang, S.; Tang, J. Graph structure learning for robust graph neural network. In Proceedings of the 26th ACM SIGKDD, International Conference on Knowledge Discovery & Data Mining, Virtual Event, 6–10 July 2020; Volume 6, pp. 66–74. [Google Scholar]
- Namata, G.; London, B.; Getoor, L.; Huang, B.; Edu, U. Query-driven active surveying for collective classification. In Proceedings of the 10th International Workshop on Mining and Learning with Graphs, Edinburgh, UK, 1 July 2012. [Google Scholar]
- Wang, C.; Pan, S.; Hu, R.; Long, G.; Jiang, J.; Zhang, C. Attributed Graph Clustering: A Deep Attentional Embedding Approach. Int. Jt. Conf. Artif. Intell. 2019, 3, 3670–3676. [Google Scholar]
- Zhang, X.; Liu, H.; Li, Q.; Wu, X.M. Attributed Graph Clustering via Adaptive Graph Convolution. Int. Jt. Conf. Artif. Intell. 2019, 2, 4327–4333. [Google Scholar]
- Caron, M.; Bojanowski, P.; Joulin, A.; Douze, M. Deep clustering for unsupervised learning of visual features. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018; Volume 1, pp. 132–149. [Google Scholar]
- Tian, F.; Gao, B.; Cui, Q.; Chen, E.; Liu, T.Y. Learning deep representations for graph clustering. In Proceedings of the AAAI Conference on Artificial Intelligence, Quebec City, QC, Canada, 2–31 July 2014; Volume 28. [Google Scholar]
- Wang, C.; Pan, S.; Long, G.; Zhu, X.; Jiang, J. Mgae: Marginalized graph autoencoder for graph clustering. In Proceedings of the 2017 ACM on Conference on Information and Knowledge Management, Singapore, 6–10 November 2017; Volume 2, pp. 889–898. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-Supervised Classification with Graph Convolutional Networks. In Proceedings of the International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar]
- Bruna, J.; Zaremba, W.; Szlam, A.; LeCun, Y. Spectral networks and deep locally connected networks on graphs. In Proceedings of the 2nd International Conference on Learning Representations, ICLR 2014—Conference Track Proceedings, Banff, AB, Canada, 14–16 April 2014; Volume 1, pp. 1–14. [Google Scholar]
- Scarselli, F.; Gori, M.; Tsoi, A.C.; Hagenbuchner, M.; Monfardini, G. The Graph Neural Network Model. IEEE Trans. Neural Netw. 2009, 20, 61–80. [Google Scholar] [CrossRef]
- Monti, F.; Boscaini, D.; Masci, J.; Rodolà, E.; Svoboda, J.; Bronstein, M.M. Geometric deep learning on graphs and manifolds using mixture model CNNs. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 5425–5434. [Google Scholar] [CrossRef]
- Gilmer, J.; Schoenholz, S.S.; Riley, P.F.; Vinyals, O.; Dahl, G.E. Neural message passing for quantum chemistry. In Proceedings of the 34th International Conference on Machine Learning, ICML, Sydney, Australia, 6–11 August 2017; Volume 3, pp. 2053–2070. [Google Scholar]
- Belkin, M.; Niyogi, P.; Sindhwani, V. Manifold Regularization: A Geometric Framework for Learning from Labeled and Unlabeled Examples. J. Mach. Learn. Res. 2006, 7, 2399–2434. [Google Scholar]
- Weston, J.; Ratle, F.; Collobert, R. Deep learning via semi-supervised embedding. In Proceedings of the 25th International Conference on Machine Learning, Helsinki, Finland, 5–9 July 2008; Volume 1, pp. 1168–1175. [Google Scholar]
- Yang, Z.; Cohen, W.W.; Salakhutdinov, R. Revisiting Semi-Supervised Learning with Graph Embeddings. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016. [Google Scholar]
- Velicković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Liò, P.; Bengio, Y. Graph attention networks. arXiv 2017, arXiv:1710.10903. [Google Scholar]
- Xiao, S.; Wang, S.; Guo, W. SGAE: Stacked Graph Autoencoder for Deep Clustering. IEEE Trans. Big Data. 2023, 9, 254–266. [Google Scholar] [CrossRef]
- Henaff, M.; Bruna, J.; Lecun, Y. Deep Convolutional Networks on Graph-Structured Data. arXiv 2015, arXiv:1506.05163. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. In Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Wang, H.; Wang, J.; Wang, J.; Zhao, M.; Zhang, W.; Zhang, F.; Xie, X.; Guo, M. Graphgan: Graph representation learning with generative adversarial nets. In Proceedings of the 32nd AAAI Conference on Artificial Intelligence, AAAI 2018, New Orleans, LA, USA, 2–7 February 2018; Volume 1, pp. 2508–2515. [Google Scholar]
- Yan, R.; Shen, H.; Qi, C.; Cen, K.; Wang, L. GraphWGAN: Graph representation learning with wasserstein generative adversarial networks. In Proceedings of the IEEE International Conference on Big Data and Smart Computing (BigComp 2020), Busan, Republic of Korea, 19–22 February 2020; Volume 1, pp. 315–322. [Google Scholar]
- Gao, X.; Ma, X.; Zhang, W.; Huang, J.; Li, H.; Li, Y.; Cui, J. Multi-View Clustering With Self-Representation and Structural Constraint. IEEE Trans. Big Data. 2022, 8, 882–893. [Google Scholar] [CrossRef]
- Xie, Y.; Lv, S.; Qian, Y.; Wen, C.; Liang, J. Active and Semi-Supervised Graph Neural Networks for Graph Classification. IEEE Trans. Big Data 2022, 8, 920–932. [Google Scholar] [CrossRef]
- Cheng, H.; Liao, L.; Hu, L.; Nie, L. Multi-Relation Extraction via A Global-Local Graph Convolutional Network. IEEE Trans. Big Data. 2022, 8, 1716–1728. [Google Scholar] [CrossRef]
- Yue, G.; Xiao, R.; Zhao, Z.; Li, C. AF-GCN: Attribute-Fusing Graph Convolution Network for Recommendation. IEEE Trans. Big Data. 2023, 9, 597–607. [Google Scholar] [CrossRef]
- Xu, B.; Shen, H.; Cao, Q.; Qiu, Y.; Cheng, X. Graph wavelet neural network. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Xu, B.; Shen, H.; Cao, Q.; Cen, K.; Cheng, X. Graph convolutional networks using heat kernel for semi-supervised learning. In Proceedings of the IJCAI International Joint Conference on Artificial Intelligence, Macao, China, 10–16 August 2019; pp. 1928–1934. [Google Scholar]
- Klicpera, J.; Bojchevski, A.; Günnemann, S. Predict then propagate: Graph neural networks meet personalized PageRank. In Proceedings of the 7th International Conference on Learning Representations, ICLR 2019, New Orleans, LA, USA, 6–9 May 2019; Volume 2, pp. 1–15. [Google Scholar]
- Wu, F.; Zhang, T.; de Souza, A.H.; Fifty, C.; Yu, T.; Weinberger, K.Q. Simplifying graph convolutional networks. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 10–15 June 2019; pp. 11884–11894. [Google Scholar]
- Hamilton, W.; Ying, R.; Leskovec, J. Inductive Representation Learning on Large Graphs. Adv. Neural Inf. Process. Syst. 2017, 2, 1024–1034. [Google Scholar]
- Atwood, J.; Towsley, D. Diffusion-Convolutional Neural Networks. In Proceedings of the Conference and Workshop on Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016. [Google Scholar]
- Vashishth, S.; Yadav, P.; Bhandari, M.; Talukdar, P. Confidence-based graph convolutional networks for semi-supervised learning. In Proceedings of the 22nd International Conference on Artificial Intelligence and Statistics, Naha, Okinawa, Japan, 16–18 April 2019. [Google Scholar]
- Feng, Y.; You, H.; Zhang, Z.; Ji, R.; Gao, Y. Hypergraph neural networks. In Proceedings of the 33rd AAAI Conference on Artificial Intelligence, AAAI 2019, Honolulu, HI, USA, 27 January–1 February 2019; Volume 3, pp. 3558–3565. [Google Scholar]
- Busbridge, D.; Sherburn, D.; Cavallo, P.; Hammerla, N.Y. Relational graph attention networks. arXiv 2019, arXiv:1904.05811. [Google Scholar]
- Xu, K.; Li, C.; Tian, Y.; Sonobe, T.; Kawarabayashi, K.I.; Jegelka, S. Representation Learning on Graphs with Jumping Knowledge Networks. Int. Conf. Mach. Learn. 2018, 1, 5453–5462. [Google Scholar]
- Zhang, Y.; Wei, X.; Zhang, X.; Hu, Y.; Yin, B. Self-Attention Graph Convolution Residual Network for Traffic Data Completion. IEEE Trans. Big Data 2023, 9, 528–541. [Google Scholar] [CrossRef]
- Ling, X.; Wu, L.; Wang, S.; Ma, T.; Xu, F.; Liu, A.X.; Wu, C.; Ji, S. Multilevel Graph Matching Networks for Deep Graph Similarity Learning. IEEE Trans. Neural Netw. Learn. Syst. 2021, 34, 799–813. [Google Scholar] [CrossRef]
- Qin, C.; Zhao, H.; Wang, L.; Wang, H.; Zhang, Y.; Fu, Y. Slow learning and fast inference: Efficient graph similarity computation via knowledge distillation. Adv. Neural Inf. Process. Syst. 2021, 34, 14110–14121. [Google Scholar]
- Li, N.; Gong, C.; Zhao, H.; Ma, Y. Space Target Material Identification Based on Graph Convolutional Neural Network. Remote Sens. 2023, 15, 1937. [Google Scholar] [CrossRef]
- Liu, W.; Liu, B.; He, P.; Hu, Q.; Gao, K.; Li, H. Masked Graph Convolutional Network for Small Sample Classification of Hyperspectral Images. Remote Sens. 2023, 15, 1869. [Google Scholar] [CrossRef]
- Shi, M.; Tang, Y.; Zhu, X.; Liu, J. Multi-Label Graph Convolutional Network Representation Learning. IEEE Trans. Big Data 2022, 8, 1169–1181. [Google Scholar] [CrossRef]
- Radford, A.; Metz, L.; Chintala, S. Unsupervised representation learning with deep convolutional generative adversarial networks. In Proceedings of the 4th International Conference on Learning Representations, ICLR 2016—Conference Track Proceedings, San Juan, Puerto Rico, 2–4 May 2016; Volume 2, pp. 1–16. [Google Scholar]
- Sen, P.; Namata, G.; Bilgic, M.; Getoor, L.; Eliassi-Rad, T. Collective Classification in Network Data Articles. Ai Mag. 2008, 29, 93–106. [Google Scholar]
- Zhu, X.; Ghahramani, Z.; Lafferty, J. Semi-Supervised Learning Using Gaussian Fields and Harmonic Functions. In Proceedings of the 20th International conference on Machine learning (ICML-03), Washington, DC, USA, 21–24 August 2003; Volume 3, pp. 912–919. [Google Scholar]
- Perozzi, B.; Al-Rfou, R.; Skiena, S. DeepWalk: Online Learning of Social Representations. KDD 2014, 29, 701–710. [Google Scholar]
- Marcheggiani, D.; Titov, I. Encoding sentences with graph convolutional networks for semantic role labeling. In Proceedings of the EMNLP 2017—Conference on Empirical Methods in Natural Language Processing, Proceedings, Copenhagen, Denmark, 7–11 September 2017; Volume 1, pp. 1506–1515. [Google Scholar]
- Liao, R.; Brockschmidt, M.; Tarlow, D.; Gaunt, A.L.; Urtasun, R.; Zemel, R. Graph partition neural networks for semi-supervised classification. arXiv 2018, arXiv:1803.06272. [Google Scholar]
- Chami, I.; Ying, R.; Ré, C.; Leskovec, J. Hyperbolic Graph Convolutional Neural Networks. Adv. Neural Inf. Process. Syst. 2019, 32, 4869–4880. [Google Scholar] [PubMed]
- Liu, Q.; Nickel, M.; Kiela, D. Hyperbolic Graph Neural Networks. Proc. Int. Conf. Neural Inf. Process. Syst. 2019, 32, 8228–8239. [Google Scholar]
- Wang, H.; Zhou, C.; Chen, X.; Wu, J.; Pan, S.; Wang, J. Graph Stochastic Neural Networks for Semi-supervised Learning. Adv. Neural Inf. Process. Syst. 2020, 33, 19839–19848. [Google Scholar]
- Chen, Y.; Wu, L.; Zaki, M.J. Iterative Deep Graph Learning for Graph Neural Networks: Better and Robust Node Embeddings. In Proceedings of the 34th Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 6–12 December 2020. [Google Scholar]
- Zeng, H.; Zhou, H.; Srivastava, A.; Kannan, R.; Prasanna, V. GraphSAINT: Graph sampling based inductive learning method. In Proceedings of the International Conference on Learning Representations, Online, 26 April–1 May 2020. [Google Scholar]
- Zhang, Y.; Wang, X.; Shi, C.; Jiang, X.; Ye, Y. Hyperbolic Graph Attention Network. IEEE Trans. Big Data 2022, 8, 1690–1701. [Google Scholar] [CrossRef]



| Datasets | Nodes | Edges | Classes | Features | Labeling Rate |
|---|---|---|---|---|---|
| Cora | 2708 | 5429 | 7 | 1433 | 0.052 |
| Citeseer | 3327 | 4732 | 6 | 3703 | 0.036 |
| Pubmed | 19,717 | 44,338 | 3 | 500 | 0.003 |
| ogbn-arxiv | 169,343 | 1,166,243 | 40 | 128 | 0.537 |
| Method | Cora | Citeseer | Pubmed | Ogbn-Arxiv |
|---|---|---|---|---|
| LP | 67.9 ± 0.1 | 45.1 ± 0.2 | 62.7 ± 0.3 | OOM |
| MLP | 56.1 ± 1.6 | 56.7 ± 1.7 | 71.4 ± 0.0 | 54.7 ± 0.1 |
| GRCN | 67.4 ± 0.3 | 67.3 ± 0.8 | 67.3 ± 0.3 | OOM |
| DeepWalk | 67.0± 1.0 | 47.8± 1.6 | 73.9 ± 0.8 | 55.6 ± 0.3 |
| GCN | 81.4 ± 0.1 | 70.1 ± 0.2 | 78.7 ± 0.3 | 69.9 ± 0.1 |
| G-GCN | 81.2 ± 0.4 | 69.6± 0.5 | 77.0 ± 0.3 | 68.2 ± 0.3 |
| GPNN | 79.0 ± 1.7 | 68.1 ± 1.8 | 73.6 ± 0.5 | 63.5 ± 0.4 |
| GAT | 83.0 ± 0.7 | 72.5 ± 0.7 | 78.8 ± 0.2 | OOM |
| SGCN | 81.0 ± 0.0 | 71.9 ± 0.1 | 78.9 ± 0.0 | 68.3 ± 0.6 |
| ConfGCN | 82.0 ± 0.3 | 72.7 ± 0.8 | 79.5 ± 0.5 | 68.9 ± 0.2 |
| GSNN-M | 83.9 ± 0.4 | 72.2 ± 0.4 | 79.1 ± 0.3 | 69.8 ± 0.2 |
| IDGL | 70.9 ± 0. 6 | 68.2 ± 0.6 | 72.3 ± 0.4 | OOM |
| HGCN | 80.5 ± 0.6 | 71.9 ± 0.4 | 79.3± 0.5 | 55.6 ± 0.2 |
| HAT | 83.6 ± 0.5 | 72.2 ± 0.6 | 79.6 ± 0.5 | OOM |
| APPNP | 81.2 ± 0.2 | 70.5 ± 0.1 | 79.8 ± 0.1 | 69.1± 0.0 |
| DGCGAN | 84.5 ± 0.1 | 73.3 ± 0.1 | 82.2 ± 0.2 | 71.2 ± 0.1 |
| Method | Cora | Citeseer | Pubmed |
|---|---|---|---|
| DeepWalk | 40.4 | 17.9 | 23.1 |
| GCN | 51.7 | 42.4 | 30.5 |
| GraphSAINT | 50.1 | 38.7 | 32.5 |
| GAT | 56.7 | 42.7 | 35.9 |
| Node2vec | 41.5 | 20.9 | 28.6 |
| HGCN | 57.2 | 42.1 | 37.2 |
| HGNN | 55.3 | 41.3 | 38.7 |
| DGCGAN | 59.2 | 44.1 | 40.2 |
| Basic Network | Methods | OA (20/80) (%) |
|---|---|---|
| AlexNet | MSCP | 85.58 ± 0.16 |
| VGG16 | MSCP | 88.93 ± 0.14 |
| AlexNet | SCCov | 87.30 ± 0.23 |
| GCN | DGCGAN | 89.73 ± 0.17 |
| Description | Propagation Model | Cora | Citeseer | Pubmed |
|---|---|---|---|---|
| MLP | XW | 55.1 | 46.5 | 71.4 |
| LT | (D-A)XW | 80.5 | 68.7 | 77.8 |
| SNLT | 81.5 | 70.3 | 79.0 |
| Parameter | Cora | Parameter | Citeseer |
|---|---|---|---|
| g = 1369 | 84.1 | g = 3600 | 72.9 |
| g = 1444 | 84.5 | g = 3721 | 73.3 |
| g = 1521 | 78.6 | g = 3844 | 72.8 |
| Parameter | Cora | Citeseer | Pubmed |
|---|---|---|---|
| s = 4208 | 78.6 | 70.6 | 80.9 |
| s = 4708 | 82.3 | 72.1 | 81.7 |
| s = 5208 | 84.5 | 72.6 | 80.7 |
| s = 5708 | 84.1 | 72.9 | 81.8 |
| s = 5906 | 83.8 | 71.3 | 80.8 |
| s = 6200 | 82.8 | 70.2 | 82.3 |
| s = 6800 | 81.6 | 68.8 | 78.8 |
| s = 7200 | 81.1 | 67.9 | 76.5 |
| s = 7800 | 79.8 | 73.3 | 74.8 |
| s = 8200 | 78.8 | 64.5 | 71.5 |
| s = 8800 | 76.5 | 62.8 | 69.5 |
| s = 21,200 | 75.8 | 60.9 | 68.7 |
| s = 22,500 | 76.8 | 59.8 | 67.5 |
| s = 23,200 | 75.2 | 57.8 | 66.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, N.; Tian, X.; Gao, W.; Jiao, L. Deep Graph-Convolutional Generative Adversarial Network for Semi-Supervised Learning on Graphs. Remote Sens. 2023, 15, 3172. https://doi.org/10.3390/rs15123172
Jia N, Tian X, Gao W, Jiao L. Deep Graph-Convolutional Generative Adversarial Network for Semi-Supervised Learning on Graphs. Remote Sensing. 2023; 15(12):3172. https://doi.org/10.3390/rs15123172
Chicago/Turabian StyleJia, Nan, Xiaolin Tian, Wenxing Gao, and Licheng Jiao. 2023. "Deep Graph-Convolutional Generative Adversarial Network for Semi-Supervised Learning on Graphs" Remote Sensing 15, no. 12: 3172. https://doi.org/10.3390/rs15123172
APA StyleJia, N., Tian, X., Gao, W., & Jiao, L. (2023). Deep Graph-Convolutional Generative Adversarial Network for Semi-Supervised Learning on Graphs. Remote Sensing, 15(12), 3172. https://doi.org/10.3390/rs15123172






