Implementation of Real-Time Space Target Detection and Tracking Algorithm for Space-Based Surveillance
Abstract
1. Introduction
2. Related Work
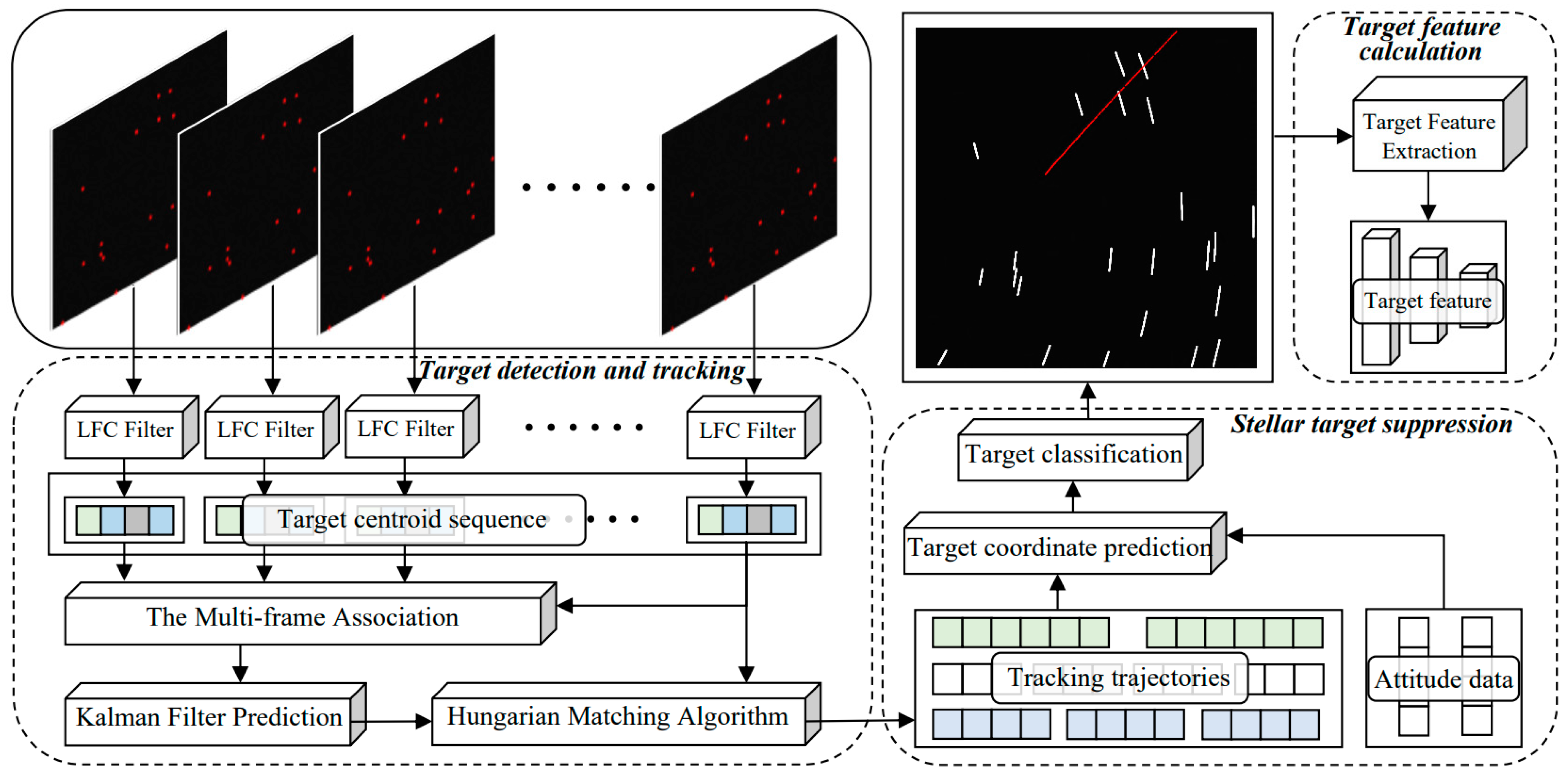
3. Methodology
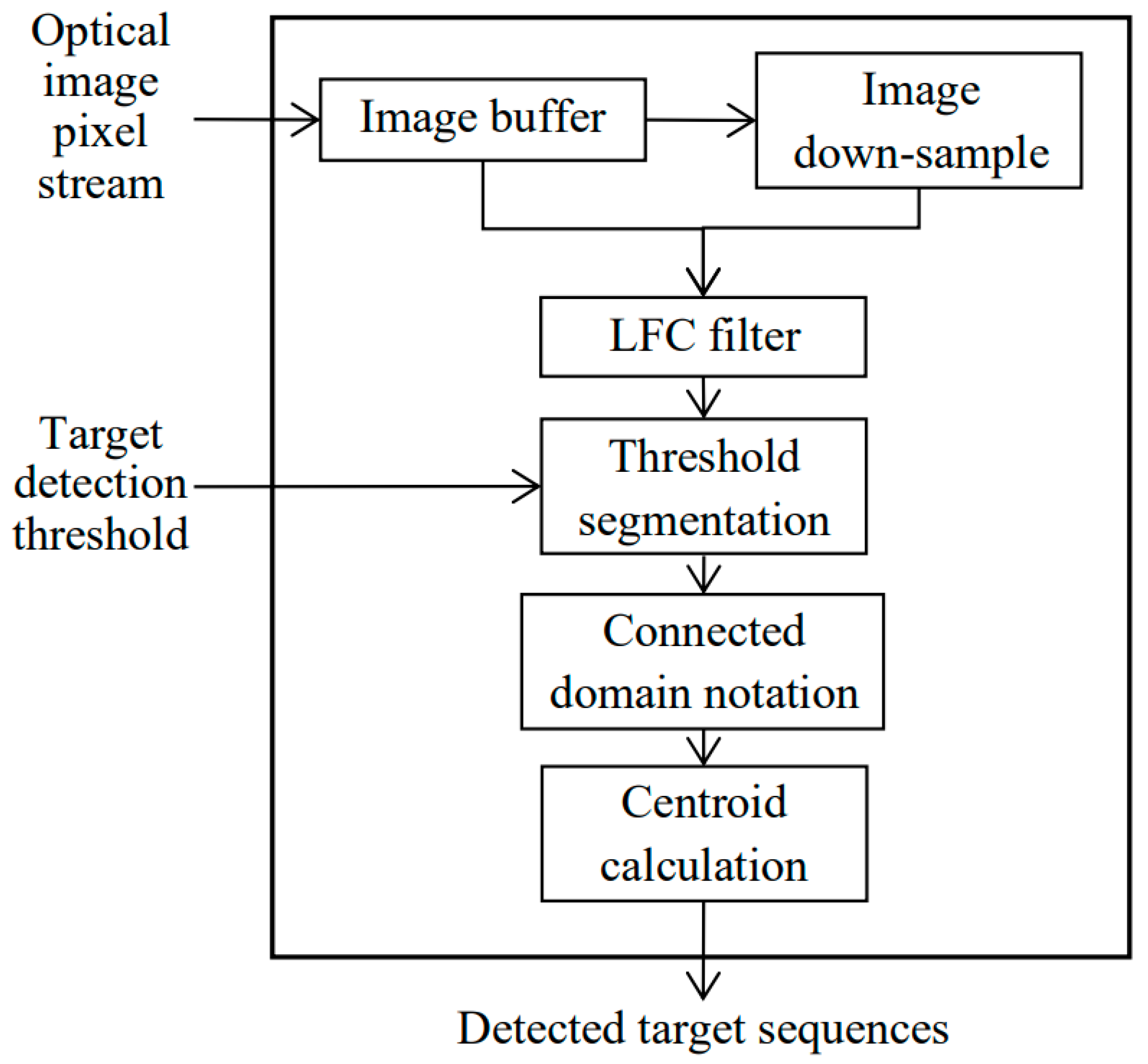
3.1. Target Detection and Tracking
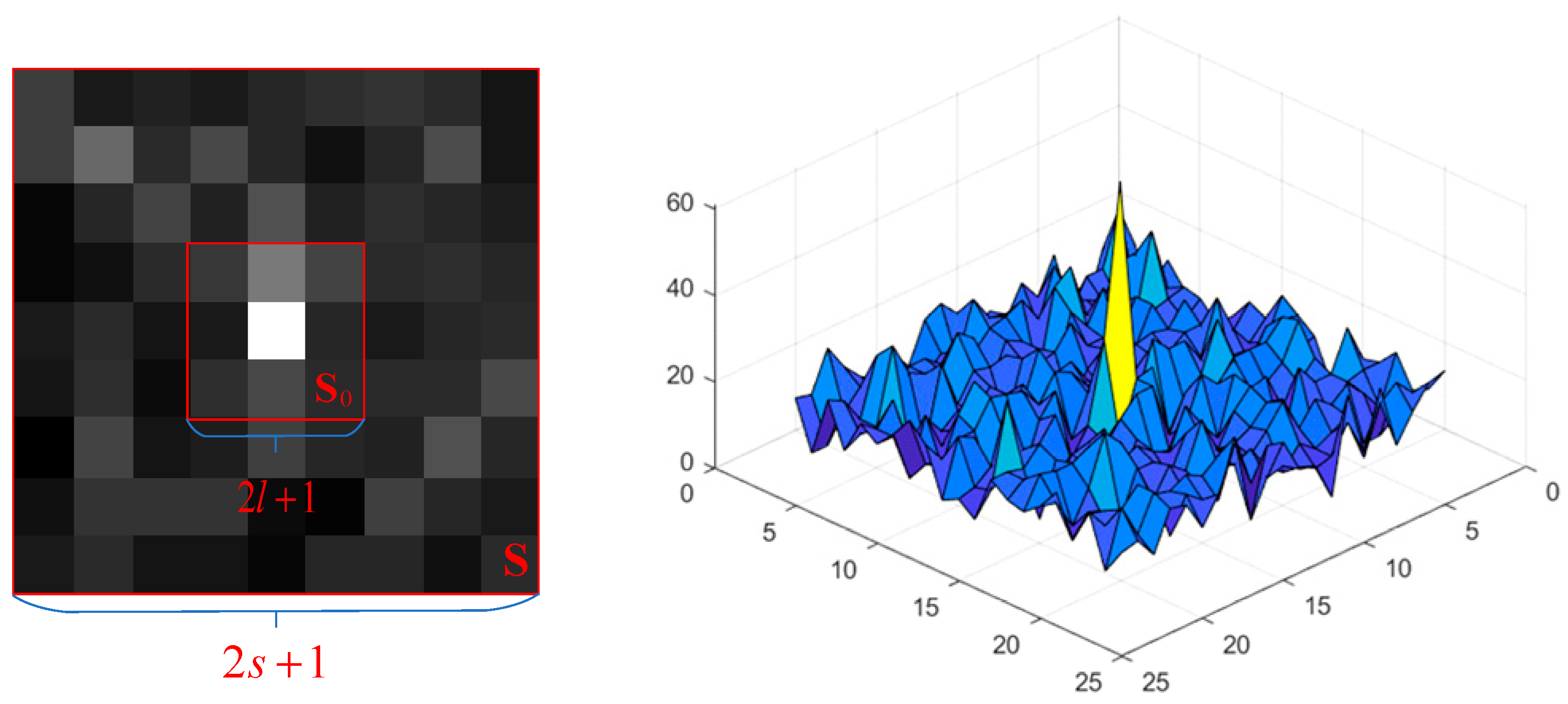
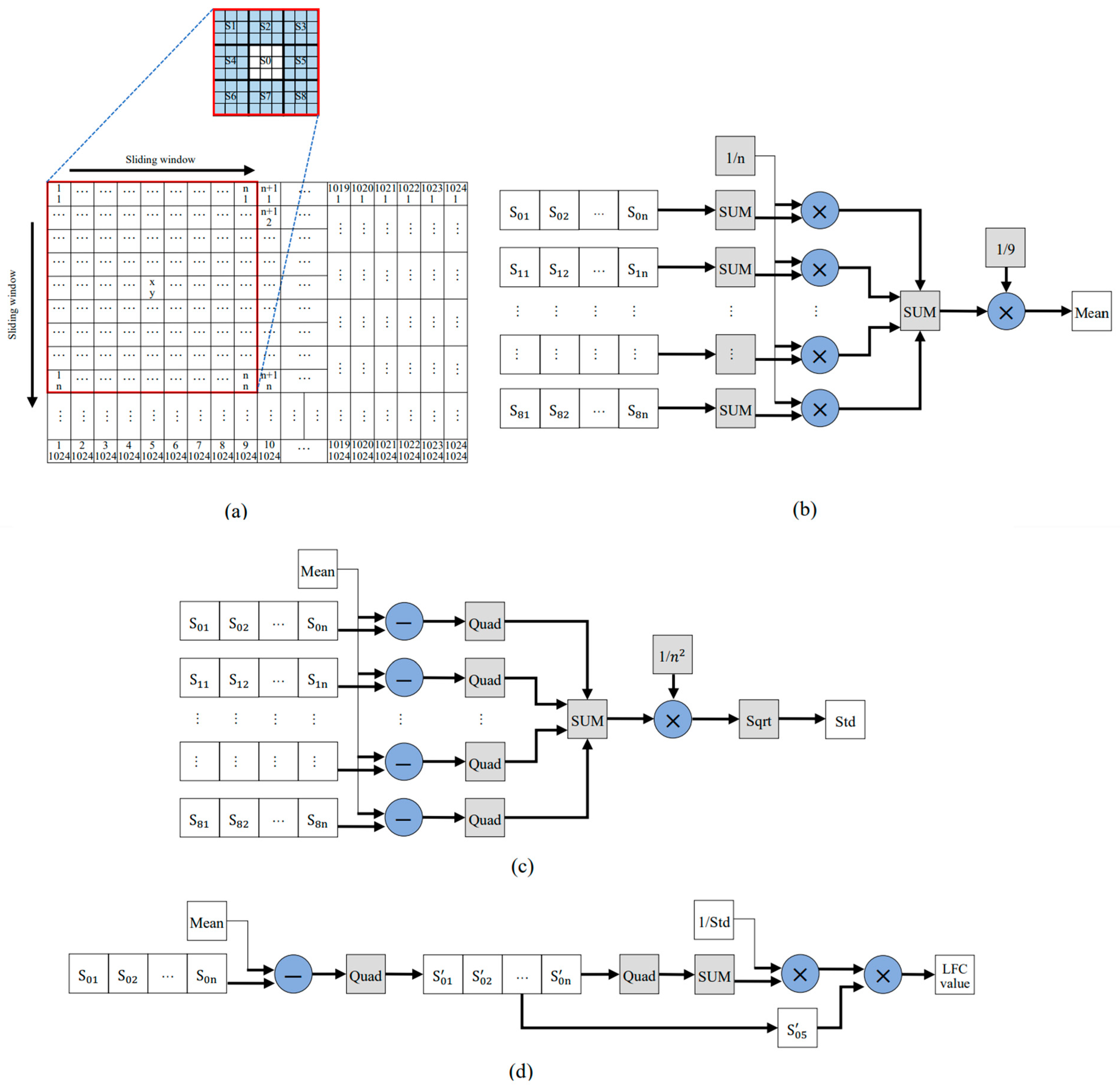
3.1.1. Target Detection Algorithm
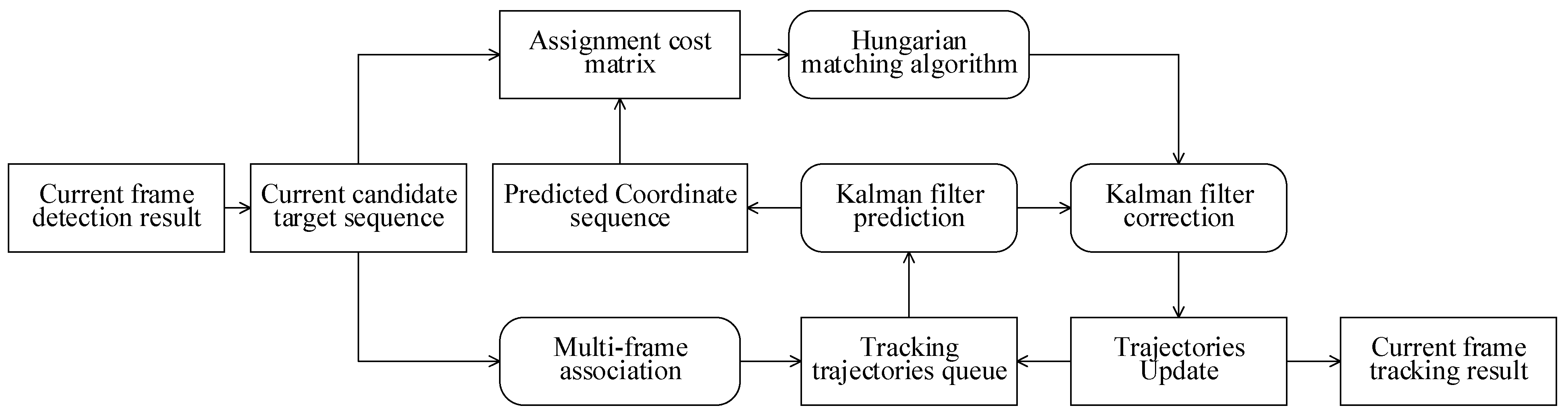
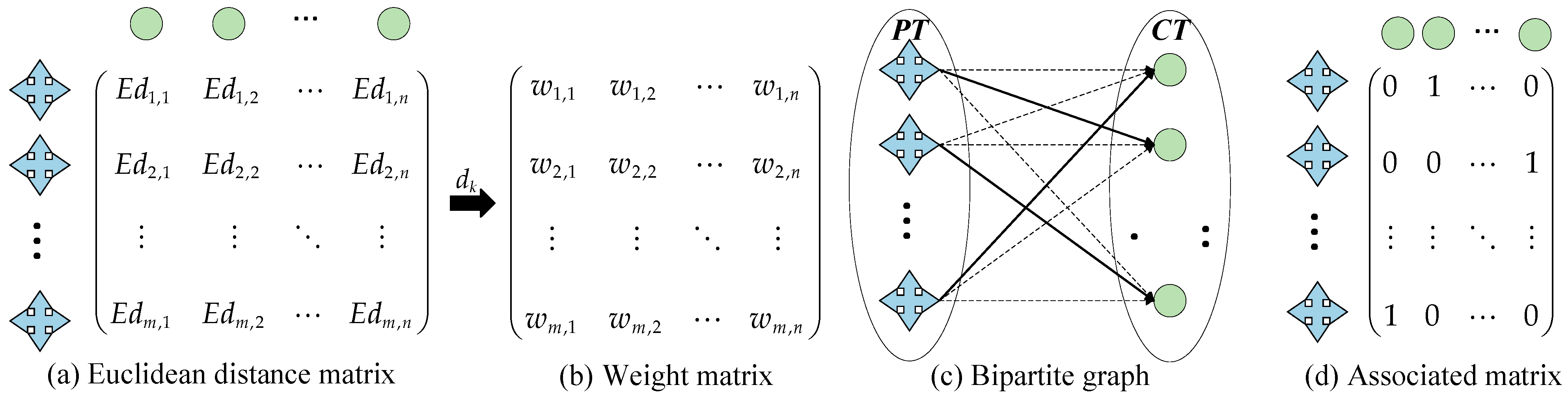
3.1.2. Target Tracking Algorithm
3.2. Stellar Target Suppression Algorithm
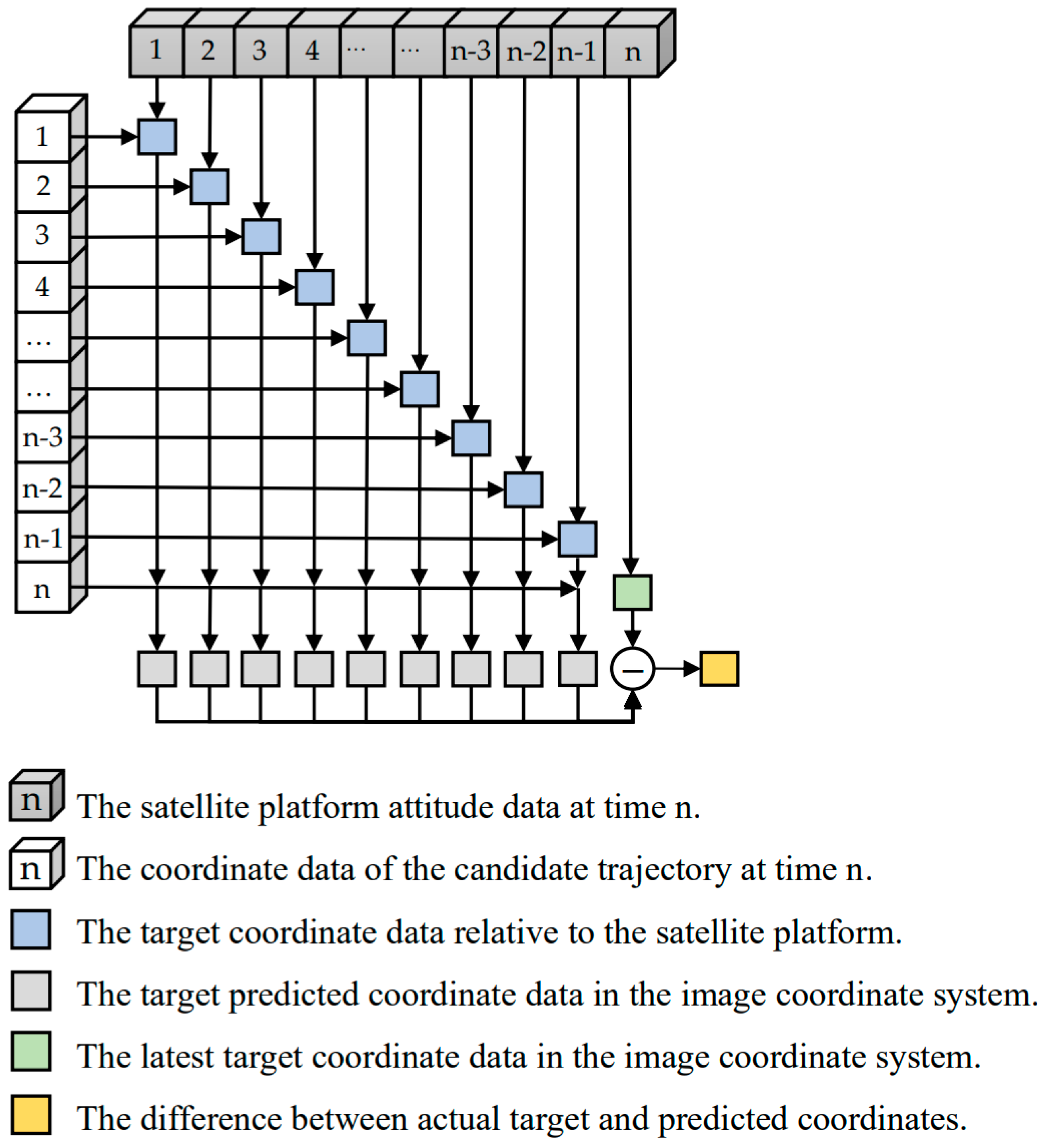
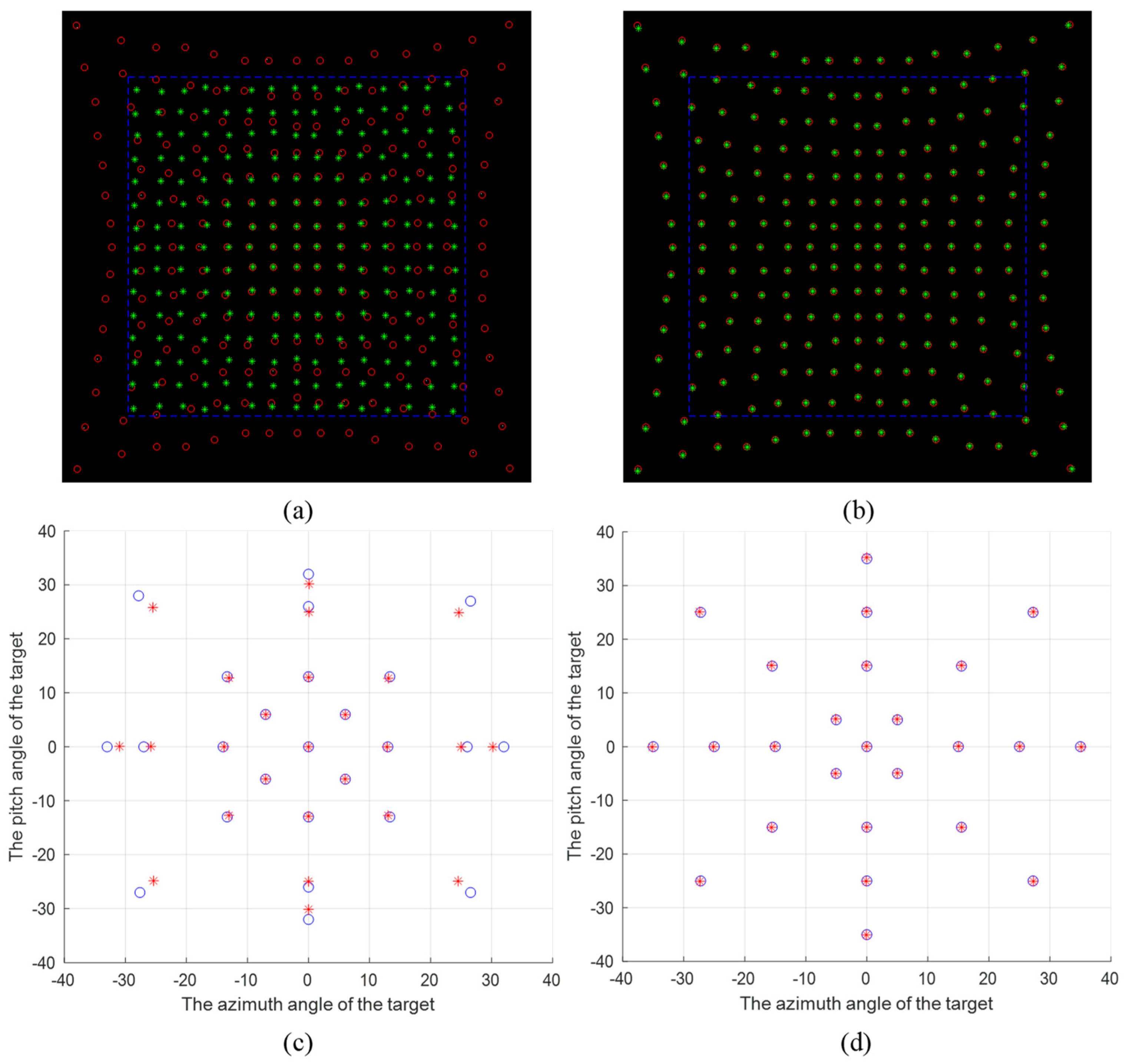
3.3. Target Angle Calculation
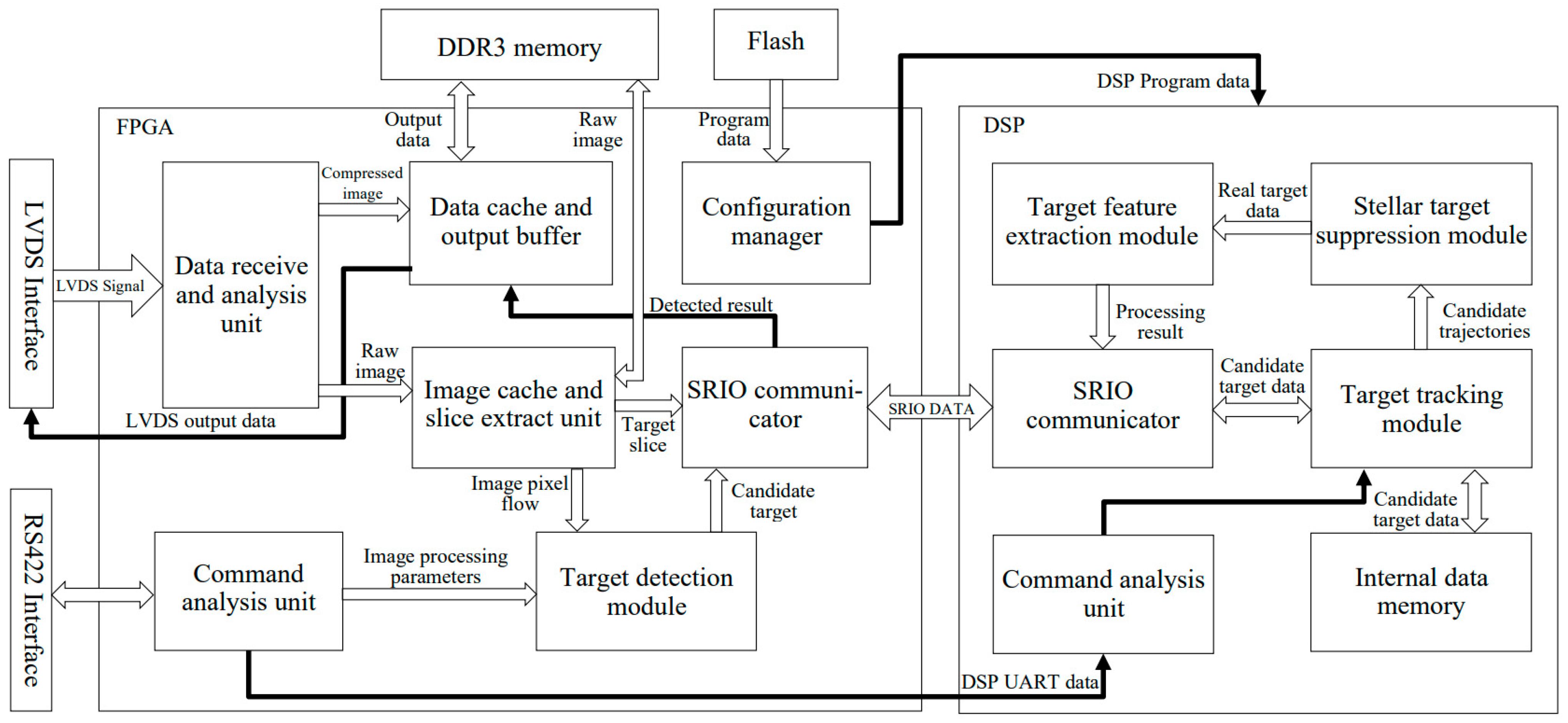
4. Hardware Implementation
4.1. Overall Hardware Design
4.2. FPGA Implementation
4.3. DSP Implementation
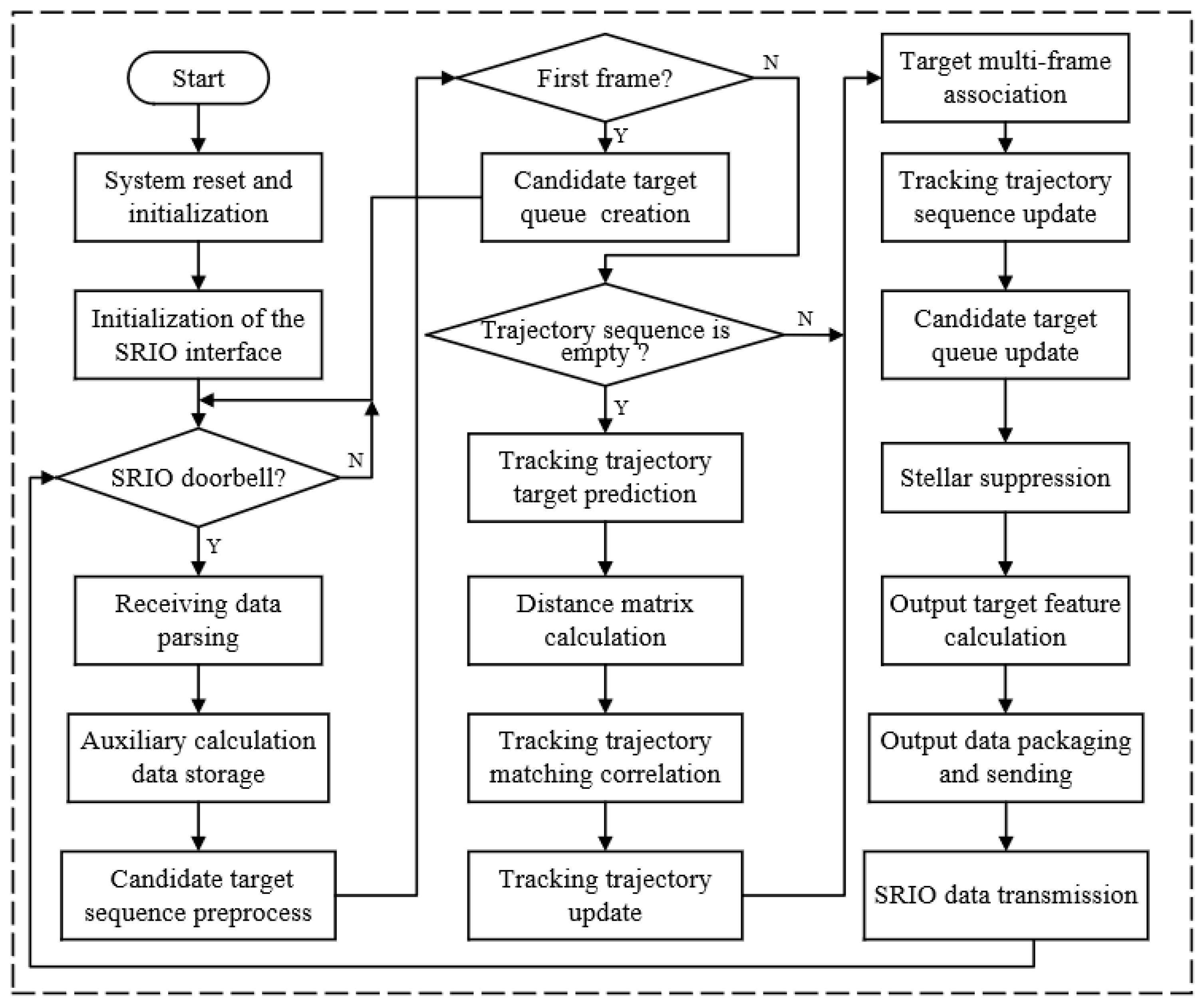
4.3.1. Target Tracking Module
4.3.2. Stellar Target Suppression Module
5. Experiment
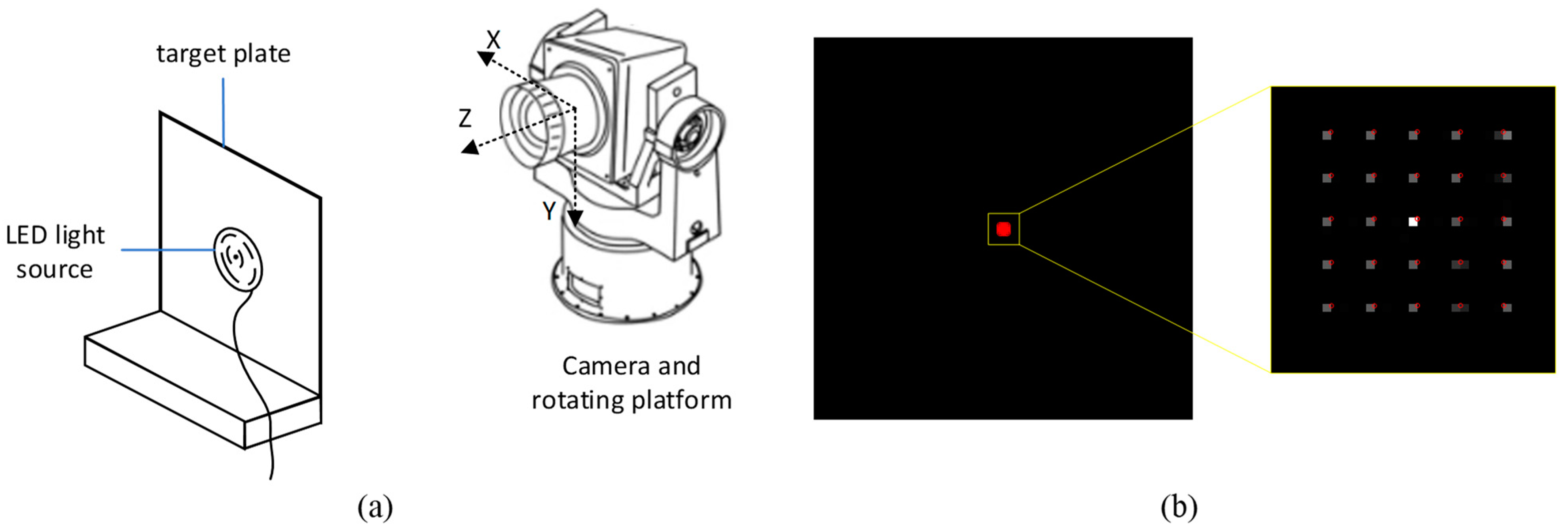
5.1. Experimental Dataset
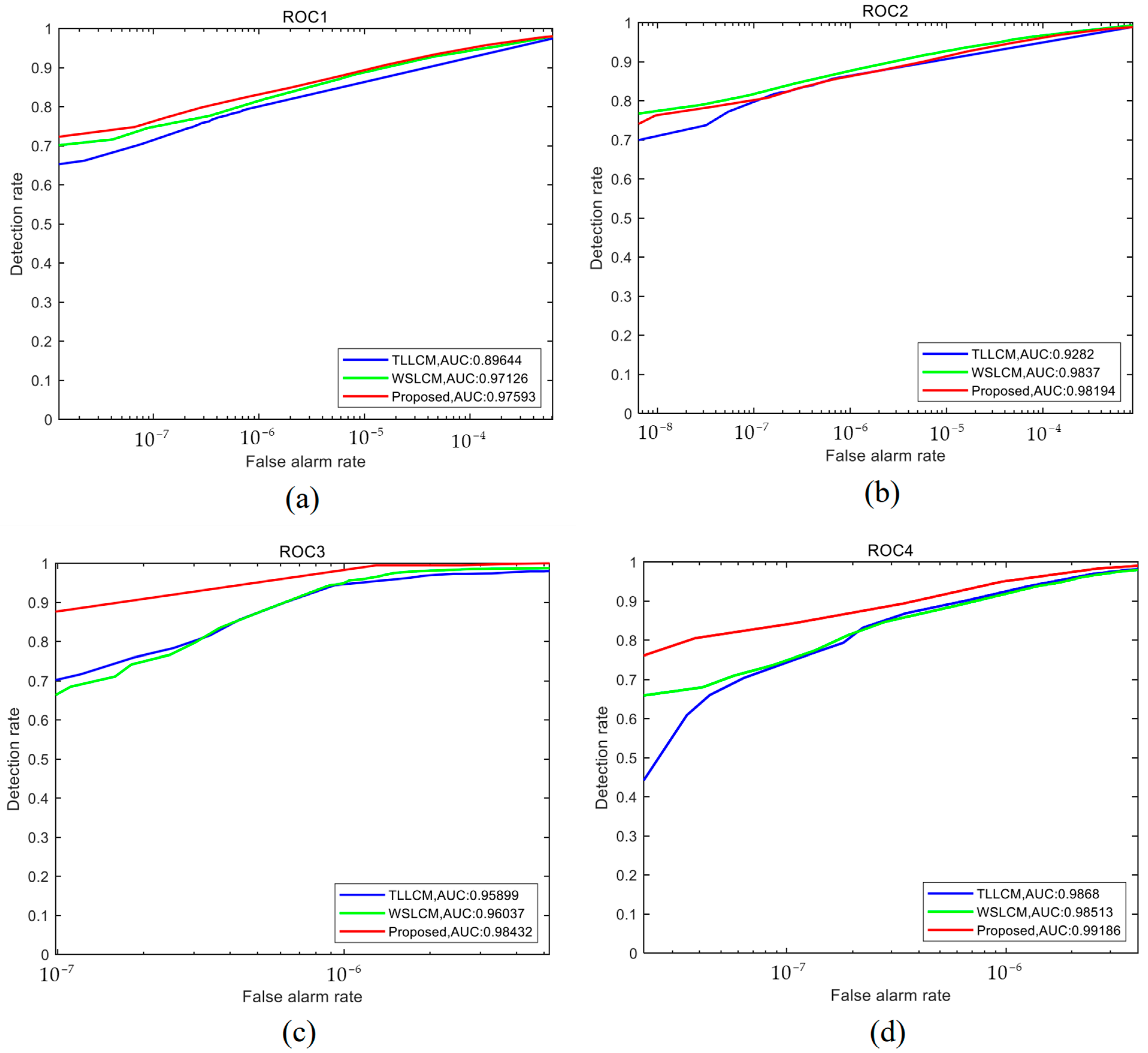
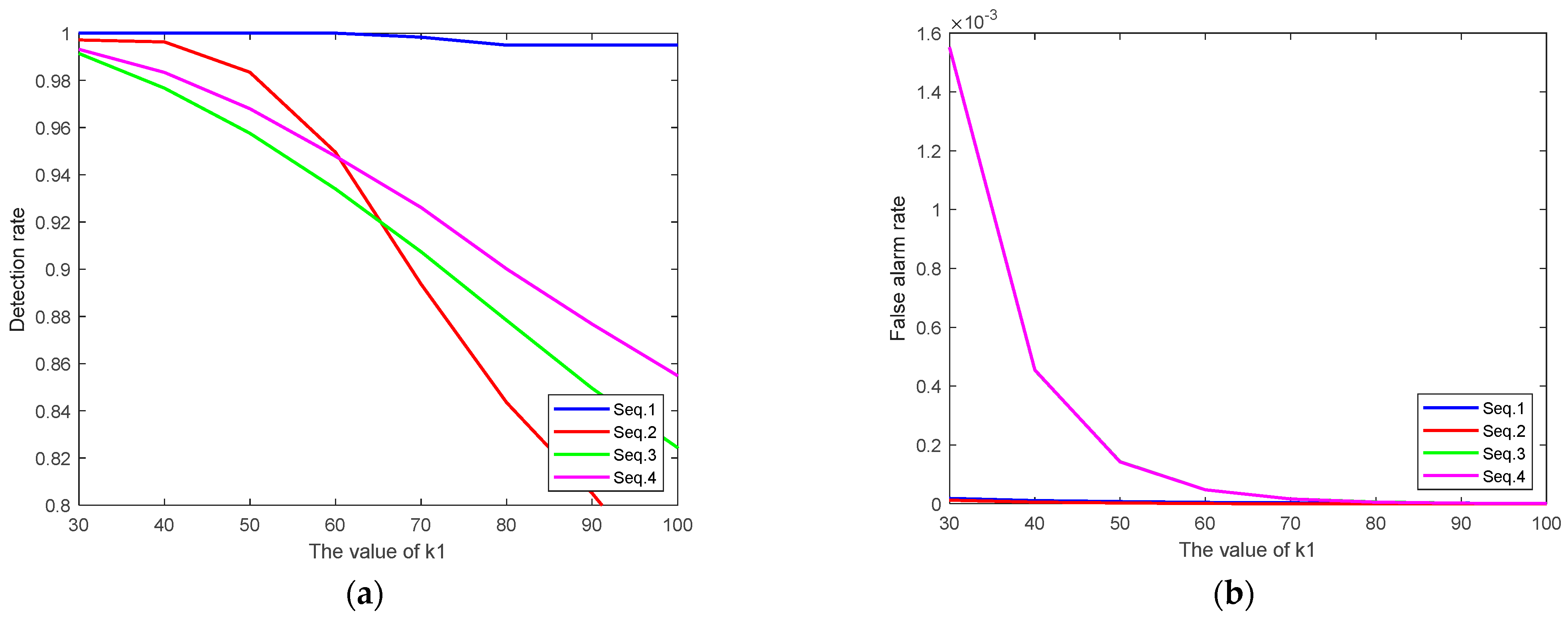
5.2. Target Detection and Tracking Experiment
5.3. Hardware System Computational Performance Analysis
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, M.; Yan, C.; Hu, C.; Liu, C.; Xu, L. Space Target Detection in Complicated Situations for Wide-Field Surveillance. IEEE Access 2019, 7, 123658–123670. [Google Scholar] [CrossRef]
- Wang, X.; Chen, Y. Application and Development of Multi-source Information Fusion in Space Situational Awareness. Spacecr. Recovery Remote Sens. 2021, 42, 11–20. [Google Scholar] [CrossRef]
- Chen, L.P.; Zhou, F.Q.; Ye, T. Design and Implementation of Space Target Detection Algorithm. Appl. Mech. Mater. 2015, 738–739, 319–322. [Google Scholar] [CrossRef]
- Barniv, Y. Dynamic programming solution for detecting dim moving targets. IEEE Trans. Aerosp. Electron. Syst. 1985, AES-21, 144–156. [Google Scholar] [CrossRef]
- Barniv, Y.; Kella, O. Dynamic programming solution for detecting dim moving targets part II: Analysis. IEEE Trans. Aerosp. Electron. Syst. 1987, AES-23, 776–788. [Google Scholar] [CrossRef]
- Doucet, A.; Gordon, N.J.; Krishnamurthy, V. Particle filters for state estimation of jump Markov linear systems. IEEE Trans. Signal Process. 2001, 49, 613–624. [Google Scholar] [CrossRef]
- Salmond, D.; Birch, H. A particle filter for track-before-detect. In Proceedings of the 2001 American Control Conference (Cat. No. 01CH37148), Arlington, VA, USA, 25–27 June 2001; pp. 3755–3760. [Google Scholar]
- Reed, I.S.; Gagliardi, R.M.; Shao, H. Application of three-dimensional filtering to moving target detection. IEEE Trans. Aerosp. Electron. Syst. 1983, AES-19, 898–905. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, B.; Zhou, X. Small target trace acquisition algorithm for sequence star images with moving background. Opt. Precision Eng. 2008, 16, 524–530. [Google Scholar]
- Cheng, J.; Zhang, W.; Cong, M.; Pan, H. Research of detecting algorithm for space object based on star map recognition. Opt. Tech. 2010, 36, 439–444. [Google Scholar]
- Zhang, J.; Ren, J.-C.; Cheng, S.-C. Space target detection in star image based on motion information. In International Symposium on Photoelectronic Detection and Imaging 2013: Optical Storage and Display Technology; SPIE: Bellingham, WA, USA, 2013; pp. 35–44. [Google Scholar]
- Xi, X.-L.; Yu, Y.; Zhou, X.-D.; Zhang, J. Algorithm based on star map matching for star images registration. In International Symposium on Photoelectronic Detection and Imaging 2011: Space Exploration Technologies and Applications; SPIE: Bellingham, WA, USA, 2011; p. 81961N. [Google Scholar]
- Boccignone, G.; Chianese, A.; Picariello, A. Small target detection using wavelets. In Proceedings of the Fourteenth International Conference on Pattern Recognition (Cat. No. 98EX170), Brisbane, QLD, Australia, 20 August 1998; pp. 1776–1778. [Google Scholar]
- Jiang, P.; Liu, C.; Yang, W.; Kang, Z.; Li, Z. Automatic Space Debris Extraction Channel Based on Large Field of view Photoelectric Detection System. Publ. Astron. Soc. Pac. 2022, 134, 024503. [Google Scholar] [CrossRef]
- Chen, C.P.; Li, H.; Wei, Y.; Xia, T.; Tang, Y.Y. A local contrast method for small infrared target detection. IEEE Trans. Geosci. Remote Sens. 2013, 52, 574–581. [Google Scholar] [CrossRef]
- Chen, L.; Rao, P.; Chen, X. Infrared dim target detection method based on local feature contrast and energy concentration degree. Optik 2021, 248, 167651. [Google Scholar] [CrossRef]
- Sun, R.-Y.; Zhan, J.-W.; Zhao, C.-Y.; Zhang, X.-X. Algorithms and applications for detecting faint space debris in GEO. Acta Astronaut. 2015, 110, 9–17. [Google Scholar] [CrossRef]
- Deshpande, S.D.; Er, M.H.; Venkateswarlu, R.; Chan, P. Max-mean and max-median filters for detection of small targets. In Signal and Data Processing of Small Targets 1999; SPIE: Bellingham, WA, USA, 1999; pp. 74–83. [Google Scholar]
- Bai, X.; Zhou, F. Infrared small target enhancement and detection based on modified top-hat transformations. Comput. Electr. Eng. 2010, 36, 1193–1201. [Google Scholar] [CrossRef]
- Lv, P.; Sun, S.; Lin, C.; Liu, G. A method for weak target detection based on human visual contrast mechanism. IEEE Geosci. Remote Sens. Lett. 2018, 16, 261–265. [Google Scholar] [CrossRef]
- Han, J.; Moradi, S.; Faramarzi, I.; Liu, C.; Zhang, H.; Zhao, Q. A local contrast method for infrared small-target detection utilizing a tri-layer window. IEEE Geosci. Remote Sens. Lett. 2019, 17, 1822–1826. [Google Scholar] [CrossRef]
- Lan, Y.; Peng, B.; Wu, X.; Teng, F. Infrared dim and small targets detection via self-attention mechanism and pipeline correlator. Digit. Signal Process. 2022, 130, 103733. [Google Scholar] [CrossRef]
- Shi, F.; Qiu, F.; Li, X.; Tang, Y.; Zhong, R.; Yang, C. A method to detect and track moving airplanes from a satellite video. Remote Sens. 2020, 12, 2390. [Google Scholar] [CrossRef]
- Fujita, K.; Hanada, T.; Kitazawa, Y.; Kawabe, A. A debris image tracking using optical flow algorithm. Adv. Space Res. 2012, 49, 1007–1018. [Google Scholar] [CrossRef]
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- La Scala, B.F.; Bitmead, R.R. Design of an extended Kalman filter frequency tracker. IEEE Trans. Signal Process. 1996, 44, 739–742. [Google Scholar] [CrossRef]
- Huang, T.; Xiong, Y.; Li, Z.; Zhou, Y.; Li, Y. Space Target Tracking by Variance Detection. J. Comput. 2014, 9, 2107–2115. [Google Scholar] [CrossRef]
- Hao, L.; Mao, Y.; Yu, Y.; Tang, Z. A method of GEO targets recognition in wide-field opto-electronic telescope observation. Opto-Electron. Eng. 2017, 44, 418–426. [Google Scholar]
- Lin, J.; Ping, X.; Ma, D. Small target detection method in drift-scanning image based on DBT. Infrared Laser Eng. 2013, 42, 3440–3446. [Google Scholar]
- Mehta, D.S.; Chen, S.; Low, K.-S. A rotation-invariant additive vector sequence based star pattern recognition. IEEE Trans. Aerosp. Electron. Syst. 2018, 55, 689–705. [Google Scholar] [CrossRef]
- Yang, L.; Niu, Y.; Zhang, Y.; Lü, J.; Li, J.; Niu, H.; Liu, W.; Zhang, Y. Research on Detection and Recognition of Space Targets Based on Satellite Photoelectric Imaging System. Laser Optoelectron. Prog. 2014, 51, 121102. [Google Scholar] [CrossRef]
- Bo, M. Research on Aerial Infrared Small Target Detection and Hardware Acceleration. Master’s Thesis, Beijing University of Technology, Beijing, China, 2016. [Google Scholar]
- Zhang, Q. Design and Implementation of Spaceborne Infrared Small Target Detection System Based on FPGA. Master’s Thesis, Huazhong University of Science and Technology, Wuhan, China, 2019. [Google Scholar]
- Liu, W. Object tracking under complicated background based on DSP+FPGA platform. Chin. J. Liq. Cryst. Disp. 2014, 29, 1151–1155. [Google Scholar]
- Seznec, M.; Gac, N.; Orieux, F.; Naik, A.S. Real-time optical flow processing on embedded GPU: An hardware-aware algorithm to implementation strategy. J. Real-Time Image Process. 2022, 19, 317–329. [Google Scholar] [CrossRef]
- Diprima, F.; Santoni, F.; Piergentili, F.; Fortunato, V.; Abbattista, C.; Amoruso, L. Efficient and automatic image reduction framework for space debris detection based on GPU technology. Acta Astronaut. 2018, 145, 332–341. [Google Scholar] [CrossRef]
- Tian, H.; Guo, S.; Zhao, P.; Gong, M.; Shen, C. Design and Implementation of a Real-Time Multi-Beam Sonar System Based on FPGA and DSP. Sensors 2021, 21, 1425. [Google Scholar] [CrossRef]
- Sun, Q.; Niu, Z.D.; Yao, C. Implementation of Real-time Detection Algorithm for Space Debris Based on Multi-core DSP. J. Phys. Conf. Ser. 2019, 1335, 012003. [Google Scholar] [CrossRef]
- Gyaneshwar, D.; Nidamanuri, R.R. A real-time FPGA accelerated stream processing for hyperspectral image classification. Geocarto Int. 2022, 37, 52–69. [Google Scholar] [CrossRef]
- Han, K.; Pei, H.; Huang, Z.; Huang, T.; Qin, S. Non-cooperative Space Target High-Speed Tracking Measuring Method Based on FPGA. In Proceedings of the 2022 7th International Conference on Image, Vision and Computing (ICIVC), Xi’an, China, 26–28 July 2022; pp. 222–231. [Google Scholar]
- Yang, B.; Yang, M.; Plaza, A.; Gao, L.; Zhang, B. Dual-mode FPGA implementation of target and anomaly detection algorithms for real-time hyperspectral imaging. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2015, 8, 2950–2961. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, J. Real-time detection algorithm for small space targets based on max-median filter. J. Inf. Comput. Sci. 2014, 11, 1047–1055. [Google Scholar] [CrossRef]
- Han, L.; Tan, C.; Liu, Y.; Song, R. Research on the On-orbit Real-time Space Target Detection Algorithm. Spacecr. Recovery Remote Sens. 2021, 42, 122–131. [Google Scholar]
- Choi, E.-J.; Yoon, J.-C.; Lee, B.-S.; Park, S.-Y.; Choi, K.-H. Onboard orbit determination using GPS observations based on the unscented Kalman filter. Adv. Space Res. 2010, 46, 1440–1450. [Google Scholar] [CrossRef]
- Babu, P.; Parthasarathy, E. FPGA implementation of multi-dimensional Kalman filter for object tracking and motion detection. Eng. Sci. Technol. Int. J. 2022, 33, 101084. [Google Scholar] [CrossRef]
- Zhang, X.; Xiang, J.; Zhang, Y. Space Object Detection in Video Satellite Images Using Motion Information. Int. J. Aerosp. Eng. 2017, 2017, 1024529. [Google Scholar] [CrossRef]
- Li, Q.; Li, R.; Ji, K.; Dai, W. Kalman filter and its application. In Proceedings of the 2015 8th International Conference on Intelligent Networks and Intelligent Systems (ICINIS), Tianjin, China, 1–3 November 2015; pp. 74–77. [Google Scholar]
- Kuhn, H.W. The Hungarian method for the assignment problem. Nav. Res. Logist. Q. 1955, 2, 83–97. [Google Scholar] [CrossRef]
- Zhu, H.; Zhou, M. Efficient role transfer based on Kuhn–Munkres algorithm. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2011, 42, 491–496. [Google Scholar] [CrossRef]
- Mirzaeinia, A.; Hassanalian, M. Minimum-cost drone–nest matching through the kuhn–munkres algorithm in smart cities: Energy management and efficiency enhancement. Aerospace 2019, 6, 125. [Google Scholar] [CrossRef]
- Luetteke, F.; Zhang, X.; Franke, J. Implementation of the hungarian method for object tracking on a camera monitored transportation system. In Proceedings of the ROBOTIK 2012: 7th German Conference on Robotics, Munich Germany, 21–22 May 2012; pp. 1–6. [Google Scholar]
- Kuipers, J.B. Quaternions and Rotation Sequences: A Primer with Applications to Orbits, Aerospace, and Virtual Reality; Princeton University Press: Princeton, NJ, USA, 1999. [Google Scholar]
- Tang, Z.; Von Gioi, R.G.; Monasse, P.; Morel, J.-M. A precision analysis of camera distortion models. IEEE Trans. Image Process. 2017, 26, 2694–2704. [Google Scholar] [CrossRef]
- Weng, J.; Cohen, P.; Herniou, M. Camera calibration with distortion models and accuracy evaluation. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 965–980. [Google Scholar] [CrossRef]
- Han, J.; Moradi, S.; Faramarzi, I.; Zhang, H.; Zhao, Q.; Zhang, X.; Li, N. Infrared small target detection based on the weighted strengthened local contrast measure. IEEE Geosci. Remote Sens. Lett. 2020, 18, 1670–1674. [Google Scholar] [CrossRef]






| Sequence | Frame | Field View | Background Details | Target Details |
|---|---|---|---|---|
| Seq.1 | 300 | Wide field | Simulated deep space background; random noise | Simulated target; 3 × 3 |
| Seq.2 | 300 | Narrow field | Simulated deep space background; random noise | Simulated target; 3 × 3 |
| Seq.3 | 300 | Wide field | Real background; sky | Civil aviation aircraft; 3 × 3 |
| Seq.4 | 300 | Narrow field | Real background; cloud and sky | Unmanned aerial vehicle; 12 × 12 |
| Sequence | Pt | Fa |
|---|---|---|
| Seq.1 | 91.72% | 1.33% |
| Seq.2 | 97.25% | 0% |
| Seq.3 | 80.9% | 0% |
| Seq.4 | 95.67% | 0% |
| Component | Number of LUTs | Number of FFs | Number of BRAMs | Number of DSPs | Number of BUFGs |
|---|---|---|---|---|---|
| Units | 4.9999 | 6.1274 | 233 | 53 | 22 |
| Percentage | 24.53% | 15.03% | 52.36% | 6.31% | 68.75% |
| Hardware Platform | Processing Time | Clock Period | Hardware Operation Frequency | Hardware Power Consumption |
|---|---|---|---|---|
| FPGA | 22.046 ms | 1,102,300 | 50 MHz | 7.02 W |
| DSP | 0.5946 ms | 595,460 | 1000 MHz | 6.168 W |
| Hardware Platform | Sequence | Seq.1 | Seq.2 |
|---|---|---|---|
| FPGA implementation | 97.37% | 96.36% | |
| 0.0332% | 0.0335% | ||
| DSP implementation | 87.27% | 88.33% | |
| 0% | 0% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, Y.; Chen, X.; Liu, G.; Cang, C.; Rao, P. Implementation of Real-Time Space Target Detection and Tracking Algorithm for Space-Based Surveillance. Remote Sens. 2023, 15, 3156. https://doi.org/10.3390/rs15123156
Su Y, Chen X, Liu G, Cang C, Rao P. Implementation of Real-Time Space Target Detection and Tracking Algorithm for Space-Based Surveillance. Remote Sensing. 2023; 15(12):3156. https://doi.org/10.3390/rs15123156
Chicago/Turabian StyleSu, Yueqi, Xin Chen, Gaorui Liu, Chen Cang, and Peng Rao. 2023. "Implementation of Real-Time Space Target Detection and Tracking Algorithm for Space-Based Surveillance" Remote Sensing 15, no. 12: 3156. https://doi.org/10.3390/rs15123156
APA StyleSu, Y., Chen, X., Liu, G., Cang, C., & Rao, P. (2023). Implementation of Real-Time Space Target Detection and Tracking Algorithm for Space-Based Surveillance. Remote Sensing, 15(12), 3156. https://doi.org/10.3390/rs15123156







