Network Collaborative Pruning Method for Hyperspectral Image Classification Based on Evolutionary Multi-Task Optimization
Abstract
1. Introduction
- A multi-task pruning algorithm: by exploiting the similarity between HSIs, different HSI classification networks can be pruned simultaneously. Through parallel optimization, the optimization efficiency of each task can be improved. The pruned networks can be applied to the classification of limited labeled sample HSIs.
- Model pruning based on evolutionary multi-objective optimization: the potential excellent sparse networks are searched by an evolutionary algorithm. Multi-objective optimization optimizes the sparsity and accuracy of the networks at the same time, and can obtain a set of sparse networks to meet different requirements.
- To ensure effective knowledge transfer, the network sparse structure is the transfer of knowledge, using knowledge transfer between multiple tasks to achieve the knowledge of the search and update. A self-adaptive knowledge transfer strategy based on the historical information of task and dormancy mechanism is proposed to effectively prevent negative transfer.The rest of this paper is organized as follows. Section 2 reviews the background. The motivation of the proposed method is also introduced. Section 3 describes the model compression methods for HSI classification in detail. Section 4 presents the experimental study. Section 5 presents the conclusions of this paper.
2. Background and Motivation
2.1. HSI Classification Methods
2.2. Neural Network Pruning
2.3. Evolutionary Multi-Task Optimization
2.4. Motivation
3. Methodology
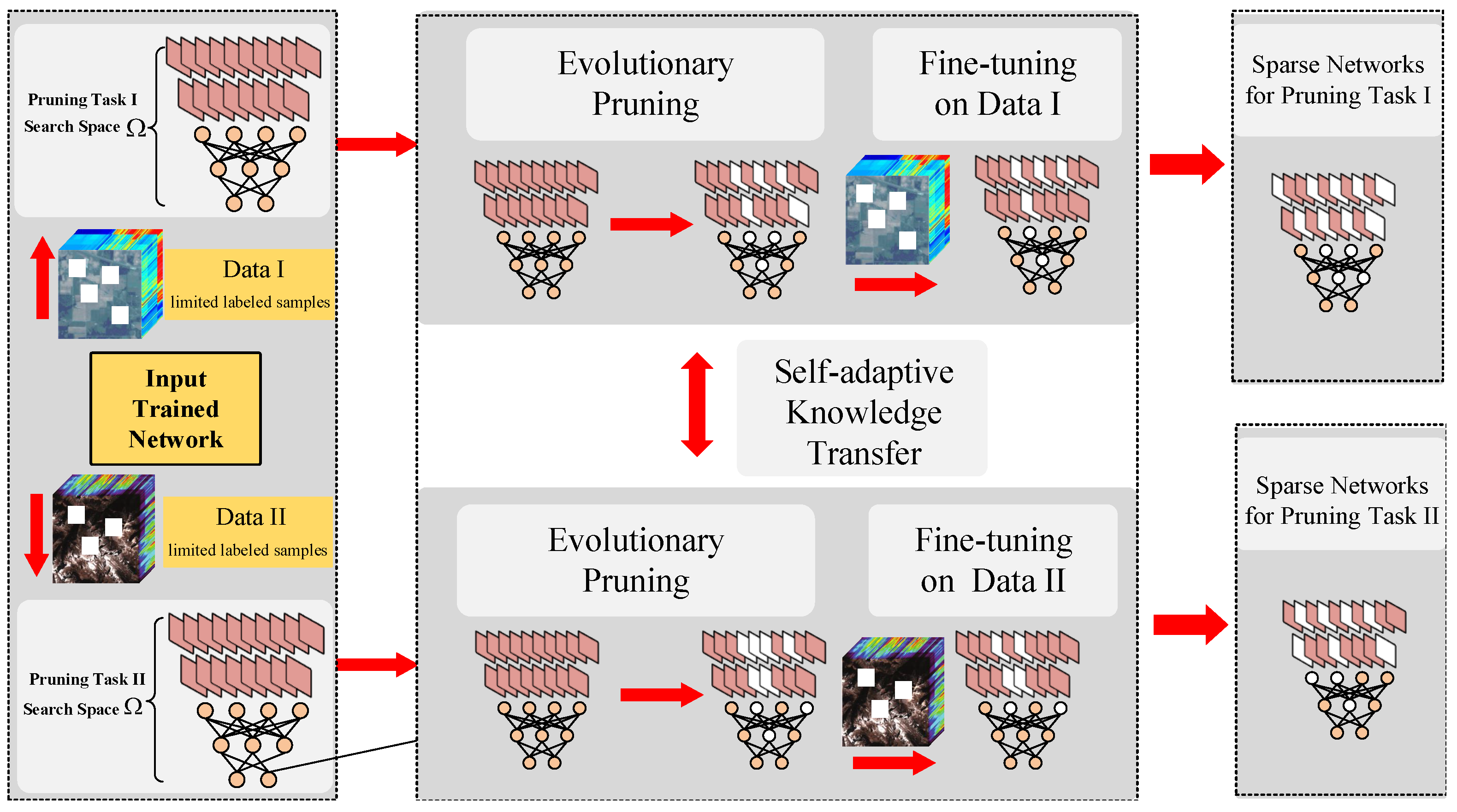
3.1. The Framework of the Proposed Network Collaborative Pruning Method for HSI Classification
3.2. Evolutionary Multi-Task Pruning Algorithm
3.2.1. Mathematical Models of Multi-Tasks
3.2.2. Overall Framework of Proposed Evolutionary Multi-Task Pruning Algorithm
| Algorithm 1 The proposed evolutionary multi-task pruning algorithm |
| Input: : task population size, t: number of evolutionary iterations, P: parent population, : random mating probability, : maximum number of generation Output: a set of trade-off sparse networks for multiple HSIs
|
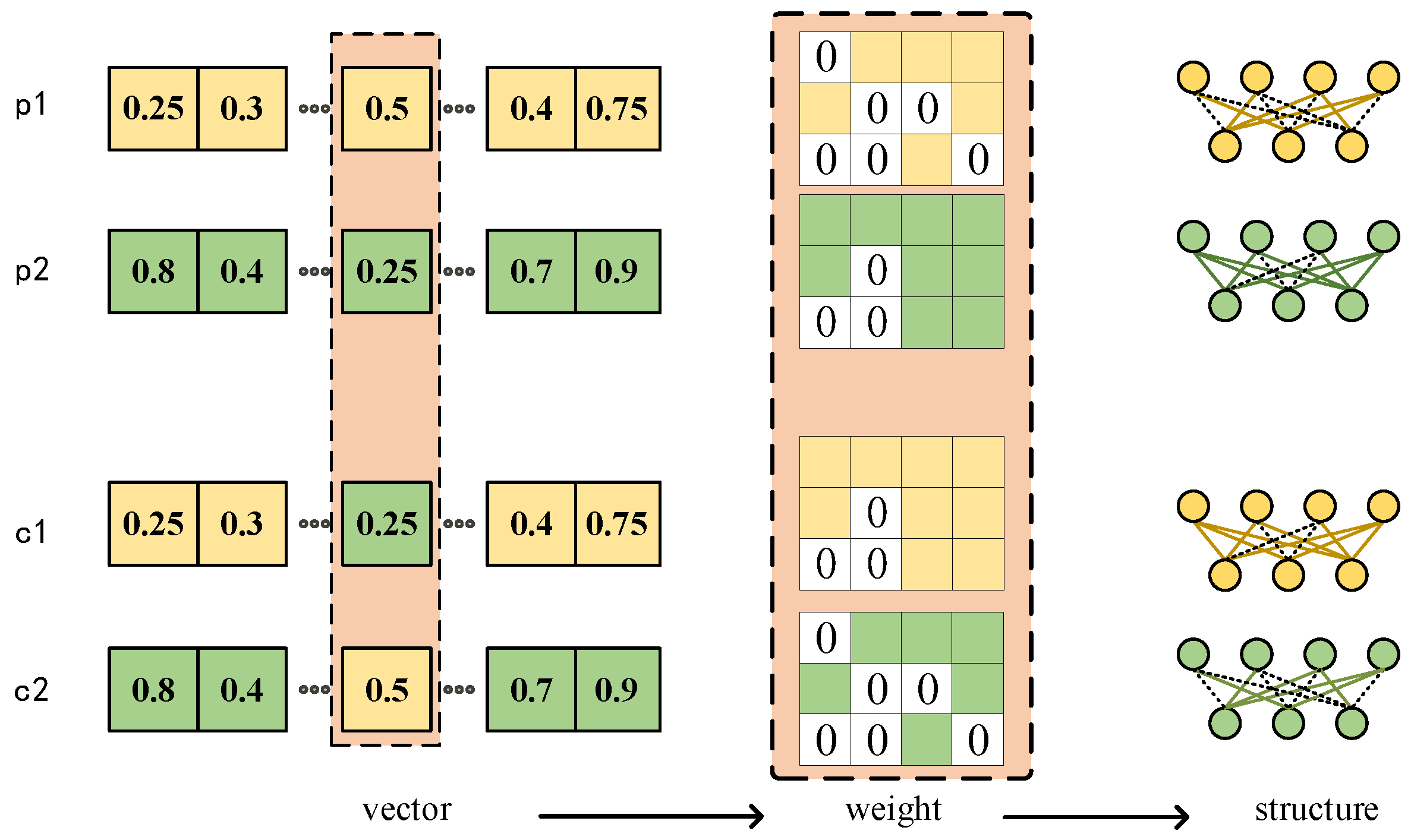
3.2.3. Representation and Initialization
3.2.4. Genetic Operator
| Algorithm 2 Genetic operations | |
| Input: : candidate parent individuals, : the skill factor of the parent, : random mating probability, : a random number between 0 and 1 Output: offspring individual
|
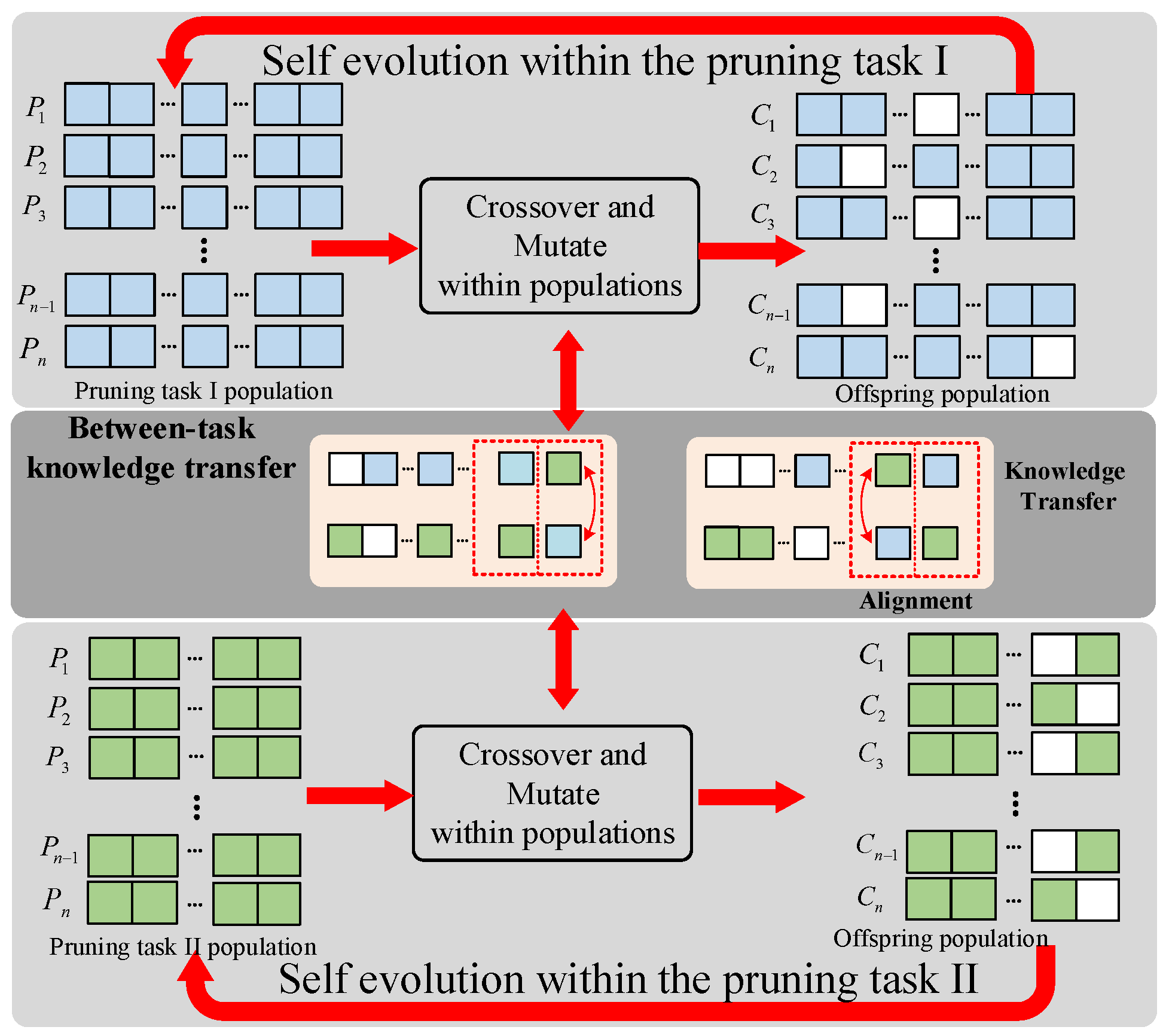
3.2.5. Self-adaptive Knowledge Transfer Strategy
| Algorithm 3 Self-adaptive knowledge transfer strategy |
| Input: : the population size in multi tasks, : minimum rank of non- dominated sort, : new individuals generated by knowledge transfer, : preset threshold Output: random mating probability
|
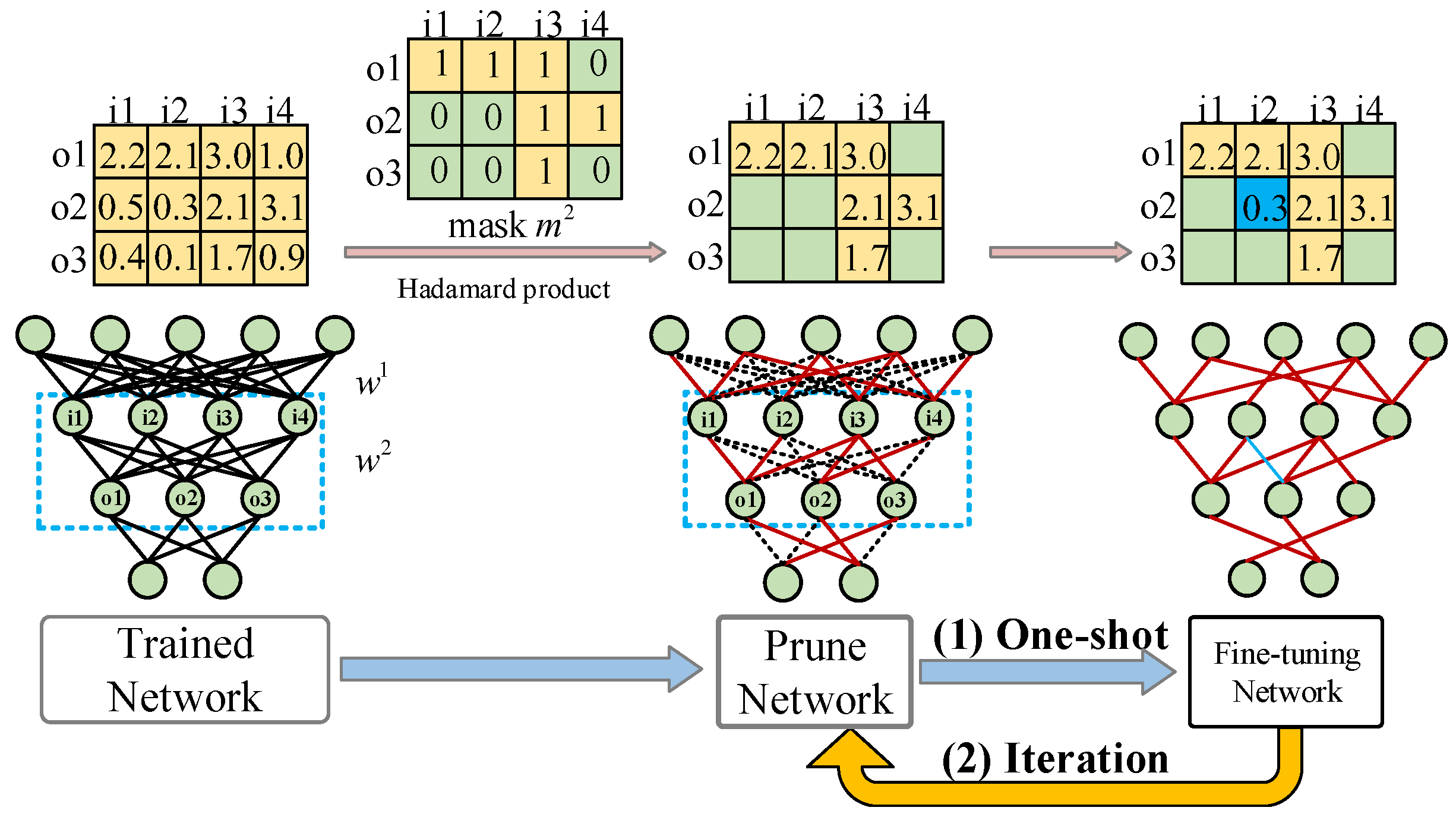
3.3. Fine-Tune Pruned Neural Networks
3.4. Computational Complexity of Proposed Method
4. Experiments
4.1. Experimental Setting
4.2. Results on HSIs
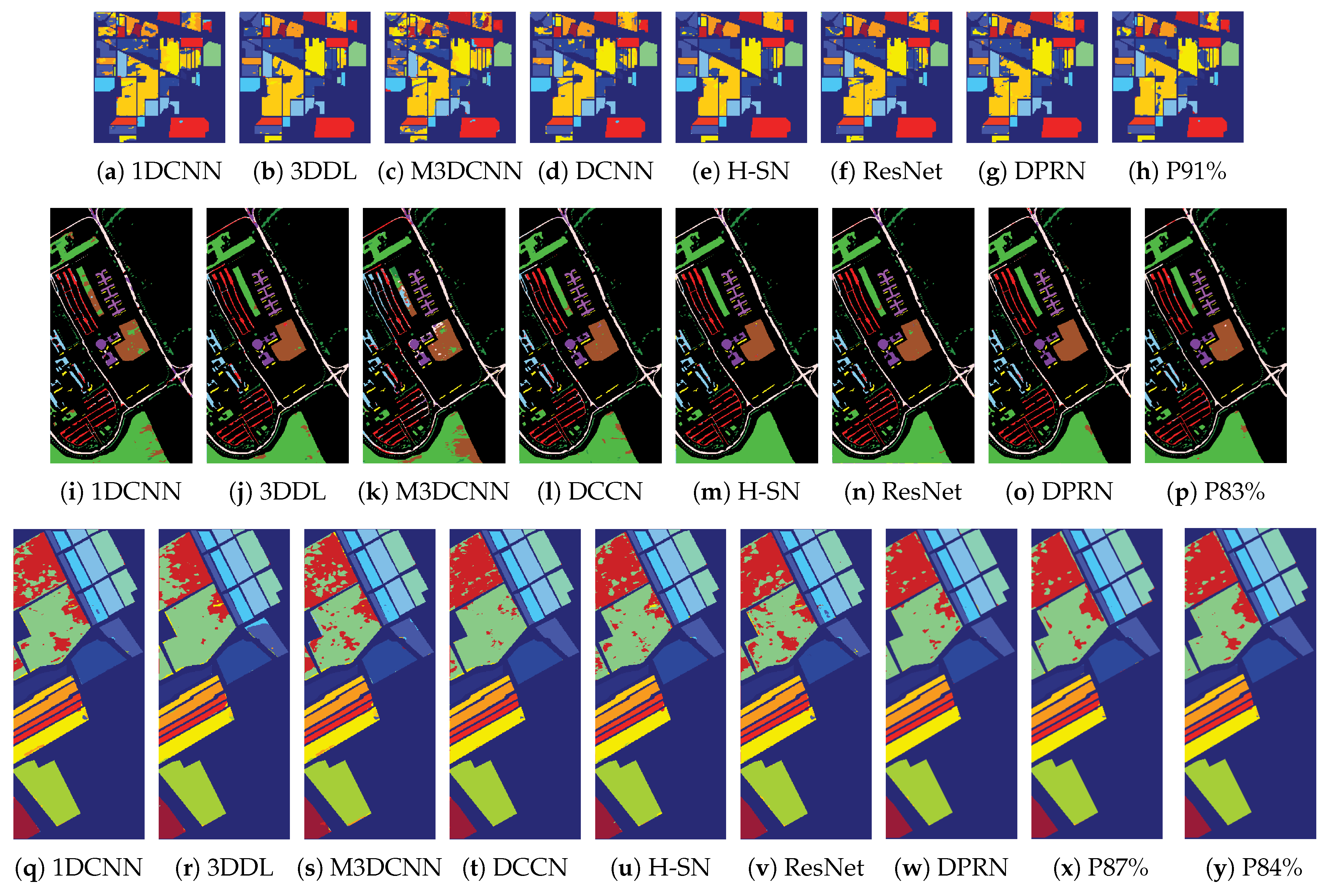
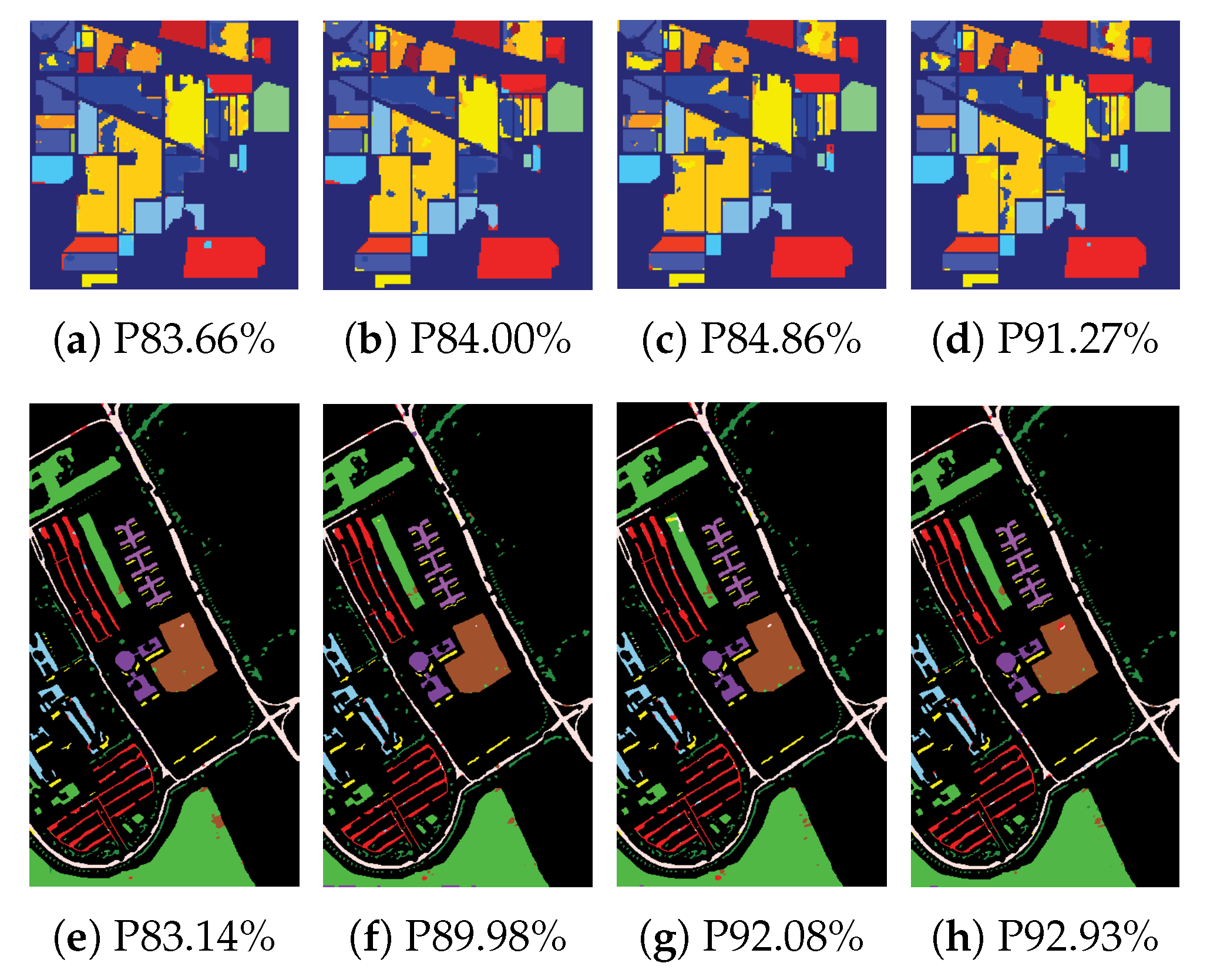
4.2.1. Classification Results
4.2.2. Comparison with other Neural Network Pruning Methods
4.2.3. Complexity Results of the Pruned Network
4.2.4. The Result of the Sparse Networks Obtained by Multi-Objective Optimization
4.2.5. Effectiveness Analysis of Self-Adaptive Knowledge Transfer strategy
- Proportion of migrated individuals: After the elite retention operation of NSGA-II, the proportion of individuals who survived through knowledge transfer in the new population is calculated in the whole population, and the overall quality of the transfer is evaluated. The higher the ratio is, the better the quality of knowledge transfer is, which can greatly promote the population optimization.
- Transfer knowledge contribution degree: the minimum non-dominated rank of all transfer individuals after non-dominated sorting of the main task. The smaller the rank is, the more excellent the transfer individual is in the population, which indicates the greater contribution of the population optimization.
- Self-adaptive knowledge transfer probability (): the variable used to control the degree of knowledge transfer in the self-adaptive transfer strategy. A larger value of represents a stronger degree of interaction.
4.2.6. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.; Zhao, X.; Zhang, Z.; Cai, W.; Yang, N.; Zhan, Y. Semi-supervised locality preserving dense graph neural network with ARMA filters and context-aware learning for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–12. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, Z.; Zhao, X.; Cai, W.; Yang, N.; Hu, H.; Huang, X.; Cao, Y.; Cai, W. Unsupervised self-correlated learning smoothy enhanced locality preserving graph convolution embedding clustering for hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5536716. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, Z.; Zhao, X.; Cai, Y.; Li, S.; Deng, B.; Cai, W. Self-supervised locality preserving low-pass graph convolutional embedding for large-scale hyperspectral image clustering. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5536016. [Google Scholar] [CrossRef]
- Zhang, M.; Li, W.; Du, Q. Diverse region-based CNN for hyperspectral image classification. IEEE Trans. Image Process. 2018, 27, 2623–2634. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. In Proceedings of the ICLR 2015: International Conference on Learning Representations 2015, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Wang, H.; Wu, Z.; Liu, Z.; Cai, H.; Zhu, L.; Gan, C.; Han, S. HAT: Hardware-Aware Transformers for Efficient Natural Language Processing. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, Online, 5–10 July 2020; pp. 7675–7688. [Google Scholar]
- Liu, Z.; Sun, M.; Zhou, T.; Huang, G.; Darrell, T. Rethinking the Value of Network Pruning. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- LeCun, Y.; Denker, J.S.; Solla, S.A. Optimal Brain Damage. Adv. Neural Inf. Process. Syst. 1989, 2, 598–605. [Google Scholar]
- Han, S.; Pool, J.; Tran, J.; Dally, W.J. Learning Both Weights and Connections for Efficient Neural Networks. In Proceedings of the 28th International Conference on Neural Information Processing Systems, NIPS’15, Montreal, QC, Canada, 7–12 December 2015; MIT Press: Cambridge, MA, USA, 2015; Volume 1, pp. 1135–1143. [Google Scholar]
- Lee, J.; Park, S.; Mo, S.; Ahn, S.; Shin, J. Layer-adaptive sparsity for the magnitude-based pruning. arXiv 2020, arXiv:2010.07611. [Google Scholar]
- Wang, Y.; Li, D.; Sun, R. NTK-SAP: Improving neural network pruning by aligning training dynamics. arXiv 2023, arXiv:2304.02840. [Google Scholar]
- Qi, B.; Chen, H.; Zhuang, Y.; Liu, S.; Chen, L. A Network Pruning Method for Remote Sensing Image Scene Classification. In Proceedings of the 2019 IEEE International Conference on Signal, Information and Data Processing (ICSIDP), Chongqing, China, 11–13 December 2019; pp. 1–4. [Google Scholar]
- Wang, Z.; Xue, W.; Chen, K.; Ma, S. Remote Sensing Image Classification Based on Lightweight Network and Pruning. In Proceedings of the 2022 China Automation Congress (CAC), Xiamen, China, 25–27 November 2022; pp. 3186–3191. [Google Scholar]
- Guo, X.; Hou, B.; Ren, B.; Ren, Z.; Jiao, L. Network pruning for remote sensing images classification based on interpretable CNNs. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–15. [Google Scholar] [CrossRef]
- Jung, I.; You, K.; Noh, H.; Cho, M.; Han, B. Real-time object tracking via meta-learning: Efficient model adaptation and one-shot channel pruning. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 11205–11212. [Google Scholar]
- He, Y.; Lin, J.; Liu, Z.; Wang, H.; Li, L.J.; Han, S. Amc: Automl for model compression and acceleration on mobile devices. In Proceedings of the European conference on computer vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 784–800. [Google Scholar]
- Zhou, Y.; Yen, G.G.; Yi, Z. Evolutionary compression of deep neural networks for biomedical image segmentation. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 2916–2929. [Google Scholar] [CrossRef]
- Wu, T.; Li, X.; Zhou, D.; Li, N.; Shi, J. Differential Evolution Based Layer-Wise Weight Pruning for Compressing Deep Neural Networks. Sensors 2021, 21, 880. [Google Scholar] [CrossRef]
- Wu, T.; Shi, J.; Zhou, D.; Lei, Y.; Gong, M. A Multi-objective Particle Swarm Optimization for Neural Networks Pruning. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, 10–13 June 2019; pp. 570–577. [Google Scholar]
- Zhou, Y.; Yen, G.G.; Yi, Z. A Knee-Guided Evolutionary Algorithm for Compressing Deep Neural Networks. IEEE Trans. Syst. Man Cybern. 2021, 51, 1626–1638. [Google Scholar] [CrossRef]
- Zhao, J.; Yang, C.; Zhou, Y.; Zhou, Y.; Jiang, Z.; Chen, Y. Multi-Objective Net Architecture Pruning for Remote Sensing Classification. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 4940–4943. [Google Scholar]
- Wei, X.; Zhang, N.; Liu, W.; Chen, H. NAS-Based CNN Channel Pruning for Remote Sensing Scene Classification. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Ma, X.; Zhao, L.; Huang, G.; Wang, Z.; Hu, Z.; Zhu, X.; Gai, K. Entire space multi-task model: An effective approach for estimating post-click conversion rate. In Proceedings of the 41st International ACM SIGIR Conference on Research & Development in Information Retrieval, Ann Arbor, MI, USA, 8–12 July 2018; pp. 1137–1140. [Google Scholar]
- Ruder, S. An overview of multi-task learning in deep neural networks. arXiv 2017, arXiv:1706.05098. [Google Scholar]
- Hou, Y.; Jiang, N.; Ge, H.; Zhang, Q.; Qu, X.; Feng, L.; Gupta, A. Memetic Multi-agent Optimization in High Dimensions using Random Embeddings. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, 10–13 June 2019; pp. 135–141. [Google Scholar] [CrossRef]
- Shi, J.; Zhang, X.; Tan, C.; Lei, Y.; Li, N.; Zhou, D. Multiple datasets collaborative analysis for hyperspectral band selection. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Liu, S.; Shi, Q. Multitask deep learning with spectral knowledge for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2020, 17, 2110–2114. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, L.; Du, B. Deep learning for remote sensing data: A technical tutorial on the state of the art. IEEE Geosci. Remote Sens. Mag. 2016, 4, 22–40. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, Z.; Zhao, X.; Wang, G.; Gu, Y. Deep learning-based classification of hyperspectral data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2094–2107. [Google Scholar] [CrossRef]
- Mou, L.; Ghamisi, P.; Zhu, X.X. Deep recurrent neural networks for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3639–3655. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, Z.; Zhao, X.; Hong, D.; Cai, W.; Yang, N.; Wang, B. Multi-scale receptive fields: Graph attention neural network for hyperspectral image classification. Expert Syst. Appl. 2023, 223, 119858. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, Z.; Zhao, X.; Hong, D.; Cai, W.; Yu, C.; Yang, N.; Cai, W. Multi-feature fusion: Graph neural network and CNN combining for hyperspectral image classification. Neurocomputing 2022, 501, 246–257. [Google Scholar] [CrossRef]
- Zhang, Z.; Ding, Y.; Zhao, X.; Siye, L.; Yang, N.; Cai, Y.; Zhan, Y. Multireceptive field: An adaptive path aggregation graph neural framework for hyperspectral image classification. Expert Syst. Appl. 2023, 217, 119508. [Google Scholar] [CrossRef]
- Hamida, A.B.; Benoit, A.; Lambert, P.; Amar, C.B. 3-D deep learning approach for remote sensing image classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4420–4434. [Google Scholar] [CrossRef]
- Li, H.C.; Lin, Z.X.; Ma, T.Y.; Zhao, X.L.; Plaza, A.; Emery, W.J. Hybrid Fully Connected Tensorized Compression Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–16. [Google Scholar] [CrossRef]
- Ahmad, M.; Khan, A.M.; Mazzara, M.; Distefano, S.; Ali, M.; Sarfraz, M.S. A fast and compact 3-D CNN for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2020, 19, 1–5. [Google Scholar] [CrossRef]
- Cao, X.; Ren, M.; Zhao, J.; Li, H.; Jiao, L. Hyperspectral imagery classification based on compressed convolutional neural network. IEEE Geosci. Remote Sens. Lett. 2019, 17, 1583–1587. [Google Scholar] [CrossRef]
- Verma, V.K.; Singh, P.; Namboodri, V.; Rai, P. A“Network Pruning Network”Approach to Deep Model Compression. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Snowmass Village, CO, USA, 1–5 March 2020; pp. 3009–3018. [Google Scholar]
- Castellano, G.; Fanelli, A.M.; Pelillo, M. An iterative pruning algorithm for feedforward neural networks. IEEE Trans. Neural Netw. 1997, 8, 519–531. [Google Scholar] [CrossRef]
- Li, H.; Kadav, A.; Durdanovic, I.; Samet, H.; Graf, H.P. Pruning filters for efficient convnets. arXiv 2016, arXiv:1608.08710. [Google Scholar]
- Zhang, S.; Stadie, B.C. One-Shot Pruning of Recurrent Neural Networks by Jacobian Spectrum Evaluation. In Proceedings of the ICLR 2020: Eighth International Conference on Learning Representations, Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- Chen, T.; Ji, B.; Ding, T.; Fang, B.; Wang, G.; Zhu, Z.; Liang, L.; Shi, Y.; Yi, S.; Tu, X. Only train once: A one-shot neural network training and pruning framework. Adv. Neural Inf. Process. Syst. 2021, 34, 19637–19651. [Google Scholar]
- Gupta, A.; Ong, Y.S.; Feng, L. Multifactorial Evolution: Toward Evolutionary Multitasking. IEEE Trans. Evol. Comput. 2016, 20, 343–357. [Google Scholar] [CrossRef]
- Gupta, A.; Ong, Y.S.; Feng, L.; Tan, K.C. Multiobjective Multifactorial Optimization in Evolutionary Multitasking. IEEE Trans. Syst. Man Cybern. 2017, 47, 1652–1665. [Google Scholar] [CrossRef]
- Tan, K.C.; Feng, L.; Jiang, M. Evolutionary transfer optimization-a new frontier in evolutionary computation research. IEEE Comput. Intell. Mag. 2021, 16, 22–33. [Google Scholar] [CrossRef]
- Thang, T.B.; Dao, T.C.; Long, N.H.; Binh, H.T.T. Parameter adaptation in multifactorial evolutionary algorithm for many-task optimization. Memetic Comput. 2021, 13, 433–446. [Google Scholar] [CrossRef]
- Shen, F.; Liu, J.; Wu, K. Evolutionary multitasking network reconstruction from time series with online parameter estimation. Knowl.-Based Syst. 2021, 222, 107019. [Google Scholar] [CrossRef]
- Tang, Z.; Gong, M.; Xie, Y.; Li, H.; Qin, A.K. Multi-task particle swarm optimization with dynamic neighbor and level-based inter-task learning. IEEE Trans. Emerg. Top. Comput. Intell. 2021, 6, 300–314. [Google Scholar] [CrossRef]
- Li, H.; Ong, Y.S.; Gong, M.; Wang, Z. Evolutionary Multitasking Sparse Reconstruction: Framework and Case Study. IEEE Trans. Evol. Comput. 2019, 23, 733–747. [Google Scholar] [CrossRef]
- Chandra, R.; Gupta, A.; Ong, Y.S.; Goh, C.K. Evolutionary Multi-task Learning for Modular Training of Feedforward Neural Networks. In Proceedings of the 23rd International Conference on Neural Information Processing, Kyoto, Japan, 16–21 October 2016; Volume 9948, pp. 37–46. [Google Scholar]
- Chandra, R.; Gupta, A.; Ong, Y.S.; Goh, C.K. Evolutionary Multi-task Learning for Modular Knowledge Representation in Neural Networks. Neural Process. Lett. 2018, 47, 993–1009. [Google Scholar] [CrossRef]
- Chandra, R. Co-evolutionary Multi-task Learning for Modular Pattern Classification. In Proceedings of the International Conference on Neural Information Processing, Guangzhou, China, 14–18 November 2017; pp. 692–701. [Google Scholar]
- Tang, Z.; Gong, M.; Zhang, M. Evolutionary multi-task learning for modular extremal learning machine. In Proceedings of the 2017 IEEE Congress on Evolutionary Computation (CEC), Donostia, Spain, 5–8 June 2017. [Google Scholar]
- Gao, W.; Cheng, J.; Gong, M.; Li, H.; Xie, J. Multiobjective Multitasking Optimization With Subspace Distribution Alignment and Decision Variable Transfer. IEEE Trans. Emerg. Top. Comput. Intell. 2021, 6, 818–827. [Google Scholar] [CrossRef]
- Deb, K.; Goyal, M. A combined genetic adaptive search (GeneAS) for engineering design. Comput. Sci. Inform. 1996, 26, 30–45. [Google Scholar]
- Caruana, R. Multitask learning. Mach. Learn. 1997, 28, 41–75. [Google Scholar] [CrossRef]
- Frankle, J.; Carbin, M. The lottery ticket hypothesis: Finding sparse, trainable neural networks. arXiv 2018, arXiv:1803.03635. [Google Scholar]
- Green, R.O.; Eastwood, M.L.; Sarture, C.M.; Chrien, T.G.; Aronsson, M.; Chippendale, B.J.; Faust, J.A.; Pavri, B.E.; Chovit, C.J.; Solis, M.; et al. Imaging spectroscopy and the airborne visible/infrared imaging spectrometer (AVIRIS). Remote Sens. Environ. 1998, 65, 227–248. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Shen, Q. Spectral–spatial classification of hyperspectral imagery with 3D convolutional neural network. Remote Sens. 2017, 9, 67. [Google Scholar] [CrossRef]
- He, M.; Li, B.; Chen, H. Multi-scale 3D deep convolutional neural network for hyperspectral image classification. In Proceedings of the 2017 IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; pp. 3904–3908. [Google Scholar]
- Hu, W.; Huang, Y.; Wei, L.; Zhang, F.; Li, H. Deep convolutional neural networks for hyperspectral image classification. J. Sens. 2015, 2015, 258619. [Google Scholar] [CrossRef]
- Yu, H.; Zhang, H.; Liu, Y.; Zheng, K.; Xu, Z.; Xiao, C. Dual-channel convolution network with image-based global learning framework for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Roy, S.K.; Krishna, G.; Dubey, S.R.; Chaudhuri, B.B. HybridSN: Exploring 3-D–2-D CNN feature hierarchy for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2019, 17, 277–281. [Google Scholar] [CrossRef]
- Roy, S.K.; Manna, S.; Song, T.; Bruzzone, L. Attention-based adaptive spectral–spatial kernel ResNet for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2020, 59, 7831–7843. [Google Scholar] [CrossRef]
- Paoletti, M.E.; Haut, J.M.; Fernandez-Beltran, R.; Plaza, J.; Plaza, A.J.; Pla, F. Deep pyramidal residual networks for spectral–spatial hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2018, 57, 740–754. [Google Scholar] [CrossRef]
- Han, S.; Mao, H.; Dally, W.J. Deep Compression: Compressing Deep Neural Networks with Pruning, Trained Quantization and Huffman Coding. In Proceedings of the ICLR 2016: International Conference on Learning Representations 2016, San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]
- Yang, Z.; Xi, Z.; Zhang, T.; Guo, W.; Zhang, Z.; Li, H.C. CMR-CNN: Cross-mixing residual network for hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 8974–8989. [Google Scholar] [CrossRef]
- Srinivas, S.; Babu, R.V. Data-free parameter pruning for deep neural networks. arXiv 2015, arXiv:1507.06149. [Google Scholar]
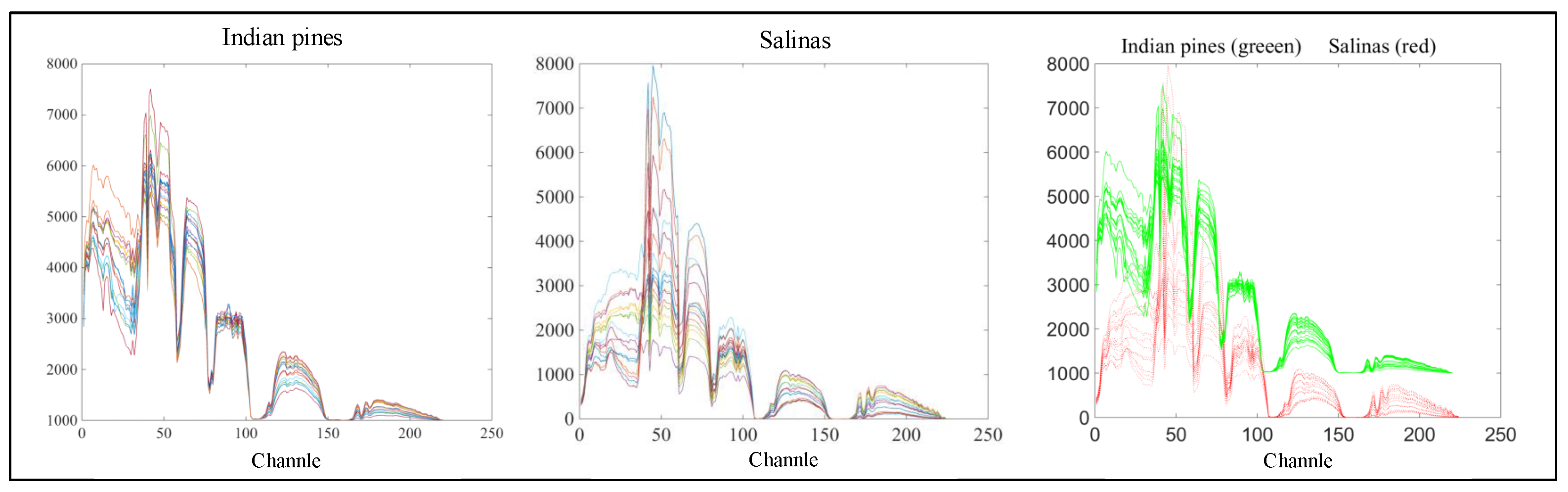




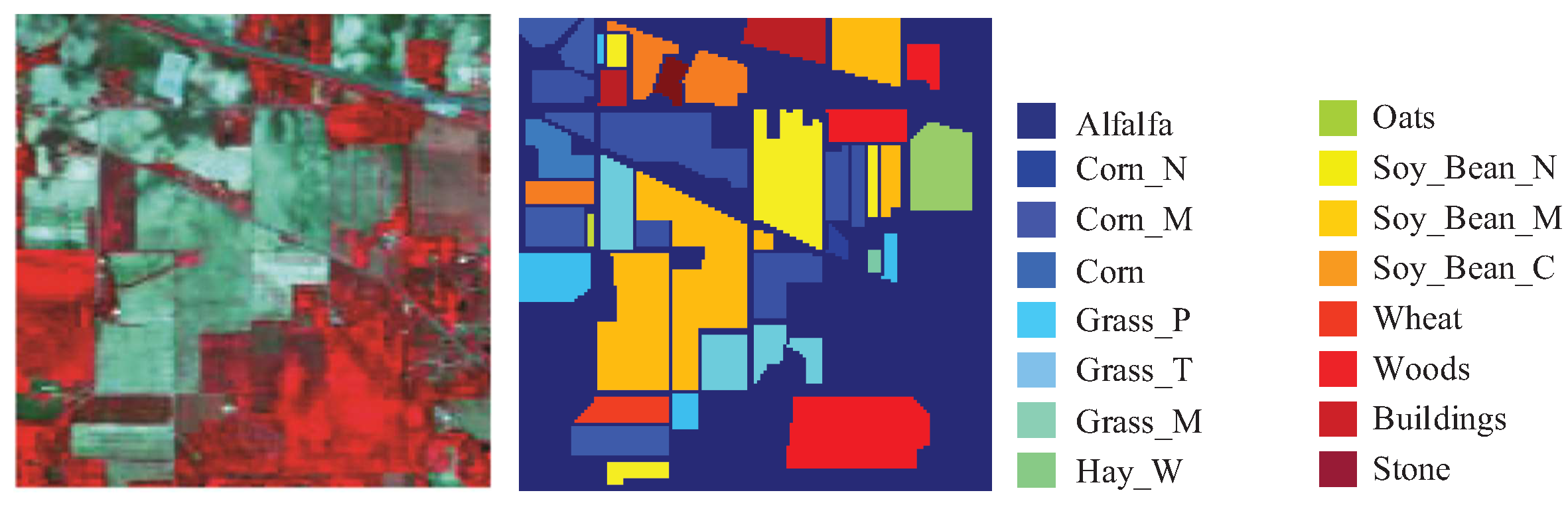

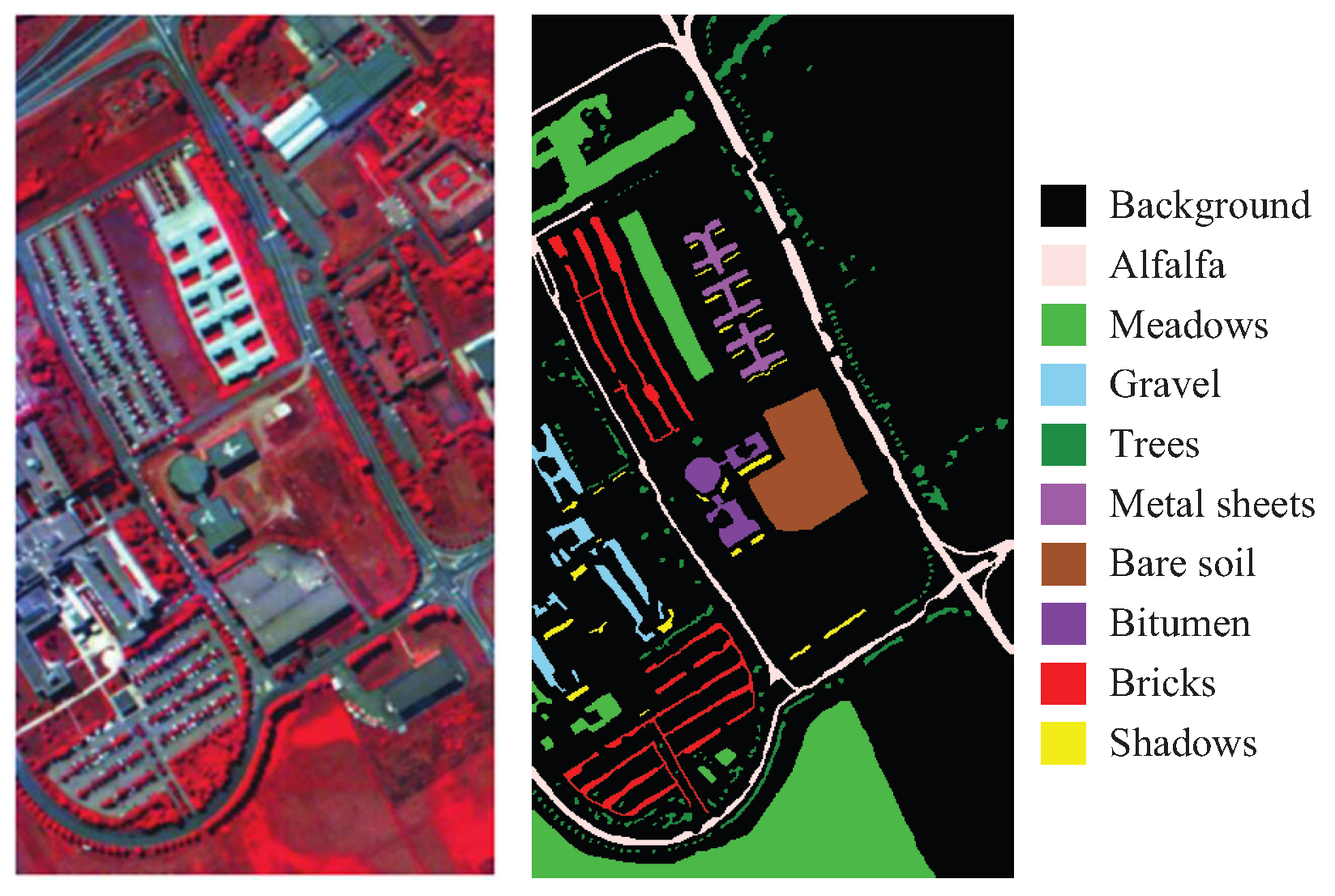
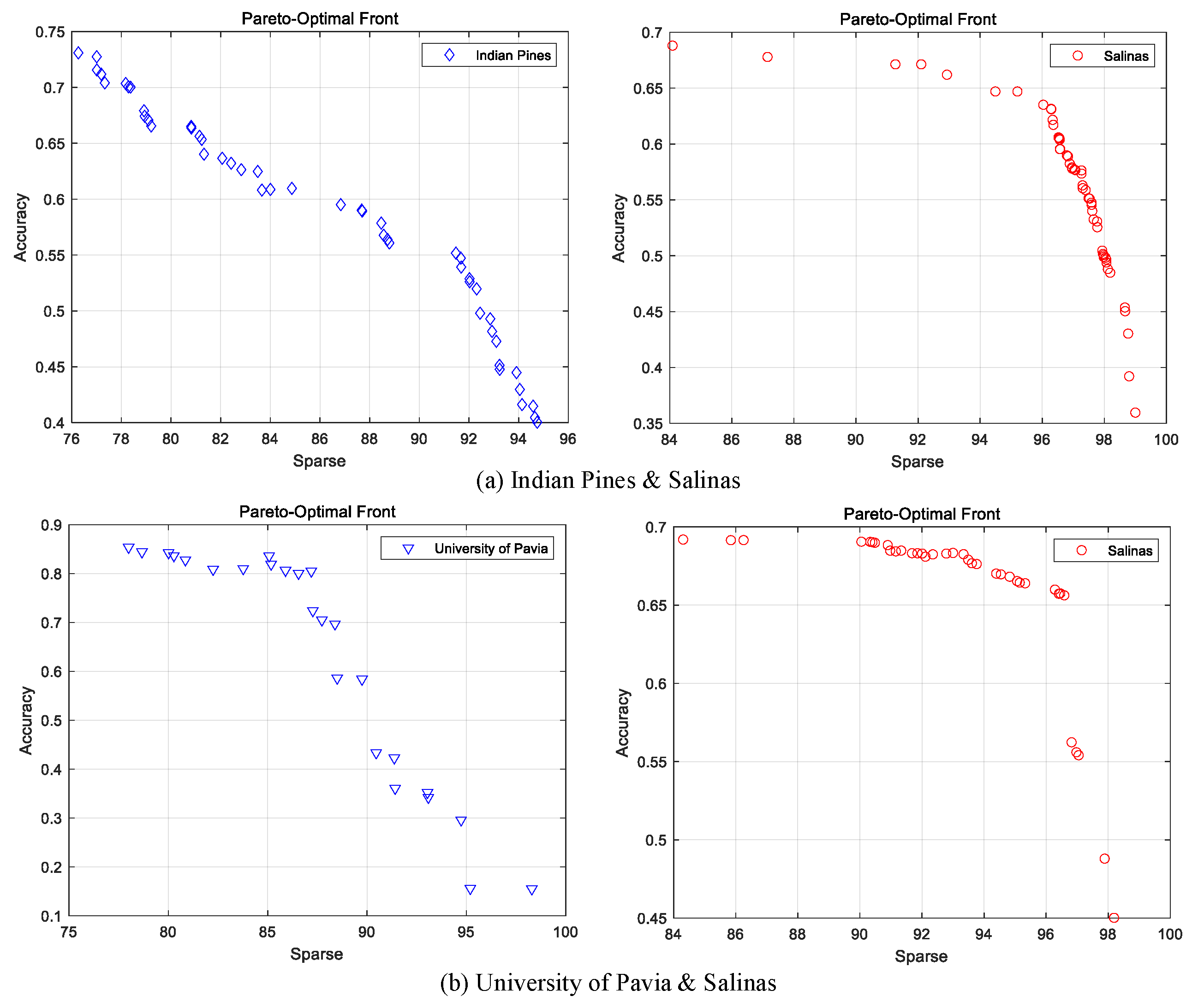
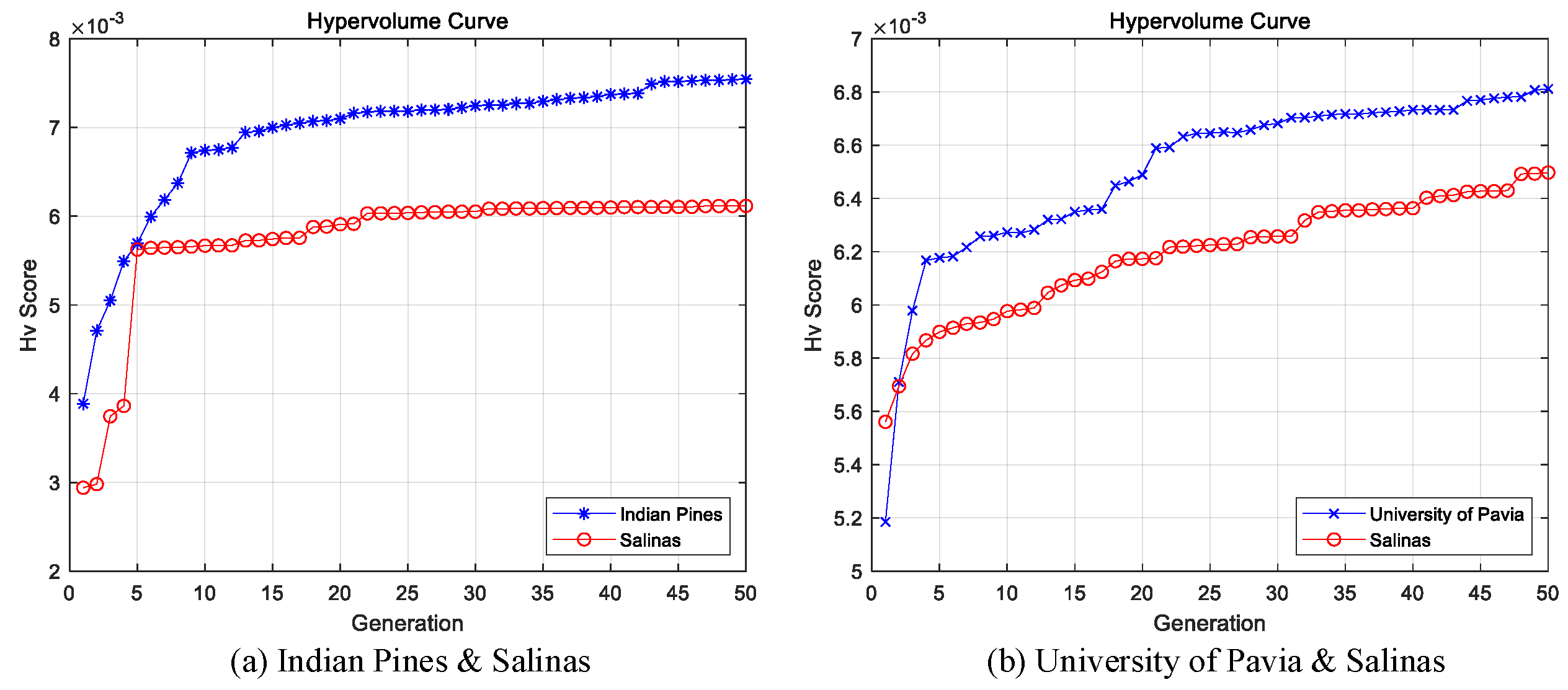


| HSI Datasets | |
|---|---|
| Offspring size in pruning task I | 50 |
| Offspring size in pruning task II | 50 |
| Maximum number of generation | 50 |
| Mutation probability | 10 |
| Crossover probability | 10 |
| The initial value of transfer | 0.5 |
| The dormancy condition | 0.1 |
| Category | 1DCNN | 3DDL | M3DCNN | DCCN | HybridSN | ResNet | DPRN | Pruned 87.15% |
|---|---|---|---|---|---|---|---|---|
| OA (%) | 91.78 ± 1.45 | 92.05 ± 1.37 | 90.51 ± 0.98 | 95.66 ± 2.06 | 91.68 ± 1.71 | 93.68 ± 1.03 | 97.14 ± 0.77 | 95.70 ± 1.31 |
| AA (%) | 96.13 ± 2.33 | 95.50 ± 2.67 | 95.41 ± 2.56 | 98.05 ± 0.42 | 96.10 ± 2.11 | 97.46 ± 1.68 | 98.59 ± 1.09 | 98.14 ± 0.69 |
| Kappa (%) | 90.87 ± 2.06 | 91.13 ± 2.01 | 89.45 ± 2.79 | 95.17 ± 1.78 | 90.77 ± 2.21 | 92.99 ± 1.51 | 96.10 ± 0.68 | 95.14 ± 0.74 |
| 1 | 99.95 | 99.90 | 99.70 | 98.45 | 98.35 | 99.75 | 99.10 | 99.70 |
| 2 | 99.59 | 99.81 | 99.27 | 99.78 | 99.81 | 100.00 | 99.88 | 100.00 |
| 3 | 98.93 | 86.33 | 97.36 | 99.84 | 98.27 | 99.39 | 100.00 | 99.24 |
| 4 | 99.78 | 99.92 | 99.28 | 98.78 | 99.71 | 99.85 | 99.03 | 99.07 |
| 5 | 98.39 | 98.99 | 99.62 | 100.00 | 96.34 | 98.80 | 99.49 | 99.03 |
| 6 | 99.99 | 99.99 | 99.98 | 99.99 | 99.99 | 100.00 | 100.00 | 99.97 |
| 7 | 99.52 | 99.30 | 99.46 | 99.94 | 99.49 | 99.97 | 99.81 | 99.47 |
| 8 | 80.09 | 88.59 | 77.82 | 85.04 | 76.69 | 78.79 | 93.17 | 88.31 |
| 9 | 99.06 | 99.64 | 98.37 | 99.91 | 98.59 | 99.48 | 99.82 | 99.77 |
| 10 | 90.69 | 95.21 | 91.03 | 96.06 | 93.47 | 97.98 | 98.42 | 98.26 |
| 11 | 99.06 | 99.90 | 99.25 | 99.06 | 98.68 | 99.06 | 100.00 | 99.34 |
| 12 | 99.01 | 97.76 | 99.01 | 100.00 | 98.96 | 99.89 | 99.71 | 99.95 |
| 13 | 99.34 | 99.45 | 99.23 | 99.01 | 98.79 | 100.00 | 100.00 | 100.00 |
| 14 | 99.06 | 97.38 | 97.75 | 99.34 | 98.69 | 98.31 | 99.55 | 100.00 |
| 15 | 77.06 | 66.82 | 72.45 | 94.04 | 81.89 | 88.44 | 89.32 | 88.37 |
| 16 | 98.61 | 99.00 | 96.90 | 99.50 | 99.88 | 99.61 | 99.74 | 99.89 |
| Category | 1DCNN | 3DDL | M3DCNN | DCNN | HybridSN | ResNet | DPRN | Pruned 91.27% |
| OA (%) | 80.93 ± 4.37 | 91.45 ± 3.62 | 95.18 ± 3.74 | 92.17 ± 3.79 | 95.38 ± 2.91 | 93.24 ± 2.86 | 97.46 ± 1.50 | 88.90 ± 1.27 |
| AA (%) | 90.15 ± 3.77 | 96.84 ± 2.81 | 98.07 ± 1.72 | 93.45 ± 2.26 | 98.12 ± 0.58 | 97.89 ± 1.43 | 98.05 ± 0.49 | 95.38 ± 0.81 |
| Kappa (%) | 78.38 ± 4.69 | 90.33 ± 2.84 | 94.52 ± 2.94 | 91.11 ± 3.19 | 94.75 ± 1.67 | 93.11 ± 2.48 | 95.97 ± 1.39 | 87.46 ± 0.93 |
| 1 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 |
| 2 | 65.68 | 96.42 | 93.20 | 82.56 | 89.28 | 91.75 | 96.68 | 76.96 |
| 3 | 73.97 | 96.14 | 97.34 | 91.20 | 97.22 | 96.26 | 98.23 | 95.66 |
| 4 | 100.00 | 100.00 | 100.00 | 95.78 | 100.00 | 100.00 | 100.00 | 100.00 |
| 5 | 96.48 | 100.00 | 100.00 | 96.27 | 99.17 | 100.00 | 100.00 | 99.37 |
| 6 | 99.31 | 99.86 | 99.45 | 98.63 | 99.86 | 100.00 | 100.00 | 98.35 |
| 7 | 100.00 | 100.00 | 100.00 | 92.86 | 100.00 | 100.00 | 100.00 | 100.00 |
| 8 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 |
| 9 | 100.00 | 100.00 | 100.00 | 90.00 | 100.00 | 100.00 | 100.00 | 100.00 |
| 10 | 64.19 | 88.58 | 93.10 | 91.67 | 100.00 | 93.18 | 97.48 | 91.15 |
| 11 | 72.66 | 73.28 | 88.55 | 91.57 | 97.42 | 81.92 | 93.74 | 76.65 |
| 12 | 75.71 | 97.97 | 98.65 | 86.34 | 90.17 | 97.95 | 99.03 | 92.91 |
| 13 | 100.00 | 100.00 | 100.00 | 100.00 | 98.14 | 100.00 | 100.00 | 100.00 |
| 14 | 95.25 | 99.84 | 98.81 | 97.00 | 100.00 | 98.37 | 99.28 | 95.81 |
| 15 | 99.22 | 97.40 | 100.00 | 95.34 | 98.89 | 100.00 | 100.00 | 99.22 |
| 16 | 100.00 | 100.00 | 100.00 | 86.02 | 99.74 | 100.00 | 100.00 | 100.00 |
| Category | 1DCNN | 3DDL | M3DCNN | DCCN | HybridSN | ResNet | DPRN | Pruned 84.30% |
|---|---|---|---|---|---|---|---|---|
| OA (%) | 91.78 ± 1.45 | 92.05 ± 1.37 | 90.51 ± 0.98 | 95.66 ± 2.06 | 91.68 ± 1.71 | 93.68 ± 1.03 | 97.14 ± 0.77 | 95.02 ± 0.98 |
| AA (%) | 96.13 ± 2.33 | 95.50 ± 2.67 | 95.41 ± 2.56 | 98.05 ± 0.42 | 96.10 ± 2.11 | 97.46 ± 1.68 | 98.59 ± 1.09 | 98.03 ± 0.30 |
| Kappa (%) | 90.87 ± 2.06 | 91.13 ± 2.01 | 89.45 ± 2.79 | 95.17 ± 1.78 | 90.77 ± 2.21 | 92.99 ± 1.51 | 96.10 ± 0.68 | 94.03 ± 1.12 |
| 1 | 99.95 | 99.90 | 99.70 | 98.45 | 98.35 | 99.75 | 99.10 | 99.60 |
| 2 | 99.59 | 99.81 | 99.27 | 99.78 | 99.81 | 100.00 | 99.88 | 99.97 |
| 3 | 98.93 | 86.33 | 97.36 | 99.84 | 98.27 | 99.39 | 100.00 | 99.60 |
| 4 | 99.78 | 99.92 | 99.28 | 98.78 | 99.71 | 99.85 | 99.03 | 99.28 |
| 5 | 98.39 | 98.99 | 99.62 | 100.00 | 96.34 | 98.80 | 99.49 | 99.44 |
| 6 | 99.99 | 99.99 | 99.98 | 99.99 | 99.99 | 100.00 | 100.00 | 99.97 |
| 7 | 99.52 | 99.30 | 99.46 | 99.94 | 99.49 | 99.97 | 99.81 | 99.66 |
| 8 | 80.09 | 88.59 | 77.82 | 85.04 | 76.69 | 78.79 | 93.17 | 84.86 |
| 9 | 99.06 | 99.64 | 98.37 | 99.91 | 98.59 | 99.48 | 99.82 | 99.97 |
| 10 | 90.69 | 95.21 | 91.03 | 96.06 | 93.47 | 97.98 | 98.42 | 98.14 |
| 11 | 99.06 | 99.90 | 99.25 | 99.06 | 98.68 | 99.06 | 100.00 | 100.00 |
| 12 | 99.01 | 97.76 | 99.01 | 100.00 | 98.96 | 99.89 | 99.71 | 99.95 |
| 13 | 99.34 | 99.45 | 99.23 | 99.01 | 98.79 | 100.00 | 100.00 | 100.00 |
| 14 | 99.06 | 97.38 | 97.75 | 99.34 | 98.69 | 98.31 | 99.55 | 99.91 |
| 15 | 77.06 | 66.82 | 72.45 | 94.04 | 81.89 | 88.44 | 89.32 | 88.06 |
| 16 | 98.61 | 99.00 | 96.90 | 99.50 | 99.88 | 99.61 | 99.74 | 100.00 |
| Category | 1DCNN | 3DDL | M3DCNN | DCCN | HybridSN | ResNet | DPRN | Pruned 83.14% |
| OA (%) | 88.32 ± 3.76 | 81.67 ± 3.17 | 94.36 ± 1.43 | 97.43 ± 1.12 | 93.47 ± 1.69 | 97.72 ± 1.19 | 98.48 ± 0.86 | 97.57 ± 1.40 |
| AA (%) | 91.29 ± 2.86 | 85.11 ± 3.84 | 94.87 ± 2.77 | 96.12 ± 2.01 | 94.81 ± 2.17 | 97.14 ± 1.28 | 98.36 ± 0.92 | 97.84 ± 0.95 |
| Kappa (%) | 84.85 ± 3.21 | 76.24 ± 3.65 | 92.59 ± 1.79 | 96.60 ± 2.24 | 91.46 ± 2.60 | 96.91 ± 1.28 | 97.19 ± 1.06 | 96.79 ± 0.69 |
| 1 | 83.47 | 69.91 | 85.03 | 95.53 | 86.98 | 92.35 | 94.12 | 95.58 |
| 2 | 87.08 | 82.99 | 96.24 | 99.52 | 93.71 | 98.92 | 99.48 | 98.14 |
| 3 | 88.42 | 74.08 | 89.09 | 88.61 | 88.58 | 95.41 | 96.86 | 96.95 |
| 4 | 96.57 | 94.48 | 96.34 | 96.01 | 96.96 | 96.99 | 97.94 | 97.74 |
| 5 | 99.99 | 99.95 | 99.99 | 100.00 | 99.99 | 100.00 | 100.00 | 99.77 |
| 6 | 91.05 | 72.51 | 98.03 | 98.01 | 97.43 | 99.97 | 99.63 | 98.60 |
| 7 | 91.42 | 83.75 | 95.78 | 97.66 | 96.76 | 98.84 | 99.60 | 99.92 |
| 8 | 84.46 | 90.82 | 94.16 | 95.54 | 93.18 | 97.48 | 94.41 | 95.05 |
| 9 | 99.15 | 97.57 | 99.15 | 94.19 | 99.47 | 99.62 | 99.52 | 98.83 |
| HSI | Method | L2Norm | MOPSO | LAMP | NCPM |
|---|---|---|---|---|---|
| Salinas | Pruned (%) | 87.00 | 85.24 | 87.00 | 87.15 |
| OA (%) | 86.66 | 90.40 | 94.28 | 95.02 | |
| AA (%) | 91.48 | 94.65 | 97.68 | 98.03 | |
| Kappa (%) | 85.24 | 89.31 | 93.64 | 94.03 | |
| Indian Pines | Pruned (%) | 91.00 | 90.23 | 91.00 | 91.27 |
| OA (%) | 66.49 | 72.68 | 89.31 | 88.90 | |
| AA (%) | 81.44 | 84.61 | 94.90 | 95.38 | |
| Kappa (%) | 62.52 | 69.23 | 87.90 | 87.46 | |
| University of Pavia | Pruned (%) | 83.00 | 84.11 | 83.00 | 83.14 |
| OA (%) | 87.03 | 90.67 | 96.86 | 97.57 | |
| AA (%) | 87.4 | 87.70 | 97.54 | 97.84 | |
| Kappa (%) | 83.1 | 87.51 | 95.87 | 96.79 |
| HSIs | Methods | 1DCNN | M3DCNN | HybridSN | ResNet | 3DDL | Pruned |
|---|---|---|---|---|---|---|---|
| Indian pines | EpochTrainTime/s | 40.5771 | 49.8241 | 73.0636 | 67.3195 | 60.1175 | 60.4814 |
| Parameter | 246,409 | 263,584 | 534,656 | 414,333 | 259,864 | 22,868 | |
| OA (%) | 80.93 | 95.18 | 95.38 | 93.24 | 91.45 | 88.90 | |
| Pavia University | EpochTrainTime/s | 40.3595 | 43.3423 | 79.7415 | 56.5454 | 41.6149 | 34.0278 |
| Parameter | 246,409 | 263,584 | 534,656 | 534,656 | 259,864 | 43,918 | |
| OA (%) | 88.32 | 94.36 | 93.47 | 97.50 | 81.67 | 95.02 | |
| Salinas | EpochTrainTime/s | 64.9641 | 85.6064 | 173.6447 | 134.5664 | 68.5989 | 65.7300 |
| Parameter | 246,409 | 263,584 | 534,656 | 534,656 | 259,864 | 33,262 | |
| OA (%) | 91.78 | 90.51 | 91.68 | 93.68 | 92.05 | 95.70 |
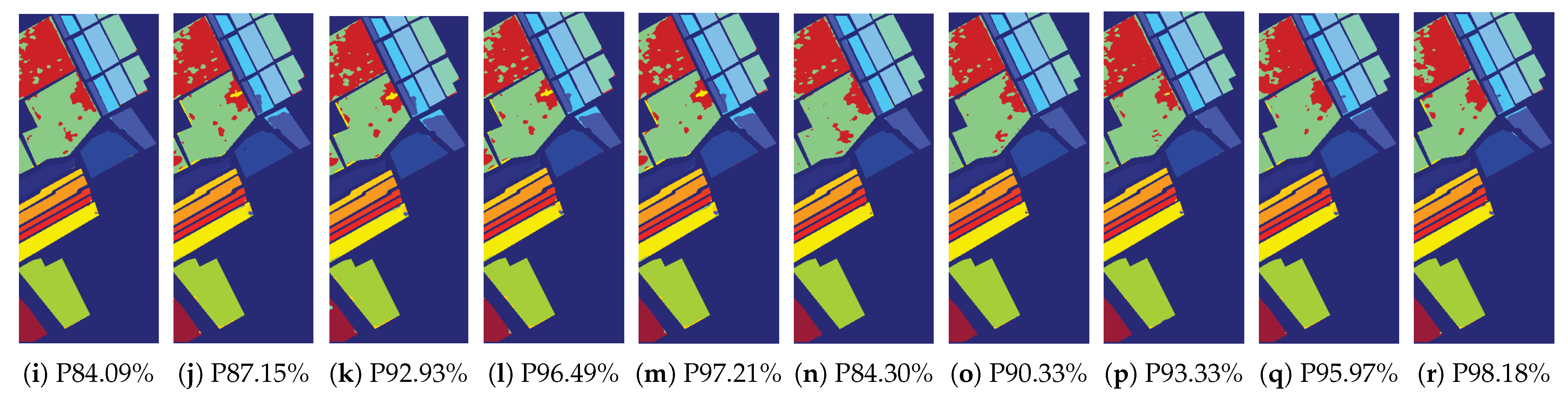
| Category | ORG | Pruned Networks in Salinas | Category | ORG | Pruned Networks in Indian Pines | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Pruned (%) | 0.00 | 84.09 | 87.15 | 92.93 | 96.49 | 97.21 | Pruned (%) | 0.00 | 83.66 | 84.00 | 84.86 | 91.27 |
| OA (%) | 92.05 | 95.25 | 95.70 | 95.42 | 95.51 | 95.42 | OA (%) | 91.45 | 89.75 | 89.87 | 89.64 | 88.90 |
| KAPPA (%) | 91.13 | 94.72 | 95.22 | 94.90 | 95.01 | 94.90 | KAPPA (%) | 90.33 | 88.39 | 88.52 | 88.29 | 87.46 |
| AA (%) | 95.50 | 97.97 | 98.14 | 97.96 | 97.98 | 97.83 | AA (%) | 96.84 | 95.02 | 94.85 | 95.02 | 95.38 |
| 1 | 99.90 | 99.55 | 99.70 | 100.00 | 99.65 | 99.65 | 1 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 |
| 2 | 99.81 | 99.75 | 100.00 | 100.00 | 100.00 | 99.86 | 2 | 96.42 | 88.16 | 79.20 | 83.89 | 76.96 |
| 3 | 86.33 | 99.24 | 99.24 | 98.83 | 99.03 | 98.07 | 3 | 96.14 | 91.20 | 95.54 | 89.75 | 95.66 |
| 4 | 99.92 | 99.56 | 99.06 | 98.42 | 99.42 | 98.63 | 4 | 100.00 | 100.00 | 97.46 | 97.46 | 100.00 |
| 5 | 98.99 | 98.84 | 99.02 | 98.73 | 99.25 | 98.31 | 5 | 100.00 | 96.48 | 94.61 | 93.78 | 99.37 |
| 6 | 99.99 | 99.94 | 99.97 | 99.97 | 99.97 | 100.00 | 6 | 99.86 | 98.63 | 96.71 | 98.08 | 98.35 |
| 7 | 99.30 | 98.60 | 99.46 | 99.66 | 99.86 | 99.46 | 7 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 |
| 8 | 88.59 | 86.65 | 88.30 | 87.96 | 89.73 | 87.75 | 8 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 |
| 9 | 99.64 | 99.59 | 99.77 | 99.48 | 99.96 | 99.14 | 9 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 |
| 10 | 95.21 | 98.35 | 98.26 | 97.13 | 97.22 | 97.31 | 10 | 88.58 | 83.12 | 86.41 | 93.10 | 91.15 |
| 11 | 99.90 | 99.90 | 99.34 | 100.00 | 99.90 | 99.81 | 11 | 73.28 | 80.61 | 85.41 | 78.28 | 76.65 |
| 12 | 97.76 | 100.00 | 99.94 | 99.89 | 99.89 | 99.74 | 12 | 97.97 | 87.52 | 91.23 | 88.36 | 92.91 |
| 13 | 99.45 | 100.00 | 100.00 | 100.00 | 99.78 | 99.89 | 13 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 |
| 14 | 97.38 | 99.43 | 100.00 | 99.81 | 99.53 | 98.87 | 14 | 99.84 | 94.70 | 91.85 | 97.94 | 95.81 |
| 15 | 66.82 | 88.23 | 88.37 | 87.65 | 84.86 | 88.96 | 15 | 97.40 | 100.00 | 99.22 | 99.74 | 99.22 |
| 16 | 99.00 | 99.94 | 99.88 | 99.88 | 99.66 | 99.88 | 16 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 |
| Category | ORG | Pruned Networks in Salinas | Category | ORG | Pruned Networks in University of Pavia | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Pruned (%) | 0.00 | 84.30 | 90.33 | 93.33 | 95.97 | 98.18 | Pruned (%) | 0.00 | 83.14 | 89.98 | 92.08 | 92.93 |
| OA (%) | 92.05 | 95.02 | 95.26 | 95.46 | 94.26 | 93.83 | OA (%) | 91.67 | 97.57 | 97.55 | 97.18 | 97.58 |
| KAPPA (%) | 91.13 | 94.46 | 94.73 | 94.95 | 93.61 | 93.13 | KAPPA (%) | 76.24 | 96.79 | 96.76 | 96.28 | 96.80 |
| AA (%) | 95.50 | 98.02 | 98.08 | 98.07 | 97.17 | 96.95 | AA (%) | 85.11 | 97.84 | 97.77 | 97.48 | 97.66 |
| 1 | 99.90 | 99.60 | 99.95 | 99.90 | 99.95 | 99.80 | 1 | 69.91 | 95.58 | 95.11 | 94.78 | 94.85 |
| 2 | 99.81 | 99.97 | 100.00 | 99.91 | 100.00 | 99.43 | 2 | 82.99 | 98.14 | 98.25 | 97.73 | 98.72 |
| 3 | 86.33 | 99.59 | 99.74 | 99.24 | 95.95 | 95.34 | 3 | 74.08 | 96.95 | 97.33 | 94.94 | 95.66 |
| 4 | 99.92 | 99.28 | 99.06 | 99.28 | 98.70 | 98.85 | 4 | 94.48 | 97.74 | 96.86 | 96.96 | 98.95 |
| 5 | 98.99 | 99.43 | 99.47 | 99.66 | 97.90 | 97.34 | 5 | 99.95 | 99.77 | 100.00 | 99.62 | 100.00 |
| 6 | 99.99 | 99.97 | 99.97 | 99.97 | 100.00 | 100.00 | 6 | 72.51 | 98.60 | 99.18 | 98.52 | 97.81 |
| 7 | 99.30 | 99.66 | 100.00 | 99.91 | 99.63 | 98.99 | 7 | 83.75 | 99.92 | 99.24 | 99.17 | 99.62 |
| 8 | 88.59 | 84.86 | 87.08 | 87.88 | 87.68 | 86.40 | 8 | 90.82 | 95.05 | 94.94 | 96.19 | 94.32 |
| 9 | 99.64 | 99.96 | 99.51 | 99.06 | 98.98 | 99.16 | 9 | 97.57 | 98.83 | 99.04 | 99.36 | 99.04 |
| 10 | 95.21 | 98.13 | 98.23 | 97.62 | 95.72 | 95.85 | ||||||
| 11 | 99.90 | 100.00 | 100.00 | 100.00 | 99.53 | 99.62 | ||||||
| 12 | 97.76 | 99.94 | 100.00 | 100.00 | 100.00 | 99.94 | ||||||
| 13 | 99.45 | 100.00 | 99.89 | 99.89 | 99.89 | 100.00 | ||||||
| 14 | 97.38 | 99.90 | 100.00 | 99.25 | 99.53 | 99.71 | ||||||
| 15 | 66.82 | 88.05 | 86.46 | 87.60 | 81.70 | 81.24 | ||||||
| 16 | 99.00 | 100.00 | 99.94 | 100.00 | 99.66 | 99.55 | ||||||
| HSIs | Salinas | Indian Pines | University of Pavia | |||
|---|---|---|---|---|---|---|
| Method | CMR-CNN | NCPM | CMR-CNN | NCPM | CMR-CNN | NCPM |
| Pruned (%) | 0.00 | 73.44 | 0.00 | 76.85 | 0.00 | 75.2 |
| TrainTime (s) | 9283 | 7909 | 2088 | 2058 | 7832 | 7082 |
| Parameter | 28,779,784 | 7,643,640 | 28,779,784 | 6,662,135 | 28,779,784 | 7,137,390 |
| OA (%) | 99.97 | 99.97 | 98.69 | 99.15 | 99.65 | 99.63 |
| AA (%) | 99.94 | 99.93 | 98.6 | 98.52 | 99.32 | 99.05 |
| Kappa (%) | 99.97 | 99.97 | 98.51 | 99.03 | 99.54 | 99.5 |
| Models | Methods | Accuracy | Parameter | Pruned (%) | CR |
|---|---|---|---|---|---|
| AlexNet | Naive-Cut | 80.33 | 564,791 | 85.00 | 6.7× |
| L2-pruning | 80.90 | 338,874 | 91.00 | 11.1× | |
| MOPSO | 80.97 | 364,854 | 90.31 | 10.3× | |
| NCPM | 95.18 | 304,610 | 91.91 | 12.4× | |
| VGG-16 | Naive-Cut | 87.47 | 6,772,112 | 53.98 | 2.17× |
| MOPSO | 83.69 | 1,358,248 | 90.77 | 10.83× | |
| NCPM | 95.91 | 2,096,970 | 85.75 | 7.017× |
| Category | 1DCNN | 3DDL | M3DCNN | DCCN | HybridSN | ResNet | DPRN | Pruned 90.88% |
|---|---|---|---|---|---|---|---|---|
| OA (%) | 88.32 | 81.67 | 94.36 | 97.43 | 93.47 | 97.72 | 98.48 | 97.45 |
| AA (%) | 91.29 | 85.11 | 94.87 | 96.12 | 94.81 | 97.14 | 98.36 | 96.25 |
| Kappa (%) | 84.85 | 76.24 | 92.59 | 96.60 | 91.46 | 96.91 | 97.19 | 96.62 |
| 1 | 83.47 | 69.91 | 85.03 | 95.53 | 86.98 | 92.35 | 94.12 | 97.78 |
| 2 | 87.08 | 82.99 | 96.24 | 99.52 | 93.71 | 98.92 | 99.48 | 99.43 |
| 3 | 88.42 | 74.08 | 89.09 | 88.61 | 88.58 | 95.41 | 96.86 | 89.37 |
| 4 | 96.57 | 94.48 | 96.34 | 96.01 | 96.96 | 96.99 | 97.94 | 96.02 |
| 5 | 99.99 | 99.95 | 99.99 | 100.00 | 99.99 | 100.00 | 100.00 | 99.85 |
| 6 | 91.05 | 72.51 | 98.03 | 98.01 | 97.43 | 99.97 | 99.63 | 95.13 |
| 7 | 91.42 | 83.75 | 95.78 | 97.66 | 96.76 | 98.84 | 99.60 | 93.08 |
| 8 | 84.46 | 90.82 | 94.16 | 95.54 | 93.18 | 97.48 | 94.41 | 96.03 |
| 9 | 99.15 | 97.57 | 99.15 | 94.19 | 99.47 | 99.62 | 99.52 | 99.57 |
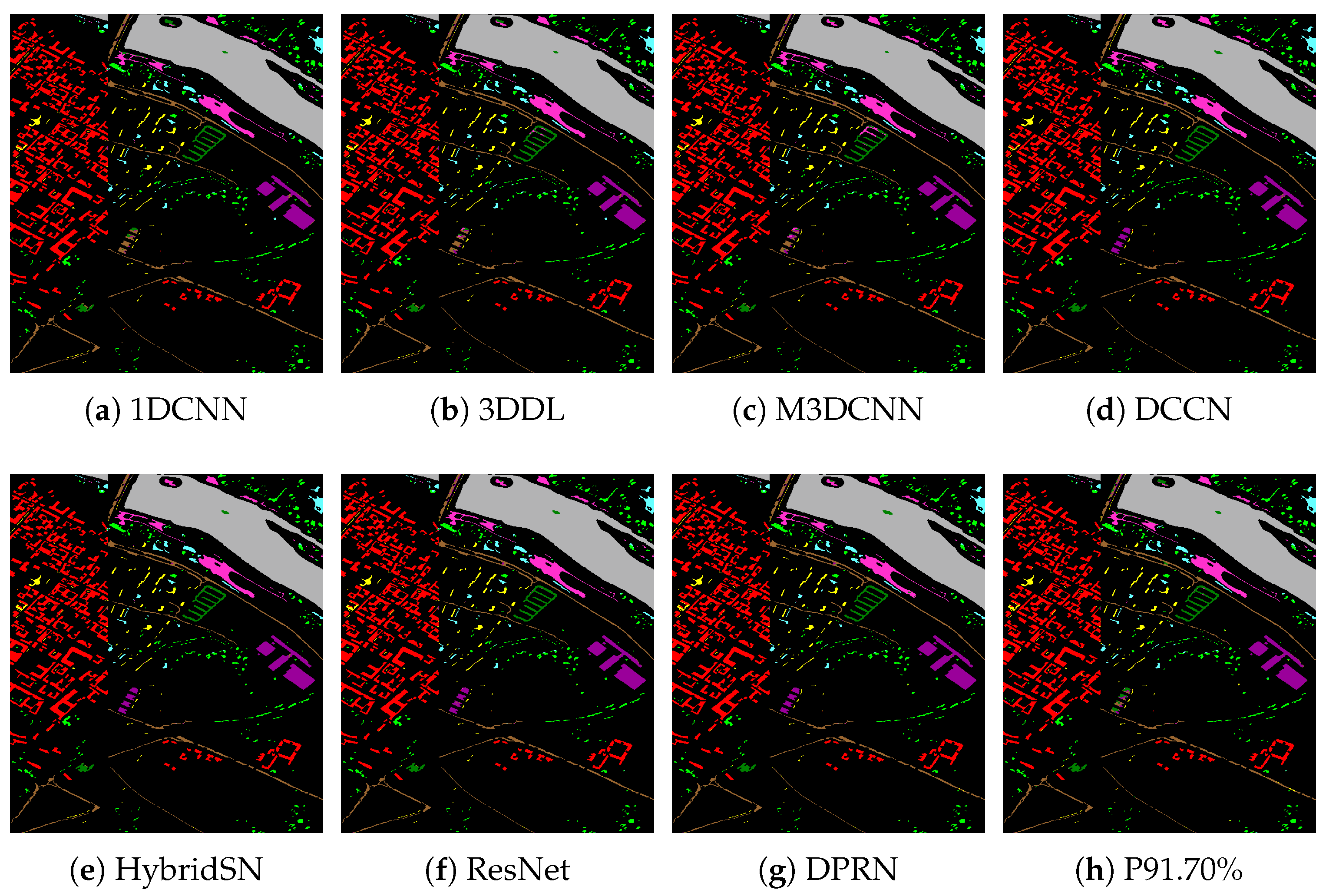
| Category | 1DCNN | 3DDL | M3DCNN | DCCN | HybridSN | ResNet | DPRN | Pruned 91.70% |
| OA (%) | 96.55 | 97.71 | 97.90 | 99.55 | 99.20 | 99.06 | 99.10 | 97.39 |
| AA (%) | 89.57 | 92.57 | 92.50 | 98.71 | 96.92 | 96.78 | 96.75 | 91.32 |
| Kappa (%) | 95.11 | 96.76 | 97.03 | 99.37 | 98.87 | 98.68 | 99.16 | 96.91 |
| 1 | 99.63 | 99.93 | 99.99 | 99.99 | 99.99 | 99.94 | 99.99 | 99.96 |
| 2 | 95.65 | 95.64 | 96.51 | 96.77 | 97.06 | 98.31 | 99.43 | 95.76 |
| 3 | 89.51 | 94.43 | 89.44 | 98.83 | 96.18 | 90.45 | 99.31 | 91.13 |
| 4 | 67.37 | 81.48 | 79.32 | 97.24 | 88.97 | 96.01 | 99.53 | 70.73 |
| 5 | 83.38 | 92.64 | 96.47 | 99.72 | 98.73 | 99.72 | 99.17 | 92.95 |
| 6 | 97.05 | 96.30 | 96.75 | 98.36 | 99.18 | 99.59 | 99.19 | 98.14 |
| 7 | 84.67 | 85.22 | 87.42 | 99.17 | 98.94 | 94.82 | 99.86 | 83.47 |
| 8 | 98.67 | 99.80 | 99.70 | 99.93 | 99.71 | 99.59 | 99.18 | 99.13 |
| 9 | 90.18 | 87.67 | 86.90 | 98.39 | 93.53 | 92.59 | 99.01 | 90.63 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, Y.; Wang, D.; Yang, S.; Shi, J.; Tian, D.; Min, L. Network Collaborative Pruning Method for Hyperspectral Image Classification Based on Evolutionary Multi-Task Optimization. Remote Sens. 2023, 15, 3084. https://doi.org/10.3390/rs15123084
Lei Y, Wang D, Yang S, Shi J, Tian D, Min L. Network Collaborative Pruning Method for Hyperspectral Image Classification Based on Evolutionary Multi-Task Optimization. Remote Sensing. 2023; 15(12):3084. https://doi.org/10.3390/rs15123084
Chicago/Turabian StyleLei, Yu, Dayu Wang, Shenghui Yang, Jiao Shi, Dayong Tian, and Lingtong Min. 2023. "Network Collaborative Pruning Method for Hyperspectral Image Classification Based on Evolutionary Multi-Task Optimization" Remote Sensing 15, no. 12: 3084. https://doi.org/10.3390/rs15123084
APA StyleLei, Y., Wang, D., Yang, S., Shi, J., Tian, D., & Min, L. (2023). Network Collaborative Pruning Method for Hyperspectral Image Classification Based on Evolutionary Multi-Task Optimization. Remote Sensing, 15(12), 3084. https://doi.org/10.3390/rs15123084








