Impact of Assimilating GK-2A All-Sky Radiance with a New Observation Error for Summer Precipitation Forecasting
Abstract
1. Introduction
2. Data and Experimental Methods
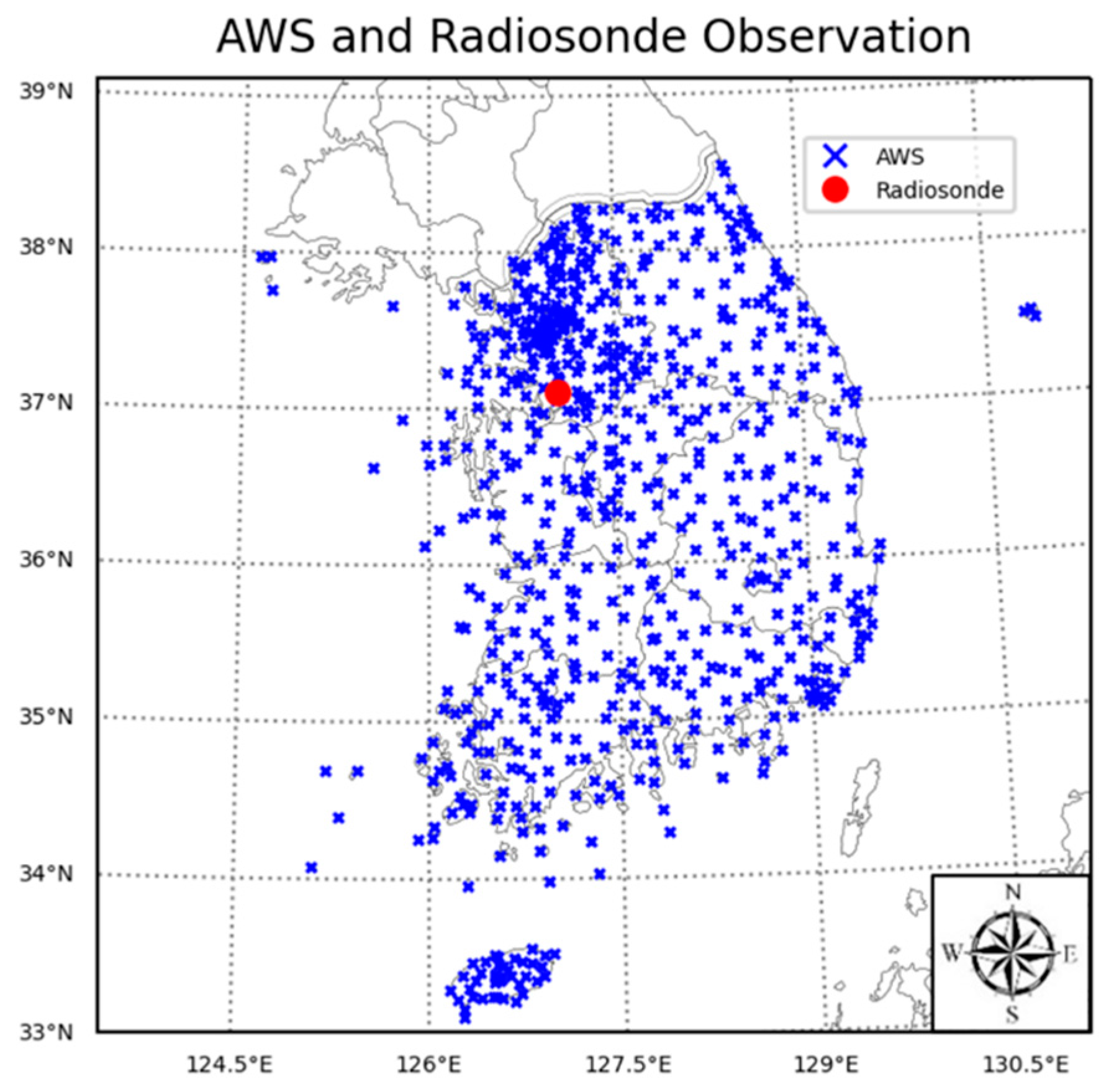
2.1. Observation Data
2.2. ASR Assimilation Method
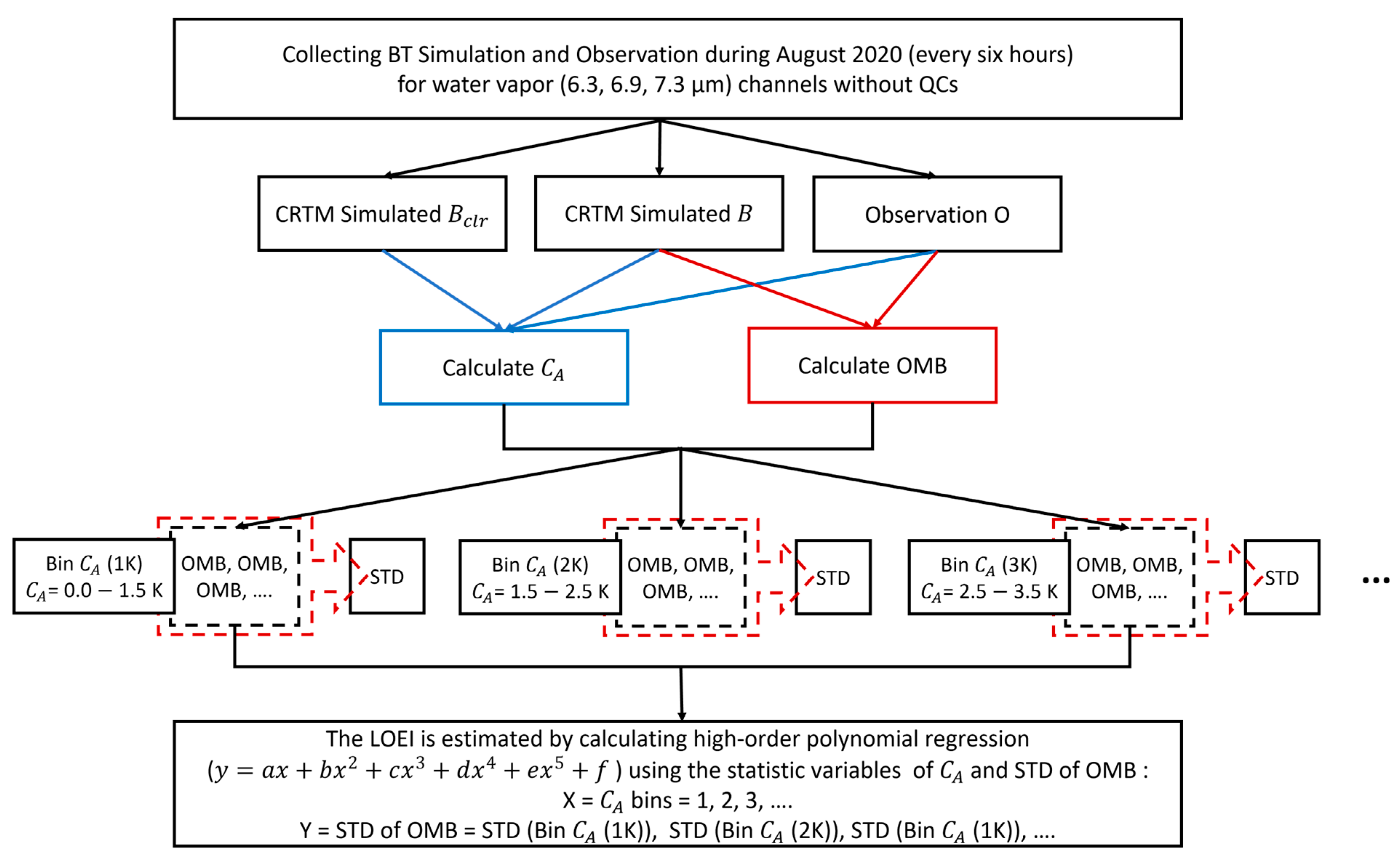
2.2.1. The LOEI Method
2.2.2. Observation Operator
2.2.3. Variational Bias Correction
2.3. WRF 3DVAR Assimilation System
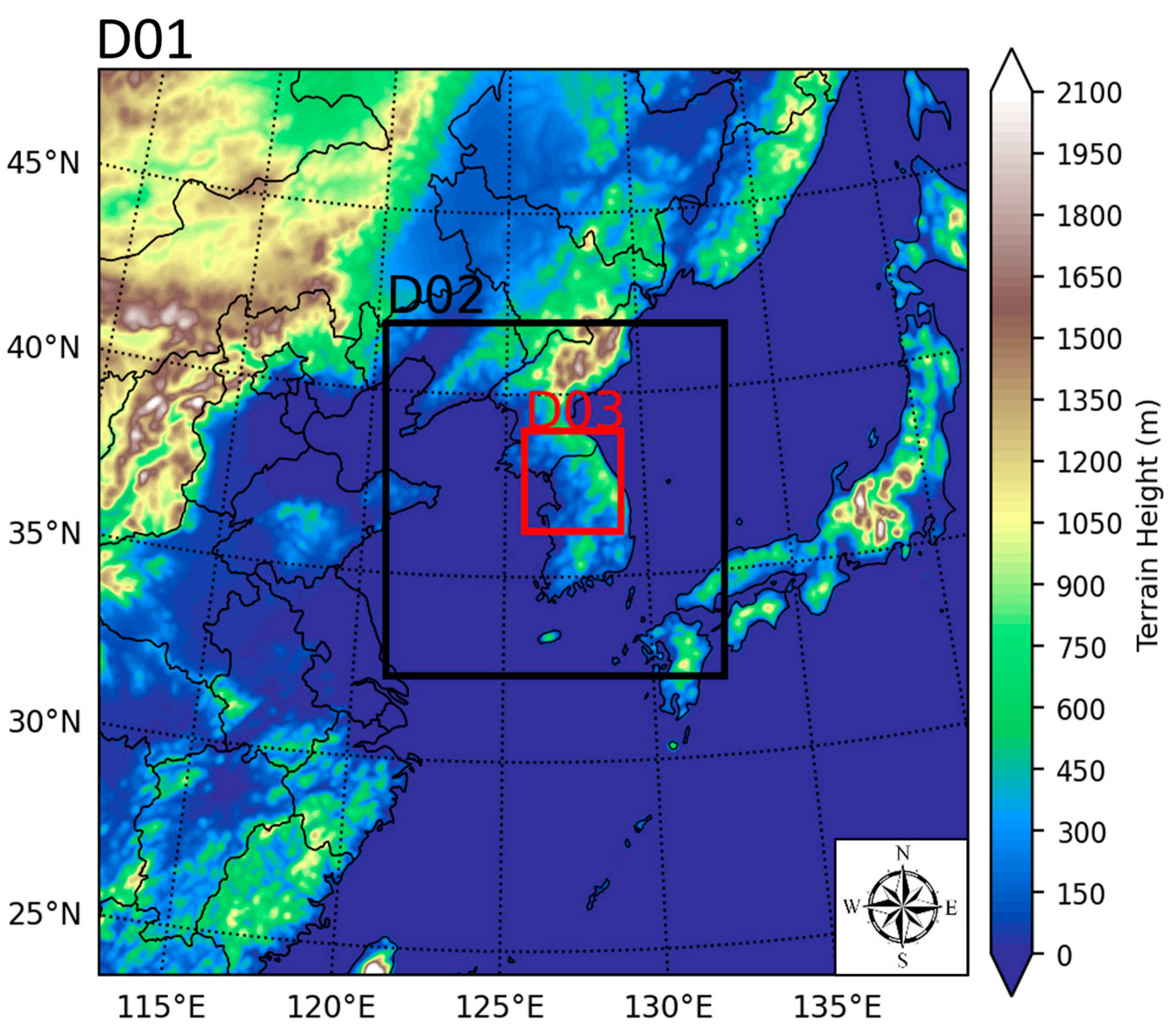
2.4. Model Configuration and Experimental Design
2.5. Overview of the Cases
2.6. Evaluation Parameters
3. Results
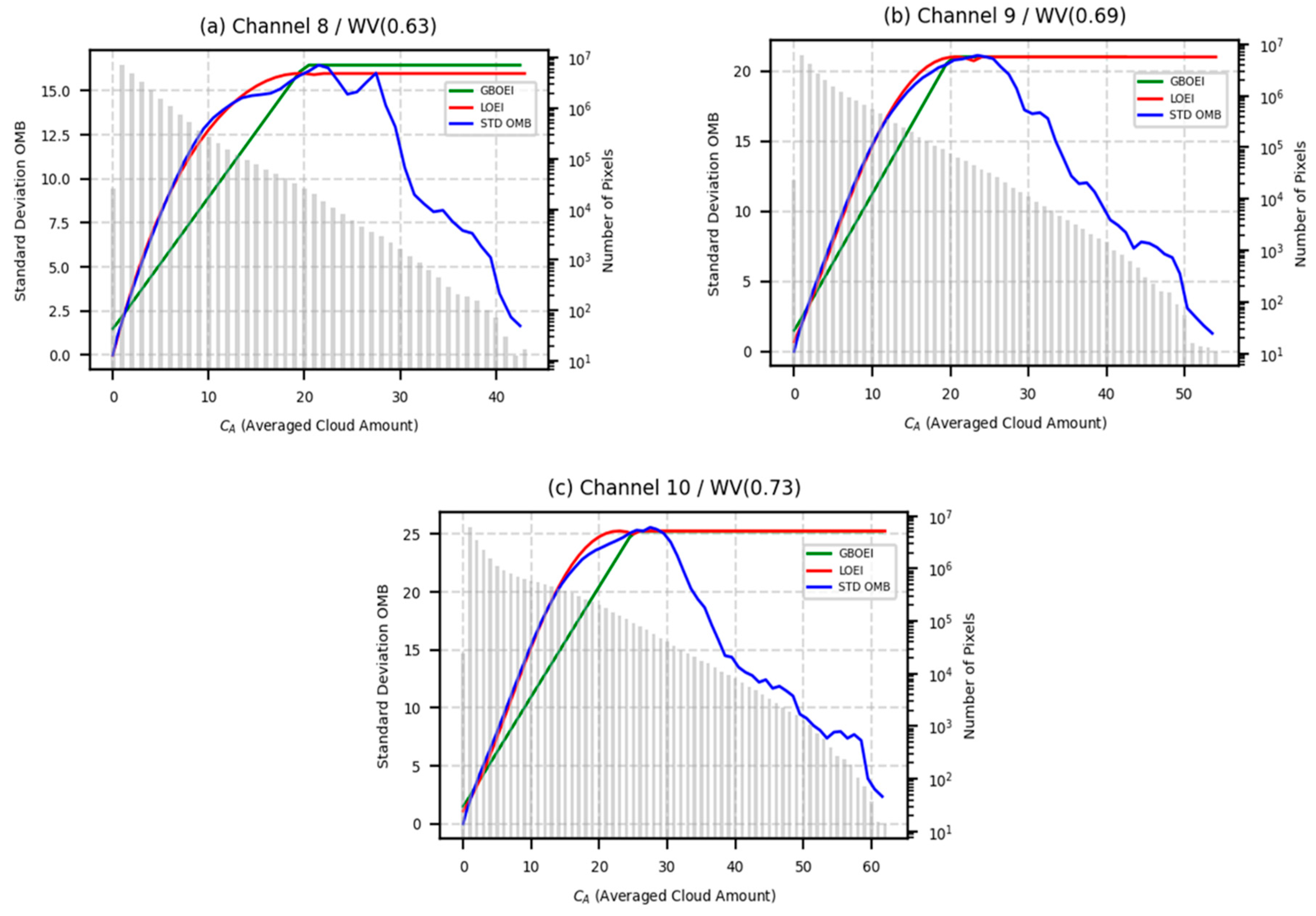
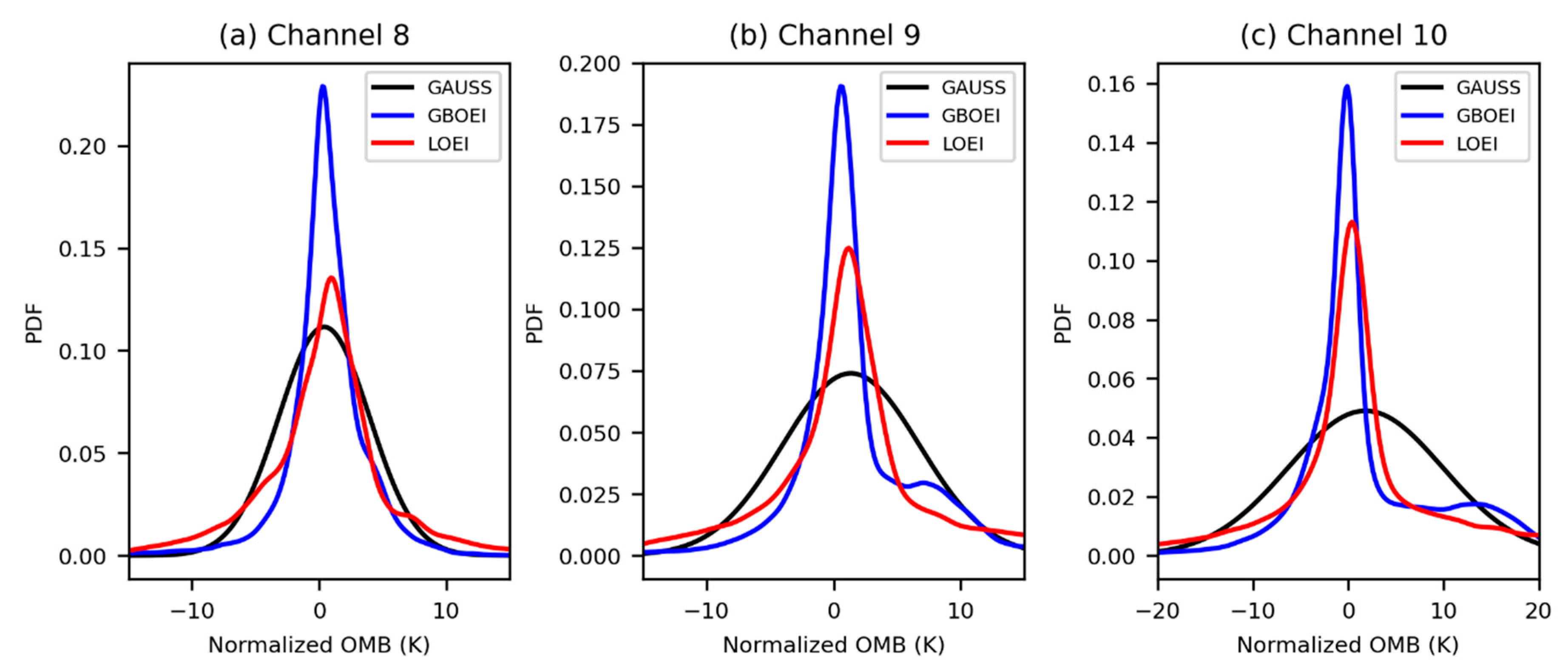
3.1. ASR Observation Error
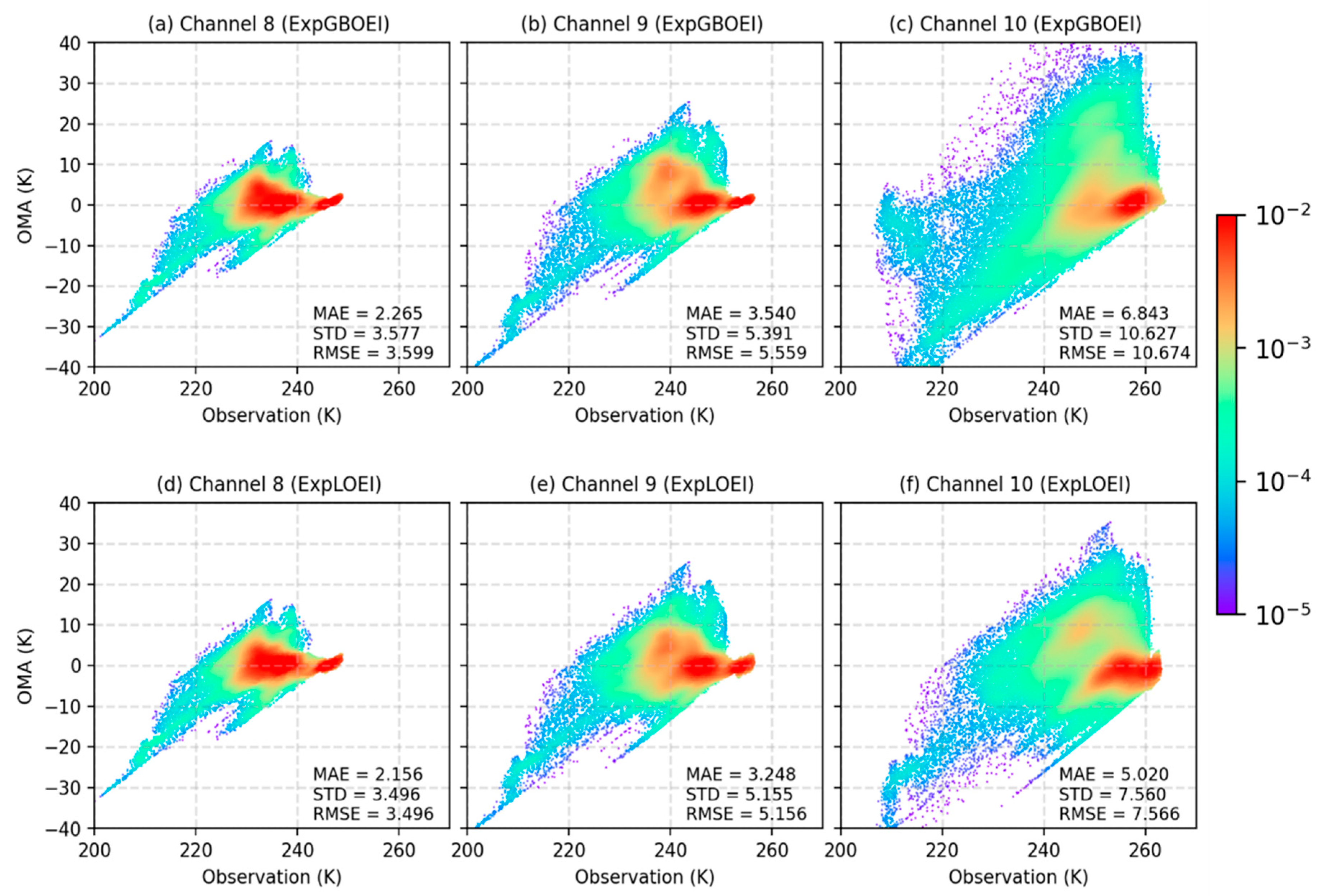
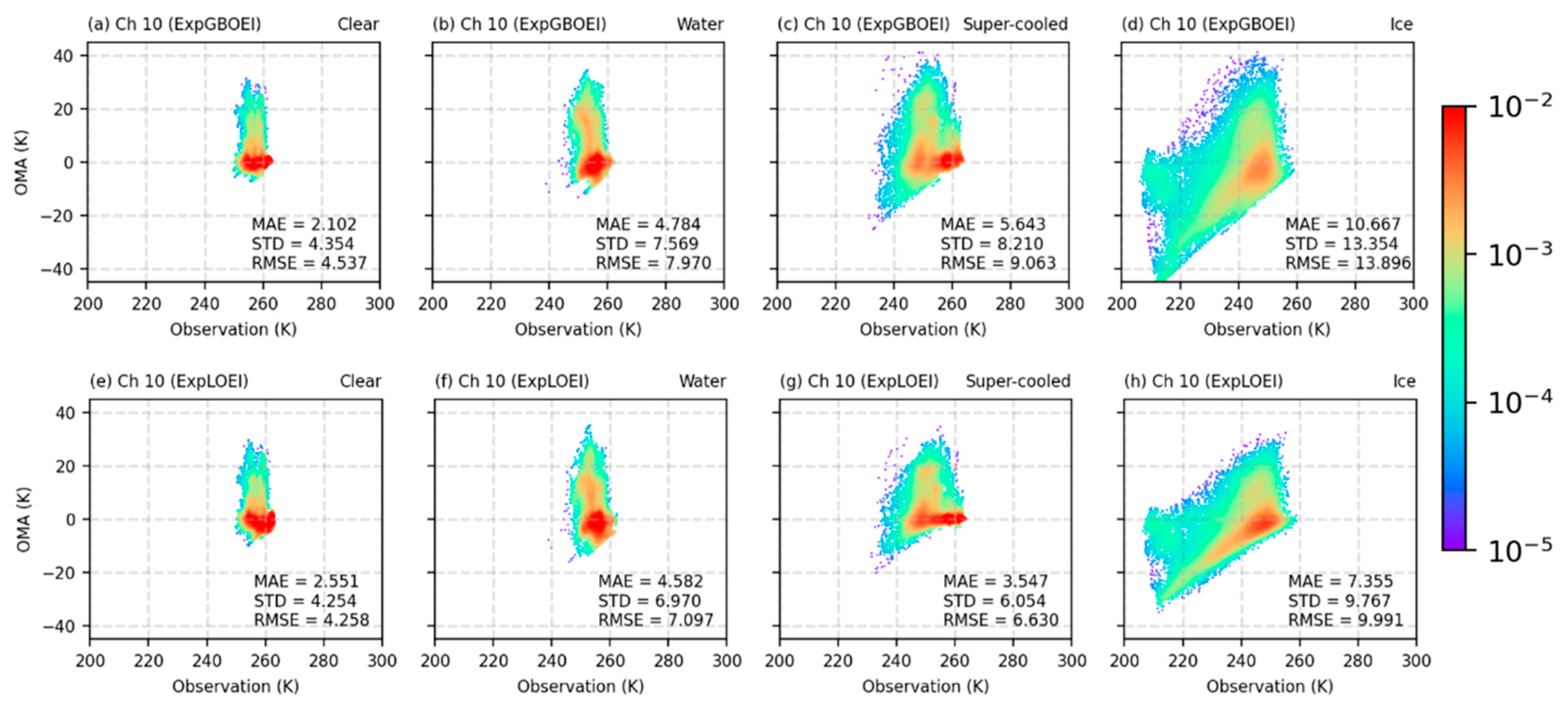
3.2. Evaluation of Simulated BT Analysis
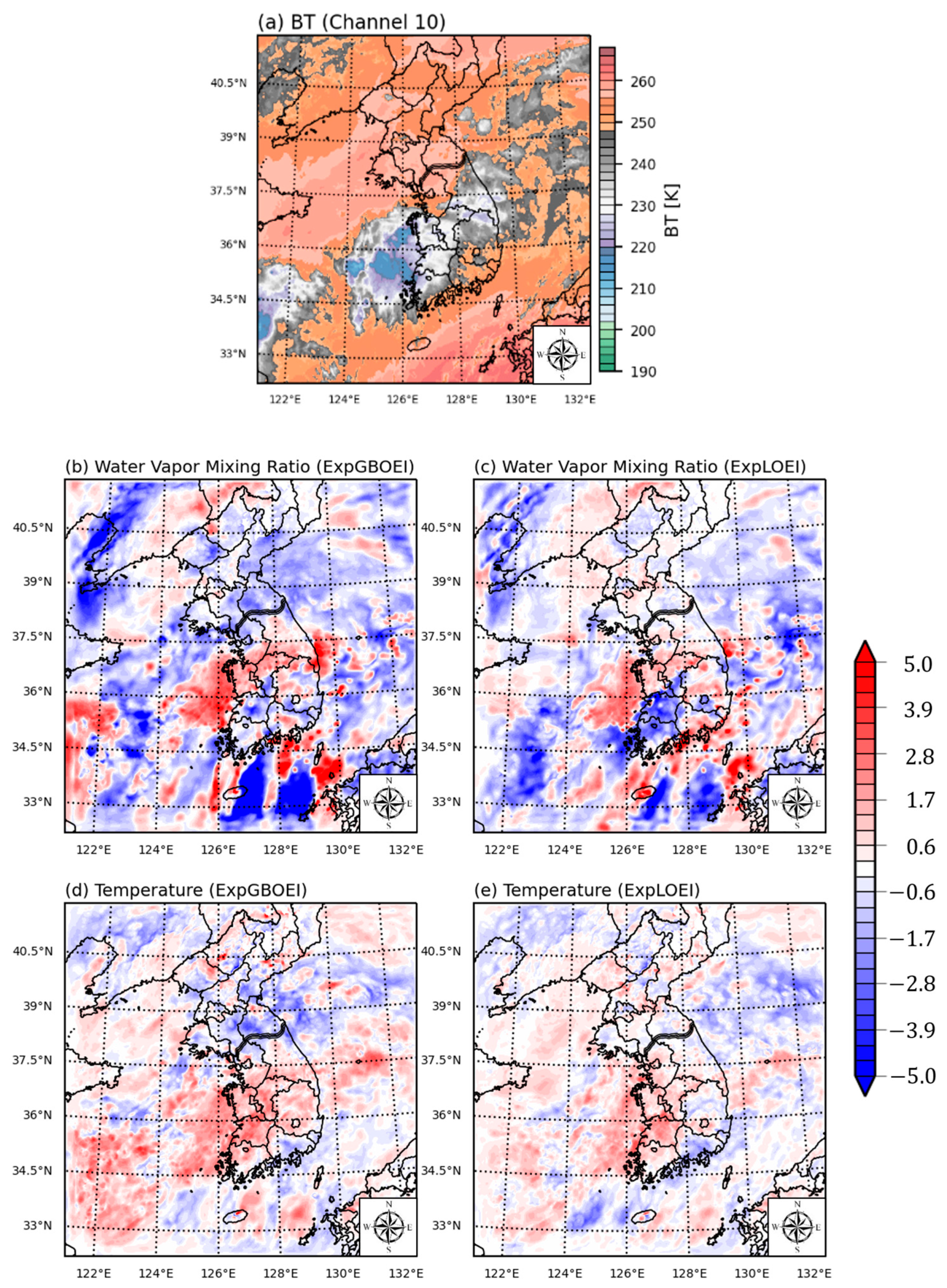
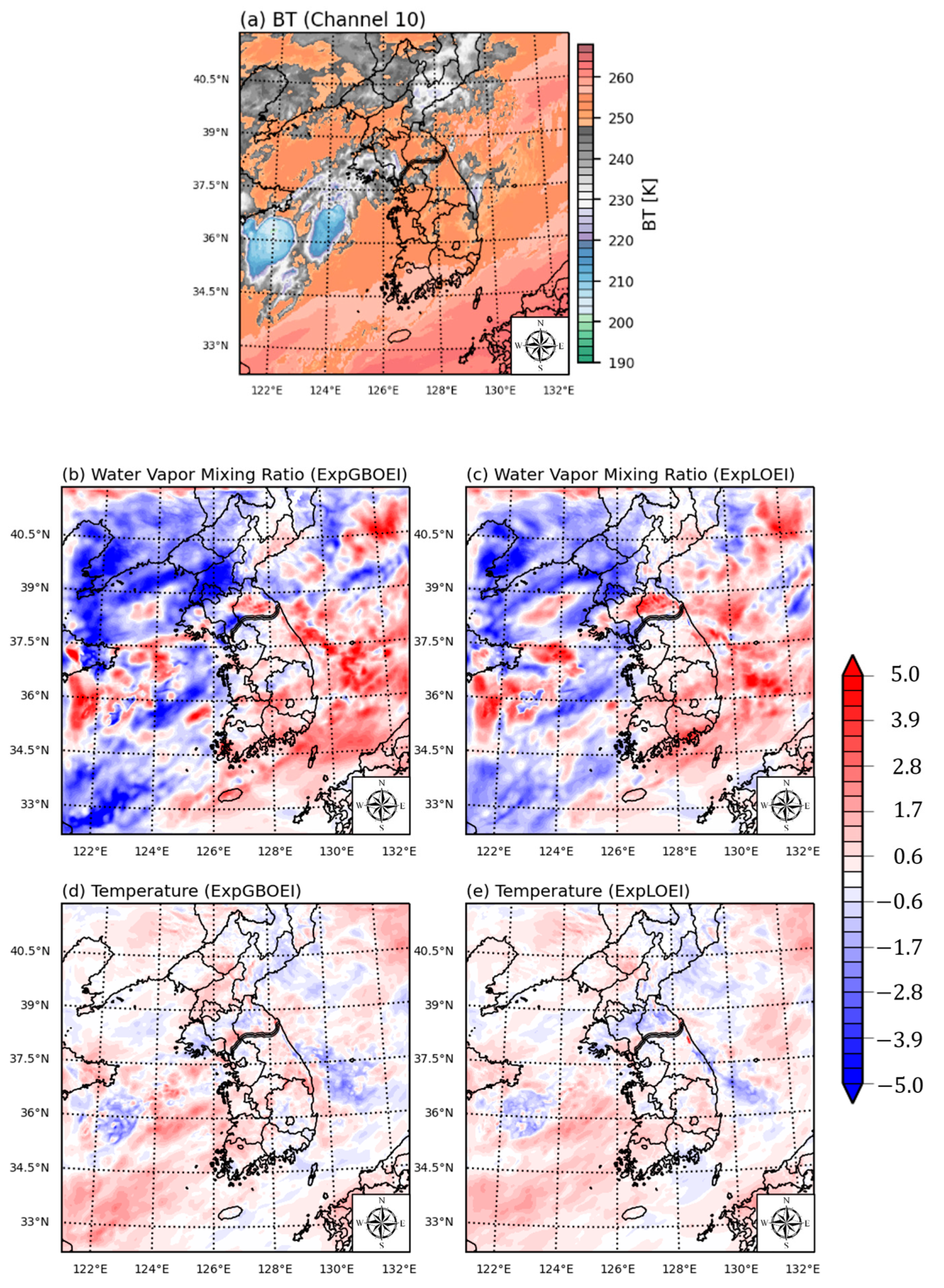
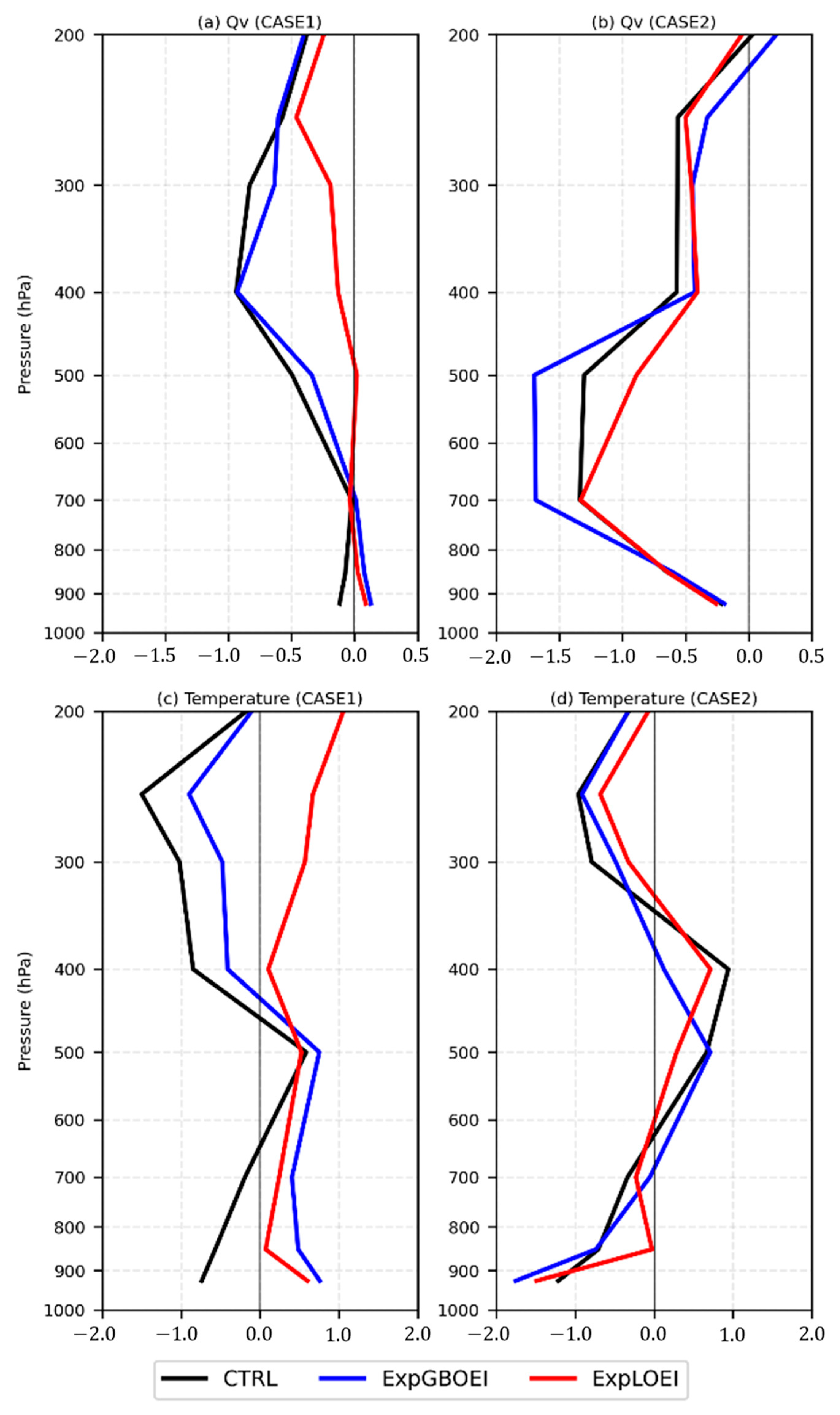
3.3. Increment of the Analysis Field
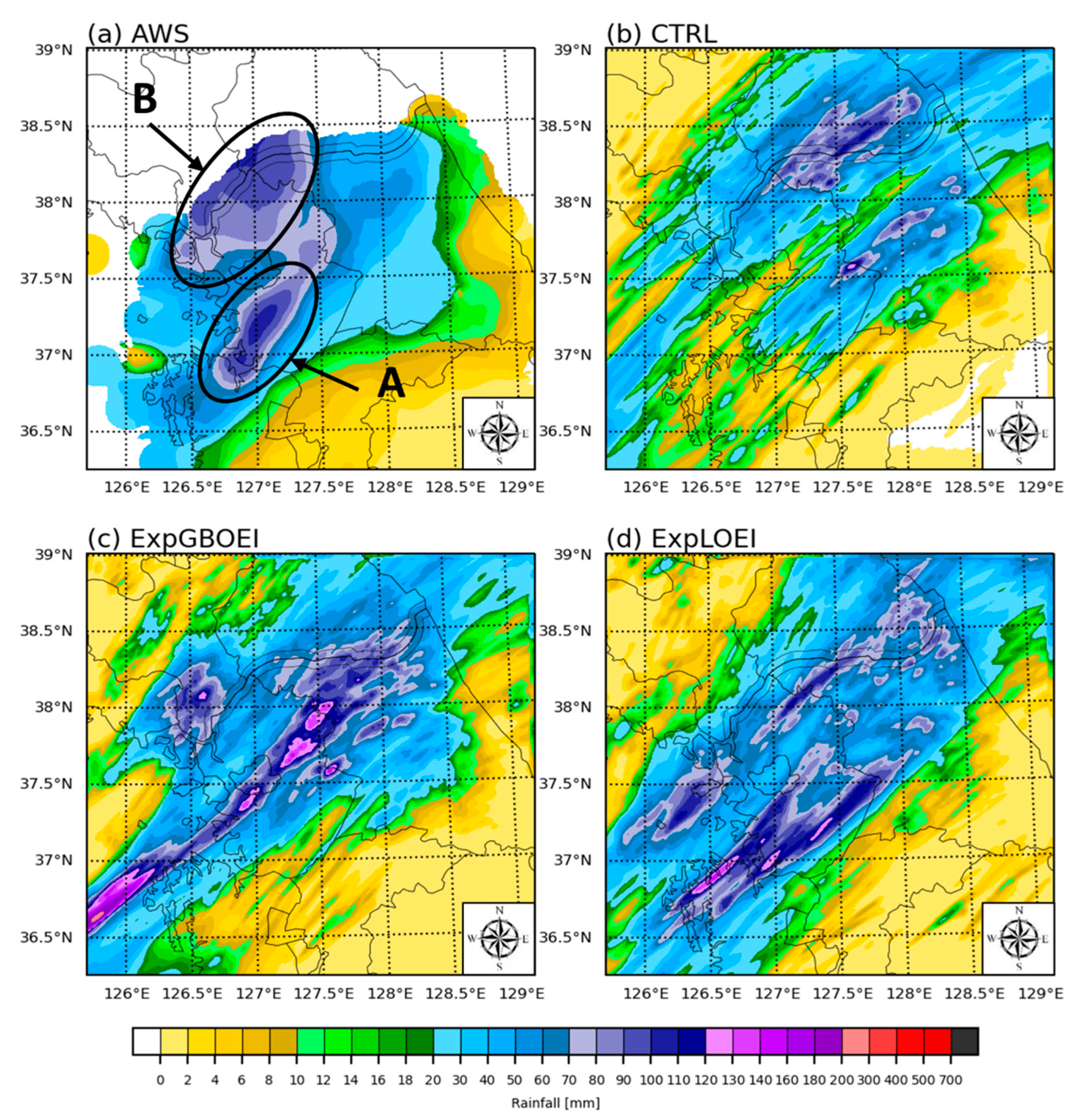
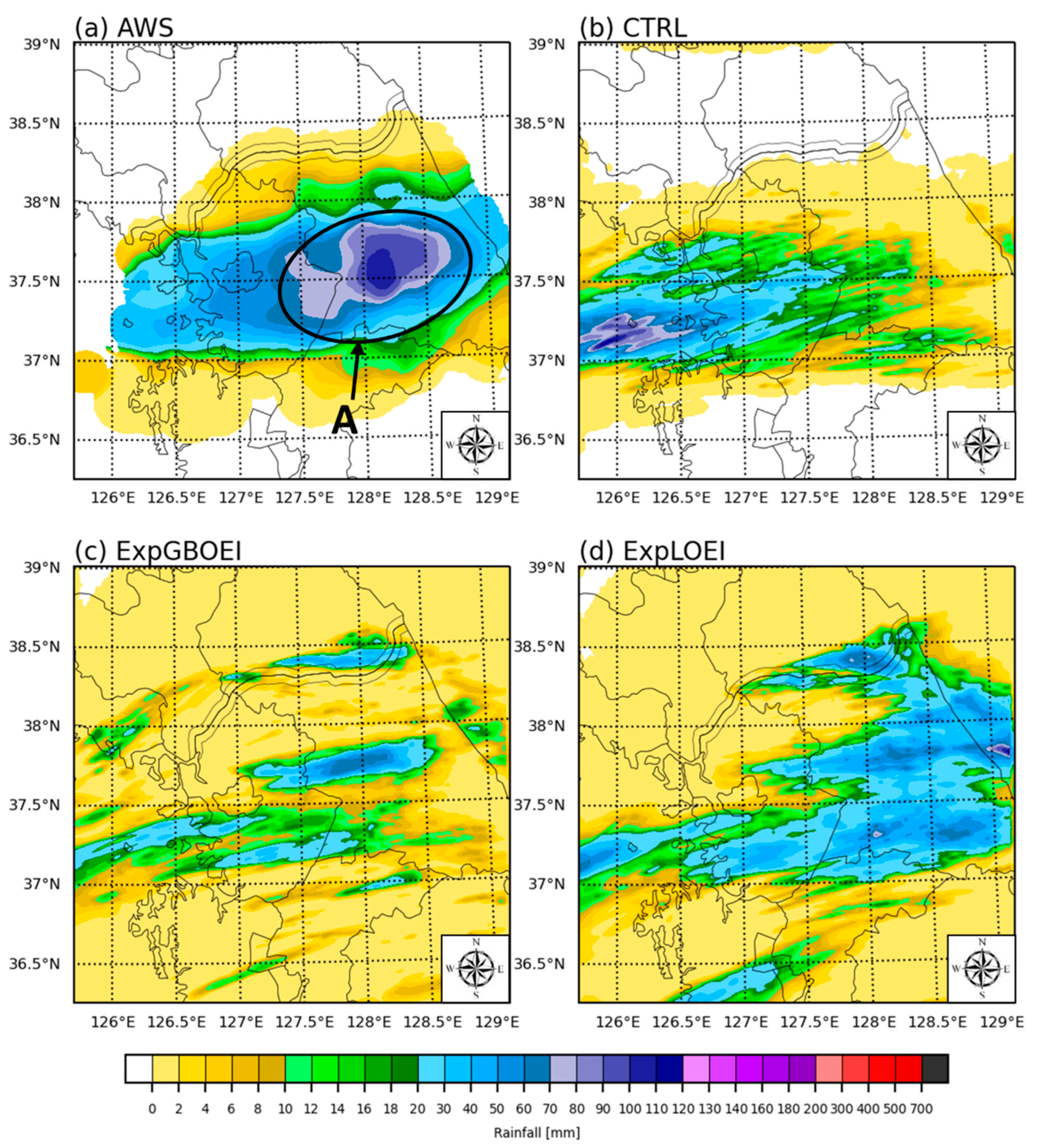
3.4. Distribution of the Cumulative Precipitation
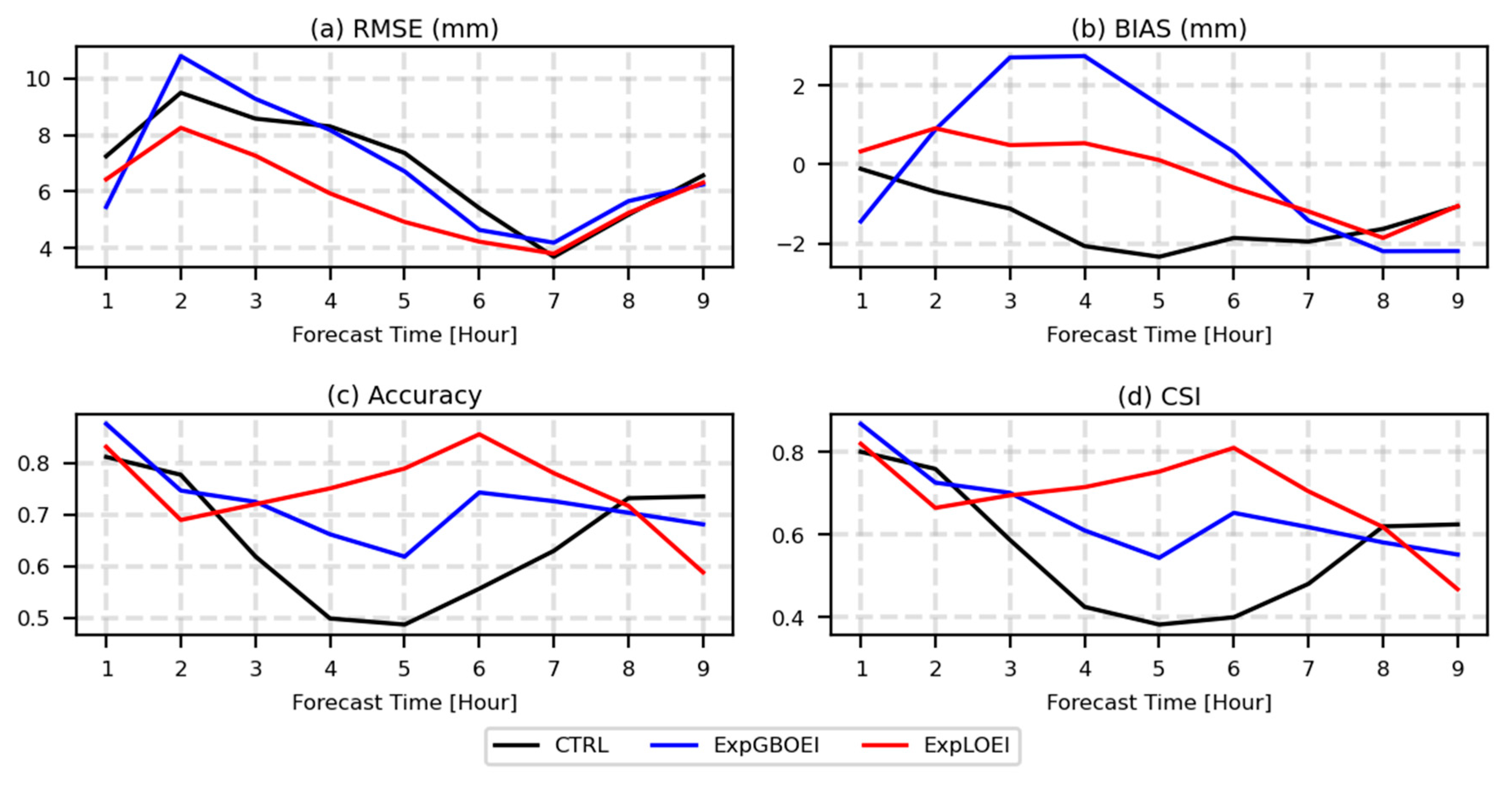
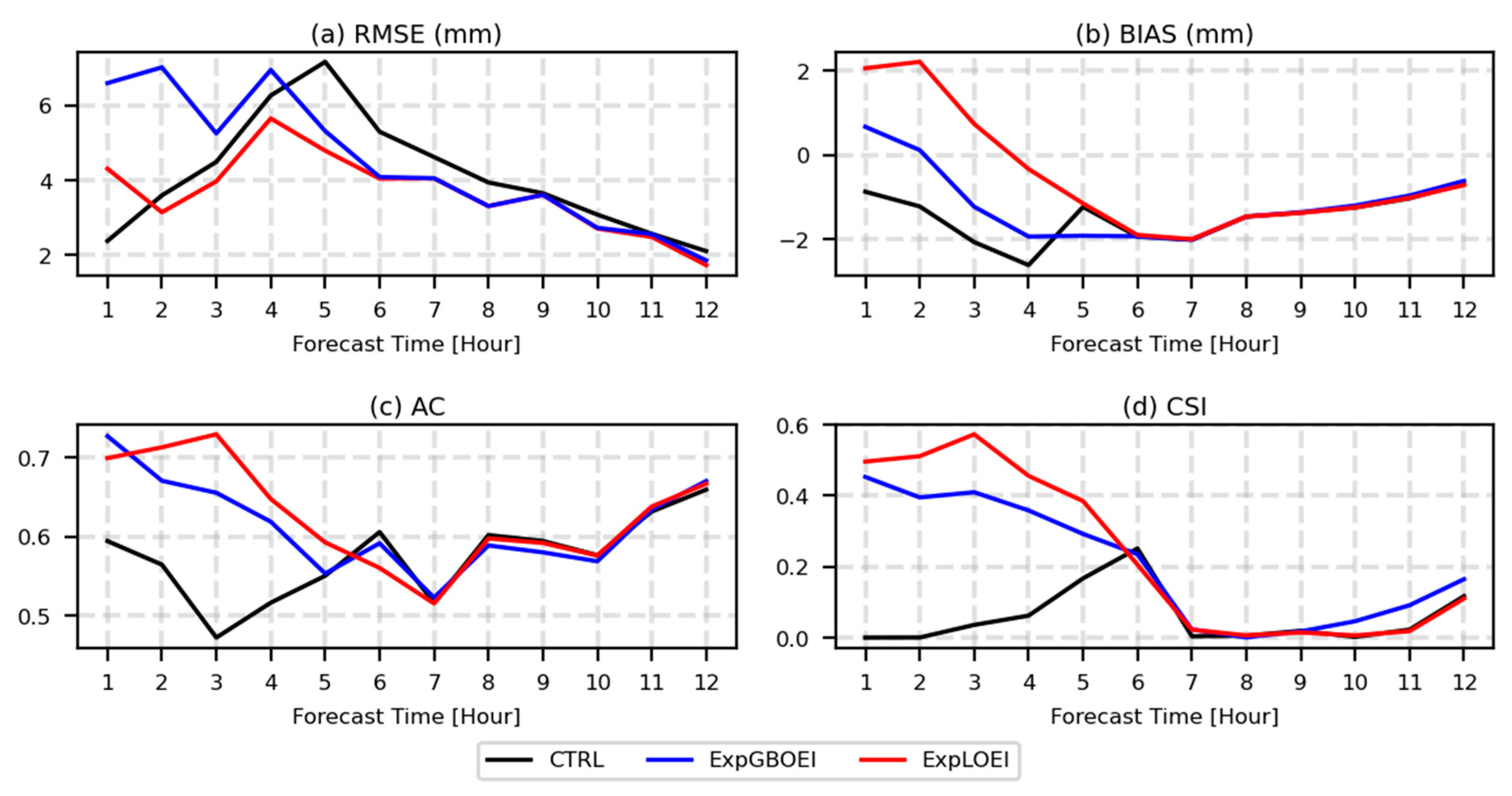
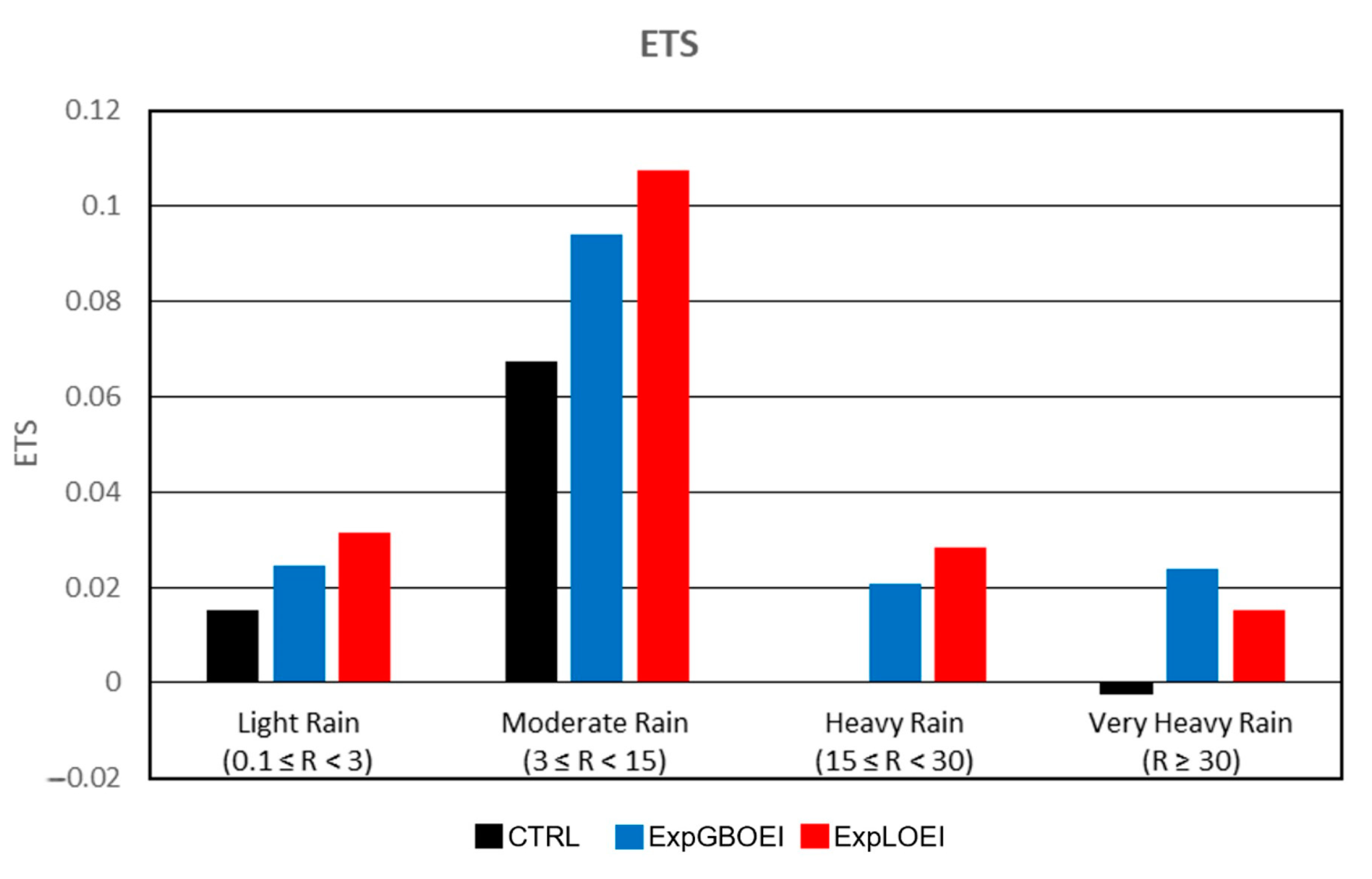
3.5. Model Verification
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hu, G.; Dance, S.L.; Bannister, R.N.; Chipilski, H.G.; Guillet, O.; Macpherson, B.; Weissmann, M.; Yussouf, N. Progress, challenges, and future steps in data assimilation for convection-permitting numerical weather prediction: Report on the virtual meeting held on 10 and 12 November 2021. Atmos. Sci. Lett. 2023, 24, e1130. [Google Scholar] [CrossRef]
- Errico, R.M.; Carvalho, D.; Privé, N.C. Sienkiewicz. Simulation of Atmospheric Motion Vectors for an Observing System Simulation Experiment. J. Atmos. Ocean. Technol. 2020, 37, 489–505. [Google Scholar] [CrossRef]
- Pan, S.; Gao, J.; Stensrud, D.J.; Wang, X.; Jones, T.A. Assimilation of Radar Radial Velocity and Reflectivity, Satellite Cloud Water Path, and Total Precipitable Water for Convective-Scale NWP in OSSEs. J. Atmos. Ocean. Technol. 2018, 35, 67–89. [Google Scholar] [CrossRef]
- Di Tomaso, E.; Bormann, N.; English, S. Assimilation of ATOVS Radiances at ECMWF: Third Year EUMETSAT Fellowship Report; EUMETSAT/ECMWF Fellowship Programme Research Report 29; ECMWF: Reading, UK, 2013; 26p. [Google Scholar]
- Pavelin, E.G.; Candy, B. Assimilation of surface-sensitive infrared radiances over land: Estimation of land surface temperature and emissivity. Q. J. R. Meteorol. Soc. 2014, 140, 1198–1208. [Google Scholar] [CrossRef]
- Bormann, N.; Bonavita, M.; Dragani, R.; Eresmaa, R.; Matricardi, M.; McNally, A. Enhancing the impact of IASI observations through an updated observation-error covariance matrix. Q. J. R. Meteorol. Soc. 2016, 142, 1767–1780. [Google Scholar] [CrossRef]
- Zou, X.; Qin, Z.; Zheng, Y. Improved tropical storm forecasts with GOES-13/15 imager radiance assimilation and asymmetric vortex initialization in HWRF. Mon. Weather Rev. 2015, 143, 2485–2505. [Google Scholar] [CrossRef]
- Jones, T.A.; Wang, X.; Skinner, P.; Johnson, A.; Wang, Y. Assimilation of GOES-13 imager clear-sky water vapor (6.5mm) radiances into a Warn-on-Forecast system. Mon. Weather Rev. 2018, 146, 1077–1107. [Google Scholar] [CrossRef]
- Wang, Y.B.; Liu, Z.Q.; Yang, S.; Min, J.Z.; Chen, L.Q.; Chen, Y.D.; Zhang, T. Added value of assimilating himawari-8 AHI water vapor radiances on analyses and forecasts for “7.19” severe storm over North China. J. Geophys. Res. 2018, 123, 3374–3394. [Google Scholar] [CrossRef]
- Yang, C.; Liu, Z.Q.; Gao, F.; Childs, P.P.; Min, J.Z. Impact of assimilating GOES imager CSR with a rapid refresh assimilation system for convection-permitting forecast over Mexico. J. Geophys. Res. 2017, 122, 5472–5490. [Google Scholar] [CrossRef]
- Otkin, J.A. Clear and cloudy sky infrared brightness temperature assimilation using an ensemble Kalman filter. J. Geophys. Res. 2010, 115, D19207. [Google Scholar] [CrossRef]
- Otkin, J.A. Assimilation of water vapor sensitive infrared brightness temperature observations during a high impact weather event. J. Geophys. Res. 2012, 117, D19203. [Google Scholar] [CrossRef]
- McNally, A.P. A note on the occurrence of cloud in meteorologically sensitive areas and the implications for advanced infrared sounders. Q. J. R. Meteorol. Soc. 2002, 128, 2551–2556. [Google Scholar] [CrossRef]
- Bocquet, M.; Pires, C.A.; Wu, L. Beyond Gaussian statistical modelling in geophysical data assimilation. Mon. Weather Rev. 2010, 138, 2997–3023. [Google Scholar] [CrossRef]
- Li, J.; Wang, P.; Han, H.; Li, J.L.; Zheng, J. On the assimilation of satellite sounder data in cloudy skies in numerical weather prediction models. J. Meteorol. Res. 2016, 30, 169–182. [Google Scholar] [CrossRef]
- Pires, C.A.; Talagrand, O.; Bocquet, M. Diagnosis and impacts of non-Gaussianity of innovations in data assimilation. Physical D 2010, 239, 1701–1717. [Google Scholar] [CrossRef]
- Kazumori, M.; Geer, A.J.; English, S.J. Effects of all-sky assimilation of GCOM-W/AMSR2 radiances in the ECMWF numerical weather prediction system. Q. J. R. Meteorol. Soc. 2016, 142, 721–737. [Google Scholar] [CrossRef]
- Errico, R.M.; Bauer, P.; Mahfouf, J.-F. Issues regarding the assimilation of cloud and precipitation data. J. Atmos. Sci. 2007, 64, 3785–3798. [Google Scholar] [CrossRef]
- Minamide, M.; Zhang, F. An adaptive background error inflation method for assimilating ASR. Q. J. R. Meteorol. Soc. 2019, 145, 805–823. [Google Scholar] [CrossRef]
- Okamoto, K.; Hayashi, M.; Hashino, T.; Nakagawa, M.; Okuyama, A. Examination of all-sky infrared radiance simulation of Himawari-8 for global data assimilation and model verification. Q. J. R. Meteorol. Soc. 2021, 147, 3611–3627. [Google Scholar] [CrossRef]
- Geer, A.; Lonitz, K.; Weston, P.; Kazumori, M.; Okamoto, K.; Zhu, Y.; Liu, E.H.; Collard, A.; Bell, W.; Migliorini, S.; et al. All-sky satellite data assimilation at operational weather forecasting centres. Q. J. R. Meteorol. Soc. 2017, 144, 1191–1217. [Google Scholar] [CrossRef]
- Okamoto, K.; Sawada, Y.; Kunii, K. Comparison of assimilating all-sky and clear- sky infrared radiances from Himawari-8 in a mesoscale system. Q. J. R. Meteorol. Soc. 2019, 145, 745–766. [Google Scholar] [CrossRef]
- Geer, A.J.; Bauer, P. Observation errors in all-sky data assimilation. Q. J. R. Meteorol. Soc. 2011, 137, 2024–2037. [Google Scholar] [CrossRef]
- Okamoto, K.; McNally, A.P.; Bell, W. Progress towards the assimilation of all-sky infrared radiances: An evaluation of cloud effects. Q. J. R. Meteorol. Soc. 2014, 140, 1603–1614. [Google Scholar] [CrossRef]
- Okamoto, K. Evaluation of IR radiance simulation for all-sky assimilation of Himawari-8/AHI in a mesoscale NWP system. Q. J. R. Meteorol. Soc. 2017, 143, 1517–1527. [Google Scholar] [CrossRef]
- Harnisch, F.M.; Weissmann, Á.P. Error model for the assimilation of cloud-affected infrared satellite observations in an ensemble data assimilation system. Q. J. R. Meteorol. Soc. 2016, 142, 1797–1808. [Google Scholar] [CrossRef]
- Xu, D.M.; Liu, Z.Q.; Fan, S.Y.; Chen, M.; Shen, F.F. Assimilating all-sky infrared radiances from Himawari-8 using the 3DVar method for the prediction of a severe storm over North China. Adv. Atmos. Sci. 2021, 38, 661–676. [Google Scholar] [CrossRef]
- Waller, J.A.; Dance, S.L.; Nichols, N.K. On diagnosing observation-error statistics with local ensemble data assimilation. Q. J. R. Meteorol. Soc. 2017, 143, 2677–2686. [Google Scholar] [CrossRef]
- Desroziers, G.; Berre, L.; Chapnik, B.; Poli, P. Diagnosis of observation, background and analysis-error statistics in observation space. Q. J. R. Meteorol. Soc. 2005, 131, 3385–3396. [Google Scholar] [CrossRef]
- Bormann, N.; Bauer, P. Estimates of spatial and interchannel observation-error characteristics for current sounder radiances for numerical weather prediction. I: Methods and application to ATOVS data. Q. J. R. Meteorol. Soc. 2010, 136, 1036–1050. [Google Scholar] [CrossRef]
- Di, D.; Ai, Y.; Li, J.; Shi, W.; Lu, N. Geostationary satellite-based 6.7 μm band best water vapor information layer analysis over the Tibetan Plateau. J. Geophys. Res. Atmos. 2016, 121, 4600–4613. [Google Scholar] [CrossRef]
- Weng, F. Advances in radiative transfer modeling in support of satellite data assimilation. J. Atmos. Sci. 2007, 64, 3799–3807. [Google Scholar] [CrossRef]
- Han, Y.; van Delst, P.; Liu, Q.; Weng, F.; Yan, B.; Han, Y. JCSDA Community radiative Transfer Model (CRTM)-Version 1. NOAA Tech. Rep. NESDIS 2006, 122, 33. [Google Scholar]
- Liu, Q.; Weng, F. Advanced doubling-adding method for radiative transfer in planetary atmosphere. J. Atmos. Sci. 2006, 63, 3459–3465. [Google Scholar] [CrossRef]
- Dee, D.; Uppala, S.M. Variational bias correction of satellite radiance data in the ERA–Interim reanalysis. Q. J. R. Meteorol. Soc. 2009, 135, 1830–1841. [Google Scholar] [CrossRef]
- Liu, Z.; Schwartz, C.S.; Snyder, C.; Ha, S. Impact of assimilating AMSU-A radiances on forecasts of 2008 Atlantic tropical cyclones initialized with a limited-area Ensemble Kalman Filter. Mon. Weather Rev. 2012, 140, 4017–4034. [Google Scholar] [CrossRef]
- Zhu, Y.; Derber, J.; Collard, A.; Dee, D.; Treadon, R.; Gayno, G.; Jung, J.A. Enhanced radiance bias correction in the National Centers for Environmental’Prediction’s Gridpoint Statistical Interpolation data assimilation system. Q. J. R. Meteorol. Soc. 2014, 140, 1479–1492. [Google Scholar] [CrossRef]
- Harris, B.A.; Kelly, G.A. Satellite radiance-bias correction scheme for data assimilation. Q. J. R. Meteorol. Soc. 2001, 127, 1453–1468. [Google Scholar] [CrossRef]
- Derber, J.C.; Wu, W.S. The use of TOVS cloud-cleared radiance in the NCEP SSI analysis system. Mon. Weather Rev. 1998, 126, 2287–2299. [Google Scholar] [CrossRef]
- Barker, D.M.; Huang, W.; Guo, Y.-R.; Bourgeois, A.J.; Xiao, Q.N. A three-dimensional variational data assimilation system for MM5: Implementation and initial results. Mon. Weather Rev. 2004, 132, 897–914. [Google Scholar] [CrossRef]
- Lee, Y.-H.; Min, K.-H. High-resolution modeling study of an isolated convective storm over Seoul Metropolitan area. Meteorol Atmos. Phys. 2019, 131, 1549–1564. [Google Scholar] [CrossRef]
- Ide, K.; Courtier, P.; Ghil, M.; Lorenc, A.C. Unified notation for data assimilation: Operational, sequential and variational. J. Meteorol. Soc. Jpn. 1999, 75, 181–189. [Google Scholar] [CrossRef]
- Parrish, D.F.; Derber, J.C. The National Meteorological Center’s spectral statistical-interpolation analysis system. Mon. Weather Rev. 1992, 120, 1747–1763. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Wang, W.; Powers, J.G.A. Description of the Advanced Research WRF Version 2; National Center for Atmospheric Research Boulder Co Mesoscale and Microscale Meteorology Div: Boulder, CO, USA, 2005. [Google Scholar]
- Kain, J.S.; Fritsch, J.M. Convective Parameterization for Mesoscale Models: The Kain-Fritsch Scheme. In The Representation of Cumulus Convection in Numerical Models. Meteorological Monographs; Emanuel, K.A., Raymond, D.J., Eds.; American Meteorological Society: Boston, MA, USA, 1993. [Google Scholar] [CrossRef]
- Lim, K.-S.S.; Hong, S.-Y. Development of an effective double-moment cloud microphysics scheme with prognostic cloud condensation nuclei (CCN) for weather and climate models. Mon. Weather Rev. 2010, 138, 1587–1612. [Google Scholar] [CrossRef]
- Dudhia, J. Numerical study of convection observed during the winter monsoon experiment using a mesoscale two-dimensional model. J. Atmos. Sci. 1989, 46, 3077–3107. [Google Scholar] [CrossRef]
- Tewari, M.; Chen, F.; Wang, W.; Dudhia, J.; LeMone, M.A.; Mitchell, K.; Cuenca, R.H. Implementation and verification of the unified NOAH land surface model in the WRF model. In Proceedings of the 20th Conference on Weather Analysis and Forecasting/16th Conference on Numerical Weather Prediction (Vol. 1115, No. 6), Seattle, WA, USA, 10 January 2004. [Google Scholar]
- Hong, S.Y.; Noh, Y.; Dudhia, J. A new vertical diffusion package with an explicit treatment of entrainment processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Koehler, A.B. Another look at measures of forecast accuracy. Int. J. Forecast. 2006, 22, 679–688. [Google Scholar]
- Jolliffe, I.T.; Stephenson, D.B. Forecast Verification: A Practitioner’s Guide in Atmospheric Science, 2nd ed.; Wiley and Sons Ltd.: Hoboken, NJ, USA, 2012; 274p. [Google Scholar]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2011; 676p. [Google Scholar]
- Devore, J. Probability and Statistics for Engineering and Science, 8th ed.; Richard Stratton: New York, NY, USA, 2012; pp. 1–712. [Google Scholar]

| Channel Number | Channel Name | Wavelength (µm) | Resolution (km) | Observation Characteristics |
|---|---|---|---|---|
| 1 | VI004 | 0.4708 | 1 | |
| 2 | VI005 | 0.5068 | 1 | |
| 3 | VI006 | 0.6394 | 0.5 | |
| 4 | VI008 | 0.8630 | 1 | Land and sea masks and vegetarian |
| 5 | NR013 | 1.3740 | 2 | Cloud physical parameter |
| 6 | NR016 | 1.6092 | 2 | |
| 7 | SW038 | 3.8316 | 2 | Low-level clouds, fog, wildfires |
| 8 | WV063 | 6.2104 | 2 | Vertical humidity profile (middle-to-upper tropospheric level) |
| 9 | WV069 | 6.9413 | 2 | |
| 10 | WV073 | 7.3266 | 2 | |
| 11 | IR087 | 8.5881 | 2 | Thin ice cloud monitoring |
| 12 | IR096 | 9.6210 | 2 | Ozone absorption |
| 13 | IR105 | 10.3539 | 2 | Ice crystals/water, lower water vapor, volcanic ash, sea surface temperature |
| 14 | IR112 | 11.2288 | 2 | |
| 15 | IR123 | 12.3664 | 2 | |
| 16 | IR133 | 13.2908 | 2 | CO2 absorption, cloud top height |
| D01 | D02 | D03 | |
|---|---|---|---|
| WRF version | v4.2 | ||
| Resolution | 9 km | 3 km | 1 km |
| Horizontal Grids | 301 × 301 | 352 × 352 | 301 × 301 |
| Vertical Grids | 60 | 60 | 60 |
| Cumulus | Multiscale Kain–Fritsch scheme | ||
| Microphysics | WRF Double Moment 6 class scheme | ||
| Planetary Boundary Layer | Yonsei University Scheme | ||
| Surface Layer | Revised MM5 Monin–Obukhov scheme | ||
| Land Surface | Unified Noah land surface model | ||
| Radiation | Rapid radiative transfer model scheme Long-wave/Dudhia Scheme Short-wave | ||
| Initial and Boundary Conditions | NCEP FNL 0.1 Degree Global Tropospheric Analysis | ||
| Experiment | Assimilation | Observation Error |
|---|---|---|
| CTRL | N/A | N/A |
| ExpGBOEI | ASR | GBOEI |
| ExpLOEI | ASR | LOEI |
| Forecast Period | Total Cumulative Precipitation (mm) | Maximum Rain Rate (mm∙h−1) | |
|---|---|---|---|
| Case 1 | 8 August 2020 at 2100 UTC— 9 August 2020 at 0600 UTC | 107.32 | 53.0 |
| Case 2 | 14 August 2020 at 1800 UTC— 15 August 2020 at 0600 UTC | 114.8 | 44.0 |
| Observation | Total | |||
|---|---|---|---|---|
| Yes | No | |||
| Forecast | Yes | Hits | False alarms | Forecast Yes |
| No | Misses | Correct negative | Forecast No | |
| Total | Observed Yes | Observed No | Total | |
| Experiment | RMSE (mm) | BIAS (mm) | AC | CSI | PC | |
|---|---|---|---|---|---|---|
| Case 1 | CTRL | 27.57 | −13.15 | 0.88 | 0.87 | 0.57 |
| ExpGBOEI | 27.01 | −2.44 | 0.91 | 0.90 | 0.63 | |
| ExpLOEI | 22.08 | 0.73 | 0.93 | 0.93 | 0.74 | |
| Case 2 | CTRL | 27.65 | −6.40 | 0.65 | 0.60 | 0.31 |
| ExpGBOEI | 26.21 | −13.87 | 0.72 | 0.69 | 0.53 | |
| ExpLOEI | 22.51 | −6.22 | 0.79 | 0.76 | 0.55 | |
| Average | CTRL | 27.61 | −9.77 | 0.76 | 0.73 | 0.44 |
| ExpGBOEI | 26.61 | −8.15 | 0.81 | 0.79 | 0.58 | |
| ExpLOEI | 22.29 | −2.74 | 0.86 | 0.84 | 0.64 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hastuti, M.I.; Min, K.-H. Impact of Assimilating GK-2A All-Sky Radiance with a New Observation Error for Summer Precipitation Forecasting. Remote Sens. 2023, 15, 3113. https://doi.org/10.3390/rs15123113
Hastuti MI, Min K-H. Impact of Assimilating GK-2A All-Sky Radiance with a New Observation Error for Summer Precipitation Forecasting. Remote Sensing. 2023; 15(12):3113. https://doi.org/10.3390/rs15123113
Chicago/Turabian StyleHastuti, Miranti Indri, and Ki-Hong Min. 2023. "Impact of Assimilating GK-2A All-Sky Radiance with a New Observation Error for Summer Precipitation Forecasting" Remote Sensing 15, no. 12: 3113. https://doi.org/10.3390/rs15123113
APA StyleHastuti, M. I., & Min, K.-H. (2023). Impact of Assimilating GK-2A All-Sky Radiance with a New Observation Error for Summer Precipitation Forecasting. Remote Sensing, 15(12), 3113. https://doi.org/10.3390/rs15123113








