Abstract
Coherence change detection (CCD) is a remote sensing technique used to map phenomena that, under certain conditions, can be directly related to changes in Interferometric SAR (InSAR) coherence. Mapping the areas affected by sediment transport events in arid environments is one of the most common applications of CCD. However, the reliability of these maps remains an unsolved issue. This paper focuses on verifying that InSAR coherence is indeed able to detect all the fluvial sediment transport events that have actually mobilised sediments in arid environments by building a classification model and validating its results. The proposed methodology is tested in three study areas in Salar de Atacama, Chile, using three years of Sentinel data plus a fourth year for validation, and meteorological records of rainfall, the relative humidity of the air and snow cover. The results prove that InSAR coherence can be used to remotely detect sediment transport events related to flash floods in arid environments, that it might have a greater detection ability than meteorological records and that the perpendicular baseline does have a relevant effect on the InSAR coherence that needs to be considered. All these findings will increase the reliability of maps based on InSAR coherence. In addition, the proposed method will allow focusing the mapping tasks only on the relevant dates and, once calibrated, the classification model will enable the automatised remote detection of new events.
1. Introduction
Interferometry with Synthetic Aperture Radar (InSAR) is a remote sensing technique able to measure subcentimetric displacements of the observed surface (either the ground or any structure on it). Its working principle consists of measuring the difference in the wave phase between two radar images acquired at different times over the same area. This phase is related to the distance between the radar and the observed surface, in such a way that the change in the phase between two instants is directly related to the displacement of the observed surface. The complexity encountered when processing SAR data (i.e., raw radar data) is that deformation is not the only factor that may alter the wave phase. Therefore, eventual displacements need to be isolated from noise and other contributions to the phase shift, such as the topographic, atmospheric and thermal expansion components. This operation can only be performed if the radar signal is stable enough, which is measured with the so-called coherence. Thus, coherence is a parameter in the SAR data processing that determines at which points of the observed scene InSAR can measure eventual displacements of the surface. More detailed and complete explanations of InSAR fundamentals can be found in [1,2,3], for instance.
More specifically, InSAR coherence is a measure of the linear correlation between two SAR images (once co-registered, i.e., geometrically matched):
where γ is the coherence of a pixel, E is the mathematical expectation, s is the complex value of the pixel, s* is its conjugated value and |s| is its module. In each pixel, a raw SAR image contains a complex number s that includes the amplitude and the phase of the backscattered radar signal. In practice, the coherence of a pixel is calculated as the average within a window around the pixel. For a window of size n × m pixels,
Since InSAR coherence is a variable linked to a pixel and its neighbours—not to the entire radar image—a map of coherence represents the effect in space of the factors affecting the coherence. Thus, if under certain conditions one factor prevails, a map of coherence will be a map of that component and, furthermore, a time series of maps of coherence will represent the evolution in time of that component. This way, coherence appears not only as a quality parameter in the InSAR processing scheme but also as an InSAR product by itself. This is the basis of the so-called coherence change detection (CCD) methods.
CCD is a highly sensitive radar technique used to remotely detect and map changes in the observed scene. Because coherence integrates information from both the amplitude and phase, it is sensitive to slight changes in the dielectrical and geometrical characteristics of the observed surface on the subpixel scale [4,5,6,7]. Thus, CCD is a promising complement to field campaigns and optical remote sensing techniques: it is suitable to monitor large and remote areas where field campaigns are costly and difficult, and it is more sensitive to surface changes than optical techniques without being constrained by cloud cover [6,7,8,9,10].
In a general case, changes in InSAR coherence might be related to four causes: (i) the perpendicular baseline, i.e., the distance between the position of the radar during the different data acquisitions in the direction perpendicular to the radar line of sight; (ii) the temporal baseline, i.e., the time lapse between radar images; (iii) atmospheric changes, mainly in the relative humidity of the air; and (iv) changes in the observed surface [9,11,12,13]. However, according to the literature, with the performance of current satellite constellations—such as Sentinel—the effects of the perpendicular baseline on the coherence [5,6,10,12]—except in rugged terrain [11,12,14]—and the temporal baseline on the coherence between consecutive SAR images [11,12] are negligible. In addition, humidity changes in arid environments are limited to during and shortly after the rare rainfall events [6,15]. Therefore, changes in the observed surface are the remaining factor that affects the coherence in arid environments, which are then suitable for CCD analysis [9]. In such environments, changes in the surface are basically due to (i) ephemeral vegetation, which only lasts for a few months after rainfall events [6,11,15]; (ii) anthropic activities, such as mining, which are easy to locate and identify [12,16]; and (iii) sediment transport [5,6]. Consequently, one of the main applications of CCD in the literature is the mapping of sediment transport phenomena in arid environments.
An early example of CCD can be found in [9]. Three ERS-1 images acquired in 1992 and 1993 over the Algerian Sahara Desert were used to detect fluvial and aeolian sediment transport events: erosion and deposition related to flash floods and the evolution of ephemeral lakes and sediment transport over dunes. Focusing on the fluvial sediment transport related to flash floods, Ref. [11] compared five pairs of Envisat SAR images from 2004 to 2010 with Tropical Rainfall Measuring Mission (TRMM) precipitation estimates and the Shuttle Radar Topography Mission (SRTM) digital elevation model (DEM) to identify areas of recent fluvial erosion in the south of the Anti-Atlas Range, Western Sahara. Unfortunately, the comparison between interferograms covering a period without rain—according to the meteorological data—indicated a substantial level of uncertainty and suggested the existence of other phenomena affecting the InSAR coherence, possibly aeolian sediment transport. With better SAR data, Ref. [6] evaluated the suitability of CCD for mapping ground modifications in an extensive area affected by erosion and sedimentation triggered by an extreme hydro-meteorological event that occurred on 23–27 March 2015 over the Atacama Desert, Chile. The combination of 15-month-long time series of Sentinel-1A InSAR coherence with optical, meteorological and field data allowed them to relate the temporal loss of coherence to variations in soil moisture and the permanent loss of coherence after 5 months to erosion and sedimentation. Some of their findings provided new insights into sediment dynamics in arid environments, proving the potential of CCD in this field.
Regarding aeolian sediment transport, the studies are often related to the management of natural hazards. Thus, using 14 TerraSAR-X images together with rainfall and wind records from a local meteorological station, Ref. [8] applied CCD to detect wind-driven sediment transport in a field of dunes along the coast of Israel in 2012, as well as the displacement of the dunes themselves. SAR data allowed the authors to describe and better understand the behaviour of dunes under the action of the wind, track the individual dynamics of each dune and produce maps of stability/instability. In another line of research, Ref. [16] explored the utility of principal component analysis (PCA), enhanced with field knowledge, to isolate aeolian erosion from other components of Sentinel-1A InSAR coherence data from 2017 of the Gobi Desert, southern Mongolia. The results were satisfactorily compared with a DEM and field observations, and they notably improved the knowledge of the dust generation in the region, where dust storms represent a major threat to public health and socio-economic activities. In another study of dunes’ motion, Ref. [7] explored the potential of InSAR coherence in supporting sand mitigation measures and used Sentinel-1 SAR data from 2015 to 2018 to detect and track the motion of sand accumulations in desert areas in the United Arab Emirates (UAE) and Egypt. Migrating dunes were detected with the average coherence (“mean short-term coherence”, MSTC) and a novel index called the Temporal Stability Index (TSI), conceived to characterise the percentage of stability of a target over time. Offset tracking was also tested, but its complexity limits its applicability.
However, the applications of CCD are not limited to the study of sediment dynamics. From the very beginning, InSAR coherence has also been used to map other characteristics and processes of the Earth’s surface. For instance, using three ERS-1 SAR images acquired over the Death Valley salt pan, USA, in 1993 and a Landsat multispectral image, Ref. [17] empirically related some ranges of InSAR coherence to different surface types (alluvial fans, bushes, lakes, wet zones, rough dry salt, smooth wet salt, …) and found lineal regressions between InSAR coherence and vegetated surfaces (in low-erosion-risk areas) and erosion (in non-vegetated and high-erosion-risk areas). According to their findings, automatic classification tools could be programmed to produce maps of the land cover based on the degree of coherence, the backscattering coefficient and the backscatter ratio of SAR data. In a similar line, Sentinel-1A and B SAR data from October 2014 to February 2018, complemented with field campaigns, allowed [15] to analyse the ability of CDD to map surface lithologies in the Atacama Desert, Chile, based on the evolution of soil moisture over time. Bringing everything together, Ref. [5] also analysed Sentinel-1 InSAR coherence over the Atacama Desert between March 2015 and December 2018 and compared it with Sentinel-2 multispectral data, TanDEM-X WorldDEM and a detailed geographic information system (GIS) database of the local hydrographic network to characterise the processes and dynamics of arid environments. Local losses of coherence were associated with low-coherence types of land cover (such as water bodies, vegetation or aeolian deposits) or with surface dynamics (mining activities, fluvial sediment transport or precipitation). For instance, linear low-coherence anomalies perfectly matched the hydrographic network; very different coherence patterns were observed before and after rain events; and stripe-like patterns matched the prevailing wind direction.
Finally, some examples of the application of CCD in hydrogeology can also be found in the literature. For example, Ref. [12] examined the evolution of Sentinel-1A InSAR coherence in the Atacama Desert from January 2015 to December 2016, notably before and after an extreme rain event on 24–26 March 2015, to better understand the water cycle in this endorreic basin, especially regarding evaporation and infiltration. Lastly, Ref. [18] used CCD for the detection of freshwater resources in desertic dunes fields. They used two pairs of Sentinel-1 SAR images, two pairs of optical Sentinel-2 images, DEM data and field observations to investigate the potential for the groundwater accumulation of active wind-blown linear dunes in Egypt that have naturally dammed wadi courses and formed lakes.
The literature review reveals some issues. First, most of the studies are based on few SAR data, so their statistical basis is limited and the validity of their conclusions for other study areas and other periods is uncertain. In fact, many of the published studies focus on a single rainfall or sediment transport event, meaning that the event was known beforehand. Thus, another issue is the ability of CCD to study unknown events, because another common aspect is that the validation of the results is partially or completely based on meteorological data, as rainfall and wind are the triggers for sediment transport events. However, since arid environments are usually remote and very sparsely populated areas, very few meteorological stations exist in these zones. Furthermore, barely any of these stations are located in less accessible but highly relevant areas, such as high-altitude summits, which often present different climate conditions compared to downstream lower-altitude zones nearby. As an alternative, satellite meteorological data are often used, but, since the models used to infer meteorological conditions are based on actual measurements from meteorological stations, their reliability in areas not covered by meteorological stations remains doubtful. On top of that, when using meteorological data for the validation of CCD results, one must keep in mind that both rain and wind must exceed certain thresholds to mobilise sediments, so a sediment transport event did not necessarily occur on every rainy or windy day according to the meteorological records.
Therefore, although the goal of applying CCD in arid environments is to map the areas affected by sediment transport events, verifying the ability to detect all the events that actually mobilised sediments is a necessary prior step: first, because CCD-derived erosion and sedimentation maps will be reliable only if CCD is able to distinguish these events; second, because if the events are first identified, CCD mapping tasks can focus only on the relevant dates, which represents a saving as significant as the study area’s extension; and third, because if CCD is able to identify the sediment transport events it will overcome the limitation related to the representativeness and completeness of meteorological data in extensive and remote regions.
Thus, the goal of this paper is to remotely detect, by means of InSAR coherence data, erosion and sedimentation events related to flash floods in arid environments, taking the Salar de Atacama, Chile, as an example to illustrate the proposed methodology. The idea is to determine the optimal marker—if there is only one—and the threshold that indicates the occurrence of events that significantly affected the InSAR coherence. These events will probably be fluvial sediment transport events. The results will show that it is indeed possible, with InSAR coherence data, to distinguish such events. Moreover, a simple classification model will allow us to automatise the task and even improve the detection capability of the meteorological data. Finally, the results will also prove that some hypotheses in the literature cannot be taken for granted.
The remaining sections are organised as follows: the second section describes the proposed methodology, presents the study area and details all the data used in this study; the third section describes and discusses the results; and the fourth section closes the paper with the main conclusions and prospects.
2. Materials and Methods
2.1. Methodology
The proposed method to identify fluvial sediment transport events in arid environments consists of verifying whether the value of markers identified as the best indicators exceeds a certain threshold or not. In other words, a classification model is built to predict whether an event has occurred or not. This model consists of some markers and thresholds, which will have to be determined for the study area. If the data used in the calibration are sufficiently representative of the dynamics of the study area, both the markers and the thresholds should already be valid for new data, i.e., new periods of time. Thus, given a study area, the model requires one single calibration.
The methodology proposed to build the model (Section 2.1.1) was tested in three study areas in order to verify that the conclusions reached in one area were also valid for the other ones. Once verified, all three models were validated with data for a new time period.
In the following subsections, a complete description of the methodology is first provided; then, Section 2.1.2 offers a more detailed explanation of the applied techniques. For the sake of clarity, from this point on, the text will refer to a classification model that includes one single marker, but the same methodology would apply to build a model with more than one marker if that is needed to improve the performance of the model.
2.1.1. Description
The proposed methodology to build the classification model is divided into six steps (Figure 1):
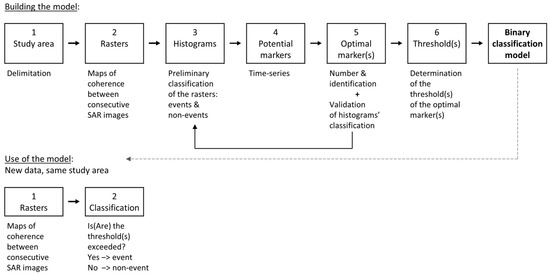
Figure 1.
Flow chart of the methodology.
- Study area. Although the results will show that a precise delimitation of the study area is not critical, the results will be clearer if the study area is limited to the area potentially affected by the phenomena of interest and avoids areas affected by other phenomena that also alter the coherence.
- Rasters of InSAR coherence. Calculation of the rasters (i.e., maps) of coherence between consecutive SAR images. Working with rasters between consecutive images allows one to (i) minimise the temporal baseline and, therefore, its effect on coherence; (ii) reduce the task load, since it reduces the number of rasters to be built (other methodologies proposed in the literature calculate the coherence for all the possible pairs of SAR images); (iii) simplify the task, since only a series of rasters are built and no previous analysis is needed to determine the pairs of images to calculate the coherence for; and (iv) automatise the task, making it more suitable for monitoring systems. Note that a raster of InSAR coherence does not correspond to a date but to a period, the time lapse between the involved SAR images.
- Histograms. Construction of the histograms of the rasters of coherence between consecutive SAR images. The results will show that most of the rasters will present similar histograms, whereas some others will present a clearly different pattern. These different histograms correspond to significant variations in coherence and, therefore, potential fluvial sediment transport events. Thus, this step will provide a preliminary visual classification of the rasters into two groups: events and non-events. Note that, in addition, the sequence of “different” histograms will also show the duration of the temporal effects of each event (such as the changes in the air humidity or the ephemeral vegetation mentioned in the Introduction).
- Potential markers. The markers need to be parameters of the histograms that evolve in time, i.e., along the series of rasters. Thus, in this step, the time series of the potential markers are calculated. The following potential markers were considered here: the average coherence, the median, the mode, the frequency of the mode, the standard deviation and the difference between percentiles 90 and 10.
- Optimal marker. Identification of the optimal marker, that with the greatest predictive classification capacity. This step is based on two techniques: partial least squares discriminant analysis (PLS-DA) and receiving operating characteristic (ROC) curves, which are explained in Section 2.1.2. In addition, the PLS-DA also evaluates how distinguishable the two groups of rasters in step 3 are (“events” and “non-events”), i.e., the PLS-DA validates the visual classification of the histograms.
- Threshold. Determination of the threshold of the optimal marker that indicates the occurrence of an event that has “significantly” affected the InSAR coherence. If the basic hypotheses are fulfilled and the changes in coherence can be related to one single phenomenon—fluvial sediment transport events, in this case—then an increase or decrease in the value of the optimal marker above or below the threshold will indicate the occurrence of this phenomenon.
Finally, as extra information, the ROC curves can also be used to easily estimate the thresholds of the meteorological variables associated with fluvial sediment transport.
The described methodology might require some clarifications. First, the classification of the histograms of the rasters of InSAR coherence is needed as an input for the PLS-DA and the ROC curves. Such classification is performed visually. However, there are not only two types of histograms, “events” and “non-events”, but also cases in between that have to be classified into one group or the other. Therefore, there is a subjectivity in the visual classification of the histograms linked to where the border between “events” and “non-events” is set. Nevertheless, as stated, the PLS-DA verifies to what extent this initial classification is correct, and, additionally, the correlation with meteorological data is a second validation.
Still, the existence of rasters that are not clearly “events” or “non-events” may raise the question of whether it would be convenient to leave such cases out of the process of building the model. A sensitivity analysis was performed with the first study area and, since the difference was minimal, all the rasters were included for the other two study areas.
Regarding the PLS-DA, the input data need to be normalised for the different markers to be comparable. Thus, the time series of each marker was “autonormalised”, i.e., the mean of the time series was subtracted from each value, which was then divided by the standard deviation of the time series. For the determination of the effective threshold of the meteorological variables, the time series of each variable was scaled, i.e., divided by its maximum value.
Finally, as for the thresholds, determined with the ROC curves, different criteria can be adopted. Here, the choice was to maximise the specificity, i.e., to minimise the “false positives”. The non-detected events (false negatives, which will therefore be increased) are the events with the least effect on the coherence or the beginning and the end of an event.
2.1.2. Methods
PLS-DA is a multivariant classification technique based on partial least squares regression (PLSR). PLSR is a regression technique that overcomes the problem of collinearity between explanatory variables in linear regression by combining them into a smaller set of uncorrelated variables, called “components” or “latent variables”. These components are linear combinations of the explanatory variables. Collinearity is a linear correlation between variables that inflates the standard errors and leads to unreliable coefficients or weights in a linear regression. The weights are the coefficients of the linear combination of variables. In PLSR, these weights are determined in such a way that the variance of both the components and the dependent variable is maximised; i.e., the covariance between the dependent and the (combined) explanatory variables is maximised, so the explanatory variables are as explanatory of the dependent variable as possible. This technique is called “partial” least squares regression because only the weights of the components are calculated through least squares regression, not the weights of the explanatory variables of the components.
The optimal number of components to include in the model can be determined through cross-validation, which, in addition, also estimates the performance of the model when applied to “new data” (data not used in the construction of the model). Cross-validation consists of a series of so-called subvalidation tests. Each test consists of, first, building a model using only a subset of data (“calibration” or “training” set) and, then, testing its performance with the data not used in its construction (“validation” or “test” set). Thus, the dataset is split into several subsets or “samples” that, for a certain fixed number of components, are used as the test sample only in one subvalidation test and for the construction of the model in the rest of the tests. As a result of each subvalidation test, we obtain an estimation of the performance of the model: accuracy, sensitivity, specificity, etc. The ensemble of the tests provides a more robust estimation of the performance of a model with the chosen number of components. Repeating the process for different numbers of components, it is possible to determine the optimal number of components that most improves the performance of the model. Several splitting methods exist. In this study, the venetian blinds method was used: if s samples are to be built, one of every s data is included in each sample, starting with datum 1 to s, respectively (i.e., sample i = {i, s + i, 2s + i, …}). Here, the number of samples s has been 10.
Since each component of the model includes all the explanatory variables, the question may arise as to how relevant each explanatory variable is or, in other words, which variables should be included in the model. One possibility is to observe the weights of each explanatory variable in each component. However, all this information is already summarised in the variable importance in projection (VIP) scores [19]. VIP scores account for the amount of variance of the dependent variable explained by each explanatory variable. Thus, the higher the VIP, the more relevant an explanatory variable is. The VIP score for explanatory variable j is as follows:
where f is the component index, F is the number of components, w_jf is the weight of explanatory variable j in component f, SSY_f is the sum of squares of the explained variance by component f and SSY_total is the total sum of squares of the explained variance of the dependent variable. Since the average of the squared VIP scores equals 1, variables with a VIP score greater than 1 are usually selected as relevant.
So far, the prediction of the dependent variable is numerical. However, what if the dependent variable is not numerical but categorical? In PLS-DA, discriminant analysis translates a numerical variable into a categorical variable through thresholds or cut-off values that define ranges associated with each category of the (dependent) variable. These cut-off values are usually determined by maximising the accuracy (i.e., minimising the errors of classification). For binary variables, the cut-off value can also be determined with the receiving operating characteristic (ROC) curve.
An ROC curve is a graphical plot that illustrates the performance of a binary classification model as its discrimination threshold or cut-off value is varied. It is usually represented as a sensitivity against a 1-specificity curve, i.e., true positives over total positives against false positives over total negatives (the specificity is true negatives over total negatives). If sensitivity and specificity are considered equally important, then the cut-off value should correspond to the point of the ROC curve the closest to the top-left corner of the plot, i.e., the one with the highest sum of sensitivity and specificity.
ROC curves also allow one to compare different binary classification models through the area under the curve (AUC), since this parameter is independent of the cut-off value. Thus, ROC curves can be used to determine the best marker by comparing models with different markers as a single explanatory variable. The AUC has a value between 0 and 1. The larger the AUC, the better the model or marker. Below 0.7, a model is considered to have a weak predictive capacity.
2.2. Case Study
Salar de Atacama is an endorreic basin in northern Chile, between latitudes 22.5° and 23.5° south and longitudes 67.5° and 68.5° west, located in the Antofagasta region, the municipality of San Pedro de Atacama, 215 km east of Antofagasta city. The Western Central Andean Range, oriented N–S and reaching as high as 6000 m.a.s.l. (metres above sea level), limits the basin to the east; the Domeyko Range, a secondary Andean range that reaches 4000 m.a.s.l., is the western limit and is oriented NNE–SSW; to the north, the Andean and Domeyko ranges merge and enclose the basin; to the south, there are the 3200 m.a.s.l. high mountains of Cordón de Lila. As an order of magnitude, the basin has an extent of 17,000 km2, and the salt flat nucleus extends over some 3000 km2 at an altitude of 2300 m.a.s.l.
The climate of Salar de Atacama is hyperarid because of the geographical barrier that the Andean range represents to the humid air masses coming from Amazonia [20]. The annual precipitation ranges from 20 mm/year in the nucleus to 160 mm/year in the eastern summits and presents a clear seasonal cyclicity [20,21]. Most of the annual precipitation (87%) occurs during the austral summer (December–March), when the more intense easterly winds bring humid air masses coming from the Atlantic Ocean via Amazonia and the Gran Chaco [21]. In addition to the altitudinal gradient, this precipitation also presents a latitudinal gradient decreasing from north to south due to the shadow effect of the Andes [22]. Minor, frontal and highly geographically irregular precipitation also occurs during the austral winter (June–September), often as snowfalls caused by westerly humid cold winds from the Pacific Ocean [21].
The hydrographical network of the Salar the Atacama is limited to two rivers (the San Pedro and Vilama rivers) flowing from north to south that discharge in the north of the nucleus and many ephemeral streams flowing from the eastern summits westward to the nucleus that disappear through infiltration in the alluvial fans located all along the eastern slopes of the basin [23].
Three study areas within the Salar de Atacama were considered in this study (Figure 2):
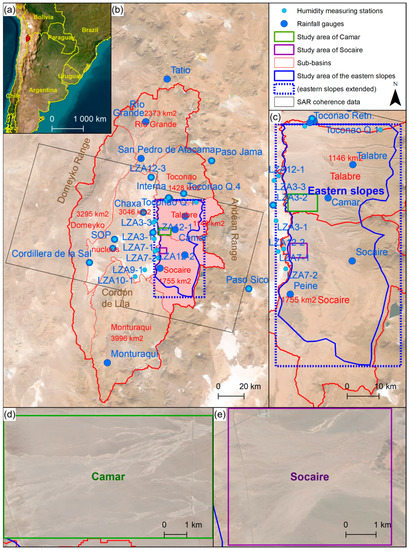
Figure 2.
Study area: (a) Location of Salar de Atacama, in the northeast of Chile; (b) Salar de Atacama. The nucleus is at 2300 m.a.s.l., and the eastern summits exceed 6000 m.a.s.l; (c) Study area of the eastern slopes of Salar de Atacama (blue); (d) Study area of Camar (green); (e) Study area of Socaire (purple).
- 7.
- Camar. A gully where there was evidence of damages caused by flash floods was selected to perform a first test. In order to avoid any interference related to the rugged topography, this study area was limited to the downstream edge of the gully and its alluvial fan.
- 8.
- Socaire. A second study area with different characteristics was selected for verification: it includes the alluvial fan of three gullies that converge.
- 9.
- Eastern slopes. Finally, in order to exploit the capacity of InSAR to cover large areas, the study area was enlarged to include all the eastern slopes of Salar de Atacama, from the summits to the alluvial fans.
2.3. Data
2.3.1. SAR Data
This study included two SAR datasets, one for the construction or calibration of the classification models (Table A1, in Appendix A) and another one for the validation of the results (Table A2). The first dataset comprised 75 SAR images from 2 April 2015 to 3 July 2018, and the second dataset spanned an extra year with 59 SAR images from 3 July 2018 to 4 July 2019. In total, this study included 134 Sentinel-1A and B SAR images, downloaded as Single Look Complex (SLC) images acquired in Interferometric Wide Swath (IWS) mode in a descending trajectory along the orbit 156. The frequency of data acquisition—i.e., the temporal baseline—ranged from 24 days in 2015 to 6 days from 2018, with some isolated exceptions and a maximum of 48 days. The perpendicular baseline ranged from 1 to 119 m with an average of 47 m for the calibration dataset, and from 1 to 156 m with an average of 62 m for the validation dataset. The InSAR coherence (Equation (2)) was calculated over a 2 × 10 pixel multilook window.
2.3.2. Meteorological Data
The results of the classification models were compared with meteorological data for validation. Three meteorological variables were considered: rainfall, the relative humidity of the air (RH) and snow cover. Daily accumulated rainfall and daily average RH records were retrieved from meteorological stations of the Dirección General de Aguas (DGA) [24], Ministry of Public Works (MOP) of Chile (Table A3). Since the records show a significant geographical variability of rainfall (see the range in Figure 3), the considered stations were located not only within the study area but also in the surroundings as complementary data for an improved interpolation in their interpretation (Figure 2).
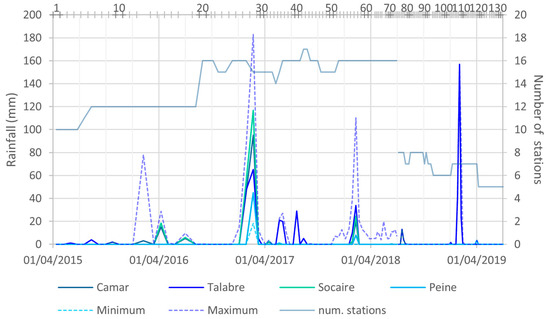
Figure 3.
Accumulated rainfall during the period between consecutive SAR images. Minimum and maximum series refer to all the stations available (see Table A3). See location of the meteorological stations in Figure 2. “num. stations” stands for the number of meteorological stations with records. The horizontal axis at the top indicates the SAR images and the ID numbers of the rasters.
The snow cover was obtained from Moderate Resolution Imaging Spectroradiometer (MODIS) snow cover product version 6. MODIS snow cover products offer a one-day temporal resolution and an approximately 500 m spatial resolution for regional snow cover mapping [25,26,27,28], with the visual obstruction caused by clouds [29,30], vegetation and rugged relief in mountainous areas [31,32] being their main limitations. In the study area, the MODIS data are affected only by the cloud cover. The snow cover products are produced with the SNOMAP algorithm, which is essentially based on the normalised difference snow index (NDSI). MODIS snow cover time series were created and downloaded with the MODIS Time Series Preprocessing (MODIStsp) R-package [33] and included data acquired by the Terra satellites (MOD10A1). The postprocessing of the data involved the removal of errors due to salts and clouds mistaken for snow, the linear interpolation of missing data during heavy snowfalls, the calculation of the extent of the snow cover in the study area, and the search for and correction of outliers. Finally, the time series of the extent of the snow cover was translated into thaw, i.e., decreases in the snow cover, negative daily variations (Figure 4).
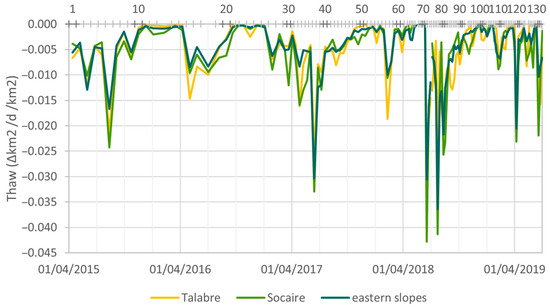
Figure 4.
Average daily rate of decrease in the snow cover during the period between consecutive SAR images. Sub-basins of Talabre and Socaire and ensemble of eastern sub-basins (Río Grande, Toconao, Talabre, Socaire and Monturaqui). Ratios per km2. See sub-basins and their extents in Figure 2. The horizontal axis at the top indicates the SAR images and the ID numbers of the rasters.
3. Results and Discussion
3.1. Construction of the Model
The changes in InSAR coherence are not uniform in space, so they do not affect all three study areas in the same way (Figure 5). Thus, the results are not exactly the same from one area to the other. However, they are consistent: in the classification of the histograms (Figure 6), a general pattern consisting of unimodal distributions with low dispersion and a mode shifted to high values is observed in all three zones. For example, for the eastern slopes, the standard deviation is 24 ± 4 and the mode ranges from 210 to 230 (the coherence is normalised to the range [0, 254]). In the same way, this general pattern is altered on specific dates that are coincident in all three zones, in which the dispersion increases and the mode adopts lower values. These are the dates classified as potential events of fluvial sediment transport (red-framed histograms in Figure 6). In this sense, PLS-DA corroborates that, in all three study areas, there are two sets of histograms (“events” or “positives” and “non-events” or “negatives”) that are clearly distinguishable (Figure 7).
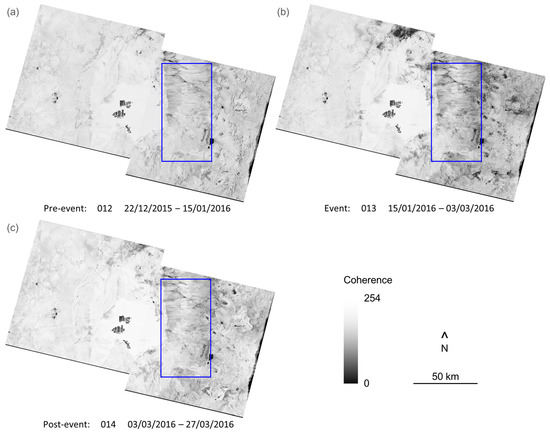
Figure 5.
Examples of rasters of coherence between consecutive SAR images. Black is null coherence; white is total coherence. Sequence of pre-event (a), during the event (b) and postevent (c): the coherence diminishes during the event and recovers afterwards but not uniformly or everywhere. For geographical reference, the study area of the eastern slopes is marked in blue.
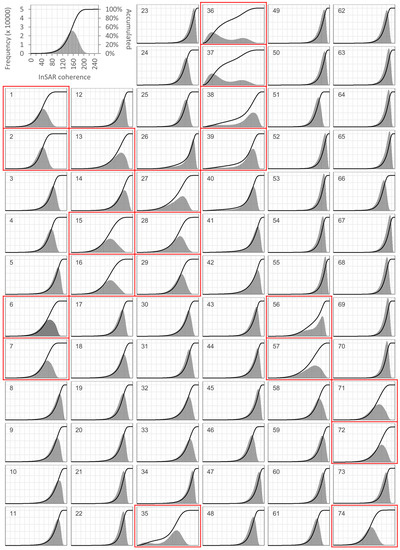
Figure 6.
Histograms of the rasters of coherence between consecutive SAR images in the study area of the eastern slopes. The numbers of the histograms identify the rasters chronologically. See dates in Table A1 and the location and extent of the study area in Figure 2: (a) Camar; (b) Socaire; (c) eastern slopes. Some histograms (framed in red) clearly differ from the general pattern, hypothetically due to fluvial sediment transport events.
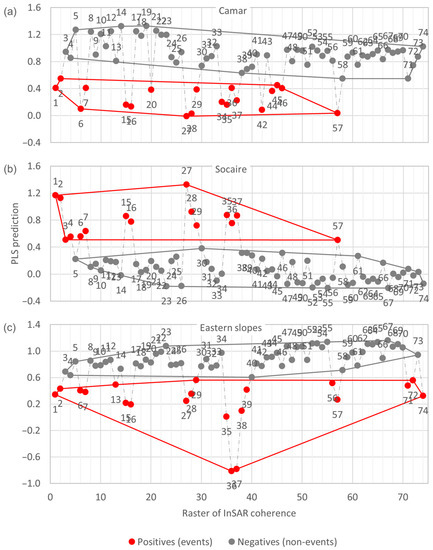
Figure 7.
PLS predictions for the rasters of coherence between consecutive SAR images, for each study area (Figure 2). The numbers of the histograms identify the rasters chronologically. The graphs show that positives (events) and negatives (non-events) are clearly distinguishable.
In fact, the two sets are so distinguishable that all the potential markers are able to classify the histograms well: both the VIP values (Figure 8 and Table 1) and the AUC (Figure 9 and Table 2) are high, in general; the VIP values are very close to or higher than 1 (remember that a marker is considered relevant if it has a VIP equal to or higher than 1); and the AUCs are always higher than 0.85 (above 0.7 is considered to have a predictive ability; remember that the AUC can be 1 at most). Therefore, a classification model including only one marker will already provide very good results, in this case.
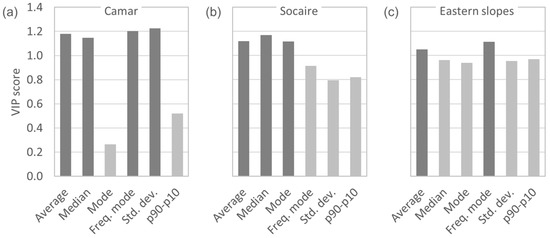
Figure 8.
Variable importance in projection (VIP) scores of the potential markers for each study area (Figure 2): (a) Camar; (b) Socaire; (c) eastern slopes. “Freq. mode” stands for the frequency of the mode; “std. dev.” stands for the standard deviation; “p90–p10” stands for the difference between percentiles 90 and 10. Values above 1 are usually considered relevant. The average is the only marker that stays within the top three in all three study areas.

Table 1.
VIP scores of the potential markers for each study area (Figure 2). “p90–p10” stands for the difference between percentiles 90 and 10.
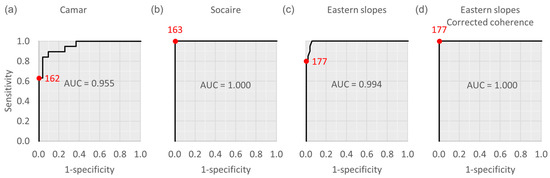
Figure 9.
Receiving operating characteristic (ROC) curves of the average coherence between consecutive SAR images for each study area (Figure 2): (a) Camar; (b) Socaire; (c) eastern slopes. AUC stands for the area under the curve, which measures the predictive capacity of the marker (the average SAR coherence, in this case). The red points are the thresholds that maximise the specificity. (d) ROC curve for the eastern slopes with coherence data corrected with the perpendicular baseline (see later in this section).

Table 2.
AUC of the ROC curves of each marker in each study area (Figure 2). It measures the predictive capacity of the marker. Again, the average is the only marker that stays within the top 3 in every study area.
However, the variability from one study area to another in both the general pattern of the spatial distribution of coherence (coherence rasters for non-events) and the variations in coherence during events means that the results between the three zones are not always exactly the same when identifying the optimal marker. Still, they are similar and, as already observed, very good for all markers, in general. Among all of them, the average stands out as the best marker: it has a VIP score above 1 and an AUC above 0.95 in all three study areas, and it is the only marker that is always in the top three in both the VIP and the AUC for all three study areas (Table 3).

Table 3.
Top 3 markers according to the VIP scores of the PLS-DA and the AUCs of the ROC curves for each study area (Figure 2). “Freq. mode” stands for the frequency of the mode; “p90–p10” stands for the difference between percentiles 90 and 10. The average is the most repeated marker.
Regarding the classification threshold, based on the ROC curves and with the criterion of maximizing specificity (i.e., minimizing “false positives”), if the average coherence between consecutive SAR images drops below 162 in Camar, 163 in Socaire or 177 in the eastern slopes, an event of fluvial sediment transport has probably occurred, with a sensitivity of 63, 100 or 80%, respectively. Note that the thresholds in Camar and Socaire are very similar, while the threshold is clearly different for the eastern slopes. This makes sense: the Camar and Socaire study areas cover only one alluvium each, whereas the eastern slopes include several gullies from top to bottom, not only the alluvium at the base.
3.2. Validation
The comparison of the results of the classification models with the meteorological data from 2015 to 2018 is good in all three study areas: there are discrepancies between the models and the meteorological data, but most of them are false negatives around events confirmed by the meteorological data (Figure 10a,c until raster 74). These false negatives could be interpreted as the model detecting the core of each event and just missing the minor affectations at the beginning and at the end of the event. Moreover, all the discrepancies are false negatives, which is coherent with the criterion chosen when determining the thresholds—minimising the false positives.
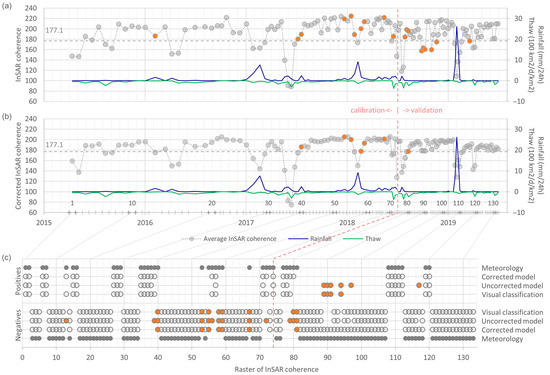
Figure 10.
Comparison between meteorological data (rainfall and thaw) and coherence between consecutive SAR images in the eastern slopes: (a) Uncorrected model, classification model based on coherence non-corrected with the perpendicular baseline; (b) Corrected model, model based on corrected coherence. In the horizontal axis, both the time (below) and the SAR images and ID numbers of the rasters (above) are indicated; (c) A visual classification of histograms is also included. Coloured circles indicate discrepancies with meteorological data. Rainfall: average daily rainfall (mm/24 h) during the period between consecutive SAR images in the meteorological station with the largest amount of rainfall accumulated in the same period. Only stations considered relevant for the eastern slopes have been included, i.e., all the stations except for Chaxa, Cordillera de la Sal, KCL, LZA10-1, LZA12-3 and SOP (Figure 2 and Table A3). Thaw: average daily decrease in the snow cover (100 km2/d) in the sub-basins of Talabre and Socaire combined (Figure 2), per unit of area (km2).
However, the comparison with the validation data (2018–2019) is not satisfactory: there are several discrepancies that are not associated with any event (Figure 10a from raster 74 onwards), and, more importantly, there is a change in the errors, from false negatives to false positives, despite the criterion used in the determination of the threshold (Figure 10c from raster 74 onwards). This change motivated a verification of the validation data to check whether there is any difference with the calibration data (2015–2018), but no difference is observed in the time series of the markers (see, for instance, the time series of the average coherence in Figure 10a before and after raster 74; the same happens with all the other markers).
Then, the main hypotheses were checked:
- Hypothesis: the relative humidity of the air only affects the InSAR coherence during and shortly after rainfall events. Confirmed: no correlation is observed (Figure 11a).
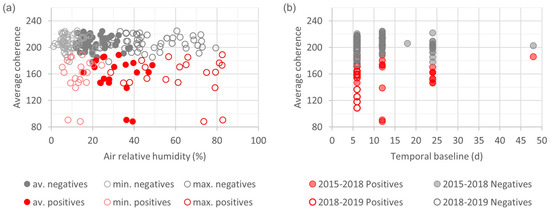 Figure 11. (a) Scatter plot of the average coherence between consecutive SAR images in the eastern slopes against the minimal, average and maximal daily average relative humidity of the air during the period between consecutive SAR images. Data from all the meteorological stations considered relevant for the eastern slopes are included, i.e., all the stations except for Chaxa, Cordillera de la Sal, KCL, LZA10-1, LZA12-3 and SOP (Figure 2 and Table A3). (b) Scatter plot of the average coherence between consecutive SAR images in the eastern slopes against the temporal baseline (days). Each circle is a raster. In both figures, red circles represent events, according to the visual classification of the histograms; grey circles represent non-events. No correlations are observed in any case, nor for the other markers.
Figure 11. (a) Scatter plot of the average coherence between consecutive SAR images in the eastern slopes against the minimal, average and maximal daily average relative humidity of the air during the period between consecutive SAR images. Data from all the meteorological stations considered relevant for the eastern slopes are included, i.e., all the stations except for Chaxa, Cordillera de la Sal, KCL, LZA10-1, LZA12-3 and SOP (Figure 2 and Table A3). (b) Scatter plot of the average coherence between consecutive SAR images in the eastern slopes against the temporal baseline (days). Each circle is a raster. In both figures, red circles represent events, according to the visual classification of the histograms; grey circles represent non-events. No correlations are observed in any case, nor for the other markers. - Hypothesis: with Sentinel, the temporal baseline does not significantly affect the coherence between consecutive SAR images. Confirmed: no correlations are observed between the temporal baseline and any of the markers (Figure 11b).
- Hypothesis: with Sentinel, the perpendicular baseline does not significantly affect the InSAR coherence either. Rejected: the highest values of the average coherence between consecutive SAR images show a clear negative linear trend with the perpendicular baseline (Figure 12a). This correlation is interpreted as the effect of the perpendicular baseline on the InSAR coherence, while the dispersion of the data for lower values is related to the events of fluvial sediment transport. Note that the validation data have the largest perpendicular baselines of the period 2015–2019, i.e., larger than the calibration data (Figure 12a,b).
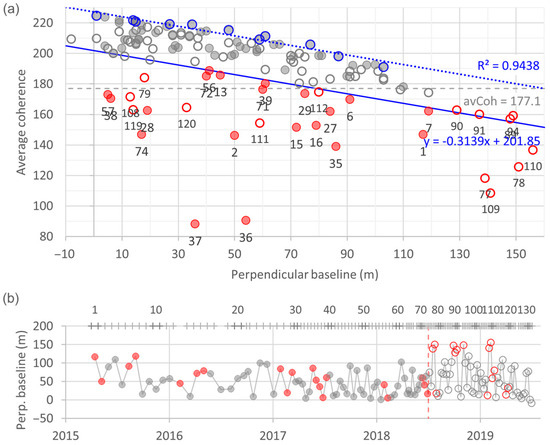 Figure 12. (a) Scatter plot of the average coherence between consecutive SAR images in the eastern slopes against the perpendicular baseline (orbit errors). Each circle is a raster: red circles are events, according to the visual classification of the histograms, whereas grey circles are non-events. Filled circles: calibration data (2015–2018); empty circles: validation data (2018–2019). The ID number of the raster is shown for events, under the red circles. A linear correlation exists for the highest values of coherence (dashed blue line). The corrected threshold to identify an event (continuous blue line) is the transposition of the correlation line that minimises the classification error for calibration data. (b) Time series of the perpendicular baseline. The horizontal axis at the top indicates the ID numbers of the rasters.
Figure 12. (a) Scatter plot of the average coherence between consecutive SAR images in the eastern slopes against the perpendicular baseline (orbit errors). Each circle is a raster: red circles are events, according to the visual classification of the histograms, whereas grey circles are non-events. Filled circles: calibration data (2015–2018); empty circles: validation data (2018–2019). The ID number of the raster is shown for events, under the red circles. A linear correlation exists for the highest values of coherence (dashed blue line). The corrected threshold to identify an event (continuous blue line) is the transposition of the correlation line that minimises the classification error for calibration data. (b) Time series of the perpendicular baseline. The horizontal axis at the top indicates the ID numbers of the rasters.
3.3. Correction of the Model
According to this finding, the model is corrected to take into account the effect of the perpendicular baseline. Due to its linear correlation with the average InSAR coherence, the classification threshold is no longer a constant value of average coherence but a straight line that relates both variables (as in Figure 12a) or, equivalently, a constant threshold for coherence data corrected according to this line (as in Figure 10b). However, it is worth noting that the correlation of the perpendicular baseline is not linear with all the markers: it is linear with the average, the median and the mode but not with the frequency of the mode, the standard deviation or the difference between percentiles 90 and 10. Therefore, in the construction of the model, the correction will need to be adapted in each case according to the optimal marker.
Thus, in this case, with the average being the optimal marker and its correlation with the perpendicular baseline being linear, in order to determine the corrected threshold, first, the range of values of the perpendicular baseline is divided into ten intervals, each containing 10% of the (calibration) data. Then, simple linear regression (dashed blue line in Figure 12a) is performed with the maxima of these intervals (blue circles in Figure 12a). Finally, the line is transposed so that the classification error is minimised (continuous blue line in Figure 12a). Thus, in summary, the model can be expressed as follows:
as represented in Figure 10b or, equivalently, it can be simplified to the following:
where is the (non-corrected) average coherence between consecutive SAR images, is the corrected average coherence, is the threshold of the average coherence determined with the ROC curves with the criterion of maximising the specificity, is the slope of the simple linear regression of the highest values of average coherence against the perpendicular baseline, is the perpendicular baseline and is the vertical intercept determined by minimising the classification error. For instance, for the eastern slopes of the Salar de Atacama, the model is as follows:
or, in a simpler way,
3.4. Validation of the Corrected Model
The corrected model fits the calibration meteorological data well: the discrepancies that remain are all false negatives around confirmed events (Figure 10b,c until raster 74). Moreover, the discrepancies are also between the visual classifications of the histograms and the meteorological data, which could be interpreted not as errors of the model but rather as problems of the meteorological or SAR data. In any case, the time series of the corrected coherence is much cleaner and stable than the non-corrected one (Figure 10a vs. Figure 10b), and its AUC is 1 (i.e., the predictive capacity is maximal) (Figure 9d). Regarding the validation data, the agreement between the corrected classification model and the meteorological data is total (Figure 10b,c from raster 74 onward).
3.5. Meteorological Variables
Finally, ROC curves can also determine the thresholds of rainfall and thaw that need to be exceeded for an event of sediment transport triggered by a flash flood to occur (i.e., somehow, effective runoff thresholds). For instance, in the eastern slopes of Salar de Atacama, a rainfall event (consecutive days with non-null precipitation) greater than 8 mm and a decrease in the snow cover greater than 13 km2 in 24 h can be associated with fluvial sediment transport events with a sensitivity of 60 and 75% and a specificity of 80 and 67%, respectively (Figure 13 and Table 4).
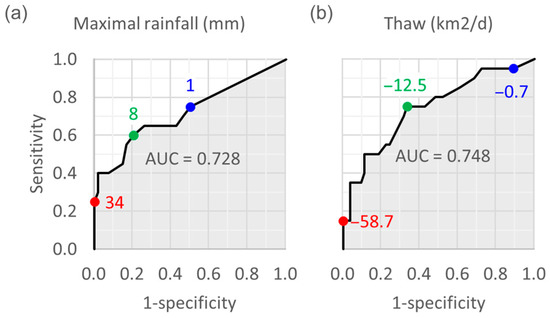
Figure 13.
ROC curves of (a) the maximal rainfall and (b) thaw in the eastern slopes (Figure 2). The red points are the thresholds that maximise specificity; blue points maximise sensitivity; green points maximise the sum of specificity and sensitivity. Rainfall data correspond to the maximal rainfall recorded at the stations considered relevant for the eastern slopes, i.e., all the stations except for Chaxa, Cordillera de la Sal, KCL, LZA10-1, LZA12-3 and SOP (Figure 2 and Table A3). Thaw: average daily decrease in the snow cover in the sub-basins of Talabre and Socaire (Figure 2).

Table 4.
Classification thresholds from ROC curves for rainfall (mm) and thaw (i.e., average daily decrease in the snow cover (km2/d)), with the corresponding sensitivities and specificities. The thresholds can be determined by maximising either the sensitivity, the specificity or the sum of both. The thresholds are estimates of the minimal necessary rainfall and thaw for a fluvial sediment transport event to occur in the eastern slopes of Salar de Atacama (sub-basins of Talabre and Socaire). Rainfall data correspond to the maximal rainfall recorded by the stations considered relevant for the eastern slopes, i.e., all the stations except for Chaxa, Cordillera de la Sal, KCL, LZA10-1, LZA12-3 and SOP (Figure 2 and Table A3).
Precisely, the AUCs of the meteorological variables (Figure 13), significantly lower than the AUCs of the statistics of the histograms of the rasters of coherence between consecutive SAR images and close to the standard threshold of predictive capacity (0.7), are a symptom of the problem of the representativity of the meteorological data. In fact, the meteorological variable with the largest AUC (0.882) is the combination of rainfall and thaw, not any of these two variables alone. In other words, rainfall records complemented with thaw data are more explanatory of the changes over time in the InSAR coherence than rainfall data alone, which could be interpreted as the records of rainfall being “incomplete”, not detecting all the precipitations or not detecting them well enough.
3.6. Sensitivity Analysis to the Study Area
The sensitivity analysis of the results to the study area closes the discussion. As stated in the explanation of the methodology, if the study area is limited to the area potentially affected by the phenomena under analysis and avoids areas affected by other phenomena, the results are clearer. However, the question remains as to how sensitive the results are to the accurate delimitation of the study area. For this purpose, an extended perimeter of the study area of the eastern slopes is analysed (Figure 2c). This extended area includes a part of the eastern margin of the nucleus of Salar de Atacama and some of the eastern summits, which are the zones that suffer the most significant changes in the InSAR coherence in the region. Despite enlarging the study area by 29% and including these zones, the results are essentially the same and, more importantly, the classification model remains the same as well (Figure 14).
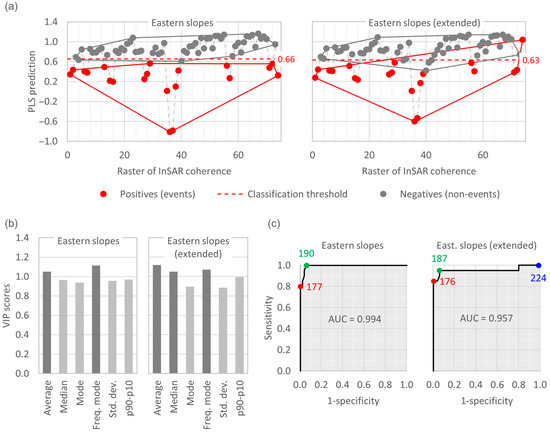
Figure 14.
Sensitivity analysis of the study area. Eastern slopes: study area used in this paper, limited to the area potentially affected by sediment transport events, versus extended tangential rectangular study area (see Figure 2c). (a) PLS predictions of the InSAR coherence maps or rasters. (b) VIP scores of the potential markers. “Freq. mode” stands for the frequency of the mode; “std. dev.” stands for the standard deviation; “p90–p10” stands for the difference between percentiles 90 and 10. (c) ROC curves of the average InSAR coherence. The coloured points are the thresholds that maximise sensitivity (blue), specificity (red) or the sum of both (green). The results of the extended study area are less clear—as expected—but remain similar, and, more importantly, the classification model remains the same.
4. Conclusions
Classification models based on InSAR coherence data have been proven to be able to remotely detect sediment transport events related to flash floods in arid environments, as illustrated in this paper with the case of Salar de Atacama (Chile).
One of the main findings of this study is that the perpendicular baseline does have a relevant effect on the InSAR coherence that needs to be taken into account when using InSAR coherence to detect fluvial sediment transport events: only when including the perpendicular baseline is the classification model developed in this work able to reproduce the meteorological observations.
However, the representativity of the meteorological data for highly remote and inaccessible yet extremely relevant areas has been proven to be insufficient in this work. For instance, the predictive capacity of the meteorological variables—measured with the AUC of the ROC curves—is clearly lower than that of the InSAR coherence and, therefore, of the classification model; rainfall and thaw combined have a greater predictive capacity than rainfall records alone.
Finally, this research has also shown that the conclusions derived from one event in one study area do not necessarily allow one to detect and characterise other events, either in the same study area or in a different one. For instance, if considered alone each one of the three study areas here analysed would have led to a classification model using a different marker to detect fluvial sediment transport events. In the same way, the validation data have led to the realisation that the model developed before verifying the hypotheses of the literature was not valid for later events. Three study areas and four years of data have allowed us to develop a more reliable classification model.
All these findings will increase the reliability of maps based on InSAR coherence. In addition, the method here proposed detects the occurrence of events that have significantly affected the coherence and the duration of the temporal effects on the coherence related to each event, which will allow focusing the mapping tasks only on the relevant dates. Finally, once calibrated, the model here developed will enable the automatised remote detection of new events.
Author Contributions
Conceptualization, J.B.i.B. and E.V.-S.; methodology, J.B.i.B., E.V.-S. and C.B.; validation, J.B.i.B.; formal analysis, J.B.i.B. and C.B.; investigation, J.B.i.B.; resources, J.B.i.B., C.B., E.V.-S., M.C.-G. and S.V.; writing—original draft preparation, J.B.i.B.; writing—review and editing, E.V.-S., C.B., M.C.-G., S.V. and M.C.; visualization, J.B.i.B.; supervision, E.V.-S.; project administration, E.V.-S.; funding acquisition, E.V.-S. and M.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by the Spanish Ministry of Economy and Competitiveness (MCIN) and State Research Agency (AEI) through the grant CEX2018-000794-S (ref. 10.13039/501100011033).
Data Availability Statement
All the data used in this study are publicly available from the referenced sources.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Rasters of coherence between consecutive SAR images. Calibration dataset.
Table A1.
Rasters of coherence between consecutive SAR images. Calibration dataset.
| Coherence Raster | 1st Image | 2nd Image | Perpendicular Baseline (m) | Temporal Baseline (d) |
|---|---|---|---|---|
| 1 | 02/04/2015 | 26/04/2015 | 117 | 24 |
| 2 | 26/04/2015 | 20/05/2015 | 50 | 24 |
| 3 | 20/05/2015 | 13/06/2015 | 90 | 24 |
| 4 | 13/06/2015 | 07/07/2015 | 110 | 24 |
| 5 | 07/07/2015 | 31/07/2015 | 41 | 24 |
| 6 | 31/07/2015 | 24/08/2015 | 91 | 24 |
| 7 | 24/08/2015 | 17/09/2015 | 119 | 24 |
| 8 | 17/09/2015 | 11/10/2015 | 16 | 24 |
| 9 | 11/10/2015 | 04/11/2015 | 50 | 24 |
| 10 | 04/11/2015 | 28/11/2015 | 29 | 24 |
| 11 | 28/11/2015 | 22/12/2015 | 54 | 24 |
| 12 | 22/12/2015 | 15/01/2016 | 58 | 24 |
| 13 | 15/01/2016 | 03/03/2016 | 45 | 48 |
| 14 | 03/03/2016 | 27/03/2016 | 10 | 24 |
| 15 | 27/03/2016 | 20/04/2016 | 72 | 24 |
| 16 | 20/04/2016 | 14/05/2016 | 79 | 24 |
| 17 | 14/05/2016 | 07/06/2016 | 71 | 24 |
| 18 | 07/06/2016 | 25/07/2016 | 28 | 48 |
| 19 | 25/07/2016 | 18/08/2016 | 30 | 24 |
| 20 | 18/08/2016 | 11/09/2016 | 58 | 24 |
| 21 | 11/09/2016 | 29/09/2016 | 66 | 18 |
| 22 | 29/09/2016 | 11/10/2016 | 77 | 12 |
| 23 | 11/10/2016 | 04/11/2016 | 9 | 24 |
| 24 | 04/11/2016 | 28/11/2016 | 100 | 24 |
| 25 | 28/11/2016 | 22/12/2016 | 97 | 24 |
| 26 | 22/12/2016 | 15/01/2017 | 16 | 24 |
| 27 | 15/01/2017 | 08/02/2017 | 84 | 24 |
| 28 | 08/02/2017 | 04/03/2017 | 19 | 24 |
| 29 | 04/03/2017 | 16/03/2017 | 75 | 12 |
| 30 | 16/03/2017 | 28/03/2017 | 49 | 12 |
| 31 | 28/03/2017 | 09/04/2017 | 52 | 12 |
| 32 | 09/04/2017 | 21/04/2017 | 43 | 12 |
| 33 | 21/04/2017 | 03/05/2017 | 4 | 12 |
| 34 | 03/05/2017 | 15/05/2017 | 22 | 12 |
| 35 | 15/05/2017 | 27/05/2017 | 86 | 12 |
| 36 | 27/05/2017 | 08/06/2017 | 54 | 12 |
| 37 | 08/06/2017 | 20/06/2017 | 36 | 12 |
| 38 | 20/06/2017 | 02/07/2017 | 6 | 12 |
| 39 | 02/07/2017 | 14/07/2017 | 61 | 12 |
| 40 | 14/07/2017 | 26/07/2017 | 68 | 12 |
| 41 | 26/07/2017 | 07/08/2017 | 11 | 12 |
| 42 | 07/08/2017 | 19/08/2017 | 15 | 12 |
| 43 | 19/08/2017 | 31/08/2017 | 51 | 12 |
| 44 | 31/08/2017 | 12/09/2017 | 34 | 12 |
| 45 | 12/09/2017 | 24/09/2017 | 17 | 12 |
| 46 | 24/09/2017 | 06/10/2017 | 92 | 12 |
| 47 | 06/10/2017 | 18/10/2017 | 9 | 12 |
| 48 | 18/10/2017 | 30/10/2017 | 80 | 12 |
| 49 | 30/10/2017 | 11/11/2017 | 27 | 12 |
| 50 | 11/11/2017 | 23/11/2017 | 15 | 12 |
| 51 | 23/11/2017 | 05/12/2017 | 87 | 12 |
| 52 | 05/12/2017 | 17/12/2017 | 4 | 12 |
| 53 | 17/12/2017 | 29/12/2017 | 35 | 12 |
| 54 | 29/12/2017 | 10/01/2018 | 48 | 12 |
| 55 | 10/01/2018 | 22/01/2018 | 1 | 12 |
| 56 | 22/01/2018 | 03/02/2018 | 41 | 12 |
| 57 | 03/02/2018 | 15/02/2018 | 5 | 12 |
| 58 | 15/02/2018 | 27/02/2018 | 7 | 12 |
| 59 | 27/02/2018 | 11/03/2018 | 14 | 12 |
| 60 | 11/03/2018 | 23/03/2018 | 38 | 12 |
| 61 | 23/03/2018 | 04/04/2018 | 103 | 12 |
| 62 | 04/04/2018 | 16/04/2018 | 59 | 12 |
| 63 | 16/04/2018 | 22/04/2018 | 17 | 6 |
| 64 | 22/04/2018 | 28/04/2018 | 26 | 6 |
| 65 | 28/04/2018 | 04/05/2018 | 15 | 6 |
| 66 | 04/05/2018 | 10/05/2018 | 81 | 6 |
| 67 | 10/05/2018 | 22/05/2018 | 14 | 12 |
| 68 | 22/05/2018 | 28/05/2018 | 28 | 6 |
| 69 | 28/05/2018 | 03/06/2018 | 40 | 6 |
| 70 | 03/06/2018 | 09/06/2018 | 61 | 6 |
| 71 | 09/06/2018 | 15/06/2018 | 60 | 6 |
| 72 | 15/06/2018 | 21/06/2018 | 40 | 6 |
| 73 | 21/06/2018 | 27/06/2018 | 64 | 6 |
| 74 | 27/06/2018 | 03/07/2018 | 17 | 6 |

Table A2.
Rasters of coherence between consecutive SAR images. Validation dataset.
Table A2.
Rasters of coherence between consecutive SAR images. Validation dataset.
| Coherence Raster | 1st Image | 2nd Image | Perpendicular Baseline (m) | Temporal Baseline (d) |
| 75 | 03/07/2018 | 09/07/2018 | 75 | 6 |
| 76 | 09/07/2018 | 15/07/2018 | 37 | 6 |
| 77 | 15/07/2018 | 21/07/2018 | 139 | 6 |
| 78 | 21/07/2018 | 27/07/2018 | 151 | 6 |
| 79 | 27/07/2018 | 02/08/2018 | 18 | 6 |
| 80 | 02/08/2018 | 08/08/2018 | 11 | 6 |
| 81 | 08/08/2018 | 14/08/2018 | 20 | 6 |
| 82 | 14/08/2018 | 20/08/2018 | 74 | 6 |
| 83 | 20/08/2018 | 26/08/2018 | 71 | 6 |
| 84 | 26/08/2018 | 01/09/2018 | 103 | 6 |
| 85 | 01/09/2018 | 07/09/2018 | 70 | 6 |
| 86 | 07/09/2018 | 13/09/2018 | 28 | 6 |
| 87 | 13/09/2018 | 19/09/2018 | 70 | 6 |
| 88 | 19/09/2018 | 25/09/2018 | 103 | 6 |
| 89 | 25/09/2018 | 01/10/2018 | 148 | 6 |
| 90 | 01/10/2018 | 07/10/2018 | 129 | 6 |
| 91 | 07/10/2018 | 13/10/2018 | 137 | 6 |
| 92 | 13/10/2018 | 19/10/2018 | 31 | 6 |
| 93 | 19/10/2018 | 31/10/2018 | 9 | 12 |
| 94 | 31/10/2018 | 06/11/2018 | 149 | 6 |
| 95 | 06/11/2018 | 12/11/2018 | 101 | 6 |
| 96 | 12/11/2018 | 18/11/2018 | 34 | 6 |
| 97 | 18/11/2018 | 24/11/2018 | 119 | 6 |
| 98 | 24/11/2018 | 30/11/2018 | 91 | 6 |
| 99 | 30/11/2018 | 06/12/2018 | 23 | 6 |
| 100 | 06/12/2018 | 12/12/2018 | 19 | 6 |
| 101 | 12/12/2018 | 18/12/2018 | 59 | 6 |
| 102 | 18/12/2018 | 24/12/2018 | 95 | 6 |
| 103 | 24/12/2018 | 30/12/2018 | 15 | 6 |
| 104 | 30/12/2018 | 05/01/2019 | 73 | 6 |
| 105 | 05/01/2019 | 11/01/2019 | 48 | 6 |
| 106 | 11/01/2019 | 17/01/2019 | 31 | 6 |
| 107 | 17/01/2019 | 23/01/2019 | 56 | 6 |
| 108 | 23/01/2019 | 29/01/2019 | 13 | 6 |
| 109 | 29/01/2019 | 04/02/2019 | 141 | 6 |
| 110 | 04/02/2019 | 10/02/2019 | 156 | 6 |
| 111 | 10/02/2019 | 16/02/2019 | 59 | 6 |
| 112 | 16/02/2019 | 22/02/2019 | 80 | 6 |
| 113 | 22/02/2019 | 28/02/2019 | 7 | 6 |
| 114 | 28/02/2019 | 06/03/2019 | 61 | 6 |
| 115 | 06/03/2019 | 12/03/2019 | 46 | 6 |
| 116 | 12/03/2019 | 18/03/2019 | 91 | 6 |
| 117 | 18/03/2019 | 24/03/2019 | 109 | 6 |
| 118 | 24/03/2019 | 30/03/2019 | 37 | 6 |
| 119 | 30/03/2019 | 05/04/2019 | 14 | 6 |
| 120 | 05/04/2019 | 11/04/2019 | 33 | 6 |
| 121 | 11/04/2019 | 17/04/2019 | 36 | 6 |
| 122 | 17/04/2019 | 23/04/2019 | 84 | 6 |
| 123 | 23/04/2019 | 29/04/2019 | 13 | 6 |
| 124 | 29/04/2019 | 05/05/2019 | 93 | 6 |
| 125 | 05/05/2019 | 17/05/2019 | 21 | 12 |
| 126 | 17/05/2019 | 23/05/2019 | 12 | 6 |
| 127 | 23/05/2019 | 29/05/2019 | 5 | 6 |
| 128 | 29/05/2019 | 04/06/2019 | 15 | 6 |
| 129 | 04/06/2019 | 10/06/2019 | 19 | 6 |
| 130 | 10/06/2019 | 16/06/2019 | 73 | 6 |
| 131 | 16/06/2019 | 22/06/2019 | 78 | 6 |
| 132 | 22/06/2019 | 28/06/2019 | 1 | 6 |
| 133 | 28/06/2019 | 04/07/2019 | −8 | 6 |

Table A3.
Meteorological records: stations and their coordinates and the time period covered by the records of daily rainfall and relative humidity of the air (RH). See the location of the stations in Figure 2.
Table A3.
Meteorological records: stations and their coordinates and the time period covered by the records of daily rainfall and relative humidity of the air (RH). See the location of the stations in Figure 2.
| Meteorological Station | Rainfall from | Rainfall to | RH from | RH to | Latitude WGS84 (°) | Longitude WGS84 (°) | Altitude (m.a.s.l.) |
| Camar | 01/01/1986 | 30/04/2018 | −23.410000 | −67.960000 | 2700 | ||
| Chaxa | 01/08/1999 | 30/06/2018 | 01/01/2015 | 28/02/2019 | −23.288920 | −68.183490 | 2307 |
| Cordillera_Sal | 19/10/2017 | 31/03/2021 | 20/10/2017 | 21/02/2019 | −23.641238 | −68.562540 | 2363 |
| Interna | 10/07/2015 | 09/10/2017 | −23.042575 | −68.129584 | 2359 | ||
| KCL | 01/01/2015 | 31/07/2018 | 01/01/2015 | 30/04/2019 | −23.542934 | −68.398893 | 2307 |
| LZA10-1 | 20/04/2015 | 21/02/2019 | −23.741353 | −68.241920 | 2309 | ||
| LZA12-1 | 19/04/2015 | 11/02/2019 | −23.348003 | −68.099744 | 2316 | ||
| LZA12-2 | 17/04/2015 | 11/02/2019 | −23.553857 | −68.086140 | 2317 | ||
| LZA12-3 | 02/06/2015 | 27/02/2019 | 19/04/2015 | 20/02/2019 | −23.042575 | −68.129584 | 2359 |
| LZA3-1 | 19/04/2015 | 22/02/2019 | −23.474659 | −68.107141 | 2306 | ||
| LZA3-2 | 09/07/2015 | 31/12/2019 | 20/04/2015 | 11/02/2019 | −23.430187 | −68.115476 | 2306 |
| LZA3-3 | 19/04/2015 | 21/02/2019 | −23.360833 | −68.113168 | 2318 | ||
| LZA7-1 | 16/04/2015 | 11/02/2019 | −23.561253 | −68.101482 | 2312 | ||
| LZA7-2 | 06/02/2015 | 11/02/2019 | −23.610295 | −68.079437 | 2311 | ||
| LZA9-1 | 20/04/2015 | 11/02/2019 | −23.693012 | −68.174465 | 2310 | ||
| Monturaqui | 01/01/2015 | 30/06/2018 | −24.345094 | −68.437070 | 3430 | ||
| Paso_Jama | 18/08/2016 | 10/01/2022 | 18/08/2016 | 23/01/2019 | −22.925545 | −67.703100 | 4825 |
| Paso_Sico | 18/08/2016 | 08/01/2022 | 19/08/2016 | 30/09/2018 | −23.825336 | −67.441728 | 4323 |
| Peine | 01/01/1986 | 30/04/2018 | −23.681879 | −68.066942 | 2460 | ||
| Rio_Grande | 01/01/1986 | 30/04/2018 | −22.651977 | −68.167375 | 3217 | ||
| San Pedro de Atacama | 01/01/1986 | 31/12/2016 | −22.910384 | −68.200528 | 2450 | ||
| Socaire | 01/01/1986 | 31/12/2016 | −23.587870 | −67.891654 | 3251 | ||
| SOP | 01/01/2015 | 31/07/2018 | 01/01/2015 | 31/03/2019 | −23.478960 | −68.385836 | 2300 |
| Talabre | 01/08/1995 | 30/04/2018 | −23.315846 | −67.889638 | 3255 | ||
| Tatio | 01/01/1986 | 13/01/2022 | −22.351323 | −68.016396 | 4370 | ||
| Toconao_DGAC | 01/01/2015 | 25/08/2018 | −23.207819 | −68.026216 | 2495 | ||
| Toconao_expe | 01/01/1986 | 28/02/2009 | −23.192581 | −67.999524 | 2500 | ||
| Toconao_P. | 11/08/2016 | 09/01/2022 | 12/08/2016 | 31/12/2017 | −23.185721 | −68.005544 | 2492 |
| Toconao_Q.1 | 19/08/2016 | 23/01/2019 | −23.217932 | −67.811939 | 3990 | ||
| Toconao_Q.4 | 18/08/2016 | 31/12/2020 | 18/08/2016 | 01/01/2019 | −23.156794 | −67.900116 | 3437 |
| Toconao_Retn | 01/01/1986 | 31/01/1991 | −23.197307 | −68.011185 | 2460 |
References
- Gabriel, A.K.; Goldstein, R.M.; Zebker, H.A. Mapping Small Elevation Changes Over Large Areas: Differential Radar Interferometry. J. Geophys. Res. 1989, 94, 9183–9191. [Google Scholar] [CrossRef]
- Bamler, R.; Hartl, P. Synthetic aperture radar interferometry. Inverse Probl. 1998, 14, R1–R54. [Google Scholar] [CrossRef]
- Rosen, P.A.; Hensley, S.; Joughin, I.R.; Li, F.K.; Madsen, S.N.; Rodríguez, E.; Goldstein, R.M. Synthetic aperture radar interferometry—Invited paper. IEEE 2000, 88, 333–382. [Google Scholar] [CrossRef]
- Zebker, H.A.; Villasenor, J. Decorrelation in interferometric radar echoes. IEEE Trans. Geosci. Remote Sens. 1992, 30, 950–959. [Google Scholar] [CrossRef]
- Ullmann, T.; Sauerbrey, J.; Hoffmeister, D.; May, S.M.; Baumhauer, R.; Bubenzer, O. Assessing Spatiotemporal Variations of Sentinel-1 InSAR Coherence at Different Time Scales over the Atacama Desert (Chile) between 2015 and 2018. Remote Sens. 2019, 11, 22. [Google Scholar] [CrossRef]
- Cabré, A.; Remy, D.; Aguilar, G.; Carretier, S.; Riquelme, R. Mapping rainstorm erosion associated with an individual storm from InSAR coherence loss validated by field evidence for the Atacama Desert. Earth Surf. Process. Landf. 2020, 45, 2091–2106. [Google Scholar] [CrossRef]
- Manzoni, M.; Molinari, M.E.; Monti-Guarnieri, A. Multitemporal InSAR Coherence Analysis and Methods for Sand Mitigation. Remote Sens. 2021, 13, 21. [Google Scholar] [CrossRef]
- Havivi, S.; Amir, D.; Schvartzman, I.; August, Y.; Maman, S.; Rotman, S.R.; Blumberg, D.G. Mapping dune dynamics by InSAR coherence. Earth Surf. Process. Landf. 2018, 43, 1229–1240. [Google Scholar] [CrossRef]
- Liu, J.G.; Black, A.; Lee, H.; Hanaizumi, H.; Moore, J.M. Land surface change detection in a desert area in Algeria using multi-temporal ERS SAR coherence images. Int. J. Remote Sens. 2001, 22, 2463–2477. [Google Scholar] [CrossRef]
- Song, Y.B.; Chen, C.B.; Xu, W.Q.; Zheng, H.W.; Bao, A.M.; Lei, J.Q.; Luo, G.P.; Chen, X.; Zhang, R.; Tan, Z.B. Mapping the temporal and spatial changes in crescent dunes using an interferometric synthetic aperture radar temporal decorrelation model. Aeolian Res. 2020, 46, 16. [Google Scholar] [CrossRef]
- Schepanski, K.; Wright, T.J.; Knippertz, P. Evidence for flash floods over deserts from loss of coherence in InSAR imagery. J. Geophys. Res. Atmos. 2012, 117, 10. [Google Scholar] [CrossRef]
- Scott, C.P.; Lohman, R.B.; Jordan, T.E. InSAR constraints on soil moisture evolution after the March 2015 extreme precipitation event in Chile. Sci. Rep. 2017, 7, 9. [Google Scholar] [CrossRef] [PubMed]
- Smith, L.C. Emerging applications of interferometric synthetic aperture radar (InSAR) in geomorphology and hydrology. Ann. Assoc. Am. Geogr. 2002, 92, 385–398. [Google Scholar] [CrossRef]
- Lee, H.; Liu, J.G. Analysis of topographic decorrelation in SAR interferometry using ratio coherence imagery. IEEE Trans. Geosci. Remote Sens. 2001, 39, 223–232. [Google Scholar] [CrossRef]
- Jordan, T.E.; Lohman, R.B.; Tapia, L.; Pfeiffer, M.; Scott, C.P.; Amundso, R.; Godfrey, L.; Riquelme, R. Surface materials and landforms as controls on InSAR permanent and transient responses to precipitation events in a hyperarid desert, Chile. Remote Sens. Environ. 2020, 237, 18. [Google Scholar] [CrossRef]
- Kim, J.; Dorjsuren, M.; Choi, Y.; Purevjav, G. Reconstructed Aeolian Surface Erosion in Southern Mongolia by Multi-Temporal InSAR Phase Coherence Analyses. Front. Earth Sci. 2020, 8, 9. [Google Scholar] [CrossRef]
- Wegmüller, U.; Strozzi, T.; Farr, T.; Werner, C.L. Arid land surface characterization with repeat-pass SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2000, 38, 776–781. [Google Scholar] [CrossRef]
- Gaber, A.; Abdelkareem, M.; Abdelsadek, I.S.; Koch, M.; El-Baz, F. Using InSAR Coherence for Investigating the Interplay of Fluvial and Aeolian Features in Arid Lands: Implications for Groundwater Potential in Egypt. Remote Sens. 2018, 10, 18. [Google Scholar] [CrossRef]
- Farrés, M.; Platikanov, S.; Tsakovski, S.; Tauler, R. Comparison of the variable importance in projection (VIP) and of the selectivity ratio (SR) methods for variable selection and interpretation. J. Chemom. 2015, 29, 528–536. [Google Scholar] [CrossRef]
- Marazuela, M.Á.; Vázquez-Suñé, E.; Custodio, E.; Palma, T.; García-Gil, A.; Ayora, C. 3D mapping, hydrodynamics and modelling of the freshwater-brine mixing zone in salt flats similar to the Salar de Atacama (Chile). J. Hydrol. 2018, 561, 223–235. [Google Scholar] [CrossRef]
- Valdivielso, S.; Vázquez-Suñé, E.; Herrera, C.; Custodio, E. Characterization of precipitation and recharge in the peripheral aquifer of the Salar de Atacama. Sci. Total Environ. 2022, 806, 14. [Google Scholar] [CrossRef] [PubMed]
- Valdivielso, S.; Hassanzadeh, A.; Vázquez-Suñé, E.; Custodio, E.; Criollo, R. Spatial distribution of meteorological factors controlling stable isotopes in precipitation in Northern Chile. J. Hydrol. 2022, 605, 12. [Google Scholar] [CrossRef]
- Marazuela, M.Á.; Vázquez-Suñé, E.; Ayora, C.; García-Gil, A.; Palma, T. The effect of brine pumping on the natural hydrodynamics of the Salar de Atacama: The damping capacity of salt flats. Sci. Total Environ. 2019, 654, 1118–1131. [Google Scholar] [CrossRef] [PubMed]
- Dirección General de Aguas (DGA). Información Oficial Hidrometeorológica y de Calidad de Aguas en Línea; Ministerio de Obras Públicas, Gobierno de Chile: Santiago de Chile, Chile, 2023.
- Gascoin, S.; Hagolle, O.; Huc, M.; Jarlan, L.; Dejoux, J.F.; Szczypta, C.; Marti, R.; Sánchez, R. A snow cover climatology for the Pyrenees from MODIS snow products. Hydrol. Earth Syst. Sci. 2015, 19, 2337–2351. [Google Scholar] [CrossRef]
- Parajka, J.; Bloschl, G. Spatio-temporal combination of MODIS images—Potential for snow cover mapping. Water Resour. Res. 2008, 44, 13. [Google Scholar] [CrossRef]
- Riggs, G.A.; Hall, D.K.; Román, M.O. MODIS Snow Products; Collection 6; User Guide; National Aeronautics and Space Administration: Washington, United States of America. 2016. Available online: https://modis-snow-ice.gsfc.nasa.gov/uploads/C6_MODIS_Snow_User_Guide.pdf (accessed on 29 March 2023).
- Villaescusa-Nadal, J.L.; Vermote, E.; Franch, B.; Santamaria-Artigas, A.E.; Roger, J.C.; Skakun, S. MODIS-Based AVHRR Cloud and Snow Separation Algorithm. IEEE Trans. Geosci. Remote Sens. 2022, 60, 13. [Google Scholar] [CrossRef]
- Parajka, J.; Bloschl, G. Validation of MODIS snow cover images over Austria. Hydrol. Earth Syst. Sci. 2006, 10, 679–689. [Google Scholar] [CrossRef]
- Kilpys, J.; Pipiraite-Januskiene, S.; Rimkus, E. Snow climatology in Lithuania based on the cloud-free moderate resolution imaging spectroradiometer snow cover product. Int. J. Climatol. 2020, 40, 4690–4706. [Google Scholar] [CrossRef]
- Hall, D.K.; Riggs, G.A. Accuracy assessment of the MODIS snow products. Hydrol. Process. 2007, 21, 1534–1547. [Google Scholar] [CrossRef]
- Hüsler, F.; Jonas, T.; Riffler, M.; Musial, J.P.; Wunderle, S. A Satellite-Based snow cover climatology (1985–2011) for the European Alps derived from AVHRR data. Cryosphere 2014, 8, 73–90. [Google Scholar] [CrossRef]
- Busetto, L.; Ranghetti, L. MODIStsp: An R package for automatic preprocessing of MODIS Land Products time series. Comput. Geosci. 2016, 97, 40–48. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).