A Simple Real LST Reconstruction Method Combining Thermal Infrared and Microwave Remote Sensing Based on Temperature Conservation
Abstract
1. Introduction
- (1)
- The first category of methods is based on statistical regression, such as multiple linear regression and random forest [32,33]. In the selection of regression factors, these approaches consider surface variables, including the vegetation index and surface albedo, as well as the influence of clouds on solar radiation received by the land surface, such as the cloud cover duration and solar radiation factor.
- (2)
- The second category of methods is based on the surface energy balance (SEB). These methods involve two steps: first, reconstructing the clear-sky LST of the target pixel, and then calculating the relationship between the LST difference and the shortwave radiation difference between the target pixel and similar pixels based on SEB. This allows for the determination of a temperature correction value for the target pixel, which is added to the clear-sky LST to obtain the real LST [34,35,36].
- (3)
- The third category of methods is based on the temporal component decomposition model of LST. These methods decompose the daily instantaneous LST into components such as the annual temperature cycle (ATC), diurnal temperature cycle (DTC), and sometimes the weather temperature component (WTC). The MODIS LST observations are used to estimate the parameters of the ATC and DTC models, reconstruct the ATC and DTC curves, and ultimately obtain the real LST [37,38].
- (4)
- The fourth category of methods is those that use reanalysis data, including Global/China Land Data Assimilation System (GLDAS/CLDAS) data and European Centre for Medium-Range Weather Forecasts (ECMWF) Reanalysis 5th Generation (ERA5) reanalysis data. These datasets are generated through data-assimilation techniques that combine physical models and observational data to simulate real surface conditions with complete spatial coverage and high temporal resolution. Various fusion methods have been proposed, such as using the Enhanced Spatial and Temporal Adaptive Reflectance Fusion Model (ESTARFM) to fuse MODIS LST and reanalysis LST [39]; or assimilating MODIS LST into a time-evolving model based on ERA5 data, using the Kalman filter algorithm, followed by bias correction using SEB theory [40].
- (5)
- The fifth category of methods is those that use passive microwave (PMW). Microwave data have the advantage of penetrating clouds and providing more complete LST information in space. The fusion of microwave LST with thermal infrared LST can achieve complementary advantages. There are three main approaches within this category: directly fusing coarse-scale microwave LST with fine-scale thermal infrared LST [41]; downscaling the microwave data and combining it with MODIS LST to obtain real LST [42]; or filling the orbital gaps in the microwave data, followed by downscaling and fusion with MODIS LST, while considering auxiliary information [43,44,45]. Recently, a deep-learning framework proposed by Wu achieved good results by fusing microwave and thermal infrared data to obtain an all-weather LST [46].
2. Materials and Methods
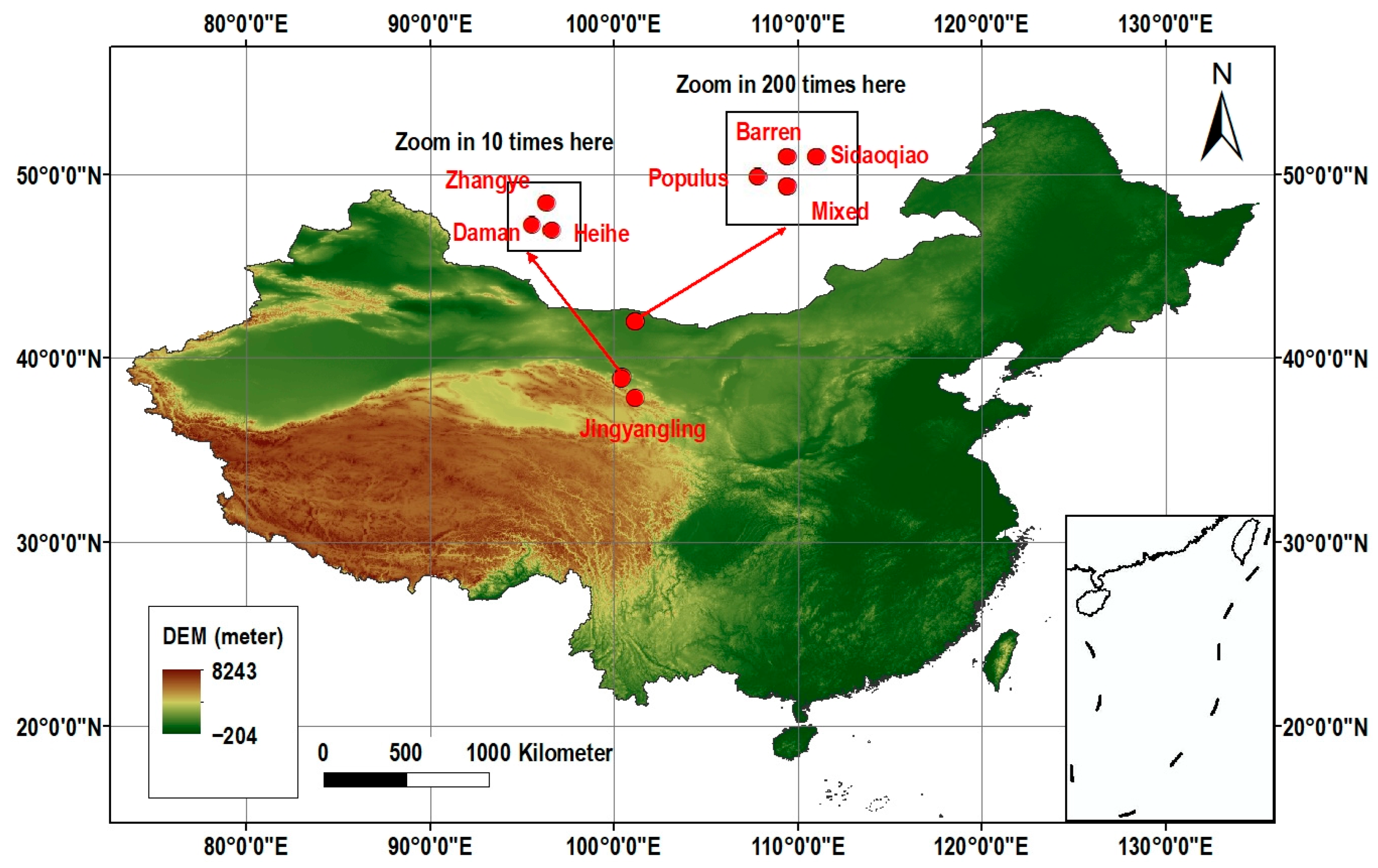
2.1. Research Area
2.2. Obtaining and Preprocessing Data
2.2.1. Satellite Data
2.2.2. In Situ Data
2.3. Method
2.3.1. TMTC Step 1: AMSR2 LST Gap Filling
2.3.2. TMTC Step 2: AMSR2 LST Downscaling
3. Results
3.1. Spatial Display of Results LSTs
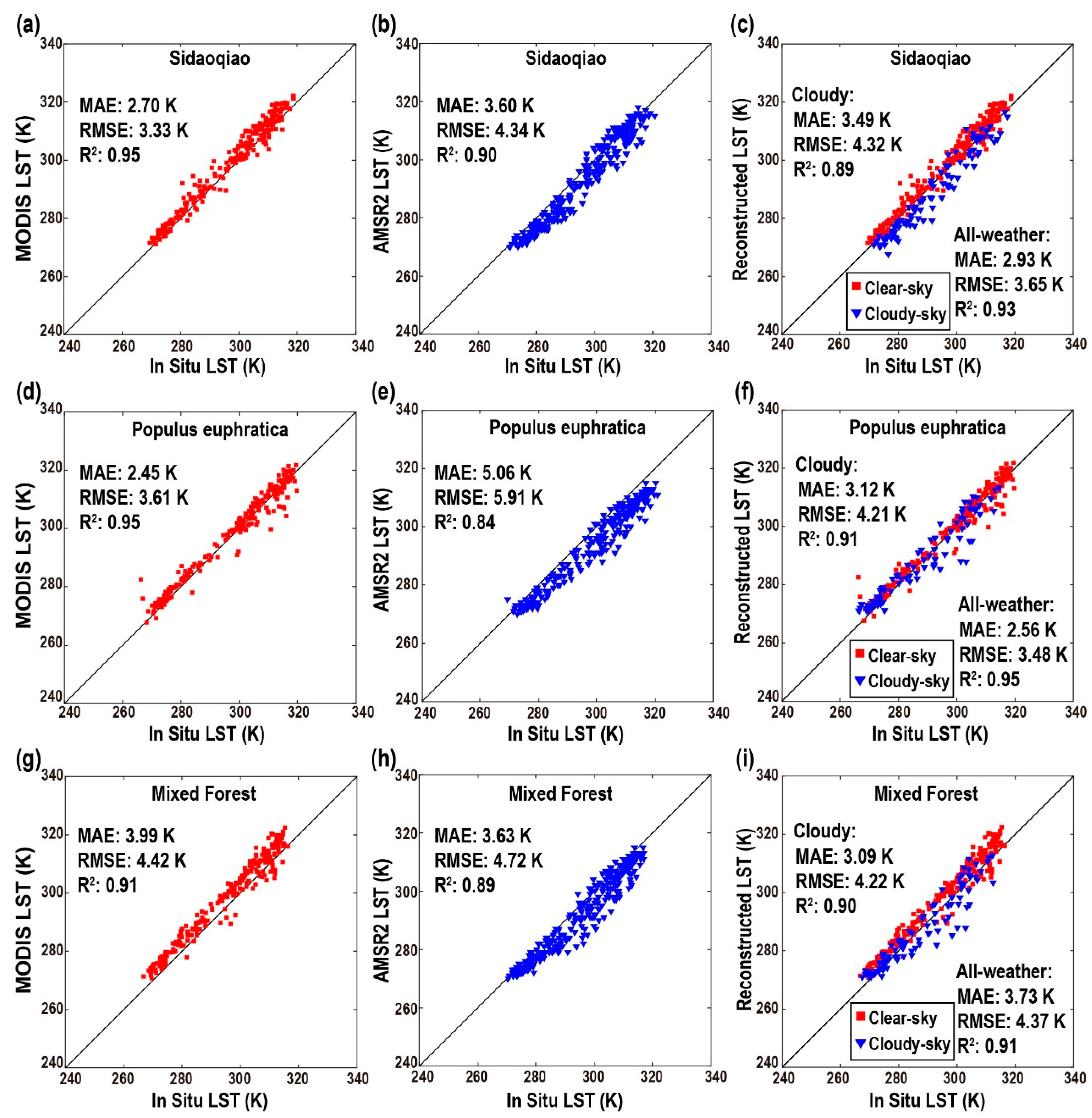
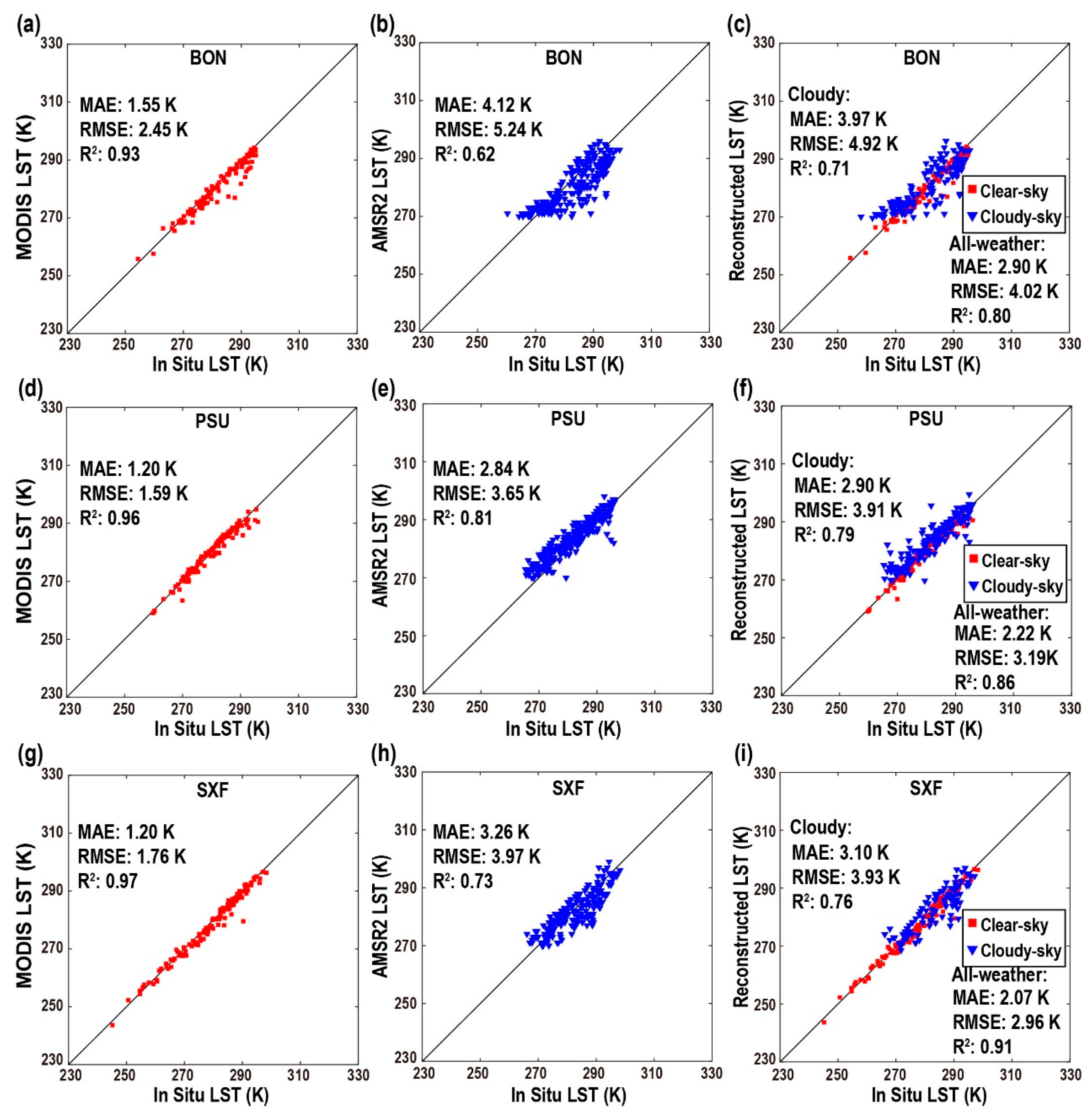
3.2. Accuracy Assessment
4. Discussion
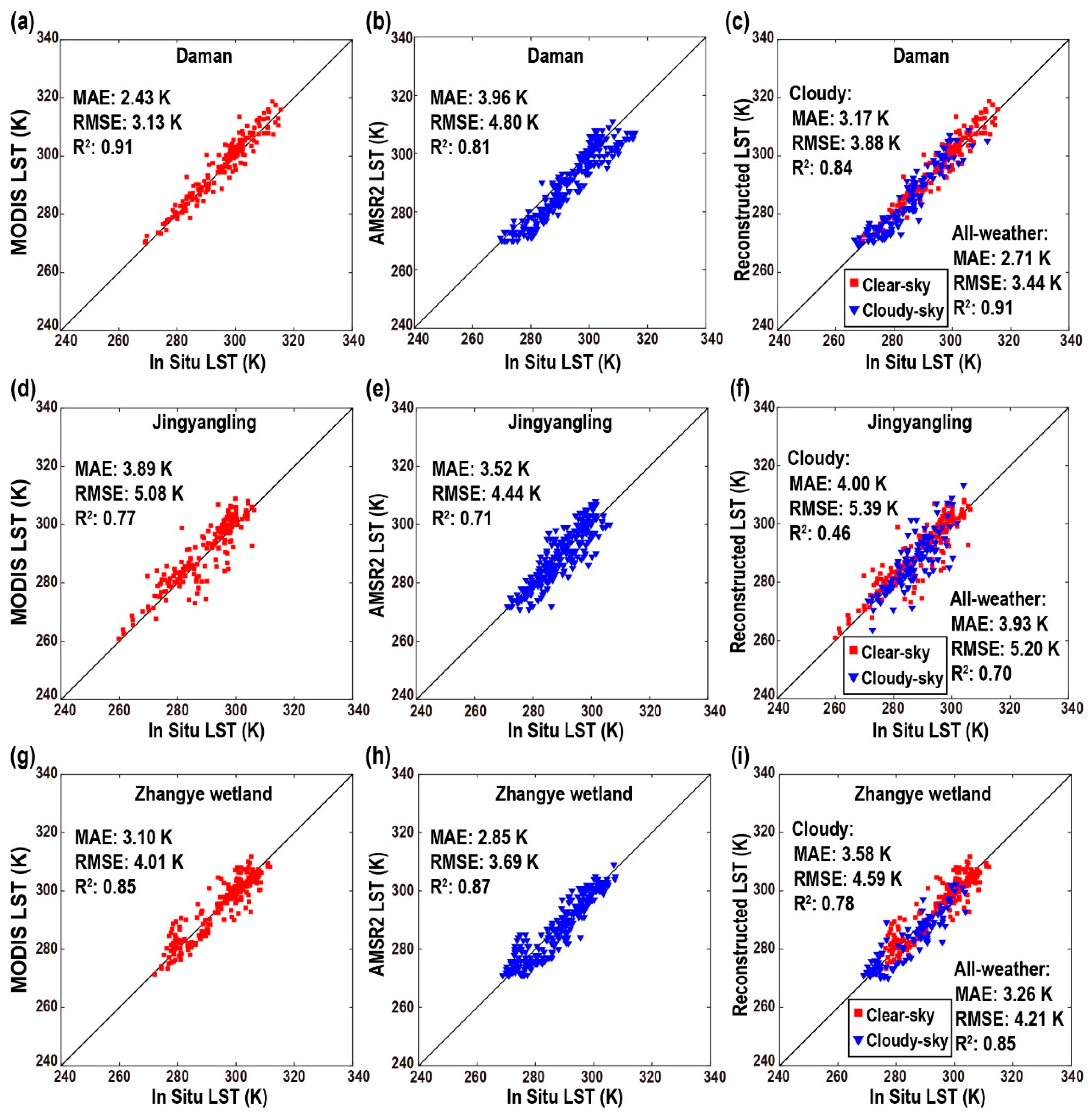
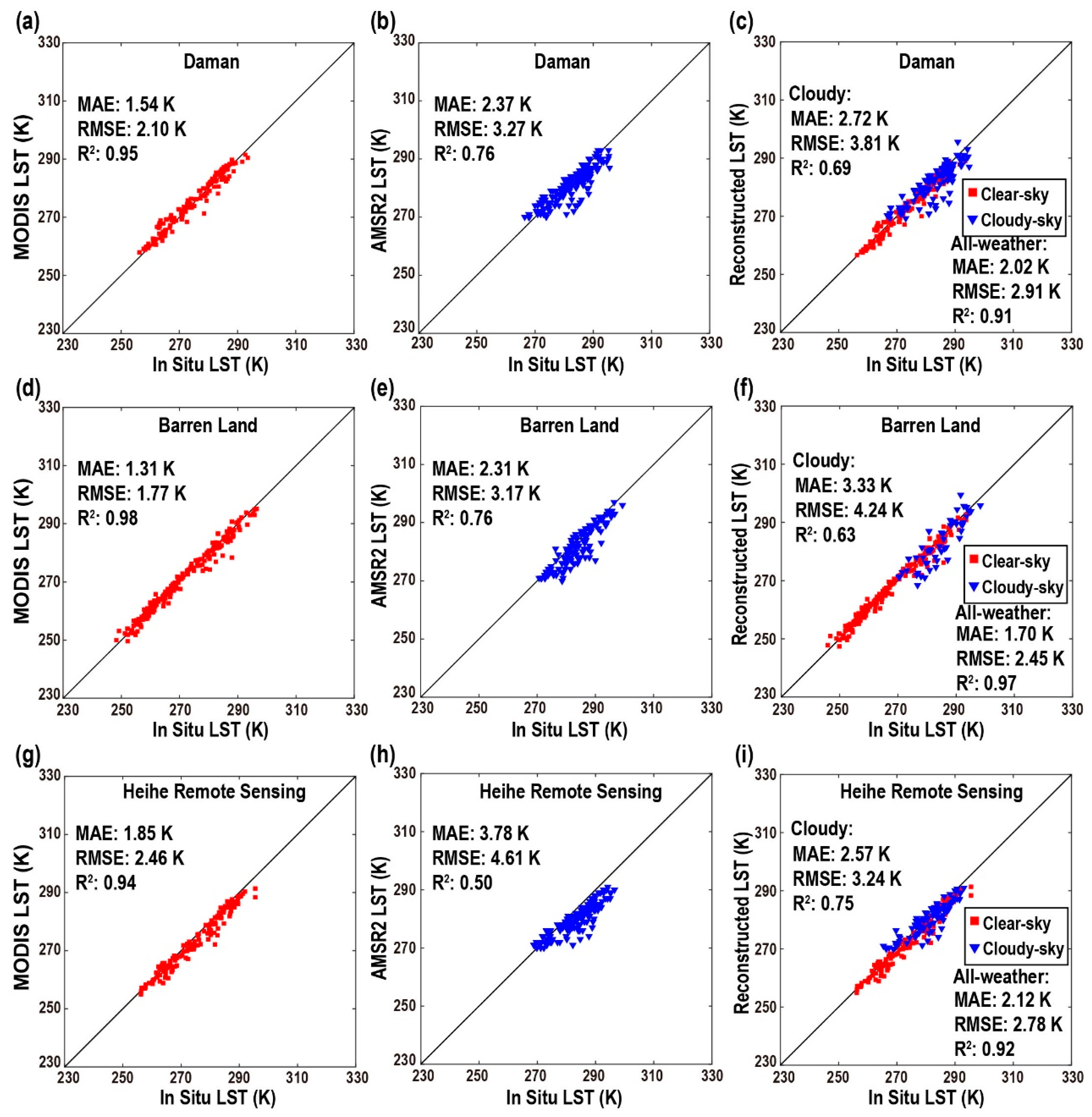
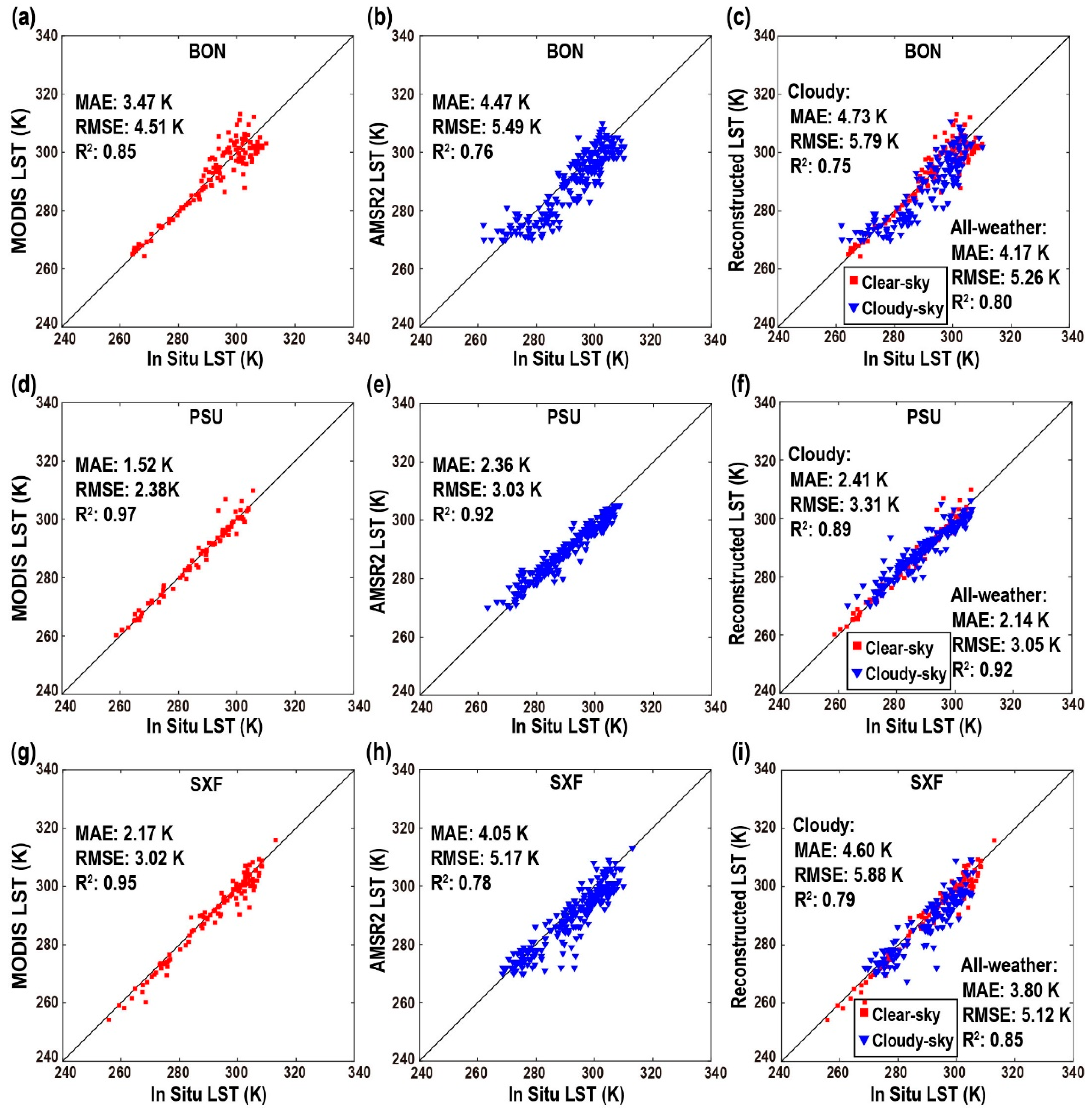
4.1. Accuracy in Other Regions
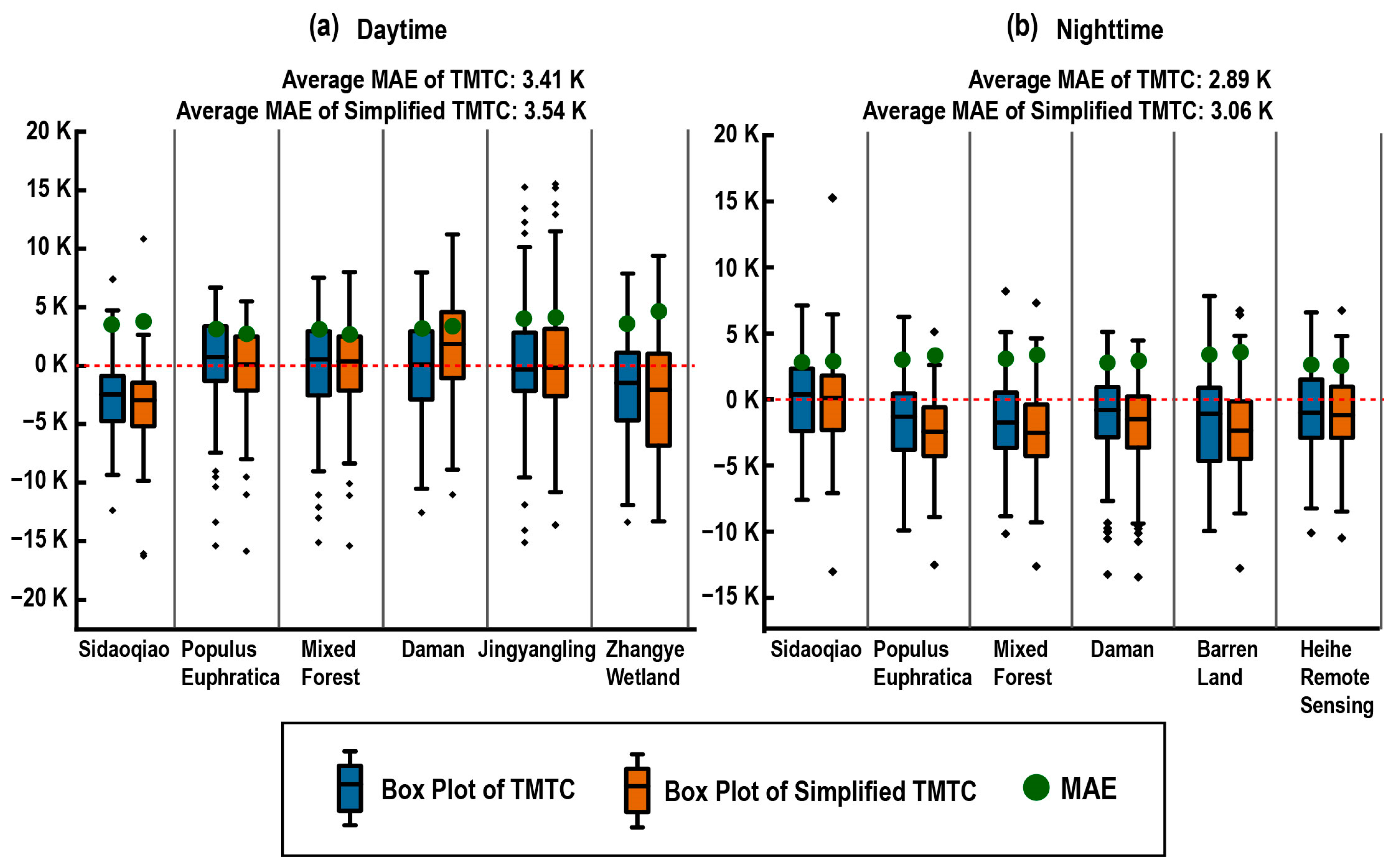
4.2. Simplified TMTC
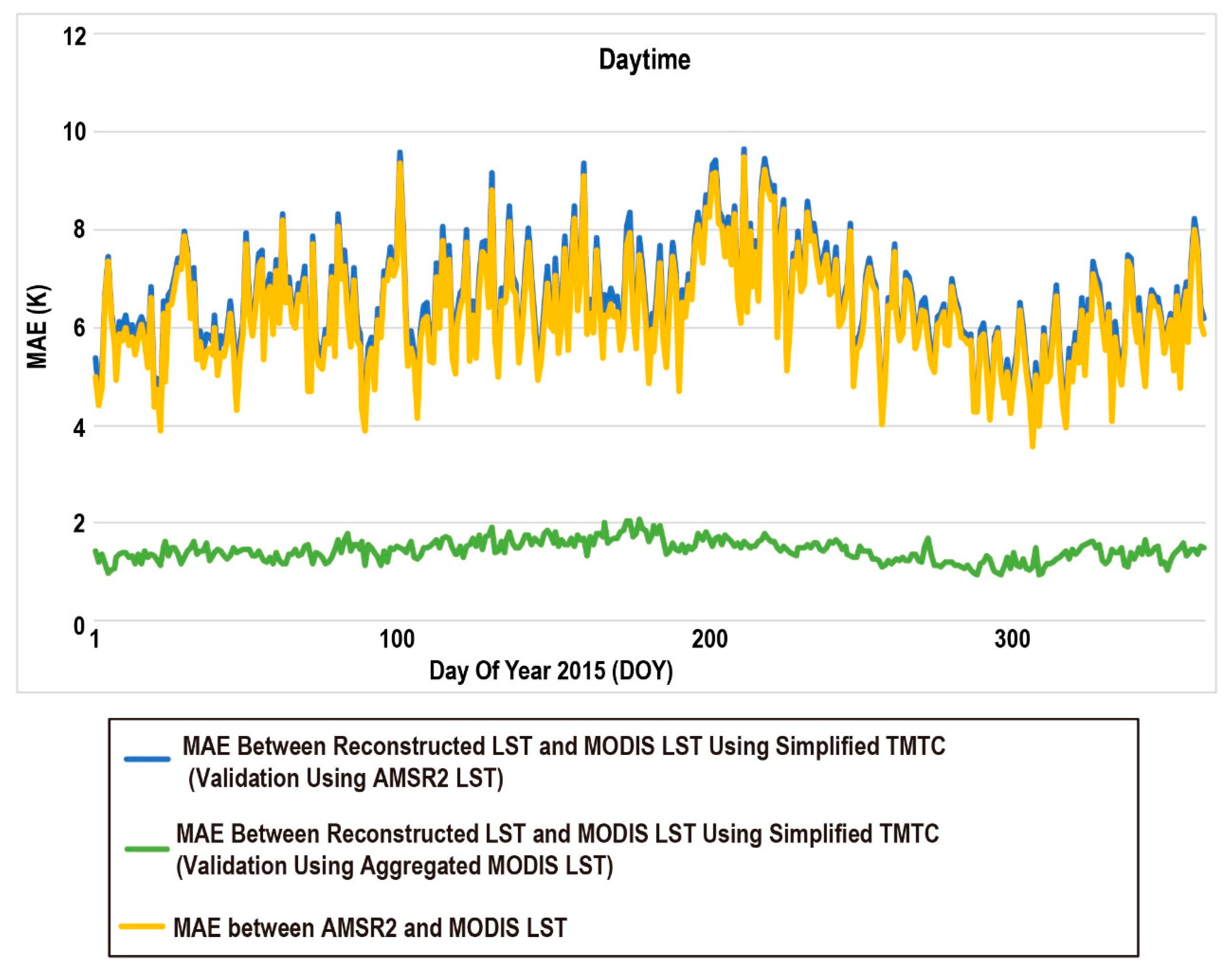
4.3. Exploration of the Accuracy Improvement (Ideal Accuracy of TMTC)
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Station Name | Lat (N)/Lon (W) | Altitude (m) | Landscape |
|---|---|---|---|
| Sidaoqiao | 42.00/101.14 | 873 | Tamarix |
| Populus euphratica | 41.99/101.12 | 876 | Populus euphratica |
| Mixed Forest | 41.99/101.13 | 874 | Populus euphratica and Tamarix |
| Daman | 38.86/100.37 | 1556 | Maize |
| Jingyangling | 37.84/101.12 | 3750 | alpine meadow |
| Zhangye wetland | 38.98/100.45 | 1460 | Reed |
| Barren Land | 41.99/101.13 | 878 | bare land |
| Heihe Remote Sensing | 38.83/100.48 | 1560 | Grassland |
| Station Name | Lat (N)/Lon (W) | Altitude (m) | State | Surface Type 1 |
|---|---|---|---|---|
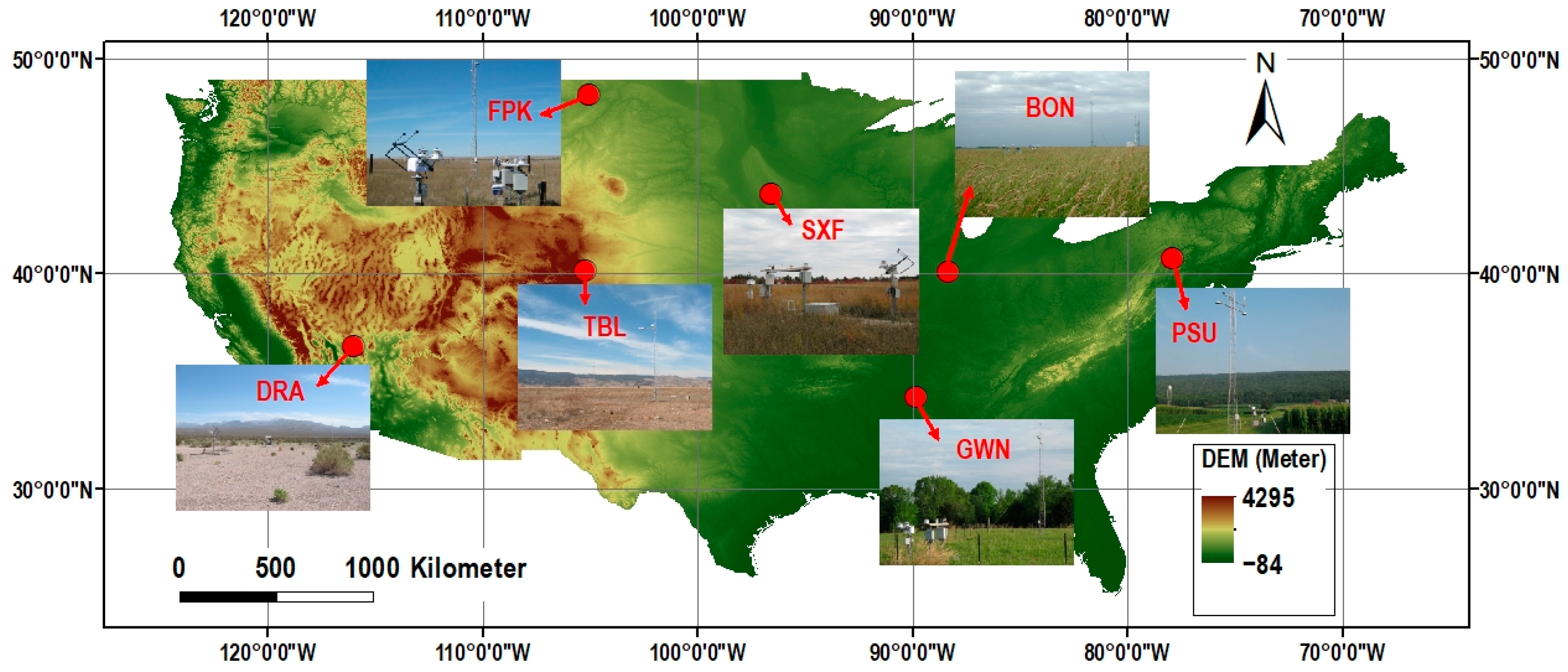
| Bondville (BON) | 40.05/88.37 | 213 | Illinois | Croplands |
| Table Mountain (TBL) | 40.13/105.24 | 1689 | Colorado | Grasslands |
| Fort Peck (FPK) | 48.31/105.10 | 634 | Montana | Grasslands |
| Goodwin Creek (GWN) | 34.25/89.87 | 98 | Mississippi | Woody Savannas |
| Penn State (PSU) | 40.72/77.93 | 376 | Pennsylvania | Croplands |
| Sioux Falls (SXF) | 43.73/96.62 | 473 | South Dakota | Croplands |
References
- Li, Z.-L.; Wu, H.; Duan, S.-B.; Zhao, W.; Ren, H.; Liu, X.; Leng, P.; Tang, R.; Ye, X.; Zhu, J.; et al. Satellite Remote Sensing of Global Land Surface Temperature: Definition, Methods, Products, and Applications. Rev. Geophys. 2023, 61, e2022RG000777. [Google Scholar] [CrossRef]
- Li, Z.-L.; Tang, B.-H.; Wu, H.; Ren, H.; Yan, G.; Wan, Z.; Trigo, I.F.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef]
- Wan, Z. New refinements and validation of the collection-6 MODIS land-surface temperature/emissivity product. Remote Sens. Environ. 2014, 140, 36–45. [Google Scholar] [CrossRef]
- Roy, D.P.; Wulder, M.A.; Loveland, T.R.; Woodcock, C.E.; Allen, R.G.; Anderson, M.C.; Helder, D.; Irons, J.R.; Johnson, D.M.; Kennedy, R. Landsat-8: Science and product vision for terrestrial global change research. Remote Sens. Environ. 2014, 145, 154–172. [Google Scholar] [CrossRef]
- Parastatidis, D.; Mitraka, Z.; Chrysoulakis, N.; Abrams, M. Online global land surface temperature estimation from Landsat. Remote Sens. 2017, 9, 1208. [Google Scholar] [CrossRef]
- Bisht, G.; Bras, R.L. Estimation of net radiation from the MODIS data under all sky conditions: Southern Great Plains case study. Remote Sens. Environ. 2010, 114, 1522–1534. [Google Scholar] [CrossRef]
- Wu, C.; Munger, J.W.; Niu, Z.; Kuang, D. Comparison of multiple models for estimating gross primary production using MODIS and eddy covariance data in Harvard Forest. Remote Sens. Environ. 2010, 114, 2925–2939. [Google Scholar] [CrossRef]
- Xu, H. A remote sensing index for assessment of regional ecological changes. China Environ. Sci. 2013, 33, 889–897. [Google Scholar]
- Zhu, W.; Lű, A.; Jia, S. Estimation of daily maximum and minimum air temperature using MODIS land surface temperature products. Remote Sens. Environ. 2013, 130, 62–73. [Google Scholar] [CrossRef]
- Kloog, I.; Nordio, F.; Coull, B.A.; Schwartz, J. Predicting spatiotemporal mean air temperature using MODIS satellite surface temperature measurements across the Northeastern USA. Remote Sens. Environ. 2014, 150, 132–139. [Google Scholar] [CrossRef]
- Karthikeyan, L.; Mishra, A.K. Multi-layer high-resolution soil moisture estimation using machine learning over the United States. Remote Sens. Environ. 2021, 266, 112706. [Google Scholar] [CrossRef]
- Chen, S.; Yang, Y.; Deng, F.; Zhang, Y.; Liu, D.; Liu, C.; Gao, Z. A high-resolution monitoring approach of canopy urban heat island using a random forest model and multi-platform observations. Atmos. Meas. Tech. 2022, 15, 735–756. [Google Scholar] [CrossRef]
- Li, X.; Wigneron, J.-P.; Fan, L.; Frappart, F.; Yueh, S.H.; Colliander, A.; Ebtehaj, A.; Gao, L.; Fernandez-Moran, R.; Liu, X.; et al. A new SMAP soil moisture and vegetation optical depth product (SMAP-IB): Algorithm, assessment and inter-comparison. Remote Sens. Environ. 2022, 271, 112921. [Google Scholar] [CrossRef]
- Liao, Y.; Shen, X.; Zhou, J.; Ma, J.; Zhang, X.; Tang, W.; Chen, Y.; Ding, L.; Wang, Z. Surface urban heat island detected by all-weather satellite land surface temperature. Sci. Total Environ. 2022, 811, 151405. [Google Scholar] [CrossRef] [PubMed]
- Pede, T.; Mountrakis, G. An empirical comparison of interpolation methods for MODIS 8-day land surface temperature composites across the conterminous Unites States. ISPRS J. Photogramm. Remote Sens. 2018, 142, 137–150. [Google Scholar] [CrossRef]
- Pham, H.T.; Kim, S.; Marshall, L.; Johnson, F. Using 3D robust smoothing to fill land surface temperature gaps at the continental scale. Int. J. Appl. Earth Obs. Geoinf. 2019, 82, 101879. [Google Scholar] [CrossRef]
- Kang, J.; Tan, J.; Jin, R.; Li, X.; Zhang, Y. Reconstruction of MODIS land surface temperature products based on multi-temporal information. Remote Sens. 2018, 10, 1112. [Google Scholar] [CrossRef]
- Xu, Y.; Shen, Y. Reconstruction of the land surface temperature time series using harmonic analysis. Comput. Geosci. 2013, 61, 126–132. [Google Scholar] [CrossRef]
- Crosson, W.L.; Al-Hamdan, M.Z.; Hemmings, S.N.; Wade, G.M. A daily merged MODIS Aqua–Terra land surface temperature data set for the conterminous United States. Remote Sens. Environ. 2012, 119, 315–324. [Google Scholar] [CrossRef]
- Neteler, M. Estimating daily land surface temperatures in mountainous environments by reconstructed MODIS LST data. Remote Sens. 2010, 2, 333–351. [Google Scholar] [CrossRef]
- Yang, J.; Wang, Y.; August, P. Estimation of land surface temperature using spatial interpolation and satellite-derived surface emissivity. J. Environ. Inform. 2004, 4, 37–44. [Google Scholar] [CrossRef]
- Zeng, C.; Shen, H.; Zhong, M.; Zhang, L.; Wu, P. Reconstructing MODIS LST based on multitemporal classification and robust regression. IEEE Geosci. Remote Sens. Lett. 2014, 12, 512–516. [Google Scholar] [CrossRef]
- Fan, X.-M.; Liu, H.-G.; Liu, G.-H.; Li, S.-B. Reconstruction of MODIS land-surface temperature in a flat terrain and fragmented landscape. Int. J. Remote Sens. 2014, 35, 7857–7877. [Google Scholar] [CrossRef]
- Sun, L.; Chen, Z.; Gao, F.; Anderson, M.; Song, L.; Wang, L.; Hu, B.; Yang, Y. Reconstructing daily clear-sky land surface temperature for cloudy regions from MODIS data. Comput. Geosci. 2017, 105, 10–20. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, Y.; Li, Y.; Xia, H.; Li, J. Reconstructing one kilometre resolution daily clear-sky LST for China’s landmass using the BME method. Remote Sens. 2019, 11, 2610. [Google Scholar] [CrossRef]
- Li, X.; Zhou, Y.; Asrar, G.R.; Zhu, Z. Creating a seamless 1 km resolution daily land surface temperature dataset for urban and surrounding areas in the conterminous United States. Remote Sens. Environ. 2018, 206, 84–97. [Google Scholar] [CrossRef]
- Wu, P.; Shen, H.; Zhang, L.; Göttsche, F.-M. Integrated fusion of multi-scale polar-orbiting and geostationary satellite observations for the mapping of high spatial and temporal resolution land surface temperature. Remote Sens. Environ. 2015, 156, 169–181. [Google Scholar] [CrossRef]
- Yu, W.; Ma, M.; Wang, X.; Tan, J. Estimating the land-surface temperature of pixels covered by clouds in MODIS products. J. Appl. Remote Sens. 2014, 8, 083525. [Google Scholar] [CrossRef]
- Metz, M.; Rocchini, D.; Neteler, M. Surface temperatures at the continental scale: Tracking changes with remote sensing at unprecedented detail. Remote Sens. 2014, 6, 3822–3840. [Google Scholar] [CrossRef]
- Weiss, D.J.; Atkinson, P.M.; Bhatt, S.; Mappin, B.; Hay, S.I.; Gething, P.W. An effective approach for gap-filling continental scale remotely sensed time-series. ISPRS J. Photogramm. Remote Sens. 2014, 98, 106–118. [Google Scholar] [CrossRef]
- Ke, L.; Ding, X.; Song, C. Reconstruction of time-series MODIS LST in Central Qinghai-Tibet Plateau using geostatistical approach. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1602–1606. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, Y.; Li, J.; Chen, X. A simple method for converting 1-km resolution daily clear-sky LST into real LST. Remote Sens. 2020, 12, 1641. [Google Scholar] [CrossRef]
- Zhao, W.; Duan, S.-B. Reconstruction of daytime land surface temperatures under cloud-covered conditions using integrated MODIS/Terra land products and MSG geostationary satellite data. Remote Sens. Environ. 2020, 247, 111931. [Google Scholar] [CrossRef]
- Yang, G.; Sun, W.; Shen, H.; Meng, X.; Li, J. An integrated method for reconstructing daily MODIS land surface temperature data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 1026–1040. [Google Scholar] [CrossRef]
- Zeng, C.; Long, D.; Shen, H.; Wu, P.; Cui, Y.; Hong, Y. A two-step framework for reconstructing remotely sensed land surface temperatures contaminated by cloud. ISPRS J. Photogramm. Remote Sens. 2018, 141, 30–45. [Google Scholar] [CrossRef]
- Yu, W.; Tan, J.; Ma, M.; Li, X.; She, X.; Song, Z. An effective similar-pixel reconstruction of the high-frequency cloud-covered areas of Southwest China. Remote Sens. 2019, 11, 336. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, J.; Liang, S.; Wang, D. A practical reanalysis data and thermal infrared remote sensing data merging (RTM) method for reconstruction of a 1-km all-weather land surface temperature. Remote Sens. Environ. 2021, 260, 112437. [Google Scholar] [CrossRef]
- Hong, F.; Zhan, W.; Göttsche, F.-M.; Lai, J.; Liu, Z.; Hu, L.; Fu, P.; Huang, F.; Li, J.; Li, H.; et al. A simple yet robust framework to estimate accurate daily mean land surface temperature from thermal observations of tandem polar orbiters. Remote Sens. Environ. 2021, 264, 112612. [Google Scholar] [CrossRef]
- Long, D.; Yan, L.; Bai, L.; Zhang, C.; Li, X.; Lei, H.; Yang, H.; Tian, F.; Zeng, C.; Meng, X.; et al. Generation of MODIS-like land surface temperatures under all-weather conditions based on a data fusion approach. Remote Sens. Environ. 2020, 246, 111863. [Google Scholar] [CrossRef]
- Jia, A.; Ma, H.; Liang, S.; Wang, D. Cloudy-sky land surface temperature from VIIRS and MODIS satellite data using a surface energy balance-based method. Remote Sens. Environ. 2021, 263, 112566. [Google Scholar] [CrossRef]
- Kou, X.; Jiang, L.; Bo, Y.; Yan, S.; Chai, L. Estimation of land surface temperature through blending MODIS and AMSR-E data with the Bayesian maximum entropy method. Remote Sens. 2016, 8, 105. [Google Scholar] [CrossRef]
- Shwetha, H.; Kumar, D.N. Prediction of high spatio-temporal resolution land surface temperature under cloudy conditions using microwave vegetation index and ANN. ISPRS J. Photogramm. Remote Sens. 2016, 117, 40–55. [Google Scholar] [CrossRef]
- Sun, D.; Li, Y.; Zhan, X.; Houser, P.; Yang, C.; Chiu, L.; Yang, R. Land surface temperature derivation under all sky conditions through integrating AMSR-E/AMSR-2 and MODIS/GOES observations. Remote Sens. 2019, 11, 1704. [Google Scholar] [CrossRef]
- Duan, S.-B.; Li, Z.-L.; Leng, P. A framework for the retrieval of all-weather land surface temperature at a high spatial resolution from polar-orbiting thermal infrared and passive microwave data. Remote Sens. Environ. 2017, 195, 107–117. [Google Scholar] [CrossRef]
- Xu, S.; Cheng, J. A new land surface temperature fusion strategy based on cumulative distribution function matching and multiresolution Kalman filtering. Remote Sens. Environ. 2021, 254, 112256. [Google Scholar] [CrossRef]
- Wu, P.; Su, Y.; Duan, S.-B.; Li, X.; Yang, H.; Zeng, C.; Ma, X.; Wu, Y.; Shen, H. A two-step deep learning framework for mapping gapless all-weather land surface temperature using thermal infrared and passive microwave data. Remote Sens. Environ. 2022, 277, 113070. [Google Scholar] [CrossRef]
- Mo, Y.; Xu, Y.; Chen, H.; Zhu, S. A Review of Reconstructing Remotely Sensed Land Surface Temperature under Cloudy Conditions. Remote Sens. 2021, 13, 2838. [Google Scholar] [CrossRef]
- Land Processes Distributed Active Archive Center (LP DAAC) Site. Available online: https://lpdaac.usgs.gov (accessed on 12 May 2023).
- Earth Observation Research Center, Japan Aerospace Exploration Agency Site. Available online: https://suzaku.eorc.jaxa.jp (accessed on 12 May 2023).
- SRTM 90m DEM Digital Elevation Database. Available online: http://srtm.csi.cgiar.org (accessed on 12 May 2023).
- Google Earth Engine Site. Available online: https://earthengine.google.com (accessed on 12 May 2023).
- Liu, S.; Li, X.; Xu, Z.; Che, T.; Xiao, Q.; Ma, M.; Liu, Q.; Jin, R.; Guo, J.; Wang, L. The Heihe Integrated Observatory Network: A basin-scale land surface processes observatory in China. Vadose Zone J. 2018, 17, 1–21. [Google Scholar] [CrossRef]
- Liu, S.M.; Xu, Z.W.; Wang, W.; Jia, Z.; Zhu, M.; Bai, J.; Wang, J. A comparison of eddy-covariance and large aperture scintillometer measurements with respect to the energy balance closure problem. Hydrol. Earth Syst. Sci. 2011, 15, 1291–1306. [Google Scholar] [CrossRef]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Li, X.; Zhang, K.; Wang, L.; Cheng, S.; Song, P. A Simple Real LST Reconstruction Method Combining Thermal Infrared and Microwave Remote Sensing Based on Temperature Conservation. Remote Sens. 2023, 15, 3033. https://doi.org/10.3390/rs15123033
Zhang Y, Li X, Zhang K, Wang L, Cheng S, Song P. A Simple Real LST Reconstruction Method Combining Thermal Infrared and Microwave Remote Sensing Based on Temperature Conservation. Remote Sensing. 2023; 15(12):3033. https://doi.org/10.3390/rs15123033
Chicago/Turabian StyleZhang, Yunfei, Xiaojuan Li, Ke Zhang, Lan Wang, Siyuan Cheng, and Panjie Song. 2023. "A Simple Real LST Reconstruction Method Combining Thermal Infrared and Microwave Remote Sensing Based on Temperature Conservation" Remote Sensing 15, no. 12: 3033. https://doi.org/10.3390/rs15123033
APA StyleZhang, Y., Li, X., Zhang, K., Wang, L., Cheng, S., & Song, P. (2023). A Simple Real LST Reconstruction Method Combining Thermal Infrared and Microwave Remote Sensing Based on Temperature Conservation. Remote Sensing, 15(12), 3033. https://doi.org/10.3390/rs15123033







