Estimation of the Soil Water Content Using the Early Time Signal of Ground-Penetrating Radar in Heterogeneous Soil
Abstract
1. Introduction
2. Materials and Methods
2.1. The Multi-Scale Stochastic Model
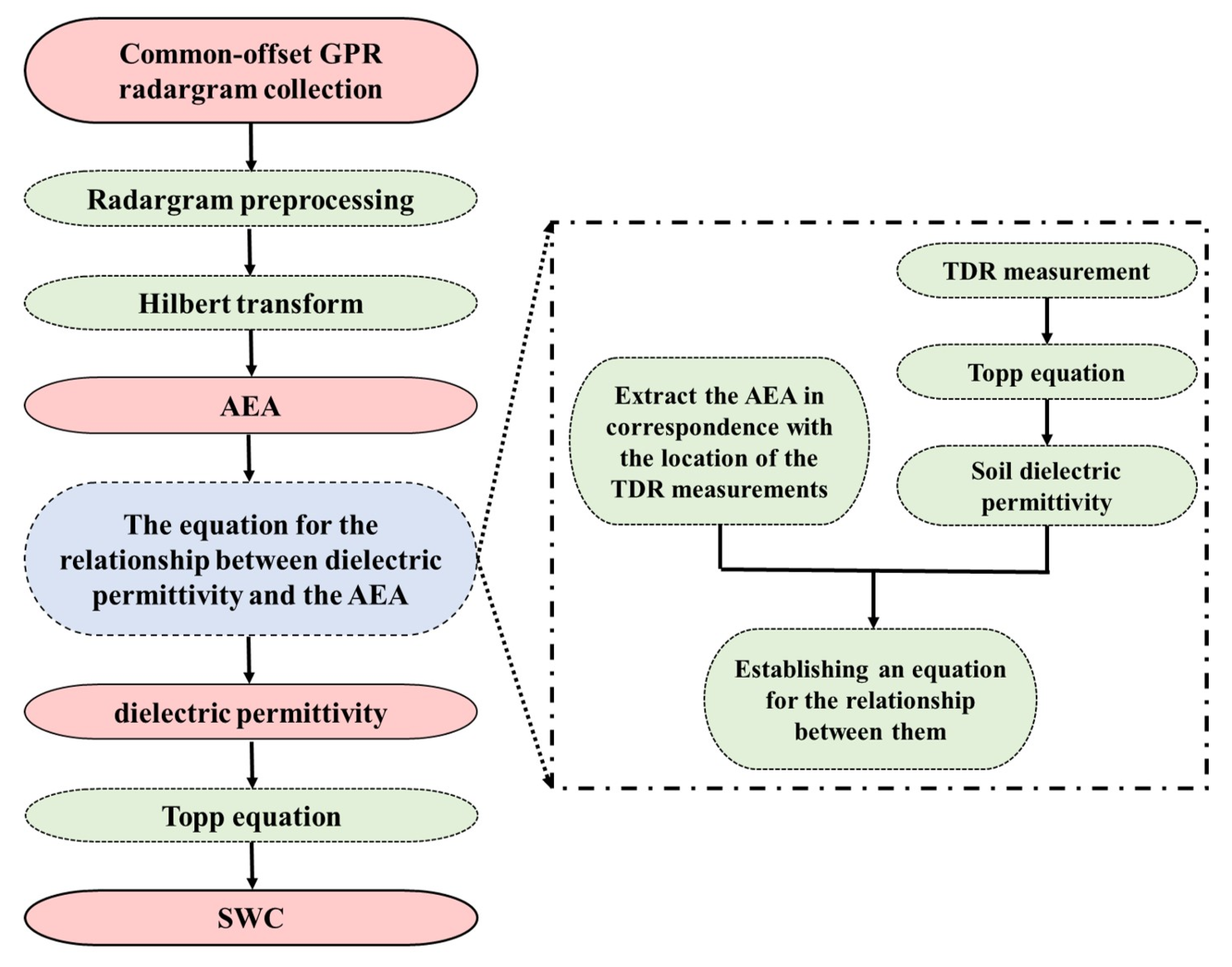
2.2. Principles for Estimating SWC with ETS
- (1)
- The obtained GPR common-offset data is preprocessed by DC filter, Band pass filter, and trace averaging to obtain ETS data that are suitable for SWC estimation.
- (2)
- To obtain the AEA, a Hilbert transform is performed on the ETS of GPR [14]. Assuming the signal obtained by GPR is , the Hilbert transform is described by:
- (3)
- A relationship is established between the dielectric permittivity and the AEA by extracting the AEA in correspondence with the location of the TDR measurements. The Topp equation [26] is used to covert the volumetric SWC by TDR measurements into the soil dielectric permittivity , which is:where is the volumetric SWC.
- (4)
- The of the soil can be estimated using the statistical relationship in step (3) with the AEA value of ETS. Then, the SWC can be calculated using the Topp equation.
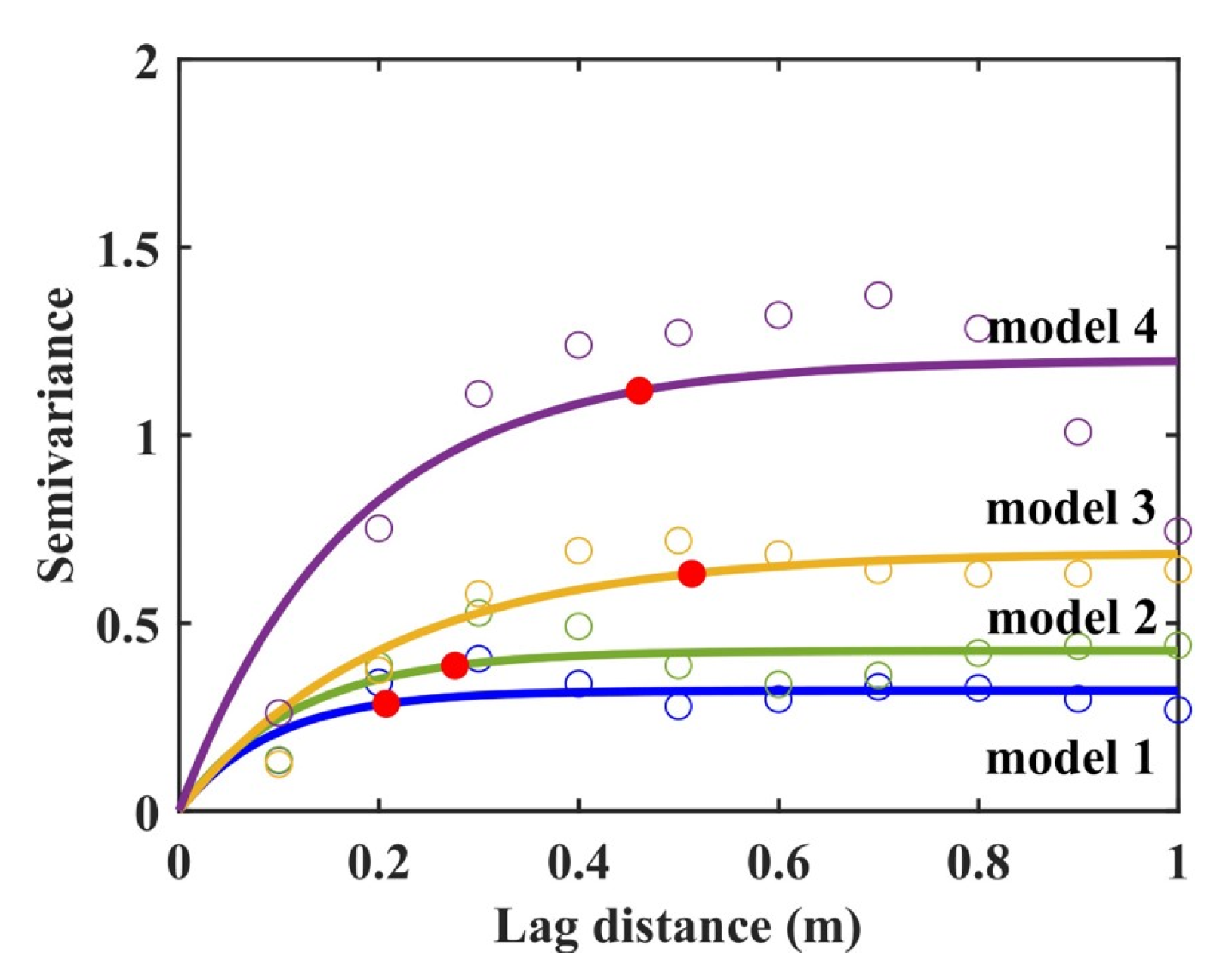
2.3. Soil Models and Heterogeneity Analysis
3. Results
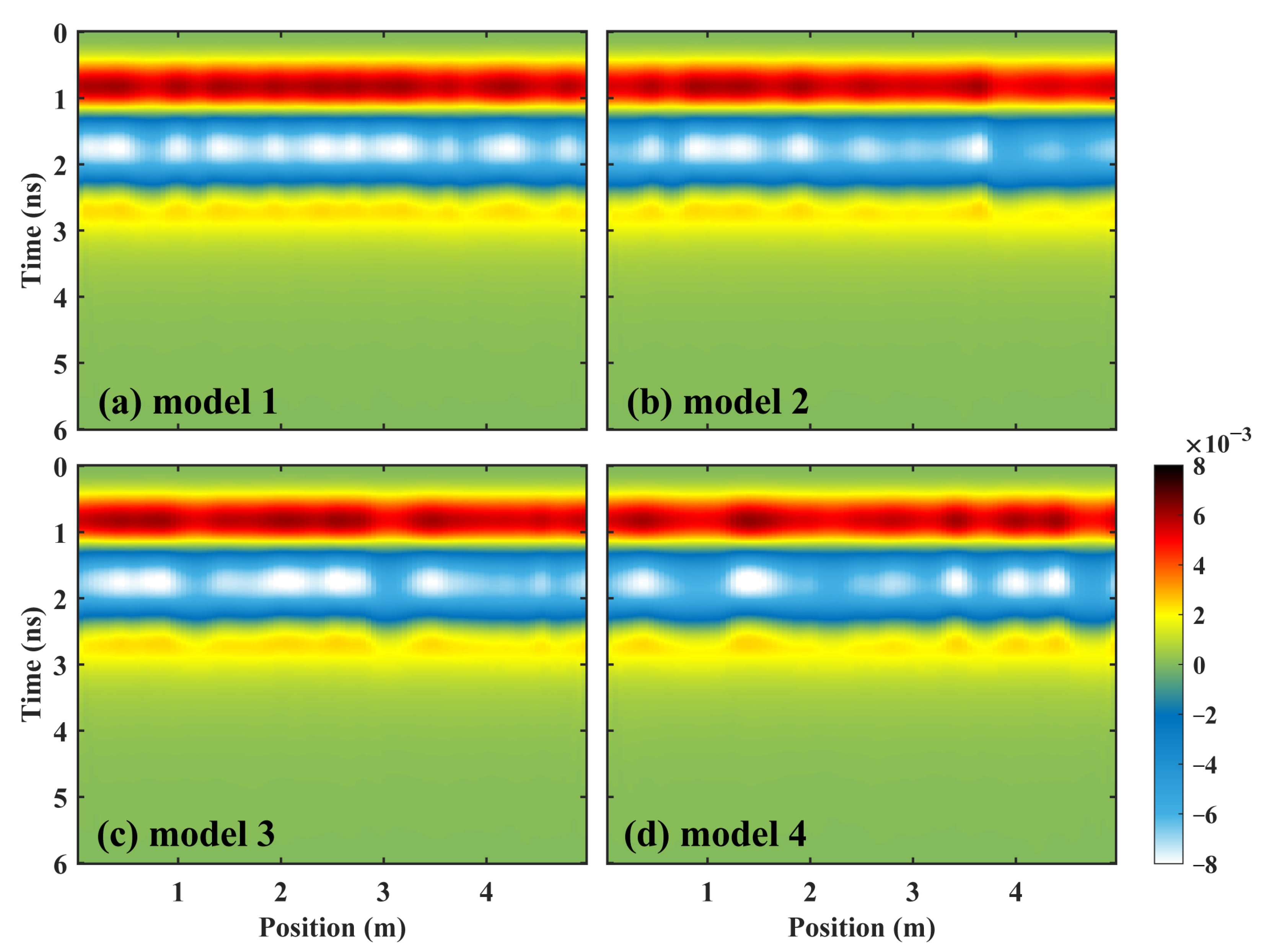
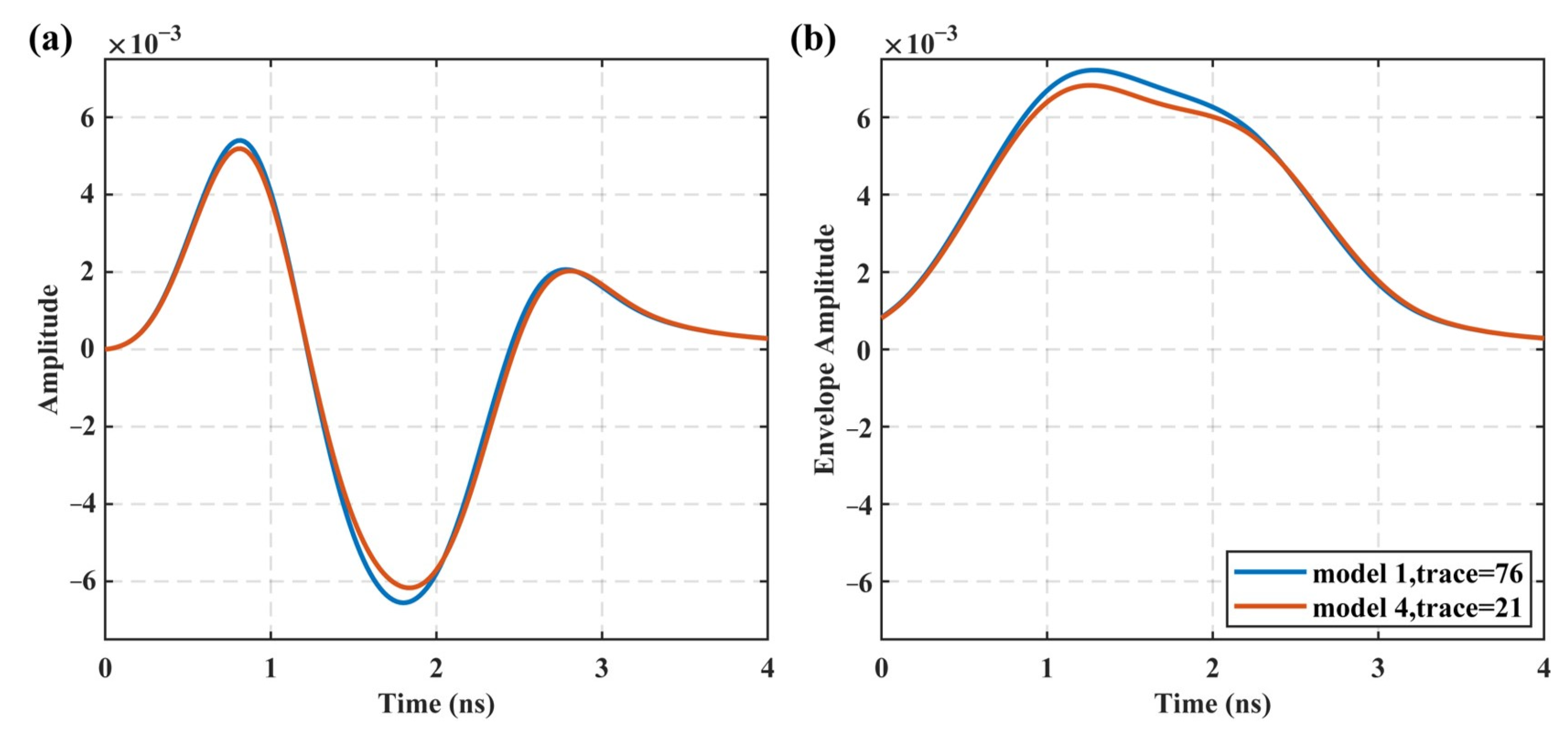
3.1. Forward Modeling and Analysis
3.1.1. FDTD Forward Modeling and ETS Characteristics
3.1.2. ETS Characteristics and Conductivity
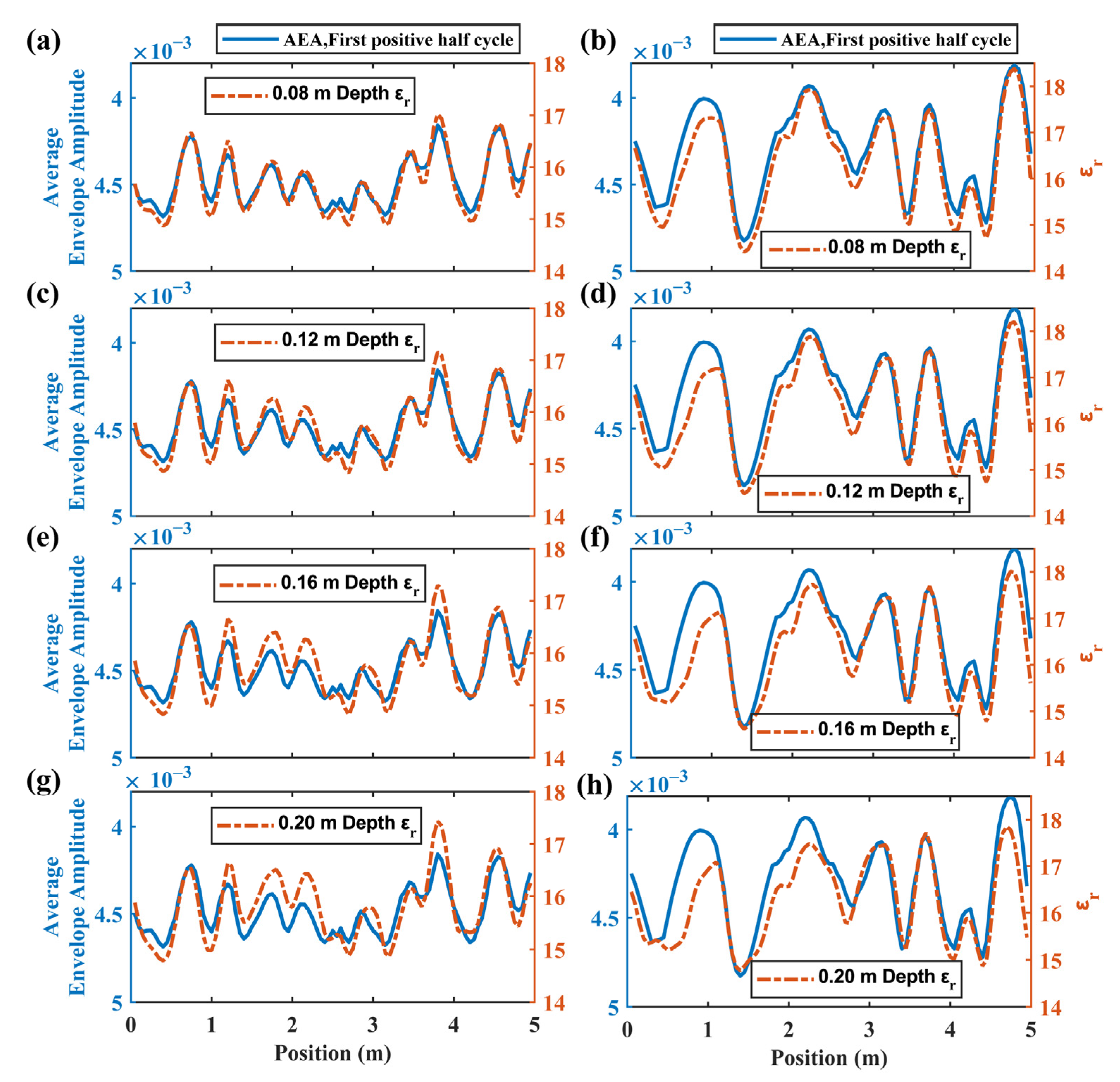
3.1.3. ETS Characteristics and Dielectric Permittivity
3.1.4. Detectable Depth of the AEA Method in Stochastic Media
3.1.5. AEA Estimation of SWC in Stochastic Media
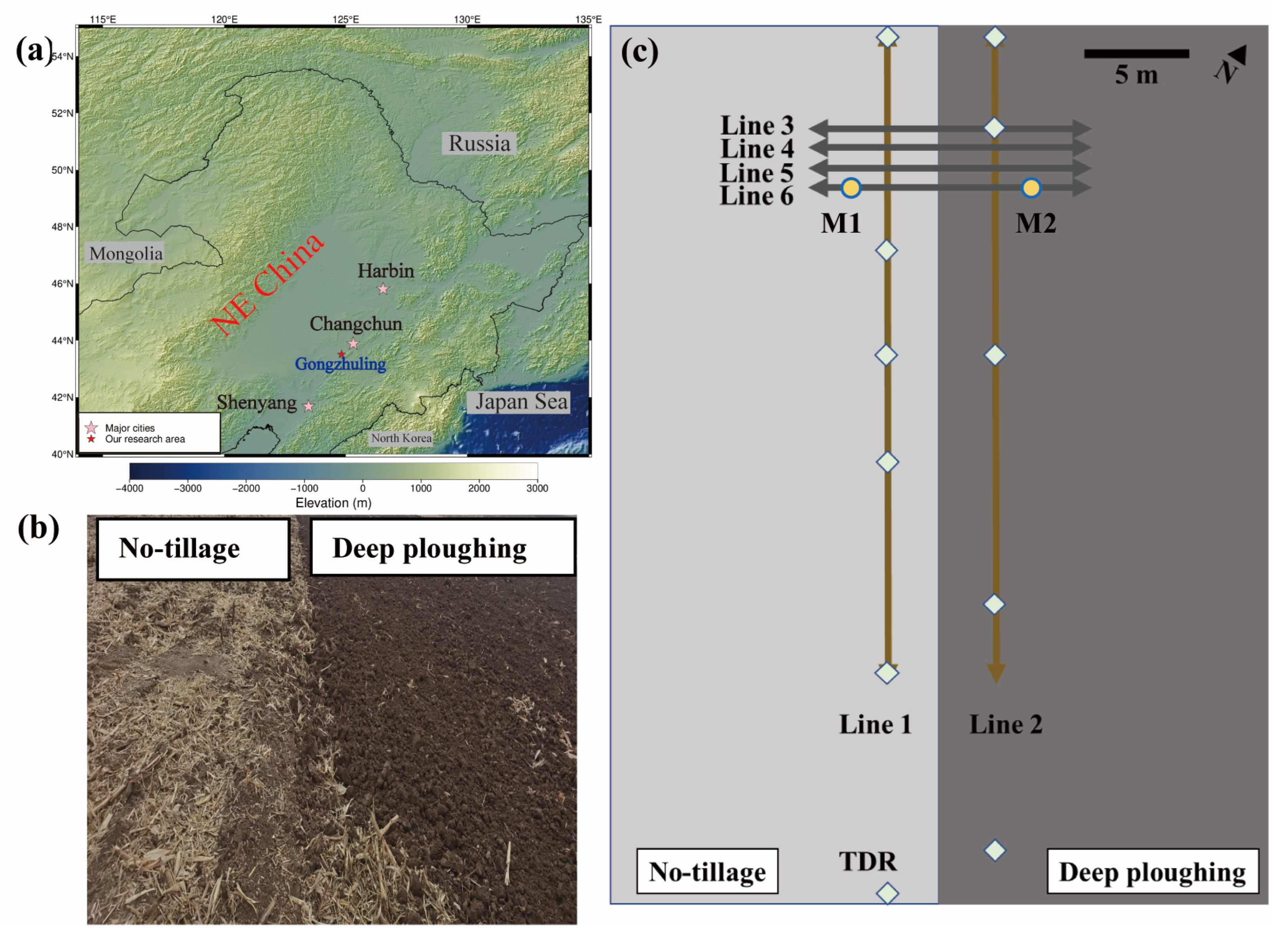
3.2. The Field Exploration Example
3.2.1. Field Experiment Data Collection
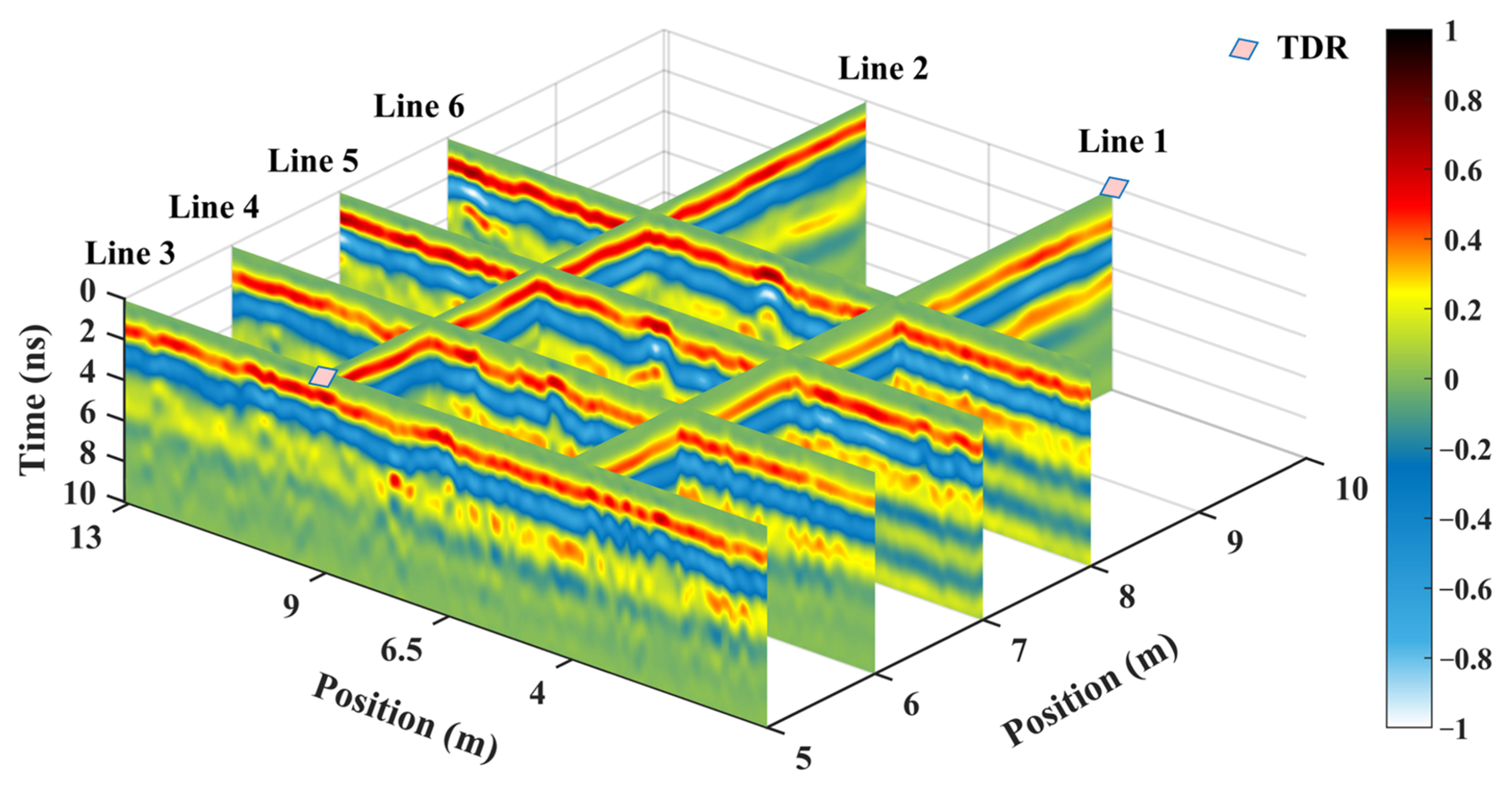
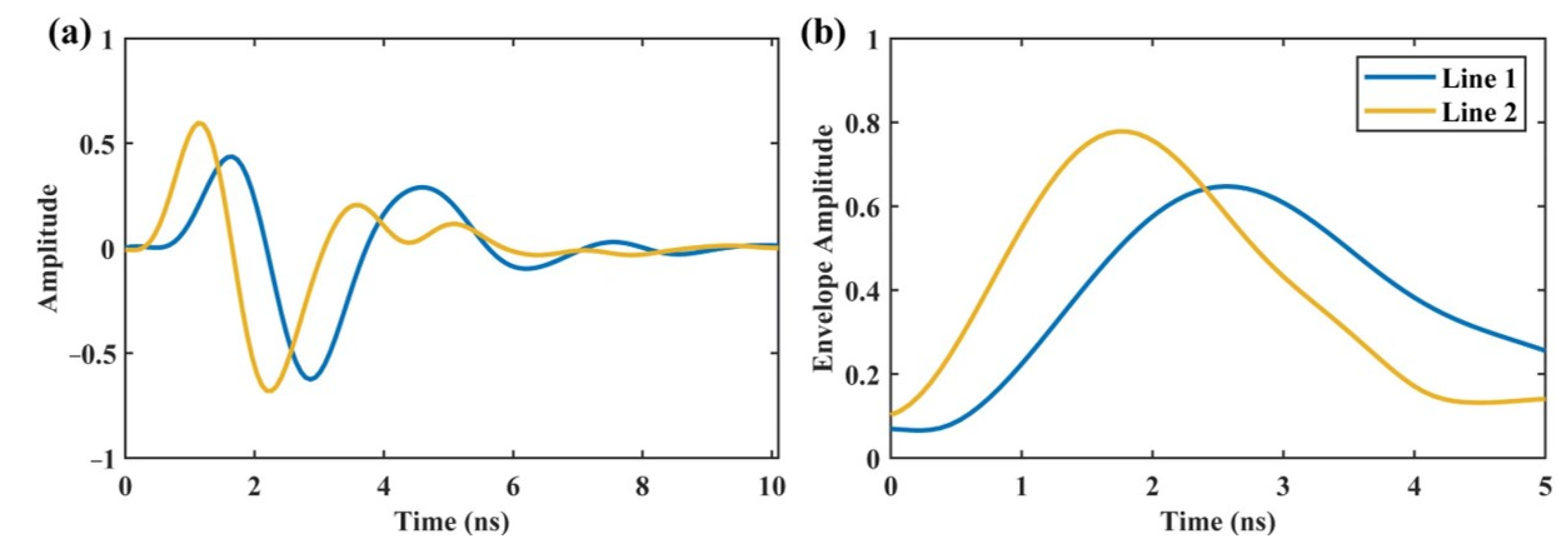
3.2.2. GPR Data Preprocessing
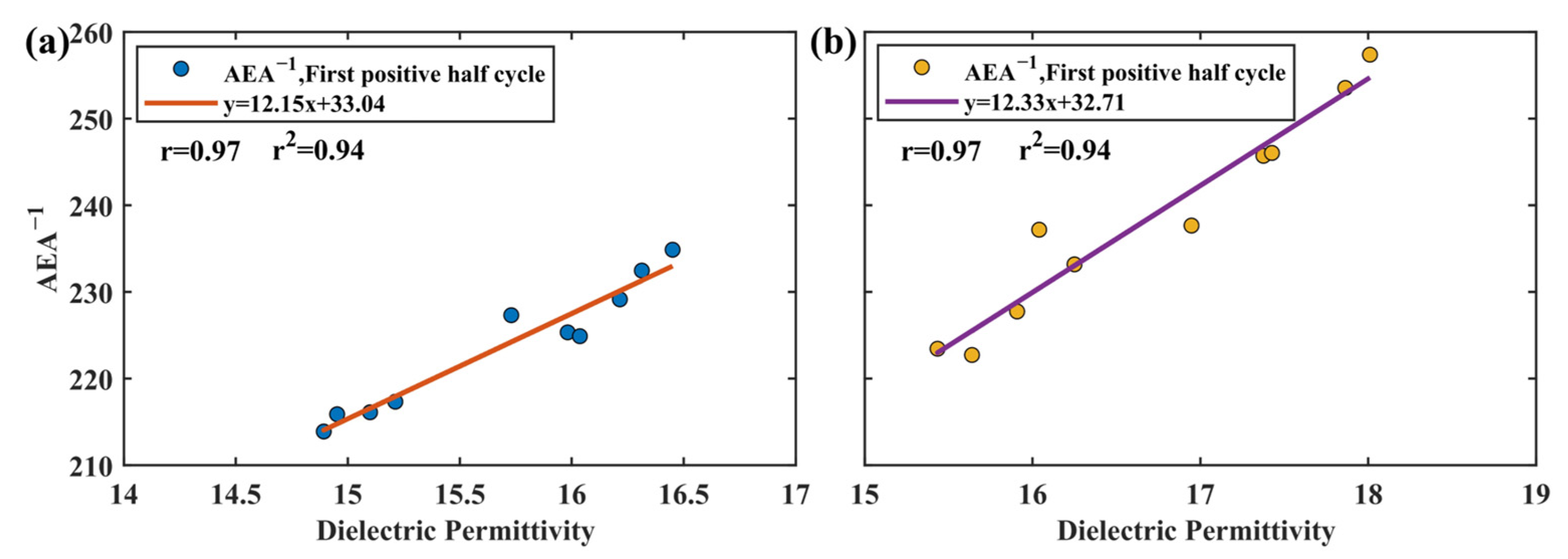
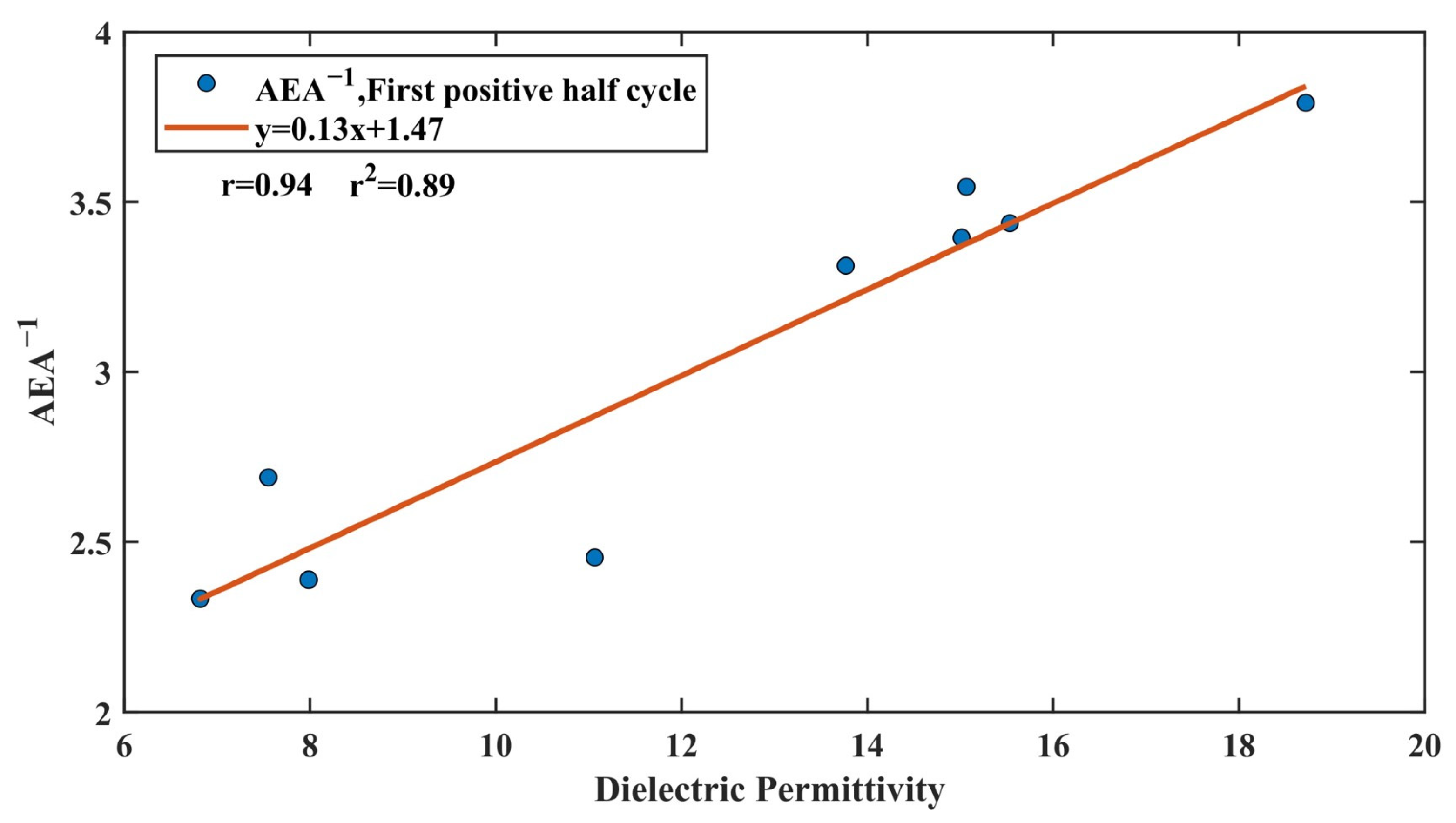
3.2.3. Fitting Relationship between the Dielectric Permittivity and AEA
3.2.4. Soil Heterogeneity
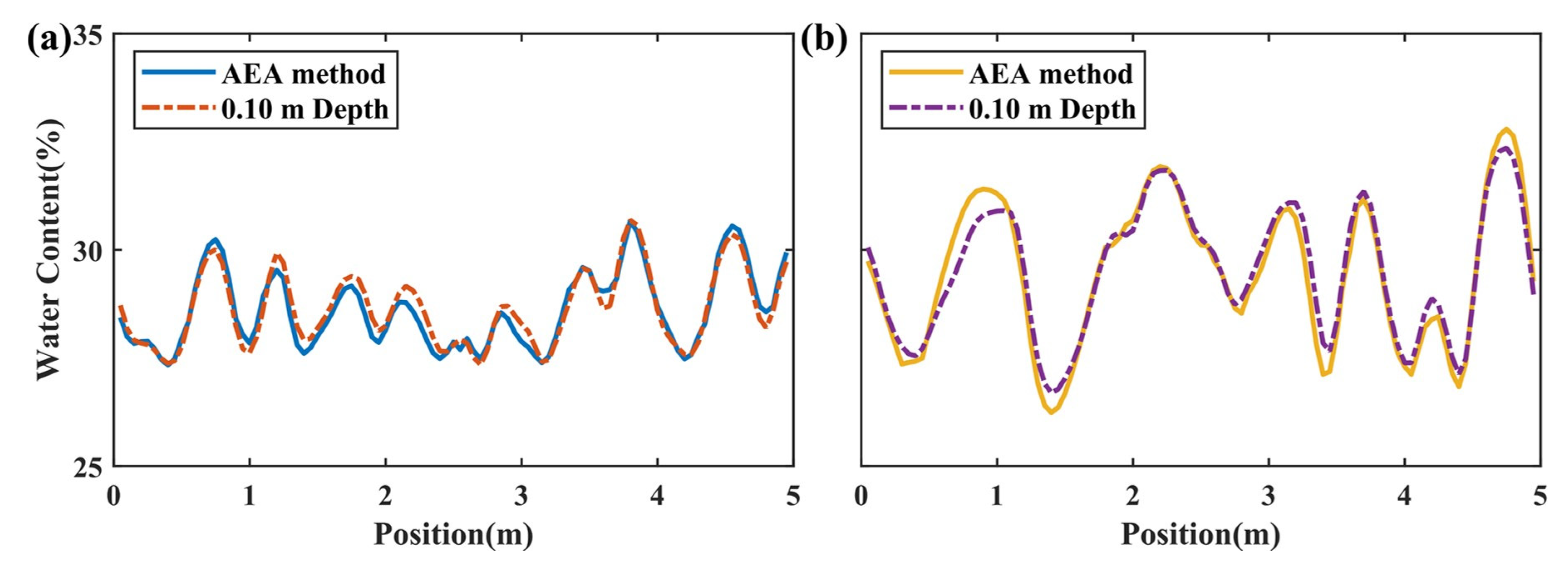
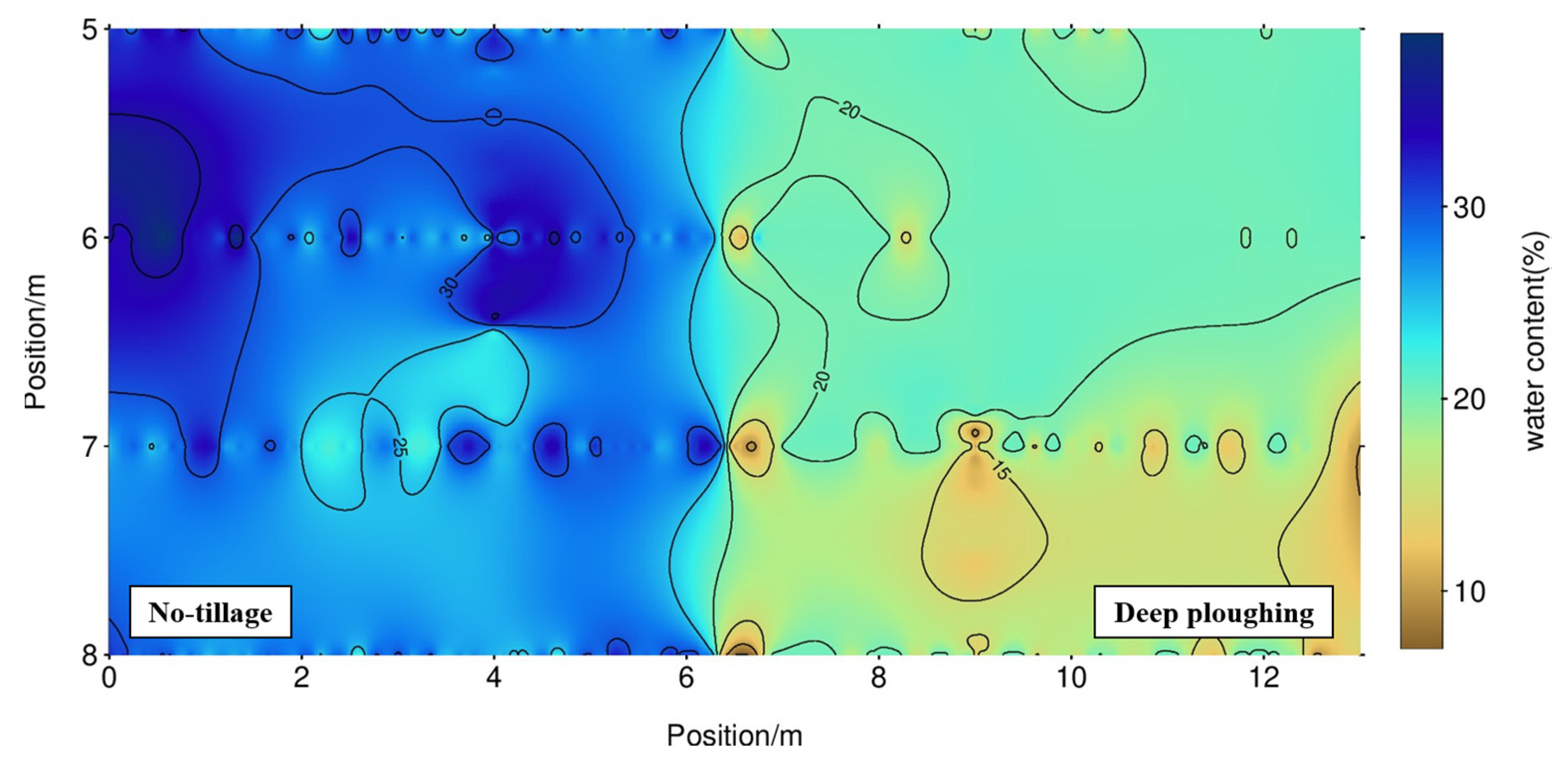
3.2.5. Estimation of SWC
4. Discussion
5. Conclusions
- (1)
- The combination of the stochastic medium modeling of GPR with the geostatistics method is useful to describe the heterogeneity of the soil medium, which can help to analyze the usability of the AEA method in heterogeneous soil. The greater the heterogeneity of the soil, the greater the error in estimating water content using the AEA method of ETS. Therefore, the soil heterogeneity should be considered when using the AEA method for estimating SWC using GPR.
- (2)
- Dielectric permittivity has a greater impact on ETS. Conductivity affects the amplitude, while dielectric permittivity affects the amplitude and time. There is a good correlation between AEA−1 and dielectric permittivity within a depth range of 1/2 λ to λ (wavelength). Therefore, the AEA method can be used to estimate SWC within a depth of 1/2 λ to λ (wavelength).
- (3)
- The AEA method based on ETS was used to estimate the SWC for two different heterogeneous farmland soils. The estimated results were compared with the TDR-measured water content, and the difference in water content was within 3%. The estimated results were compared the water content values obtained by the thermo-gravimetric method, and the difference in water content was within 3%. Although heterogeneity can increase the error value in estimating SWC using the AEA method, this error is acceptable. Therefore, the AEA method can be used for soils with moderate heterogeneity.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vereecken, H.; Huisman, J.; Bogena, H.; Vanderborght, J.; Vrugt, J.; Hopmans, J. On the value of soil moisture measurements in vadose zone hydrology: A review. Water Resour. Res. 2008, 44, 4. [Google Scholar] [CrossRef]
- Robinson, D.A.; Campbell, C.S.; Hopmans, J.W.; Hornbuckle, B.K.; Jones, S.B.; Knight, R.; Ogden, F.; Selker, J.; Wendroth, O. Soil moisture measurement for ecological and hydrological watershed-scale observatories: A review. Vadose Zone J. 2008, 7, 358–389. [Google Scholar] [CrossRef]
- SU, S.L.; Singh, D.N.; Baghini, M.S. A critical review of soil moisture measurement. Measurement 2014, 54, 92–105. [Google Scholar] [CrossRef]
- Peng, J.; Loew, A.; Merlin, O.; Verhoest, N.E. A review of spatial downscaling of satellite remotely sensed soil moisture. Rev. Geophys. 2017, 55, 341–366. [Google Scholar] [CrossRef]
- Wang, L.; Qu, J.J. Satellite remote sensing applications for surface soil moisture monitoring: A review. Front. Earth Sci. China 2009, 3, 237–247. [Google Scholar] [CrossRef]
- Huisman, J.A.; Hubbard, S.S.; Redman, J.D.; Annan, A.P. Measuring soil water content with ground penetrating radar: A review. Vadose Zone J. 2003, 2, 476–491. [Google Scholar] [CrossRef]
- Weihermüller, L.; Huisman, J.; Lambot, S.; Herbst, M.; Vereecken, H. Mapping the spatial variation of soil water content at the field scale with different ground penetrating radar techniques. J. Hydrol. 2007, 340, 205–216. [Google Scholar] [CrossRef]
- Bian, Z.; Lei, S.; Inyang, H.I.; Chang, L.; Zhang, R.; Zhou, C.; He, X. Integrated method of RS and GPR for monitoring the changes in the soil moisture and groundwater environment due to underground coal mining. Environ. Geol. 2009, 57, 131–142. [Google Scholar] [CrossRef]
- Weiler, K.W.; Steenhuis, T.S.; Boll, J.; Kung, K.J.S. Comparison of Ground Penetrating Radar and Time-Domain Reflectometry as Soil Water Sensors. Soil Sci. Soc. Am. J. 1998, 62, 1237–1239. [Google Scholar] [CrossRef]
- Turesson, A. Water content and porosity estimated from ground-penetrating radar and resistivity. J. Appl. Geophys. 2006, 58, 99–111. [Google Scholar] [CrossRef]
- Huisman, J.; Sperl, C.; Bouten, W.; Verstraten, J. Soil water content measurements at different scales: Accuracy of time domain reflectometry and ground-penetrating radar. J. Hydrol. 2001, 245, 48–58. [Google Scholar] [CrossRef]
- Grote, K.; Hubbard, S.; Rubin, Y. Field-scale estimation of volumetric water content using ground-penetrating radar ground wave techniques. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Serbin, G.; Or, D. Near-surface soil water content measurements using horn antenna radar: Methodology and overview. Vadose Zone J. 2003, 2, 500–510. [Google Scholar] [CrossRef]
- Pettinelli, E.; Vannaroni, G.; Di Pasquo, B.; Mattei, E.; Di Matteo, A.; De Santis, A.; Annan, P.A. Correlation between near-surface electromagnetic soil parameters and early-time GPR signals: An experimental study. Geophysics 2007, 72, A25–A28. [Google Scholar] [CrossRef]
- Di Matteo, A.; Pettinelli, E.; Slob, E. Early-time GPR signal attributes to estimate soil dielectric permittivity: A theoretical study. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1643–1654. [Google Scholar] [CrossRef]
- Ferrara, C.; Barone, P.; Steelman, C.; Pettinelli, E.; Endres, A. Monitoring shallow soil water content under natural field conditions using the early-time GPR signal technique. Vadose Zone J. 2013, 12, 1–9. [Google Scholar] [CrossRef]
- Pettinelli, E.; Di Matteo, A.; Beaubien, S.E.; Mattei, E.; Lauro, S.E.; Galli, A.; Vannaroni, G. A controlled experiment to investigate the correlation between early-time signal attributes of ground-coupled radar and soil dielectric properties. J. Appl. Geophys. 2014, 101, 68–76. [Google Scholar] [CrossRef]
- Algeo, J.; Van Dam, R.L.; Slater, L. Early-Time GPR: A method to monitor spatial variations in soil water content during irrigation in clay soils. Vadose Zone J. 2016, 15, 1–9. [Google Scholar] [CrossRef]
- Comite, D.; Galli, A.; Lauro, S.E.; Mattei, E.; Pettinelli, E. Analysis of GPR early-time signal features for the evaluation of soil permittivity through numerical and experimental surveys. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 9, 178–187. [Google Scholar] [CrossRef]
- Takahashi, K.; Igel, J.; Preetz, H.; Sato, M. Sensitivity analysis of soil heterogeneity for ground-penetrating radar measurements by means of a simple modeling. Radio Sci. 2015, 50, 79–86. [Google Scholar] [CrossRef]
- Deutsch, C.V.; Wang, L. Hierarchical object-based stochastic modeling of fluvial reservoirs. Math. Geol. 1996, 28, 857–880. [Google Scholar] [CrossRef]
- Ikelle, L.; Yung, S.; Daube, F. 2-D random media with ellipsoidal autocorrelation functions. Geophysics 1993, 58, 1359–1372. [Google Scholar] [CrossRef]
- Zhu, P.; Fung, A.; Wong, K. Effective propagation constants in dense random media under effective medium approximation. Radio Sci. 1987, 22, 234–250. [Google Scholar] [CrossRef]
- Jiang, Z.; Zeng, Z.; Li, J.; Liu, F.; Li, W. Simulation and analysis of GPR signal based on stochastic media model with an ellipsoidal autocorrelation function. J. Appl. Geophys. 2013, 99, 91–97. [Google Scholar] [CrossRef]
- Zhang, L.; Xu, Y.; Zeng, Z.; Li, J.; Zhang, D. Simulation of Martian near-surface structure and imaging of future GPR data from Mars. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–12. [Google Scholar] [CrossRef]
- Topp, G.C.; Davis, J.; Annan, A.P. Electromagnetic determination of soil water content: Measurements in coaxial transmission lines. Water Resour. Res. 1980, 16, 574–582. [Google Scholar] [CrossRef]
- Noborio, K.; McInnes, K.; Heilman, J. Field measurements of soil electrical conductivity and water content by time-domain reflectometry. Comput. Electron. Agric. 1994, 11, 131–142. [Google Scholar] [CrossRef]
- Rhoades, J.; Raats, P.; Prather, R. Effects of liquid-phase electrical conductivity, water content, and surface conductivity on bulk soil electrical conductivity. Soil Sci. Soc. Am. J. 1976, 40, 651–655. [Google Scholar] [CrossRef]
- Deutsch, C.V.; Journel, A.G. Geostatistical Software Library and User’s Guide; Oxford University Press: Oxford, UK, 1992; Volume 8. [Google Scholar]
- Rea, J.; Knight, R. Geostatistical analysis of ground-penetrating radar data: A means of describing spatial variation in the subsurface. Water Resour. Res. 1998, 34, 329–339. [Google Scholar] [CrossRef]
- McBratney, A.; Webster, R. Choosing functions for semi-variograms of soil properties and fitting them to sampling estimates. J. Soil Sci. 1986, 37, 617–639. [Google Scholar] [CrossRef]
- Goovaerts, P. Geostatistics for Natural Resources Evaluation; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Irving, J.; Knight, R. Numerical modeling of ground-penetrating radar in 2-D using MATLAB. Comput. Geosci. 2006, 32, 1247–1258. [Google Scholar] [CrossRef]
- Zhou, H.; Li, B.; Lu, Y. Micromorphological analysis of soil structure under no tillage management in the black soil zone of Northeast China. J. Mt. Sci. 2009, 6, 173–180. [Google Scholar] [CrossRef]


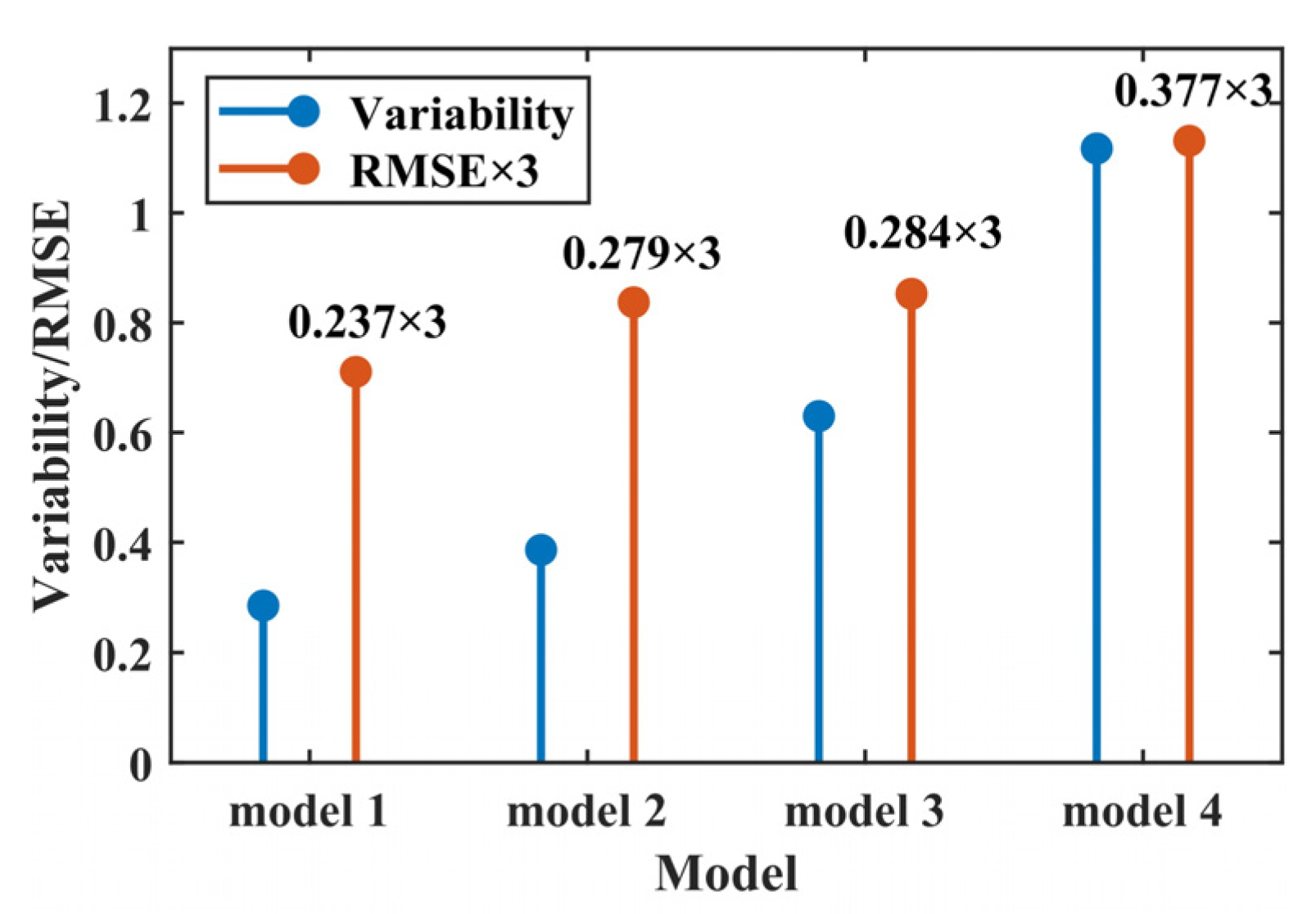

| Depth (m) | Model 1 | Model 2 | Model 3 | Model 4 | ||||
|---|---|---|---|---|---|---|---|---|
| r | RN | r | RN | r | RN | r | RN | |
| 0.08 | 0.98 | 0.90 | 0.98 | 0.89 | 0.99 | 0.90 | 0.99 | 0.93 |
| 0.12 | 0.06 | 0.13 | 0.07 | 0.18 | 0.07 | 0.18 | 0.08 | 0.20 |
| 0.16 | 0.94 | 0.85 | 0.95 | 0.82 | 0.96 | 0.82 | 0.96 | 0.88 |
| 0.20 | 0.10 | 0.15 | 0.12 | 0.23 | 0.12 | 0.24 | 0.14 | 0.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Q.; Liu, K.; Zeng, Z.; Liu, S.; Li, R.; Xia, L.; Guo, S.; Li, Z. Estimation of the Soil Water Content Using the Early Time Signal of Ground-Penetrating Radar in Heterogeneous Soil. Remote Sens. 2023, 15, 3026. https://doi.org/10.3390/rs15123026
Lu Q, Liu K, Zeng Z, Liu S, Li R, Xia L, Guo S, Li Z. Estimation of the Soil Water Content Using the Early Time Signal of Ground-Penetrating Radar in Heterogeneous Soil. Remote Sensing. 2023; 15(12):3026. https://doi.org/10.3390/rs15123026
Chicago/Turabian StyleLu, Qi, Kexin Liu, Zhaofa Zeng, Sixin Liu, Risheng Li, Longfei Xia, Shilong Guo, and Zhilian Li. 2023. "Estimation of the Soil Water Content Using the Early Time Signal of Ground-Penetrating Radar in Heterogeneous Soil" Remote Sensing 15, no. 12: 3026. https://doi.org/10.3390/rs15123026
APA StyleLu, Q., Liu, K., Zeng, Z., Liu, S., Li, R., Xia, L., Guo, S., & Li, Z. (2023). Estimation of the Soil Water Content Using the Early Time Signal of Ground-Penetrating Radar in Heterogeneous Soil. Remote Sensing, 15(12), 3026. https://doi.org/10.3390/rs15123026









