1. Introduction
Accurate localization within indoor environments is considered a crucial component of intelligent urban infrastructure. Due to the intricate and multifaceted nature of indoor spaces, it is imperative to develop autonomous and cost-effective indoor positioning services. A variety of existing indoor positioning systems (IPSs), including Wireless Fidelity (Wi-Fi) [
1], Bluetooth Low Energy (BLE) [
2], ultra-wideband (UWB) [
3], sound source [
4], and integrated sensors [
5], have been developed to provide indoor positioning with varying degrees of precision. However, further advancements are necessary to ensure optimal performance in complex indoor environments, which are typical of modern smart cities. Among IPSs, at this stage, the existing positioning systems mostly rely on local facilities or wireless signals, and meter-level localization precision can be achieved with a combination of external signals and smartphone-integrated sensors, which is labor-consuming and high cost. A comparison between existing IPSs is shown in
Table 1.
The autonomous localization system (ALS) is advanced by its autonomy characteristics because no additional facilities or pre-collected fingerprinting database are required in the positioning phase, and the efficacy of the ALS is hindered by the imprecise nature of the trajectory data obtained from smartphones. This inaccuracy may be attributed to the varied ways in which users hold their devices [
14], and the accumulation of errors within the sensors integrated into mobile terminals [
15]. As a result, the accuracy of the ALS could be significantly improved through the development of more precise trajectory data collection methods and optimization of the sensor technology in mobile devices. The existing problems include complex human motion modes [
16] and a lack of an efficient combination of built-in sensor-based location sources and an existing indoor map or pedestrian network information [
17], which are the main factors that affect the accuracy of ALS.
Numerous research studies have been conducted to address the aforementioned issues. For instance, Yan et al. [
18] proposed a robust smartphone-based RIDI system that estimates walking speed and localization information accurately, even with varying handheld positions. Their approach yielded more efficient and similar accuracy than the traditional visual inertial odometry (VIO) method. Additionally, they developed the RoNIN network to enhance the precision and stability of inertial odometry using a new dataset comprising more than 40 h of data from smartphone-integrated sensors under complex pedestrian motion modes [
19]. Guo et al. [
20] proposed a machine learning-based classification approach to estimate walking speed under complex pedestrian motion modes by incorporating a handheld mode awareness strategy. Various mobile data were collected, and model training processes were conducted to evaluate the accuracy of the proposed speed estimator. Similarly, Zhang et al. [
21] developed the SmartMTra framework, which leverages feature extraction and motion detection techniques, along with handheld mode classification, to achieve robust dead reckoning performance. Furthermore, Poulose et al. [
22] comprehensively evaluated the heading calculation precision using different multi-sensor fusion algorithms—namely the Kalman filter (KF), extended Kalman filter (EKF), unscented Kalman filter (UKF), particle filter (PF), and complementary filters (CF). Their evaluation results demonstrated that the UKF realized much better heading estimation accuracy, while PF showed the lowest accuracy, which is not suitable for heading calculation. These studies have highlighted the importance of developing robust and accurate solutions for indoor positioning and tracking in complex urban environments.
Indoor mapping information is essential for generating and updating crowdsourced databases with high accuracy. To improve map-matching precision while reducing calculation complexity, Wu et al. [
23] proposed the HTrack system, which takes into account pedestrian heading and geospatial data. Xia et al. [
24] combined the pedestrian dead reckoning model with BLE-based distance measurement and map constraints. The particle filter was applied to enhance localization robustness and precision, resulting in an RMSE of 1.48 m. Li et al. [
25] introduced a fingerprinting precision-level predictor that can autonomously evaluate the performance of Wi-Fi- and magnetic field-provided locations based on wireless indexes, map information, and database-related characteristics. This approach significantly increases the precision of integrated positioning based on the crowd-sensing trajectories. The importance of accurate and efficient indoor mapping approaches has been demonstrated by these studies, as they are critical for achieving reliable indoor tracking and positioning.
Detecting the correct floor level is crucial for enhancing the effectiveness and accuracy of classifying trajectory data collected through crowd-sourcing, as well as for generating comprehensive databases. In a study by Zhao et al. [
26], they proposed an HYFI system that estimates the initial floor level based on the distribution of local wireless access points (APs). To minimize the effects of environmental factors, the system also integrated pressure information into its approach. The authors reported an accuracy rate exceeding 96.1% when compared to using only a single source. Similarly, Shao et al. [
27] introduced an adaptive algorithm for detecting floors using wireless technology, which is especially suitable for large-scale indoor areas with multiple floors. Their method involves analyzing the Wi-Fi radio signal strength indicator (RSSI) and spatial similarity features and segmenting local environments using block models, and achieved an average accuracy rate of 97.24%. These studies have demonstrated the importance of developing robust and accurate floor detection approaches to ensure reliable indoor tracking and positioning in complex indoor environments. Thus, it is crucial to continue the research on improving floor detection algorithms to enhance the overall performance of indoor positioning systems.
The classical smartphone-based indoor mapping and trajectory optimization structures include Walkie-Markie [
28], PiLoc [
29], and MPiLoc [
30], among others. In Walkie-Markie, the indoor pathway is generated using the basis of the detection of Wi-Fi AP-based landmarks and trajectory matching. The limitation is that the collected RSSI value is subjected to changeable indoor environments and the absolute location of the generated pathway cannot be acquired. PiLoc classifies similar crowdsourced trajectories by their shapes and the similarity of collected Wi-Fi RSSI information and merges the similar trajectories using point-to-point fusion. MPiLoc further extends the floor plan from 2D to 3D and uses the sparsely acquired GNSS-reported locations as the absolute points. The disadvantage is that both PiLoc and MPiLoc rely on the accurate estimation of heading information, while the precise absolute heading may not be available all the time. Li et al. [
31] presented the IndoorWaze system, using the crowdsourced Wi-Fi fingerprinting data and POI information collected by shopping mall employees to generate a robust and marked floor plan. The final experiments showed that the designed IndoorWaze framework can accurately mark the pathways and location of the store for indoor navigation purposes.
Integrated navigation technology has become more and more popular due to its improved robustness and precision compared to single-location sources in complex indoor environments. Several fusion methods, such as the Kalman filter (KF) [
32], extended Kalman filter (EKF) [
33], unscented Kalman filter (UKF) [
34], and particle filter (PF) [
35], are applied as the typical integration methods for multi-source fusion-based indoor localization. Huang et al. [
36] developed a cost-effective and user-convenient indoor localization technique that utilizes existing Li-Fi lighting and Wi-Fi infrastructure to achieve significantly improved positioning accuracy. Their technique involves Li-Fi-assisted coefficient calibration and was experimentally verified. Chen et al. [
37] developed an indoor dynamic positioning method that utilizes the symmetrical characteristics of human motion to quickly define the basis of the human motion process and address existing issues. They introduced an ultra-wideband (UWB) method and applied an unscented Kalman filter to fuse inertial sensors and UWB data. Inertial positioning compensated for UWB signal obstacles, while UWB positioning overcame the error accumulation of the inertial positioning. Chen et al. [
38] proposed an INS and Wi-Fi integration model that utilizes multi-dimensional dynamic time warping (MDTW) to calculate the distance between the measured signals and fingerprints in a database. They also introduced an MDTW-based weighted least squares (WLS) method for fusing multiple fingerprint localization results, resulting in improved positioning accuracy and robustness.
To further enhance the performance of smartphone-integrated sensor-based pedestrian trajectory estimation and optimization, and indoor network extraction and trajectory matching, this paper proposes an ML-ISNM framework, which realizes accurate multi-floor positioning performance without the assistance of local facilities. The main contributions of this work are summarized as follows:
- (1)
This paper proposes a robust data and model dual-driven pedestrian trajectory estimator for accurate integrated sensor-based positioning in complex motion modes and disturbed environments. The proposed approach considers factors such as handheld modes, lateral errors, and step-length constraints while updating the location based on a period of observations rather than solely relying on the last moment;
- (2)
A new floor detection algorithm based on Bi-LSTM is implemented to offer floor index references for estimated trajectories. This involves extracting hybrid features from wireless signals, human motion, and map-related data to improve the recognition precision, leading to a more accurate initial location and floor information provided to users;
- (3)
This work models an extracted pedestrian indoor network, formulates it as the combination of a matrix, and develops a grid search algorithm for network matching and further walking route calibration with the reference of the initial location and floor detection results. The matched network information is further applied as the observation under the fusion phase;
- (4)
Using the outcomes of trajectory estimation, floor recognition, and indoor network matching, an error ellipse-supported unscented Kalman filter (EE-UKF) is suggested to robustly combine data from integrated sensors, pedestrian motion, and indoor network information. This approach can achieve meter-level positioning accuracy without requiring additional local facilities for assistance.
The following content is outlined in the sections of this article.
Section 2 provides an overview of the trajectory estimator based on a data and model dual-driven approach.
Section 3 describes the developed Bi-LSTM-based floor recognition, trajectory matching, calibration, and error ellipse-supported UKF-based intelligent integration.
Section 4 discusses the evaluation results of the developed ML-ISNM. Finally,
Section 5 presents a conclusion of this work.
2. Data and Model Dual-Driven Trajectory Estimator
This research introduces an ML-ISNM framework, which combines trajectory estimation, multi-level observations, and indoor network information to enable the autonomous detection of the user’s location and floors without requiring local facilities, while also facilitating accurate multi-source fusion. The proposed trajectory estimator integrates sensor data from tri-gyroscopes, tri-accelerometers, tri-magnetometers, and barometers to obtain the raw 3D location, speed, and attitude vectors. Next, Bi-LSTM-based floor detection and pedestrian indoor network matching are applied to provide an accurate initial reference location and floor indexes for the proposed trajectory estimator. In addition, non-holonomic constraints, a quasi-static magnetic field, and an indoor network reference are generated as the multi-level observations and combined with the trajectory estimator by an enhanced EE-UKF, and the forward trajectory is further calibrated by the backward EE-UKF after obtaining the network’s extracted landmark points. The overall structure of the developed ML-ISNM framework is described in
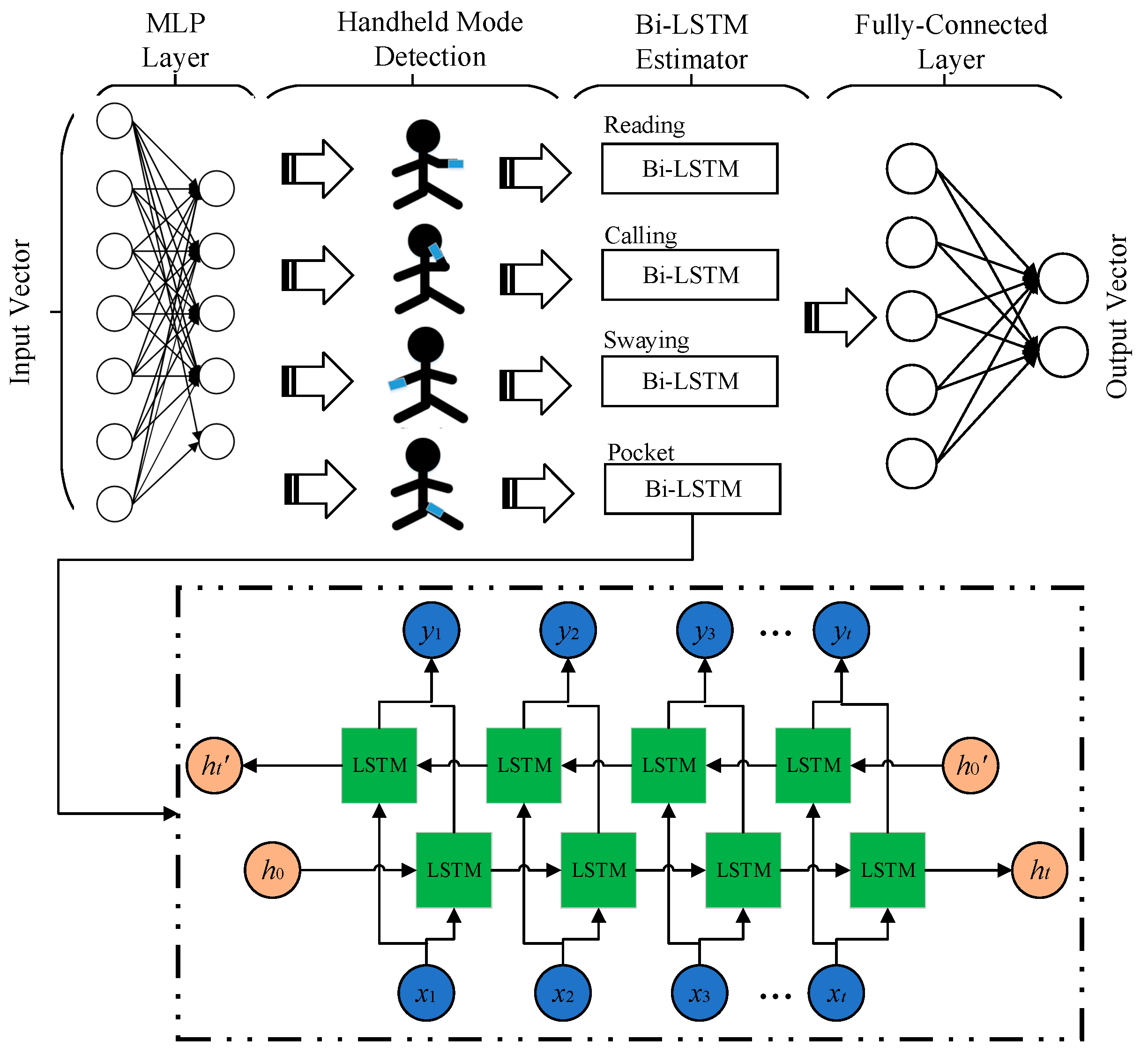
Figure 1. This part presents an accurate data and model dual-driven trajectory estimator under complex handheld modes and disturbed indoor environments, and the estimated trajectory information is further integrated with other observations in order to realize much more accurate and robust positioning performance.
2.1. Hybrid Deep-Learning Model Enhanced Walking Speed Prediction
When it comes to achieving inertial odometry for mobile devices that depend on indoor pedestrian localization, INS and PDR mechanisms are viewed as viable solutions. However, conventional approaches using INS/PDR have limited precision because of the varied handheld modes of these devices and accumulated errors in their inertial sensors. Furthermore, relying solely on the previous moment for location updates through these methods may result in missing crucial motion information during the chosen walking period.
To address these limitations, this work proposes a novel data and model dual-driven trajectory estimation approach that leverages advanced machine learning techniques to enhance the accuracy and robustness of inertial odometry. This approach considers factors such as handheld positioning, lateral error, and step-length constraints while updating the location based on a period of observations rather than solely relying on the last moment. By incorporating these techniques into INS/PDR-based systems, the resulting inertial odometry is significantly more accurate and reliable, making them ideal for deployment in complex indoor environments.
This research addresses the limitations of the existing dead reckoning (DR) methods by proposing an enhanced deep learning-based walking velocity estimator. The aim was to realize precise speed observation for PDR mechanization, taking into account the varied handheld modes of mobile terminals and overcoming cumulative errors that can limit accuracy. To detect the different handheld modes of existing smartphones, this approach leverages MLP models that consider period-specific acceleration vectors, the angular speed vector, and related modeled characteristics. Additionally, the Bi-LSTM structure is used to predict pedestrians’ continuous walking speed using similar inputs.
Figure 2 depicts the whole framework of the developed deep-learning-based approach for walking velocity prediction. By utilizing these advanced machine learning techniques, the resulting PDR mechanism achieves significantly higher accuracy and robustness in indoor tracking and positioning, which makes it ideal for deployment in challenging indoor environments where signal interference and other environmental factors can pose significant challenges.
The above diagram depicts the structure of the proposed walking speed estimator, which relies on deep learning. The model comprises several components, with the MLP serving as the initial element to detect handheld modes. The detected modes and generated features are then input into the Bi-LSTM model, which provides precise estimates of pedestrian walking speed-originated features. Lastly, a fully-connected layer is utilized for final-result modeling to deliver real-time estimations of pedestrian moving velocity information. By integrating these advanced machine learning techniques into the design of the PDR mechanism, the resulting system achieves higher accuracy and robustness in indoor tracking and positioning. This can substantially improve the user experience, particularly in complex indoor environments where traditional dead reckoning methods can result in significant inaccuracies due to cumulative errors and signal interference.
To correspondingly estimate walking speed and detect handheld modes, the accelerometer and gyroscope’s smoothed data are employed as input features in the MLP. The detected handheld modes derived from these features are then utilized to train a Bi-LSTM framework that can predict walking velocity information under different handheld modes. For increasing the speed estimation precision, an input vector of 3 s in overall length is chosen from a dataset sampled at a rate of 50 Hz. These enhanced input features can then be used to generate more precise estimates of walking speed while also detecting handheld modes with greater accuracy.
Finally, the MLP network
MLP() is applied as the first layer of the developed deep-learning model, the raw sensor data are extracted as the input vector of MLP, and the four different handheld modes are adopted as the output vector of the MLP network [
39]:
where
indicates the output vector of the MLP, which contains four different handheld modes of smartphones, and
is the input vector of the sensor data.
Next is the Bi-LSTM layer. The input vector of the Bi-LSTM model is the pre-processed sensor data and the detected handheld mode of the smartphones. The relationships among the different Bi-LSTM parameters are presented as follows [
40]:
In the following equation , , and denote the input, forget, and output units of the Bi-LSTM network, respectively. represents the input vector of the Bi-LSTM layer under each time period, and denotes the hidden state vector, which is considered the output of the Bi-LSTM layer and is further applied as the input of the full connection layer. The sigmoid function is denoted by , while is the candidate vector that is merged with the output vector to form the memorized state under the recorded time.
In our deep learning-based speed estimator framework, we utilize walking velocity as the expected output vector of the model training procedure. It is important to note that the initial predicted walking speed lacks real-world geospatial reference and can only be considered as the forward velocity. This forward speed is defined as follows:
where
is presented according to the step-length calculation result.
To obtain the pedestrian’s forward speed, it is necessary to transform the estimated walking speed according to the results obtained from handheld mode detection. The calculation for obtaining the forward velocity under the n-frame follows the formula outlined in [
7]. This step ensures that the final output accurately reflects the pedestrian’s true forward speed and takes into account any identified variations in handheld modes during the data collection:
In the above equation, represents the NHC-based speed that has been converted. The attitude matrix calculated between the b-frame and the ENU frame is denoted by . The translation matrix related to handheld modes, denoted by , converts the axis related to heading into the reading mode-based heading-related axis in accordance with the results of the handheld mode recognition. Finally, the translation matrix from the ENU coordinate system to the NED coordinate system is indicated by .
The estimated location of the pedestrian can be determined by combining both the heading and walking velocity values in a time period.
In the above equation, represents the walking velocity value provided in a recognized step period and needs to be converted into the n-frame. The real-world position is then calculated according to the formal location information.
2.2. Data and Model Dual-Driven Trajectory Estimator
INS mechanization is proposed for inertial sensor-based localization. The information of the acceleration and angular rate acquired from MEMS sensors are integrated by INS mechanization for the estimation of the 3D position, velocity, and attitude of the moving object with a high update rate, which is shown below [
5]:
In the following equation, denotes the real-time 3D location of the pedestrian. The 3D velocity is represented by , while indicates the rotation matrix of the b-frame and n-frame. represents the collected local gravity vector, and denotes the rotation angular rate between the ECEF frame and i-frame. Additionally, indicates the rotation angular rate between the navigation coordinate system and the ECEF coordinate system. A 3 × 3 matrix related to the latitude and the ellipsoidal altitude of the selected object is denoted by .
Due to the low precision of MEMS sensors, the Earth-related angular rate error vectors,
and
, can be ignored. Hence, the simplified error model of INS can be described as follows [
5]:
In the following equation, , , and denote the measured errors of the 3D position, velocity, and attitude information, respectively. and represent the biases of the gyroscope and accelerometer, respectively. indicates the converted acceleration data in the n-frame, while and represent the parameters related to sensor noise. Additionally, and are the measured noises of and , respectively.
Using the INS error model presented above, the state vector can be described in the AUKF as follows:
The discrete-time EE-UKF system equation and observation equation are:
where
and
represent the state vector and observed vector at the moment
t;
indicates the observation matrix at the moment
t.
and
indicate the state noise and measurement noise at the timestamp
t;
indicates the
state transition matrix, which is shown below:
In the above equation, represents the update interval of the INS mechanization, while represents the collected accelerometer vector under the n-frame.
To address the influence of the indoor artificial magnetic fields added to the accuracy of the heading calculation, a pseudo-observation is extracted to constrain the heading divergence error. This observation is obtained by calculating the heading deviation from the straightforward motion mode during the quasi-static magnetic field (QSMF) periods [
5]. Incorporating this observation helps to reduce any interference caused by indoor magnetic fields and improves the overall precision of the heading estimation.
In the above equation, and denote the heading observation extracted from the detected QSMF period data for the first epoch and other epochs, respectively. represents the measurement noise.
The observation model for the calculated walking speed under the n-frame in the deep learning model is modeled as follows:
In the following equation,
represents the INS mechanization-provided walking velocity, while
denotes the results of deep learning-based velocity prediction. The observation model for position increment is expressed as follows:
In the above equation, denotes the position cumulated by INS mechanization, while denotes the results of the location update based on the deep learning model.
3. Floor Detection, Network Matching, and Intelligent Fusion
To enhance the efficiency and precision of indoor network information extraction and intelligent integration, a deep-learning approach was developed. This framework aims to achieve autonomous floor recognition, indoor network matching, and calibration, as well as the EE-UKF-based integration of indoor network and MEMS sensors.
3.1. Bi-LSTM-Enhanced Floor Recognition
To utilize useful observations obtained from daily-life trajectory data and local indoor environments, a time-continuous approach for detecting floors is proposed in this work. This method employs a Bi-LSTM network that considers a period of trajectory data to enhance the precision of floor recognition. The input vector for the Bi-LSTM network is constructed by combining features from Wi-Fi, barometer, and magnetic sources:
- (1)
To capture the wireless features of the selected floor, the modeled RSSI values obtained from some representative Wi-Fi access points (APs) are utilized as a part of the input vector in the training procedure of the Bi-LSTM model. These collected RSSI values are deemed to be the most representative and are critical for ensuring accurate predictions:
In the following description, represents the collected RSSI vector of a selected Wi-Fi access point, while denotes the set standard for RSSI filtering.
- (2)
The mean RSSI value of the selected representative RSSI values: In order to capture the overall description index of the RSSI collection, the mean RSSI value is also computed and included as an input value for the developed Bi-LSTM model. This additional input helps to provide a more comprehensive understanding of the RSSI vector, enabling the model to make more accurate predictions based on both individual signal strengths and the overall average signal strength:
In the above description, denotes the calculated mean RSSI value.
- (3)
Deviation between the collected representative RSSI values: The calculated deviation in the scanned RSSI vector can significantly capture the dynamic changes in the surrounding buildings and is therefore considered a crucial feature. By utilizing this feature, the proposed model can better adapt to variations in the environment and provide more accurate estimations as a result. Incorporating real-time differences between the scanned RSSI vectors enhances the model’s ability to detect subtle changes in the signal strength over time, allowing it to generate more reliable predictions:
where
represents the RSSI deviation vector.
- (4)
The norm vector of the extracted local magnetic data is calculated as follows:
where
,
, and
represent the magnetometer outputted data.
- (5)
The barometric pressure increment values based on the initial data are calculated as follows:
where
indicates the pressure increment compared to the initial data, and
and
are the real-world acquired pressure values.
- (6)
The deviation between the adjacent collected pressure data is calculated as follows:
where
and
represent the pressure outputs obtained at two consecutive timestamps, and their variation can indicate changes in the elevation during a pedestrian’s movement. This information is crucial for indoor positioning systems that estimate the user’s vertical displacement and determine their current floor level, with applications in wayfinding, asset tracking, and environmental monitoring.
3.2. Indoor Network Matching and Trajectory Calibration
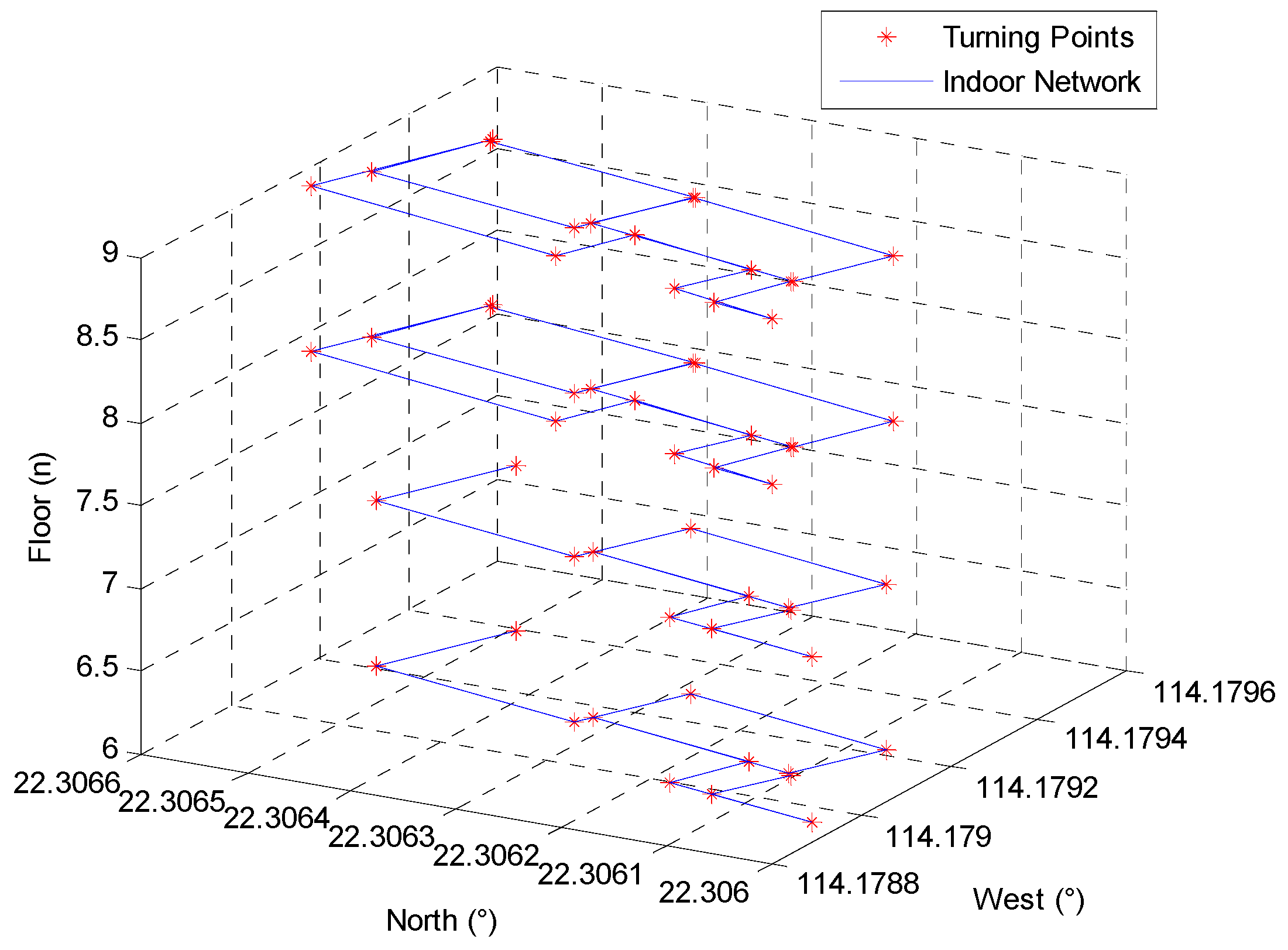
Pedestrian network information extracted from an indoor map can provide effective location references in the procedure of pedestrian walking. The principle of indoor network matching is to find the optimal reference point in the network to provide accurate location observation to the data and model dual-driven trajectory estimator, which can effectively reduce the cumulative error of the integrated sensor-based positioning approach. Compared to the traditional map-matching approach, network matching can significantly reduce the calculation complexity and provide effective location references. This research focuses on the representation of indoor pedestrian networks from multiple floors in the form of matrices. The network is extracted by marking intersection points as matrix elements, with each element containing information on the heading and the length between two intersections. This approach allows for an accurate depiction of the entire indoor network, enabling efficient navigation and localization. Moreover, this method enables the creation of a corresponding network matrix, which provides a clear visual representation of the indoor network’s topology and facilitates further analysis.
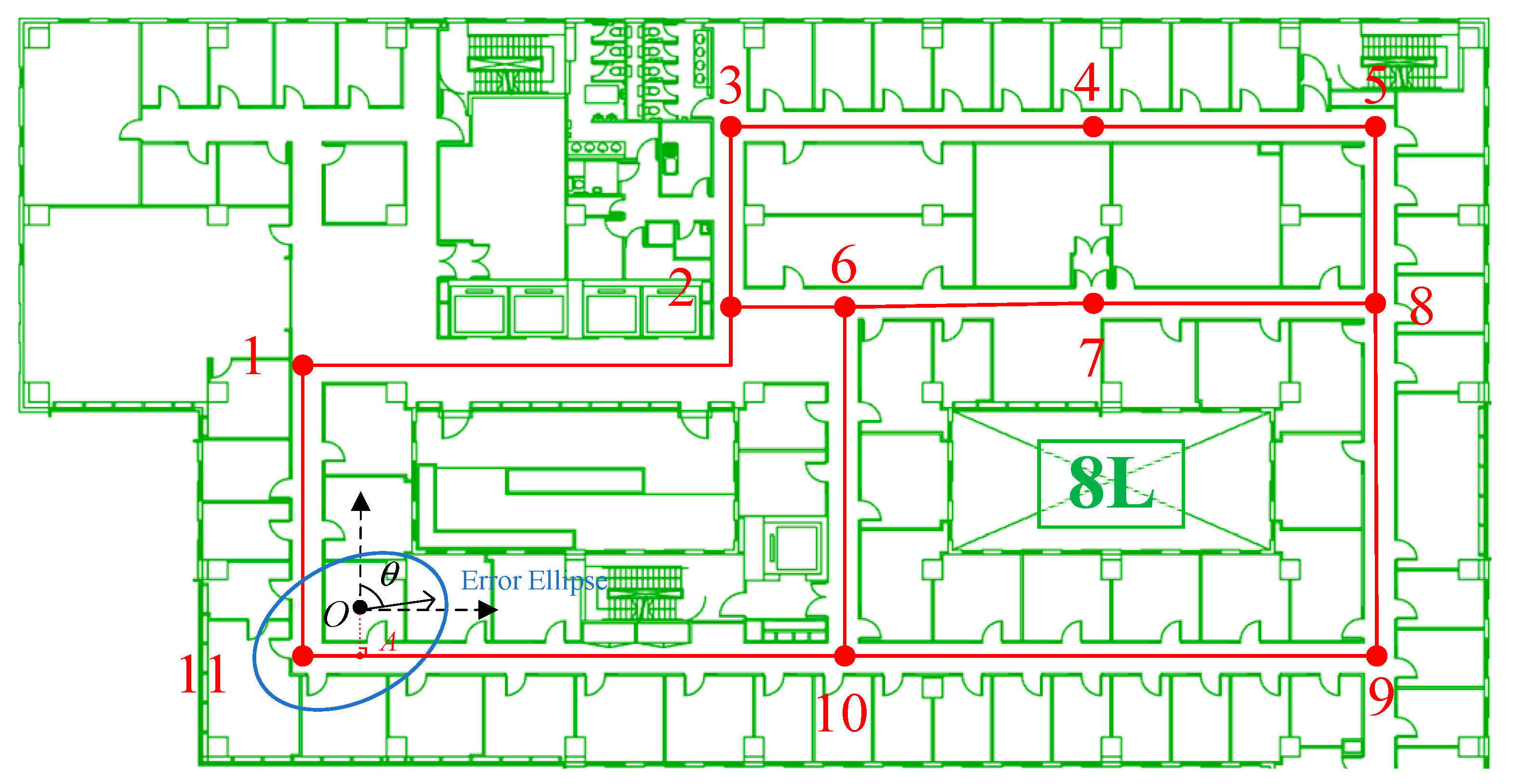
Figure 3 presents a detailed illustration of the extracted indoor network and its corresponding matrix, highlighting the usefulness of this representation method.
Figure 3 demonstrates the division of the indoor pedestrian network into a combination of straight lines and turning points. Each straight line is characterized by two features: heading and gait length, which serve as the feature-matching parameters for comparing with the results provided by the deep-learning-based trajectory estimator. By utilizing the described approach, we can accurately estimate the user’s position in the indoor environment and determine their trajectory. In the network matrix generated from this representation, adjacent turning points are marked as 1, while non-adjacent turning points are identified as 0. This allows for an efficient and intuitive representation of the indoor network’s topology, which can facilitate path-planning and navigation tasks. Overall, this method provides a comprehensive and reliable solution for indoor localization and positioning, with potential applications in various fields such as logistics, security, and healthcare.
The above equation describes the relationship between each pair of turning points, which is divided as connected-1 and non-connected-0. The network matrix generated from the indoor pedestrian network extraction process has dimensions equivalent to the amount of turning points in the network. For each pair of adjacent turning points, the related characteristics are recorded, including the heading and gait length during a normal walking period. This information can be utilized for various applications, such as path planning, navigation, and localization. By representing the indoor environment as a matrix, we can efficiently capture and process data, facilitating real-time decision making and improving the user’s experience. The grid search algorithm is proposed for network matching and compares the extracted reference network information in Equation (20) and the real-time collected and divided trajectory. Overall, this approach offers a comprehensive and reliable solution for indoor positioning and navigation that can be applied in diverse settings from healthcare to logistics:
In which and denote the heading and distance between each pair of adjacent intersection points, calculated based on the user’s normal walking trajectory between the two turning points. This information is crucial for accurately representing the indoor pedestrian network and facilitating indoor positioning and navigation. By utilizing this approach, we can efficiently capture and process data, enabling real-time decision making and improving the user’s experience. Furthermore, this representation provides a comprehensive solution for various applications, such as asset tracking, security, and emergency response. Overall, this method offers a reliable and versatile approach for indoor localization and positioning.
In this study, a grid search algorithm was developed to perform trajectory matching and calibration of the estimated trajectory and the extracted network information from a constructed network matrix. By utilizing this approach, the model can effectively identify optimal matches between the two datasets, allowing for more accurate localization and tracking of pedestrians within indoor environments. By leveraging the insights gained from the constructed network matrix, the proposed approach can help to improve the overall accuracy of trajectory matching and calibration, making it a valuable tool for indoor navigation and location-based services. This method utilizes the information contained in the network matrix to accurately estimate the user’s position and trajectory in real-time. By implementing this technique, we can enhance the precision and reliability of IPSs, improving the user’s experience and facilitating various applications, such as asset tracking and emergency response. Overall, this approach offers a comprehensive and practical solution for indoor localization and navigation tasks:
- (1)
To detect turning points during pedestrian movement, a hybrid deep-learning framework is utilized to detect changeable handheld modes and determine the walking direction. This approach is particularly useful in complex environments where pedestrians may adopt various postures or holding positions. After identifying the forward direction, the turning points are calculated by peak recognition, similar to a step detection method proposed previously [
1]. By incorporating these techniques, we can accurately estimate the user’s position and trajectory in indoor environments, facilitating effective navigation and positioning tasks. Moreover, this approach can be applied in diverse settings, such as healthcare, logistics, and security, enhancing the overall performance of indoor positioning systems;
- (2)
To reduce the incidence of false matching, we exclusively considered the results provided by the trajectory estimator that contained more than three turning points, which can be further applied for network matching purposes. This algorithm was proven to significantly increase the precision of trajectory matching;
- (3)
To effectively match trajectories with the existing indoor network, the proposed approach employs both the correlation coefficient value and the dynamic time warping (DTW) index. These two techniques are used in tandem to provide a more comprehensive understanding of the similarities and differences between different trajectories, enabling the model to identify optimal matches with greater accuracy. By incorporating both the correlation coefficient index and the DTW index, the proposed approach can enhance the overall performance of trajectory matching, paving the way for more precise location-based services within indoor environments. These indices enable us to identify similar trajectories by analyzing the detected turning points in each trajectory [
14]. By employing this method, we can enhance the overall performance of indoor positioning systems, making them suitable for various applications such as logistics, security, and healthcare.
where
represents the cumulated distance covered between two turning points vectors, while
represents the Euclidean distance calculated by each pair of points within these distributions.
where
and
indicate the results of the correlation coefficient on the
x- and
y-axes, respectively.
- (4)
Following the map-matching phase, the matched turning points on the extracted pedestrian network are utilized as absolute references for the trajectory calibration phase of straight lines. This approach enables us to accurately estimate the user’s position and trajectory, improving the overall performance of indoor positioning systems. By incorporating this method, we can facilitate various applications, such as asset tracking, navigation, and emergency response. Overall, this technique achieves a robust and practical approach for indoor localization tasks:
where
and
indicate the state and measurement vectors presented in Equation (8).
3.3. Error Ellipse-Enhanced UKF for Intelligent Fusion
In this section, the error ellipse-enhanced unscented Kalman filter (EE-UKF) is used to integrate all of the results provided by the integrated sensors, pedestrian indoor network matching, and floor detection for achieving meter-level indoor localization precision. The error ellipse is generated based on the previous integration result of the indoor network observation and data and model dual-driven trajectory estimator.
First, the INS mechanization applied in the data and model dual-driven trajectory estimator is applied as the state equation of the final EE-UKF, described in Equation (6). Then, the deep-learning-based walking speed prediction results, multi-level human motion constraints, and reference location and floor information provided by the network matching and floor detection are adopted as the observations in order to decrease the cumulative error of the INS mechanization and maintain the positioning accuracy under complex human motion and handheld modes and in disturbed indoor environments.
Furthermore, the enhancement of the localization performance involves implementing constraints on the indoor grid and mapping. Initially, the algorithm identifies the closest pair of adjacent turning points of observation using the current location data acquired through the integration of the sensory inputs and indoor network information. The segment of the indoor network is then represented in the model as follows:
Hence, the current coordinates (
x1,
y1) can be utilized to compute the closest point of observation in the indoor network. Consequently, the resulting representation of the indoor network is defined as follows:
where
and
represent the indoor network-provided location and walking velocity values,
and
denote the trajectory estimator-provided location and velocity prediction results.
Lastly, with respect to the characterization of confidence ellipses in engineering [
41], the focal point of the error ellipse is designated as the origin of the major semi-axis of the ellipse, which can be expressed as follows:
The minor semi-axis of the error ellipse is calculated as:
The azimuth of the major semi-axis of the error ellipse is described as:
Following the error ellipse-assisted network constraint check, eligible observations will be automatically incorporated into the UKF (unscented Kalman Filter) update procedure. This step helps to improve the overall accuracy of the filter by allowing it to integrate new observations into its predictions with greater precision. By incorporating eligible observations after the error ellipse-assisted network constraint check, the proposed approach can help to minimize errors and improve the quality of location estimates within indoor environments.
4. Experimental Results of ML-ISNM
This section outlines a series of comprehensive experiments devised to assess the efficacy of ML-ISNM. To this end, one publicly available dataset and a multi-floor indoor environment representative of real-world scenarios were chosen as experimental sites. Google Pixel 3 and Google Pixel 4 were applied as the experimental terminals, and Samsung Galaxy A7 was adopted for data collection in a public dataset. The proposed techniques, including trajectory estimator Bi-LSTM-based floor recognition, network matching, calibration, and EE-UKF, were tested and compared with state-of-art approaches or frameworks.
In configuring the model setting, the Adam optimizer was utilized due to its efficiency in handling large amounts of training data. Specifically, the learning rate was set at 0.002 for optimal performance. Additionally, the deep-learning-based speed estimator module employed an input vector dimension of 11, consistent with that of the integrated sensor data. The output hidden state from the Bi-LSTM layer was set at a dimension of 30, while the dimension of the input vector remained at 11. These settings were carefully selected to ensure optimal performance in the subsequent evaluations.
For the model training of the proposed data and model dual-driven trajectory estimator, a daily-life dataset containing a time period of more than 56 h of trajectory data provided by a number of 30 users under 4 different handheld modes (reading, phoning, swaying, and pocket) was collected with the reference of a Lidar-based positioning system (LPS) as the benchmark trajectory. For the accuracy evaluation, the trajectories estimated by the data and model dual-driven estimator were compared with the LPS for positioning error calculation, and then compared with the state-of-art algorithms based on the same test route and handheld modes. In our experiments, a public dataset was first applied to evaluate the long-term performance of the proposed trajectory estimator, and the existing state-of-the-art algorithms were also applied for the robustness and significance comparison of ML-ISNM. In addition, a real-world scene was further adopted for evaluation and comparison purposes.
4.1. Performance Evaluation of Trajectory Estimator
To assess the efficacy of the proposed data and model dual-driven trajectory estimator, a public dataset from the IPIN-2018 competition [
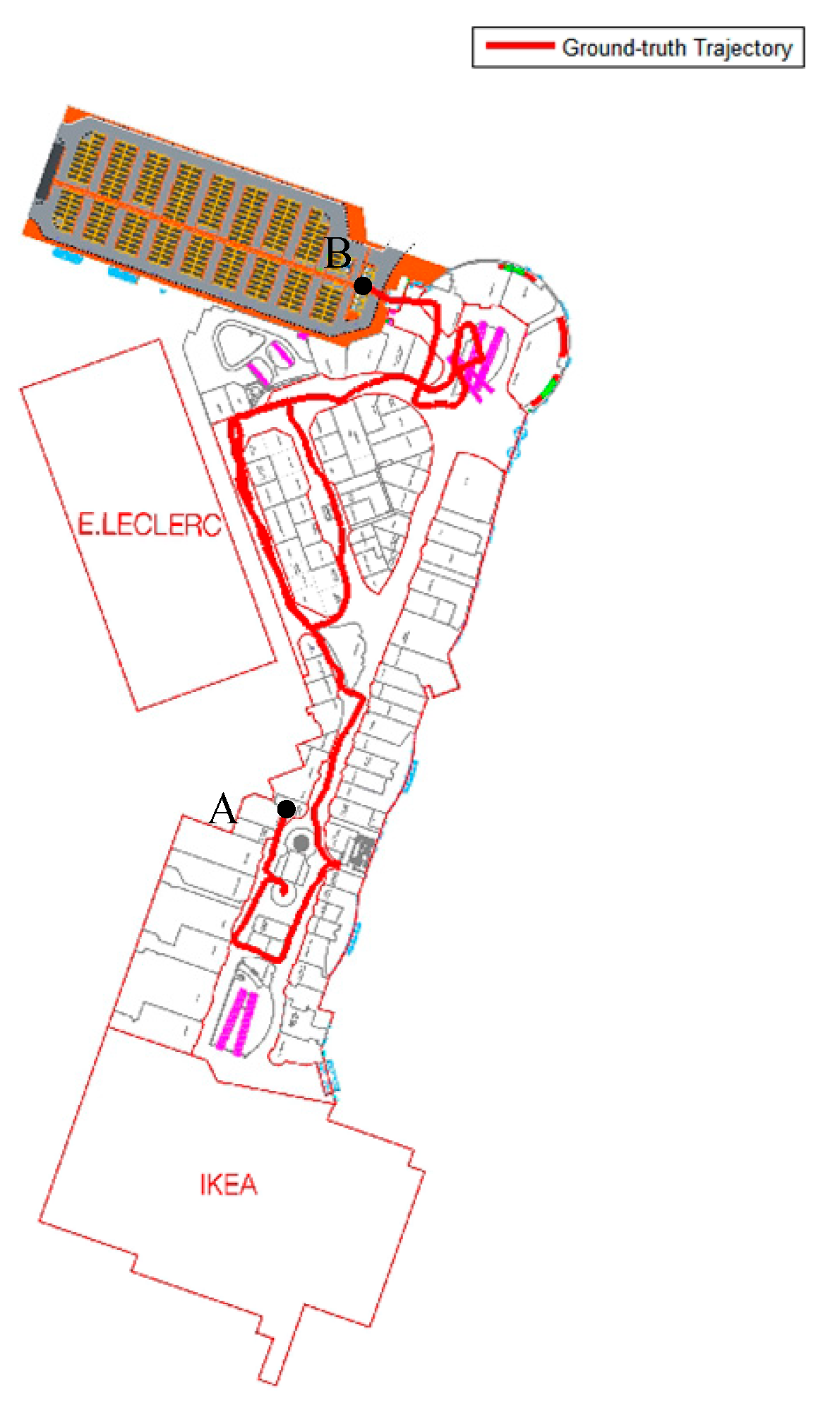
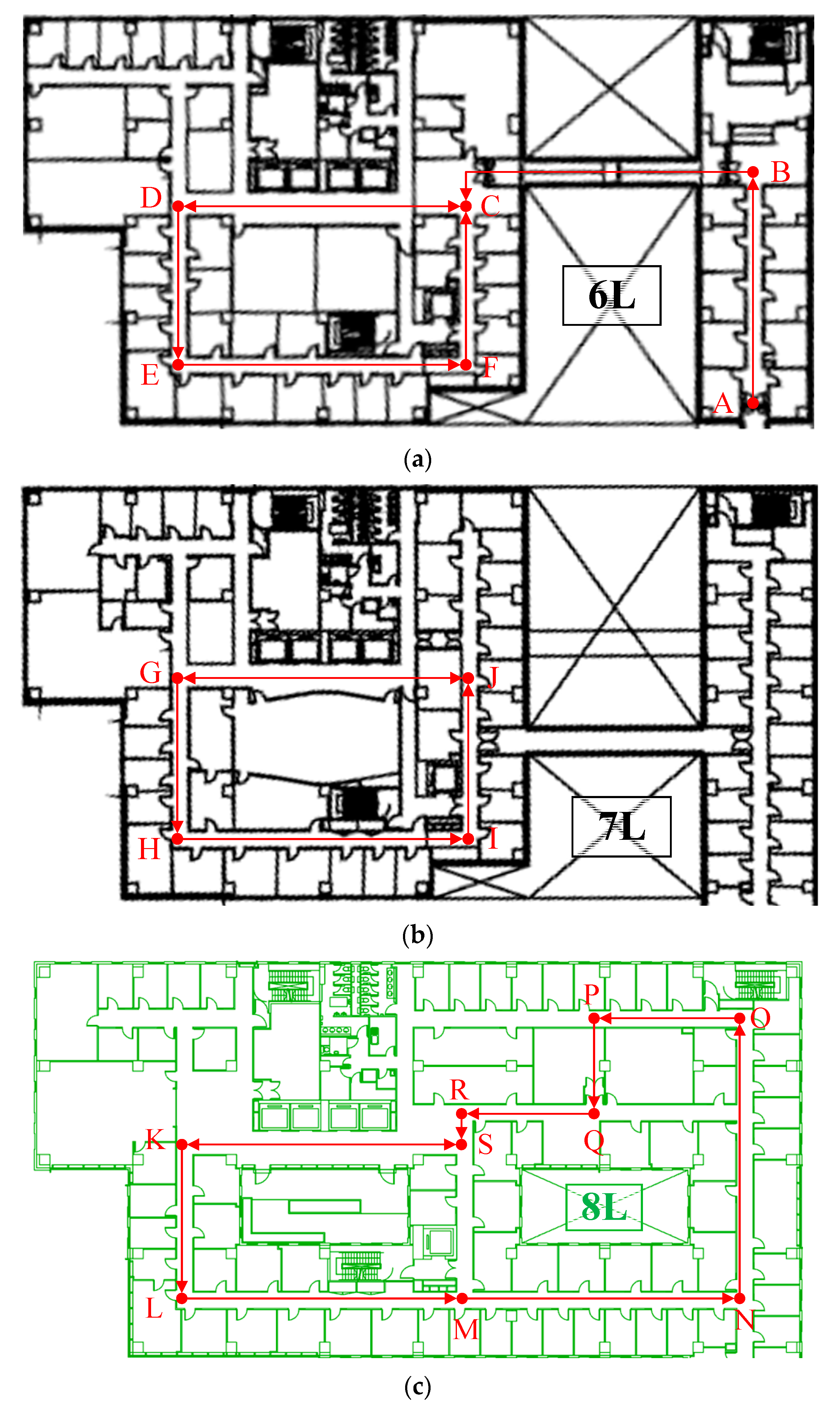
42] was utilized to estimate the accuracy with changeable handheld modes. For this purpose, different indoor environments containing multiple floors were selected, as illustrated in
Figure 4. The evaluation process involved starting at point A and conducting tests over an extended duration of approximately 20 min to evaluate the long-term performance of the proposed estimator. The chosen experimental setup allowed for a thorough assessment of the algorithm’s ability to accurately estimate the trajectories across varying conditions. The use of a publicly available dataset ensured that the results obtained were reproducible and could be compared with those of other studies conducted using the same dataset. Furthermore, the selection of a multi-floor environment enabled the evaluation of the proposed technique’s effectiveness in accurately estimating trajectories in complex indoor settings.
In order to assess the trajectory estimator’s long-term performance, a comparison was conducted with an enhanced INS-PDR framework [
5], utilizing identical smartphone data and a shared walking route. High-precision control points were utilized to evaluate the positioning errors. The respective estimated trajectories produced by the two algorithms were then compared, with the results presented in
Figure 5.
Based on the data presented in
Figure 5, it is apparent that the suggested inertial odometry achieved noticeably superior and accurate long-term location determination in comparison to the lone PDR mechanism. In order to obtain a more comprehensive evaluation of the positioning precision of both algorithms, a group of ten individuals retraced the same walking path multiple times, and their calculated positioning errors are depicted in
Figure 6.
The results described in
Figure 6 illustrate that the developed trajectory estimator maintained a long-term error of no more than 5.95 m in 75% of cases, which is superior to the INS-PDR approach, which had an error of up to 9.73 m in 75% of cases. This improvement can be attributed to the hybrid observations and constraints utilized by the proposed estimator.
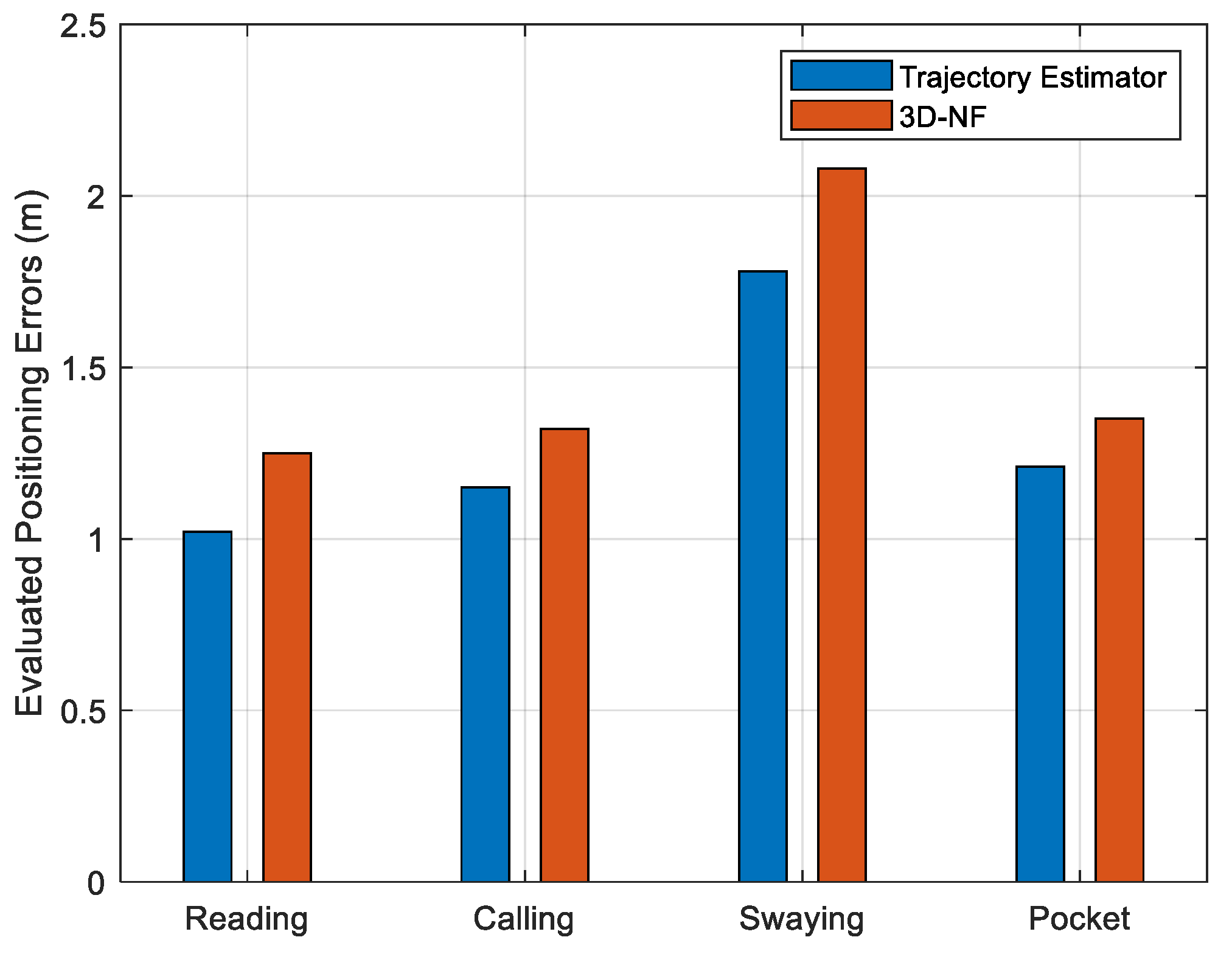
To further assess the performance of the data and model dual-driven trajectory estimator under varying handheld modes, we compared it with the state-of-the-art 3D navigation framework (3D-NF) [
14]. The mean positioning inaccuracies were computed for four distinct portable modes utilizing the identical pedestrian pathway specified in the reference material [
14], and the resultant mean positioning inaccuracies were contrasted.
According to
Figure 7, the proposed path estimator attained notably superior positioning precision across all four distinct portable modes, with mean positioning inaccuracies of 1.02 m (reading), 1.15 m (calling), 1.78 m (swaying), and 1.21 m (pocket) along the prolonged test pathway. This stands in contrast to the 3D-NF algorithm, which registered mean positioning inaccuracies of 1.25 m (reading mode), 1.32 m (calling mode), 2.08 m (swaying mode), and 1.35 m (pocket mode).
4.2. Performance Evaluation of Floor Recognition
This manuscript addresses the issue of lacking an initial floor observation in raw estimated trajectories. To overcome this limitation, a Bi-LSTM network was implemented to improve floor recognition precision on multiple floors in a contained building by incorporating data from local wireless signals and environment-related characteristics before the map-matching phase. To ensure comprehensive coverage of the indoor scenes, a 2.5 h trajectory dataset from five different floors was collected for training purposes, while a 0.5 h trajectory dataset was utilized for accuracy evaluation. The developed Bi-LSTM-based floor recognition model was compared with the classical 1D-CNN model [
16] and the classical MLP model [
1], with the accuracy comparison results presented in
Figure 8.
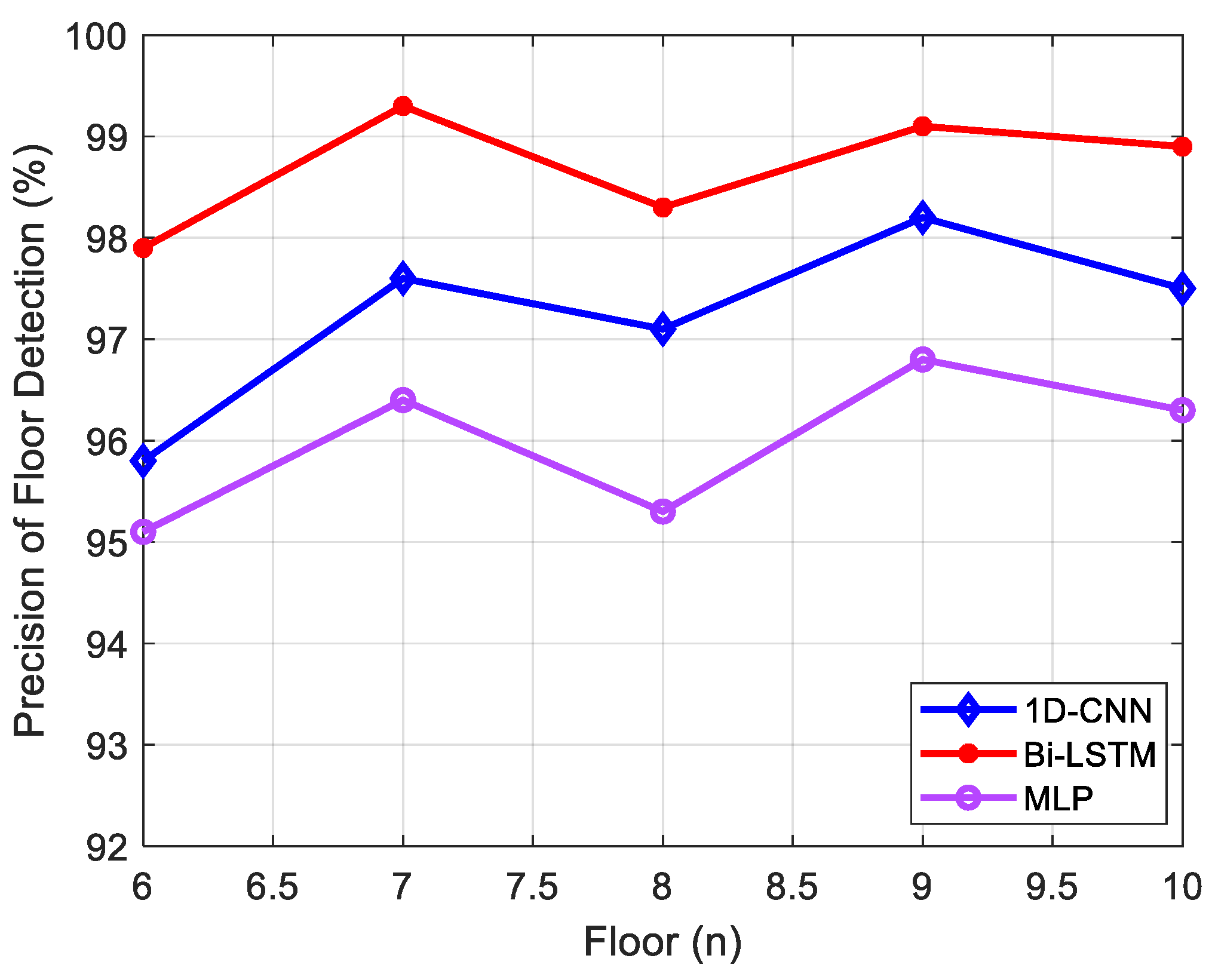
As shown in
Figure 8, the Bi-LSTM-based floor recognition model proposed in this study demonstrated superior accuracy compared to the 1D-CNN and MLP algorithms. The test dataset achieved an average accuracy of over 98.7% using the proposed approach, whereas the 1D-CNN-based approach and MLP-based approach resulted in average accuracies of 97.2% and 95.98%, respectively.
4.3. Precision Evaluation of Error Ellipse-Assisted UKF
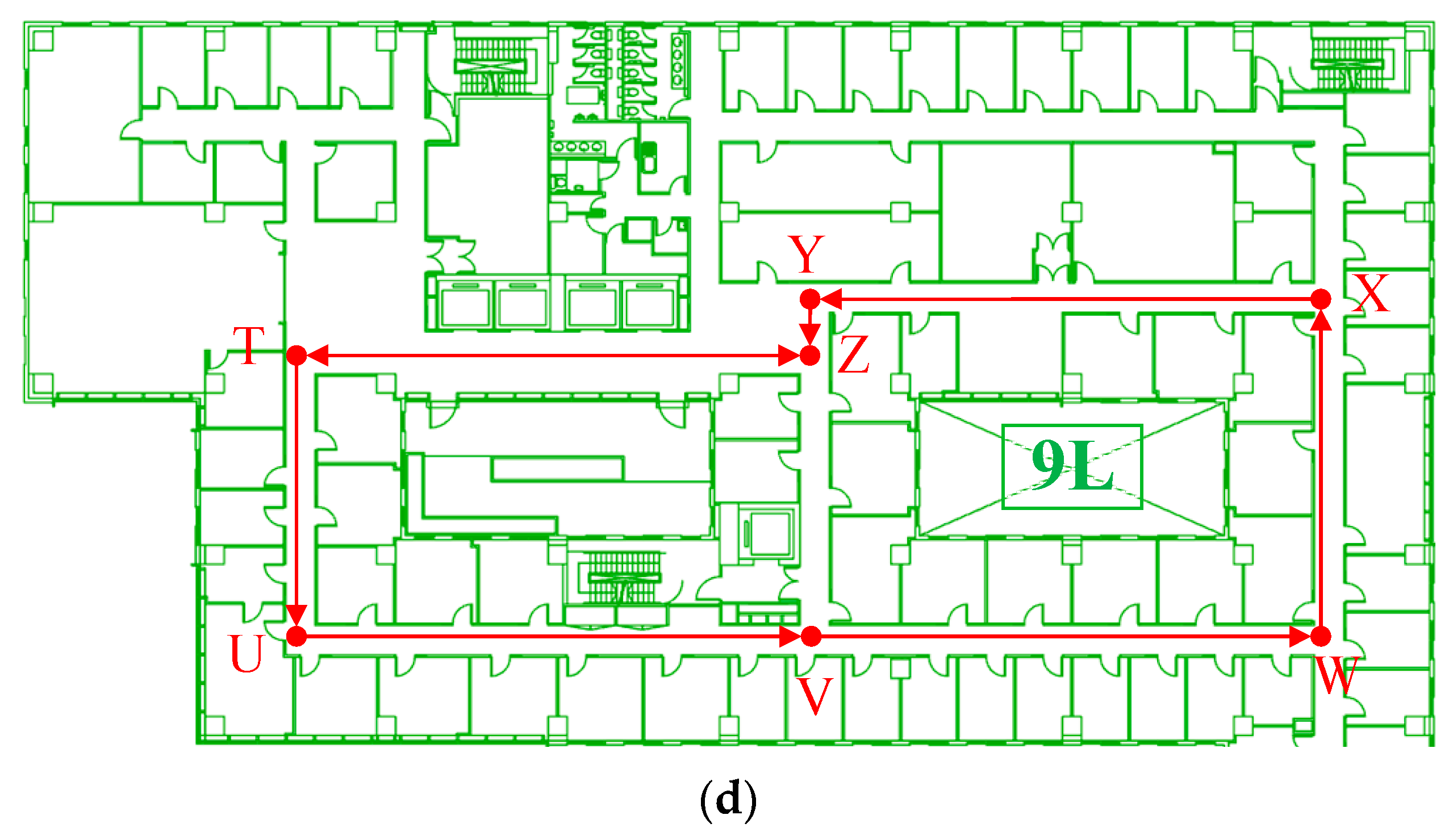
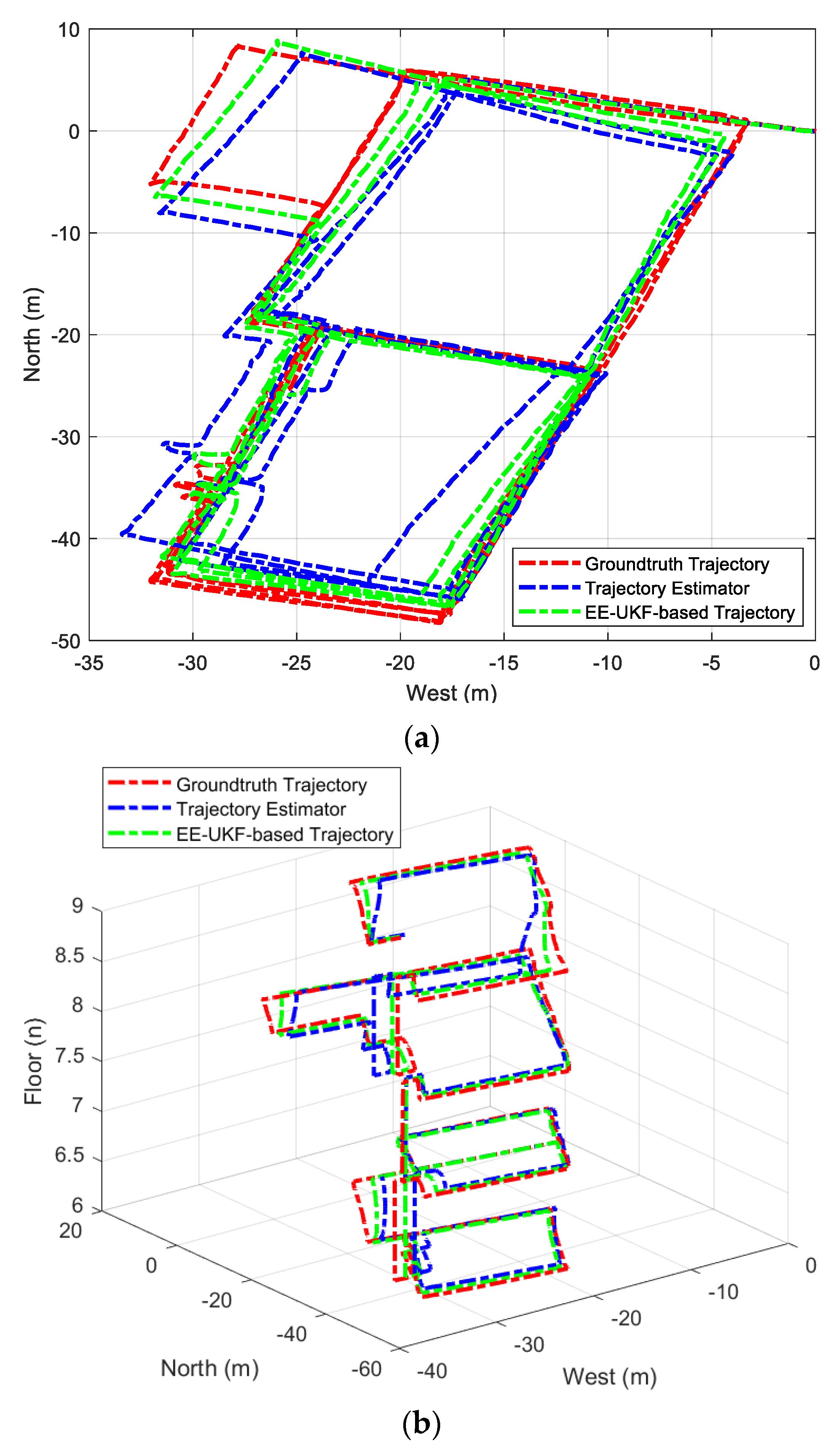
In order to assess the efficacy of map-matching and the fusion of the trajectory estimator and pedestrian indoor network, a multi-floor 3D indoor environment comprising four distinct floors with corresponding pedestrian indoor networks (as depicted in
Figure 9) was selected for evaluation. In this scenario, the indoor networks collected from different floors were modeled as a combination of nodes and segments and applied for trajectory matching, as illustrated in
Figure 10:
As illustrated in
Figure 10, the extracted indoor network comprehensively covers all pedestrian walking route and turning point information within multi-floor contained indoor building environments. Therefore, this study proposes an indoor network matching algorithm to enable absolute turning point references for optimizing and calibrating raw trajectory estimator results, while the floor recognition algorithm is employed to achieve dynamic floor indices of the trajectory estimator.
To evaluate the efficacy of the final ML-ISNM structure, a 3D indoor environment containing four adjacent floors was selected. The evaluator proceeded with uninterrupted walking from the 6th floor to the 9th floor, following the explicit pedestrian path delineated in
Figure 9. In this setting, an EE-UKF-driven amalgamation algorithm was suggested to astutely merge diverse location origins, involving MEMS sensors integrated into smartphones and indoor pedestrian network data. To refine the path estimator, the error ellipse was utilized to delimit the exploration range of the indoor network and to correlate relevant indoor network data. A comparison between the single trajectory estimator (TE), EE-UKF-based TE, and the indoor network integration model was conducted by examining the estimated trajectories.
As shown in
Figure 11, despite the multi-level based constraints and observations, the trajectory estimator remained susceptible to cumulative errors. However, the integration model of the pedestrian indoor network and trajectory estimator significantly enhanced single TE performance, while the integration of pedestrian network data further reduced the TE localization error and brought the estimated trajectory closer to the ground-truth reference. A localization error comparison between the two different combinations of location sources is presented below.
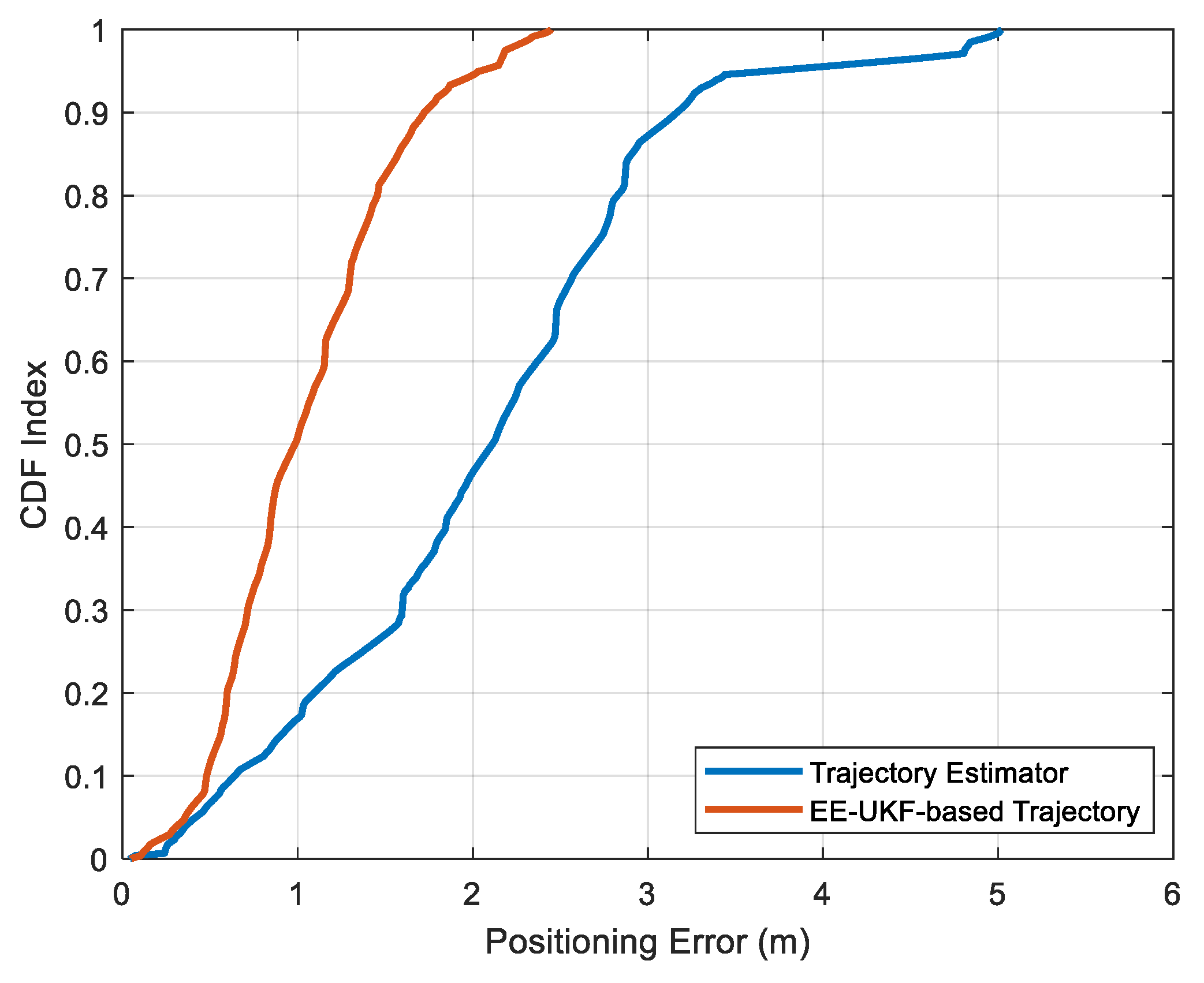
As depicted in
Figure 12, the amalgamation of indoor networks achieved indoor positioning accuracy at the meter level, with a positioning inaccuracy of less than 1.35 m in 75% of cases, outperforming the single trajectory estimator, which acquired a precision of 2.73 m in 75% of cases.
Lastly, to ensure impartiality, the proposed multi-source fusion algorithm based on EE-UKF was compared with two cutting-edge systems: the HTrack system [
23] and the map-assisted particle filter (MA-PF) [
43], utilizing the same pedestrian path. A comparison of the 3D positioning inaccuracies among these three distinct algorithms is presented in
Table 2.
In accordance with
Table 2, the proposed EE-UKF technique attained superior integration performance of multi-sourced data in contrast to the MA-PF and HTrack methodologies, thanks to the error ellipse-oriented UKF amalgamation strategy. The realized average positioning inaccuracy was lower than 1.13 m, which was remarkably lower compared to the MA-PF and HTrack schemes (which registered average inaccuracies of 1.31 m and 1.68 m, respectively).
5. Conclusions
To improve the positioning ability in complex and changeable urban buildings, this paper presents an autonomous multi-floor localization framework using smartphone-integrated sensors and pedestrian network matching (ML-ISNM). A robust data and model dual-driven pedestrian trajectory estimator is proposed for accurate integrated sensor-based positioning under different handheld modes and disturbed environments. The Bi-LSTM network was further developed for floor recognition using extracted environmental features and pedestrian motion features, and further combined with the indoor network matching algorithm for acquiring accurate location and floor observations. In the multi-source fusion phase, an error ellipse-enhanced unscented Kalman filter is presented to realize the multi-source fusion of the trajectory estimator, human motion constraints, and indoor network information. The empirical outcomes validate that the proposed ML-ISNM achieves self-directed and accurate 3D indoor localization performance in intricate and extensive indoor settings, with an average estimated positioning inaccuracy below 1.13 m, and without any reliance on wireless amenities.
The advantages of the proposed ML-ISNM contain the following aspects. Firstly, no additional local facilities are required for positioning purposes. The proposed ML-ISNM framework uses only smartphone-integrated sensors and extracted indoor network information for accurate multi-floor localization. Secondly, the proposed ML-ISNM has proven accurate and stable positioning performance under complex human motion and handheld modes and in disturbed indoor environments based on the EE-UKF fusion model. Thirdly, the proposed ML-ISNM can acquire precise initial location and floor information according to network matching and floor detection results, which is more autonomous than the existing approaches and applicable to providing universal location-based services.
The proposed ML-ISNM also has some limitations. The human trajectory is usually disordered and complex, which decreases the performance of pedestrian network matching. Thus, a more robust network matching algorithm is expected to enhance the matching accuracy for disordered trajectories. In addition, more complex human motion and handheld modes need to be considered to improve the robustness and precision of the data and model dual-driven method, which is more suitable for real-world applications.
The future work of this research includes the enhancement of the current ML-ISNM framework, improving the adaptability to more complex human motion and handheld modes, and developing more robust network matching and floor detection algorithms, which can be applied for the fast calibration of initial location/floor information and for providing more accurate observation information to the trajectory estimator. In addition, other advanced deep-learning frameworks [
44] can also be attempted for human trajectory prediction and estimation using multi-sensor data, for instance, a new automatic pruning method—sparse connectivity learning (SCL)—proposed by Tang et al. [
45], a channel-pruning method via class-aware trace ratio optimization (CATRO) proposed by Hu et al. [
46], and the weight-quantized SqueezeNet model developed by Huang [
47].