Ground-Penetrating Radar and Electromagnetic Induction: Challenges and Opportunities in Agriculture
Abstract
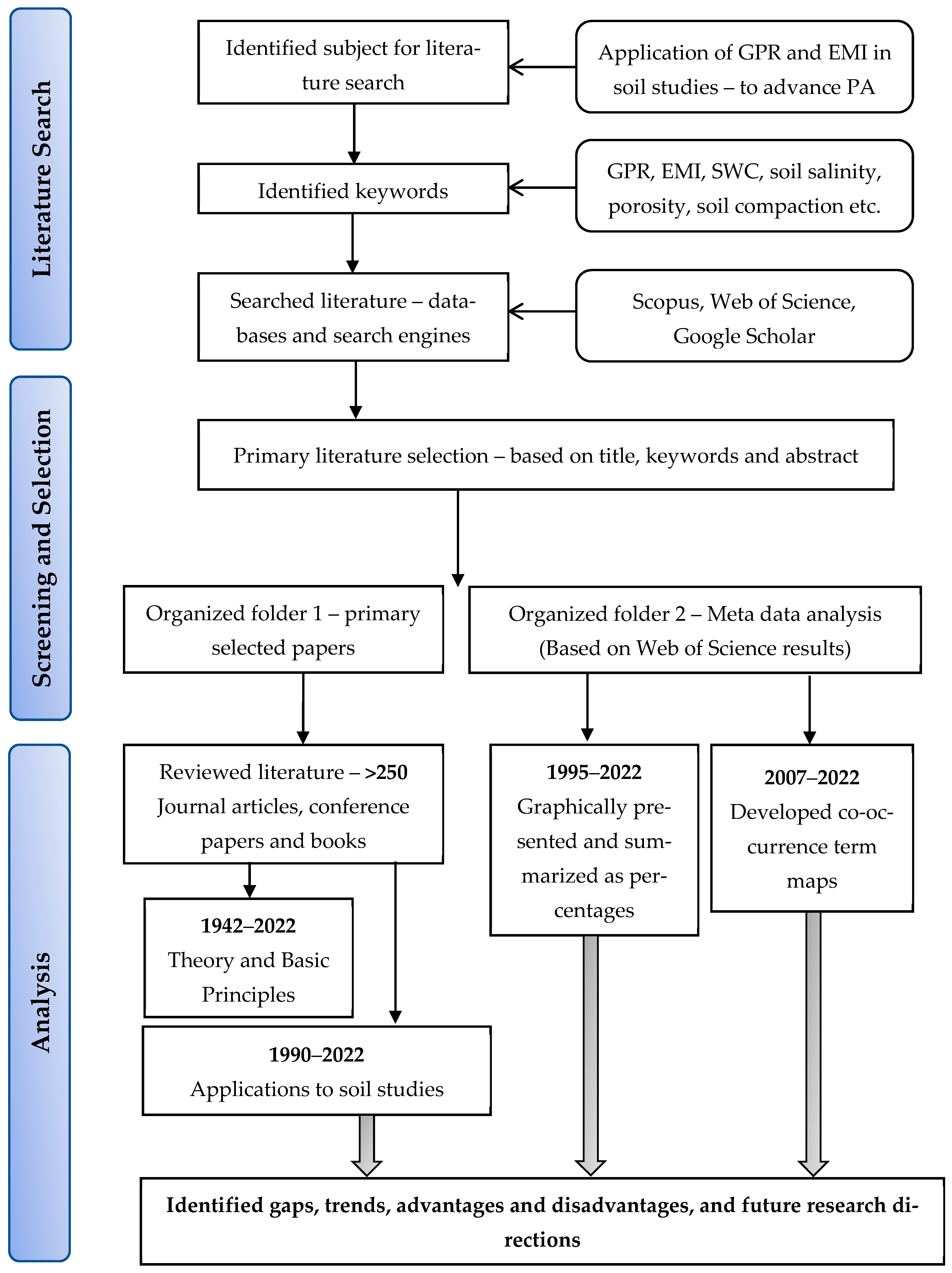
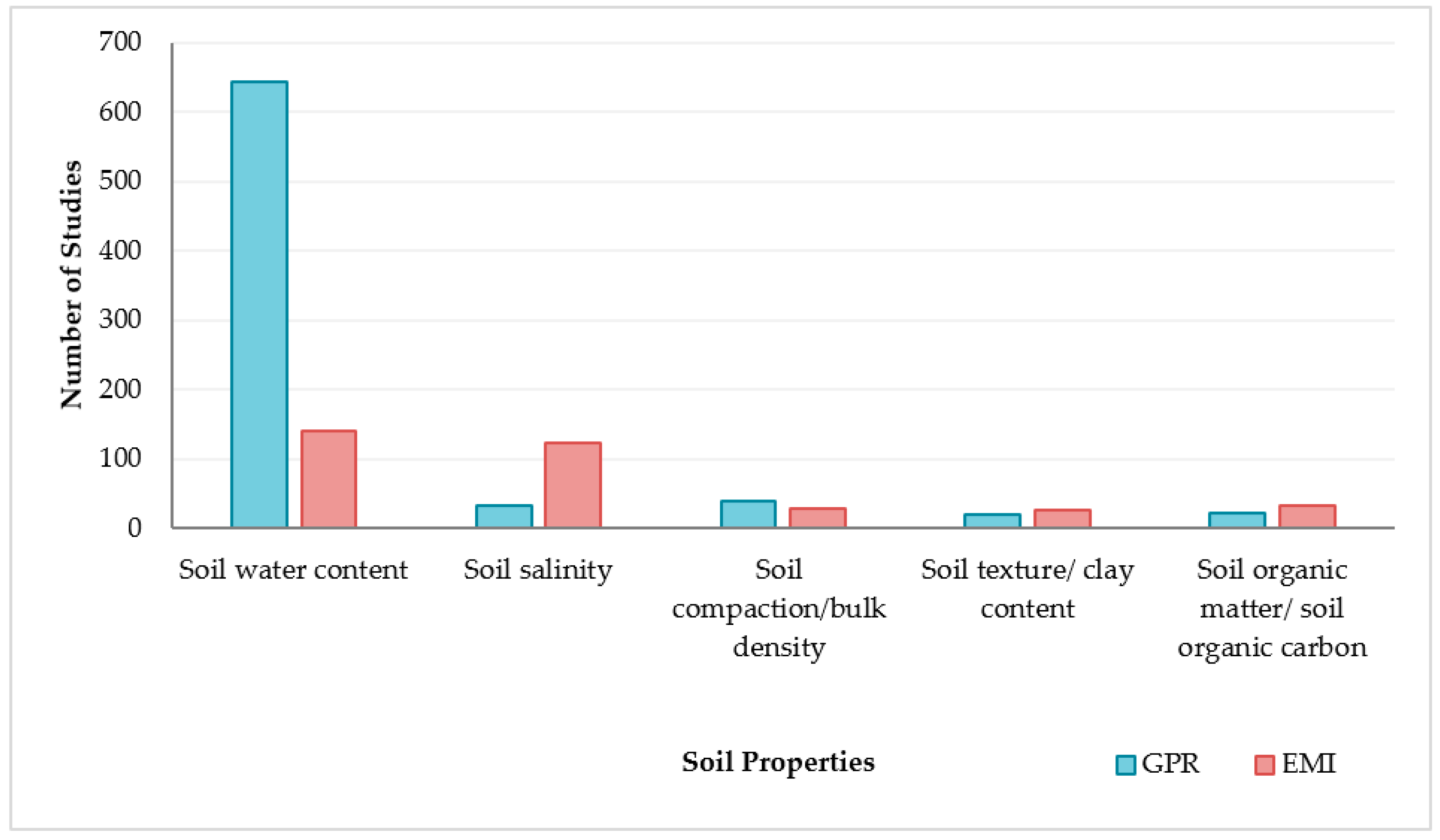
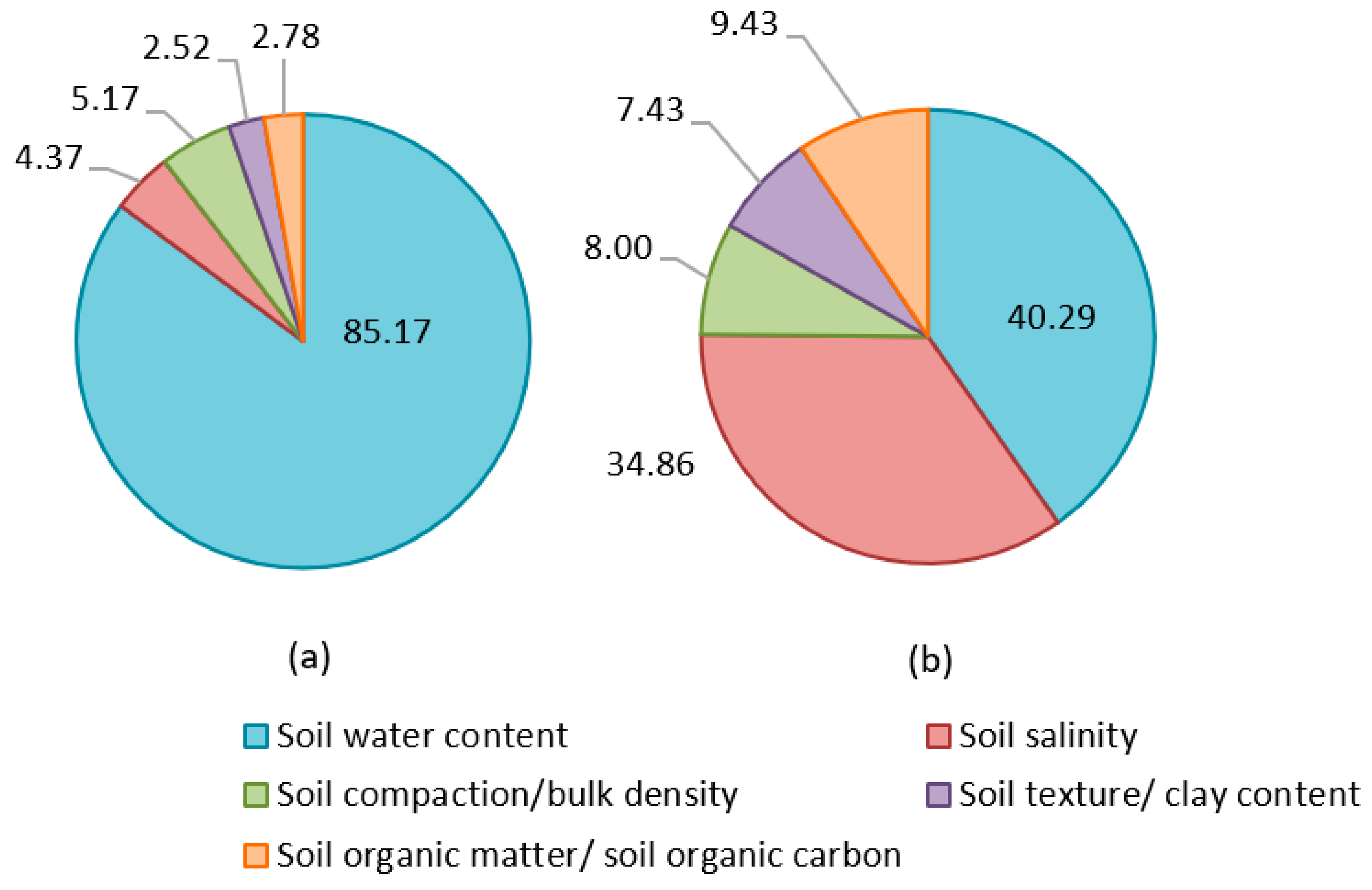
1. Introduction
2. Electromagnetic Methods
2.1. Theoretical and Empirical Equations and Models Used in Applications of Electromagnetic Methods
2.1.1. Topp’s Equation
2.1.2. Archie’s Equation
2.1.3. Complex Refractive Index Model
2.1.4. Rhoades’s Equation
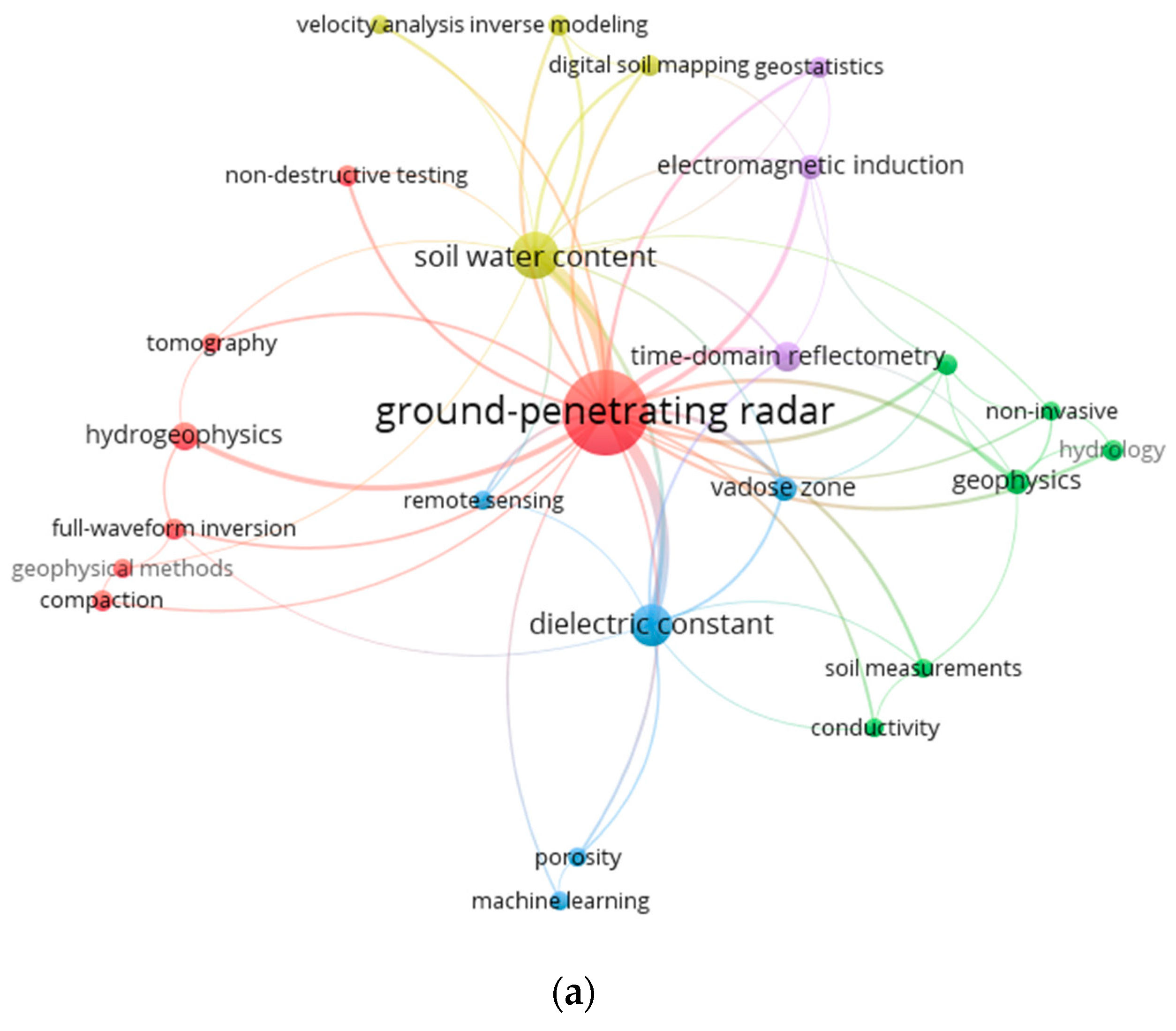
3. Ground-Penetrating Radar
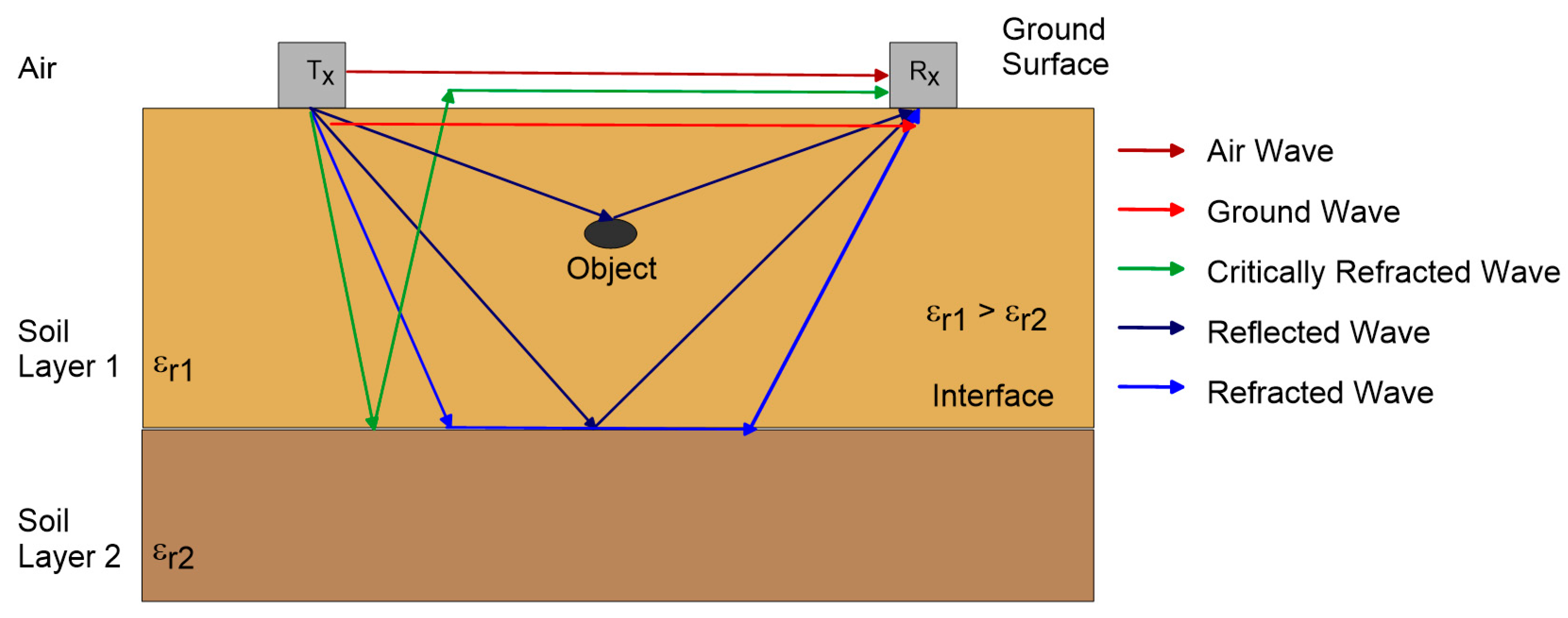
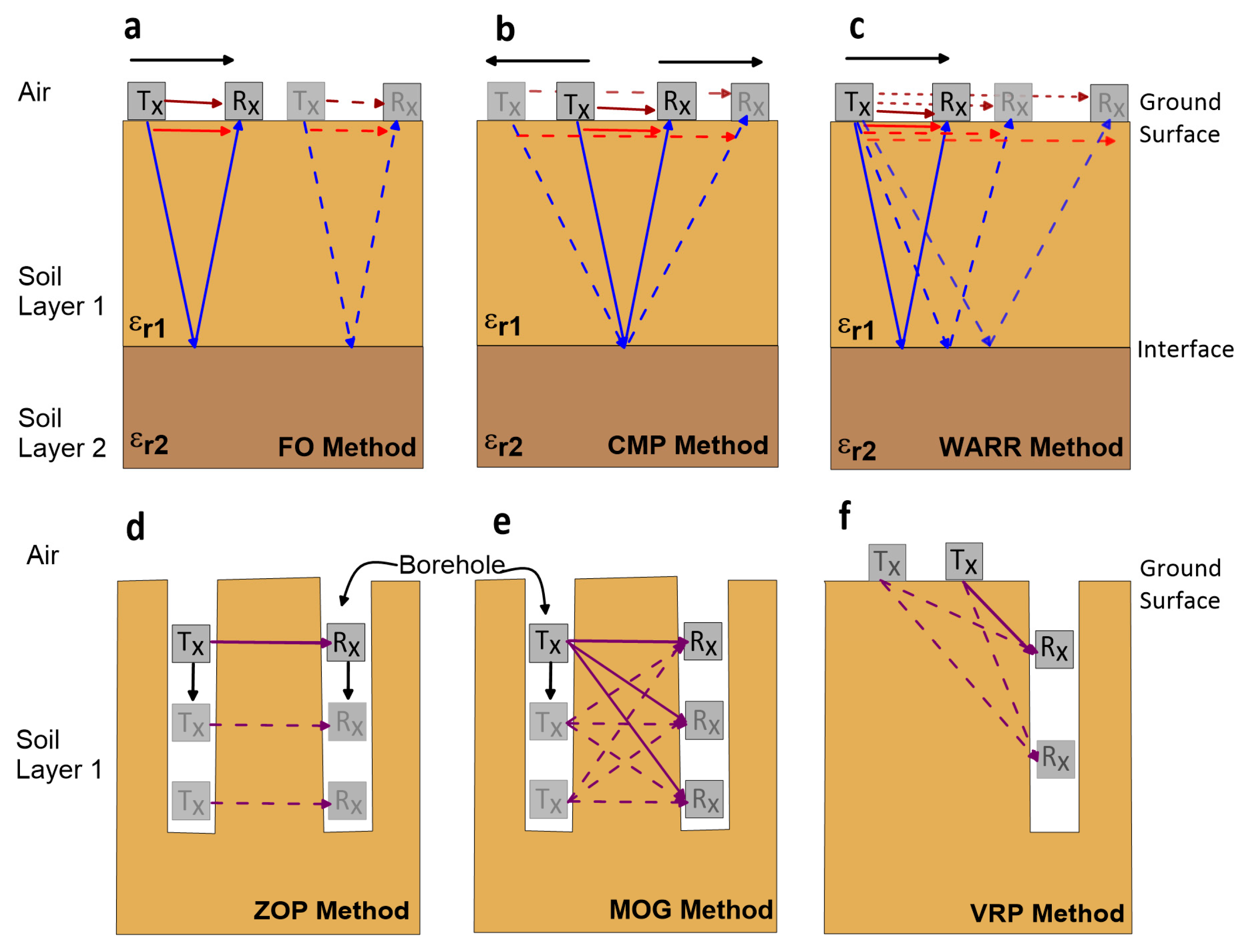
3.1. Basic Operating Principles of Ground-Penetrating Radar
3.2. Applications of Ground-Penetrating Radar in Soil Studies
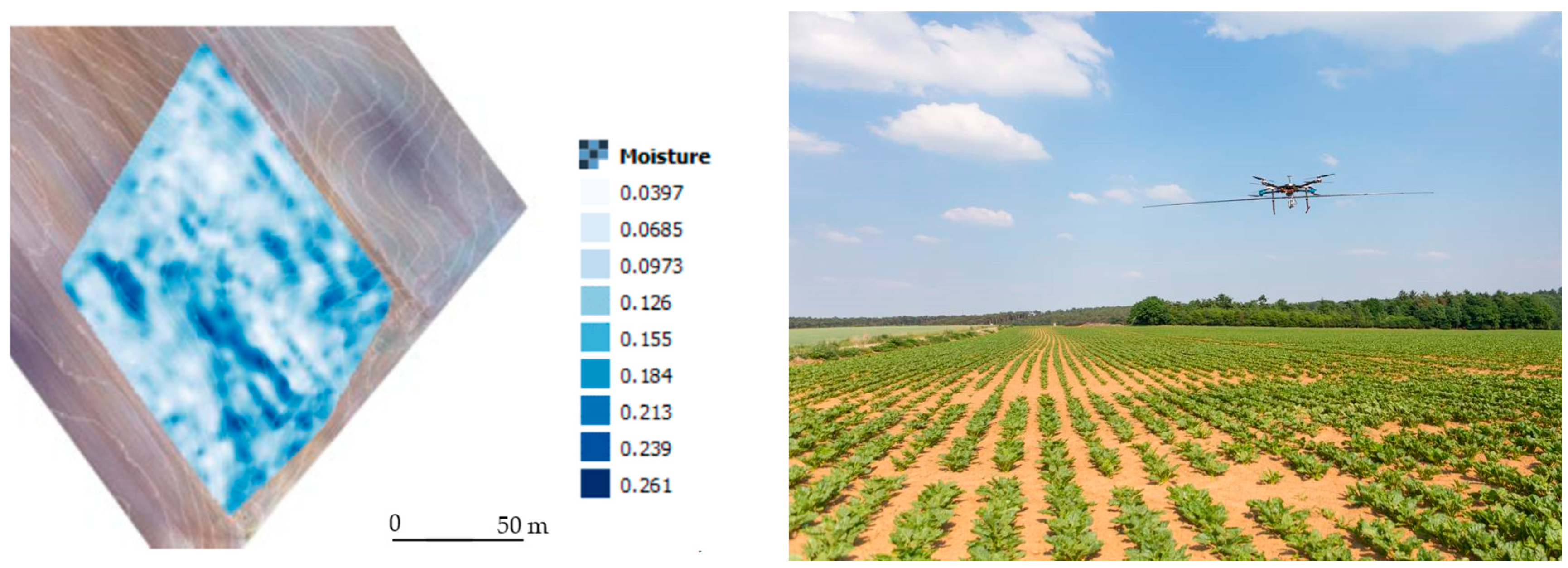
3.2.1. Soil Water Content
- Reflected wave velocity method
- b.
- Direct ground wave velocity method
- c.
- Transmitted wave velocity method
- d.
- Surface reflection coefficient method
- e.
- Average envelope amplitude method
- f.
- Full waveform inversion method
3.2.2. Soil Porosity and Soil Compaction
3.2.3. Soil Salinity
3.2.4. Soil Hydraulic Properties
3.2.5. Groundwater Table and Capillary Fringe Reflection
3.2.6. Other Soil Properties
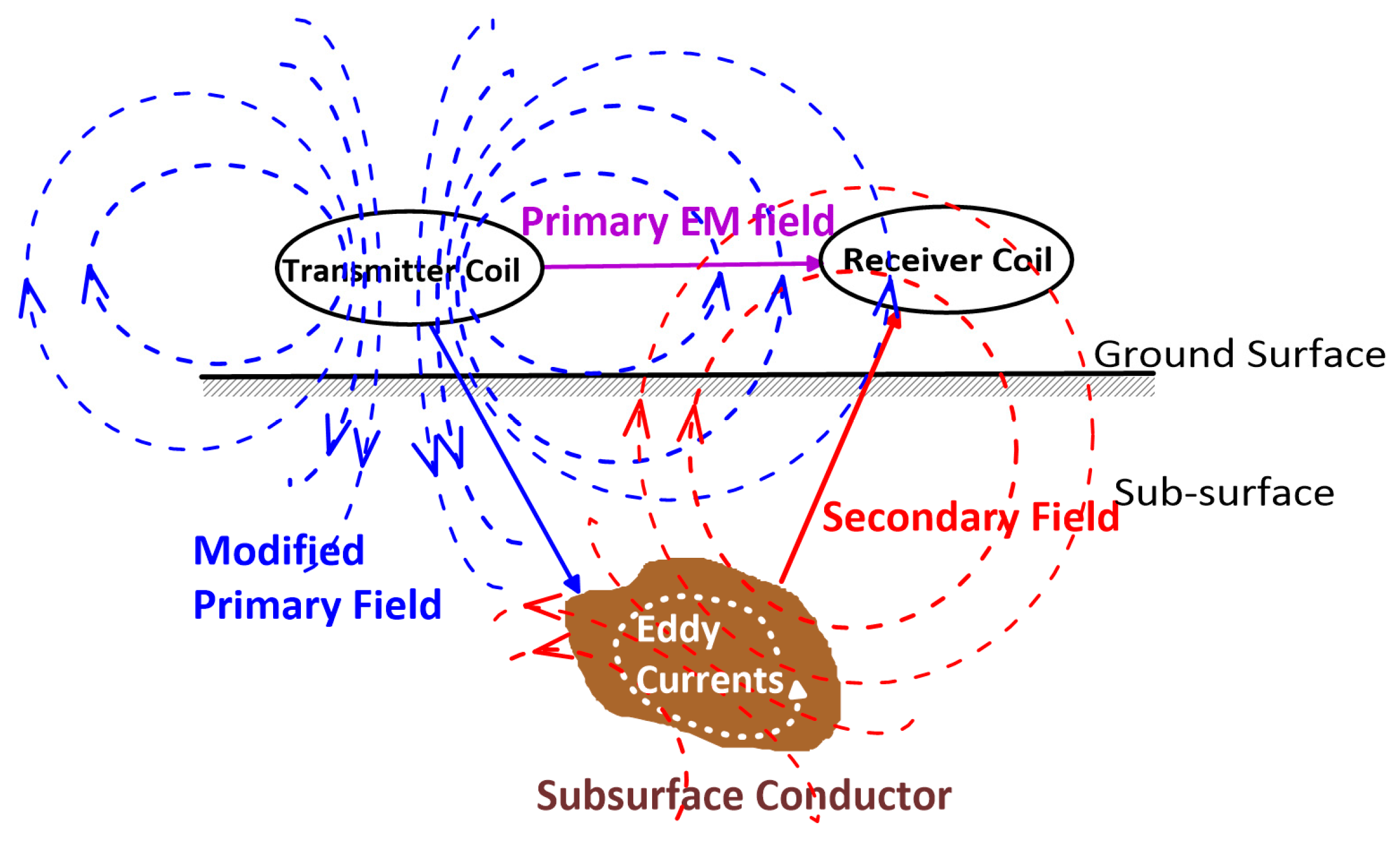
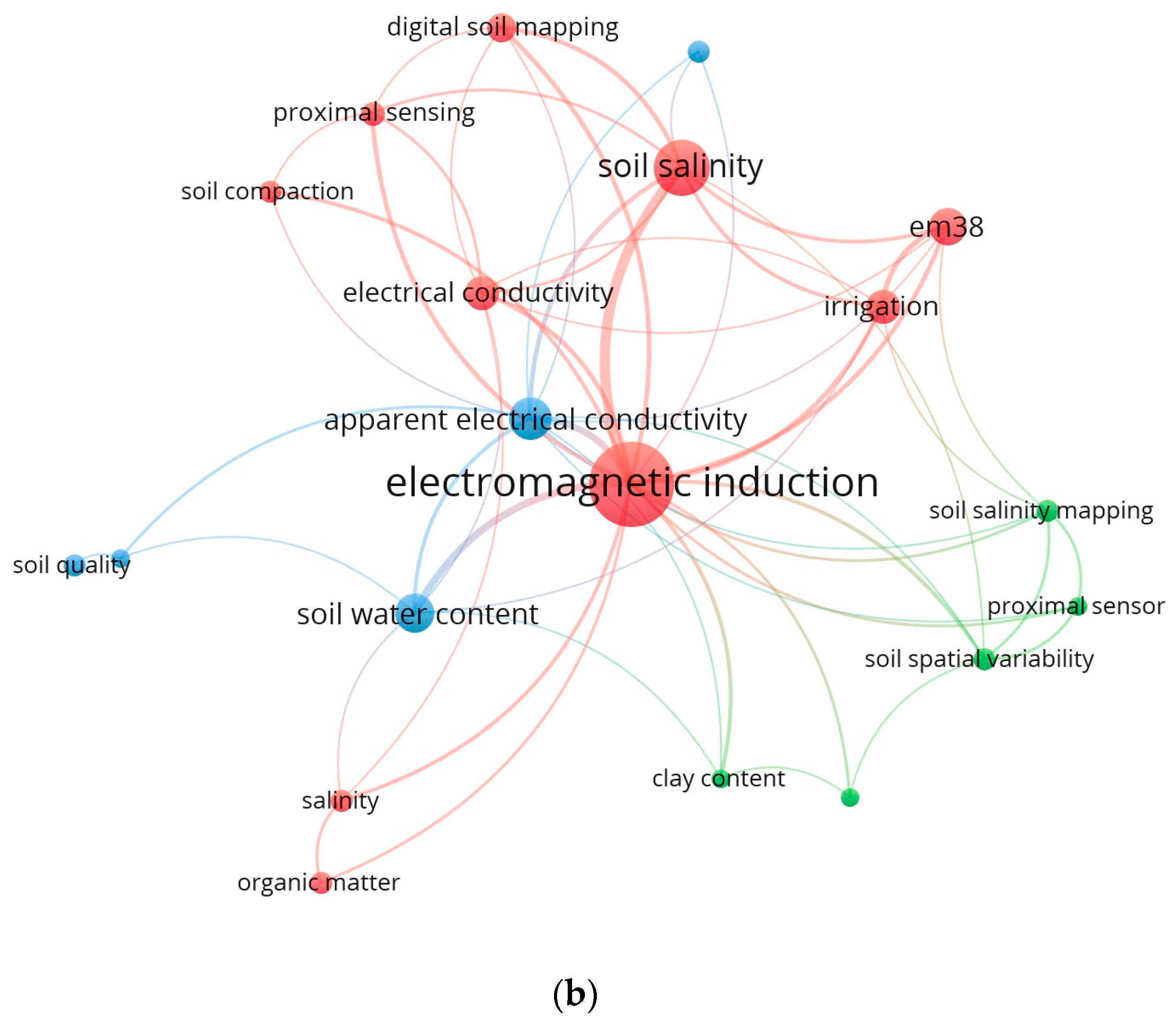
4. Electromagnetic Induction
4.1. Basic Operating Principles of Electromagnetic Induction

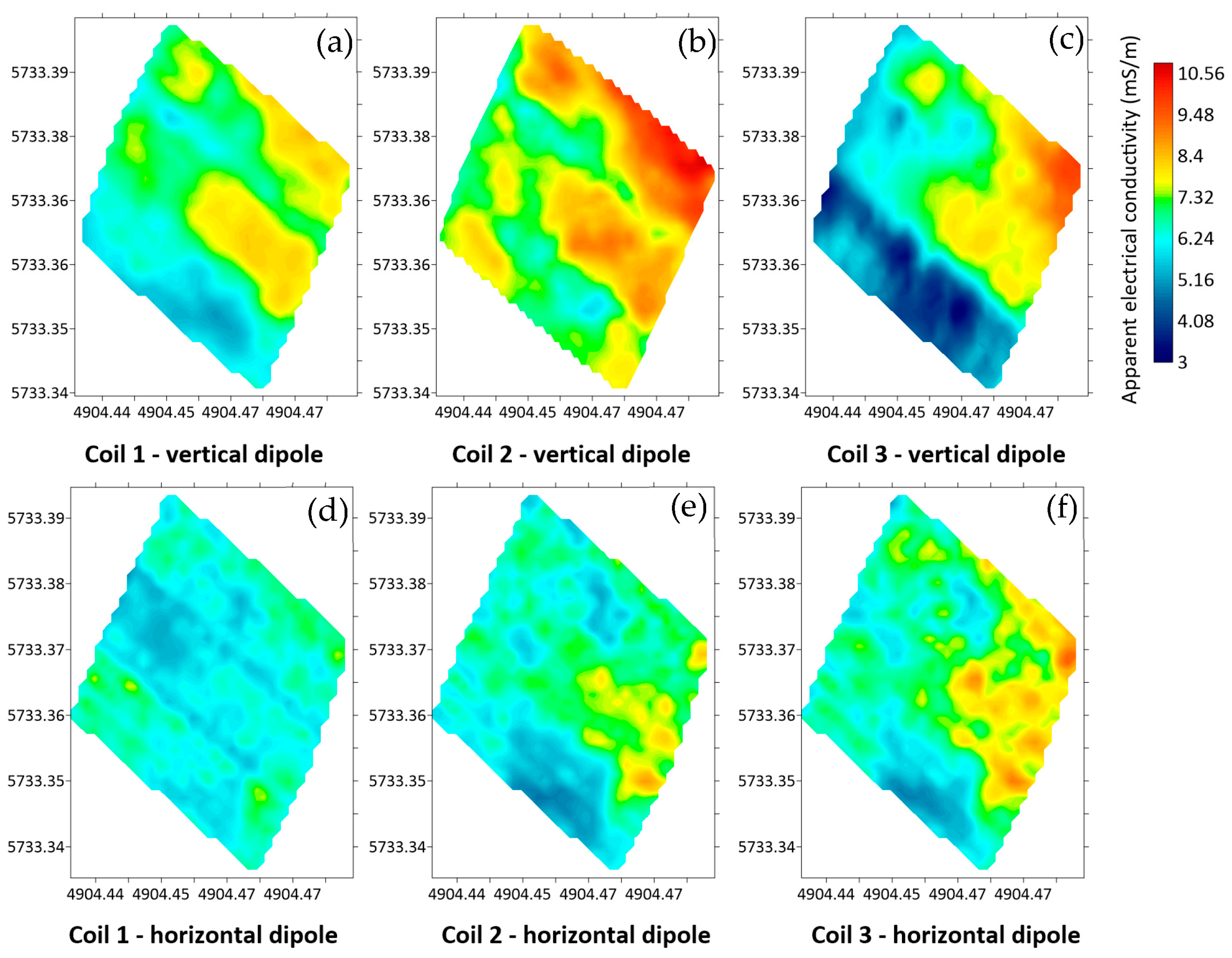
4.2. Applications of Electromagnetic Induction in Soil Studies
4.2.1. Soil Salinity
4.2.2. Soil Water Content
4.2.3. Bulk Density and Soil Compaction
4.2.4. Other Soil Properties
4.2.5. Apparent Magnetic Susceptibility
5. Synthesis and Critical Analysis
6. Summary and Future Directions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bongiovanni, R.; Lowenberg-DeBoer, J. Precision agriculture and sustainability. Precis. Agric. 2004, 5, 359–387. [Google Scholar] [CrossRef]
- Aubert, B.A.; Schroeder, A.; Grimaudo, J. IT as enabler of sustainable farming: An empirical analysis of farmers’ adoption decision of precision agriculture technology. Decis. Support Syst. 2012, 54, 510–520. [Google Scholar] [CrossRef]
- Shafi, U.; Mumtaz, R.; García-Nieto, J.; Hassan, S.A.; Zaidi, S.A.R.; Iqbal, N. Precision agriculture techniques and practices: From considerations to applications. Sensors 2019, 19, 3796. [Google Scholar] [CrossRef]
- Goel, R.K.; Yadav, C.S.; Vishnoi, S.; Rastogi, R. Smart agriculture—Urgent need of the day in developing countries. Sustain. Comput. Inform. Syst. 2021, 30, 100512. [Google Scholar] [CrossRef]
- Xia, Y.; Zhang, M.; Tsang, D.C.W.; Geng, N.; Lu, D.; Zhu, L.; Igalavithana, A.D.; Dissanayake, P.D.; Rinklebe, J.; Yang, X.; et al. Recent advances in control technologies for non-point source pollution with nitrogen and phosphorous from agricultural runoff: Current practices and future prospects. Appl. Biol. Chem. 2020, 63, 8. [Google Scholar] [CrossRef]
- Stafford, J.V. Implementing precision agriculture in the 21st century. J. Agric. Eng. Res. 2000, 76, 267–275. [Google Scholar] [CrossRef]
- Becker, S.M.; Franz, T.E.; Abimbola, O.; Steele, D.D.; Flores, J.P.; Jia, X.; Scherer, F.T.; Rudnick, R.D.; Neale, C.M. Feasibility assessment on use of proximal geophysical sensors to support precision management. Vadose Zone J. 2022, 21, e20228. [Google Scholar] [CrossRef]
- Friedl, M.A. Remote sensing of croplands. In Comprehensive Remote Sensing—Elsevier Earth Systems and Environmental Science; Liang, S., Ed.; Elsevier: Amsterdam, The Netherlands, 2018; Volume 6, pp. 78–95. [Google Scholar] [CrossRef]
- Pallottino, F.; Biocca, M.; Nardi, P.; Figorilli, S.; Menesatti, P.; Costa, C. Science mapping approach to analyze the research evolution on precision agriculture: World, EU and Italian situation. Precis. Agric. 2018, 19, 1011–1026. [Google Scholar] [CrossRef]
- Nicol, L.A.; Nicol, C.J. Adoption of precision agriculture to reduce inputs, enhance sustainability and increase food production: A study of Southern Alberta, Canada. WIT Trans. Ecol. Environ. 2018, 217, 1743–3541. [Google Scholar] [CrossRef]
- Hammond, M.W.; Mulla, D.J.; Fairchild, D.S. Development of management maps for soil variability. In Proceedings of the 39th Annual Far West Regional Fertilizer Conference, Bozeman, MT, USA, 11–13 July 1988; pp. 67–76. [Google Scholar]
- Mulla, D.J.; Hammond, M.W. Mapping of soil test results from large irrigation circles. In Proceedings of the 39th Annual Far West Regional Fertilizer Conference, Bozeman, MT, USA, 11–13 July 1988; pp. 169–176. [Google Scholar]
- Schmidhalter, U.; Maidl, F.X.; Heuwinkel, H.; Demmel, M.; Auernhammer, H.; Noack, P.O.; Rothmund, M. Precision farming–adaptation of land use management to small scale heterogeneity. In Perspectives for Agroecosystem Management: Balancing Environmental and Socio-Economic Demands; Schröder, P., Pfadenhauer, J., Munch, J.C., Eds.; Elsevier: Amsterdam, The Netherlands, 2008; Chapter 2.3; pp. 121–199. [Google Scholar] [CrossRef]
- Pinaki, M.; Tewari, V.K. Present status of precision farming: A review. Int. J. Agric. Res. 2010, 5, 1124–1133. [Google Scholar] [CrossRef]
- Mulla, D.; Khosla, R. Historical evolution and recent advances in precision farming. In Soil Specific Farming: Precision Agriculture; Lal, R., Stewart, B.A., Eds.; Taylor and Francis: Boca Raton, FL, USA, 2015; Chapter 1; pp. 1–36. [Google Scholar]
- Alix, A.; Capri, E. Modern agriculture in Europe and the role of pesticides. In Advances in Chemical Pollution, Environmental Management and Protection; Capri, E., Alix, A., Eds.; Elsevier: Amsterdam, The Netherlands, 2018; Volume 2, pp. 1–22. [Google Scholar] [CrossRef]
- Kashyap, B.; Kumar, R. Sensing methodologies in agriculture for soil moisture and nutrient monitoring. IEEE Access 2021, 9, 14095–14121. [Google Scholar] [CrossRef]
- Hammond, M.W.; Mulla, D.J. Field variation in soil fertility: Its assessment and management for potato production. In Proceedings of the 28th Annual Washington State Potato Conference, Moses Lake, WA, USA, 2 February 1989. [Google Scholar]
- Jarolímek, J.; Stočes, M.; Masner, J.; Vaněk, J.; Šimek, P.; Pavlík, J.; Rajtr, J. User-technological index of precision agriculture. Agris On-Line Pap. Econ. 2017, 9, 69–75. [Google Scholar] [CrossRef]
- Fairchild, D.; Hammond, M. Using computerized fertilizer application equipment for efficient soil fertility management. In Proceedings of the 39th Annual Regional Fertilizer Conference, BoTeman, MT, USA, 11–13 July 1988; Jacobsen, J.S., Ed.; pp. 77–82. [Google Scholar]
- Mulla, D.J. Using geostatistics and spectral analysis to study spatial patterns in the topography of southeastern Washington State, U.S.A. Earth Surf. Process. 1988, 13, 389–405. [Google Scholar] [CrossRef]
- Vereecken, H.; Binley, A.; Cassiani, G.; Revil, A.; Titov, K. Applied hydrogeophysics. In Applied Hydrogeophysics: NATO Science Series; Vereecken, H., Binley, A., Cassiani, G., Revil, A., Titov, K., Eds.; Springer Dordrecht: Berlin, Germany, 2006; Volume 71, pp. 1–8. [Google Scholar] [CrossRef]
- Rubin, Y.; Hubbard, S.S. Hydrogeophysics; Springer: Cham, Switzerland, 2005; Volume 50. [Google Scholar] [CrossRef]
- Lambot, S.; Binley, A.; Slob, E.C.; Hubbard, S. Foreword to the special issue on ground-penetrating radar in hydrogeophysics. Vadose Zone J. 2008, 7, 137–139. [Google Scholar] [CrossRef]
- Binley, A.; Cassiani, G.; Deiana, R. Hydrogeophysics: Opportunities and challenges. Boll. Geofis. Teor. Ed Appl. 2010, 51, 267–284. [Google Scholar]
- Vereecken, H.; Hubbard, S.; Binley, A.; Ferre, T. Hydrogeophysics: An introduction from the guest editors. Vadose Zone J. 2004, 3, 1060–1062. [Google Scholar] [CrossRef]
- Blazevic, L.A.; Bodet, L.; Pasquet, S.; Linde, N.; Jougnot, D.; Longuevergne, L. Time-lapse seismic and electrical monitoring of the vadose zone during a controlled infiltration experiment at the Ploemeur hydrological observatory, France. Water 2020, 12, 1230. [Google Scholar] [CrossRef]
- Hubbard, S.S. Hydrogeophysics; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2011. [Google Scholar]
- Doolittle, J.A.; Brevik, E.C. The use of electromagnetic induction techniques in soils studies. Geoderma 2014, 223–225, 33–45. [Google Scholar] [CrossRef]
- De Benedetto, D.; Montemurro, F.; Diacono, M. Mapping an agricultural field experiment by electromagnetic Induction and ground penetrating radar to improve soil water content estimation. Agronomy 2019, 9, 638. [Google Scholar] [CrossRef]
- Slob, E.; Sato, M.; Olhoeft, G. Surface and borehole ground-penetrating-radar developments. Geophysics 2010, 75, 75A103–75A120. [Google Scholar] [CrossRef]
- Zajícová, K.; Chuman, T. Application of ground penetrating radar methods in soil studies: A review. Geoderma 2019, 343, 116–129. [Google Scholar] [CrossRef]
- Huisman, J.A.; Hubbard, S.S.; Redman, J.D.; Annan, A.P. Measuring soil water content with ground penetrating radar: A review. Vadose Zone J. 2003, 2, 476–491. [Google Scholar] [CrossRef]
- van Dam, R.L. Calibration functions for estimating soil moisture from GPR dielectric constant measurements. Commun. Soil Sci. Plant Anal. 2014, 45, 392–413. [Google Scholar] [CrossRef]
- Liu, X.; Chen, J.; Cui, X.; Liu, Q.; Cao, X.; Chen, X. Measurement of soil water content using ground penetrating radar: A review of current methods. Int. J. Digit. Earth 2017, 12, 95–118. [Google Scholar] [CrossRef]
- Klotzsche, A.; Jonard, F.; Looms, M.C.; van der Kruk, J.; Huisman, J.A. Measuring soil water content with ground penetrating radar: A decade of progress. Vadose Zone J. 2018, 17, 1–9. [Google Scholar] [CrossRef]
- Zhang, M.; Feng, X.; Bano, M.; Xing, H.; Wang, T.; Liang, W.; Zhou, H.; Dong, Z.; An, Y.; Zhang, Y. Review of ground penetrating radar applications for water dynamics studies in unsaturated zone. Remote Sens. 2022, 14, 5993. [Google Scholar] [CrossRef]
- Olhoeft, G.R. Electrical, magnetic, and geometric properties that determine ground penetrating radar performance. In Proceedings of the 7th International Conference on Ground Penetrating Radar, The University of Kansas, Lawrence, KS, USA, 27–30 May 1998; pp. 177–182. [Google Scholar]
- Annan, A.P. Ground Penetrating Radar Principles, Procedures, and Applications; Workshop Notes, Sensors and Software Inc.: Mississauga, ON, Canada, 2004. [Google Scholar]
- Annan, A.P. Electromagnteic principles of ground penetrating radar. In Ground Penetrating Radar Theory and Applications; Jol, H.M., Ed.; Elsevier: Amsterdam, The Netherlands, 2009; pp. 3–37. [Google Scholar] [CrossRef]
- Weiler, K.W.; Steenhuis, T.S.; Boll, J.; Kung, K.J.S. Comparison of ground penetrating radar and time-domain reflectometry as soil water sensors. Soil Sci. Soc. Am. J. 1998, 62, 1237–1239. [Google Scholar] [CrossRef]
- Topp, G.C.; Davis, J.L.; Annan, A.P. Electromagnetic determination of soil water content: Measurements in coaxial transmission lines. Water Resour. Res. 1980, 16, 574–582. [Google Scholar] [CrossRef]
- Turesson, A. Water content and porosity estimated from ground-penetrating radar and resistivity. J. Appl. Geophy. 2006, 58, 99–111. [Google Scholar] [CrossRef]
- Roth, K. Calibration of time domain reflectometry for water content measurement using a composite dielectricity approach. Water Resour. Res. 1990, 26, 2267–2273. [Google Scholar] [CrossRef]
- White, I.; Knight, J.H.; Zegelin, S.J.; Topp, G.C. Comments on ‘Considerations on the use of time-domain reflectometry (TDR) for measuring soil water content’ by W. R. Whalley. Eur. J. Soil Sci. 1994, 45, 503–508. [Google Scholar] [CrossRef]
- Wanniarachchi, D.; Cheema, M.; Thomas, R.; Galagedara, L. Effect of biochar on TDR-based volumetric soil moisture measurements in a loamy sand podzolic soil. Soil Syst. 2019, 3, 49. [Google Scholar] [CrossRef]
- Archie, G.E. The electrical resistivity log as an aid in determining some reservoir characteristics. Trans. Am. Inst. Min. 1942, 146, 54–62. [Google Scholar] [CrossRef]
- Shah, P.H.; Singh, D.N. Generalized archie’s law for estimation of soil electrical conductivity. J. ASTM Int. 2005, 2, 145–164. [Google Scholar]
- Ewing, R.P.; Hunt, A.G. Dependence of the electrical conductivity on saturation in real porous media. Vadose Zone J. 2006, 5, 731–741. [Google Scholar] [CrossRef]
- Glover, P.W.J. A generalized Archie’s law for n phases. Geophysics 2010, 75, 247–265. [Google Scholar] [CrossRef]
- Glover, P.W.J. Archie’s law—A reappraisal. Solid Earth 2016, 7, 1157–1169. [Google Scholar] [CrossRef]
- Birchak, J.R.; Gardner, C.G.; Hipp, J.E.; Victor, J.M. High dielectric constant microwave probes for sensing soil moisture. Proc. IEEE 1974, 62, 93–98. [Google Scholar] [CrossRef]
- Lai, W.L.; Tsang, W.F.; Fang, H.; Xiao, D. Experimental determination of bulk dielectric properties and porosity of porous asphalt and soils using GPR and a cyclic moisture variation technique. Geophysics 2006, 71, K93. [Google Scholar] [CrossRef]
- Mount, G.J.; Comas, X. Estimating porosity and solid dielectric permittivity in the Miami Limestone using high-frequency ground penetrating radar (GPR) measurements at the laboratory scale. Water Resour. Res. 2014, 50, 7590–7605. [Google Scholar] [CrossRef]
- Zadhoush, H.; Giannopoulos, A.; Giannakis, I. Optimising the complex refractive index model for estimating the permittivity of heterogeneous concrete models. Remote Sens. 2021, 13, 723. [Google Scholar] [CrossRef]
- Rhoades, J.D.; Raats, P.A.C.; Prather, R.J. Effects of liquid-phase electrical conductivity, water content, and surface conductivity on bulk soil electrical conductivity. Soil Sci. Soc. Am. J. 1976, 40, 651–655. [Google Scholar] [CrossRef]
- Baker, G.S.; Jordan, T.E.; Pardy, J. An introduction to ground penetrating radar (GPR). In Stratigraphic Analyses Using GPR; Baker, G.S., Jol, H.M., Eds.; Geological Society of America: Boulder, CO, USA, 2007; Volume 432, pp. 1–18. [Google Scholar] [CrossRef]
- Davis, J.L.; Annan, A.P. Ground penetrating radar for high-resolution mapping of soil and rock stratigraphy. Geophys. Prospect. 1989, 37, 531–551. [Google Scholar] [CrossRef]
- Reynolds, J.M. An Introduction to Applied and Environmental Geophysics, 2nd ed.; A John Wiley & Sons Ltd.: West Sussex, UK, 2011. [Google Scholar]
- Knight, R. Ground penetrating radar for environmental applications. Annu. Rev. Earth Planet. Sci. 2001, 29, 229–255. [Google Scholar] [CrossRef]
- Annan, A.P. Ground penetrating radar. In Near-Surface Geophysics; Butler, D.K., Ed.; Society of Exploration Geophysics: Tulsa, OK, USA, 2005; pp. 434–557. [Google Scholar] [CrossRef]
- Cassidy, N.J. Electrical and magnetic properties of rocks, soils, fluids. In Ground Penetrating Radar Theory and Applications; Jol, H.M., Ed.; Elsevier: Amsterdam, The Netherlands, 2009; Chapter 2; pp. 41–67. [Google Scholar] [CrossRef]
- Sperl, C. Determination of Spatial and Temporal Variation of the Soil Water Content in an Agro-Ecosystem with Ground-Penetrating Radar. Ph.D. Thesis, Technische Universitat München, Munich, Germany, 1999. [Google Scholar]
- Lambot, S.; Rhebergen, J.; van den Bosch, I.; Slob, E.C.; Vanclooster, M. Measuring the soil water content profile of a sandy soil with an off-ground monostatic ground penetrating radar. Vadose Zone J. 2004, 3, 1063–1071. [Google Scholar] [CrossRef]
- Zhang, J.; Lin, H.; Doolittle, J. Soil layering and preferential flow impacts on seasonal changes of GPR signals in two contrasting soils. Geoderma 2014, 213, 560–569. [Google Scholar] [CrossRef]
- Chew, W.C. Waves and Fields in Inhomogeneous Media; Wiley-IEEE Press: Piscataway, NJ, USA, 1995. [Google Scholar]
- Galagedara, L.W.; Parkin, G.W.; Redman, J.D. An analysis of the ground penetrating radar direct ground wave method for soil water content measurement. Hydrol. Process. 2003, 17, 3615–3628. [Google Scholar] [CrossRef]
- Galagedara, L.W.; Parkin, G.W.; Redman, J.D.; Endres, A.L. Assessment of soil moisture content measured by borehole GPR and TDR under transient irrigation and drainage. J. Environ. Eng. Geophys. 2003, 8, 77–86. [Google Scholar] [CrossRef]
- Wijewardana, Y.G.N.S.; Galagedara, L.W. Estimation of spatio-temporal variability of soil water content in agricultural fields with ground penetrating radar. J. Hydrol. 2010, 391, 24–33. [Google Scholar] [CrossRef]
- Chanzy, A.; Tarussov, A.; Bonn, F.; Judge, A. Soil water content determination using a digital ground penetrating radar. Soil Sci. Soc. Am. J. 1996, 60, 1318–1326. [Google Scholar] [CrossRef]
- van Overmeeren, R.A.; Sariowan, S.V.; Gehrels, J.C. Ground penetrating radar for determining volumetric soil water content; results of comparative measurements at two test sites. J. Hydrol. 1997, 197, 316–338. [Google Scholar] [CrossRef]
- Hubbard, S.; Grote, K.; Rubin, Y. Mapping the volumetric soil water content of a california vineyard using high-frequency GPR ground wave data. Lead. Edge 2002, 21, 552. [Google Scholar] [CrossRef]
- Huisman, J.A.; Bouten, W. Accuracy and reproducibility of mapping surface soil water content with the ground wave of ground-penetrating radar. J. Environ. Eng. Geophys. 2003, 8, 67–75. [Google Scholar] [CrossRef]
- Galagedara, L.W.; Parkin, G.W.; Redman, J.D.; Von Bertoldi, P.; Endres, A.L. Field studies of the GPR ground wave method for estimating soil water content during irrigation and drainage. J. Hydrol. 2005, 301, 182–197. [Google Scholar] [CrossRef]
- Galagedara, L.W.; Parkin, G.W.; Redman, J.D. Measuring and modeling of direct ground wave depth penetration under transient soil moisture conditions. Subsurf. Sens. Technolo. Appli. 2005, 6, 193–205. [Google Scholar] [CrossRef]
- Illawathure, C.; Parkin, G.; Lambot, S.; Galagedara, L. Evaluating soil moisture estimation from ground-penetrating radar hyperbola fitting with respect to a systematic time-domain reflectometry data collection in a boreal podzolic agricultural field. Hydrol. Process. 2020, 34, 1428–1445. [Google Scholar] [CrossRef]
- Grote, K.; Hubbard, S.; Rubin, Y. Field-scale estimation of volumetric water content using ground penetrating radar ground wave techniques. Water Resour. Res. 2003, 39, 1–14. [Google Scholar] [CrossRef]
- Wollschläger, U.; Roth, K. Estimation of temporal changes of volumetric soil water content from ground-penetrating radar reflections. Subsurf. Sens. Technol. Appli. 2005, 6, 207–218. [Google Scholar] [CrossRef]
- Lu, Y.; Song, W.; Lu, J.; Wang, X.; Tan, Y. An examination of soil moisture estimation using ground penetrating radar in desert steppe. Water 2017, 9, 521. [Google Scholar] [CrossRef]
- Lunt, I.A.; Hubbard, S.S.; Rubin, Y. Soil moisture content estimation using ground-penetrating radar reflection data. J. Hydrol. 2005, 307, 254–269. [Google Scholar] [CrossRef]
- Ercoli, M.; Di Matteo, L.; Pauselli, C.; Mancinelli, P.; Frapiccini, S.; Talegalli, L.; Cannata, A. Integrated GPR and laboratory water content measures of sandy soils: From laboratory to field scale. Constr. Build. Mater. 2018, 159, 734–744. [Google Scholar] [CrossRef]
- Stoffregen, H.; Zenker, T.; Wessolek, G. Accuracy of soil water content measurements using ground penetrating radar: Comparison of ground penetrating radar and lysimeter data. J. Hydrol. 2002, 267, 201–206. [Google Scholar] [CrossRef]
- Loeffler, O.; Bano, M. Ground penetrating radar measurements in a controlled vadose zone: Influence of the water content. Vadose Zone J. 2004, 3, 1082–1092. [Google Scholar] [CrossRef]
- Zhou, L.; Yu, D.; Wang, Z.; Wang, X. Soil water content estimation using high-frequency ground penetrating radar. Water 2019, 11, 1036. [Google Scholar] [CrossRef]
- Cui, X.; Guo, L.; Chen, J.; Chen, X.; Zhu, X. Estimating tree-root biomass in different depths using ground-penetrating radar: Evidence from a controlled experiment. IEEE Trans. Geosci. Remote Sens. 2019, 51, 3410–3423. [Google Scholar] [CrossRef]
- Liu, X.; Cui, X.; Guo, L.; Chen, J.; Li, W.; Yang, D.; Cao, X.; Chen, X.; Liu, Q.; Lin, H. Non-invasive estimation of root zone soil moisture from coarse root reflections in ground-penetrating radar images. Plant Soil 2019, 436, 623–639. [Google Scholar] [CrossRef]
- Sham, J.F.C.; Lai, W.W.-L.; Leung, C.H.C. Effects of homogeneous/heterogeneous water distribution on GPR wave velocity in a soil’s wetting and drying process. In Proceedings of the 16th International Conference on Ground Penetrating Radar, Hong Kong, China, 13–16 June 2016; IEEE: Manhattan, NY, USA, 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Steelman, C.M.; Endres, A.L. Assessing vertical soil moisture dynamics using multi-frequency GPR common-midpoint soundings. J. Hydrol. 2012, 436–437, 51–66. [Google Scholar] [CrossRef]
- Huisman, J.A.; Sperl, C.; Bouten, W.; Verstraten, J.M. Soil water content measurements at different scales: Accuracy of time domain reflectometry and ground-penetrating radar. J. Hydrol. 2001, 245, 48–58. [Google Scholar] [CrossRef]
- Huisman, J.A.; Snepvangers, J.J.J.C.; Bouten, W.; Heuvelink, G.B.M. Monitoring temporal development of spatial soil water content variation: Comparison of ground penetrating radar and time domain reflectometry. Vadose Zone J. 2003, 2, 519–529. [Google Scholar] [CrossRef]
- Huisman, J.A.; Snepvangers, J.J.J.C.; Bouten, W.; Heuvelink, G.B.M. Mapping spatial variation in surface soil water content: Comparison of ground-penetrating radar and time domain reflectometry. J. Hydrol. 2002, 269, 194–207. [Google Scholar] [CrossRef]
- Grote, K.; Anger, C.; Kelly, B.; Hubbard, S.; Rubin, Y. Characterization of soil water content variability and soil texture using GPR groundwave techniques. J. Environ. Eng. Geophys. 2010, 15, 93–110. [Google Scholar] [CrossRef]
- Minet, J.; Bogaert, P.; Vanclooster, M.; Lambot, S. Validation of ground penetrating radar full-waveform inversion for field scale soil moisture mapping. J. Hydrol. 2012, 424, 112–123. [Google Scholar] [CrossRef]
- Ardekani, M.R.M. Off- and on-ground GPR techniques for field-scale soil moisture mapping. Geoderma 2013, 200–201, 55–66. [Google Scholar] [CrossRef]
- Thitimakorn, T.; Kummode, S.; Kupongsak, S. Determination of spatial and temporal variations of volumetric soil water content using ground penetrating radar: A case study in Thailand. Appl. Environ. Res. 2016, 38, 33–46. [Google Scholar] [CrossRef]
- Cao, Q.; Song, X.; Wu, H.; Gao, L.; Liu, F.; Yang, S.; Zhang, G. Mapping the response of volumetric soil water content to an intense rainfall event at the field scale using GPR. J. Hydrol. 2020, 583, 124605. [Google Scholar] [CrossRef]
- Weihermüller, L.; Huisman, J.A.; Lambot, S.; Herbst, M.; Vereecken, H. Mapping the spatial variation of soil water content at the field scale with different ground penetrating radar techniques. J. Hydrol. 2007, 340, 205–216. [Google Scholar] [CrossRef]
- Pallavi, B.; Saito, H.; Kato, M. Application of GPR ground wave for mapping of spatiotemporal variations in the surface moisture content at a natural field site. In Proceedings of the 19th World Congress of Soil Science: Soil Solutions for a Changing World, Brisbane, Australia, 1–6 August 2010; Gilkes, R.J., Prakougkep, N., Eds.; Australian Society of Soil Science: Warragul, Australia, 2010; pp. 13–16. [Google Scholar]
- Galagedara, L.W.; Redman, J.D.; Parkin, G.W.; Annan, A.P.; Endres, A.L. Numerical modeling of GPR to determine the direct ground wave sampling depth. Vadose Zone J. 2005, 4, 1096–1106. [Google Scholar] [CrossRef]
- Pallavi, B.; Saito, H.; Kato, M. Estimating depth of influence of GPR ground wave in lysimeter experiment. J. Arid. Land Stud. 2009, 19, 121–124. [Google Scholar]
- Binley, A.; Winship, P.; West, L.J.; Pokar, M.; Middleton, R. Seasonal variation of moisture content in unsaturated sandstone inferred from borehole radar and resistivity profiles. J. Hydrol. 2002, 267, 160–172. [Google Scholar] [CrossRef]
- Strobach, E.; Harris, B.D.; Dupuis, J.C.; Kepic, A.W. Time-lapse borehole radar for monitoring rainfall infiltration through podosol horizons in a sandy vadose zone. Water Resour. Res. 2014, 50, 2140–2163. [Google Scholar] [CrossRef]
- Klotzsche, A.; Lärm, L.; Vanderborght, J.; Cai, G.; Morandage, S.; Zörner, M.; Vereecken, H.; Kruk, J. Monitoring soil water content using time-lapse horizontal borehole GPR data at the field-plot scale. Vadose Zone J. 2019, 18, 190044. [Google Scholar] [CrossRef]
- Yu, Y.; Klotzsche, A.; Weihermüller, L.; Huisman, J.A.; Vanderborght, J.; Vereecken, H.; van der Kruk, J. Measuring vertical soil water content profiles by combining horizontal borehole and dispersive surface ground penetrating radar data. Near Surf. Geophys. 2020, 18, 275–294. [Google Scholar] [CrossRef]
- Rucker, D.F.; Ferré, T.P.A. Near-surface water content estimation with borehole ground penetrating radar using critically refracted waves. Vadose Zone J. 2003, 2, 247–252. [Google Scholar] [CrossRef]
- Rucker, D.F.; Ferré, T.P.A. Correcting water content measurement errors associated with critically refracted first arrivals on zero offset profiling borehole ground penetrating radar profiles. Vadose Zone J. 2004, 3, 278–287. [Google Scholar] [CrossRef]
- Rucker, D.F.; Ferré, T.P.A. Automated water content reconstruction of zero-offset borehole ground penetrating radar data using simulated annealing. J. Hydrol. 2005, 309, 1–16. [Google Scholar] [CrossRef]
- Lambot, S.; Weihermüller, L.; Huisman, J.A.; Vereecken, H.; Vanclooster, M.; Slob, E.C. Analysis of air-launched ground-penetrating radar techniques to measure the soil surface water content. Water Resour. Res. 2006, 42, W11403. [Google Scholar] [CrossRef]
- al Hagrey, S.A.; Müller, C. GPR study of pore water content and salinity in sand. Geophys. Prospect. 2000, 48, 63–85. [Google Scholar] [CrossRef]
- Redman, J.D.; Davis, J.L.; Galagedara, L.W.; Parkin, G.W. Field studies of GPR air launched surface reflectivity measurements of soil water content. In Proceedings of the 9th International Conference on Ground Penetrating Radar, Santa Barbara, CA, USA, 29 April–2 May 2002; Koppenjan, S.K., Lee, H., Eds.; SPIE: Bellingham, WA, USA, 2002; Volume 4758, pp. 156–161. [Google Scholar] [CrossRef]
- Redman, D.; Galagedara, L.; Parkin, G. Measuring soil water content with the ground penetrating radar surface reflectivity method: Effects of spatial variability. In Proceedings of the 2003 ASABE Annual Meeting (Paper 032276), Las Vegas, NV, USA, 27 July 2003; American Society of Agricultural and Biological Engineers: St. Joseph, MI, USA, 2003. [Google Scholar]
- Pettinelli, E.; Vannaroni, G.; Di Pasquo, B.; Mattei, E.; Di Matteo, A.; De Santis, A.; Annan, A.P. Correlation between near-surface electromagnetic soil parameters and early-time GPR signals: An experimental study. Geophysics 2007, 72, A25–A28. [Google Scholar] [CrossRef]
- Pettinelli, E.; Di Matteo, A.; Beaubien, S.E.; Mattei, E.; Lauro, S.E.; Galli, A.; Vannaroni, G. A controlled experiment to investigate the correlation between early-time signal attributes of ground-coupled radar and soil dielectric properties. J. Appl. Geophys. 2014, 101, 68–76. [Google Scholar] [CrossRef]
- Algeo, J.; Van Dam, R.L.; Slater, L. Early-time GPR: A method to monitor spatial variations in soil water content during irrigation in clay soils. Vadose Zone J. 2016, 15, 1–9. [Google Scholar] [CrossRef]
- Ferrara, C.; Barone, P.M.; Steelman, C.M.; Pettinelli, E.; Endres, A.L. Monitoring shallow soil water content under natural field conditions using the early-time GPR signal technique. Vadose Zone J. 2013, 12, 1–9. [Google Scholar] [CrossRef]
- Ferrara, C.; Barone, P.M.; Mattei, E.; Galli, A.; Comite, D.; Lauro, S.E.; Vannaroni, G.; Pettinelli, E. An evaluation of the early-time GPR amplitude technique for electrical conductivity monitoring. In Proceedings of the IWAGPR 2013—7th International Workshop on Advanced Ground Penetrating Radar, Nantes, France, 2–5 July 2013; IEEE: Manhattan, NY, USA, 2013; pp. 1–4. [Google Scholar] [CrossRef]
- Algeo, J.; Slater, L.; Binley, A.; Van Dam, R.L.; Watts, C. A comparison of ground-penetrating radar early-time signal approaches for mapping changes in shallow soil water content. Vadose Zone J. 2018, 17, 1–11. [Google Scholar] [CrossRef]
- Ernst, J.R.; Green, A.G.; Maurer, H.; Holliger, K. Application of a new 2D timedomain full-waveform inversion scheme to crosshole radar data. Geophysics 2007, 72, J53–J64. [Google Scholar] [CrossRef]
- Klotzsche, A.; van der Kruk, J.; Meles, G.A.; Doetsch, J.; Maurer, H.; Linde, N. Full-waveform inversion of crosshole groundpenetrating radar data to characterize a gravel aquifer close to the Thur River, Switzerland. Near Surf. Geophys. 2010, 8, 635–649. [Google Scholar] [CrossRef]
- Meles, G.A.; van der Kruk, J.; Greenhalgh, S.A.; Ernst, J.R.; Maurer, H.; Green, A.G. A new vector waveform inversion algorithm for simultaneous updating of conductivity and permittivity parameters from combination crosshole/borehole-to-surface GPR data. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3391–3407. [Google Scholar] [CrossRef]
- Klotzsche, A.; van der Kruk, J.; Bradford, J.; Vereecken, H. Detection of spatially limited highporosity layers using crosshole GPR signal analysis and full-waveform inversion. Water Resour. Res. 2014, 50, 6966–6985. [Google Scholar] [CrossRef]
- Gueting, N.; Vienken, T.; Klotzsche, A.; van der Kruk, J.; Vanderborght, J.; Caers, J.; Vereecken, H.; Englert, A. High resolution aquifer characterization using crosshole GPR full-waveform tomography: Comparison with direct-push and tracer test data. Water Resour. Res. 2017, 53, 49–72. [Google Scholar] [CrossRef]
- Yu, Y.; Huisman, J.A.; Klotzsche, A.; Vereecken, H.; Weihermüller, L. Coupled full-waveform inversion of horizontal borehole ground penetrating radar data to estimate soil hydraulic parameters: A synthetic study. J. Hydrol. 2022, 610, 127817. [Google Scholar] [CrossRef]
- Lambot, S.; Slob, E.; Chavarro, D.; Lubczynski, M.; Vereecken, H. Measuring soil surface water content in irrigated areas of southern Tunisia using full-waveform inversion of proximal GPR data. Near Surf. Geophys. 2008, 6, 403–410. [Google Scholar] [CrossRef]
- Lambot, S.; André, F. Full-wave modeling of near-field radar data for planar layered media reconstruction. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2295–2303. [Google Scholar] [CrossRef]
- Jonard, F.; Weihermuller, L.; Jadoon, K.Z.; Schwank, M.; Vereecken, H.; Lambot, S. Mapping field-scale soil moisture with L-band radiometer and ground-penetrating radar over bare soil. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2863–2875. [Google Scholar] [CrossRef]
- Jonard, F.; Weihermüller, J.; Vereecken, H.; Lambot, S. Accounting for soil surface roughness in the inversion of ultrawideband offground GPR signal for soil moisture retrieval. Geophysics 2012, 77, H1–H7. [Google Scholar] [CrossRef]
- de Mahieu, A.; Ponette, Q.; Mounir, F.; Lambot, S. Using GPR to analyze regeneration success of cork oaks in the Maâmora forest (Morocco). NDT E Int. 2020, 115, 102297. [Google Scholar] [CrossRef]
- Wu, K.; Lambot, S. Analysis of low-frequency drone-borne GPR for root-zone soil electrical conductivity characterization. IEEE Trans. Geosci. Remote Sens. 2022, 60, 2006213. [Google Scholar] [CrossRef]
- Tran, A.P.; Vanclooster, M.; Lambot, S. Improving soil moisture profile reconstruction from ground-penetrating radar data: A maximum likelihood ensemble filter approach. Hydrol. Earth Syst. Sci. 2013, 17, 2543–2556. [Google Scholar] [CrossRef]
- De Coster, A.; Tran, A.P.; Lambot, S. Fundamental analyses on layered media reconstruction using GPR and full-wave inversion in near-field conditions. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5143–5158. [Google Scholar] [CrossRef]
- Wu, K.; Desesquelles, H.; Cockenpot, R.; Guyard, L.; Cuisiniez, V.; Lambot, S. Ground-penetrating radar full-wave inversion for soil moisture mapping in Trench-Hill potato fields for precise irrigation. Remote Sens. 2022, 14, 6046. [Google Scholar] [CrossRef]
- Lambot, S.; Slob, E.C.; van den Bosch, I.; Stockbroeckx, B.; Vanclooster, M. Modeling of ground-penetrating radar for accurate characterization of subsurface electric properties. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2555–2568. [Google Scholar] [CrossRef]
- Nimmo, J.R. Porosity and pore size distribution. Ency. Soils Environ. 2001, 3, 295–303. [Google Scholar] [CrossRef]
- Ghose, R.; Slob, E.C. Quantitative integration of seismic and GPR reflections to derive unique estimates for water saturation and porosity in subsoil. Geophys. Res. Lett. 2006, 33, 2–5. [Google Scholar] [CrossRef]
- Khalil, M.A.; Hafez, M.A.; Santos, F.M.; Ramalho, E.C.; Mesbah, H.S.A.; El-Qady, G.M. An approach to estimate porosity and groundwater salinity by combined application of GPR and VES: A case study in the Nubian sandstone aquifer. Near Surf. Geophys. 2010, 8, 223–233. [Google Scholar] [CrossRef]
- Hillel, D. Environmental Soil Physics; Academic Press: San Diego, CA, USA, 1998. [Google Scholar]
- Bradford, J.H.; Clement, W.P.; Barrash, W. Estimating porosity with ground-penetrating radar reflection tomography: A controlled 3-D experiment at the boise hydrogeophysical research site. Water Resour. Res. 2009, 46, 1–11. [Google Scholar] [CrossRef]
- Akinsunmade, A.; Tomecka-Suchoń, S.; Pysz, P. Correlation between agrotechnical properties of selected soil types and corresponding GPR response. Acta Geophys. 2019, 67, 1913–1919. [Google Scholar] [CrossRef]
- Akinsunmade, A. GPR imaging of traffic compaction effects on soil structures. Acta Geophys. 2021, 69, 643–653. [Google Scholar] [CrossRef]
- Akinsunmade, A.; Tomecka-Suchoń, S.; Kiełbasa, P.; Juliszewski, T.; Pysz, P.; Karczewski, J.; Zagórda, M. GPR geophysical method as a remediation tool to determine zones of high penetration resistance of soil. J. Phys. Conf. Ser. 2021, 1782, 012001. [Google Scholar] [CrossRef]
- Wang, P.; Hu, Z.; Zhao, Y.; Li, X. Experimental study of soil compaction effects on GPR signals. J. Appl. Geophys. 2016, 126, 128–137. [Google Scholar] [CrossRef]
- Jonard, F.; Mahmoudzadeh, M.; Roisin, C.; Weihermüller, L.; André, F.; Minet, J.; Lambot, S. Characterization of tillage effects on the spatial variation of soil properties using ground-penetrating radar and electromagnetic induction. Geoderma 2013, 207, 310–322. [Google Scholar] [CrossRef]
- Muñiz, E.; Shaw, R.K.; Gimenez, D.; Williams, C.A.; Kenny, L. Use of ground-penetrating radar to determine depth to compacted layer in soils under pasture. In Digital Soil Morphometrics; Hartemink, A.E., Minasny, B., Eds.; Springer Nature: Cham, Switzerland, 2016; pp. 411–421. [Google Scholar] [CrossRef]
- Saarenketo, T. Electrical properties of water in clay and silty soils. J. Appl. Geophys. 1998, 40, 73–88. [Google Scholar] [CrossRef]
- Awak, E.A.; George, A.M.; Urang, J.G.; Udoh, J.T. Determination of soil electrical conductivity using ground penetrating radar (GPR) for precision agriculture. Int. J. Sci. Eng. Res. 2017, 8, 1971–1977. [Google Scholar]
- Corwin, D.L.; Scudiero, E. Review of soil salinity assessment for agriculture across multiple scales using proximal and/or remote sensors. In Advances in Agronomy; Sparks, D.L., Ed.; Elsevier: Amsterdam, The Netherlands, 2019; Volume 158, pp. 1–130. [Google Scholar] [CrossRef]
- Miller, J.J.; Curtain, D. Electrical conductivity and soluble ions. In Soil Sampling and Methods of Analysis, 2nd ed.; Carter, M.R., Gregorich, E.G., Eds.; CRC Press, Taylor & Francis Group: Oxfordshire, UK, 2008; pp. 161–171. [Google Scholar] [CrossRef]
- Corwin, D.L.; Lesch, S.M. Application of soil electrical conductivity to precision agriculture: Theory, principles, and guidelines. Agron. J. 2003, 95, 455–471. [Google Scholar] [CrossRef]
- Corwin, D.L.; Lesch, S.M. Apparent soil electrical conductivity measurements in agriculture. Comput. Electron. Agric. 2005, 46, 11–43. [Google Scholar] [CrossRef]
- Altdorff, D.; Galagedara, L.; Nadeem, M.; Cheema, M.; Unc, A. Effect of agronomic treatments on the accuracy of soil moisture mapping by electromagnetic induction. Catena 2018, 164, 96–106. [Google Scholar] [CrossRef]
- Badewa, E.; Unc, A.; Cheema, M.; Kavanagh, V.; Galagedara, L. Soil moisture mapping using multi-frequency and multi-coil electromagnetic induction sensors on managed podzols. Agronomy 2018, 8, 224. [Google Scholar] [CrossRef]
- Badewa, E.; Unc, A.; Cheema, M.; Galagedara, L. Temporal stability of soil apparent electrical conductivity (ECa) in managed podzols. Acta Geophys. 2019, 67, 1107–1118. [Google Scholar] [CrossRef]
- Wu, B.; Li, X.; Zhao, K.; Jiang, T.; Zheng, X.; Li, X.; Gu, L.; Wang, X. A nondestructive conductivity estimating method for saline-alkali land based on ground penetrating radar. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2605–2614. [Google Scholar] [CrossRef]
- Rhoades, J.D.; Corwin, D.L.; Lesch, S.M. Geospatial measurements of soil electrical conductivity to assess soil salinity and diffuse salt loading from irrigation. In Geophysical Monograph Series: Assessment of Non-Point Source Pollution in the Vadose Zone; Corwin, D.L., Loague, K., Ellsworth, T.R., Eds.; American Geophysical Union: Washington, DC, USA, 1998; Volume 108, pp. 197–215. [Google Scholar] [CrossRef]
- Mimrose, D.M.C.S.; Galagedara, L.W.; Parkin, G.W.; Wijewardana, Y.G.N.S. Investigating the effect of electrical conductivity in irrigation water on reflected wave energy of GPR. Trop. Agric. 2011, 159, 29–46. [Google Scholar]
- Alsharahi, G.; Driouach, A.; Faize, A. Performance of GPR influenced by electrical conductivity and dielectric constant. Proc. Technol. 2016, 22, 570–575. [Google Scholar] [CrossRef]
- Wijewardana, N.S.; Galagedara, L.W.; Mowjood, M.I.M. Assessment of groundwater contamination by landfill leachate with ground penetrating radar. In Proceedings of the 14th International Conference on Ground Penetrating Radar, Shanghai, China, 4–8 June 2012; pp. 728–732. [Google Scholar] [CrossRef]
- Wijewardana, Y.N.S.; Galagedara, L.W.; Mowjood, M.I.M.; Kawamoto, K. Assessment of inorganic pollutant contamination in groundwater using ground penetrating radar (GPR). Trop. Agric. Res. 2015, 26, 700–706. [Google Scholar] [CrossRef]
- Wijewardana, Y.N.S.; Shilpadi, A.T.; Mowjood, M.I.M.; Kawamoto, K.; Galagedara, L.W. Ground-penetrating radar (GPR) responses for sub-surface salt contamination and solid waste: Modeling and controlled lysimeter studies. Environ. Monit. Assess. 2017, 189, 57. [Google Scholar] [CrossRef]
- Tsoflias, G.P.; Becker, M.W. Ground-penetrating-radar response to fracture-fluid salinity: Why lower frequencies are favorable for resolving salinity changes. Geophysics 2008, 73, J25–J30. [Google Scholar] [CrossRef]
- Di Prima, S.; Winiarski, T.; Angulo-Jaramillo, R.; Stewart, R.D.; Castellini, M.; Abou Najm, M.R.; Ventrella, D.; Pirastru, M.; Giadrossich, F.; Capello, G.; et al. Detecting infiltrated water and preferential flow pathways through time-lapse ground-penetrating radar surveys. Sci. Total Environ. 2010, 726, 138511. [Google Scholar] [CrossRef] [PubMed]
- Jury, W.A.; Gardner, W.R.; Gardner, W.H. Soil Physics, 5th ed.; John Wiley: Hoboken, NY, USA, 1991. [Google Scholar]
- Cassiani, G.; Binley, A. Modeling unsaturated flow in a layered formation under quasi-steady state conditions using geophysical data constraints. Adv. Water Resour. 2005, 28, 467–477. [Google Scholar] [CrossRef]
- Kowalsky, M.B.; Finsterle, S.; Peterson, J.; Hubbard, S.; Rubin, Y.; Majer, E.; Ward, A.; Gee, G. Estimation of field-scale soil hydraulic and dielectric parameters through joint inversion of GPR and hydrological data. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- Jadoon, K.Z.; Slob, E.; Vanclooster, M.; Vereecken, H.; Lambot, S. Uniqueness and stability analysis of hydrogeophysical inversion for time-lapse ground penetrating radar estimates of shallow soil hydraulic properties. Water Resour. Res. 2008, 44, W09421. [Google Scholar] [CrossRef]
- Jadoon, K.Z.; Weihermuller, L.; Scharnagl, B.; Kowalsky, M.B.; Bechtold, M.; Hubbard, S.S.; Vereecken, H.; Lambot, S. Estimation of soil hydraulic parameters in the field by integrated hydrogeophysical inversion of time-lapse ground-penetrating radar data. Vadose Zone J. 2012, 11. [Google Scholar] [CrossRef]
- Igel, J.; Stadler, S.; Guenther, T. High-resolution investigation of the capillary transition zone and its influence on GPR signatures. In Proceedings of the 16th International Conference on Ground Penetrating Radar (GPR), Hong Kong, China, 13–16 June 2016; IEEE: Manhattan, NY, USA, 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Essam, D.; Ahmed, M.; Abouelmagd, A.; Soliman, F. Monitoring temporal variations in groundwater levels in urban areas using ground penetrating radar. Sci. Total Environ. 2020, 703, 134986. [Google Scholar] [CrossRef]
- van Overmeeren, R.A. Radar facies of unconsolidated sediments in The Netherlands: A radar stratigraphic interpretation method for hydrogeology. J. Appl. Geophys. 1998, 40, 1–18. [Google Scholar] [CrossRef]
- Doolittle, J.A.; Jenkinson, B.; Hopkins, D.; Ulmer, M.; Tuttle, W. Hydropedological investigations with ground-penetrating radar (GPR): Estimating water-table depths and local ground-water flow pattern in areas of coarse-textured soils. Geoderma 2006, 131, 317–329. [Google Scholar] [CrossRef]
- Mahmoudzadeh, M.R.; Frances, A.P.; Lubczynski, M.; Lambot, S. Using ground penetrating radar to investigate the water table depth in weathered granites—Sardon case study, Spain. J. Appl. Geophys. 2012, 79, 17–26. [Google Scholar] [CrossRef]
- Paz, C.; Alcalá, F.J.; Carvalho, J.M.; Ribeiro, L. Current uses of ground penetrating radar in groundwater-dependent ecosystems research. Sci. Total Environ. 2017, 595, 868–885. [Google Scholar] [CrossRef]
- Nguyen, B.L.; Bruining, J.; Slob, E.C.; Hopman, V. Delineation of air/water capillary transition zone from GPR data. SPE Reserv. Eng. 1998, 1, 319–324. [Google Scholar] [CrossRef]
- Onishi, K.; Rokugawa, S.; Katoh, Y.; Tokunaga, T. Influence of capillary fringe on the groundwater survey using ground-penetrating radar. ASEG Ext. Abstr. 2004, 1, 1–4. [Google Scholar] [CrossRef]
- Bano, M. Effects of the transition zone above a water table on the reflection of GPR waves. Geophys. Res. Lett. 2006, 33, L13309. [Google Scholar] [CrossRef]
- Illawathure, C.; Cheema, M.; Kavanagh, V.; Galagedara, L. Distinguishing capillary fringe reflection in a GPR profile for precise water table depth estimation in a boreal podzolic soil field. Water 2020, 12, 1670. [Google Scholar] [CrossRef]
- Endres, A.L.; Clement, W.P.; Rudolph, D.L. Ground penetrating radar imaging of an aquifer during a pumping test. Ground Water 2000, 38, 566–576. [Google Scholar] [CrossRef]
- Bentley, L.R.; Trenholm, N.M. The accuracy of water table elevation estimates determined from ground penetrating radar data. J. Environ. Eng. Geophys. 2002, 7, 37–53. [Google Scholar] [CrossRef]
- Daniels, J.J.; Allred, B.; Binley, A.; Labrecque, D.; Alumbaugh, D. Hydrogeophysical case studies in the vadose zone. In Hydrogeophysics; Rubin, Y., Hubbard, S.S., Eds.; Springer: Basel, Switzerland, 2005; Volume 50, pp. 413–440. [Google Scholar] [CrossRef]
- Costall, R.; Harris, B.D.; Teo, B.; Schaa, R.; Wagner, F.M.; Pigois, J.P. Groundwater throughflow and seawater intrusion in high quality coastal aquifers. Sci. Rep. 2020, 10, 9866. [Google Scholar] [CrossRef]
- Kowalczyk, S.; Lejzerowicz, A.; Kowalczyk, B. Groundwater table level changes based on ground penetrating radar images: A case study. In Proceedings of the 17th International Conference on Ground Penetrating Radar, Rapperswil, Switzerland, 18–21 June 2018; IEEE: Manhattan, NY, USA, 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Annan, A.P.; Cosway, S.W.; Redman, J.D. Water table detection with ground-penetrating radar. In SEG Technical Program Expanded Abstracts 1991; Society of Exploration Geophysicists: Houston, TX, USA, 1991; pp. 494–496. [Google Scholar] [CrossRef]
- Meadows, D.G.; Young, M.H.; McDonald, E.V. Estimating the fine soil fraction of desert pavements using ground penetrating radar. Vadose Zone J. 2006, 5, 720–730. [Google Scholar] [CrossRef]
- De Benedetto, D.; Castrignano, A.; Sollitto, D.; Modugno, F.; Buttafuoco, G.; lo Papa, G. Integrating geophysical and geostatistical techniques to map the spatial variation of clay. Geoderma 2012, 171, 53–63. [Google Scholar] [CrossRef]
- Benedetto, F.; Tosti, F. GPR spectral analysis for clay content evaluation by the frequency shift method. J. Appl. Geophys. 2013, 97, 89–96. [Google Scholar] [CrossRef]
- Tosti, F.; Patriarca, C.; Slob, E.; Benedetto, A.; Lambot, S. Clay content evaluation in soils through GPR signal processing. J. Appl. Geophys. 2013, 97, 69–80. [Google Scholar] [CrossRef]
- van Dam, R.L.; van den Berg, E.H.; van Heteren, S.; Kasse, C.; Kenter, J.A.M.; Groen, K. Influence of Organic Matter in Soils on Radar-Wave Reflection: Sedimentological Implications. J. Sediment. Res. 2002, 72, 341–352. [Google Scholar] [CrossRef]
- Comas, X.; Terry, N.; Hribljan, J.A.; Lilleskov, E.A.; Suarez, E.; Chimner, R.A.; Kolka, R.K. Estimating belowground carbon stocks in peatlands of the Ecuadorian paramo using ground penetrating radar (GPR). J. Geophys. Res. 2017, 122, 370–386. [Google Scholar] [CrossRef]
- Shen, X.; Foster, T.; Baldi, H.; Dobreva, I.; Burson, B.; Hays, D.; Tabien, R.; Jessup, R. Quantification of soil organic carbon in biochar-amended soil using ground penetrating radar (GPR). Remote Sens. 2019, 11, 2874. [Google Scholar] [CrossRef]
- De Benedetto, D.; Barca, E.; Castellini, M.; Popolizio, S.; Lacolla, G.; Stellacci, A.M. Prediction of soil organic carbon at field scale by regression kriging and multivariate adaptive regression splines using geophysical covariates. Land 2022, 11, 381. [Google Scholar] [CrossRef]
- Ryazantsev, P.A.; Hartemink, A.E.; Bakhmet, O.N. Delineation and description of soil horizons using ground-penetrating radar for soils under boreal forest in Central Karelia (Russia). Catena 2022, 214, 106285. [Google Scholar] [CrossRef]
- Doolittle, J.A.; Collins, M.E. A comparison of EM induction and GPR methods in areas of karst. Geoderma 1998, 85, 83–102. [Google Scholar] [CrossRef]
- Stroh, J.C.; Archer, S.; Doolittle, J.A.; Wilding, L. Detection of edaphic discontinuities with ground-penetrating radar and electromagnetic induction. Landsc. Ecol. 2001, 16, 377–390. [Google Scholar] [CrossRef]
- André, F.; van Leeuwen, C.; Saussez, S.; Van Durmen, R.; Bogaert, P.; Moghadas, D.; de Rességuier, L.; Delvaux, B.; Vereecken, H.; Lambot, S. High-resolution imaging of a vineyard in south of France using ground-penetrating radar, electromagnetic induction and electrical resistivity tomography. J. Appl. Geophys. 2012, 78, 113–122. [Google Scholar] [CrossRef]
- Nováková, E.; Karous, M.; Zajíček, A.; Karousová, M. Evaluation of ground penetrating radar and vertical electrical sounding methods to determine soil horizons and bedrock at the locality Dehtáře. Soil Water Res. 2013, 8, 105–112. [Google Scholar] [CrossRef]
- Winkelbauer, J.; Völkel, J.; Leopold, M.; Bernt, N. Methods of surveying the thickness of humous horizons using ground penetrating radar (GPR): An example from the Garmisch-Partenkirchen area of the Northern Alps. Eur. J. For. Res. 2011, 130, 799–812. [Google Scholar] [CrossRef]
- Allred, B.J.; Ehsani, M.R.; Daniels, J.J. General Considerations for Geophysical Methods Applied to Agriculture. In Handbook of Agricultural Geophysics, 1st ed.; Allred, B.J., Daniels, J.J., Ehsani, M.R., Eds.; CRC Press, Taylor and Francis Group: Boca Raton, FL, USA, 2008; pp. 3–16. [Google Scholar]
- Allred, B.J.; Ehsani, M.R.; Saraswat, D. The impact of temperature and shallow hydrologic conditions on the magnitude and spatial pattern consistency of electromagnetic induction measured soil electrical conductivity. Trans. ASABE 2005, 48, 2123–2135. [Google Scholar] [CrossRef]
- Padhi, J.; Misra, R.K. Sensitivity of EM38 in determining soil water distribution in an irrigated wheat field. Soil Tillage Res. 2011, 117, 93–102. [Google Scholar] [CrossRef]
- Robinson, D.A.; Abdu, H.; Lebron, I.; Jones, S.B. Imaging of hill-slope soil moisture wetting patterns in a semi-arid oak savanna catchment using time-lapse electromagnetic induction. J. Hydrol. 2012, 416, 39–49. [Google Scholar] [CrossRef]
- Visconti, F.; de Paz, J.M. Sensitivity of soil electromagnetic induction measurements to salinity, water content, clay, organic matter and bulk density. Precis. Agric. 2021, 22, 1559–1577. [Google Scholar] [CrossRef]
- Sheets, K.R.; Hendrickx, J.M.H. Non-invasive soil water content measurement using electromagnetic induction. Water Resour. Res. 1995, 31, 2401–2409. [Google Scholar] [CrossRef]
- McNeill, J.D. Electromagnetic Terrain Conductivity Measurement at Low Induction Numbers; Technical Note TN-6; Geonics Ltd.: Mississauga, ON, Canada, 1980; Available online: http://www.geonics.com/pdfs/technicalnotes/tn6.pdf (accessed on 15 June 2020).
- De Carlo, L.; Vivaldi, G.A.; Caputo, M.C. Electromagnetic induction measurements for investigating soil salinization caused by saline reclaimed water. Atmosphere 2021, 13, 73. [Google Scholar] [CrossRef]
- De Smedt, P.; Saey, T.; Lehouck, A.; Stichelbaut, B.; Meerschman, E.; Islam, M.M.; Van De Vijver, W.; Van Meirvenne, M. Exploring the potential of multi-receiver EMI survey for geoarchaeological prospection: A 90 ha dataset. Geoderma 2013, 199, 30–36. [Google Scholar] [CrossRef]
- Altdorff, D.; Bechtold, M.; van der Kruk, J.; Vereecken, H.; Huisman, J.A. Mapping peat layer properties with multi-coil offset electromagnetic induction and laser scanning elevation data. Geoderma 2016, 261, 178–189. [Google Scholar] [CrossRef]
- Altdorff, D.; Sadatcharam, K.; Unc, A.; Krishnapillai, M.; Galagedara, L. Comparison of multi-frequency and multi-coil electromagnetic induction (EMI) for mapping properties in shallow Podsolic soils. Sensors 2020, 20, 2330. [Google Scholar] [CrossRef]
- Keiswetter, D.A.; Won, I.J. Multifrequency electromagnetic signature of the Cloud Chamber, Nevada Test Site. J. Environ. Eng. Geophys. 1997, 2, 99–103. [Google Scholar] [CrossRef]
- Corwin, D.L.; Lesch, S.M. A simplified regional-scale electromagnetic induction—Salinity calibration model using ANOCOVA modeling techniques. Geoderma 2014, 230–231, 288–295. [Google Scholar] [CrossRef]
- Farzamian, M.; Autovino, D.; Basile, A.; De Mascellis, R.; Dragonetti, G.; Monteiro Santos, F.; Binley, A.; Coppola, A. Assessing the dynamics of soil salinity with time-lapse inversion of electromagnetic data guided by hydrological modelling. Hydrol. Earth. Syst. Sci. 2021, 25, 1509–1527. [Google Scholar] [CrossRef]
- Narjary, B.; Kumar, S.; Meena, M.; Kamra, S.K.; Sharma, D.K. Spatio-temporal mapping and analysis of soil salinity: An integrated approach through electromagnetic induction (EMI), multivariate and geostatistical techniques. Geocarto Int. 2021, 37, 8602–8623. [Google Scholar] [CrossRef]
- Ganjegunte, G.K.; Sheng, Z.; Clark, J.A. Soil salinity and sodicity appraisal by electromagnetic induction in soils irrigated to grow cotton. Land Degrad. Dev. 2014, 25, 228–235. [Google Scholar] [CrossRef]
- Yao, R.-J.; Yang, J.-S.; Wu, D.-H.; Xie, W.-P.; Cui, S.-Y.; Wang, X.-P.; Yu, S.-P.; Zhang, X. Determining soil salinity and plant biomass response for a farmed coastal cropland using the electromagnetic induction method. Comput. Electron. Agric. 2015, 119, 241–253. [Google Scholar] [CrossRef]
- Yao, R.-J.; Yang, J.-S.; Wu, D.-H.; Xie, W.-P.; Gao, P.; Wang, X.-P. Geostatistical monitoring of soil salinity for precision management using proximally sensed electromagnetic induction (EMI) method. Environ. Earth Sci. 2016, 75, 1–18. [Google Scholar] [CrossRef]
- Corwin, D.L.; Scudiero, E.L.I.A.; Zaccaria, D. Modified ECa–ECe protocols for mapping soil salinity under micro-irrigation. Agric. Water Manag. 2022, 269, 107640. [Google Scholar] [CrossRef]
- Diaz, L.; Herrero Isern, J. Salinity estimates in irrigated soils using electromagnetic induction. Soil Sci. 1992, 154, 151–157. Available online: http://hdl.handle.net/10261/10707 (accessed on 8 January 2022). [CrossRef]
- Doolittle, J.; Petersen, M.; Wheeler, T. Comparison of two electromagnetic induction tools in salinity appraisals. J. Soil Water Conserv. 2001, 56, 257–262. [Google Scholar]
- Urdanoz, V.; Aragüés, R. Comparison of Geonics EM38 and Dualem 1S electromagnetic induction sensors for the measurement of salinity and other soil properties. Soil Use Manag. 2012, 28, 108–112. [Google Scholar] [CrossRef]
- Akramkhanov, A.; Brus, D.J.; Walvoort, D.J.J. Geostatistical monitoring of soil salinity in Uzbekistan by repeated EMI surveys. Geoderma 2014, 213, 600–607. [Google Scholar] [CrossRef]
- Šimůnek, J.; van Genuchten, M.T.; Šejna, M. Development and applications of the HYDRUS and STANMOD software packages and related codes. Vadose Zone J. 2008, 7, 587–600. [Google Scholar] [CrossRef]
- Kachanoski, R.G.; Wesenbeeck, I.V.; Gregorich, E.G. Estimating spatial variations of soil water content using noncontacting electromagnetic inductive methods. Can. J. Soil Sci. 1988, 68, 715–722. [Google Scholar] [CrossRef]
- Brevik, E.C.; Fenton, T.E.; Lazari, A. Soil electrical conductivity as a function of soil water content and implications for soil mapping. Precis. Agric. 2006, 7, 393–404. [Google Scholar] [CrossRef]
- Robinet, J.; von Hebel, C.; Govers, G.; van der Kruk, J.; Minella, J.P.; Schlesner, A.; Ameijeiras-Mariño, Y.; Vanderborght, J. Spatial variability of soil water content and soil electrical conductivity across scales derived from electromagnetic induction and time domain reflectometry. Geoderma 2018, 314, 160–174. [Google Scholar] [CrossRef]
- Moghadas, D.; Jadoon, K.Z.; McCabe, M.F. Spatiotemporal monitoring of soil water content profiles in an irrigated field using probabilistic inversion of time-lapse EMI data. Adv. Water Resour. 2017, 110, 238–248. [Google Scholar] [CrossRef]
- Tang, S.; Farooque, A.A.; Bos, M.; Abbas, F. Modelling DUALEM-2 measured soil conductivity as a function of measuring depth to correlate with soil moisture content and potato tuber yield. Precis. Agric. 2020, 21, 484–502. [Google Scholar] [CrossRef]
- Zare, E.; Li, N.; Khongnawang, T.; Farzamian, M.; Triantafilis, J. Identifying potential leakage zones in an irrigation supply channel by mapping soil properties using electromagnetic induction, inversion modelling and a support vector machine. Soil Syst. 2020, 4, 25. [Google Scholar] [CrossRef]
- Shaukat, H.; Flower, K.C.; Leopold, M. Quasi-3D mapping of soil moisture in agricultural fields using electrical conductivity sensing. Agric. Water Manag. 2022, 259, 107246. [Google Scholar] [CrossRef]
- Pedrera-Parrilla, A.; Van De Vijver, E.; Van Meirvenne, M.; Espejo-Pérez, A.J.; Giráldez, J.V.; Vanderlinden, K. Apparent electrical conductivity measurements in an olive orchard under wet and dry soil conditions: Significance for clay and soil water content mapping. Precis. Agric. 2016, 17, 531–545. [Google Scholar] [CrossRef]
- Islam, M.M.; Meerschman, E.; Saey, T.; De Smedt, P.; Van De Vijver, E.; Van Meirvenne, M. Comparing apparent electrical conductivity measurements on a paddy field under flooded and drained conditions. Precis. Agric. 2012, 13, 384–392. [Google Scholar] [CrossRef]
- Hezarjaribi, A.; Sourell, H. Feasibility study of monitoring the total available water content using non-invasive electromagnetic induction-based and electrode-based soil electrical conductivity measurements. Irrig. Drain. 2007, 56, 53–65. [Google Scholar] [CrossRef]
- Huth, N.I.; Poulton, P.L. An electromagnetic induction method for monitoring variation in soil moisture in agroforestry systems. Soil Res. 2007, 45, 63–72. [Google Scholar] [CrossRef]
- Misra, R.K.; Padhi, J. Assessing field-scale soil water distribution with electromagnetic induction method. J. Hydrol. 2014, 516, 200–209. [Google Scholar] [CrossRef]
- Altdorff, D.; von Hebel, C.; Borchard, N.; van der Kruk, J.; Bogena, H.R.; Vereecken, H.; Huisman, J.A. Potential of catchment-wide soil water content prediction using electromagnetic induction in a forest ecosystem. Environ. Earth Sci. 2017, 76, 111. [Google Scholar] [CrossRef]
- Martini, E.; Werban, U.; Zacharias, S.; Pohle, M.; Dietrich, P.; Wollschläger, U. Repeated electromagnetic induction measurements for mapping soil moisture at the field scale: Validation with data from a wireless soil moisture monitoring network. Hydrol. Earth Syst. Sci. 2017, 21, 495–513. [Google Scholar] [CrossRef]
- Turkeltaub, T.; Wang, J.; Cheng, Q.; Jia, X.; Zhu, Y.; Shao, M.-A.; Binley, A. Soil moisture and electrical conductivity relationships under typical Loess Plateau land covers. Vadose Zone J. 2022, 21, e20174. [Google Scholar] [CrossRef]
- Calamita, G.; Perrone, A.; Brocca, L.; Onorati, B.; Manfreda, S. Field test of a multi-frequency electromagnetic induction sensor for soil moisture monitoring in southern Italy test sites. J. Hydrol. 2015, 529, 316–329. [Google Scholar] [CrossRef]
- Friedman, S.P. Soil properties influencing apparent electrical conductivity: A review. Comput. Electron. Agric. 2005, 46, 45–70. [Google Scholar] [CrossRef]
- Reedy, R.C.; Scanlon, B.R. Soil water content monitoring using electromagnetic induction. J. Geotech. Geoenviron. Eng. 2003, 129, 1028–1039. [Google Scholar] [CrossRef]
- Saey, T.; Van Meirvenne, M.; Vermeersch, H.; Ameloot, N.; Cockx, L. A pedotransfer function to evaluate the soil profile textural heterogeneity using proximally sensed apparent electrical conductivity. Geoderma 2009, 150, 389–395. [Google Scholar] [CrossRef]
- Martínez, G.; Vanderlinden, K.; Giráldez, J.V.; Espejo, A.J.; Muriel, J.L. Field-scale soil moisture pattern mapping using electromagnetic induction. Vadose Zone J. 2010, 9, 871–881. [Google Scholar] [CrossRef]
- Brevik, E.C.; Fenton, T.E. Influence of soil water content, clay, temperature, and carbonate minerals on electrical conductivity readings taken with an EM-38. Soil Survey Horizons 2002, 43, 9–13. [Google Scholar] [CrossRef]
- Hoefer, G.; Bachmann, J.; Hartge, K.H. Can the EM38 probe detect spatial patterns of subsoil compaction? In Proximal Soil Sensing: Progress in Soil Science; Viscarra Rossel, R.A., McBratney, A.B., Minasny, B., Eds.; Springer: Dordrecht, The Netherlands, 2010; pp. 265–273. [Google Scholar] [CrossRef]
- Galambošová, J.; Macák, M.; Rataj, V.; Barát, M.; Misiewicz, P.A. Determining trafficked areas using soil electrical conductivity–a pilot study. Acta Technol. Agric. 2020, 23, 1–6. [Google Scholar] [CrossRef]
- Al-Gaadi, K.A. Employing electromagnetic induction technique for the assessment of soil compaction. Am. J. Agric. Biol. Sci. 2012, 7, 425–434. [Google Scholar] [CrossRef]
- Besson, A.; Cousin, I.; Samouelian, A.; Boizard, H.; Richard, G. Structural heterogeneity of the soil tilled layer as characterized by 2D electrical resistivity surveying. Soil Tillage Res. 2004, 79, 239–249. [Google Scholar] [CrossRef]
- Ren, L.; D’Hose, T.; Borra-Serrano, I.; Lootens, P.; Hanssens, D.; De Smedt, P.; Cornelis, W.M.; Ruysschaert, G. Detecting spatial variability of soil compaction using soil apparent electrical conductivity and maize traits. Soil Use Manag. 2022, 38, 1749–1760. [Google Scholar] [CrossRef]
- Johnson, C.K.; Doran, J.W.; Duke, H.R.; Wienhold, B.J.; Eskridge, K.M.; Shanahan, J.F. Field-scale electrical conductivity mapping for delineating soil condition. Soil Sci. Soc. Am. J. 2001, 65, 1829–1837. [Google Scholar] [CrossRef]
- Vitharana, U.W.A.; Van Meirvenne, M.; Simpson, D.; Cockx, L.; de Baerdemaeker, J. Key soil and topographic properties to delineate potential management classes for precision agriculture in the European loess area. Geoderma 2008, 143, 206–215. [Google Scholar] [CrossRef]
- Rodrigues, F.A., Jr.; Bramley, R.G.V.; Gobbett, D.L. Proximal soil sensing for precision agriculture: Simultaneous use of electromagnetic induction and gamma radiometrics in contrasting soils. Geoderma 2015, 243, 183–195. [Google Scholar] [CrossRef]
- Atwell, M.A.; Wuddivira, M.N. Electromagnetic-induction and spatial analysis for assessing variability in soil properties as a function of land use in tropical savanna ecosystems. SN Appl. Sci. 2019, 1, 856. [Google Scholar] [CrossRef]
- Rentschler, T.; Werban, U.; Ahner, M.; Behrens, T.; Gries, P.; Scholten, T.; Teuber, S.; Schmidt, K. 3D mapping of soil organic carbon content and soil moisture with multiple geophysical sensors and machine learning. Vadose Zone J. 2020, 19, e20062. [Google Scholar] [CrossRef]
- Maher, B.A. Characterisation of soils by mineral magnetic measurements. Phys. Earth Planet. 1986, 42, 76–92. [Google Scholar] [CrossRef]
- Sadatcharam, K.; Altdorff, D.; Unc, A.; Krishnapillai, M.; Galagedara, L. Depth sensitivity of apparent magnetic susceptibility measurements using multi-coil and multi-frequency electromagnetic induction. J. Environ. Eng. Geophys. 2020, 25, 301–314. [Google Scholar] [CrossRef]
- Shirzaditabar, F.; Heck, R.J. Characterization of soil magnetic susceptibility: A review of fundamental concepts, instrumentation, and applications. Can. J. Soil Sci. 2022, 102, 231–251. [Google Scholar] [CrossRef]
- Shirzaditabar, F.; Heck, R.J. Characterization of soil drainage using electromagnetic induction measurement of soil magnetic susceptibility. Catena 2021, 207, 105671. [Google Scholar] [CrossRef]
- McLachlan, P.; Schmutz, M.; Cavailhes, J.; Hubbard, S.S. Estimating grapevine-relevant physicochemical soil zones using apparent electrical conductivity and in-phase data from EMI methods. Geoderma 2022, 426, 116033. [Google Scholar] [CrossRef]
- Toy, C.W.; Steelman, C.M.; Endres, A.L. Comparing electromagnetic induction and ground penetrating radar techniques for estimating soil moisture content. In Proceedings of the 13th International Conference on Ground Penetrating Radar, Lecce, Italy, 21–25 June 2010; IEEE: New York, NY, USA, 2010; pp. 1–6. [Google Scholar] [CrossRef]
- Barca, E.; De Benedetto, D.; Stellacci, A.M. Contribution of EMI and GPR proximal sensing data in soil water content assessment by using linear mixed effects models and geostatistical approaches. Geoderma 2019, 343, 280–293. [Google Scholar] [CrossRef]
- Moghadas, D.; André, F.; Slob, E.C.; Vereecken, H.; Lambot, S. Joint full-waveform analysis of off-ground zero-offset ground penetrating radar and electromagnetic induction synthetic data for estimating soil electrical properties. Geophys. J. Int. 2010, 182, 1267–1278. [Google Scholar] [CrossRef]


| Description/Property | Low-Frequency Method Electromagnetic Induction | High-Frequency Method Ground-Penetrating Radar |
|---|---|---|
| Operating frequency range | 1–100 kHz | 10–3600 MHz |
| Dominant current | Conduction current | Displacement and conduction currents |
| Operation method | EM induction (Strength of the electromagnetic field) | Wave propagation (Reflection, Refraction, scattering) |
| Primary physical property | Electrical conductivity | Dielectric permittivity |
| Frequency (MHz) | Soil Type | Effective Depth (m) | Source |
|---|---|---|---|
| 200 | Silty clay | 0–0.10 (wet condition) | Chanzy et al. [70] |
| 200 | Aeolian sand (Podzolic) | 0–1.20 | van Overmeeren et al. [71] |
| 50 | Aeolian sand (Podzolic) | 0–3.00 | van Overmeeren et al. [71] |
| 900 | Clay to loamy sand | 0–0.20 | Hubbard et al. [72] |
| 450 | Sandy loam | 0–0.20 (wet condition) | Galagedara et al. [67] |
| 450 | Sandy loam and sandy clay loam | 0–0.11 (wet condition) 0–0.14 (dry condition) | Grote et al. [77] |
| 900 | Sandy loam and sandy clay loam | 0–0.07 (wet condition) 0–0.10 (dry condition) | Grote et al. [77] |
| 100 | Sandy loam | 0–0.85 (A) 0–0.50 (B) | * Galagedara et al. [99] |
| 200 | Sandy loam | 0–0.38 (A) 0–0.26 (B) | * Galagedara et al. [99] |
| 450 | Sandy loam | 0–0.26 (A) 0–0.16 (B) | * Galagedara et al. [99] |
| 900 | Sandy loam | 0–0.13 (A) 0–0.09 (B) | * Galagedara et al. [99] |
| 250 | Sand | 0–0.15 | Pallavi et al. [100] |
| 400 | Loamy soil | 0.10–0.20 (wet condition) 0.10–0.30 (dry condition) | Thitimakoran et al. [95] |
| Aspect | GPR | EMI |
|---|---|---|
| SWC | estimates SWC by measuring εr relationship between εr and SWC is quite independent from other properties does not require site-specific calibration | estimates SWC by measuring soil σa relationship between σa and SWC is affected by other properties such as soil salinity, clay content, temperature, and porosity requires site-specific calibration |
| Soil salinity | lack of studies | well-studied |
| Other soil properties | lack of studies with other soil properties | σa depends on several factors; therefore, different studies related σa to other soil properties |
| Mapping layers | provide high-resolution imaging of soil structure, layering, stratigraphy, groundwater table, and root architecture by utilizing wave reflections | detect roots, layering, contaminated zones, and groundwater table indirectly by measuring changes in soil σa, even though the resolution is much lower than GPR |
| Influence of soil type | works well in sandy soils (low conductive soils), and some difficulties (e.g., limit the penetration depth) in clay-rich and/or high-conductive soils | works well in clay-rich soils (high conductive soils) and some difficulties in sand-rich (resistive) soils |
| Field surveys | have contact issues for on-ground (ground-coupling) surveys on rough surfaces (e.g., shrubs) | no contact issues since the instrument is generally placed above the ground |
| Multiple depth sensing/depth of penetration | senses multiple depths with different frequencies and different waves (direct ground wave, reflected wave) antennas should be changed to investigate deeper depths with lower resolution or shallow depths with higher resolution | senses different depths with different frequencies, inter-coil spacings, and coil orientation senses different depths simultaneously, unlike GPR |
| Set up and operation | may be challenging for non-technical individuals without advanced geophysics knowledge newest technologies are making automated robotics to address this issue | relatively straightforward for non-technical individuals without advanced geophysical knowledge |
| Instrument cost | relatively expensive compared to EMI | relatively affordable compared to GPR |
| Data processing | requires sophisticated data processing and interpretation skills | basic data processing and interpretation are straightforward |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pathirana, S.; Lambot, S.; Krishnapillai, M.; Cheema, M.; Smeaton, C.; Galagedara, L. Ground-Penetrating Radar and Electromagnetic Induction: Challenges and Opportunities in Agriculture. Remote Sens. 2023, 15, 2932. https://doi.org/10.3390/rs15112932
Pathirana S, Lambot S, Krishnapillai M, Cheema M, Smeaton C, Galagedara L. Ground-Penetrating Radar and Electromagnetic Induction: Challenges and Opportunities in Agriculture. Remote Sensing. 2023; 15(11):2932. https://doi.org/10.3390/rs15112932
Chicago/Turabian StylePathirana, Sashini, Sébastien Lambot, Manokarajah Krishnapillai, Mumtaz Cheema, Christina Smeaton, and Lakshman Galagedara. 2023. "Ground-Penetrating Radar and Electromagnetic Induction: Challenges and Opportunities in Agriculture" Remote Sensing 15, no. 11: 2932. https://doi.org/10.3390/rs15112932
APA StylePathirana, S., Lambot, S., Krishnapillai, M., Cheema, M., Smeaton, C., & Galagedara, L. (2023). Ground-Penetrating Radar and Electromagnetic Induction: Challenges and Opportunities in Agriculture. Remote Sensing, 15(11), 2932. https://doi.org/10.3390/rs15112932








