Modified Dynamic Routing Convolutional Neural Network for Pan-Sharpening
Abstract
1. Introduction
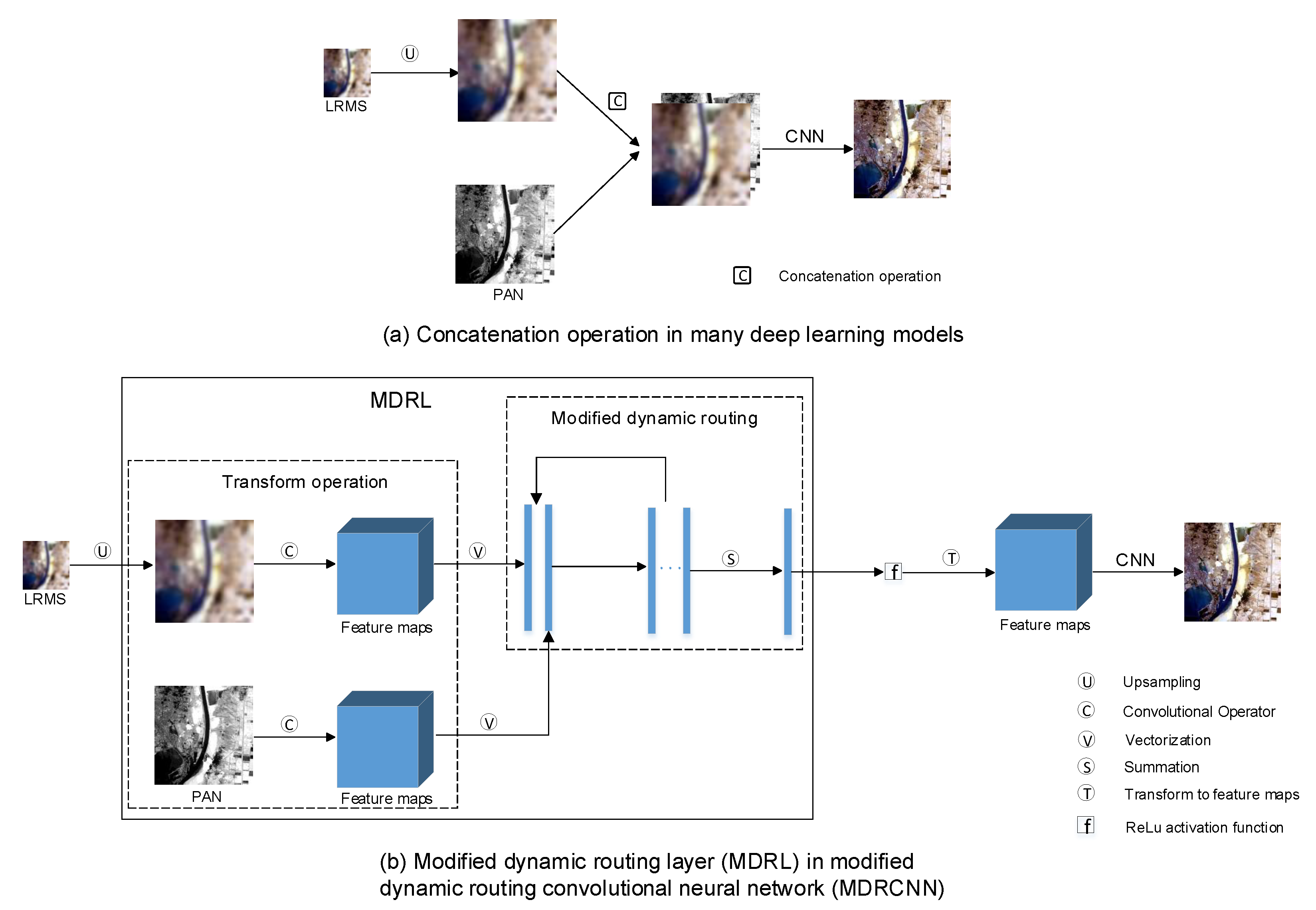
- To replace addition or concatenation operations in many deep learning models, we modify the dynamic routing algorithm to construct a modified dynamic routing layer (MDRL), where MDRL may be the first try to fuse LRMS images and PAN images by modifying the information transmission mode of capsules for pan-sharpening. In addition, the addition and concatenation operations are illustrated as special cases of our MDRL.
- In MDRL, the spatial location information is preserved in our model based on the convolutional operator in transform operation and the vectorize operation. Furthermore, the coupling coefficients are learned by the MDR algorithm, which make MDRL fuse the information of PAN images and LRMS images more effectively than with a simple concatenation or summation operation.
- Based on two baseline models (i.e., MIPSM and DRPNN), the proposed MDRL is inserted into them to generate our two neural networks named MDR–MIPSM and MDR–DRPNN. Quantitative experiments on three benchmark datasets demonstrate the superiority of our method.
2. Materials and Methods
2.1. Dynamic Routing Algorithm
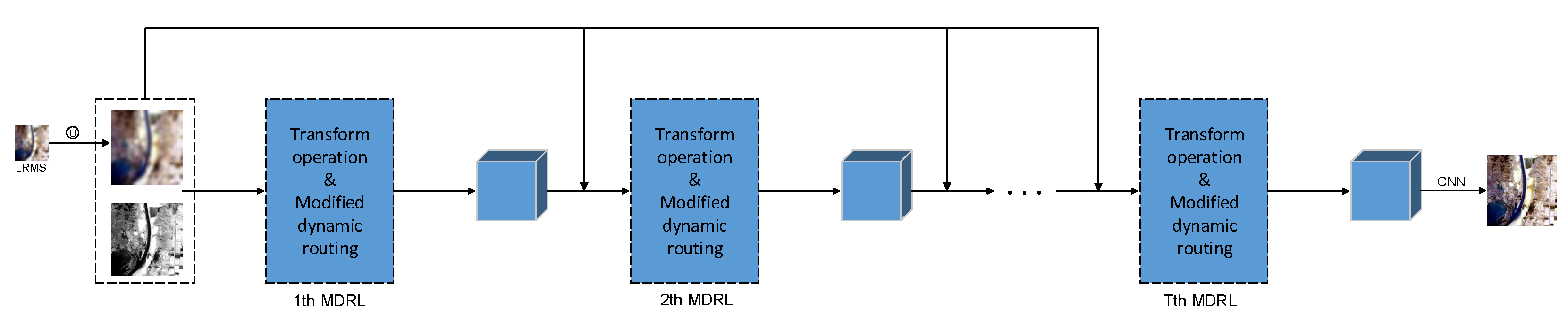
2.2. MDRL and MDRCNN
| Algorithm 1 MDR for pan-sharpening. |
| Input: Prediction vectors: . The number of iterations: r. The number of capsules in layer l: M. The number of capsules in layer (l + 1): N. Initialization: Initialize all capsules i in layer l and capsules j in layer (l + 1): 0. For r iterations do for all capsules i in layer l and capsules j in layer (l + 1): use Equation (7) to obtain . for all capsules j in layer (l + 1): use Equation (2) to obtain . for all capsules i in layer l and capsules j in layer (l + 1): . End for For all capsules j in layer (l + 1): ReLU(). output: . |
2.3. The Relationship between the MDRL and Addition or Concatenation Operations
2.4. Dataset and Evaluation Metrics
3. Experimental Results
3.1. Comparison Methods and Training Details
3.2. Performance Comparison
4. Discussion
4.1. Influence of the Number of MDRL
4.2. Influence of the Number of Iterations in MDR
4.3. Parameter Numbers
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cao, X.; Zhou, F.; Xu, L.; Meng, D.; Xu, Z.; Paisley, J. Hyperspectral image classification with markov random fields and a convolutional neural network. IEEE Trans. Image Process. 2018, 27, 2354–2367. [Google Scholar] [CrossRef] [PubMed]
- Cao, X.; Yao, J.; Xu, Z.; Meng, D. Hyperspectral image classification with convolutional neural network and active learning. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4604–4616. [Google Scholar] [CrossRef]
- Cao, X.; Fu, X.; Xu, C.; Meng, D. Deep spatial-spectral global reasoning network for hyperspectral image denoising. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5504714. [Google Scholar] [CrossRef]
- Hong, D.; Gao, L.; Yao, J.; Zhang, B.; Plaza, A.; Chanussot, J. Graph convolutional networks for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2020, 59, 5966–5978. [Google Scholar] [CrossRef]
- Hong, D.; Gao, L.; Yokoya, N.; Yao, J.; Chanussot, J.; Du, Q.; Zhang, B. More diverse means better: Multimodal deep learning meets remote-sensing imagery classification. IEEE Trans. Geosci. Remote Sens. 2020, 59, 4340–4354. [Google Scholar] [CrossRef]
- Wu, X.; Hong, D.; Chanussot, J. Convolutional neural networks for multimodal remote sensing data classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5517010. [Google Scholar] [CrossRef]
- Yao, J.; Cao, X.; Hong, D.; Wu, X.; Meng, D.; Chanussot, J.; Xu, Z. Semi-active convolutional neural networks for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5537915. [Google Scholar] [CrossRef]
- Hong, D.; Hu, J.; Yao, J.; Chanussot, J.; Zhu, X. Multimodal remote sensing benchmark datasets for land cover classification with a shared and specific feature learning model. ISPRS J. Photogramm. Remote Sens. 2021, 178, 68–80. [Google Scholar] [CrossRef]
- Hong, D.; Han, Z.; Yao, J.; Gao, L.; Zhang, B.; Plaza, A.; Chanussot, J. Spectralformer: Rethinking hyperspectral image classification with transformers. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5518615. [Google Scholar] [CrossRef]
- Prades, J.; Safont, G.; Salazar, A.; Vergara, L. Estimation of the number of endmembers in hyperspectral images using agglomerative clustering. Remote Sens. 2020, 12, 3585. [Google Scholar] [CrossRef]
- Zhu, X.; Yue, K.; Junmin, L. Estimation of the number of endmembers via thresholding ridge ratio criterion. IEEE Geosci. Remote Sens. Mag. 2019, 58, 637–649. [Google Scholar] [CrossRef]
- Dhaini, M.; Berar, M.; Honeine, P.; Van Exem, A. End-to-End Convolutional Autoencoder for Nonlinear Hyperspectral Unmixing. Remote Sens. 2022, 14, 3341. [Google Scholar] [CrossRef]
- Liu, J.; Yuan, S.; Zhu, X.; Huang, Y.; Zhao, Q. Nonnegative matrix factorization with entropy regularization for hyperspectral unmixing. Int. J. Remote Sens. 2021, 42, 6359–6390. [Google Scholar] [CrossRef]
- Cao, X.; Fu, X.; Hong, D.; Xu, Z.; Meng, D. Pancsc-net: A model-driven deep unfolding method for pansharpening. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5404713. [Google Scholar] [CrossRef]
- Vivone, G.; Dalla Mura, M.; Garzelli, A.; Restaino, R.; Scarpa, G.; Ulfarsson, M.O.; Alparone, L.; Chanussot, J. A new benchmark based on recent advances in multispectral pansharpening: Revisiting pansharpening with classical and emerging pansharpening methods. IEEE Geosci. Remote Sens. Mag. 2020, 9, 53–81. [Google Scholar] [CrossRef]
- Meng, X.; Shen, H.; Li, H.; Zhang, L.; Fu, R. Review of the pansharpening methods for remote sensing images based on the idea of meta-analysis: Practical discussion and challenges. Inf. Fusion 2019, 46, 102–113. [Google Scholar] [CrossRef]
- Gillespie, A.R.; Kahle, A.B.; Walker, R.E. Color enhancement of highly correlated images. I. Decorrelation and HSI contrast stretches. Remote Sens. Environ. 1986, 20, 209–235. [Google Scholar] [CrossRef]
- Laben, C.A.; Brower, B.V. Process for Enhancing the Spatial Resolution of Multispectral Imagery Using Pan-Sharpening. U.S. Patent 6,011,875, 4 January 2000. [Google Scholar]
- Haydn, R. Application of the ihs color transform to the processing of multisensor data and image enhancement. In Proceedings of the International Symposium on Remote Sensing of Arid and Semi-Arid Lands, Cairo, Egypt, 19–25 January 1982. [Google Scholar]
- Khan, M.M.; Chanussot, J.; Condat, L.; Montanvert, A. Indusion: Fusion of multispectral and panchromatic images using the induction scaling technique. IEEE Geosci. Remote Sens. Lett. 2008, 5, 98–102. [Google Scholar] [CrossRef]
- Liu, J.G. Smoothing filter-based intensity modulation: A spectral preserve image fusion technique for improving spatial details. Int. J. Remote Sens. 2000, 21, 3461–3472. [Google Scholar] [CrossRef]
- Otazu, X.; González-Audícana, M.; Fors, O.; Núñez, J. Introduction of sensor spectral response into image fusion methods. Application to wavelet-based methods. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2376–2385. [Google Scholar] [CrossRef]
- Garzelli, A.; Nencini, F.; Capobianco, L. Optimal mmse pan sharpening of very high resolution multispectral images. IEEE Trans. Geosci. Remote Sens. 2007, 46, 228–236. [Google Scholar] [CrossRef]
- He, X.; Condat, L.; Bioucas-Dias, J.; Chanussot, J.; Xia, J. A new pansharpening method based on spatial and spectral sparsity priors. IEEE Trans. Image Process. 2014, 23, 4160–4174. [Google Scholar] [CrossRef] [PubMed]
- Fang, F.; Li, F.; Shen, C.; Zhang, G. A variational approach for pan-sharpening. IEEE Trans. Image Process. 2013, 22, 2822–2834. [Google Scholar] [CrossRef] [PubMed]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21 July 2017. [Google Scholar]
- Masi, G.; Cozzolino, D.; Verdoliva, L.; Scarpa, G. Pansharpening by convolutional neural networks. Remote Sens. 2016, 8, 594. [Google Scholar] [CrossRef]
- Wei, Y.; Yuan, Q.; Shen, H.; Zhang, L. Boosting the accuracy of multispectral image pansharpening by learning a deep residual network. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1795–1799. [Google Scholar] [CrossRef]
- Yuan, Q.; Wei, Y.; Meng, X.; Shen, H.; Zhang, L. A multiscale and multidepth convolutional neural network for remote sensing imagery pan-sharpening. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 978–989. [Google Scholar] [CrossRef]
- Xiong, Z.; Guo, Q.; Liu, M.; Li, A. Pan-sharpening based on convolutional neural network by using the loss function with no-reference. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 14, 897–906. [Google Scholar] [CrossRef]
- Guo, Q.; Li, S.; Li, A. An Efficient Dual Spatial–Spectral Fusion Network. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Shao, Z.; Cai, J. Remote sensing image fusion with deep convolutional neural network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1656–1669. [Google Scholar] [CrossRef]
- Liu, L.; Wang, J.; Zhang, E.; Li, B.; Zhu, X.; Zhang, Y.; Peng, J. Shallow–deep convolutional network and spectral-discrimination-based detail injection for multispectral imagery pan-sharpening. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1772–1783. [Google Scholar] [CrossRef]
- Vivone, G.; Dalla Mura, M.; Garzelli, A.; Pacifici, F. A benchmarking protocol for pansharpening: Dataset, preprocessing, and quality assessment. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 6102–6118. [Google Scholar] [CrossRef]
- Jin, Z.; Zhuo, Y.; Zhang, T.; Jin, X.; Jing, S.; Deng, L. Remote sensing pansharpening by full-depth feature fusion. Remote Sens. 2022, 14, 466. [Google Scholar] [CrossRef]
- Wang, W.; Zhou, Z.; Liu, H.; Xie, G. MSDRN: Pansharpening of multispectral images via multi-scale deep residual network. Remote Sens. 2021, 13, 1200. [Google Scholar] [CrossRef]
- Zhang, E.; Fu, Y.; Wang, J.; Liu, L.; Yu, K.; Peng, J. Msac-net: 3d multi-scale attention convolutional network for multi-spectral imagery pansharpening. Remote Sens. 2022, 14, 2761. [Google Scholar] [CrossRef]
- Sara, S.; Nicholas, F.; Geoffrey, E.H. Dynamic routing between capsules. In Proceedings of the Neural Information Processing Systems, Long Beach, CA, USA, 4 December 2017. [Google Scholar]
- Hinton, G.E.; Sabour, S.; Frosst, N. Matrix capsules with em routing. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April 2018. [Google Scholar]
- Sun, K.; Zhang, J.; Liu, J.; Yu, R.; Song, Z. Drcnn: Dynamic routing convolutional neural network for multi-view 3d object recognition. IEEE Trans. Image Process. 2020, 30, 868–877. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June 2016. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Wald, L.; Ranchin, T.; Mangolini, M. Fusion of satellite images of different spatial resolutions: Assessing the quality of resulting images. Photogramm. Eng. Remote Sens. 1997, 63, 691–699. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Wald, L. Data Fusion: Definitions and Architectures: Fusion of Images of Different Spatial Resolutions; Presses des MINES: Paris, France, 2002. [Google Scholar]
- Quan, H.-T.; Ghanbari, M. Scope of validity of psnr in image/video quality assessment. Electron. Lett. 2008, 44, 800–801. [Google Scholar]
- Yuhas, R.H.; Goetz, A.F.H.; Boardman, J.W. Discrimination among semi-arid landscape endmembers using the spectral angle mapper (sam) algorithm. In JPL, Summaries of the Third Annual JPL Airborne Geoscience Workshop; AVIRIS Workshop: Pasadena, CA, USA, 1992. [Google Scholar]
- Schowengerdt, R.A. Reconstruction of multispatial, multispectral image data using spatial frequency content. Photogramm. Eng. Remote Sens. 1980, 46, 1325–1334. [Google Scholar]
- Yang, J.; Fu, X.; Hu, Y.; Huang, Y.; Ding, X.; Paisley, J. Pannet: A deep network architecture for pan-sharpening. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22 October 2017. [Google Scholar]
- Deng, X.; Dragotti, P.L. Deep convolutional neural network for multi-modal image restoration and fusion. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 43, 3333–3348. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Z.; Zhan, J.; Xu, S.; Sun, K.; Huang, L.; Liu, J.; Zhang, C. Fgf-gan: A lightweight generative adversarial network for pansharpening via fast guided filter. In Proceedings of the IEEE International Conference on Multimedia and Expo, Virtual, 5 July 2021. [Google Scholar]
- Xie, Q.; Zhou, M.; Zhao, Q.; Xu, Z.; Meng, D. Mhf-net: An interpretable deep network for multispectral and hyperspectral image fusion. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 1457–1473. [Google Scholar] [CrossRef]
- Liang, Y.; Zhang, P.; Mei, Y.; Wang, T. PMACNet: Parallel multiscale attention constraint network for pan-sharpening. IEEE Geosci. Remote Sens. Lett. 2022, 19, 3170904. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]



| Datasets | Training | Validation | Test | Bands | Spatial Up-Scaling Ratio (SUR) |
|---|---|---|---|---|---|
| QuickBird | 474 | 103 | 100 | 4 | 4 |
| Landsat8 | 350 | 50 | 100 | 10 | 2 |
| GaoFen2 | 350 | 50 | 100 | 4 | 4 |
| Method | PSNR ↑ | SSIM ↑ | SAM ↓ | ERGAS ↓ |
|---|---|---|---|---|
| BDSD [23] | 23.5540 | 0.7156 | 0.0765 | 4.8874 |
| Brovey [17] | 25.2744 | 0.7370 | 0.0640 | 4.2085 |
| GS [18] | 26.0305 | 0.6829 | 0.0586 | 3.9498 |
| HPF [50] | 25.9977 | 0.7378 | 0.0588 | 3.9452 |
| IHS [19] | 24.3826 | 0.6742 | 0.0647 | 4.6208 |
| Indusion [20] | 25.7623 | 0.6377 | 0.0674 | 4.2514 |
| SFIM [21] | 24.0351 | 0.6409 | 0.0739 | 4.8282 |
| MIPSM [21] | 27.7323 | 0.8411 | 0.0522 | 3.1550 |
| DRPNN [30] | 31.0415 | 0.8993 | 0.0378 | 2.2250 |
| MSDCNN [31] | 30.1245 | 0.8728 | 0.0434 | 2.5649 |
| RSIFNN [34] | 30.5769 | 0.8898 | 0.0405 | 2.3530 |
| PANNET [51] | 30.9631 | 0.8988 | 0.0368 | 2.2648 |
| CUNet [52] | 30.3612 | 0.8876 | 0.0428 | 2.4178 |
| FGF-GAN [53] | 30.3465 | 0.8761 | 0.0407 | 2.4103 |
| MHNet [54] | 31.1557 | 0.8947 | 0.0368 | 2.1931 |
| PMACNet [55] | 31.0974 | 0.9020 | 0.0384 | 2.3141 |
| MDR–MIPSM (ours) | 29.8426 | 0.8837 | 0.0431 | 2.6694 |
| MDR–DRPNN (ours) | 31.4626 | 0.9038 | 0.0358 | 2.1348 |
| Method | PSNR ↑ | SSIM ↑ | SAM ↓ | ERGAS ↓ |
|---|---|---|---|---|
| BDSD [23] | 33.8065 | 0.9128 | 0.0255 | 1.9128 |
| Brovey [17] | 32.4030 | 0.8533 | 0.0206 | 1.9806 |
| GS [18] | 32.0163 | 0.8687 | 0.0304 | 2.2119 |
| HPF [50] | 32.6691 | 0.8712 | 0.0250 | 2.0669 |
| IHS [19] | 32.8772 | 0.8615 | 0.0245 | 2.3128 |
| Indusion [20] | 30.8476 | 0.8168 | 0.0359 | 2.4216 |
| SFIM [21] | 32.7207 | 0.8714 | 0.0248 | 2.0775 |
| MIPSM [21] | 35.4891 | 0.9389 | 0.0209 | 1.5769 |
| DRPNN [30] | 37.3639 | 0.9613 | 0.0173 | 1.3303 |
| MSDCNN [31] | 36.2536 | 0.9581 | 0.0176 | 1.4160 |
| RSIFNN [34] | 37.0782 | 0.9547 | 0.0172 | 1.3273 |
| PANNET [51] | 38.0910 | 0.9647 | 0.0152 | 1.3021 |
| CUNet [52] | 37.0468 | 0.9610 | 0.0179 | 1.3430 |
| FGF-GAN [53] | 38.0832 | 0.9533 | 0.0165 | 1.2714 |
| MHNet [54] | 37.0049 | 0.9566 | 0.0189 | 1.3509 |
| PMACNet [55] | 38.3271 | 0.9670 | 0.0158 | 1.2278 |
| MDR–MIPSM (ours) | 37.3317 | 0.9614 | 0.0171 | 1.4071 |
| MDR–DRPNN (ours) | 38.5876 | 0.9685 | 0.0153 | 1.2012 |
| Method | PSNR ↑ | SSIM ↑ | SAM ↓ | ERGAS ↓ |
|---|---|---|---|---|
| BDSD [23] | 30.2114 | 0.8732 | 0.0126 | 2.3963 |
| Brovey [17] | 31.5901 | 0.9033 | 0.0110 | 2.2088 |
| GS [18] | 30.4357 | 0.8836 | 0.0101 | 2.3075 |
| HPF [50] | 30.4812 | 0.8848 | 0.0113 | 2.3311 |
| IHS [19] | 30.4754 | 0.8639 | 0.0108 | 2.3546 |
| Indusion [20] | 30.5359 | 0.8849 | 0.0113 | 2.3457 |
| SFIM [21] | 30.4021 | 0.8501 | 0.0129 | 2.3688 |
| MIPSM [21] | 32.1761 | 0.9392 | 0.0104 | 1.8830 |
| DRPNN [30] | 35.1182 | 0.9663 | 0.0098 | 1.3078 |
| MSDCNN [31] | 33.6715 | 0.9685 | 0.0090 | 1.4720 |
| RSIFNN [34] | 33.0588 | 0.9588 | 0.0112 | 1.5658 |
| PANNET [51] | 34.5774 | 0.9635 | 0.0089 | 1.4750 |
| CUNet [52] | 33.6919 | 0.9630 | 0.0184 | 1.5839 |
| FGF-GAN [53] | 35.0450 | 0.9449 | 0.0089 | 1.4351 |
| MHNet [54] | 33.8930 | 0.9291 | 0.0176 | 1.3697 |
| PMACNet [55] | 35.3506 | 0.9678 | 0.0101 | 1.2658 |
| MDR–MIPSM (ours) | 34.2735 | 0.9530 | 0.0105 | 1.5150 |
| MDR–DRPNN (ours) | 35.6512 | 0.9704 | 0.0091 | 1.2177 |
| Landsat8 | QuickBird | |||||
|---|---|---|---|---|---|---|
| Method | QNR↑ | ↓ | ↓ | QNR↑ | ↓ | ↓ |
| BDSD | 0.7632 | 0.1064 | 0.1469 | 0.6061 | 0.1660 | 0.2741 |
| GS | 0.8195 | 0.0580 | 0.1310 | 0.7134 | 0.0937 | 0.2157 |
| HPF | 0.8764 | 0.0475 | 0.0801 | 0.7626 | 0.1062 | 0.1484 |
| IHS | 0.7381 | 0.1360 | 0.1470 | 0.5547 | 0.1975 | 0.3095 |
| Indusion | 0.9239 | 0.0235 | 0.0539 | 0.8104 | 0.1083 | 0.0923 |
| SFIM | 0.8865 | 0.0464 | 0.0706 | 0.7573 | 0.1062 | 0.1544 |
| CUNet | 0.9132 | 0.0265 | 0.0621 | 0.7864 | 0.1367 | 0.0894 |
| RSIFNN | 0.9273 | 0.0278 | 0.0468 | 0.7709 | 0.1064 | 0.1392 |
| MHNet | 0.9117 | 0.0373 | 0.0535 | 0.8408 | 0.0760 | 0.0902 |
| MSDCNN | 0.9380 | 0.0237 | 0.0392 | 0.7419 | 0.1246 | 0.1557 |
| PANNET | 0.9499 | 0.0214 | 0.0293 | 0.8383 | 0.0865 | 0.0824 |
| MIPSM | 0.9273 | 0.0172 | 0.0566 | 0.7850 | 0.1290 | 0.0998 |
| DRPNN | 0.9380 | 0.0252 | 0.0378 | 0.7999 | 0.1087 | 0.1025 |
| MDR–MIPSM (ours) | 0.9354 | 0.0192 | 0.0471 | 0.7939 | 0.1028 | 0.1167 |
| MDR–DRPNN (ours) | 0.9500 | 0.0170 | 0.0339 | 0.8469 | 0.0680 | 0.0916 |
| #MDRL | PSNR ↑ | SSIM ↑ | SAM ↓ | ERGAS ↓ |
|---|---|---|---|---|
| 1 | 31.4074 | 0.9022 | 0.0354 | 2.1382 |
| 2 | 31.4626 | 0.9038 | 0.0358 | 2.1348 |
| 3 | 31.3480 | 0.9029 | 0.0358 | 2.1617 |
| #Iterations | PSNR ↑ | SSIM ↑ | SAM ↓ | ERGAS ↓ |
|---|---|---|---|---|
| 1 | 31.4626 | 0.9038 | 0.0358 | 2.1348 |
| 2 | 31.4435 | 0.9036 | 0.0362 | 2.1193 |
| 3 | 31.3661 | 0.9049 | 0.0353 | 2.1509 |
| Method | MIPSM | MDR–MIPSM | DRPNN | MDR–DRPNN |
|---|---|---|---|---|
| #Parameters (million) | 87,047 | 68,551 | 375,293 | 302,595 |
| PSNR | 27.7323 | 29.8426 | 31.0415 | 31.4626 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, K.; Zhang, J.; Liu, J.; Xu, S.; Cao, X.; Fei, R. Modified Dynamic Routing Convolutional Neural Network for Pan-Sharpening. Remote Sens. 2023, 15, 2869. https://doi.org/10.3390/rs15112869
Sun K, Zhang J, Liu J, Xu S, Cao X, Fei R. Modified Dynamic Routing Convolutional Neural Network for Pan-Sharpening. Remote Sensing. 2023; 15(11):2869. https://doi.org/10.3390/rs15112869
Chicago/Turabian StyleSun, Kai, Jiangshe Zhang, Junmin Liu, Shuang Xu, Xiangyong Cao, and Rongrong Fei. 2023. "Modified Dynamic Routing Convolutional Neural Network for Pan-Sharpening" Remote Sensing 15, no. 11: 2869. https://doi.org/10.3390/rs15112869
APA StyleSun, K., Zhang, J., Liu, J., Xu, S., Cao, X., & Fei, R. (2023). Modified Dynamic Routing Convolutional Neural Network for Pan-Sharpening. Remote Sensing, 15(11), 2869. https://doi.org/10.3390/rs15112869






