Abstract
The finite-element (FE) method for three-dimensional (3D) airborne electromagnetic (AEM) modeling can flexibly simulate complex geological structures at high accuracy. However, it has low efficiency and high computational requirements. To solve these problems, one needs to generate meshes more reasonably. In view of this, we develop an adaptive octree meshing scheme for frequency-domain AEM modeling. The octree meshes have the characteristics of regularity and flexibility, while the adaptive algorithm can effectively refine the mesh locally. In our adaptive mesh generation, the posterior errors and weighted coefficients are used to construct the final weighted posterior errors. We verify the accuracy of our method by comparing its results with semi-analytical solutions for a half-space model. Furthermore, we use the spectral-element (SE) method and our method to calculate EM responses for an abnormal block model and compare their computational costs. The results show that our adaptive scheme has obviously technical advantages over SE method for AEM modeling with multiple frequencies and multiple survey stations. Finally, we calculate a model with complex geological structures to verify the feasibility of our algorithm in complex geological circumstances.
1. Introduction
AEM is an efficient exploration tool that has been widely used in geological mapping, mineral exploration, environmental and engineering investigations, and groundwater exploration [1,2,3]. To model the topography and complex underground structures, various 3D numerical methods have been developed, such as the integral equations (IE) method [4,5], the finite-difference (FD) method [6,7,8,9], the finite-volume (FV) method [10,11,12], the finite-element (FE) method [13,14,15], and the spectral-element (SE) method [16]. Among these numerical methods, the IE method can only simulate simple models, while the FD method has low accuracy. The FV method can simulate complex models, but its accuracy is not high. The SE method can achieve high modeling accuracy, but its computational cost is high. In comparison to these methods, the FE method can work on flexible meshes, so it can model the terrain and complex underground structures. However, its accuracy and efficiency strongly depend on the quality of the meshes.
In this paper, the vector FE method is implemented in combination with the adaptive octree mesh for AEM forward modeling, and a goal-oriented adaptive meshing scheme is developed to locally refine the octree mesh so that the modeling efficiency can be improved while the accuracy is maintained. The octree mesh has been used in FE method since the 1990s [17]. It has regularity and flexibilty and can be refined locally. However, a process to effectively generate appropriate octree meshes is the key to EM modeling. The traditional mesh generation is based largely on the experience of operators, but it cannot ensure that the generated mesh is optimal, nor can it ensure that the forward modeling can deliver high-precision results. Especially when the distribution of underground structures is complex, an over-sparse mesh cannot deliver high-precision results, while a dense mesh can ensure accuracy, but an over-dense mesh largely reduces the efficiency and wastes computational resources. Only a reasonable mesh can deliver accurate results at high efficiency. Starting with the traditional octree mesh, we try in this paper to develop an adaptive scheme to refine only those elements that create large calculation errors and make large contributions to EM signals, so that the number of elements to be refined can be reduced and the modeling efficiency can be improved while the modeling accuracy is assured.
The posterior error estimation in the adaptive mesh refinement scheme is generally based on the continuity of the EM field or the current density across adjacent elements [18] and the super-convergence characteristics of the potential field [19,20,21]. In this paper, the posterior errors are estimated based on the continuity condition of the current density. The process of using only posterior errors to guide mesh refinement is called the global adaptive algorithm. This algorithm can improve the forward-modeling accuracy at all locations in the calculation area. However, from the classical theory-of-error analysis in FE method [22], once the density of the global mesh reaches a certain level, the accuracy of FE solutions are strongly affected by the local mesh density. Considering that in the AEM method, we are only interested in EM signals around the survey points [2], the global adaptive algorithm is not very suitable because it would reduce the modeling efficiency, while the accuracy may not be improved at the locations of the survey points. Therefore, in this paper we introduce a goal-oriented adaptive scheme for mesh refinement. In addition to a posterior error estimation for each element, we also calculate a weighting coefficient from the influence function for each element based on the model parameters and the location of the receiving points. Then, the weighted posterior errors are used to determine which element needs to be refined. In this way, the modeling efficiency can be improved while the calculation accuracy is ensured.
In the sequence, we will first briefly introduce the FE forward modeling for AEM using octree meshes, and then focus our attention on the goal-oriented adaptive meshing scheme. After that, we will introduce how to implement the adaptive scheme to the octree mesh for our 3D modeling based on FE method. To test the effectiveness of the algorithm, we compare our results with 1D semi-analytical solutions for a homogeneous half-space model. To demonstrate the advantages of our goal-oriented adaptive method over the globally adaptive one, the number of unknowns is compared for these two methods under the condition that the same accuracy is obtained. Furthermore, to verify the effectiveness of our algorithm for forward-modeling a multi-frequency and multi-receiver AEM system, we use, respectively, the single frequency and the combined frequencies to generate adaptive meshes for the calculation of AEM responses and demonstrate the advantages of the adaptive mesh generated by the combined frequencies in AEM modeling. Considering that the terrain has serious impacts on AEM responses [23,24,25], we use a 2D rough surface to create a terrain model with complex underground structures and use the goal-oriented adaptive octree mesh to discretize it, and then we calculate AEM responses based on the goal-oriented adaptive octree mesh. The calculation results verify the effectiveness of our algorithm for simulating terrain and complex underground structures.
2. Methods
2.1. AEM forward Modeling Based on Octree Mesh
Assuming a time dependence of eiωt, Maxwell’s equation in the frequency domain can be written as
where E and H are, respectively, the electric and magnetic field; ω is the angular frequency; μ0 is the free-space permeability; σ is the conductivity; and Jp is the source current density, . In order to eliminate the singularity of the source field, the total field is divided into primary and secondary parts, i.e., E = Ep + Es, H = Hp + Hs. Then, we have
where , , and σ0 is the background conductivity. The vertical magnetic dipole in a free space is taken for calculating the primary field [26]. To ensure the uniqueness of the solution, the Dirichlet boundary condition is introduced [7], i.e.,
Defining the Hilbert vector space as , where L2 represents the square integrable function in the Hilbert space, then the inner products in the Hilbert space can be written as
Taking the dot product of Equation (3) with vector interpolation function [27] and applying the first Green’s theorem, the following equation for the secondary field [28] can be obtained, i.e.,
To solve Equation (7), an octree mesh is used to discretize the model. Referring to Figure 1a, we take a 2D mesh as an example to explain the hierarchical relationship between the octree elements and the division rules. The elements that are not divided are called the root cell. The elements that are divided once (blue ones) have a level 1, the elements that are divided twice (green ones) have a level 2, and so on. The octree mesh is divided according to a 2:1 rule, which means that the level difference of adjacent elements cannot exceed one. Thus, the orange elements in Figure 1a are illegal. Therefore, for an octree element, the number of adjacent cells in one element face can only be four or one (Figure 1b). When an octree mesh is refined, it has different mesh levels on both sides and generates hanging faces (namely, the number of elements on each side of the face is inconsistent). The edges on the hanging faces are called hanging edges. Different element levels on both sides of the hanging face will cause field discontinuity, which will destroy the convergence of the Galerkin method. Thus, measures need to be taken to limit it. As shown in Figure 1c, a total of 12 hanging edges exist, which can be further classified into hanging edges at the edges (solid lines) and hanging edges on the face (dotted lines). The simplest way to deal with hanging edges is to impose continuity conditions via algebraic constraints [29]. Thus, for hanging edges at the edge, we assume
Meanwhile, for hanging edges on the face, we assume
where , , , and are the field values corresponding to the long edges formed by the relevant short edges.
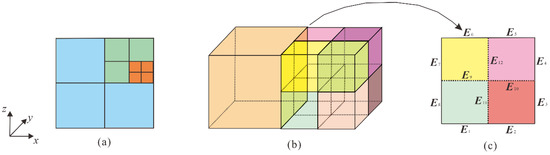

Figure 1.
(a) Illegal quadtree mesh; (b) octree mesh; (c) hanging surface in (b).
For the regular hexahedral meshes, the field value at any point in an element can be obtained by interpolation, i.e.,
where denotes the vector interpolation functions for the corresponding edge in the element, while denotes the tangential electric field at the corresponding edge.
For the octree mesh, we can substitute Equations (8) and (9) into Equation (10) and integrate Equation (7). Then, we can assemble the matrix for each element together into a large linear equation system and obtain
where K1 denotes the stiffness matrix, K2 denotes the mass matrix, es is the secondary-field vector to be solved at the edges, and ep is the primary-field vector. The direct solver PARDISO [30] is used to solve Equation (11). After obtaining the electric field at each edge, the electric field at any point can be calculated by interpolation, while the magnetic field at the receiving point can be calculated by Faraday’s law.
2.2. Adaptive Scheme for Octree Mesh
2.2.1. Posterior Errors Estimation for Octree Meshes
As we know, when the current flows across an interface of different media, its normal component is continuous, so the posterior error of each element can be evaluated based on the continuity of the normal component of the current flow. Since the FE method divides the model domain into many small elements for the numerical calculation of AEM responses, numerical errors can occur in the calculation results, so the continuity conditions of normal current density at an interface cannot be strictly guaranteed. In this paper, the discontinuity of normal current densities of adjacent elements caused by numerical errors is used as a criterion for posterior error estimation. Defining Г as the common face between the octree elements Oi and Oj and E+ and E− as the electric fields at the common face calculated using the vector FE algorithm based on the octree mesh, then if the calculation results are accurate, we have
where nГ denotes the normal vector of surface Г, J− = σ−E−, J+ = σ+E+, and σ+ and σ− are the conductivities corresponding to elements Oi and Oj, respectively. It is seen from the above discussion that Equation (12) is difficult to satisfy in EM forward modeling due to the existence of numerical errors. However, the posterior errors can be estimated from (12) by calculating the difference in current density from the calculation results.
For 3D forward modeling in frequency-domain AEM, we solve the secondary electric field. The normal current density of the secondary field does not meet the continuity condition, so we need to modify Equation (12). For this purpose, the total electric field is rewritten as
Considering that the background field Ep is selected as that of a magnetic dipole in a free space, the real part of the background field is 0 [26], so the real part of the secondary field is equal to the real part of the total field. Therefore, the continuity condition of the real part of the normal secondary current density can be used as an estimation of the posterior errors. Based on this, the posterior error of the secondary field can be defined as
where Гi is the ith face of the octree mesh, Esr− and Esr+ are the real parts of the electric field at the common face Гi, while σ− and σ+ are the conductivities on both sides of Гi.
For octree meshes, the posterior errors are estimated, respectively, for the following three cases:
- For element O1 in Figure 2a, the relationship between elements O1 and O2 is one face to one face. Thus, when calculating the posterior error, only the differences of normal current densities between Г1 and Г2 need to be calculated.
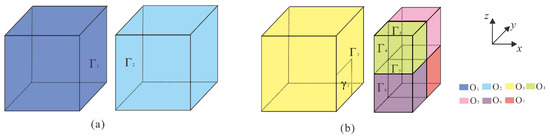 Figure 2. Schematic diagram of posterior error calculation for octree meshes. (a) Schematic diagram of the first case. (b) Schematic diagram of the second and third case.
Figure 2. Schematic diagram of posterior error calculation for octree meshes. (a) Schematic diagram of the first case. (b) Schematic diagram of the second and third case. - For element O3 in Figure 2b, the relationships with elements O4, O5, O6, and O7 are one face to four faces. Thus, when calculating the posterior error, the differences of normal current densities between Г3 and Г4, Г5, Г6, and Г7 need to be calculated.
- For elements O4, O5, O6, or O7 in Figure 2b, the relationship between them and O3 is one face to one face. Thus, when calculating the posterior errors, the differences of normal current densities between the faces Г4, Г5, Г6, Г7, and their corresponding areas on Г3 need to be calculated.
In actual calculations, for the first case, the electric fields , , , and at four points of Г1 and , , , and at four points of Г2 can be calculated from Equation (10). Then, we can divide the area into four small equal rectangles f1, f2, f3, and f4, with each containing one point, and calculate the posterior error at the common surfaces of Г1 and Г2 by
For the second case, we take 4 points at Г3 in the area corresponding to Г4, Г5, Г6, Г7 and obtain the electric fields , , , and according to Equation (10). Similarly, we can obtain the corresponding electric fields , , , and at Г4, Г5, Г6, and Г7 and calculate the posterior error of Г3 by
For the third case, we take element O6 as an example. It is seen from Figure 2b that the face corresponding to Г6 is γ3. The electric fields , , , and of four points at Г6 can be obtained from Equation (10), where the area is divided into four small equal rectangles, f5, f6, f7, and f8, with each containing one point. Similarly, we can obtain the electric fields , , , and for four points corresponding to surface γ3 and calculate the posterior error of Г6 by
2.2.2. Influence Function
The globally adaptive mesh refinement based only on posterior errors will improve the calculation accuracy of AEM forward modeling in the whole calculation area. However, when the mesh is refined to a certain level, the global mesh refinement will lead to a situation where the number of elements is largely increased, but the accuracy is not much improved. At this time, further mesh refinements cannot improve the accuracy, but instead greatly increase the computational cost. Since in AEM, we are only interested in EM responses at the receiver locations, the subdivision of underground space under EM receivers is very important. The difference between the globally adaptive refinement and the goal-oriented adaptive refinement is that the former refines the mesh globally, while the latter tends to refine the elements that have a large impact on the receiver responses while ignoring those that have small impacts on the receiver responses. To achieve this, we introduce a goal-oriented adaptive meshing scheme to achieve local refinement only at the abnormal bodies and electrical interfaces, which will greatly reduce the number of computations while ensuring the accuracy.
To realize the goal-oriented adaptive mesh refinement, we introduce in this paper a weighted coefficient into the posterior error estimation by solving the dual problem of the above forward modeling. Assuming that the linear equation system satisfied by the electric fields within elements where the receivers are located is L(E), the adaptive algorithm aims to reduce the value of the linear error function L(e) by refining the mesh, where e = E − Eh is the error between the numerical solution Eh and the real solution E, and L(E) is only related to the elements containing the receivers. Furthermore, the dual problem of the forward modeling can be defined as
where W is the influence function [31] and is the dual form of . Since is self-dual, Equation (18) can be rewritten as
Defining w as the error of W, i.e., w = W − Wh, where Wh is the FE solution of W, then from (19), L(e) can be expressed as [22]
while w can be obtained from
L(N) is a linear functional of N, where [18]. The specific form of can be written as
Using (20) and the Cauchy–Schwarz inequality, the maximum value of L(e) can be estimated by [32]
where Cn is a positive constant, and is the energy norm for the ith element that is defined as . Since the true value of E cannot be obtained, e cannot be obtained, either. From the physical meaning of , one can see that it reflects the errors caused by using the finite dimensional numerical results to replace the true values. Equation (14) just reflects this error, so we can substitute by , i.e.,
where is the weighted posterior error for element i, and . After calculating for each element, we can select those elements with larger than the preset threshold and then refine them.
Figure 3 shows the flow chart of our FE forward modeling for AEM based on adaptive octree meshes. In the figure, Niter is the number of iterations, Nmaxiter is the maximum number of iterations, Nunknown is the number of unknowns, while Nmaxunknown is the maximum number of unknowns. ζm,n denotes the relative errors between the forward results at each frequency (m) and receiver point (n) of the last three iterations, and ζt is the threshold set for ζm,n. V is the element volume, and Vmin is the smallest volume among all elements. is the normalized weighted posterior error, while is the threshold set for .
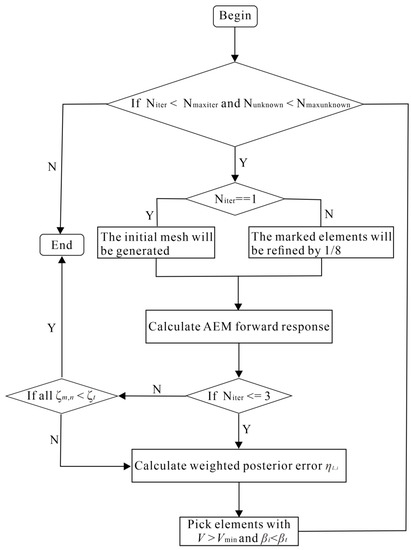
Figure 3.
Flow chart of FE forward modeling based on goal-oriented adaptive octree meshes.
3. Numerical Experiments
To verify the accuracy of the algorithm presented in this paper, we first assume a uniform half-space model and compare the forward responses calculated by our adaptive octree mesh with the semi-analytical solutions. We also compare the results from our goal-oriented adaptive algorithm and the globally adaptive one. The half-space has a resistivity of 10 Ω·m, the transmitting and receiving dipoles are both located in the air at the height of 45 m, and the offset between them is 8 m. The frequency is 25,000 Hz. Note that for convenience, we used the resistivity instead of the conductivity and the horizontal coplanar coil (HCP) system in all our numerical experiments. Figure 4 shows the globally adaptive mesh and that generated by the goal-oriented adaptive algorithm, the forward responses, and the relative errors with respect to the semi-analytical solutions. It is seen from Figure 4a,b that with an increasing number of elements, the forward results from the two adaptive algorithms converge quickly; the relative errors of the goal-oriented adaptive algorithm and the globally adaptive one both decrease rapidly. When the number of unknowns increases to a certain level, the relative errors tend to become stable. However, the comparison shows that the relative errors of our goal-oriented adaptive algorithm decrease faster than the globally adaptive one, meaning that when using the goal-oriented adaptive algorithm, one can obtain the same accuracy as the global adaptive algorithm with fewer elements and unknowns. Comparing the meshes in Figure 4c–f, one can clearly see that our goal-oriented adaptive scheme is more inclined to refine the elements in the underground near the transmitting and receiving dipoles than the global adaptive algorithm, so the goal-oriented adaptive algorithm presented here is more target-oriented in the process of mesh refinement.
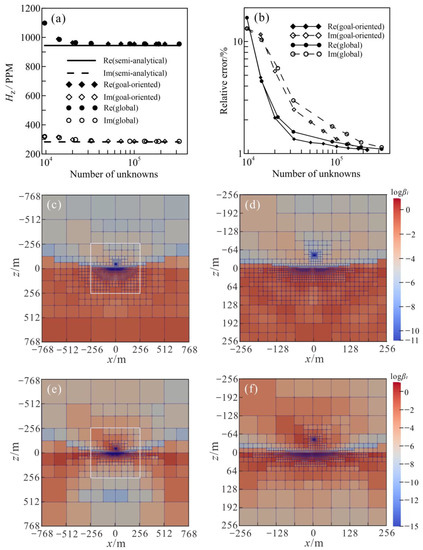
Figure 4.
Mesh generation and forward-modeling results for a half-space model. (a) The results calculated using a global adaptive mesh and a goal-oriented adaptive one are compared with 1D semi-analytical solutions; (b) their relative errors versus the number of unknowns; (c) global adaptive mesh; (d) local view of the mesh marked by the white box in (c); (e) goal-oriented adaptive mesh; (f) local view of the mesh marked by the white box in (e). β is the normalized weighted posterior error.
To further validate our algorithm for the modeling of multi-frequency and multi-receiver problems in AEM, we respectively calculate (1) Hz responses at 1600 Hz using the goal-oriented adaptive mesh generated for 1600 Hz; (2) Hz responses at 25,000 Hz using the goal-oriented adaptive mesh generated for 25,000 Hz; and (3) Hz responses at 1600 Hz and 25,000 Hz, with Hz calculated using the goal-oriented adaptive mesh created for the combined frequencies of 1600 Hz and 25,000 Hz. Then, we compare these results with those obtained from the fourth order of spectral-element method [16]. Figure 5 shows the model. The transmitting and receiving dipoles are both located at the height of 30 m with an offset of 10 m. The abnormal body has a size of 80 m × 80 m × 60 m and a top depth of 40 m. The resistivity of the half-space is 100 Ω·m, while the resistivity of the abnormal body is 1 Ω·m. Figure 6 shows the meshes with different adaptive refinement strategies, while Figure 7 shows the calculation results. It is seen from Figure 6a,b that at low frequencies, the EM system has a large penetration depth, and thus, a big range of adaptive mesh is generated so that both the abnormal body and the deep earth are refined. From Figure 6c,d, it is seen that at high frequencies, the EM system has a small penetration depth, so our adaptive method only refines the mesh close to the surface and the upper part of the abnormal body. From Figure 6e,f, it is seen that when the adaptive mesh is generated by considering two frequencies together, the surface and abnormal body are both well-refined. This implies that the mesh generated by combining the high and low frequencies takes care of both the shallow and deep earth. From the model results shown in Figure 7a,b, one sees that the forward responses using the single-frequency adaptive octree mesh and the octree mesh from combined frequencies are in good agreement with those of the fourth order of SE method, as the maximum relative errors of results calculated by the single-frequency meshes and the mesh of combined frequencies are both less than 2.2% (Figure 7c,d). This indicates that our adaptive algorithm is effective in dealing with the multi-frequency and multi-receiver AEM modeling problem.
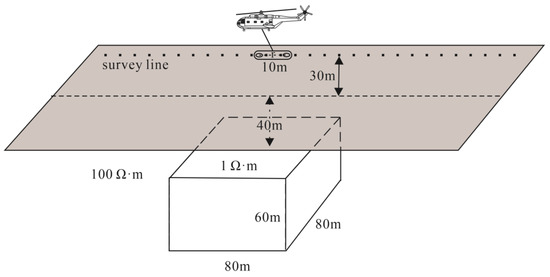
Figure 5.
An abnormal body embedded in a homogenous half-space.

Figure 6.
Mesh generation for a block abnormal body embedded in a half-space in Figure 5. (a) Mesh generated with single frequency of 1600 Hz; (b) local view of the mesh marked by the white box in (a); (c) mesh generated with single frequency of 25,000 Hz; (d) local view of the mesh marked by the white box in (c); (e) mesh generated using the combined frequencies of 1600 Hz and 25,000 Hz; (f) local view of the mesh marked by the white box in (e). β is the normalized weighted posterior error.
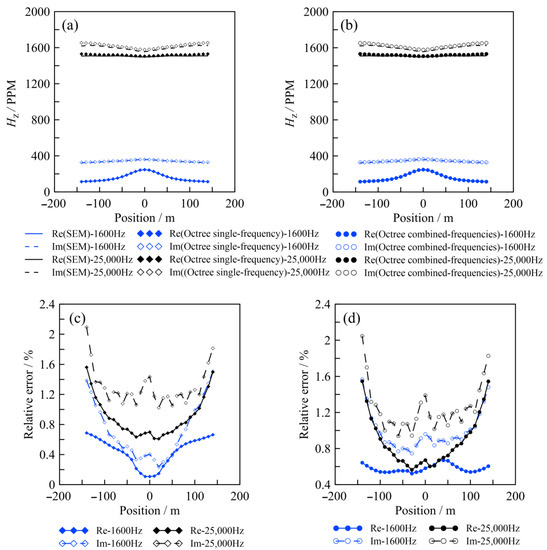
Figure 7.
AEM responses for the model in Figure 6 and their relative errors to those calculated by the fourth-order SE method. (a) Results of 1600 Hz and 25,000 Hz using the mesh for a single frequency in comparison to those of SE method; (b) results using mesh of combined frequencies in comparison to the SE method; (c,d) are corresponding relative errors between our modeling results and those of SE method.
It should be pointed out that although the single-frequency adaptive mesh can deliver accurate EM results for the corresponding frequency, one needs to generate an adaptive mesh for each frequency. For a multi-frequency AEM system, it will take much time to generate these meshes, which will seriously affect the modeling efficiency. In contrast, using our combined-frequency strategy, one can create a mesh once that can be used to model AEM responses for multiple frequencies. This can save lots of computing resources.
Table 1 shows the comparison of the number of unknowns, time, and memory requirement for our FE method based on adaptive octree mesh for combined frequencies and SE method for the block model in Figure 5 under the condition that roughly the same accuracy is obtained for both methods. We use a Dell workstation with a single processor, Intel Xeon gold6254 CPU @ 3.10 GHz (Santa Clara, CA, USA). It is seen from the table that when the relative errors of both algorithms are less than 2.2% (see Figure 7d), our FE method based on the adaptive octree mesh is more than 2.3 times faster than the fourth-order SE method. The memory requirement is also largely reduced.

Table 1.
Comparison between SE and adaptive FE method using the octree mesh generated by combined frequencies.
To further verify the effectiveness of our adaptive algorithm for modeling the complex geology, an undulating terrain and complex underground structure shown in Figure 8 are simulated in this section. The terrain was generated as a 2D random Gaussian rough surface [33]. The abnormal body has a size of about 332 m × 198 m × 168 m and a top depth of about 70 m. The half-space has a resistivity of 100 Ω·m, while the abnormal body has a resistivity of 1 Ω·m. The flight altitude is 30 m, and the transmitter–receiver offset is 10 m.

Figure 8.
A complex abnormal body embedded in a half-space with undulating terrain. The dashed line indicates the survey line.
First, we generate an adaptive mesh for the combined frequencies of 1600 Hz and 25,000 Hz, shown in Figure 9. It is seen that our adaptive refinement algorithm created a good mesh for the complex geological model. The interfaces between the air and the earth surface as well as between the abnormal body and its surrounding areas were all refined. From Figure 9a,b, it is seen that when the frequency is low, the range of the adaptive mesh generated is large, and the interfaces between the abnormal body, the surrounding rock, and the deep earth are refined. When the frequency is high, the penetration depth gets smaller, and only the elements close to the earth’s surface are refined (c.f. Figure 9c,d). From Figure 9e,f, it is seen that the mesh for combined frequencies has the characteristics of both low- and high-frequency meshes. The mesh is refined both at the undulating surface and at the location of the abnormal body, while the elements in the deep earth are not much refined. Figure 10 shows the forward responses using the mesh in Figure 9. It is seen that the responses for each frequency calculated by the single-frequency mesh are in good agreement with the results calculated by the mesh of combined frequencies. This indicates again that the mesh generated for combined frequencies can be used to replace the single-frequency mesh for AEM forward modeling and the calculation efficiency can be largely improved. Additionally, from the results in Figure 10, it is seen that there is an obvious mirror relationship between high-frequency EM responses and the terrain, meaning that the terrain has a serious effect on AEM responses at high frequencies.

Figure 9.
Mesh generation for the complex model in Figure 8. (a) Single-frequency mesh for 1600 Hz; (b) local view of the mesh marked by the white box in (a); (c) single-frequency mesh for 25,000 Hz; (d) local view of the mesh marked by the white box in (c); (e) mesh for combined frequencies of 1600 Hz and 25,000 Hz; (f) local view of the mesh marked by the white box in (e). β is the normalized weighted posterior error.

Figure 10.
AEM responses for the complex model in Figure 8 for different frequencies.
4. Conclusions
In this paper, based on the goal-oriented adaptive octree mesh scheme, we have successfully developed a finite-element algorithm for the AEM modeling of multi-frequency and multi-receiver problems. Considering the difference in mesh generations for hanging faces and common faces, we separately calculated the posterior errors based on the characteristics of the faces. Comparisons of the meshes generated by the globally adaptive method and our goal-oriented adaptive method and their calculation results confirmed that our goal-oriented adaptive algorithm is more suitable for AEM forward modeling. It can largely improve the modeling efficiency while ensuring the computational accuracy. Moreover, the comparison with the fourth-order SE method showed that under the same accuracy, our adaptive FE method can improve the efficiency and save memory by up to threefold. Finally, for the multi-frequency and multi-receiver AEM system, the mesh generation method developed here for combined frequencies can create an optimal mesh for multi-frequency AEM modeling. The numerical experiments showed that this kind of mesh can deliver results at the same accuracy as the single-frequency meshes; however, lots of time is saved compared to when generating the single-frequency meshes. It is expected that the presented algorithm will provide an effective means for 3D AEM forward modeling.
Author Contributions
Conceptualization, X.H. (Xue Han) and C.Y.; Data curation, X.H. (Xue Han), X.H. (Xin Huang), J.Z. and Y.L.; Formal analysis, X.H. (Xue Han); Funding acquisition, C.Y., B.Z., Y.L., X.R. and Y.S.; Investigation, X.H. (Xue Han), X.H. (Xin Huang) and J.Z.; Methodology, X.H. (Xue Han), C.Y. and B.Z.; Software, X.H. (Xue Han) and B.Z.; Validation, X.H. (Xue Han), J.N. and B.Z.; Visualization, X.H. (Xue Han), J.N., Y.L. and X.R.; Writing—original draft, X.H. (Xue Han); Writing—review and editing, X.H. (Xue Han), J.N. and C.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (42030806, 42174167, 42274093) and the China National Postdoctoral Program for Innovative Talents (BX20220130).
Data Availability Statement
Data associated with this research are available and can be obtained by contacting the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pfaffhuber, A.A.; Monstad, S.; Rudd, J. Airborne electromagnetic hydrocarbon mapping in Mozambique. Explor. Geophys. 2009, 40, 237–245. [Google Scholar] [CrossRef]
- Yin, C.; Zhang, B.; Liu, Y.H.; Ren, X.; Cai, J. Review on airborne EM technology and developments. Chin. J. Geophys. 2015, 58, 2637–2653. [Google Scholar]
- Gottschalk, I.; Knight, R.; Asch, T.; Abraham, J.; Cannia, J. Using an airborne electromagnetic method to map saltwater intrusion in the northern Salinas Valley, California. Geophysics 2020, 85, B119–B131. [Google Scholar] [CrossRef]
- Walker, P.W.; West, G.F. A robust integral equation solution for electromagnetic scattering by a thin plate in conductive media. Geophysics 1991, 56, 1140–1152. [Google Scholar] [CrossRef]
- Zhdanov, M.S.; Lee, S.K.; Yoshioka, K. Integral equation method for 3D modeling of electromagnetic fields in complex structures with inhomogeneous background conductivity. Geophysics 2006, 71, G333–G345. [Google Scholar] [CrossRef]
- Yee, K. Numerical solution of initial boundary value problems involving Maxwell’s equations in isotropic media. IEEE Trans. Antennas Propag. 1966, 14, 302–307. [Google Scholar] [CrossRef]
- Newman, G.A.; Alumbaugh, D.L. Frequency-domain modelling of airborne electromagnetic responses using staggered finite differences. Geophys. Prospect. 1995, 43, 1021–1042. [Google Scholar] [CrossRef]
- Frank, A.M. Fast finite-difference time-domain modeling for marine-subsurface electromagnetic problem. Geophysics 2007, 72, A19–A23. [Google Scholar] [CrossRef]
- Streich, R. 3D finite-difference frequency-domain modeling of controlled-source electromagnetic data: Direct solution and optimization for high accuracy. Geophysics 2009, 74, F95–F105. [Google Scholar] [CrossRef]
- Haber, E.; Ascher, U.M. Fast finite volume simulation of 3Delectromagnetic problems with highly discontinuous coefficients. SIAM J. Sci. Comput. 2001, 22, 1943–1961. [Google Scholar] [CrossRef]
- Yang, B.; Xu, Y.; He, Z.; Sun, W. 3D frequency-domain modeling of marine controlled source electromagnetic response with topography using finite volume method. Chin. J. Geophys. 2012, 55, 1390–1399. [Google Scholar]
- Jahandari, H.; Farquharson, C.G. A finite-volume solution to the geophysical electromagnetic forward problem using unstructured grids. Geophysics 2014, 79, E287–E302. [Google Scholar] [CrossRef]
- Mitsuhata, Y. 2-D electromagnetic modeling by finite-element method with a dipole source and topography. Geophysics 2000, 65, 465–475. [Google Scholar] [CrossRef]
- Schwarzbach, C.; Haber, E. Finite element-based inversion for time-harmonic electromagnetic problems. Geophys. J. Int. 2013, 193, 615–634. [Google Scholar] [CrossRef]
- Yin, C.; Zhang, B.; Liu, Y.; Cai, J. 2.5-D forward modeling of the time-domain airborne EM system in areas with topographic relief. Chin. J. Geophys. 2015, 58, 1411–1424. [Google Scholar]
- Huang, X.; Yin, C.; Farquharson, C.G.; Cao, X.; Zhang, B.; Huang, W.; Cai, J. Spectral element method with arbitrary hexahedron meshes for time-domain 3D airborne electromagnetic forward modeling. Geophysics 2019, 84, E37–E46. [Google Scholar] [CrossRef]
- Young, D.P.; Melvin, R.G.; Bieterman, M.B.; Johnson, F.T.; Samant, S.S.; Bussoletti, J.E. A locally refined rectangular grid finite element method-Application to computational fluid dynamics and computational physics. J. Comput. Phys. 1991, 92, 1–66. [Google Scholar] [CrossRef]
- Ren, Z.; Kalscheuer, T.; Greenhalgh, S.; Maurer, H. A goal-oriented adaptive finite-element approach for plane wave 3D electromagnetic modeling. Geophys. J. Int. 2013, 187, 63–74. [Google Scholar] [CrossRef]
- Key, K.; Weiss, C. Adaptive finite-element modeling using unstructured grids: The 2D magnetotelluric example. Geophysics 2006, 71, G291–G299. [Google Scholar] [CrossRef]
- Ren, Z.; Tang, J. 3D direct current resistivity modeling with unstructured mesh by adaptive finite-element method. Geophysics 2010, 75, H7–H17. [Google Scholar] [CrossRef]
- Schwarzbach, C.; Borner, R.; Spitzer, K. Three-dimensional adaptive higher order finite element simulation for geo-electromagnetics-Amarine CSEM example. Geophys. J. Int. 2011, 187, 63–74. [Google Scholar] [CrossRef]
- Brenner, S.; Scott, L. The Mathematical Theory of Finite Element Methods; Springer: New York, NY, USA, 2008. [Google Scholar]
- Sasaki, Y.; Nakazato, H. Topographic effects in frequency-domain helicopter-borne electromagnetic. Explor. Geophys. 2003, 34, 24–28. [Google Scholar] [CrossRef]
- Nam, M.J.; Kim, H.J.; Song, Y.; Lee, T.J.; Son, J.S. 3D magneto-telluric modelling including surface topography. Geophys. Prospect. 2007, 55, 277–287. [Google Scholar] [CrossRef]
- Liu, Y.; Yin, C. 3D inversion for frequency-domain HEM data. Chin. J. Geophys. 2013, 56, 4278–4287. [Google Scholar]
- Ward, S.H.; Hohmann, G.W. Electromagnetic Theory for Geophysical. In Applications Electromagnetic Method in Applied Geophysics; Nabighian, M.N., Ed.; Society of Exploration Geophysicists: Houston, TX, USA, 1988; Volume 1, p. 176. [Google Scholar]
- Jin, J. The Finite Element Method in Electromagnetics; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Cai, H.; Xiong, B.; Han, M.; Zhdanov, M. 3D controlled-source electromagnetic modeling in anisotropic medium using edge-based finite element method. Comput. Geosci. 2014, 73, 164–176. [Google Scholar] [CrossRef]
- Legrain, G.; Allais, R.; Cartraud, P. On the use of the extended finite element method with quadtree/octree meshes. Int. J. Numerical. Methods Eng. 2011, 86, 717–743. [Google Scholar] [CrossRef]
- Bollhöfer, M.; Eftekhari, A.; Scheidegger, S.; Schenk, O. Large-Scale Sparse Inverse Covariance Matrix Estimation. SIAM J. Sci. Comput. 2019, 41, A380–A401. [Google Scholar] [CrossRef]
- Oden, J.T.; Prudhomme, S. Goal-oriented error estimation and adaptive for the finite element method. Comput. Math. Appl. 2001, 41, 735–756. [Google Scholar] [CrossRef]
- Zdunek, A.; Rachowicz, W. A goal-oriented hp-adaptive finite element approach to radar scattering problems. Comput. Methods Appl. Mech. Eng. 2005, 194, 657–674. [Google Scholar] [CrossRef]
- Kobayashi, T.; Oya, H.; Ono, T. A-scope analysis of subsurface radar sounding of lunar mare region. Earth Planets Space 2002, 54, 973–982. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).