Attention-Aware Spectral Difference Representation for Hyperspectral Anomaly Detection
Abstract
1. Introduction
- (1)
- An attention-aware spectral difference representation module is proposed to generate a noise distribution that better matches the background by employing the attention mechanism and spectral difference strategy, which can guide the construction of a more accurate background model in situations where the types of land covers are diverse and complex.
- (2)
- A compound loss function is designed to better detect anomalies, which simultaneously calculates the reconstruction errors between the original input image and the reconstructed image from both the spectrum intensity and angle perspectives.
- (3)
- The proposed HAD-ASDR method is verified on five hyperspectral data sets and achieves better or comparable HAD performance than the comparison HAD methods.
2. Related Work
2.1. Hyperspectral Anomaly Detection Method
2.2. Convolutional Auto-Encoder
2.3. Attention Mechanism
3. Method
3.1. Attention-Aware Spectral Difference Representation Module
3.2. Convolutional Auto-Encoder Based Background Reconstruction Module
3.3. Joint Spectrum Intensity and Angle Based Anomaly Detection Module
3.4. The Process of HAD-ASDR
| Algorithm 1 The process of HAD-ASDR. |
| Input: |
| The hyperspectral images X. |
| Initialization: |
| 1. Adam optimizer is used in the ASDR model, and the learning rate is set to 1 × 10. |
| The loss function is MSELoss, and the number of epochs is set to 50. |
| 2. The Adam optimizer is used in the CAE-BRM, the learning rate is set to 1 × 10, and the loss function is used in Equation (3). |
| Step: |
| 1. Feed X into the block to obtain . |
| 2. Feed the learned to the block to obtain . |
| 3. The initial background is calculated by Equation (1). |
| 4. Feed to to generate the reconstructed background . |
| 5. Update all the parameters by utilizing Adam optimizer to minimize MSELoss. |
| Until: achieve the optimal ASDR model after a fixed number of epochs. |
| 6. Calculate the noise of the background by Equation (2). |
| 7. Feed to CAE-BRM to obtain the reconstructed background . |
| 8. Compute the overall loss according to Equation (3). |
| 9. Update all the parameters by minimizing utilizing Adam optimizer. |
| Until: achieve the optimal CAE-BRM model after a fixed number of epochs. |
| 10. The anomaly detection map is achieved by calculating reconstruction errors between X and obtained from the optimal ASDR and CAE-BRM by Equation (6). |
| Output: |
| 1. The anomaly detection map. |
| 2. Area Under Curve (AUC) values. |
4. Experiments and Analysis
4.1. Data Sets
- (1)
- AVIRIS Airplane Data: The AVIRIS sensor is utilized to shoot the specific area of San Diego, CA, USA to acquire the AVIRIS airplane data. The AVIRIS airplane data has a spatial resolution of 20 m and a spectral resolution of 10 nm, whose spectral wavelengths span from 370 to 2510 nm. The AVIRIS airplane image has the spatial size of and 224 spectral bands. A total of 189 spectral bands are retained because of removing the bad or noise bands. In the hyperspectral image, three airplanes are classified as anomalies. The visualization of the AVIRIS airplane data and its corresponding ground truth are shown in Figure 2.
- (2)
- HYDICE Urban Data: The HYDICE airborne sensor is employed to collect HYDICE urban data. The HYDICE urban image has pixels in the spatial dimension and includes 210 spectral bands, with wavelengths ranging between 400 and 2500 nm. 162 valid spectral bands have remained after removing bad bands such as low-SNR and water absorbing bands. The cars and roofs in these data are considered as anomalies. The HYDICE urban data and its corresponding ground truth are illustrated in Figure 3.
- (3)
- Salinas Scene Data: The AVIRIS sensor is utilized to shoot the Salinas valley of California, USA to acquire the Salinas scene data. The Salinas scene image has pixels in the spatial dimension and includes 224 spectral bands. Vegetables, vineyard fields, and bare soils are considered as anomalies in the Salinas scene. Figure 4 shows the Salinas scene data and their corresponding ground truth.
- (4)
- Abu-airport-3 Data: The AVIRIS sensor is utilized to collect Abu-airport-3 Data, which represents the airport in Los Angeles, USA. The Abu-airport-3 image consists of a spatial dimension of pixels and includes 205 spectral bands after removing bad bands. Airplanes in these data are considered anomalies. Figure 5 illustrates the Abu-airport-3 data and their corresponding ground truth.
- (5)
- Abu-urban-4 Data: The AVIRIS sensor is employed to capture data from the urban area in Los Angeles, USA, resulting in the Abu-urban-4 data. These data are collected using the same equipment as the Abu-airport-3 data. It has the spatial size of and 205 spectral bands after eliminating the bad or noise bands. Houses in these data are considered anomalies. Figure 6 displays the Abu-urban-4 data and their corresponding ground truth.
4.2. Evaluation Criteria
4.3. Training Parameters
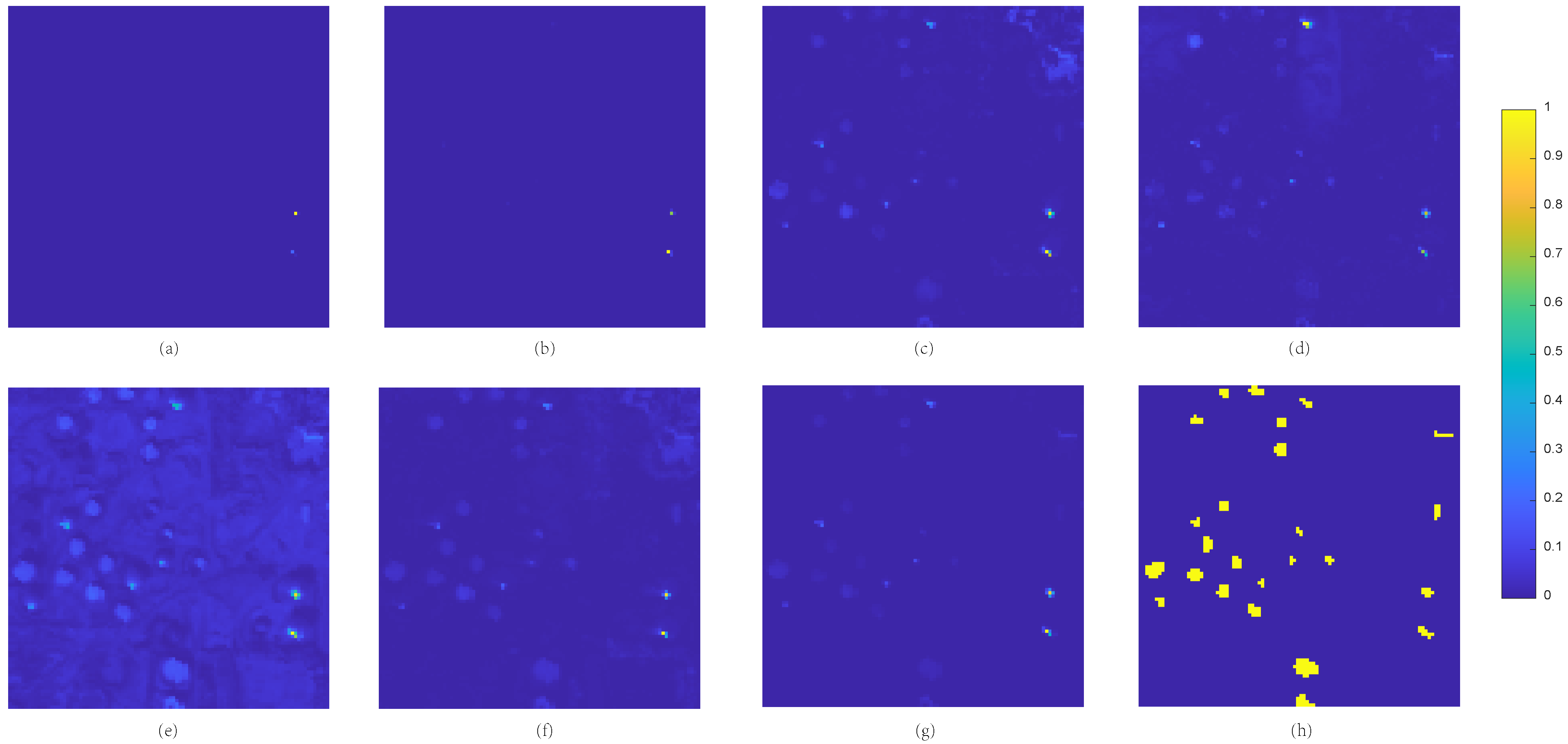
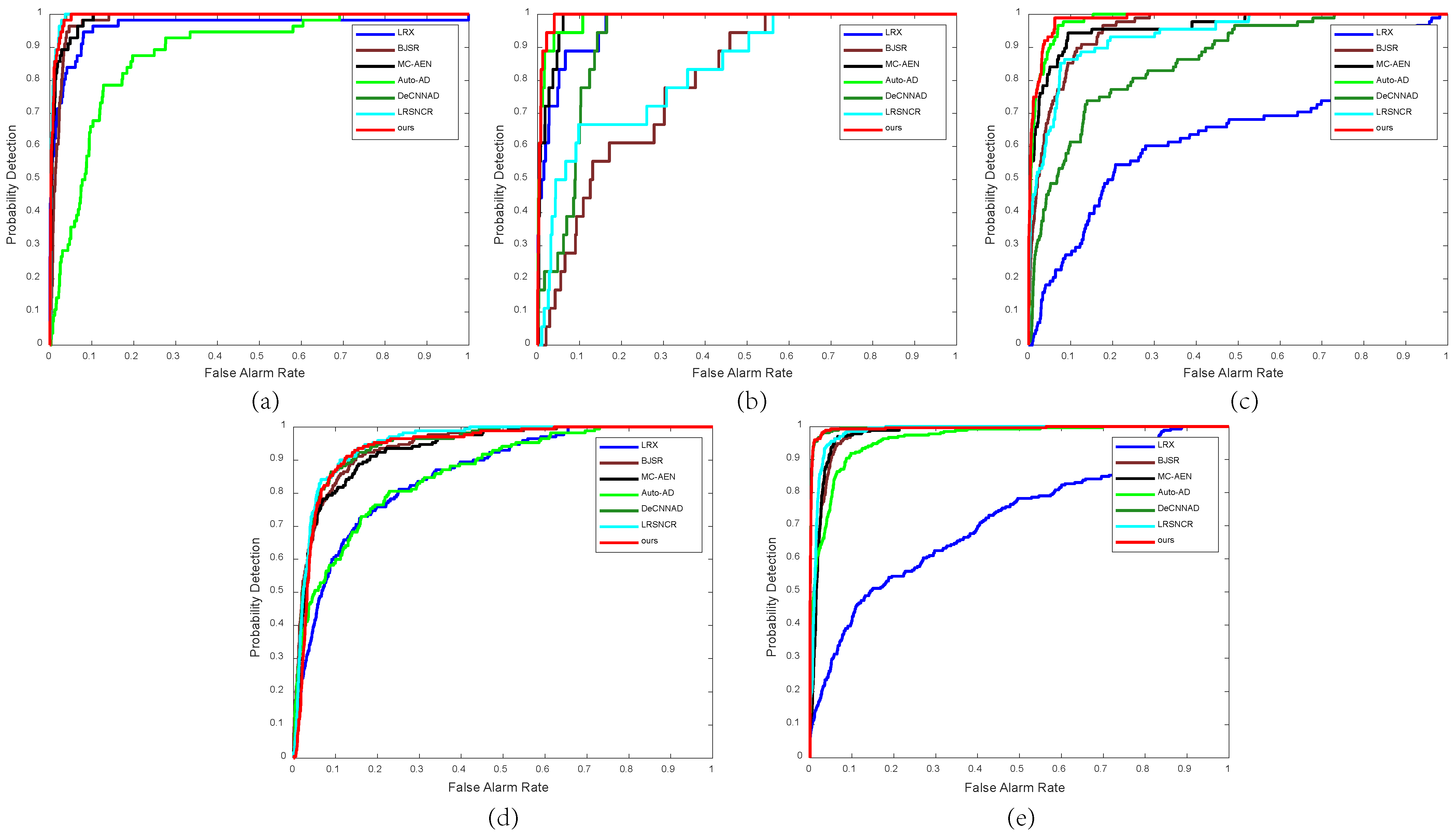
4.4. Comparison with State-of-the-Arts
- (1)
- Local RX (LRX) [45] uses the strategy of the double sliding window for estimating local background statistics. It has the ability to identify anomalies by computing the Mahalanobis distance between a pixel under consideration and its surrounding pixels.
- (2)
- The Background Joint Sparse Representation (BJSR) [25] based method makes the assumption that each pixel can be represented by the constructed background dictionary and a specific coefficient, and employs the reconstructed errors to identify anomalies with large reconstructed errors.
- (3)
- Manifold Constrained AutoEncoder Network (MC-AEN) [46] based method extracts latent features by the auto-encoders with constraints by the manifold structure, and calculates the global and local reconstructed errors to detect anomalies.
- (4)
- The Autonomous Hyperspectral Anomaly Detection Network (Auto-AD) [47] method designs a fully convolutional auto-encoder architecture, which incorporates skip connections to reconstruct the background. An adaptive-weighted loss function is utilized to reduce the influence of potential anomalous pixels with large reconstruction errors in order to distinguish anomalies effectively.
- (5)
- DeCNN-AD algorithm [28] uses the clustering strategy to construct a new dictionary and incorporates a flexible denoiser as a prior for the representation coefficients in the dictionary to enhance the accuracy of HAD.
- (6)
- The LRSNCR algorithm [48] is a non-convex regularized approximation technique that builds on the improved RPCA for HAD. LRSNCR improves the discriminative ability between anomalies and the background significantly through the use of non-convex regularization.
4.5. Algorithm Time Cost
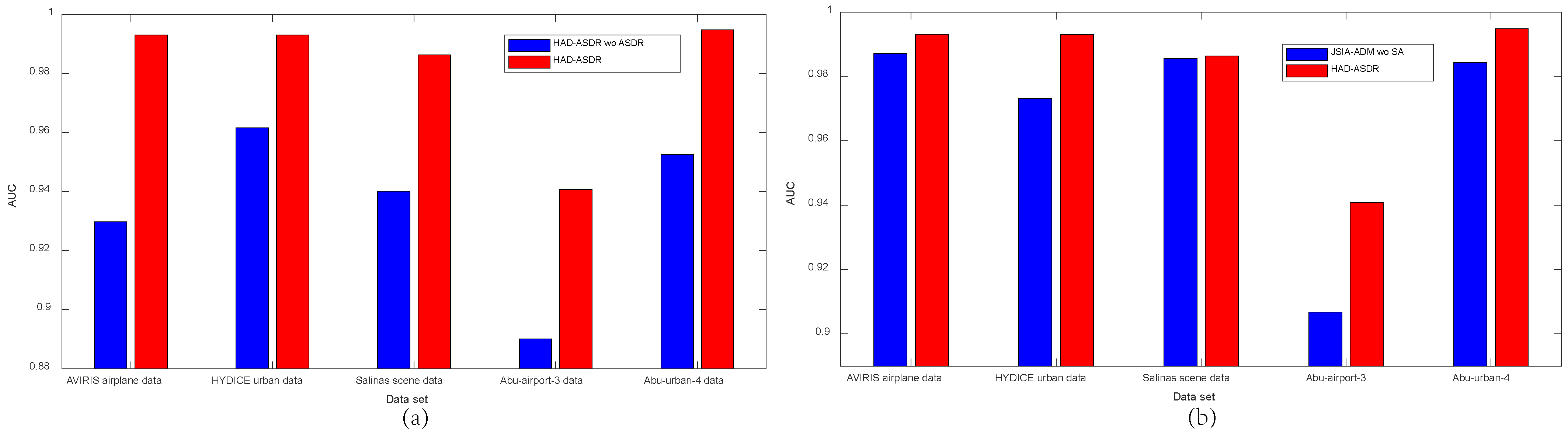
4.6. Ablation Study
4.6.1. The Effective of ASDR
4.6.2. The Effective of JSIA-ADM
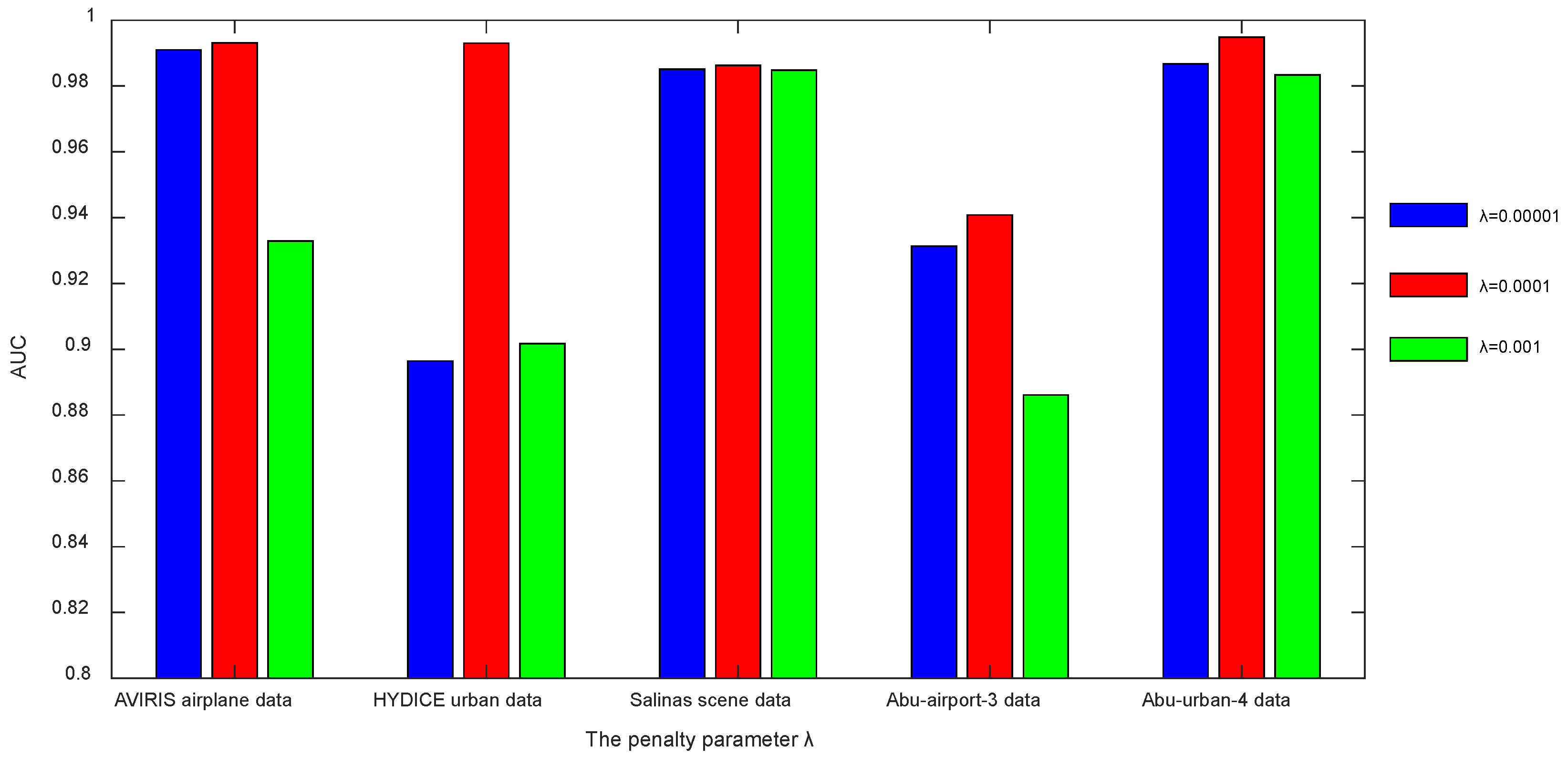
4.6.3. The Effectiveness of the Penalty Parameter α
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chang, C.I.; Chiang, S.S. Anomaly detection and classification for hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1314–1325. [Google Scholar] [CrossRef]
- Liu, S.; Marinelli, D.; Bruzzone, L.; Bovolo, F. A review of change detection in multitemporal hyperspectral images: Current techniques, applications, and challenges. IEEE Geosci. Remote Sens. Mag. 2019, 7, 140–158. [Google Scholar] [CrossRef]
- Hu, X.; Xie, C.; Fan, Z.; Duan, Q.; Zhang, D.; Jiang, L.; Wei, X.; Hong, D.; Li, G.; Zeng, X.; et al. Hyperspectral anomaly detection using deep learning: A review. Remote Sens. 2022, 14, 1973. [Google Scholar] [CrossRef]
- Theiler, J.; Wohlberg, B. Local coregistration adjustment for anomalous change detection. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3107–3116. [Google Scholar] [CrossRef]
- Khazai, S.; Safari, A.; Mojaradi, B.; Homayouni, S. An approach for subpixel anomaly detection in hyperspectral images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 6, 769–778. [Google Scholar] [CrossRef]
- Zhang, X.; Wen, G.; Dai, W. A tensor decomposition-based anomaly detection algorithm for hyperspectral image. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5801–5820. [Google Scholar] [CrossRef]
- Chalapathy, R.; Chawla, S. Deep learning for anomaly detection: A survey. arXiv 2019, arXiv:1901.03407. [Google Scholar]
- Nayak, R.; Pati, U.C.; Das, S.K. A comprehensive review on deep learning-based methods for video anomaly detection. Image Vis. Comput. 2021, 106, 104078. [Google Scholar] [CrossRef]
- Reed, I.S.; Yu, X. Adaptive multiple-band CFAR detection of an optical pattern with unknown spectral distribution. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 1760–1770. [Google Scholar] [CrossRef]
- Zhao, C.; Li, X.; Ren, J.; Marshall, S. Improved sparse representation using adaptive spatial support for effective target detection in hyperspectral imagery. Int. J. Remote Sens. 2013, 34, 8669–8684. [Google Scholar] [CrossRef]
- Du, B.; Zhang, L. Random-selection-based anomaly detector for hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2010, 49, 1578–1589. [Google Scholar] [CrossRef]
- Hinton, G.E. Deep belief networks. Scholarpedia 2009, 4, 5947. [Google Scholar] [CrossRef]
- Tschannen, M.; Bachem, O.; Lucic, M. Recent advances in autoencoder-based representation learning. arXiv 2018, arXiv:1812.05069. [Google Scholar]
- Gu, J.; Wang, Z.; Kuen, J.; Ma, L.; Shahroudy, A.; Shuai, B.; Liu, T.; Wang, X.; Wang, G.; Cai, J.; et al. Recent advances in convolutional neural networks. Pattern Recognit. 2018, 77, 354–377. [Google Scholar] [CrossRef]
- Medsker, L.R.; Jain, L. Recurrent neural networks. Des. Appl. 2001, 5, 64–67. [Google Scholar]
- Graves, A.; Graves, A. Long Short-Term Memory. Supervised Sequence Labelling with Recurrent Neural Networks. Ph.D. Thesis, Technical University of Munich, Munich, Germany, 2012; pp. 37–45. [Google Scholar]
- Creswell, A.; White, T.; Dumoulin, V.; Arulkumaran, K.; Sengupta, B.; Bharath, A.A. Generative adversarial networks: An overview. IEEE Signal Process. Mag. 2018, 35, 53–65. [Google Scholar] [CrossRef]
- Ma, N.; Peng, Y.; Wang, S.; Leong, P.H. An unsupervised deep hyperspectral anomaly detector. Sensors 2018, 18, 693. [Google Scholar] [CrossRef]
- Su, H.; Wu, Z.; Zhang, H.; Du, Q. Hyperspectral anomaly detection: A survey. IEEE Geosci. Remote Sens. Mag. 2021, 10, 64–90. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, L.; Du, B.; Zhang, L. Hyperspectral anomaly detection based on machine learning: An overview. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 3351–3364. [Google Scholar] [CrossRef]
- Zheng, X.; Chen, W.; Lu, X. Spectral super-resolution of multispectral images using spatial–spectral residual attention network. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5404114. [Google Scholar] [CrossRef]
- Kwon, H.; Nasrabadi, N.M. Kernel RX-algorithm: A nonlinear anomaly detector for hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2005, 43, 388–397. [Google Scholar] [CrossRef]
- Zhao, R.; Du, B.; Zhang, L. A robust nonlinear hyperspectral anomaly detection approach. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1227–1234. [Google Scholar] [CrossRef]
- Su, H.; Wu, Z.; Zhu, A.X.; Du, Q. Low rank and collaborative representation for hyperspectral anomaly detection via robust dictionary construction. ISPRS J. Photogramm. Remote Sens. 2020, 169, 195–211. [Google Scholar] [CrossRef]
- Li, J.; Zhang, H.; Zhang, L.; Ma, L. Hyperspectral anomaly detection by the use of background joint sparse representation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2523–2533. [Google Scholar] [CrossRef]
- Li, S.; Wang, W.; Qi, H.; Ayhan, B.; Kwan, C.; Vance, S. Low-rank tensor decomposition based anomaly detection for hyperspectral imagery. In Proceedings of the 2015 IEEE International Conference on Image Processing (ICIP), Quebec City, QC, Canada, 27–30 September 2015; pp. 4525–4529. [Google Scholar]
- Kang, X.; Zhang, X.; Li, S.; Li, K.; Li, J.; Benediktsson, J.A. Hyperspectral anomaly detection with attribute and edge-preserving filters. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5600–5611. [Google Scholar] [CrossRef]
- Fu, X.; Jia, S.; Zhuang, L.; Xu, M.; Zhou, J.; Li, Q. Hyperspectral anomaly detection via deep plug-and-play denoising CNN regularization. IEEE Trans. Geosci. Remote Sens. 2021, 59, 9553–9568. [Google Scholar] [CrossRef]
- Bati, E.; Çalışkan, A.; Koz, A.; Alatan, A.A. Hyperspectral anomaly detection method based on auto-encoder. In Proceedings of the Image and Signal Processing for Remote Sensing XXI., Virtual, 10 November 2015; SPIE: Washington, DC, USA, 2015; Volume 9643, pp. 220–226. [Google Scholar]
- Xie, W.; Liu, B.; Li, Y.; Lei, J.; Du, Q. Autoencoder and adversarial-learning-based semisupervised background estimation for hyperspectral anomaly detection. IEEE Trans. Geosci. Remote Sens. 2020, 58, 5416–5427. [Google Scholar] [CrossRef]
- Chang, S.; Du, B.; Zhang, L. A sparse autoencoder based hyperspectral anomaly detection algorihtm using residual of reconstruction error. In Proceedings of the IGARSS 2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 5488–5491. [Google Scholar]
- Jiang, T.; Li, Y.; Xie, W.; Du, Q. Discriminative reconstruction constrained generative adversarial network for hyperspectral anomaly detection. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4666–4679. [Google Scholar] [CrossRef]
- Zhu, D.; Du, B.; Zhang, L. EDLAD: An encoder-decoder long short-term memory network-based anomaly detector for hyperspectral images. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 4412–4415. [Google Scholar]
- Zheng, X.; Chen, X.; Lu, X.; Sun, B. Unsupervised change detection by cross-resolution difference learning. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5606616. [Google Scholar] [CrossRef]
- Zhang, Y. A Better Autoencoder for Image: Convolutional Autoencoder. In Proceedings of the ICONIP17-DCEC. 2018. Available online: http://users.cecs.anu.edu.au/Tom.Gedeon/conf/ABCs2018/paper/ABCs2018_paper_58.pdf (accessed on 23 March 2017).
- Zheng, X.; Gong, T.; Li, X.; Lu, X. Generalized scene classification from small-scale datasets with multitask learning. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5609311. [Google Scholar] [CrossRef]
- Zheng, X.; Wang, B.; Du, X.; Lu, X. Mutual attention inception network for remote sensing visual question answering. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5606514. [Google Scholar] [CrossRef]
- Zhao, W.; Guo, Z.; Yue, J.; Zhang, X.; Luo, L. On combining multiscale deep learning features for the classification of hyperspectral remote sensing imagery. Int. J. Remote Sens. 2015, 36, 3368–3379. [Google Scholar] [CrossRef]
- Hosseiny, B.; Shah-Hosseini, R. A hyperspectral anomaly detection framework based on segmentation and convolutional neural network algorithms. Int. J. Remote Sens. 2020, 41, 6946–6975. [Google Scholar] [CrossRef]
- Shi, Y.; Li, J.; Yin, Y.; Xi, B.; Li, Y. Hyperspectral target detection with macro-micro feature extracted by 3-D residual autoencoder. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 4907–4919. [Google Scholar] [CrossRef]
- Zheng, X.; Sun, H.; Lu, X.; Xie, W. Rotation-invariant attention network for hyperspectral image classification. IEEE Trans. Image Process. 2022, 31, 4251–4265. [Google Scholar] [CrossRef]
- Chen, L.; Maddox, R.K.; Duan, Z.; Xu, C. Hierarchical cross-modal talking face generation with dynamic pixel-wise loss. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 7832–7841. [Google Scholar]
- Cai, W.; Wei, Z. Remote sensing image classification based on a cross-attention mechanism and graph convolution. IEEE Geosci. Remote Sens. Lett. 2020, 19, 8002005. [Google Scholar] [CrossRef]
- Ju, M.; Luo, J.; Wang, Z.; Luo, H. Adaptive feature fusion with attention mechanism for multi-scale target detection. Neural Comput. Appl. 2021, 33, 2769–2781. [Google Scholar] [CrossRef]
- Nasrabadi, N.M. Regularization for spectral matched filter and RX anomaly detector. In Proceedings of the Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery XIV, Virtual, 2 August 2002; SPIE: Washington, DC, USA, 2008; Volume 6966, pp. 28–39. [Google Scholar]
- Lu, X.; Zhang, W.; Huang, J. Exploiting embedding manifold of autoencoders for hyperspectral anomaly detection. IEEE Trans. Geosci. Remote Sens. 2019, 58, 1527–1537. [Google Scholar] [CrossRef]
- Wang, S.; Wang, X.; Zhang, L.; Zhong, Y. Auto-AD: Autonomous hyperspectral anomaly detection network based on fully convolutional autoencoder. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5503314. [Google Scholar] [CrossRef]
- Yao, W.; Li, L.; Ni, H.; Li, W.; Tao, R. Hyperspectral anomaly detection based on improved RPCA with non-convex regularization. Remote Sens. 2022, 14, 1343. [Google Scholar] [CrossRef]










| Block | Layer | Input | Kernel Size | Stride Size | Output |
|---|---|---|---|---|---|
| Spectral chanel attention | Avg_pool | (C,H,W) | - | - | (C,1,1) |
| Conv2d | (1,C,1,1) | (1,1) | (1,1) | (1,C,1,1) | |
| Conv2d | (1,C,1,1) | (1,1) | (1,1) | (1,C,1,1) | |
| Max_pool | (1,C,1,1) | - | - | (C,1,1) | |
| Conv2d | (1,C,1,1) | (1,1) | (1,1) | (1,C,1,1) | |
| Conv2d | (1,C,1,1) | (1,1) | (1,1) | (1,C,1,1) | |
| Spatial attention | Concat | 2 × (1,1,H,W) | - | - | (1,2,H,W) |
| Conv2d | (1,2,H,W) | (7,7) | (1,1) | (1,1,H,W) | |
| Auto-encoder | Conv2d | (1,C,H,W) | (3,3) | (1,1) | (1,128,H,W) |
| Conv2d | (1,128,H,W) | (3,3) | (1,1) | (1,64,H,W) | |
| Conv2d | (1,64,H,W) | (3,3) | (1,1) | (1,32,H,W) | |
| ConvTranspose2d | (1,32,H,W) | (3,3) | (1,1) | (1,64,H,W) | |
| ConvTranspose2d | (1,64,H,W) | (3,3) | (1,1) | (1,128,H,W) | |
| ConvTranspose2d | (1,128,H,W) | (3,3) | (1,1) | (1,C,H,W) |
| Dataset | LRX | BJSR | MC-AEN | Auto-AD | DeCNNAD | LRSNCR | HAD-ASDR |
|---|---|---|---|---|---|---|---|
| AVIRIS airplane data | 0.8976 | 0.9810 | 0.9871 | 0.8822 | 0.9937 | 0.9938 | 0.9931 |
| HYDICE urban data | 0.9214 | 0.7988 | 0.9836 | 0.9875 | 0.9856 | 0.8362 | 0.9930 |
| Salinas scene data | 0.7595 | 0.9533 | 0.9608 | 0.9831 | 0.8609 | 0.9377 | 0.9863 |
| Abu-airport-3 data | 0.8587 | 0.9401 | 0.9335 | 0.8637 | 0.9463 | 0.9526 | 0.9408 |
| Abu-urban-4 data | 0.7219 | 0.9796 | 0.9774 | 0.9626 | 0.9955 | 0.9844 | 0.9955 |
| Average AUC value | 0.8318 | 0.9310 | 0.9685 | 0.9358 | 0.9564 | 0.9410 | 0.9817 |
| Dataset | LRX | BJSR | MC-AEN | Auto-AD | DeCNNAD | LRSNCR | HAD-ASDR |
|---|---|---|---|---|---|---|---|
| AVIRIS airplane data | 34.81 | 3085.96 | 214.05 | 38.57 | 34.27 | 20.52 | 126.54 |
| HYDICE urban data | 61.67 | 6958.46 | 482.01 | 28.66 | 27.96 | 29.68 | 117.87 |
| Salinas scene data | 131.60 | 9944.59 | 689.31 | 35.97 | 28.66 | 22.57 | 125.67 |
| Abu-airport-3 data | 44.88 | 3071.55 | 213.25 | 30.59 | 29.14 | 19.77 | 116.70 |
| Abu-urban-4 data | 42.46 | 3140.95 | 215.52 | 31.25 | 25.63 | 21.05 | 119.66 |
| Average time | 63.08 | 5240.30 | 362.82 | 33.08 | 29.13 | 22.72 | 121.29 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Guo, H.; Liu, S.; Wu, S. Attention-Aware Spectral Difference Representation for Hyperspectral Anomaly Detection. Remote Sens. 2023, 15, 2652. https://doi.org/10.3390/rs15102652
Zhang W, Guo H, Liu S, Wu S. Attention-Aware Spectral Difference Representation for Hyperspectral Anomaly Detection. Remote Sensing. 2023; 15(10):2652. https://doi.org/10.3390/rs15102652
Chicago/Turabian StyleZhang, Wuxia, Huibo Guo, Shuo Liu, and Siyuan Wu. 2023. "Attention-Aware Spectral Difference Representation for Hyperspectral Anomaly Detection" Remote Sensing 15, no. 10: 2652. https://doi.org/10.3390/rs15102652
APA StyleZhang, W., Guo, H., Liu, S., & Wu, S. (2023). Attention-Aware Spectral Difference Representation for Hyperspectral Anomaly Detection. Remote Sensing, 15(10), 2652. https://doi.org/10.3390/rs15102652







