Sensitivity of Vegetation to Climate in Mid-to-High Latitudes of Asia and Future Vegetation Projections
Abstract
1. Introduction
2. Materials and Methods
2.1. Observational Climate and Vegetation Data
2.2. CMIP6 Model Data
2.3. Quantitative Analysis of the Contributions of Climate Elements to Vegetation Change
2.4. Bias Correction of CMIP6 Data
2.5. Machine Learning Methods
3. Results
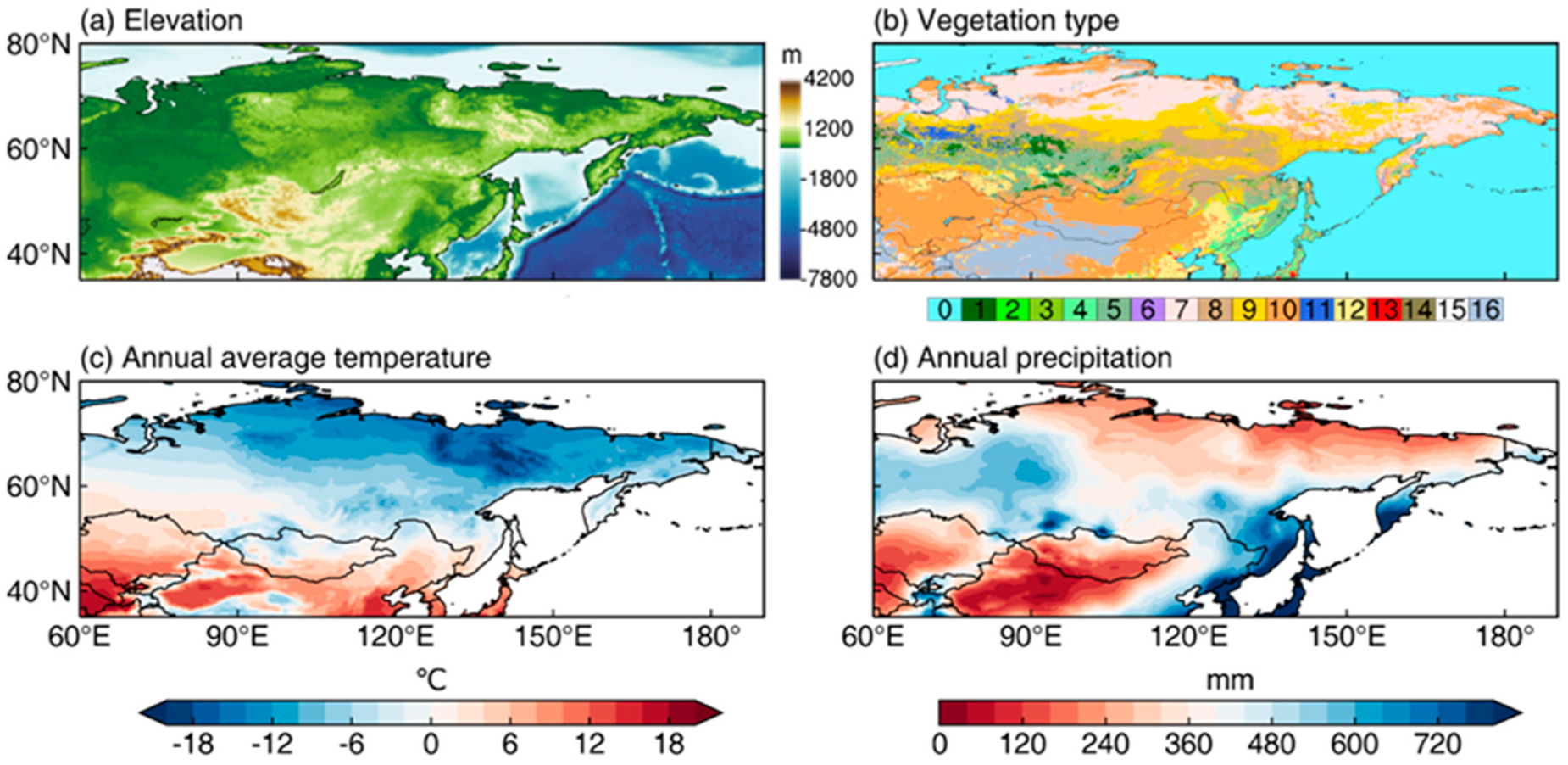
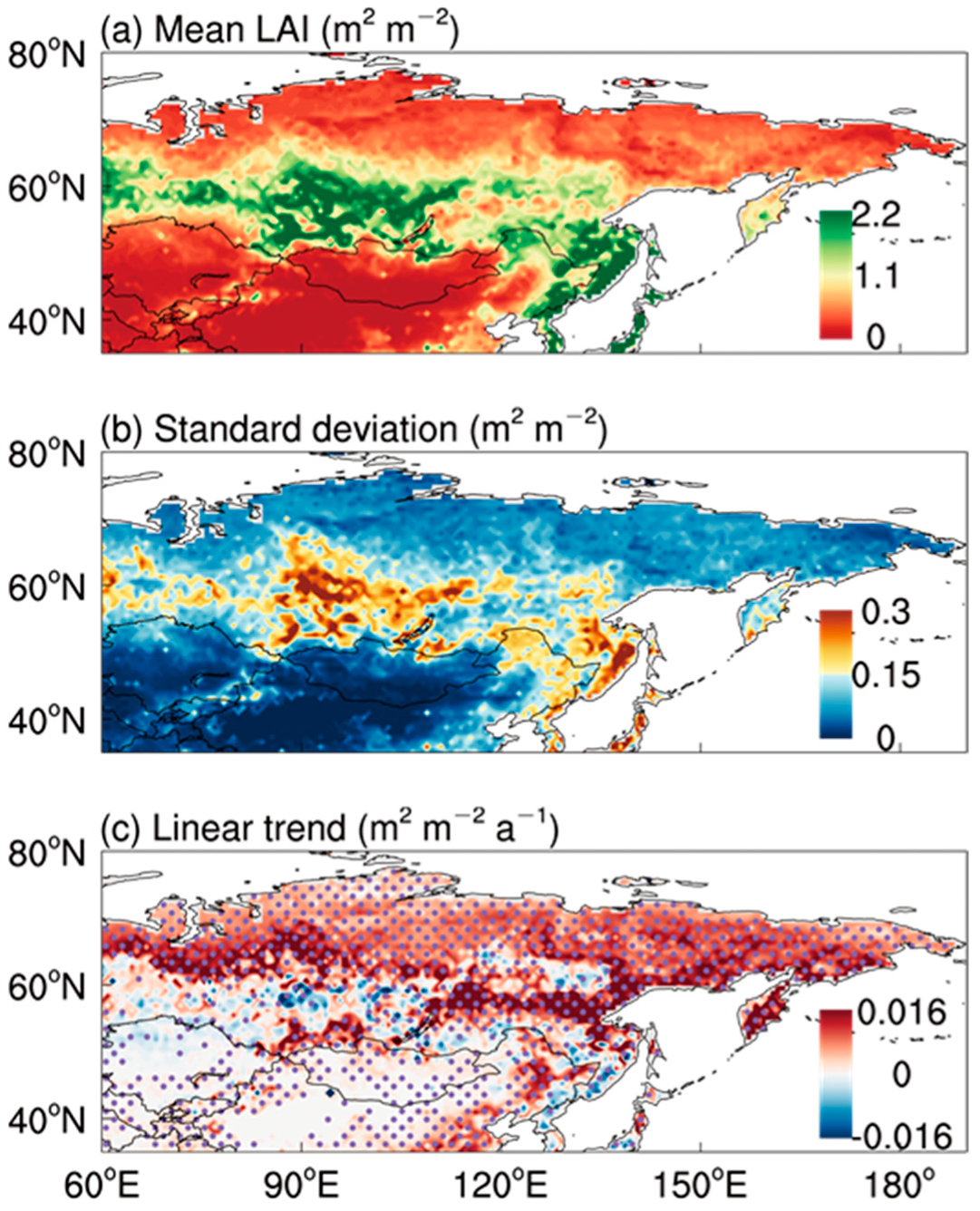
3.1. Climate and Vegetation in the MHA
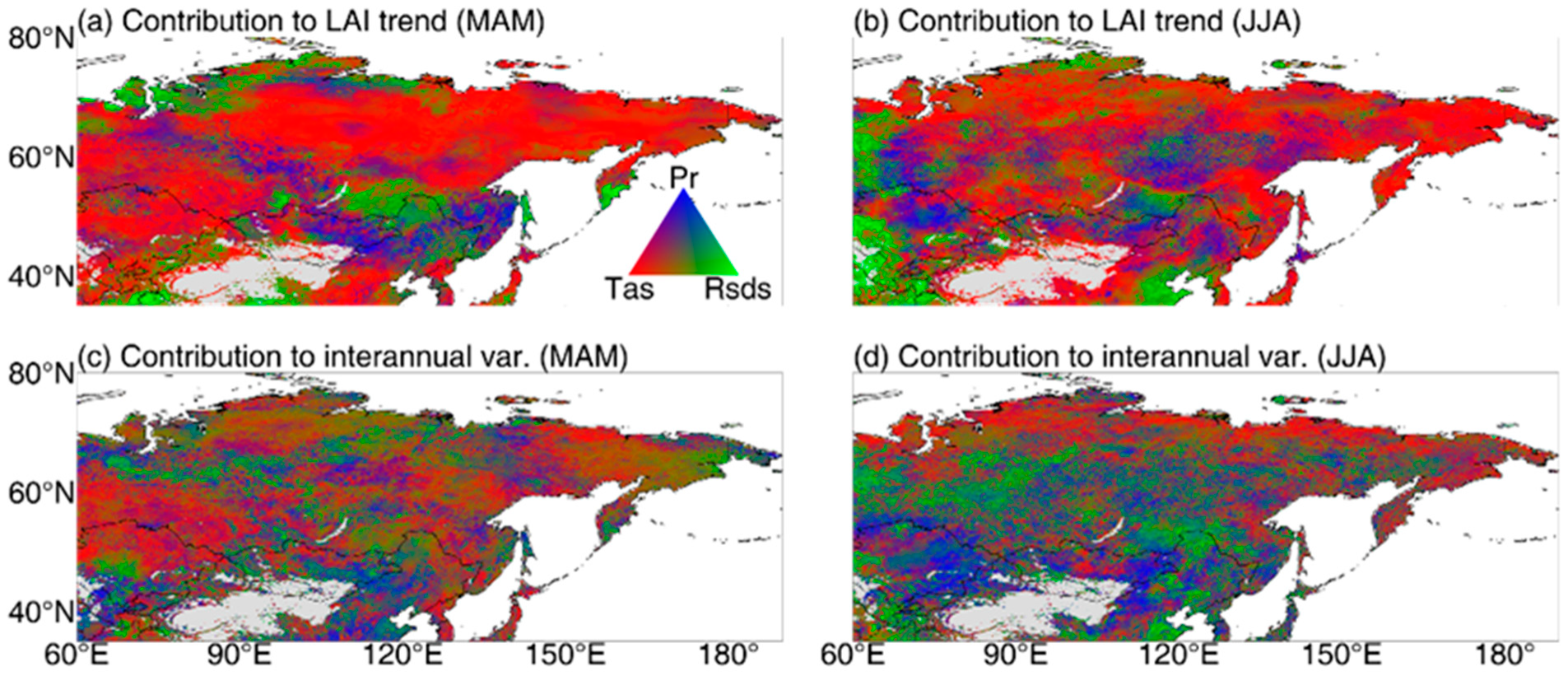
3.2. Climate Elements Affecting the Trend and Interannual Variation of LAI
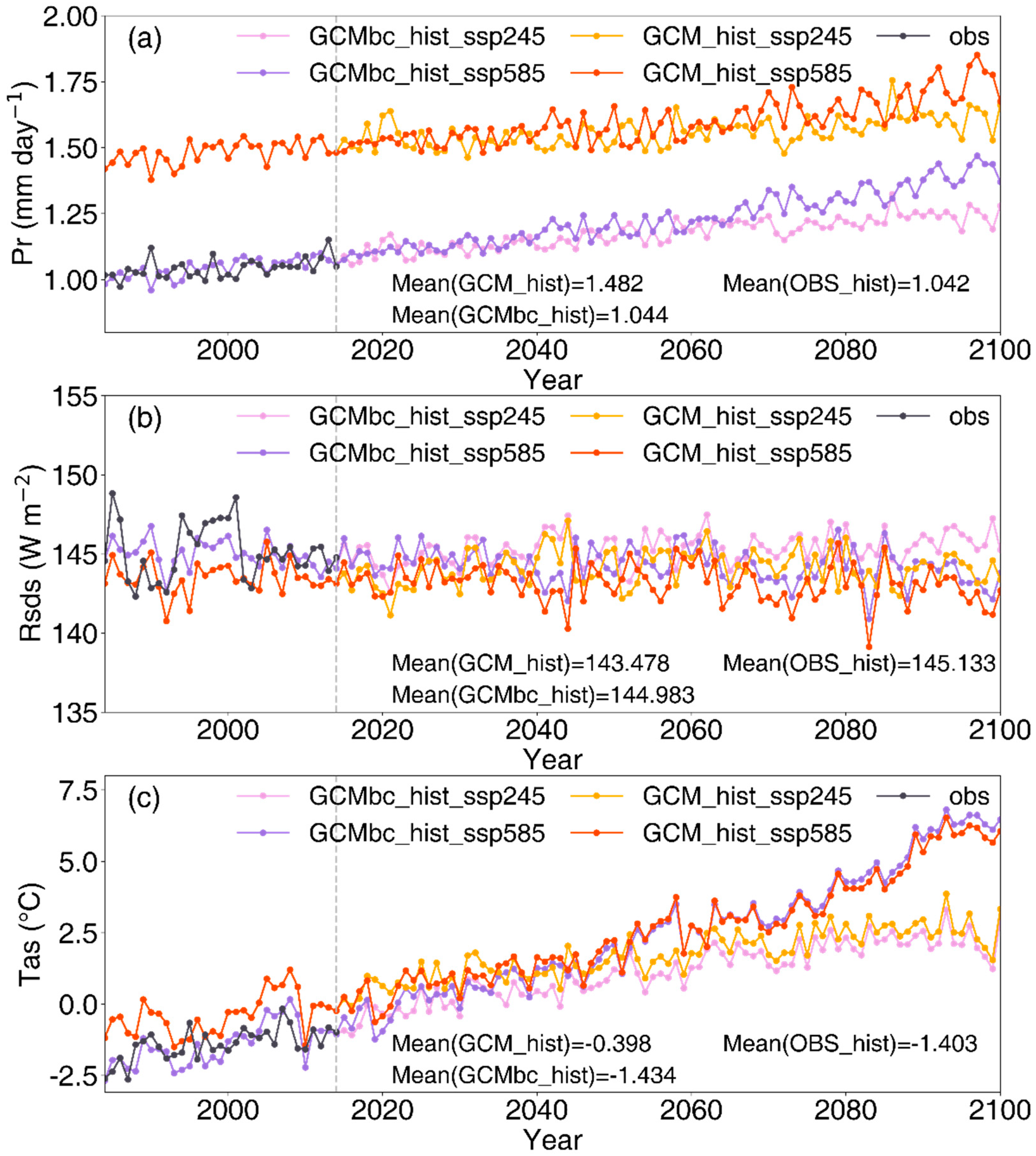
3.3. Bias Correction for CMIP6 Data
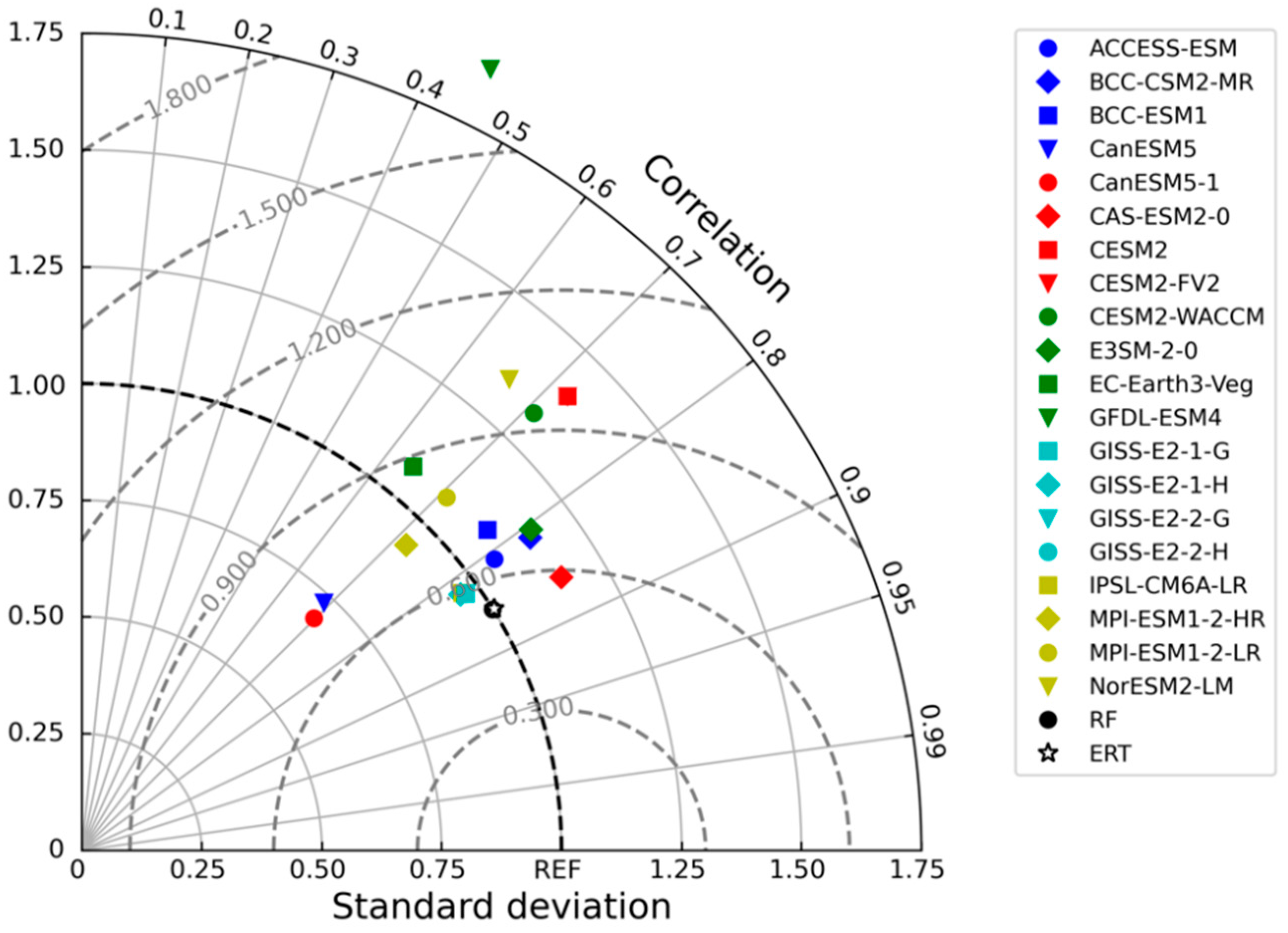
3.4. Evaluation of Machine Learning Models
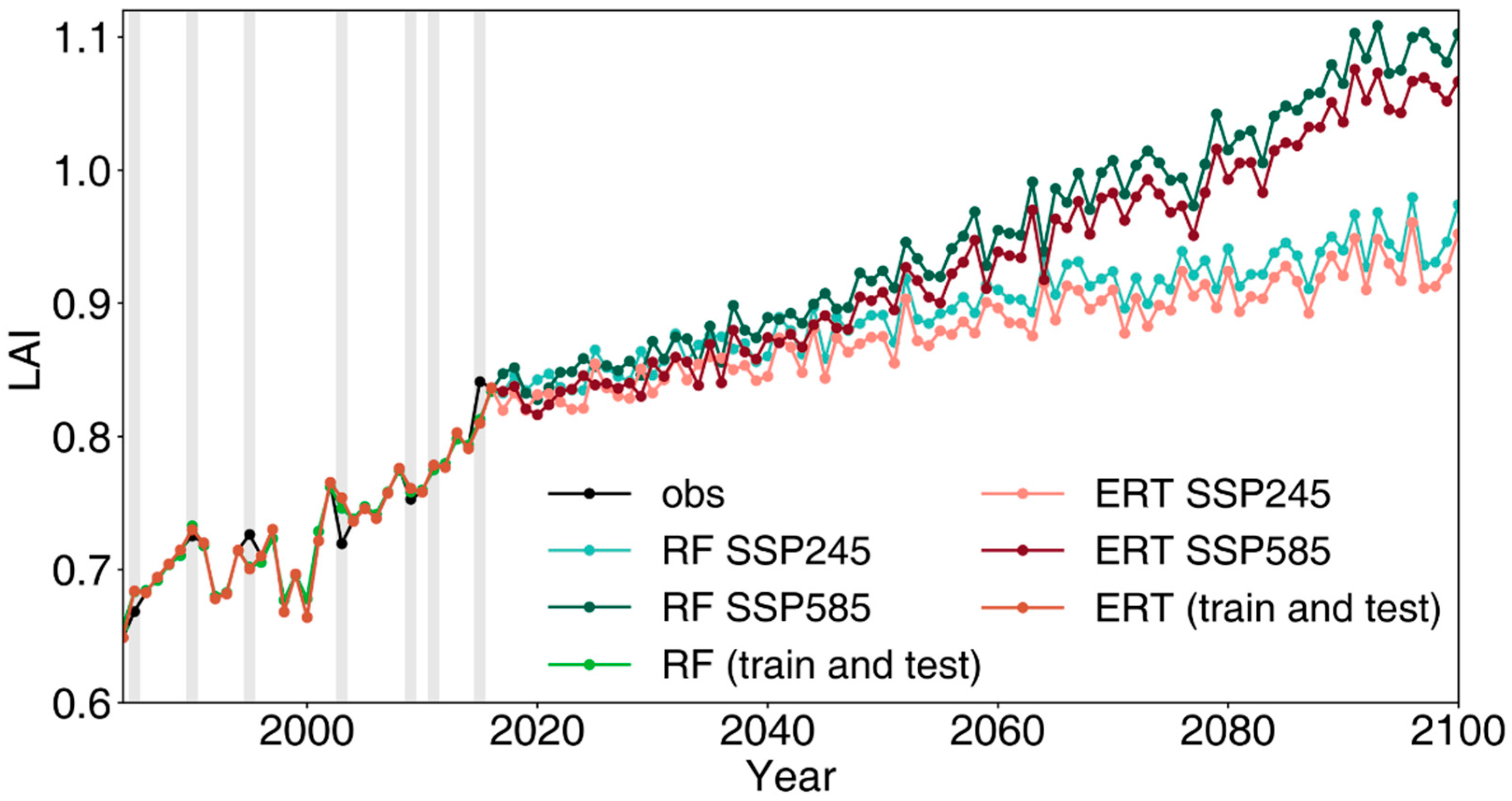
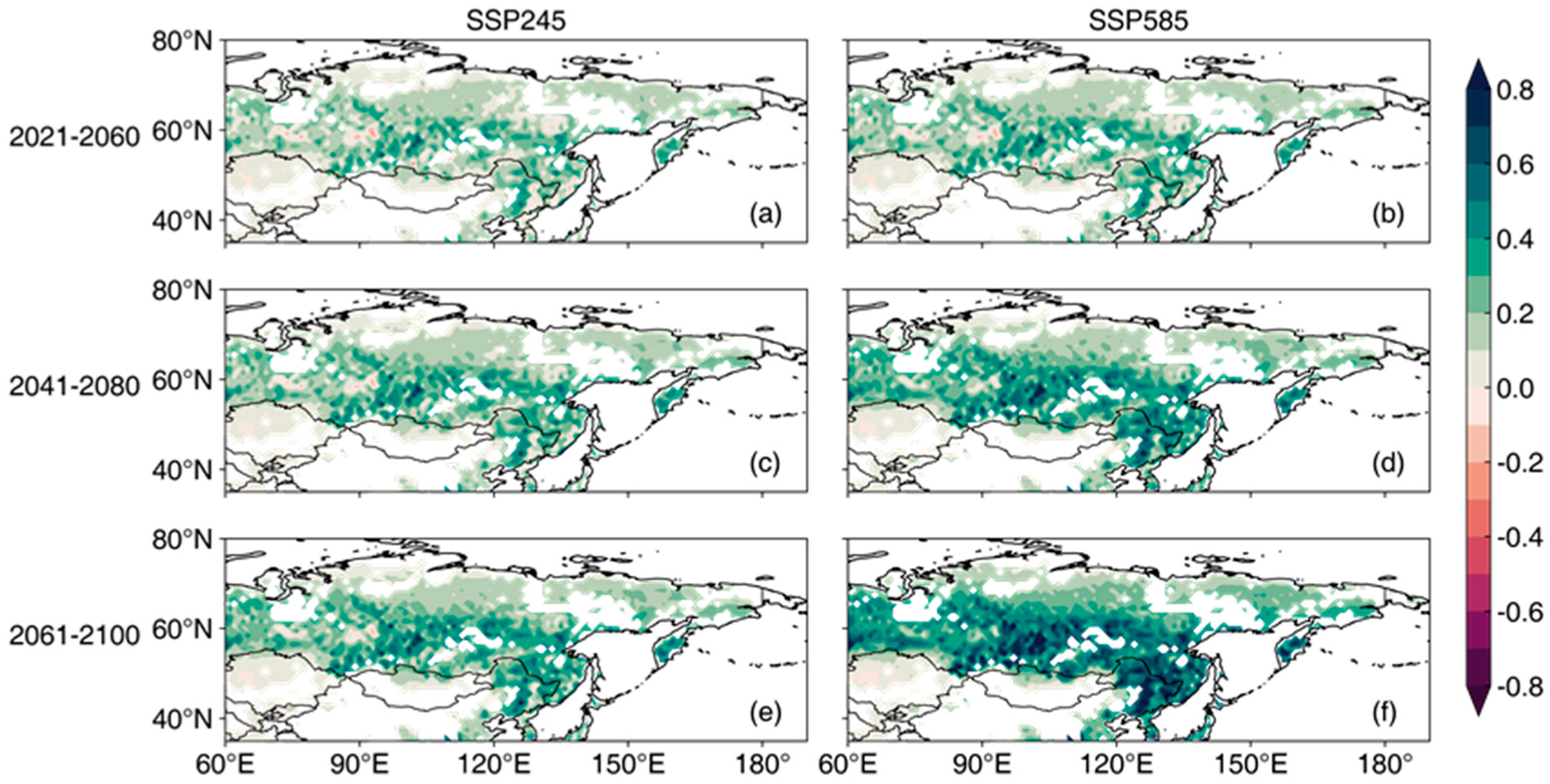
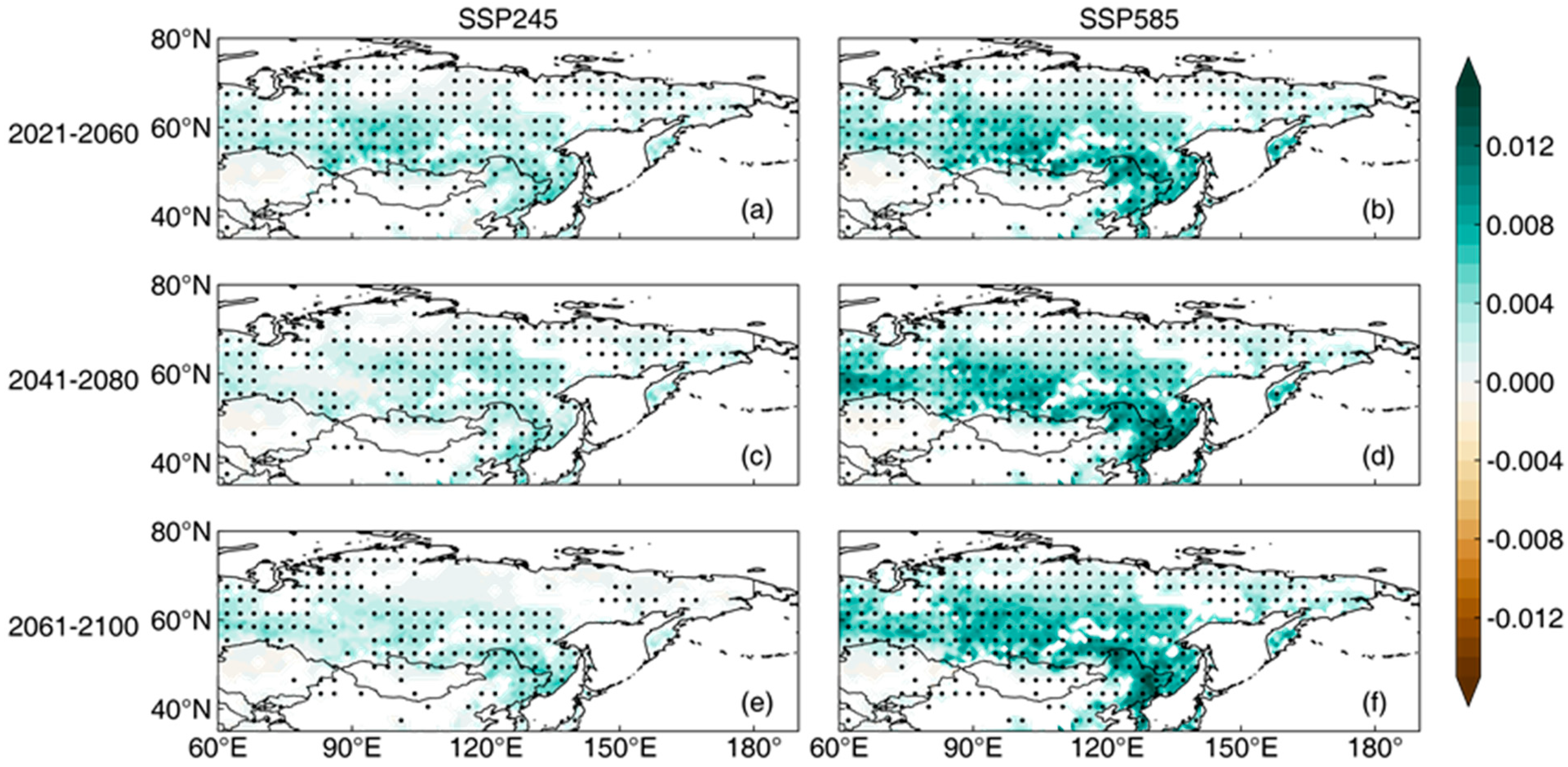
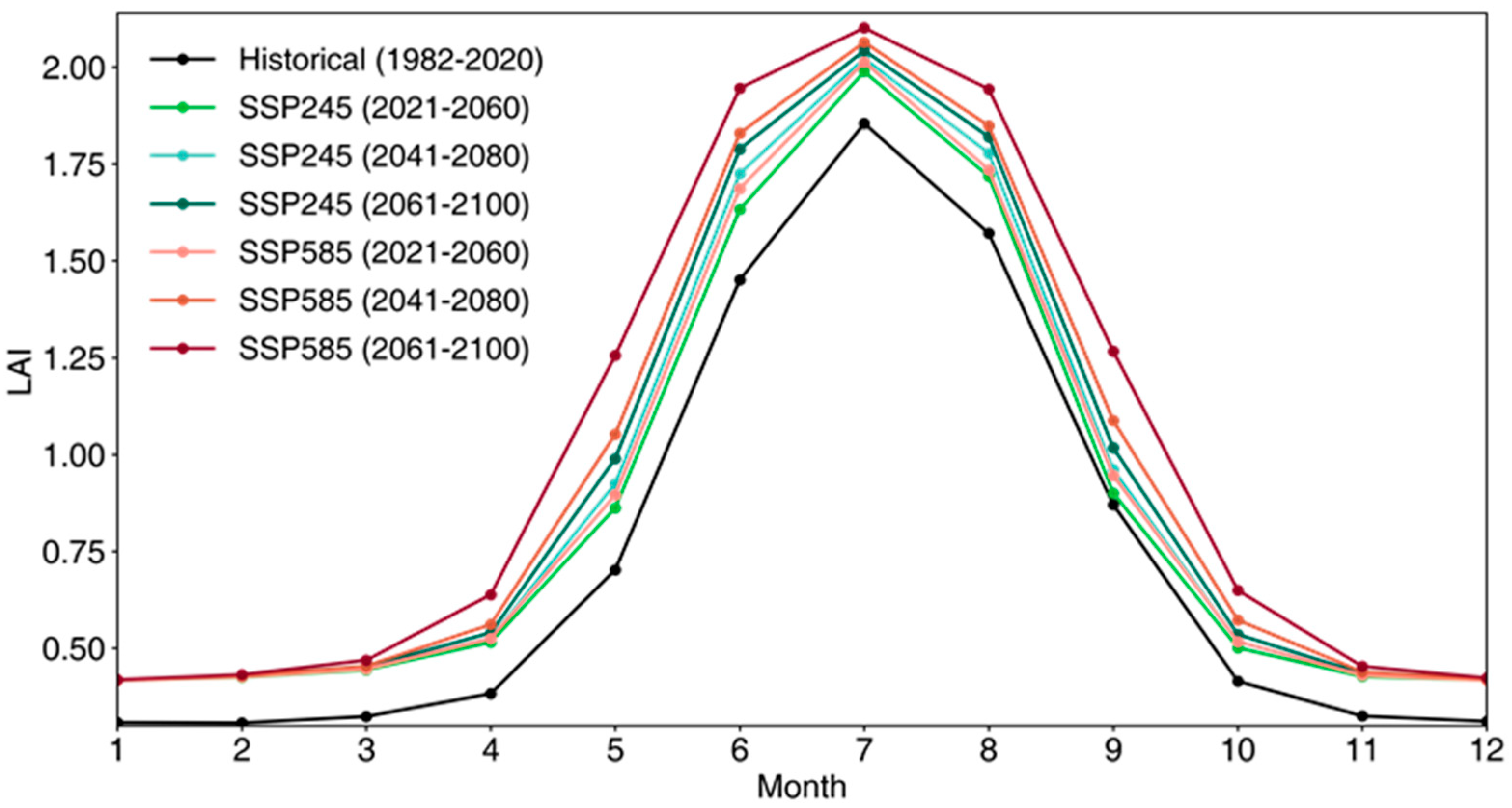
3.5. Projection of Future Vegetation
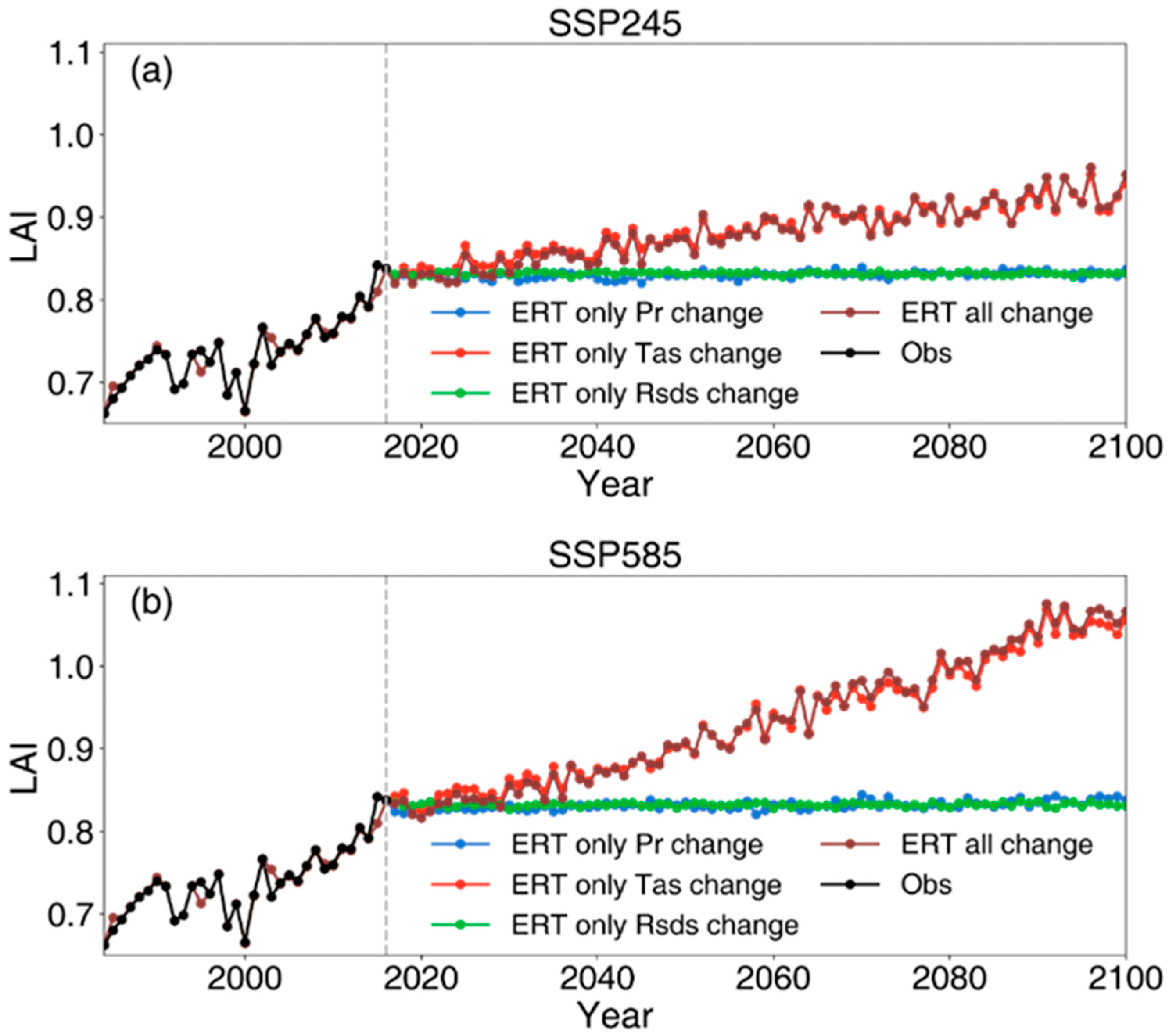
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Beer, C.; Reichstein, M.; Tomelleri, E.; Ciais, P.; Jung, M.; Carvalhais, N.; Rödenbeck, C.; Arain, M.A.; Baldocchi, D.; Bonan, G.B.; et al. Terrestrial Gross Carbon Dioxide Uptake: Global Distribution and Covariation with Climate. Science 2010, 329, 834–838. [Google Scholar] [CrossRef] [PubMed]
- Jones, C.D.; Cox, P.M. On the Significance of Atmospheric CO2 Growth Rate Anomalies in 2002–2003. Geophys. Res. Lett. 2005, 32, L14816. [Google Scholar] [CrossRef]
- Piao, S.; Nan, H.; Huntingford, C.; Ciais, P.; Friedlingstein, P.; Sitch, S.; Peng, S.; Ahlström, A.; Canadell, J.G.; Cong, N.; et al. Evidence for a Weakening Relationship between Interannual Temperature Variability and Northern Vegetation Activity. Nat. Commun. 2014, 5, 5018. [Google Scholar] [CrossRef]
- Nemani, R.R.; Keeling, C.D.; Hashimoto, H.; Jolly, W.M.; Piper, S.C.; Tucker, C.J.; Myneni, R.B.; Running, S.W. Climate-Driven Increases in Global Terrestrial Net Primary Production from 1982 to 1999. Science 2003, 300, 1560–1563. [Google Scholar] [CrossRef]
- Craine, J.M.; Nippert, J.B.; Elmore, A.J.; Skibbe, A.M.; Hutchinson, S.L.; Brunsell, N.A. Timing of Climate Variability and Grassland Productivity. Proc. Natl. Acad. Sci. USA 2012, 109, 3401–3405. [Google Scholar] [CrossRef]
- Seddon, A.W.R.; Macias-Fauria, M.; Long, P.R.; Benz, D.; Willis, K.J. Sensitivity of Global Terrestrial Ecosystems to Climate Variability. Nature 2016, 531, 229–232. [Google Scholar] [CrossRef]
- Zhou, L.; Tian, Y.; Myneni, R.B.; Ciais, P.; Saatchi, S.; Liu, Y.Y.; Piao, S.; Chen, H.; Vermote, E.F.; Song, C.; et al. Widespread Decline of Congo Rainforest Greenness in the Past Decade. Nature 2014, 509, 86–90. [Google Scholar] [CrossRef]
- De Andrade, A.M.; Michel, R.F.M.; Bremer, U.F.; Schaefer, C.E.G.R.; Simões, J.C. Relationship between Solar Radiation and Surface Distribution of Vegetation in Fildes Peninsula and Ardley Island, Maritime Antarctica. Int. J. Remote Sens. 2018, 39, 2238–2254. [Google Scholar] [CrossRef]
- Zhou, L.; Tucker, C.J.; Kaufmann, R.K.; Slayback, D.; Shabanov, N.V.; Myneni, R.B. Variations in Northern Vegetation Activity Inferred from Satellite Data of Vegetation Index during 1981 to 1999. J. Geophys. Res. Atmos. 2001, 106, 20069–20083. [Google Scholar] [CrossRef]
- Fensholt, R.; Langanke, T.; Rasmussen, K.; Reenberg, A.; Prince, S.D.; Tucker, C.; Scholes, R.J.; Le, Q.B.; Bondeau, A.; Eastman, R.; et al. Greenness in Semi-Arid Areas across the Globe 1981–2007—An Earth Observing Satellite Based Analysis of Trends and Drivers. Remote Sens. Environ. 2012, 121, 144–158. [Google Scholar] [CrossRef]
- Cong, N.; Wang, T.; Nan, H.; Ma, Y.; Wang, X.; Myneni, R.B.; Piao, S. Changes in Satellite-Derived Spring Vegetation Green-up Date and Its Linkage to Climate in China from 1982 to 2010: A Multimethod Analysis. Glob. Chang. Biol. 2013, 19, 881–891. [Google Scholar] [CrossRef]
- Zelikova, T.J.; Williams, D.G.; Hoenigman, R.; Blumenthal, D.M.; Morgan, J.A.; Pendall, E. Seasonality of Soil Moisture Mediates Responses of Ecosystem Phenology to Elevated CO2 and Warming in a Semi-Arid Grassland. J. Ecol. 2015, 103, 1119–1130. [Google Scholar] [CrossRef]
- Garonna, I.; de Jong, R.; de Wit, A.J.W.; Mücher, C.A.; Schmid, B.; Schaepman, M.E. Strong Contribution of Autumn Phenology to Changes in Satellite-Derived Growing Season Length Estimates across Europe (1982–2011). Glob. Chang. Biol. 2014, 20, 3457–3470. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Piao, S.; Sun, Y.; Rogers, B.M.; Li, X.; Lian, X.; Liu, Z.; Chen, A.; Peñuelas, J. Future Reversal of Warming-Enhanced Vegetation Productivity in the Northern Hemisphere. Nat. Clim. Chang. 2022, 12, 581–586. [Google Scholar] [CrossRef]
- Shinoda, M.; Nandintsetseg, B. Soil Moisture and Vegetation Memories in a Cold, Arid Climate. Glob. Planet. Change 2011, 79, 110–117. [Google Scholar] [CrossRef]
- Lin, Y.; Xin, X.; Zhang, H.; Wang, X. The Implications of Serial Correlation and Time-Lag Effects for the Impact Study of Climate Change on Vegetation Dynamics—A Case Study with Hulunber Meadow Steppe, Inner Mongolia. Int. J. Remote Sens. 2015, 36, 5031–5044. [Google Scholar] [CrossRef]
- Mohammat, A.; Wang, X.; Xu, X.; Peng, L.; Yang, Y.; Zhang, X.; Myneni, R.B.; Piao, S. Drought and Spring Cooling Induced Recent Decrease in Vegetation Growth in Inner Asia. Agric. For. Meteorol. 2013, 178–179, 21–30. [Google Scholar] [CrossRef]
- Reichstein, M.; Ciais, P.; Papale, D.; Valentini, R.; Running, S.; Viovy, N.; Cramer, W.; Granier, A.; Ogée, J.; Allard, V.; et al. Reduction of Ecosystem Productivity and Respiration during the European Summer 2003 Climate Anomaly: A Joint Flux Tower, Remote Sensing and Modelling Analysis. Glob. Chang. Biol. 2007, 13, 634–651. [Google Scholar] [CrossRef]
- Iwasaki, H. NDVI Prediction over Mongolian Grassland Using GSMaP Precipitation Data and JRA-25/JCDAS Temperature Data. J. Arid Environ. 2009, 73, 557–562. [Google Scholar] [CrossRef]
- Wang, S.; Huang, G.H.; Huang, W.; Fan, Y.R.; Li, Z. A Fractional Factorial Probabilistic Collocation Method for Uncertainty Propagation of Hydrologic Model Parameters in a Reduced Dimensional Space. J. Hydrol. 2015, 529, 1129–1146. [Google Scholar] [CrossRef]
- Huang, S.; Ming, B.; Huang, Q.; Leng, G.; Hou, B. A Case Study on a Combination NDVI Forecasting Model Based on the Entropy Weight Method. Water Resour. Manag. 2017, 31, 3667–3681. [Google Scholar] [CrossRef]
- Yuan, W.; Wu, S.-Y.; Hou, S.; Xu, Z.; Pang, H.; Lu, H. Projecting Future Vegetation Change for Northeast China Using CMIP6 Model. Remote Sens. 2021, 13, 3531. [Google Scholar] [CrossRef]
- Liu, B.; Tang, Q.; Zhou, Y.; Zeng, T.; Zhou, T. The Sensitivity of Vegetation Dynamics to Climate Change across the Tibetan Plateau. Atmosphere 2022, 13, 1112. [Google Scholar] [CrossRef]
- Zhou, Z.; Ding, Y.; Shi, H.; Cai, H.; Fu, Q.; Liu, S.; Li, T. Analysis and Prediction of Vegetation Dynamic Changes in China: Past, Present and Future. Ecol. Indic. 2020, 117, 106642. [Google Scholar] [CrossRef]
- Parton, W.J.; Scurlock, J.M.O.; Ojima, D.S.; Gilmanov, T.G.; Scholes, R.J.; Schimel, D.S.; Kirchner, T.; Menaut, J.-C.; Seastedt, T.; Garcia Moya, E.; et al. Observations and Modeling of Biomass and Soil Organic Matter Dynamics for the Grassland Biome Worldwide. Global Biogeochem. Cycles 1993, 7, 785–809. [Google Scholar] [CrossRef]
- McGuire, D.A.; Melillo, J.M.; Kicklighter, D.W.; Pan, Y.; Xiao, X.; Helfrich, J.; Moore, B., III; Vorosmarty, C.J.; Schloss, A.L. Equilibrium Responses of Global Net Primary Production and Carbon Storage to Doubled Atmospheric Carbon Dioxide: Sensitivity to Changes in Vegetation Nitrogen Concentration. Global Biogeochem. Cycles 1997, 11, 173–189. [Google Scholar] [CrossRef]
- White, M.A.; Thornton, P.E.; Running, S.W.; Nemani, R.R. Parameterization and sensitivity analysis of the BIOME-BGC terrestirial ecosystem model: Net primary production controls. Earth Interact. 2000, 4, 1–85. [Google Scholar] [CrossRef]
- Foley, J.A.; Prentice, I.C.; Ramankutty, N.; Levis, S.; Pollard, D.; Sitch, S.; Haxeltine, A. An integrated biosphere model of land surface processes, terrestrial carbon balance, and vegetation dynamics. Glob. Biogeochem. Cycles 1996, 10, 603–628. [Google Scholar] [CrossRef]
- Sitch, S.; Smith, B.; Prentice, I.C.; Arneth, A.; Bondeau, A.; Cramer, W.; Kaplan, J.O.; Levis, S.; Lucht, W.; Sykes, M.T.; et al. Evaluation of ecosystem dynamics, plant geography and terrestrial carbon cycling in the LPJ dynamic global vegetation model. Glob. Chang. Biol. 2003, 9, 161–185. [Google Scholar] [CrossRef]
- Chen, Z.; Liu, H.; Xu, C.; Wu, X.; Liang, B.; Cao, J.; Chen, D. Modeling Vegetation Greenness and Its Climate Sensitivity with Deep-Learning Technology. Ecol. Evol. 2021, 11, 7335–7345. [Google Scholar] [CrossRef]
- Huang, S.; Chang, J.; Huang, Q.; Chen, Y. Monthly Streamflow Prediction Using Modified EMD-Based Support Vector Machine. J. Hydrol. 2014, 511, 764–775. [Google Scholar] [CrossRef]
- Navarro-Racines, C.; Tarapues, J.; Thornton, P.; Jarvis, A.; Ramirez-Villegas, J. High-Resolution and Bias-Corrected CMIP5 Projections for Climate Change Impact Assessments. Sci. Data 2020, 7, 7. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.; Han, Y.; Tam, C.-Y.; Yang, Z.-L.; Fu, C. Bias-Corrected CMIP6 Global Dataset for Dynamical Downscaling of the Historical and Future Climate (1979–2100). Sci. Data 2021, 8, 293. [Google Scholar] [CrossRef] [PubMed]
- Nakamura, Y.; Krestov, P.; Omelko, A.; Vladivostok. Russia Bioclimate and Zonal Vegetation in Northeast Asia: First Approximation to an Integrated Study. Phytocoenologia 2007, 37, 443–470. [Google Scholar] [CrossRef]
- Lee, J.-Y.; Marotzke, J.; Bala, G.; Cao, L.; Corti, S.; Dunne, J.P.; Engelbrecht, F.; Fischer, E.; Fyfe, J.C.; Jones, C.; et al. Future Global Climate: Scenario-Based Projections and Near-Term Information. In Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Masson-Delmotte, V.P., Zhai, A., Pirani, S.L., Connors, C., Péan, S., Berger, N., Caud, Y., Chen, L., Goldfarb, M.I., Gomis, M., et al., Eds.; Cambridge University Press: Cambridge, UK, 2021; pp. 553–672. [Google Scholar]
- Harris, I.; Osborn, T.J.; Jones, P.; Lister, D. Version 4 of the CRU TS monthly high-resolution gridded multivariate climate dataset. Sci. Data 2020, 7, 109. [Google Scholar] [CrossRef]
- Amante, C.; Eakins, B. ETOPO1 1 Arc-Minute Global Relief Model: Procedures, Data Sources and Analysis; NOAA: Boulder, CO, USA, 2009. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, R.; Chen, J.M. Retrospective Retrieval of Long-Term Consistent Global Leaf Area Index (1981–2011) from Combined AVHRR and MODIS Data. J. Geophys. Res. Biogeosci. 2012, 117. [Google Scholar] [CrossRef]
- Fang, H.; Jiang, C.; Li, W.; Wei, S.; Baret, F.; Chen, J.M.; Garcia-Haro, J.; Liang, S.; Liu, R.; Myneni, R.B.; et al. Characterization and Intercomparison of Global Moderate Resolution Leaf Area Index (LAI) Products: Analysis of Climatologies and Theoretical Uncertainties. J. Geophys. Res. Biogeosci. 2013, 118, 529–548. [Google Scholar] [CrossRef]
- Jiang, C.; Ryu, Y.; Fang, H.; Myneni, R.; Claverie, M.; Zhu, Z. Inconsistencies of Interannual Variability and Trends in Long-Term Satellite Leaf Area Index Products. Glob. Chang. Biol. 2017, 23, 4133–4146. [Google Scholar] [CrossRef]
- Friedl, M.A.; McIver, D.K.; Hodges, J.C.F.; Zhang, X.Y.; Muchoney, D.; Strahler, A.H.; Woodcock, C.E.; Gopal, S.; Schneider, A.; Cooper, A.; et al. Global Land Cover Mapping from MODIS: Algorithms and Early Results. Remote Sens. Environ. 2002, 83, 287–302. [Google Scholar] [CrossRef]
- Zhang, M.; Lin, H.; Long, X.; Cai, Y. Analyzing the Spatiotemporal Pattern and Driving Factors of Wetland Vegetation Changes Using 2000–2019 Time-Series Landsat Data. Sci. Total Environ. 2021, 780, 146615. [Google Scholar] [CrossRef]
- Wu, W.-Y.; Lo, M.-H.; Wada, Y.; Famiglietti, J.S.; Reager, J.T.; Yeh, P.J.-F.; Ducharne, A.; Yang, Z.-L. Divergent Effects of Climate Change on Future Groundwater Availability in Key Mid-Latitude Aquifers. Nat. Commun. 2020, 11, 3710. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble Empirical Mode Decomposition: A Noise-Assisted Data Analysis Method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Fernández-Giménez, M.E.; Batkhishig, B.; Batbuyan, B. Cross-Boundary and Cross-Level Dynamics Increase Vulnerability to Severe Winter Disasters (Dzud) in Mongolia. Glob. Environ. Chang. 2012, 22, 836–851. [Google Scholar] [CrossRef]
- Tan, M.; Li, X. Does the Green Great Wall Effectively Decrease Dust Storm Intensity in China? A Study Based on NOAA NDVI and Weather Station Data. Land Use Policy 2015, 43, 42–47. [Google Scholar] [CrossRef]
- Wei, J.; Jin, Q.; Yang, Z.-L.; Zhou, L. Land–Atmosphere–Aerosol Coupling in North China during 2000–2013. Int. J. Climatol. 2017, 37, 1297–1306. [Google Scholar] [CrossRef]
- Zhu, Z.; Piao, S.; Myneni, R.B.; Huang, M.; Zeng, Z.; Canadell, J.G.; Ciais, P.; Sitch, S.; Friedlingstein, P.; Arneth, A.; et al. Greening of the Earth and its drivers. Nat. Clim. Chang. 2016, 6, 791–795. [Google Scholar] [CrossRef]
- Hernanz, A.; García-Valero, J.A.; Domínguez, M.; Rodríguez-Camino, E. A critical view on the suitability of machine learning techniques to downscale climate change projections: Illustration for temperature with a toy experiment. Atmos. Sci. Lett. 2022, 23, e1087. [Google Scholar] [CrossRef]
- Kashinath, K.; Mustafa, M.; Albert, A.; Wu, J.L.; Jiang, C.; Esmaeilzadeh, S.; Azizzadenesheli, K.; Wang, R.; Chattopadhyay, A.; Singh, A.; et al. Physics-informed machine learning: Case studies for weather and climate modelling. Phil. Trans. Roy Soc. A 2021, 379, 20200093. [Google Scholar] [CrossRef]



| No. | Model | Institution/Country (Region) | Grid Size (lon × lat) |
|---|---|---|---|
| 1 | ACCESS-CM2 | ACCESS/Australia | 1.875° × 1.25° |
| 2 | ACCESS-ESM1-5 | ACCESS/Australia | 1.875° × 1.25° |
| 3 | CanESM5 | CCCma/Canada | 2.81° × 2.81° |
| 4 | BCC-CSM2-MR | BCC/China | 1.125° × 1.125° |
| 5 | FGOALS-f3-L | CAS/China | 1.25° × 1° |
| 6 | FGOALS-g3 | CAS/China | 2° × 2.25° |
| 7 | EC-Earth3 | EC-Earth/Europe | 0.70° × 0.70° |
| 8 | EC-Earth3-Veg | EC-Earth/Europe | 0.70° × 0.70° |
| 9 | IPSL-CM6A-LR | IPSL/France | 2.5° × 1.27° |
| 10 | AWI-CM-1-1MR | AWI/Germany | 0.94° × 0.94° |
| 11 | MPI-ESM1-2-HR | MPI/Germany | 0.94° × 0.94° |
| 12 | MPI-ESM1-2-LR | MPI/Germany | 1.875° × 1.875° |
| 13 | MIROC6 | AORI-UT-JAMSTEC-NIES/Japan | 1.41° × 1.41° |
| 14 | MRI-ESM2-0 | MRI/Japan | 1.125° × 1.125° |
| 15 | NorESM2-LM | NCC/Norway | 2.5° × 1.89° |
| 16 | CESM2-WACCM | NCAR/USA | 1.25° × 0.94° |
| 17 | GFDL-ESM4 | NOAA-GFDL/USA | 1.25° × 1.0° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, J.; Liu, X.; Zhou, B. Sensitivity of Vegetation to Climate in Mid-to-High Latitudes of Asia and Future Vegetation Projections. Remote Sens. 2023, 15, 2648. https://doi.org/10.3390/rs15102648
Wei J, Liu X, Zhou B. Sensitivity of Vegetation to Climate in Mid-to-High Latitudes of Asia and Future Vegetation Projections. Remote Sensing. 2023; 15(10):2648. https://doi.org/10.3390/rs15102648
Chicago/Turabian StyleWei, Jiangfeng, Xiaocong Liu, and Botao Zhou. 2023. "Sensitivity of Vegetation to Climate in Mid-to-High Latitudes of Asia and Future Vegetation Projections" Remote Sensing 15, no. 10: 2648. https://doi.org/10.3390/rs15102648
APA StyleWei, J., Liu, X., & Zhou, B. (2023). Sensitivity of Vegetation to Climate in Mid-to-High Latitudes of Asia and Future Vegetation Projections. Remote Sensing, 15(10), 2648. https://doi.org/10.3390/rs15102648







