Abstract
Monitoring global greenhouse gas concentration information via satellite remote sensing has become a critical area of research to support the further understanding of global carbon emissions. The Greenhouse-gases Absorption Spectrometer-2 (GAS-2) is being developed as the primary payload of the Fengyun-3H (FY-3H), which will be launched in 2024. Achieving high-precision mesurements of greenhouse gases requires precise spectral calibration. However, currently, there is no method for assessing the detection accuracy of GAS-2 using spectral calibration light sources, and quantitative studies are lacking. In this study, the influence model of calibration light sources on spectral calibration accuracy is established, and the spectral radiance acquired via GAS-2 is simulated using the line-by-line radiative transfer model (LBLRTM). We investigated the impact of different linewidths and wavelength stabilities of the calibration light source on its accuracy in four wavelength bands. This study is the first to examine the effects of the linewidth and wavelength stability of a calibration light source on the spectral radiance acquired via GAS-2. The initial results demonstrate that if the linewidth of the calibration light source is approximately 100 MHz and the wavelength stability is in the order of subpicometers, the radiance error obtained by GAS-2 is less than 10%. Among the four bands, the 2.06 m (strong-) band is more affected by the calibration light source than the other three bands. In addition, the wavelength stability of the light source has a greater influence on the error than the linewidth of the light source under the same error condition. The research findings can be used to guide and reference the selection of light sources in the laboratory spectral calibration of GAS-2, ultimately contributing to the instrument’s quantitative development level.
1. Introduction
Carbon dioxide () and methane () are two significant greenhouse gases responsible for the rising global temperatures and increasing frequency of extreme weather events in recent decades [1,2]. The rapid increase in greenhouse gas emissions has raised significant concerns within the international community [3], necessitating urgent measures to reduce these emissions and slow the global temperature rise [4]. The accurate detection and monitoring of greenhouse gas concentrations in the atmosphere are crucial for gaining a better understanding of the carbon cycle and the impact of human activities on the environment. The second global carbon stocktake, scheduled for 2028, will provide valuable information for scientific decisions on global warming and support efforts to mitigate its effects.
Traditional ground-based observation networks, such as the Total Carbon Column Observing Network (TCCON) established by the National Oceanic and Atmospheric Administration(NOAA) of the United States, offer high accuracy and reliability in monitoring greenhouse gas concentrations [5,6]. However, they suffer from limitations such as uneven station distribution and insufficient coverage. In recent years, satellite remote sensing detection technology has rapidly developed, providing significant improvements in the coverage of greenhouse gas monitoring. This technology has enabled the acquisition of global atmospheric concentrations, compensating for the limitations of ground-based observation sites and obtaining large regional spatial data from the ground to high altitudes [7]. As such, satellite-based greenhouse gas monitoring has become a research subject of significance in major spacefaring countries and regions, providing crucial data support for global distribution and regional source emissions [8,9,10]. There are two main types of space-based greenhouse gases GHGs detectors currently in orbit and under development. In the first category, there are comprehensive satellite-based passive sounding instruments that use mature technology to observe both and other trace gases in the atmosphere, such as AIRS, SCIAMACHY, and IASI [9], and the detection accuracy is low. In recent years, for higher spectral resolutions, spatial resolution GHG detection satellites such as OCO-2, GOSAT, CarbonSat, TanSat, and GAS [11,12,13,14] have been developed. They can detect the concentration of greenhouse gases with high accuracy, such as an OCO-2 detection accuracy of 1 ppm [15]. In the second category, there are active lidar detectors, such as ASCENDS, A-SCOPE, and DQ-1 [16,17]. Passive satellite-based atmospheric monitoring mainly employs the theory of atmospheric radiative transfer [18]. Research shows that the thermal infrared band is sensitive to the change in concentration in the middle and upper atmosphere, but less sensitive to the in the ground atmosphere [19]. In contrast, the short-wave infrared band is more sensitive to the observation of concentration near the ground [20]. Therefore, most recent greenhouse gas detection instruments, including OCO-2/3, TanSat, GAS, and GMI, utilize the short-wave infrared band to detect the concentration and obtain the concentration distribution at near-ground levels [21]. The basic principle of the satellite detection of greenhouse gas concentrations using short-wave infrared is that the energy of solar radiation passes through the atmosphere, reaches the ground, and is reflected back into space. During this process, various gas molecules in the atmosphere form different specific absorption spectra and intensities due to their absorption properties in specific wavelength bands, and are affected by aerosols [22]. The characteristic absorption peaks and absorption intensities can reflect the content of the target gas concentration in the atmosphere, with the intensity of gas absorption strengthening with increasing concentration. Using this principle, satellite-based greenhouse gas sensors can monitor and record these characteristic spectral lines, and the distribution of concentration in the target region can be obtained through subsequent data processing, such as high-precision inversion algorithms [23].
High-precision calibration is crucial for obtaining highly quantitative information using remote sensing instruments. There are two types of calibration: radiometric and spectral, with the latter being the foundation for the former [24]. For imaging spectrometers, the central wavelength and spectral resolution of each spectral band are crucial parameters that directly affect the accuracy of radiometric calibration [25]. Studies by the Jet Propulsion Laboratory have shown that spectral calibration errors of 5% and 10% cause significant errors in measured radiance in the solar reflectance band [26,27,28]. Therefore, accurate laboratory spectral calibration before launch is important for obtaining high-precision data quality [26,29]. The main objective of spectral calibration is to determine the central wavelength and spectral resolution of each pixel of the detector in a remote sensing instrument. During the implementation of laboratory spectral calibration, the central wavelength of each pixel and the spectral resolution are obtained by scanning a monochromatic light source in specific steps. This usually has certain requirements on the calibration light source, especially the linewidth and wavelength stability of the monochromatic light source; for example, when OCO-2 is used for laboratory spectral calibration, the calibration light source’s linewidth must be less than 300 KHz, and its wavelength stability must be in the order of picometers [30]. Thus, the linewidth and wavelength stability of the spectral calibration light source are two critical factors in laboratory spectral calibration. Currently, there are several laboratory spectral calibration methods available, including spectral calibration using spectral line lamps, monochromatic collimation calibration, gas absorption cell spectral calibration, and tunable laser calibration, each with advantages and disadvantages [31,32,33,34]. Both monochromator-based wavelength scanning spectral calibration methods and gas absorber cell-based spectral calibration methods require an appropriate calibration light source. For example, the monochromatic parallel light calibration method requires the spectral linewidth of the calibration source to be less than one-tenth of the spectral resolution of the imaging spectrometer, and the wavelength stability of the calibration source is also required accordingly [33]. However, the influence of the calibration light source’s linewidth and wavelength stability on the spectral radiance obtained by the instrument has not been comprehensively analyzed or discussed. While there have been studies on the impact of atmospheric parameters, surface reflectance parameters, and aerosol optical thickness on the spectral radiance acquired by the instrument in the literature [35,36,37], there is limited research on the influence of the spectral calibration light sources on the acquisition of spectral radiance by greenhouse gas hyperspectral remote sensing instruments such as GAS-2.
The Greenhouse-gases Absorption Spectrometer-2 (GAS-2) is a critical payload of the FengYun-3 (FY3-H) satellite being developed by the Shanghai Institute of Technology and Physics, Chinese Academy of Sciences. This advanced instrument is designed to provide accurate and detailed information on the concentration distribution of various greenhouse gases, including and , throughout the Earth’s atmosphere. With its ability to enable high-precision monitoring of greenhouse gas levels at both regional and global scales, the GAS-2 instrument will provide critical data to support the distribution of global carbon sources and sinks.
In order to improve the accuracy of satellite-based atmospheric greenhouse gas monitoring, this study evaluates the impact of the spectral calibration light source on the spectral radiance acquired via GAS-2 using the radiative transfer model based on atmospheric transport theory. Firstly, a model is developed to analyze the influence of the linewidth of the calibration light source on the spectral resolution of GAS-2. Subsequently, the impact of the output wavelength shift and the spectral spread of the calibration light source on the spectral radiance of GAS-2 is simulated using the line-by-line radiative transfer model(LBLRTM) [38,39]. The upwelling radiance spectrum obtained from LBLRTM and the spectral response function are convolved to derive different radiances by shifting the wavelength position and spreading the spectral shape of the GAS-2 spectral channel. Finally, the root-mean-square error (RMSE), absolute error (AE), and relative error (RE) are employed to assess the effect of the calibration light sources on the accuracy of the spectral radiance acquired via GAS-2. This research is a crucial preliminary step in the laboratory spectral calibration process, serving as a guide and reference for the selection of suitable spectral calibration light sources before the launch of GAS-2. Improving spectral calibration accuracy by choosing an appropriate calibration light source can eventually contribute to global efforts to improve the precision of greenhouse gas concentration measurement.
2. GAS-2
The Greenhouse-gases Absorption Spectrometer-2 (GAS-2) is a significant payload carried by the second-generation polar-orbiting satellite Fengyun-3H (FY-3H), which is scheduled to be launched in 2024. GAS-2 employs one near-infrared and three short-wave infrared spectral bands for the continuous monitoring of greenhouse gases. To obtain highly accurate quantitative data, the precise calibration of GAS-2 is essential. Achieving an accurate calibration of spectral calibration parameters requires the use of a calibration light source with a narrow linewidth and high wavelength stability. GAS-2 enables the global coverage and continuous uniform detection of sensitive global climate change factors, facilitating the understanding of the distribution and changing trends of , -based greenhouse gases in the atmosphere. This information aids in the analysis of the global carbon cycle and the process of greenhouse gas sources and sinks in the natural world [40], providing valuable data support for the second global carbon stocktake.
The GAS-2 instrument has a spatial resolution of 3 km and a swath width of 100 km, and the subsatellite point-to-earth observations are shown in Figure 1. GAS-2 has spectral resolutions of 0.04 nm, 0.07 nm, 0.09 nm, and 0.1 nm for the 0.76 m (), 1.61 m (weak-), 2.06 m (strong-), and 2.3 m () bands, respectively. Compared with the previous greenhouse gas detection satellites OCO-2 and TANSAT, GAS-2 has an additional 2.3 m band, which is mainly used to detect . This band is also used in the literature [6] to detect and CO. The technical indicators of GAS-2 are shown in Table 1 below, and its main technical indicators reach the advanced levels of similar payloads worldwide. GAS-2 utilizes a grating spectroscopy method that optimizes grating parameters to achieve high diffraction efficiency in narrow spectral bands, while GAS-1 is a Fourier transform spectrometer that employs interference spectroscopy similar to the GOSAT [41,42]. The optical schematic diagram of GAS-2 can be seen in Figure 2. The optical system for the four bands shares a front-light optical system. The radiation from the atmosphere enters the front optical system and converges to the slit after passing through the two-dimensional pointing mirror. Subsequently, the beam is expanded into parallel light by the collimating beam-expanding mirror. The beam splitter separates the four channels, and the four channels are respectively diffracted by the grating and converged to the detectors of their respective channels through the focusing mirror.
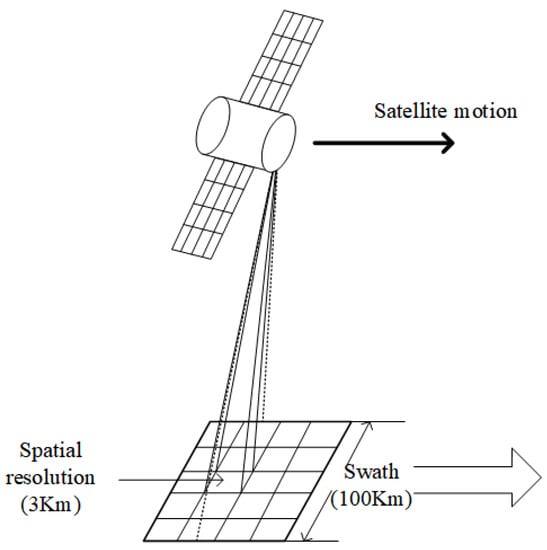
Figure 1.
Spatial resolution and swath of the Greenhouse-gases Absorption Spectrometer-2 (GAS-2).

Table 1.
Main parameters of Greenhouse-gases Absorption Spectrometer-2 (GAS-2).
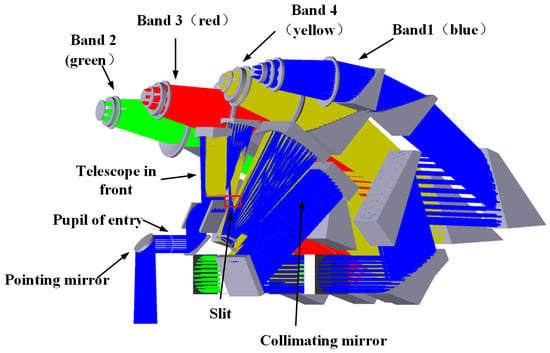
Figure 2.
The optical schematic of GAS-2.
GAS-2 has three observation modes: the nadir observation mode, sun-glint observation mode, and the target observation mode, as shown in Figure 3. Figure 3a depicts the nadir observation mode, which utilizes the diffuse reflection characteristics of the ground for monitoring. The two-dimensional pointing mirror on GAS-2 remains fixed on the ground during the satellite’s passage, providing information on greenhouse gas concentrations on the ground surface [43]. In Figure 3b, the flare observation mode is shown, which can observe carbon dioxide over the sea surface. When the satellite flies over the ocean, the mirror reflection of the sun on the sea surface is leveraged to improve the signal-to-noise ratio. The two-dimensional pointing mirror on GAS-2 points at the sun’s reflection point and tracks it to gather information on greenhouse gas concentrations over the sea surface [44]. Figure 3c displays the target observation mode, which involves observing a specific target during flight. The two-dimensional pointing mirror on GAS-2 remains fixed at the location of the specific monitoring target to obtain greenhouse gas concentration information of the target. This mode is useful for monitoring hot spots of emergencies and verifying the data with ground stations, such as the TCCON ground station.
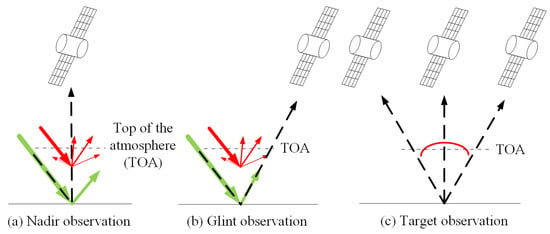
Figure 3.
The observation modes of GAS-2. (a) Nadir observation mode; (b) glint observation mode; (c) target observation mode.
A two-dimensional pointing mirror is a device that enables the precise direction of light to be controlled in two dimensions [45]. It is commonly used in optical instruments such as telescopes and spectrometers, and is a critical component in remote sensing instruments that require precise targeting and pointing. The two-dimensional pointing mirror can be adjusted to different angles in both the horizontal and vertical directions, which allows for a wide range of pointing capabilities. By reflecting light from the target area to the sensor, the two-dimensional pointing mirror ensures that the sensor receives the necessary information for accurate data collection. The mirror is typically controlled by a motor, which allows for a rapid and precise movement to track the target area. The design and performance of a two-dimensional pointing mirror are crucial factors in ensuring the overall accuracy and effectiveness of GAS-2, particularly in achieving high spatial resolution and precise targeting.
3. Methods
3.1. Model
During satellite-based remote sensing, the majority of light emitted from a target is produced by diffuse reflections resulting from the surrounding environmental sources, in the form of diffuse or direct radiation on the rough surface of the target. As illustrated in Figure 4, the radiation reaching the surface of the remote sensor is a combination of direct solar light with directional incidence, and diffuse light with hemispheric incidence from various sources such as the sky, clouds, and ground objects. These two types of light produce distinct reflectance patterns, and understanding their contributions is critical in accurately interpreting remote sensing data. The accurate measurement of both direct and diffuse light is therefore essential for the interpretation of remote sensing data and the development of models for atmospheric correction and radiative transfer.
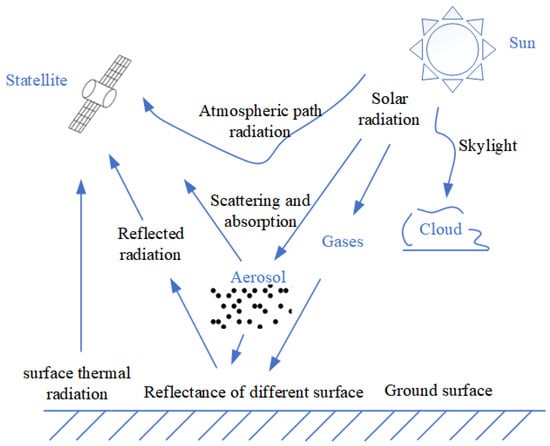
Figure 4.
Schematic diagram of remote sensor in environmental radiation.
Various gas components in the atmosphere exhibit selective absorption properties that are dependent on their molecular and atomic structures and their state of motion. When electromagnetic radiation passes through the atmosphere, different gas components absorb specific wavelengths of the radiation. Short-wave infrared remote sensing utilizes the short-wave infrared part of solar radiation, which is absorbed by molecules to create absorption spectral lines. The absorption spectra of are a result of the rotational–vibrational coupling and occur at 1.61 m and 2.06 m. The depth of the absorption lines intensifies with an increasing amount of content. Modeling methods can be used to calculate path transmittance and radiance under specific atmospheric conditions. LBLRTM is an accurate and efficient line-by-line radiative transfer model that was originally derived from the Fast Atmospheric Signature Code (FASCODE). It has been extensively validated against atmospheric radiance spectra across a broad range of wavelengths, from ultraviolet to submillimeter [39]. LBLRTM is continuously updated and validated against highly accurate spectral measurements, with the updates in spectroscopic factors derived from the high-resolution transmission molecular absorption (HITRAN) database version 2012 (HITRAN2012) [46]. A spectral resolution and sampling interval of 0.001 cm are sufficient for GAS-2 because the spectral resolution of the 0.76 m band is 0.69 cm, 1.61 m is 0.27 cm, 2.06 m is 0.21 cm, and the 2.3 m band is 0.19 cm.
Under atmospheric clear-sky conditions, the radiation intensity observed by the instrument can be expressed as [36]
In Equation (1), is the observed radiation intensity at wavelength ; and are the observed zenith and azimuth angles, and and are the corresponding solar zenith and azimuth angles; is the top-of-atmosphere solar flux; is the surface reflectivity; and denote the absorption cross section and number density of the gas on the optical path, respectively; the integral path denotes the path of the incident solar light entering the atmosphere from the top of the atmosphere, reflecting from the surface to the air, and finally reaching the instrument; “⟨⟩” denotes the average of the possible transmitted optical paths [36].
The radiation transmission pattern is a high-resolution simulation of the spectrum calculated under certain conditions. The actual spectral radiance obtained by the instrument can be expressed as the radiance at the pupil of the instrument and the convolution of the spectral response function of the instrument, of which the specific Equation (2) is shown below.
The atmospheric transfer model, LBLRTM, was utilized to simulate the interaction between atmospheric molecules and solar radiation using a high-spectral-resolution transfer model. The simulation calculated the standard atmosphere of the United States 1976 with a concentration of 400 ppm, 0.76 um (13,029–13,290 cm), 1.6 um (6153–6270 cm), 2.06 um (4807–4902 cm), and 2.3 um (4301–4401 cm) bands, and calculated the radiance spectrum obtained by the instrument. The radiance spectrum was acquired at the top of the atmosphere (altitude 100 Km) under the conditions of solar zenith angle of 30 degrees, surface reflectance of 0.05, vertical observation, and clear sky without clouds. LBLRTM is a highly regarded radiative transfer model with a spectral resolution of up to 0.0014 cm, which fulfills the resolution requirements of the four spectral bands used via GAS-2. Furthermore, it is used as a value of reference. The specific parameters are shown in Table 2 below.

Table 2.
LBLRTM parameters set during simulation.
3.2. Characterization Methods for GAS-2
To characterize GAS-2, the spectral response function of the spectral channel is commonly represented by a Gaussian function, which has been found to be feasible in practical applications, such as OCO-2/3 and Tansat. The actual spectral radiance measured via the GAS-2 instrument can be obtained by convolving the upwelling radiance spectrum with the spectral response function of the instrument, as seen in Equation (2). During spectral calibration, the instrument line shape (ILS) function of GAS-2, which is also the spectral response function, is obtained and needs to be normalized to a Gaussian line shape. The full width at half maxima (FWHM) of the Gaussian line represents the spectral resolution of GAS-2, and the center wavelength of the Gaussian line corresponds to the response center wavelength of the spectral channel. The spectral resolution and response center wavelength of each spectral channel of GAS-2, as well as the upwelling radiance spectrum, affect the amplitude of the spectral radiance obtained via GAS-2. When the input conditions are determined, the upwelling radiance spectrum at the top of the atmosphere is considered constant. Thus, this study focuses on two factors that affect the spectral radiance obtained via GAS-2, namely the central wavelength of the spectral response of each channel and the effect of the FWHM on the radiance spectrum.
A schematic diagram of the GAS-2 acquisition of radiance is presented in Figure 5. Figure 5a displays the upwelling radiance spectrum of the top of the atmosphere obtained with LBLRTM. This spectrum contains rich information and exhibits many absorption peaks and valleys, which are formed due to the interaction of sunlight with the atmosphere. Figure 5b shows the instrumental line shape (ILS) function of the spectral channel, which is commonly represented by a Gaussian function, where the FWHM of the Gaussian function indicates the spectral resolution of the instrument. A smaller FWHM indicates higher spectral resolution. Figure 5c represents the spectral radiance acquired via GAS-2, which is calculated as the convolution of the upwelling radiance spectrum and the ILS. The amplitude of the radiance image obtained after convolution becomes smaller and more details are lost in the image. However, an interesting phenomenon can be observed in Figure 5c at around 7880 cm, where a singularity is present. This is due to the convolution process, which is also a smoothing process. The Gaussian filter used in the instrument line shape (ILS) function passes low-frequency signals but blocks high-frequency signals. As a result, when the processed data (upwelling radiance near 7880 cm) have high-frequency changes in amplitude, as shown in Figure 6a, these high-frequency data will be attenuated by the filter, leading to the singularity phenomenon observed in Figure 6c. The higher spectral resolution of the instrument enables more upwelling radiance spectrum details to be captured. However, the spectral resolution of the instrument is limited by the signal-to-noise ratio and the manufacturing process of the grating, necessitating a trade-off between spectral resolution and other instrument parameters.
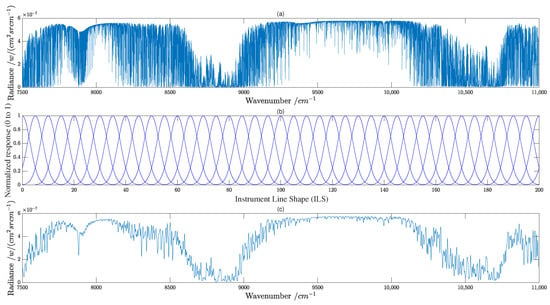
Figure 5.
Schematic representation of the convolution of the upwelling radiance spectrum with the instrument line shape (ILS). (a) The upwelling radiance spectrum obtained with MODTRAN5.2.1; (b) The instrumental line shape (ILS) function of the spectral channel; (c) Spectral radiance acquired by the instrument, which is the convolution of (a,b).
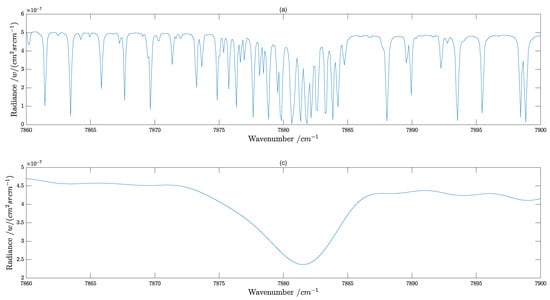
Figure 6.
The local magnification of (a) and (c) in Figure 5; the wavenumber range is from 7860 cm to 7960 cm, and (a) and (c) in Figure 6 correspond one-to-one to (a) and (c) in Figure 5. (a) The upwelling radiance spectrum obtained with MODTRAN 5.2.1. (c) Spectral radiance acquired by the instrument, which is the convolution of (a) and ILS (Gaussian function).
3.3. Effect of the Calibration Light Source on ILS
For an optical remote sensing instrument with N channels, the relative spectral response function of the i-th channel of the system is
where is the optical efficiency of the system, in Equation (3), and is the transfer function of the dispersive system of the remote sensing instrument. is the spectral responsivity of the detector. is the spectral responsivity of the electronic system. Considering the effects of different diaphragm forms and the system in , and , the spectral response curve of the system can be expressed as a Gaussian response curve [47]:
Equation (5) represents the full width at half maxima of the Gaussian function of Equation (4), which is the spectral resolution of the system.
The essence of spectral calibration is to obtain the spectral response curve of the detector image element of the remote sensing instrument for each spectral band. The principle of spectral calibration via monochromatic scanning method is to use continuous-output monochromatic collimated light to scan in the spectral range of the instrument in certain scanning steps, and the hyperspectral imager continuously records the output data and their corresponding wavelength to obtain the wavelength-DN (digital number) curve of each image element [30]. This is a waveform similar to a Gaussian curve, to which a Gaussian fit is performed to derive the spectral resolution of each channel and the central wavelength of the response, as shown in Figure 7.
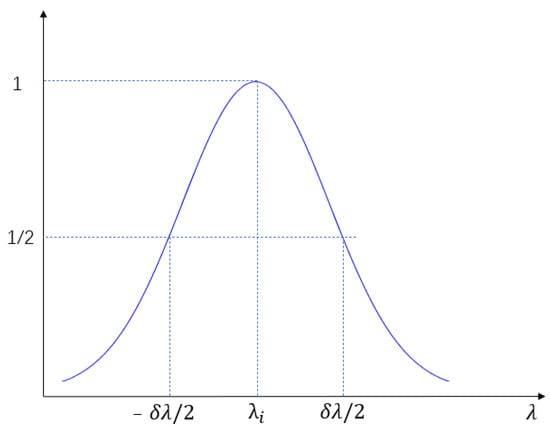
Figure 7.
Spectral response function of hyperspectral imaging spectrometer.
By analyzing the principle of spectral calibration, the ideal spectral calibration light source is monochromatic light with zero linewidth, but zero linewidth also means no energy output, inability to complete the spectral calibration, and no practical significance, so the calibration light source has a certain linewidth. The actual monochromatic light has a certain linewidth and generally obeys Gaussian distribution. The calibrated spectral response of the hyperspectral imaging spectrometer is the convolution of the ILS of the remote sensing instrument and the monochromatic light (calibration light source), as shown in the following equation:
In Equation (6), is the spectral function of the calibration source, which obeys Gaussian distribution. is the spectral response function of the remote sensing instrument, which is related to the incident slit function and the outgoing slit function. If we consider the case of the actual optical system with point diffusion function, let the point diffusion function of the spectral system (only the point diffusion function in the spectral direction is considered) be ; then, the spectral response function of the instrument is [48]
The incident slit function and the outgoing slit function in Equation (7) are both rectangular gate functions, and the point spread function of the spectral system is a Gaussian function, and the best energy utilization is achieved when the incoming and outgoing slits are matched and the optical efficiency of the system is high, which is generally satisfied by the design of remote sensing instruments. The spectral response function can be modeled by a Gaussian function.
The following is an attempt to derive the relationship between the linewidth of the calibration light source and the spectral resolution in spectral calibration. The monochromatic light of the calibration source obeys a Gaussian distribution, and the expression is assumed to be
The linewidth of the calibration source can be expressed as
The spectral response function of the remote sensing instrument is assumed to be expressed as
The spectral resolution (full width at half maximum) is
Then, the problem can be transformed into a convolution of two functions:
By processing the convolution of the two Gaussian functions operationally, we obtain
The spectral resolution (full width at half maximum) after convolution is
Through the theoretical analysis of spectral calibration, we conclude that two key parameters in the instrument line shape (ILS)—the central wavelength of spectral response and the spectral resolution FWHM—are mainly influenced by the calibration light source. The specific influence relationship is as follows: the central response wavelength is affected by the output wavelength of the calibration light source, for example, the central response wavelength of a channel of GAS-2 is , but due to the instability of the output wavelength of the calibration light source, the central response wavelength of the channel obtained via the spectral calibration is , which causes the error of the spectral response wavelength of the channel of GAS-2, and this leads to the error of the acquired spectral radiance. The spectral resolution FWHM is affected by the linewidth of the calibration light source, and we see that the linewidth of the calibration light source causes the spreading of the spectral resolution FWHM of GAS-2 by Equation (14).
3.4. Effect of the Calibration Light Source on the Spectral Radiance Obtained via GAS-2
The wavelength stability and linewidth of the spectral calibration light source affect the ILS during spectral calibration, which are the response center wavelength and FWHM of the detector image element of GAS-2, respectively. GAS-2 acquires spectral radiance as a convolution of the pupil radiance and the ILS so that the relationship between the spectral calibration light source and the GAS-2-acquired spectral radiance is established. Figure 8 clearly shows how to establish the connection between the effect of the spectral calibration light source on the acquired spectral radiance of GAS-2. It should be stated here that the influence of the calibration light source to be studied on the spectral radiance acquired via GAS-2 is assumed to be constant atmospheric conditions. The instrument works in a sun-synchronous orbit, so the radiance of the top of atmosphere (TOA) is selected.
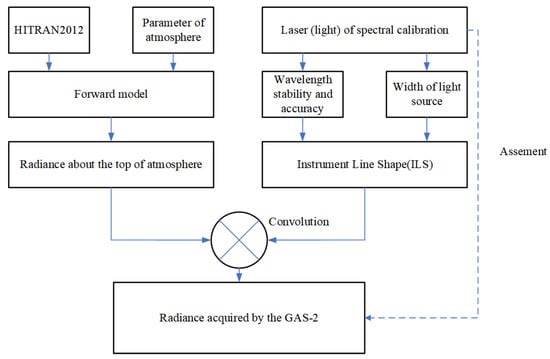
Figure 8.
Flowchart for assessing the effect of spectral calibration light source on the spectral radiance obtained via GAS-2.
The spectral radiance error caused by the central wavelength of the response of GAS-2 is modeled by the systematic wavelength shift of the spectral channel. Poor wavelength stability or accuracy of the calibration light source leads to errors in the response of the center wavelength of the spectral channel in the spectral calibration results, which in turn causes errors in the acquisition of spectral radiance via GAS-2. Here, for simplicity, the wavelength stability or accuracy of the calibration light source is considered to be in one-to-one correspondence with the center wavelength shift of the spectral channel after calibration. The specific calculation method is illustrated by 1.61 um bands (6153–6270 cm) with a spectral resolution of 0.27 cm, and the upwelling radiance spectrum values obtained at 0.1 cm sampling interval are simulated using LBLRTM and then convolved via a Gaussian function with an FWHM of 0.27 cm to obtain the spectral radiance of GAS-2. Furthermore, this value is taken as the reference value without introducing errors. Then, the results are calculated and analyzed by offsetting 0.0027 cm, 0.0135 cm, 0.027 cm, 0.081 cm, and 0.162 cm, representing the wavelength shift error of 1%, 5%, 10%, 30%, and 60%, respectively. The other three bands are calculated in a similar way.
The spectral radiance error caused by the linewidth of the calibration light source was simulated via the spreading of the FWHM of the spectral channel. The simulated conditions of LBLRTM were the same as those described above to obtain the upwelling radiance spectrum with a Gaussian function FWHM of 0.27 cm. The simulated radiance of GAS-2 was obtained by convolving the top-of-atmosphere radiance and FWHM. Furthermore, this value was taken as the reference value without introducing errors. In assessing the effect of FWHM broadening, the results were calculated by convolving 0.2727 cm, 0.2835 cm, 0.297 cm, 0.351 cm and 0.432 cm, representing a spectral resolution broadening of 1%, 5%, 10%, 30% and 60%, respectively, and the error was analyzed. The other three bands were calculated in a similar way.
3.5. Indicators for the Evaluation
LBLRTM is a radiative transfer model that provides high spectral resolution, which makes it a suitable reference for evaluating the effects of calibration light source wavelength stability and linewidth on the spectral radiance obtained via GAS-2. In this evaluation, the high-resolution LBLRTM value serves as the reference value, while the observed value is obtained by convolving the instrument line shape function. To evaluate the impact of a 1% shift in the calibration light source wavelength stability, the LBLRTM values are spaced at 1% of the instrument spectral resolution values. For example, in the 1.61 m (weak-) band, the LBLRTM has a spectral resolution of 0.27 cm, requiring an LBLRTM interval of 0.0027 cm.
The AE (absolute error), AE (relative error), and RMSE (root-mean-square error), were used to evaluate the error between the observed value and the reference value. Their definitions are shown below.
Absolute error (AE) is defined as
Relative error (RE) is defined as
Root-mean-square error (RMSE) is defined as
where represents the spectral radiance value, the observed value by GAS-2 at wavenumber i; and represents the spectral radiance of the LBLRTM at wave number i, which represents the reference value.
4. Results
In this paper, we first quantitatively analyzed the effect of spectral calibration light source linewidth on the spectral resolution spreading of GAS-2 from theory. Then, the effects of spectral resolution spreading and wavelength shift on the spectral radiance of GAS-2 were simulated via the LBLRTM, and the effects of light source output wavelength stability and light source linewidth on the spectral radiance of the surface of land, clear sky without clouds, and countryside visibility of 25 km were obtained. The effects were also evaluated via indicators of AE, RE, and RMSE.
4.1. Influence of the Linewidth of the Calibration Light Source on Spectral Resolution
According to Section 3.3, the analysis methods of the influence of the calibration light source on the ILS and the simulation of the influence of the spectral calibration light source linewidth on the spectral resolution were performed in theory. The simulation results are shown in Figure 9 below, where the horizontal coordinate is the ratio of the linewidth of the calibration light source to the spectral resolution of GAS-2. The vertical coordinate is the relative error between the spectral resolution obtained and the real spectral resolution value.
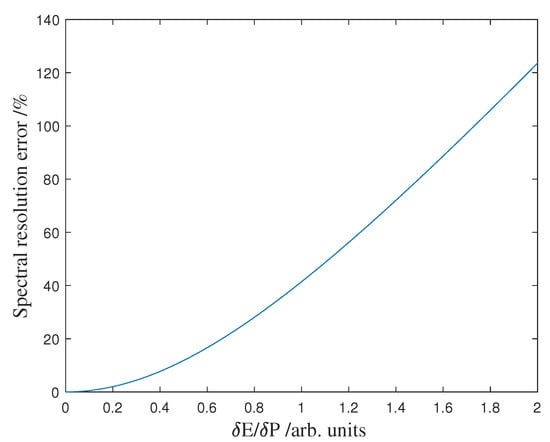
Figure 9.
Simulation results of spectral resolution error caused by linewidth of the calibration light source.
As can be seen from Figure 9, the spectral resolution error of the spectral calibration of the instrument increases with the increase in the linewidth of the calibration light source. When the linewidth of the calibration light source accounts for a 0.1 ratio of the spectral resolution of GAS-2, the spectral resolution error is about 1%; when the linewidth of the calibration light source accounts for a 0.46 ratio of the spectral resolution of the GAS-2, the spectral resolution error is 10%. This indicates that the narrower the linewidth of the calibration light source, the smaller the influence on the spectral resolution error. In practice, the narrow-linewidth calibration light source is usually a laser, and the accuracy of spectral resolution is ensured by choosing a suitable linewidth calibration light source in combination with the development level and process limitation of the laser. It should be noted that the distribution of the calibration source and the distribution of the instrument line shape function are symmetrically distributed, so the linewidth of the calibration source has no effect on the calibration of the central wavelength of the instrument. However, the calibration of the center wavelength of the instrument is affected by the wavelength stability or accuracy of the calibration light source.
4.2. Influence of the Linewidth of the Calibration Light Source on the Acquired Spectral Radiance
4.2.1. Spectral Radiance
According to Section 4.1, the linewidth of the calibration light source causes spectral resolution errors in spectral calibration. To determine the effect of GAS-2 spectral resolution on its acquired spectral radiance, forward-mode simulations were performed in this paper. In the simulation, a Gaussian function was used to simulate the ILS of GAS-2 and convolve it with the upwelling radiance spectrum to obtain the spectral radiance acquired via GAS-2 at different spectral resolutions. The parameters set for the simulation are shown in Table 2.
As can be seen from Figure 10, the narrower the calibration light source’s linewidth, the smaller the FWHM error of the spectral calibration, and the gas absorption characteristics are visibly and approximately close to the reference spectral radiance. When the calibration light source’s linewidths are 2.9 GHz, 1.1 GHz, 890 MHz, and 794 MHz, respectively, and the spectral resolution is broadened by 1%, the resulting spectral radiance is close to the reference spectral radiance. The maximum relative errors (MAXREs) in the four bands are 1.28%, 1.21%, 4.35%, and 4.79%, which are all below 5%. Taking the weak- band as an example, the observed spectral radiance error at the wave number 6237.42 cm is 1.21% when the line width of the calibration light source is 2.9 GHz. However, when the linewidth of the calibration light source is increased to 6.6 GHz, the observed radiance error also increases to 3.6%. Furthermore, when the linewidth of the calibration light source is further increased to 17.2 GHz, the observed radiance error increases to 5.93%. Finally, at a linewidth of 25.9 GHz, the observed radiance error increases substantially to 27.02%. This means that the larger the spectral resolution error is, the weaker the bimodal structure is and the larger the spectral radiance error it causes, which directly influences the accuracy regarding greenhouse gas concentration.
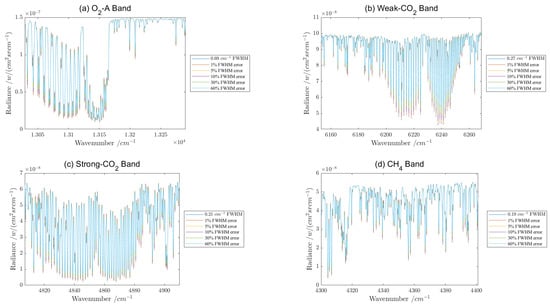
Figure 10.
Comparison of the spectral radiance of the FWHM error obtained from calibration sources with different linewidths. (a) The spectral radiance obtained via GAS-2 in the -A band with FWHM errors of 1%, 5%, 10%, 30%, and 60% due to calibration light source’s linewidth, respectively; (b) the spectral radiance obtained via GAS-2 in the weak- band with FWHM errors of 1%, 5%, 10%, 30%, and 60% due to calibration light source’s linewidth, respectively; (c) the spectral radiance obtained via GAS-2 in the strong- band with FWHM errors of 1%, 5%, 10%, 30%, and 60% due tocalibration light source’s linewidth, respectively; (d) the spectral radiance obtained via GAS-2 in the band with FWHM errors of 1%, 5%, 10%, 30%, and 60% due to calibration light source’s linewidth, respectively.
4.2.2. Accuracy Evaluation
In order to perform the evaluation of the accuracy of the linewidth of the calibration light source on the spectral radiance acquired via GAS-2, the AE, RE, and RMSE indicators were used for evaluation, and the definitions of each metric are given in Section 3.5. The effect of the FWHM error caused by the source linewidth on the radiometric accuracy of GAS-2 is expressed by the introduction and nonintroduction of the acquired FWHM error. The absolute errors (AE) in the -A band, weak- band, strong- band, and band are shown in Figure 11.
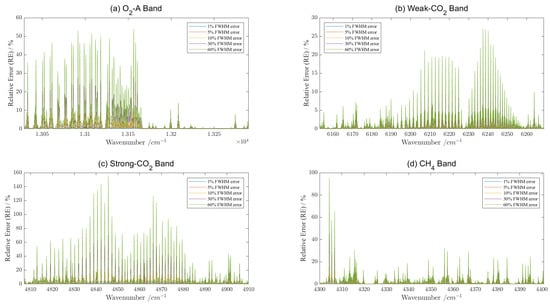
Figure 11.
Comparison of relative error (RE) of spectral radiance obtained via GAS-2 in four bands with different FWHM errors of 1%, 5%, 10%, 30%, and 60%. (a) -A band, the relative error (RE) of spectral radiance; (b) weak- band, the relative error (RE) of spectral radiance; (c) strong- band, the relative error(RE) of spectral radiance; (d) band, the relative error (RE) of spectral radiance.
The RMSE, maximum of the relative error (MAXRE), and maximum of the absolute error (MAXAE) indicators are used for evaluation, and their accuracy evaluation indicators are shown in Appendix A Table A1, Table A2, Table A3 and Table A4, respectively. According to the evaluation results of the four tables, it can be seen that the narrower the linewidth of the calibration source, the smaller the spectral resolution error, and the spectral radiance detected via GAS-2 is closer to the actual spectral radiance. Especially at the gas absorption peaks and valleys, small spectral resolution errors can cause relatively large deviations in the spectral radiance.
Among the four bands, the strong- band appears to be the most sensitive to variations in the same error. For example, under the condition of 5% FWHM broadening, the four calibration light sources’ linewidths of 6.6 GHz, 2.6 GHz, 2.0 GHz and 1.8 GHz result in maximum relative errors of 5.11% for the O2-A band, 3.60% for the weak- band, 15.73% for the strong- band, and 9.72% for the band. The other FWHM errors have similar results. This phenomenon is caused by the fact that is a strong absorption band at 4807–4910 cm, caused by molecular vibrations, etc. This indicates that the linewidth of the light source in this band puts a higher requirement in the spectral calibration. Moreover, it is an interesting phenomenon that the relative error of the -A band is less affected by the linewidth in the second half of the whole band 13,171–13,290 cm, even at 60% spectral resolution error, wherein the maximum relative error is less than 15%, which may be related to the fact that the absorption peaks and valleys of the gas in this band are fewer.
4.3. Effect of Wavelength Stability of the Calibration Light Source on the Acquired Spectral Radiance
The wavelength stability of the calibration light source affects the accuracy of the central response wavelength of the spectral calibration, which affects the spectral radiance of GAS-2. For convenience, the wavelength stability of the calibration light source and the shift of the central wavelength of the spectral calibration were approximated to correspond one-to-one. The effect of wavelength stability was evaluated by calculating the error of the spectral radiance due to the center wavelength shift.
The spectral radiance calculated by GAS-2 in the -A band with a spectral resolution of 0.690 cm was compared with the spectral radiance calculated at wavelength offsets of 1% (0.4 pm), 5% (2 pm), 10% (4 pm), 30% (12 pm), and 60% (24 pm). Similarly, in the weak- band with a spectral resolution of 0.27 cm, the strong- band with a spectral resolution of 0.21 cm, and the band with a spectral resolution of 0.19 cm, the spectral radiance was calculated for wavelength shifts of 1%, 5%, 10%, 30%, and 60%, respectively.
Based on the simulation results, RMSE, absolute deviation (AE), and relative deviation (RE) were used for evaluation, respectively. The wavelength without introducing shift was used as a reference for comparison calculation. The relative errors (REs) of the four wavelengths are shown in Figure 12 below. The remaining evaluation indicators RMSE, MAXAE, and MAXRE are shown in Table A5, Table A6, Table A7 and Table A8 for four bands, respectively.
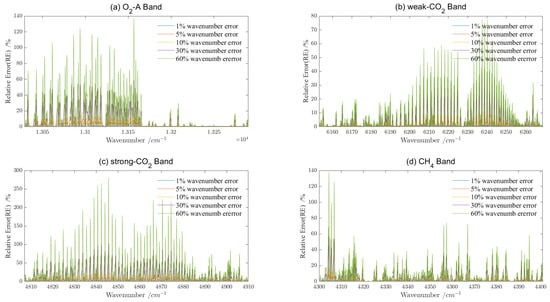
Figure 12.
Comparison of relative error (RE) of spectral radiance acquired via GAS-2 due to 1%, 5%, 10%, 30%, 60% shift in center wavelength. (a) -A band, the relative error (RE) of spectral radiance due to central wavelength shift; (b) weak- band, the relative error (RE) of spectral radiance due to central wavelength shift; (c) strong- band, the relative error (RE) of spectral radiance due to central wavelength shift; (d) band, the relative error (RE) of spectral radiance due to central wavelength shift.
From Figure 12, it can be concluded that the errors of the obtained spectral radiance are most evident in the wavelength region with a large variation in radiance, especially at the absorption peaks and valleys of greenhouse gases causing large errors of radiance. By comparison, it can be seen that the lesser the central wavelength shift is, the more accurate and the smaller the relative error (RE) is in the spectral radiance obtained via GAS-2 in all four bands. The more that the central wavelength is shifted, the more inaccurate the spectral radiance obtained via GAS-2. For example, in the weak- band, for the 1% (0.7 pm) wavelength shift, the maximum relative error is 2.64% and the RMSE is ; for the 5% (3.5 pm) wavelength shift, the maximum relative error is 13.09% and the RMSE is ; for the 10% (7 pm) wavelength shift, the maximum relative error is 25.72% and the RMSE is ; for the 30% (21 pm) wavelength shift, the maximum relative error is 65.98% and the RMSE is ; for the 60% (42 pm) wavelength shift, the maximum relative error is 77.41% and the RMSE is . The situation is similar for the other three bands. This shows that the smaller the central wavelength shift, the smaller the error and the higher the accuracy of the acquired data.
The comparison between the four bands shows that the strong- band is most affected by the relative error of spectral radiance under the same spectral resolution error, and the relative error of 13171–13290 cm in the latter band -A is less affected by the stability of the light source in the whole band, which is similar to the above FWHM error situation. This also shows that the locations where these spectral radiance changes are larger are at the absorption peaks and valleys.
In addition, by comparing Figure 11 and Figure 12, the effects of the linewidth and wavelength stability of the calibration light source on the spectral radiance obtained via GAS-2, we can see that the effect of wavelength stability is greater than the effect of the linewidth for the same error ratio, which is the same case in all four bands. As an example, in the weak band, when the linewidth of the calibration light source is 1.1 GHz, it results in a 1% FWHM error, and the wavelength stability of the calibration light source is 0.7 pm, which also causes a 1% wavelength shift error. The maximum relative errors are 1.21% and 2.64%, respectively, and the RMSEs are and , respectively. When the linewidth of the calibration light source is 2.6 GHz, resulting in a 5% FWHM error, and the wavelength stability of the calibration light source is 3.5 pm, which also causes a 5% wavelength shift error, the maximum relative errors are 3.60% and 13.09%, respectively. The RMSEs are and , respectively. When the linewidth of the calibration light source is 3.7 GHz, resulting in a 10% FWHM error, and the wavelength stability of the calibration light source is 7 pm, which also causes a 10% wavelength shift error, the maximum relative errors are 5.93% and 25.72%, respectively. The RMSEs are and , respectively. When the linewidth of the calibration light source is 6.7 GHz, resulting in a 30% FWHM error, and the wavelength stability of the calibration light source is 21 pm, which also causes a 30% wavelength offset error, the maximum relative errors are 14.75%, and 65.98%, respectively. The RMSEs are and , respectively. When the linewidth of the calibration light source is 10.1 GHz, causing a 60% FWHM error, and the wavelength stability of the calibration light source is 42 pm, which also causes a 60% wavelength shift error, the maximum relative errors are 27.02%, and 77.41%, respectively. The RMSEs are and , respectively. The remaining three bands are similar to these results. This indicates that the wavelength stability accuracy requirement of the calibration light source in spectral calibration is higher than the requirement of the linewidth of the calibration light source. In order to ensure the accuracy of data acquisition, the calibration of the central wavelength of GAS-2 should be more accurate, which puts higher requirements on the wavelength stability of the calibration light source.
4.4. Combined Effect of Wavelength Stability and the Linewidth of the Calibration Light Source on the Acquired Spectral Radiance
In practical calibration processes, the linewidth and wavelength stability of the calibration source often coexist, rather than varying independently. Section 4.2 and Section 4.3, respectively, explore the effects of the spectral radiance caused by a single variable. This section investigates the variation in the acquired spectral radiance of GAS-2 resulting from the simultaneous presence of both factors and evaluates its accuracy. GAS-2 acquires spectral radiance results for each band of its 25 situations, which is a combination of wavelength errors 1%, 5%, 10%, 30%, 60% and of spectral resolution errors 1%, 5%, 10%, 30% and 60%, respectively. The relative error (RE) for each band is represented by five subplots. The following Figure 13, Figure 14, Figure 15 and Figure 16 show the combined effect of the wavelength stability and the linewidth of the calibration light source on the acquired spectral radiance via GAS-2 for four bands.
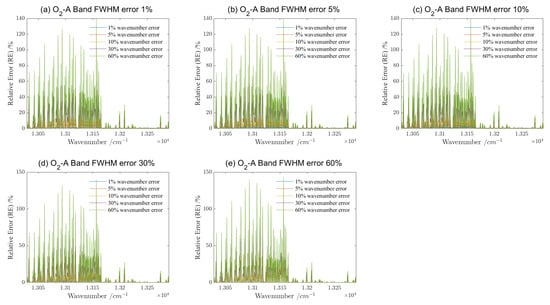
Figure 13.
Comparison of relative error (RE) of spectral radiance acquired via GAS-2 in four bands due to 1%, 5%, 10%, 30%, 60% shift in center wavelength and 1%, 5%, 10%, 30%, 60% spectral resolution (FWHM) error in -A band. (a) -A band, relative error (RE) of spectral radiance due to different wavelength errors when the FWHM error is 1%; (b) -A band, relative error (RE) of spectral radiance due to different wavelength errors when the FWHM error is 5%; (c) -A band, relative error (RE) of spectral radiance due to different wavelength errors when the FWHM error is 10%; (d) -A band, relative error (RE) of spectral radiance due to different wavelength errors when the FWHM error is 30%; (e) -A band, relative error (RE) of spectral radiance due to different wavelength errors when the FWHM error is 60%.
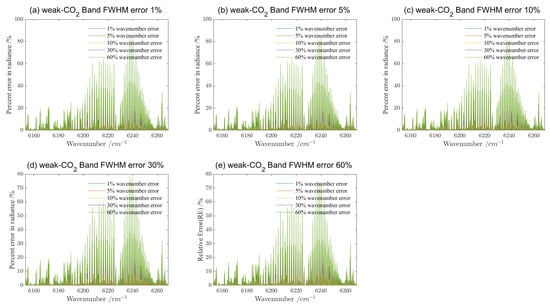
Figure 14.
Comparison of relative error (RE) of spectral radiance acquired via GAS-2 in four bands due to 1%, 5%, 10%, 30%, 60% shift in center wavelength and 1%, 5%, 10%, 30%, 60% spectral resolution (FWHM) error in weak- band. (a) weak- band, relative error (RE) of spectral radiance due to different wavelength error when the FWHM error is 1%; (b) weak- band, relative Error (RE) of spectral radiance due to different wavelength error when the FWHM error is 5%; (c) weak- band, relative error (RE) of spectral radiance due to different wavelength error when the FWHM error is 10%; (d) weak- band, relative error (RE) of spectral radiance due to different wavelength error when the FWHM error is 30%; (e) weak- band, relative error (RE) of spectral radiance due to different wavelength error when the FWHM error is 60%.
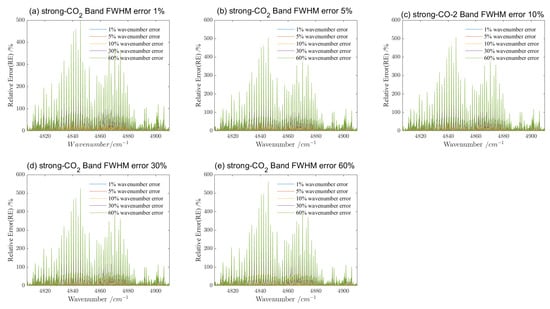
Figure 15.
Comparison of relative error (RE) of spectral radiance acquired via GAS-2 in four bands due to 1%, 5%, 10%, 30%, 60% shift in center wavelength and 1%, 5%, 10%, 30%, 60% spectral resolution (FWHM) error in strong- band. (a) strong- band, relative error (RE) of spectral radiance due to different wavelength error when the FWHM error is 1%; (b) strong- band, relative error (RE) of spectral radiance due to different wavelength error when the FWHM error is 5%; (c) strong- band, relative error (RE) of spectral radiance due to different wavelength error when the FWHM error is 10%; (d) strong- band, relative error (RE) of spectral radiance due to different wavelength error when the FWHM error is 30%; (e) strong- band, relative error (RE) of spectral radiance due to different wavelength error when the FWHM error is 60%.
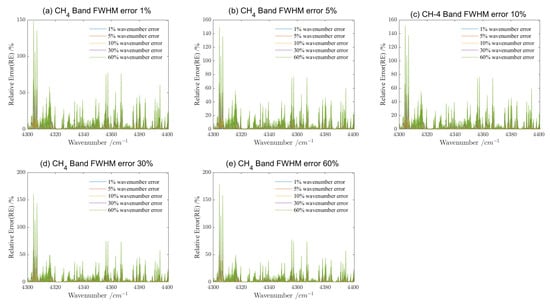
Figure 16.
Comparison of relative error (RE) of spectral radiance acquired via GAS-2 in four bands due to 1%, 5%, 10%, 30%, 60% shift in center wavelength and 1%, 5%, 10%, 30%, 60% spectral resolution (FWHM) error in band. (a) band, relative error (RE) of spectral radiance due to different wavelength error when the FWHM error is 1%; (b) band, relative error (RE) of spectral radiance due to different wavelength error when the FWHM error is 5%; (c) band, relative error (RE) of spectral radiance due to different wavelength error when the FWHM error is 10%; (d) band, relative error (RE) of spectral radiance due to different wavelength error when the FWHM error is 30%; (e) band, relative error (RE) of spectral radiance due to different wavelength error when the FWHM error is 60%.
The findings presented above indicate that the combined effect of both wavelength stability and linewidth of the calibration light source has a greater impact on the acquired spectral radiance than the effect of a single factor. The comparisons of Section 4.2 and Section 4.3 reveal that the simultaneous effect of both factors is not a simple addition of individual factors. For example, in the weak band, the maximum relative error (MAXRE) of the spectral radiance obtained via GAS-2 is 1.21% due to the 1% FWHM error caused by the linewidth of the calibration light source (1.1 GHz). The maximum relative error (MAXRE) of the obtained spectral radiance via GAS-2 is 2.64% due to the 1% wavelength shift error caused by the 0.7 pm wavelength stability of the calibration light source. However, when considering both factors, the maximum relative error (MAXRE) is 4.42%. Similar results were observed for the other three bands. This indicates that the influence of the calibration source on the spectral radiance obtained via GAS-2 cannot be considered a single factor, and the wavelength stability and the linewidth of the source should be taken into account in the actual calibration process.
Figure 17, Figure 18 and Figure 19 depict the evaluation results of the errors in the acquired spectral radiance of GAS-2 when both the calibration light source wavelength stability and linewidth are considered for four bands. The evaluation metrics, including RMSE, MAXRE, and MAXAE, are used to assess the accuracy of the acquired spectral radiance. It is worth noting that the combined effect of the two factors is considered in the evaluation. The results suggest that the influence of the calibration light source on the spectral radiance obtained via GAS-2 cannot be treated as a single factor, and both the wavelength stability and linewidth of the light source should be taken into account in the actual calibration process.
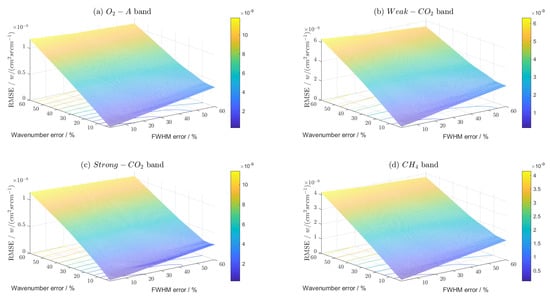
Figure 17.
Comparison of RMSE results of spectral radiance acquired via GAS-2 in four bands due to wavelength stability and linewidth of the calibration light source. (a) -A band, the RMSE results of spectral radiance due to two factors operating simultaneously; (b) weak- band, the RMSE results of spectral radiance due to two factors operating simultaneously; (c) strong- band, the RMSE results of spectral radiance due to two factors operating simultaneously; (d) band, the RMSE results of spectral radiance due to two factors operating simultaneously.
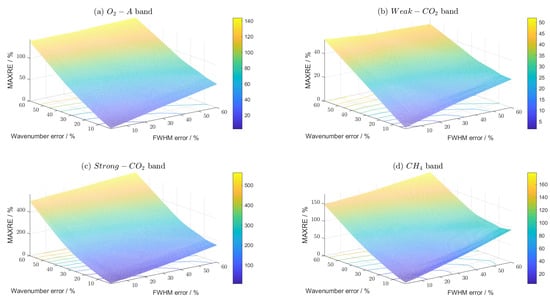
Figure 18.
Comparison of RE results of spectral radiance acquired via GAS-2 in four bands due to wavelength stability and linewidth of the calibration light source. (a) -A band, the RE results of spectral radiance due to two factors operating simultaneously; (b) weak- band, the RE results of spectral radiance due to two factors operating simultaneously; (c) strong- band, the RE results of spectral radiance due to two factors operatimg simultaneously; (d) band, the RE results of spectral radiance due to two factors operating simultaneously.
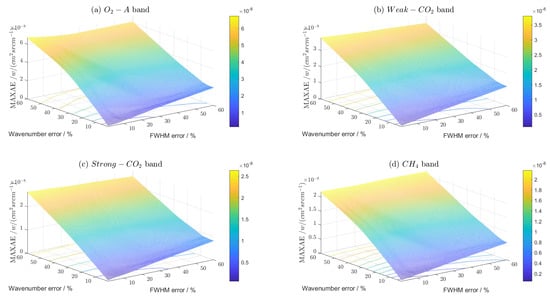
Figure 19.
Comparison of AE results of spectral radiance acquired via GAS-2 in four bands due to wavelength stability and linewidth of the calibration light source. (a) -A band, the AE results of spectral radiance due to two factors operating simultaneously; (b) weak- band, the AE results of spectral radiance due to two factors operating simultaneously; (c) strong- band, the AE results of spectral radiance due to two factors operating simultaneously; (d) band, the AE results of spectral radiance due to two factors operating simultaneously.
Based on the findings presented in Figure 17, Figure 18 and Figure 19, it is evident that the spectral radiance obtained via GAS-2 is more significantly impacted by the simultaneous presence of the wavelength stability and linewidth of the light source than by either factor alone, as demonstrated by all three evaluation indicators. Notably, the strong- band is the most affected among the four bands, regardless of whether a single or both factors are present. Additionally, the proportion of the light source wavelength stability is higher than that of the light source linewidth when both factors are present, which is consistent with the findings of Section 4.2 and Section 4.3. These results highlight the criticality of considering both the stability and linewidth of the light source when considering the spectral calibration of GAS-2.
5. Discussion
5.1. Reasonableness
5.1.1. Reasonableness of the Study
The theoretical analysis of the spreading of the spectral resolution via the linewidth of the calibration light source is reasonable. Due to the fact the convolution of two Gaussian functions is considered when building the model, the result of the convolution will cause the spreading of the spectral resolution of GAS-2. For example, for the spectral calibration of the 0.27 cm spectral resolution band, the light source is generally chosen to be a laser, and the laser fundamental transverse mode lies in a Gaussian-type distribution of intensity in the vertical plane of the beam advance direction. The instrument line function of GAS-2 is a Gaussian distribution, and the instrument line function measured using the principle prototype is also a Gaussian distribution. Therefore, it is reasonable to model the spectral resolution spreading by convolving two Gaussian functions in this paper.
In this study, it is reasonable to determine the errors in GAS-2 acquiring radiance via the spectral resolution spreading and the central wavelength shift of the spectral channel. In the simulation of the observations using the LBLRTM, the atmospheric input conditions are guaranteed to be constant, such as the surface reflectance of 0.05 and the US 1976 standard atmospheric conditions, while observation geometry is fixed and an upwelling radiance spectrum is obtained. The spectral radiance obtained via GAS-2 is the result of the convolution of the upwelling radiance spectrum with the ILS. In other words, the spectral radiance signal is smoothed in the process of convolution with the ILS of GAS-2. The linewidth of the calibration source leads to a broadening of the spectral resolution, and the wider the spectral resolution, the more powerful the smoothing of the upwelling radiance spectrum, the more details are lost, and the detection accuracy is reduced. The wavelength stability of the light source directly affects the accuracy of the center wavelength of the GAS-2 channel. For example, the central wavelength of the response of one of the image elements of the detector is , but due to the wavelength instability of the light source (laser), the calibration result is . This will inevitably cause GAS-2 to acquire spectral radiance errors, especially at the peaks and valleys of gas absorption. This directly affects the accuracy of radiation calibration and causes inaccurate inversion accuracy of GAS-2.
5.1.2. Reasonableness of the Calibration Light Source
This paper presents a quantitative analysis of the error of spectral radiance caused by different calibration sources in GAS-2. Specifically, the influence of linewidth and wavelength stability of calibration sources on spectral radiance is studied, using the weak- band as an example. The results show that the maximum spectral radiance errors of the instrument are 1.54%, 3.44%, and 5.4% when the linewidth of the light source is 1.1 GHz and the wavelength stability is 0.7 pm, when the linewidth is 2.5 GHz and the wavelength stability is 0.7 pm, and when the linewidth is 2.5 GHz and the wavelength stability is 3.5 pm, respectively. To discuss the reasonable error of the light source, a forward model is used, and the control variable method is employed when the detection accuracy of GAS-2 is 2 ppm or 4 ppm. The analysis is conducted with a fixed spectral resolution of 0.27 cm, while the concentration of in the atmosphere increases by 2 ppm or 4 ppm. The simulation results reveal the relative error (RE) of GAS-2 under different scenarios, which are shown in Figure 20.
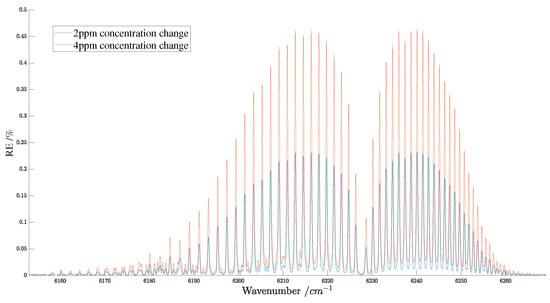
Figure 20.
Relative error in spectral radiance for 2 ppm and 4 ppm changes in atmospheric concentration.
The Figure 20 shows that when the detection accuracy is 2 ppm, the maximum allowable relative error is about 0.25%. If the instrument working band covers only one of the relative change peak-valley cycles, in order to detect the 2 ppm and 4 ppm concentration changes, the relative spectral radiance errors should theoretically be less than 0.25% and 0.5%, respectively. This requires a high signal-to-noise ratio of the instrument to detect the signal change. In the retrieval process, the instrument operating wavelength covers N absorption peaks, and the noise decreases by about times based on the best-fitting estimation method of the full spectrum. In the weak- band range, there are about 42 absorption peaks that are sensitive to the change in column concentration. In the case of other influencing factors being unchanged, if the detection accuracy is better than 2 ppm, the allowable relative spectral radiance error is about 1.62%. If the detection accuracy is better than 4 ppm, the allowable relative spectral radiance error is about 3.24%. Therefore, when discussing the influence of the light source, the weak- band is taken as an example to illustrate that when the linewidth of the calibration light source is 1.1 GHz and the wavelength stability is 0.7 pm, the maximum allowable spectral radiance error is 1.54% (less than 1.6%), which meets the detection accuracy requirement of 2 ppm. If GAS-2 is required to meet the detection accuracy requirement of 4 ppm, the linewidth of the calibration light source should be less than 2.5 GHz, and the wavelength stability should be better than 0.7 pm.
In practice, the actual selection of calibration light source parameters should be improved by one or even several orders of magnitude. For instance, during spectral calibration of NASA’s OCO and OCO-2, the tunable laser selected had a linewidth less than 1 MHz and 300 KHz, respectively, and the wavelength stability is also required accordingly [30,32]. These results sufficiently illustrate the important research significance of spectral calibration light sources. It should be mentioned here that the simulations are all under ideal conditions, and the margin is not considered when considering the calibration light source parameters.
5.2. Limitations of Study
While this study provides valuable insights into the effect of the linewidth and wavelength stability of the calibration light source on the spectral radiance acquired via GAS-2, it is important to recognize its limitations. The quantitative analysis is based on a simulation experiment using an atmospheric model assumed to be constant, which may not fully represent the actual atmospheric conditions. In addition, the results of this study depend on the radiative transfer model, and different models have different results. As a result, this study may have some limitations. However, the limitations of the atmospheric model do not affect the analysis of the influence of the calibration light source on the spectral radiance obtained via GAS-2. It is important to note that this study is focused on analyzing the effect of two key parameters of the light source on the radiance measurements, and this analysis provides valuable information for selecting appropriate calibration light sources. For future prelaunch spectral calibration, it is recommended to employ an end-to-end approach that incorporates the retrieval process over a wide range of atmospheric conditions. This will provide a more comprehensive assessment of the calibration accuracy, including the effects of the atmosphere on the spectral radiance measurements. In conclusion, this study emphasizes the significance of selecting suitable calibration light sources for precise spectral radiance measurements and provides a foundation for future research in this area.
5.3. Future Research Directions
To better evaluate the impact of the calibration light source on spectral radiance obtained via GAS-2, further analyses and studies should be conducted on the power magnitude and power stability of the light source, in addition to the quantitative analysis of the wavelength stability and linewidth. Short-wave infrared tunable lasers, which have high wavelength stability and narrow linewidth, typically have very low output power, typically at the mW level. In the selection of laser models, it is important to consider the laser output power, as an instrument may not respond if the power is too small. The power stability of the light source affects the normalization of the instrument line function during spectral calibration, which also affects the accuracy of the spectral radiance obtained via GAS-2. Therefore, these parameters need to be studied quantitatively in the future to achieve the high-precision detection of greenhouse gases.
6. Conclusions
GAS-2 is one of the main payloads carried by the second-generation polar-orbiting satellite Fengyun-3H(FY-3H), whose main objective is to obtain high-precision quantitative data of global atmospheric greenhouse gases (, etc.). In this paper, we quantify the influence of the linewidth and wavelength stability of the calibration light source on the errors of the spectral radiance obtained via GAS-2. Although the simulated atmospheric conditions in this paper are different from the real ones, the simulated wavelength stability and linewidth of the calibration source affecting the errors of the spectral radiance obtained via GAS-2 are applicable and reasonable under the condition that the observation conditions remain unchanged.
In this paper, we investigated the influence of spectral radiance obtained in four bands of GAS-2 (-A, weak- absorption band, strong- absorption band, and absorption band) by the linewidth and wavelength stability of the calibration source. The main conclusions of this work are described as follows:
- (1)
- The linewidth of the calibration light source will cause the spreading of the spectral resolution, thus affecting the accuracy of the spectral radiance obtained via GAS-2. The narrower the linewidth of the light source, the richer the spectral radiance information received by GAS-2, and the closer it is to the real radiance spectrum. In the actual spectral calibration process, GAS-2 puts forward new requirements on the linewidth of the spectral calibration light source.
- (2)
- The wavelength stability of the calibration light source directly affects the accuracy of the central wavelength of the spectral calibration. The greater the shift in the central wavelength, the greater the error of the spectral radiance received by GAS-2. Compared with the influence of the linewidth and wavelength stability, the wavelength stability of the calibration light source has a greater impact. This is a higher requirement for GAS-2 on the wavelength stability of the spectral calibration light source.
- (3)
- The two factors of calibration light source with linewidth and wavelength stability simultaneously have more influence on the spectral radiance than a single factor, especially at the peaks and valleys of greenhouse gas absorption, which will directly affect the accuracy of greenhouse gas detection. Therefore, the linewidth and wavelength stability of the light source must be considered simultaneously in the spectral calibration.
In conclusion, this paper quantitatively investigates the effects of the linewidth and wavelength stability of the calibration light source on the radiance of GAS-2. In the research and manufacture of the spectral calibration instrument, it is necessary to focus on solving the two major problems of linewidth and wavelength stability of the calibration light source to reduce the uncertainty of the spectral calibration, so as to ensure the accuracy of the spectral calibration and improve the precision of the spectral radiance acquired via GAS-2. This paper provides guidance and reference for the development of laboratory spectral calibration equipment for GAS-2. If the spectral radiance error in each band of GAS-2 is required to be less than 10%, the linewidth of the light source should be around 100 MHz and the wavelength stability of the light source should be at the subpicometer level. The requirements are higher if the error effects of the actual situation are considered. In the future, we will study the influence of the power magnitude and power stability of the calibration light source on the spectral radiance obtained via GAS-2.
Author Contributions
Conceptualization, S.L., H.Y., X.W. and L.D.; methodology, S.L. and L.C.; software, S.L.; validation, S.L., L.C. and H.Y.; formal analysis, H.Y. and L.C.; investigation, S.L. and L.C.; resources, L.D.; data curation, S.L. and L.C.; writing—original draft preparation, S.L.; writing—review and editing, L.D., H.Y., L.C. and X.W.; visualization, S.L.; supervision, L.D.; project administration, L.D.; funding acquisition, L.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China grant number 12141305 and Innovation Program, Shanghai Institute of Technical Physics, Chinese Academy of Sciences grant number CX-384.
Data Availability Statement
All the data generated or analyzed during this study are included in this article.
Acknowledgments
We would like to thank the Pengyu Huang and Yong Hu of the Shanghai Institute of Technical Physics, Chinese Academy of Sciences, for the technical help of software.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Linewidths of different calibration light sources in -A band and evaluation results of spectral radiance errors obtained via GAS-2.
Table A1.
Linewidths of different calibration light sources in -A band and evaluation results of spectral radiance errors obtained via GAS-2.
| Band | LW * (cm) | PSRR ** (%) | RMSE (W/cm · sr · cm) | MAXAE (W/cm · sr · cm) | MAXRE (%) |
|---|---|---|---|---|---|
| B1 (0.69 cm) | 0.097 (2.9 GHz) | 1 | 1.28 | ||
| 0.22 (6.6 GHz) | 5 | 5.11 | |||
| 0.317 (9.5 GHz) | 10 | 5.11 | |||
| 0.573 (17.2 GHz) | 30 | 28.01 | |||
| 0.862 (25.9 GHz) | 60 | 54.13 |
* LW represents the linewidth of the calibration light source. ** PSRR represents the percentage spectral resolution error.

Table A2.
Linewidths of different calibration light sources in weak- band and evaluation results of spectral radiance errors obtained via GAS-2.
Table A2.
Linewidths of different calibration light sources in weak- band and evaluation results of spectral radiance errors obtained via GAS-2.
| Band | LW (cm) | PSRR (%) | RMSE (W/cm · sr · cm) | MAXAE (W/cm · sr · cm) | MAXRE (%) |
|---|---|---|---|---|---|
| B2 (0.27 cm) | 0.0378 (1.1 GHz) | 1 | 0.54 | ||
| 0.0864 (2.5 GHz) | 5 | 1.21 | |||
| 0.1237 (3.7 GHz) | 10 | 3.60 | |||
| 0.2241 (6.7 GHz) | 30 | 5.93 | |||
| 0.3372 (10.1 GHz) | 60 | 27.02 |

Table A3.
Linewidths of different calibration light sources in strong- band and evaluation results of spectral radiance errors obtained via GAS-2.
Table A3.
Linewidths of different calibration light sources in strong- band and evaluation results of spectral radiance errors obtained via GAS-2.
| Band | LW (cm) | PSRR (%) | RMSE (W/cm · sr · cm) | MAXAE (W/cm · sr · cm) | MAXRE (%) |
|---|---|---|---|---|---|
| B3 (0.21 cm) | 0.0294 (890 MHz) | 1 | 4.35 | ||
| 0.0672 (2.0 GHz) | 5 | 15.73 | |||
| 0.0962 (2.9 GHz) | 10 | 22.90 | |||
| 0.1743 (5.2 GHz) | 30 | 70.57 | |||
| 0.2623 (7.9 GHz) | 60 | 156.15 |

Table A4.
Linewidths of different calibration light sources in band and evaluation results of spectral radiance errors obtained via GAS-2.
Table A4.
Linewidths of different calibration light sources in band and evaluation results of spectral radiance errors obtained via GAS-2.
| Band | LW (cm) | PSRR (%) | RMSE (W/cm · sr · cm) | MAXAE (W/cm · sr · cm) | MAXRE (%) |
|---|---|---|---|---|---|
| B4 (0.19 cm) | 0.0266 (794 MHz) | 1 | 4.79 | ||
| 0.0608 (1.8 GHz) | 5 | 9.72 | |||
| 0.087 (2.5 GHz) | 10 | 16.49 | |||
| 0.1577 (4.7 GHz) | 30 | 45.56 | |||
| 0.2373 (7.0 GHz) | 60 | 95.11 |

Table A5.
Wavelength stability of different calibration light sources in -A band and evaluation results of spectral radiance errors obtained via GAS-2.
Table A5.
Wavelength stability of different calibration light sources in -A band and evaluation results of spectral radiance errors obtained via GAS-2.
| Band | Wavelength shift (cm) | Wavelength shift/SR0 * (%) | RMSE (W/cm · sr · cm) | MAXAE (W/cm · sr · cm) | MAXRE (%) |
|---|---|---|---|---|---|
| B1 (0.69 cm) | 0.0069 (0.4 pm) | 1 | 1.59 | ||
| 0.0345 (2 pm) | 5 | 8.19 | |||
| 0.069 (4 pm) | 10 | 58.65 | |||
| 0.207 (12 pm) | 30 | 58.65 | |||
| 0.414 (24 pm) | 60 | 137.3 |
* SR0 is the spectral resolution of this band of GAS-2.

Table A6.
Wavelength stability of different calibration light sources in weak- band and evaluation results of spectral radiance errors obtained via GAS-2.
Table A6.
Wavelength stability of different calibration light sources in weak- band and evaluation results of spectral radiance errors obtained via GAS-2.
| Band | Wavelength shift (cm) | Wavelength shift/SR0 (%) | RMSE (W/cm · sr · cm) | MAXAE (W/cm · sr · cm) | MAXRE (%) |
|---|---|---|---|---|---|
| B2 (0.27 cm) | 0.0027 (0.7 pm) | 1 | 2.64 | ||
| 0.0135 (3.5 pm) | 5 | 13.09 | |||
| 0.027 (7 pm) | 10 | 25.72 | |||
| 0.081 (21 pm) | 30 | 65.98 | |||
| 0.162 (42 pm) | 60 | 77.41 |

Table A7.
Wavelength stability of different calibration light sources in strong- band and evaluation results of spectral radiance errors obtained via GAS-2.
Table A7.
Wavelength stability of different calibration light sources in strong- band and evaluation results of spectral radiance errors obtained via GAS-2.
| Band | Wavelength shift (cm) | Wavelength shift/SR0 (%) | RMSE (W/cm · sr · cm) | MAXAE (W/cm · sr · cm) | MAXRE (%) |
|---|---|---|---|---|---|
| B3 (0.21 cm) | 0.0021 (0.9 pm) | 1 | 2.42 | ||
| 0.0105 (4.5 pm) | 5 | 12.69 | |||
| 0.021 (9 pm) | 10 | 26.93 | |||
| 0.063 (27 pm) | 30 | 102.12 | |||
| 0.126 (54 pm) | 60 | 280.28 |

Table A8.
Wavelength stability of different calibration light sources in band and evaluation results of spectral radiance errors obtained via GAS-2.
Table A8.
Wavelength stability of different calibration light sources in band and evaluation results of spectral radiance errors obtained via GAS-2.
| Band | Wavelength shift (cm) | Wavelength shift/SR0 (%) | RMSE (W/cm · sr · cm) | MAXAE (W/cm · sr · cm) | MAXRE (%) |
|---|---|---|---|---|---|
| B4 (0.19 cm) | 0.0019 (1 pm) | 1 | 2.08 | ||
| 0.0095 (5 pm) | 5 | 9.97 | |||
| 0.019 (10 pm) | 10 | 18.92 | |||
| 0.057 (30 pm) | 30 | 56.81 | |||
| 0.114 (60 pm) | 60 | 137.79 |
References
- Nadeau, K.C.; Agache, I.; Jutel, M.; Annesi Maesano, I.; Akdis, M.; Sampath, V.; d’Amato, G.; Cecchi, L.; Traidl-Hoffmann, C.; Akdis, C.A. Climate change: A call to action for the united nations. Allergy 2022, 77, 1087–1090. [Google Scholar] [CrossRef] [PubMed]
- Elum, Z.; Momodu, A. Climate change mitigation and renewable energy for sustainable development in Nigeria: A discourse approach. Renew. Sust. Energ. Rev. 2017, 76, 72–80. [Google Scholar] [CrossRef]
- Ritchie, H.; Roser, M.; Rosado, P. CO2 and Greenhouse Gas Emissions. Our World in Data. 2020. Available online: https://ourworldindata.org/co2-and-greenhouse-gas-emissions (accessed on 30 April 2023).
- O’Connor, R.E.; Bord, R.J.; Yarnal, B.; Wiefek, N. Who wants to reduce greenhouse gas emissions? Soc. Sci. Q. 2002, 83, 1–17. [Google Scholar] [CrossRef]
- Mustafa, F.; Wang, H.; Bu, L.; Wang, Q.; Shahzaman, M.; Bilal, M.; Zhou, M.; Iqbal, R.; Aslam, R.W.; Ali, M.A.; et al. Validation of gosat and oco-2 against in situ aircraft measurements and comparison with carbontracker and geos-chem over Qinhuangdao, China. Remote Sens. 2021, 13, 899. [Google Scholar] [CrossRef]
- Shao, L.; Fang, B.; Zheng, F.; Qiu, X.; He, Q.; Wei, J.; Li, C.; Zhao, W. Simultaneous detection of atmospheric CO and CH4 based on TDLAS using a single 2.3 μm DFB laser. Spectrochim. Acta A Mol. Biomol. 2019, 222, 117118. [Google Scholar] [CrossRef]
- Gao, R. Research Progress of Atmospheric CO2 Monitoring by Satellite Remote Sensing. J. Phys. 2022, 2386, 12028. [Google Scholar] [CrossRef]
- Stephan, C.; Alpers, M.; Millet, B.; Ehret, G.; Flamant, P.; Deniel, C. MERLIN: A space-based methane monitor. In Proceedings of the Lidar Remote Sensing for Environmental Monitoring XII, San Diego, CA, USA, 21–25 August 2011; SPIE: Bellingham, WA, USA, 2011; Volume 8159, pp. 87–101. [Google Scholar]
- Barkley, M.P.; Monks, P.S.; Engelen, R.J. Comparison of SCIAMACHY and AIRS CO2 measurements over North America during the summer and autumn of 2003. Geophys. Res. Lett. 2006, 33, 20. [Google Scholar] [CrossRef]
- Crisp, D. A Constellation Architecture for Monitoring Carbon Dioxide and Methane from Space. Prepared by the CEOS Atmospheric Constellation Greenhouse Gas Team, Version 1.0, 8 October 2018. Available online: https://ceos.org/document_management/Virtual_Constellations/ACC/Documents/CEOS_AC-VC_GHG_White_Paper_Publication_Draft2_20181111.pdf (accessed on 30 April 2023).
- Schwandner, F.M.; Gunson, M.R.; Miller, C.E.; Carn, S.A.; Eldering, A.; Krings, T.; Verhulst, K.R.; Schimel, D.S.; Nguyen, H.M.; Crisp, D.; et al. Spaceborne detection of localized carbon dioxide sources. Science 2017, 358, eaam5782. [Google Scholar] [CrossRef]
- Chevallier, F.; Palmer, P.I.; Feng, L.; Boesch, H.; O’Dell, C.W.; Bousquet, P. Toward robust and consistent regional CO2 flux estimates from in situ and spaceborne measurements of atmospheric CO2. Geophys. Res. Lett. 2014, 41, 1065–1070. [Google Scholar] [CrossRef]
- Sierk, B.; Caron, J.; Bezy, J.L.; Loscher, A.; Meijer, Y.; Jurado, P. The CarbonSat candidate mission for imaging greenhouse gases from space: Concepts and system requirements. In Proceedings of the International Conference on Space Optics—ICSO 2014, Tenerife, Spain, 6–10 October 2014; SPIE: Bellingham, WA, USA, 2017; Volume 10563, pp. 1010–1018. [Google Scholar]
- Zhang, X.; Wang, F.; Wang, W.; Huang, F.; Chen, B.; Gao, L.; Wang, S.; Yan, H.; Ye, H.; Si, F.; et al. The development and application of satellite remote sensing for atmospheric compositions in China. Atmos. Res. 2020, 245, 105056. [Google Scholar] [CrossRef]
- Frankenberg, C.; Pollock, R.; Lee, R.; Rosenberg, R.; Blavier, J.F.; Crisp, D.; O’Dell, C.; Osterman, G.; Roehl, C.; Wennberg, P.; et al. The Orbiting Carbon Observatory (OCO-2): Spectrometer performance evaluation using pre-launch direct sun measurements. Atmos. Meas. Tech. 2015, 8, 301–313. [Google Scholar] [CrossRef]
- Wang, S.; Ke, J.; Chen, S.; Zheng, Z.; Cheng, C.; Tong, B.; Liu, J.; Liu, D.; Chen, W. Performance evaluation of spaceborne integrated path differential absorption lidar for carbon dioxide detection at 1572 nm. Remote Sens. 2020, 12, 2570. [Google Scholar] [CrossRef]
- Meng, G.; Wen, Y.; Zhang, M.; Gu, Y.; Xiong, W.; Wang, Z.; Niu, S. The status and development proposal of carbon sources and sinks monitoring satellite system. Carbon Neutrality 2022, 1, 32. [Google Scholar] [CrossRef]
- Thies, B.; Bendix, J. Satellite based remote sensing of weather and climate: Recent achievements and future perspectives. Meteorol. Appl. 2011, 18, 262–295. [Google Scholar] [CrossRef]
- Deeter, M.; Martínez-Alonso, S.; Edwards, D.; Emmons, L.; Gille, J.; Worden, H.; Pittman, J.V.; Daube, B.; Wofsy, S. Validation of MOPITT Version 5 thermal-infrared, near-infrared, and multispectral carbon monoxide profile retrievals for 2000–2011. J. Geophys. Res. Atmos. 2013, 118, 6710–6725. [Google Scholar] [CrossRef]
- Zhang, L.; Jiang, H.; Zhang, X. Comparison analysis of the global carbon dioxide concentration column derived from SCIAMACHY, AIRS, and GOSAT with surface station measurements. Int. J. Remote Sens. 2015, 36, 1406–1423. [Google Scholar] [CrossRef]
- Wu, H.; Wang, X.; Ye, H.; Jiang, Y.; Duan, F. Error analysis of the greenhouse-gases monitor instrument short wave infrared XCO 2 retrieval algorithm. J. Appl. Remote Sens. 2018, 12, 16015. [Google Scholar] [CrossRef]
- Sierk, B.; Bezy, J.L.; Loscher, A.; Meijer, Y. The European CO2 Monitoring Mission: Observing anthropogenic greenhouse gas emissions from space. In Proceedings of the International Conference on Space Optics—ICSO 2018, Chania, Greece, 9–12 October 2018; SPIE: Bellingham, WA USA, 2019; Volume 11180, pp. 237–250. [Google Scholar]
- Stohl, A.; Seibert, P.; Arduini, J.; Eckhardt, S.; Fraser, P.; Greally, B.; Lunder, C.; Maione, M.; Mühle, J.; O’doherty, S.; et al. An analytical inversion method for determining regional and global emissions of greenhouse gases: Sensitivity studies and application to halocarbons. Atmos. Chem. Phys. 2009, 9, 1597–1620. [Google Scholar] [CrossRef]
- Chapman, J.W.; Thompson, D.R.; Helmlinger, M.C.; Bue, B.D.; Green, R.O.; Eastwood, M.L.; Geier, S.; Olson-Duvall, W.; Lundeen, S.R. Spectral and radiometric calibration of the next generation airborne visible infrared spectrometer (AVIRIS-NG). Remote Sens. 2019, 11, 2129. [Google Scholar] [CrossRef]
- Zhang, C.; Qi, C.; Yang, T.; Gu, M.; Zhang, P.; Lee, L.; Xie, M.; Hu, X. Evaluation of FY-3E/HIRAS-II Radiometric Calibration Accuracy Based on OMB Analysis. Remote Sens. 2022, 14, 3222. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, D.; Wang, Y. Preflight spectral calibration of airborne shortwave infrared hyperspectral imager with water vapor absorption characteristics. Sensors 2019, 19, 2259. [Google Scholar] [CrossRef] [PubMed]
- Green, R.O.; Eastwood, M.L.; Sarture, C.M.; Chrien, T.G.; Aronsson, M.; Chippendale, B.J.; Faust, J.A.; Pavri, B.E.; Chovit, C.J.; Solis, M.; et al. Imaging Spectroscopy and the Airborne Visible/Infrared Imaging Spectrometer (AVIRIS). Remote. Sens. Environ. 1998, 65, 227–248. [Google Scholar] [CrossRef]
- Green, R.O. Spectral calibration requirement for Earth-looking imaging spectrometers in the solar-reflected spectrum. Appl. Opt. 1998, 37, 683–690. [Google Scholar] [CrossRef] [PubMed]
- Han, Y.; Revercomb, H.; Cromp, M.; Gu, D.; Johnson, D.; Mooney, D.; Scott, D.; Strow, L.; Bingham, G.; Borg, L.; et al. Suomi NPP CrIS measurements, sensor data record algorithm, calibration and validation activities, and record data quality. J. Geophys. Res. Atmos. 2013, 118, 12–734. [Google Scholar] [CrossRef]
- Lee, R.A.; O’Dell, C.W.; Wunch, D.; Roehl, C.M.; Osterman, G.B.; Blavier, J.F.; Rosenberg, R.; Chapsky, L.; Frankenberg, C.; Hunyadi-Lay, S.L.; et al. Preflight spectral calibration of the Orbiting Carbon Observatory 2. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2499–2508. [Google Scholar] [CrossRef]
- Yang, Z.; Zhen, Y.; Yin, Z.; Lin, C.; Bi, Y.; Liu, W.; Wang, Q.; Wang, L.; Gu, S.; Tian, L. Laboratory spectral calibration of the TanSat atmospheric carbon dioxide grating spectrometer. Geosci. Instrum. Methods Data Syst. 2018, 7, 245–252. [Google Scholar] [CrossRef]
- Day, J.O.; O’Dell, C.W.; Pollock, R.; Bruegge, C.J.; Rider, D.; Crisp, D.; Miller, C.E. Preflight spectral calibration of the Orbiting Carbon Observatory. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2793–2801. [Google Scholar] [CrossRef]
- Yu, X.; Sun, Y.; Fang, A.; Qi, W.; Liu, C. Laboratory spectral calibration and radiometric calibration of hyper-spectral imaging spectrometer. In Proceedings of the The 2014 2nd International Conference on Systems and Informatics (ICSAI 2014), Shanghai, China, 15–17 November 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 871–875. [Google Scholar]
- Vane, G.; Chrien, T.G.; Miller, E.A.; Reimer, J.H. Spectral and radiometric calibration of the airborne visible/infrared imaging spectrometer. Imaging Spectrosc. II 1987, 834, 91–107. [Google Scholar]
- Ye, H.-H.; Wang, X.-H.; Wu, J.; Fang, Y.-H. Sensitivity for retrieval of atmospheric column carbon dioxide with high accuracy. J. Atmos. Environ. Opt. 2011, 6, 208. [Google Scholar]
- Wang, Q.; Yang, Z.D.; Bi, Y.M. Spectral parameters and signal-to-noise ratio requirement for TANSAT hyper spectral remote sensor of atmospheric CO2. In Proceedings of the Remote Sensing of the Atmosphere, Clouds, and Precipitation V, Beijing, China, 13–16 October 2014; SPIE: Bellingham, WA, USA, 2014; Volume 9259, pp. 351–366. [Google Scholar]
- Zhang, D.; Zheng, Y. High spectral resolution remote sensing detection system for atmosphere greenhouse gas. In Proceedings of the Hyperspectral Remote Sensing Applications and Environmental Monitoring and Safety Testing Technology, Beijing, China, 9–11 May 2016; SPIE: Bellingham, WA, USA, 2016; Volume 10156, pp. 482–487. [Google Scholar]
- Clough, S.A.; Iacono, M.J.; Moncet, J.L. LBLRTM: Line-By-Line Radiative Transfer Model; ascl: 1405.001; Astrophysics Source Code Library: Online, 2014. [Google Scholar]
- Alvarado, M.; Cady-Pereira, K. Welcome to the Atmospheric and Environmental Research (AER) Radiative Transfer Working Group Website. Available online: http://rtweb.aer.com/lblrtm.html (accessed on 30 April 2023).
- Mikhaylov, A.; Moiseev, N.; Aleshin, K.; Burkhardt, T. Global climate change and greenhouse effect. Entrep. Sustain. Issues 2020, 7, 2897. [Google Scholar] [CrossRef]
- Bi, Y.; Zhang, P.; Yang, Z.; Wang, Q.; Zhang, X.; Liu, C.; Xu, P.; Hou, L.; Ke, J.; Zhang, N. Fast CO2 Retrieval Using a Semi-Physical Statistical Model for the High-Resolution Spectrometer on the Fengyun-3D Satellite. J. Meteorol. Res. 2022, 36, 374–386. [Google Scholar] [CrossRef]
- Bai, W.; Zhang, P.; Zhang, W.; Li, J.; Ma, G.; Qi, C.; Liu, H. Jacobian matrix for near-infrared remote sensing based on vector radiative transfer model. Sci. China Earth Sci. 2020, 63, 1353–1365. [Google Scholar] [CrossRef]
- Kuze, A.; Suto, H.; Nakajima, M.; Hamazaki, T. Thermal and near infrared sensor for carbon observation Fourier-transform spectrometer on the Greenhouse Gases Observing Satellite for greenhouse gases monitoring. Appl. Opt. 2009, 48, 6716–6733. [Google Scholar] [CrossRef]
- Nelson, R.R.; Crisp, D.; Ott, L.E.; O’Dell, C.W. High-accuracy measurements of total column water vapor from the Orbiting Carbon Observatory-2. Geophys. Res. Lett. 2016, 43, 12–261. [Google Scholar] [CrossRef]
- Eldering, A.; Taylor, T.E.; O’Dell, C.W.; Pavlick, R. The OCO-3 mission: Measurement objectives and expected performance based on 1 year of simulated data. Atmos. Meas. Tech. 2019, 12, 2341–2370. [Google Scholar] [CrossRef]
- Line Parameter Database Description. Available online: http://rtweb.aer.com/line_param_description.html (accessed on 30 April 2023).
- Wang, J.; Wang, Y.; Li, C. Noise model of hyperspectral imaging system and influence on radiation sensitivity. J. Remote Sens. 2010, 4, 1. [Google Scholar]
- Guo, Y.x.; Li, Y.q.; Zong, X.y. Research on spectral calibration for hyper-spectral imager. In Proceedings of the 6th International Symposium on Advanced Optical Manufacturing and Testing Technologies: Advanced Optical Manufacturing Technologies, Beijing, China, 13–16 October 2014; SPIE: Bellingham, WA, USA, 2012; Volume 8416, pp. 402–406. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).