Abstract
With the capability of capturing a target’s two-dimensional information, Inverse Synthetic Aperture Radar (ISAR) imaging is widely used in Radar Automatic Target Recognition. However, changes in the ship target’s attitude can lead to the scatterers’ rotation, occlusion, and angle glint, reducing the accuracy of ISAR image recognition. To solve this problem, we proposed a Triangle Preserving level-set-assisted Triangle-Points Affine Transform Reconstruction (TP-TATR) for ISAR ship target recognition. Firstly, three geometric points as initial information were extracted from the preprocessed ISAR images based on the ship features. Combined with these points, the Triangle Preserving level-set (TP) method robustly extracted the fitting triangle of targets depending on the intrinsic structure of the ship target. Based on the extracted triangle, the TP-TATR adjusted all the ship targets from the training and test data to the same attitude, thereby alleviating the attitude sensitivity. Finally, we created templates by averaging the adjusted training data and matched the test data with the templates for recognition. Experiments based on the simulated and measured data indicate that the accuracies of the TP-TATR method are 87.70% and 90.03%, respectively, which are higher than those of the contrast algorithms and have a statistical difference. These demonstrate the effectiveness and robustness of our proposed TP-TATR method.
1. Introduction
Synthetic Aperture Radar (SAR) plays a potential role in ocean dynamics and ship detection investigations [1]. It is a powerful tool that can provide high-resolution images of the ocean surface, allowing researchers to study ocean currents [2], waves [3], and even detect oil spills [4]. Additionally, SAR can be employed for ship detection and tracking, making it an important tool for maritime surveillance and security [5]. In this view, Synthetic Aperture Radar’s site contains Inverse Synthetic Aperture Radar (ISAR). ISAR is used to create two-dimensional images of a moving target, such as a ship or aircraft, by processing the radar reflections received from it. It is commonly used in maritime and aviation applications for target identification and classification. Inverse Synthetic Aperture Radar (ISAR) produces images to detect ship targets at sea in all weather, day or night. It is possible to extract the features of these ISAR images and then recognize ships owing to the range and cross-range dimensional high resolution. During ISAR detection, however, the attitude change of the ship target directly affects the feature extraction. The target scattering point not only appears in rotation and occlusion, but its electromagnetic properties also change, i.e., angle glint [6]. These further lead to a decreased correlation among ISAR images, which reduces the accuracy of recognition. Therefore, a robust recognition method insensitive to attitude changes is critical for ISAR images.
The recognition methods for ISAR images can be categorized into three groups: the neural network-based [7,8,9,10,11,12], transform domain-based [13,14,15,16,17,18,19,20,21,22,23], and geometrical features-based [24,25,26,27,28] methods.
These recognition methods are all studied for the attitude change. Before the neural network for recognition, Bai et al. [7] used the spatial transformer network model to tackle the unknown deformation of ISAR images caused by the attitude change of targets. The recognition accuracy is 89.03% with combined deformation ISAR images. However, the difference is only five degrees in elevation angle between training and testing. This approach requires a large number of images (at least 2880) to train the network, which can be challenging to implement because ISAR images are difficult to obtain. Zhao et al. [8] proposed a pre-trained network for small datasets. There are seven classes of targets based on the aspect angle of 150 or 210 degrees and the robustness needs to be evaluated with a broader range of aspect angles.
Among the transform domain methods, Karine et al. [13] utilized the relative phases of complex wavelet coefficients and then fed the feature into the sparse representation-based classification. This method uses 780 samples for training data and the recognition accuracy is 87.99%. However, this method is sensitive to the quotient of training samples. Kim et al. [14] mapped the ISAR image to polar coordinates to eliminate the rotation of the ISAR image. However, the robustness of recognition will greatly reduce if the ideal centroid of the target mismatches the actual one. To address this issue, Park et al. [15] processed the ISAR image with two-dimensional fast Fourier transform and mapped it to polar coordinates to achieve the rotation center invariance. These methods [14,15] both deal with aspect angles ranging from 0 to 180 degrees. However, the elevation angles are the same. These methods only focus on the rotation and translation, but not on the stretching and other deformations. The training data consist of 108 and 222 samples, respectively. Nevertheless, the effectiveness of this method may reduce as the shape of targets’ images varies with their attitude. Lee et al. [16] obtained more robust features by mapping the image along the estimated principal axis. This method deals with data with the azimuth angle ranging from −10 to 10 degrees and the elevation angle ranging from −2 to 6 degrees. Saidi et al. [17] combined several transform features and the best accuracy of the ISAR image is 87.4%. However, these transform domain methods suffer from the loss of target structure and shape features.
The recognition methods based on geometric feature typically recognize targets by extracting features such as the target’s centerline [24], length [25], area [26], edges [27], and the centroided points of interest [24]. However, the extraction accuracy of these features dramatically decreases when the ISAR target is distorted or stretched caused by the attitude change, resulting in poor recognition. Manno-Kovacs et al. [27] first extracted texture features from ISAR images, then identified targets based on the extracted features and the result gained 70% accuracy. However, the unstable cross-range resolution may impair the texture features, subsequently reducing the accuracy of recognition. Kurowska et al. [25] classified ships by extracting the ship target’s length and width and the result gained a 95.7% accuracy. However, the classification accuracy is seriously reduced due to the targets’ distortion. Kawaharay et al. [28] introduced co-occurrence histograms of oriented gradients to extract feature vectors to alleviate the effects of target image distortion and occlusion. The accuracy of a 60-degree aspect drops, and certain categories drop to 7.2%. The effectiveness of this method is limited by its small observation angles. In general, these methods retain the target’s structure in order to adopt various classifiers for further processing. However, there is a clear trend for all the above methods: as the angle range increases and the number of training samples decreases, the accuracy decreases as well. This indicates that the low correlation between the training data and test data may lead to a decrease in the accuracy of recognition and the effectiveness of the classifier severely depends on the target rotation, occlusion, and angle glint.
Recently, Xie et al. [29] utilized template matching to calculate the accuracy between the ISAR image and the CAD model. However, this method requires the CAD model and accurate matching points. A natural approach is to match the test data and template ISAR images, which requires robust feature points. As we know, a ship target includes the bow, stern, and island. If the boundaries of the ISAR image can be extracted, the feature points can be founded by calculating the intersection points of the boundaries. These feature points represent the structures of the ship, which are robust and easy to match. However, the boundaries are always blurry in ISAR images. Chan et al. [30] proposed a CV variational level-set segmentation model, which has the advantage of good noise-robustness and can segment targets with blurry boundaries. Building on this, Feng et al. [31] proposed a CV variational level set target segmentation method that preserves a rectangle shape. This segmentation method can incorporate prior rectangle information and extract targets with blurred boundaries that are prone to interference. And we find that the boundaries of ISAR images present this blurry feature. Therefore, inspired by the CV variational level set method based on rectangle preservation, this paper introduced a Triangle Preserving level-set (TP) combined with the inherent structure of the ship target. The ship target comprises the bow, stern, and island, which forms a triangular structure in ISAR imaging. The TP method can accurately extract these structural position of ship targets. In addition, we introduce an Affine Transform method to the extracted triangle structure, which maps the ISAR image of the ship target to a given standard attitude. Considering the extracted structure, a Triangle-Points Affine Transform Reconstruction (TP-TATR) was proposed to map and reconstruct the ISAR image to remove attitude sensitivity.
Combining the advantages of the above two methods, we proposed a Triangle Preserving level-set and Triangle-Points Affine Transform Reconstruction (TP-TATR) for ship target recognition. First, we preprocessed the ISAR images by compressing dynamic range and thresholding, subsequently extracting three initial points to construct a triangle. Following that, the triangle was tightly fitted with the ship’s structures utilizing the TP method. With this stable triangle, we mapped the training and test data to the same attitude utilizing the TATR so as to alleviate the attitude sensitivity. Then, we matched the test data with templates generated by averaging the adjusted training data to evaluate the matching degree. The correlation was by Normalized Product (NProd) [32] to achieve the final recognition. The contributions of this paper are described as follows:
- We introduced the TP method to accurately fit ship structure, with the robustness of speckle noise. Additionally, the TP method can deal with blurred targets, making it more suitable for ISAR images.
- We proposed the TP-TATR to alleviate the target rotation, occlusion, and angle glint induced by the attitude sensitivity. Since a ship generally consists of the bow, stern, and island, the triangle-points clearly match the ship structure more than the quadrangle.
- We proposed an effective and robust framework for ISAR ship target recognition. As our TP-TATR method adjusts all data to the same attitude, the attitude sensitivity is greatly moderated, allowing the insertion of other powerful classification methods.
2. ISAR Signal Model
In this section, we will introduce the ISAR signal model briefly.
ISAR imaging utilizes a synthetic aperture to achieve high cross-range resolution. If there is relative motion between the radar and the target, a long-time coherent accumulation can be used to obtain the synthetic aperture. The relative motion between the target and radar can be decomposed into translational motion and rotation. The translational motion is always useless to ISAR imaging, and the motion compensation is carried out to reduce the influence.
Ideally, there is only rotation after the motion compensation between the radar and target, as shown in Figure 1. The target rotates with the center point O and the distance to radar is . Let the x-axis be the Line of Sight (LOS), and a scatterer P coordinate be (). The distance to O is , and the distance to the radar is r. The angle between the OP and the positive direction of the x-axis is . As , we have
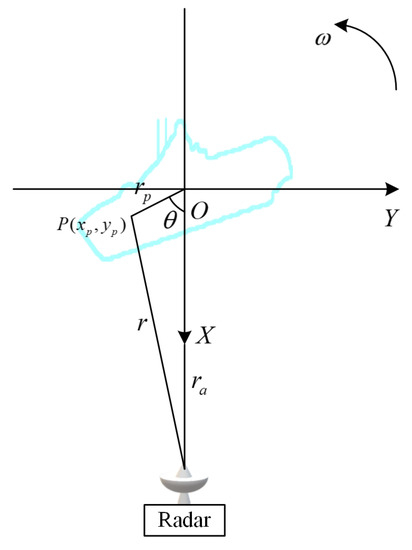
Figure 1.
Ideal ISAR imaging model.
Then, the changes with time t as
where the is the angular velocity.
The Doppler frequency of P can be derived as
where the , and the .
From Equation (3), the Doppler frequency is proportional to the azimuth position of the scattering point, then the azimuth resolution can be realized by resolving the Doppler frequency.
As the cross-range is calculated by the Doppler of the target, the target’s ISAR image is dependent on its movement. The Image Projection Plane (IPP) is defined by the LOS and the target’s movement.
For the rotating ship, the coordinate system was established, where the origin of coordinates is the center of rotation O and the x-axis is the LOS. The angular rotation vector is perpendicular to the rotation plane. The projection of the rotation vector to the plane of is the effective rotation vector , as shown in Figure 2, where the plane is perpendicular to the LOS. The effective rotation vector is the normal vector of the IPP. The ISAR image is the target’s projection onto the IPP [33].
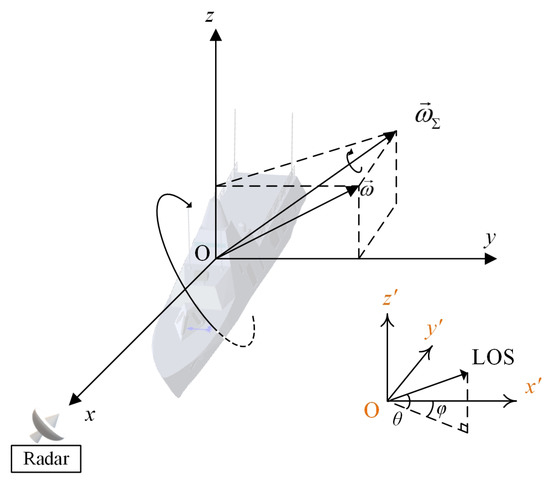
Figure 2.
The IPP of ISAR image.
Then the target local coordinate system was built, where the origin of coordinates is the center of rotation O and the x-axis is the direction of the ship’s bow. The elevation angle is the angle between the LOS and the plane. The azimuth angle is the angle between the projection of LOS to the plane and the x-axis.
The image of ISAR is influenced by IPP, which is determined by the LOS and the movement of the target. With different IPP, the ISAR image might experience translation, scaling, and rotation [7], and decrease the accuracy of recognition. Therefore, in the next section, the algorithm is proposed to mitigate the impact of the change with IPP.
3. Proposed Methods
3.1. Framwork
In this section, we introduce the framework of the TP-TATR and the template matching for the recognition of ISAR ship target. The flowchart is shown as Figure 3.
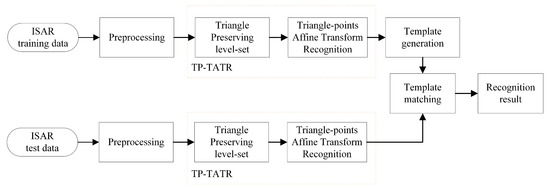
Figure 3.
The flowchart of TP-TATR and the template matching for ISAR ship target recognition.
The first step involves preprocessing the images to remove speckle noise and stripes. In the second step, three potential feature points and a centroid point are extracted. These candidate points are then evolved using the TP method to obtain stable points, which serve as the vertices of a triangle. The third step involves reconstructing the ISAR image through affine transform using TATR with stable points. The combination of the second and third steps is referred to as the TP-TATR method, which reduces the impact of the target’s attitude sensitivity as much as possible. Finally, to demonstrate the effectiveness and robustness of TP-TATR, the template matching algorithm is utilized to recognize the ISAR images. The training data can generate the template, and the correlation coefficient between the test data and the templates is calculated by pixel-to-pixel matching. Then the recognition results are given. We describe each step in more detail as follows.
3.2. Preprocessing
The first step is preprocessing the ISAR images. The ISAR target is composed of a few extremely strong scatterers and many weak scatterers. In order to reduce its dynamic range, it is necessary to use decibel mapping, which involves taking the logarithm of the amplitude of the ISAR image to change its amplitude to dB. Next, threshold processing is needed. Although the scatterers are different in amplitude, they typically have more noticeable grayscale distribution differences compared to the background. Therefore, global thresholding can be considered for preprocessing. However, the fixed thresholding is not satisfied with the ISAR image, so automatic threshold estimation is performed for each image, and a common iterative algorithm is used [34].
Removing strong scatterers and stripes through global thresholding can be challenging. To address this, we proposed a method that correlates the threshold with the distance to the target centroid. This approach effectively removes noise while retaining the ship’s structure, such as its masts. Here are the specific steps involved in our approach:
- Step 1: Calculate the cross-range coordinate of the centroid of the target.
- Step 2: Accumulate the target ISAR image along the range to get the projection .
- Step 3: Binarize the projection and calculate the width of the connected domain where the target centroid is located.
- Step 4: Multiply the global threshold by a coefficient , which varies with the cross-range coordinate x and satisfies this formula,
This preprocessing can avoid the problem of filtering out structures such as masts while partially removing stripes of the ISAR ship target.
3.3. Triangle Preserving Level-Set Model
To effectively eliminate the influence of attitude sensitivity, which can cause scatterers’ rotation, occlusion, and angle glint, TATR requires at least three stable feature points after preprocessing. However, extracting these feature points from ISAR images can be challenging due to the presence of speckle noise around the ship, sidelobes of strong scatterers, and angle glints, which can interfere with the process. Moreover, extracting these feature points from ISAR images can be challenging due to the presence of speckle noise around the ship, sidelobes of strong scatterers, and stripes, which can interfere with the process. The structural scatters are obscured and disappear, and the stripes also change. In Figure 4, as the elevation angle changes from 7.96 degrees to 7.01 degrees, the scatterers corresponding to the bow of the ship disappear.
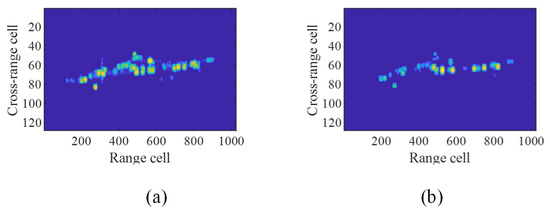
Figure 4.
ISAR image with different elevation angle (a) An ISAR image of a ship with an elevation angle 7.96 degrees (b) An ISAR image of a ship with an elevation angle 7.01 degrees.
Common point matching methods may produce a large number of mismatches, especially when dealing with ships with different attitudes and in the presence of noise and angle glint [35]. Therefore, we need to extract the stable feature points. Since we were processing the side view of the ship, we chose the ship’s bow, stern, and island as the three structures for feature point extraction. This was because most ships have these structures, and scatterers belonging to these structures are often strong and located on the edge of the ISAR image. Therefore, this section extracts these three parts as three key feature points.
A natural idea is using the Hough transform to extract the boundaries. However, there are three lines, which consist of the bow and island, the stern and island, and the bow and stern, respectively. As the resolution of the ISAR image changes, the line might be close together and be hardly distinguished using Hough transform. We were inspired by the segmentation model based on the shape preserving and CV variational level-set [30,31] method, which is known for its excellent anti-noise performance and ability to accurately segment targets with blurry boundaries. This method incorporates a prior shape to address the problem of targets under partial occlusion. Here, we provide a detailed description of this method, including how it works and its advantages over other segmentation techniques. We then describe how this method was introduced into our three-point feature extraction.
3.3.1. CV Model
For the traditional CV model, the energy function model is:
where C is the curve, represents the average gray value of the inner area of the curve and represents the average gray value of the outer area of the curve. means the image, is positive fixed parameters. The first two terms are fitting terms of the evolution of curve C, which are used to make curve C as close as possible to the contour of image u. The last two terms are regularizing terms of the curve C, representing the length and area of the curve C, respectively. By minimizing the energy function, the final contour line C, as well as the and , can be obtained.
Let a Lipschitz function represent the curve C implicitly: . The evolution of the curve can be given by taking the zero-level curve of the function at a given time t. The relationship between C and is shown in the Figure 5.
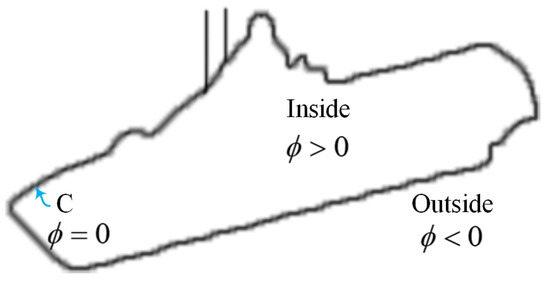
Figure 5.
The relationship between C and .
Then, rewrite the Equation (5) as:
where is the image area, and represent the Heaviside function and its derivative, the Dirac function, respectively. They are always defined by:
where is the parameter of the regularized Heaviside function and its derivative.
Equation (6) is the energy function of the CV level-set model.
3.3.2. Line Preserving and Level-Set Model
In order to solve the problem that the CV model cannot handle active contours with prior information, this energy model is established as [36]:
where is fixed parameters, and
where is a level-set function representing shape prior.
Comparing the Formulas (5) and (8), it can be found that, due to the constraint of the shape prior, the regularizing terms are omitted. Due to constraining the shape of boundaries, the evolution process can be simplified without the constraint of , using line shape preserving instead of an affine transformation. Since the regularization term in also constrains the boundary shape, we can also omit this term by constraining the level set function directly, and the formula is:
Since the function of a single line in the plane is
where is the angle between the normal of the line and the positive direction of the x-axis, and is the distance from the line to the origin.
Hence, as Figure 6 shown, let the level-set function as:
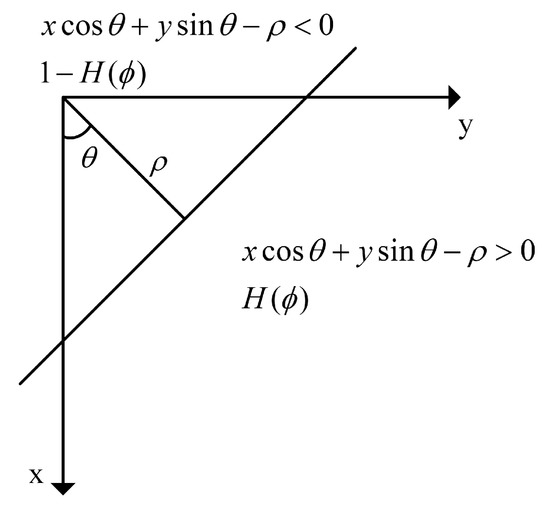
Figure 6.
Level-set function with line preserving.
Then, Equation (10) can be solved by applying the gradient descent method. As the parameters and change with time t during the evolution of the line, the evolution equation is obtained as [31]:
By the gradient descent method, use
to iterative solution, where a is a small constant, representing the learning rate; represents the gradient of . The is the variable during the iteration and the k is the iteration number.
After the iteration stops, segment the straight edge of image u.
3.3.3. Triangle Preserving Level-Set Model
Considering the triangular region as the intersection of three lines and detecting them one by one, the triangular target could be segmented.
Similar to the line model, the energy function of the Triangle Preserving level-set (TP) method is:
where the represents a triangle area, which is shown in Figure 7. is written as:
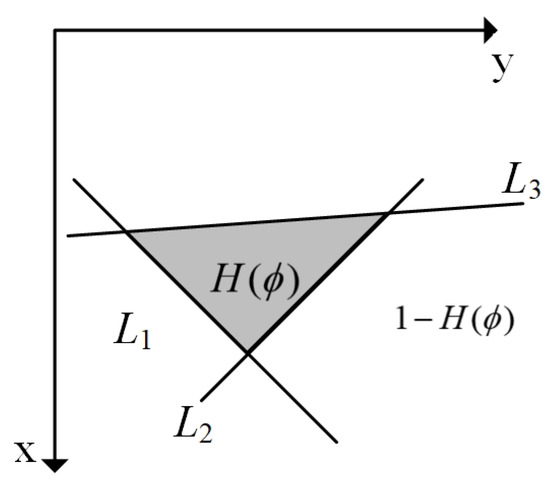
Figure 7.
Level-set function with triangle preserving.
When a line evolves, other lines are considered fixed, which means and are constants when solving for . Therefore, set and , then reduce the problem from Equation (15) to Equation (10), and solve as Equation (13). The other two lines are the same; then, the evolution formulae of Equation (15) are:
where the are the distances from the three lines forming the triangle to the origin, are the angles of these three lines, are the Heaviside function, and are the Dirac function.
Similar to the line preserving level-set model, the gradient descent method is used to iteratively obtain the contour of the target. The algorithm flow is depicted in Algorithm 1.
| Algorithm 1: Triangle Preserving level-set. |
Input: image u, initial parameters of triangle 1: Initialization: learning rate a, positive fixed parameters , 2: while not converged do 4: calculate the average gray and of area and 1- area, respectively 5: calculate the gradient by Equation (17) with the fixed 6: calculate the gradient by Equation (17) with the fixed 7: calculate the gradient by Equation (17) with the fixed 9: update by gradient descent method 10: end while |
Note that there is another possible form of the . The details can be found in Appendix A.
The intersection points of the three lines are the three robust feature points. Assume that the lines and intersect at point , then we have
and the solution is
The two other intersections are similar to this.
3.3.4. Process of Ship Target with TP
Before using the TP method for image segmentation, providing suitable initial values of can accelerate the iteration. Different from the previous section, three initial lines are estimated by three initial feature points in this section, further obtaining the initial values . Although these scatterers may be affected by speckle noise, stripes, and angle glint, they will be stably detected by the TP method.
In summary, the process of extracting feature points from a ship with the TP method can be achieved through the following steps:
- Step 1: Calculate the centroid of the preprocessed image u.
- Step 2: Extract two scatterers farthest from the centroid in opposite directions one by one, then connect them as a line to obtain the scattered point farthest from the line. Record the three points as the initial points.
- Step 3: Use these three points as the intersection points of three lines to calculate the initial values for .
- Step 4: Apply Algorithm 1 to obtain the stable triangle.
- Step 5: Obtain three intersection points of the corresponding three lines belonging to the triangle, and output them together with the centroid for the next algorithm.
After performing the TP method on the ship images, four points are outputs, including three feature points and one centroid point.
3.4. Triangle-Points Affine Transform Reconstruction
In the previous section, we extracted three stable points corresponding to the ship’s bow, stern, and island. Besides the three points, the centroid point is also considered as a robust point with less impact from speckle noise, stripes, and ship attitude. Therefore, adding the fourth point, the centroid point, can further reduce the impact of noise and improve the robustness of the TATR algorithm. Based on the three geometric feature points and one centroid point—a total of four points—the affine transform could be used to reconstruct the ISAR image to a standard attitude, reducing the sensitivity of attitude. The process is referred to as the Triangle-Points Affine Transform Reconstruction (TP-TATR).
The coordinates of the four points are written as where the , are the coordinates of the four points. The coordinates of the four points after reconstruction are defined as , i = 1, 2, ..., 4. The affine transform can be written as:
where
and are coefficients of the affine transformation.
Since there are six coefficients of the affine transformation existing in the matrix A, only six equations are needed to obtain the solution. However, there are eight equations due to four points, bringing the equation group into the overdetermination. Therefore, we utilized the generalized inverse of the matrix to obtain the squares solution, which is:
where the is the estimated affine transformation matrix.
In summary, the steps of TATR include:
- Step 1: Based on the ISAR image, rewrite the four pairs of matching points’ coordinates as a matrix, including the bow, stern, island and the centroid.
- Step 2: Estimate the transform matrix using Equation (22).
- Step 3: Warp the ISAR image using the transform matrix , and output the result for recognition.
By applying an affine transformation using the to the ISAR image, the reconstructed image is the output of the TATR algorithm.
3.5. Template Matching
For the training data, the templates belonging to different categories can be obtained by averaging the standard ISAR images obtained by the TP-TATR method. Since the ISAR images after TP-TATR are robust with attitude sensitivity, only a few samples (five samples in this paper) are needed to complete the training. For the test data, after the TP-TATR, the images are matched with templates using the Normalized Product correlation (NProd) method [32]. The formula is:
where and are the ith pixel of test data images and templates, respectively.
The P ranges from 0 to 1, where 1 indicates a perfect correlation and 0 means no correlation. The samples are classified into the category of the template with the highest P.
4. Results and Discussion
4.1. Simulated Data
The 3D ship models were utilized to acquire the ISAR images from computational electromagnetics software for recognition processing. The simulation parameters were: center frequency = 8.5 GHz, bandwidth B = 150 MHz, and pulse interval stepping angle 0.01 degrees. The elevation angle ranges from 0 to 35 degrees. There were 128 cross-range points and 1024 range points in each ISAR image.
We selected three types of ships for modeling, and their 3D models and ISAR images are shown in Figure 8. Target 1 has 77 ISAR images, target 2 has 127 ISAR images, and target 3 also has 127 ISAR images, adding up to 331 ISAR images.
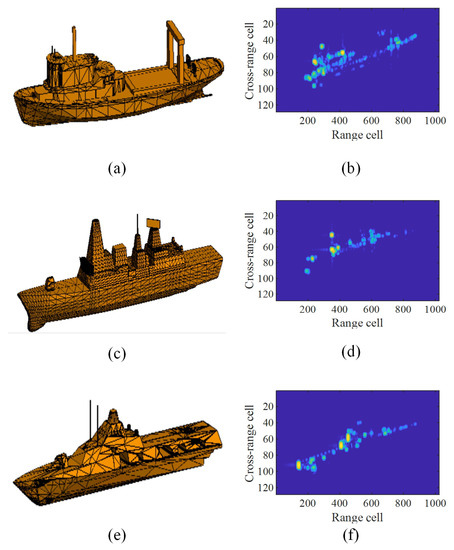
Figure 8.
The 3D models with different simulated ships and their ISAR images. (a) The 3D model of target 1. (b) One of the ISAR image of target 1. (c) The 3D model of target 2. (d) One of the ISAR image of target 2. (e) The 3D model of target 3. (f) One of the ISAR image of target 3.
In Figure 8a, the ship’s island is biased to one side and there is a cylindrical structure above the island, with most of the scatterers mainly concentrated on the left side and a stronger scatterer at the top in Figure 8b. In Figure 8c, the ship contains multiple vertical structures and the island is mainly concentrated in the center of the ship, which is reflected in Figure 8d as more scattering points in the center position. In Figure 8e, the ship has an island and two vertical structures but, in Figure 8f, the ISAR image only shows the island in the center of the ship, and the scatterers’ intensity of the two vertical structures is weak. It is obvious that the part of the relatively unique geometric structures of the ships can be reflected in the ISAR images.
All the simulation ISAR images were preprocessed. Then the centroid was calculated, and three geometric structure feature points were extracted and are marked in Figure 9. Compared Figure 9a with Figure 9c, some scatterers of structures disappear due to angle glint. Compared Figure 9b with Figure 9d, the location of the left feature point changes due to the scatterers weakened. The weakened scatterers interfere with the extraction of feature points. Therefore, we needed to extract robust feature points based on the TP method.
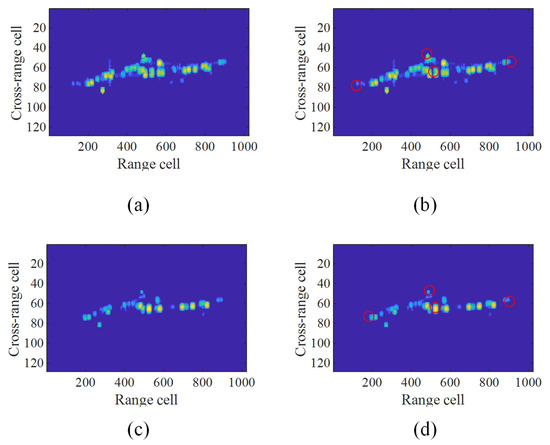
Figure 9.
Changes of feature points caused by angle glint. (a) An ISAR image of a ship with an elevation angle of 7.96 degrees. (b) The location of the four feature points when the ship’s elevation angle is 7.96 degrees. (c) An ISAR image of a ship with an elevation angle of 7.01 degrees. (d) The location of the four feature points when the ship’s elevation angle is 7.01 degrees.
After the TP method, the results are shown in Figure 10. Despite the differences between the input, the TP method can still stably segment the fitting triangle. We adopted the vertices of the triangle and the centroid point and applied the TATR algorithm.
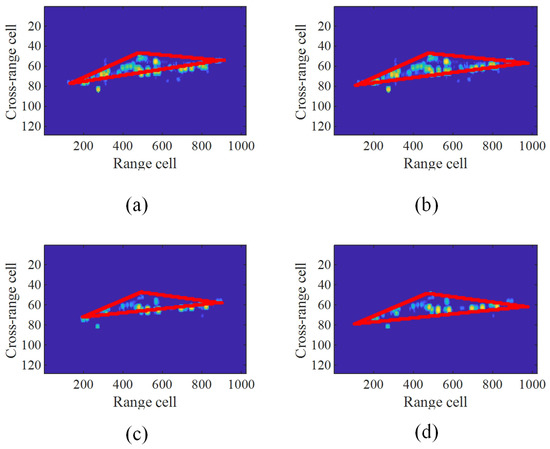
Figure 10.
The influence of different initial feature points on the segmentation results. (a) The initial triangle with an elevation angle of 7.96 degrees. (b) The evolution result of the triangle of the ISAR image with 7.96 degrees elevation angle. (c) The initial triangle with an elevation angle of 7.01 degrees. (d) The evolution result of the triangle of the ISAR image with 7.01 degrees elevation angle.
The results of TATR are shown in Figure 11. The targets are mostly corrected to horizontal postures, basically eliminating the elevation before TATR. From the result, we constructed a template for this type of target.
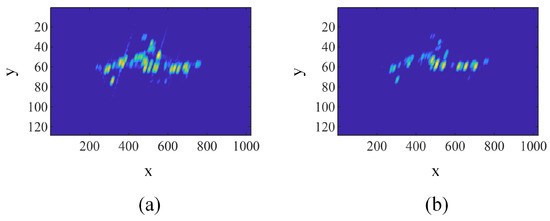
Figure 11.
The results using TATR. (a) The TATR result of the ISAR image with an elevation angle of 7.96 degrees. (b) The TATR result of the ISAR image with an elevation angle of 7.01 degrees.
We used three ISAR images for each target type to construct templates, as shown in Figure 12. The templates indicate that different images can be roughly overlapped after TATR reconstruction, and the ship’s position is relatively horizontal, demonstrating the stability of our algorithm.
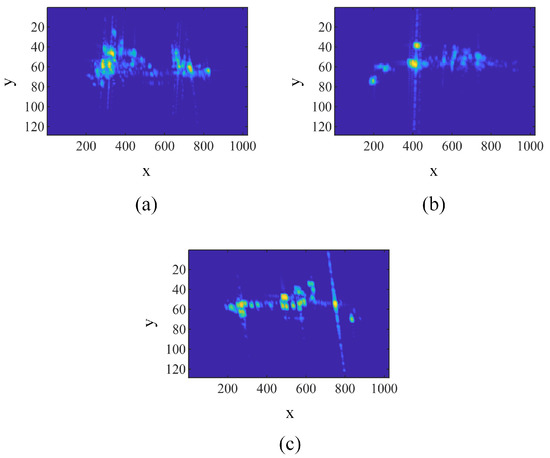
Figure 12.
The templates with simulated data generated by TP-TATR. (a) The template of target 1. (b) The template of target 2. (c) The template of target 3.
To demonstrate the effectiveness of our algorithm, we designed comparative experiments with different algorithms. For fairness, each algorithm uses the same preprocessing and ISAR images to generate templates. The compared algorithms included the “only centroid” algorithm, which only aligns the centroid point to generate templates and matching, and the QATR [34] algorithm, which uses the four vertices of the boundary rectangle and the centroid to reconstruct the ISAR images.
The templates generated by the above two algorithms and the proposed algorithm are shown in Figure 13. The templates generated by the “only centroid” algorithm are difficult to use to recognize and identify useful information. Although the QATR algorithm performs better than the “only centroid” algorithm, the points may still be affected by the stripes caused by strong scattering points. As a result, sometimes the feature points deviate from the correct position, as shown in the template for target 1. Moreover, the angle glint may cause the template to appear “unfocused,” as shown in the template for target 3. Note that the template for target 3 appears to have two stripes, as the stripes caused by the same scatterers are not reconstructed to the same position.
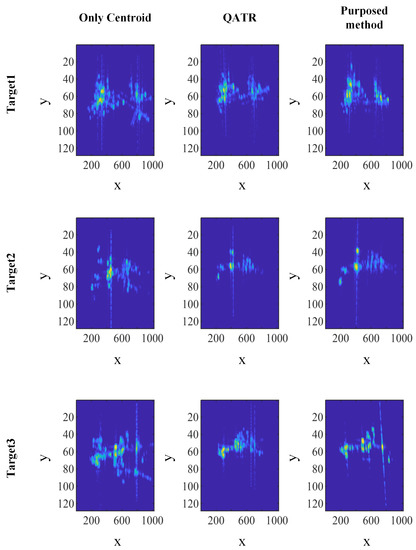
Figure 13.
The templates with simulated data generated by the “only centroid” algorithm, QATR, and TP-TATR.
In contrast, our proposed algorithm reconstructs ISAR images stably, and the obtained templates are advantageous for matching and recognition.
We used template matching on test data based on these templates. The Receiver Operating Characteristic (ROC) was drawn using the correlation of NProd, and the Area Under the Curve (AUC) was calculated [37]. The result is shown in Figure 14.
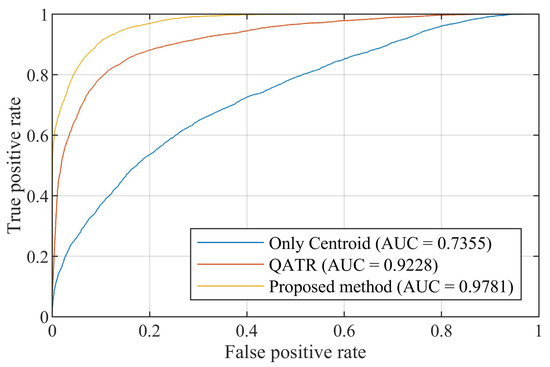
Figure 14.
The ROC of simulated data.
According to the figure, the “only centroid” method’s curve is the closest to the diagonal line, which means the worst recognition capability, and the AUC is lowest at 0.7355, accordingly. The curve of QATR is in the middle, meaning the recognition capability is better than “only centroid” but worse than our proposed method, and the AUC is in the middle—0.9228. The ROC curve demonstrates that our proposed method has the best recognition capability, as its curve is closest to the top-left, with the highest AUC at 0.9781. Each image was classified into the category of the template with the highest matching score. The accuracy of each algorithm is shown in Table 1. This paper used Welch’s t-test [38] with statistical comparison. The p-values of “only centroid” and QATR with the proposed method were calculated, and were p < 0.001 and p = 0.039 < 0.05, respectively. The results indicate that the accuracies of both methods are significantly different from that of the proposed method. It is clearly seen that the proposed method outperforms the others, further demonstrating the stability of our method.

Table 1.
The accuracy of the three algorithms on the simulated data (mean ± std).
4.2. Measured Data
The measured data were used to further verify the proposed method’s effectiveness.
The measured data were acquired using an X-band ISAR radar system with a bandwidth of 400 MHz. Each ISAR image was 128 points in the cross-range and 1024 points in the range direction. There were 66 ISAR images of a three-masted sailing ship, 42 ISAR images of a cargo ship, and 152 ISAR images of a transport ship, totaling 260 ISAR images.
Figure 15 shows the optical images of different targets and the corresponding ISAR image for each target. The ship in Figure 15a has three masts, while in Figure 15b it has three bright lines. The ship in Figure 15c has four vertical structures and a ship island at the stern, which is also reflected in Figure 15d. The ship in Figure 15e has one vertical structure and a ship island, which is also obviously depicted in Figure 15f.
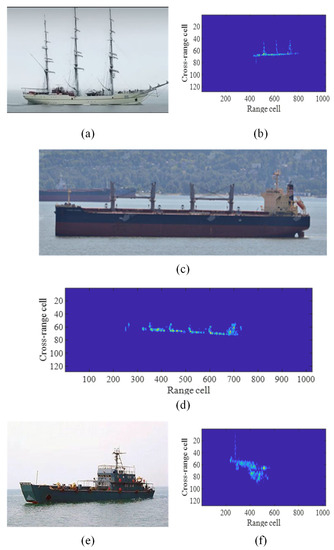
Figure 15.
The optical and ISAR images of several targets. (a) The optical image of target 1. (b) One of the ISAR images of target 1. (c) The optical image of target 2. (d) One of the ISAR images of target 2. (e) The optical image of target 3. (f) One of the ISAR images of target 3.
Similar to the simulated data, the proposed method was validated on the measured data. Templates were obtained for the three types of targets using three, two, and five ISAR images, respectively, due to the disparity in the number of ISAR images for each target. The templates generated by our proposed method are shown in Figure 16. The templates of measured data show that all the masts are almost overlapped at the same position, which are always vertical with the ship body in the image. The body of the ship is relatively horizontal. The stripes in the ISAR images of target 3 hardly disturb our algorithm. As a result, the stripes slope after TP-TATR. The templates demonstrate that different images can be roughly overlapped after TP-TATR reconstruction, indicating the stability of our algorithm with measured data. The templates obtained by the three algorithms are shown in Figure 17, which shows the effectiveness of the proposed method.
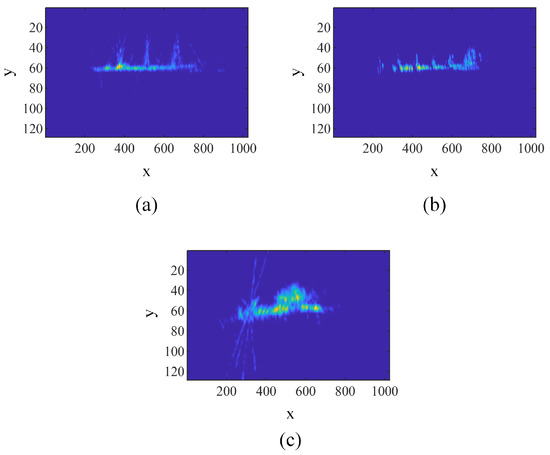
Figure 16.
The templates of measured data generated by TP-TATR. (a) The template of target 1. (b) The template of target 2. (c) The template of target 3.
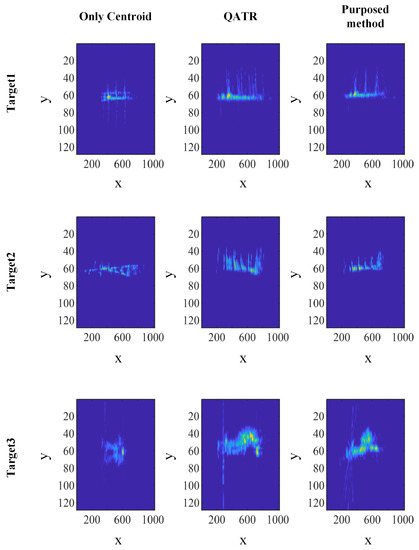
Figure 17.
The templates with measured data generated by the “only centroid” algorithm, QATR, and TP-TATR.
For target 1, our method accurately aligns the slightly thinner structures, such as masts. For target 2, our algorithm can avoid the interference of stripes and accurately aligns the hull to the horizontal position. For target 3, the stripes converge near the scattering point near the bow of the ship, which indicates that the proposed algorithm can successfully align the scattering points near the bow under the interference of stripes, verifying the effectiveness and robustness of the proposed algorithm.
Similarly, by matching all ISAR images with the templates, the ROC was drawn using the correlation of NProd, and the AUC was calculated. The results are presented in Figure 18.
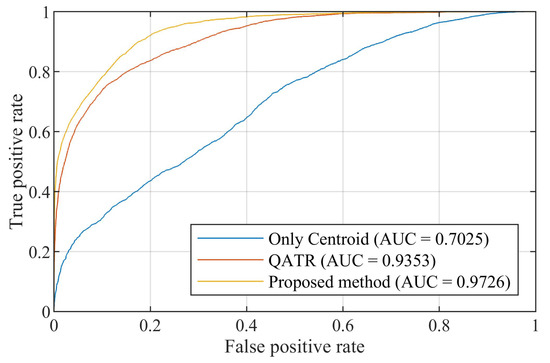
Figure 18.
The ROC of measured data.
Consistent with the results of simulated data, the “only centroid” method has the worst recognition capability, with its curve closest to the diagonal line and the lowest AUC at 0.7025. The QATR is in the middle, with both its curve and AUC at 0.9353. The best is our proposed method, with the curve closest to the top-left corner and the highest AUC at 0.9726.
The recognition results are shown in Table 2. Welch’s t-test was also used for hypothesis statistical testing. The results show that both the "only centroid” and the QATR algorithms have statistically significant differences with the algorithm proposed (with p < 0.001 and p = 0.005 < 0.05, respectively).

Table 2.
The accuracy of the three algorithms on the measured data.
As this paper calculated the correlation between the test data and the templates to recognize ISAR images, the accuracy reflects the similarity of images after reconstruction. If the test data are similar to the templates, this means that the reconstruction process effectively reduces the influence of attitude sensitivity. Therefore, the recognition accuracy reflects the robustness of the reconstruction algorithm. The “only centroid” method only translates the ISAR images to the center, and the different images are uncorrelated, as influenced by the rotation. Therefore, the accuracy is the lowest. As with the proposed method, QATR also affines the image. However, the matching pairs of feature points are not accurate, which is influenced by the noise, strips, and angle glint, leading to rotated reconstructions that differ from the templates. The correlation between rotated images is lower, resulting in lower accuracy. The proposed method has the best robustness among these methods, and can adjust the images with different attitudes, resulting in the highest accuracy. which further proves the effectiveness of the proposed algorithm. In the future, we will focus on the effect of TP-TATR on more types of ships and different noise levels.
5. Conclusions
This paper proposed the TP-TATR method to alleviate the target attitude sensitivity, ensuring the accuracy of the ISAR ship recognition. Three initial geometric feature points of the ship target were extracted in the preprocessing. Based on this, the TP method fit the ship ISAR image into a stable triangular structure. With the extracted triangle, the proposed TP-TATR method is allowed to robustly reconstruct the ISAR image into a standard attitude. The averaged standard-attitude ISAR images generate a recognition template via the TP-TATR method. Finally, the template matching recognition is achieved by calculating the correlation between the images and templates. The proposed method was evaluated using a simulation and measured data, and was compared with others using the ROC and AUC. The AUC of the proposed method is the highest, at 0.971 and 0.9726 for the simulated and measured data, respectively. The accuracies are also the highest, at 87.70% and 90.03% for the simulated and measured data, respectively, which exceed those of the other methods and are statistically significant. These results demonstrate that our method can stably reconstruct and recognize ISAR images with a small number of training data, proving the effectiveness and robustness of our proposed TP-TATR method.
Author Contributions
Conceptualization, X.J. and F.S.; methodology, X.J.; software, X.J.; validation, X.J.; investigation, X.J., H.L. and J.D.; resources, F.S.; data curation, X.J.; writing—original draft preparation, X.J., Z.X. and H.L.; writing—review and editing, X.J., Z.X. and H.L.; visualization, Z.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
The authors would like to thank the editors and anonymous reviewers for their competent comments and suggestions to improve this article. And special thanks are given to Sijia Fan for the help with the formula.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SAR | Synthetic Aperture Radar |
| ISAR | Inverse Synthetic Aperture Radar |
| TP-TATR | Triangle Preserving level-set assisted Triangle-points Affine Transform Reconstruction |
| TP | Triangle Preserving level-set |
| TATR | Triangle-points Affine Transform Reconstruction |
| RATR | Radar Automatic Target Recognition |
| NProd | Normalized Product |
| ROC | Receiver Operating Characteristic |
| LOS | Line of Sight |
| IPP | Image Projection Plane |
| CV model | Chan and Vese model |
| AUC | Area Under the Curve |
Appendix A
Suppose the triangular region is regarded as the intersection of three straight lines. In that case, there is another possibility for the , not the case shown in Figure 7, which can also achieve segmentation of the triangle.
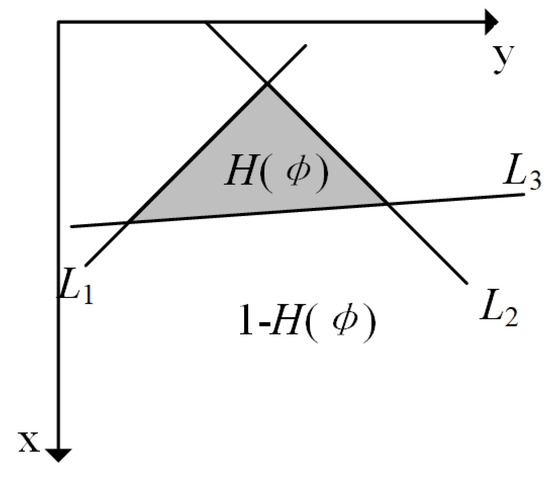
Figure A1.
Another form of level-set function with triangle preserving.
As shown in Figure A1, to make the conform to the triangle, we have:
Like before, we assume that one line evolves at the same time. Therefore, the parameter evolution equation of Equation (17) is slightly different, and becomes:
References
- Marghany, M. Nonlinear Ocean Dynamics: Synthetic Aperture Radar; Elsevier: Amsterdam, The Netherlands, 2021; pp. 1–2. [Google Scholar]
- Kudryavtsev, V.; Kozlov, I.; Chapron, B.; Johannessen, J. Quad-polarization SAR features of ocean currents. J. Geophys. Res. Ocean. 2014, 119, 6046–6065. [Google Scholar] [CrossRef]
- Wu, K.; Li, X.M.; Huang, B. Retrieval of ocean wave heights from spaceborne SAR in the Arctic Ocean with a neural network. J. Geophys. Res. Ocean. 2021, 126, e2020JC016946. [Google Scholar] [CrossRef]
- Marghany, M. Utilization of a genetic algorithm for the automatic detection of oil spill from RADARSAT-2 SAR satellite data. Mar. Pollut. Bull. 2014, 89, 20–29. [Google Scholar] [CrossRef] [PubMed]
- Kang, K.-M.; Kim, D.-J. Ship velocity estimation from ship wakes detected using convolutional neural networks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 4379–4388. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, Q.; Deng, B.; Qin, Y.; Wang, H. Estimation of Translational Motion Parameters in Terahertz Interferometric Inverse Synthetic Aperture Radar (InISAR) Imaging Based on a Strong Scattering Centers Fusion Technique. Remote Sens. 2019, 11, 1221. [Google Scholar] [CrossRef]
- Bai, X.; Zhou, X.; Zhang, F.; Wang, L.; Xue, R.; Zhou, F. Robust pol-ISAR target recognition based on ST-MC-DCNN. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9912–9927. [Google Scholar] [CrossRef]
- Zhao, W.; Heng, A.; Rosenberg, L.; Nguyen, S.T.; Hamey, L.; Orgun, M. ISAR Ship Classification Using Transfer Learning. In Proceedings of the 2022 IEEE Radar Conference (RadarConf22), New York City, NY, USA, 21–25 March 2022; pp. 1–6. [Google Scholar]
- Xue, B.; Tong, N. Real-world ISAR object recognition using deep multimodal relation learning. IEEE Trans. Cybern. 2019, 50, 4256–4267. [Google Scholar] [CrossRef] [PubMed]
- Xue, R.; Bai, X.; Zhou, F. SAISAR-Net: A robust sequential adjustment ISAR image classification network. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–15. [Google Scholar] [CrossRef]
- Lu, W.; Zhang, Y.; Yin, C.; Lin, C.; Xu, C.; Zhang, X. A deformation robust ISAR image satellite target recognition method based on PT-CCNN. IEEE Access 2021, 9, 23432–23453. [Google Scholar] [CrossRef]
- Ni, P.; Liu, Y.; Pei, H.; Du, H.; Li, H.; Xu, G. CLISAR-Net: A Deformation-Robust ISAR Image Classification Network Using Contrastive Learning. Remote Sens. 2022, 15, 33. [Google Scholar] [CrossRef]
- Karine, A.; Toumi, A.; Khenchaf, A.; El Hassouni, M. Target recognition in ISAR images based on relative phases of complex wavelet coefficients and sparse classification. In Proceedings of the 2018 4th International Conference on Advanced Technologies for Signal and Image Processing (ATSIP), Sousse, Tunisia, 21–24 March 2018; pp. 1–5. [Google Scholar]
- Kim, K.T.; Seo, D.K.; Kim, H.T. Efficient classification of ISAR images. IEEE Trans. Antennas Propag. 2005, 53, 1611–1621. [Google Scholar]
- Park, S.H.; Jung, J.H.; Kim, S.H.; Kim, K.T. Efficient classification of ISAR images using 2D Fourier transform and polar mapping. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 1726–1736. [Google Scholar] [CrossRef]
- Lee, S.J.; Park, S.H.; Kim, K.T. Improved classification performance using ISAR images and trace transform. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 950–965. [Google Scholar] [CrossRef]
- Saidi, M.N.; Daoudi, K.; Khenchaf, A.; Hoeltzener, B.; Aboutajdine, D. Automatic target recognition of aircraft models based on ISAR images. In Proceedings of the 2009 IEEE International Geoscience and Remote Sensing Symposium, Cape Town, South Africa, 12–17 July 2009; Volume 4, pp. IV–685–IV–688. [Google Scholar] [CrossRef]
- Yang, H.; Zhang, Y.; Ding, W. A fast recognition method for space targets in ISAR images based on local and global structural fusion features with lower dimensions. Int. J. Aerosp. Eng. 2020, 2020, 3412582. [Google Scholar] [CrossRef]
- Toumi, A.; Khenchaf, A. Target recognition using IFFT and MUSIC ISAR images. In Proceedings of the 2016 2nd International Conference on Advanced Technologies for Signal and Image Processing (ATSIP), Monastir, Tunisia, 21–23 March 2016; pp. 596–600. [Google Scholar]
- Bozkurt, H.; Erer, I. Information preserving preprocessing for improved radar target classification accuracy. In Proceedings of the 2017 8th International Conference on Recent Advances in Space Technologies (RAST), Istanbul, Turkey, 19–22 June 2017; pp. 161–165. [Google Scholar]
- Park, S.H.; Kim, H.T.; Kim, K.T. Cross-range scaling algorithm for ISAR images using 2-D Fourier transform and polar mapping. IEEE Trans. Geosci. Remote Sens. 2010, 49, 868–877. [Google Scholar] [CrossRef]
- Elyounsi, A.; Tlijani, H.; Bouhlel, M.S. Shape detection by mathematical morphology techniques for radar target classification. In Proceedings of the 2016 17th International Conference on Sciences and Techniques of Automatic Control and Computer Engineering (STA), Sousse, Tunisia, 19–21 December 2016; pp. 352–356. [Google Scholar]
- Cexus, J.C.; Toumi, A.; Riahi, M. Target recognition from ISAR image using polar mapping and shape matrix. In Proceedings of the 2020 5th International Conference on Advanced Technologies for Signal and Image Processing (ATSIP), Sousse, Tunisia, 2–5 September 2020; pp. 1–6. [Google Scholar]
- Sathyendra, H.M.; Stephan, B.D. Data fusion analysis for maritime automatic target recognition with designation confidence metrics. In Proceedings of the 2015 IEEE Radar Conference (RadarCon), Arlington, VA, USA, 10–15 May 2015; pp. 0062–0067. [Google Scholar]
- Kurowska, A.; Kulpa, J.S.; Giusti, E.; Conti, M. Classification results of ISAR sea targets based on their two features. In Proceedings of the 2017 Signal Processing Symposium (SPSympo), Jachranka, Poland, 12–14 September 2017; pp. 1–6. [Google Scholar]
- Jarabo-Amores, P.; Giusti, E.; Rosa-Zurera, M.; Bacci, A.; Capria, A.; Mata-Moya, D. Target classification using passive radar ISAR imagery. In Proceedings of the 2017 European Radar Conference (EURAD), Nuremberg, Germany, 11–13 October 2017; pp. 155–158. [Google Scholar]
- Manno-Kovacs, A.; Giusti, E.; Berizzi, F.; Kovács, L. Automatic target classification in passive ISAR range-crossrange images. In Proceedings of the 2018 IEEE Radar Conference (RadarConf18), Oklahoma City, OK, USA, 23–27 April 2018; pp. 0206–0211. [Google Scholar]
- Kawahara, T.; Toda, S.; Mikami, A.; Tanabe, M. Automatic ship recognition robust against aspect angle changes and occlusions. In Proceedings of the 2012 IEEE Radar Conference, Atlanta, GA, USA, 7–11 May 2012; pp. 0864–0869. [Google Scholar]
- Xie, S.D.; Pan, M.; Li, D. Robust method for ship recognition based on ISAR imaging using 3D model. J. Eng. 2019, 2019, 6777–6780. [Google Scholar] [CrossRef]
- Chan, T.F.; Vese, L.A. Active contours without edges. IEEE Trans. Image Process. 2001, 10, 266–277. [Google Scholar] [CrossRef] [PubMed]
- Feng, J.; Xiao, Y.; Wang, E. Rectangle object segmentation based on shape preserving and CV variational level set. In Proceedings of the International Symposium on Optoelectronic Technology and Application 2014: Image Processing and Pattern Recognition, Beijing, China, 13–15 May 2014; Volume 9301, pp. 754–759. [Google Scholar]
- Bailey, H.; Blackwell, F.; Lowery, C.; Ratkovic, J. Image Correlation: Part 1. Simulation and Analysis; Technical Report; Rand Corp.: Santa Monica, CA, USA, 1976. [Google Scholar]
- Wehner, D.R. High Resolution Radar; Artech House: Norwood, MA, USA, 1987; pp. 361–363. [Google Scholar]
- Jin, X.; Su, F. Aircraft Recognition Using ISAR Image Based on Quadrangle-points Affine Transform. In Proceedings of the 2022 15th International Congress on Image and Signal Processing, BioMedical Engineering and Informatics (CISP-BMEI), Beijing, China, 5–7 November 2022; pp. 1–6. [Google Scholar]
- Xu, D.; Bie, B.; Sun, G.C.; Xing, M.; Pascazio, V. ISAR Image Matching and Three-Dimensional Scattering Imaging Based on Extracted Dominant Scatterers. Remote Sens. 2020, 12, 2699. [Google Scholar] [CrossRef]
- Chan, T.; Zhu, W. Level set based shape prior segmentation. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; Volume 2, pp. 1164–1170. [Google Scholar]
- Davis, J.; Goadrich, M. The relationship between Precision-Recall and ROC curves. In Proceedings of the 23rd International Conference on Machine Learning, Pittsburgh, PA, USA, 25–29 June 2006; pp. 233–240. [Google Scholar]
- Welch, B.L. The generalization of ‘STUDENT’S’problem when several different population varlances are involved. Biometrika 1947, 34, 28–35. [Google Scholar] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).