H-RNet: Hybrid Relation Network for Few-Shot Learning-Based Hyperspectral Image Classification
Abstract
1. Introduction
- (1)
- An H-RNet method is proposed for improved HSI classification that only requires a few labeled samples. In hybrid 3-D/2-D CNNs, spectral–spatial features are first obtained by 3D convolution, followed by further spatial information by 2D convolution, resulting in more discriminative features. In the relation learning module, sample pairing is used to efficiently obtain the relation scores under a small number of labeled samples for classification.
- (2)
- By innovatively combining the 3-D/2-D CNNs in a hybrid module with an end-to-end relation learning module, the H-RNet can more effectively extract the spatial and spectral features for improved classification of HSIs.
- (3)
- Experiments on three benchmark HSI datasets have demonstrated the superior performance of our approach over a few existing models.
2. Related Work
2.1. HSI Classification Based on CNNs
2.2. HSI Classification Based on Few-Shot Learning
3. The Proposed Methodology
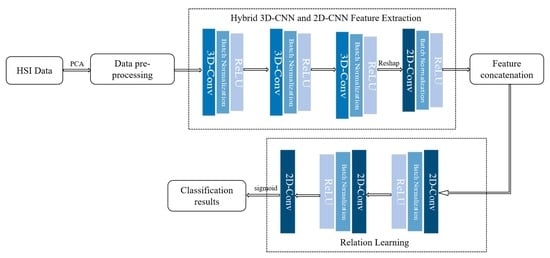
3.1. Overall Structure
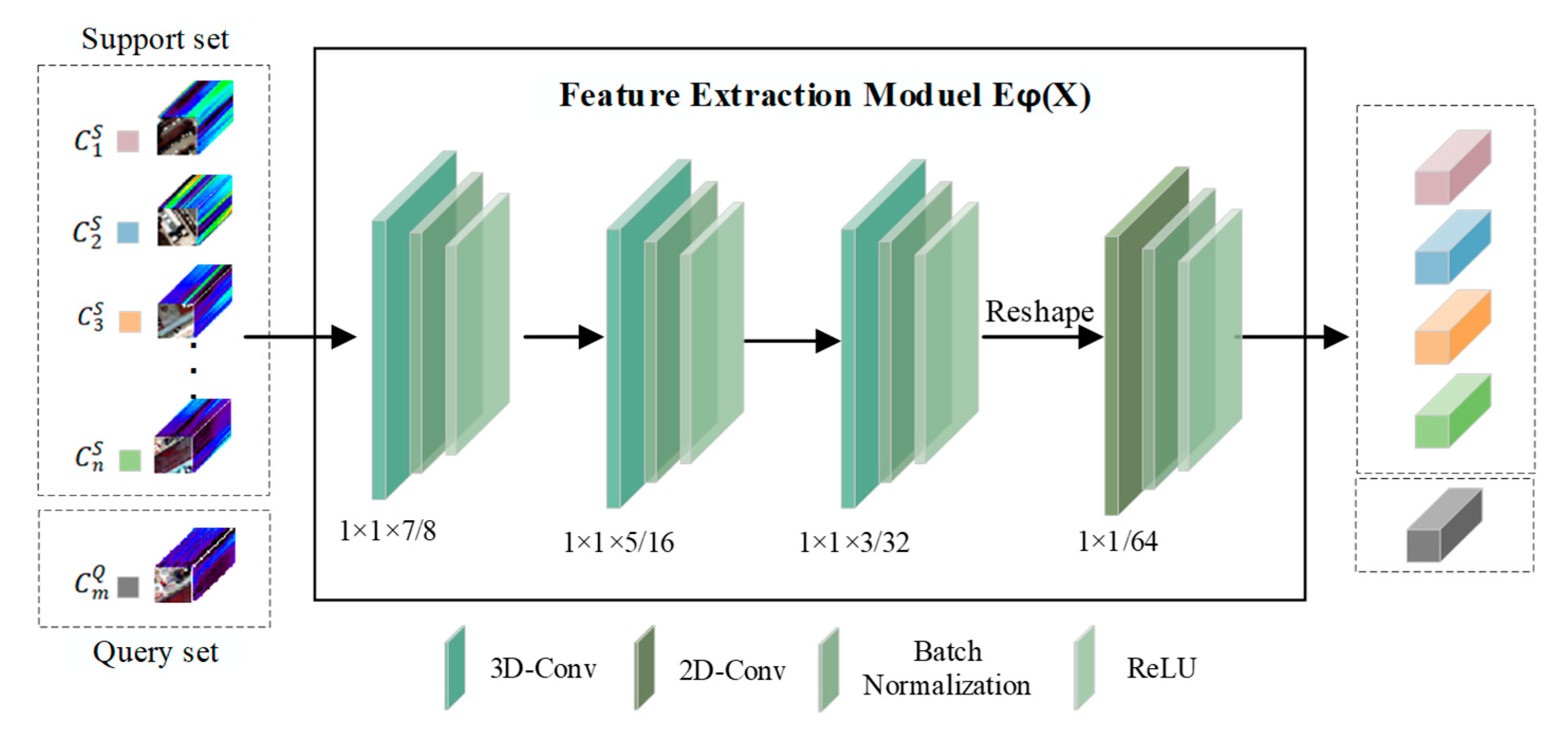
3.2. Hybrid 3D-CNN and 2D-CNN Feature Extraction Module
3.3. Relation Learning Module
| Algorithm 1 H-RNet model training process |
| Input: Support set and Query set for each iteration. Initializing feature extraction module and relation learning module . Output: Update the parameters of module . |
| 1. for (x′, y′) in Q do 2: for (x, y) in S do 3: The feature extraction module obtains the features and from x and x′; 4: Update the relation score by Equation (3); 5: pdate the loss by Equation (4); 6: end for 7: end for 8: Update the parameters of and by L back propagation. 9: Repeat iterations until the completion of the training process. |
4. Experiment and Discussion
4.1. Dataset Description
4.2. Experimental Settings
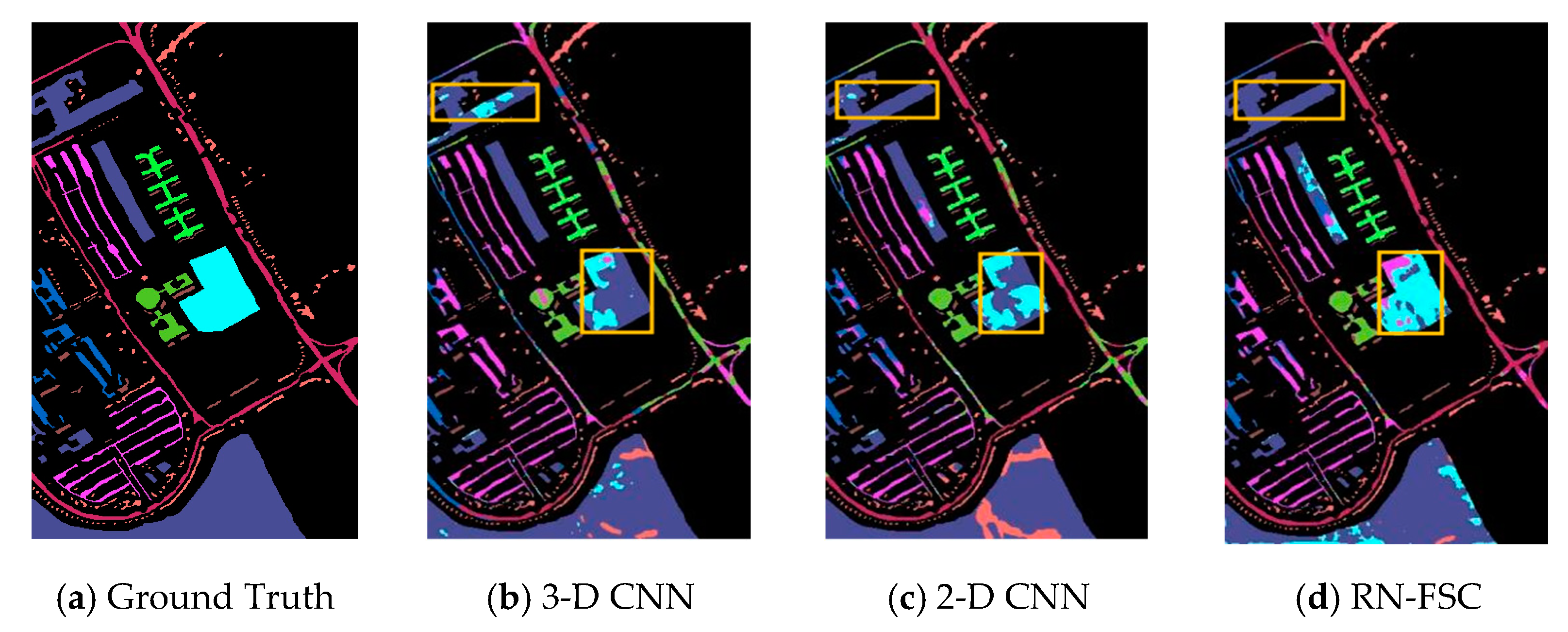
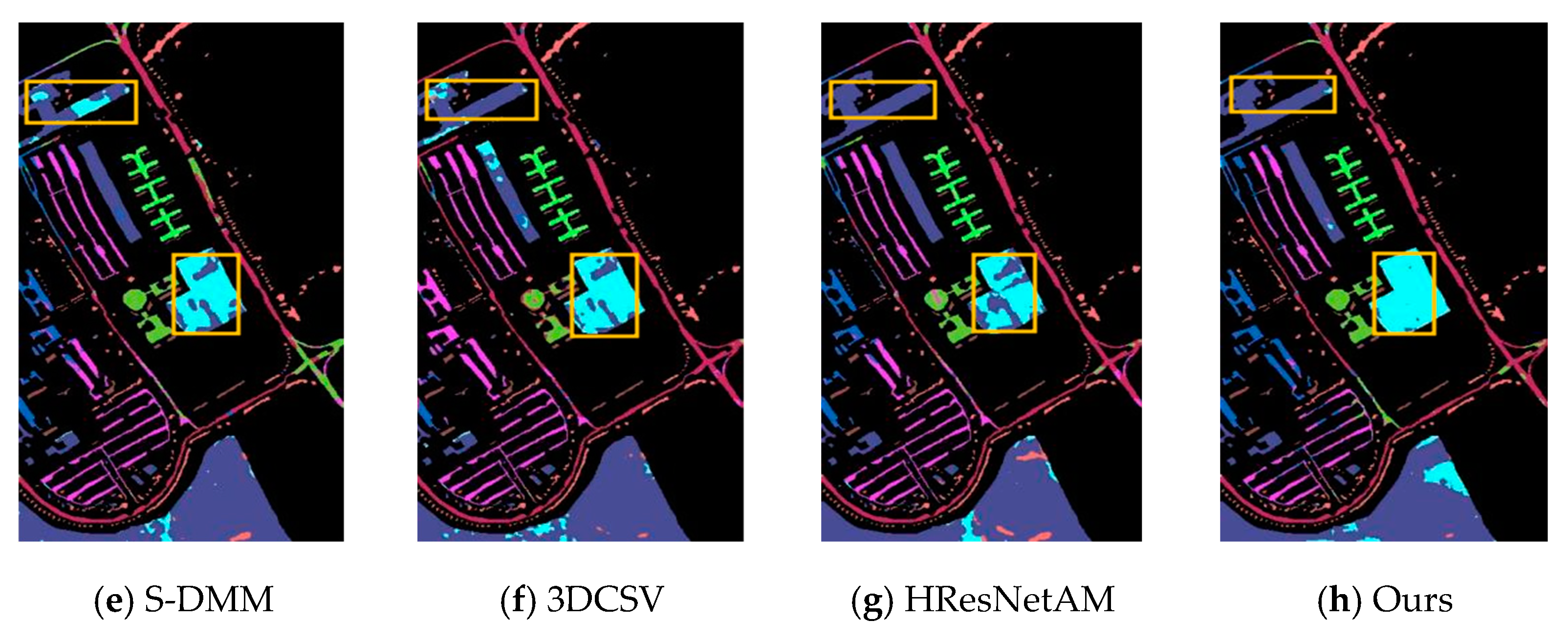
4.3. Classification Results
| Class | 2D-CNN | TWO-CNN | 3D-CNN | DFSL-NN | S-DMM | 3DCSN | RN-FSC | HResNetAM | H-RNet (Ours) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 98.80 | 88.22 | 96.99 | 98.54 | 99.45 | 100.0 | 96.35 | 99.67 | 99.89 |
| 2 | 98.77 | 78.09 | 99.25 | 98.12 | 99.21 | 98.97 | 100.0 | 99.60 | 99.76 |
| 3 | 95.48 | 74.80 | 92.60 | 96.08 | 96.70 | 99.49 | 100.0 | 96.76 | 99.99 |
| 4 | 98.36 | 98.19 | 97.21 | 99.56 | 99.56 | 100.0 | 86.88 | 95.37 | 99.37 |
| 5 | 92.55 | 96.54 | 92.99 | 97.01 | 97.12 | 91.07 | 99.88 | 99.79 | 98.42 |
| 6 | 99.96 | 96.89 | 98.54 | 99.54 | 89.64 | 98.55 | 100.0 | 99.93 | 99.88 |
| 7 | 99.61 | 92.52 | 97.65 | 99.33 | 99.82 | 99.49 | 100.0 | 98.92 | 99.92 |
| 8 | 77.51 | 54.32 | 70.21 | 78.62 | 70.53 | 70.74 | 89.44 | 86.71 | 81.48 |
| 9 | 97.19 | 81.22 | 95.00 | 97.23 | 99.02 | 99.90 | 99.93 | 98.84 | 99.97 |
| 10 | 89.23 | 75.18 | 84.54 | 92.38 | 91.13 | 96.51 | 99.19 | 93.41 | 95.12 |
| 11 | 95.45 | 92.26 | 92.83 | 99.10 | 97.56 | 100.0 | 97.34 | 94.21 | 99.61 |
| 12 | 99.96 | 86.40 | 98.09 | 99.34 | 99.87 | 89.77 | 90.61 | 99.26 | 99.75 |
| 13 | 99.22 | 98.18 | 95.62 | 97.84 | 99.25 | 99.01 | 84.09 | 99.45 | 99.67 |
| 14 | 96.80 | 96.10 | 93.50 | 96.17 | 96.30 | 98.11 | 88.57 | 95.20 | 99.03 |
| 15 | 72.03 | 55.60 | 65.37 | 72.69 | 72.28 | 94.11 | 70.06 | 71.20 | 85.61 |
| 16 | 94.07 | 92.39 | 93.61 | 98.59 | 95.29 | 93.87 | 89.98 | 99.94 | 98.14 |
| OA (%) | 91.31 ±0.53 | 77.54 ±2.15 | 85.93 ±1.48 | 89.86 ±0.84 | 89.69 ±2.98 | 91.59 ±1.39 | 91.45 ±1.72 | 91.56 ±0.84 | 93.67 ±0.72 |
| AA (%) | 94.06 ±0.39 | 84.94 ±1.72 | 90.56 ±1.02 | 95.01 ±0.63 | 93.92 ±0.92 | 95.60 ±0.85 | 93.27 ±1.04 | 95.54 ±0.66 | 97.23 ±0.26 |
| × 100 | 90.12 ±0.20 | 76.17 ±2.69 | 82.68 ±0.25 | 89.51 ±0.31 | 88.69 ±3.26 | 90.68 ±0.94 | 90.52 ±0.74 | 90.62 ±0.23 | 92.96 ±0.79 |
| F1-score | 0.951 ±0.064 | - | 0.901 ±0.062 | - | 0.937 ±0.034 | 0.946 ±0.017 | 0.910 ±0.040 | 0.954 ±0.021 | 0.963 ±0.057 |
| Class | TWO-CNN | 3D-CNN | DFSL-NN | S-DMM | 3DCSN | HResNetAM | H-RNet (Ours) |
|---|---|---|---|---|---|---|---|
| 1 | 98.72 | 98.97 | 97.28 | 99.95 | 96.42 | 99.98 | 99.87 |
| 2 | 95.82 | 97.88 | 95.46 | 94.56 | 92.64 | 98.51 | 92.19 |
| 3 | 80.29 | 84.58 | 85.46 | 88.31 | 84.57 | 81.02 | 95.71 |
| 4 | 61.95 | 62.59 | 84.69 | 92.67 | 99.47 | 73.85 | 96.32 |
| 5 | 95.67 | 94.86 | 94.10 | 95.22 | 98.53 | 96.26 | 93.39 |
| 6 | 90.58 | 92.47 | 93.46 | 92.03 | 91.14 | 89.72 | 99.02 |
| 7 | 93.20 | 91.38 | 96.61 | 97.50 | 97.84 | 98.54 | 90.73 |
| 8 | 98.27 | 95.45 | 99.98 | 99.84 | 99.56 | 99.89 | 99.37 |
| 9 | 97.75 | 86.97 | 96.07 | 98.16 | 84.08 | 96.42 | 99.81 |
| OA (%) | 95.47 ±1.06 | 95.07 ±0.38 | 97.79 ±0.51 | 96.98 ±1.21 | 96.54 ±1.78 | 97.74 ±0.63 | 98.23 ±0.45 |
| AA (%) | 90.25 ±1.79 | 89.32 ±2.24 | 93.68 ±0.87 | 95.36 ±0.94 | 93.81 ±1.28 | 92.69 ±0.47 | 96.28 ±1.36 |
| × 100 | 93.69 ±0.97 | 92.45 ±1.94 | 97.02 ±0.14 | 96.25 ±0.81 | 95.14 ±1.02 | 96.81 ±0.89 | 97.49 ±0.63 |
| F1-score | - | - | - | 0.900 ±0.018 | 0.926 ±0.054 | 0.904 ±0.053 | 0.944 ±0.049 |
4.4. Ablation Study
4.4.1. Impact of the Number of Principal Components
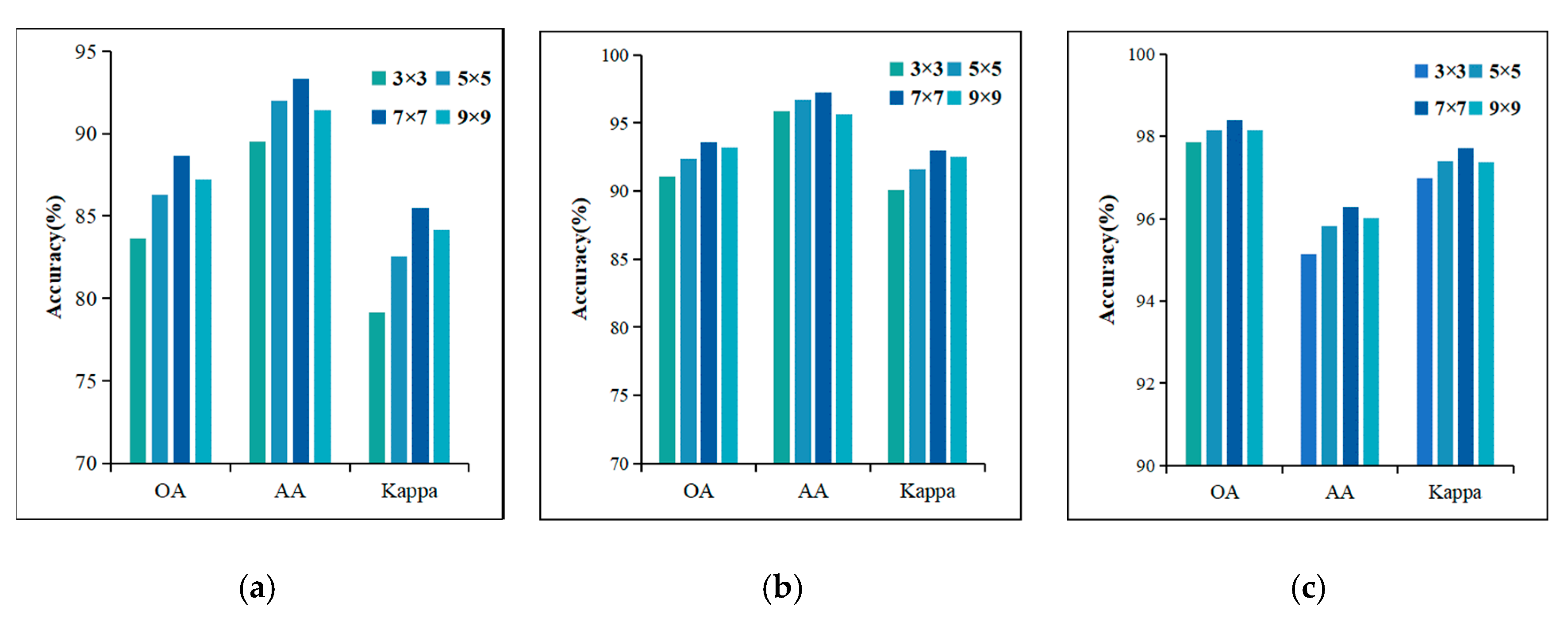
4.4.2. Impact of the Patch Size
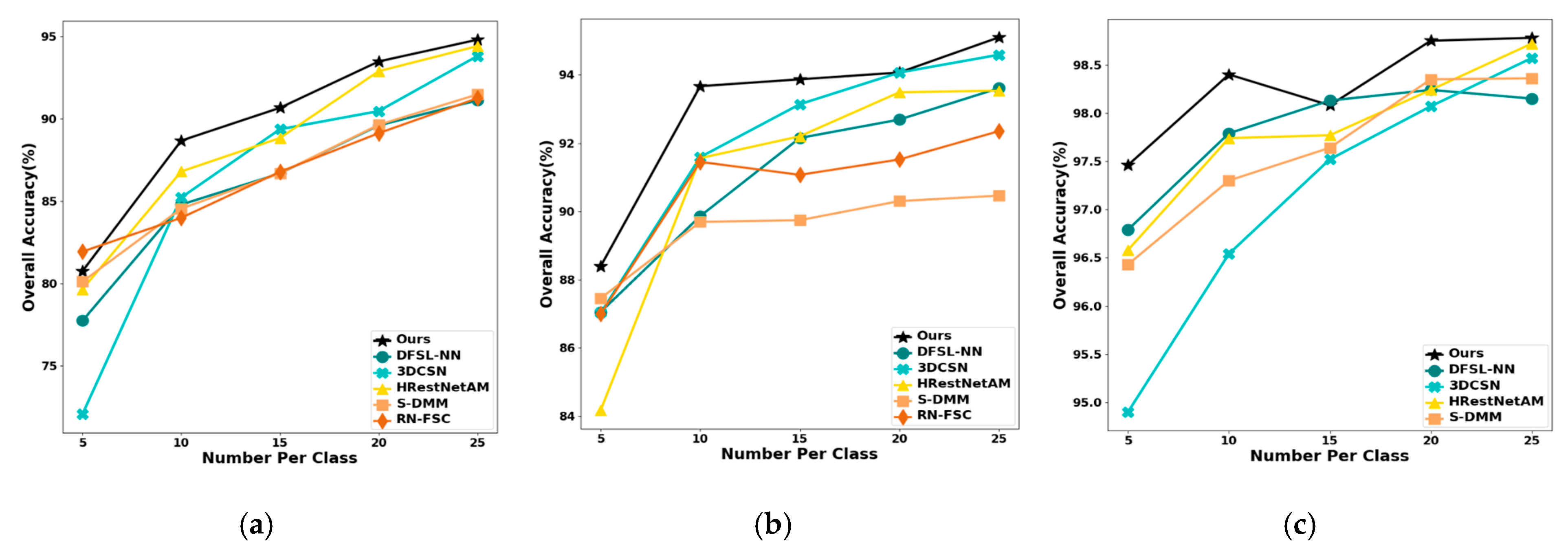
4.4.3. Impact of the Number of Labeled Samples per Class
4.5. Computational Complexity Analysis
| Model | FLOPs (M) | Params (M) |
|---|---|---|
| 2D-CNN | 1.77 | 35,536 |
| TWO-CNN | 239.02 | 1,574,506 |
| HResNetAM | 803.05 | 343,587 |
| DFSL-NN | 416.48 | 56,848 |
| 3DCSN | 1967.95 | 1,537,256 |
| S-DMM | 82.29 | 28,929 |
| RN-FSC | 816.44 | 402,465 |
| H-RNet (Ours) | 72.98 | 55,845 |
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kumar, B.; Dikshit, O.; Gupta, A.; Singh, M.K. Feature Extraction for Hyperspectral Image Classification: A Review. Int. J. Remote Sens. 2020, 41, 6248–6287. [Google Scholar] [CrossRef]
- Huang, K.; Deng, X.; Geng, J.; Jiang, W. Self-Attention and Mutual-Attention for Few-Shot Hyperspectral Image Classification. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 2230–2233. [Google Scholar] [CrossRef]
- Yalamarthi, S.; Joga, L.K.; Madem, S.R.; Vaddi, R. Deep Net based Framework for Hyperspectral Image Classification. In Proceedings of the 2022 7th International Conference on Communication and Electronics Systems (ICCES), Coimbatore, India, 22–24 June 2022; pp. 1475–1479. [Google Scholar] [CrossRef]
- Yuan, Y.; Wang, C.; Jiang, Z. Proxy-Based Deep Learning Framework for Spectral–Spatial Hyperspectral Image Classification: Efficient and Robust. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5501115. [Google Scholar] [CrossRef]
- Chen, R.; Huang, H.; Yu, Y.; Ren, J.; Wang, P.; Zhao, H.; Lu, X. Rapid Detection of Multi-QR Codes Based on Multistage Stepwise Discrimination and A Compressed MobileNet. IEEE Internet Things J. 2023; early access. [Google Scholar] [CrossRef]
- Zheng, X.; Chen, W.; Lu, X. Spectral Super-Resolution of Multispectral Images Using Spatial-Spectral Residual Attention Network. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5404114. [Google Scholar] [CrossRef]
- Li, Y.; Ren, J.; Yan, Y.; Petrovski, A. CBANet: An End-to-end Cross Band 2-D Attention Network for Hyperspectral Change Detection in Remote Sensing. IEEE Trans. Geosci. Remote Sens. 2023, in press. [Google Scholar]
- Zhao, J.; Hu, L.; Dong, Y. A combination method of stacked autoencoder and 3D deep residual network for hyperspectral image classification. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102459. [Google Scholar] [CrossRef]
- Zhao, C.; Li, C.; Feng, S.; Li, W. Spectral-Spatial Anomaly Detection via Collaborative Representation Constraint Stacked Autoencoders for Hyperspectral Images. IEEE Geosci. Remote Sens. Lett. 2022, 19, 5503105. [Google Scholar] [CrossRef]
- Zabalza, J.; Ren, J.; Zheng, J. Novel segmented stacked autoencoder for effective dimensionality reduction and feature extraction in hyperspectral imaging. Neurocomputing 2016, 185, 1–10. [Google Scholar] [CrossRef]
- Hang, R.; Liu, Q.; Hong, D.; Ghamisi, P. Cascaded Recurrent Neural Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5384–5394. [Google Scholar] [CrossRef]
- Li, H.C.; Li, S.S.; Hu, W.S.; Feng, J.H.; Sun, W.W.; Du, Q. Recurrent Feedback Convolutional Neural Network for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2022, 19, 5504405. [Google Scholar] [CrossRef]
- Mughees, A.; Tao, L. Multiple Deep-Belief-Network-Based Spectral-Spatial Classification of Hyperspectral Images. Tsinghua Sci. Technol. 2019, 24, 183–194. [Google Scholar] [CrossRef]
- Shi, C.; Liao, D.; Zhang, T.; Wang, L. Hyperspectral Image Classification Based on Expansion Convolution Network. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5528316. [Google Scholar] [CrossRef]
- Wang, X.; Tan, K.; Du, P.; Pan, C.; Ding, J. A Unified Multiscale Learning Framework for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4508319. [Google Scholar] [CrossRef]
- Li, C.; Fan, T.; Chen, Z.; Gao, H. Directionally separable dilated CNN with hierarchical attention feature fusion for hyperspectral image classification. Int. J. Remote Sens. 2022, 43, 812–840. [Google Scholar] [CrossRef]
- Imani, M.; Ghassemian, H. An overview on spectral and spatial information fusion for hyperspectral image classification: Current trends and challenges. Inf. Fusion 2020, 59, 59–83. [Google Scholar] [CrossRef]
- Yu, S.; Jia, S.; Xu, C. Convolutional neural networks for hyperspectral image classification. Neurocomputing 2017, 219, 88–98. [Google Scholar] [CrossRef]
- Li, X.; Ding, M.; Pižurica, A. Deep Feature Fusion via Two-Stream Convolutional Neural Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 58, 2615–2629. [Google Scholar] [CrossRef]
- Hamida, A.B.; Benoit, A.; Lambert, P.; Amar, C.B. 3-D Deep Learning Approach for Remote Sensing Image Classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4420–4434. [Google Scholar] [CrossRef]
- Wu, P.; Cui, Z.; Gan, Z.; Liu, F. Two-Stage Attention Network for hyperspectral image classification. Int. J. Remote Sens. 2021, 42, 9249–9284. [Google Scholar] [CrossRef]
- Sharifi, O.; Mokhtarzade, M.; Beirami, B.A. A Deep Convolutional Neural Network based on Local Binary Patterns of Gabor Features for Classification of Hyperspectral Images. In Proceedings of the 2020 International Conference on Machine Vision and Image Processing (MVIP), Qom, Iran, 18–20 February 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Li, W.; Chen, C.; Zhang, M.; Li, H.; Du, Q. Data Augmentation for Hyperspectral Image Classification with Deep CNN. IEEE Geosci. Remote Sens. Lett. 2019, 16, 593–597. [Google Scholar] [CrossRef]
- Liu, Q.; Peng, J.; Zhang, G.; Sun, W.; Du, Q. Deep Contrastive Learning Network for Small-Sample Hyperspectral Image Classification. J. Remote Sens. 2023, 3, 25. [Google Scholar] [CrossRef]
- Liu, B.; Yu, X.; Zhang, P.; Yu, A.; Fu, Q.; Wei, X. Supervised Deep Feature Extraction for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1909–1921. [Google Scholar] [CrossRef]
- Li, W.; Wu, G.; Zhang, F.; Du, Q. Hyperspectral Image Classification Using Deep Pixel-Pair Features. IEEE Trans. Geosci. Remote Sens. 2017, 55, 844–853. [Google Scholar] [CrossRef]
- Ma, X.; Ji, S.; Wang, J.; Geng, J.; Wang, H. Hyperspectral Image Classification Based on Two-Phase Relation Learning Network. IEEE Trans. Geosci. Remote Sens. 2019, 57, 10398–10409. [Google Scholar] [CrossRef]
- Yang, L.; Hamouda, M.; Ettabaa, K.S.; Bouhlel, M.S. Smart Feature Extraction and Classification of Hyperspectral Images based on Convolutional Neural Networks. IET Image Process. 2020, 14, 1999–2005. [Google Scholar] [CrossRef]
- Yang, Y.; Yang, J.; Zhao, N.; Wu, L.; Wang, L.; Wang, T. FusionNet: A Convolution-Transformer Fusion Network for Hyperspectral Image Classification. Remote Sens. 2022, 14, 4066. [Google Scholar] [CrossRef]
- Hu, W.; Huang, Y.; Wei, L.; Zhang, F.; Li, H. Deep Convolutional Neural Networks for Hyperspectral Image Classification. J. Sens. 2015, 2015, 258619. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Y.; Zhang, Y.; Shen, Q. Spectral-spatial classification of hyperspectral imagery using a dual-channel convolutional neural network. Remote Sens. 2017, 8, 438–447. [Google Scholar] [CrossRef]
- Meng, Z.; Jiao, L.; Liang, M.; Zhao, F. Hyperspectral Image Classification with Mixed Link Networks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 2494–2507. [Google Scholar] [CrossRef]
- Zheng, X.; Sun, H.; Lu, X.; Xie, W. Rotation-Invariant Attention Network for Hyperspectral Image Classification. IEEE Trans. Image Process. 2022, 31, 4251–4265. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep Feature Extraction and Classification of Hyperspectral Images Based on Convolutional Neural Networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef]
- Qing, Y.; Huang, Q.; Feng, L.; Qi, Y.; Liu, W. Multiscale Feature Fusion Network Incorporating 3D Self-Attention for Hyperspectral Image Classification. Remote Sens. 2022, 14, 742. [Google Scholar] [CrossRef]
- Zhong, Z.; Li, J.; Luo, Z.; Chapman, M. Spectral–Spatial Residual Network for Hyperspectral Image Classification: A 3-D Deep Learning Framework. IEEE Trans. Geosci. Remote Sens. 2018, 56, 847–858. [Google Scholar] [CrossRef]
- Xue, Z.; Yu, X.; Liu, B.; Tan, X.; Wei, X. HResNetAM: Hierarchical Residual Network with Attention Mechanism for Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 3566–3580. [Google Scholar] [CrossRef]
- Ghaderizadeh, S.; Abbasi-Moghadam, D.; Sharifi, A.; Tariq, A.; Qin, S. Multiscale Dual-Branch Residual Spectral–Spatial Network with Attention for Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 5455–5467. [Google Scholar] [CrossRef]
- Ren, M.; Triantafillou, E.; Ravi, S.; Snell, J.; Swersky, K.; Tenenbaum, J.; Larochelle, H.; Zemel, R. Meta-Learning for Semi-Supervised Few-Shot Classification. arXiv 2018, arXiv:1803.00676. [Google Scholar]
- Liu, B.; Gao, K.; Yu, A.; Ding, L.; Qiu, C.; Li, J. ES2FL: Ensemble Self-Supervised Feature Learning for Small Sample Classification of Hyperspectral Images. Remote Sens. 2022, 14, 4236. [Google Scholar] [CrossRef]
- Xi, B.; Li, J.; Li, Y.; Song, R.; Hong, D.; Chanussot, J. Few-Shot Learning with Class-Covariance Metric for Hyperspectral Image Classification. IEEE Trans. Image Process. 2022, 31, 5079–5092. [Google Scholar] [CrossRef]
- Zhang, C.; Yue, J.; Qin, Q. Global Prototypical Network for Few-Shot Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 4748–4759. [Google Scholar] [CrossRef]
- Liu, B.; Yu, X.; Yu, A.; Zhang, P.; Wan, G.; Wang, R. Deep Few-Shot Learning for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 2290–2304. [Google Scholar] [CrossRef]
- Cao, Z.; Li, X.; Jiang, J. 3D convolutional siamese network for few-shot hyperspectral classification. J. Appl. Remote Sens. 2020, 14, 048504. [Google Scholar] [CrossRef]
- Alkhatib, M.Q.; Al-Saad, M.; Aburaed, N.; Almansoori, S.; Zabalza, J.; Marshall, S.; Al-Ahmad, H. Tri-CNN: A three branch model for hyperspectral image classification. Remote Sens. 2023, 15, 316. [Google Scholar] [CrossRef]
- Deng, B.; Jia, S.; Shi, D. Deep Metric Learning-Based Feature Embedding for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2020, 58, 1422–1435. [Google Scholar] [CrossRef]
- Rao, M.; Tang, P.; Zhang, Z. Spatial–Spectral Relation Network for Hyperspectral Image Classification with Limited Training Samples. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 5086–5100. [Google Scholar] [CrossRef]
- Gao, K.; Liu, B.; Yu, X.; Qin, J.; Zhang, P.; Tan, X. Deep Relation Network for Hyperspectral Image Few-Shot Classification. Remote Sens. 2020, 12, 923. [Google Scholar] [CrossRef]
- Jia, S.; Jiang, S.; Lin, Z.; Li, N.; Xu, M.; Yu, S. A Survey: Deep Learning for Hyperspectral Image Classification with Few Labeled Samples. Neurocomputing 2021, 448, 179–204. [Google Scholar] [CrossRef]
- Yang, J.; Zhao, Y.Q.; Chan, J.C.W. Learning and Transferring Deep Joint Spectral–Spatial Features for Hyperspectral Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4729–4742. [Google Scholar] [CrossRef]
- Liu, X.; Sun, Q.; Meng, Y.; Fu, M.; Bourennane, S. Hyperspectral Image Classification Based on Parameter-Optimized 3D-CNNs Combined with Transfer Learning and Virtual Samples. Remote Sens. 2018, 10, 1425. [Google Scholar] [CrossRef]
- Li, W.; Liu, Q.; Wang, Y.; Li, H. Transfer Learning with Limited Samples for the same Source Hyperspectral Remote Sensing Images Classification. The International Archives of Photogrammetry. Remote Sens. Spat. Inf. Sci. 2022, 43, 405–410. [Google Scholar]
- Zhang, X.; Sun, G.; Jia, X.; Wu, L.; Zhang, A.; Ren, J.; Fu, H.; Yao, Y. Spectral-Spatial Self-Attention Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5512115. [Google Scholar] [CrossRef]
- Fang., B.; Liu, Y.; Zhang, H.; He, J. Hyperspectral Image Classification Based on 3D Asymmetric Inception Network with Data Fusion Transfer Learning. Remote Sens. 2022, 14, 1711. [Google Scholar] [CrossRef]
- Roy, S.K.; Krishna, G.; Dubey, S.R.; Chaudhuri, B.B. HybridSN: Exploring 3-D–2-D CNN Feature Hierarchy for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2020, 17, 277–281. [Google Scholar] [CrossRef]
- Yu, Z.; Ying, C.; Chao, S.; Shan, G.; Chao, W. Pyramidal and conditional convolution attention network for hyperspectral image classification using limited training samples. Int. J. Remote Sens. 2022, 43, 2885–2914. [Google Scholar] [CrossRef]
- Ma, P.; Ren, J.; Sun, G.; Zhao, H.; Jia, X.; Yan, Y.; Zabalza, J. Multiscale superpixelwise prophet model for noise-robust feature extraction in hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5508912. [Google Scholar] [CrossRef]







| Layer Name | Filter Size | Output Size | BN + Relu | Parameters (M) |
|---|---|---|---|---|
| Feature Extraction Module | ||||
| Input_1 | N/A | (1, 30, 7, 7) | N | 0 |
| Conv3D_1 | (8, 7, 1, 1) | (8, 24, 7, 7) | Y | 80 |
| Conv3D_2 | (16, 5, 1, 1) | (16, 20, 7, 7) | Y | 688 |
| Conv3D_3 | (32, 3, 1, 1) | (32, 18, 7, 7) | Y | 1632 |
| Reshape | N/A | (576, 7, 7) | N | 0 |
| Conv2D_1 | (64, 1, 1) | (64, 7, 7) | Y | 37,636 |
| Total trainable params: 40,036 | ||||
| Relation Learning Module | ||||
| Input_1 | (128, 7, 7) | (128, 7, 7) | N | 0 |
| Conv2D_1 | (64, 1, 1) | (64, 7, 7) | Y | 8384 |
| Conv2D_2 | (64, 1, 1) | (64, 7, 7) | Y | 4288 |
| Conv2D_3 | (1, 7, 7) | (1, 1, 1) | N | 3137 |
| Total trainable params: 15,809 | ||||
| Class | 2D-CNN | TWO-CNN | 3D-CNN | DFSL-NN | S-DMM | 3DCSN | RN-FSC | HResNetAM | H-RNet (Ours) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 83.13 | 71.80 | 67.68 | 84.15 | 94.34 | 66.57 | 87.14 | 98.37 | 94.07 |
| 2 | 73.84 | 88.27 | 77.93 | 80.13 | 73.13 | 87.49 | 90.90 | 96.29 | 82.69 |
| 3 | 77.32 | 47.58 | 73.25 | 76.71 | 86.85 | 86.60 | 66.84 | 70.64 | 90.31 |
| 4 | 90.45 | 96.29 | 84.23 | 89.60 | 95.04 | 98.95 | 85.02 | 98.74 | 96.42 |
| 5 | 99.28 | 94.99 | 98.79 | 90.11 | 99.98 | 100.0 | 100.0 | 99.81 | 100.0 |
| 6 | 76.25 | 49.75 | 46.16 | 85.43 | 85.58 | 99.48 | 58.04 | 60.08 | 94.30 |
| 7 | 91.92 | 58.65 | 89.66 | 89.42 | 98.55 | 99.84 | 83.23 | 75.17 | 98.48 |
| 8 | 88.01 | 66.95 | 84.88 | 86.17 | 86.47 | 69.06 | 89.81 | 77.36 | 83.74 |
| 9 | 99.65 | 97.15 | 98.68 | 93.24 | 99.81 | 81.00 | 89.81 | 98.33 | 99.89 |
| OA (%) | 80.06 ±4.25 | 78.61 ±1.23 | 74.89 ±2.78 | 83.35 ±2.92 | 84.55 ±3.26 | 85.22 ±3.54 | 83.99 ±2.18 | 86.80 ±2.09 | 88.97 ±3.23 |
| AA (%) | 86.65 ±2.35 | 74.60 ±3.41 | 80.14 ±2.23 | 86.10 ±2.82 | 91.08 ±2.64 | 87.66 ±3.27 | 82.51 ±0.84 | 86.08 ±3.05 | 93.32 ±1.29 |
| × 100 | 75.31 ±0.50 | 74.41 ±2.17 | 67.00 ±0.30 | 80.07 ±3.34 | 83.89 ±2.86 | 82.45 ±2.98 | 79.00 ±2.79 | 82.95 ±1.51 | 85.51 ±3.98 |
| F1-score | 0.862 ±0.014 | - | 0.830 ±0.016 | - | 0.877 ±0.022 | 0.842 ±0.004 | 0.795 0.041 | 0.893 ±0.015 | 0.902 ±0.007 |
| Dataset | Accuracy Metric | 20 | 30 | 40 | 50 |
|---|---|---|---|---|---|
| PU | OA (%) | 86.49 | 86.78 | 84.46 | 82.41 |
| κ × 100 | 83.99 | 84.25 | 80.45 | 77.85 | |
| AA (%) | 92.36 | 92.40 | 90.29 | 88.44 | |
| SA | OA (%) | 91.48 | 91.68 | 86.98 | 85.79 |
| κ × 100 | 90.53 | 90.67 | 85.59 | 84.24 | |
| AA (%) | 96.16 | 96.15 | 92.22 | 92.62 | |
| PA | OA (%) | 98.12 | 98.22 | 98.15 | 98.29 |
| κ × 100 | 97.15 | 97.49 | 97.39 | 97.58 | |
| AA (%) | 95.97 | 95.99 | 96.14 | 96.28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Dong, Z.; Li, H.; Ren, J.; Zhao, H.; Li, H.; Chen, W.; Xiao, Z. H-RNet: Hybrid Relation Network for Few-Shot Learning-Based Hyperspectral Image Classification. Remote Sens. 2023, 15, 2497. https://doi.org/10.3390/rs15102497
Liu X, Dong Z, Li H, Ren J, Zhao H, Li H, Chen W, Xiao Z. H-RNet: Hybrid Relation Network for Few-Shot Learning-Based Hyperspectral Image Classification. Remote Sensing. 2023; 15(10):2497. https://doi.org/10.3390/rs15102497
Chicago/Turabian StyleLiu, Xiaoyong, Ziyang Dong, Huihui Li, Jinchang Ren, Huimin Zhao, Hao Li, Weiqi Chen, and Zhanhao Xiao. 2023. "H-RNet: Hybrid Relation Network for Few-Shot Learning-Based Hyperspectral Image Classification" Remote Sensing 15, no. 10: 2497. https://doi.org/10.3390/rs15102497
APA StyleLiu, X., Dong, Z., Li, H., Ren, J., Zhao, H., Li, H., Chen, W., & Xiao, Z. (2023). H-RNet: Hybrid Relation Network for Few-Shot Learning-Based Hyperspectral Image Classification. Remote Sensing, 15(10), 2497. https://doi.org/10.3390/rs15102497