Estimation of Ground Subsidence Deformation Induced by Underground Coal Mining with GNSS-IR

Abstract

In this paper, GNSS interferometric reflectometry (GNSS-IR) is firstly proposed to estimate ground surface subsidence caused by underground coal mining. Ground subsidence on the main direction of a coal seam is described by using the probability integral model (PIM) with unknown parameters. Based on the laws of reflection in geometric optics, model of GNSS signal-to-noise (SNR) observation for the tilt surface, which results from differential subsidence of ground points, is derived. Semi-cycle SNR observations fitting method is used to determine the phase of the SNR series. Phase variation of the SNR series is used to calculate reflector height of ground specular reflection point. Based on the reflector height and ground tilt angle, an iterative algorithm is proposed to determine coefficients of PIM, and thus subsidence of the ground reflection point. By using the low-cost navigational GNSS receiver and antenna, an experimental campaign was conducted to validate the proposed method. The results show that, when the maximum subsidence is 3076 mm, the maximum relative error of the proposed method-based subsidence estimation is 5.5%. This study also suggests that, based on the proposed method, the navigational GNSS instrument can be treated as a new type of sensor for continuously measuring ground subsidence deformation in a cost-effective way.

1. Introduction

Coal is one of the most important sources of electricity worldwide, currently providing more than 36% of global electricity. Coal-fueled power plants account for nearly one-quarter of the electricity in the United States, and account for a larger proportion in the developing countries like China and India [1]. A larger amount of coal comes from underground mining in areas where surface mining is impractical or uneconomical [2]. Underground coal mining could induce ground subsidence affecting water supplies, transportation, vegetation and farming. Continuously monitoring underground coal mining induced ground subsidence is crucial for assessment of environmental impacts of coal mining and prevention of the possible damage arose from them [3]. However, traditional subsidence measuring methods such as levelling or GNSS can only provide subsidence observations in few ground points with heavy cost; although the techniques can be used to measure the ground subsidence with millimeter to centimeter precision [4].

In addition to the fundamental applications of positioning, navigation and timing service, GNSS signals have also been widely used for remotely sensing a series of environmental parameters, resulting in two GNSS based remote sensing techniques: GNSS reflectometry (GNSS-R) and GNSS interferometric reflectometry (GNSS-IR). By making use of the interfered signal collected by ground-based GNSS receiver and antenna, GNSS-IR can be used to estimate snow depth, water level, vegetation height, or topographic profile [5,6,7,8,9,10]. Due to the obvious environmental degradation of the coal mining area especially in China over recent years, there has been increasingly more attention on the evaluation and mitigation of the environmental impacts induced by the ground subsidence due to underground coal mining. Meanwhile, a cost-effective way of monitoring ground subsidence with high temporal and spatial resolution is crucial for the evaluation and mitigation. Hence, the purposes of this study are as follows:

(a)

Exploration of a new low-cost subsidence monitoring technique based on GNSS-IR;

(b)

Establishment of the mathematic model and estimating algorithm for the GNSS-IR based subsidence retrieval; and

(c)

Validation and analyzation of the initial results derived from the GNSS-IR ground subsidence monitoring technique.

The remainder of this paper is organized as follows. In Section 2, materials related to the research are provided. Section 3 presents the details of the proposed method. An experimental campaign conducted in Jining mining area, Shandong Province, China, and the experimental results of GPS L1 band signal are provided in Section 4. The results are discussed in Section 5. Section 6 concludes this paper.

2. Materials

2.1. Application of GNSS Analysis in Crust Monitoring

The Earth’s thin and deformable crustal layer is affected by endogenous and exogenous agents, which are dominated by gravitation. Crust deformation involves phenomena characterized by a large wavelength, the crustal movements, and local displacements characterized by a small wavelength [11]. In general, studies of long wavelength phenomena such as plate motion and seismic occurrences require that the geodetic observations are not affected by the local displacements. On the other hand, for the engineering applications such as landslide and underground coal mining-induced ground subsidence, monitoring of the local deformations is required. During the last 30 years, GNSS analyses have been used in both the cases, which improve the understanding of geodynamical processes of those deformations significantly.

GNSS is a powerful technique for geodetic observations with precision of about 1 and 3 mm in horizontal and vertical component, respectively, as reported in [12,13]. Relative precision of GNSS geodetic observations can reach 10⁻⁷ to 10⁻⁸ for baselines of tens to hundreds of kilometers and can reach 10⁻⁹ for the baselines of thousands of kilometers [14]. Due to a larger number of GNSS Continuously Operating Reference Stations (CORS) established over the world, the vertical and horizontal displacements on different directions with different spatial scales can be measured simultaneously; thereby, the information related to spatial developments of crustal deformations can be obtained based on analyzation of the GNSS monitoring results, for example, velocity and deformation fields [15,16].

For the local phenomenon monitoring, utilization of GNSS is to detect and estimate movements and deformations of an entity such as the ground surface within a small scale. The local monitoring site is equipped with GNSS instruments and a control system saving raw data; and the systems can also estimate the solution in near-real time or post processing mode. As an alternative solution to the CORS, the site can be monitored by GNSS survey campaigns repeated at fixed intervals; this solution is the most frequently chosen in the case of small areas, such as landslide monitoring [17].

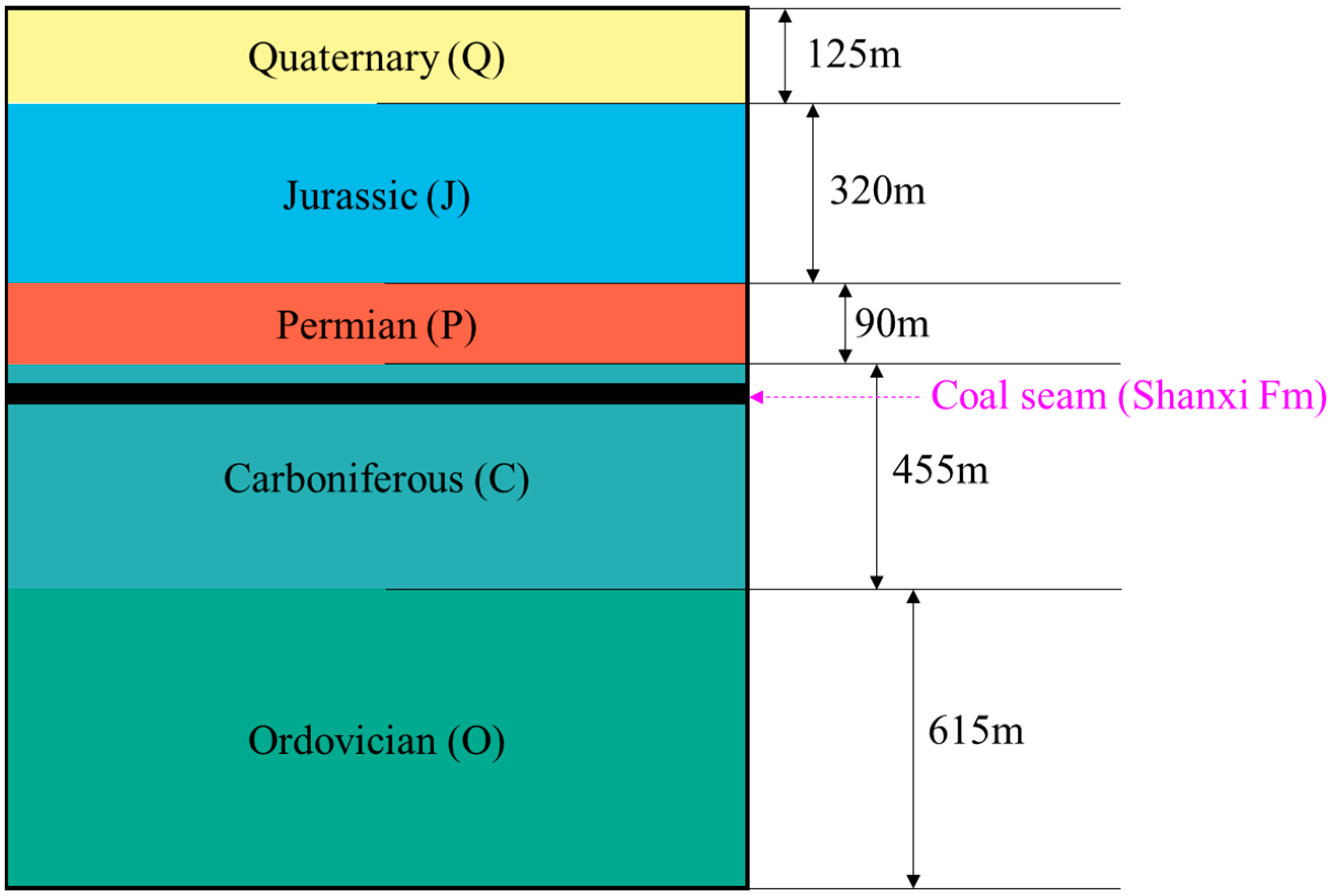
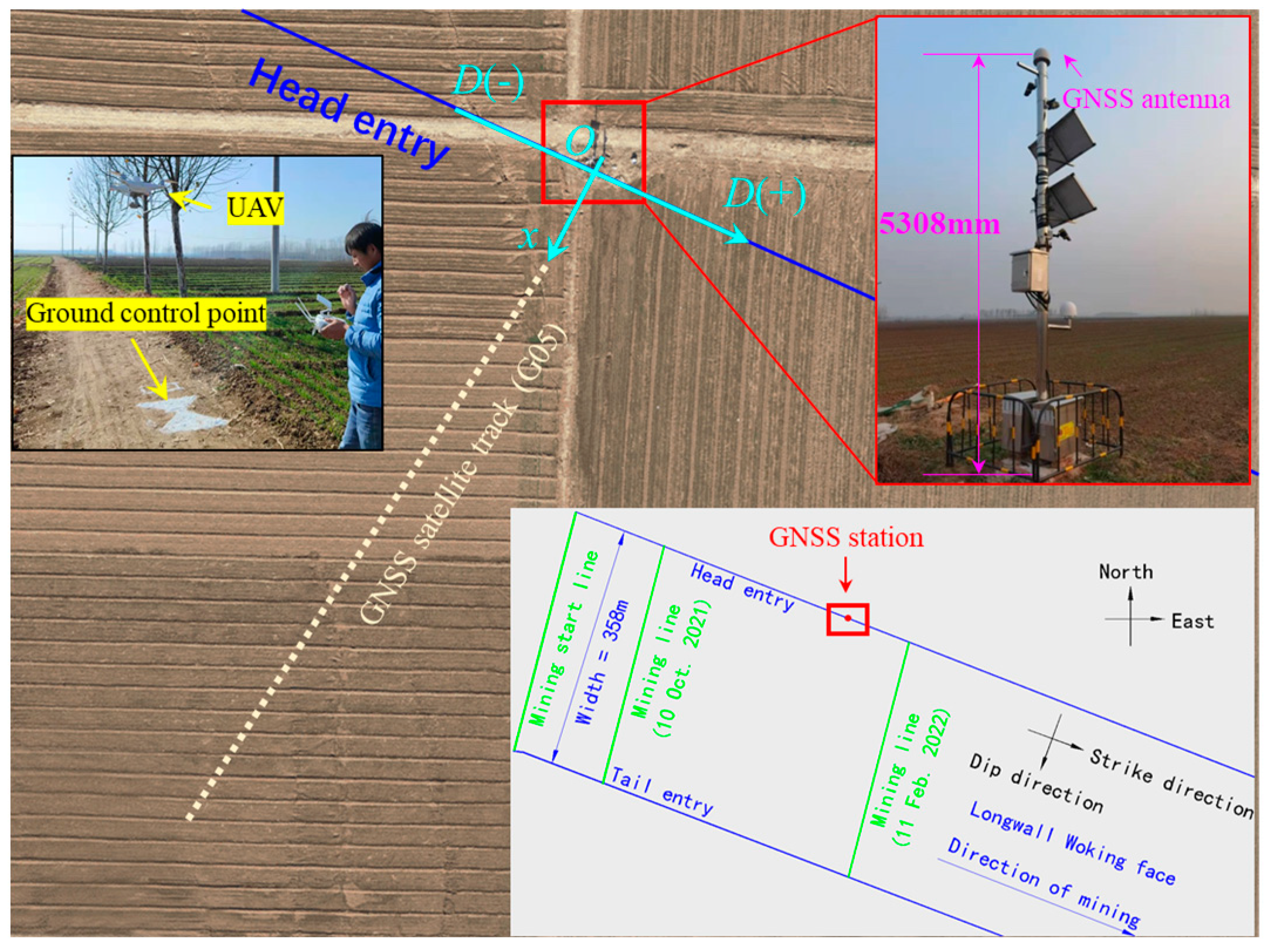
2.2. Geological Regime

The study area is located in Jining mining area, Shandong Province, China. The area belongs to Quaternary alluvial plain; land form within the area is relative flat and the ground elevation ranges from +~42 to +~52 m. The stratums of the study area exposed by the bore holes include Quaternary, Jurassic, Permian, Carboniferous, and Ordovician. Distributions of those stratums are shown in Figure 1. Thickness of the stratums is about 125, 320, 90, 455, and 615 m, respectively. Coal seam of the area mainly exists in the top of stratum of Carboniferous; and the coal seam located sub-stratum is also named as Shanxi Formation (Fm) in China. The average of the coal seam thickness in the mining area is 9.0 m. The coal-bearing coefficient in the sub-stratum is 9.52%. The degree of geological structure complexity in the area is classified as moderate complexity; geological structure is mainly composed of the wide and gradual fold associating with a certain amount of fault. There has no evidence indicating intrusion of the igneous rock into the coal-existing stratum so far.

3. Methods

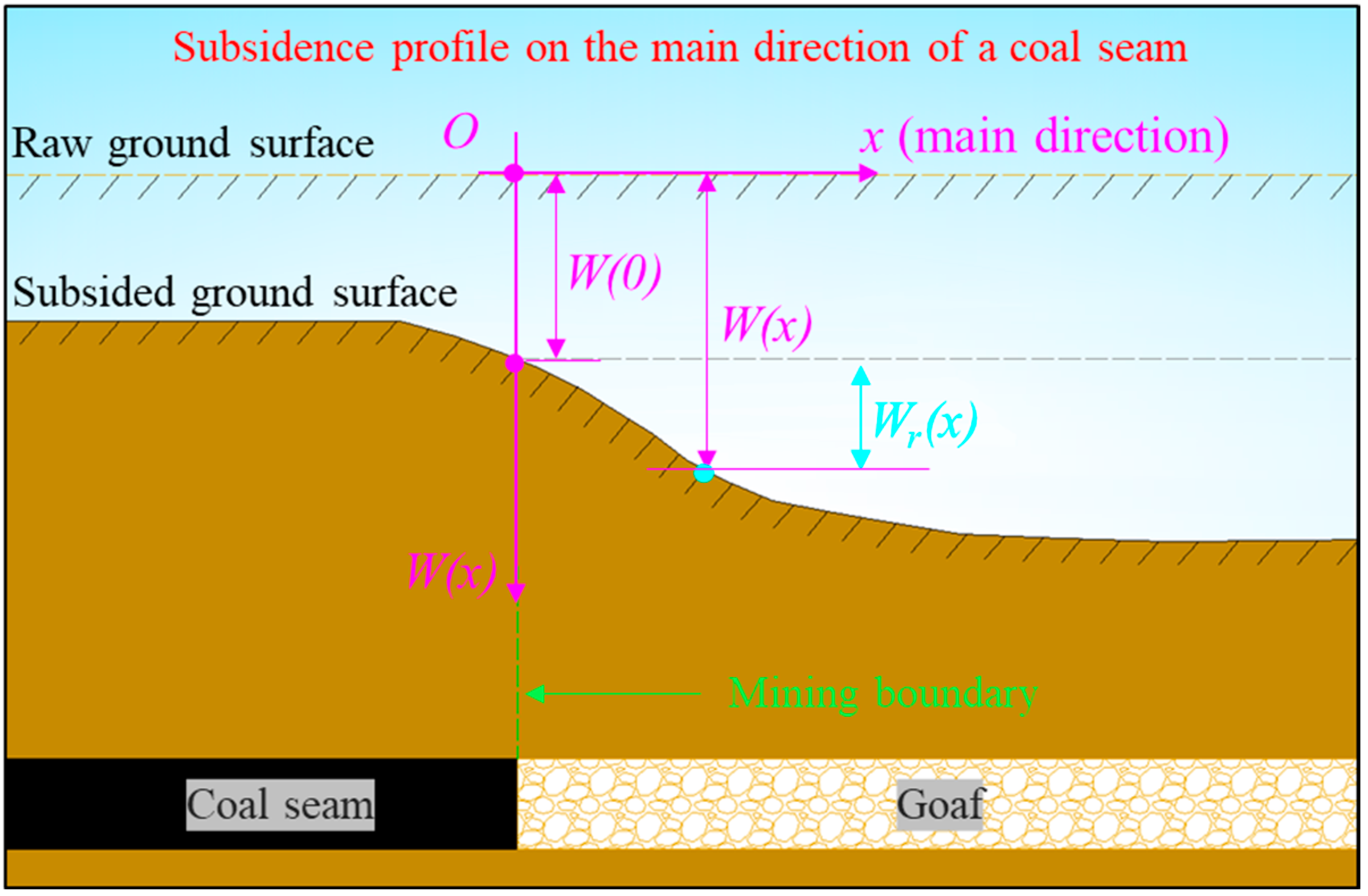
3.1. Mathematical Model of Ground Sudidence on the Main Direction of a Coal Seam

Before underground coal mining, the rock and soil above a coal seam are supported by the coal seam. Underground coal mining will remove the support from the overlying rock and soil, resulting in sag and separation of the immediate roof strata along bedding planes. As the overlying roof strata falls into the mined zone (i.e., goaf), subsidence of the overlying strata and thus the ground surface commences.

In the past several decades, many mathematical models have been proposed to describe the ground subsidence pattern caused by underground coal mining, e.g., Knothe model, Reddish Model, and probability integral model (PIM) [18,19,20]. Among these models, the PIM has been widely used in many countries especially in China, because of clear physical mechanism and concise coefficients of the model. On the main direction (i.e., dip or strike direction) of a coal seam, the coordinate system can be established, as shown in Figure 2. The origin of the coordinate system is the intersection point of mining boundary of the coal seam and the raw ground surface. According to the PIM, on the main direction of a coal seam, underground coal mining-induced subsidence at a ground point can be described by [18]:

$$W(x)=\frac{a_1}{2}\left[\mathrm{erf}(\frac{\sqrt{\pi }}{a_2}x)+1\right]$$

(1)

where W(x) is subsidence of the ground point with horizontal coordinate of x; in the mining engineering field, W(x) and x are usually expressed in units of millimeters (mm) and meters (m) respectively. a₁ and a₂ refer to coefficients of the PIM; and erf(*) is the Gauss error function. Clearly, subsidence at the ground point relative to that at the origin (or, relative subsidence) can be obtained by:

$$W_r(x)=W(x)-W(0)=\frac{a_1}{2}\left[\mathrm{erf}(\frac{\sqrt{\pi }}{a_2}x)-\mathrm{erf}(0)\right]$$

(2)

Basically, the magnitude of the subsidence at different ground points is different, resulting in tilt of the ground surface. Tilt is calculated as the change in subsidence between two ground points divided by the horizontal distance between those points; thus, tilt is also equal to the first derivative of the ground subsidence with units of mm/m:

$$T(x)={\left[W(x)\right]}^{\prime }={\left[W_r(x)\right]}^{\prime }=\frac{a_1}{a_2}{e}^{-\pi \frac{x^2}{a_2^2}}$$

(3)

Then, ground tilt angle due to the differential subsidence can be derived from (3) by:

$$\alpha \left(x\right)=\mathrm{atan}\left[T\left(x\right)\cdot 0.001\right]$$

(4)

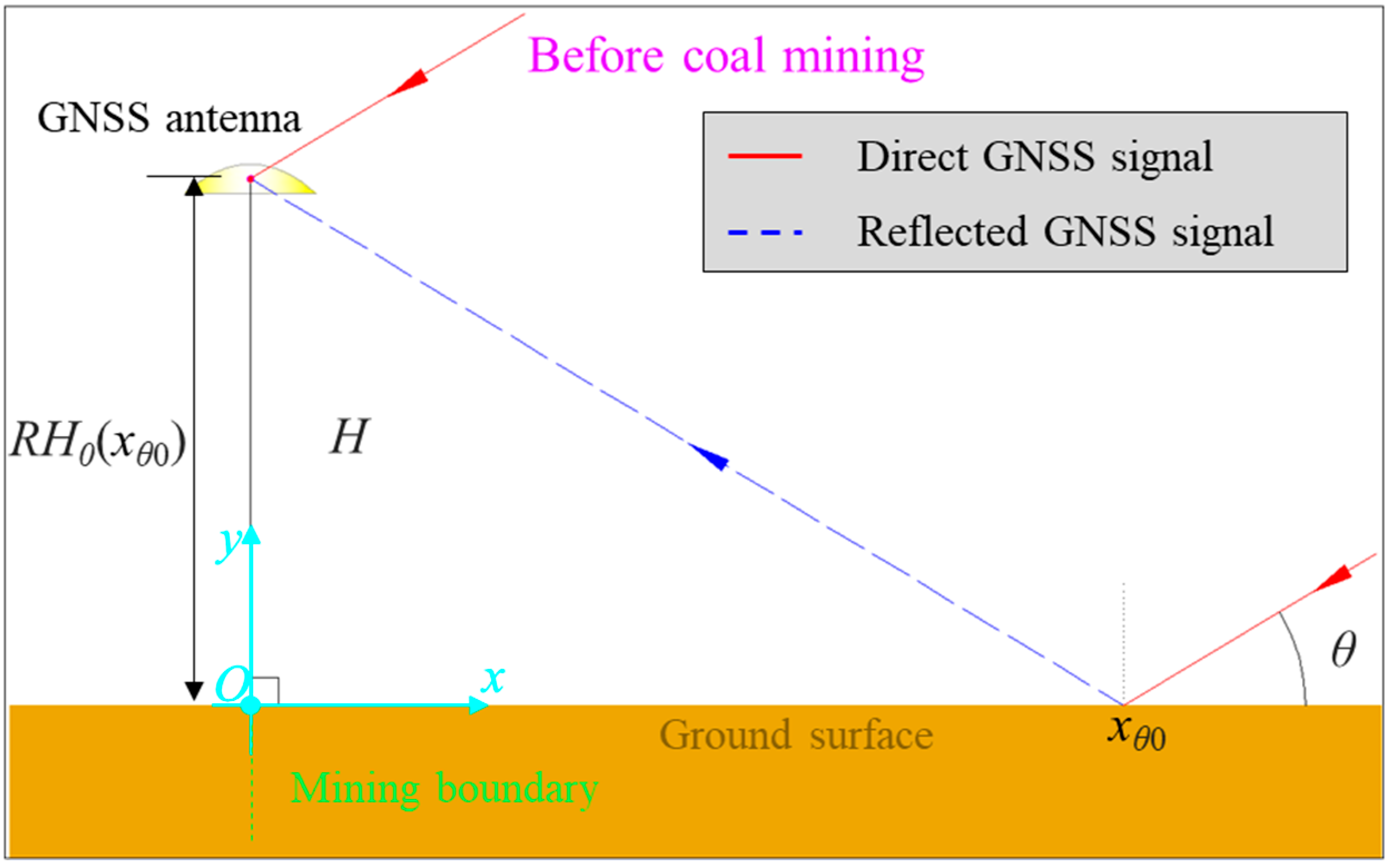
3.2. GNSS Reflection Model for Subsided Ground Surface

As shown in Figure 3, a GNSS antenna is vertically fixed on the ground surface above mining boundary; and the antenna height (or, length of pole connecting the GNSS antenna) is H in units of mm. Assuming the ground surface is flat and mirrorlike before coal mining, only specular reflection occurs, and the signal reflected at the specular point will arrive at the GNSS antenna. In addition to the reflected signal, the direct GNSS signal can also be received by the antenna, producing the interference signal. Therefore, the raw SNR observations collected by the GNSS antenna and receiver can be written as [21]:

$$\left\{\begin{array}{l}SNR=A_{\mathit{d}}^2+2A_{\mathit{d}}{A}_{\mathit{m}}\cos {\mathsf{\Phi }}_0(x_{\theta 0})+A_m^2\\ {\mathsf{\Phi }}_0(x_{\theta 0})=\frac{4\pi \sin \theta }{\lambda }\cdot R{H}_0(x_{\theta 0})\end{array}\right.$$

(5)

where A_d and A_m are amplitude of the direct and reflected signal respectively; θ is GNSS satellite elevation angle; λ is wavelength of the GNSS signal in units of mm; x_θ0 is horizontal position of the ground specular reflection point in units of m, when the elevation angle is θ; Φ₀(x_θ0) is phase of the SNR series at the specular reflection point in units of radians; RH₀(x_θ0) is the reflector height at the reflection point in units of mm, and the height is equal to the antenna height for each reflection point:

$$R{H}_0(*)=H$$

(6)

The direct signal component of the raw SNR series can be obtained by using the low-order polynomial fitting method. Subtracting the direct component from the raw SNR series, the detrended SNR series can be obtained, and is given by:

$$SN{R}_0^{\mathrm{de}}=A_0\cos {\mathsf{\Phi }}_0(x_{\theta 0})$$

(7)

where A₀ = 2A_dA_m is amplitude of the detrended SNR series.

Based on the laws of reflection in geometric optics, the GNSS reflection model for the subsided ground surface caused by underground coal mining can be derived; and the geometry of the reflection model is illustrated in Figure 4. Compare with the direct signal, the reflected signal travels an additional path length to reach the GNSS antenna. Based on the geometric relationship shown in Figure 4, the additional path length Δ(x_θ1) can be calculated by:

$$\left\{\begin{array}{l}\Delta (x_{\theta 1})=2\cdot R{H}_1(x_{\theta 1})\cdot \sin \beta (x_{\theta 1})\\ \beta (x_{\theta 1})=\theta +\alpha (x_{\theta 1})\end{array}\right.$$

(8)

where x_θ1 is horizontal position of specular reflection point when the elevation angle is θ; RH₁(x_θ1) is the reflector height at the reflection point in units of mm; α(x_θ1) is ground surface tilt angle at the reflection point. Obviously, the reflection excess phase (or, phase of the SNR series) can be obtained by:

$${\mathsf{\Phi }}_1(x_{\theta 1})=\frac{2\pi }{\lambda }\Delta (x_{\theta 1})=\frac{4\pi \sin \beta (x_{\theta 1})}{\lambda }\cdot R{H}_1(x_{\theta 1})$$

(9)

Consequently, the detrended SNR series for the subsided ground surface can be written as:

$$SN{R}_1^{\mathrm{de}}=A_1\cos {\mathsf{\Phi }}_1(x_{\theta 1})$$

(10)

where A₁ is amplitude of the detrended SNR series.

Note that, the realistic ground surface is usually not perfectly mirrorlike but rough, so the reflection is diffuse and the GNSS antenna will capture signals reflected from many points of the ground surface. Among all the captured reflected signals, the signal reflected at the specular point has the shortest propagation path and is the first one to arrive at the GNSS antenna. The signal energy captured by the antenna mostly comes from the first Fresnel zone, and the signals reflected around the specular point contribute the most. Therefore, only considering the specular reflection would be reasonable for simplicity in theoretical modeling.

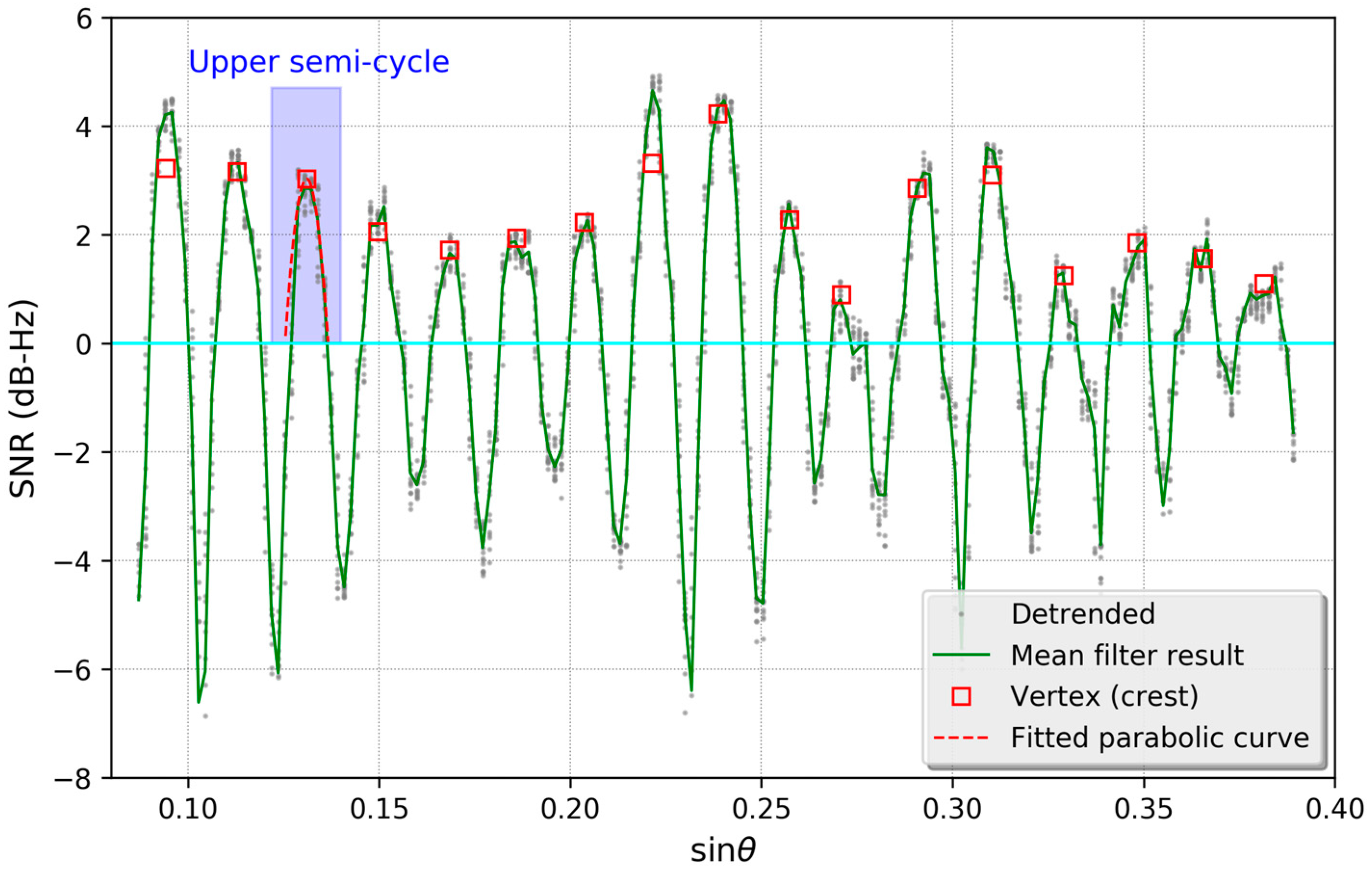
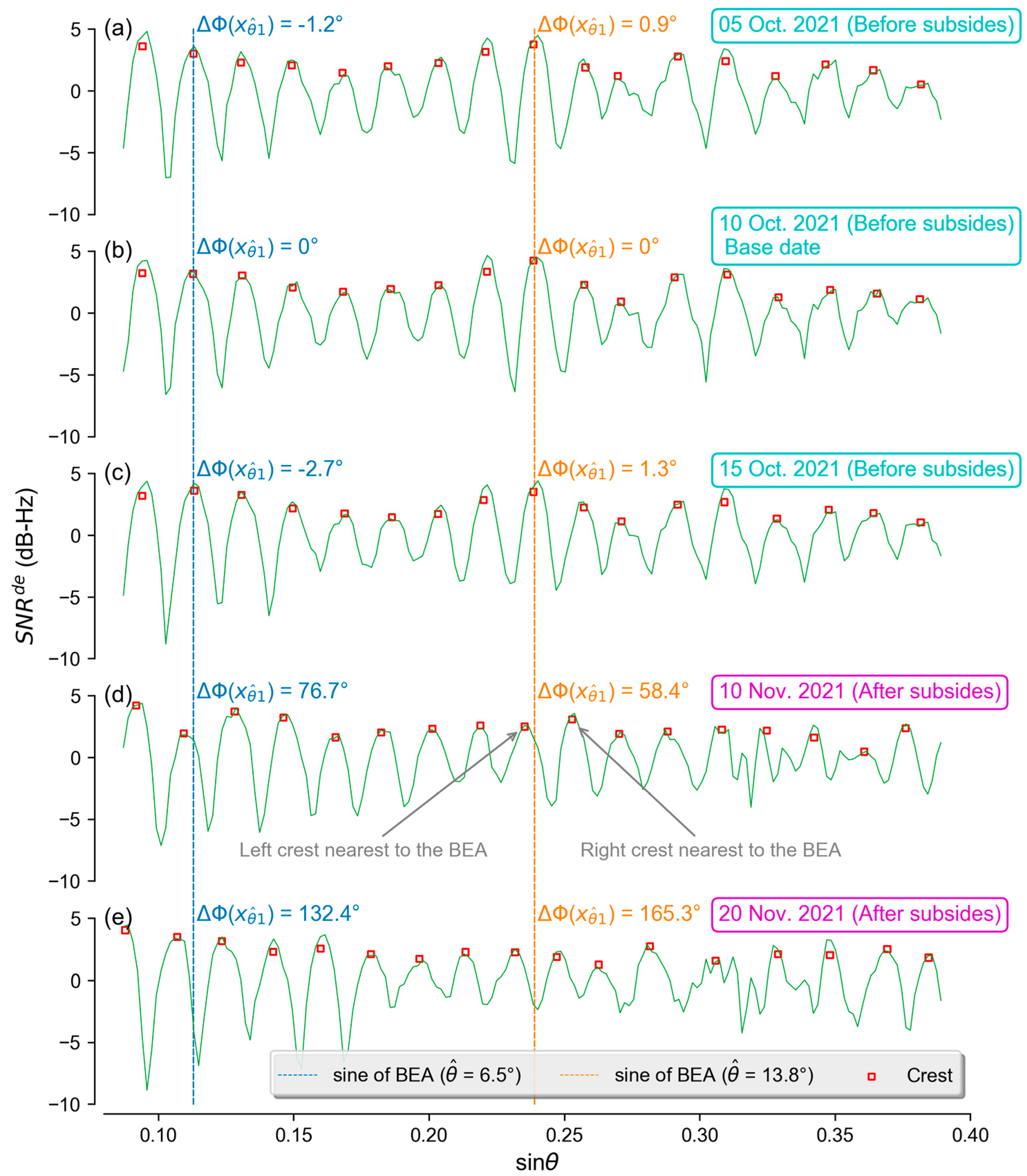
3.3. Phase Variation of the Detrended SNR Series Induced by Ground Subsidence

The detrended SNR series is a quasi-sinusoidal signal at low elevation angle (e.g., 5° to 25°), periodically oscillating with respect to sine of elevation angle, as shown in Figure 5. Note that, due to affection of observing noise, the detrended series has many glitches or high-frequency oscillations. For improving quality of the series, the SNR observations with elevation angle difference less than 0.1º are treated as one observation at a given elevation angle; then, the mean filtering method can be used to reduce observing noise of the series. Fitting the filtered result over each upper semi-cycle with parabolic curve and taking the vertex of the fitted curve as the crest of the SNR series, the crest sequence of the series can be obtained. Obviously, the phase of the detrended SNR series at the k-th crest can be written as:

$$\mathsf{\Phi }=2k_0\pi +2k\pi ,\begin{array}{cc}& k=1,2,3\dots \end{array}$$

(11)

where k₀ is an unknown constant of integer.

Selecting a date before ground subsides due to underground coal mining as the base date, GNSS satellite elevation angle corresponding to the crest of detrended SNR series collected on the day is taken as the base elevation angle (BEA). Clearly, the phase of detrended SNR series at k-th BEA (say, $\widehat{\theta }$) before ground subsides can be written as:

$${\mathsf{\Phi }}_0(x_{\widehat{\theta }0})=2k_0\pi +2k\pi =\frac{4\pi \sin \widehat{\theta }}{\lambda }\cdot R{H}_0(x_{\widehat{\theta }0})$$

(12)

After ground subsides, phase of detrended SNR series at the BEA can be written as:

$${\mathsf{\Phi }}_1(x_{\widehat{\theta }1})=2k_0\pi +2k\pi +\Delta \mathsf{\Phi }(x_{\widehat{\theta }1})=\frac{4\pi \sin \beta (x_{\widehat{\theta }1})}{\lambda }\cdot R{H}_1(x_{\widehat{\theta }1})$$

(13)

where $\Delta \mathsf{\Phi }(x_{\widehat{\theta }1})$ is phase variation of the detrended SNR series (or, multipath relative phase variation, MRPV) at the BEA, which is induced by ground subsidence due to underground coal mining. For a given detrended SNR series, MRPV at a BEA can be calculated through the linearly interpolating method:

$$\Delta \mathsf{\Phi }(x_{\widehat{\theta }1})=2\pi \frac{\sin \widehat{\theta }-\sin {\theta }_{left}}{\sin {\theta }_{right}-\sin {\theta }_{left}}$$

(14)

where θ_left is the elevation angle of the left crest nearest to the BEA; and θ_right is the elevation angle of the right crest nearest to the BEA.

Figure 6a–c shows three typical detrend SNR series collected in a mining area before ground subsides. It can be seen from the figures that MRPV at the BEA is marginal basically when the ground surface is subsidence-free. For example, at BEA of 13.8°, MRPV is 0.9° and 1.3° for SNR series collected on 5 October 2021 and on 15 October 2021, respectively. On 10 November 2021, the ground surface was affected by the underground coal mining, resulting in ground subsidence. As subsidence at the ground reflection point is larger than that at the ground point fixing GNSS antenna, reflector height increases; accordingly, MRPV increases to 76.7° and to 58.4° at the BEA of 6.5° and 13.8°, respectively. With aggravation of differential subsidence, the reflector height and thus MRPV continuously increases. On 20 November 2021, MRPV at those two BEAs increases to 132.4° and to 165.3°, as shown in Figure 6e; and the corresponding increase of reflector height at those two BEAs is about 300 and 180 mm, respectively.

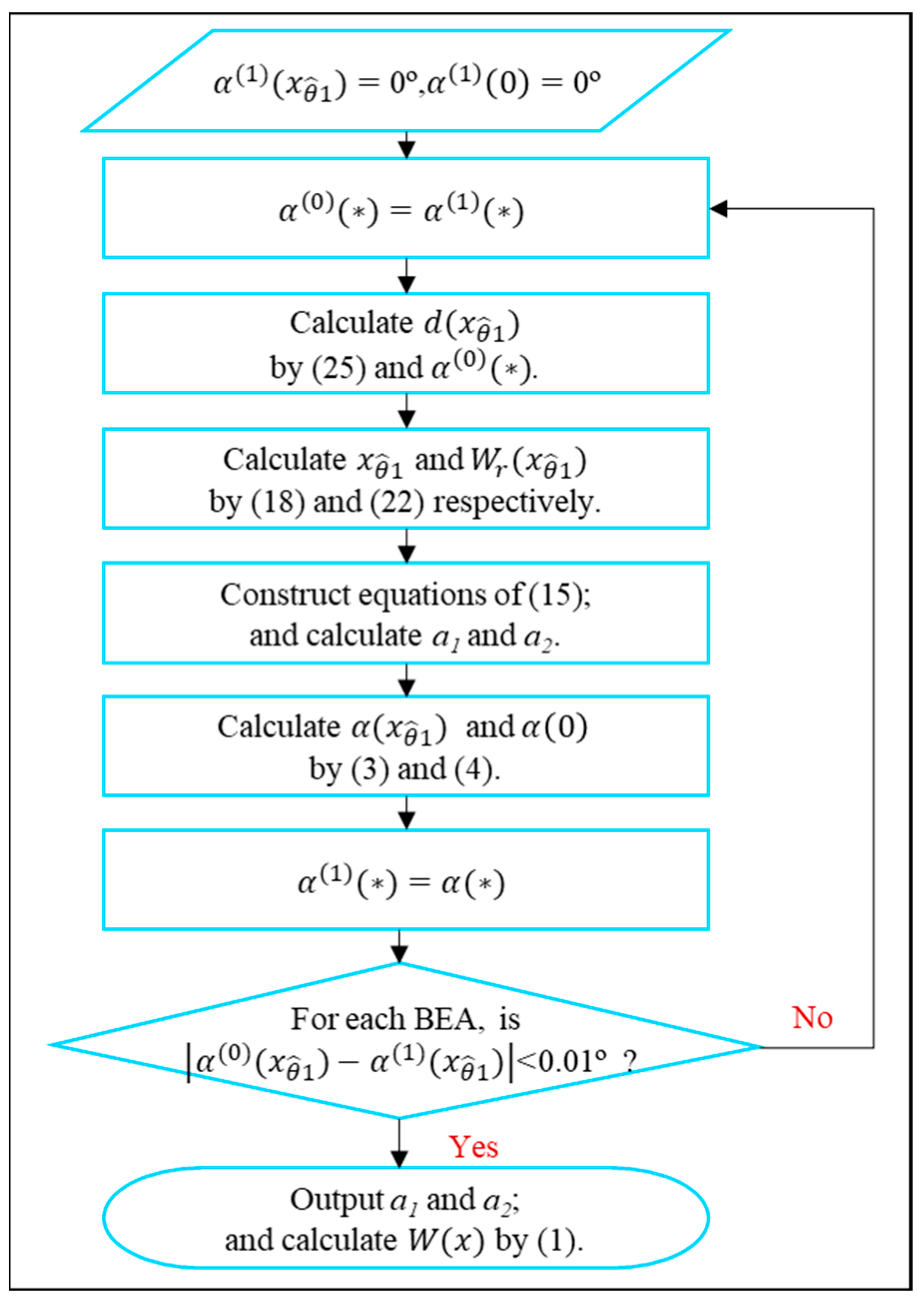
3.4. Estimation of Ground Subsidence with MRPV

If horizontal position and relative subsidence of the ground reflection point at the BEA, i.e., $x_{\widehat{\theta }1}$ and $W_r(x_{\widehat{\theta }1})$, can be determined by using MRPV, k equations with two unknown PIM coefficients (a₁ and a₂) can be obtained:

$$\left\{\begin{array}{l}{W}_r(x_{\widehat{\theta }1\_1}^{})=\frac{a_1}{2}\left[\mathrm{erf}(\frac{\sqrt{\pi }}{a_2}{x}_{\widehat{\theta }1\_1}^{})-\mathrm{erf}(0)\right]\\ W_r(x_{\widehat{\theta }1\_2}^{})=\frac{a_1}{2}\left[\mathrm{erf}(\frac{\sqrt{\pi }}{a_2}{x}_{\widehat{\theta }1\_2}^{})-\mathrm{erf}(0)\right]\\ \dots \\ W_r(x_{\widehat{\theta }1\_k}^{})=\frac{a_1}{2}\left[\mathrm{erf}(\frac{\sqrt{\pi }}{a_2}{x}_{\widehat{\theta }1\_k}^{})-\mathrm{erf}(0)\right]\end{array}\right.$$

(15)

Based on the least squares criterion, the optimal coefficients of PIM can be calculated through (15). Substituting the optimal coefficients into (1), ground subsidence on the main direction of a coal seam can be obtained.

Clearly, the premise of the above method is estimating horizontal position and relative subsidence of the ground reflection point at the BEA. By making use of geometric relationship shown in Figure 4, horizontal position of reflection point at the BEA can be obtained by:

$$\begin{array}{c}{x}_{\widehat{\theta }1}=0.001\cdot d(x_{\widehat{\theta }1})\cdot \cos \left[\beta (x_{\widehat{\theta }1})+\alpha (x_{\widehat{\theta }1})\right]+\delta x\\ =0.001\cdot d(x_{\widehat{\theta }1})\cdot \cos \left[\widehat{\theta }+2\alpha (x_{\widehat{\theta }1})\right]+\delta x\end{array}$$

(16)

where $d(x_{\widehat{\theta }1})$ is distance from the ground reflection point to the GNSS antenna in units of mm; δx is horizontal deviation of the GNSS antenna in units of m, which can be related to ground tilt angle at the GNSS station, α(0), by:

$$\delta x=0.001\cdot H\sin \alpha (0)$$

(17)

Substituting (17) into (16), horizontal position of the ground reflection point at the BEA can be rewritten as:

$$x_{\widehat{\theta }1}=0.001\cdot \left\{d(x_{\widehat{\theta }1})\cdot \cos \left[\widehat{\theta }+2\alpha (x_{\widehat{\theta }1})\right]+H\sin \alpha (0)\right\}$$

(18)

Relative subsidence of the ground reflection point at the BEA can also be derived from the geometric relationship shown in Figure 4, obtaining:

$$W_r(x_{\widehat{\theta }1})=H_1(x_{\widehat{\theta }1})+\delta y-H$$

(19)

where $H_1(x_{\widehat{\theta }1})$ is vertical height from the ground reflection point to the GNSS antenna in units of mm; δy is ground tilt induced vertical position deviation of the GNSS antenna, and can be calculated by:

$$\delta y=H\left[1-\cos \alpha (0)\right]$$

(20)

The vertical height $H_1(x_{\widehat{\theta }1})$ can also be related to distance from the ground reflection point to the GNSS antenna by:

$$\begin{array}{ll}{H}_1(x_{\widehat{\theta }1})& =d(x_{\widehat{\theta }1})\cdot \sin \left[\beta (x_{\widehat{\theta }1})+\alpha (x_{\widehat{\theta }1})\right]\\ & =d(x_{\widehat{\theta }1})\cdot \sin \left[\widehat{\theta }+2\alpha (x_{\widehat{\theta }1})\right]\end{array}$$

(21)

Substituting (20) and (21) into (19), relative subsidence of the ground reflection point at the BEA can be rewritten as:

$$W_r(x_{\widehat{\theta }1})=d(x_{\widehat{\theta }1})\cdot \sin \left[\widehat{\theta }+2\alpha (x_{\widehat{\theta }1})\right]-H\cos \alpha (0)$$

(22)

It can be seen from (18) and (22) that, both horizontal position and relative subsidence of the ground reflection point are related to the distance from the ground reflection point to the GNSS antenna; and the distance can be related to reflector height at the BEA by:

$$d(x_{\widehat{\theta }1})=\frac{R{H}_1(x_{\widehat{\theta }1})}{\sin \beta (x_{\widehat{\theta }1})}$$

(23)

Subtracting (12) from (13) and with some manipulations, reflector height at the BEA after the ground subsides can be calculated by:

$$R{H}_1(x_{\widehat{\theta }1})=\frac{1}{\sin \beta (x_{\widehat{\theta }1})}\left[\frac{\lambda }{4\pi }\Delta \mathsf{\Phi }(x_{\widehat{\theta }1})+R{H}_0(x_{\widehat{\theta }0})\sin \widehat{\theta }\right]$$

(24)

Substituting (24) into (23) and making use of (6) and the second equation of (8), distance from the ground reflection point to the GNSS antenna can be rewritten as:

$$d(x_{\widehat{\theta }1})=\frac{1}{{\sin }^2\left[\widehat{\theta }+\alpha (x_{\widehat{\theta }1})\right]}\left[\frac{\lambda }{4\pi }\Delta \mathsf{\Phi }(x_{\widehat{\theta }1})+H\sin \widehat{\theta }\right]$$

(25)

Obviously, if tilt angle (or ground tilt) of the reflection point is determined, distance from the reflection point to the GNSS antenna can be calculated through MRPV with (25). Subsequently, horizontal position and relative subsidence of the reflection point at the BEA can be obtained by (18) and (22), respectively. Finally, the optimal PIM coefficients and thus ground subsidence can be derived by making use of (15) with the least squares criterion.

However, the ground tilt angle is also subsidence-related (or relative subsidence-related), as indicated in (3) and (4). This means, ground subsidence is required for determination of ground tilt angle; conversely, ground tilt angle is also required for the calculation of ground subsidence. Thus, an iterative algorithm can be performed to calculate the ground subsidence (as well as the ground tilt angle) induced by underground coal mining.

Flowchart of the iterative algorithm based GNSS-IR ground subsidence estimation is shown in Figure 7. The estimating process is described as follows:

(a)

Set initial value of tilt angle equal to 0° for each BEA;

(b)

Use initial value of tilt angle and MRPV calculating distance from the ground reflection point to the GNSS antenna through (25); Note that, height of the GNSS antenna in (25) can be obtained by exploiting Lomb–Scargle spectral analysis to the detrended SNR series collected on the base date;

(c)

Calculate the horizontal position and relative subsidence of the reflection point using (18) and (22), respectively;

(d)

Construct equation of (15) using horizontal position and relative subsidence derived from (c); and calculate the optimal PIM coefficients;

(e)

Calculate the tilt angle using the optimal PIM coefficients derived from (d) through equations of (3) and (4);

(f)

For each BEA, judge absolute error between the initial tilt angle and the angle derived from (e);

(g)

For each BEA, if the absolute error is less than 0.01°, which corresponds to ground tilt of about 0.2 mm/m, output the optimal PIM coefficients and calculate ground subsidence by (1) using the PIM coefficients; and

(h)

If the absolute error is larger than 0.01º, assign the tilt angle derived from (e) to the initial tilt angle and go to step (b).

Note that, GPS satellites operate in circular orbits at an altitude of 20,180 km, an inclination of 55º and each satellite completes the orbit in approximately 11 h 58 min. This means that for a stationary observer the same satellite is visible at the same point in the sky every (sidereal) day [22], which ensures the coincidence of the multi-day trajectories of the same satellite, as shown in Figure 8. This is critical, because it is the MRPV in different periods under the coincident trajectory of the same satellite that is used by the proposed method to obtain ground subsidence. In addition, since the GNSS receiver can be used to monitor the ground deformation continuously, tilt angles of the previous period can be taken as the initial tilt angles of the current period for guaranteeing convergence of the iterative algorithm and reducing computation time.

4. Results

An experimental campaign was conducted in the study area from 10 October 2021 to 11 February 2022. A GNSS station was established in a farmland above mining boundary (head entry) of an underground longwall working face on 7 September 2021, as shown in Figure 9. As a typical farmland of the North China Plain, ground surface around the GNSS station is flat enough before coal mining; in addition, since the experimental campaign was conducted in the mid-autumn and winter, the effect of ground vegetation is marginal. The width of the underground working face is about 358 m; the average of mining thickness and depth of the working face are about 8500 and 580 m, respectively. Mining direction of the working face is from northwest to southeast.

A low-cost GNSS instrument, which is developed based on navigational GNSS chips of u-blox M8N and antenna of u-blox ANN-MB as detailed in [23], was used to collect the GPS L1 band signal. The vertical height of the antenna is 5308 mm before the ground subsides. As the ground reflection track of GPS satellite G05 is in the main direction (i.e., dip direction) of the working face, as shown in Figure 9, SNR observations of the satellite within the elevation angle of 5° to 25° are used to calculate the ground subsidence with the proposed method. On 10 October 2021, distance from the mining line to the GNSS station was about 298 m; due to the distant mining line, the mining operation could not affect the ground surface around the GNSS station. Therefore, this date is taken as the base date of the experimental campaign. Seventeen elevation angles, which correspond to seventeen crests of the SNR series collected on the base date, are selected as the BEAs.

In addition to the GPS data, unmanned aerial vehicle (UAV) photogrammetry was also performed in the experiment to measure digital elevation model (DEM) around the GNSS station, as shown in Figure 9. Four field measurements of DEM (i.e., 10 October 2021, 20 November 2021, 2 December 2021, and 11 February 2022) are used to validate the proposed method. Subtracting DEM of the last three measurements from DEM of the first measurement respectively, ground subsidence of the last three measurements can be obtained. The DEM-based ground subsidence coincided with the G05 satellite ground reflection track is taken as the in-situ one to compare with the proposed method based ground subsidence.

Figure 10 shows 6-days ground subsidence estimations on the GPS satellite reflection track derived by the proposed method during the experimental campaign. Note that, the term of D in the figure and in Figure 9 denotes the distance from the mining line to the GNSS station. Negative sign of D indicates the mining line is in back of the station, which means the coal seam under the station had not been mined; while the positive sign indicates the mining line is in front of the station, which means the coal seam under the station had been mined. In addition to the proposed method derived ground subsidence, three datasheets of the in-situ ground subsidence are also shown in Figure 10. Figure 11 shows the velocity curve derived from the GNSS-IR based ground subsidence observations at x of 50 m during the experimental campaign.

Table 1. Mean, STD and RMS of errors for the proposed method-based ground subsidence estimation.

Date	Mean (mm)	STD (mm)	RMSE (mm)	Maximum RE (%)
20 November 2021	109.3	13.1	110.1	4.7
02 December 2021	155.4	7.0	155.6	5.5
11 February 2022	91.5	29.4	96.2	5.3

shows the mean error, error STD, and RMSE of the GNSS-IR-derived ground subsidence estimations.

Table 2. Economic cost comparison between the proposed method and two traditional ground-based subsidence monitoring methods.

Method	Point Count	Monitoring Period (Days)	Unit Price (Dollars per Point)	Total Price (Dollars)
GNSS-IR	20	730	-	1140
GNSS-RTK	20	730	2.1	32,186
Levelling	20	730	3.6	52,143

shows the economic cost comparison between the proposed method and two traditional ground-based subsidence monitoring methods, i.e., GNSS-RTK and levelling method;

Table 3. Efficiency comparison between the proposed method and two traditional ground-based subsidence monitoring methods.

Method	Point Count	Monitoring Period (Days)	Unit Time (Minutes per Point)	Total Time (Minutes)
GNSS-IR	20	730	Near-real time	Near-real time
GNSS-RTK	20	730	2 (Manual)	30,400
Levelling	20	730	5 (Manual)	76,000

shows efficiency comparison between the proposed method and the two traditional monitoring methods.

5. Discussion

5.1. Estimating Error Analyzation for the GNSS-IR Based Ground Subsidence Observations

It can be seen from Figure 10 and Table 1 that there exists a significant mean error for the GNSS-IR-based ground subsidence estimations. This should be mainly caused by inaccuracy of PIM in description of the realistic ground subsidence pattern. In fact, subsidence estimation derived from MRPV of SNR series is relative subsidence on the ground reflection point (i.e., W_r(x)), instead of the absolute subsidence (i.e., W(x)); and the former is related to the latter through absolution subsidence at the GNSS station using PIM, as indicated in (2). However, due to complexity of the ground subsidence pattern, there could exist deviation between the PIM estimated absolute subsidence at the station and the actual one, resulting in a systematic error of subsidence estimations on the ground reflection track.

Besides, variation of ground soil moisture may also affect MRPV, inducing subsidence estimating error for the proposed method; and the MRPV is about 30º for the geodetic GNSS instrument collected SNR series, when soil moisture is in the range of 0.05 to 0.40 cm³/cm³ [24]. Nevertheless, thus affection needs to be further proved for the low-cost navigational GNSS instrument collected SNR series (e.g., the instrument used in the experimental campaign), because of the significantly different characteristics of SNR series collected by the two type instruments, as analyzed in [23,25].

The in-situ maximum subsidence is 3076 mm on the GNSS satellite ground reflection track during the experimental campaign. By making a ratio of the absolute error of the proposed method-based subsidence estimation to the in-situ maximum subsidence, relative error (RE) of the subsidence estimation can be obtained. In the realistic, the relative error within 10% is enough for many engineering applications, e.g., evaluation of farmland damaging degree and design of remediation plan for the subsidence basin [26]. Meanwhile, the maximum relative error of the proposed method is 5.5%, although the absolute error of the proposed method is relatively larger with the maximum RMSE of 155.6 mm. This also indicates that the proposed method performs well for monitoring underground coal mining-induced ground subsidence in some extent.

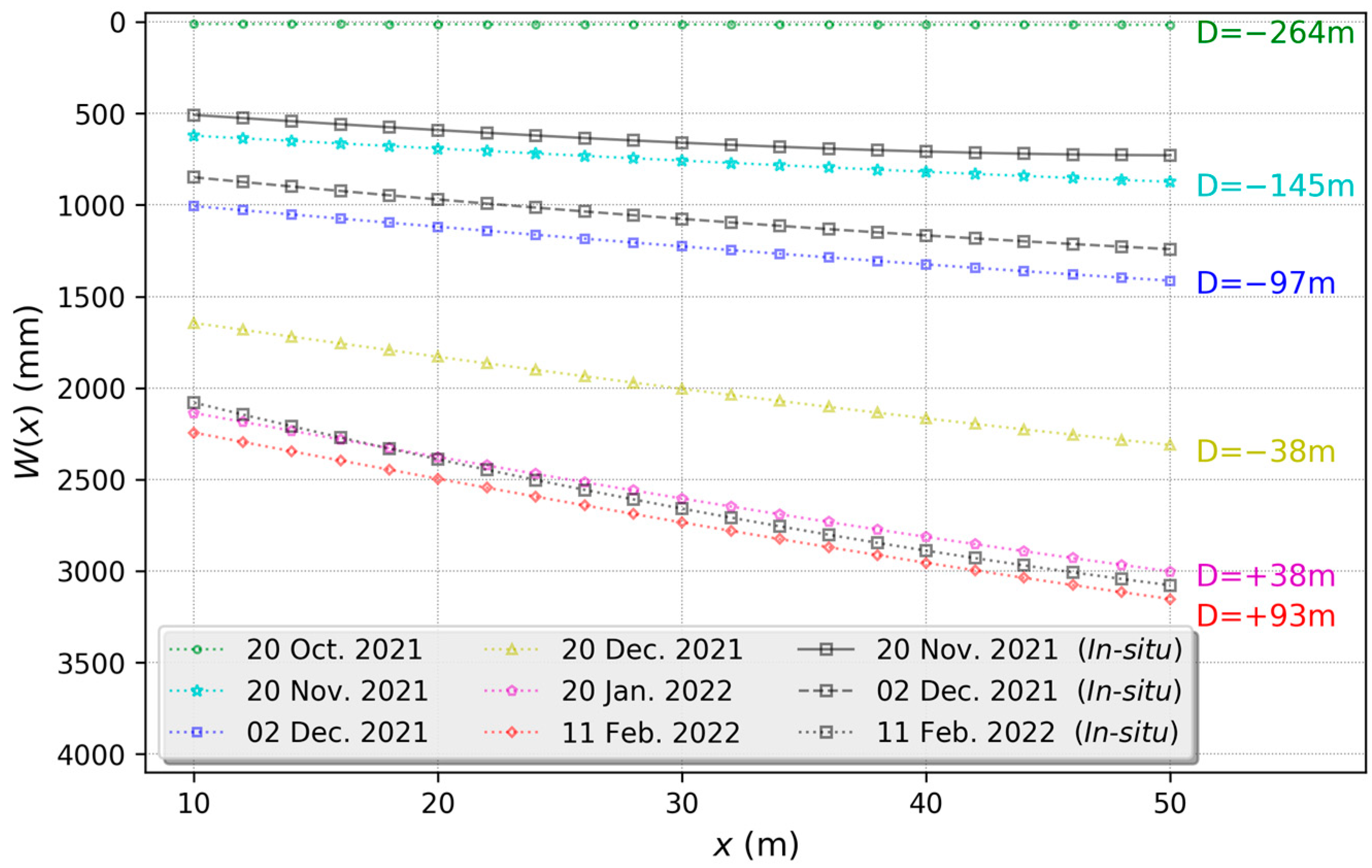
5.2. Spatial Characteristics of Ground Subsidence in the Study Area

Underground coal mining-induced land subsidence is a space- and time-dependent complicated process, and is related to many affecting factors (e.g., advance rates of working face, depth of coal seam, and geological conditions). In the spatial dimension, coal mining would cause appearance of a bowl-shape subsidence trough (also named as subsidence basin), the area of which is much larger than the mined area in general. Meanwhile, the GNSS-IR-derived ground subsidence results show that ground surface around the GNSS station subsides significantly on 20 November 2021, e.g., with ground subsidence of 866 mm at x of 50 m, although the coal seam under the GNSS station had not been extracted. This observation is in accordance with the spatial subsidence pattern documented by the previous works of [26,27].

In addition, as described in [27], for a given ground point on the subsidence basin, the magnitude of subsidence of the point is inversely proportional to horizontal distance from the point to the goaf center; that is, the ground subsidence increases with the decrease of the horizontal distance. This is also compatible with the GNSS-IR-derived subsidence results shown in Figure 10. For example, on 11 February 2022, subsidence at the ground points with x of 10 and 50 m were 2268 and 3173 mm, respectively; and horizontal distances from those two points to the goaf center were 169 and 129 m, respectively.

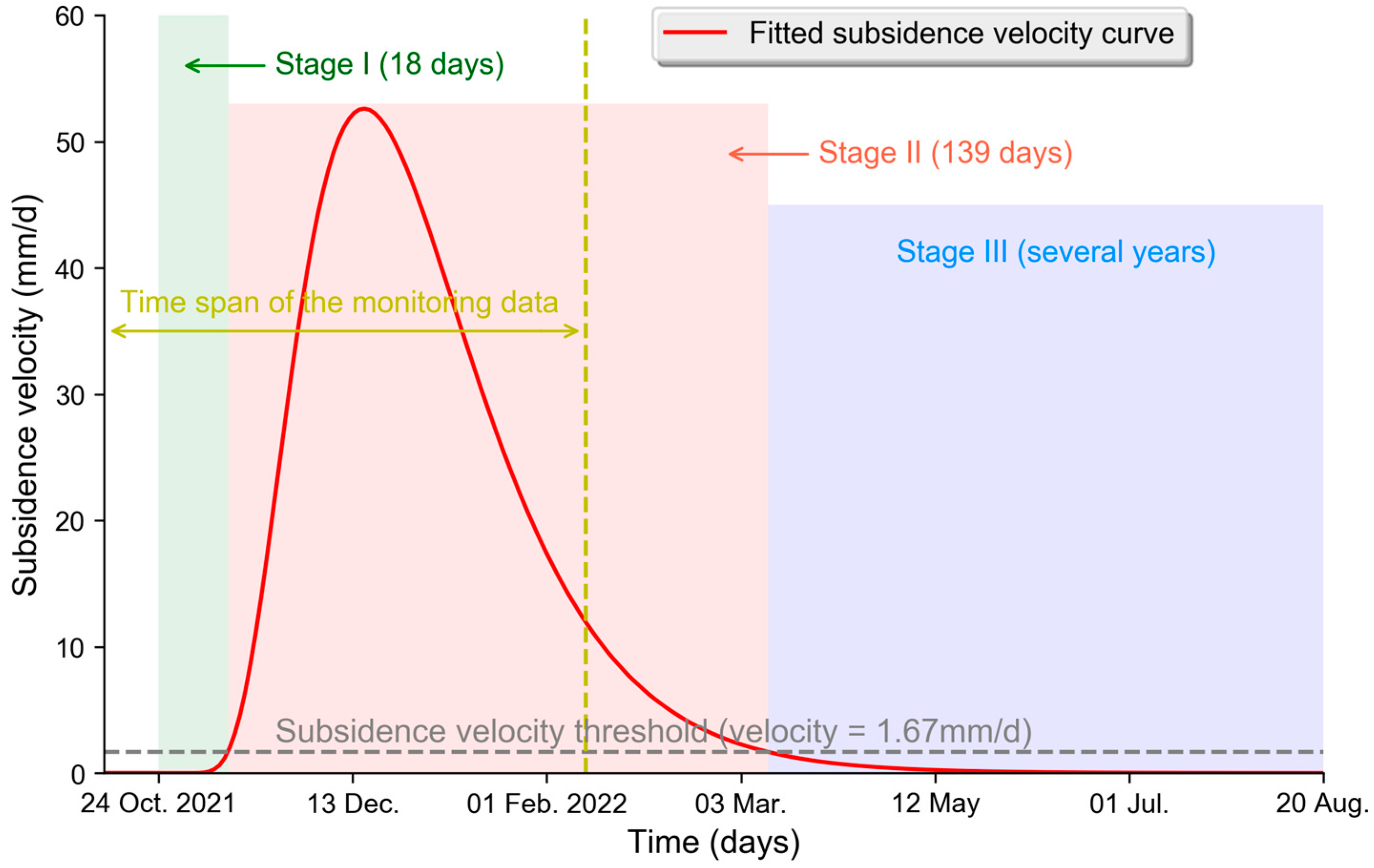
5.3. Temporal Characteristics of Ground Subsidence in the Study Area

In the temporal dimension, ground subsidence is not uniform over time. Subsidence of a ground point with respect to time can be described as the inverse S-shaped curve (or, time function curve) [28,29,30]. By making the first derivative of the curve, the subsidence velocity curve of the point can be obtained, as shown in Figure 11, which shows the velocity curve derived from the GNSS-IR based ground subsidence observations during the experimental campaign. On the basis of subsidence velocity of 1.67 mm/d, the whole process of ground subsidence induced by underground coal mining can be divided into three stages traditionally: the initial stage (stage I), the active stage (stage II), and the stable stage (stage III) [29]. It can be seen from Figure 11 that, at stage I, the subsidence velocity is very low (less than 1.67 mm/d); and the subsidence increases slowly from 0 mm/d. At stage II, subsidence velocity increases to its maximum rapidly as the ground subsidence increases sharply; and then the velocity decreases while the ground subsidence continues to increase. At stage III, the subsidence velocity is less than 1.67 mm/d and decreases continuously; and the ground subsidence increases very slightly. The previous studies reveal that the duration is about a few of days to a dozen of days for stage I, about 4 to 6 months for stage II, and about a few of years to several decades for stage III [30]. Meanwhile, the GNSS-IR observations derived duration of the stage I and II of the study area are 18 and 139 days, respectively, which are in agreement with the previous results.

Note that, although duration of the stage Ⅱ is relatively short compared with the whole subsidence period, the majority of land damage happened over the stage; and ground subsidence occurred in the stage accounts for more than 70% of the total subsidence of the ground surface in general [31]. Thus, the stage is also termed as the “dangerous stage” in the mining engineering. As the time span of the actual monitoring data collected in the experimental campaign covers the most part of the active stage, validating the proposed method with the data is adequate in terms of underground coal mining-induced land disaster monitoring.

5.4. Economic Cost and Efficiency Comparison

In order to exhibit the advantages of the GNSS-IR subsidence monitoring technique in terms of economic cost and efficiency, two traditional ground-based subsidence monitoring techniques, which are GNSS-RTK and levelling method, were compared with the proposed technique. For a ground survey line used to monitor the underground coal mining-induced subsidence, the count of ground monitoring point on the line is about 20 in general; suppose that the monitoring period is two years (730 days). According to the market price in China, the cost of the GNSS-RTK and levelling method is about 2.1 and 3.6 dollars per monitoring point; therefore, the sum of the economic cost of the two methods is $32,186 and $52,143, respectively, for the two years of subsidence monitoring, as shown in Table 2. Comparatively, there only exists the instrument cost and the cost of station construction for the proposed method, which is about $1140; and the subsidence observations on the survey line can be provided freely and continuously for several years with the proposed method. The total economic cost of the proposed method accounts for about thirtieth and fiftieth of the GNSS-RTK and levelling method, respectively, which clearly indicates the advantage of the proposed method in terms of economic cost.

As to the time cost which includes the instrument check time and measuring time, the GNSS-RTK and levelling method is about 2 and 5 min for measurement of a ground point. The total time cost for the two years monitoring period is 30,400 and 76,000 min in the case of utilization of the GNSS-RTK and levelling method, respectively, as shown in Table 3; while the proposed method can measure the ground subsidence automatically with near-real time way. Obviously, ground subsidence monitoring efficiency of the proposed method is much better than that of the traditional GNSS-RTK and levelling method.

6. Conclusions

In this paper, GNSS-IR is firstly proposed to estimate the underground mining-induced ground subsidence on the main direction of the longwall working face. The low-cost GNSS instrument is used to collect GPS L1 band signal in an experimental campaign to validate the proposed method. The main conclusions of this paper are summarized as follows:

(a)

The maximum absolute error and the maximum relative error of the GNSS-IR-derived ground subsidence are 155.6 mm and 5.5% respectively, when the maximum ground subsidence induced by underground coal mining is 3076 mm. The SNR phase estimation error and the error of model describing ground subsidence pattern are the main reasons causing the GNSS-IR subsidence estimating error;

(b)

The influence distance of underground coal mining operation in the study area is about 145 m; and duration of the initial stage and the active stage is 18 and 139 days, respectively. The spatial and temporal characteristics of ground subsidence in the study area are compatible with the general pattern of subsidence caused by the underground caving mining; and

(c)

Economic cost of the proposed GNSS-IR subsidence monitoring technique is about a thirtieth of the GNSS-RTK technique, and is about fiftieth of the levelling subsidence monitoring method. Efficiency of the GNSS-IR method is also far better than the traditional GNSS-RTK and levelling method for monitoring ground subsidence induced by underground coal mining.

In the next work, an improved model (e.g., B-spline line function model) will be used to describe underground coal mining-induced ground subsidence profile on the GNSS satellite reflection track for improving the estimating precision; the effect of variation of ground soil moisture on the subsidence estimation will be evaluated. In addition, the field actual measurements over a longer period such as two years will also be used to validate the proposed method in the future.